MILP formulations for highway petrol station replenishment in initiative distribution mode

Abstract

To investigate highway petrol station replenishment in initiative distribution mode, this paper develops a mixed-integer linear programming (MILP) model with minimal operational costs that includes loading costs, unloading costs, transport costs and the costs caused by unpunctual distribution. Based on discrete representation, the working day is divided into equal time intervals, and the truck distribution process is decomposed into a pair of tasks including driving, standby, rest, loading and unloading. Each truck must execute one task during a single interval, and the currently executing task is closely related to the preceding and subsequent tasks. By accounting for predictive time-varying sales at petrol stations, real-time road congestion and a series of operational constraints, the proposed model produces the optimal truck dispatch, namely, a detailed task assignment for all trucks during each time interval. The model is tested on a real-world case of a replenishment system comprising eight highway petrol stations, one depot, one garage and eight trucks to demonstrate its applicability and accuracy.

1 Introduction

1.1 Background

As necessary facilities for urban transportation, petrol stations play a critical role in the steady supply of refined products (Fernandes et al. 2013), and efficient distribution of refined products is also important in the smooth operation of cities. To daily replenish petrol stations, the transport company must simultaneously determine detailed routes and product assignments for each truck (Cattaruzza et al. 2014; Liu and Jiang 2012). As we know, product oil distribution between refineries and oil depots is usually carried by pipelines (Fernandes et al. 2013), and there are distribution stations along the pipelines. Researchers often focus on the formulation of scheduling plans (Zhang et al. 2016) and transmission plans (Fernandes et al. 2013). Zhang et al. (2017) established a MILP model to solve problems, and some researchers (Moradi et al. 2019) had also proposed efficient algorithm to solve scheduling studies. Liang et al. (2012) considered regional differences in electricity prices along the pipeline, established an optimization model for a multi-product pipeline which has a known delivery demand and operation plan for each off-take station. Different from the distribution between refineries and oil depots, the replenishment of petrol stations takes truck transportation as the mode of transportation, which is easier to be affected by the condition of road congestion. The replenishment of petrol stations is mainly classified into two types: passive distribution and initiative distribution. For passive distribution, petrol stations order products before the next working day, specifying the minimum and maximum quantity to be delivered for each ordered product. The minimum quantity is often determined by the stations’ average daily sales, while the maximum quantity is determined by the difference between the capacity of the station’s storage tanks and an estimation of the remaining stock before the next replenishment. Generally, petrol stations specify that products be replenished during periods when sales are low and not during peak periods. However, passive distribution has the following problems. First, the specified replenishment time of different petrol stations may be highly similar, so that trucks are extremely busy during these periods and idle when the petrol stations are busy and unable to replenish stock. Second, a single petrol station may receive a variety of products several times from transportation companies in a single day, and it is difficult to estimate and coordinate each distribution time. By contrast, with initiative distribution, petrol stations do not order products but instead forecast the sales for each station, while the transport company assigns the specific time to deliver the products. The advantage of initiative distribution is that it treats the whole replenishment process as an integrated system, and the replenishment time is determined by the system instead of the petrol stations. This approach allows the working time of trucks in a day to be more balanced, thereby avoiding the inefficiency created by concentrated periods of demand. Overall, initiative distribution improves efficiency in the dispatch of trucks and therefore in the running of the entire replenishment system.

1.2 Related work

One of the first articles addressing the issue of petrol station replenishment was published by Brown and Graves (1981). They developed an integer programming model to address the problem of a nationwide bulk delivery fleet of petroleum tanker trucks. The objective function was to minimize transport costs under the constraints of equitable manpower and equipment workload distributions, safety, customer service, and equipment compatibility restrictions. The model was applied to a scale of more than 80 bulk terminals on a fleet exceeding 300 vehicles with approximately 2600 loads per day. Brown et al. (1987) extended the work of Brown and Graves (1981) for a real-time, transaction-driven information management system that could solve the problem for 120 bulk terminals and more than 430 vehicles.

Apart from mathematical programming methods, heuristic algorithms (Azad et al. 2017; Kasivisvanathan et al. 2014; Nambirajan et al. 2016), intelligent optimization (Diaby et al. 2016; Marinakis et al. 2013; Soto et al. 2017) and hybrid algorithm (Alinaghian and Shokouhi 2018; Shi et al. 2017) had also been widely used in dealing with the scheduling optimization issue. For example, focusing on the truck assignment and routing problem of a Hong Kong petrol distribution company, Ng et al. (2008) proposed a decision support system that combines heuristic clustering and optimal routing to determine the optimal fleet assignment and routing. Multiple objective functions included the minimal number of used trucks, the minimal number of drops in each trip, the maximal profits in terms of total products delivered and the maximal utilization of resources. For the multi-depot petrol station replenishment problem, Cornillier et al. (2008) presented a heuristic that contained route construction and truck loading procedures, a route packing procedure and two procedures enabling the anticipation or the postponement of deliveries. Next, Cornillier et al. (2009) studied the filling station replenishment problem with time intervals (PSRPTW). The introduction of time intervals leads to a great increase in model scale and computational effort, so they proposed an MILP model and two heuristics for this problem to determine the quantity of each product to deliver, the assignment of products to truck compartments, delivery routes and schedules. In fact, petroleum products are stored in a number of different depots, and they are delivered to a set of petrol distribution stations. Each depot has its own fleet of heterogeneous and compartmented tanker trucks. Therefore, in their later work, Cornillier et al. (2012) developed a heuristic procedure to generate a restricted set of promising feasible trips beforehand for the multi-depot petrol station replenishment problem with time intervals (MPSRPTW). Wang et al. (2018) established a mixed-integer linear model and proposed an improved heuristics algorithm to solve the petrol truck scheduling problem which considered multi-path selection and congestion. Boctor et al. (2011) firstly introduced a generalized trip packing problem, in which trucks have different capacities and trip net revenues depend on the trucks used. Meanwhile, some construction, improvement and neighborhood search solution heuristics are proposed to solve a real-life case.

In addition to petrol station replenishment issues, a large number of studies have also focused on the vehicle routing problem (VRP), which focuses on the use of efficient algorithms (Li et al. 2012; Goodson et al. 2012; Schyns 2015). Brandão and Mercer (1997) presented a novel tabu search heuristic algorithm to solve the multi-trip routing and scheduling problem (VRSP) with respect to constraints in which a vehicle can make more than one trip each day and the customers impose delivery time intervals. Based on the adaptive memory procedure, Olivera and Viera (2007) described a heuristic method to solve the vehicle routing problem with multiple trips. To solve a wide range of different types of VRPs, Gromicho et al. (2012) presented a highly flexible framework accommodating various real-life restrictions. Wang et al. (2019) established a mathematical model to solve the petrol truck routing problem and proposed a heuristic algorithm based on a local branch-and-bound search with a tabu list, several inequalities are added to accelerate the solving process. A comparison with state-of-the-art local search methods indicates the superiority of this new framework in practical applications.

This paper studies on highway petrol station replenishment in the initiative distribution mode. Different from classical petrol station VRP problem, highways have a large and various demand for refined products in this study, so a single petrol station on a highway may be replenished more than once during a working day. Moreover, highway petrol stations receive a variety of refined products transported from depots, and a reasonable replenishment time for each type of product is difficult to predict only considering each petrol station. In fact, the replenishment mode studied in previous relevant work belongs to the passive distribution type, in which the quantity and delivery timing of each product are given by petrol stations. Compared with initiative distribution, passive distribution is dominated by human factors and often results in impractical truck allocation and low distribution efficiency. With the increasing popularity of Internet technology, the shift from passive distribution to initiative distribution is a compelling trend among petroleum enterprises looking to accomplish the daily information-based management of oil resources. However, to the best of our knowledge, this paper is the first research work that addresses this replenishment problem in an initiative distribution mode rather than a passive distribution mode. None of the abovementioned papers have simultaneously determined the quantities, timing and replenishment object of each product to be delivered by each truck through a comprehensive consideration of time-varying sales at petrol stations, real-time road congestion and the state monitoring of all trucks.

1.3 Contributions of this work

• With a focus on highway petrol station replenishment in the initiative distribution mode, an MILP approach is proposed to provide a more reasonable schedule for trucks and improve efficiency for the entire replenishment system.

• Various factors appearing in practice, such as time-varying sales, task time limitations, real-time road congestion, different unit transport costs under full-load or no-load conditions, road capacity, the detailed operational mode (namely, loading, unloading, rest and standby) and operational limitations, are all taken into consideration.

• The optimal distribution plan, including the quantities, specific time and replenishment object of each product to be delivered by each truck, is solved by the proposed model.

• A real case study is given to demonstrate the practicality of this method.

1.4 Paper organization

The adopted methodology and details of the mathematical model are given in Sects. 2 and 3, respectively. Section 4 provides a real case study in China and demonstrates the model’s practicability. Finally, conclusions are presented in Sect. 5.

2 Methodology

2.1 Problem description

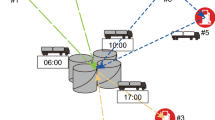
Figure 1 illustrates the highway petrol station replenishment system studied in this paper. There are three types of destinations, namely garages, depots and petrol stations. At the initial time of one working day, trucks departure from garages to depots and then cover refined products to the petrol stations which are short of oil. Considering the limited number of loading arms, an upper limit is set for the number of trucks that are loading simultaneously. Therefore, trucks need to wait when there is no free loading arm. Additionally, all trucks are stored in the garage at the end of the working day. Since the petrol stations are sparsely distributed along the highway, the distance between any petrol stations is rather long and an oil depot can serve only a small number of petrol stations. It usually takes a long time for a truck to complete a single delivery task, which brings higher-level demands for truck scheduling from oil tankers. Distributing trucks according to the reports from petrol stations may result in higher demand in some busy time periods and no demand in other times, thereby greatly reducing the efficiency of the dispatch system.

Fig. 1

Work flow for highway petrol station replenishment

In order to overcome the lack of passive distribution model stated above and provide a more reasonable schedule for trucks and reduce cost, this paper develops a discrete-time MILP model in the initiative distribution mode and incorporates the constraint of sales predictions as an addition to other constraints. In the proposed model, the truck distribution process is decomposed into a pair of tasks, including driving, standby, rest, loading and unloading, and each task is closely related to the preceding and subsequent task. For any truck, a complete replenishment process involves driving to a depot, loading, driving to a petrol station and unloading. In practical engineering, a truck can replenish the oil supply of multiple petrol stations or of a single petrol station repeatedly for 1 day. Therefore, there are several tasks that must be completed at specified destinations for each truck. Moreover, the entire scheduling time horizon is divided into several equal time intervals, and each truck must execute one task during each interval.

2.2 Model requirements

The model is formulated as MILP, and MATLAB R2014a is employed to calculate the detailed truck routing and scheduling of petrol station replenishment.

Given:

• The time horizon of the working day.

• The locations of garages, depots and petrol stations.

• The delivery plan of the depot (delivery volume during each time interval) and the sales plan of the petrol stations (sales volume during each time interval).

• The inventory of the depot and petrol stations for each product.

• The congestion condition during each time interval.

• The basic information of trucks.

Determine:

• The detailed scheduling of trucks: the executed task during each time interval.

• The departure point and the corresponding destination of each transport task.

• The quantity and type of product being loaded (unloaded) of each load (unload) task.

• The inventory variations of depots and petrol stations.

• The total operational costs.

Objective:

The objective is to create a distribution plan with minimal operational costs while respecting a variety of operational and technical constraints. To establish and solve the model effectively, assumptions are made as follows.

• The trucks drive at a constant speed and can only load one type of specified product during each time interval.

• After the truck arrives at the depot or petrol station, it needs time to load or unload the petrol products, and the speed of loading and unloading is constant.

• During a single workday, all trucks start from the garage and return to the garage after completing all tasks.

• Petroleum companies predict the daily sales plan of the petrol stations and a daily delivery plan for the depots beforehand.

• The standby times and rest times of each vehicle during the working day should be within the allowed limits.

• The transport time between any two destinations is closely related to their real distance and real-time congestion conditions.

3 Mathematical model

This paper develops the MILP model based on discrete representation (Shaik and Bhat 2014). The studied system is made up of a set of nodes j $\in$ J, including depots (f_PDj = 1), petrol stations (f_PPj = 1) and garages (f_PGj = 1). Time nodes t $\in$ T is used to divide the working day into several equal time intervals, and the truck distribution process is decomposed into a pair of tasks. Each truck must execute one task during a single interval, and the currently executing task is closely related to the preceding and subsequent task. By accounting for predictive time-varying sales at petrol stations, real-time road congestion and a series of operational constraints, the proposed model produces the optimal truck dispatch, i.e., the detailed task assignment of all trucks during each time interval.

Overall, the model involves five sets: the set of trucks (I); the set of tasks (B_i); the set of nodes (J); the set of product types (K); and the set of time nodes (T) chronologically arranged. Moreover, this model comprises of positive continuous variables controlling the product inventory at petrol stations (V_Pj,k,t) and depots (V_Dj,k,t), the accumulated rest time of trucks (T_Ri,b), transport costs (C_Ti,b) and the costs for unpunctual distribution (C_Ot,j,k). Beyond that, a series of key binary variables are also introduced to identify if truck i are loading/unloading/resting/driving/standing by during its task b (in case S_Li,b,k, S_Ui,b, S_Ri,b, S_Di,b, S_Ri,b = 1), if truck i is filled with product k during its task b (in case P_Li,b,k = 1), if truck i’s task b starts at time node t(in case E_BTi,b,t = 1), and if truck i is staying at node j when its task b starts (in case N_Ci,b,j = 1).

3.1 Objective function

The objective function is the minimum operational cost, including the loading operation cost ($\sum\nolimits_{i \in I} {\sum\nolimits_{{b \in B_{i} }} {\sum\nolimits_{k \in K} {c_{{\text{L}}} S_{{{\text{L}}\,i,b,k}} } } }$), the unloading operation cost ($\sum\nolimits_{i \in I} {\sum\nolimits_{{b \in B_{i} }} {c_{{\text{U}}} S_{{{\text{U}}{\mkern 1mu} i,b}} } }$), the transport cost ($\sum\nolimits_{i \in I} {\sum\nolimits_{{b \in B_{i} }} {C_{{{\text{T}}{\mkern 1mu} i,b}} } }$) and the cost caused by the late distribution for petrol stations ($\sum\nolimits_{t \in T} {\sum\nolimits_{{j \in J_{P} }} {\sum\nolimits_{k \in K} {C_{{{\text{O}}{\mkern 1mu} t,j,k}} } } }$).

$$\min F = \sum\limits_{i \in I} {\sum\limits_{{b \in B_{i} }} {\left( {\sum\limits_{k \in K} {c_{{\text{L}}} S_{{{\text{L}}\,i,b,k}} } + c_{{\text{U}}} S_{{{\text{U}}\,i,b}} + C_{{{\text{T}}\,i,b}} } \right)} } + \sum\limits_{t \in T} {\sum\limits_{{j \in J_{P} }} {\sum\limits_{k \in K} {C_{{{\text{O}}\,t,j,k}} } } }$$

(1)

3.2 Trucks’ state constraints

This paper introduces binary variables to indicate the position of all trucks. N_Ci,b,j equals 1 when truck i is located at node j at the start time of task b. During any task, a truck can only stay at one node.

$$\sum\limits_{j \in J} {N_{{{\text{C}}\,i,b,j}} } = 1\quad i \in I,\;b \in B_{i}$$

(2)

There are two states for all trucks: one is full-load, and the other is no-load. If truck i is filled with product k at the start time of its task b, P_Li,b,k = 1, and otherwise P_Li,b,k = 0. In this way, $\sum\nolimits_{k \in K} {P_{{{\text{L}}i,b,k}} } { = 1}$ stands for full-load while $\sum\nolimits_{k \in K} {P_{{{\text{L}}i,b,k}} } = 0$ stands for no-load. Furthermore, the trucks are also divided into two types: one stores gasoline, and the other stores diesel oil. Equations (3) and (4) ensure that each truck only transports one type of specified oil during a single task. Note that the binary parameter f_Li,k in Eq. (3) is used to indicate if truck i can load product k.

$$\sum\limits_{k \in K} {P_{{{\text{L}}\,i,b,k}} } \le {1}\quad i \in I,\;b \in B_{i}$$

(3)

$$\sum\limits_{{b \in B_{i} }} {P_{{{\text{L}}\,i,b,k}} } \le f_{{{\text{L}}\,i,k}} \quad i \in I,\;k \in K$$

(4)

The executable operations of all trucks include load, unload, rest, drive and standby, only one of which can be executed during a single task:

$$\sum\limits_{k \in K} {S_{{{\text{L}}\,i,b,k}} } + S_{{{\text{U}}\,i,b}} + S_{{{\text{R}}\,i,b}} + S_{{{\text{D}}\,i,b}} + S_{{{\text{S}}\,i,b}} = 1\quad i \in I,\;b \in B_{i}$$

(5)

3.3 Loading constraints

For any truck i, the loading operation can only be executed at depots. In other words, the binary variable of the loading operation (S_Li,b,k) can equal one when truck i is located at node j, with node j being a depot (i.e., N_Ci,b,j = 1, f_PDj = 1).

$$\sum\limits_{k \in K} {S_{{{\text{L}}\,i,b,k}} } \le \sum\limits_{j \in J} {N_{{{\text{C}}\,i,b,j}} f_{{{\text{PD}}\,j}} } \quad i \in I,\;b \in B_{i}$$

(6)

Constraint (7) states that only no-load trucks can execute loading operations. If truck i loads product k during its task b, it will be filled with product k at the start time of its next task, that is to say, P_Li,b+1,k would be one if S_Li,b,k is equal to 1 [see constraint (8)]. Otherwise, the truck without product $k$ will remain unchanged. As seen in constraint (9), if P_Li,b,k is zero P_Li,b+1,k must be zero.

$$S_{{{\text{L}}\,i,b,k}} \le 1 - P_{{{\text{L}}\,i,b,k}} \quad i \in I,\;b \in B_{i} ,\;k \in K$$

(7)

$$S_{{{\text{L}}\,i,b,k}} \le P_{{{\text{L}}\,i,b{ + 1},k}} \quad i \in I,\;b < bm_{i} ,\;k \in K$$

(8)

$$P_{{{\text{L}}\,i,b{ + 1},k}} \le P_{{{\text{L}}\,i,b,k}} + S_{{{\text{L}}\,i,b,k}} \quad i \in I,\;b < bm_{i} ,\;k \in K$$

(9)

3.4 Unloading constraints

For any truck i, the unloading operation can only be executed at a petrol station. Specifically, the binary variable of the unloading operation (S_Ui,b) equals one when truck i is located at node j, while node j is a petrol station.

$$S_{{{\text{U}}\,i,b}} \le \sum\limits_{j \in J} {N_{{{\text{C}}\,i,b,j}} f_{{{\text{PP}}\,j}} } \quad i \in I,\;b \in B_{i}$$

(10)

Constraint (11) states that only full-load trucks can execute the unloading operation. If truck i unloads oil during its task b, it will be empty at the start time of its next task, that is to say, $\sum\nolimits_{k \in K} {P_{{{\text{L}}i,b{ + 1},k}} }$ must be zero as long as S_Ui,b is equal to one [see constraint (12)]. If it does not unload oil, the truck that is filled with product k will remain unchanged. As seen in constraint (13), if P_Li,b,k is one P_Li,b+1,k must be one.

$$S_{{{\text{U}}\,i,b}} \le \sum\limits_{k \in K} {P_{{{\text{L}}\,i,b,k}} } \quad i \in I,\;b \in B_{i}$$

(11)

$$S_{{{\text{U}}\,i,b}} \le 1 - \sum\limits_{k \in K} {P_{{{\text{L}}\,i,b{ + 1},k}} } \quad i \in I,\;b < bm_{i}$$

(12)

$$P_{{{\text{L}}\,i,b,k}} \le P_{{{\text{L}}\,i,b{ + 1},k}} + S_{{{\text{U}}\,i,b}} \quad i \in I,\;b < bm_{i} ,\;k \in K$$

(13)

3.5 Rest, standby and driving constraints

Only when the truck stops at the garage at the work start time can it rest. By constraint (14), S_Ri,b can be one only when $\sum\nolimits_{j \in J} {N_{{{\text{C}}{\mkern 1mu} i,b,j}} f_{{{\text{PG}}{\mkern 1mu} j}} } { = 1}$.

$$S_{{{\text{R}}\,i,b}} \le \sum\limits_{j \in J} {N_{{{\text{C}}\,i,b,j}} f_{{{\text{PG}}\,j}} } \quad i \in I,\;b \in B_{i}$$

(14)

Due to safety concerns, full-load trucks cannot rest. This operation condition is enforced by constraint (15). The binary variable of rest operation (S_Ri,b) must be zeros if $\sum\nolimits_{k \in K} {P_{{{\text{L}}{\mkern 1mu} i,b,k}} } { = 1}$.

$$\sum\limits_{k \in K} {P_{{{\text{L}}\,i,b,k}} } \le 1 - S_{{{\text{R}}\,i,b}} \quad i \in I,\;b \in B_{i}$$

(15)

To ensure safety, trucks can only stand by at some particular nodes. By constraint (16), S_Si,b can be one only when $\sum\nolimits_{j \in J} {N_{{{\text{C}}\,i,b,j}} f_{{{\text{PS}}\,j}} } \, = \, 1$.

$$S_{{{\text{S}}\,i,b}} \le \sum\limits_{j \in J} {N_{{{\text{C}}\,i,b,j}} f_{{{\text{PS}}\,j}} } \quad i \in I,\;b \in B_{i}$$

(16)

At the end of the weekday, all trucks must be at a rest station, and the last task must be rest, as seen in Eq. (17).

$$\sum\limits_{j \in J} {N_{{{\text{C}}\,i,bm_{i} ,j}} f_{{{\text{PG}}\,j}} } = 1\quad i \in I,\;j \in J$$

(17)

All trucks cannot standby twice continuously. In constraint (18), only one of two adjacent tasks b and b + 1 can be standby.

$$S_{{{\text{S}}\,i,b}} { + }S_{{{\text{S}}\,i,b + 1}} \le {1}\quad i \in I,\;b < bm_{i}$$

(18)

If truck i’s position at the start time of task b is different from that at task b + 1, then we can conclude that truck i’s task b is driving. As constraint (19) states, S_Di,b is bounded by the maximum value of N_Ci,b+1,j − N_Ci,b,j.

$$N_{{{\text{C}}\,i,b + 1,j}} - N_{{{\text{C}}\,i,b,j}} \le S_{{{\text{D}}\,i,b}} \quad i \in I,\;b < bm_{i} ,\;j \in J$$

(19)

3.6 Time constraints

To develop the constraints between time and tasks, this paper introduces a binary variable (E_BTi,b,t), which equals 1 when truck i’s task b starts at time node t. By constraint (20), each task must start at one time node. Constraint (21) determines that no task start be earlier than the start time of the preceding task. Furthermore, the last task of any truck must start before the study horizon, which is stated in constraint (22).

$$\sum\limits_{t \in T} {E_{{{\text{BT}}\,i,b,t}} } = 1\quad i \in I,\;b \in B_{i}$$

(20)

$$\sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b,t}} } \le \sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b + 1,t}} } \quad i \in I,\;b \in B_{i}$$

(21)

$$\sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,bm_{i} ,t}} } \le \tau m\quad i \in I$$

(22)

If the truck is loading products during its task b (i.e., $\sum\nolimits_{k \in K} {S_{{{\text{L}}{\mkern 1mu} i,b,k}} } { = 1}$), the time consumed by this task is related to the truck’s capacity and the loading flow rate. If the truck is not loading products, constraints (23)–(24) are redundant, and the interval duration can then match the value computed from the time constraints of another unload, rest, drive and standby.

$$\sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b + 1,t}} } - \sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b,t}} } \le \frac{{v_{{{\text{NU}}\,i}} }}{{r_{{\text{L}}} }} + \Delta \tau + \left( {1 - \sum\limits_{k \in K} {S_{{{\text{L}}\,i,b,k}} } } \right)\tau m\quad i \in I,\;b < bm_{i}$$

(23)

$$\sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b + 1,t}} } - \sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b,t}} } \ge \frac{{v_{{{\text{NU}}\,i}} }}{{r_{{\text{L}}} }} + \left( {\sum\limits_{k \in K} {S_{{{\text{L}}\,i,b,k}} } - {1}} \right)\tau m\quad i \in I,\;b < bm_{i}$$

(24)

Similarly, if truck i is unloading products during its task b (i.e., S_Ui,b = 1), the time consumed by this task is related to the truck’s capacity and unloading flowrate. Otherwise, constraints (25)–(26) are redundant and the interval duration is bounded by other operations.

$$\sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b + 1,t}} } - \sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b,t}} } \le \frac{{v_{{{\text{NU}}\,i}} }}{{r_{{\text{U}}} }} + \Delta \tau + \left( {1 - S_{{{\text{U}}\,i,b}} } \right)\tau m\quad i \in I,\;b < bm_{i}$$

(25)

$$\sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b + 1,t}} } - \sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b,t}} } \ge \frac{{v_{{{\text{NU}}\,i}} }}{{r_{{\text{U}}} }} + \left( {S_{{{\text{U}}\,i,b}} - 1} \right)\tau m\quad i \in I,\;b < bm_{i}$$

(26)

If truck i is resting during its task b (i.e., S_Ri,b = 1), the rest time of this truck should be equal to the accumulated rest time before task b plus the duration of task b [i.e., constraints (27)–(28)]. If not, the rest time of this truck should be equal to the accumulated rest time before task b [i.e., constraints (29)–(30)]. The total rest time of each truck should be limited to a range [i.e., constraint (31)].

$$T_{{{\text{R}}\,i,b + 1}} \le T_{{{\text{R}}\,i,b}} + \sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b + 1,t}} } - \sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b,t}} } + \left( {1 - S_{{{\text{R}}\,i,b}} } \right)\tau m\quad i \in I,\;b < bm_{i}$$

(27)

$$T_{{{\text{R}}\,i,b + 1}} \ge T_{{{\text{R}}\,i,b}} + \sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b + 1,t}} } - \sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b,t}} } + \left( {S_{{{\text{R}}\,i,b}} - 1} \right)\tau m\quad i \in I,\;b < bm_{i}$$

(28)

$$T_{{{\text{R}}\,i,b + 1}} \le T_{{{\text{R}}\,i,b}} + S_{{{\text{R}}\,i,b}} \tau m\quad i \in I,\;b < bm_{i}$$

(29)

$$T_{{{\text{R}}\,i,b + 1}} \ge T_{{{\text{R}}\,i,b}} - S_{{{\text{R}}\,i,b}} \tau m\quad i \in I,\;b < bm_{i}$$

(30)

$$t_{{{\text{R}}\,\min }} \le T_{{{\text{R}}\,i,bm}} \le t_{{{\text{R}}\,\max }} \quad i \in I$$

(31)

If truck i is driving during its task b (i.e., S_Di,b = 1), the time consumed must be related to the average of the driving distance, the speed of the truck and the coefficient of road congestion during this time period. Specifically, if truck i’s task b is to move from node j to node j′ during time interval t (i.e., S_Di,b, N_Ci,b+1,j′, N_Ci,b+1,j = 1), inequation constraints (32)–(33) work as an equation constraint. By doing so, the transport time is equal to the driving distance between node j and node j′(l_j,j′) being divided by the truck speed (r_D) and then being multiplied by the congestion coefficient during interval t(Z_t,j,j′).

$$\begin{aligned} \sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b + 1,t}} } - \sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b,t}} } & \le \frac{{l_{{j,j^{\prime}}} }}{{r_{{\text{D}}} }}\left( {\frac{{\sum\limits_{t \in T} {z_{{t,j,j^{\prime}}} E_{{{\text{BT}}\,i,b + 1,t}} + \sum\limits_{t \in T} {z_{{t,j,j^{\prime}}} E_{{{\text{BT}}\,i,b,t}} } } }}{2}} \right) + \Delta \tau \\ & + \left( {1 - S_{{{\text{D}}\,i,b}} } \right)\tau m{ + }\left( {{1} - \frac{{N_{{{\text{C}}\,i,b + 1,j^{\prime}}} + N_{{{\text{C}}\,i,b,j}} }}{2}} \right)\tau m\quad \quad i \in I,\;b < bm_{i} ,\;j,j^{\prime} \in J \\ \end{aligned}$$

(32)

$$\begin{aligned} \sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b + 1,t}} } - \sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b,t}} } & \ge \frac{{l_{{j,j^{\prime}}} }}{{r_{{\text{D}}} }}\left( {\frac{{\sum\limits_{t \in T} {z_{{t,j,j^{\prime}}} E_{{{\text{BT}}\,i,b + 1,t}} + \sum\limits_{t \in T} {z_{{t,j,j^{\prime}}} E_{{{\text{BT}}\,i,b,t}} } } }}{2}} \right) \\ & \quad + \left( {S_{{{\text{D}}\,i,b}} - 1} \right)\tau m + \left( {\frac{{N_{{{\text{C}}\,i,b + 1,j^{\prime}}} + N_{{{\text{C}}\,i,b,j}} }}{2} - 1} \right)\tau m\quad i \in I,\;b < bm_{i} ,\;j,j^{\prime} \in J \\ \end{aligned}$$

(33)

If truck i is standing by during its task b (i.e., S_Si,b = 1), the standby time should not be too long. Constraints (34)–(35) impose the lower and upper bounds on the standby time.

$$\sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b + 1,t}} } - \sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b,t}} } \le t_{{{\text{Smax}}}} + \left( {1 - S_{{{\text{S}}\,i,b}} } \right)\tau m\quad i \in I,\;b < bm_{i}$$

(34)

$$\sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b + 1,t}} } - \sum\limits_{t \in T} {t\Delta \tau E_{{{\text{BT}}\,i,b,t}} } \ge t_{{{\text{Smin}}}} + \left( {S_{{{\text{S}}\,i,b}} - 1} \right)\tau m\quad i \in I,\;b < bm_{i}$$

(35)

3.7 Petrol station constraints

The binary variable E_PVi,j,b,k,t denotes the completed status of replenishment and equals one when a full-load truck i finishes unloading product k to node j at time node t. By constraints (36)–(37), if any value of binary variables S_Ui,b E_BTi,b+1,t, N_Ci,b+1,j and P_Li,b,k is equal to zero, E_PVi,j,b,k,t must be zero. Conversely, if these variables are all equal to one, E_PVi,j,b,k,t must be one.

$$E_{{{\text{PV}}\,i,j,b,k,t}} \ge Mi + \frac{{S_{{{\text{U}}\,i,b}} + E_{{{\text{BT}}\,i,b + 1,t}} + N_{{{\text{C}}\,i,b + 1,j}} + P_{{{\text{L}}\,i,b,k}} }}{4} - 1\quad i \in I,\;j \in J,\;b < bm_{i} ,\;k \in K,\;t \in T$$

(36)

$$E_{{{\text{PV}}\,i,j,b,k,t}} \le 1 - \left( {1 - \frac{{S_{{{\text{U}}\,i,b}} + E_{{{\text{BT}}\,i,b + 1,t}} + N_{{{\text{C}}\,i,b + 1,j}} + P_{{{\text{L}}\,i,b,k}} }}{4}} \right)Mi\quad i \in I,\;j \in J,\;b < bm_{i} ,\;k \in K,\;t \in T$$

(37)

If $\sum\nolimits_{i \in I} {\sum\nolimits_{{b \in B_{i} }} {\sum\nolimits_{k \in K} {E_{{{\text{PV}}{\mkern 1mu} i,j,b,k,t}} } } }$ is more than one, the received volume of node j during time interval (t, t + 1) equals the sum of the capacities of the corresponding trucks. Otherwise, the received oil volume is zero. The inventory of node j equals the inventory at the last time node plus the received oil volume and minus the sales volume during the last time interval.

$$V_{{{\text{P}}\,j,k,t}} = V_{{{\text{P}}\,j,k,t - 1}} { + }\sum\limits_{i \in I} {\sum\limits_{{b \in B_{i} }} {E_{{{\text{PV}}\,i,j,b,k,t}} v_{{{\text{NU}}\,i}} } } - v_{{{\text{S}}\,j,k,t - 1}} \quad j \in J,\;k \in K,\;t > 1$$

(38)

During any time interval t, the inventory of the petrol station should meet certain limits. To obtain a feasible solution when faced with stockouts caused by falling product prices, there is no lower limit for the inventory of the petrol station. However, this model has added the costs caused by unpunctual distribution into the objective function to ensure that each petrol station keeps a stock of petrol products.

$$V_{{{\text{P}}\,j,k,t}} \le v_{{{\text{Pmax}}\,j,k}} \quad j \in J,\;k \in K,\;t \in T$$

(39)

3.8 Depot constraints

This paper introduces three types of binary variables to represent the start, finish and process of the loading operation. Specifically, E_DVBi,j,b,k,t equals one when a no-load truck i starts loading product k from node j at time node t [i.e., constraints (40)–(41)], while E_DVNi,j,b,k,t equals one when the truck has just finished loading oil [i.e., constraints (42)–(43)]. As constraint (44) shows, E_DVi,j,b,k,t is bounded by E_DVBi,j,b,k,t and E_DVNi,j,b,k,t, and it equals one when truck i is loading product k from node j during time interval (t, t + 1).

$$E_{{{\text{DVB}}\,i,j,b,k,t}} \ge Mi + \frac{{S_{{{\text{L}}\,i,b,k}} + E_{{{\text{BT}}\,i,b,t}} + N_{{{\text{C}}\,i,b,j}} }}{3} - 1\quad i \in I,\;j \in J,\;b < bm_{i} ,\;k \in K,\;t \in T$$

(40)

$$E_{{{\text{DVB}}\,i,j,b,k,t}} \le 1 - \left( {1 - \frac{{S_{{{\text{L}}\,i,b,k}} + E_{{{\text{BT}}\,i,b,t}} + N_{{{\text{C}}\,i,b,j}} }}{3}} \right)Mi\quad i \in I,\;j \in J,\;b < bm_{i} ,\;k \in K,\;t \in T$$

(41)

$$E_{{{\text{DVN}}\,i,j,b,k,t}} \ge Mi + \frac{{S_{{{\text{L}}\,i,b,k}} + E_{{{\text{BT}}\,i,b + 1,t}} + N_{{{\text{C}}\,i,b + 1,j}} }}{3} - 1\quad i \in I,\;j \in J,\;b < bm_{i} ,\;k \in K,\;t \in T$$

(42)

$$E_{{{\text{DVN}}\,i,j,b,k,t}} \le 1 - \left( {1 - \frac{{S_{{{\text{L}}\,i,b,k}} + E_{{{\text{BT}}\,i,b + 1,t}} + P_{{{\text{C}}\,i,b + 1,j}} }}{3}} \right)Mi\quad i \in I,\;j \in J,\;b < bm_{i} ,\;k \in K,\;t \in T$$

(43)

$$E_{{{\text{DV}}\,i,j,b,k,t}} = E_{{{\text{DV}}\,i,j,b,k,t - 1}} + E_{{{\text{DV}}\,{\text{B}}i,j,b,k,t}} - E_{{{\text{DV}}\,{\text{N}}i,j,b,k,t}} \quad i \in I,\;j \in J,\;b < bm_{i} ,\;k \in K,\;t > 1$$

(44)

Due to the limited number of loading arms, a depot can only permit a limited number of trucks to load oil during a single time interval.

$$\sum\limits_{i \in I} {\sum\limits_{{b \in B_{i} }} {E_{{{\text{DV}}\,i,j,b,k,t}} } } \le h_{{{\text{L}}\,\max j,k}} \quad j \in J_{i} ,\;k \in K,\;t \in T$$

(45)

If $\sum\nolimits_{i \in I} {\sum\nolimits_{{b \in B_{i} }} {\sum\nolimits_{k \in K} {E_{{{\text{DV}}{\mkern 1mu} i,j,b,k,t}} } } }$ is more than one, the discharged volume of node j during time interval (t, t + 1) is equal to the aggregate capacities of the trucks that are loading. Otherwise, the discharged volume is zero. Hence, the inventory at node j is equal to the inventory of the last time node plus the received volume from refineries and minus the discharged oil volume during the last time interval.

$$V_{{{\text{D}}\,j,k,t}} = V_{{{\text{D}}\,j,k,t - 1}} + v_{O\,j,k,t - 1} - \sum\limits_{i \in I} {\sum\limits_{{b \in B_{i} }} {E_{{{\text{DVN}}\,i,j,b,k,t}} v_{{{\text{NU}}\,i}} } } \quad j \in J,\;k \in K,\;t \in T$$

(46)

During any time interval t, the inventory of all depots should meet certain limits.

$$v_{{{\text{Dmin}}\,j,k}} \le V_{{{\text{D}}\,j,k,t}} \le v_{{{\text{Dmax}}\,j,k}} \quad j \in J,\;k \in K,\;t \in T$$

(47)

3.9 Cost constraints

For a given transport route, fuel consumption increases with the load. Hence, the transport costs are calculated by transportation distance and truck status, as shown in constraints (48)–(49). More specifically, transport costs for all empty trucks only depend on the product of unit cost and transportation distance. However, if truck i is full of product k, the transport costs must be a bitter higher than the costs of empty trucks. Therefore, the parameter α_k in constraints (48)–(49) is used to compute the extra costs for carrying v_NUi m³ of product k.

$$C_{{{\text{T}}\,i,b}} \le c_{{{\text{UT}}}} l_{{j,j^{\prime}}} \left( {1 + \sum\limits_{k \in K} {P_{{{\text{L}}\,i,b,k}} v_{{{\text{NU}}\,i}} \alpha_{k} } } \right) + \left( {1 - \frac{{N_{{{\text{C}}\,i,b + 1,j^{\prime}}} + N_{{{\text{C}}\,i,b,j}} }}{2}} \right)M\quad i \in I,\;j,\;j^{\prime} \in J,\;b < bm_{i} ,\;t \in T$$

(48)

$$C_{{{\text{T}}\,i,b}} \ge c_{{{\text{UL}}}} l_{{j,j^{\prime}}} \left( {1 + \sum\limits_{k \in K} {P_{{{\text{L}}\,i,b,k}} v_{{{\text{NU}}\,i}} \alpha_{k} } } \right) + \left( {\frac{{N_{{{\text{C}}\,i,b + 1,j^{\prime}}} + N_{{{\text{C}}\,i,b,j}} }}{2} - 1} \right)M\quad i \in I,\;j,\;j^{\prime} \in J,\;b < bm_{i} ,\;t \in T$$

(49)

It is forbidden for the truck to be delivering oil if its location remains unchanged. If this occurs, then the corresponding costs are at the maximum level. By constraint (50), transport costs ($C_{{{\text{T}}\,i,b}}$) would be greater than a sufficiently large value (1/2M) when binary variables S_Di,b, N_Ci,b+1,j, N_Ci,b,j are all equal to one.

$$C_{{{\text{T}}\,i,b}} \ge \frac{1}{2}M + \left( {S_{{{\text{D}}\,i,b}} - 1} \right)M + \left( {\frac{{N_{{{\text{C}}\,i,b + 1,j}} + N_{{{\text{C}}\,i,b,j}} }}{2} - 1} \right)M\quad i \in I,\;j \in J,\;b < bm_{i}$$

(50)

As for any petrol station, a negative inventory stands for unpunctual distribution, which leads to economic losses. The right term of constraint (51) is a positive value when the inventory V_Pj,k,t is negative, and thus imposes a lower bound for the costs of unpunctual distribution C_Ot,j,k.

$$C_{{{\text{O}}\,t,j,k}} \ge - c_{{{\text{UO}}}} V_{{{\text{P}}\,j,k,t}} \Delta \tau \quad j \in J,\;k \in K,\;t \in T$$

(51)

4 Results and discussion

4.1 Basic data

This section is to validate our model and the superiority of initiative distribution by using a real-world case of a highway in Beijing, China. Figure 2 illustrates a real-world block where there are eight petrol stations (S1, S2, S3, S4, S5, S6, S7 and S8), a garage and a depot. The depot is located at the center of the block and is responsible for the product supplies of these petrol stations. A daily distribution plan starts at 6:00 and finishes at 24:00. During the workday, all trucks start from the garage and return to the garage after completing all tasks. For this replenishment system, there are a total of eight available trucks (C1, C2, C3, C4, C5, C6, C7 and C8) to transport three types of products (P1, P2 and P3). To avoid contamination, C1, C2 and C3 can only load P1, while C4, C5, C6, C7 and C8 are usable for P2 and P3. However, each truck can only load one type of product at a time. The oil tank capacity of each truck is 20 m³, and the inventory of the petrol station is 30 m³. There are 2, 1 and 1 loading arms for P1, P2 and P3 in the depot, respectively. The unit labor cost and wastage cost of loading or unloading oil each time is 50 CNY, and the unit cost caused by unpunctual distribution is 600 CNY/(m³ h) During the transport task, the unit transport cost for an empty truck is 10.9 CNY per kilometer, while it is 16.7 CNY per kilometer for a full-load truck. The trucks’ speeds when loading, unloading and driving are 60 m³/h, 60 m³/h and 60 km/h, respectively. And the replenishment speeds of P1, P2 and P3 of the depot are 71.67 m³/h, 56.67 m³/h and 60 m³/h, respectively. Within the study horizon of the study, the sales rate of petrol station will change several times and is shown in Fig. 3. Standby time should be less than 1.5 h, while the total rest time for each driver should be less than 3 h.

Fig. 2

Positions of the depot, garage and petrol stations

Fig. 3

Sales rates of petrol stations

4.2 Real-world scheduling plan

To demonstrate our advantages in the following part, we first give an overview of the actual scheduling plan premade by the company, which can be seen as a classic example of passive distribution. All the petrol station only puts forward the ordered products capacity and has no specific requirements on the delivery time. It only requires the products to be delivered on today. The total cost of this real-world scheduling plan is 82,706 CNY, including 2600 CNY for loading and unloading operations, 78,775 CNY for transporting operations and 1331 CNY for the costs caused by the late distribution for petrol stations.

Figure 4 shows the detailed distribution plan. Green represents the transportation task, yellow represents the standby task, orange represents the loading task, gray represents the rest task and blue represents the unloading task. The orange mark represents the type of product that needs to be loaded and unloaded, and the blue mark represents the petrol station that needs to be replenished. One complete replenishment plan for a truck, including the loaded product type and the replenishing object, is closely associated with the current inventory of all petrol stations, one complete replenishment plan for a truck, including the loaded product type and the replenishing object. At the start time, all trucks go from the garage to the depot and then perform the loading operation under the constraints of the number of loading arms and the demanded oil types. Afterward, each truck drives to the petrol station to unload oil and finally back to the garage to rest. Overall, C2 and C5 replenish petrol stations four times a day, and the others replenish petrol stations three times a day.

Fig. 4

Detailed distribution plan of passive distribution

Figures 5 and 6 depict the inventory variation of petrol stations and depots. It can be seen from Fig. 8 that sometimes oil shortage occurs in a few petrol stations. Specifically, P1 is out of stock in S1 at 20:40, P2 is out of stock in S2 at 16:00, P2 is out of stock in S5 at 18:30, and P3 is out of stock in S8 at 13:40. The stock out of S2 is the most severe and lasts almost 3 h.

Fig. 5

Inventory variation of petrol stations

Fig. 6

Inventory variation of depots

4.3 Optimal scheduling plan

To obtain the optimal scheduling plan of initiative distribution, we develop a mathematical model according to Sect. 3. The model is solved by the Gurobi Optimizer under the hardware environment of the Intel Core i7-4770k (3.50 GHz). The Gurobi Optimizer is a state-of-the-art mathematical programming solver able to handle all large-scale problem types. This solver was designed from the ground up to exploit modern architectures and multicore processors by using the latest implementations of the latest algorithms. Furthermore, the solver supports matrix-oriented interfaces for MATLAB. Given the same MILP model, Gurobi can solve it faster and use less memory than the nested solver of MATLAB. The optimal distribution plan of trucks is shown in Fig. 7. Its total cost during the research time horizon is 79,254 CNY, including 2600 CNY for loading and unloading operations and 76,654 CNY for transportation. Each petrol station is replenished before its inventory is low; thus, there is no cost caused by unpunctual distribution. In contrast to the real-world result, the cost of transportation and out of stock is greatly saved.

Fig. 7

Detailed distribution plan solved by the proposed method

As is known from Fig. 7, C2 and C6 replenish petrol stations four times a day, while the others replenish petrol stations three times a day. The loading order depends on the loading arm constraint and the truck’s destination. Taking the 7th and 8th time intervals (i.e., 7:10–7:30) as an example, all trucks except C6 arrive at the depot, while only C2, C3, C4 and C5 are loaded because there are 2, 1 and 1 loading arms for P1, P2 and P3 in the depot, respectively. Moreover, there are three trucks that need to load P3 during the first loading operation, but the loading order is C4 (replenish for S2), C7 (replenish for S6) and C8 (replenish for S5). From Fig. 5, it can be seen that the first station to reach the lower limitation is S2, followed by S5 and S6. Considering that the transportation distance of S6 is longer than that of S5, C7 loads P3 ahead of C8. With a comprehensive consideration of the transportation time and out-of-stock time, initiative distribution is able to optimize the delivery sequence for all petrol stations. After the optimization, the time to replenish P1 at S1, P2 at S2, P2 at S5 and P3 at S8 is brought forward to 20:00, 13:10, 18:10 and 13:10, thus avoiding the out of stock occurred under the mode of passive distribution.

Besides, most trucks’ final task is to replenish the petrol stations that are relatively close to the garage, such as S1 and S4, and then to return back to the garage to rest after completing the loading task. From Fig. 7, C1 and C3 are the first trucks to arrive at the garage (at 21:00), and they have a 3-h rest time. Figure 8 illustrates that all the petrol stations would receive timely replenishments when their inventories are close to their lower limits, and the inventory during the study horizon stays within the allowable range. This also indicates that initiative distribution enables petrol stations to control their inventory at a relatively low but safe level and gives a potential advantage of reducing inventory handling cost when compared to passive distribution. The inventory variation of the depot is depicted in Fig. 9 and meets the capacity constraints during the entire study horizon.

Fig. 8

Inventory variation of petrol stations

Fig. 9

Inventory variation of depots

5 Conclusions

In order to improve efficiency for the entire replenishment system of highway petrol stations, this paper establishes a MILP model which sets the minimum operating cost as the objective function and considers the detailed truck status and a series of operational constraints. In the cost component, loading and unloading operating cost, transportation cost and cost caused by out of stock are taken into account. One step further than previous studies is that the proposed model is capable of dealing with a variety of products, time-varying sales rates and congestion conditions. For a real-world case containing eight petrol stations, one depot with three types of oil products and one garage with eight trucks, the detailed truck dispatch plan is optimized using this model. During the 18 h of the study period, the sales rate of each petrol station varies several times and every truck has a detailed task assignment in each time interval. And it also visualizes the inventory change of each petrol station and depot. Compared to the actual scheduling plan in passive mode premade by the company, initiative mode leads to less operational cost while controlling the inventory of all the petrol stations at low but safe level. In the initiative mode, inventory is predicted scientifically and the products are sent to the petrol station in a suitable time, which effectively improves the efficiency of product oil resource allocation and enhances the stability of the supply of petrol station.

However, the truck scheduling problem is an NP-hard problem with strict demands on computational time and space. For a mathematical model, it is suitable for obtaining the optimal solution for a relatively small problem because the solving efficiency is closely related to the model’s scale. Therefore, developing a highly efficient meta-heuristic algorithm to solve increasingly complex truck scheduling problems within an acceptable time is important for future works.