Supply-based optimal scheduling of oil product pipelines

Abstract

Oil product pipelines have features such as transporting multiple materials, ever-changing operating conditions, and synchronism between the oil input plan and the oil offloading plan. In this paper, an optimal model was established for a single-source multi-distribution oil product pipeline, and scheduling plans were made based on supply. In the model, time node constraints, oil offloading plan constraints, and migration of batch constraints were taken into consideration. The minimum deviation between the demanded oil volumes and the actual offloading volumes was chosen as the objective function, and a linear programming model was established on the basis of known time nodes’ sequence. The ant colony optimization algorithm and simplex method were used to solve the model. The model was applied to a real pipeline and it performed well.

1 Introduction

Approximately, 17.95 million barrels of oil products are imported and exported everyday around the world (BP 2014), most of which are transported to different cities by pipelines. As oil product pipelines are developing at an incredible pace, the topological structure and operation of oil product pipelines are becoming more complex than ever, adding difficulty in making schedules. The main issues concerned are how to make a more rational batch-scheduling plan and how to meet the consumption demand of each region along the pipeline in a safe and economic way. The oil products pipeline has features such as multiple oil products, ever-changing working conditions, and synchronism between the injection plan of the pipeline’s initial station and the offloading plan of the offloading stations along the pipeline. Milidiú and dos Santos Liporace (2003) proved that the scheduling plan of oil batches is a non-deterministic polynomial complete (NPC) issue if the batch sequence constraint is considered. Presently, batch-dispatchers use manual or semi-automatic methods to create the batch-scheduling plan for most of the supply-based pipelines. In other words, there exists no mature algorithm that can automatically make the scheduling plan that meets with the demands of actual operation.

Much research focuses on these complex scheduling issues. Determination of time expression is a fundamental step of building a scheduling model, and can directly affect the size of the model and the selection of algorithm. Currently, there are two major time expressions for scheduling models available, namely discrete-time and continuous-time expression.

Discrete-time expression, dividing the period studied into several isometric- or length-specified time-windows, takes the time node of time-windows as the scheduling plan’s event nodes and analyzes the logical relationship between variables. Using the method of discrete-time expression can simplify the non-linear coupling relationship between variables as well as reduce the difficulty of building and solving a model. The research of Rejowski and Pinto (2003) embodied the advantage of a discrete-time expression when dealing with time-related electrical price issues. Magatão et al. (2004), using a discrete-time expression, solved the issue of pipeline network scheduling plans, which also reflects its preponderance in simplifying large and complex models. Zyngier and Kelly (2009) proved that the introduction of a stock constraint will add to the model’s complexity and improve the discrete-time expression. Herrán et al. (2010) resolved the issue of multi-injection and tracking batch interfaces through discrete-time expression. de Souza Filho et al. (2013) combined a discrete-time expression with a heuristic algorithm and set up a mixed integer linear programming (MILP) model to resolve the issue of scheduling aiming at minimizing power costs. Despite the fact that the research above has demonstrated that discrete-time expression works well when dealing with sub-problems like tracking batch interfaces, the final solution given by a discrete-time expression may not possess practical applicability in that the practical planning cycle is more than a week and the long-time step length may lead to poor optimality, while the short one may result in excessive model and dimension disasters.

Continuous-time expressions divide the time-window according to the happening and ending of an event, the beginning and ending time of which are known or unknown. In other words, there exists an uncertainty for time-window’s length and time nodes. Analyzing the occurring and ending condition of events and inter-connection between events is essential for continuous-time expressions. Although the adoption of continuous-time expressions may lead to a more complex model structure and stronger coupling link between variables, it can minimize the size of a model and improve the solving efficiency. Based on the previous research of the MILP discrete method for dendritic pipeline network scheduling, MirHassani and Ghorbanalizadeh (2008) have proposed a continuous-time MILP method, the result of which demonstrates that the introduction of continuous-time can apparently enhance the calculating efficiency. During the past several years, optimizing of schedule issues on the basis of continuous-time models for different pipelines has become an issue of interest in academia. For instance, some researchers aim at single-source pipelines (Cafaro and Cerdá 2004, 2008; Relvas et al. 2006), some focus on tree-structure pipelines (Mirhassani and Ghorbanalizadeh 2008; Castro 2010; Cafaro and Cerdá 2011), or mesh-structure pipelines (Cafaro and Cerdá 2012). However, at present, the scheduling plan given by a continuous-time MILP model is just an approximate scheduling which contains only a general time zone and approximate injection as well as offtake volume for each station instead of a detailed operating time.

In the subsequent research, many researchers began to study the algorithm for a detailed scheduling plan on the basis of an approximate scheduling plan. Cafaro et al. (2011) chose the simplest monophyletic transfer pipe as the research object, and obtained an approximate scheduling plan and then developed a step-by-step algorithm for detailed planning. Whereafter, a detailed scheduling plan that can achieve simultaneously offloading operations was developed (Cafaro et al. 2012). Recently, on the basis of the previous research, Cafaro et al. (2015) established a mixed integer non-linear programming (MINLP) model and made a detailed scheduling plan for a real monophyletic pipeline, considering the hydraulic coupling non-linear constraint.

Nevertheless, the current continuous-time expression MILP model ignores the time nodes such as batches’ arrival and batch delivery operation’s starting and ending moment, which will inevitably bring about uneconomical operating period distribution and excessive time-window offset. Those will decrease the model’s practicability. Moreover, a large number of models take the limit of download and injection size as known parameters which are time-related. It would be more reasonable if it is replaced by a limit of operating flow rate. This paper uses the time-continuous expression method to establish a LP model on the basis of known time nodes’ sequence. The objective function is the minimum deviation between the demand batch volume and the actual offloading volume at each station. To accelerate solving speed, the hybrid algorithm of ACO (ant colony optimization) and the SM (simplex method) is used to solve the model.

Section 2 of this paper describes the scheduling issue and gives the model’s assumption conditions. Section 3 establishes the objective function of the model and describes the constraints of the model. In Sect. 4, the model-solving process is discussed. Section 5 verifies the correctness and applicability of the model with two examples. We end with our conclusions in Sect. 6.

2 Problem description

2.1 Supply-based scheduling of single-source products pipeline

Some products pipelines serve the refinery, with the responsibility of transporting the refined oil to the downstream market. Firstly, the refinery’s production plan is made on the basis of the downstream market’s demand. Next, the injecting plan at the initial station is made according to the production plan. The batch-dispatchers can work out the offloading plan based on the supply of the initial station, called the supply-based schedule. Thus, the demand of the downstream market can be satisfied in time, and at the same time, human resources are saved and inventory cost is sharply reduced.

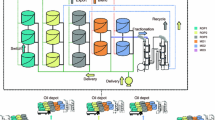
There are three kinds of stations in the single-source pipeline system: initial station (input station), offloading stations (intermediate stations), and terminal station, as shown in Fig. 1. The initial station is linked with a refinery and the terminal station is an oil depot with a large storage capacity. The oil products are sequentially transported in the pipeline and the batch sequence is known. The optimal research about the pipeline scheduling plan based on supply is to determine the offloading station’s actual offloading volume on the basis of known conditions, including the input schedule at the initial station and demanded volumes at offloading stations.

Fig. 1

Oil products pipeline system

Parameters are taken into account, including pipeline information, oil input sequence, volume and flow rate of the initial station in a certain period of time, demand volumes of each offloading station, upper and lower limits of flow rate, and each station’s offloading flow rate limits. The decision variables are actual offloading volumes and the starting and ending time of offloading operation.

2.2 Modeling hypotheses

The scheduling of an oil products pipeline system is subject to several constraints. In order to improve solving efficiency, some assumptions are made:

• (1) Inventory constraints of the terminal station are neglected and it can receive any type of oil at any time.

• (2) When batches move in products pipeline in order, contamination will occur inevitably between the two adjacent oils. The mixed oil section is considered as an interface.

• (3) The offloading stations along the pipeline own a certain number of tanks, which can store the oil temporarily. The paper assumes that the demands given by each offloading station have considered stock volumes, irrespective of the tank capacity constraints, and oil storage conditions of each intermediate station.

• (4) The oil is incompressible.

• (5) Any offloading flow rate of each offloading station is constant within a time-window.

3 Mathematical formula

3.1 Objective function

The minimum deviation between each batch demanded volume of each station and the actual offloading volume is defined as the objective function.

$$\hbox{min}\; f = \sum\limits_{i} {\sum\limits_{j} {\left| {V_{{{\text{x}}i,j}} - V_{{{\text{s}}i,j}} } \right|} } \quad i \in I,\,j \in J$$

(1)

Since this objective function is non-continuous, it is difficult to solve. Artificial relaxation variables and artificial tightening variables are introduced to linearize the objective function.

$$\hbox{min}\; f = \sum\limits_{i} {\sum\limits_{j} {(M_{1i,j} } } + M_{2i,j} )\quad i \in I,\;j \in J$$

(2)

M _1i,j , M _2i,j mentioned above should meet the following constraints:

$$V_{{{\text{x}}i,j}} - V_{{{\text{s}}i,j}} + M_{1i,j} \ge 0$$

(3)

$$V_{{{\text{s}}i,j}} - V_{{{\text{x}}i,j}} + M_{ 2i,j} \ge 0$$

(4)

$$M_{1i,j} \ge 0,M_{2i,j} \ge 0\quad i \in I,j \in J$$

(5)

If $V_{{{\text{x}}i,j}} - V_{{{\text{s}}i,j}} \ge 0,$ according to Eq. (3), the minimum value of M _1i,j is 0. The minimum value of M _2i,j is equal to $V_{{{\text{x}}i,j}} - V_{{{\text{s}}i,j}}$ according to Eq. (4). If $V_{{{\text{x}}i,j}} - V_{{{\text{s}}i,j}} \le 0,$ according to Eq. (3), the minimum value of M _1i,j is equal to $V_{{{\text{s}}i,j}} - V_{{{\text{x}}i,j}} .$ The minimum value of M _2i,j is 0. Therefore, Eq. (2) is equivalent to Eq. (1).

3.2 Model constraints

3.2.1 Time node constraints

If the order of all the time nodes is known—Sect. 4 will describe how to determine the order—all the time nodes are numbered. The following is the corresponding expression:

$$t_{\tau } \le t_{\tau + 1} \quad \tau \in T_{\text{C}} ,t_{\tau } \in T.$$

(6)

For any given station, the arrival time of any batch’s oil head cannot be later than that of the next batch oil head.

$$\tau_{{{\text{a}}i,j}} < \tau_{{{\text{a}}i,j + 1}} \quad i \in I,j \in J,\tau_{{{\text{a}}i,j}} \in T_{\text{C}}$$

(7)

For the same batch, the arrival time of the oil head at any station cannot be later than that of the next station.

$$\tau_{{{\text{a}}i,j}} < \tau_{{{\text{a}}i + 1,j}} \quad i \in I,j \in J,\tau_{{{\text{a}}i,j}} \in T_{\text{C}}$$

(8)

The time when a station starts to offload the demanded batch cannot be earlier than oil head’s arriving time. The time when a station finishes offloading the demanded batch cannot be later than the arrival time of the next batch.

$$\tau_{{{\text{a}}i,j}} < \tau_{{{\text{c}}i,j}}$$

(9)

$$\tau_{{{\text{a}}i,j + 1}} > \tau_{{{\text{b}}i,j}} \quad i \in I,j \in J,\tau_{{{\text{a}}i,j}} ,\tau_{{{\text{c}}i,j}} ,\tau_{{{\text{b}}i,j}} \in T_{\text{C}}$$

(10)

The time that a station starts to offload the batch cannot be later than the ending time.

$$\tau_{{{\text{c}}i,j}} < \tau_{{{\text{b}}i,j}} \quad i \in I,j \in J,\tau_{{{\text{c}}i,j}} ,\tau_{{{\text{b}}i,j}} \in T_{\text{C}}$$

(11)

The time when a station starts and ends to offload the batch cannot be earlier than the scheduled starting time and cannot be later than the scheduled ending time.

$$\tau_{\text{tc}} < \tau_{{{\text{c}}i,j}} < \tau_{\text{tb}}$$

(12)

$$\tau_{\text{tc}} < \tau_{{{\text{b}}i,j}} < \tau_{\text{tb}} \quad i \in I,j \in J,\tau_{{{\text{c}}i,j}} ,\tau_{{{\text{b}}i,j}} \in T_{\text{C}}$$

(13)

3.2.2 Offloading plan constraints

The actual offloading volume of any batch at any station is the sum of offloading volumes during all the time-windows from offloading staring time node to the ending node.

$$V_{{{\text{s}}i,j}} = \sum\limits_{{\tau = \tau_{{{\text{c}}i,j}} }}^{{{\tau_{\text{b}}}_{{i,j^{ - 1} }} }} {V_{{{\text{p}}i,\tau }} } \quad i \in I,j \in J,\tau_{{{\text{c}}i,j}} ,\tau_{{{\text{b}}i,j}} \in T_{\text{C}}$$

(14)

Due to the limit of the offloading flow rate, the offloading volume within any time-window should not be larger than that of the maximum offloading flow rate multiplied by the length of the time-window or less than that of the minimum offloading flow rate multiplied by the length of the time-window.

$$V_{{{\text{p}}i,\tau }} \le t_{\tau + 1} Q_{{{\text{x}}\hbox{max} i}} - t_{\tau } Q_{{{\text{x}}\hbox{max} i}}$$

(15)

$$V_{{{\text{p}}i,\tau }} \ge t_{\tau + 1} Q_{{{\text{x}}\hbox{min} i}} - t_{\tau } Q_{{{\text{x}}\hbox{min} i}} \quad i \in I,\tau \in \{ \tau_{{{\text{c}}i,j}} , \ldots ,\tau_{{{\text{b}}i,j}} - 1\} ,\,j \in J$$

(16)

3.2.3 Batch transportation constraints

Considering the hydraulic constraints, the flow rate of the pipeline should be within a certain range. When there exists a gasoline and diesel mixed interface, in order to reduce the amount of mixed oil, the Reynolds number of the fluid in the pipeline must be larger than the critical Reynolds number. The minimum flow rate of the pipeline between station i and station i + 1 multiplied by the length of the time-window should not be larger than the difference between the volume input by the initial station within this time-window and the offloading volumes of station i and all stations before station i within the time-window. The allowable maximum flow rate of the pipeline between station i and station i + 1 multiplied by the length of time-window should not be less than the difference between the volume input by the first station within this time-window and the offloading volumes of station i and all stations before station i within the time-window.

$$t_{\tau + 1} Q_{{{\text{c}}\hbox{min} i}}^{\tau } - t_{\tau } Q_{{{\text{c}}\hbox{min} i}}^{\tau } \le t_{\tau + 1} Q_{{{\text{k}}\tau }} - t_{\tau } Q_{{{\text{k}}\tau }} - \sum\limits_{{i^{{\prime }} = 1}}^{i} {V_{{{\text{p}}i^{{\prime }} ,\tau }} }$$

(17)

$$t_{\tau + 1} Q_{{{\text{c}}\hbox{max} i}}^{\tau } - t_{\tau } Q_{{{\text{c}}\hbox{max} i}}^{\tau } \ge t_{\tau + 1} Q_{{{\text{k}}\tau }} - t_{\tau } Q_{{{\text{k}}\tau }} - \sum\limits_{{i^{\prime} = 1}}^{i} {V_{{{\text{p}}i^{{\prime }} ,\tau }} } \quad i \in I,\tau \in T_{\text{C}} ,t_{\tau } \in T$$

(18)

According to the conservation of volume, the volume coordinate of batch j plus the total input volume of the initial station before time $t_{{\tau_{{{\text{a}}i,j}} }}$ minus the total offloading volumes at stations before station i during the time-windows from $t_{{\tau_{{{\text{a}}i,j}} }}$ to $t_{{\tau_{{{\text{c}}i,j}} }}$ is equal to the volume coordinate of station i.

$$V_{{{\text{o}}j}} + \sum\limits_{\tau = 1}^{{\tau_{{{\text{a}}i,j^{ - 1} }} }} {(t_{\tau + 1} Q_{{{\text{k}}\tau }} - t_{\tau } Q_{{{\text{k}}\tau }} } ) - \sum\limits_{{i^{\prime} = 1}}^{i - 1} {\sum\limits_{{\tau = \tau_{{{\text{c}}i^{{\prime }} ,j}} }}^{{\tau_{{{\text{a}}i,j^{ - 1} }} }} {V_{{{\text{p}}i^{{\prime }} ,\tau }} } } = V_{i} \quad i \in I,j \in J,\tau_{{{\text{c}}i,j}} ,\tau_{{{\text{a}}i,j}} \in T_{\text{C}} ,t_{\tau } \in T$$

(19)

4 Model solving

According to the objective function and the constraints if the sequence of all the time nodes is determined (all of the discrete variables are determined), an LP model can be established as shown in Sect. 3 and solved by SM. Therefore, finding the optimal sequence of time nodes is significant to solve this issue. While, as coupling with a large-scale LP model, this issue is more complex than traditional sequencing issues, such as the traveling salesman problem (TSP). Dynamic programming is one of the widely used algorithms for such kinds of issue. However, when dealing with a large quantity of time nodes, due to the curse of dimensionality, the practicability will be limited when solving the model through this method. On the other hand, intelligence algorithms have been utilized to solve complex programming issues, for instance, genetic algorithm (GA), particle swarm optimization algorithm (PSO), ant colony optimization algorithm (ACO), etc. Considering the constraints of the model and the fact that the optimal sequence does not have much difference with each feasible sequence, the ACO algorithm is more suitable to solve the model as it has better convergence in terms of optimizing the sequence.

In the ACO algorithm, all artificial ants are placed at an initial position of a multi-dimension space at the beginning. The objective for these ants is to find the food’s position (the optimal solution). The objective function can be regarded as the food concentration to evaluate each position. During each iteration operation, each ant will select an orientation randomly and move in a specific step length to explore a new position, and then ants will be reallocated to a few best explored positions. In this way, as the explored region expands, the result will converge to a better solution. Finally, the optimal solution can be found.

As the target is to find the optimal sequence of time nodes, the positions in the ACO algorithm can be represented by sequences. A possible time node sequence is necessary since the initial position is very important for the ACO algorithm. Given that all the offloading stations do not offload batches, because the injecting plan is known, the batch interface can be traced and batch’s arrival at stations can be simulated accordingly. Thus, the sequence of time nodes when batches arrive at stations, the injecting flow rate changes, and study horizon’s beginning as well as end can be further calculated. The batch’s offloading starting moment is close to the one when the batch’s head reaches the station, and the finish time is close to one when the next batch’s head reaches the station, providing that the batch’s arrival is within the study horizon. The start of the offloading operation should be close to the head of the study horizon and the ending moment should be next to the end of the study horizon if the batch’s arriving time is beyond the study horizon. In this way, the initial time node sequence is generated. During each iteration operation, two time nodes will be selected randomly and the firstly chosen one is plugged after the second one, and then we judge whether this changed sequence can meet the formulas (7)–(13). If not, two new time nodes’ orders will be exchanged randomly until they meet those constraints. Then an LP model can be established and solved by the simplex method. Therefore, a detailed scheduling plan and the value of its objective function can be obtained. Sorting all the explored positions on the basis of the value of their objective function, ants are reallocated to a few of the best positions, awaiting the next round of relocation.

The structure of the algorithm is as follows:

• (1) To calculate the initial sequence and take it as the initial position of ants.

• (2) To make ants move randomly to generate new sequences.

• (3) According to those new sequences, establish the LP models and solve them by SM to obtain their objective function values.

• (4) Sorting all the explored positions on basis of their objective function values and allocating ants to a few of the best positions.

• (5) Repeat step 2 until the value of the objective function is less than the allowable maximum error or the iteration number is the maximum.

• (6) To output the optimizing result.

The flowchart of the algorithm is shown in Fig. 2.

Fig. 2

Flowchart of the algorithm

5 Example

In this section, two examples aiming at a certain real pipeline are given through the proposed model, using an Intel Core i7-4770k (3.50 GHz) computer with 8 parallel threads and MATLAB calculating software. In the first example, an operation case in summer is presented, in which all the demand of offloading stations is rational. In other words, there exists a promising solution that is capable of satisfying all stations’ offloading demands. In the second example, another example in wintertime is presented, in which an irrational demand has arisen. By virtue of it, the convergence of the model is demonstrated.

5.1 Basic data

Taking an oil products pipeline as the research object, if the batch input plan of the initial station and the oil-filled state in the pipeline at the initial moment and the demanded volume by each offloading station are known, the scheduling plan for the pipeline can be made in the studied horizon. The length of the pipeline is 112 km. This pipeline transports different types of gasoline and diesel. There are six stations: the initial station (IS), 1# offloading station (1#OS), 2# offloading station (2#OS), 3# offloading station (3#OS), 4# offloading station (4#OS), and the terminal station (TS). Table 1 shows the basic data of the pipeline.

Table 1 Basic pipeline data

Considering the hydraulic requirements, the flow rate of the pipeline between stations should be controlled within a certain range, as shown in Table 2.

Table 2 Allowable flow rate range of the pipeline segment between stations

According to the design pressure constraint, restrictions on equipment such as pumps, and the application range of flow rate meters in the offloading stations, there exists flow rate range constraints of the stations as shown in Table 3.

Table 3 Flow rate range of all stations

The ant colony algorithm parameters are assigned as follows: The number of ants is 50 and the maximum number of iterations is 100. Considering the slight computational and round-off errors, the maximum error is set at 5.

5.2 Example one

The starting time of the plan is 0 and the end time of the plan is set at 71.8 h. In summer, each offloading station gives the demanded volumes based on the market requirements. Combined with the oil-filled state in the pipeline at the initial moment, the offloading plan of each offloading station within the study horizon can be made. The sequence of the batch is 95# gasoline–92# gasoline–0# diesel–92# gasoline–95# gasoline–92# gasoline. There is a mixed oil interface between 95# and 92# gasoline in the pipeline at the initial moment, at a location of 18.5 km away from the initial station. Table 4 shows the volume of the new batch input at the initial station:

Table 4 Example one: first station input volumes of the new batches

Table 5 shows the volume coordinate of each batch calculated. The volume coordinates of old batches are positive values, and the volume coordinates of new batches are negative values.

Table 5 Example one: volume coordinate of each batch

Table 6 shows the inputting flow rate of the initial station.

Table 6 Example one: input flow rate of the first station

Table 7 shows the volume of each batch that offloading stations demand.

Table 7 Example one: each offloading station’s demanded volume of each batch

With known conditions and model above, the offloading plan can be made as shown in Table 8.

Table 8 Example one: offloading plan of each station

Table 9 shows the total offloading amount of each batch and the deviation between each batch’s offloading volume and the demanded volume.

Table 9 Example one: offloading volume and deviation

As Table 9 shows, the deviation between the demanded and offloading volume is small enough to be accepted. The offloading volumes normally satisfy the volumes demanded of each station.

The batch transportation diagram, which is shown in Fig. 3, is based on the initial state as well as the inputting and offloading plans. In the diagram, the 95# gasoline is in blue, while the 92# gasoline is red, and 0# diesel is green. The rectangles on the left side of vertical axis denote the initial state of the pipeline. The rectangles on the horizontal axis represent the injection plan at the initial station. As for other rectangles in the diagram, they define the offloading plans. The quantity of offloading and injection flow is in accordance with the width of these rectangles. The black line in the diagram represents the batch interface’s migration process. As Fig. 3 shows, each offloading operation is conducted within an allowable time range.

Fig. 3

Example one: batch transportation diagram (blue the 95# gasoline; red the 92# gasoline; green the 0# diesel)

Figure 4 shows the flow rate in each pipeline segment. All the intermediate stations are only allowed to offtake instead of injecting, since the studied pipeline is one with single-source and multiple distributions. Thus, the flow rate between 4#OS and TS is the minimum one along the pipeline. As illustrated in formulas 17 and 18, the minimum flow rate should be adjusted if there is an interface between gasoline and diesel. During the periods from 13.27 to 41.27 and 44.07 to 71.80 h, there exists a diesel oil–gasoline interface in the pipeline. Therefore, during these periods the lower limit of flow rate is 50 m³/h. From Fig. 4, the flow rate of the terminal station at any time is no less than the lower limit.

Fig. 4

Example one: flow rate in each pipeline segment and its lower limit

Because the demands of each offloading station are satisfied, the value of the objective function is less than the maximum error in the iteration process, and hence the computing program stops. The computational results of this example are shown in Table 10.

Table 10 Computational results

5.3 Example two

For the same pipeline, a scheduling plan lasting 71.8 h in winter season is made. Each offloading station gives the demanded volume of specific batch based on the market. The sequence is 95# gasoline–92# gasoline–−10# diesel–92# gasoline–95# gasoline–92# gasoline. There is a mixed oil interface between 95# and 92# gasoline in the pipeline at the initial moment, at a location of 65 km away from the initial station. Table 11 shows the volume of the new batches input at the initial station:

Table 11 Example two: first station input volumes of the new batches

Table 12 shows the volume coordinate of each calculated batch.

Table 12 Example two: volume coordinate of each batch

Table 13 shows the inputting flow rate of the initial station.

Table 13 Example two: First station input flow rate

Table 14 shows the volume of each batch that each offloading station demands.

Table 14 Example two: each offloading station’s demanded volume of each batch

With known conditions and model above, the offloading plan can be made as shown in Table 15.

Table 15 Example two: offloading plan of each station

Table 16 shows the total offloading amount of each batch and the deviation between each batch’s offloading volume and the demanded volume.

Table 16 Example two: offloading volume and deviation

As the sum of the fifth batch’s demand volumes is larger than the total input volume of the fifth batch, this means that the demand is not reasonable. The results show that there exists a big deviation between the actual offloading volume and the demanded volume of the fifth batch at 4#OS, in accordance with the real situation. The offloading volumes of the rest of the batches all meet the demanded volumes.

The batch transportation diagram is shown in Fig. 5. In the diagram, the −10# diesel is in yellow. All the offloading operations are conducted within a reasonable time range.

Fig. 5

Example two: batch transportation diagram (−10# diesel is in yellow)

The diesel oil-gasoline interfaces exist in the pipeline during the period from 14.18 h to 69.98 h. Therefore, the lower limit is 50 m³/h. For other periods, the lower limit is 30 m³/h. Figure 6 shows the flow rate in each pipeline segment. As shown in Fig. 6, the flow rate along the pipeline is always within the reasonable range.

Fig. 6

Example two: flow rate in each pipeline segment and its lower limit

The computational results of example two are shown in Table 10. Since the objective function has no zero-solution in this example, the calculation runs until it reaches the maximum allowable iteration number. Thus, the convergence and stability need to be further discussed. Using same data in example 2, the calculation is repeated four times, and the iterating processes are shown in Fig. 7. The calculations, converging until they have iterated for respectively 61, 66, 69, 72, and 77 times, all converge to the same value in the end. The stability and convergence are demonstrated.

Fig. 7

Example two: process of iterations

6 Conclusions

The proposed model considers the batches’ arriving time as time nodes and takes the influence of mixed oil interface on minimum flow rate into account, which increases the difficulty of calculation. Thus, a continuous-time expression scheduling model is built and then a hybrid algorithm consisting of ACO and SM is applied to solve the model. As shown in the examples, the calculation speed is relatively fast although the model is large. The scheduling plan obtained in this model has minimum deviation from the demand, which is also in accordance with the actual field situation, At the same time, the model’s convergence and stability are verified. Therefore, the accuracy, efficiency, and practicability of this model are evident, and the results can provide guidance to the scheduling plan for the actual operation. In further research, pipeline’s hydraulic calculation will be taken into consideration in order to enhance the model’s practicability and accuracy.