Abstract
Accurate fluid flow simulation in geologically complex reservoirs is of particular importance in construction of reservoir simulators. General approaches in naturally fractured reservoir simulation involve use of unstructured grids or a structured grid coupled with locally unstructured grids and discrete fracture models. These methods suffer from drawbacks such as lack of flexibility and of ease of updating. In this study, I combined fracture modeling by elastic gridding which improves flexibility, especially in complex reservoirs. The proposed model revises conventional modeling fractures by hard rigid planes that do not change through production. This is a dubious assumption, especially in reservoirs with a high production rate in the beginning. The proposed elastic fracture modeling considers changes in fracture properties, shape and aperture through the simulation. This strategy is only reliable for naturally fractured reservoirs with high fracture permeability and less permeable matrix and parallel fractures with less cross-connections. Comparison of elastic fracture modeling results with conventional modeling showed that these assumptions will cause production pressure to enlarge fracture apertures and change fracture shapes, which consequently results in lower production compared with what was previously assumed. It is concluded that an elastic gridded model could better simulate reservoir performance.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
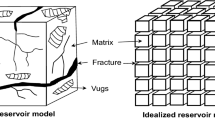
To handle the complexity of reservoir heterogeneity which comes from natural fractures, the nature of the reservoir should be determined in advance (Agar and Hampson 2014). The complexity in reservoir modeling either comes from reservoir characterization (e.g., heterogeneity and anisotropy in permeability) or from the process of oil recovery (e.g., capillarity, gravity and phase behavior), or from both (Kresse et al. 2013). To resolve this complexity, a dual-porosity model (Nie et al. 2012) and recently a triple-porosity model (Huang et al. 2015; Sang et al. 2016) have been introduced to simulate fractured reservoirs. Despite many useful features of the dual-porosity model, it cannot provide reliable results in reservoirs in which fractures do not intersect (Karimi-Fard and Firoozabadi 2003). Applicability of the classic double-porosity model with a constant shape factor to low-permeability reservoir simulation is questionable (Cai et al. 2015). It also does not describe discrete fractures, which are the main source of challenge in naturally fractured reservoirs (Chen et al. 2008; Presho et al. 2011; Soleimani 2016a). History matching of naturally fractured reservoirs becomes more challenging particularly when these models are represented using discrete fracture network (DFN) models in carbonate rocks (Bahrainian et al. 2015). DFN models were also represented using generally unstructured grids to achieve high degrees of geological realism. Karimi-Fard et al. (2004) introduced an efficient discrete fracture model applicable for general-purpose reservoir simulators. Accurate representation of each individual fracture requires use of unstructured grids which can consider effects of the fracture aperture (Mi et al. 2014). Jiang and Younis (2015) implemented a lower-dimensional DFN model based on unstructured gridding for handling complex fracture geometry in simulated formation. Although DFN models have several advantages, they cannot be used directly with standard history matching techniques for strongly heterogeneous reservoirs with complex fracture geometry (Yan et al. 2016). Figure 1a shows a real structure and shape of different porosities in a limestone cube. Figure 1b, c shows conventional dual-porosity and DFN approaches that model the realistic fractures in a limestone fractured reservoir. In such models, if in the course of history matching, more fractures are added, moved or deleted, the model must be re-gridded from the beginning (Salimi and Bruining 2010).
Dual-porosity conventional model a actual porosity model, b sugar cube representation and c discrete fracture model for a fractured reservoir (Biryukov and Kuchuk 2012)
In this study, we try to increase realism of the fracture model by considering shape of the fracture and the variation of its properties through production and pressure regime change in fluid flow procedure. Fracture characteristics which change through time of production are included in elastic properties of fractures. The elastic gridding scheme was introduced in this study into the fracture modeling scheme to handle heterogeneity of a complex reservoir. This approach was then applied on a fractured limestone reservoir in southwest Iran. Results of the application of the proposed strategy for fracture modeling in the study field show production of more water in comparison with conventional fracture modeling result.
2 Fracture simulation methods for carbonate rocks
The intersection relationships of fractures are probably very complex in a realistic DFN model (Zhang 2015). Bisdom et al. (2016) investigated impact of in situ stress and outcrop fracture geometry on hydraulic apertures in reservoirs. They stated that each fracture network containing fractures is created of at least one fracture set, but is not necessarily limited to it. By proposing a fracture propagation model using multiple planar fractures with a mixed model, Jang et al. (2016) stated that there is a large discrepancy in reservoir volume stimulation, because of a number of intersections of fracture connectivity. Heffer and King (2006) introduced a spatial correlation function of fractures as displacement strain vectors using renormalization techniques in representation of stochastic tensor fields for strain modeling. Masihi and King (2007) applied this method to generate fracture networks based on the assumption that the elastic energy in the fractured media follows a Boltzmann distribution. Koike et al. (2012) used geostatistical fracture distribution and fracture orientation (strike and dip) in simulation of the fracture system to estimate the hydraulic conductivity. Bisdom et al. (2016) also proved that the fracture orientation and the associated hydraulic aperture distribution have stronger impact on equivalent permeability than length or spacing. Thus, spatial correlation of fractures is the most important parameter in any fracture networks model or gridding scheme. To make this correlation between fractures, various methods are introduced for assigning precise values from fracture characteristics to the model of fractures. Among them, various approaches of using outcrop fracture characteristics such as fracture spatial distribution, length, height, orientation, spacing and aperture are widely used for model regularization (Wilson et al. 2011; Hooker et al. 2012). Lapponi et al. (2011) used outcrop data to construct a 3D model in a dolomitized carbonate reservoir rock from the Zagros Mountains, southwest Iran. Lee et al. (2011) studied the spatial fracture intensity effect on hydraulic flow in fractured rock. They used outcrop for simulation of spatial fracture intensity distribution. They have built three spatial fracture intensity distribution models and showed that flow vectors are strongly affected by spatial fracture intensity. They also proved that the higher the fracture intensity, the higher flow velocity. Boro et al. (2014) presented a workflow to construct an upscaled fracture model based on outcrop studies in a carbonate platform. It is important to note that fractures in the outcrop might have been affected by surface processes like weathering and stress release. The overall analysis, however, can help to constrain possible scenarios on fracture populations that may be relevant to the subsurface reservoir. Malinouskaya et al. (2014) illustrated a method to rapidly estimate permeability of a fracture network, using fracture data from outcrops of a Jurassic carbonate ramp. The method proposed by Maffucci et al. (2015) used outcrop data combined with a discrete fracture network (DFN) model to increase the reliability of fracture system characterization in the case of limited data for carbonate rocks. Connectivity of fracture networks in carbonate rock is dependent on orientation, size distribution and densities of the different fracture sets. These parameters also define size of the blocks enveloped by fractures (i.e., the matrix block size), which is generally used to model transfer of fluids between the matrix and fractures (Wennberg et al. 2016). To incorporate interaction between the matrix and fractured media, Huang et al. (2014) divided the fractured porous medium into two non-overlapping subdomains. One domain has a continuum model in the rock matrix, and the other, in deep fractured and fissure zones, is described by a DFN model. Then, they coupled these domains to simulate groundwater flow in their case study. However, Boro et al. (2014) stated that in general, fracture intensities, apertures and their intrinsic permeability would have more significant impact on the permeability of the field. Fracture shape and orientations are more important in affecting connectivity. Bisdom et al. (2016) also showed the strong importance of fracture orientation and associated hydraulic aperture distribution on equivalent permeability. In general, it is widely believed that fluid flow is affected by heterogeneities at all scales, from millimeter scale (porosity) to kilometer scale (Shekhar et al. 2014). In the present work, field evidence of different solutions and fractures in limestone is used to certify the nature of elasticity of fractures through time of production.
The proposed strategy also exposes incorrect assumptions in conventional fracture modeling, which has a great impact on history matching studies. Afterward, the concept of allocating each fracture to a fracture set and subsequently to a fracture network was considered by comparing the formation outcrop and considering the elasticity nature of the fractures, which comes from formation fluid pressure and/or regional stress in modeling.
3 Elastic fracture modeling
Dennis et al. (2010) stated that the physical structure properties and complexity of fracture characterization both have a significant effect on fluid flow in fractured rock. Thus, they proposed that the fracture zone should be characterized fully before simulation. Wang et al. (2016) studied the flow stress damage and reservoir responses to injection rate under different DFN-connected configuration states. Their results proved significant influence of the hydraulic pressure flow on the properties of hydraulic fractures. Generally, Gan and Elsworth (2016) stated that in any fracture modeling for complex reservoirs, the upcoming assumptions should not be neglected: Fractures initiate from flaws and the process is controlled by the elastic stress around them, the material surrounding the flaws can be viewed as continuum media, and individual flaws are spaced widely enough so that stress anomalies associated with each do not overlap. These assumptions are necessary for analytical formulation and therefore will be retained in the analysis, although a slight degree of plasticity is allowed (Wang and Shahvali 2016). However, in any elastic gridding, it should be kept in mind that a fracture is initiated when the maximum stress concentration occurring on the critical flaw boundary reaches the strength of the material which surrounds the flaw. Fracture extension also occurs from the tensile and not the compressive stress concentrations under both tensile and compressive loading. Fan et al. (2012) stated that microcracks induced by the excess oil/gas pressure may propagate and form an interconnected fracture network. This indicates also that during production, different pressure regimes could change characteristics of fractures. Not only might they be closed in the case of pressure drop or reservoir depletion, but they also might be widened due to high production rates and excessive pressure of fluid flow to the walls of fractures or cracks. It also might create fractures which make connections between vugs, while cracks could be widened and/or become fractures. Fan et al. (2012) investigated mechanism of fracture propagation by a linear elastic model. They have shown that critical crack propagation takes place if the intensity of the induced stress reaches the fracture toughness of the reservoir rock. On the other hand, subcritical crack propagation occurs in the rock when the stress intensity has not reached the fracture toughness of the reservoir rock, but exceeds a threshold value, which is usually a fraction (e.g., 20%–50%) of fracture toughness of the reservoir rock. This conclusion states how important it is to consider fracture–matrix interaction and/or boundary condition of fractures in accurate flow simulation. Subsequently, Hassanzadeh and Pooladi-Darvish (2006) considered the time variability of the fracture boundary condition by the Laplace domain analytical solutions of the diffusivity equation for different geometries of fractures in constant fracture pressure through a large number of pressure steps. Guerriero et al. (2013) proposed an analytical model that could pave the way to a full numerical model allowing one to calculate the pore pressure within fractures, at several scales of observation, in a reasonable time. They also suggested that the model also allows one to obtain a better understanding of the hydraulic behavior of fractured porous rock. However, not only the pressure regime change, but other factors affecting fracture shape and apertures could be accounted for by considering elastic behavior of fractures in the model construction during gridding and throughout production history matching investigation.
Bisdom et al. (2016) stated relationships between the fracture geometrical parameters and some other parameters such as the stress applied in the medium. However, for this specific case, accurate relationship between degree of elasticity and fracture’s aperture would be defined only by core analyses in a wide range of applied stresses from pore fluid to the walls of fractures. However, previous studies have shown that this relationship is linear in a narrow range of applied stress (Bisdom et al. 2016).
Elastic gridding is a variant of the grid optimization-based technique on a length functional with a non-Euclidean metric tensor. In creation of the grid, it is considered to be a system of springs connecting neighboring grid vertices along the grid lines. On the other hand, the problem of grid optimization is thereby reduced to a problem of elasticity and the problem of translating grid optimization criteria into criteria for assigning spring constants to grid lines. After having assigned values to the spring constants of the elastic grid, the grid vertex positions can be found by solving the equilibrium equation for the elastic system. In case of reservoirs with parallel flow channels, strong pressure regime change will cause fracture apertures to become wider to some extent. However, not all the fractures in carbonate rocks, regardless of their sizes, are responsible for fluid flow. Observations of fractures in core and outcrop indicate that flow in open fractures in carbonate rock tends to be channeled rather than through fissures. Most of the flow takes place along a few dominating channels in the fracture plane, whereas most of the fracture plane is not effective for fluid flow. Wennberg et al. (2016) stated that the effect of channeled flow should be taken into account during evaluation of fractured carbonate reservoirs and building dynamic flow models. However, the consequence of the aperture variation is that the fluid flow in fractured carbonate reservoirs will tend to be channeled instead of that of fissure-type flow, which is the assumption in most flow simulators (Wennberg et al. 2016). Figure 2 shows different solutions and fractures of the Sarcheshmeh limestone formation outcrops in the Shahrood area, Iran. Major fractures shown by black lines (which are considered as the pathway of fluid) are oriented normal to the maximum stress direction, while red lines show minor fractures crosscut the major ones. The nature of major fractures is that these are the main fluid flow channels, while minor fractures are not necessarily important for that purpose. This is a typical fracture pattern in limestone reservoirs in Iran. This pattern would make only those parallel fractures, which are the only pathway of fluid flow, undergo effects of pressure regime change through high rate production. This effect will cause aperture widening, which changes the shape of the fracture, the parameter that is going to be considered in fracture modeling in this study. Another high production rate effect in such reservoirs is connecting vugs by propagation and/or widening of fractures. Lapponi et al. (2011) showed that vuggy porosity seems to increase porosity only locally and to a limited extent, developing a non-connected pore network. However, fracture propagation under pressure or high production rate would make connections between vugs. This is not an important effect in production, since these connecting fractures show small apertures, not appropriate for fluid flow. Figure 3 shows an outcrop of the same formation in the same location and an example of vugs connected by fracture propagation under pressure.
Outcrop of the Sarcheshmeh Formation, same location as in Fig. 2, Iran. a Various porosity types in the outcrop, b connected and non-connected vugs and worm channels (red lines)
However, in this study reservoir, the thermal fracturing is not planned in the master development plan of the field and the production history of the reservoir also shows some degree of overpressure fluid in the first periods of initial production, when accurate data were not available. Thus, neither the thermal fluid injection nor the fluid overpressure was considered here. The majority of fractures that we had in the study reservoir were of the type of fractures shown in Fig. 2.
As was previously mentioned, some fractures connect vugs, which results in fracture propagation and/or fracture shape. All the main fractures responsible for fluid flow are modeled as flat planes in fracture modeling and are fixed through the production simulation procedure. However, in the proposed strategy, these fractures will change in shape through history matching. This is what we called the elastic gridding modeling. Figure 4 shows an example of an elastic grid and the elastic nature of fractures in modeling. As it was previously mentioned, fracture properties might change through high pressure regime change.
a Conventional model of matrix and fractures (Karimi-Fard 2013). b an example of change in shape of a fracture modeled by elastic fracture modeling, c another change in shape and d change in fracture aperture modeled by elastic fracture modeling
The more the pressure regime changes in a short time, the more this will cause more change in the shape of fractures. Figure 4a shows a conventional model of fractures. Figure 4b, c illustrates shape change in the same fracture after high pressure regime change, modeled by elastic fracture modeling. Figure 4d also shows change in fracture aperture modeled by elastic fracture modeling. However, the most important parameter that changes the permeability of the reservoir rock is the dilation of fractures. Unlike other fracture parameters, the dilation degree of a fracture under stress cannot be described from core sample tests. Clearly, long fractures cause the core to fall apart during the experiment. Core recovery is also very poor in intensely fractured intervals, and the stress release when the core is taken to the surface will affect the observed apertures (Wennberg et al. 2016). Use of electrical image logs also suffers from uncertainty if the absolute aperture is large. This problem would be boosted if we want to accurately measure the dilation of the fracture. Therefore, it necessitates that the relationship between aperture dilation and applied stress is defined by numerical analysis and other permeability tests in various conditions. Taron et al. (2014) tested fracture dilation in a geothermal system.
However, Min et al. (2004) and Farahmand et al. (2015) derived relationships between aperture dilation and applied stress. Min et al. (2004) studied completely all cases and we used the results that they derived in their complete study. Min et al. (2004) have stated that the exact extent of shear dilations of fractures can only be identified through numerical experiments. Their experiments showed that on the one hand, equivalent permeability decreases with increase in stresses, when the differential stress is not large enough to cause shear dilation of fractures. On the other hand, the equivalent permeability increases with the increase in differential stresses, when the stress ratio was large enough to cause continued shear dilation of fractures. In this case, shear dilation is the dominating mechanism in characterizing the stress-dependent permeability. They have proved that the maximum contribution of dilation is more than one order of magnitude in permeability. Thus, we have used this role in our study for fracture dilation.
Since the elastic system is attached to the boundary of the model, it would not collapse. For both convex and concave domains, the elastic method is also very flexible in fracture geometry and robust to system collapse (Fig. 5). Figure 5 shows an example of a conventional grid, and Fig. 5b illustrates only a schematic of the same system but with elastic grids. Since we do not exactly know how the grids would differ during simulation, the applied pressure and elastic properties of rock would define that thus Fig. 5b is an example of any shape of grids with the unique geometry. Figure 6a depicts a simple case of conventional fracture modeling in a medium. Figure 6b shows example of a low allowed degree of elasticity and/or low pressure regime change, and Fig. 6c exhibits a sample of high degree of elasticity allowed in the model due to possible high production rates with high fluctuation in the pressure regime. Every parameter that is going to model the elastic behavior of a fracture should be defined by numerous experimental tests on core samples.
a Conventional modeling in which fractures were modeled by flat planes with no change in shape through production (Karimi-Fard 2013), b Low degree of elasticity allowed, and c high degree of elasticity allowed in elastic fracture modeling in the proposed strategy
The pore fluid effects needed to calculate elastic properties of fluid-saturated rock could be obtained also in each study from the simulation case. However, in this study, we did not have enough data to derive an implicit model for elastic behavior simulation of a fracture. However, it is not only the matter of data, but it is about the matter of accurate and implicit relationship between the applied stress and strain of the medium and elastic properties and behavior of fractures. Thus, in this study, we used an explicit relationship between the stress applied to a fracture and the allowed degree of elasticity of the fracture. Consequently, we should define a maximum degree of change in shape that we consider for a fracture and the value of changes in curvature of the fracture. The former is defined based on the Bulk and/or Young’s modulus of the rock. For hard rocks, the lowest grade of change in shape is allowed and it is vice versa for soft rocks. The latter needs more explanation. At first, it should define whether curvature has any effect on permeability change or it is only a fracture shape change, without effect on permeability. According to Fig. 4, it changes the permeability only if both sides of the fracture experience convex curvature, which increases the permeability. In case of same convexity or concavity of fracture walls, no changes in permeability would happen. In this study, we assumed the first case for our fractures, as shown in Fig. 4d. The degree of curvature is defined based on the toughness of rock. Although the exact degree of convexity and curvature of the fracture wall should be defined by core sample test, it could be defined as a linear function of applied stress for medium to rocks.
4 The study reservoir
The study reservoir is an extensively faulted anticline 74 km long and 6–8 km wide, located in the Dezful Embayment, southwest Iran (Fig. 7a). The study anticline is an asymmetrical anticline with a NW–SE trend and a sinuous axis. The target formation is a prominent carbonate unit of Oligocene and early Miocene age called the Asmari Formation. This formation in the study field contains limestone, dolomite and minor marl and shale (Abdollahie Fard et al. 2006). The study field was divided into five sectors based on geological and engineering data. Most of the boundaries of these sectors are in agreement with faults. These sectors are depicted in the underground contour (UGC) map of the target formation shown in Fig. 7b. It should be mentioned that the UGC map in Fig. 7b was obtained from time–depth conversation of 3D migrated seismic data with well top adjustment supervision. However, an advanced migration algorithm is needed for imaging in such complex media (Soleimani 2016b). Limited lateral communication, the presence of faults acting as barriers, hydrodynamic system and imbalanced offtake have caused the Asmari Formation to be divided into several compartments (Sherkati and Letouzey 2004). The oil production from the study reservoir has been very imbalanced mainly because early development took place in the central and northwestern part of the field, where oil column was thicker and the wells had higher productivity. In spite of extensive fracturing of the Asmari Formation, a pressure differential has developed in the gas zone across the field due to imbalanced oil and gas production.
a Location of the study field is shown by the rectangle (Soleimani and Jodeiri-Shokri 2015). b Zonation of the study field and underground contour map (UGC) of top of the Asmari Formation
4.1 Petrophysical data
Limited cores were cut from the Asmari Formation for routine and special analyses. Total length of cores cut was 550 m out of which 421 m was recovered. The mean porosity of plugs cut from 421 m of cores in six wells was 9.8%, while 21% of samples have porosities less than 4% and only 3% of samples have porosity more than 20%, implying that the Asmari Formation is a low porosity reservoir (Hoseinzadeh et al. 2015). The median permeability of cores was calculated to be 0.43 mD with 60% of samples having permeability of less than one milli-darcy, indicating a very low permeable carbonate rock matrix. Production logging tools (PLT) logs were recorded in 15 oil wells and in 5 gas wells. Reviewing of the PLT log results indicates that distance between flowing intervals varies from 1 m to the maximum of 44 m. This indicates an active mechanism of fracture production in this field.
5 Zonation and fracture study
Porosity distribution in the Asmari Formation is very diverse. Therefore, division of this formation into several zones and subzones is unavoidable. Based on petrophysical and petrographic characteristics, the target formation was divided into seven different oil-bearing zones with the water column as zone 8. Consequently, zones 1, 2, 6 and 7 were divided into two subzones (Table 3 of Appendix). From the study of cores, some parameters were extracted such as type of fracture; spacing (number of fractures per meter); dip of fractures (relative to the core axis in the core description tables and relative to horizontal in the interpretation); width of fractures measured in laboratory conditions; and filling mineral type. Among these parameters, type of fracture and filling mineral type are classified and coded as shown in Tables 1 and 2, respectively. Occurrence of anomalous losses of mud during drilling is often the first indirect indication of the existence of a naturally fractured interval. Comparison of the mud loss rate in different wells may give the intensity of fracturing in different parts of the reservoir (Xia et al. 2015).
In spite of the fact that there are many parameters that can affect the mud loss rate and inherent errors in the results, such as mud weight, weight on bit, stroke per minute of pumps and rock type, the mud loss rate is one of the most important parameters in indirect observations of fractures. Other information that could be useful in fracture studies includes productivity index (PI), PLT data and maximum daily flow rate. Production rate is usually dependent on the extent of fracturing of the formation in this low-matrix permeability reservoir (Xia et al. 2015a). Therefore, higher production rates correspond to a more extensive fracturing of the strata in the well location (Fig. 8). To determine the fractured zones within the reservoir, a radius of curvature method (Yoshida et al. 2016) was used. The 3D curvature model was not shown here, but it was obtained from 3D migrated seismic data and application of maximum and minimum curvature attributes. After applying this method to the target formation, we have concluded that the most common types of fracture are type 1 (cross-axial tensional and conjugate shear fractures) and type 2 (axial tensional and conjugate shear fractures). Interpretation of mud losses, daily flow rate, PI, PLT and other data suggest that sector 1N and partially sector 4 are highly fractured. Fracturing in sector 3 is relatively intensive and not extensive in sector 1S. Figure 9a shows the fracture quality map, and Fig. 9b illustrates strain distribution map on top of the target formation. The strain regime here is of shortening type. The mud loss, PI and PLT integration was performed by finding the relationship between fracture quality index and these three parameters in GIS media.
6 Elastic fracture model generation
All the required data for elastic fracture and geological model construction were collected. Petrophysical data contain two series of net-to-gross (NTG) ratio, porosity and water saturation related to each horizon. Monte Carlo statistical simulation was used to obtain a 3D distribution of fracture spacing density and, consequently, matrix block size. Input probabilistic frequencies were scaled in such a way as to have the mode of matrix block height distributions changing from approximately 3 m at the top to approximately 6 m at the bottom of the Asmari Formation, respectively. Matrix–fracture communication was defined by considering elasticity behavior of fractures. At that stage, matrix and fracture properties were considered as first approximations to be modified during history matching. After construction of the model, a geological model containing 633 × 451 × 12 (3,425,796 cells) mesh cells was prepared including all faults. Configuration of the elastic gridding model was based on fault traces and a contour line of −2600 m from the structure map on top of the Asmari Formation. The elastic grid has 133 blocks in one direction and 17 blocks in the other direction with 30 layers. The elastic grid structural elevations were obtained from underground contour maps and verified against well picks. Gross thickness of zones (subzones) was based on isopach and isochore maps. Porosity versus normalized depth profiles were used as guides to split zones (subzones) into 30 layers. Figure 10 displays a map view of the elastic grids on the top of the target formation. Zone (subzone) matrix porosity and NTG ratio were obtained from geologic maps and then downscaled to layers based on the porosity–normalized depth profiles.
Matrix permeability was based on matrix porosity and permeability–porosity correlations. A fracture porosity distribution was generated based on the fracture porosity map. This map was horizontally scaled according to the qualitative map of fracture intensity. It was vertically scaled also in accordance with empirical correlations reflecting reduction in fracture intensity from top to bottom of the Asmari Formation (Fig. 11). Well trajectories and perforation, production, and static pressure histories were incorporated in the model. Sporadic information about salt and/or water production was only available for a limited number of oil wells. Individual well gas/oil ratios were found to have resulted from prorating rather than from measurements; on this basis, they were excluded from history matching.
6.1 Model initialization
Providing the model with initial distributions of water saturation, reservoir pressure and hydrocarbon components were the subject of this part of the study. To obtain distribution models of these characteristics, we took seven available drainage capillary pressure curves (not shown here) and scaled them in accordance with the following equation:
where R w is the formation water resistivity, R t is the formation resistivity, and w = f(R w, R, ø). The right side of Eq. (1) was derived from well logs and averaged for different regions and zones (subzones). To have a reasonable value for the right side of equation, a primary blocking step of the target formation was performed for averaging in each block. Subsequently, a weighted averaging based on the thickness of each zone/subzone was performed. Due to the large number of obtained maps with different blocking approaches and based on different interpretation of the averaged map result with the help of geological and hydrological data, the maps are not shown here. Then, S wi was estimated from Eq. (1) for each simulation model elastic grid block based on its matrix porosity. The resulting S wi values were introduced in the model as connate water saturation. To obtain different oil–water contacts (OWC), two aquifers and six equilibration regions were introduced into the model (Fig. 12). Two analytical aquifers were introduced instead of one aquifer, while the northwest part of the reservoir was completely disconnected from any analytical aquifer. Aquifer 2 is stronger than the other aquifers. The aquifers are separated by faults, while six OWC zones are controlled by the pressure regime of the field. The water saturation in the matrix also could affect the OWC in different zones.
Thus for model initiation, the pressure regime and the matrix water saturation (besides the fracture water saturation) should be introduced as the initial condition for model running. Figure 13 shows the pressure regime and matrix water saturation in the model.
6.2 Preliminary simulation
The study field’s production history is complicated, and the aquifer strength varies from the southeast to the northwest of the field. Thus, introducing the elastic behavior of fractures into the model was proposed here to realize the history matching of the reservoir production.
However, running time was a significant issue right from the beginning of the matching process. Only using advanced hardware (a total of 12 CPUs of 3 GHz each) and implementing extensive debugging allowed the reduction of the running time for a history match to nearly 75 h. In the first step, the conventional history matching objectives in the traditional gridded model showed the entire field’s solution of gas production and water production only in the oil wells located southwest of the field. To introduce the elastic behavior of fractures into the model, initial global modifications involved elevating the aquifer permeability, elevating fracture permeability in x direction by a factor of 10 and reducing fracture permeability in z direction by a factor of 10 to compensate for the elasticity of microfracturing observed in the cores. Examination of elastic model runs showed that oil flow from matrix to fractures should be increased to match water and gas production from the oil wells. Elevating of this oil transfer was done by modifying the imbibition capillary pressure. Individual oil well modifications included changing capillary pressure curves assigned to the matrix grid blocks surrounding the well, varying the height of matrix blocks, modification of the pore volume of initially oil- and gas-saturated grid blocks and modification of the fracture permeability in x, y and z directions. Figure 14 shows the conventional and elastic fracture water saturation model. As it can be seen on the elastic fracture model, wells located in the southeast (SE) of the field may produce more water. This is due to the increase in cracks and/or fracture apertures, which means previous small cracks were filled with water. Figure 15 shows elastic and conventional models of fracture oil saturation. Again, the southeast (SE) part of the field does not produce more oil after a while according to the elastic modeling results. This phenomenon is less observed for gas saturation. Figure 16 shows result of elastic and conventional fracture modeling. As a result, change in shape of fractures, (increasing aperture) would replace oil by gas in the vicinity of oil-gas contact. This is obvious in Fig. 16.
7 Conclusions
There are many problems in fractured reservoirs that may require new approaches in fracture modeling based on advanced concepts. Some problems cannot be simplified beyond a certain limit. The complexity, scale and uncertainty of natural systems are the primary reasons for most of the modeling difficulties which have to be handled.
The objective of this work was to develop a prototype workflow for history matching in naturally fractured reservoirs. This concern is also with the problem of generating more realistic computational grids for reservoir simulations. Here we face the particular problems connected to the complexity of the reservoir. The proposed strategy combines the accuracy of fracture modeling with the efficiency of elastic gridding. Elastic gridding is very simple, and in principle, the method should be well suited for weighing between mutually conflicting optimization criteria with highly nonlinear and discontinuous cost functions. The strategy was applied on a complex reservoir from southwest Iran. The strategy was observed to be reasonably effective in achieving field-level agreement in total oil and water production rates. Aperture increase in cracks will mean they will be filled by water, while it replaces gas by oil in the vicinity of the gas oil contact. Thus, elastic fracture modeling shows that more water will be produced compared to what was assumed by conventional fracture models, which do not take into account fracture properties change through production.
References
Abdollahie Fard I, Braathen A, Mokhtari M, Alavi A. Interaction of the Zagros fold–thrust belt and the Arabian-type, deep-seated folds in the Abadan plain and the Dezful embayment SW Iran. Pet Geosci. 2006. doi:10.1144/1354-079305-706.
Agar SM, Hampson GJ. Fundamental controls on flow in carbonates: an introduction. Pet Geosci. 2014. doi:10.1144/petgeo2013-090.
Bahrainian SS, Daneh Dezfuli A, Noghrehabadi A. Unstructured grid generation in porous domains for flow simulations with discrete-fracture network model. Transport Porous Media. 2015. doi:10.1007/s11242-015-0544-3.
Biryukov D, Kuchuk FJ. Transient pressure behavior of reservoirs with discrete conductive faults and fractures. Transport Porous Media. 2012. doi:10.1007/s11242-012-0041-x.
Bisdom K, Bertott G, Nick HM. The impact of in situ stress and outcrop-based fracture geometry on hydraulic aperture and upscaled permeability in fractured reservoirs. Techtonophysics. 2016. doi:10.1016/j.tecto.2016.04.006.
Boro H, Rosero E, Bertotti G. Fracture-network analysis of the Latemar Platform (northern Italy): integrating outcrop studies to constrain the hydraulic properties of fractures in reservoir models. Pet Geosci. 2014. doi:10.1144/petgeo2013-007.
Cai L, Ding DY, Wang C, Wu YS. Accurate and efficient simulation of fracture–matrix interaction in shale gas reservoirs. Transport Porous Media. 2015. doi:10.1007/s11242-014-0437-x.
Chen Y, Cai D, Fan Z, Li K, Ni J. 3D geological modeling of dual porosity carbonate reservoirs: a case from the Kenkiyak pre-salt oilfield Kazakhstan. Pet Explor Dev. 2008. doi:10.1016/S1876-3804(08)60097-X.
Dennis I, Pretorius J, Steyl G. Effect of fracture zone on DNAPL transport and dispersion: a numerical approach. Environ Earth Sci. 2010. doi:10.1007/s12665-010-0468-8.
Fan ZQ, Jin ZH, Johnson SE. Gas-driven subcritical crack propagation during the conversion of oil to gas. Pet Geosci. 2012. doi:10.1144/1354-079311-030.
Farahmand K, Baghbanan A, Shahriar K, Diederichs MS. Effect of fracture dilation angle on stress-dependent permeability tensor of fractured rock. In: 49th U.S. Rock mechanics/geomechanics symposium, San Francisco, 2015, ARMA-2015-542.
Gan Q, Elsworth D. A continuum model for coupled stress and fluid flow in discrete fracture networks. Geomech Geophy Geo Energy Geo Resour. 2016. doi:10.1007/s40948-015-0020-0.
Guerriero V, Mazzoli S, Iannace A, Vitale S, Carravetta A, Strauss C. A permeability model for naturally fractured carbonate reservoirs. Mar Pet Geol. 2013. doi:10.1016/j.marpetgeo.2012.11.002.
Hassanzadeh H, Pooladi-Darvish M. Effects of fracture boundary conditions on matrix-fracture transfer shape factor. Transport Porous Media. 2006. doi:10.1007/s11242-005-1398-x.
Heffer KJ, King PR. Spatial scaling of effective modulus and correlation of deformation near the critical point of fracturing. Pure Appl Geophys. 2006. doi:10.1007/978-3-7643-8124-010.
Hoseinzadeh M, Daneshian J, Moallemi SA, Solgi A. Facies analysis and depositional environment of the Oligocene-Miocene Asmari Formation, Bandar Abbas hinterland Iran. Open J Geol. 2015. doi:10.4236/ojg.2015.54016.
Hooker JN, Gomez LA, Laubach SE, Gale JFW, Marrett R. Effects of diagenesis (cement precipitation) during fracture opening on fracture aperture-size scaling in carbonate rocks. Geol Soc Lond Spec Publ. 2012. doi:10.1144/SP370.9.
Huang T, Guo X, Chen F. Modeling transient flow behavior of a multiscale triple porosity model for shale gas reservoirs. J Nat Gas Sci Eng. 2015. doi:10.1016/j.jngse.01.022.
Huang Y, Zhou Z, Wang J, Dou Z. Simulation of groundwater flow in fractured rocks using a coupled model based on the method of domain decomposition. Environ Earth Sci. 2014. doi:10.1007/s12665-014-3184-y.
Jang A, Kim J, Ertekin T, Sung W. Fracture propagation model using multiple planar fracture with mixed mode in naturally fractured reservoir. J Pet Sci Eng. 2016. doi:10.1016/j.petrol.02.015.
Jiang J, Younis RM. Numerical study of complex fracture geometries for unconventional gas reservoirs using a discrete fracture-matrix model. J Nat Gas Sci Eng. 2015. doi:10.1016/j.jngse.2015.08.013.
Karimi-Fard M, Firoozabadi A. Numerical simulation of water injection in fractured media using discrete-fracture model and the Galerkin method. SPE Reserv Eval Eng. 2003. doi:10.2118/83633-PA.
Karimi-Fard M, Durlofsky LJ, Aziz K. An efficient discrete fracture model applicable for general-purpose reservoir simulators. SPE J. 2004. doi:10.2118/88812-PA.
Karimi-Fard M. Modeling tools for fractured systems: gridding, discretization, and upscaling. Stanford University. 2013. http://cees.stanford.edu/docs/KarimiFard13.
Koike K, Liu C, Sanga T. Incorporation of fracture directions into 3D geostatistical methods for a rock fracture system. Environ Earth Sci. 2012. doi:10.1007/s12665-011-1350-z.
Kresse O, Weng XW, Gu HR, Wu RT. Numerical modeling of hydraulic fractures interaction in complex naturally fractured formations. Rock Mech Rock Eng. 2013. doi:10.1007/s00603-012-0359-2.
Lapponi F, Casini G, Sharp I, Blendinger W, Fernández N, Romaire I, Hunt D. From outcrop to 3D modelling: a case study of a dolomitized carbonate reservoir, Zagros Mountains Iran. Pet Geosci. 2011. doi:10.1144/1354-079310-040.
Lee CC, Lee CH, Yeh HF, Lin HI. Modeling spatial fracture intensity as a control on flow in fractured rock. Environ Earth Sci. 2011. doi:10.1007/s12665-010-0794-x.
Maffucci R, Bigi S, Corrado S, Chiodi A, Di Paolo L, Giordano G, Invernizzi C. Quality assessment of reservoirs by means of outcrop data and discrete fracture network models: the case history of Rosario de La Frontera (NW Argentina) geothermal system. Tectonophysics. 2015. doi:10.1016/j.tecto.2015.02.016.
Malinouskaya I, Thovert JF, Mourzenko VV, Adler PM, Shekhar R, Agar S, Rosero E, Tsenn M. Fracture analysis in the Amellago outcrop and permeability predictions. Pet Geosci. 2014. doi:10.1144/petgeo2012-094.
Masihi M, King PR. A correlated fracture network: modeling and percolation properties. Water Resour Res. 2007. doi:10.1029/2006WR005331.
Mi L, Jiang H, Li J, Li T, Tian Y. The investigation of fracture aperture effect on shale gas transport using discrete fracture model. J Nat Gas Sci Eng. 2014. doi:10.1016/j.jngse.09.029.
Min KB, Rutqvist J, Tsang CF, Jing L. Stress-dependent permeability of fractured rock masses: a numerical study. Int J Rock Mech Min Sci. 2004. doi:10.1016/j.ijrmms.2004.05.005.
Nie RS, Meng YF, Jia YL, Zhang FX, Yang XT, Niu XN. Dual porosity and dual permeability modeling of horizontal well in naturally fractured reservoir. Transport Porous Media. 2012. doi:10.1007/s11242-011-9898-3.
Presho M, Woc S, Ginting V. Calibrated dual porosity, dual permeability modeling of fractured reservoirs. J Pet Sci Eng. 2011. doi:10.1016/j.petrol.2011.04.007.
Salimi H, Bruining H. Upscaling in vertically fractured oil reservoirs using homogenization. Transport Porous Media. 2010. doi:10.1007/s11242-009-9483-1.
Sang G, Elsworth D, Miao X, Mao X, Wang J. Numerical study of a stress dependent triple porosity model for shale gas reservoirs accommodating gas diffusion in kerogen. J Nat Gas Sci Eng. 2016. doi:10.1016/j.jngse.2016.04.044.
Shekhar R, Sahni I, Benson G, et al. Modelling and simulation of a Jurassic carbonate ramp outcrop, Amellago, High Atlas Mountains. Morocco. Pet Geosci. 2014. doi:10.1144/petgeo2013-010.
Sherkati S, Letouzey J. Variation of structural style and basin evolution in the central Zagros (Izeh zone and Dezful Embayment) Iran. Mar Pet Geol. 2004. doi:10.1016/j.marpetgeo.01.007.
Soleimani M, Jodeiri-Shokri B. 3D static reservoir modeling by geostatistical techniques used for reservoir characterization and data integration. Environ Earth Sci. 2015. doi:10.1007/s12665-015-4130-3.
Soleimani M. Seismic imaging by 3D partial CDS method in complex media. J Pet Sci Eng. 2016a. doi:10.1016/j.petrol.2016.02.019.
Soleimani M. Seismic image enhancement of mud volcano bearing complex structure by the CDS method, a case study in SE of the Caspian Sea shoreline. Russ Geol Geophs. 2016b. doi:10.1016/j.rgg.2016.01.020.
Taron J, Hickman S, Ingebritsen SE, Williams C. Using a fully coupled, open-source THM simulator to examine the role of thermal stresses in shear stimulation of enhanced geothermal systems. In: 48th US Rock mechanics/geomechanics symposium held in Minneapolis, 2014, ARMA 14-7525.
Wang Y, Shahvali M. Discrete fracture modeling using Centroidal Voronoi grid for simulation of shale gas plays with coupled nonlinear physics. Fuel. 2016. doi:10.1016/j.fuel.2015.09.038.
Wang Y, Li X, Tang CA. Effect of injection rate on hydraulic fracturing in naturally fractured shale formations: a numerical study. Environ Earth Sci. 2016. doi:10.1007/s12665-016-5308-z.
Wennberg OP, Casini G, Jonoud S, et al. The characteristics of open fractures in carbonate reservoirs and their impact on fluid flow: a discussion. Pet Geosci. 2016. doi:10.1144/petgeo2015-003.
Wilson CE, Aydin A, Karimi-Fard M, et al. From outcrop to flow simulation: constructing discrete fracture models from a LIDAR survey. AAPG Bull. 2011. doi:10.1306/03241108148.
Xia Y, Jin Y, Chen M. Comprehensive methodology for detecting fracture aperture in naturally fractured formations using mud loss data. J Pet Sci Eng. 2015a. doi:10.1016/j.petrol.10.017.
Xia Y, Jin Y, Chen M, et al. Hydrodynamic modeling of mud loss controlled by the coupling of discrete fracture and matrix. J Pet Sci Eng. 2015b. doi:10.1016/j.petrol.2014.07.026.
Yan X, Huang Z, Yao J, Li Y, Fan D. An efficient embedded discrete fracture model based on mimetic finite difference method. J Pet Sci Eng. 2016. doi:10.1016/j.petrol.2016.03.013.
Yoshida N, Levine JS, Stauffer PH. Investigation of uncertainty in CO2 reservoir models: a sensitivity analysis of relative permeability parameter values. Int J Greenh Gas Control. 2016. doi:10.1016/j.ijggc.2016.03.008.
Zhang QH. Finite element generation of arbitrary 3-D fracture networks for flow analysis in complicated discrete fracture networks. J Hydrol. 2015. doi:10.1016/j.jhydrol.2015.08.065.
Author information
Authors and Affiliations
Corresponding author
Additional information
Edited by Jie Hao
Appendix
Appendix
Table 3 shows zonation of the target formation. As was mentioned in the text, the target formation is divided into seven zones with the aquifer as zone 8. This zonation is based on the geological and petrophysical information. In each zone and subzone, lithology porosity, permeability and NTG of the zone are fully described. This zonation was used as the base of the reservoir modeling and simulation.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Soleimani, M. Naturally fractured hydrocarbon reservoir simulation by elastic fracture modeling. Pet. Sci. 14, 286–301 (2017). https://doi.org/10.1007/s12182-017-0162-5
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12182-017-0162-5