Introduction

Fluid flow in fractured geological strata should be accurately predicted in many subsurface applications, including groundwater management, hydrocarbon exploitation, carbon dioxide sequestration, and geothermal energy extraction (Yang et al. 2019; Dong et al. 2019). For unconventional oil/gas development, hydraulic fracturing is the most effective technique to achieve economic production (Thomas et al. 2017; Vidic et al. 2013; Zhang et al. 2017). The appropriate scale separation for the modeling of fluid transport is hardly possible due to the complexity and heterogeneity of the fracture network (Ren et al. 2018). Accurate fracture representation continues to be a big challenge for oil/gas production performance analysis. As such, accurate and efficient methods are essential for the modeling of fluid flow in hydraulically fractured media.

Seismic monitoring, a commonly used technology to detect fracture networks, can only provide limited information of fractures. Mayerhofer et al. (2010) put forward the concept of “stimulated reservoir volume (SRV)” based on microseismic-fracture-mapping, which is an effective method in hydraulic fracture diagnostic. It describes the distribution of complex fracture network around the horizontal wells formed after hydraulic fracturing treatment. The well production is closely determined by the SRV properties including the size, shape, and conductivity. Figure 1 shows the microseismic-fracture-mapping of well XY with 24 fracture stages. The SRV has a very complex 3D structure, and the distribution is irregular both in horizontal and vertical planes. The complexity of SRV is strongly influenced by the preexisting natural fractures and in situ stresses in the formation (Weng et al. 2014). In formations that contain a large number of natural fractures and with mild stress anisotropy, the SRV is inclined to be large. While for the formation with no natural fracture development but strong stress anisotropy, the induced fractures are always in planar shape.

Fig. 1
figure 1

Schematic representation of microseismic mapping and stimulated reservoir volume for a hydraulically fractured horizontal well: a. shows the microseismic-fracture-mapping; b. shows the stimulated reservoir volume region from side view; c. shows the stimulated reservoir volume region from top view

Full size image

It is a great technical challenge to characterize the stimulated reservoir volume (SRV) and unstimulated reservoir volume (USRV). One of the major difficulties is that hydraulic fracturing causes significant level of fracture complexity in SRV region. Effective models capable of simulating the flow in different regions should be established carefully. Currently, the existing methods suitable for SRV characterization fall mainly into two classes, namely the equivalent continuum model and discrete fracture model. The equivalent continuum approach has been extensively used by the well performance analysis community for its straightforwardness, and various extended approaches have been proposed based on a similar philosophy. The dual continuum model is a traditional approach of modeling naturally fractured rocks in which the matrix is the main media for fluid storage, and the natural fracture is the main media contributing to the fluid conductivity (Warren and Root 1963; Russell and Truitt 1964; Gringarten and Ramey 1973, 1974). The dual continuum model requires the existence of representative elementary volume (REV), i.e., it assumed the formation has a large number of natural fractures and the fractured domain can achieve a good scale separation. A trilinear flow model coupling linear flows in three sequential flow regions was proposed to analyze the SRV effect on well performance. The inner formation between adjacent hydraulic fractures can be regarded as the SRV in which the dual continuum flow model is used (Brown et al. 2011; Ozkan et al. 2011). The analytical trilinear flow solution to simulate the well behaviors of SRV is computationally convenient and capable of providing the dominant flow regimes. As an extension of the trilinear flow model, the five-region model is proposed to enable the subdivision of the reservoir into five regions. Accordingly, the model can simulate the hydraulic fractures that are surrounded by a stimulated region of a limited extent, while incorporating the other regions that remain unstimulated (Stalgorova and Mattar 2013). The SRV in this case is taken as a media with a single-porosity type. The equivalent hydraulic properties in SRV can be upscaled from the spatial information and conductivity of both fracture and matrix. The demand for accurate characterization of the transient flow between matrix and fracture call for the fine division of matrix. Therefore, the multiple interacting continua (MINC) model becomes increasingly popular (Jiang and Younis 2015, 2016; Wang et al. 2017). The concept of MINC model is to divide a matrix REV into a series of nested subcells to represent the multiple interconnected continua distributed all over the formation domain (Wu and Pruess 1988; Pruess 1985).

Because of the advantages in computational efficiency and simplicity of implementation, the equivalent continuum model is widely adopted for the analysis of subsurface fluid flow through fractured rock system (March et al. 2018; Kuhlman et al. 2015). However, the continuum model has shown some limitations because the model assumptions are not always appropriate (Karimi-Fard et al. 2006; Zhang et al. 2018). In certain cases, it is necessary to characterize the distribution of fracture network in detail, and the discrete fracture model (DFM) demonstrates great advantages in this respect. DFM is a typical discontinuum method in which the hydraulic fractures or natural fractures in SRV are represented explicitly. A series of DFMs are successfully developed and some showed good adaptability. A prerequisite for the DFM simulation is to determine the spatial distribution and conductivity of the fractures. One way to obtain the information of the hydraulic fracture networks is through direct hydraulic fracturing stimulation (Weng et al. 2015; Li et al. 2016). The major difficulty of this approach is to collect the information of preexisting natural fractures and in situ stresses in the formation. The uncertainty associated with the preexisting natural fractures and in situ stresses significantly reduces the accuracy of the hydraulic fracturing simulation. Another way is to extract the fracture information from microseismic observations, which, however, is still insufficient to achieve an accurate representation of fracture distribution. In order to simplify the simulation workflow, the SRV is assumed to be a group of fractures perpendicular to each other (Mayerhofer et al. 2006). When performing the simulation, the PEBI meshing technique is capable of capturing the local small-scale characteristics (Sun et al., 2016a, 2016b).

Through mesh refinement, Voronoi cells are constructed and optimized to accommodate the exact fracture geometry. However, the PEBI meshing technique always leads to a huge grid number and high computational cost. In recent years, the embedded discrete fracture model (EDFM) has drawn more and more attention. EDFM is firstly proposed as a hierarchical modeling method to treat small-, medium-, and large-scale fractures separately (Lee et al. 1999, 2001; Li and Lee 2008). EDFM does not employ the sugar cube approximation for matrix as in dual continuum model or need fine unstructured grid discretization as in conventional DFM model. Besides, test cases indicate that EDFM is computationally efficient. The classical embedded discrete fracture model needs to address different types of connections that may occur between different cells, such as connection between a fracture cell and its neighboring matrix grid, connection between two intersecting fracture cells, and connection between two grid domains of an individual fracture. The calculation rules for connection transmissibility are well-documented in the existing literature. A holistic review of existing studies on EDFM is given in Table 1. EDFM approach has been employed for compositional simulator development, fractured vuggy reservoir modeling, fracture inversion, and upscaling purposes. As conventional EDFM can only achieve good accuracy for the simulation of high conductivity fracture. An improved approach, known as the projection-based embedded discrete fracture model (pEDFM) (Ţene et al., 2017; Jiang and Younis 2017; Ren et al. 2018), accurately simulates the low conductivity fractures by adding extra non-neighbor connections (NNCs). As an effective tool, the improved pEDFM can produce good accuracy for both low conductivity fracture case and multiple fluid saturation case. Considering the merits and drawbacks of continuum model and DFM approaches, the combination of both methods proved to be more effective (Zhang et al. 2018, 2020). DFM is used to treat the main hydraulic fracture and the continuum model is adopted to model the SRV region. In a recent study, the large-scale fractures were dealt with EDFM method, while micro-fractures were represented by DP model. Considering the low permeability of matrix, transient transfer model between matrix and natural fracture was adopted (Xu et al. 2019).

Table 1 Application of EDFM
Full size table

In this paper, we present a new workflow to predict the evolution of pressure field of unconventional oil/gas reservoirs with stimulated reservoir volume. The workflow is based on a newly developed method, i.e., the Laplace-transform embedded discrete fracture model method. The numerical method is firstly proposed as the Laplace-transform finite difference (LTFD) (Moridis and Reddell 1991; Moridis et al. 1994). When using this method, the time domain is solved semi-analytically so the accuracy and stability of the simulation will not be affected by the back finite difference of time in real space. The space derivatives in the governing equations are still approximated by numerical finite difference method. This method allows for the consideration of reservoir heterogeneities and flow simulation with a 3D SRV configuration. The method initially can only treat vertical well, but significant improvement was made by combining the LTFD concept with a discrete fracture model, i.e., the embedded discrete fracture model. Three family of methods to characterize the SRV are proposed. A general option is to treat all possible fractures with EDFM model instead of using the hybrid model, which, however, can substantially increase the calculation time. Thus, the MINC model and equivalent model are used in the modeling of fluid flow in SRV region, while the EDFM is used to deal with the main hydraulic fracture. We present some numerical test results compared with DFM. We compare the solutions and some integrated quantities by choosing different solution methods. Our results show that Laplace-transform EDFM can provide good accuracy. The paper is organized as follows. We present the detailed formulations of the described problem in Sect. 2, while Sect. 3 elaborates on the numerical solution strategy. The numerical results obtained from different methods are shown in Sect. 4 based on synthetic test cases, after which the analysis will be focused on application of LTEDFM.

Methodology

Physical model description

A properly designed physical model is necessary for the accurate simulation of the fractured horizontal well with SRV. In view of the complexity of a real producing reservoir, a wide range of scales should be considered for the fractures. Hence, detailed modeling of fractures remains unattainable at present. The SRV concept was shown to be a simple and effective alternative method. As shown in Fig. 2, four cases are generally considered: Case-A shows a hydraulically fractured horizontal well with four main fractures, around which no SRV was created; Case-B shows a hydraulically fractured horizontal well with SRV around each hydraulic fracture, the volume and conductivity may be different among the four SRVs; Case-C shows a hydraulically fractured horizontal well with all main hydraulic fractures contained in a single SRV, which means the SRVs are linked with each other after hydraulic fracturing treatment; Case-D shows the complex fracture system around the well, and this case explicitly presents all hydraulic fractures of different scales. We will analyze all the above cases using the newly developed numerical simulation model.

Fig. 2
figure 2

Schematic representation of fractured horizontal well:(1) shows a fractured horizontal well where \(\Omega_{USRV}\) is the matrix domain and \(\Omega_{F}\) is the hydraulic fracture domain; (2) shows a fractured horizontal well with SRV around each hydraulic fracture where \(\Omega_{SRV}\) is the SRV domain; (3) shows a fractured horizontal well with SRV contains all hydraulic fractures; (4) shows the complex fracture system around the well explicitly

Full size image

Mathematical model

The microseismic monitoring and fracture propagation modeling can be used to understand the hydraulic fracture distribution. Once the fracture information is determined (though in most cases only partially determined), the theoretical flow model should be established to take the complex fracture system into consideration. Figure 3 shows a simple reservoir example. The distribution of fractures around the horizontal well is complex, and the whole domain can be divided into three regions: the hydraulic fracture domain \(\Omega_{F}\), the SRV domain \(\Omega_{SRV}\), and the USRV domain \(\Omega_{USRV}\). In the following analysis, case (2) in Sect. 2.1 will be chosen as the basic physical model with which the mathematical model is established. Then, we will show how to extend the model to the other three cases. Some assumptions should be followed to restrict the solution: (1) The flow domain is two-dimensional or three-dimensional, which means the main hydraulic fracture and SRV can have a 3D structure; (2) Three flow regions are considered from USRV to SRV to hydraulic fractures one by one; (3) Isothermal condition is considered; (4) Flow is single phase; (5) The fluid is slightly compressible.

Fig. 3
figure 3

Schematic representation of the physical model: four perforation points distribute along the well and complex hydraulic fractures form after fracturing fluid is injected. The red lines present the complex hydraulic fractures with high conductivity. The yellow regions are stimulated reservoir volume (SRV) containing the secondary fracture and matrix. The outer region is the unstimulated reservoir volume (USRV) which is modeled as single-porosity media. Fluids first flow into the wellbore from the SRV and then from USRV to SRV

Full size image

Flow in hydraulic fracture

As shown in Fig. 3, the flow equation describing the fluid transport in hydraulic fractures can be expressed as:

$$\partial_{t} \left( {\phi_{F} \rho } \right) + \nabla \cdot \left( {\rho v_{F} } \right) = q_{F}^{W} + q_{fs - F}^{{}} \;{\text{on }}\Omega_{F}$$
(1)

where \(\phi_{F}\) is the fracture porosity; \(\rho\) is fluid density; \(q_{F}^{W}\) denotes the source and sink terms from fracture; \(v_{F}\) is the flow velocity in fracture; \(q_{fs - F}^{{}}\) is the fluid flux between main fracture and secondary fracture in SRV.

Flow in SRV region

The SRV region contains two kinds of media: secondary fractures and matrix. The flow equation in secondary fractures can be expressed as:

$$\partial_{t} \left( {\phi_{fs} \rho } \right) + \nabla \cdot \left( {\rho v_{fs} } \right) = - q_{fs - F} + q_{fs - m} \;{\text{on }}\Omega_{SRV}$$
(2)

where \(\phi_{fs}\) is the secondary fracture porosity; \(v_{fs}\) is the flow velocity in secondary fracture; \(q_{sf - m}^{{}}\) is the fluid flux between secondary fracture and matrix.

The flow equation of matrix in SRV can be expressed as:

$$\partial_{t} \left( {\phi_{m} \rho } \right) + \nabla \cdot \left( {\rho v_{m} } \right) = - q_{fs - m} \;{\text{on }}\Omega_{m}$$
(3)

where \(\phi_{m}\) is matrix porosity; \(v_{m}\) is the flow velocity in matrix.

Flow in USRV region

The flow equation of matrix in USRV can be expressed as:

$$\partial_{t} \left( {\phi_{USRV} \rho } \right) + \nabla \cdot \left( {\rho v_{USRV} } \right) = 0\;{\text{on }}\Omega_{USRV}$$
(4)

where \(\phi_{USRV}\) is matrix porosity; \(v_{USRV}\) is the flow velocity in matrix.

Darcy Law is applied to calculate the flow velocity in both SRV and USRV regions:

$$v = - \frac{k}{\mu }\nabla p$$
(5)

where \(\mu\) is the viscosity of fluid; \(k\) is the permeability; \(p\) is the fluid pressure.

The outer boundary condition is set to satisfy the Neumann boundary condition:

$$v_{USRV} \cdot n_{\Gamma } = 0\;{\text{on }}\Gamma_{out}$$
(6)

where \(n_{\Gamma }\) is the outward unit normal vector.

The continuity condition of the flow rate at the interface between the SRV domain \(\Omega_{SRV}\) and USRV domain \(\Omega_{USRV}\) is considered which can be described as:

$$v_{USRV} \cdot n_{\Gamma } = v_{SRV} \cdot n_{\Gamma } \;{\text{on }}\Gamma_{SRV - USRV}$$
(7)

Transformation of the flow equations

In order to achieve the solution in the whole domain, we transform the above mathematical model into Laplace space.

Generally, the liquid density can be defined as:

$$\rho { = }\rho_{STC} \beta_{0} R$$
(8)

where \(\beta_{0} R\) is the inverse of formation volume factor. Here, \(\rho_{0} { = }\rho_{STC} \beta_{0}\).

Subsequently, a general form of flow equation will be derived for main hydraulic fractures, SRV region, and USRV region.

The flow equation in hydraulic fractures

\(R_{F}\) is calculated as the following equation:

$$R_{F} { = }\exp \left[ {c_{f} (p_{F} - p_{0} )} \right]\;{\text{for main fracture}}$$
(9)

where \(c_{f}\) is the fluid compressibility, \(p_{0}\) is the reference pressure.

The porosity is a weak function of pressure which can be described as:

$$\varphi_{F} { = }\varphi_{0,F} \exp \left[ {c_{fm,F} (p_{F} - p_{0,F} )} \right]$$
(10)

Expanding the first term of the left-hand side of Eq. (1):

$$\partial_{t} \left( {\phi_{F} \rho } \right){ = }\rho_{0} \left( {\phi_{F} + R_{F} \frac{{\partial \phi_{F} }}{{\partial p_{F} }}\frac{{\partial p_{F} }}{\partial R}} \right)\frac{{\partial R_{F} }}{\partial t} = \rho_{0} C_{TF} \frac{{\partial R_{F} }}{\partial t}$$
(11)

where

$$C_{TF} { = }\phi_{0} \left( {1 + \frac{{c_{fm,F} }}{{c_{f} }}} \right)R^{{\left( {c_{fm,F} /c_{f} } \right)}}$$
(12)

For slightly compressible liquid, \(R \approx 1\) and \(C_{TF}\) is reduced into Eq. (13):

$$C_{TF} { = }\phi_{0} \left( {1 + \frac{{c_{fm,F} }}{{c_{f} }}} \right)$$
(13)

Expansion of the second term of the left-hand side of Eq. (1) gives:

$$\nabla \cdot \left( {\rho v_{F} } \right){ = }\frac{\partial }{\partial (x,y,z)}\left[ { - k\frac{\rho }{\mu }\left( {\frac{{\partial p_{F} }}{\partial (x,y,z)}} \right)} \right] = \frac{\partial }{\partial (x,y,z)}\left[ { - k\frac{{\rho_{0} }}{{\mu c_{f} }}\frac{{\partial R_{F} }}{\partial (x,y,z)}} \right]$$
(14)

Then, Eq. (1) becomes:

$$C_{TF} \frac{{\partial R_{F} }}{\partial t} + \nabla \cdot \left( { - \frac{{k_{F} }}{{\mu c_{f} }}\nabla R_{F} } \right) = Q_{F}^{W} - Q_{fs - F} \;{\text{on }}\Omega_{f}$$
(15)

Rewriting Eq. (15) in terms of \(\Delta R_{F}\) yields:

$$C_{TF} \frac{{\partial \left( {\Delta R_{F} } \right)}}{\partial t} + \nabla \cdot \left( { - \frac{{k_{F} }}{{\mu c_{f} }}\frac{{\partial \left( {\Delta R_{F} } \right)}}{\partial x}} \right) = Q_{F}^{W} - Q_{fs - F}^{{}}$$
(16)

where

$$R_{F} { = }1 + \Delta R_{F} ,R_{F}^{2} = 1 + 2\Delta R_{F} + \left( {\Delta R_{F} } \right)^{2}$$
(17)

Taking Laplace transform of Eq. (16):

$$C_{TF} \left[ {s\psi_{F} - \Delta R_{F} \left( 0 \right)} \right] + \nabla \cdot \left( { - \frac{{k_{F} }}{{\mu c_{f} }}\frac{{\partial \psi_{F} }}{\partial x}} \right) = \overline{{Q_{F}^{W} }} - \overline{{Q_{fs - F}^{{}} }}$$
(18)

where

$$\overline{{Q_{F}^{W} }} = L\left\{ {Q_{F}^{W} } \right\}$$
(19)
$$\psi_{F} = L(\Delta R_{F} )$$
(20)
$$\overline{{Q_{fs - F}^{{}} }} = L\left\{ {Q_{fs - F}^{{}} } \right\}$$
(21)

where \(s\) is the Laplace space parameter; \(\Delta R_{F} \left( 0 \right)\) is the initial distribution of \(\Delta R_{F}\) at \(t = 0\).

The flow equation in SRV region

\(R_{m}\) and \(R_{fs}\) are calculated as the following equation:

$$R_{m} { = }\exp \left[ {c_{f} (p_{m} - p_{0} )} \right]\;{\text{for matrix}}$$
(22)
$$R_{fs} { = }\exp \left[ {c_{f} (p_{fs} - p_{0} )} \right]\;{\text{for secondary fracture}}$$
(23)

Again, the porosity is a weak function of pressure:

$$\varphi_{fs} { = }\varphi_{0,fs} \exp \left[ {c_{fm,fs} (p_{fm} - p_{0,fs} )} \right]$$
(24)
$$\varphi_{{\text{m}}} { = }\varphi_{0,m} \exp \left[ {c_{fm,m} (p_{m} - p_{0,m} )} \right]$$
(25)

where \(\varphi_{0,m}\) and \(\varphi_{0,fs}\) are the porosity at the reference pressure for matrix and secondary fracture (\(p_{0,m}\) and \(p_{0,fs}\)), respectively. \(c_{fm,m}\) is the matrix rock compressibility, and \(c_{fm,fs}\) is the secondary fracture rock compressibility.

Expanding the first term of the left-hand side of Eq. (2):

$$\partial_{t} \left( {\phi_{fs} \rho } \right){ = }\rho_{0} \left( {\phi_{fs} + R_{fs} \frac{{\partial \phi_{fs} }}{{\partial p_{fs} }}\frac{{\partial p_{fs} }}{\partial R}} \right)\frac{{\partial R_{fs} }}{\partial t} = \rho_{0} C_{Tfs} \frac{{\partial R_{fs} }}{\partial t}$$
(26)

Expansion of the first term of the left-hand side of Eq. (3) yields:

$$\partial_{t} \left( {\phi_{m} \rho } \right){ = }\rho_{0} \left( {\phi_{m} + R_{m} \frac{{\partial \phi_{m} }}{\partial p}\frac{{\partial p_{m} }}{\partial R}} \right)\frac{{\partial R_{m} }}{\partial t} = \rho_{0} C_{Tm} \frac{{\partial R_{m} }}{\partial t}$$
(27)

where

$$C_{Tfs} { = }\phi_{0} \left( {1 + \frac{{c_{fm,fs} }}{{c_{f} }}} \right)R^{{\left( {c_{fm,fs} /c_{f} } \right)}}$$
(28)
$$C_{Tm} { = }\phi_{0} \left( {1 + \frac{{c_{fm,m} }}{{c_{f} }}} \right)R^{{\left( {c_{fm,m} /c_{f} } \right)}}$$
(29)

For slightly compressible liquid, \(R \approx 1\) and \(C_{T}\) is reduced into Eq. (30) and (31):

$$C_{Tfs} \approx \phi_{0} \left( {1 + \frac{{c_{fm,fs} }}{{c_{f} }}} \right)$$
(30)
$$C_{Tm} \approx \phi_{0} (1 + \frac{{c_{fm,m} }}{{c_{f} }})$$
(31)

Expanding the second term of the left-hand side of Eq. 2\(\nabla \cdot \left( {\rho v_{m} } \right)\):

$$\nabla \cdot \left( {\rho v_{fs} } \right){ = }\frac{\partial }{\partial (x,y,z)}\left[ { - k\frac{\rho }{\mu }\left( {\frac{{\partial p_{fs} }}{\partial (x,y,z)}} \right)} \right] = \frac{\partial }{\partial (x,y,z)}\left[ { - k\frac{{\rho_{0} }}{{\mu c_{f} }}\frac{{\partial R_{fs} }}{\partial (x,y,z)}} \right]$$
(32)

Expanding the second term of the left-hand side of Eq. 3\(\nabla \cdot \left( {\rho v_{m} } \right)\):

$$\nabla \cdot \left( {\rho v_{m} } \right){ = }\frac{\partial }{\partial (x,y,z)}\left[ { - k\frac{\rho }{\mu }\left( {\frac{{\partial p_{m} }}{\partial (x,y,z)}} \right)} \right] = \frac{\partial }{\partial (x,y,z)}\left[ { - k\frac{{\rho_{0} }}{{\mu c_{f} }}\frac{{\partial R_{m} }}{\partial (x,y,z)}} \right]$$
(33)

Considering the compressibility of rock and liquid. The general nonlinear equations, Eq. (2) and Eq. (3), become:

$$C_{Tfs} \frac{{\partial R_{fs} }}{\partial t} + \nabla \cdot \left( { - \frac{{k_{F} }}{{\mu c_{f} }}\nabla R_{fs} } \right) = - Q_{fs - F} + Q_{fs - m} \;{\text{on }}\Omega_{fs}$$
(34)
$$C_{Tm} \frac{{\partial R_{m} }}{\partial t} + \nabla \cdot \left( { - \frac{{k_{m} }}{{\mu c_{f} }}\nabla R_{m} } \right) = - Q_{fs - m} \;{\text{on }}\Omega_{{\text{m}}}$$
(35)

Define the following equations:

$$R_{fs} { = }1 + \Delta R_{fs} ,R_{fs}^{2} = 1 + 2\Delta R_{fs} + \left( {\Delta R_{fs} } \right)^{2}$$
(36)
$$R_{m} { = }1 + \Delta R_{m} ,R_{m}^{2} = 1 + 2\Delta R_{m} + \left( {\Delta R_{m} } \right)^{2}$$
(37)

Then, Eqs. (34) and (35) are reformulated as:

$$C_{Tfs} \frac{{\partial \left( {\Delta R_{fs} } \right)}}{\partial t} + \nabla \cdot \left( { - \frac{{k_{fs} }}{{\mu c_{f} }}\frac{{\partial \left( {\Delta R_{fs} } \right)}}{\partial x}} \right) = - Q_{fs - F}^{{}} + Q_{fs - m}^{{}}$$
(38)
$$C_{Tm} \frac{{\partial \left( {\Delta R_{m} } \right)}}{\partial t} + \nabla \cdot \left( { - \frac{{k_{m} }}{{\mu c_{f} }}\frac{{\partial \left( {\Delta R_{m} } \right)}}{\partial x}} \right) = - Q_{fs - m}^{{}}$$
(39)

Taking Laplace transform of Eqs. (38) and (39) results in:

$$C_{Tfs} \left[ {s\psi_{fs} - \Delta R_{fs} \left( 0 \right)} \right] + \nabla \cdot \left( { - \frac{{k_{fs} }}{{\mu c_{f} }}\frac{{\partial \psi_{fs} }}{\partial x}} \right) = \overline{{Q_{fs - m}^{W} }} - \overline{{Q_{fs - F}^{{}} }}$$
(40)
$$C_{Tm} \left[ {s\psi_{m} - \Delta R_{m} \left( 0 \right)} \right] + \nabla \cdot \left( { - \frac{{k_{m} }}{{\mu c_{f} }}\frac{{\partial \psi_{m} }}{\partial x}} \right) = - \overline{{Q_{fs - m}^{{}} }}$$
(41)

Equations (40) and (41) are the general flow equations in SRV.

The flow equation in USRV region

\(R_{USRV}\) is calculated using the following equation:

$$R_{USRV} { = }\exp \left[ {c_{f} (p_{USRV} - p_{0} )} \right]\;{\text{for matrix}}$$
(42)

Similarly, the porosity–pressure relationship follows:

$$\varphi_{USRV} { = }\varphi_{0,USRV} \exp \left[ {c_{fm,USRV} (p_{USRV} - p_{0,USRV} )} \right]$$
(43)

Equation (4) can then be rewritten as:

$$\partial_{t} \left( {\phi_{USRV} \rho } \right){ = }\rho_{0} \left( {\phi_{USRV} + R_{USRV} \frac{{\partial \phi_{USRV} }}{{\partial p_{USRV} }}\frac{{\partial p_{USRV} }}{\partial R}} \right)\frac{{\partial R_{USRV} }}{\partial t} = \rho_{0} C_{TUSRV} \frac{{\partial R_{USRV} }}{\partial t}$$
(44)

where

$$C_{TUSRV} { = }\phi_{0} \left( {1 + \frac{{c_{fm,USRV} }}{{c_{f} }}} \right)R^{{\left( {c_{fm,USRV} /c_{f} } \right)}}$$
(45)

For slightly compressible fluids, \(R \approx 1\) and \(C_{TUSRV}\) is reduced into Eq. (46):

$$C_{TUSRV} { = }\phi_{0} \left( {1 + \frac{{c_{fm,USRV} }}{{c_{f} }}} \right)$$
(46)

Expanding the second term of the left-hand side of Eq. 4:

$$\nabla \cdot \left( {\rho v_{USRV} } \right){ = }\frac{\partial }{\partial (x,y,z)}\left[ { - k\frac{\rho }{\mu }\left( {\frac{{\partial p_{USRV} }}{\partial (x,y,z)}} \right)} \right] = \frac{\partial }{\partial (x,y,z)}\left[ { - k\frac{{\rho_{0} }}{{\mu c_{f} }}\frac{{\partial R_{USRV} }}{\partial (x,y,z)}} \right]$$
(47)

Then, Eq. 4 can be rewritten as:

$$C_{TUSRV} \frac{{\partial R_{USRV} }}{\partial t} + \nabla \cdot \left( { - \frac{{k_{USRV} }}{{\mu c_{f} }}\nabla R_{USRV} } \right) = 0\;{\text{on}}\;\Omega_{USRV}$$
(48)

where

$$R_{USRV} { = }1 + \Delta R_{USRV} ,R_{USRV}^{2} = 1 + 2\Delta R_{USRV} + \left( {\Delta R_{USRV} } \right)^{2}$$
(49)

Reformulating Eq. (48) in terms of \(\Delta R_{USRV}\):

$$C_{TUSRV} \frac{{\partial \left( {\Delta R_{USRV} } \right)}}{\partial t} + \nabla \cdot \left( { - \frac{{k_{USRV} }}{{\mu c_{f} }}\frac{{\partial \left( {\Delta R_{USRV} } \right)}}{\partial (x,y,z)}} \right) = 0$$
(50)

Then, taking Laplace transform of Eq. (50) yields:

$$C_{TUSRV} \left[ {s\psi_{USRV} - \Delta R_{USRV} \left( 0 \right)} \right] + \nabla \cdot \left( { - \frac{{k_{USRV} }}{{\mu c_{f} }}\frac{{\partial \psi_{USRV} }}{\partial (x,y,z)}} \right) = 0$$
(51)

Coupling model among different media

  1. (1)

    Fluid transport in SRV

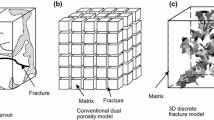
The classical definition of shape factor that assumes a pseudo-steady mass transfer between fracture and matrix is not applicable for tight reservoir rock, so transient transfer should be considered instead. The MINC model is a reasonable method to describe the unsteady mass transfer between secondary fracture and matrix. Figure 4 shows the coupling strategy. The main hydraulic fracture is modeled using EDFM because of the high conductivity. The coupling of secondary fracture and matrix is modeled using MINC model.

Fig. 4
figure 4

Coupling model of different media in SRV: the red line represents the main hydraulic fractures, the blue line shows the secondary fractures. After upscaling, the coupling of secondary fracture and matrix can be described by the MINC model

Full size image

In the MINC model, each matrix cell is subdivided into a series of nested subcells. We define the flux across each pair connection (subcell–subcell connection) as:

$$f_{i,j} = Ak\frac{\rho }{\mu }\frac{\partial p}{{\partial (x,y,z)}}$$
(52)

Introducing Eqs. (8, 9) transforms Eq. (52) as:

$$f_{i,j} = Ak\frac{\rho }{\mu }\frac{\partial p}{{\partial (x,y,z)}}{ = }Ak\frac{{\rho_{0} }}{{\mu c_{f} }}\frac{\partial R}{{\partial (x,y,z)}}$$
(53)

Reformulating Eq. (53) in terms of \(\Delta R\):

$$f_{i,j} { = }Ak\frac{{\rho_{0} }}{{\mu c_{f} }}\frac{\partial R}{{\partial (x,y,z)}}{ = }Ak\frac{{\rho_{0} }}{{\mu c_{f} }}\frac{{\partial \left( {1 + \Delta R} \right)}}{\partial (x,y,z)} = Ak\frac{{\rho_{0} }}{{\mu c_{f} }}\frac{\partial \Delta R}{{\partial (x,y,z)}}$$
(54)

Laplace transform to Eq. (54) gives:

$$\overline{{f_{i,j} }} { = }Ak\frac{{\rho_{0} }}{{\mu c_{f} }}\frac{\partial \psi }{{\partial (x,y,z)}}$$
(55)

Without considering \(\rho_{0}\), the connection can be defined as:

$$\overline{{F_{i,j} }} = Ak\frac{1}{{\mu c_{f} }}\frac{\partial \psi }{{\partial (x,y,z)}} = T\frac{1}{{\mu c_{f} }}\left( {\psi_{i} - \psi_{j} } \right)$$
(56)
  1. (2)

    Main fracture and secondary fracture coupling

EDFM was proposed by Li and Lee (2008). Three connections should be defined in the implementation of EDFM: the connection between a fracture cell and its neighboring matrix grid, connection between two intersecting fracture cells in the same grid, and connection between two grids of an individual fracture. When considering the secondary fracture, the first connections should be replaced by a fracture cell and its neighboring secondary fracture grid. The average normal distance from secondary fracture to fracture should be defined and computed.

For EDFM, the flux at each pair connection is calculated by:

$$C_{i,j} = T_{i,j} (p_{i} - p_{j} ){ = }\frac{\rho kA}{{\mu d}}(p_{i} - p_{j} )$$
(57)

For LTEDFM, we define the flux between each connected pair as:

$$C_{i,j} = Ak\frac{\rho }{\mu }\left( {\frac{\partial p}{{\partial (x,y,z)}}} \right)$$
(58)

Introducing Eqs. (8) and (9):

$$C_{i,j} { = }Ak\frac{{\rho_{0} }}{{\mu c_{f} }}\frac{\partial R}{{\partial (x,y,z)}}$$
(59)

Taking the Laplace transform of Eq. (59):

$$\overline{{C_{i,j} }} { = }Ak\frac{{\rho_{0} }}{{\mu c_{f} }}\frac{\partial \psi }{{\partial (x,y,z)}}$$
(60)

Without considering \(\rho_{0}\), the NNC flux term becomes:

$$\overline{{C_{i,j} }} = \frac{Ak}{d}\frac{1}{{\mu c_{f} }}\left( {\psi_{i} - \psi_{j} } \right)$$
(61)

As indicated above, LTEDFM introduced different connection lists compared with EDFM. Figure 5 shows a simple example for the connection list both with and without considering SRV. The whole domain is discretized into 25 matrix grids for the situation without SRV. The “ + ” shape fracture is discretized into six cells by the matrix grid boundaries. The total number of connections is 51, including five main fracture–main fracture cell connections, six matrix–fracture connections, and 40 matrix–matrix grid connections. The connection lists are the same as the classical EDFM. The connection calculation of classical EDFM can be used for the simulation of case 1 and case 4. However, the connection types are quite different when SRV is considered. As shown in Fig. 5(b), the whole space domain is discretized into 25 grids, including nine SRV grids and 16 matrix grids. The main hydraulic fracture cells are connected to the SRV grids directly. The connection list includes five main fracture–main fracture cell connections, 45 MINC subcell–subcell connections, six main fracture–SRV grid connections, 16 matrix–matrix grid connections, 12 SRV–SRV grid connections, and 12 matrix–SRV connections. It should be noted that the SRV grid must use the effective permeability and porosity when computing the connection between secondary fracture and matrix. Namely, in this example, grid 7, 8, 9, 12, 13, 14, 17, 18, and 19 should use the effective properties. The above connection calculation method can be used for the simulation of case 2 and case 3.

Fig. 5
figure 5

Schematics of the grid system of the fracture and matrix for different cases. a connection relationship without SRV; b connection relationship with SRV

Full size image

Solution strategy

EDFM are commonly employed to solve for pressure field directly in real space. We extended it to the Laplace space in Sect. 2. The LTEDFM system of simultaneous equations is:

$$\left\{ M \right\}\left[ \Psi \right] = \left[ D \right]$$
(62)

where the term \(M\) yields after dealing with all connection lists and the accumulation term. \(\Psi\) store the unknowns.\(D\) is a known right-hand side matrix.

The equation system can be solved to obtain the pressure field in Laplace space. Then, the Stehfest numerical inversion algorithm is used to calculate the pressure in real time space. Figure 6 shows the solution workflow. Some procedures to execute are summarized, as follows: (1) Define the matrix and fracture grids. Determine hydraulic fracture cells, SRV grids, and USRV grids; (2) Prepare the connections for hydraulic fracture, SRV, and USRV regions; (3) Generate the connection list. Each list contains the left domain, right domain, and transmissibility. The transmissibility is calculated according to the method shown in Sect. 2; (4) Identify fracture segments intersected by wells and calculate the well index of the corresponding fracture control volumes; (5) Calculate the system of equations \(\left\{ M \right\}\left[ \Psi \right] = \left[ D \right]\) and then transform the pressure into real space; (6) Stop the simulation until the final time step.

Fig. 6
figure 6

Calculation procedures of Laplace-transform embedded discrete fracture models

Full size image

Validation

Comparison with the existing solution methods

In this section, the developed new model is validated by comparing the pressure distribution of the discrete fracture method (DFM) and the EDFM method in real space. The discrete fracture method (DFM) proposed by Karimi-Fard and Firoozabadi (2001) is used to obtain the benchmark solution. This model is proposed for two-phase flow simulation initially and can be readily modified into single-phase flow simulation. The discretization is based on the standard Galerkin finite element method; thus, the unstructured triangular mesh should be used. To realize DFM, the software COMSOL Multiphysics is chosen as the mesh discretization tool. The dimension of fracture is reduced by one. Grid refinement is performed near the well and fractures to better capture the pressure profile. The weak form equation of fracture flow is derived from Eq. (1) and set in COMSOL directly. This strategy solves the problem in real space and is taken as the reference solution. The EDFM method in real space refers to our previous work (Xu et al. 2019). To achieve a robust verification and capture the characteristic of flow in complex fracture system, four models are considered corresponding to the cases in Sect. 2.1: case-A, case-B, case-C, and case-D.

  1. (1)

    Case-A: fractured horizontal well with planar fractures

In this section, we validate the LTEDFM for fractured horizontal well with planar fractures. Figure 7(1) shows the fractured horizontal well benchmark case under the condition of constant production rate with no flow outer boundary. The size of 2D geometry is 600 m × 600 m, and the formation thickness is 10 m. Four planar fractures are located along the horizontal well. There is no SRV around the main hydraulic fractures. Thus, the mass transfer happens between the main fractures and matrix directly. The main fracture width is 0.0001 m, the absolute permeability is 7.5 × 10(−10) m2 calculated according to Eq. (63).

$$k_{F} = \phi_{F} \frac{{b^{2} }}{12}$$
(63)
Fig. 7
figure 7

Case-A: (1) Conceptual model of fractured horizontal well with four fractures (the red line represents the fractures); (2) Triangular meshes for DFM; (3) Square grids for EDFM and LTEDFM

Full size image

Figure 7(2) shows the grid system for DFM model. The space domain is discretized with 13,340 triangular meshes. Figure 7(3) shows the grid system for EDFM model and LTEDFM model. The space domain is divided into 3600 square grids. Each main hydraulic fracture is discretized into ten cells. Totally, 40 fracture cells are divided. The simulation parameters of the problem are listed in Table 2.

Table 2 Basic parameters for case-A
Full size table

To validate the LTEDFM model, we compare the fracture and matrix pressure with those obtained from DFM and EDFM in real space. Figure 8 shows the pressure distribution for DFM, EDFM, and LTEDFM, respectively. The pressure distribution is symmetric with respect to the center of the reservoir. All three simulation methods are able to capture the typical fracture effect that the pressure spreads fast around the fracture. To allow for qualitative analysis between different methods, we compare all grid pressures between two different simulation methods in Fig. 9. The curves show an excellent agreement between the simulation results of the LTEDFM method and other methods. Figure 9 also shows that most grid pressures are above 5 MPa after 400 days of production. The calculation time for LTEDFM and EDFM is compared. A total of 110 time steps are simulated, with 253 Newton’s iterations for EDFM in real space. The calculation time is 88.75 s. However, when the proposed LTEDFM is imposed to solve the same problem, the calculation time is 4.72 s. The new solution protocol becomes Newton’s iteration free and the main computational expense is the Stehfest inversion process. Hence, the computational speed would be significantly enhanced.

  1. (2)

    Case-B: SRV around each fracture

Fig. 8
figure 8

Pressure distribution of case-A (400 days)

Full size image
Fig. 9
figure 9

Grid pressure relationship for DFM, EDFM, and LTEDFM (400 days)

Full size image

Figure 10(1) shows a fractured horizontal well benchmark case considering SRV. In this case, we discuss the problem of hydraulic fracture–SRV–matrix coupling. There is a rectangular SRV around each hydraulic fracture. The size of SRV is 40 m × 160 m. Figure 10(2) shows the grid system for DFM model. The space domain is discretized with 12,024 triangular meshes. All secondary fractures are explicitly displayed. Figure 10(3) shows the grid system for EDFM model and LTEDFM model. It should be noted that the secondary fracture permeability and porosity need to be converted to the corresponding effective continuum properties when using EDFM and LTEDFM. After conversion, the effective fracture porosity is 0.000008, and the effective fracture permeability is 8.33 × 10(−16) m2. Figure 10(4) shows the MINC elements. Each matrix element is subdivided into five continua. The simulation parameters of the problem are listed in Table 3.

Fig. 10
figure 10

Case-B: (1) Conceptual model of fractured horizontal well with four fractures with SRV around each main hydraulic fracture; (2) Triangular meshes for DFM; (3) Square grids for EDFM and LTEDFM. (4) MINC element including five continua

Full size image
Table 3 Basic parameters for case-B
Full size table

Figure 11 shows the pressure distribution of case-B for different simulation models. The simulation results manifest the fast spread of pressure in SRV because of the high conductivity comparing to the USRV region. As a result, the pressure drop in SRV is much larger than USRV regions. The drawdown for the medium two SRVs is the largest to maintain at a fixed production rate. We compare all grid pressures between two different simulation methods, as shown in Fig. 12. The results show that the LTEDFM method produces good accuracy when considering SRV around main hydraulic fractures. The difference in pressure distribution is noticeable by comparing Case-A and Case-B. Comparing Fig. 8 and Fig. 11, the pressure drop for Case-B is much smaller at 400 days around the well. For Case-B, all grid pressures are above 10 MPa. The main reason is that the SRV significantly decreases the flow resistance near the wellbore region.

Fig. 11
figure 11

Pressure distribution of case-B using MINC model (400 days)

Full size image
Fig. 12
figure 12

Grid pressure relationship using MINC model (400 days)

Full size image

Another method to simulate the flow in fracture and matrix system is the equivalent model. Different from the MINC, the equivalent model resembles the single-porosity model by upscaling the matrix and fracture properties mainly including porosity and permeability. We compute the equivalent parameters for each grid within SRV region, which works out to be 0.1 for equivalent SRV porosity and 8.43 × 10(−16) m2 for equivalent SRV permeability. The permeability and porosity remain unchanged for USRV.

Figure 13 shows the pressure distribution for DFM, EDFM, and LTEDFM using the equivalent model. The pressure distribution is consistent with that of EDFM + MINC model. Thus, the equivalent model is a reasonable choice for the SRV simulation problem, which is why some classical models, such as the five-region flow model (Stalgorova and Mattar, 2013), regarded SRV region as a single media. We also compare all grid pressures between two different simulation methods in Fig. 14. The results show that the LTEDFM method exhibits good calculation accuracy for the equivalent model.

  1. (3)

    Case 3-SRV around all fractures

Fig. 13
figure 13

Pressure distribution of case-B using equivalent model (400 days)

Full size image
Fig. 14
figure 14

Grid pressure relationship using equivalent model (400 days)

Full size image

Figure 15(1) shows a fractured horizontal well benchmark case considering a large size SRV. In this case, we set a rectangular SRV in which all main hydraulic fractures are located. The size of SRV is 400 m × 200 m. Figure 15(2) shows the grid system for DFM model. The space domain is discretized into 18,336 triangular meshes. All secondary fractures are explicitly displayed. Figure 15(3) shows the grid system for EDFM model and LTEDFM model. Figure 15(4) shows the MINC elements. Each matrix element is subdivided into five continua. To demonstrate the SRV effect on pressure distribution, we have simulated the flow of three different models. Figure 16 shows the pressure distribution for DFM, EDFM, and LTEDFM considering a large size SRV. We compare all grid pressures between two different simulation methods as shown in Fig. 17. The results show that the LTEDFM method exhibits good calculation accuracy when considering SRV considering a large size SRV. The simulation results indicate that all grid pressures are greater than 14 MPa after 400 days. The pressure drop for Case-C is the smallest among the first three cases in 400 days. The SRV greatly enhances the fluid mobility, and thus the fluid pressure can be maintained at a high level. We also run the simulations using the equivalent model. The upscaling properties is the same as case-B. Figure 18 shows the pressure distribution for DFM, EDFM, and LTEDFM using equivalent model. We also compare all grid pressures between two different simulation methods in Fig. 19, in which the LTEDFM results match very well with the DFM results for equivalent model.

  1. (4)

    Complex fracture system

Fig. 15
figure 15

Case-C: (1) Conceptual model of fractured horizontal well with four fractures with large size SRV; (2) Triangular meshes for DFM; (3) Square grids for EDFM and LTEDFM. (4) MINC element including five continua

Full size image
Fig. 16
figure 16

Pressure distribution of case-C using MINC model (400 days)

Full size image
Fig. 17
figure 17

Grid pressure relationship using MINC model (400 days)

Full size image
Fig. 18
figure 18

Pressure distribution of case-C using equivalent model (400 days)

Full size image
Fig. 19
figure 19

Grid pressure relationship using equivalent model (400 days)

Full size image

Figure 20(1) shows the schematics of a fractured horizontal well with complex fracture system. In this case, all hydraulic fractures are explicitly characterized. Totally, there are eight fracture and two perforation points located at (215, 295) m and (345, 355) m. Figure 20(2) shows the grid system for DFM model. The space domain is discretized with 5688 triangular meshes. Figure 20(3) shows the grid system for EDFM model and LTEDFM model. All fractures are discretized into 110 cells. Figure 21 shows the pressure distribution for DFM, EDFM, and LTEDFM considering complex fracture system. Figure 22 demonstrates the comparison of the pressure distribution obtained from different simulation methods, and a good agreement is observed between LTEDFM and other methods. The simulation results indicate that the fluid flow is strongly dependent on the fracture geometry, as the pressure wave firstly diffuses along the fracture and then spread to far field.

Fig. 20
figure 20

Case-D: (1) Conceptual model of complex fractured well; (2) Triangular meshes for DFM; (3) Square grids for EDFM and LTEDFM

Full size image
Fig. 21
figure 21

Pressure distribution of case-D (400 days)

Full size image
Fig. 22
figure 22

Grid pressure relationship of case-D (400 days)

Full size image

Application of LTEDFM

SRV effect on flow performance

All simulation above are under the condition with a constant well production rate. A very interesting topic is to analyze the SRV effect on wellbore pressure performance. Figure 23 shows the pressure drop of horizontal well for case-A, B, C, and D. As can be seen, case-A without considering SRV yields a rapid pressure drop compared with the other three models. The pressure drop obtained from case-C and case-D is slow because the SRV/complex fracture reduces the flow resistance around the well. Comparisons between the simulation results of case-B and case-C indicate that a larger SRV size contributes to a higher conductivity for fluid flow.

Fig. 23
figure 23

Pressure drop of horizontal well for case-A, B, C, and D

Full size image

Pressure analysis considering reservoir heterogeneity

In this part, we design a 2D case considering heterogeneity of both SRV and USRV. The object-based modeling is used to generate the permeability. The azimuth angle is set to 0, and the correlation length is set to 1000 m in both the major and minor correlation direction. The mean and deviation of the petrophysical parameter for each individual facies are given in Table 4. The vertical permeability field is set to equal to horizontal permeability. Figure 24 shows three classes of sampling result. The first class is for case-A and case-D without considering SRV. The second class is for case-B and the third class is for case-C.

Table 4 Mean and variance of permeability for SRV and USRV
Full size table
Fig. 24
figure 24

Permeability distribution of four cases

Full size image

Figure 25 shows the pressure drawdown versus time for different simulation cases. The figures show that the pressure drop of different cases diverge obviously from each other when considering permeability heterogeneity. All curves show a rapid pressure drop initially, but the speed of pressure drawdown gradually decreases with the elapse of time. For case-A, the pressure is much lower than other three cases because of the lowest conductivity around the well. It indicates that a larger-scale SRV is beneficial to maintain the pressure level. In Fig. 26, the effect of heterogeneity on pressure performance is assessed by different sampling with and without considering SRV. The pressure performance is notably different for different sampling models. After 1,000,0000 s production, the pressure has not yet spread to the reservoir boundary because of the low conductivity of USRV. When SRV exists, the pressure can diffuse to a relative farther distance from the well. For the same case, the pressure distribution varies from each other for different permeability heterogeneity. Therefore, neglecting the reservoir heterogeneity may lead to inaccurate forecast of pressure transient behavior.

Fig. 25
figure 25

Pressure drop of horizontal well considering reservoir heterogeneity

Full size image
Fig. 26
figure 26

Grid pressure for four cases

Full size image

Production rate variable versus time

The LTEDFM method can also be used to analyze the well production performance when the well rate varies with time. Case-A is taken as the basic simulation model, and five time intervals are set according to Table 5. The pressure distribution is presented in Fig. 27. For case 1, the pressure spreads slower because of the low production rate at initial time, while for case 3, the pressure spreads faster because of the high production rate at initial time. At 500 days, the reservoir boundary has undergone notable pressure drawdown. Production rate always changes with time for field practice, and the LTEDFM can simulate this situation and facilitate the history matching process.

Table 5 Production rate of three cases
Full size table
Fig. 27
figure 27

Grid pressure for three cases (500 days)

Full size image

3D SRV

In this subsection, the problem with a 3D SRV structure is presented. We extend the 2D model into a five-layer 3D model. Figure 28 shows the physical model of the considered reservoir with a size of 600 × 600 × 50 m. As shown, no SRV is created in the top and bottom layers. The SRV size is 40 m × 160 m × 10 m for layer 2 and layer 4, while the SRV size is 400 m × 200 m × 10 m for layer 3. The background grid size is 10 × 10 × 10 m. We set four main hydraulic fractures which have the same profile as test case-A–D. The four fractures are all vertical and fully penetrates the whole five layers. The well perforation points locate at the third layer. The total background grid number is 18000, while the total main hydraulic fracture cell number is 200. The main hydraulic fractures are discretized by two-dimensional planar cells in space but expanded to equi-dimensional cells during computation. The width of the main hydraulic fracture is 0.0001 m, and each fracture cell volume is 0.001 m3. The connection number between fracture cell and fracture cell belonging to different matrix grids is 180 in the horizontal direction and 160 in the vertical direction. The connection number between the background grid and main hydraulic fracture cell is 200. The production rate for each fracture is 0.5 m3/day. Figure 29 shows the pressure distribution of five layers at t = 10 days. There is a contrast between the pressure distribution of different layers and the pressure diffusion in layer 3 in the fastest among all layers. The reason is that layer 3 has the biggest SRV volume; thus, the flow resistance is significantly reduced. As a comparison, the pressure spreads very slowly in layer 1 and layer 5 as there is no SRV created in both layers. Figure 30 shows the pressure distribution of five layers at t = 2000 days. The pressure distribution of five layers tends to be consistent, which indicates that the SRV in layer 3 influences the pressure diffusion not only in horizontal direction, but also in the vertical direction.

Figure28
figure 28

Geological model of a 3D test case

Full size image
Fig. 29
figure 29

Pressure distribution of five layers at t = 10 days

Full size image
Fig. 30
figure 30

Pressure distribution of five layers at t = 2000 days

Full size image

Conclusion

We developed a novel numerical simulation model for fluid production from a complex fracture network. The mathematical model for flow in the main hydraulic fracture, SRV, and USRV is derived. The Laplace-transform embedded discrete fracture model is developed to solve for the pressure evolution. We applied the model to four kinds of hydraulic fracturing situations, namely hydraulically fractured horizontal well without SRV, hydraulically fractured horizontal well with SRV around each hydraulic fracture, hydraulically fractured horizontal well with an SRV containing all hydraulic fractures, and complex fracture system around the well. Some important conclusions are drawn as follows:

  1. (1)

    The EDFM method is extended to Laplace space to capture the main fracture geometry. By coupling the EDFM and MINC, the flow characteristics in SRV is precisely captured. The present solution for a series of test cases is validated by comparing the simulation results with other simulation methods, including the EDFM and DFM.

  2. (2)

    The detailed simulation of the four considered cases shows that SRV has a strong impact on pressure distribution. Generally, a larger SRV size leads to a lower flow resistance that is beneficial for fluid production.

  3. (3)

    Both equivalent model and multiple continuum model can be used for SRV description. The equivalent model concept has been used in some forward modeling studies as it can group the fracture and matrix system into a single-porosity media. The equivalent model can obtain an accurate prediction of pressure distribution as the multiple continuum model does.

  4. (4)

    The proposed workflow can be extended to more complex problems, including pressure analysis considering reservoir heterogeneity, variable production rate, and 3D SRV simulation, which reveal the strong practicality of the Laplace-transform embedded discrete fracture model.