Abstract
Oil depots along products pipelines are important components of the pipeline transportation system and down-stream markets. The operating costs of oil depots account for a large proportion of the total system’s operating costs. Meanwhile, oil depots and pipelines form an entire system, and each operation in a single oil depot may have influence on others. It is a tough job to make a scheduling plan when considering the factors of delivering contaminated oil and batches migration. So far, studies simultaneously considering operating constraints and contaminated oil issues are rare. Aiming at making a scheduling plan with the lowest operating costs, the paper establishes a mixed-integer linear programming model, considering a sequence of operations, such as delivery, export, blending, fractionating and exchanging operations, and batch property differences of the same oil as well as influence of batch migration on contaminated volume. Moreover, the paper verifies the linear relationship between oil concentration and blending capability by mathematical deduction. Finally, the model is successfully applied to one of the product pipelines in China and proved to be practical.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Background
At present, oil products are still one of the major energy sources in industries, such as power generation, transportation, metallurgy, chemical industry and light industry. According to statistics, refinery throughput is 76.8 × 106 bbl/d (BP 2014) and pipelines can provide an economic transportation mode for petroleum industries. As a result, in both producing and consuming countries, a large amount of oil products is transported from refineries or wharfs to oil depots through pipelines and then pumped to down-stream markets (Li et al. 2015; Liang et al. 2012a). Oil depots connecting up-stream sources and down-stream markets, play a vital role in the entire transportation system (Duan et al. 2016). However, it is complex to make a scheduling plan. On the one hand, oil depots have large turn-round volume and complex operations. On the other hand, the delivery of contaminated oil to the down-stream stations is a systematic issue and the operation of each oil depot is interrelated with others.
Until now, scheduling plans for most large and dynamic oil depot systems are made by field engineers subjectively and from experience. Therefore, the plans may not be globally optimum and lead to much higher operating costs (Barzin et al. 2015; Mitra et al. 2013). Based on the systematic optimal theory, a mathematic model in this paper is established to make scheduling plans for oil depots. The results show that the proposed method can improve the accuracy of scheduling, shorten the time of making decision and reduce operating costs.
1.2 Related work
Presently, many researchers have devoted themselves to pipeline scheduling, synthetically considering pipeline structure, time representation, modeling types, and solution approaches. The pipeline topological structures include: single source (Cafaro and Cerda 2008; Herrán et al. 2011; Relvas et al. 2009), multiple sources (MirHassani et al. 2013), tree-structure pipeline (Cafaro and Cerda 2011; Castro 2010; MirHassani and Jahromi 2011) and mesh-structure pipeline (Cafaro and Cerda 2012). The time representation usually includes discrete-time (Zhang et al. 2015) and continuous-time (Zhang et al. 2016b) representation. The MILP (Rejowski and Pinto 2004) and mixed-integer nonlinear programming (MINLP) (Cafaro et al. 2015b) models are established and solved by brand and bound algorithms, hybrid computational approach (Zhang et al. 2017) or heuristic algorithms (Rejowski and Pinto 2003) to work out the scheduling scheme. Research on oil depot constraints along pipelines has been focused and the pipeline and depot can be perceived as a whole system through related simplification. Mostafaei and Hadigheh (2014) and Ghaffari-Hadigheh and Mostafaei (2015) solved the scheduling issue with continuous-time representation based on the integration of MILP models, and they took minimum operation costs of the pipeline as the objective to satisfy depot requirements. Cafaro et al. (2015a) solved the same scheduling issue with a continuous-time MILP model which can accelerate the solving speed. The work of Cafaro and Cerda (2010) and MirHassani and BeheshtiAsl (2013) also considered dual purpose depots. Herran et al. (2012) proposed a multi-period MINLP model to optimize the plan to produce and transport multiple petroleum products from a refinery plant to several depots. Cafaro et al. (2015b) considered the pressure loss due to friction along single source pipelines with multiple depots, using nonlinear equations to rigorously track power consumption at each pipeline segment. These pipeline operation scheduling models consider the inventory of depots as a constraint. However, operation costs of each depot tank are not considered in their work.
Meanwhile, the depot operation is too complex to be described by a constraint. Some researchers have paid attention to this issue. Relvas et al. (2006) have considered a system that has a pipeline pumping oil from a refinery to an oil depot. Three different stages are considered in the process: loading from pipeline, performing settling and approving tasks, and unloading for clients. It combines the optimal pipeline schedule with tank inventory management. Relvas et al. (2013) have improved the model and make it easier to determine feasible time intervals or the number of pumping batches. Neiro et al. (2014) focused on the scheduling of an in-line diesel blending and distribution subsystem of an oil refinery, considering crude oil unloading, mixing, and inventory control, production unit scheduling, and finished product blending and shipping. However, these models are not comprehensive enough. In the real world, there are more than three stages in oil tanks. Operation among the oil tanks and operation of oil blending should be considered, and the differences of oil properties should also be taken into account.
When products are transported sequentially in pipelines, contaminated oil cannot be avoided, and it will influence the detailed scheduling (Liang et al. 2012b). A blending operation is one main method to deal with the contaminated oil. In previous research, the blending operations were taken into account as an important issue (Kolodziej et al. 2013; Pan and Wang 2006). Neiro et al. (2006) presented a stochastic multi-period model with two Lagrangian decomposition strategies to represent a petroleum refinery under uncertainty. Shi et al. (2014) presented a MILP discrete-time refinery scheduling model, establishing several controllable and realizable operation modes for production units by unit-wide predictive control. And a two-stage Lagrangian decomposition approach was applied to decompose a refinery scheduling problem (Shi et al. 2015). However, it is difficult to apply these methods above in dealing with scheduling of oil depots considering the special technological constraints for contaminated oil processing.
1.3 Contributions of this work
-
All the previous studies ignored the differences in the physical properties of different batches of one type of oil. While due to the production parameters, material ratio and other differences, the same type of oil produced at different times will also have differences in physical properties. The paper takes these differences into consideration.
-
The paper verifies the linear relationship between contaminated-oil concentration and blending capacity.
-
The paper considers the following operations in the oil depot: delivery, export, blending, fractionation and maintenance.
-
An approach for dealing with oil depot scheduling problem by MILP models is presented.
-
A Chinese case-study, a large scale of oil depot system of a refined oil products pipeline, is under research.
1.4 Paper organization
The adopted methodology and details of the mathematical model are given in Sects. 2 and 3 respectively. In Sect. 4 a real case in China is taken as an example, then the detailed scheduling in each oil depot is drawn, and the model’s feasibility is verified. Conclusions are provided in Sect. 5.
2 Methodology
2.1 Issue description
This work mainly focuses on making a schedule scheme with the least cost for transit depots to operate tank switching, contaminated oil delivery, back tail and treatment, under the condition that all the constraints can be satisfied. To deal with the issue, three aspects need to be considered: depot operation, oil blending and contaminated batches.
2.1.1 Operations in oil depots
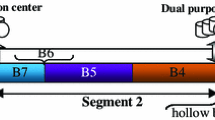
The transportation mode of product pipelines is multi-batch sequential transportation as shown in Fig. 1. The products are injected at the initial station and delivered at intermediate oil depots and the terminal depot. The exporting schedules of oil depots will be made according to the demand of down-stream markets. When batches migrate in the pipelines, contaminated oil cannot be avoided due to thermal diffusion and turbulent diffusion and its volume will increase with the migration of the interface between two batches. In actual production, contaminated oil is usually treated in two ways: blending and fractionation. The blending operation means contaminated oil can be blended with the oil in the exporting pipeline according to a certain proportion. Fractionation means contaminated oil is fractionated to qualified oil, and recycled to the oil tank. When a tank needs to be repaired, it is necessary to transfer the oil into other tanks with the same kind of oil in advance. It is called a tank switching operation. All of these operating processes are shown in Fig. 1. There are three kinds of refined oil products (ROP1, ROP2 and ROP3) and three kinds of contaminated oil (MO1, MO2 and MO3), which are given in different colors. In Fig. 1, green solid lines denote delivery lines; green dashed lines denote export lines; blue solid lines denote fractionation lines; blue dashed lines denote recycle lines; red dashed lines denote blending lines; and black lines denote switching lines.
2.1.2 Blending capacity
Compared with the fractionation operation, blending is more effective since it is simpler and more cost-effective. Blending operation can be classified into the following two cases. One is to put the light component oil into the heavy one, and the other the opposite, putting the heavy component oil into the light one. There are a variety of indicators to evaluate the quality of refined products, such as oxidation stability, sulfur content, octane number, ash, copper corrosion, moisture, mechanical impurities, lubricity, kinematic viscosity, pour point, cold filter plugging point, flash point, distillation range, density. The quality of the original oil is no doubt affected by the blending operation. The blending capacity means that maximum volume of contaminated oil can be treated under the premise of ensuring the oil’s standard. In actual production, due to production parameters, material ratio and other differences, the same kind of oil produced at different times will also have some differences. In other words, the oil may have different blending capacities. Considering the nonlinear effects of the blending oil on the physical properties and the mixing of different kinds of oils with different physical properties in a tank, the problem is more complex.
In the situation of heavy component oil blended with light contaminated oil, Li et al. (2011) have concluded that flash point is the most sensitive item according to the result of comparing test data with standards’ control indexes. With the increase in the proportion of light component oil in heavy oil, flash point decreases faster while other items change insensitively. Furthermore, when flash point becomes unqualified, others can still meet the requirements of the standard. By comparing test data of different mixing ratios with the result solved by each recommended experiential formula, Li et al. (2011) have concluded that the formula (1) agrees well with the experimental results, and the formula (1) can be used to calculate heavy component oil’s blending capacity.
where \(Vg_{c,j}\) denotes the blending capacity of heavy component oil \(c\) per unit volume mixing with contaminated oil \(j\); \(\lambda g_{j}\) denotes contaminated oil \(j\)’s ratio of containing light component oil; \(Ts_{c}\) denotes heavy component oil \(c\)’s flash point; and \(\overline{Ts}\) denotes the lowest flash point allowed.
The experiential formula of calculating contaminated oil’s flash point:
where \(Tsm_{1}\), \(Tsm_{2}\) denotes previously respective flash point of two same kinds of oil before mixing; \(\mu_{1}\), \(\mu_{2}\) denotes mixing ratio.
If light component contaminated oil is blended into heavy contaminated oil composed of two heavy components oil, the blending capacity of per unit volume of heavy contaminated oil will be:
where \(Vge_{c,j}\) denotes the blending capacity of heavy component oil \(c\) per unit volume mixing with contaminated oil \(j\) calculated by a standard formula.
Formula (3) is derived from physical equations, thus it can be used as a standard equation to calculate the blending capacity of contaminated heavy component oil per unit volume mixed with light oil.
If blending capacity is calculated by linear sum according to the blending proportion, it can be denoted by formula (4).
where \(Vgc_{c,j}\) denotes the blending capacity of heavy component oil \(c\) per unit volume mixing with contaminated oil \(j\) calculated by linear sum according to the blending proportion. \(e\) denotes the differences of formulas (3) and (4). If \(\mu_{2} = 1 - \mu_{1}\), \(\mu_{1} \in \left[ {0,1} \right]\) is given, \(e\) can be expressed by formula (5).
If \(\lambda g_{j}\) is a constant, the variables of \(e\) are only \(Ts_{1}\) and \(Ts_{2}\).
Within the scope of oil flash point, the differences of the results calculated by formulas (3) and (4) are very small, just as shown in Fig. 2. In other words, after mixing of the same kind of oil produced at different times, its blending capacity of mixing light component oil can be calculated by linear summing of these oils’ previous blending capacities.
In the situation of light component oil blended with heavy contaminated oil, Li et al. (2011) have concluded that the dry point is the most sensitive item according to the experimental data fitting and sensitivity analysis. In other words, other items can still meet the requirements of the standard when the dry point is just higher than its allowable limit. Therefore, in the mixed proportional range, formula (6) denotes the linear relation between dry point and mixing proportion. Moreover, formula (7) can be used to calculate the blending capacity of light component oil per unit volume mixing with heavy component oil.
where \(Vd_{c,j}\) denotes the blending capacity of light component oil \(c\) per unit volume mixing with contaminated oil \(j\); \(\lambda d_{j}\) denotes the proportion of heavy component oil included in contaminated oil \(j\); \(Tz_{c}\) denotes the dry point of light component oil \(c\); \(\overline{Tz}\) denotes the highest dry point allowed by the standard; \(Tzm_{1}\), \(Tzm_{2}\) denote the dry points of two same types of oil before blending.
The blending capacity of light component oil, mixed by the same kind of oil produced at different times can be calculated by linear summing of the two previous oils’ blending capacities from formulas (6) and (7).
Based on the analysis above, it is verified that the blending capacities of the same kind of oil can be added linearly. Besides, the blending capacity ratio regarding different sorts of contaminated oil of a certain kind of oil product should meet the condition:
2.1.3 Contaminated oil batch
The products, pumped in sequence at the initial station, will generate two different types of contaminated oil with the migration in the pipeline. The first one is caused by two kinds of oil with similar components. The other is caused by two kinds of oil with different components.
The first kind of contaminated oil is usually neglected in actual production because it has little influence on physical properties of qualified oil. The intermediate stations usually cut the contaminated oil into two segments. In other words, the contaminated oil is cut at the middle position and offloaded into two qualified oil tanks respectively. As shown in Fig. 1, intermediate oil depots and the terminal oil depot do not have contaminated oil tanks for MO3 because the components of ROP1 and ROP2 are similar. The two segments of MO3 are transported, respectively, into corresponding qualified oil tanks. Therefore, MO3 is not taken into consideration in the paper.
The second kind of contaminated oil is usually cut into four segments. As shown in Fig. 1, ROP2 and ROP3 have large differences. When contaminated oil is caused by ROP2 and ROP3, the beginning and the ending segments of contaminated oil are delivered into the qualified oil tank, and the other two segments are, respectively, delivered into two different contaminated oil tanks. The former part MO2 of the two intermediate segments includes more ROP3, while the latter part includes more ROP2.
The volume of contaminated oil continuously increases with the migration of contaminated oil in the pipeline due to the influence of convection and diffusion. Meanwhile, due to the nonlinear growth of the volume of contaminated oil, the delivery plan for contaminated oil at one station may have effects on the oil volume and the arrival time at other stations, thereby affecting other stations’ schedules. Moreover, the delivery plan for contaminated oil is related to the plan of blending and fractionation; thus, it also has effects on other stations’ scheduling plans such as export and switch. As a result, considering the nonlinear volatility of the volume of contaminated oil in the pipeline, the entire scheduling of oil depots along products pipeline will form a unified entity with its sub-parts affecting each other, which makes the solution of scheduling plan much more complex. According to Austin et al. (1963), formula (9) is mostly used to calculate the volume of contaminated oil.
If the injection scheduling of the initial station and the delivery scheduling of other stations are known, the flow rate and oil type in each time window can be obtained, and \(Re_{i - 1,km}\) is known. Formula (9) is a nonlinear equation \(Lmd_{i,km} = f_{i,km} (Lmc_{i - 1,km} )\) as shown in Fig. 3. A nonlinear equation would add to the complexity of the optimal model. This paper comes up with a method of linearization in the following stages: the independent variable is divided into several sections, and at each section, the solution of all the independent variables is represented by the solution of the average value of the independent variable. In this way, the nonlinear equation can be converted into a sectional linear equation like stairs. As shown in Fig. 3, \(Lmc_{i - 1,km}\) is divided into several sections. If \(Lmc_{i - 1,km}\) belongs to section \(b\), \(Lmc_{i - 1,km} \in [Lmi_{i - 1,km,b} ,Lma_{i - 1,km,b} ]\). In this section, \(Lmd_{i,km}\) identically equals \(f_{i,km} \left( {\frac{{Lma_{i - 1,km,b} - Lmi_{i - 1,km,b} }}{2}} \right)\).
2.2 Model requirements
The model is formulated as MILP and the optimization is executed using MATLAB R2014a. A detailed scheduling of oil depots along product pipeline can be obtained by solving the model.
Given:
-
Time horizon of studying.
-
Basic information of pipeline and stations: pipeline information, station location, the count of oil tanks and contaminated oil tanks, inventory limits of oil tanks, the capacity of fractionation facilities, the initial storage and blending capacities of oil in tanks.
-
Injection order and volume of oil in the initial station, the blending capacities of batches.
-
Approximate scheduling of delivery: starting and ending time of delivery operations at oil depots, and delivery volume.
-
Approximate scheduling of export: starting and ending time, oil type and volume of export operations.
-
Approximate scheduling of maintenance: starting and ending time of oil tank’s maintenance.
Determine:
-
Detailed scheduling of delivery: the volume of delivered oil at oil tanks, the actual time and volume of delivering oil, the number of contaminated oil tanks.
-
Detailed scheduling of export: the number of exporting oil tanks and the corresponding volume needed to be exported.
-
Detailed scheduling of blend: the type of contaminated oil, the number of contaminated oil tanks and the volume of oil.
-
Detailed scheduling of fractionation: the type of contaminated oil, operating time, the volume of contaminated oil, the number of contaminated oil tanks.
Objective:
Minimize the total costs of delivery, export, blending, fractionation and tank switching operations of all the oil tanks during the study horizon to schedule the oil tanks’ detailed operation under various operational and technical constraints.
In order to build and solve the model effectively, assumptions are made as follows:
-
(1)
In the light of the lower flowrate of contaminated oil delivered at intermediate stations and the shorter contaminated length, the influence of contaminated oil delivery operation on batches’ flowrate and time of arriving at stations is not taken into consideration.
-
(2)
The oil physical properties do not change with temperature.
-
(3)
The given scheduling for batch delivery and oil export at transit oil tanks is reasonable, which can be satisfied with batch migration, hydraulic and tank inventory constraints.
-
(4)
Supposing that the oil in the tank and the oil from the pipeline have been fully mixed, and their physical properties are same.
3 Mathematical model
3.1 Time windows
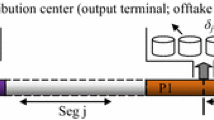
The time nodes, usually fixed, of export and delivery at stations are given in the paper. However, considering the solution of the detailed scheduling plan, the way of just dividing time windows by fixed nodes cannot meet the model’s requirement. The reason is that the approximate scheduling plan is different from a detailed scheduling plan which needs to determine the exact time nodes of each operation and the corresponding oil volume of each tank. So each operation at the oil depots must specify an object in each time window, and the starting and ending time of each time window must correspond with each operation. If the time windows were divided only by fixed time nodes, they would be too sparse to affect the solution. As shown in Fig. 4a, all the fixed time nodes are sorted by time order, and the space between two adjacent time nodes is a time window. Taking time window 6 as an example, according to scheduling requirements and operation constraints, product oil cannot be delivered into several tanks at one time, that is, the product oil can only be delivered into one oil tank during the entire time window. If time window 6 is long enough that the planned volume of oil is more than each oil tank’s capacity, the model will have no solution due to its contradictory constraints.
To solve the issue above, in this paper we bring up a fixed-continuous mixed time expression. As illustrated in Fig. 4b, just like the method of dividing fixed time windows, all the time nodes are sorted by time order and several continuous time nodes are inserted into the space between fixed time nodes. Those continuous time nodes need to meet the requirements of the time order. In this way, the whole study horizon is divided into more time windows than that in previous studies. As shown in Fig. 4, the time window 6, divided by fixed time expressions, is divided into three time windows, 10, 11 and 12, using fixed-continuous mixed time expressions. Therefore, the oil, which used to be delivered in time window 6, can be mostly delivered into three tanks, so the oil scheduling system is more flexible than that in previous studies.
3.2 Objective function
The objective of the model is to draw up a lowest cost scheduling plan while meeting each constraint. The cost of oil depots along a products pipeline mainly includes blending costs, fractionation costs and switching costs. The blending costs are related to the volume of oil need to be disposed of. The expression of the objective function is:
3.3 Delivery constraints
If the binary variable denoting the delivery state of an oil tank is 0, the delivery volume is 0. Supposing M is a large constant.
During the time when contaminated oil j is passing through the intermediate station i, the intermediate station i can choose to deliver contaminated oil j or not. In order to reduce the effect of delivering operations on the batch transportation, the ratio of the volume of contaminated oil need to be delivered and the volume of arriving oil in the period should be smaller than the allowable maximum value.
When contaminated oil arrives at the terminal station, all of it should be delivered.
Moreover, the delivering flow rate must be larger than the minimum flow rate.
If contaminated oil j has not arrived at station i, it cannot be delivered at station i.
During the time when station i is delivering oil c, there must be one oil tank receiving the oil each time.
If station \(i\) is not delivering oil \(c\), its binary variable denoting the state of oil tank’s delivery is 0.
According to the definition of a binary variable, only when the state binary variable of last moment and this moment are 0 and 1, respectively, can the operation binary variable of this moment be 1. Because the objective function is to obtain the minimal costs and is positively correlated with operation binary variables, the variable can be constrained only by determining its lower bound.
During the delivering time at a station, the amount of delivery for all the tanks is equal to the total volume of oil arriving at the station in the corresponding period.
3.4 Export constraints
Due to the constraints of export facilities, only one oil tank is allowed to export oil at a station at the same time.
If the state binary variable of an oil tank is 0, its blending capacity of exporting oil is 0.
The state binary variable of an oil tank is 0 if it is not exporting an oil.
During the time of export, the sum of the volume of export and blending operations in all time windows should be in the allowable range.
According to formula (8a, 8b), the blending capacity’s percentage for export oil blended with different kinds of contaminated oil is a constant value.
The relationship between export operating binary variable and export state binary variable is similar to formula (19).
3.5 Blending constraints
If the blending state binary variable of a contaminated oil tank is 0, the blending volume oil is 0.
According to the processing requirements, a blending operation happens only when oil is exported to other stations. If there is no export operation, all oil tanks’ state binary variables are 0.
During blending operations, the blending volume of contaminated oil should be less than its blending capacity. Moreover, the flow of blending operation should be more than the minimum flow rate.
The relationship of blending operation binary variable and blending state binary variable is similar to formula (19).
Due to the constraints of blending devices, only one contaminated oil tank at a station is allowed to blend contaminated oil at a time.
3.6 Fractionation constraints
If the fractioning state binary variable of a contaminated oil tank is 0, the volume of fractionation is 0.
The volume of fractionating contaminated oil should be within the upper and lower bounds at any moment.
The relationship of the fractionating operation binary variable and fractionating state binary variable is the same as formula (19).
The fractionated oil should be pumped into the corresponding oil tank. The fractionated volume of all kinds of oil is related to the contaminated oil’s previous volume, type and fractionation loss.
If the fractionating recycle state binary variable of an oil tank is 0, its fractionating blending volume is 0.
The relationship of a fractionating recycle operating binary variable and the fractionating blending state binary variable is the same as formula (19).
3.7 Maintenance and switch-tank constraints
If a tank needs repair, oil should be pumped into other oil tanks storing the same kind of oil. If the switching state binary variable of a contaminated oil tank is 0, the volume of switch-tank oil is 0.
If the switching state binary variable of a contaminated oil tank is 0, its blending capacity of exchanging to other oil tanks is 0.
The relationship of switching operation binary variable and switching state binary variable is the same as formula (19).
According to formula (19), the blending capacity ratio of exchanging oil blended with different kinds of contaminated oil is a constant.
3.8 Oil tank and contaminated oil tank constraints
The current inventory of a contaminated oil tank is the sum of the accumulated oil of last moment, the contaminated oil delivered at this moment and the switching oil minus blended and fractionated oil.
Without maintenance, the inventories of contaminated oil tanks are in the allowed range.
A contaminated oil tank is not allowed to take two operations such as blend, switch and fractionation at the same time.
The blending capacity of an oil tank is the sum of its blending capacity of last moment, delivery, recycle and switching oil’s blending capacity during this period minus export oil’s blending capacity.
The inventory of an oil tank is the sum of its volume at the last moment, delivered and switched volume during this period minus the volume of export.
Without maintenance, the blending capacity of oil stocked in oil tanks has certain limitation due to the inventory of oil tanks.
The inventory of oil tanks, the volume of switch and export operation should be in a range of volume.
There should be a certain ratio between the inventory of oil tanks and the blending capacity of oil tanks.
No oil tank is allowed to do delivery, export, switch, blending and fractionation operations simultaneously at the same time.
3.9 Contaminated oil batch constraints
After linearizing Austin’s formula, the length of contaminated oil of each batch when arriving at stations can be denoted as follows:
The length of contaminated oil when it leaves the station is equal to its arriving length minus the delivering volume divided by pipeline cross-sectional area. All contaminated oil should be delivered to the terminal oil depot.
Arriving and leaving time of mixed oil at one station can be modified by the calculated length of contaminated oil.
When cutting the contaminated oil into four segments, the time of the former contaminated oil batch leaving the station is equal to the time of the latter arriving, and is also equal to the average time of the sum of contaminated oil batches in and out.
3.10 Time node constraints
The following time nodes cannot be sorted earlier than the time nodes in the front, while the time nodes in the front cannot be sorted later than the time node behind.
All time nodes, such as the starting and ending time of delivery, export, maintenance and study horizon, the arriving time of contaminated oil batch, are regarded as the model’s time nodes. Because the fixed time nodes are given as model’s known parameters, the sorting order of time nodes are also the model’s known parameters sorted by fixed-continuous time expression. Taking \(k\tau_{t}\) and \(k\theta_{t}\) as internal variables, their expressions and constrains are shown as follows:
4 Results and discussion
4.1 Example 1
Provided that there is a single delivery station, the model will be simplified as a depot scheduling model. The model is solved by MATLAB 2014b solver with Intel Core i7-4770k (3.50 GHz) hardware.
There is a transit depot, which can respectively stock 0# diesel (0#D), 93# gasoline (93#G) and 97# gasoline (97#G), as well as include oil tanks for high diesel-cut contaminated oil (DMO) and high gasoline-cut contaminated oil (GMO). The basic parameters of each oil tank are shown in Table 1. And the physical properties of each batch of oil are shown in Table 2.
In this paper, the MILP model is established for the transit depot. The studying horizon is 243 h. There are a total of six times for oil delivery and export. The scheduling scheme of delivery and export are shown in Tables 3 and 4.
In this paper, the cost of oil and contaminated oil tank’s operation is 100 CNY per unit, and the cost of fractionating contaminated oil is 10 CNY/m3. Because blending contaminated oil can increase the benefits of enterprise, the cost of contaminated oil is −1 CNY/m3. According to the method in the paper, a MILP model is established to solve the oil transit depot scheduling issue and the results are shown in Table 5.
According to Tables 3 and 4, the model is established to solve the detailed scheduling scheme. With the prerequisite that the scheduling of delivery and export and the tank inventory are met, oil can be delivered (or exported) into (or from) specific tanks in turn and switching frequency of tanks can be reduced as much as possible. The contaminated oil delivered is going into back tail treatment. The detailed scheduling scheme of oil tanks obtained by the model is shown in Fig. 5, and the detailed scheduling scheme of contaminated oil tanks is shown in Fig. 6. Figures 5 and 6 illustrate that the oil tank scheduling can fully meet the needs of the entire system. During the period of export, the volume sum of exporting oil and blending contaminated oil is equal to the export demand.
The inventory of each oil tank varies with time as shown in Fig. 7, and the inventory variation of contaminated oil tanks with time is shown in Fig. 8. The results indicate that if every time the oil delivery (or export) into (or from) tanks for only once is guaranteed, both the operating cost and oil evaporation loss will be cut down. However, the large amount of the second delivery of diesel leads to the need for two diesel tanks. GMO and DMO should go to back tail as far as possible before oil is to be exported every time. Therefore, at the moment when the scheduling ends, the tank level of each contaminated oil tank is below the lower limit.
Inventory of oil tanks. Notes: 1#I denotes the inventory of 1# oil tank. 2#I denotes the inventory of 2# oil tank. LU denotes the upper bound of the oil tank. LL denotes the lower bound of the oil tank. 1#BCH denotes the blending capacity of 1# oil tank blending with heavy component oil. 2#BCH denotes the blending capacity of 2# oil tank blending with heavy component oil. 1#BCL denotes the blending capacity of 1# oil tank blending with light component oil. 2#BCL denotes the blending capacity of 2# oil tank blending with light component oil. BC denotes the blending capacity
Inventory of contaminated oil tanks. Notes: 1#HI denotes the inventory of 1# heavy component oil tank. 2#HI denotes the inventory of 2# heavy component oil tank. 1#LI denotes the inventory of 1# light component oil tank. 2#LI denotes the inventory of 2# light component oil tank. LU denotes the upper bound of the oil tank. LL denotes the lower bound of the oil tank
4.2 Example 2
In this section, a real-world case of a depot system in China is given and its mathematic model is established according to the proposed MILP formulation. The model is solved by MATLAB 2014b solver on a computer with Intel Core i7-4770k (3.50 GHz) hardware.
There are 3 oil depots (1#OD, 2#OD and 3#OD) along the products pipeline, which can respectively stock 0# diesel (0#D), 93# gasoline (93#G) and 97# gasoline (97#G). The basic parameters are shown in Table 6. In the whole system, only a contaminated oil fractionation equipment with 20 m3/h processing capacity is settled at 3#OD. Before optimization, a large amount of contaminated oil is transported to 3#OD, for the scheduling concern of 1#OD and 2#OD. When a lot of contaminated oil cannot be blended with export operation at 3#OD, it is necessary to fractionate contaminated oil by fractionation equipment, which increases the production costs.
In this paper, the MILP model is established for this oil depot system. The studying horizon is 175 h. 0#D(2#) and 93#G(2#) in 3#OD, respectively, need to be repaired during 25.5–69.4 and 120.1–165.9 h. The approximate delivery scheduling plan is shown in Fig. 9. There are five batches (B1, B2, B3, B4 and B5), and the physical properties of each batch of oil are shown in Table 7. Each oil depot needs to accept a specific volume of delivered oil at the specified time according to the scheduling plan. Moreover, oil depots need to export oil in the specified time according to the demand of down-stream markets. The scheduling plan of export is also shown in Fig. 9.
In this paper, the cost of oil and contaminated oil tank’s operation is 100 CNY per unit, and the cost of fractionating contaminated oil is 10 CNY/m3. Because blending contaminated oil can increase the benefits of enterprise, the cost of contaminated oil is -1 CNY/m3. According to the method in the paper, a MILP model is established to solve the oil depot system scheduling issue and the results are shown in Table 8.
The detailed scheduling plan of oil tanks is shown in Fig. 10, and the detailed scheduling plan of contaminated oil tanks is shown in Fig. 11. Figures 10 and 11 show that the oil tank scheduling can fully meet the needs of the entire system. During the period of export, the volume sum of exporting oil and blending contaminated oil is equal to the export demand. For example, the volume of 0#D needed to be exported in 1#OD is 9200 m3 during 43.1–52.4 h. The corresponding result after optimization is that 0#D(2#) exports 9105 m3 oil and DMO(1#) is blended with 95 m3 high diesel-cut contaminated oil. At the same time, the model takes the tank’s maintenance into consideration. Before the maintenance of 0#D(2#) and 93#G(2#) in 3#OD, the oil in them are switched into other oil tanks with the same kind of oil.
During 92.4–116.6 h, 1#OD is required to delivery 93# gasoline oil of 11,234 m3. Due to the upper limit of 10,000 m3, there should be two oil tanks for receiving oil in turn and 1#OD should take first. When it comes to 110 h, 1#OD is required to export 93# gasoline oil of 8724 m3. Since the model aims to minimize the switching times of tanks and only 1#OD inventory can satisfy the export requirement, 1#OD should start to export instead of receiving oil, while 2#OD should start to receive oil.
The inventory of each oil tank varies with time as shown in Fig. 12. Considering the limit of inventory, some operating plan should be divided into several periods, for instance, the same kind of oil is stocked into different oil tanks and is exported from different oil tanks. For example, 3#OD needs to deliver 8279 m3 97#G during 150.3–165.9 h and the results are divided into 3 periods. Firstly, during 150.3–160.1 h, 2784 m3 oil is delivered into 97#G(1#). Secondly, after this period, the station needs to export 97#G. However, the capacity of 97#G(1#) is low so it is necessary to stop delivering oil into 97#G(1#) and to start exporting 97#G. Therefore, the oil is delivered into 97#G(2#). Thirdly, 97#G(1#) reaches the lower bound at 165.1 h, so it is necessary to stop exporting oil from 97#G(1#) and to start delivering oil. Finally, 97#G(2#) takes export operation.
The inventory variation of contaminated oil tanks with time is shown in Fig. 13. The volume variation of two contaminated-oil batches in the pipeline is shown as Fig. 14. It can be seen that, although the initial inventory of the tank is relatively high, using only the blending operation can better balance the contaminated oil to avoid the fractionation operation, thereby reducing the operating costs.
Inventory of contaminated oil tanks. Notes: 1#HI denotes the inventory of 1# heavy component oil tank. 2#HI denotes the inventory of 2# heavy component oil tank. 1#LI denotes the inventory of 1# light component oil tank. 2#LI denotes the inventory of 2# light component oil tank. LU denotes the upper bound of the oil tank. LL denotes the lower bound of the oil tank
In the light of the above results, it is general to finish the valve opening operation only once when oil delivery and export are performed every time. Since DMO can be easily contaminated by diesel oil, it should be treated with back tail for the sake of satisfying the inventory constraints of contaminated oil tanks. Similarly, so does gasoline oil when exported. But for some special cases such as 97# gasoline oil flowing into 3#OD, it is necessary to operate two tanks simultaneously because the scheduling time overlaps and both the gasoline oil tanks are 5000 m3. When delivery starts, the 1#OD should be first opened and then the 2#OD; and when it turns to the 2#OD, the 1#OD should carry out export. In the light of 3#OD as the terminal depot, thus, it required to blend some DMO so as to ensure contaminated tanks can once receive DMO from B5 batch for once. When the 1#OD inventory comes up to the lower limit, the 2#OD is blended with GMO for export. It is seen from the Austin formula that the contaminated oil volume will come be the lowest in a scheduling scheme if there is no contaminated oil delivery. A large amount of contaminated oil needs to be delivered in 3#OD at the terminal station, yet there is not enough space for DMO delivered last time which remains unprocessed, leading to some DMO should be shared at intermediate stations.
5 Conclusion
The paper puts forward a new view of oil blending capacity and verifies the linear relationship of mixing oil concentration and oil blending capacity. The paper also presents a new method for detailed scheduling of oil depots along a product pipeline based on a MILP model. The model established in this paper considers the issues such as differences of oil physical properties, the growth of contaminated-oil batches, the type of contaminated oil and the different operation modes in oil depots and those issues make the formulation more practicable but more complex. The model, aiming at solving the minimum cost scheduling of oil depots system, takes the cost of blending and fractionation as well as the operation of oil and contaminated oil tanks into consideration. The MILP model, considering the constraints of delivery, export, blending, fractionation, maintenance, switching, oil and contaminated oil tank, contaminated oil batch and time node, is solved by MATLAB 2014.
This method is successfully applied to a Chinese actual oil depot system, which includes three oil depots. All of them can deliver and export 0# diesel, 93# and 97# gasoline. There are, respectively, 7 oil tanks in 1# and 2# oil depot, and 10 oil tanks in 3# oil depot. By solving the model, a 175 h detailed scheduling plan is given. Moreover, the contaminated oil is properly dealt with in real time by blending operations, so the plan effectively avoids the accumulation of contaminated oil in 3# oil depot, which increases the profits of oil depots. At the same time, there is no need to make fractionation operation which saves a lot of costs. As a result, the model is feasible and effective.
Product pipeline scheduling plans are closely related to the oil depots along the pipeline. The paper takes batch migration as a known condition and only focuses on oil depots scheduling plan. In the future, the authors intend to do more research on an entire optimization of batch migration and oil depot scheduling plans. When establishing the optimization model, the contaminated plug in pipelines is regarded as a contamination interface. While in the real pipeline operation, the contaminated plug will influence the time of batches arriving at stations, resulting in lower accuracy of scheduling schemes. Thus the further research should take the contaminated plug into consideration. Moreover, the following points should be paid attention during oil delivery and export:
-
Minimize the volume fluctuation when oil tanks receive and export oil.
-
Switching operation should better happen in the daytime.
-
Avoid start or stop pumps during the peak period of electricity consumption as much as possible.
In this way, there will be further development to improve the model if the listed factors above are taken into account.
Abbreviations
- \(\forall i \in I = \{ 1, \ldots ,i_{\hbox{max} } \}\) :
-
The set of the numbers of stations in the system, \(i_{\hbox{max} }\) denotes the maximum number of stations
- \(\forall j \in J = \{ 1, \ldots ,j_{\hbox{max} } \}\) :
-
The set of the numbers of all kinds of contaminated oil in the system, 1 denotes high gasoline-cut contaminated oil, \( j_{\hbox{max}} = 2\), in this work, denotes high diesel-cut contaminated oil
- \(\forall c \in C = \{ 1,2, \ldots, c_{\hbox{max} } \}\) :
-
The set of the numbers of all kinds of oil in the system, \(c_{\hbox{max} }\) denotes the maximum number of oil types
- \(\forall gm \in Gm_{i,j} = \{ 1,2, \ldots, mm_{i,j} \}\) :
-
The set of the numbers of contaminated oil j tanks at station i, \(mm_{i,j}\) denotes the maximum number of those oil tanks
- \(\forall go \in Go_{i,c} = \{ 1,2, \ldots, mo_{i,c} \}\) :
-
The set of the numbers of oil c tanks at station i, \(m{\text{o}}_{i,c}\) denotes the maximum number of those oil tanks
- \(\forall t \in T = \{ 1,2, \ldots ,t_{\hbox{max} } \}\) :
-
The set of the numbers of all time nodes sorted in order in the study horizon, \(t_{\hbox{max} }\) denotes the maximum number of time nodes
- \(Tdy_{i,j,km}\) :
-
The set of the numbers of time nodes during batch \(km\)’s contaminated oil \(j\) crossing over station \(i\)
- \(Tdn_{i,j}\) :
-
The set of the numbers of time nodes during contaminated oil \(j\) not crossing over station \(i\)
- \(Toy_{i,kd}\) :
-
The set of the numbers of time nodes during station \(i\) delivering oil at first \(kd\) times
- \(Ton_{i,c}\) :
-
The set of the numbers of time nodes during station \(i\) not delivering oil \(c\)
- \(Tey_{i,kt}\) :
-
The set of the numbers of time nodes during station \(i\) exporting oil at first \(kt\) times
- \(Ten_{i}\) :
-
The set of the numbers of time nodes during station \(i\) not exporting oil
- \(\forall p \in P\) :
-
The set of the numbers of sections after linearizing Austin’s formula
- \(\forall b \in B\) :
-
The set of the numbers of the volume divided in sections
- \(\forall kd \in KD_{i}\) :
-
The set of the times of station \(i\) delivering oil
- \(\forall kt \in KT_{i}\) :
-
The set of the times of station \(i\) exporting oil
- \(\forall km \in KM_{i}\) :
-
The set of the times of contaminated oil batches crossing station \(i\)
- \(\forall ks \in KS_{i}\) :
-
The set of the times of station \(i\) in maintenances
- \(\lambda_{1j}\) :
-
The cost of blending contaminated oil \(j\) per unit volume
- \(\lambda_{2j}\) :
-
The cost of fractionating oil \(j\) per unit volume
- \(\lambda_{3}\) :
-
The operating cost of oil tanks and contaminated oil tanks
- \(\alpha_{\hbox{max} }\) :
-
The maximum ratio of delivering volume of contaminated oil and the volume of oil existed
- \(Qg_{i}^{t}\) :
-
The flow arriving at station \(i\) through pipeline at time node \(t\), m3/h
- \(Qmd_{\hbox{min} }\) :
-
The minimum delivering flow of contaminated oil, m3/h
- \(Qmh_{\hbox{min} }\) :
-
The minimum flow of blending operation, m3/h
- \(Qfax_{i}\) :
-
The maximum flow of fractionation operation at station \(i\)
- \(Qfin_{i}\) :
-
The minimum flow of fractionation operation at station \(i\)
- \(Voy_{i,c,kd}\) :
-
The volume of oil \(c\) at station \(i\) at first \(kd\) times
- \(Vay_{i,c,kd,j}\) :
-
The total blending capacity of oil \(c\) per unit volume, delivered at station \(i\) at first \(kd\) times, to blend contaminated oil \(j\), m3
- \(\beta in_{j}\) :
-
The minimum value of blending capacity of total oil per unit volume in study system to blend contaminated oil \(j\), m3
- \(\beta ax_{j}\) :
-
The maximum value of blending capacity of total oil per unit volume in study system to blend contaminated oil \(j\), m3
- \(\eta_{{j,j^{{\prime }} }}\) :
-
The blending capacity ratio of oil to blend contaminated oil \(j\) and to blend contaminated oil \(j^{{\prime }}\), m3
- \(Veax_{i,c,kt}\) :
-
The upper limit of exporting oil \(c\) at station \(i\) at first \(kt\) times, m3
- \(Vein_{i,c,kt}\) :
-
The lower limit of exporting oil \(c\) at station \(i\) at first \(kt\) times, m3
- \(\varphi_{c,j}\) :
-
The blending capacity of oil \(c\) fractionated per unit volume to blend contaminated oil \(j\), m3
- \(Vmx_{i,j,gm}\) :
-
The upper limit of contaminated oil \(j\) tank \(gm\) at station \(i\), m3
- \(Vmn_{i,j,gm}\) :
-
The lower limit of contaminated oil \(j\) tank \(gm\) at station \(i\), m3
- \(Vsx_{i,c,go}\) :
-
The upper limit of contaminated oil \(c\) tank \(go\) at station \(i\), m3
- \(Vsn_{i,c,go}\) :
-
The lower limit of contaminated oil \(c\) tank \(go\) at station \(i\), m3
- \(\xi_{j,c}\) :
-
The volume of oil \(c\) fractionated by contaminated oil \(j\) per unit volume, m3
- \(\delta\) :
-
The loss ratio of fractionation
- \(\omega_{i,km,p}\) :
-
The calculated equivalent of contaminated oil batches length at \(p\) linear section during the contaminated oil arriving at station \(i\) at first \(km\) times
- \(Lma_{p}\) :
-
The upper limit of contaminated oil at \(p\) linear section calculated by Austin’s formula, m
- \(Lmi_{p}\) :
-
The lower limit of contaminated oil at \(p\) linear section calculated by Austin’s formula, m
- \(Voma_{b}\) :
-
The upper limit of the volume in section b, m3
- \(Vomi_{b}\) :
-
The lower limit of the volume in section b, m3
- \(Lmg_{i,km}\) :
-
The predicted length of contaminated oil arriving at station \(i\) at first \(km\) times, m
- \(\Delta \tau g_{i,km}\) :
-
The predicted time of contaminated oil crossing over station \(i\) at first \(km\) times, h
- \(\tau dg_{i,j,km}\) :
-
The predicted time of the head of total contaminated oil batch arriving at station \(i\) at first \(km\) times, h
- \(\tau cg_{i,j,km}\) :
-
The predicted time of the end of total contaminated oil batch arriving at station \(i\) at first \(km\) times, h
- \(\tau odb_{i,kd}\) :
-
The starting time of delivering oil at station \(i\) at first \(kd\) times, h
- \(\tau odn_{i,kd}\) :
-
The ending time of delivering oil at station \(i\) at first \(kd\) times, h
- \(\tau oeb_{i,kt}\) :
-
The starting time of exporting oil at station \(i\) at first \(kt\) times, h
- \(\tau oen_{i,kt}\) :
-
The ending time of exporting oil at station \(i\) at first \(kt\) times, h
- \(\tau osb_{i,ks}\) :
-
The starting time of maintenance at station \(i\) at first \(ks\) times, h
- \(\tau osn_{i,ks}\) :
-
The ending time of maintenance at station \(i\) at first \(ks\) times, h
- \(\tau b\) :
-
The starting moment at study horizon, h
- \(\tau n\) :
-
The ending moment at study horizon, h
- \(ds_{i,c,kd}\) :
-
The binary variables of delivering oil. If oil \(c\) is delivered at station \(i\) at first \(kd\) times, \(ds_{i,kd,c} = 1\), if not, \(ds_{i,kd,c} = 0\)
- \(es_{i,c,kt}\) :
-
The binary variables of exporting oil. If oil \(c\) is exported at station \(i\) at first \(kt\) times, \(es_{i,c,kt} = 1\), if not, \(es_{i,c,kt} = 0\)
- \(mv_{i,j,gm}^{t}\) :
-
The binary variables of contaminated oil tank’s maintenance. If contaminated oil \(j\) tank \(gm\) at station \(i\) needs to be required during moment \(t\) to \(t + 1\), \(mv_{i,j,gm}^{t} = 1\), if not \(mv_{i,j,gm}^{t} = 0\)
- \(ov_{i,c,go}^{t}\) :
-
The binary variables of contaminated oil tank’s maintenance. If contaminated oil \(c\) tank \(go\) at station \(i\) needs to be required during time node \(t\) to \(t + 1\), \(ov_{i,c,go}^{t} = 1\), if not, \(ov_{i,c,go}^{t} = 0\)
- \(ik_{j,km}\) :
-
The distinguishing binary variables of the contaminated oil in front. If the contaminated oil \(j\) is ahead of others with the contaminated oil at first \(km\) times crossing over the station \(i\),\(ik_{j,km} = 1\), if not, \(ik_{j,km} = 0\)
- \(ikd_{t,kd}\) :
-
The distinguishing binary variables of delivering moments. If time node \(t\) is in the period of delivering oil at first \(kd\) times, \(ikd_{t,kd} = 1\), if not, \(ikd_{t,kd} = 0\)
- \(\theta odb_{i,kd,t}\) :
-
The distinguishing binary variables of the starting moments sorted for delivering oil. All the time nodes are in ascending order, so if the starting moment of delivering oil at station \(i\) at first \(kd\) times is sorted in first \(t\) place, \(\theta odb_{i,kd,t} = 1\), if not, \(\theta odb_{i,kd,t} = 0\)
- \(\theta odn_{i,kd,t}\) :
-
The distinguishing binary variables of the ending moments sorted for delivering oil
- \(\theta oeb_{i,kt,t}\) :
-
The distinguishing binary variables of the starting moments sorted for exporting oil
- \(\theta oen_{i,kt,t}\) :
-
The distinguishing binary variables of the ending moments sorted for exporting oil
- \(\theta osb_{i,ks,t}\) :
-
The distinguishing binary variables of the starting moments sorted for maintenance
- \(\theta osn_{i,ks,t}\) :
-
The distinguishing binary variables of the ending moments sorted for maintenance
- \(\theta md_{i,j,km,t}\) :
-
The distinguishing binary variables of the starting moments sorted for delivering contaminated oil
- \(\theta mc_{i,j,km,t}\) :
-
The distinguishing binary variables of the ending moments sorted for delivering contaminated oil
- \(\theta sb_{t}\) :
-
The distinguishing binary variables of the starting moments at study horizon
- \(\theta sn_{t}\) :
-
The distinguishing binary variables of the ending moments at study horizon
- \(Vmd_{i,j,gm}^{t}\) :
-
The volume of contaminated oil \(j\) stocked to tank \(gm\) at station \(i\) from \(t\) to \(t + 1\), m3
- \(Vod_{i,c,go}^{t}\) :
-
The volume of contaminated oil \(c\) stocked to tank \(go\) at station \(i\) from \(t\) to \(t + 1\), m3
- \(Vmh_{i,j,gm,c,go}^{t}\) :
-
The volume of contaminated oil \(j\) from tank \(gm\) at station \(i\) blended to tank \(go\) with exporting oil from \(t\) to \(t + 1\), m3
- \(Vat_{i,c,go,j}^{t}\) :
-
The blending capacity of the exporting oil \(c\) from oil tank \(go\) at station \(i\) to blend contaminated oil \(j\) from \(t\) to \(t + 1\), m3
- \(Vmf_{i,j,gm}^{t}\) :
-
The fractionation volume of contaminated oil \(j\) tank \(gm\) at station \(i\) from \(t\) to \(t + 1\), m3
- \(Vof_{i,c,go}^{t}\) :
-
The blending volume of oil \(c\) fractionated by contaminated oil to oil tank \(go\) at station \(i\) from \(t\) to \(t + 1\), m3
- \(Vmo_{{i,j,gm^{{\prime }} ,gm}}^{t}\) :
-
The volume of contaminated oil \(j\) switched from contaminated oil tank \(gm\) to \(gm^{{\prime }}\) from \(t\) to \(t + 1\), m3
- \(Voo_{{i,c,go,go^{{\prime }} }}^{t}\) :
-
The volume of oil \(c\) from oil tank \(go\) to \(go^{{\prime }}\) from \(t\) to \(t + 1\), m3
- \(Vao_{{i,c,go,go^{{\prime }} ,j}}^{t}\) :
-
The blending capacity of oil \(c\) switched from oil tank \(go\) to \(go^{{\prime }}\) mixing with contaminated oil \(j\) at station \(i\) from \(t\) to \(t + 1\), m3
- \(Vm_{i,j,gm}^{t}\) :
-
The stock volume of contaminated oil \(j\) tank \(gm\) at station \(i\) at time node \(t\), m3
- \(Vo_{i,c,go}^{t}\) :
-
The inventory of oil c tank go at station i at time node t, m3
- \(Vam_{i,c,go,j}^{t}\) :
-
The blending capacity of oil c in tank \(go\) to blend contaminated oil \(j\) at time node t, m3
- \(Lmc_{i,km}\) :
-
The actual length of contaminated oil out of station i at first \(km\) times, m
- \(Lmd_{i,km}\) :
-
The actual length of contaminated oil arriving at station i at first \(km\) times, m
- \(\tau md_{i,j,km}\) :
-
The actual time of the head of contaminated oil \(j\) arriving at station i at first \(km\) times, h
- \(\tau mc_{i,j,km}\) :
-
The actual time of the end of contaminated oil \(j\) arriving at station i at first \(km\) times, h
- \(\tau_{t}\) :
-
The time of number t, h
- \(Cmh_{i,j,gm,c,go}^{t}\) :
-
The binary variables of the contaminated oil tank’s blending operation. If contaminated oil \(j\) from tank \(gm\) at time node \(t\) blends with oil \(c\) from tank \(go\), \(Cmh_{i,j,gm,c,go}^{t} = 1\), if not, \(Cmh_{i,j,gm,c,go}^{t} = 0\)
- \(Cmf_{i,j,gm}^{t}\) :
-
The binary variables of contaminated oil tank’s fractionation operation. If contaminated oil \(j\) from tank \(gm\) at station \(i\) is fractionated at time node \(t\), \(Cmf_{i,j,gm}^{t} = 1\), if not, \(Cmf_{i,j,gm}^{t} = 0\)
- \(Cmd_{i,j,gm}^{t}\) :
-
The binary variables of contaminated oil tank’s delivery operation. If contaminated oil \(j\) is delivered into contaminated oil tank \(gm\) at station \(i\) at time node \(t\), \(Cmi_{i,j,gm}^{t} = 1\), if not, \(Cmi_{i,j,gm}^{t} = 0\)
- \(Cmo_{{i,j,gm,gm^{{\prime }} }}^{t}\) :
-
The binary variables of contaminated oil tank’s switching operation. If contaminated oil \(j\) is switched to contaminated oil tank \(gm^{{\prime }}\) from tank \(gm\) at station \(i\) at time node \(t\), \(Cmo_{{i,j,gm,gm^{{\prime }} }}^{t} = 1\), if not, \(Cmo_{{i,j,gm,gm^{{\prime }} }}^{t} = 0\)
- \(Cod_{i,c,go}^{t}\) :
-
The binary variables of contaminated oil tank’s delivery operation. If oil \(c\) is delivered into oil tank \(go\) at station \(i\) at time node \(t\), \(Cod_{i,c,go}^{t} = 1\), if not, \(Cod_{i,c,go}^{t} = 0\)
- \(Cop_{i,c,go}^{t}\) :
-
The binary variables of contaminated oil tank’s export operation. If oil \(c\) is exported from oil tank \(go\) at station \(i\) at time node \(t\), \(Cop_{i,c,go}^{t} = 1\), if not, \(Cop_{i,c,go}^{t} = 0\)
- \(Cof_{i,c,go}^{t}\) :
-
The binary variables of contaminated oil tank’s fractionation and recycle operation. If oil \(c\) after fractionation is recycled into oil tank \(go\) at station \(i\) at time node \(t\), \(Cof_{i,c,go}^{t} = 1\), if not, \(Cof_{i,c,go}^{t} = 0\)
- \(Coo_{{i,c,go,go^{{\prime }} }}^{t}\) :
-
The binary variables of oil tank’s switching operation. If oil \(c\) is switched to oil tank \(go^{{\prime }}\) from tank \(go\) at station \(i\) at time node \(t\), \(Coo_{{i,c,go,go^{{\prime }} }}^{t} = 1\) if not, \(Coo_{{i,c,go,go^{{\prime }} }}^{t} = 0\)
- \(Smd_{i,j,gm}^{t}\) :
-
The state binary variables of contaminated oil tank’s delivery. If contaminated oil \(j\) is delivered into contaminated oil tank \(gm\) at station \(i\) at time node \(t\), \(Smd_{i,j,gm}^{t} = 1\), if not, \(Smd_{i,j,gm}^{t} = 0\)
- \(Sod_{i,c,go}^{t}\) :
-
The state binary variables of oil tank’s delivery. If oil \(c\) is delivered into contaminated oil tank \(go\) at station \(i\) at time node \(t\), \(Sod_{i,c,go}^{t} = 1\), if not, \(Sod_{i,c,go}^{t} = 0\)
- \(Sop_{i,c,go}^{t}\) :
-
The state binary variables of oil tank’s export. If oil \(c\) in oil tank \(go\) is being exported from station \(i\) at time node \(t\), \(Sop_{i,c,go}^{t} = 1\), if not, \(Sop_{i,c,go}^{t} = 0\)
- \(Smh_{i,j,gm,c,go}^{t}\) :
-
The state binary variables of contaminated oil tank’s blend. If contaminated oil \(j\) in contaminated oil tank \(gm\) is being blended with oil tank \(go\) exporting oil \(c\) at station \(i\), \(Smh_{i,j,gm,c,go}^{t} = 1\), if not, \(Smh_{i,j,gm,c,go}^{t} = 0\)
- \(Smf_{i,j,gm}^{t}\) :
-
The state binary variables of contaminated oil tank’s fractionation. If contaminated oil \(j\) in contaminated oil tank \(gm\) is being fractionated at station \(i\), \(Smf_{i,j,gm}^{t} = 1\), if not, \(Smf_{i,j,gm}^{t} = 0\)
- \(Sof_{i,c,go}^{t}\) :
-
The state binary variables of contaminated oil tank’s recycle. If oil \(c\) after fractionation is being recycled into tank \(go\) at station \(i\), \(Sof_{i,c,go}^{t} = 1\), if not, \(Sof_{i,c,go}^{t} = 0\)
- \(Smo_{{i,j,gm,gm^{{\prime }} }}^{t}\) :
-
The state binary variables of contaminated oil switch-tank. If contaminated oil \(j\) is switched from contaminated oil tank \(gm\) to \(gm^{{\prime }}\) at station \(i\), \(Smo_{{i,j,gm,gm^{{\prime }} }}^{t} = 1\), if not, \(Smo_{{i,j,gm,gm^{{\prime }} }}^{t} = 0\)
- \(Soo_{{i,c,go,go^{{\prime }} }}^{t}\) :
-
The state binary variables of contaminated oil switch-tank. If oil \(c\) is switched from contaminated oil tank \(go\) to \(go^{{\prime }}\) at station \(i\), \(Soo_{{i,c,go,go^{{\prime }} }}^{t} = 1\), if not, \(Soo_{{i,c,go,go^{{\prime }} }}^{t} = 0\)
- \(Cm_{i,km,p}\) :
-
The distinguishing binary variables of the linear section divided by Austin’s formula. If the batch state of contaminated oil arriving at station \(i\) is in section \(p\), \(Cm_{i,km,p} = 1\), if not, \(Cm_{i,km,p} = 0\)
- \(Cb_{i,c,go,t,b}\) :
-
The distinguishing binary variables of the volume of oil tanks’ inventory. If the inventory of oil c tanks go at station i at time node t is in period b, \(Cb_{i,c,go,t,b} = 1\), if not, \(Cb_{i,c,go,t,b} = 0\)
- \(Cbo_{{i,c,go,go^{{\prime }} ,b}}\) :
-
The distinguishing binary variables of the volume of switching tank operation. Just like the definition of \(Cb_{i,c,go,t,b}\)
- \(Cbt_{i,c,go,t,b}\) :
-
The distinguishing binary variables of the volume of export operation. Just like the definition of \(Cb_{i,c,go,t,b}\)
References
Austin JE, Palfrey JR, Austin JE, et al. Mixing of miscible but dissimilar liquids in serial flow in a pipeline. Proc Inst Mech Eng. 1963;1963(178):377–95.
Barzin R, Chen JJJ, Young BR, et al. Peak load shifting with energy storage and price-based control system. Energy. 2015;92:505–14. doi:10.1016/j.energy.2015.05.144.
BP (2014) BP statistical review of world energy. www.bp.com/statisticalreview2014.
Cafaro DC, Cerda J. Dynamic scheduling of multiproduct pipelines with multiple delivery due dates. Comput Chem Eng. 2008;32(4–5):728–53. doi:10.1016/j.compchemeng.2007.03.002.
Cafaro DC, Cerda J. Operational scheduling of refined products pipeline networks with simultaneous batch injections. Comput Chem Eng. 2010;34(10):1687–704. doi:10.1016/j.compchemeng.2010.03.005.
Cafaro DC, Cerda J. A rigorous mathematical formulation for the scheduling of tree-structure pipeline networks. Ind Eng Chem Res. 2011;50(9):5064–85. doi:10.1021/Ie101462k.
Cafaro DC, Cerda J. Rigorous scheduling of mesh-structure refined petroleum pipeline networks. Comput Chem Eng. 2012;38:185–203. doi:10.1016/j.compchemeng.2011.11.007.
Cafaro VG, Cafaro DC, Mendez CA, et al. MINLP model for the detailed scheduling of refined products pipelines with flow rate dependent pumping costs. Comput Chem Eng. 2015a;72:210–21. doi:10.1016/j.compchemeng.2014.05.012.
Cafaro VG, Cafaro DC, Mendez CA, et al. Optimization model for the detailed scheduling of multi-source pipelines. Comput Ind Eng. 2015b;88:395–409. doi:10.1016/j.cie.2015.07.022.
Castro PM. Optimal scheduling of pipeline systems with a resource-task network continuous-time formulation. Ind Eng Chem Res. 2010;49(22):11491–505. doi:10.1021/ie1010993.
Duan ZG, Liang YT, Guo Q, et al. An automatic detailed scheduling method of refined products pipeline. In: IEEE international conference on control and automation. 2016. p. 816–23.
Ghaffari-Hadigheh A, Mostafaei H. On the scheduling of real world multiproduct pipelines with simultaneous delivery. Optim Eng. 2015;3:1–34.
Herrán A, Defersha FM, Chen M, et al. An integrated multi period planning of the production and transportation of multiple petroleum products in a single pipeline system. Int J Ind Eng Comput. 2011;2(1):19–44.
Herran A, de la Cruz JM, de Andres B. Global Search Metaheuristics for planning transportation of multiple petroleum products in a multi-pipeline system. Comput Chem Eng. 2012;37:248–61. doi:10.1016/j.compchemeng.2011.10.003.
Kolodziej SP, Grossmann IE, Furman KC, et al. A discretization-based approach for the optimization of the multiperiod blend scheduling problem. Comput Chem Eng. 2013;53:122–42. doi:10.1016/j.compchemeng.2013.01.016.
Li H, Liang J, Zhu F, et al. Mixing experiment and critical proportion calculation for contamination of products. Oil Gas Storage Transp. 2011;30(3):180–2 (in Chinese).
Li WQ, Dai YP, Ma LW, et al. Oil-saving pathways until 2030 for road freight transportation in China based on a cost-optimization model. Energy. 2015;86:369–84. doi:10.1016/j.energy.2015.04.033.
Liang YT, Li M, Li JF. Hydraulic model optimization of a multi-product pipeline. Pet Sci. 2012a;9(4):521–6. doi:10.1007/s12182-012-0237-2.
Liang YT, Li M, Zhang N. A study on optimizing delivering scheduling for a multiproduct pipeline. Comput Chem Eng. 2012b;44:127–40. doi:10.1016/j.compchemeng.2012.05.007.
MirHassani SA, Abbasi M, Moradi S. Operational scheduling of refined product pipeline with dual purpose depots. Appl Math Model. 2013;37(8):5723–42. doi:10.1016/j.apm.2012.11.009.
MirHassani SA, BeheshtiAsl N. A heuristic batch sequencing for multiproduct pipelines. Comput Chem Eng. 2013;56:58–67. doi:10.1016/j.compchemeng.2013.05.007.
MirHassani SA, Jahromi HF. Scheduling multi-product tree-structure pipelines. Comput Chem Eng. 2011;35(1):165–76. doi:10.1016/j.compchemeng.2010.03.018.
Mitra S, Sun LG, Grossmann IE. Optimal scheduling of industrial combined heat and power plants under time-sensitive electricity prices. Energy. 2013;54:194–211. doi:10.1016/j.energy.2013.02.030.
Mostafaei H, Hadigheh AG. A general modeling framework for the long-term scheduling of multiproduct pipelines with delivery constraints. Ind Eng Chem Res. 2014;53(17):7029–42. doi:10.1021/ie4038032.
Neiro SM, Pinto JM. Langrangean decomposition applied to multiperiod planning of petroleum refineries under uncertainty. Latin Am Appl Res Pesquisa aplicada latino americana = Investigación aplicada latinoamericana. 2006;36(4):213–20.
Neiro SMS, Murata VV, Pinto JM. Hybrid time formulation for diesel blending and distribution scheduling. Ind Eng Chem Res. 2014;53(44):17124–34. doi:10.1021/ie5009103.
Pan H, Wang L. Blending scheduling under uncertainty based on particle swarm optimization with hypothesis test. Lect Notes Comput Sci. 2006;4115:109–20.
Rejowski R, Pinto JM. Scheduling of a multiproduct pipeline system. Comput Chem Eng. 2003;27(8–9):1229–46. doi:10.1016/S0098-1354(03)00049-8.
Rejowski R, Pinto JM. Efficient MILP formulations and valid cuts for multiproduct pipeline scheduling. Comput Chem Eng. 2004;28(8):1511–28.
Relvas S, Barbosa-Povoa APFD, Matos HA. Heuristic batch sequencing on a multiproduct oil distribution system. Comput Chem Eng. 2009;33(3):712–30. doi:10.1016/j.compchemeng.2008.10.012.
Relvas S, Magatao SNB, Barbosa-Povoa APFD, et al. Integrated scheduling and inventory management of an oil products distribution system. Omega Int J Manag Sci. 2013;41(6):955–68. doi:10.1016/j.omega.2013.01.001.
Relvas S, Matos HA, Barbosa-Povoa APFD, et al. Pipeline scheduling and inventory management of a multiproduct distribution oil system. Ind Eng Chem Res. 2006;45(23):7841–55. doi:10.1021/ie060309c.
Shi L, Jiang YH, Wang L, et al. Refinery production scheduling involving operational transitions of mode switching under predictive control system. Ind Eng Chem Res. 2014;53(19):8155–70. doi:10.1021/ie500233k.
Shi L, Jiang YH, Wang L, et al. A novel two-stage Lagrangian decomposition approach for refinery production scheduling with operational transitions in mode switching. Chin J Chem Eng. 2015;23(11):1793–800. doi:10.1016/j.cjche.2015.08.017.
Zhang H, Liang Y, Wang N, et al. Optimal scheduling of multi-source single-distribution pipeline with multi-batch sequential transportation. Acta Pet Sin. 2015;36(9):1148–55 (in Chinese).
Zhang H, Liang Y, Liao Q, et al. A hybrid computational approach for detailed scheduling of products in a pipeline with multiple pump stations. Energy. 2017;119(15):612–28. doi:10.1016/j.energy.2016.11.027.
Zhang HR, Liang YT, Xiao Q, et al. Supply-based optimal scheduling of oil product pipelines. Pet Sci. 2016;13(2):355–67. doi:10.1007/s12182-016-0081-x.
Acknowledgements
This work was part of the Program of “Study of the mechanism of complex heat and mass transfer during batch transport process in product pipelines” funded under the National Natural Science Foundation of China, Grant Number 51474228. The authors are grateful to all study participants.
Author information
Authors and Affiliations
Corresponding author
Additional information
Edited by Xiu-Qin Zhu
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhang, HR., Liang, YT., Liao, Q. et al. An MILP approach for detailed scheduling of oil depots along a multi-product pipeline. Pet. Sci. 14, 434–458 (2017). https://doi.org/10.1007/s12182-017-0151-8
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12182-017-0151-8