A notable bounded probability distribution for environmental and lifetime data

Abstract

In this article, we introduce a notable bounded distribution based on a modification of the epsilon function that creates an upper bound on the domain of a distribution. Further, a key feature of the distribution is to have asymptotic connections with the famous Lindley distribution, which is a weighted variant of the exponential distribution and also a mixture of exponential and gamma distributions. In some ways, the proposed distribution provides a flexible solution to the modeling of bounded characteristics that can be almost well-fitted by the Lindley distribution if the domain is restricted. Moreover, we have also explored its application, particularly with reference to lifetime and environmental points of view, and found that the proposed model exhibits a better fit among the competing models. Namely, we demonstrate the practical applicability of the new distribution on two data sets containing lifetime data, as well as on two other data sets of rainfall data. Further, from the annual rainfall analysis, the proposed model exhibits a realistic return period of the rainfall.

Introduction

While observing real life phenomena, one usually comes across finite range of changes. Such finite changes generally give rise to bounded domain distributions. Among these bounded distributions, an upper bound is very helpful in analysing the annual stream flow and annual rainfall data (see (Phien and Ajirajah 1984)). The most common bounded domain distributions are the uniform, power, Bates, arcsine, Kumaraswamy, Topp-Leone, beta, triangular, raised cosine, and von Mises distributions. As an alternative to these distributions, (Dombi et al. 2018) recently introduced the epsilon distribution (EpD). Mathematically, it is based on the epsilon function defined by

$$ \begin{array}{@{}rcl@{}} \varepsilon_{\lambda,d}(x) = \begin{cases} \left( \frac{d+x}{d-x} \right)^{\lambda \frac{d }{2}}, & \text{if }-d< x <d, \\ 0, & \text{otherwise}, \end{cases} \end{array} $$

where $\lambda \in \mathbb {R}$, λ≠ 0 and d > 0. This function is derived from the first-order epsilon differential equation, and it has the following exponential limit property: For any x ∈ (−d,+d), if $d \rightarrow \infty$, then $\varepsilon _{\lambda ,d}(x) \rightarrow e^{\lambda x}$. Hence, a continuous random variable X is said to have an epsilon distribution with the parameters λ > 0 and d > 0 if its cumulative distribution function (CDF) is given by

$$ \begin{array}{@{}rcl@{}} F^{*}_{\lambda, d}(x) = \begin{cases} 0, & \text{if }x \leq 0, \\ 1 - \varepsilon_{-\lambda,d}(x), & \text{if }0< x <d, \\ 1, & \text{if }x \geq d. \end{cases} \end{array} $$

As a result, the epsilon distribution is a bounded domain distribution with two parameters, and it satisfies the following limit property: $\lim _{d\rightarrow +\infty } F^{*}_{\lambda , d}(x) = F^{*}_{\lambda }(x)$, where $F^{*}_{\lambda }(x)$ is the CDF of the exponential distribution with parameter λ. Among the applications, according to (Dombi et al. 2018), the epsilon distribution can be used to describe the mortality and useful life cycle in the sense of reliability management under the assumption of a typical bathtub-shaped failure (hazard) rate.

In this paper, we propose a notable two-parameter distribution that is also based on the epsilon function, but connected to the famous Lindley distribution, instead of the exponential distribution. The Lindley distribution has a plural interest. First, it was created by Lindley (see (Lindley 1958) and (Lindley 1965)). It was first coined to express the distinction between fiducial and posterior distributions, and it has been widely used in mathematical theory and practice in recent years. Let us recall that the CDF of the Lindley distribution with a parameter λ > 0 is given by

$$ \begin{array}{@{}rcl@{}} F^{o}_{\lambda}(x) = \begin{cases} 0, & \text{if }x \leq 0, \\ 1- \left( 1+\frac{\lambda x}{1+\lambda} \right)e^{-\lambda x}, & \text{if } x>0. \\ \end{cases} \end{array} $$

The Lindley distribution has been used to analyze large amounts of data, especially in the context of stress resistance and reliability modeling. There is a substantial literature on the Lindley distribution. Let us mention the Lindley distribution’s dominance over the exponential distribution of banking customers’ waiting times until service, as highlighted by (Ghitany et al. 2008), the Lindley distribution’s applications in lifetime data in the context of competing risks, as presented by (Mazucheli and Achcar 2011), and a comparison study of the adequacy of exponential and Lindley distributions, as presented by (Shanker and Mishra 2013) and (Shanker et al. 2015), among others.

By capturing the idea of the epsilon distribution and adapting it to reach the Lindley distribution as a limit, we motivate the use of the following function:

$$ \begin{array}{@{}rcl@{}} F_{\lambda, d}(x) =\left\{ \begin{array}{lll} 0, &\quad \text{if }x \leq 0, \\ \displaystyle 1-\left( 1+\frac{\lambda }{1+\lambda}\frac{dx}{d-x} \right) \varepsilon_{-\lambda,d}(x), & \quad\text{if }0< x <d, \\ 1, &\quad \text{if }x \geq d, \end{array}\right. \end{array} $$

(1)

where λ > 0 and d > 0. The distribution defined by F_λ,d(x) is called the epsilon-Lindley distribution (EpLD). Then, one can prove that it is a valid CDF, which satisfies $\lim _{d\rightarrow +\infty } F_{\lambda , d}(x) = F^{o}_{\lambda }(x)$; the Lindley distribution is a limit case of the EpLD, which is a rare property for a bounded support distribution. Furthermore, the related functions, such as the probability density function (PDF) and hazard rate function (HRF) are very flexible in their behaviour, as shown later. More precisely, by using a graphical analysis, the PDF adopts various shapes, like skewed to the right with J-shapes as well as an upside down U-shape. In all these cases, we observe a positive skewness and leptokurtic nature of the curve, which clearly indicates that it is designed to model the heavy-tailed phenomenon. Such phenomena are generally common in reliability applications, queuing theory and environmental aspects. In this regard, we focus on the environmental aspect and also lifetime direction. Our application section will help the reader to reach a decision to forecast the next generation’s future in a better way. Environmental data analysis is based on the most efficient bounded models. One can mention the three-parameter lognormal distribution, generalized extreme value type II distribution, generalized extreme value type III distribution, three-parameter gamma distribution, and three-parameter log-Pearson distribution, among others. The non-closed form of the CDF in these popular hydrological models is a fundamental flaw, whereas the suggested model is based on only two parameters and has a closed form of its basic functions, including its CDF, which makes the determination of the return period considerably easier.

Further, the HRF adopts various shapes, from bathtub to increasing failure rate with a left skewed J-shape. This functional flexibility is a true plus for the EpLD from the modeling viewpoint. On the mathematical plan, the EpLD is a weighted version of the EpD. This weighted version not only models ascertainment biases but also a linear combination of probability distributions. We thus develop the statistical features offered by the EpLD through diverse aspects, including theoretical and practical facts. The practical lines interested in fitting, modeling and analysis of lifetime and environmental data are outlined by the proposed model. Here, we demonstrate the practical applicability of the EpLD on two data sets containing lifetime data, as well as on two other data sets of rainfall data. Further, from the annual rainfall analysis, we found a realistic return period of the rainfall by the proposed model.

The organization of the paper is as follows. Section Some related functions, properties with estimations presents some other functions of interest in the EpLD, like moments and parameter estimation. Section Model compatibility and its application to real-world data covers the application area of the proposed model. Section Conclusions and future research plans deals with conclusion and closing comments about the proposed distribution with future research plans.

Some related functions, properties with estimations

Related functions

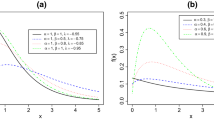
We now illustrate the shape behavior of the main functions of the EpLD. First, let us focus on the CDF as defined in Eq. 1. Figure 1 presents some graphs of this CDF for several values of the parameters.

Fig. 1

Graphs of the CDF of the EpLD

Figure 1 depicts that for smaller values of both d and λ, the convergence of CDF to 1 is very slow compared to that for larger d and λ values.

Let us now focus on the related PDF. The PDF of the EpLD is expressed as

$$ \begin{array}{c} f_{\lambda, d}(x) = \begin{cases} \frac{\lambda d^{2}}{\left( 1+\lambda \right) \left( d^{2}-x^{2}\right) }\left[ 1 + \lambda \!-\frac{d+x-\lambda dx}{d-x} \right] \varepsilon_{-\lambda,d}(x), & \text{if $0< x <d$,} \\ 0, & \text{otherwise}. \end{cases} \end{array} $$

(2)

Figure 2 presents some graphs of this PDF for several parameter values.

Fig. 2

Graphs of the PDF of the EpLD; unimodal shapes skewed to the right and J shapes

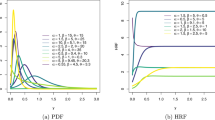
From Figs. 2 and 3, we see that the PDF of the EpLD also adopts various shapes, like unimodal shapes skewed to the right, various J-shapes, as well as an upside down U-shapes. In particular, Fig. 2 indicates that, when the rate parameter λ decreases, it increases the probability of events whatever the boundary value of d is. Thus, the PDF of the EpLD distribution is extremely flexible, and, as developed in the introductive section, motivates the use of the EpLD for various modelling purposes, including the heavy-tailed phenomenon.

Fig. 3

Graphs of the PDF of the EpLD; U-J shapes and upside down U-shapes

In addition to its practical ability, the PDF of the EpLD has interesting mathematical decompositions. Indeed, one can view f_λ,d(x) as follows:

• It is a weighted version of the PDF of the EpD, because it can be written as $f_{\lambda , d}(x) = w_{\lambda ,d}(x) f^{*}_{\lambda , d}(x)$, where

  $$w_{\lambda,d}(x)=1 -\frac{d+x-\lambda dx}{(1+\lambda)(d-x)}$$

  and $f^{*}_{\lambda , d}(x)$ refers to the PDF of the epsilon distribution.

• If λ > 2/d, by noticing that

  $$ \frac{d+x-\lambda dx}{(1+\lambda)(d-x)}=\frac{1}{1+\lambda}\left[\frac{\lambda}{4} (d-x) +\left( 1- \frac{\lambda}{4} (d+x)\right) \frac{d+x}{d-x} \right], $$

  we can also write f_λ,d(x) as a linear combination of PDFs and lenght biased PDFs of the EpD as

  $$ \begin{array}{@{}rcl@{}} f_{\lambda, d}(x) &=&\!\!\left( 1-\frac{\lambda}{4(1+\lambda)} (d-x)\right)f^{*}_{\lambda, d}(x) \\ &&\!\!-\frac{\lambda d}{(1+\lambda)(\lambda d-2)}\left( 1- \frac{\lambda}{4} (d+x)\right) f^{*}_{\lambda-2/d, d}(x) \\ &=& \!\!\left( 1-\frac{\lambda d}{4(1+\lambda)} \right)f^{*}_{\lambda, d}(x)\\&& \!\!-\frac{\lambda d}{(1+\lambda)(\lambda d-2)}\left( 1- \frac{\lambda d}{4} \right) f^{*}_{\lambda-2/d, d}(x) \\ &&\!\!+ \frac{\lambda}{4(1 + \lambda)} x f^{*}_{\lambda, d}(x) + \frac{\lambda^{2} d}{4(1 + \lambda)(\lambda d - 2)}x f^{*}_{\lambda-2/d, d}(x). \end{array} $$

  (3)

  This expansion is useful to determine several probabilistic quantities related to the EpLD.

As a major reliability function (see, e.g., (Nair et al. 2018)) of the EpLD, the HRF is specified as

$$ \begin{array}{@{}rcl@{}} h_{\lambda, d}(x) =\! \begin{cases} \frac{\lambda d^{2}}{\left( 1+\lambda \right) \left( d^{2}-x^{2}\right) }\!\left[ \!1 + \lambda - \frac{d+x-\lambda dx}{d-x} \!\right] \!\left( \!1 + \frac{\lambda }{1+\lambda}\frac{dx}{d-x} \!\right)^{\!-1},\!\! & \text{if }0< x <d, \\ 0, & \text{otherwise}. \end{cases} \end{array} $$

Figure 4 provides some graphs of this HRF for selected values of the parameters.

Fig. 4

Graphs of the HRF of the EpLD

The graphs in Fig. 4 clearly portray the HRF behaviour like increasing and bathtub-shaped in an impressive way.

We end this part by discussing the quantile analysis of the EpLD. As we know, in traditional probability and statistics as well as in stochastic analysis, the quantile function (QF) deals with a valuable way of describing a static or vigorous distribution, as a result, knowing how to use this function indicates certain advantages not available straight from the CDF or PDF. For example, the simplest way of simulating any non-uniform random variable is by applying its QF to uniform deviates. Similarly, from an environmental point of view, these functions usually help environmental scientists to calculate the return period and return level of any distribution.

In view of above, the QF of the EpLD, denoted by Q_λ,d(u) with u ∈ (0,1), is the solution of the following non-linear equation:

$$\left( 1+\frac{\lambda }{1+\lambda}\frac{d Q_{\lambda,d}(u)}{d- Q_{\lambda,d}(u)} \right) \varepsilon_{-\lambda,d}[Q_{\lambda,d}(u)]=1-u.$$

To evaluate Q_λ,d(u) at given u and parameters, it is clear that a mathematical software is required.

Moments

In mathematics, and in statistics in particular, the word moments of a function are reckonable procedures associated to the shape of the function’s graph. If the function represents density or mass function, then the first moment represent the center of the mass or expected value, and the second moment is the rotational inertia or the variance. So, the moments about the origin of the EpLD can be determined by using the expansion in Eq. 3. For a random variable Y_λ,d following the epsilon distribution with parameters λ and d and a random variable X following the EpLD, the r-th moment of X can be obtained as

$$ \begin{array}{@{}rcl@{}} \mu_{r}^{\prime} &=& E(X^{r}) \\ &=& \left( 1-\frac{\lambda d}{4(1+\lambda)} \right)E(Y_{\lambda,d}^{r})\\&& -\frac{\lambda d}{(1+\lambda)(\lambda d-2)}\left( 1- \frac{\lambda d}{4} \right) E(Y_{\lambda-2/d,d}^{r})\\ &&+ \frac{\lambda}{4(1{}+{}\lambda)} E(Y_{\lambda,d}^{r+1}) {}+{} \frac{\lambda^{2} d}{4(1{}+{}\lambda)(\lambda d{}-{}2)}E(Y_{\lambda-2/d,d}^{r+1}). \end{array} $$

The r-th and (r + 1)-th moments of Y_λ,d are well established, see (Okorie and Nadarajah 2019). In a similar way, we can express the incomplete moments of X in terms of incomplete moments of Y_λ,d. Thus, the mean and variance of X can be obtained.

Similarly, the ratio of third mean moment to the square of second mean moment are the skewness and the ratio fourth moment about mean to second moment about mean is the kurtosis. From these moments, we are now able to interpret the shape and kurtosis behaviour of the EpLD. In this regard, Fig. 5 portrays that the proposed model can exhibit versatile shapes ranging from negative to positive behaviour. In addition, we see that the distribution also has the leptokurtic, mesokurtic and platykurtic behaviour.

Fig. 5

Graphs of skewness and kurtosis of the EpLD

Parameters estimation

Due to the importance of statistical inference, here, we adopt the maximum likelihood method, giving the maximum likelihood estimates (MLEs) of the unknown parameters. MLEs are designed to follow the regularity conditions, which are usually helpful for constructing the confidence intervals and the test statistics. For these estimators, the large sample theory yields straightforward approximations that work well in finite samples. In order to achieve better approximation distributions, statisticians frequently strive to estimate quantities, such as the distribution of a test statistic that depends on the sample size. The resulting MLE approximation in distribution theory can be handled analytically or numerically with ease. Only complete samples are used to calculate the MLEs of the EpLD parameters. In this regard, let x₁,…,x_n be a realization of a random sample of size n from the EpLD given by Eq. 2. Then, the log-likelihood function of the EpLD is given by

$$ \begin{array}{@{}rcl@{}} \ell(\lambda,d)& = &2 n\log d+ n\log\lambda - n\log(1+\lambda)\\&&- \left( 1+\frac{d \lambda }{2}\right)\sum\limits_{i=1}^{n} \log\left( \frac{d+x_{i}}{d-x_{i}}\right) \\ &&+ \sum\limits_{i=1}^{n} \log\left[d \lambda +x_{i}((d-1) \lambda -2)\right]-3 \sum\limits_{i=1}^{n} \log(d-x_{i}). \end{array} $$

(4)

The log-likelihood can be maximized either directly by using the Mathematica [12.0] or by solving the nonlinear likelihood equations obtained by differentiating Eq. 4. In particular, we have

$$ \begin{array}{@{}rcl@{}} \frac{\partial \ell(\lambda,d)}{\partial \lambda }&=&\frac{n}{\lambda }-\frac{n}{1+\lambda }-\frac{d}{2} \sum\limits_{i=1}^{n} \log\left( \frac{d+x_{i}}{d-x_{i}}\right)\\&&+\sum\limits_{i=1}^{n} \frac{d+(d-1) x_{i}}{d \lambda +((d-1) \lambda -2) x_{i}}=0. \end{array} $$

The MLE of the parameter λ is obtained by solving the nonlinear system ∂ℓ(λ,d)/∂λ = 0. As mentioned earlier, this equation cannot be solved analytically, so we prefer to use statistical packages like Mathematica [12.0]. For this purpose, we use Global MLE of the proposed model that take the Lindley distribution MLE as seed value. However, we observe that we cannot obtain the estimate of d from Eq. 4. Consequently, we adopt the methodology described as follows: since d is free from x and it is the upper limit in the domain of x, we consider x₍₁₎,x₍₂₎,…,x_(n), the ordered sample corresponding to x₁,x₂,…,x_n, and, based on them, the estimate d as $\hat {d}={\max \limits } (x_{1},x_{2},\ldots ,x_{n})+\upsilon$, where υ > 0 denotes an arbitrary constant. However, when we start estimating d using the sample, we undertake that all the elements in the sample are in the domain of the random variable. This is because the sample should be comprised of independent observations. Since the value of parameter d determines the domain of attraction of the random variable that has a EpLD, in the estimation, it is a necessity that d is greater than the maximal element in the sample. So we are looking for the robust value of $\hat {d}$, which will probably be established under the condition that $\hat {d}$ is greater than the largest element in the sample. For more details, see (Dombi et al. 2018), (Dombi et al. 2019), (Dombi and Jónás 2020) and (Dombi and Jónás 2021).

Model compatibility and its application to real-world data

In this section, we concentrate on the modelling process’s model selection and model validation. However, model selection is a challenging task and the prime of a suitable model and it is produced with the use of well-considered judgement based on whatever information is available. It is essential that the chosen model be malleably sufficient to model the confronted data amply, while considering the settlement between simplicity of evaluation and the intricacy of the model. Moreover, outstanding attention must be devoted to modeling behavior for large and small values of the variable of interest. In this regard, the modelling process includes validating the model, which includes various goodness-of-fit tests and graphical procedures. These statistical techniques for assessing hypothesised models are known as goodness-of-fit tests. An unsatisfactory fit, either analytical or graphical, may occur for the following reasons: i) The model is incorrectly specified. ii) The model specification is correct, but unfortunately carries a huge bias. In general, validation necessitates more data, other information, and further testing, as well as a careful examination of the consequences.

Goodness-of-fit tests

As in such tests, researchers usually make a null hypothesis, H₀: The given data comes from a CDF with a specified form. For this purpose, we have considered four tests. The first test is the famous χ² test (Chi Square), due to Karl Pearson. It includes grouping observed data into intervals and may be used to assess the fit of data to any specified distribution (continuous or discrete). When using this test, a sample of size n is assumed, with each observation falling into one of k potential classifications. The observed and expected frequencies in the interval i are denoted by o_i and e_i, respectively. The test statistic is

$$ \begin{array}{@{}rcl@{}} \chi^{2}=\sum\limits_{i=1}^{k} \frac{(o_{i}-e_{i})^{2}}{e_{i}}. \end{array} $$

However, this test has the advantages of being easy to apply and being applicable even when parameters are unknown (see (Murthy et al. 2004)). In addition, this test is not of much use in small or sometimes even modest size samples (see (Murthy et al. 2004)). The next three tests are based on the empirical cumulative distribution function (ECDF) and hence are often referred to as ECDF tests.

Kolmogorov-Smirnov (KS) Test

The Kolmogorov-Smirnov (KS) test is grounded on the ECDF. Given n ordered observations Z₁,Z₂,…,Z_k, then the ECDF is defined as E_k = m_i/k where m_i is the number of points less than Z_i and the Z_i are ordered from smallest to largest value. At the value of each ordered data point, this step function rises by 1/k. The greatest distance between the hypothesised CDF and ECDF is the test statistic KS. The mathematical expression of the KS test statistic is given by

$$ \begin{array}{@{}rcl@{}} \text{KS}= \max_{1\leq i\leq k} \left\lbrace \frac{i}{k}-z_{i},z_{i}-\frac{i-1}{k}\right\rbrace, \end{array} $$

where z_i = F(Z_i), and F is the theoretical CDF of the distribution being tested. Other goodness-of-fit tests, like the Anderson-Darling test and the Cramér-von Mises test, are alternatives of the KS test. As these modified tests are usually measured to be more powerful than the conventional KS test, many analysts prefer them.

Anderson-Darling (AD$_{0}^{\ast }$) Test

The Anderson-Darling (AD$_{0}^{\ast }$) test is an alternative of the KS test and usually attaches more weight to the tails than the KS test. Its test statistic is

$$ \begin{array}{@{}rcl@{}} A_{0}^{\ast}=\left( \frac{2.25}{k^{2}} + \frac{0.75}{k} + 1\!\right)\!\left\lbrace \!-k\!- \frac{1}{k}{\sum}_{i=1}^{k}(2i - 1)\log(z_{i}(1 - z_{k-i+1})) \!\right\rbrace\!. \end{array} $$

Cramér-von Mises (CVM$_{0}^{\ast }$) Test

The CVM$_{0}^{\ast }$ test is also a modification of the KS test, which is usually considered to be more powerful than the original KS test. The CVM$_{0}^{\ast }$ test statistic is expressed as

$$ W_{0}^{\ast}=\sum\limits_{i=1}^{k}\left( z_{i}-\frac{2i-1}{2k}\right)^{2}+\frac{1}{ 12k}. $$

A relative comparison of the selection of these tests indicates that: i) The ECDF tests are more powerful than the χ² test. ii) The KS test is the most well-known ECDF test, but it is often much less powerful than the other ECDF tests (AD$_{0}^{\ast }$ and CVM$_{0}^{\ast }$ tests) (see (Murthy et al. 2004)). Moreover, we have also applied information criteria for model selection purposes, such as Akaike information criterion (AIC), Bayesian information criterion (BIC), corrected Akaike information criterion (AICc), Hannan-Quinn information criterion (HQIC) and consistent Akaike information criterion (CAIC). The following are the definitions of AIC, AICc, HQIC, and CAIC:

$$ \begin{array}{@{}rcl@{}} \text{AIC}=2 \hslash - 2 l,\!\! \quad\text{AICc} = \text{AIC} + \frac{2\hslash(\hslash+1)}{n-\hslash-1},\!\!\quad \text{BIC} = \hslash \log(n) -2 l, \end{array} $$

$$ \begin{array}{@{}rcl@{}} \text{HQIC}=-2 l+\hslash \log(\log (n)), \qquad \text{CAIC}=-2 l+\frac{2 \hslash n}{n-\hslash-1}, \end{array} $$

where l denotes the estimate of the maximm log-likehood function, $\hslash$ is the number of parameters to be estimated and n is the number of data.

Along with these model selection procedures, we have also used the Kullback-Leibler information criterion philosophy and applied the Vuong test proposed by (Vuong 1989).

Vuong test

The Vuong test is a closeness test based on the likelihood-ratio-based test for model selection using the Kullback-Leibler information criterion philosophy. This test may be used for non-nested models, and it generally compares the null hypothesis that two competing models are equally near to the actual data against the alternative that one model performs better. Further discussion about the Vuong test can be found in (Hussain et al. 2019).

Competing models

We compare the proposed model with the following well-known models: epsilon probability distribution (EpD) (see (Dombi et al. 2018)), two-parameter Lindley distribution (TPLD) (see (Shanker et al. 2015)), A quasi Lindley distribution (QLD) (see (Shanker and Mishra 2013)), Lindley distribution (LD) (see (Lindley 1958)) and exponential distribution (ED). For the sake of transparency, these competitors are defined by the following PDFs:

• for the EpD:

  $$ f^{EpD}_{\lambda, d} (x)= \frac{\lambda d^{2}}{d^{2}-x^{2}}\varepsilon_{-\lambda ,d}(x), \quad 0<x<d, $$

  and $f^{EpD}_{\lambda , d} (x)=0$ for x∉[0,d], with d > 0,

• for the TPLD:

  $$ f^{TPLD}_{\lambda ,d}(x) =\frac{\lambda^{2}(1+dx)}{d+\lambda }e^{-\lambda x},\quad x>0, $$

  and $f^{TPLD}_{\lambda ,d}(x)=0$ for x ≤ 0, with λ > 0 and d > − 1,

• for the QLD:

  $$ f^{QLD}_{\lambda ,d}(x) =\frac{\lambda (d+\lambda x)}{d+1}e^{-\lambda x}, \quad x>0, $$

  and $f^{QLD}_{\lambda ,d}(x) =0$ for x ≤ 0, with λ > 0 and d > − 1,

• for the LD:

  $$ f^{LD}_{\lambda}(x ) =\frac{\lambda^{2}(1+x)}{1+\lambda }e^{-\lambda x}, \quad x>0, $$

  and $f^{LD}_{\lambda }(x )=0$ for x ≤ 0, with λ > 0,

• for the ED:

  $$ f^{ED}_{\lambda }(x) =\lambda e^{-\lambda x}, \quad x>0, $$

  and $f^{ED}_{\lambda }(x)=0$ for x ≤ 0, with λ > 0.

We consider four different real-world data sets.

Lifetime data sets

Data sets I and II.

The first and second data sets are taken from (Walpole et al. 2012) and (Andrews and Herzberg 1985), respectively. The first data are about the length of life in years, measured to the nearest tenth of 30 similar fuel pumps, while the second data represent the life of fatigue fracture of Kevlar 373 epoxy that is subjected to constant pressure at the 90 stress level until all have failed. The measurements of the first data set are 2.0, 3.0, 0.3, 3.3, 1.3, 0.4, 0.2, 6.0, 5.5, 6.5, 0.2, 2.3, 1.5, 4.0, 5.9, 1.8, 4.7, 0.7, 4.5, 0.3, 1.5, 0.5, 2.5, 5.0, 1.0, 6.0, 5.6, 6.0, 1.2, 0.2. The second data set measurements are given as: 0.0251, 0.0886, 0.0891, 0.2501, 0.3113, 0.3451, 0.4763, 0.5650, 0.5671, 0.6566, 0.6748, 0.6751, 0.6753, 0.7696, 0.8375, 0.8391, 0.8425, 0.8645, 0.8851, 0.9113, 0.9120, 0.9836, 1.0483, 1.0596, 1.0773, 1.1733, 1.2570, 1.2766, 1.2985, 1.3211, 1.3503, 1.3551, 1.4595, 1.4880, 1.5728, 1.5733, 1.7083, 1.7263, 1.7460, 1.7630, 1.7746, 1.8275, 1.8375, 1.8503, 1.8808, 1.8878, 1.8881, 1.9316, 1.9558, 2.0048, 2.0408, 2.0903, 2.1093, 2.1330, 2.2100, 2.2460, 2.2878, 2.3203, 2.3470, 2.3513, 2.4951, 2.5260, 2.9911, 3.0256, 3.2678, 3.4045, 3.4846, 3.7433, 3.7455, 3.9143, 4.8073, 5.4005, 5.4435, 5.5295, 6.5541, 9.0960. In this regard, we have compiled the descriptive statistics, which are listed in Table 1, and the total time on test (TTT) plots introduced by (Aarset 1987), which are portrayed in Fig. 6 for Data sets I and II.

Table 1 Descriptive statistics for Data sets I and II

Fig. 6

Estimated TTT plots of Data sets I and II

Discussion and analysis of lifetime data sets

Tables 1 and 2 reveal that theoretical and observed descriptive statistics show a remarkable closeness to each other and it seems that both data sets are being simulated by the proposed model.

Table 2 Theoretical statistics from the EpLD

Note that as the parameter d specifies the support of the PDF of the EpLD in Equation (2), i.e., it is positive only if x ∈ (0,d). This means that the value of parameter d must meet the requirement $d > \max \limits _{i = 1,2,\ldots ,n}(x_{i})$, see (Dombi et al. 2019). That is why we observed that $\hat {d}$ is large for any data set, as shown in the related tables. From the TTT-plot for Data set I, we can see that the curve has three characteristic phases: (1) a first convex phase, where the failure rate is decreasing; (2) a second quasi linear phase with a constant failure rate; (3) and a third concave phase, where the failure rate is increasing. That is, the TTT-plot for Data set I (see Fig. 6) portrays a bathtub-shaped like failure rate curve. Noting the TTT-plot for Data set II in Fig. 6, from which we can conclude that it exhibits an increasing failure rate phenomenon of the empirical failure rate function. Hence, both of the above data sets are efficiently modelled by the proposed model. These results are in line with the fact that the HRF of the EpLD can be bathtub-shaped or increasing (see Fig. 4). Since d is large, the EpLD is almost identical to the LD, and so they have almost the same goodness-of-fit statistics values. Such a suitability of the proposed model is reflected in Tables 3 and 4, where the EpLD yields a smallest value of the goodness-of-fit statistics along with highest p-vlaue for χ² statistics. In addition, we have also assessed the performance of the model with respect to the LD via the log-likelihood ratio test, which is usually applicable for nested models, and we drew the same conclusion.

Table 3 MLEs and goodness-of-fit statistics for Data set I

Table 4 MLEs and goodness-of-fit statistics for Data set II

However, Tables 5 and 6 portray that the QLD and LD yield minimum values of information criterion, which seem to be a penalty of over parametrization, particularly with reference to the LD model. Previously we pointed out that the LD distribution may be viewed as an asymptotic EpLD distribution, i.e., if $d \to \infty$, then the EpLD distribution is identical to the LD distribution. We can observe a practical implication of this finding in Tables 3–6. Namely, when a data set can be modelled well by the LD distribution, then it can also be modelled well by the EpLD distribution with a sufficiently large value of the parameter d, and vice versa. Certainly, in such a case, the estimates of the λ parameter and the corresponding goodness-of-fit statistics are very close.

Table 5 Estimates of the maximum log-likelihood and information criteria for Data set I

Table 6 Estimates of the maximum log-likelihood and information criteria for Data set II

Furthermore, Table 7 also pleads for the suitability of the proposed model. But Vuong statistics show that QLD and LD are strong competitors for the proposed model.

Table 7 Vuong test statistics for Data sets I and II

Furthermore, by the histogram analysis performed in Fig. 7, we see that the proposed model matches the data in a better way than the competing models.

Fig. 7

Data sets I and II fits via histograms

Environmental Data Sets

Data sets III and IV. The third and fourth data sets are the total amount of rainfall in mm of Pakistani cities Lasbella and Bunji, which covers a period of 30 years (1981 to 2010) with 30 values of annual rainfall in each set. They were reported by (Hussain et al. 2019). The third data set measurements are as follows: 138.11818, 89.5, 246.5, 142.6, 143.5, 47.4, 105.7, 182.6, 153.7, 119.9, 56.5, 272.8, 99.9, 426.1, 205.6, 169.8, 308.3, 80.5, 104.0, 37.7, 223.0, 9.2, 474.6, 25.3, 209.6, 182.5, 196.2, 254.9, 103.6, 117.6. The fourth data set contains the following rainfall measurements: 248.8, 82.2, 102.2, 217.9, 113.2, 248.2, 244.1, 122.2, 144.9, 63.2, 62.8, 139, 228.7, 216.4, 144.8, 252.6, 144.8, 157.2, 168.5, 139.1, 74.3, 154.6, 339.4, 154.1, 156.3, 200.7, 97.5, 96.3, 155.2, 298.8. The descriptive statistics of these data sets and corresponding theoretical statistics from the EpLD are presented in Tables 8 and 9, respectively. Box-plots of the data are given in Fig. 8.

Table 8 Descriptive statistics for Data sets III and IV

Table 9 Theoretical statistics from the EpLD

Fig. 8

Box-plots for Data sets III and IV

In order to analyse the environmental data, we have also checked some features of the environmental data, namely homogeneity, independence and stationarity. For this purpose, we applied the Mann-Whitney (M-W) test for testing homogeneity and stationarity, and the Mann-Kendall (M-K) test for trend detection. In this regard, we have observed that both data sets accept the hypotheses of homogeneity and stationarity at a 5 percent level of significance with Z-scores of 0.3568 and -0.2777, respectively. Similarly, the hypothesis of independence and identically distributed distribution is accepted at a 5 percent level of significance with Z-scores of 0.4817 and -0.6943, respectively. For details of these tests, readers are referred to (Haktanir et al. 2013).

Analysis and discussion of environmental data

From Table 8 and Fig. 8 as well as Table 9, it is obvious that the empirical and theoretical aspects of the data sets in the presence of outliers in Data set III are in close agreement. These indicate that the model can effectively be used if the data are positively skewed and leptokurtic in nature, which are the obvious characteristics of environmental data. Such findings are further consolidated by viewing Tables 10 and 11, which portray that the EpLD exhibits minimum values of goodness-of-fit statistics.

Table 10 MLEs and goodness-of-fit statistics for Data set III

Table 11 MLEs and goodness-of-fit statistics for Data set IV

Tables 10 and 11 indicate that ECDF test statistics for goodness-of-fit tests are low, which ensures that the EpLD is a good competitor to the QLD and LD.

However, likelihood aspects and information criterion values also favour the proposed model, which can be visualized in Tables 12 and 13, respectively.

Table 12 Estimates of the maximum log-likelihood and information criteria for Data set III

Table 13 Estimates of the maximum log-likelihood and information criteria for Data set IV

Furthermore, the shape of our proposed model, as shown in Fig. 9, matches the data in a better way compared to the competing models.

Fig. 9

Data sets III and IV fits via histograms

Furthermore, the Vuong statistics as depicted in Table 14 also show the capability of the proposed model.

Table 14 Vuong test statistics for Data sets III and IV

Hydrological parameters

The annual series is very common in frequency analysis for two reasons. The earliest is its accessibility, as most data are managed in such a way that the annual series is commonly available. The other one is that there is a simple hypothetical basis for deducing the frequency of annual series data beyond the range of observation (see (World Meteorological Organization 2009)). Moreover, we observed that both series are valid and approved by the M-W and M-K tests, as shown in the earlier section.

Therefore, it can be settled that, according to the consequences of relevant tests, both the annual rainfall series documented at Lasbella (Pakistan) and Bounji (Pakistan) are homogeneous, independent, non-periodic and trend-free. Hence, classical frequency analyses are applied to all of the annual rainfall series. From the above mentioned analysis, we can conjecture that the EpLD is a suitable model for the above mentioned data sets, so we have decided to portray its return period for those interested in environmental data, which is being studied in the coming subsection.

Return period

The average number of years in which an event is predicted to be equalled or exceeded only once is the return period $\mathfrak {T}$ of a particular level. The return period is the reciprocal of the probability of exceeding the threshold in a particular year (see (World Meteorological Organization 2009)). The link between the annual return time and the exceedance probability may be stated as follows if the yearly exceedance probability is designated $1/\mathfrak {T}$. Since the probability of exceedance is $P\left (X>x_{\mathfrak {T}}\right )=1/\mathfrak {T}$, this implies a return level with a return period of $\mathfrak {T}=1/\mathfrak {p}$ is a high threshold $x_{\mathfrak {T}}$ whose probability of exceedance is $\mathfrak {p}$.

In this regard, we have found that the EpLD yields a realistic return period that can be visualized from Fig. 10.

Fig. 10

Return periods of the competing models for Data sets III and IV

Conclusions and future research plans

In this article, we proposed a notable bounded distribution under the name epsilon Lindley distribution (EpLD). Since the Lindley distribution is a limit case of the EpLD, which is a rare property for a bounded support distribution, the EpLD may be treated as a bounded alternative to the Lindley distribution. Therefore, this new distribution provides a flexible solution to the problem of modeling bounded characteristics. We pointed out that the PDF and HRF of the EpLD are very flexible, i.e., they can exhibit various shapes. The fact that the PDF of the EpLD can have a positive skewness and a leptokurtic nature indicates that this new distribution can be used to model the heavy-tailed phenomenon, which is generally common in reliability applications, queuing theory and environmental aspects. We found that the HRF of the EpLD can adopt various shapes from bathtub to increasing failure rate with a left skewed J-shape. All that make this distribution suitable for modeling purposes in a wide range of practical problems. The environmental data analyses are mainly based on the most efficient bounded models, such as the three-parameter lognormal distribution, generalized extreme value type II distribution, generalized extreme value type III distribution, three-parameter gamma distribution, and three-parameter log-Pearson distribution. A significant issue in many common hydrological models is the non-closed form of the CDF. At the same time, the EpLD has only two parameters and has a closed form of its basic functions, including its CDF. This property of the EpLD makes it useful in practical hydrological modeling applications. We should mention that the EpLD is a weighted variant of the EpD from a theoretical standpoint. This weighted variant includes a linear mixture of probability distributions as well as ascertainment biases. In this study, we estimated the parameters of EpLD using the maximum likelihood method. Next, we studied the applications of the proposed distribution both in lifetime and environmental data modeling. Based on the empirical results, we could conclude that the proposed methodology works quite well. In particular, for the annual rainfall data, the EpLD yields a realistic return period when compared with other competing models.

As part of our research activities, we plan to study how the epsilon-Lindley distribution can be utilized in other areas of statistics, including regression analyses and classification modeling.