Introduction

An ecosystem is a set of species, each of finite population size that interact by competing for finite resources that fuel their growth. A single ecosystem can involve dynamics that occurs over a wide range of length and timescales (Azaele et al. 2016); Darwin already eloquently referred to this in his “tangled bank” remark. The seemingly universal nature of a species’ emergence, adaptation and extinction in such ecosystems, has inspired many to describe the phenomenology of ecosystem dynamics with simple modeling with only a few ingredients that are independent of the specific physical mechanisms at play (Nowak 2006; Azaele et al. 2016). What is then the simplest quantitative description that displays all the salient dynamical features of evolution? This question has a long list of partial answers (Nowak 2006; Tikhonov 2016; Posfai et al. 2017), although much work in the field concerns equilibria (MacArthur and Wilson 1963; MacArthur 1955; Chesson 1990; Hubbell 2001). Here, we show that the already successful variants of MacArthur models can be amended with a simple stochastic mechanism that introduces new species, which allows us to show many of the biologically relevant dynamical features of evolution even when the starting point for the dynamics is a single primordial ancestor. In particular, our MacArthur model variant can describe the growth dynamics of an ecosystem in terms of species richness, its evolution towards a dynamic equilibrium size, and even its adaptation to resource influx changes. The predictions of the model are consistent with other existing modeling on, for example, equilibrium dynamics and reasonably in line with common observations on, for example, resource shock experiments.

The speciating MacArthur model

Evolutionary dynamics modeling including MacArthur type models usually starts with describing population dynamics as \(\dot{{\textbf {n}}}(t) = {\textbf {n}}(t)f({{{\textbf {n}}}})\) with \({\textbf {n}}\) the set of species population sizes and the dot denotes a time derivative. The crux is that \(f({\textbf {n}})\) is not constant but a growth rate determining function that depends on ecosystem features such as population sizes and coupling constants which specify inter-species competition and preying efficiency (Wangersky 1978; Cressman and Tao 2014). This general approach is tremendously successful even in capturing quantitative experimental observations of low-dimension systems (Korolev et al. 2011). However, describing the dynamics of larger ecosystems with many evolving species is challenging, as high-dimensional systems quickly lose their numerical and analytical tractability, even without incorporating the additional complexity of the evolution of each species.

We address this complexity by adding evolutionary dynamics to multi-species ecosystem models by quantifying the growth rate within the context of the ecosystem properties. It has become customary in recent years to define every species j by a strategy vector \({\textbf {s}}_j\) (Posfai et al. 2017; Tikhonov and Monasson 2017; Pacciani-Mori et al. 2020; Caetano et al. 2021) that couples the growth dynamics \(\dot{{\textbf {n}}}(t) = {\textbf {n}}(t)f({{{\textbf {n}}}})\) to a dynamic resource vector \({\textbf {r}}(t)\) which represents the amount of available resources at time t. Here, each component i of \({\textbf {s}}_j\) describes which fraction of each resource \(r_i\) is used by every species j at every time step. The time-dependent growth factor is then naturally captured by the alignment \({\textbf {s}}_j\cdot {\textbf {r}}\). We can write for each element \(\dot{{\textbf {n}}}_j = {\textbf {n}}_jf_j({\textbf {n}},{\textbf {s}}_j\cdot {\textbf {r}})\) while introducing resource time-dependence via a function \(\dot{{\textbf {r}}} = g({\textbf {n}},{\textbf {s}})\), where \({\textbf {s}}\) is the matrix with strategies \({\textbf {s}}_j\) as its columns. The concept of a strategy vector \({\textbf {s}}_j\) that every species \(j \in \{1\ldots k\}\) has in order to harvest resources is central in the model. Each component of \({\textbf {s}}_j\) represents a strategy for a particular resource, the ensemble of which is characterized by a time-dependent vector \({\textbf {r}} = \{r_1,r_2,\ldots , r_l\}\) where l is the number of resources. \({\textbf {s}}_j\) quantifies how much of each resource every individual would like to take out of the resource bath. We consider the concept of a resource component \(r_i\) as extremely general: it can refer to a specific molecule, a chemical energy influx, or even to a certain amount of space available in a habitat. Each species has limited energy and time to spend harvesting. Thus, species need to optimize their foraging behavior by choosing how to be efficient as regards different resource consumption (MacArthur and Pianka 1966). To express the interdependence of resources, one simple way is to fix a norm of the strategy vector to an arbitrary quantity. For convenience we choose \(\Vert {\textbf {s}}_j\Vert _2 = 1\), but other norms and values can be chosen. This choice does have a biological significance (Caetano et al. 2021). For now, we will focus on speciation with this fixed choice, but in “Comparison with adaptive dynamics: Convergence of strategies” section, we will see that this choice has important consequences. Note that our definition for the strategy vector is in analogy with how individuals with different genetics are represented in so-called ‘tangled nature models’ (TaNas) in the genotype space (Christensen et al. 2002; Hall et al. 2002; Anderson and Jensen 2005). The fundamental difference is that, in TaNa and other similar approaches (Higgs and Derrida 1992; Gavrilets 1999; Eigen et al. 1988), the strategy vector’s components can assume discrete values, usually representing alleles of genes while in our case, the strategy vector assumes continuous values. The extension of the TaNa definition to phenotype space is straightforward (Laird and Jensen 2006).

We assume that the total demand for resources is proportional to \({\textbf {s}}_j\) and the population size of each species \(n_j\). The time dynamics of every resource component \(r_i\) is then described by the following:

$$\begin{aligned} \frac{\text {d}{r_i}}{\text {d}{t}} = -\beta \sum _{j=1\ldots k} s_{ij}n_j + \gamma _i. \end{aligned}$$
(1)

Here, \(\beta\) is a timescale, and \(\gamma _i\) is the resource replenishment factor of resource i, essentially representing a chemostat (Posfai et al. 2017). In this simplified linearized resource dynamics, \(r_i\) is not strictly positive, which is unphysical. When \(r_i<0\), we set it to zero. We find that the time dependence of the model is very sensitive to the choice of the rate of consumption (and growth). However, the approach of a dynamic equilibrium while adding species to the ecosystem is preserved regardless of the choice of growth rate factor.

If the preferred resource intake of the species is similar to the composition of the resource environment \({\textbf {r}}\), the growth rate should be maximal; in the case where \({\textbf {s}}_j\) and \({\textbf {r}}\) are not aligned, the species should perform poorly. A species goes extinct when its population size is below a threshold value. We verified that threshold choice is not important for much of the dynamics observed. We do note that setting the threshold lower trivially increases the total ecosystem size. It is now natural to write for \(n_j\) that

$$\begin{aligned} \frac{\text {d}{n_j}}{\text {d}{t}} = \left( \alpha \, {\textbf {s}}_j\cdot {\textbf {r}}- \delta \right) n_j. \end{aligned}$$
(2)

Writing explicitly that \({\textbf {s}}_j\cdot {\textbf {r}} \equiv \sum _{i=1\ldots l}s_{ij}r_i\) makes clear that \(s_{ij}\) is the resource utilization coefficient of species j for resource i. \(\alpha\) is, again, a time constant; \(\delta\) sets the population decay rate. Equations (1) and (2) are simplified versions of MacArthur equations (MacArthur 1970; Chesson 1990; Haygood 2002). However, we interpret the coupling matrix \(s_{ij}\) much more specifically: it is essential to see how \({\textbf {s}}_j\) here serves as the definition of species j (Posfai et al. 2017).

Stochastic speciation

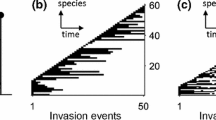
So far, we did not consider any stochasticity: the skeleton of the dynamics is deterministic and embeds a selection for the fittest species (Vellend 2010). The novel feature in this work is that we add speciation dynamics in two ways: (1) by adding species and (2) by ensuring the added species can be different from existing ones. We choose to make (i) mutants appear randomly, adding a new species equation to the system in a Monte Carlo way. We shall see that this captures both evolution and invasion. (ii) The strategy vector of the newborn species is stochastically generated (Posfai et al. 2017; Pacciani-Mori et al. 2020; Drake 1990; Serván et al. 2018; May 1972). Thus, the community assembly happens sequentially at random times with randomly evolved species—see Fig. 1. We call our speciating MacArthur approach towards ecosystem dynamics “SMA” for brevity.

Fig. 1
figure 1

The phylogenetic tree derived from the emergence of species in the evolution of one realization. Time is expressed in terms of integration time steps. The species lifetime is indicated in color to provide the chronology of emerged species in the tree. Leaf 1 indicates the emergence of the last spawned species and so on. The red line shows the lineage of the species with which the tree started; it went extinct around \(t \sim 4.4\times 10^4\) steps

Full size image

We can now use \({\textbf {s}}_j\) to specify how a species evolves with a simple Monte Carlo evolutionary model: mutants are generated from existing species from which they differ only in terms of the harvesting strategy vector. The initial species in the ecosystem is defined by uniformly drawing an ancestral strategy vector \({\textbf {s}}_1\), with elements in the range (0, 1), and normalizing it to one in the Euclidean norm. A new species can be spawned for every time step and for every alive species, when a random number, drawn from a standard normal distribution, is larger than \(\nu\) standard deviations. We can thus define a mutant \(k+1\) by taking any existing species strategy \({\textbf {s}}_j\) and by adding a noise vector:

$$\begin{aligned} {\textbf {s}}_{k+1} = \frac{\mid {\textbf {s}}_j + \eta {\boldsymbol{\psi }}\mid }{\Vert {\textbf {s}}_j + \eta {\boldsymbol{\psi }}\Vert _2}. \end{aligned}$$
(3)

The noise vector is composed of a random vector drawn from a normal distribution, \({\boldsymbol{\psi }}\), weighted by a parameter \(\eta\) quantifying the amplitude of the mutation. Therefore, the noise vector represents a shift in the species’ resource utilization composition as a consequence of mutations. Note that by “phenotypically” defining our species solely in terms of \({\textbf {s}}_j\), a natural link to genetic variation within a species is lost.

The stochastic arrival of a new species and the resource richness influence the local selection outcome by possibly inducing historical contingency and priority effect in the community assembly (Fukami 2015; Almany 2003; Sale 1977). The level of historical dependency on species’ arrival hinges on the value of \(\eta\) and the number of different resource types. We assume that a small \(\eta\) represents an infinitesimal evolutionary mutation in a species’ survival strategies, originating speciation events in response to the dynamic resource landscape. Indeed, \(\eta\) defines the degree of strategies’ divergence from parent species to daughter species. On the contrary, foreign invasions are modeled by considering the arrival of a new species with an entirely new set of characteristics, uncorrelated with the ones already present in the system. We call such case \(\eta \rightarrow \infty\) and will be discussed more in detail in “The role of \(\eta\)” section. As we will see, SMA does show a remarkable ability to reproduce behaviors that can be interpreted in any eco-evolutionary context. We will discuss the interpretation of \(\eta\) in more detail in “Interpreting the role of\(\eta\)” section.

Biological example: Biofilms

Despite the sober mathematical formulation, SMA conceptually captures some essential features of ecological systems: in several natural ecosystems, ecological successions are intertwined with populations’ adaptation to environmental conditions. Moreover, both native species’ evolution and alien species’ invasion contribute to determining the community’s fate, together with environmental responses or sudden changes. One simple yet effective example is that of microbial communities in biofilm formation, where evolutionary and ecological timescales are comparable (Hansen et al. 2007; Goyal et al. 2022). In subaerial biofilms, such as those that grow in monumental buildings, the substrate of stones is firstly colonized by pioneer airborne microbes, which then leads to further successive stages with the subsequent invasions of other microorganisms  (Gorbushina 2007). The different substrate characteristics and environmental conditions define the dynamic resource richness, which in SMA is rendered via the types of resources and their influx vector (Gaylarde 2020; Ariño et al. 2010; Caneva et al. 2004). Moreover, microorganisms not only can feed on others’ metabolic discards, but are also able to evolve rapidly via strains’ mutations, which in our model are captured by the signs and mutations in the strategy vectors (Gorbushina 2007). As a result, several biofilms quickly show resistance to chemical anti-degradation treatments, often leading to unexpected and new community structures (Simões et al. 2009; Gorbushina 2007).

It is evident that biofilms are much more complex ecosystems than the ones described by SMA. In biofilm formation, both evolutionary speciation and ecological invasion act simultaneously, while in the current version of SMA, we consider these processes separately for simplicity. SMA can of course include both effects simultaneously, yet we aim to disentangle the dynamics observed in a simple general framework that captures existing natural systems. Many other interpretations besides biofilms are possible and welcome.

Implementation

We run all ecosystems starting from one species, with \(\alpha = 0.005\), \(\beta = 0.01\), \(\delta = 0.1\). We assume that all resources have an equal influx rate given by \(\gamma _i=1\). We focus on the case of \(\nu =3.8\), and we consider systems where we vary l. The value for l can be representative of several different community scales. For example, when considering microbial communities, 100 or more different resource types are an appropriate choice (Fischbach and Clardy 2007; Fischbach and Sonnenburg 2011; Tikhonov and Monasson 2017). We then varied \(\eta\) within previously defined limits and studied the ecosystem’s evolution.

Solver

To integrate the species dynamics in Eq. (2), we employ a fourth-order Runge–Kutta (RK4) method with stochastic elements that can only generate one new species per existing one at every time step. We checked that the RK4 accuracy used in all our calculations does not affect the results. We verified that our custom implementation provides similar performance to the standard MATLAB ode45 solver for the deterministic \(l=1\), \(k=1\) case, with \(\alpha = 0.05\), \(\beta = 0.01\), \(\gamma _i = 1\), \(\delta = 0.2\). In the stochastic setting, we loop in every time step over the extant species, compute for each species the RK4 step, and add a new species when a number drawn from a standard normal distribution is, in absolute value, larger than \(\nu\). After the loop over the species, we perform an Euler forward step for the resource dynamics Eq. (1) where we use the updated values for the species. Then, we set all negative values for \(r_i\) to zero to ensure the positivity of the resources. A representative code is provided on Zenodo (Bellavere et al. 2022).

Example ecosystem: \(l=5\), \(k=1\)

The SMA model can show a wide range of different dynamics, depending on the (initial) number of species k, total number of resources l, and other parameters. The phenomenology of speciation embedded in the SMA can however already be observed for starting evolution with the most stringent starting condition of one species, that is, \(k=1\). Note that capturing the emergence of an ecosystem with interacting species from a single primordial reproducing entity is one explicit aim of the current modeling approach. Evolving an ecosystem from a single species is, for example, not possible in the classical MacArthur, Lotka-Volterra (LV), or replicator equation contexts.

In this example, we choose an \(l=5\) resource space and set \(r_i(0)=10\) for all i as the initial resource amount available. Due to the presence of multiple species, the vector \({\textbf {r}}(t)\) will be time-dependent and may not always be aligned with a particular species vector \({\textbf {s}}_j\). We use \(\alpha = 0.005\), \(\beta = 0.01\), \(\gamma _i = 1\), \(\delta = 0.1\), \(\nu = 3.7\) and \(\eta = 1\) and evolve the system for up to \(10^5\) time steps of size \(h=0.1\). Note that the value of \(\nu\) is intrinsically linked to the choice of h because h also sets the frequency at which new species are generated; we come back to this point in “Transient scaling with\(\nu\)” section. We consider a species extinct if its size is smaller than \(0.1n_\textrm{start}\), where \(n_\textrm{start}\) is the initial size of the population; this threshold effectively captures the role of fluctuations in small populations (Reichenbach et al. 2006; Parker and Kamenev 2009; Huang et al. 2015). The specific value for the extinction threshold does not affect the essence of the evolutionary dynamics of \({\textbf {r}}\) and \({\textbf {n}}\). For repeated independent ecosystem calculations, we generate a new \({\textbf {s}}_1\) for every iteration.

Figure 2 shows the typical ecosystem evolution initiated from one species \(k=1\) starting at size \(n_1 = 10\). Due to the stochastic nature of species emergence and extinction, every realization of ecosystem dynamics is different. However, several important qualitative features reproduce and are visible in this and any example: (i) The initial species size oscillates in time until a viable new species has emerged; in sync, the resource dynamics is also oscillatory for the smallest component of \({\textbf {s}}\) as all the other resources get quenched to zero (Huang et al. 2017). Note that this excludes the case when an \(s_i\) is strictly zero, which is possible but rare. This is such that the resulting behavior dynamically balances the resource usage with the resource influx. (ii) The emergence of new species affects the timescale of periodic oscillations; also, new species can make older species go extinct. (iii) Later in the evolution, the population fluctuations shift in frequency and decay in amplitude, and multiple resources are utilized. The interpretation of these three trends is clear: the randomly selected initial species favors the survival of one resource, for which \(s_{i}\) is the smallest. After this transient, the dynamics follow the \(l=1\), \(k=1\) system which is pseudo-LV in character and allows for periodic orbits of fixed frequency. In this phase, the possibility of the random emergence of new species is consequential: the emergence of new species that are \(\eta \boldsymbol{\psi }\) different from their parents will suppress the dominant role of the first species and limit its overuse of other resources, thus making the remaining resources emerge again as they are always continuously replenished at rate \(\gamma _i\). We will make these statements more quantitative in the next sections.

Fig. 2
figure 2

a \(n_j(t)\) for the first (blue) and all subsequently emerged species; color indicates the spawning time, the dot the emergence of a new species. For visual simplicity, we displayed 22 over the 220 species spawned during the community evolution. b \(r_i(t)\) for the five resources available in the evolving ecosystem. At later times, multiple resources emerge after initial depletion

Full size image

Main phenomenology

The first significant result from SMA is the naturally bounded ecosystem it produces in both size and structure while we neither fix the (maximum) number of hosted species in the community nor the maximum population size of the individual species; only the influx of resources \(\boldsymbol{\gamma }\) is bounded. In modeling, this is traditionally captured with logistic growth models and/or to restrict oneself to probing the dynamics of an ecosystem with a fixed number of species (MacArthur 1970; Chesson 1990; Haygood 2002; Grover et al. 1997; Posfai et al. 2017; Tikhonov and Monasson 2017; Grilli et al. 2017). SMA embeds size limitations naturally, as we observe that for enough simulation time, the number of species grows towards a long-term stationary value—see below. This maximum number of coexisting species is solely determined by the distribution of strategies and resource availability. The bounded growth feature allows us to explore the long-term species abundance distribution (SAD) (Hubbell 2001; McGill et al. 2007), with the knowledge that a system will maintain, on average, a constant number of competitors and, as we will see, a finite global size. Note that during equilibrium size, the model allows for and will randomly let species emerge and go extinct; the ceiling represents a dynamic equilibrium. Note that in much of the dynamics explored, \(\nu\) mostly sets the speciation rate for the system evolution and is thus a timescale.

Growth towards equilibrium dynamics

Rather than considering each species or resource type separately, we gain insight into the system evolution as a whole by considering the total number of individuals (N) and the total amount of resources (R). Interest in the total abundance dynamics for similar trophic species is seldom suggested and, to our knowledge, rarely explored (Posfai et al. 2017). Yet, empirical evidence shows that the aggregate biomass could provide valid information on the stability and composition of a community (Tilman et al. 1997; Doak et al. 1998). Thus, studying the evolution of total abundances allows us to explore the system behavior in greater depth from a new perspective and, simultaneously, reduces the variables involved. Resultant equilibrium dynamics for ecosystem averages for different l are shown in Fig. 3a. The inset shows how the equilibrium is reached for a particular example setting of \(l=2\). We find a family of fixed points for the (R, N) dynamics that are all on a line defined by

$$\begin{aligned} \frac{R}{N}=\frac{l}{\sum _i \gamma _i}\frac{\delta \beta }{\alpha }. \end{aligned}$$
(4)
Fig. 3
figure 3

(R, N) phase space of the last \(10^4\) out of \(10^5\) time steps for 150 realizations (indicated by lines of different colors) with \(\nu = 3.8\), \(\eta \rightarrow \infty\) and different values of l (arrows). For \(l=100\) the simulations ended after \(8\times 10^4\) time steps due to memory load issues, and the figure displays the last \(10^4\) time steps of the runs. The fixed points lie on a line with slope \(\frac{l}{\sum \gamma _i}\frac{\delta \beta }{\alpha }\) (black dashed line). b Evolution of a single realization in (R, N) space with \(l=2\) with initial conditions \(R=20\) and \(N=10\). The system gradually displays asymptotic limit cycles. Different colors indicate different ecosystem realizations

Full size image

This total abundance dynamics can be understood by simply considering separately the sum of the resources R and the sum of the species N. In this way, the dynamically evolving dimension of the system reduces to a two-dimensional problem

$$\begin{aligned} \begin{aligned}&\frac{d R}{d t} = \sum _{i}^{l} \gamma _i - \beta \sum _{i}^{l} \sum _{j}^{k(t)} s_{ij} n_j,\\&\frac{d N}{d t} = \alpha \sum _{i}^{l} \sum _{j}^{k(t)} r_i s_{ij} n_j - \delta \sum _{j}^{k(t)} n_j. \end{aligned} \end{aligned}$$
(5)

Here, we emphasize that the number of living species, k, is a function of time: the equilibrium is dynamic in nature. The stationary solution \((R^*,N^*)\) of this system should solve the equations

$$\begin{aligned} {\begin{matrix} \sum\limits_{i}^{l} \sum\limits_{j}^{k(t)} s_{ij} n_j&{}= \frac{\sum _{i}^{l} \gamma _i}{ \beta },\\ \sum\limits_{i}^{l} \sum\limits_{j}^{k(t)} r_i s_{ij} n_j &{}= \frac{\delta }{\alpha }N^*, \end{matrix}} \end{aligned}$$
(6)

but note again that the elements that make up \(R^*\) and \(N^*\) do not have to be stationary. Inspired by Fig. 2, we now assume \(r_i\) is approximately constant in i, meaning that the mean abundance per resource does not vary too much per resource, we can pull \(r_i=\frac{R^*}{l}\) out of the sum, resulting indeed in the fraction

$$\begin{aligned} \frac{R^*}{N^*} = \frac{\delta l \beta }{\alpha \sum _{i} \gamma _i}. \end{aligned}$$
(7)

It turns out that this equation predicts the slope of the line in the (R, N) phase space on which all the attractors of the total abundance dynamics lie, as is shown in Fig. 3a. Note however that the pictures shown are for a constant \(\boldsymbol{\gamma }\), and numerical results seem to indicate that the assumption \(r_i\approx \frac{R^*}{l}\) becomes less valid when \(\gamma _i\ne \gamma _j\). Using the results from Posfai et al. (2017), we can understand why this line has such predictive power. In the deterministic version of our model, i.e., without speciation, any number of species can coexist. That is, as long as the geometric conditions introduced in Posfai et al. (2017) on the strategy vectors \(\textbf{s}_j\) and the replenishment \(\boldsymbol{\gamma }\) are met. When these conditions are met, the system converges to a fixed point where all \(r_i\) attain the same value. Hence, what we observe is that every time a new species is introduced (or an old one removed), the dynamics converges to a new fixed point that is indistinguishable from the old one in the R-N dynamics. We conclude that the stochasticity in our system always results in an ecosystem where the necessary geometric conditions for the coexistence of many species are met. To be precise, in Posfai et al. (2017) results were obtained for a nonlinear version of our model, such as Eq. (8), with normalization in \(L^1\) instead of the Euclidean norm. This norm changes some of the details; see “Comparison with adaptive dynamics: Convergence of strategies” section. Also, the nonlinear version of the model changes the slope of Eq. (7) somewhat, while making it valid under more general types of \(\boldsymbol{\gamma }\).

Transient scaling with \(\nu\)

A second feature in SMA is that the speciation threshold, \(\nu\), induces a timescale \(\tau\) for the evolution. At every time step, each species has a probability \(p_m\) to mutate. This probability is given by the tail (\(\ge \nu\)) of the standard normal distribution, i.e., \(p_m=\text {erfc}(\nu /\sqrt{2})\). Therefore, in absence of extinction, we expect the average number of species \(\langle S_a\rangle\) to grow as \(\sim \exp (\text {erfc}(\nu /\sqrt{2})t)\). However, it should be noted that \(\nu\) is intrinsically entangled with the choice of the time step h: indeed, \(\nu\) defines the probability of an alive species generating a new species in the h time unit. In our simulations, we always kept h constant at the value 0.1 which ensures the stability of the solver. Because of this choice, we must take \(\langle S_a\rangle \sim \exp (\text {erfc}(\nu /\sqrt{2})t/h)\).

For \(\nu\) to set such a timescale, the average behavior of a dynamic observable obtained for different values of \(\nu\), when plotted as a function of \(\tau =\exp (\text {erfc}(\nu /\sqrt{2})t/h)\), should collapse into the same master curve. We explored this possibility by considering as observable the time-dependent average of living species \(\langle S_a\rangle\) over 150 realizations, keeping \(\eta\) and l fixed but setting \(\nu =3.8,3.9\) and 4.

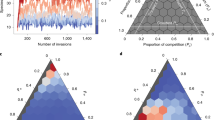
We rescaled the time axis of each curve associated with a different value of \(\nu\) to \(\tau\). For small l and high values of \(\eta\), we observe that \(\nu\) does induce a timescale for the overall evolution: indeed, the \(\langle S_a \rangle\) curves associated with the different \(\nu\) tend to collapse towards a single curve—see Fig. 4a, b in which we display results for \(l=2\) and \(l=100\) respectively and \(\eta \rightarrow \infty\). It follows that for low \(\nu\) the evolution is faster, while high values of \(\nu\) slow the community’s formation.

Fig. 4
figure 4

a Time-scaling of the average number of living species, \(\langle S_a \rangle\), over 150 realizations of systems with \(l=2\) and \(\eta \rightarrow \infty\). Curves associated to \(\nu =3.8\), \(\nu =3.9\) and \(\nu =4\) are displayed in orange, blue, and black, respectively. The curves are rescaled according to \(\tau =\exp (\text {erfc}(\nu /\sqrt{2})t/h)\). The red arrow indicates \(\tau \approx 4\), for which the three curves diverge. b Same as (a) for a system with \(l=100\). The blue arrow indicates \(\tau \approx 12\) for which the three curves diverge. c Time-scaling of the average extinction, \(\langle S_e \rangle\), for the same system as displayed in (a). The colors are consistent with (a). The red arrow indicates the value of \(\tau\) for which \(\langle S_e \rangle = 1\). For all three different curves \(\langle S_e \rangle = 1\) for \(\tau \approx 4\), value for which the curves diverge in (a). d Same as (c) for the system described in (b). The blue arrow, indicating the value of \(\tau\) for which \(\langle S_e \rangle = 1\), is consistent with (b) for all three curves (\(\tau \approx 12\))

Full size image

It is also clear from the figures that \(\tau\) is a valid timescale for small communities. When the number of species grows, extinction becomes important, and the curves for \(\langle S_a \rangle\) deviate weakly from the timescale \(\tau\). Quantitatively, when the average number of extinctions \(\langle S_e \rangle > 1\), we find that the rescaling becomes less accurate. Curiously, the rescaling works very well for all \(\langle S_e \rangle\).

Adaptation

The resource alignment interpretation of SMA clearly gives it many physically meaningful links to real-world ecosystem dynamics. Empirically, a promising constraint is to provide a time-varying resource influx by introducing \(\gamma _i(t)\), sometimes also called a “pulse” experiment (Tilman 1987; Hiltunen et al. 2015). We demonstrate in what follows that SMA shows adaptation under such conditions. Additionally, we explore how the magnitude of changes in subsequent generations as characterized by \(\eta\) affects adaptation dynamics.

Rank abundance

To demonstrate the effects of a “pulse,” we focus on the results obtained for a system characterized solely by invasion events, and \(l = 100\). We chose to make the resource shock occur at \(t_c = 8\times 10^{4}\) steps, and we doubled the length of the simulation to provide enough time for the system to respond to the perturbation. For \(t < t_c\), the influx rates are \(\gamma _i =1\) for all i; when \(t \ge t_c\), the new \(\sum _i\gamma _i\) is three times that before the perturbation. We chose to distribute \(75 \%\) of the new \({\varvec{\gamma }}\) among only \(25 \%\) of the resources. This abrupt change in resource influx induces adaptation dynamics by the ecosystem. Solving SMA with time-dependent resource influx over several realizations at previously defined \(\alpha , \beta , \delta \text{ and } \nu\), we observe that ecosystems are able to recover from such a resource shock: when the perturbation occurs, there is an initial stage, after which R(t) and N(t) gradually restore their limit cycles (not shown). However, for the linear model used here, the position of the attractor in the (R, N) phase space changes according to the new resource influx rates. The center of the oscillations does not lie on the line with slope \(\frac{l}{\sum _i \gamma _i}\frac{\delta \beta }{\alpha }\) anymore. On the contrary, given the unevenness of the new resource influx vector, the correct slope seems now proportional to the average influxes of the resource types that are not fully depleted, which in general are the ones associated with the highest resource influx.

We quantify the pulse response by probing species occurrence. Interestingly, the number of coexisting species is strongly affected by the resource shock. In the absence of perturbations, the number of living species hosted in the system spontaneously grows until it reaches an average maximum value in time—see Fig. 5a. When the perturbation occurs, the increase in available resources initially encourages the system to welcome new species, resulting in a sharp peak in the number of coexisting species. Subsequently, the living species curve decays with a characteristic timescale until it reaches a substantially lower new stationary value—see Fig. 5a. The new rank abundance distribution corresponds to having fewer species that are all large in population size.

Fig. 5
figure 5

a The number of living species, \(S_a\), for a single realization of a system with \(l=100\), \(\nu =3.8\) and \(\eta \rightarrow \infty\). (i) From \(t \approx 4.5\times 10^{4}\) steps on, the curve reaches a plateau; (ii) the resource shock perturbs the system at \(t_c = 8\times 10^{4}\) steps; and (iii) after the shock, a second plateau is reached. b Rank-abundance plot for the realization in (a). The curves show the trend at every 1000 time steps from \(t = 8 \times 10^{4}\) to \(t = 9.1 \times 10^{4}\). From \(t = 9.1 \times 10^{4}\) to the end of the simulation, corresponding to when the \(S_a\) reach the second plateau in (a), the rank-abundance curves are displayed every 14,000 time steps. The color scheme follows the colors on the left. The solid red line is the curve when the shock occurs. The arrows indicate the time immediately after the perturbation

Full size image

Remarkably, the shock also influences the SAD—see Fig. 5b. Before the resource shock occurs, the rank-abundance plot, also known as Whittaker plot (Magurran 2013), displays a curve that gradually collapses towards lognormal-like behavior in the tail. Such behavior resembles that observed in empirical data (Sugihara 1980; Longino et al. 2002; Baldridge et al. 2016; Magurran 2013; May 1975), although a few methodological aspects that give rise to such distribution are still debated (Magurran 2013; May 1975). After the perturbation, the curve still preserves its characteristic shape. However, its slope gets steeper in time, and the curve reaches a new asymptotic behavior characterized by less species evenness. Curiously, for systems with \(l=2\), the rank-abundance trend shows a strongly uneven species distribution that is often associated with harsh environments or early stages of successions (Magurran 2013; McGill et al. 2007) (not shown). Further generalizations of SMA are discussed in “Generalizations of SMA” section.

The role of \(\eta\)

The noise amplitude \(\eta\) has two biologically different limiting cases. For \(\eta \rightarrow 0\), the community’s evolution proceeds via infinitesimal steps, with all the new species occupying the same niche. On the contrary, we can imagine a scenario in which a foreign species invades the community from an external pool. In this case, we assume that the foreign species evolved from a different ancestral species. Thus, we define its strategy by drawing a new ancestral one and adding a noise vector with the maximum noise amplitude \(\eta =1\). This approach preserves the biological interpretation of the ancestral strategy and the mutations, originating from two different distributions: uniform and standard normal. For simplicity, we will refer to this scenario with the term \(\eta \rightarrow \infty\), although mathematically we do not explore the limit of \(\eta \rightarrow \infty\).

The case of \(\eta \rightarrow 0\)

As discussed, by decreasing \(\eta\), the realizations start to depend on their initial conditions. When \(\eta\) is infinitesimal, ecosystem dynamics are mainly determined by the ancestor features. However, such development of a neutral community at a species level (MacArthur and Wilson 1967) is made dynamic by a priority effect. Simply put, a small \(\eta\) is likely to lead to a successful species only if its ancestor was also successful. For small values of l, each realization still defines limit cycles around a fixed point. By increasing l, the dynamics becomes aperiodic. When l is small, as expected, the family of fixed points lies along the line defined by the ratio \(\frac{l}{\sum \gamma _i}\frac{\delta \beta }{\alpha }\). Also for \(l = 100\), the dynamics, even though aperiodic, is still contained in a region of the phase space close to the line—see Fig. 6.

Fig. 6
figure 6

a (R, N) heatmap of the last \(2\times 10^4\) out of \(10^5\) time steps for 150 realizations with \(\nu = 3.8\), \(\eta \rightarrow 0\), specifically \(\eta =0.005\), and \(l=2\), colored according to the logarithm of the number of counts. Each realization displays limit cycles around a different fixed point. In red, the line with slope \(\frac{l}{\sum \gamma _i}\frac{\delta \beta }{\alpha }\). The red dot on the red line but close to the origin identifies the late time dynamics for \(l=2\) and \(\eta \rightarrow \infty\) as shown in Fig. 3 in the main text. b Same as (a) but with \(l=100\). Most of the aperiodic trajectories are in the proximity of the line

Full size image

We conclude that tuning \(\eta\) allows us to apply SMA to both evolutionary and invasion-type dynamics. The so embedded co-occurrence of both selection and priority effect mirrors empirical evidence and theoretical hypotheses suggesting that stochasticity and determinism in community assembly work hand in hand (Chase and Myers 2011; Dumbrell et al. 2010; Luan et al. 2020; Cavender-Bares et al. 2009; Zhou and Ning 2017; Losos et al. 1998).

The case of \(\eta \rightarrow \infty\)

For systems invaded by foreign species, the dynamics of several different realizations of one system exhibit the same attractor and qualitative behavior—see Fig. 3. From said figure, it is clear that at long timescales, the dynamics settles on quasiperiodic orbits around points on the line of fixed points defined by Eq. (4), and higher values of l result in higher values of R and N. Varying the parameters \(\alpha\), \(\beta\), \(\boldsymbol{\gamma }\), and \(\delta\) gives similar results, only changing the slope of the line. Moreover, for high \(\eta\), in the range [0.5, 1], the results are similar to those obtained for \(\eta \rightarrow \infty\). In this limit of \(\eta\), especially the large l limit is interesting, because at small l, the ecosystem quickly selects the best adjusted strategies, all the others going extinct. For large l, species’ strategies are constantly evolving towards an existing optimum that is however statistically unlikely to achieve, leading to slow dynamics. The effect of introducing new species is now also determined by their time of arrival, which now defines their competitiveness, inducing a priority effect (Fukami 2015; Almany 2003; Sale 1977) that we will see is the dominant driver of dynamics in the case \(\eta \rightarrow \infty\).

Priority effect for \(\eta \rightarrow \infty\)

In the simulations, we see that species that spawn at the end of the simulation have a lower chance of surviving than at the start of the simulation. This can be interpreted as a priority effect. In order to quantify this, we count in a given time interval the number of species that went extinct immediately, i.e., decayed exponentially from the initial population to the extinction threshold. Dividing this number by the total number of spawned species in the same interval gives us an immediate extinction probability \(P_\textrm{ext}.\) When the number of spawned species is large enough, we can divide the list of species up into bins and calculate \(P_\textrm{ext}\) for each bin separately which indicates how \(P_\textrm{ext}\) changes over time. Figure 7 shows a clear trend for an example ecosystem which indicates that there indeed is a priority effect.

Fig. 7
figure 7

Extinction probability for a single realization with \(\nu =3.8\), \(\eta \rightarrow \infty\), and \(l=50\). After \(6\times 10^4\) time steps, 984 species spawned which we divided in 12 bins of size 82

Full size image

Interpreting the role of \(\eta\)

Noise, priority effects, and historical contingency

We observed that the SMA dynamics solely depends on the number of different resources if the community assembly emerges from adding essentially random species. This scenario comes about in the limit of large \(\eta\), thus with more significant differentiation between parent and child species, resulting eventually in always the same type of community structure and species’ distribution. The late-time community that emerges in this limit is commonly referred to as the climax community and indicates the final ecological succession of the community formation (Morin 2009; Weiher and Keddy 1995). The species, specifically the strategies selected to survive in the climax community, are considered resistant to the invasion of new strategies’ variants, which might be considered a type of “priority effect.”

On the other limit, we observe that the community assembly is affected by the history of the species’ arrival for low values of \(\eta\). The community is thus historically contingent (Morin 2009; Belyea and Lancaster 1999; Schröder et al. 2005), an observation that is coherent with the literature. The smaller values of \(\eta\) result in more minor divergences between parent and child species. The community is locally neutral because the species belong to similar trophic levels and have comparable survival probabilities. Thus, the community assembly is likely susceptible to the species’ arrival history and the pioneer species’ features (Fukami et al. 2007).

Resource-noise interactions

What is the influence of evolutionary noise when there is not much room to be different in resource space? What is the role of noise when there are many resources? Clearly, l and \(\eta\) span a phase space of dynamics that we briefly explore for the biologically relevant dynamics it can describe.

For most realizations of systems with \(\eta \rightarrow 0\) and \(l=2\), the number of living species \(S_a\) per realization displays a sigmoidal behavior in time—see Fig. 8a. This results from the resource-consumer feedback: the total number of consumers increases by consuming resources before reducing again due to excessive competition and resource lack. However, in this scenario, the species are almost equivalent in their competitiveness, and they can only go extinct if they arrive in the community at an unfavorable time. It seems reasonable to assume that when \(l=2\), only a limited pool of strategies can survive in what we can call a “harsh” environment. Consequently, the majority of invading species do not present the necessary conditions and quickly go extinct. Successful invasions become rare events, and the growth of \(S_a\) stalls, reaching an equilibrium.

Fig. 8
figure 8

a The number of living species, \(S_a\), for 5 realizations uniformly drawn from a 150 pool of a system with \(l=2\), \(\nu =3.8\), and \(\eta \rightarrow 0\). b Same as a for a system with \(l=100\), \(\nu =3.8\), and \(\eta \rightarrow \infty\). The simulation length of the system in (b) is \(8 \times 10^4\) steps due to memory load issues. For both the system in (a) and (b), the \(S_a\) curves reach a long time plateau whose values are different for each realization

Full size image

Similarly, systems with \(\eta \rightarrow \infty\) and \(l=100\) also show a long-term stationary value for \(S_a\)—see Fig. 8b. Here, the strong species selection provides additional resource-consumer feedback by choosing the most convenient strategies, leading the less fit species to extinction. Regardless of the interpretation, it is notable that again we observe that long-term stability is achieved under very different settings. Note also the much larger number of species that manage to coexist in the limit \(\eta \rightarrow \infty\) and \(l=100\) than when l is small.

On the contrary, for the case with \(\eta \rightarrow 0\), \(l=100\), the system does not present any long-term stationary value for the number of living species within the available computation time (data not shown). In this limit, the species take a long time to adjust their size according to the availability of the many resource types.

In the limit of \(\eta \rightarrow \infty\) and \(l=2\), many realizations of the system hint at the existence of a long-time plateau value of \(S_a\). Also here, it is reasonable to assume that when \(l=2\), a limited pool of strategies can survive in such a harsh environment, but apparently invasion in harsh environments is notably different in its dynamics than evolutionary speciation.

Generalizations of SMA

SMA allows for many further generalizations (MacArthur 1970; Chesson 1990; Haygood 2002). In Eq. (1) we have only considered that species consume resources; however, they may also provide resources—see “Negative strategies” section. Oxygenic photosynthesis (Knoll and Nowak 2017) is one example; on a different scale, gut microbes also provide natural resources for each other (Faust and Raes 2012; Vet et al. 2018). Besides, predator dynamics can be introduced by adding another predator coupling matrix term \(\sum _im_{ij}n_i\), which can have both positive and negative elements, when species j is a predator or prey respectively. Growth rates can be made an explicit function of \(r_i\), preserving much of the dynamics presented here but adding more biologically relevant constraints. Several other choices can be modified, such as making the speciation rate or \(\eta\) a function of \(\textbf{n}\). Making \(r_i < 0\) for some i can account for stressors. We discuss some of these aspects in this section.

Negative strategies

Enabling the components of the strategies \({\textbf {s}}_j\) to also have negative values is a natural choice or ecological dynamical modeling, as it allows for species to contribute to the resources of other species. We find that allowing for the sign change of \({\textbf {s}}_j\) results in a significantly different transient. For example, when one samples \({\textbf {s}}_j\) from the full normal distribution, we observe that for infinitesimal mutations, \(\eta \rightarrow 0\), and small numbers of resources, l, no negative strategy appears or survives. For high l and \(\eta\) values, on the contrary, a portion of negative strategies survives. As a result, the total abundance dynamics presents aperiodic behavior, as the negative strategies work as an additional resource influx rate, with an intrinsic stochastic nature given by the random arrival of species with such features—see Fig. 9.

Fig. 9
figure 9

(R, N) heatmap of the last \(2 \times 10^4\) time steps for 150 realizations of a system with \(l=100\), \(\eta \rightarrow \infty\) and \(\nu =3.8\). Both positive or negative components can define the species strategy vectors, so that \(s_{ij} \in \mathbb {R}\). The colormap displays the logarithm of the number of counts. The dynamics are aperiodic but still constrained in a region in the proximity of the line of slope \(\frac{l}{\sum \gamma _i}\frac{\delta \beta }{\alpha }\) (solid red line). The red dot indicates the position of the fixed point for a system with only \(s_{ij} > 0\)

Full size image

Consumption and growth rates as Monod functions

Until now, we assumed that the resource consumption rate \(\beta\) was constant, but it can be reasonable to assume that \(\beta\) is a function of the resource availability, so \(\beta =\beta (r_i)\). The consumption rate then depends on the species’ opportunity to find and consume resources. It turns out that also for SMA, this consumption rate function is an important factor that determines certain characteristics of the dynamics.

To explore the role of the consumption rate function, one relevant choice for \(\beta (r_i)\) is the Monod function (Monod 1949): \(\beta _\textrm{max} \frac{r_i}{K + r_i}\), where K (\(K > 0\)) defines the half-saturation constant, that is, the resource availability that is present in the system when the consumption rate reaches half-speed, \(\beta =\beta _\textrm{max}/2\). The Monod function usually describes bacterial communities’ growth dependency on substrate concentration outside the lag phase (Liu 2020). However, we employ it here to express the intuitive concept that the consumption rate will vary depending on the substrate concentration, assuming \(\beta (0)=0\), and saturating over a certain level of resource availability \(\beta _\textrm{max}\). More generally, K could be different for each resource; for simplicity, we set it equal for all the resource types.

Similar to many other resource-consumer models, we further assume that resource uptake by the species is, up to a constant, equal to the depletion of the resources (Posfai et al. 2017; Pacciani-Mori et al. 2020). Consequently, \(\alpha (r_i)\) in Eq. (2) of the main text also becomes a Monod function, differing from \(\beta (r_i)\) only on the proportionality constant \(\alpha _\textrm{max}\): \(\alpha (r_i)= \alpha _\textrm{max} \frac{r_i}{K + r_i}\).

Summarizing, it follows that the equation for the system dynamics now becomes

$$\begin{aligned} \frac{d r_i}{d t}&= -\beta (r_i)\sum _{j=1\ldots k} s_{ij}n_j + \gamma _i,\end{aligned}$$
(8a)
$$\begin{aligned} \frac{d n_j}{d t}&= \left( \textbf{s}_j\cdot \alpha (\textbf{r}) - \delta \right) n_j. \end{aligned}$$
(8b)

Concretely, we explore the scenario in which \(\eta \rightarrow \infty\) and varied l and K. The choice of K affects both the resource depletion and the species growth timescales. The dynamics in (R, N) space does not display limit-cycles as observed for the linearized resource dynamics defined by the systems described in Eqs. (1) and (2) (see Fig. 2). However, in the Monod-version of SMA, the attractors still lie along a vertical line, now defined by \(N^*= \frac{\alpha _\textrm{max} \sum _i\gamma _i}{\delta \beta _\textrm{max}}\), obtained by the total abundances dynamics stationary solution. This can be observed in Fig. 10a for \(l=2\) and Fig. 11a for \(l=100\).

Fig. 10
figure 10

a (R, N) phase space of the last \(2 \times 10^4\) time steps for 20 realizations (different colors) of a system with \(\nu = 3.6\), \(\eta \rightarrow \infty\), \(l=2\) and different values of K(arrows). Both consumption and species growth rates are described by a Monod function. Here, similarly to Posfai et al. (2017), \(\alpha _\textrm{max}\) and \(\beta _\textrm{max}\) were set both to 1. The attractors lie on a vertical line \(N=\frac{\alpha _\textrm{max} \sum _i\gamma _i}{\delta \beta _\textrm{max}}\). b Examples of living species curve, one for each system with different K, as described in (a)

Full size image
Fig. 11
figure 11

(R, N) phase space of the entire evolution of exemplifying realizations (different colors), one for each system with \(\nu = 3.8\), \(\eta \rightarrow \infty\), \(l=100\) and different values of K (arrows). Both consumption and species growth rates are described by a Monod function. Here, \(\alpha _\textrm{max}=0.5\) and \(\beta _\textrm{max}=1\). We notice a fast evolution towards the attractor. b Examples of living species curve, one for each system with different K, as described in (a). All the systems reach a long-time stationary value

Full size image

The long-term stationary state reached is also reproduced by the Monod version of SMA. In Figs. 10b and 11b for both cases \(l=2,100\), we see that independently of K, all the systems reach a long-time stationary value. In fact, the \(S_a\) associated with \(l=2\) and \(\eta \rightarrow \infty\) reach a plateau. This might result from the fact that when a Monod function describes both consumption and growth rates, the systems with low \(\nu\) are still computable, while in the linearized version of the model, a low \(\nu\) value leads to a too large number of species for the system to remain computationally tractable (but would presumably otherwise reach equilibrium). We see that a long-time plateau is reached for many parameter choices and functional implementations of SMA, strongly suggesting that this feature is a robust property of the SMA model proposed. Of course, the obtained plateau values do depend on the choice of model details.

Comparison with adaptive dynamics: Convergence of strategies

The simplifying time-dependent dynamics provided by the use of Monod functions provides us with an opportunity to compare SMA dynamics to adaptive dynamics (Brännström et al. 2013). As observed in Fig. 11a, the (R, N) dynamics seems to minimize the sum of the resources R. Will adaptive dynamics do the same? We systematically investigate this question by considering the following extreme case: we assume that there is an equilibrium where all species have an identical strategy vector \(\textbf{s}^*\) with nonzero components. First, we introduce for convenience the notation \(g(r)=\frac{r}{K+r}\). From Eq. (8a), we then deduce that in equilibrium we have the equality

$$\begin{aligned} \beta _\textrm{max} g(r^*_i)\textbf{s}^*_iN^*=\gamma _i, \end{aligned}$$
(9)

while from Eq. (8b), we conclude that in equilibrium we must have

$$\begin{aligned} \sum _i \textbf{s}^*_i\alpha _\textrm{max} g(r^*_i)=\delta . \end{aligned}$$
(10)

Hence, we can express \(g(r_i^*)\) in terms of \(s^*_i\), but Eq. (10) gives us just one condition for l components. Therefore, we add that we want to minimize \(\sum _ig(r^*_i)\) given that we had also assumed an interdependence of resources via the arbitrary choice of \(\Vert \textbf{s}^*\Vert _2=1\). To highlight the role of the normalization, we will do the derivation for a general \(p-\)value. Hence, we look for a vector \(\mathbf {s^*}\) that solves

$$\begin{aligned} \text {Max}\hspace{2mm} -\sum _ig(r^*_i), \hspace{3mm} \text {subject to} \hspace{2mm} \Vert \textbf{s}^*\Vert _p^p=1. \end{aligned}$$
(11)

Using Lagrange multipliers, we find that a solution exists when there is a \(\lambda\) such that the following holds for all i:

$$\begin{aligned} -\partial _{s_i^*}\sum _ig(r^*_i)=\lambda \partial _{s_i^*}\Vert \textbf{s}^*\Vert _p^p. \end{aligned}$$
(12)

Using Eq. (9), we find

$$\begin{aligned} \frac{\gamma _i}{\sum _i\gamma _i}\frac{\delta }{\alpha _\text {max}}\frac{1}{(s_i^*)^2}=\lambda p (s_i^*)^{p-1}. \end{aligned}$$
(13)

As \(\lambda\) must be independent of i, we must take

$$\begin{aligned} s_i^*=c\left( \frac{\gamma _i}{\sum _i\gamma _i}\right) ^{\frac{1}{1+p}}. \end{aligned}$$
(14)

The constant c can now be used to normalize \(\textbf{s}^*\), so the unique solution for \(\textbf{s}^*\) is then

$$\begin{aligned} s_i^*=\frac{\gamma _i^{\frac{1}{1+p}}}{\left(\sum _i\gamma _i^{\frac{p}{1+p}}\right)^{\frac{1}{p}}}. \end{aligned}$$
(15)

On the other hand, in Caetano et al. (2021), the same equations for equilibrium of Eq. (8a) are solved as

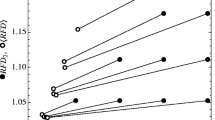
$$\begin{aligned} \textbf{s}^*_i=\left( \frac{\gamma _i}{\sum _i\gamma _i}\right) ^{\frac{1}{p}}, \end{aligned}$$
(16)

using adaptive dynamics (Brännström et al. 2013), i.e., this solution is an Evolutionarily Stable State (ESS). We can compare this strategy vector with our resource-minimizing strategy vector using simulations.Footnote 1 In Fig. 12, we show a simulation of the SMA for \(l=3\) and \(\eta =0.02\) for a long integration time. In Fig. 12a, we see that R is initially indeed minimized, before it slowly increases to the value predicted by the ESS. When we make a ternary plot of the strategies at the end of the simulation, we observe that they are all centered around the ESS, not the resource-minimizing strategy. Therefore, in the language of adaptive dynamics, the resource-minimizing strategy could be a dynamically unstable ESS.

The choice of the norm \(\Vert \textbf{s}^*\Vert _2=1\) does have consequences, which we can clarify quantitatively. For the strategy vector in Eq. (16), we can find the total amount of resources in equilibrium \(R^*\) by summing over the individual \(r^*_i\) and get

$$\begin{aligned} R^*=\sum _ig^{-1}\left( \frac{\delta }{\alpha _\textrm{max}}\left( \frac{\gamma _i}{\sum _i\gamma _i}\right) ^{1-1/p}\right) . \end{aligned}$$
(17)

Note that when we choose \(p=1\), all \(r_i^*\) will become independent of \(\varvec{\gamma }\), explaining the results from Posfai et al. (2017). Furthermore, when \(p<1\), we see that all \(r_i^*\) become smaller when we choose specialization as the preferred strategy (opposite to assuming that all components of \(\varvec{s}^*\) are nonzero). This highlights that also in SMA, the choice of normalization, which models how a species distributes its finite amount of energy, influences the selection of different types of strategies.

Fig. 12
figure 12

a The blue line shows the evolution of the total resource abundance from \(t=10^4\) onward. The green line represents the stationary value connected to the resource minimizing state, Eq. (15), and the red line represents the ESS from Eq. (16). b This figure shows the strategies from SMA (blue dots) together with the minimizing strategy (green) and the ESS (red). The strategies clearly center around the ESS. Here, \(\alpha _\textrm{max}=0.5\), \(\beta _\textrm{max}=1\), \(\eta =0.02\), \(\nu =4\), and \(\boldsymbol{\gamma }= (1.5,0.5,5)\). \(\boldsymbol{\gamma }\) is deliberately chosen very uneven to highlight the differences between the two strategies

Full size image

Limitations

After studying several extensions, we must look at the limitations of our approach. We noted that the deterministic version of our model can have an arbitrarily large number of coexisting species in absence of an extinction threshold (Posfai et al. 2017). Unfortunately, this is not a generic property of the model. Indeed, when we perturb the constraint that all species have their strategy normalized to the same value, i.e., by letting the value of the normalization depend on the species, we observe that the complex communities collapse back towards a number of species that is in line with the competitive exclusion principle. It is however very well possible that in, for example, plankton communities, many species have similar functional traits (Borics et al. 2021; Graco-Roza et al. 2021). Therefore, our model might not be the full description of a complex ecosystem, but it can give us insight into the dynamics in a single “cluster” of similar traits.

We would like to further add that speciation is a complex process, not been fully uncovered (Matute and Cooper 2021; Gavrilets 2014). Because our aim is model simplicity, we do not consider, e.g., a specific mode of reproduction or reproductive isolation (Higgs and Derrida 1991; Manzo and Peliti 1994; Yamaguchi and Iwasa 2013; Gavrilets 2004). Our definition of speciation is more similar to a neutral speciation rate, as it is represented by the probability that an offspring originates a new species (Gavrilets 2014). Our approach is clearly not relatable to neutral models, e.g., Azaele et al. (2016), Volkov et al. (2003), Chave (2004), Kopp (2010). Nonetheless, for infinitesimal \(\eta\), a certain degree of invariance for strategies’ identities, and thus for species shuffling, remains valid.

Conclusions

We showed that adding speciation in a MacArthur model adds a host of dynamical features reminiscent of commonly observed evolutionary biology. Even when one starts the dynamics with a single species, by introducing new species of slightly different types into an existing ecosystem, we observe equilibration to a maximum number of species on a timescale that is a simple function of the spawning rate. We observe that the system self-maximizes the number of coexisting species, reaching a long-term stationary value. The stationary behavior represents a dynamic equilibrium as an attractor in (R, N) space. Parameters that set the stochastic strength allow the model to explore both invasive and evolutionary dynamics; the size of the resource pool affects the dynamical ability to converge to a niche community (Fisher and Mehta 2014). Community aggregate behavior is also stable under perturbations: the system adjusts its features after a resource influx shock; rank abundance plots are in line with commonly observed features. Much phenomenology is robust when different choices are made for resource consumption rates and other model features, and some analytical features of the model are consistent with literature results. The perspective embedded in SMA and the range of biologically relevant phenomena it produces offer a flexible interpretation of the term “species” that gives a simple computational tool for a more quantitative understanding of evolution and ecology. One significant open question for this framework is whether the completely random speciation introduced here can also result in the emergence of “clusters” of similar species vectors (Maynard et al. 2018). Such clustering of species that consume resources in a complementary way would be a computationally tractable representation of a true “tangled bank.”