Coexistence in spatiotemporally fluctuating environments

Abstract

Ecologists have put forward many explanations for coexistence, but these are only partial explanations; nature is complex, so it is reasonable to assume that in any given ecological community, multiple mechanisms of coexistence are operating at the same time. Here, we present a methodology for quantifying the relative importance of different explanations for coexistence, based on an extension of the Modern Coexistence Theory. Current versions of Modern Coexistence Theory only allow for the analysis of communities that are affected by spatial or temporal environmental variation, but not both. We show how to analyze communities with spatiotemporal fluctuations, how to parse the importance of spatial variation and temporal variation, and how to measure everything with either mathematical expressions or simulation experiments. Our extension of Modern Coexistence Theory shows that many more species can coexist than originally thought. More importantly, it allows empiricists to use realistic models and more data to better infer the mechanisms of coexistence in real communities.

Introduction

Modern Coexistence Theory (MCT) is a framework for understanding ecological coexistence (Chesson 1994, 2000; see Barabás et al. 2018 for a recent review). MCT has two main strengths. First, MCT gives us the relative importance of different explanations for coexistence, and thus tells us how species are coexisting, not simply whether they are coexisting. Second, MCT is general because it is a framework for analyzing arbitrary models of population dynamics (which could represent all kinds of different communities). This feature of MCT stands in contrast to several big theories in community ecology—such as neutral theory, maximum entropy, and metacommunity theory—in which highly constrained models are used to make inferences about many communities. MCT has been successfully used to derive theoretical insights (e.g., Chesson and Huntly 1997; Stump and Chesson 2015; Li and Chesson 2016; Snyder and Chesson 2003; Chesson 2008; Kuang and Chesson 2010; Schreiber 2021), and to infer the mechanisms of coexistence in real communities (Cáceres 1997; Adler et al. 2006; Angert et al. 2009; Sears and Chesson 2007; Usinowicz et al. 2012; Descamps-Julien and Gonzalez 2005; Chu and Adler 2015; Usinowicz et al. 2017; Ignace et al. 2018; Towers et al. 2020).

Despite MCT’s successes, there are a handful of problems that limit its applicability. One such problem is that currently, MCT can be used to analyze models where the environment fluctuates over space or time, but not both. Here, we extend Modern Coexistence Theory (MCT) to show how models with spatiotemporal fluctuations can be analyzed. Furthermore, we show how to parse the importance of spatial fluctuations and temporal fluctuations, and how to measure everything with mathematics or simulations. While a couple papers (Chesson 1985; Snyder et al. 2005; Snyder 2008) have examined the effects of spatiotemporal fluctuations in particular models, our approach permits the analysis of a broad variety of models and is thus targeted towards empirical applications.

MCT is based on invasion growth rates, the average per capita growth rates of species that have been perturbed to low density. However, the appropriate average is not trivial to compute in spatiotemporal models. A simple arithmetic average over space and time is not appropriate, due to a fundamental difference in how populations grow over space and time: with respect to the geometric mean of the finite rate of increase (the quantity predictive of persistence; Lewontin and Cohen 1969; Dempster 1955; Stearns 2000; Metz et al. 1992), contributions from populations across space are additive, but contributions from populations across time are multiplicative. Therefore, the appropriate spatiotemporal averaging involves a density-weighted spatial average, followed by a temporal average on the log-scale.

The ability to analyze models with spatiotemporal fluctuations helps us better understand coexistence in real ecological communities: MCT necessarily interfaces with the real world through empirically calibrated models, and good representations of real communities will undoubtedly involve spatiotemporal variation. But the addition of spatiotemporal fluctuations is not realism for realism’s sake: failure to include spatiotemporal fluctuations will typically lead to underestimates of fluctuation-dependent coexistence mechanisms, which could lead to poor downstream inferences about the nature of coexistence and macroecological patterns that entail coexistence (e.g., metacommunity structure, species abundance distributions). Furthermore, our extension of MCT permits a more fine-grained quantification of coexistence mechanisms. With Spatiotemporal MCT, one can compare the relative importance of spatial variation, temporal variation, and classical coexistence mechanisms (e.g., resource partitioning); one can partition an individual coexistence mechanism—like the storage effect—into its spatial and temporal constituents. The ability to analyze models with spatiotemporal fluctuations can also lead to novel theoretical insights. For instance, we show that (1) temporal variation can promote the storage effect in the lottery model, even in the case of non-overlapping generations (Section “Example: The spatiotemporal lottery model”); (2) that it is (nearly) impossible for the competitive exclusion principle to hold true in the presence of spatiotemporal fluctuations (Section “Discussion”); and (3) the inclusion of spatiotemporal fluctuations exactly doubles the maximum number of species that can coexist due to fluctuation-dependent coexistence mechanisms (Section “Discussion”).

Table 1 The symbols and terminology of Spatiotemporal Modern Coexistence Theory (MCT)

	Description
MCT-specific terminology
Invader	A rare species; for mathematical convenience, the per capita growth rate of this species is approximated by perturbing population density to zero
Resident	A common species, more precisely understood as a species at its typical abundances
Invasion growth rate	The long-term average of the per capita growth rate of an invader
Partition	A scheme for breaking up an invasion growth rate into a sum of component parts
Coexistence mechanism	A class of explanations for coexistence; corresponds to a component of the invasion growth rate partition of Spatiotemporal MCT
Space-time decomposition	A type of partition which parses the effects of spatial and temporal variation on the invasion growth rate
Invader–resident comparison	A comparison between an invader and the resident species; measures a rare-species advantage
Generation time quotient	Scales resident growth rates, hypothetically converting the population-dynamical speeds of resident species to that of the invader; corrects for average fitness differences in the invader–resident comparison; replaces the scaling factors, also known as comparison quotients, from previous versions of MCT
Variable
x	A location in space
t	A point in time
j	Species index (subscript)
$n_j(x,t)$	The population density of species j at patch x and time t
$\nu _j(x,t)$	Relative density, calculated as local population density divided by the spatial average of population density, i.e., $n_j(x,t) / \mathbb {E}_{x} \left[ n_j \right]$
$\lambda _j$(x,t)	The local finite rate of increase. In non-spatial models, $\lambda _j$ is defined as $n_{j}(x,t+1)/n_{j}(x,t)$. However, in spatial models, $\lambda _j$ is defined as $n_{j}'(x,t)/n_{j}(x,t)$, where $n_{j}'(x,t)$ is the population size after the local growth phase, but before the dispersal phase
$\widetilde{\lambda }_j(t)$	The metapopulation finite rate of increase, defined as a density-weighted average of $\lambda _j$ over patches: $\widetilde{\lambda }_j = \mathbb {E}_{x} \left[ (n_j / \mathbb {E}_{x} \left[ n_j \right] ) \lambda _j \right]$
$\mathbb {E}_{t} \left[ \log (\widetilde{\lambda }_j) \right]$	The long-term average per capita growth rate; for resident species, this is zero by definition; for invader, this is the invasion growth rate
$E_j(x,t)$	The environmental parameter, more generally understood as the effects of density-independent factors
$C_j(x,t)$	The competition parameter, more generally understood as the effects of density-dependent factors
$g_j$	A function that gives the local finite rate of increase: $\lambda _j(x,t) = g_j(E_j(x,t), C_j(x,t))$
$E_j^*$	The equilibrium environmental parameter, defined so that $g_j(E_j^*, C_j^*) = 1$
$C_j^*$	The equilibrium competition parameter, defined so that $g_j(E_j^*, C_j^*) = 1$
$\sigma$	The scale of environmental fluctuations: $E_j(x,t) - E_j^* = \mathcal {O}(\sigma )$; it is sometimes the case that $\sigma$ controls the size of fluctuations in $n_j$, $E_j$, and $C_j$, see Appendix “Small-noise assumptions”
S	The total number of species in the community; $S-1$ is the number of residents, assuming that all residents can coexist
$GT_j$	The generation time of species j, evaluated at equilibrium; the quantity $1/GT_j$ is a measure of the speed of population dynamics—the intrinsic capacity to grow or decline quickly
$\frac{GT_r}{GT_i}$	Generation time quotient; effectively converts the population-dynamical speed of resident r to that of the invader i
$\overline{\mathscr {E}_j}$	The main effect of density-independent factors on the average per capita growth rate, defined as $\mathbb {E}_{t} \left[ \log (\mathbb {E}_{x} \left[ g_j(E_j,C_j^*) \right] ) \right]$
$\overline{\mathscr {C}_j}$	The main effect of density-dependent factors on the average per capita growth rate, defined as $\mathbb {E}_{t} \left[ \log (\mathbb {E}_{x} \left[ g_j(E_j^*, C_j) \right] ) \right]$
$\overline{\mathscr {I}_j}$	The interaction effect of density-dependent and density-independent factors on the average per capita growth rate, defined as $\mathbb {E}_{t} \left[ \log (\mathbb {E}_{x} \left[ g_j(E_j, C_j) \right] ) \right] - \overline{\mathscr {E}_j} - \overline{\mathscr {C}_j}$
$\overline{\mathscr {K}_j}$	The main effect of allowing relative density to vary, on the average per capita growth rate, defined as $\mathbb {E}_{t} \left[ \log (\mathbb {E}_{x} \left[ \nu _j g_j(E_j,C_j) \right] ) \right] - \mathbb {E}_{t} \left[ \log (\mathbb {E}_{x} \left[ g_j(E_j,C_j) \right] ) \right]$
Coexistence mechanisms
$\Delta E_i$	Density-independent effects; the degree to which density-independent factors favor the invader
$\Delta \rho _i$	Linear density-dependent effects; specialization on resources and/or natural enemies
$\Delta N_i$	Relative nonlinearity; specialization on the spatiotemporal variance of resources and/or natural enemies
$\Delta I_i$	The storage effect; specialization on different states of a spatiotemporally varying environment
$\Delta \kappa _i$	Fitness-density covariance; the differential ability of rare species to end up in locations with high ecological fitness
Taylor series coefficients
$\alpha _{j}^{(1)}$	The linear effects of fluctuations in $E_j$, defined as $\frac{\partial g_j}{\partial E_j}\Bigr |_{\begin{array}{c} E_j = E_{j}^{*}\\ C_j = C_{j}^{*} \end{array}} = \frac{\partial g_j {(E_j^*, C_j^*)}}{\partial E_j}$
$\alpha _{j}^{(2)}$	The nonlinear effects of of fluctuations in $E_j$, defined as $\frac{\partial ^2 g_j{(E_j^*, C_j^*)}}{\partial E^2_j}$
$\beta _{j}^{(1)}$	The linear effects of fluctuations in $C_j$, defined as $\frac{\partial g_j{(E_j^*, C_j^*)}}{\partial C_j}$
$\beta _{j}^{(2)}$	The nonlinear effects of fluctuations in $C_j$, defined as $\frac{\partial ^2 g_j {(E_j^*, C_j^*)}}{\partial ^2 C_j}$
$\zeta _{j}^{(1)}$	The non-additive (i.e., interaction) effects of fluctuations in $E_j$ and $C_j$, defined as $\zeta _j = \frac{\partial ^2 g_j {(E_j^*, C_j^*)}}{{\partial E_j}{\partial C_j}}$
Superscripts and subscripts
Subscripts
j	Index of an arbitrary species
i	Index of the invader
r	Index of a resident
x	Indicates that a summary statistic (e.g., mean, covariance, variance) is calculated by summing across space
t	Indicates that a summary statistic (e.g., mean, covariance, variance) is calculated by summing across time
A	Denotes the effect of average conditions in the space-time decomposition
S	Denotes the main effect of spatial variation in the space-time decomposition
T	Denotes the main effect of temporal variation in the space-time decomposition
R	Denotes the interaction effect of spatial and temporal variation in the space-time decomposition
Superscripts
(e)	Denotes exact coexistence mechanisms, or intermediate products in the calculation of exact coexistence mechanisms
$\#$	Indicates that the elements of a vector or matrix have been shuffled (sampled randomly without replacement)
Operators
$\mathbb {E}_{x,t} \left[ \cdot \right]$	The spatiotemporal sample arithmetic mean; for a variable Z that varies over K patches and T time points,
	$\mathbb {E}_{x} \left[ Z \right] = (1/K)\sum _{x = 1}^{K} Z(x,t)$,
	$\mathbb {E}_{t} \left[ Z \right] = (1/T)\sum _{t = 1}^{T} Z(x,t)$, and
	$\mathbb {E}_{x,t} \left[ Z \right] = (1/(T K)) \sum _{t = 1}^{T} \sum _{x = 1}^{K} Z(x,t)$
$\mathrm {Var}_{x,t} \left( \cdot \right)$	The spatiotemporal sample variance; for a variable Z that varies over K patches and T time points,
	$\mathrm {Var}_{x} \left( Z\right) = (1/K)\sum _{x = 1}^{K} (Z(x,t) - \mathbb {E}_{x} \left[ Z \right] )^2$,
	$\mathrm {Var}_{t} \left( Z\right) = (1/T)\sum _{t = 1}^{T} (Z(x,t) - \mathbb {E}_{t} \left[ Z \right] )^2$, and
	$\mathrm {Var}_{x,t} \left( Z\right) = (1/(T K)) \sum _{t = 1}^{T} \sum _{x = 1}^{K} (Z(x,t) - \mathbb {E}_{x,t} \left[ Z \right] )^2$
$\mathrm {Cov}_{x,t} \left( \cdot , \cdot \right)$	The spatiotemporal sample covariance; for variables W and Z that vary over K patches and T time points,
	$\mathrm {Cov}_{x} \left( W, Z \right) = (1/K)\sum _{x = 1}^{K} (W(x,t) - \mathbb {E}_{x} \left[ W \right] )(Z(x,t) - \mathbb {E}_{x} \left[ Z \right] )$,
	$\mathrm {Cov}_{t} \left( W, Z \right) = (1/T)\sum _{t = 1}^{T} (W(x,t) - \mathbb {E}_{t} \left[ W \right] )(Z(x,t) - \mathbb {E}_{t} \left[ Z \right] )$, and
	$\mathrm {Cov}_{x,t} \left( W, Z \right) = (1/(T K)) \sum _{t = 1}^{T} \sum _{x = 1}^{K} (W(x,t) - \mathbb {E}_{x,t} \left[ W \right] )(Z(x,t) - \mathbb {E}_{x,t} \left[ Z \right] )$

Spatiotemporal coexistence mechanisms

Overview

At the coarsest level of description, the Modern Coexistence Theory (MCT) has two steps: “decompose and compare” (Ellner et al. 2019). First, decompose the average per capita growth rate of each species into terms that correspond to conceptually distinct processes (e.g., growth that can be attributed to resource consumption). Second, compare the like-terms of rare species (termed invaders) and common species (termed residents) in order to discover which processes tend to help rare species. These invader–resident comparisons, called coexistence mechanisms, correspond to classes of explanations for coexistence. The sum of coexistence mechanisms is the invasion growth rate, the long-term average per capita growth rate of a species that has been perturbed to near-zero density.

How do invasion growth rates and coexistence mechanisms relate to coexistence? The main idea is that invasion growth rates measure the tendency to recover from rarity, so a set of S species can be said to coexist if each species has a positive invasion growth rate in the sub-community of $S-1$ resident species. This is known as the mutual invasibility criterion for coexistence (Turelli 1978; Chesson 2000; Chesson and Ellner 1989; Grainger et al. 2019).

In truth, the relationship between invasion growth rates and coexistence is not so simple. The mutual invasibility criterion fails when the elimination of one species causes knock-on extinctions, such that the $S-1$ residents cannot coexist. For the mutual invasibility criterion to work, we must either assume that all $S-1$ residents can coexist (Case 2000), or limit ourselves to two-species competitive communities (Ellner 1989). When the mutual invasibility criterion fails, one can still use invasion growth rates as inputs to the Hofbauer criterion for coexistence (Hofbauer 1981; Benaïm and Schreiber 2019, Eq. 3.4), a sufficient condition for a type of global stability called permanence or uniform persistence (Schreiber 2000; Garay and Hofbauer 2003; Schreiber et al. 2011; Roth and Schreiber 2014). But this criterion potentially combines invasion growth rates in many sub-communities (with $S-n$ residents, for $n = 1, 2, \ldots , S$), so it is unclear to how to average over sub-communities to obtain species-level coexistence mechanisms or community-average coexistence mechanisms (as in Chesson 2003, Eq. 16).

Invasion growth rates are used in the mutual invasibility criterion and the Hofbauer criterion, both of which test for global stability. However, global stability can sometimes be too strong a notion of coexistence: under a certain set of scenarios (e.g., Allee effects, obligate mutualisms, and intransitive competition), negative invasion growth rates can erroneously indicate a failure to coexistence, since all species would be able to coexist if simultaneously introduced at higher densities. We leave all of these issues to future research; thus, we temporarily use these concepts heuristically: larger coexistence mechanisms $\rightarrow$ larger invasion growth rate $\rightarrow$ stronger coexistence. We deliberately avoid models with obligate mutualisms and Allee effects; if placing a species in the invader state causes knock-on extinctions, we forge onward, measuring coexistence mechanisms with the reduced number of residents.

In this paper, we will define two types of coexistence mechanisms. The first is small-noise coexistence mechanisms, which closely approximate the invasion growth rate when environmental fluctuations are small. The second type is exact coexistence mechanisms, which always sum exactly to the invasion growth rate. Small-noise coexistence mechanisms are calculated with Taylor series expansions (i.e., a linearization of population dynamics about an equilibrium), whereas exact coexistence mechanisms are calculated with simulation data (an approach pioneered by Ellner et al. (2016, 2019)). To be clear, small-noise coexistence mechanisms do not assume that environmental fluctuations are unimportant or that the fluctuation-independent mechanisms drive coexistence. Small-noise refers to a technical assumption that environmental fluctuations are small relative to other parameters in a model of population growth. This assumption (when paired some additional assumptions; Appendix “Small-noise assumptions”) allows us to derive analytical expressions for the coexistence mechanisms.

There has been recent debate about how exactly coexistence mechanisms should be defined (Barabás et al. 2018; Chesson 2020; Barabás and D’Andrea 2020), with Chesson claiming that true coexistence mechanisms are exact (Chesson 2020, Eq. 9) contradicting previous work (Chesson 1994, Eq. 22). Some expositions of MCT mix-and-match both types of coexistence mechanisms (e.g., Chesson 1994, Eq. 19–22), adding to the confusion. We present the two types of coexistence mechanisms separately, partially for clarity, but primarily because they have distinct pros and cons.

Even though small-noise coexistence mechanisms only approximate the invasion growth rate, there are situations in which small-noise coexistence mechanisms are preferred. For one, the small-noise approximations can be calculated quickly, which is important in empirical applications where coexistence mechanisms are calculated for many draws from a posterior or bootstrap distribution of model parameters. Secondly, small-noise coexistence mechanisms sometimes permit analytical expressions (for a worked example, see Section “Example: The spatiotemporal lottery model”), whereas the exact coexistence mechanisms almost never do. Finally, the small-noise coexistence mechanisms could correspond more closely to our verbal/textual explanations for coexistence, and thus could be more interpretable. On the other hand, the primary advantage of the exact coexistence mechanisms is that they sum exactly to the invasion growth rate. We will derive both the small-noise coexistence mechanisms (Section “Small-noise coexistence mechanisms”) and the exact coexistence mechanisms (Section “Exact coexistence mechanisms”), but we leave it to the reader to determine which is more relevant to their work.

Our exposition focuses on discrete-time models with spatial structure but without age/stage structure. In Appendix “Generalization of MCT to different classes of models”, we discuss generalizations of Spatiotemporal MCT to different classes of models, including continuous-time models and age/stage-structured models. For the time being, community dynamics are governed by a system of difference equations,

$$\begin{aligned} n_j(x,t+1) = n_{j}(x,t) \; \lambda _{j}(x,t) + c_j(x,t) - e_j(x,t) \qquad j = (1, 2, ..., S), \end{aligned}$$

(1)

where $n_{j}(x,t)$ is the local density of species j, $\lambda _j$ is the local finite rate of increase, x is a discrete patch in space, t is a discrete point in time, and S is the number of species in the community. The terms $c_j$ and $e_j$ represent immigration and emmigration respectively, in units of population density. We require that the sum of $c_j$ and $e_j$ across space (i.e., net dispersal) vanishes (Appendix “Spatial averaging and fitness-density covariance”), which occurs generically when either 1) the system is closed (i.e., no individuals can enter or leave the system of patches), or 2) that the system of patches is representative of a larger metacommunity, such that it receives roughly as many immigrants as it loses emigrants.

A few notes on notation are necessary. For convenience, we will often write out random variables without the explicit dependence on space and time; for example, we will write $\lambda _j$ instead of $\lambda _j(x,t)$. We use the operator $\mathbb {E}_{} \left[ Z \right]$ to denote the average of some random variable Z, with subscripts to denote whether the average is being taken across space or time, or both. For example, in a system with K patches that has been observed for T time-steps, $\mathbb {E}_{x} \left[ Z \right] = (1/K)\sum _{x = 1}^{K} Z(x,t)$, $\mathbb {E}_{t} \left[ Z \right] = (1/T)\sum _{t = 1}^{T} Z(x,t)$, and $\mathbb {E}_{x,t} \left[ Z \right] = (1/(T K)) \sum _{t = 1}^{T} \sum _{x = 1}^{K} Z(x,t)$. We use the operators $\mathrm {Var}_{x,t} \left( .\right)$ and $\mathrm {Cov}_{x,t} \left( ., . \right)$ in a similar fashion, to the denote the sample variance and sample covariance respectively.

Our use of the expectation operator is unorthodox: it usually denotes the average across an infinite number of instantiations of the stochastic population process at one point in time, not the temporal average of one instantiation. However, the sample average is asymptotically equivalent to the expectation if the stochastic process is stationary and ergodic; see Section “Computational tricks for measuring invasion growth rates”. Additionally, $\mathbb {E}_{x,t} \left[ . \right]$ is visually similar to $\mathrm {Var}_{x,t} \left( .\right)$ and $\mathrm {Cov}_{x,t} \left( ., . \right)$, whereas the subscripts “x, t” are located incongruously in more conventional notation for the mean, e.g., $\langle Z \rangle _{x,t}$, $\overline{Z}^{\{x,t\}}$.

The local finite rate of increase is defined as $\lambda _j = n'_j(x,t+1)/n_j(x,t)$, where $n'_j(x,t+1)$ is the population density after a bout of local population growth, but before the dispersal phase. The metapopulation finite rate of increase, $\widetilde{\lambda }_j = \mathbb {E}_{x} \left[ (n_j / \mathbb {E}_{x} \left[ n_j \right] ) \lambda _j \right]$, is the density-weighted spatial average of $\lambda _j$. The average growth rate rate, $\mathbb {E}_{t} \left[ \log (\widetilde{\lambda }_j) \right]$, is the quantity whose sign is predictive of long-term growth (Schreiber et al. 2011). The average growth rate of the invader is called the invasion growth rate. The subscript i references an invader species, the subscript r references a resident species, and the subscript j references a generic species whose status as a resident or invader is impertinent.

Small-noise coexistence mechanisms

A full derivation of small-noise spatiotemporal coexistence mechanisms is provided in Appendix “Deriving small-noise coexistence mechanisms”. Here, we summarize the main steps:

• 1. The local finite rate of increase is expressed as a function of an environmental parameter $E_j$, and a competition parameter $C_j$: $\lambda _j(x,t) = g_j(E_j(x,t), C_j(x,t))$. The environmental parameter $E_j$ has also been referred to as “the environmentally dependent parameter,” “the environmental response,” or simply, “the environment.” It is more generally defined as some parameter that depends on spatiotemporally fluctuating density-independent factors (e.g., the germination probability of a seed, which depends on precipitation). Similarly, the competition parameter $C_j$, also known as “competition,” is more generally defined as some parameter that depends on density-dependent factors. As such, $C_j$ may represent resource competition, apparent competition, or even mutualism. The competition parameter can often be expressed as function of multiple regulating factors (see Appendix “Multiple regulating factors”), such as resources, refugia, competitors’ densities, and predators.

• 2. The local finite rate of increase is approximated with a second-order Taylor series expansion of $g_j$ about the equilibrium parameters, $E_j^*$ and $C_j^*$, constants which are specified by the user of MCT but must satisfy the constraint $g_j(E_j^*, C_j^*) = 1$. The resulting second-order polynomial will lead to an accurate approximation of the invasion growth rate, but only if some assumptions about the magnitude of environmental fluctuations are met (see Appendix “Small-noise assumptions”). To help satisfy these assumptions, it is important to select the equilibrium parameters so that they are close to their spatiotemporal means, $\mathbb {E}_{x,t} \left[ E_j \right]$ and $\mathbb {E}_{x,t} \left[ C_j \right]$, respectively.

• 3. The appropriate spatial and temporal averaging is applied in order to express average growth rates entirely in terms of moments of local growth, $\lambda _j$, and relative density, $\nu _j = n_j / \mathbb {E}_{x} \left[ n_j \right]$:

  $$\begin{aligned} \begin{aligned} \mathbb {E}_{t} \left[ \log (\widetilde{\lambda }_j) \right] \approx \mathbb {E}_{x,t} \left[ \lambda _j \right] + \mathbb {E}_{t} \left[ \mathrm {Cov}_{x} \left( \nu , \lambda _j \right) \right] - 1 - \frac{1}{2} \mathrm {Var}_{t} \left( \mathbb {E}_{t} \left[ \lambda _j \right] \right) \end{aligned} \end{aligned}$$

  (2)

• 4. The Taylor series approximation of $\lambda _j$ (see step 2) is substituted into the expression for the average growth rate Eq. (2), resulting in a long expression for species j’s average growth rate:

  $$\begin{aligned} \begin{aligned} \mathbb {E}_{t} \left[ \log (\widetilde{\lambda }_j) \right] &\approx \;\alpha _j^{(1)} \mathbb {E}_{x,t} \left[ (E_j - E_{j}^{*}) \right] + \beta _j^{(1)} \mathbb {E}_{x,t} \left[ (C_j - C_{j}^{*}) \right] \\ &\quad+\; \frac{1}{2} \alpha _j^{(2)} \mathrm {Var}_{x,t} \left( E_j\right) + \frac{1}{2} \beta _j^{(2)} \mathrm {Var}_{x,t} \left( C_j\right) + \zeta _j \mathrm {Cov}_{x,t} \left( E_j, C_j \right) \\ &\quad+ \mathbb {E}_{t} \left[ \mathrm {Cov}_{x} \left( \nu _j, \alpha _j^{(1)} (E_j - E_{j}^{*}) + \beta _j^{(1)} (C_j - C_{j}^{*}) \right) \right] \\ &\quad- \frac{1}{2} \alpha _j^{(1)^{2}} \mathrm {Var}_{t} \left( \mathbb {E}_{x} \left[ E_j \right] \right) - \frac{1}{2} \beta _j^{(1)^{2}} \mathrm {Var}_{t} \left( \mathbb {E}_{x} \left[ E_j \right] \right)\\ &\quad-\alpha _j^{(1)}\beta _j^{(1)} \mathrm {Cov}_{t} \left( \mathbb {E}_{x} \left[ E_j \right] , \mathbb {E}_{x} \left[ C_j \right] \right) , \end{aligned} \end{aligned}$$

  (3)

  where the coefficients of the Taylor series,

  $$\begin{aligned} \begin{aligned} &\alpha _j^{(1)} = \frac{\partial g_j {(E_j^*, C_j^*)}}{\partial E_j}, \quad \beta _j^{(1)} = \frac{\partial g_j {(E_j^*, C_j^*)}}{\partial C_j}, \\& \alpha _j^{(2)} = \frac{\partial ^2 g_j {(E_j^*, C_j^*)}}{\partial E_j^2}, \quad \beta _j^{(2)} = \frac{\partial ^2 g_j {(E_j^*, C_j^*)}}{\partial C_j^2},\\& \zeta _j = \frac{\partial ^2 g_j {(E_j^*, C_j^*)}}{{\partial E_j}{\partial C_j}}, \quad \end{aligned} \end{aligned}$$

  (4)

  are all evaluated at the user-specified equilibrium values $E_j = E_j^*$ and $C_j = C_j^*$, as implied by the notation. The additive terms in the above Eq. (3), which we may call growth rate components, can be conceptualized as distinct processes. For example, the second term $\beta _j^{(1)} \mathbb {E}_{x,t} \left[ (C_j - C_{j}^{*}) \right]$ is the effect of the mean level of competition on the average growth rate.

• 5. The invader is compared to the residents. Because coexistence is about a rare-species advantage, we do not care so much about the invader’s growth rate components, but rather their magnitude relative to the corresponding components of residents. Since every resident species cannot grow or decline on average (i.e., $\mathbb {E}_{t} \left[ \log (\widetilde{\lambda }_r) \right] = 0$), we may subtract a linear combination of the $S-1$ resident species from the invasion growth rate

  $$\begin{aligned} \mathbb {E}_{t} \left[ \log (\widetilde{\lambda }_i) \right] = \mathbb {E}_{t} \left[ \log (\widetilde{\lambda }_i) \right] - \frac{1}{S-1} \sum \limits _{r \ne i}^S \frac{GT_r}{GT_i} \mathbb {E}_{t} \left[ \log (\widetilde{\lambda }_r) \right] , \end{aligned}$$

  (5)

  without any distortion of the invasion growth rate. The weighting by $1/(S-1)$ assumes that all $S-1$ species can coexist; if perturbing a species to the invader state causes knock-on extinctions, then we only average over extant residents. The coefficients $GT_r/GT_i$ are quotients of species’ generation times and function to hypothetically convert the population-dynamical speed of the residents to that of the invader (Johnson and Hastings 2022a). They will be discussed further in a few paragraphs. The long decomposition of the average growth rate Eq. (3) can be substituted into the above Eq. (5), and like-terms can be grouped such that the invasion growth rate is expressed as a sum of invader–resident comparisons. These comparisons are the coexistence mechanisms.

The density-independent effects ($\Delta E_i$) is the degree to which all density-independent factors favor the invader. The linear density-dependent effects ($\Delta \rho _i$) represents a rare-species advantage due to specialization on regulating factors (i.e., resources and/or natural enemies). Relative nonlinearity ($\Delta N_i$) is a rare-species advantage due to specialization on variation in regulating factors. The storage effect ($\Delta I_i$) is the rare-species advantage due to specialization on certain states of a variable environment. Fitness-density covariance ($\Delta \kappa$) is the differential ability of a rare species’ individuals to end up in locations where they have high fitness. Note that “coexistence mechanism” is a misnomer when it comes to $\Delta E_i$, since $\Delta E_i$ can only support a single species in the absence of all other mechanisms. See Barabás et al. (2018) for a more thorough discussion of the canonical coexistence mechanisms and their interpretations.

Experts in coexistence theory may notice several differences between spatiotemporal MCT and previous versions of MCT (i.e., Chesson 1994, Chesson 2000; Barabás et al. 2018), aside from the inclusion of spatiotemporal fluctuations. First, we keep the equilibrium competition parameters, $C_j^*$, as part of $\Delta \rho _i$, whereas previous versions of MCT shunted the $C_j^*$ to the density-independent effects, which are then denoted by $r_i'$ (see Barabás et al. 2018, Eq. 19). Second, we scale resident growth rates by a quotient of generation times, whereas previous versions of MCT scaled resident growth rates by the so-called scaling factors. Both the shunting of $C_j^*$ and the scaling factors have a very specific function: to cancel $\Delta \rho _i$. As we have argued elsewhere (Johnson and Hastings 2022a), cancelling $\Delta \rho _i$ can be useful in the context of theoretical research, but is not recommended for “measuring coexistence” (i.e., using MCT to infer the mechanisms of coexistence in real communities). In the myopic quest to cancel $\Delta \rho _i$, the scaling factors can dramatically modulate the values of other coexistence mechanisms, potentially leading to incorrect inferences about coexistence.

Retaining the $C_j^*$ terms in $\Delta \rho _i$ helps with the interpretability of $\Delta \rho _i$: the term $\alpha _j^{(1)} (\mathbb {E}_{x,t} \left[ C_j \right] -C_j^*)$ can be interpreted as the effect (on per capita growth rates) of the average deviation from equilibrium competition, whereas $\alpha _j^{(1)} \mathbb {E}_{x,t} \left[ C_j \right]$ has no clear meaning. That being said, it will sometimes make sense to present the sum of $\Delta \rho _i$ and $\Delta E_i$, the total contribution of fluctuation-independent forces (e.g., Johnson and Hastings 2022a, SI Table 1–2; Ellner et al. 2019, Table 2, “Fluctuation-free growth rate”).

To ensure that species with fast life cycles do not dominate the invader–resident comparison, we multiply each residents’ average growth rate by a quotient of generation times, $GT_r / GT_i$. Because $1/GT_j$ is a measure of population-dynamical speed, the scaling quotients can be thought of as converting the speed of resident dynamics to that of the invader: resident speed, $1/GT_r$, is canceled by the speed implicit in the resident’s average growth rate, leaving only the invader’s speed, $1/GT_i$. When the species under consideration do not have dramatically different generation times, it is often reasonable (and in some models, considerably simpler) to fix $GT_r/GT_i = 1$ for all i and r. This approach, dubbed the simple comparison by Johnson and Hastings (2022a), was originally performed by Ellner et al. (2016, 2019), who also retained $\Delta \rho _i$ (using different notation).

There is no single definition of generation time, but many definitions are quantitatively equivalent in a stable population (Ellner 2018). Thus, to minimize arbitrariness, we fix model parameters at their equilibrium values and operationalize generation time as the weighted average of parent age across all births at one time, with weights equal to the reproductive value of offspring. This quantity can be calculated with a simple formula in structured population models (Bienvenu and Legendre 2015, Eq. 12; Ellner 2018, Eq. 13), or via simulation in more complex models. In simple models where individuals are identical (i.e., there is no variation in reproductive values) and reproduction is independent of parent age, the generation time is simply the average age of adults; if then mortality occurs at a density-independent rate $\delta$, the distribution of adult age is given by a geometric distribution (or exponential distribution in continuous-time models) with mean $1/\delta$.

Exact coexistence mechanisms

The sum of small-noise coexistence mechanisms merely approximates the invasion growth rate Eq. (6). The approximation will be good if environmental fluctuations are small (see Appendix “Small-noise assumptions” for all assumptions), but in empirically calibrated models there is no guarantee that the small-noise assumptions will be met. An alternative approach is to define a set of coexistence mechanisms that sum exactly to the invasion growth rate. We call these exact coexistence mechanisms and demarcate them with the superscript “(e),” e.g., the exact relative nonlinearity is $\Delta N_i^{(e)}$.

The average growth rate of species j can be broken into two terms:

$$\begin{aligned} \mathbb {E}_{t} \left[ \log (\widetilde{\lambda }_j) \right] = \underbrace{\mathbb {E}_{t} \left[ \log (\mathbb {E}_{x} \left[ \lambda _j \right] ) \right] }_{\textcircled {1}} + \underbrace{\mathbb {E}_{t} \left[ \log (\widetilde{\lambda }_j) \right] - \mathbb {E}_{t} \left[ \log (\mathbb {E}_{x} \left[ \lambda _j \right] ) \right] }_{{\textcircled {2}}}. \end{aligned}$$

(12)

Term $\textcircled {1}$ captures the appropriate spatiotemporal average of fitness. Term $\textcircled {2}$ captures the effects of variation in relative density, which can be seen either by noting that $\mathbb {E}_{t} \left[ \log (\widetilde{\lambda }_j) \right] = \mathbb {E}_{t} \left[ \log (\mathbb {E}_{x} \left[ \lambda _j \right] ) \right]$ when fitness-density covariance is zero Eq. (2), or that the second term will approximate $\mathbb {E}_{t} \left[ \mathrm {Cov}_{x} \left( \nu _j, \lambda _j \right) \right]$ when the small-noise assumptions (Appendix “Small-noise assumptions”) are met.

Term $\textcircled {1}$ can be further decomposed with the following schema:

$$\begin{aligned} \mathbb {E}_{t} \left[ \log ( \mathbb {E}_{x} \left[ \lambda _j \right] ) \right] = \overline{\mathscr {E}_j} + \overline{\mathscr {C}_j} + \overline{\mathscr {I}_j} \end{aligned}$$

(13)

$$\begin{aligned} \overline{\mathscr {E}_j} = \mathbb {E}_{t} \left[ \log (\mathbb {E}_{x} \left[ g_j(E_j,C_j^*) \right] ) \right] \end{aligned}$$

(14)

$$\begin{aligned} \overline{\mathscr {C}_j} = \mathbb {E}_{t} \left[ \log (\mathbb {E}_{x} \left[ g_j(E_j^*, C_j) \right] ) \right] \end{aligned}$$

(15)

$$\begin{aligned} \overline{\mathscr {I}_j} = \mathbb {E}_{t} \left[ \log (\mathbb {E}_{x} \left[ g_j(E_j, C_j) \right] ) \right] - \left( \overline{\mathscr {E}_j} + \overline{\mathscr {C}_j} \right) \end{aligned}$$

(16)

The term $\overline{\mathscr {E}_j}$ is the main effect of the environment on the average growth rate, $\overline{\mathscr {C}_j}$ is the main effect of competition, and $\overline{\mathscr {I}_j}$ is the effect of interactions between environment and competition, in analogy with a two-way ANOVA. These new terms are analogous to the temporal or spatial means of the standard parameters, quantities that played an important role in previous iterations of MCT (e.g., Chesson 1994, Eqs. 8–9; Chesson 2000, Eqs. 28–29). However, they are not equivalent, despite sharing similar notation.

Term $\textcircled {2}$ can be re-expressed as

$$\begin{aligned} \mathbb {E}_{t} \left[ \log (\widetilde{\lambda }_j) \right] - \mathbb {E}_{t} \left[ \log (\mathbb {E}_{x} \left[ \lambda _j \right] ) \right] = \overline{\mathscr {K}_j}, \end{aligned}$$

(17)

$$\begin{aligned} \overline{\mathscr {K}_j} = \mathbb {E}_{t} \left[ \log (\mathbb {E}_{x} \left[ \nu _j g_j(E_j,C_j) \right] ) \right] - \mathbb {E}_{t} \left[ \log (\mathbb {E}_{x} \left[ g_j(E_j,C_j) \right] ) \right] , \end{aligned}$$

(18)

so that $\overline{\mathscr {K}_j}$ is the main effect of allowing relative density, $\nu _j = n_j / \mathbb {E}_{x} \left[ n_j \right]$, to vary across space.

The intermediate quantities—$\overline{\mathscr {E}_j}$, $\overline{\mathscr {C}_j}$, $\overline{\mathscr {I}_j}$, and $\overline{\mathscr {K}_j}$—can be computed generically using simulation data. Simply run a simulation of a model while archiving a record of the $E_j$’s, $C_j$’s, and $\nu _j$’s; specify the equilibrium parameters $E_j^*$ and $C_j^*$; and plug everything into the above equations.

To preempt a point of potential confusion, we emphasize that simulation data is never created while holding $E_j$ or $C_j$ at their equilibrium values. To compute $\overline{\mathscr {C}_j}$, one must evaluate $g_j$ function while holding the environment at $E_j^*$ and allowing $C_j$ to vary; but we still use the $C_j$ that we would have obtained had we not held the environment at $E_j^*$. To obtain these unadulterated $C_j$, we first run a business-as-usual simulation while recording $E_j$ and $C_j$.

To calculate the exact coexistence mechanisms, our new quantities ($\overline{\mathscr {E}_j}$, $\overline{\mathscr {C}_j}$, and $\overline{\mathscr {I}_j}$) are used in the invader–resident comparison Eq. (5) in lieu of the appropriately averaged Taylor series terms (i.e., the additive terms in Eq. (3)).

The space-time decomposition of small-noise coexistence mechanisms

Ideally, we would like to take any coexistence mechanism that relies on spatiotemporal variation, and perform a space-time decomposition to generate four additive components: the contribution of average $E_j$ and $C_j$, the contribution of spatial variation, the contribution of temporal variation, and the contribution of the interaction between spatial and temporal variation. For example, we would like to write the density-independent effects as $\Delta E_{i} = \Delta E_{i,A} + \Delta E_{i,S} + \Delta E_{i,T} + \Delta E_{i,R}$, with the subscripts A, S, T, and R respectively corresponding to the average component, the space component, the time component, and the space-time interaction. The letter R was chosen because the space-time interaction is calculated as a $\underline{R}$emainder (Eq. 32), and because the letter I is already used in $\Delta I_i$ and $\overline{\mathscr {I}_i}$.

Before decomposing entire coexistence mechanisms, we will decompose $\mathrm {Var}_{x,t} \left( E_j\right)$, a building block of the $\Delta E_i$ coexistence mechanism. The space-time decomposition of $\mathrm {Var}_{x,t} \left( E_j\right)$ is

$$\begin{aligned} \mathrm {Var}_{x,t} \left( E_j\right) = S_j + T_j + R_j \end{aligned}$$

(29)

$$\begin{aligned} S_j =\mathrm {Var}_{x} \left( \mathbb {E}_{t} \left[ E_j \right] \right) \end{aligned}$$

(30)

$$\begin{aligned} T_j =\mathrm {Var}_{t} \left( \mathbb {E}_{x} \left[ E_j \right] \right) \end{aligned}$$

(31)

$$\begin{aligned} \begin{aligned} R_j&= \mathrm {Var}_{x,t} \left( E_j\right) - (S_j +T_j) \\&= \mathbb {E}_{x} \left[ \mathrm {Var}_{t} \left( E_j\right) \right] - \mathrm {Var}_{t} \left( \mathbb {E}_{x} \left[ E_j \right] \right) \\&= \mathbb {E}_{t} \left[ \mathrm {Var}_{x} \left( E_j\right) \right] - \mathrm {Var}_{x} \left( \mathbb {E}_{t} \left[ E_j \right] \right) . \end{aligned} \end{aligned}$$

(32)

The last two expressions for $R_j$ are obtained using the law of total variance. A close examination confirms our space-time decomposition satisfies some minimal requirements: $S_j = 0$ when there is no spatial variation in $E_j$, $T_j = 0$ when there is no temporal variation, and $R_j = 0$ when there is either no spatial or temporal variation.

The components of the space-time decomposition of $\mathrm {Var}_{x,t} \left( E_j\right)$ can be thought of as differences between hypothetical worlds in which spatial and/or temporal variation has been turned on or off. For example, the space term, $S_j$, is the difference between the variance of $E_j$ in a world where temporal variation has been turned off (by setting $E_j(x,t)$ to $\mathbb {E}_{t} \left[ E_j \right]$, leaving only spatial variation), and the variance of $E_j$ in a reference world where both spatial and temporal variation has been turned off (which is necessarily zero). Adding only spatial variation to the reference state of “no variation” gives the main effect of spatial variation. The interaction effect of spatial and temporal variation is the marginal effect of turning on both spatial and temporal variation; it is the extent to which the combination of spatial and temporal variation exceeds the sum of its parts, which is why the interaction term (Eq. 32) involves subtracting both main effects.

Our talk of “hypothetical worlds” and “turning off variation” may give our space-time decomposition a speciously ad hoc aura. However, it is ordinary scientific practice to measure the causal effect of X as the marginal effect of X in relation to some reference state (VanderWeele 2015); think of a clinical trial where the effect of drug X is the difference in health outcomes between the control and treatment groups. In Appendix “Justification of the space-time decomposition”, we justify our space-time decomposition by (1) showing that the result it gives in a toy model accords with intuition, and (2) using the philosophical literature to show that our decomposition results in terms that can be interpreted as the causal effects of spatial and temporal variation.

In Eqs. (29)–(32), we defined the space-time decomposition of $\mathrm {Var}_{x,t} \left( E_j\right)$. The oher variance/covariance terms featured in the small-noise coexistence mechanisms (i.e., $\mathrm {Var}_{x,t} \left( C_j\right)$ and $\mathrm {Cov}_{x,t} \left( E_j, C_j \right)$) can be decomposed in analogous fashion, by turning on/off $E_j$ and $C_j$ in tandem. To obtain the space-time decomposition of the small-noise coexistence mechanisms, we propagate the small-noise decompositions of $\mathrm {Var}_{x,t} \left( E_j\right)$, $\mathrm {Var}_{x,t} \left( C_j\right)$, and $\mathrm {Cov}_{x,t} \left( E_j, C_j \right)$ though the expressions for the small-noise coexistence mechanisms (Eqs. 7–11). For example, since the variance of $E_j$ is the purview of the density-independent effects ($\Delta E_{i}$), and because the space component of $\mathrm {Var}_{x,t} \left( E_j\right)$ is $\mathrm {Var}_{x} \left( \mathbb {E}_{t} \left[ E \right] \right)$, it follows that all terms involving $\mathrm {Var}_{x} \left( \mathbb {E}_{t} \left[ E \right] \right)$ will belong to $\Delta E_{i,S}$, the space component of the density-independent effects.

How should the space-time components of coexistence mechanisms be interpreted? In the abstract, they are the causal effects of spatial or temporal variation (or their interaction) on particular coexistence mechanisms. For example, the space component of the storage effect, $\Delta I_{i,S}$, is the rare-species advantage that results from species specializing on persistent spatial heterogeneity. Because models without temporal variation will generate a $\Delta I_{i,S}$ that is quantitatively identical to the spatial storage effect of Chesson’s (2000) spatial coexistence theory, we may call $\Delta I_{i,S}$ the spatial storage effect, with the notable caveat that $\Delta I_{i,S}$ does not capture all the effects of spatial variation ($\Delta I_{i,R}$ also depends on spatial variation). The space-time components may have more precise ecological interpretations—beyond “the causal effects of spatial (temporal) variation on X coexistence mechanism”—but these will depend on the idiosyncrasies of particular models.

All averages over space and time are shunted into the “Average” components of the space-time decomposition, denoted with the subscript A. Note that relative nonlinearity ($\Delta N_i$) has no average component because the average effect of $C_j$ is captured in the linear density-dependent effects ($\Delta \rho _i$). Also note that the average component of the storage effect ($\Delta I_{i,A}$) equals zero, since the covariance between two constants is always zero.

The space-time decomposition of exact coexistence mechanisms

In this section, we will describe how the space-time decomposition of the exact coexistence mechanisms can be computed using data from simulations. Our exposition is focused on the storage effect because it is the most difficult exact coexistence mechanism to quantify.

Ellner et al. (2016) showed how simulations could be used to calculate the exact temporal storage in a model with only temporal variation. Their procedure can be naturally extended to models with spatiotemporal variation:

• 1. Simulate the model. For each species, record a matrix of $E_j(x,t)$’s and a matrix of $C_j(x,t)$’s with each row corresponding to a location in space, and each column corresponding to a point in time. Call these matrices $E_j$ and $C_j$.

• 2. For each species, shuffle the elements of $E_j$. That is, fill in a matrix with equivalent dimensions by randomly sampling without replacement from the flattened $E_j$. Call this new matrix $E_j^{\#}$. Shuffling (i.e., randomly sampling without replacement, or permuting) destroys the covariance between environment and competition (as well as any higher order mixed moments) that is integral to the storage effect.

• 3. For each species, estimate the interaction effect as $\overline{\mathscr {I}_j} = \mathbb {E}_{t} \left[ \log (\mathbb {E}_{x} \left[ g_j(E_j, C_j) \right] ) \right] - \mathbb {E}_{t} \left[ \log (\mathbb {E}_{x} \left[ g_j(E_j^\#, C_j) \right] ) \right]$. Note here that we are averaging finite rates of increase across patches instead of individuals. This ensures that our estimate of ${\Delta I_{i}}^{(e)}$ does not include any bit omf growth rate that can be attributed to the fitness-density covariance, $\Delta \kappa _i$.

• 4. Calculate the exact storage effect as ${\Delta I_{i}}^{(e)} = \overline{\mathscr {I}_i} - \sum _{r \ne i}^S \frac{GT_r}{GT_i} \overline{\mathscr {I}_r}$.

Ellner et al.'s (2016) critical idea—shuffling an archive of environmental parameters—can also be utilized to calculate the space-time decomposition of the exact storage effect. To illustrate, we will discuss how one may calculate the space component of the precursor to the exact storage effect: $\mathscr {I}_{j,S}$. To measure the causal effect of spatial covariation, we must compare a (reference) hypothetical world with only spatial variation to a reference hypothetical world with only spatial variation and no EC covariation. We obtain the former world by squashing temporal variation, i.e., by setting $E_j(x,t)$ to $\mathbb {E}_{t} \left[ E_j \right]$ and setting $C_j(x,t)$ to $\mathbb {E}_{t} \left[ C_j \right]$. This produces the growth rate $\log (\mathbb {E}_{x} \left[ g_j(\mathbb {E}_{t} \left[ E_j \right] ,\mathbb {E}_{t} \left[ C_j \right] ) \right] )$. We obtain the latter world (with no temporal nor spatial covariation) by squashing temporal variation just as we did before, and then shuffling the vector of $\mathbb {E}_{t} \left[ E_j \right]$. This produces the growth rate $\log (\mathbb {E}_{x} \left[ g_j(\mathbb {E}_{t} \left[ E_j \right] ^\#,\mathbb {E}_{t} \left[ C_j \right] ) \right] )$. The effect of spatial covariation (and higher order mixed moments) on species j’s average growth rate is simply the difference between the growth rates corresponding to the two hypothetical worlds. Put into symbols, we say that $\overline{\mathscr {I}}_{j,S} = \log (\mathbb {E}_{x} \left[ g_j(\mathbb {E}_{t} \left[ E_j \right] ,\mathbb {E}_{t} \left[ C_j \right] ) \right] ) - \log (\mathbb {E}_{x} \left[ g_j(\mathbb {E}_{t} \left[ E_j \right] ^\#,\mathbb {E}_{t} \left[ C_j \right] ) \right] )$.

Instead of writing out steps for quantifying every space-time component of every exact coexistence mechanism, we will provide formulas that indicate how simulated data are to be used. Of notable importance to the storage effect is the previously introduced shuffle operator, denoted by the superscript $\#$, which indicates that the elements of a matrix or vector are to be shuffled, i.e., randomly sampled without replacement.

Note that $\overline{\mathscr {I}}_{j,A}$, the precursor to the “Average” component of the storage effect, is not necessarily zero (as it was in the analogous small noise expression) though it should be small in the limit of small noise. Unlike $\overline{\mathscr {E}}_{j,A}$ and $\overline{\mathscr {C}}_{j,A}$, which could reasonably be called the effects of the average environment and average competition (respectively), $\overline{\mathscr {I}}_{j,A}$ has no good interpretation—it is the effect of setting the environment and competition parameters to their spatiotemporal averages, which is simply a textual reiteration of the mathematical definition.

Computational tricks for measuring invasion growth rates

We have given formulas for computing coexistence mechanisms, but the components of those formulas ($E_j$ and $C_j$) must be measured in a specific context. Specifically, the invasion growth rate and coexistence mechanisms must be measured in the context where (1) the invader’s environment (which includes the resident species) has attained its limiting dynamics, and (2) the invader has attained its quasi-steady spatial distribution.

Here, “the invader’s environment” does not refer to the environmental parameter $E_i$, but rather all variables that influence the invader’s per capita growth rate (e.g., resident densities, resources, temperature). Previous expositions of MCT required that the invader’s environment be an ergodic stationary stochastic process (Chesson 1994, p. 236). This assumption is convenient because ergodicity implies that initial conditions are irrelevant, and stationarity allows the long-term average (inherent in the invasion growth rate) to be replaced with the expectation over the stationary distribution of the state of the invader’s environment; as we will see, there are several well-established tricks for calculating stationary distributions. However, requiring a stationary distribution excludes any models where parameters change over time, including models with seasonality and models that track weather patterns. Instead, we only a require that the invader’s environment has a unique, asymptotic, time-average distribution (Glynn and Sigman, 1998). This requirement technically excludes models with unidirectional environmental change, but we discuss several workarounds in Section “Discussion”.

In many ecological models, the time-average distribution of invader’s environment is a stationary distribution (Nisbet and Gurney 1982). In homogeneous (i.e., time-invariant) Markov chain models with a finite number of states, the stationary distribution can be computed as the dominant eigenvector of the transition probability matrix or the generator matrix (the terminology changes depending on whether the model is in discrete time or continuous time; Allen 2010, p. 67). When the state space is the natural numbers (i.e., there are a countable but infinite number of states), one may approximate the stationary distribution as the dominant eigenvector of a truncated transition probability matrix (or generator matrix) where rows and columns corresponding to states of improbably high abundance have been removed (e.g., Allen 2010, p. 107). Alternatively, one may obtain an approximate stationary distribution using the Wentzel-Kramers-Brillouin (WKB) approximation (Assaf and Meerson 2010; Pande and Shnerb 2020). For models that take the form of stochastic differential equations, the stationary distribution can be obtained by solving a second-order differential equation (Karlin and Taylor 1981, Ch. 15.3). Alternatively, one may obtain an approximate stationary distribution by finding the minimum action of a path integral (Chow and Buice 2015; Kamenev et al. 2008). However, because the volume of state space (of joint abundances/densities) increases exponentially with the number of species, the computation time for all the aforementioned methods scales exponentially with the number of species under consideration.

For models with many species, or models where the notion of stationarity is not appropriate, one may have to take a brute-force approach: simulate a model forward in time, recording the frequency distribution of different states after a sufficiently long burn-in period. To determine the length of the burn-in period, one may simply “eye-ball” a time series plot, perhaps selecting $2\;\times$ the time it takes for the residents to visually attain typical densities. When one must obtain the time-average distribution for many different parameter combinations, the “eye-ball” approach becomes impractical. Instead, one can employ heuristic tests for determining the length of the burn-in period (for examples, see Caswell and Etter 1993; Hiebeler and Millett 2011).

MCT assumes that all populations have infinite population sizes; otherwise, the invader could go extinct before it experiences a representative collection of environmental states, in which case the invasion growth rate would depend on the initial conditions of the invader’s environment. Because the resident species can also go extinct in finite-population models, the concept of the stationary distribution can be replaced with the quasi-stationary distribution (QSD): the distribution of resident densities conditioned on non-extinction. In single-resident birth-death models, there is an iterative numerical procedure for finding the QSD (Nisbet and Gurney 1982, pp. 183–184). Unlike the stationary distribution, the QSD cannot be computed with naive simulation. The problem is that a simulation must run for a long time in order for the frequency distribution to converge, but the longer the simulation, the more likely extinction is. One solution is the Fleming-Voit method (Ferrari and Maric 2007; Blanchet et al. 2016), where a number of simulations are run in parallel so that extinct simulations can be restarted with initial conditions equal to the state of one of the extant simulations. A similar method restarts extinct simulations by drawing randomly from an archive of past states (Groisman and Jonckheere 2012).

To avoid simulations, one may approximate the QSD by analyzing an auxiliary model. This auxiliary model is exactly like the original model, except either (1) each transition from a non-zero state to the zero state (i.e., extinction) has a probability equal to zero (Pielou 1969, p. 27; Allen 2010, p. 127), or (2) one individual is immortal for all time (Weiss and Dishon 1971; Norden 1982). The stationary distribution of the auxiliary model (computed using the methods in the previous paragraphs) is an approximation of the quasi-stationary distribution of the original model. The auxiliary model no. 1 leads to better results for populations with long mean extinction times, whereas the auxiliary model no. 2 leads to better results for populations with short mean extinction times (Nåsell 2001; Kryscio and Lefévre 1989).

A unique challenge in spatiotemporal models (with either infinite or finite populations) is determining the quasi-steady spatial distribution of the invader, not to be confused with the previously discussed quasi-stationary distribution of resident densities. To accurately measure the invasion growth rate, one must inoculate the invader and then wait until it has attained its natural spatial distribution, which we might technically define as a second-order stationary and isotropic process (Cressie 2015). However, the longer one waits for the invader to attain this distribution, the larger the invader population becomes (assuming a positive invasion growth rate and barring stochastic extinction), leading to inaccurate measurements of the invasion growth rate. One hopes that the dynamics of spatial correlations operate on a much faster timescale than the dynamics of total density, such that a quasi-steady spatial distribution of the invader’s density is attained long before the total density changes too much. The requisite time-scale separation can be verified with parametric plots of spatial correlations against total density (as in Le Galliard et al. 2003, Fig. 7). Analytical expressions for the quasi-steady distribution are only available in simple spatially implicit models (see Appendix “Deriving the small-noise fitness-density covariance for the spatiotemporal lottery model” for a worked example) or in simple spatially explicit models with the help of pair approximation (Ferrière and Galliard 2001).

In more complex models, simulation experiments are needed to compute the quasi-steady spatial distribution of the invader. After virtually inoculating the invader species and waiting through a sufficiently long burn-in period, one can begin measuring the invasion growth rate. If the regional invader population density exceeds a user-specified ceiling (i.e., the invader becomes common), then the simulation can be restarted. Indeed, this general strategy can be used to compute other kinds of quasi-steady distributions, such as the invader’s stable-age distribution. In finite population models, the invader may go extinct. To circumvent this problem, one may apply the previously discussed Fleming-Voit method (Ferrari and Maric 2007; Blanchet et al. 2016).

Example: The spatiotemporal lottery model

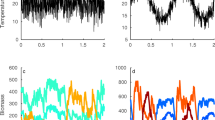
To give readers a sense of how Spatiotemporal MCT may be used in practice, we analyze the lottery model (Chesson and Warner 1981; Chesson 1994) with spatiotemporal fluctuations. The lottery model is one of the simplest models that features fluctuation-dependent coexistence mechanisms, and has thus become a canonical model in theoretical ecology. We derive analytical expressions for the special case of two species with similar demographic parameters (Eqs. 99–114). Additionally, we compute exact coexistence mechanisms in a three-species system with dissimilar parameters (Fig. 1).

Imagine several fish species inhabiting territories on a coral reef. During each time-step, an individual of species j produces $\xi _j(x,t)$ larvae; per capita larval production fluctuates over space and time. The remaining life history is very simple. Adult fish die with the density-independent probability $\delta _j$. Within a single patch, the larvae inherit the empty territories with a per-larva recruitment probability equal to the number of empty sites, divided by the total number of larvae. The remaining larvae perish. Note that “empty territories” and “total larvae” here are patch-specific quantities; so far, we have only described local population dynamics. The uniform per-larva probability of recruitment explains the lottery model’s name (Sale 1977).

If there are S species, the local dynamics of the lottery model can be encoded in a S-dimensional difference equation:

$$\begin{aligned} \lambda _j(x,t) = \overbrace{1-\delta _j}^{\text {survival prob.}} + \; \overbrace{\xi _{j}(x,t)}^{{\text {per capita fecundity}}} \left[ \frac{ \overbrace{ \sum \limits _{j \ne i}^{S} \delta _j n_{j}(x,t)}^{\text {open territories}}}{ \underbrace{\sum \limits _{j \ne i}^{S} \xi _{j}(x,t) n_{j}(x,t)}_{{\text {total larvae}}}}\right], \qquad j = (1, 2, ..., S). \end{aligned}$$

(95)

Selecting $E_j = \log \, (\xi _j)$ and $C = \log \, ( \frac{\sum \limits _{j \ne i}^{S} \xi _{j} n_{j} }{\sum \limits _{j \ne i}^{S} \delta _j n_{j}})$, the local finite rate of increase takes the simple form,

$$\begin{aligned} g_{j}(E_j(x,t), C_j(x,t)) = 1 - \delta _j + \exp {E_j(x,t) - C(x,t)}. \end{aligned}$$

(96)

Both species share the same equilibrium competition parameter, $C^* = \frac{1}{S} \sum _{i=1}^{S} \mathbb {E}_{x,t} \left[ C_{i} \right]$, which is the average competition experienced by the invader, averaged over all species acting as the invader. This equilibrium competition parameter fixes the species-specific equilibrium environmental parameter at $E_j^* = \log (\delta _j) + C^*$. With the equilibrium parameters in hand, we can now compute the Taylor series coefficients for the small-noise coexistence mechanisms: we find that $\alpha _j^{(1)} = \delta _j$, $\beta _j^{(1)} = -\delta _j$, $\alpha _j^{(2)} = \delta _j$, $\beta _j^{(2)} = \delta _j$, and $\zeta _j = -\delta _j$. The generation time quotients (see Section “Small-noise coexistence mechanisms”) are $GT_r/GT_i = \delta _i / \delta _r$.

In the second segment of each time-step, after local growth occurs, a fraction of individuals, $q_j$, are retained at site x while the $1-q_j$ fraction of dispersing individuals are distributed evenly across all K patches. This particular form of dispersal dynamics, which we may call local retention with global dispersal, is easy to simulate and is analytically tractable. The full dynamics of species j can now be written as

$$\begin{aligned} n_j(x,t+1) &= q_j n_j(x,t) g_j(E_j(x,t), C_j(x,t))\\&\quad+ \frac{1 - q_j}{K} \sum \limits _{s=1}^{K} n_j(s,t) g_j(E_j(s,t), C_j(s,t)). \end{aligned}$$

(97)

Finally, we must describe the structure of environmental variation. The environmental parameter, $E_j(x,t)$, is the sum of a patch effect a(x), a time effect b(t), and their interaction, which is scaled by the interaction coefficient $\theta _j$:

$$\begin{aligned} E_j(x,t) = a_j(x) + b_j(t) + \theta _j a_j(x) b_j(t) \end{aligned}$$

(98)

For simplicity, $a_j(x)$ and $b_j(t)$ are independently drawn from normal distributions with standard deviations $\sigma _j^{(x)}$ and $\sigma _j^{(t)}$, respectively. There is no autocorrelation, but there are cross-species correlations: the correlation between $a_j(x)$ and $a_k(x)$ is $\phi _{jk}^{(x)}$, and the correlation between $b_j(t)$ and $b_k(t)$ is $\phi _{jk}^{(t)}$. Under the small-noise assumptions of MCT, the term $\theta _j a_j(x) b_j(t)$ will become negligibly small when squared, and thus the space-time interaction component of the space-time decomposition will be zero. For purely illustrative purposes, we will assume that $\theta _j = \mathcal {O}(\sigma ^{-1})$, as this allows us to obtain a non-zero interaction component while still keeping the simple form of Eq. 98.

We now analyze a particularly simple case of the spatiotemporal lottery model in which two species are similar in many respects. The two species have equal death probabilities $\delta$, equal spatial variances ${\sigma ^{(t)}}^2$, equal temporal variances ${\sigma ^{(t)}}^2$, equal space-time interaction coefficients $\theta$, and equal retention fractions, q. The two species only differ in how they respond to the environment (i.e., $\phi ^{(x)} < 1$, and $\phi ^{(t)} < 1$).

Various tricks can be used to simplify the expressions for the small-noise coexistence mechanisms. In order to calculate the variance and covariance terms inherent in the small-noise coexistence mechanisms, the competition parameter can be expressed in terms of the environmental parameter, by (1) Taylor-series expanding competition with respect to the $E_j$ and $n_j$, (2) substituting the expansions into the covariance terms and truncating at first order in accordance with the small-noise assumptions, (3) recognizing that $\mathrm {Cov}_{} \left( E_j, n_j \right) = 0$ due to the absence of spatial or temporal autocorrelation, and (4) recognizing that $\mathrm {Var}_{} \left( n_r\right) = 0$ in the case of two species, since $n_r$ is fixed at 1. To compute fitness-density covariance, $\Delta \kappa$, we must first calculate the quasi-steady spatial distribution of the invader (see Section “Computational tricks for measuring invasion growth rates”). In Appendix “Deriving the small-noise fitness-density covariance for the spatiotemporal lottery model”, we derive an approximation of this distribution using perturbation theory, recursion, and the geometric series.

Fig. 1

Values of exact coexistence mechanisms in the spatiotemporal lottery model with 3 species. The mechanisms are color coded, with the components of the space-time decomposition taking a lighter hue. Coexistence can be attributed to the storage effect and fitness-density covariance. Parameter values and code can be found in lottery_model_example.R at https://github.com/ejohnson6767/spatiotemporal_coexistence

We first use the small-noise coexistence mechanisms above to look at edge cases where there is no spatial nor temporal variation. When there is no spatial variation (i.e., $\sigma ^{(x)} = 0$), the lottery model analyzed in this section collapses to the temporal lottery model of Chesson (1994). The entire invasion growth rate is $\delta (1 - \delta ) \left( \sigma ^{(t)}\right) ^2 ( 1-\phi ^{(t)})$, which transparently shows that stable coexistence is not possible if species’ responses to the environment are perfectly correlated (i.e., if $\phi ^{(t)} = 1$), or if generations are non-overlapping (i.e., if $\delta = 1$). This latter result speaks to the storage effect’s namesake: coexistence “... relies on such buffering effects of persistent stages...” (Chesson 2003).

When there is no temporal variation and we assume no local retention (i.e., $\sigma ^{(t)} = 0$ and $q = 0$), our lottery model collapses to the spatial lottery model of Chesson (2000). In this case, the invasion growth rate is $\delta \left( \sigma ^{(x)}\right) ^2 \left( 1-\phi ^{(x)} \right)$, which demonstrates that the spatial storage effect can promote coexistence in the face of non-overlapping generations.

Finally, we consider the spatiotemporal lottery model. The invasion growth rate, minus fitness-density covariance and any space-time interaction terms is $\Delta I_{i,T} + \Delta I_{i,S} = \delta \sigma ^{{(t)}^2} \left( 1 - \delta \right) \left( 1-\phi ^{(t)} \right) + \delta \sigma ^{{(x)}^2} \left( 1-\phi ^{(x)}\right)$, the sum of invasion growth rates in the only-temporal-variation case and the only-spatial-variation case. This quantity shows us that while spatial and temporal variation both tend to promote coexistence, they do not do so symmetrically. Specifically, compared to spatial variation, temporal variation is discounted by a factor of $(1-\delta )$. This discrepancy can be explained by the tendency of temporal variation to decrease the geometric mean of $\lambda _j$ (Lewontin and Cohen 1969).

Next, consider the sum of all space-time interaction terms from the space-time decomposition, which is equal to $\delta \theta ^2 (1- \phi ^{(x)} \phi ^{(t)}) \left( \sigma ^{(x)} \sigma ^{(t)}\right) ^2$. Both this quantity and the small-noise fitness-density covariance Eq. (114) reveal that even when generations are overlapping and responses to time-effects are perfectly correlated across species (i.e., $\phi ^{(t)} = 1$), temporal variation can still promote coexistence by effectively amplifying species-specific responses to spatial variation, with strength according to the interaction coefficient $\theta$. Note, however, that this result is a consequence of the assumption that the interaction between spatial and temporal variation, $\theta$, is large (to counteract the fact that $\sigma ^{(x)} \sigma ^{(t)}$ is very small). Also note that when both species respond identically to patch effects and time effects, the space-time interaction terms disappear, confirming the perennial fact that niche differences are required for stable coexistence.

When we consider the general case of multiple residents and asymmetric demographic parameters, the small-noise coexistence mechanisms become more complicated. However, plotting the exact coexistence mechanisms (Fig. 1) corroborates the idea that coexistence in the lottery model is achieved via the storage effect and fitness-density covariance. In empirical applications of MCT, Coefficient plots (such as Fig. 1) should always include error bars representing parameter uncertainty, and potentially model uncertainty, propagated through to the level of coexistence mechanisms.

Here we have examined the space-time decomposition of coexistence mechanisms. In general, there are many ways to partition the invasion growth rate, each potentially leading to ecological insights. One may wish to aggregate terms in various ways, e.g., all space terms, all terms containing partial derivatives of C (i.e., both $\Delta \rho _i$ and $\Delta N_i$). Conversely, the invasion growth rate partition can be made even more fine-grained. Ellner et al. (2019) decomposed $\Delta E_{i}$ into multiple terms, and partitioned the invasion growth rates with respect to trait values (as opposed to E and C). In many models, the competition parameter $C_j$ can be expressed as a function of multiple regulating factors (see Appendix “Multiple regulating factors”), so naturally, $\Delta \rho _i$, $\Delta N_i$, and $\Delta I_i$ can be broken down further into terms which measure the contributions of individual (or subsets of) regulating factors.

Discussion

In this paper, we have shown how the invasion growth rate can be partitioned so as to isolate the effects of spatial variation and temporal variation. With this new capability, one can determine whether species are coexisting because of spatial heterogeneity or temporally changing environmental conditions, or both. Furthermore, one can break down individual coexistence mechanisms (such as the storage effect) into contributions from spatial and temporal variation, e.g., the spatial storage effect and the temporal storage effect can be extracted from a complex model with spatiotemporal variation.

In addition to the partitioning of spatiotemporal variation, the framework presented here contains several improvements on previous iterations of Modern Coexistence Theory (MCT). (1) Resident growth rates are scaled by quotients of generation times, as opposed to the conventional but infamously confusing scaling factors (see Section “Small-noise coexistence mechanisms”; Johnson and Hastings 2022a). (2) Coexistence mechanisms based on small-noise approximations are clearly delineated from exact coexistence mechanisms (Section “Overview”). (3) Both small-noise and exact coexistence mechanisms can be extracted from a diversity of model types, including discrete-time models, continuous-time models (including stochastic differential equations), models with multiple regulating factors, and structured population models (Appendix “Generalization of MCT to different classes of models”). We have presented canonical coexistence mechanisms (e.g., the storage effect), but more exotic coexistence mechanisms can be derived with a generalized partition (following Ellner et al. 2019); replace the arguments of the growth function $g_j$ with any number of variables, and apply the logic of Section “Spatiotemporal coexistence mechanisms”.

Spatiotemporal MCT allows for the analysis of more realistic models, which naturally lead to better inferences regarding mechanisms of coexistence in real communities. Although generating realistic models requires immense amounts of system-specific knowledge, data collection, and statistical expertise, all of this hard work can be thought of as a safeguard against bad inferences. When simplistic statistical approaches are used to understand community structure, the data are often overdetermined by theory. For example, left skew in a species abundance distribution could indicate neutral population dynamics (Hubbell 2001); or temporal autocorrelation in sampling (McGill 2003); or an excess of transient species (Magurran and Henderson 2003); or a sequential stick-breaking model (Nee et al. 1991); or a log-normal distribution paired with a zero-sum constraint (Pueyo 2006). Randomization-based null models for detecting interspecific competition can implicitly exclude or include the effects of competition (Connor and Simberloff 1979, Diamond and Gilpin 1982). A saturating curve on a plot of regional vs. local species richness could indicate environmental filtering (Cornell and Lawton 1992) or dispersal limitation (Fox et al. 2000).

While data is always overdetermined by theory to some extent (Duhem 1954), the problem can be abated by MCT’s model-based approach and a few best practices. First, one ought to use large and flexible models. As Leonard Savage used to say, all models should be “as big as a house” (qtd in Draper 1995). Big models tend to be less biased and implicitly capture structural uncertainty in the form of parameter uncertainty (Draper 1995). As a statistical example of this phenomenon, consider a Student t-distribution, which interpolates between a Gaussian distribution and a Cauchy distribution depending on the degrees of freedom parameter. An ecological example is MacArthur’s resource-consumer model (MacArthur 1970; Chesson 1990), which interpolates between an explicit resource-consumer model and the Lotka Volterra model depending on the speed of resource dynamics. Simple template models (like the annual plant model; Law and Watkinson 1987; Chesson 1994, Section 5; Godoy and Levine 2014) can be made complex through the process of continuous, iterative model expansion (Box 1980; Draper 1995; Gelman et al. 2020).

When dealing with complex models, there is a legitimate fear of overfitting (Hastie et al. 2009, Ch. 7). However, overfitting can be addressed by regularization, the general term for penalizing model complexity in the parameter-tuning process (Gelman and Vehtari 2021), as opposed to penalizing complexity in the model selection process (using AIC, cross-validation, etc.). Regularization can be enforced via model-fitting algorithms (such as the LASSO, ridge-regression, or least-angle regression; Hastie et al. 2009, Ch. 3), prior distributions in the Bayesian context (see horseshoe priors for sparsity-inducing regularization; Carvalho et al. 2009), and hierarchical model structures (Gelman and Hill 2006). Hierarchical model structures are the obvious way of reducing estimation variance for large matrixes of competition coefficients (S species $\rightarrow$ $S^2$ competition coefficients!); alternatively, the number of parameters can be reduced by grouping species based on phylogeny, ecological function, or traits (Martyn et al. 2021). It is worth noting that overfitting can be largely avoided simply by using a Bayesian model-fitting framework: MCMC methods explore the typical set (the volume where the posterior density is close to its expected value; Gelman et al. 2020), not the posterior mode, and are therefore unlikely to sample parameter values with spuriously high likelihoods.

Another modelling best practice is to propagate uncertainty in model parameters through to the level of coexistence mechanisms, which can be generically accomplished by sampling from bootstrap or posterior distributions of model parameters. To our knowledge, only one empirical application of MCT (Ellner et al. 2016, Section SI.8) has performed this crucial step. Without uncertainty propagation, it is difficult to say whether estimates of coexistence mechanisms reflect reality or sampling error.

MCT assumes that the statistical properties of the environment (e.g., the mean level and variance) do not change in a directional manner (i.e., a unique time-averaged distribution of the invader’s environment exists; Section “Computational tricks for measuring invasion growth rates”), an assumption that is certainly false in many cases. However, MCT can still be used when unidirectional environmental change is considerably slower than demographic change (Fig. 2). For example, temperate lake phytoplankton can invade on the time scale of years, but are appreciably affected by climate change on the time scale of decades (Izmest’eva et al. 2011). Therefore, it may be reasonable to not incorporate climate change projections into one’s model of phytoplankton dynamics, with the understanding that the validity of one’s inferences regarding coexistence only extends so far into the future.

Fig. 2

How the utility of MCT changes with the type and speed of environmental change. Red indicates that MCT is a not a suitable tool; yellow indicates that some coexistence mechanisms are automatically absent, or that MCT can be used with caveats; green indicates that MCT can be used without worry. a When environmental change is directional but slow, one can estimate invasion growth rates by treating the current statistical characteristics of the environment (e.g., the mean, variance) as constant. b When environmental change is directional and appreciable, quasi invasion growth rates can be calculated, but they are conditional on initial conditions and the time period over which growth rates are averaged. c Invasion growth rates are dominated by the trend component of the environment; coexistence mechanisms do not matter. d When environmental change is slow relative to the speed of population dynamics, the environment is effectively constant on ecological time-scales; the temporal storage effect and environment-induced temporal relative nonlinearity will be zero, but MCT can still be used to quantify spatial coexistence mechanisms, temporal relative nonlinearity via endogenous population cycles (sensu Armstrong and McGehee 1976, 1980), and to partition the linear density-dependent effects (Appendix “Multiple regulating factors”). e There are no problems applying MCT in this regime. f When the environment fluctuates too quickly, there is not enough time for population buildup to occur during favorable periods, thus enervating the high intraspecific competition felt by common species; in the limit of a fast environment, the temporal storage effect is zero (Li and Chesson 2016; Johnson and Hastings 2022b).

When the time scales of demographic change and directional environmental change are commensurate, it is still possible to use MCT. Invasion growth rates can be calculated under projected environmental change, but their values will depend on the initial conditions and the length of the period over which growth rates are averaged. While this subjectivity is undesirable, there are reasonable methods for dealing with it. One could select the initial conditions to be time-dependent equilibrium parameters, the most recent observation, or a range of recent observations (in which case marginalizing invasion growth rates would be necessary). The dependence of invasion growth rates on the time frame of measurement cannot be circumvented, but it can be acknowledged by plotting a temporal moving-average of growth rates (i.e., a local invasion growth rate) and subsequent coexistence mechanisms across time.

When environmental change is much slower than demographic change, the infinite population assumption of MCT (Section “Computational tricks for measuring invasion growth rates”) breaks down: in theory, long periods of unfavorable conditions can be offset by sufficiently favorable conditions; in reality, long periods of unfavorable conditions lead to extinction. In the limit of strong environmental autocorrelation, the environment is effectively fixed in its initial conditions (Kamenev et al. 2008) and competitive exclusion occurs in the absence of other coexistence-promoting mechanisms. Regardless of the relative speed of environmental change, one ought to be wary of calculating invasion growth rates over long time scales. Even though the invasion growth rate of a tree species may converge after 500,000 years—perhaps after the effects of anthropogenic climate change have been attenuated by several Milankovitch cycles—our models of contemporary population dynamics will certainly be poor representations of the far future.

A few basic insights emerge from Spatiotemporal Modern Coexistence Theory (MCT). The inclusion of spatiotemporal fluctuations (as opposed to only spatial or only temporal fluctuations) exactly doubles the maximum number of species that the fluctuation-dependent coexistence mechanisms can support (Table 2). The reason is laid bare in the space-time decomposition of the small-noise coexistence mechanisms (Eqs. 33–52): species may specialize on either spatial variation or temporal variation. It is worth noting that this result depends on the veracity of the small-noise assumptions (Appendix “Small-noise assumptions”); even more species could potentially coexist by specializing on higher-order moments (Zicarelli 1975; Levins 1979), such as the spatial skew of resource concentrations.

Table 2 The maximum number of species that can coexist via various coexistence mechanisms, in a system with L discrete resources, M discrete environmental states, and K discrete patches. In the column headings, spatial variation and temporal variation refer to variation in the environment, regulating factors, and relative density. The entries in this table were derived as follows: only one species will have the largest $\Delta E$, and in the absence of other influences on the per capita growth rates, this species’ relative frequency will approach 1 over time. The entries for $\Delta \rho$ simply express the competitive exclusion principle. The entries for $\Delta N$ follow from recognizing that the covariances between regulating factors can be treated as honorary regulating factors, and then by applying the competitive exclusion principle. The entries for $\Delta I$ are derived in the same way, and are an obvious extrapolation of the work by Miller and Klausmeier (2017). The entries for $\Delta \kappa$ come from Appendix “The maximum number of species that can coexist via fitness-density covariance”. It is well known that many species can coexist if patches have different resource supply points (Levin 1974; Tilman 1982; Chase and Leibold 2003); this manifests as the $M \times L$ term in the entries for $\Delta \kappa$, where M is the number of distinct resource supply points. We have not formally analyzed the case where fitness-density covariance is caused by aggregating behavior (such as swarming or schooling) or preferential dispersal (Barabás et al. 2018, Appendix S5), but we imagine that behaviors or patch preferences can be treated as density-independent variables; and therefore, that the table entries for $\Delta \kappa$ are still accurate

Table 2 reveals that with even a modest number of regulating factors and environmental states, there are more than enough ways for species to coexist. This highlights the importance of actually measuring coexistence mechanisms in real communities. Table 2 also shows the enormous potential of the fluctuation-dependent coexistence mechanisms, relative to classical explanations for coexistence (i.e., $\Delta \rho _i$). While this may be interesting, it is not likely to drive diversity patterns in the real world. For one, it has been argued that regulating factors are plentiful if you look hard enough (Levin 1970; Haigh and Smith 1972; Abrams 1988). Second, biodiversity is affected by many forces, including structural stability (Gyllenberg and Meszéna 2005), evolutionary/developmental/physiological constraints on extreme forms of specialization, and extinction–speciation balance.

Spatiotemporal MCT also strengthens an a priori refutation of the competitive exclusion principle, the idea that no more than L species can coexist on L regulating factors). The competitive exclusion principle was originally based on equilibrium theory (Volterra 1926, Lotka 1932, Gause 1934), but the principle still applies in fluctuating environments when there are no fluctuation-dependent coexistence mechanisms (Hening and Nguyen 2020; Barabás et al. 2018, p. 295). Of course, for this to occur, there must be linear responses to regulating factors (this precludes relative nonlinearity) and no interaction effect between environment and competition (this precludes the storage effect). Spatiotemporal MCT shows that species’ responses to regulating factors cannot simultaneously be linear with respect to fluctuations on the natural scale (i.e., $\frac{\partial g_j(E_j^*, C_j^*)}{\partial ^2 C_j} = \beta _j^{(2)} = 0$), which is necessary for spatial averaging, and linear with respect to fluctuations on the log-scale (i.e., $\frac{\partial ^2\log (g_j(E_j^*, C_j^*))}{\partial C^2_j} = \beta _j^{(2)} - \beta _j^{(1)^2} = 0$), which is necessary for temporal averaging. This shows that the competitive exclusion principle is unlikely to have real-world relevance.

The competitive exclusion principle has been challenged from many angles: it is trivial (Cole 1960; Ayala 1969) and tautological (Gilbert et al. 1952), relies on the false assumption of a stable equilibrium (Armstrong and McGehee 1980), has stymied the development of a broader research program (Simha et al. 2022), and is irrelevant on ecologically relevant time scales, since similar species can co-occur for a long time (Hurtt and Pacala 1995). Nevertheless, the competitive exclusion principle and its interrogative form—the paradox of the plankton (Hutchinson 1961)—are frequently used to motivate coexistence research (Simha et al. 2022, supplement 1), probably because authors need to cite something other than their personal interest in biodiversity. The competitive exclusion principle does deserve to be recognized, not for making believable predictions, but for its role in the dialectical narrative of coexistence research.

The Hegelian dialectic is a model of history in which a thesis is met with an antithesis, and the conflict itself produces synthesis. In our current context, the thesis is the presumption of competitive exclusion, an idea that started with Darwin and was formalized with the competitive exclusion principle. Charles Darwin, not knowing the genetic basis for inheritance, believed that evolution necessitated fierce competition; otherwise, favorable mutations would be blended with the wild type until the population was phenotypically uniform (Lewens 2010). Indeed, Darwin (1859, p. 322) writes “We need not marvel at extinction; if we must marvel, let it be at our own presumption in imagining for a moment that we understand the many complex contingencies on which the existence of each species depends.”

It is plausible that Darwin’s emphasis on competition and exclusion was influenced not only by the faulty of theory of blending inheritance, but also by the upper-class milieu of 1800s England—Darwin was a member of the Whig party during the era of the New Poor Law and was predominantly influenced by the work of the eugenicist Thomas Malthus—consequently, he endorsed the depredation (via disease, famine, economic deprivation) of poor and colonized people in the name of creative destruction, all while detesting slavery and violent genocide (Moore and Desmond 1991). The presumption of competitive exclusion evolved into the competitive exclusion principle, though the exact reason for the principle’s prominence is unclear. Explanations include the attention of a few superstar authors (namely Robert MacArthur and G.E. Hutchinson, see Schoener 1982), the naturalization of capitalist ideology (Simha et al. 2022), and the fact that mutualism—the conceptual reciprocal of competition—does not play nice with the tools of theoretical ecology (May 1981, p. 95).

The antithesis of competitive exclusion emerged from the discovery of fluctuation-dependent mechanisms (Armstrong and McGehee 1976; Chesson and Warner 1981), the realization that spatial and temporal variances could be treated as regulating factors (Levins 1979), and formulae suggesting that an arbitrary number of species could coexist on a single resource (e.g., Chesson 1994, Eq. 81). The focal question flipped from “Why are there so many species?” to “Why are there so few species?” These two questions, laid side-by-side, reveal the absurdity of trying to make strong quantitative predictions without an underlying model. Depending on one’s theoretical commitments, biodiversity can be bounded in whatever way one chooses; recall that the bounds in Table 2 depend on the small-noise assumptions (Appendix “Small-noise assumptions”) and the assumption that both resources and environmental states are fundamentally discrete. The conflict between the thesis and antithesis suggests the synthesis: the question “Why is the number of species that which we observe?” By serving as a methodology for measuring coexistence, Spatiotemporal MCT is poised to help answer this question.

Although we have extended MCT to more complex models, there remain a number of problems with MCT (see Section “Overview”). But we should not be surprised nor disheartened that such problems exist: MCT was invented to explain the role of environmental variation in coexistence (Barabás et al. 2018, p. 288, Chesson 2020, p. 6), not to be a measurement tool. There has been a recent surge of interest in the interpretation and application of MCT (Ellner et al. 2016, 2019; Grainger et al. 2019; Song et al. 2020; Pande et al. 2020; Ellner et al. 2020; Barabás et al. 2018; Chesson 2020; Barabás and D’Andrea 2020; Johnson and Hastings 2022a, b), but more work needs to be done.

Appendices

Appendix 1: Deriving small-noise coexistence mechanisms

The derivation of spatiotemporal coexistence mechanisms can be broken into four parts. In part 1, the local finite rate of increase is expressed in a common format: a polynomial of $E_j$ and $C_j$. This requires re-writing a model of population dynamics in terms of $E_j$ and $C_j$ (Appendix “Justification of the space-time decomposition”), assuming that environmental fluctuations are small (Appendix “Small-noise assumptions”), and applying a Taylor series expansion (Appendix “Decomposing the finite rate of increase: The quadratic approximation”). In part 2, the appropriate spatial (Appendix “Spatial averaging and fitness-density covariance”) and temporal (Appendix “Temporal averaging”) averaging is applied in order to express the invasion growth rate in terms of local finite rates of increase. In part 3, The approximations derived in parts 1 and 2 are combined to create a lengthy expression for each species’ average growth rate (Appendix “Putting it all together: A decomposition of the average growth rate”). In part 4, the small-noise coexistence mechanisms are finally produced (formulas presented in the main text) by comparing the invader to the residents.

Why does our exposition feature discrete-time populations dynamics? For one, the connection with data-based modelling of real communities is more transparent, since data is collected at discrete points in time, and as a consequence, ecologists primarily fit discrete-time models. Secondly, the expressions for the small-noise coexistence mechanisms in the case of discrete-time are identical to those in case of continuous-time when environmental stochasticity is proportional to white noise (Appendix “Stochastic differential equations (SDEs)”).

A brief technical note: throughout the paper, we use the notation $E_j$ as shorthand for $E_j(x,t)$; it is not the case that $E_j$ is a random variable and that $E_j(x,t)$ is a realization of said random variable, as the notation seems to imply. As Chesson (2000) points out, the notation can be made more precise by adding the seed number/ sample path as an additional argument, such that $E_j(x,t,\omega )$ is a realization of the random variable $E_j(x,t)$. Throughout this paper, when we apply the expectation operator (or covariance or variance operators), we sum over space and/or time while fixing the sample path $\omega$.

Justification of the space-time decomposition

The local finite rate of increase, $\lambda _j$, is given by the function $g_j(E_j, C_j)$, where $E_j$ represents the effects of density-independent factors and $C_j$ represents the effects of density-dependent factors (also known as regulating factors or limiting factors).

The parameter $E_j$ has many names: the environmentally dependent parameter, the response to the environment, the environmental parameter, or the environment. It is typically a demographic parameter that depends on the abiotic environment, such as per capita fecundity or the probability of seed germination, hence the terminology response to the environment. But $E_j$ may also be a literal environmental variable, such as annual precipitation, degree days, or soil type. It is important to keep in mind that $E_j$ need not represent the effects of the abiotic environment, since not all density-independent factors are part of the abiotic environment (e.g., mortality from a generalist predator), and not all density-dependent factors are biotic (e.g., refugia, soil nutrients).

The parameter $C_j$ is often called the competition parameter, or simply competition. Concrete examples of the competition parameter are the number of juvenile fish competing per open territory in the lottery model, or a linear combination of population densities, as in the competitive Lotka-Volterra model. The focus on competition reflects MCT’s intellectual origin (and more generally, ecology’s bias towards competition; Mittelbach 2019, p. 164) but the density-dependent $C_j$ can just as easily represent predation pressure (Kuang and Chesson 2010; Chesson and Kuang 2010; Stump and Chesson 2015, 2017) or mutualistic benefits (Stump et al. 2018).

We note that in some papers (e.g., Chesson 1994, 2018; Ellner et al. 2016), $C_{j}^{\{-i \}}$ or $C_{j\backslash i}$ is used to denote the competition parameter of species j when species i is absent. We use $C_j$ to denote the same, since we are always considering a community in which one species is the invader.

Decomposing the finite rate of increase: The quadratic approximation

We will decompose $g_j(E_j,C_j)$ via a second-order Taylor series expansion. First though, we must select equilibrium values of the environment and competition to expand about. These values, denoted $E_j^*$ and $C_j^*$, must be selected so that $g_j(E_j^*,C_j^*) = 1$, a constraint that functions to eliminate the zeroth-order Taylor series coefficient (see Eq. (119)).

In general, there is no unique choice of $E_j^*$ and $C_j^*$, though as Chesson (1994) notes, fixing one parameter will determine the other. That being said, not all choices are equally appropriate. In particular, for every term in the Taylor series expansion to be the same order of magnitude—and thus of commensurate importance—we must simultaneously select $E_j^*$ to be close to $\mathbb {E}_{x,t} \left[ E_j \right]$, and $C_j^*$ to be close to $\mathbb {E}_{x,t} \left[ C_j \right]$ (the reasoning will be explained in the following section, Appendix “Small-noise assumptions”).

There is a canonical method for selecting $E_j^*$ and $C_j^*$: virtually eliminate environmental noise, select $E_j^*$ as the environmental parameter in the resulting deterministic skeleton, and then select $C_j^*$ based on the constraint $g_j(E_j^*,C_j^*) = 1$. In models with multiple regulating factors (see Appendix “Multiple regulating factors”), there are an infinite number of ways to select equilibrium parameters—there are many unknowns and just one constraint (i.e. $g_j(E_j^*,C_j^*) = 1$)—but there are several reasonable strategies (see Johnson and Hastings 2022a, Appendix 1).

With the appropriate selection of the equilibrium parameters, we expand the local finite rate of increase with a second-order Taylor Series about $E_{j}^{*}$ and $C_{j}^{*}$:

$$\begin{aligned} \begin{aligned} g_{j}(E_j,C_j) \approx \; 1&+ \alpha _j^{(1)} (E_j - E_{j}^{*}) + \beta _j^{(1)} (C_j - C_{j}^{*}) \\&+ \frac{1}{2} \alpha _j^{(2)} (E_j - E_{j}^{*})^{2} + \frac{1}{2} \beta _j^{(2)} (C_j - C_{j}^{*})^{2} \\&+ \zeta _j (E_j - E_{j}^{*}) (C_j - C_{j}^{*}). \end{aligned} \end{aligned}$$

(119)

The coefficients of the Taylor series are

$$\begin{aligned} \begin{aligned} &\alpha _j^{(1)} = \frac{\partial g_j{(E_j^*, C_j^*)}}{\partial E_j}, \quad \beta _j^{(1)} = \frac{\partial g_j{(E_j^*, C_j^*)}}{\partial C_j}, \\&\alpha _j^{(2)} = \frac{\partial ^2 g_j{(E_j^*, C_j^*)}}{\partial E_j^2}, \quad \beta _j^{(2)} = \frac{\partial ^2 g_j {(E_j^*, C_j^*)}} {\partial C_j,^2} \\&\zeta _j = \frac{\partial ^2 g_j {(E_j^*, C_j^*)}}{{\partial E_j}{\partial C_j}}. \end{aligned} \end{aligned}$$

(120)

Small-noise assumptions

In order for the second-order Taylor series expansion (the r.h.s. of Eq. 119) to be a good approximation of $g_j(E_j, C_j)$, we must make some assumptions about the magnitude of environmental fluctuations. First, we assume that the environmental parameter $E_j$ fluctuates about $E_j^*$ in a small finite range, and that the size of this range in controlled by a small parameter $\sigma$. Here, we use the conventional “big-oh” notation to denote an upper bound on magnitude of fluctuations:

$$\begin{aligned} E_j - E_j^* = \mathcal {O}(\sigma ). \end{aligned}$$

(121)

This means that ${|E_j - E_j^*|} < k \sigma$, with some constant k as $\sigma \rightarrow 0$. Our next assumption states that environmental fluctuations are even smaller when averaged across space and time:

$$\begin{aligned} \mathbb {E}_{x,t} \left[ E_j \right] - E_j^* = \mathcal {O}(\sigma ^2). \end{aligned}$$

(122)

The justification of the above assumption is either (1) that positive and negative fluctuations cancel out, or (2) that large fluctuations (which set the magnitude of $E_j - E_j^*$) are overpowered by many smaller fluctuations. Functionally, the assumption ensures that the effects of spatiotemporal averages are on the same order of magnitude as the effects of spatiotemporal variance; note that Eqs. 121 and 122 imply that $\mathrm {Var}_{x,t} \left( E\right) = \mathcal {O}(\sigma ^2)$.

To help make sense of the above assumptions, consider an environmental parameter $E_j(x,t) = a(x) + b(t)$. Both the patch effect a(x) and time effect b(t) independently take the value $+\sigma$ or $-\sigma$ with probability $= 0.5$. By construction, the first assumption, Eq. (121), is met. If we then select $E_j^* = 0$, the relevant bounds are ${|E_j - E_j^*|} \le 2\sigma$, ${|\mathbb {E}_{t} \left[ E_j \right] - E_j^*|} \le \sigma$, and ${|\mathbb {E}_{t} \left[ E_j \right] - E_j^*|} \le \sigma$. Here we see that spatial and temporal averages of environmental fluctuations are on the same order of magnitude as the raw fluctuations, $E_j - E_j^*$. Furthermore, we see that $\mathbb {E}_{x,t} \left[ E_j \right] - E_j^* = 0$, which neatly demonstrates that the spatiotemporal average of fluctuations is exceedingly small (Eq. 122).

In order for environment and competition to have commensurate effects on per capita growth rates, we must assume analogous bounds for the competition parameter ($C_j - C_j^* = \mathcal {O}(\sigma )$ and $\mathbb {E}_{x,t} \left[ C_j \right] - C_j^* = \mathcal {O}(\sigma ^2)$) and for relative density ($\nu _j - 1 = \mathcal {O}(\sigma )$ and $\mathbb {E}_{x,t} \left[ \nu _j \right] - 1 = \mathcal {O}(\sigma ^2)$). In some situations, these bounds are not pure assumptions, but rather the result of some conditions. Heavily paraphrased, the conditions are (1) that species have a shared competition parameter (Chesson 1994, p. 268) or have very similar competition parameters (Chesson 1994, p. 270, second equation), (2) that competition is a function of population densities and environmental responses (Chesson 1994, p. 269); (3) that competition does not amplify itself over time (Chesson 1994, p. 269); and (4) that “... any increase in local density due to dispersal cannot increase competition any more than $\mathcal {O}(\sigma)$ above the maximum competition applicable if there were no dispersal.” (Chesson 2000, p. 234). Additionally, if there are more residents than regulating factors, then the scaling factors can be used to cancel the $\Delta \rho _i$ coexistence mechanisms, and concerns about bounding $C_j$ are moot. For all the details, see Appendix 2 of Chesson (1994) and Appendix 3 of Chesson (2000).

The small-noise assumptions serve two primary purposes. First, they allow us to truncate the Taylor series Eq. (119) at second order, thus limiting the number of coexistence mechanisms that we might simultaneously consider. Second, the small-noise assumptions allow us to use the small-noise approximation for dynamical systems (Gardiner 1985), resulting in simple stochastic models that permit analytical expressions for important quantities, e.g., the covariance between environment and competition (see Schreiber 2021 for an example).

When the small-noise assumptions (and the auxiliary conditions above) are not met, one can proceed with two risks. First, the small-noise coexistence mechanisms may not sum approximately to the invasion growth rate; they will “miss” important processes that promote or hinder coexistence. Second, the exact coexistence mechanisms may capture unknown processes that involve large environmental fluctuations, thus making the exact coexistence mechanism less interpretable.

The small-noise assumptions above require large fluctuations to be impossible, not just improbable. Restricting fluctuations to a finite range ensures that growth rates will not be dominated by low-probability, high-impact events. The gain in internal validity comes at the cost of external validity: it is often reasonable to model the environmental response by a random variable with support on the positive real numbers. For example, recruitment in some marine animals appears to follow lognormal distributions (Hennemuth et al. 1980; Ripley and Caswell 2006). However, the exact coexistence mechanisms circumvent the finite range assumption entirely, as long as we exclude from consideration the unlikely scenario where the distributions of $E_j$ and $C_j$ are so fat-tailed that spatial, temporal, or spatiotemporal averages of $E_j$ and $C_j$ do not exist. Given the plethora of assumptions implicit in any ecological model, a violation of the finite range assumption is just one of the many ways in which the results of an MCT analysis are provisional.

Spatial averaging and fitness-density covariance

Next, we will derive a decomposition of the metapopulation finite rate of increase, $\widetilde{\lambda }_j(t)$. Consider a community with K distinct patches. The metapopulation finite rate of increase can be calculated as a simple average of each individual’s finite rate of increase, or equivalently, a weighted average of each patch’s finite rate of increase, with weights equal to the relative density of the population in that patch. To see the logic of the latter scheme, first note that

$$\begin{aligned} \widetilde{\lambda }_j(t) = \frac{\sum \limits _{x=1}^K n_j(x,t+1)}{\sum \limits _{x=1}^K n_j(x,t)} = \frac{\sum \limits _{x=1}^K n_j(x,t+1)}{ K\; \mathbb {E}_{x} \left[ n_j(t) \right] }. \end{aligned}$$

(123)

Using the local dynamics Eq. (1) to substitute for $n_j(x,t+1)$ , we find that

$$\begin{aligned} \widetilde{\lambda }_j(t) =& \frac{1}{K \; \mathbb {E}_{x} \left[ n_j(t) \right] } \; \sum \limits _{x=1}^K \left( n_j(x,t) \; g_j(E_j(x,t), C_j(x,t)) \right)\\ & + \frac{1}{K \; \mathbb {E}_{x} \left[ n_j(t) \right] } \; \sum \limits _{x=1}^K \left( c_j(x,t) - e_j(x,t) \right) . \end{aligned}$$

(124)

To simplify the above expression, we would like second additive term (the spatial sum of net dispersal) to vanish. This can be accomplished by assuming either (1) that the system is closed, i.e., no individuals can enter or leave the system of patches, or (2) that the community receives roughly as many immigrants as it loses emigrants. Scenario 1 is likely to be approximately true for communities that span entire ecosystems, or for communities with very specific habitat requirements (e.g., Californian plants endemic to serpentine soils; Harrison et al. 2006). In either case, there is no immigration into the metacommunity, and emmigration out of the metacommunity results in mortality that can be treated as part of the local dynamics of marginal patches. Scenario 2 is likely to be approximately true when the habitat surrounding the focal area is similar enough to the habitat within the focal area, such that immigration and emigration are balanced over the margin of the focal area. The focal area (which itself is not closed) is representative of a larger metacommunity which is effectively closed.

Assuming that dispersal is negligible at the spatial scale of the metapopulation, dropping the notation for explicit time-dependence, and rearranging terms, Eq. (124) simplifies significantly,

$$\begin{aligned} \widetilde{\lambda }_j = \mathbb {E}_{x} \left[ \frac{n_j}{\mathbb {E}_{x} \left[ n_j \right] } g_j(E_j, C_j) \right] , \end{aligned}$$

(125)

thus revealing that the metapopulation finite rate of increase is a density-weighted average of local finite rates of increase. $\widetilde{\lambda }_j$ can be decomposed further with the law of total covariance:

$$\begin{aligned} \begin{aligned} \widetilde{\lambda }_j&= \mathbb {E}_{x} \left[ \frac{n_j}{\mathbb {E}_{x} \left[ n_j \right] } \right] \mathbb {E}_{x} \left[ g_j(E_j, C_j) \right] + \mathrm {Cov}_{x} \left( \frac{n_j}{\mathbb {E}_{x} \left[ n_j \right] }, g_j(E_j, C_j) \right) \\&= \mathbb {E}_{x} \left[ g_j(E_j, C_j) \right] + \mathrm {Cov}_{x} \left( \nu _j, g_j(E_j, C_j) \right) \end{aligned} \end{aligned}$$

(126)

where $\nu _j$ is the relative density of species j, defined precisely as $\nu _j(x,t) = \frac{n_j(x,t)}{\mathbb {E}_{x} \left[ n_j(t) \right] }$.

The first term in Eq. 126 is the spatial average of local per capita growth rates. The second term is the covariance between relative density and growth rates, which captures the ability of a species j to end up in locations where it has high fitness (though the mechanism of this ability is completely unspecified). This term is the precursor to fitness-density covariance.

Temporal averaging

The quantity which is predictive of persistence is not $\mathbb {E}_{t} \left[ \widetilde{\lambda }_k \right]$, but rather $\mathbb {E}_{t} \left[ \log \widetilde{\lambda }_j \right]$. The logarithmic transformation converts a product of $\widetilde{\lambda }_j$ into a sum of $\log (\widetilde{\lambda }_j)$, which facilitates the application of an arithmetic average.

Conditions on the magnitude of fluctuations in $E_j$, $C_j$, and $\nu _j$ (Appendix “Small-noise assumptions”) can be used to show that $\widetilde{\lambda }_j = 1 + \mathcal {O}(\sigma )$ and $\mathbb {E}_{t} \left[ \widetilde{\lambda }_j \right] = 1 + \mathcal {O}(\sigma ^2)$. The logarithm can now be decomposed with a Taylor series expansion

$$\begin{aligned} \begin{aligned} \log (\widetilde{\lambda }_j) \approx \widetilde{\lambda }_j - 1 - \frac{1}{2} \left( \widetilde{\lambda }_j - 1 \right) ^2. \end{aligned} \end{aligned}$$

(127)

Utilizing the fact that $\mathbb {E}_{t} \left[ \left( \widetilde{\lambda }_j - 1 \right) ^2 \right] = \mathrm {Var}_{t} \left( \widetilde{\lambda }_j\right) + \mathcal {O}(\sigma ^4)$, we take the average over time to obtain the average growth rate:

$$\begin{aligned} \mathbb {E}_{t} \left[ \log (\widetilde{\lambda }_j) \right] \approx \mathbb {E}_{t} \left[ \widetilde{\lambda }_j \right] - 1 - \frac{1}{2} \mathrm {Var}_{t} \left( \widetilde{\lambda }_j\right) . \end{aligned}$$

(128)

Plugging the decomposition of $\widetilde{\lambda }_j$ Eq. (126) into Eq. (128), we find that the invasion growth rate can be approximated entirely by moments of $\lambda _j$ and $\nu _j$.

$$\begin{aligned} \begin{aligned} \mathbb {E}_{t} \left[ \log (\widetilde{\lambda }_j) \right] \approx \mathbb {E}_{x,t} \left[ \lambda _j \right] + \mathbb {E}_{t} \left[ \mathrm {Cov}_{x} \left( \nu _j(t), \lambda _j \right) \right] - 1 - \frac{1}{2} \mathrm {Var}_{t} \left( \mathbb {E}_{t} \left[ \lambda _j \right] \right) . \end{aligned} \end{aligned}$$

(129)

Putting it all together: A decomposition of the average growth rate

The Taylor series decomposition of $g_j(E_k,C_j)$ Eq. (119) can be plugged into Eq. (129), producing a fine-grained partition of species j’s average growth rate

$$\begin{aligned} \begin{aligned} \mathbb {E}_{t} \left[ \log (\widetilde{\lambda }_j) \right]&\approx \alpha _j^{(1)} \mathbb {E}_{x,t} \left[ (E_j - E_{j}^{*}) \right] + \beta _j^{(1)} \mathbb {E}_{x,t} \left[ (C_j - C_{j}^{*}) \right] \\&\quad+ \frac{1}{2} \alpha _j^{(2)} \mathrm {Var}_{x,t} \left( E_j\right) + \frac{1}{2} \beta _j^{(2)} \mathrm {Var}_{x,t} \left( C_j\right) + \zeta _j \mathrm {Cov}_{x,t} \left( E_j, C_j \right) \\&\quad+ \mathbb {E}_{t} \left[ \mathrm {Cov}_{x} \left( \nu _j, \alpha _j^{(1)} (E_j - E_{j}^{*}) + \beta _j^{(1)} (C_j - C_{j}^{*}) \right) \right] \\&\quad- \frac{1}{2} \alpha _j^{(1)^{2}} \mathrm {Var}_{t} \left( \mathbb {E}_{x} \left[ E_j \right] \right) - \frac{1}{2} \beta _j^{(1)^{2}} \mathrm {Var}_{t} \left( \mathbb {E}_{x} \left[ E_j \right] \right) - \alpha _j^{(1)}\beta _j^{(1)} \mathrm {Cov}_{t} \left( \mathbb {E}_{x} \left[ E_j \right] , \mathbb {E}_{x} \left[ C_j \right] \right) . \end{aligned} \end{aligned}$$

(130)

The additive terms in Eq. 130 can be thought of as components of the average growth rate, each of which captures some “effect” on population growth. The components are not generally independent, which correctly implies that the subsequent coexistence mechanisms are not generally independent (Song et al. 2020; Kuang and Chesson 2010; Yuan and Chesson 2015). For instance, in the spatiotemporal lottery model (Section “Example: The spatiotemporal lottery model” in the main text), the mortality parameter modulates all coexistence mechanisms. However, growth rate components may be conceptualized as distinct processes, just as ecology and evolution are interdependent but conceptually distinct.

Note that the term $\mathbb {E}_{x,t} \left[ (E_j-E_j^*)(C_j-C_j^*) \right]$ has been replaced with $\mathrm {Cov}_{x,t} \left( E_j, C_j \right)$, since $\mathrm {Cov}_{x,t} \left( E_j, C_j \right) = \mathbb {E}_{x,t} \left[ (E_j-E_j^*)(C_j-C_j^*) \right] + \mathcal {O}(\sigma ^3)$ via the small-noise assumptions. Analogous replacements have been made for other variance and covariance terms in Eq. (130). These replacements are not a necessary part of MCT, but they do make the mathematical expressions shorter and more comprehensible.

Appendix 2: Justification of the space-time decomposition

To isolate the effects of spatial and temporal variation, we first define a reference state where both spatial and temporal variation are turned off; then, we separately turn on spatial (temporal) variation, and identify the difference as the main effect of spatial (temporal) variation. Put in such colloquial terms, this procedure may appear ad hoc at first glance. However, we show that this procedure agrees with intuition in a simple example (Appendix “A toy model with only spatially or only temporally varying abiotic factors”), and is concordant with philosophical accounts of causation (Appendix “The space-time decomposition measures causation”).

A toy model with only spatially or only temporally varying abiotic factors

Here we analyze the edge case where the environmental response $E_j$ is a function of abiotic factors that individually vary over only space or time. This case is simple enough that we can describe our intuitions regarding what a space-time decomposition should do: the space component should only include the effects of the spatially varying abiotic factors, and the time component should only include the effects of the temporally varying abiotic factors.

To be more concrete, consider two abiotic factors, W and Y. The factor W only varies over space (i.e., at a particular location, W does not vary from year-to-year) and Y only varies over time (i.e., at a single point in time, all locations have the same value of Y). Select the equilibrium values of the abiotic resources, $W^*$ and $Y^*$, so that $E_j^* = f_j(W^*, Y^*)$, where $f_j$ is a function that maps abiotic factors to species j’s environmental response. The small-noise assumptions of MCT imply that $W - W^* = \mathcal {O}(\sigma )$, $Y - Y^* = \mathcal {O}(\sigma )$, $\mathbb {E}_{x,t} \left[ W - W^* \right] = \mathbb {E}_{x} \left[ W - W^* \right] =\mathcal {O}(\sigma ^2)$, and $\mathbb {E}_{x,t} \left[ Y - Y^* \right] = \mathbb {E}_{t} \left[ Y - Y^* \right] = \mathcal {O}(\sigma ^2)$. Using this information, we can derive expressions for the space-time decomposition of $\mathrm {Var}_{x,t} \left( E_j\right)$. Applying a Taylor series of $f_j$ about $W^*$ and $Y^*$, plugging the resulting expression into the space-time decomposition Eqs. (30)–(32), and utilizing the fact that the variance of a constant equals zero (e.g., $\mathrm {Var}_{t} \left( W\right) = 0$), we find that

$$\begin{aligned}&S_j = \left[ \frac{\partial f_j(W^*, Y^*)}{\partial W} \right] ^2 \mathrm {Var}_{x} \left( W\right) + \mathcal {O}(\sigma ^3) \end{aligned}$$

(131)

$$\begin{aligned}&T_j = \left[ \frac{\partial f_j(W^*, Y^*)}{\partial Y} \right] ^2 \mathrm {Var}_{t} \left( Y\right) + \mathcal {O}(\sigma ^3), \quad \text {and} \end{aligned}$$

(132)

$$\begin{aligned}&R_j = \left[ \frac{\partial ^2 f_j(W^*, Y^*)}{{\partial W}{\partial Y}} \right] ^2 \mathrm {Var}_{x} \left( W\right) \mathrm {Var}_{t} \left( Y\right) + \mathcal {O}(\sigma ^5). \end{aligned}$$

(133)

The Taylor series coefficients show that $S_j$ captures the main effect of the spatially varying abiotic factor, $T_j$ captures the main effect of the temporally varying abiotic factor, and that $R_j$ captures the interaction effect between the two abiotic factors. This model is exceedingly simple, but it is the first line of evidence that our space-time decomposition behaves as desired.

The space-time decomposition measures causation

Counterfactual theories of causation posit that causation can be explained in terms of counterfactual dependency (Hume 1748, Section XII; Mill 1856, Lewis 1973, Pearl and Mackenzie 2018). To say “A caused B,” is to say “if A had not occurred, then B would not have occurred.” To operationalize causation, we may calculate differences (with respect to some outcome of interest) between possible worlds, where the possible worlds are similar in every relevant way except for some focal causal factor. The comparison of possible worlds is crucial, which is why the counterfactual account of causation is sometimes called the difference-making account of causation. Lewis (1973) explains “We think of a cause as something that makes a difference, and the difference it makes must be a difference from what would have happened without it.”

The exposition above makes our challenge clear: to justify our space-time decomposition on the grounds that it captures causation, we must (1) describe $S_j$, $T_j$, and $R_j$ (see Eqs. (30)–(32)) in terms of differences between possible worlds, as has been done in the main text (Section “Exact coexistence mechanisms”) and (2) argue that the possible worlds in question are close in some relevant sense, following Lewis’ (1979) guideline that possible worlds “...maximize the spatiotemporal region thorough-out which perfect match of particular fact prevails.” By using spatial (temporal) averaging to squash spatial (temporal) variation, we are doing just that: the sequence of spatial averages $A(t) = \mathbb {E}_{x} \left[ E_j \right]$ minimizes the squared error $\sum _{x,t} \left( E_j(x,t) -A(t) \right) ^2$, under the constraints that there is no spatial variation, and that spatial variation must be squashed using only information from the $E_j$’s within each individual time-step.

Appendix 3: Deriving the small-noise fitness-density covariance for the spatiotemporal lottery model

Like all coexistence mechanisms, the fitness-density covariance coexistence mechanism is $\mathcal {O}(\sigma ^2)$, which implies that the leading-order approximation for the covariance will involve $\mathcal {O}(\sigma )$ approximations of $\nu _j(t)$ and $\lambda _j(t)$. To this end, we take a perturbative approach, expanding both parameters in powers of $\sigma$, $\nu _{j}(x,t) = \nu _{j,0}(x,t) + \sigma \nu _{j,1}(x,t) + ...$; and $\lambda _{j}(x,t) = \lambda _{j,0}(x,t) + \sigma \lambda _{j,1}(x,t) + ...$.

Matching like-terms in the perturbative expansion and the Taylor series expansion of $\lambda _j$ (Eq. 119), we find that $\lambda _{j,0}(x,t) = 1$ and $\sigma \lambda _{j,1}(x,t) = \alpha _j^{(1)} (E_j(x,t) - E_{j}^{*}) + \beta _j^{(1)} (C_j(x,t) - C_{j}^{*})$. The solution $\lambda _{j,0}(x,t) = 1$ implies that $\nu _{j,0}(x,t) = 1$. Noting the constancy of the zeroth-order solutions, the covariance can now be approximated as

$$\begin{aligned} \begin{aligned} \mathrm {Cov}_{x} \left( v_j(t), \lambda _j(t) \right)&= \mathrm {Cov}_{x} \left( v_{j,0}(t) + \sigma v_{j,1}(t) + ..., \lambda _{j,0}(t) + \sigma \lambda _{j,1}(t) + ... \right) \\&\approx \mathrm {Cov}_{x} \left( \sigma v_{j,1}(t), \sigma \lambda _{j,1}(t) \right) . \end{aligned} \end{aligned}$$

(134)

We now seek to simplify by expressing $v_{j,1}(x,t)$ in terms of the environmental parameter. Dividing both sides of the population map (Eq. 97) by $\mathbb {E}_{x} \left[ n_j(t) \right]$ gives the relative-density map.

$$\begin{aligned} \nu _j(x,t+1) = q_j \nu _j(x,t) \frac{\lambda _j(x,t)}{\widetilde{\lambda }_j(t)} + 1 - q_j. \end{aligned}$$

(135)

The small-noise assumptions (Appendix “Small-noise assumptions”) allow us to make the substitution, $\widetilde{\lambda }_j(x,t) = 1 + \mathcal {O}(\sigma )$, which simplifies the relative density map to

$$\begin{aligned} \nu _j(x,t+1) = q_j \nu _j(x,t) \lambda _j(x,t) + 1 - q_j. \end{aligned}$$

(136)

We now expand $v_j$ in powers of $\sigma$ and match terms of order $\sigma$.

$$\begin{aligned} \mathcal {O}(\sigma ): \quad \quad \nu _{j,1}(x,t+1) = q_j \nu _{j,1}(x,t) + q_j \lambda _{j,1}(x,t). \end{aligned}$$

(137)

Substituting the above expression into the covariance produces

$$\begin{aligned} \begin{aligned} \mathrm {Cov}_{x} \left( v_j(t), \lambda _j(t) \right)&\approx \mathrm {Cov}_{x} \left( \sigma v_{j,1}(t), \sigma \lambda _{j,1}(t) \right) \\&= \sigma ^2 \mathrm {Cov}_{x} \left( q v_{j,1}(t-1) + \lambda _j(t-1), \lambda _{j,1}(t) \right) \\&= \sigma ^2 \mathrm {Cov}_{x} \left( q^2 v_{j,1}(t-2) + q \lambda _{j,1}(t-2) \right. \\ &\quad\left.+ \lambda _{j,1}(t-1), \lambda _{j,1}(t) \right) \\ \vdots \\&= \sigma ^2 \sum \limits _{i=1}^{\infty } q^i \mathrm {Cov}_{x} \left( \lambda _{j,1}(t-i), \lambda _{j,1}(t) \right) . \end{aligned} \end{aligned}$$

(138)

Substituting $\alpha _j^{(1)} (E_j(x,t) - E_{j}^{*}) + \beta _j^{(1)} (C_j(x,t) - C_{j}^{*}) + \mathcal {O}(\sigma ^2)$ for $\sigma \lambda _{j,1}$, we get

$$\begin{aligned} \begin{aligned} \mathrm {Cov}_{x} \left( v_i(t), \lambda _i(t) \right)&\approx \sum \limits _{s=1}^{\infty } q^s \mathrm {Cov}_x \bigl (\alpha _i^{(1)} (E_i(x,t-s) - E_{i}^{*}) \\&\quad+ \beta _i^{(1)} (C_i(x,t-s) - C_{i}^{*}), \alpha _i^{(1)} \\&\quad(E_i(x,t) - E_{i}^{*}) + \beta _i^{(1)} (C_i(x,t) - C_{i}^{*}) \bigl ). \end{aligned} \end{aligned}$$

(139)

Next, we express the invader’s competition parameter fluctuation in terms of the resident’s environmental response. In the two-species lottery model of Section “Example: The spatiotemporal lottery model”, $C_i(x,t) - C_{i}^{*} = E_r(x,t) - E_{r}^{*} + \mathcal {O}(\sigma ^2)$. The covariance expression is now

$$\begin{aligned} \begin{aligned} \mathrm {Cov}_{x} \left( v_i(t), \lambda _i(t) \right) \approx& \sum \limits _{s=1}^{\infty } q^s \mathrm {Cov}_x \bigl (\alpha _i^{(1)} (E_i(x,t-s) - E_{i}^{*})\\& + \beta _i^{(1)} (E_r(x,t-s) - E_{r}^{*}) , \alpha _i^{(1)} (E_i(x,t)\\& - E_{i}^{*}) + \beta _i^{(1)} (E_r(x,t) - E_{r}^{*}) \bigl ). \end{aligned} \end{aligned}$$

(140)

Finally, we write the environmental fluctuations in terms of patch and time effects (Eq. 98), evaluate the above expression using the geometric series and the symbols introduced in the Section “Example: The spatiotemporal lottery model” (e.g., $\mathrm {Cov}_{x} \left( a_i, a_r \right) = \phi _{ir}^{(x)} \sigma _{i}^{(x)} \sigma _{r}^{(x)}$), and take the average across time:

$$\begin{aligned} \begin{aligned} \mathbb {E}_{t} \left[ \mathrm {Cov}_{x} \left( v_i, \lambda _i \right) \right] \approx \frac{q}{1-q}\biggl [&{\alpha _i^{(1)}}^2 {\sigma _i^{(x)}}^2 + {\beta _i^{(1)}}^2 {\sigma _r^{(x)}}^2 + 2\alpha _i^{(1)}\beta _i^{(1)} \phi _{ir}^{(x)} \sigma _i^{(x)}\sigma _r^{(x)} \\&+ {\alpha _i^{(1)}}^2 \theta _i^2 {\sigma _i^{(x)}}^2 {\sigma _i^{(t)}}^2 + {\beta _i^{(1)}}^2 \theta _r^2 {\sigma _r^{(x)}}^2 {\sigma _r^{(t)}}^2 \\&+ 2\alpha _i^{(1)}\beta _i^{(1)} \theta _i \theta _r \phi _{ir}^{(x)} \phi _{ir}^{(t)} \sigma _i^{(x)} \sigma _i^{(t)} \sigma _r^{(x)} \sigma _r^{(t)} \biggl ]. \end{aligned} \end{aligned}$$

(141)

In the lottery model, there are always more larvae produced than are necessary to compensate for adult mortality. If there is only one resident, its local density will be exactly 1 everywhere after the local growth phase. Since global dispersal with local retention acts symmetrically on all patches, the resident’s density will still be 1 everywhere after the dispersal phase. Therefore, the resident’s covariance term is zero, and the fitness-density covariance coexistence mechanism is simply the expression above, (Eq. 141); i.e., $\Delta \kappa _i = \mathbb {E}_{t} \left[ \mathrm {Cov}_{x} \left( v_i, \lambda _i \right) \right]$. When symmetries in demographic parameters are taken into consideration, Eq. 141 reduces to the result in the main text, Eq. 114.

Appendix 4: Generalization of MCT to different classes of models

In the main text (Section “Spatiotemporal coexistence mechanisms”), we presented formulas for coexistence mechanisms in models with discrete-time dynamics and no age/stage-structure . With slight modification, these same formulas can be used to calculate coexistence mechanisms in other classes of models.

In continuous-time models, $g_j$ represents the local per capita growth rate, $dn_j(t)/dt$ (as opposed to the finite rate of increase in the discrete-time case). In models with multiple regulating factors, the $C_j$ argument is replaced with an arbitrary number of arguments representing regulating factors, and finer-grained fluctuation-dependent coexistence mechanisms are computed by allowing one or two of these factors to vary while holding the rest constant. In structured population models, the function $g_j$ represents the finite rate of increase of the sum of states, i.e., $\Vert n(t+1) \Vert / \Vert n(t) \Vert$, where $\Vert n(t) \Vert$ is the sum (or integral) of population densities across all traits/ages/stages.

Stochastic differential equations (SDEs)

A stochastic differential equation (SDE) is a continuous-time process in which stochastic perturbations occur at an infinitesimal time scale. Ecological SDEs are usually not physically motivated, and can often be viewed as approximations to stochastic difference equations as the length of the time step shrinks to zero (Turelli 1977). Such approximations are useful because they permit analytical results (e.g., the stationary distribution of population densities in Hatfield and Chesson 1989).

A univariate, non-spatial SDE can be written as

$$\begin{aligned} dn(t) = n(t) \left[ a(n(t)) dt + b(n(t)) dW(t) \right] , \end{aligned}$$

(142)

where a(n(t)) is the infinitesimal per capita mean and b(n(t)) is the infinitesimal per capita scale. These two quantities are respectively defined as the expectation and variance of per capita population growth, conditioned on n(t), in the limit of small time steps; or in symbols,

$$\begin{aligned} a(n) = \lim _{\Delta t \rightarrow 0} \frac{\mathbb {E}_{} \left[ n(t+\Delta t) \right] - n(t)}{n(t) \Delta t}, \quad \text {and} \end{aligned}$$

(143)

$$\begin{aligned} b(n) = \lim _{\Delta t \rightarrow 0} \sqrt{\frac{\mathrm {Var}_{} \left( n(t+\Delta t) - n(t)\right) }{n(t) \Delta t}}. \end{aligned}$$

(144)

To solve the SDE, we use Ito’s lemma to perform a change of variables. Ito’s lemma (Karlin and Taylor 1981, pp. 347–348) states that for an arbitrary SDE,

$$\begin{aligned} d X(t) = A(X,t) dt + B(X,t) dW(t), \end{aligned}$$

(145)

the SDE for the transformation f(X, t) is

$$\begin{aligned} d f = \left[ \frac{\partial f}{\partial t} + A(X,t) \frac{\partial f}{\partial x} + \frac{B(X,t)^2}{2} \frac{\partial ^2 f}{\partial ^2 x} \right] dt + B(X,t) \frac{\partial f}{\partial x} dW(t). \end{aligned}$$

(146)

We define the transformation $f(n,t) = \log (n(t))$. The SDE is

$$\begin{aligned} d f = \left[ a(n(t)) - \frac{b(n(t))^2}{2} \right] dt + b(n(t)) dW(t), \end{aligned}$$

(147)

which reveals that the tendency for population density to increase/decrease is given by the sign of $\lim _{t\rightarrow \infty } \int _0^t a(n(s)) - \frac{b(n(s))^2}{2} ds$. For resident species, $\mathbb {E}_{t} \left[ a(n) - \frac{b(n)^2}{2} \right] = 0$. In SDEs, the quantity $a(n) - \frac{b(n)^2}{2}$ plays the same role that the logged finite rate of increase plays in discrete time models. The discounting of the expected per capita growth rate by half of the variance should be reminiscent of (Eq. 128).

For illustrative purposes, we have thus far looked at a univariate, non-spatial SDE. To make the general SDE notation more congruent with the formalism of spatiotemporal MCT, we first define the local per capita growth rate, $r_j$, as the output of the function $g_j$:

$$\begin{aligned} r_j := g_j(E_j, C_j) = a_j(C_j) + b_j(C_j)(E_j-E_j^*). \end{aligned}$$

(148)

The model has been parameterized so that $\mathrm {Var}_{} \left( E_j(x,t)\right)$ (the variance of $E_j(x,t)$ across sample paths) is not proportional to the time step. For example, consider the Lotka Volterra model with spatiotemporal environmental noise

$$\begin{aligned} n'_j(x,t+dt) - n_j(x,t) = \left( 1-\sum _{k=1}^{S} \alpha _{jk} n_k(x,t)\right) dt + \epsilon _j(x)dt + \sigma _j dW_j(t), \end{aligned}$$

(149)

where $\epsilon _j(x)$ is the effect of location x on environmental noise, $\sigma _j$ is the scale of temporal environmental fluctuations, and $n'_j(x,t)$ is the population density after the local population growth phase, but before the dispersal phase. Here, the competition parameter is $C_j(x,t) = \sum _{k=1}^{S} \alpha _{jk} n_k(x,t)$ by convention (Chesson 1994, Section 5). The environmental parameter is $E_j(x,t) = \epsilon _j(x) + \sigma _j dW_j(t)/\sqrt{dt}$; because $\mathbb {E}_{} \left[ dW \right] = dt$ (Karlin and Taylor 1981, p.347), division by $\sqrt{dt}$ ensures that variances of $E_j$ will not be proportional to the time step. With $E_j$ and $C_j$ defined in this way, we have $\mathrm {Var}_{} \left( E_j(x,t)\right) = \sigma _j^2$ and $g_j(E_j,C_j) = (1-C_j) + E_j$.

Following the logic of Appendix “Spatial averaging and fitness-density covariance”, the metapopulation per capita growth rate is

$$\begin{aligned} \widetilde{r}_j = \mathbb {E}_{x} \left[ r \right] + \mathrm {Cov}_{x} \left( \nu _j, r_j \right) , \end{aligned}$$

(150)

To approximate the average per capita growth rate, we approximate $\mathbb {E}_{t} \left[ \widetilde{r_j} \right]$ and $\mathrm {Var}_{t} \left( \widetilde{r_j}\right)$ with Taylor series of $g_j$ about $E_j$ and $C_j$; and truncate using the small-noise assumptions (Appendix “Small-noise assumptions”). The result is

$$\begin{aligned} \begin{aligned} \Biggl (\mathbb {E}_{t} \left[ \widetilde{r_j} \right] - \frac{\mathrm {Var}_{t} \left( \widetilde{r_j}\right) }{2}\Biggr ) \approx \;&\alpha _j^{(1)} \mathbb {E}_{x,t} \left[ (E_j - E_{j}^{*}) \right] + \beta _j^{(1)} \mathbb {E}_{x,t} \left[ (C_j - C_{j}^{*}) \right] \\&+ \frac{1}{2} \alpha _j^{(2)} \mathrm {Var}_{x,t} \left( E_j\right) + \frac{1}{2} \beta _j^{(2)} \mathrm {Var}_{x,t} \left( C_j\right) + \zeta _j \mathrm {Cov}_{x,t} \left( E_j, C_j \right) \\&+ \mathbb {E}_{t} \left[ \mathrm {Cov}_{x} \left( \nu _j, \alpha _j^{(1)} (E_j - E_{j}^{*}) + \beta _j^{(1)} (C_j - C_{j}^{*}) \right) \right] \\&- \frac{1}{2} \alpha _j^{(1)^{2}} \mathrm {Var}_{t} \left( \mathbb {E}_{x} \left[ E_j \right] \right) - \frac{1}{2} \beta _j^{(1)^{2}} \mathrm {Var}_{t} \left( \mathbb {E}_{x} \left[ E_j \right] \right) \\ &- \alpha _j^{(1)}\beta _j^{(1)} \mathrm {Cov}_{t} \left( \mathbb {E}_{x} \left[ E_j \right] , \mathbb {E}_{x} \left[ C_j \right] \right) , \end{aligned} \end{aligned}$$

(151)

which is nearly identical to the corresponding discrete-time approximation (Eq. 130), the only difference being that the function $g_j(E_j, C_j)$ generates the per capita growth rate as opposed to the finite rate of increase, such that the Taylor series coefficients have different meanings. Because of the correspondence between the continuous-time and discrete-time approximations of the average growth rate, equations from the main text (Eqs. 7–11 & 33–52) can be used to calculate the small-noise coexistence mechanisms for SDE models, again with the caveat that the Taylor series coefficients may have different meanings.

The derivation of exact coexistence mechanisms follows Section “Exact coexistence mechanisms” from the main text, except that $r_j - \frac{\left( r_j - \mathbb {E}_{t} \left[ r_j \right] \right) ^2}{2}$ is used in place of $\log (\lambda )$.

Continuous-time models (non-SDEs)

When the dynamics of population density are not governed by SDEs (even when $E_j$ or $C_j$ are governed by SDEs, as in Li and Chesson, 2016), a simple arithmetic average over space and time gives the correct average growth rate. With the function $g_j$ generating the per capita growth rate, $dn_j/dt$, the average growth rate can be approximated as

$$\begin{aligned} \begin{aligned} \mathbb {E}_{t} \left[ \widetilde{r_j} \right] \approx \;&\alpha _j^{(1)} \mathbb {E}_{x,t} \left[ (E_j - E_{j}^{*}) \right] + \beta _j^{(1)} \mathbb {E}_{x,t} \left[ (C_j - C_{j}^{*}) \right] \\&+ \frac{1}{2} \alpha _j^{(2)} \mathrm {Var}_{x,t} \left( E_j\right) + \frac{1}{2} \beta _j^{(2)} \mathrm {Var}_{x,t} \left( C_j\right) + \zeta _j \mathrm {Cov}_{x,t} \left( E_j, C_j \right) \\&+ \mathbb {E}_{t} \left[ \mathrm {Cov}_{x} \left( \nu _j, \alpha _j^{(1)} (E_j - E_{j}^{*}) + \beta _j^{(1)} (C_j - C_{j}^{*}) \right) \right] . \end{aligned} \end{aligned}$$

(163)

Here, there is no discounting for temporal variation, so spatial and temporal variation are treated symmetrically (with the exception of fitness-density covariance). The small-noise and exact coexistence mechanisms are as follows:

Multiple regulating factors

In the spatiotemporal lottery model, competition is a function of just one regulating factor: open reef territories. In more realistic models, we may want to cast competition as function of L regulating factors, $\varvec{F} = (F_1, F_2, ..., F_L)$, which may be species densities, refugia, resources, natural enemies:

$$\begin{aligned} C_j = \phi _j(\varvec{F}). \end{aligned}$$

(181)

In previous work (e.g., Barabás et al. 2018; Chesson 2020), the finite rate of increase is directly expanded with respect to the regulating factors. We will expand the competition-generating function $\phi _j$ with respect to the regulating factors, and then substitute the expansion for $C_j$ within the mathematical expressions for small-noise coexistence mechanisms. Our approach makes the formulas slightly longer (unlike previous theory, the coefficients $\beta _j^{(1)}$ and $\beta _j^{(2)}$ are not absorbed into $\phi _{jk}^{(1)}$ and $\phi _{jkl}^{(2)}$, the Taylor series coefficients of $\phi _j$), but in substituting $\phi _j(\varvec{F})$ for $C_j$, we demonstrate that the case of multiple regulating factors is not different from what is presented in the main text. Note however that in some models, the only reasonable choice for the competition parameter results in $C_j = \lambda _j$, such that $\beta _j^{(1)} = \beta _j^{(2)} = 1$.

Formulas for small-noise coexistence mechanisms which explicitly use the regulating factors can be obtained by taking the formulas for small-noise coexistence mechanisms in the main text (Eqs. 7–11), substituting in the Taylor series expansion of $\phi _j$ in place of $C_j$, and truncating using the small-noise assumptions. To Taylor-expand $\phi _j$, one must select equilibrium values $\varvec{F^{*j}}$ such that $C_j^* = \phi _j(\varvec{F}^{*j})$. This task may be guided by the conditions $F_k - F_k^{*j} = \mathcal {O}(\sigma )$ and $\mathbb {E}_{x,t} \left[ F_k \right] - F_k^{*j} = \mathcal {O}(\sigma ^2)$, which are implied by the small-noise assumptions (Appendix “Small-noise assumptions”). Note that the equilibrium levels of the regulating factors can be species-specific (hence the superscript “j”). There is no best way to select the equilibrium parameters, but various strategies are discussed briefly by Johnson and Hastings 2022a, Appendix 1. The Taylor series coefficients are denoted $\phi _{jk}^{(1)} = \frac{\partial \phi _j(\varvec{F^{*j}})}{\partial F_k}$ and $\phi _{jkl}^{(2)} = \frac{\partial ^2 \phi _j(\varvec{F^{*j}})}{\partial F_k \partial F_l}$.

The regulating factors have additive effects on the coexistence mechanisms, thus allowing the contribution of subsets of regulating factors to be extracted. We will demonstrate how this partitioning would work, using examples with a single regulating factor, $F_k$.

The contribution of regulating factor $F_k$ to the linear density-dependent effects, i.e., species i’s degree of specialization on $F_k$:

$$\begin{aligned} \begin{aligned} \beta _i^{(1)} \phi _{ik}^{(1)} \mathbb {E}_{x,t} \left[ F_k - F_k^{*i} \right] - \frac{1}{S-1} \sum \limits _{r \ne i}^S \frac{GT_r}{GT_i} \beta _r^{(1)} \phi _{rk}^{(1)} \mathbb {E}_{x,t} \left[ F_k - F_k^{*r} \right] . \end{aligned} \end{aligned}$$

The contribution of regulating factor $F_k$ to the storage effect:

$$\begin{aligned}&\left[ \zeta _{i} \phi _{ik}^{(1)} \mathrm {Cov}_{x,t} \left( E_i, F_k \right) - \alpha _i^{(1)}\beta _i^{(1)} \phi _{ik}^{(1)} \mathrm {Cov}_{t} \left( \mathbb {E}_{x} \left[ E_i \right] , \mathbb {E}_{x} \left[ F_k \right] \right) \right] \\&- \frac{1}{S-1} \sum \limits _{r \ne i}^S \frac{GT_r}{GT_i} \left[ \zeta _{r} \phi _{rk}^{(1)} \mathrm {Cov}_{x,t} \left( E_r, F_k \right)\right. \\ & \left.\right. \\ & \left. - \alpha _r^{(1)}\beta _r^{(1)} \phi _{rk}^{(1)} \mathrm {Cov}_{t} \left( \mathbb {E}_{x} \left[ E_r \right] , \mathbb {E}_{x} \left[ F_k \right] \right) \right] \end{aligned}$$

It should also be straightforward to derive the space-time decompositions of the small-noise coexistence mechanisms. For example, the contribution of $F_k$ to the time component of the storage effect is

$$\begin{aligned}& \left( \zeta _i \phi _{ik}^{(1)} - \alpha _i^{(1)}\beta _i^{(1)} \phi _{ik}^{(1)} \right) \mathrm {Cov}_{t} \left( \mathbb {E}_{x} \left[ E_i \right] , \mathbb {E}_{x} \left[ F_k \right] \right) - \frac{1}{S-1} \sum \limits _{r \ne i}^S \frac{GT_r}{GT_i} \\&\left( \zeta _r \phi _{rk}^{(1)} - \alpha _r^{(1)}\beta _r^{(1)} \phi _{rk}^{(1)} \right) \mathrm {Cov}_{t} \left( \mathbb {E}_{x} \left[ E_r \right] , \mathbb {E}_{x} \left[ F_k \right] \right) . \end{aligned}$$

(188)

The contribution of regulating factor $F_k$ to relative nonlinearity Arguably, there are several ways to partition relative nonlinearity further with respect to individual regulating factors.

• 1. The contribution of $F_k$’s variance to relative nonlinearity, or equivalently, the degree of specialization on the variance in $F_k$:

  $$\begin{aligned} \begin{aligned}&\frac{1}{2} \left[ \beta _i^{(2)} \phi _{ikk}^{(2)} \mathrm {Var}_{x,t} \left( F_k\right) - {\beta _i^{(1)}}^2 \phi _{ik}^{(1)} \phi _{ik}^{(1)} \mathrm {Var}_{t} \left( \mathbb {E}_{x} \left[ F_k \right] \right) \right] \\&- \frac{1}{S-1} \sum \limits _{r \ne i}^S \frac{GT_r}{GT_i} \frac{1}{2} \left[ \beta _r^{(2)} \phi _{rkk}^{(2)} \mathrm {Var}_{x,t} \left( F_k\right)\right. \\ & \left.- {\beta _r^{(1)}}^2 \phi _{rk}^{(1)} \phi _{rk}^{(1)} \mathrm {Var}_{t} \left( \mathbb {E}_{x} \left[ F_k \right] \right) \right] \end{aligned} \end{aligned}$$

  (189)

• 2. The contribution of covariance between $F_k$ and $F_l$ ($k \ne l$) on relative nonlinearity, or equivalently, the degree of specialization on the covariance between $F_k$ and $F_l$:

  $$\begin{aligned} \begin{aligned}&\left[ \beta _i^{(2)} \phi _{ikl}^{(2)} \mathrm {Cov}_{x,t} \left( F_k, F_l \right) - {\beta _i^{(1)}}^2 \phi _{ik}^{(1)} \phi _{il}^{(1)} \mathrm {Cov}_{t} \left( \mathbb {E}_{x} \left[ F_k \right] , \mathbb {E}_{x} \left[ F_l \right] \right) \right] \\&- \frac{1}{S-1} \sum \limits _{r \ne i}^S \frac{GT_r}{GT_i} \left[ \beta _r^{(2)} \phi _{rkl}^{(2)} \mathrm {Cov}_{x,t} \left( F_k, F_l \right) \right. \\ & \left.- {\beta _r^{(1)}}^2 \phi _{rk}^{(1)} \phi _{rl}^{(1)} \mathrm {Cov}_{t} \left( \mathbb {E}_{x} \left[ F_k \right] , \mathbb {E}_{x} \left[ F_l \right] \right) \right] \end{aligned} \end{aligned}$$

  (190)

• 3. The total contribution of $F_k$ to relative nonlinearity, including the contribution of the variance of $F_k$, and the contribution of covariances between $F_k$ and other regulating factors:

  $$\begin{aligned} \begin{aligned}&\left[ \frac{1}{2} \left( \beta _i^{(2)} \phi _{ikk}^{(2)} \mathrm {Var}_{x,t} \left( F_k\right) - {\beta _i^{(1)}}^2 \phi _{ik}^{(1)} \phi _{ik}^{(1)} \mathrm {Var}_{t} \left( \mathbb {E}_{x} \left[ F_k \right] \right) \right) \right] \\ -&\left[ \frac{1}{S-1} \sum \limits _{r \ne i}^S \frac{GT_r}{GT_i} \frac{1}{2} \left( \beta _r^{(2)} \phi _{rkk}^{(2)} \mathrm {Var}_{x,t} \left( F_k\right) - {\beta _r^{(1)}}^2 \phi _{rk}^{(1)} \phi _{rk}^{(1)} \mathrm {Var}_{t} \left( \mathbb {E}_{x} \left[ F_k \right] \right) \right) \right] \\ +&\left[ \sum \limits _{l \ne k}^L \left( \beta _i^{(2)} \phi _{ikl}^{(2)} \mathrm {Cov}_{x,t} \left( F_k, F_l \right) - {\beta _i^{(1)}}^2 \phi _{ik}^{(1)} \phi _{il}^{(1)} \mathrm {Cov}_{t} \left( \mathbb {E}_{x} \left[ F_k \right] , \mathbb {E}_{x} \left[ F_l \right] \right) \right) \right] \\ -&\left[ \frac{1}{S-1} \sum \limits _{r \ne i}^S \frac{GT_r}{GT_i} \left[ \sum \limits _{l \ne k }^L \left( \beta _r^{(2)} \phi _{rkl}^{(2)} \mathrm {Cov}_{x,t} \left( F_k, F_l \right) \right.\right.\right.\\&\left.\left.\left.- {\beta _r^{(1)}}^2 \phi _{rk}^{(1)} \phi _{rl}^{(1)} \mathrm {Cov}_{t} \left( \mathbb {E}_{x} \left[ F_k \right] , \mathbb {E}_{x} \left[ F_l \right] \right) \right) \right] \right] \end{aligned} \end{aligned}$$

  (191)

The exact coexistence mechanisms can be obtained by following the directions implied by the formulas in the main text (Eqs. 20–27). For example, the formula for $\Delta {\rho _{i}}^{(e)}$ (Eq. 22) directs the user to set $C_j$ to $\mathbb {E}_{x,t} \left[ C_j \right]$; because $C_j = \phi _j(\varvec{F})$, one would set $\phi _j(\varvec{F})$ to $\mathbb {E}_{x,t} \left[ \phi _j(\varvec{F}) \right]$.

However, to partition the coexistence mechanisms further into contributions from individual regulating factors, we need a slightly different approach: fix all regulating factors at $\varvec{F^{*j}}$ and then modify the regulating factors one at a time. For example, when partitioning $\Delta {\rho _{i}}^{(e)}$, we set $\phi _j(F_1, \ldots , F_L)$ to $\phi _j(F_1^{*j}, \ldots , \mathbb {E}_{x,t} \left[ F_k \right] , \ldots , F_L^{*j})$, one regulating factor at at a time, and then sum the L resulting pieces of invasion growth rate to approximate $\Delta {\rho _{i}}^{(e)}$. Unless $\phi _j$ is a linear function of the regulating factors, the aforementioned procedure will not exactly equal $\Delta {\rho _{i}}^{(e)}$ as defined in the main text (Section “Exact coexistence mechanisms”). This is discussed further below.

To define these exact coexistence mechanisms in a reasonable amount of page-space, new notation is required. Let $\left\{ \varvec{v}^{-\{k\}}, a \right\}$ be a vector $\varvec{v}$ where the k-th element has been replaced with a. Similarly, let $\left\{ \varvec{v}^{-\{k,l\}}, a, b \right\}$ be a vector $\varvec{v}$ where the k-th element has been replaced with a, and the l-th element has been replaced by b. The notation introduced here allows us to express ideas such as holding all elements of $\varvec{F}$ at their equilibrium values, except for $F_k$, which is held at its spatiotemporal average: $\left\{ \varvec{F^*}^{-\{k\}}, \mathbb {E}_{x,t} \left[ F_k \right] \right\}$. The following formulas look complicated, but they express the simple idea, pioneered by Ellner et al. (2016, 2019), that coexistence mechanisms can be measured as the marginal effects of allowing some parameters to vary while holding the rest constant.

The exact coexistence mechanisms here are different from those presented in the main text (Section “Exact coexistence mechanisms”: Eqs. 20–27), due to the fact that the competition parameter is generically a nonlinear function of the regulating factors, i.e., $\mathbb {E}_{x,t} \left[ \phi _j(\varvec{F}) \right] \ne \sum _{k = 1}^L \phi _j \left( \left\{ \varvec{F^{*j}}^{-\{k\}}, \mathbb {E}_{x,t} \left[ F_k \right] \right\} \right)$). Normally, the precursor to the exact fitness-density covariance, $\overline{\mathscr {K}}_{j}$, is defined as a deviation from the average growth rate. Above, we have defined $\overline{\mathscr {K}}_{j}$ differently—as deviations summed across regulating factors—and captured the remainder of the average growth rate with $\epsilon _j$. The benefit of defining exact coexistence mechanisms in this way is that all canonical coexistence mechanisms can be partitioned into contributions from subsets of regulating factors.

Structured population models

In structured population models, the average per capita growth rate is replaced with the concept of the dominant lyapunov exponent (also known as the stochastic growth rate; Caswell 2001, Section 14.3.3). Small-noise approximations of the stochastic growth rate tend to be complicated (Tuljapurkar 1982), so we do not pursue them here.

The exact coexistence mechanisms can be computed using the formulas in the main text (Section “Exact coexistence mechanisms”: 20–27) with one modification. Because the distribution of future population density is determined by $\sum _{t = 0}^\infty \log (\Vert \varvec{n_j'}(x,t+1) \Vert / \Vert \varvec{n_j}(x,t) \Vert )$ (Tuljapurkar and Orzack 1980), the function $g_j(E_j,C_j)$ now is taken to generate $\Vert \varvec{n_j'}(x,t+1) \Vert / \Vert \varvec{n_j}(x,t) \Vert$. Here, $\varvec{n_j}(x,t)$ is the vector of population densities corresponding to each age or stage class at location x and time t; $\varvec{n_j'}(x,t+1)$ contains the population densities after the growth phase, but before the dispersal phase; and the operator $\Vert . \Vert$ computes the sum across of all elements in a vector. In models with continuous population structure (e.g., integral projection models with size-dependent demographic rates), the population density becomes a function of continuous variables (e.g., $n_j(x,t,z)$, where z is body size), and $\Vert . \Vert$ computes the integral across said variables.

Appendix 5: The maximum number of species that can coexist via fitness-density covariance

When there is no temporal variation, Eq. 139 in Appendix “Deriving the small-noise fitness-density covariance for the spatiotemporal lottery model” reduces to

$$\begin{aligned} \begin{aligned} \mathbb {E}_{t} \left[ \mathrm {Cov}_{x} \left( v_j, \lambda _j \right) \right]&\approx \frac{q}{1-q} \mathrm {Var}_{x} \left( \alpha _j^{(1)} (E_j(x) - E_{j}^{*}) + \beta _j^{(1)} (C_r(x) - C_{r}^{*})\right) \\&\approx \frac{q}{1-q} \left[ {\alpha _j^{(1)}}^2 \mathrm {Var}_{x} \left( E_j\right) + 2 \alpha _j^{(1)} \beta _j^{(1)} \mathrm {Cov}_{x} \left( E_j, C_j \right) \right. \\ & \qquad\qquad\left.+ {\beta _j^{(1)}}^2 \mathrm {Var}_{x} \left( C_j\right) \right] . \end{aligned} \end{aligned}$$

(206)

The competition parameter $C_j$ can be expanded as a function of L regulating factors (see Appendix “Multiple regulating factors”): $C_j = \phi _j(\varvec{F})$, where $\varvec{F} = (F_1, F_2, ..., F_L)$. The environment parameter can be expressed a vector of M discrete states: $E_j \in \varvec{E}'$, where $\varvec{E}' = (E'_{1}, E'_{2}, ..., E'_{M})$. Then, there are $M \times L$ “effective regulating factors” with the form $\mathrm {Cov}_{x} \left( E'_{m}, F_k \right)$; and $L(L-1)/2$ “effective regulating factors” with the form $\mathrm {Cov}_{x} \left( F_k, F_l \right)$. This result shows that fitness-density covariance can potentially support a large number of species.