Abstract
Exchange of diseases between domesticated and wild animals is a rising concern for conservation. In the ocean, many species display life histories that separate juveniles from adults. For pink salmon (Oncorhynchus gorbuscha) and parasitic sea lice (Lepeophtheirus salmonis), infection of juvenile salmon in early marine life occurs near salmon sea-cage aquaculture sites and is associated with declining abundance of wild salmon. Here, we develop a theoretical model for the pink salmon/sea lice host–parasite system and use it to explore the effects of aquaculture hosts, acting as reservoirs, on dynamics. Because pink salmon have a 2-year lifespan, even- and odd-year lineages breed in alternate years in a given river. These lineages can have consistently different relative abundances, a phenomenon termed “line dominance”. These dominance relationships between host lineages serve as a useful probe for the dynamical effects of introducing aquaculture hosts into this host–parasite system. We demonstrate how parasite spillover (farm-to-wild transfer) and spillback (wild-to-farm transfer) with aquaculture hosts can either increase or decrease the line dominance in an affected wild population. The direction of the effect depends on the response of farms to wild-origin infection. If aquaculture parasites are managed to a constant abundance, independent of the intensity of infections from wild to farm, then line dominance increases. On the other hand, if wild-origin parasites on aquaculture hosts are proportionally controlled to their abundance then line dominance decreases.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In recent decades, exchange of diseases and parasites between wild and domesticated animals has become a prominent concern for conservation and disease emergence (Daszak et al. 2000), as well as management of pest species in food production (Bengis et al. 2002; Costello 2009). The occurrence of “spillover”, transfer of infection from wildlife to domestic hosts, and “spillback”, transfer from domestic hosts to wildlife, has been demonstrated in a wide variety of taxa with migratory life histories, including terrestrial mammals (Cervus canadensis, Bison bison, Saiga tatarica; Cheville et al. 1998; Morgan et al. 2005), birds (Anseriformes:Anatidae; Gilbert et al. 2006; Muzaffar et al. 2006), and fishes (Oncorhynchus gorbuscha, O. keta; Krkošek et al. 2006, 2007b). Host migration plays an important role in determining the effects of spillover and spillback on conservation (Morgan et al. 2005; Krkošek et al. 2007b) and disease spread (Kilpatrick et al. 2006). Foundational host–parasite and epidemiological models, however, do not include host movement or migration (Morgan et al. 2004). Thus, efforts to understand the role of host migration in parasite and disease systems often employ complex tools, e.g. data-intensive statistical models (Kilpatrick et al. 2006) or parameter-heavy, spatially explicit simulation models (Morgan et al. 2007).
One application where simple models are successful in understanding the effects of host migration and disease exchange is in linking the declines of wild salmon populations in Europe and North America to their association with sea-cage salmon aquaculture production (Ford and Myers 2008). One proposed explanation for the declines, at least in the Pacific, is that spillover and spillback of parasitic sea lice (Lepeophtheirus salmonis) between wild salmonids and farm salmon leads to infections of juvenile wild salmon in early marine life (Krkošek et al. 2006, 2007a; Costello 2006, 2009). Without farms, infections do not occur until later in life because the migratory behaviour of salmon results in a spatial separation of juveniles in early marine life from adults and their parasites, a characteristic termed migratory allopatry; host migration creates a barrier to adult–juvenile transmission during early marine entry (Krkošek et al. 2007b). Studies of sea lice and salmon have described how aquaculture can break down this migratory barrier when farms containing adult fish are placed on migration corridors for wild juvenile salmonids (recent reviews: Krkošek 2010; Costello 2009). Rather than develop complex, spatially explicit models of host–parasite population dynamics, these studies have focused on the consequences of infections during early marine life (that are due to the interaction of host migration and aquaculture). Using this approach, Krkošek et al. (2007a) demonstrated declines in pink salmon populations associated with epizootics in aquaculture regions. Another theoretical paper reports a probabilistic analysis of infection pressures generated by various stocking levels of farms to explain these declines (Frazer 2009). To date the primary focus, however has been effects on equilibrium abundance of wild hosts. Salmon farming effectively augments host diversity, and according to epidemiological theory, this should affect behaviour of population dynamics as well (Dobson 2004).
Here, to understand the implications of parasite spillover and spillback with farm hosts for population dynamics, we introduce a model for the host–parasite system of wild pink salmon and parasitic sea lice. In keeping with the approach of earlier work, we use the classic Ricker (1954) model for pink salmon population dynamics, which we couple with a simple transmission model derived under the assumption of migratory allopatry. This permits a rather simple, spatially implicit, formulation of the model as a system of discrete-time equations. Because pink salmon have a 2-year lifespan, even- and odd-year lineages breed in alternate years in a given river. These lineages can have consistently different relative abundances of adults, a phenomenon termed “line dominance” in the salmon literature (Groot and Margolis 1991). Mathematically, line dominance arises in our model through a period-doubling bifurcation, which links the degree of dominance with the strength of inter-lineage interactions. To understand the effects of introduced aquaculture hosts on wild host population dynamics, we focus on changes in this dominance relationship, demonstrating that a line dominance naturally maintained by negative density-dependent interactions between lineages can be altered by the introduction of farm hosts.
Models
Sea lice are native copepod ectoparasites common on both adult wild hosts and in sea-cage salmon aquaculture (Costello 2009). These parasites have a direct life cycle, being transmitted primarily as planktonic larvae that become infective copepodids after surviving through a naupliar period lasting between 1 to 9 days (Johnson and Albright 1991). Once the copepodite attaches to a host fish, lice develop through a sequence of attached chalimus stages before becoming motile pre-adults and adult lice. Adult lice reproduce sexually on a host fish, with the female extruding eggstrings from which nauplii hatch, completing the life cycle. The feeding activity of lice on host surface tissues can cause morbidity and mortality of host fish, as well as sublethal effects that may influence survival via predation risk.
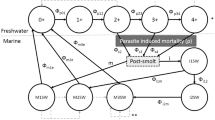
Pink salmon, like many fish, display migratory allopatry in which juvenile fish are spatially separated from adult fish due to differences in habitat requirements, food supply, natural enemies, and migration. With a 2-year generation time, a pink salmon population consists of two distinct lineages, or year classes, that use river (breeding) and ocean (maturing) habitat sequentially in time. Without farms (Fig. 1a), pink salmon of different lineages potentially interact through two means: (1) through effects on the environments (river and ocean habitat) that are sequentially used by the juvenile and adult age classes in alternate years, and (2) through transmission of a specialist parasite from adult hosts to juvenile hosts, i.e. between lineages.
Schematic depiction of interactions between two lineages of wild host without (a) and with (b) farm hosts. The solid and dashed–dotted lines correspond to the two lineages, dashed lines correspond to the parasite population. The y-axis depicts spatial extent of migration between breeding and maturing ranges, the x-axis depicts continuous time (τ). Without farms, parasite transmission is only inter-lineage, from adults to juveniles, and occurs in space and time within the gray “infection windows” as adults of one lineage share space with juveniles of the other. Infection of juveniles by adult-origin parasites during inter-lineage transmission and subsequent parasite-induced mortality is depicted in the dotted boxes at each census time (t, t + 1, t + 2,...). With farms (light gray bar), static in space and acting as reservoir hosts, both inter- and intra-lineage transmission can occur, with the latter mediated by farm hosts. Intra-lineage transmission through the farm is shown as short dashed lines within the light gray bar
Interactions of the first type occur through changes in the biotic or abiotic environment of the river or ocean habitat due to host density and include a variety of mechanisms proposed by Ricker (1962) to explain line dominance in pink salmon, including direct suppressive interactions between lineages, fouling of the rearing environment by large runs, and competition for food in ocean habitat (Groot and Margolis 1991). Interactions of the second type occur due to parasite transmission, when the offspring of parasites associated with adults of one lineage infect juveniles of the other lineage as the two age classes of host temporarily share space during migration. These “infection windows” are shown as shaded regions of Fig. 1a between the river and ocean habitat. We assume that the density-dependent interactions of both types act to increase mortality.
Introduction of farmed hosts to migration routes between river and ocean habitats (Fig. 1b) can lead to infection of hosts early in life. Juveniles migrating out from the river are infected earlier in time and closer to the river in space by “spillover” infection from farms than when farms are not present (Fig. 1a). Farm infection status may, in turn, be influenced by “spillback” infection from parasites of wild adult hosts to farm salmon. In this case, the farm provides a route of transmission within a lineage that is not present without farms (Fig. 1a). This intra-lineage transmission mediated by the farm is shown in Fig. 1b. When adult hosts migrate from ocean to river, they bring parasites that influence farm infections. These adult hosts breed to produce juveniles that out-migrate and receive infections from farms. For example, in Fig. 1a adults of dash–dot lineage are migrating to the river at census time t. These adults breed, producing offspring that out-migrate and receive infections from farms just before census time t + 1.
We derive two models here, one for the case without farms (Fig. 1a) and one for the case with farms (Fig. 1b). We track numbers of wild adult (A) and juvenile (J) hosts, and average abundance of juvenile-associated parasites P w . We are concerned with the parasite population attached to hosts, which provide a convenient sampling unit of the parasite population (Hudson and Dobson 1995). Thus we track parasites in terms of average abundance per host. In our models we census the salmon and parasite populations just after summer sympatry of juveniles and adults. That is, after the period of transmission from adult-to-juvenile fish in coastal marine environments.
By “transmission” we mean infection of juveniles by copepodid-stage offspring of mature parasites on adult hosts. In a well-mixed coastal environment, the probability that any one larva both survives to become infective and attaches to a host is low. Furthermore, the number of juveniles at census is attenuated from the large numbers at initial out-migration. We use an approximation that assumes the number of juvenile hosts is low relative to the inverse probability of any one infective larva becoming a mature parasite, which enters our model as a transmission coefficient. The approximation states that the average load of juvenile-associated parasites P w following transmission increases with the number of mature parasites on returning adults at time of transmission. This approximation reflects the basic physics of lice transmission, that more mature lice in a region produce more infective copepodid larvae and increase the equilibrium level of infection (Frazer 2009). The local concentration of infective larvae produced by mature adults is termed infection “pressure” (Krkošek et al. 2005). A full derivation of our transmission approximation is given in Appendix 1.
Importantly, our models substitute temporal heterogeneity in transmission for the spatial dynamics of migratory hosts. This captures the main effect of space and migration on host–parasite dynamics without farms: determining the timing of adult–juvenile transmission. Thus, our transmission function is derived by assuming that infection occurs only within “infection windows” that are brief relative to the yearly census time and defined by periods of sympatry between wild juveniles and adults: farm-wild transmission requires sympatry with farm adults (Fig. 1b); wild–wild transmission requires sympatry with wild adults (Fig. 1a).
Host–parasite system with migratory allopatry
To model the farm-free case (Fig. 1a), we begin with the Ricker (1954) model, which for a species with a 2-year life cycle like pink salmon is \(A_{t+2} = A_te^{r-bA_t}\). The parameter r is intrinsic growth rate of the host and the term exp(− bA (t )) represents density-dependent mortality arising from competition for food among juvenile salmon or increased mortality of eggs at high spawner density. To this classic model, we introduce age structure to track both adult and juvenile fish. We also add two forms of general negative density-dependent interactions between lineages. The first, exp(− c 0 J (t )), represents reduced survival of juveniles due to lagged influences of prior-year populations on the nursery environment. Such an interaction could occur if detritus from large runs fouled river habitats (Groot and Margolis 1991). The second, exp(− c 1 A(t)), represents reduction in survival of juveniles to become adults due to lagged influence of prior-year adults on the marine environment. This type of interaction could be due to direct suppressive effects, e.g. cannibalism, or to competition for food at sea during summer sympatry (Groot and Margolis 1991). We also add a term for parasite impacts on juveniles, exp(− a w P w (t)), consistent with the parasite impact term used in empirical studies (Krkošek et al. 2007a). Finally, we add a model for average parasite transmission between wild adults and juveniles. This function is a combination of transmission, during the period of summer sympatry (the infection window of length Δ w ), and growth of the parasite population during the period of allopatry (the remainder of the year, of length 1 − Δ w ); see Appendix 1 for the derivation. This gives our full host–parasite model for pink salmon and lice without farms,
where s 0, s 1 and s 2 are survival probabilities, and f is the expected fecundity of salmon. Note that we assume inter-lineage negative density-dependent effects are less strong than the intra-lineage negative density dependence of the traditional Ricker model, i.e. c 1 < b. Table 1 summarizes our notation.
We introduce a scaling of Eq. 1 to obtain the non-dimensional equations,
Dynamical variables are N 0 = b s 1 J, N 1 = b A and P = a w P w . Host growth rate is \(e^r = s_0s_1s_2 f\). The non-dimensional parameter for parasite-mediated density dependence is
Host–parasite system with farms
The parasites originating from farms affect the juveniles prior to census, which follows the period of summer sympatry between wild adults and juveniles in coastal marine waters (Fig. 1b). Farm-origin infections occur during a period of sympatry between wild juveniles and farms of length Δ f . The resulting model has modified transmission (Eq. 4c) and adult-to-juvenile (Eq. 4a) maps,
With farm-origin infections the model differs relative to Eq. 1. At census, juveniles J are decreased, while their average parasite load P w is increased. The effects of farm-origin and wild-origin parasites on juvenile wild fish in our models are not equivalent, and accordingly these parasites are assigned separate virulences, a f and a w . In parameterizing this model, the virulences may differ not only in host–parasite biology, but also in the timing of census relative to parasite-induced juvenile mortality. While farm-origin parasites affect juveniles prior to census, wild-origin parasites affect juveniles after census. Thus, a f may exceed a w due to stronger effects of parasites on smaller juveniles. On the other hand, a f includes effects of parasites over a relatively short infection window Δ f , and so may be smaller than host–parasite biology would otherwise indicate.
The number of parasites per juvenile, P w , is the sum of contributions from parasites hosted by wild returning adults (first term) and by farm hosts (second term). For consistency with our method of tracking parasites on wild hosts, we describe farm infections as average lice per farm fish P f times the number of fish on the farm N. We assume throughout that the number of fish on the farm, N, is constant. With this assumption, controlling the number of parasites per fish on the farm is equivalent to controlling the total number of parasites per farm, i.e. the infection pressure. Table 2 summarizes notation for the system with farms (Eq. 4).
The number of parasites on the farm NP f depends on several factors. Farm infections are influenced by the wild-associated parasite population. Perfect infection control, i.e. P f = 0 is not obtainable, and management of infections on farms can proceed in two broad ways: control lice abundance to a constant level or to some function of the number of parasites from wild hosts. The simplest mathematical expression of the first case is that the number of parasites per fish on the farm is a constant each year P f (t + 1) = γ 1. For the second case, the simplest assumption is that farm status depends linearly on prior-year wild infections, P f (t + 1) = γ 2 λ(1 − Δ w )A(t) P w (t − 1), where the expression on the right hand side of the equation is the number of adult-associated parasites at time t. The index on variable P w , the average number of parasites on juveniles tracked in model (Eq. 1), is lagged 1 year relative to the index on variable A, the adults, to obtain the number of parasites on adults at time t. Combining these expressions, parasites on farm hosts are the sum of two terms, a contribution from constant management and a contribution dependent on wild-origin infection: P f (t + 1) = γ 1 + γ 2 λ(1 − Δ w )A(t) P w (t − 1).
We also introduce a scaling of Eq. 4 to obtain non-dimensional equations
where scaled dynamical variables are as in Eq. 2. Note that the ratio of virulences \(\frac{a_f}{a_w}\) appears in the non-dimensional model. This scaling introduces a non-dimensional parameter that represents farm-mediated transmission,
which incorporates the effect of prior-year wild infections on farms. The scaling Eq. 5 also introduces a non-dimensional parameter that represents constant infection pressure from farms,
Methods
We analysed the dynamical behaviour of systems without farms (Eq. 1) and with the effects of farm hosts (Eq. 4). Our focus was on line dominance relationships between host lineages, specifically how farm hosts can change these relationships. Because model (Eq. 1) includes both adult and juvenile hosts in each year, it represents both lineages. The adults, A(t), in model (Eq. 1) represent the odd-year lineage in odd years, and the even-year lineage in even years. The opposite holds for the juveniles J(t). Mathematically, line dominance corresponds to a two-cycle system (Eq. 1). In Eq. 1, transition from a fixed point to a two-cycle system occurs through a period-doubling bifurcation. Thus we use stability and bifurcation analysis, with a combination of analytical and numerical methods, to analyse changes to dominance induced by farm hosts.
In Eq. 1, density- and parasite-independent survivorship is partitioned among host-age classes according to terms s 0, s 1, and s 2. We show in Appendix 2 that this partitioning does not affect equilibrium dynamics, which are governed by a combined host growth parameter r, where r = log(f s 0 s 1 s 2). The empirical estimate of host reproduction r for pink salmon is r * ≈ 1.2 (Myers et al. 1999). Our interest is in the biological interpretation for pink salmon. Accordingly, we focus on behaviour for r < 2 because above 2, increases in r will drive a period-doubling cascade. When numerical analysis required fixing a value for r, we use the empirical estimate, which is consistent with the range of pink salmon population growth rates estimated for numerous stocks from Washington through Alaska (Dorner et al. 2008).
Without farms, the behaviour of the model (Eq. 1) depends on host population growth rate r, on negative density-dependent interactions between hosts, i.e c 0 and c 1, and on parasite-mediated interactions summarized by the non-dimensional parameter η defined in Eq. 3. For systems with no nursery competition (c 0 = 0), the farm-free system (Eq. 1) is amenable to standard analysis of qualitative behaviour from the theory of dynamical systems (Hale and Kocak 1991). Because of our assumption that inter-lineage density dependence is less strong than intra-lineage density dependence, we require c 1 < b. Full details are in Appendix 2. When c 0 > 0, transcendental equations define the equilibria so we use numerical tools.
With farms, the dynamics are governed by model (Eq. 5). The modified parasite dynamics (Eq. 5c) include parameters η f , representing farm-mediated transmission under proportional management defined in Eq. 6, and ϕ, representing farm input under constant management defined in Eq. 7. Relative to the case without farms (Eq. 2c), the parasite dynamics (Eq. 5c) include two additional terms. The second term, when η f > 0, modifies the dynamical structure of Eq. 2 because its effect depends on the values of dynamical variables. The third term, when ϕ > 0, is independent of dynamical variable values and is assumed constant at each time. We examined two cases: where parasites are managed to a constant abundance, i.e. η f = 0 but ϕ > 0, and where parasites depend on prior-year wild infections, i.e. ϕ = 0 but η f > 0. For the first case, an analytical solution for the equilibria is impossible, and in the second case it is difficult. Therefore for both, we used the numerical continuation package cl_matcontM (Dhooge et al. 2003) to compute stability diagrams for the location of the period-doubling bifurcation as a function of the farm parameters, η f or ϕ.
Numerical computation of a period-doubling bifurcation also gives a quantitative prediction of how dominance varies as a function of the parameters with which we conducted bifurcation analysis. Dividing the equilibrium abundance of the non-dominant line by that of the dominant line yields an inverse measure of dominance, the “equivalence ratio.” An equivalence ratio of unity means that both lineages have the same equilibrium abundance, which occurs at a fixed point of Eq. 1.
Results
For a migratory allopatric host with a 2-year lifespan and no farms, negative density-dependent inter-lineage interactions of sufficient strength can result in line dominance. These interactions include both parasite-mediated and environment-mediated negative density dependence, and a sufficiently strong combination of these is enough to produce line dominance. As shown below, introduction of farm hosts can either decrease or increase the line dominance, depending on the manner in which farm management responds to wild-origin infections. If farm management controls parasites to a constant abundance regardless of the intensity of wild infections, the presence of the farm increases line dominance. On the other hand, if farm control of infection is only proportional to the intensity of wild infections, then the farm’s presence decreases line dominance.
Host–parasite dynamics without farms
Without farms, the model (Eq. 1), has several distinct qualitative behaviours that depend on parameters governing host growth, r and on negative density-dependent interactions between hosts, i.e c 0 and c 1. Parasite-mediated interactions also influence system behaviour, and though Eq. 1 has many parameters governing parasites, these are summarized by the non-dimensional parameter η defined in Eq. 3. Negative density-dependent inter-lineage interactions, both general, c i , and parasite-mediated, η, have similar qualitative effects on dynamics. Stability diagrams for two pairings of parameters are in Fig. 2. The dashed lines in Fig. 2 separate regions labelled “stable,” where both age classes of the host has a constant abundance at every time step, from regions labelled “dominance,” where age-class abundance alternates between relatively abundant and less-abundant years. Two-year lifespans mean the hosts exist in lineages that breed independently, e.g. the odd- and even-year lineages in pink salmon, thus behaviour in the “dominance” region corresponds to constant abundance within a given lineage, but with abundance differing between lineages.
Behaviour of host–parasite system without farms in parameter space. In the “host-only” regions, the parasite population cannot persist. In the “stable” regions, the system (Eq. 2) has a stable 1-year periodic equilibrium. Along the dashed lines, this equilibrium bifurcates through period-doubling to a 2-year periodic equilibrium. Above the dotted line, which corresponds to a Neimark–Sacker bifurcation, cycles of period greater than two occur. The 2-year periodic behaviour in the “dominance” regions corresponds to line dominance, see Fig. 3. The panels show different parameter spaces: inter-lineage transmission η and host growth r (a) with changes due to various values of scaled inter-lineage negative density dependence (coefficient \(\tfrac{c_1}{b}\)) given in legend and c 0 = 0; and inter-lineage transmission η and scaled negative density dependence \(\tfrac{c_1}{b}\) (b) for r = r * = 1.2 and c 0 = 0. Note that within the “host-only” region, for r > 2, increasing r drives host dynamics on a period-doubling cascade consistent with the Ricker equation. The period-doubling and Neimark–Sacker bifurcations were identified and curves computed by numerical continuation using Cl_matcontM (Dhooge et al. 2003)
In the “stable” regions of parameter space shown in Fig. 2, dynamics of the system (Eq. 1) are a 1-year periodic equilibrium. In the “dominance” regions, dynamics are a 2-year periodic equilibrium. Transition between these regions in parameter space is through a period-doubling bifurcation. The bifurcation arises as negative density-dependent interactions between host lineages increase in strength. Dominance results from a sufficiently strong combination of general negative density-dependent interactions, c i , between host lineages and inter-lineage transmission, η. In our model, inter-lineage transmission acts as a form of parasite-mediated negative density dependence. Parasites have a negative effect on juvenile hosts that increases with the average parasite abundance per juvenile P w following transmission. Parasites on juveniles arise through inter-lineage transmission from parasites of adult hosts, and P w increase with the absolute abundance of parasites on adults. Because we track the average parasites per host, the absolute parasite population is larger when the abundance of adult hosts is greater. Thus, increased abundance of adult hosts in one lineage result in increased infections in juveniles of the other lineage, a negative density-dependent interaction between the lineages.
A sufficient combination of the two types of negative density dependence (general and parasite mediated) will induce line dominance. Figure 2a shows stable and dominance regions in parameters space of intra-lineage transmission and host growth. For moderate values of r, sufficiently strong intra-lineage transmission results in dominance. Increasing general negative density dependence, e.g. c 1 in legend, reduces the strength of transmission needed for dominance. In the “host-only” region there is no stable equilibrium with coexistence of the parasite and host at positive abundance. In the “cycles” region, equilibria with periods that exceed 2 years occur. Figure 2b shows the regions of qualitative dynamics in the parameter space of inter-lineage transmission (parameter η) and the negative density-dependent interactions that occur between lineages in the ocean habitat (parameter c 1), explicitly illustrating the trade-off along the dashed line. The regions of host-only dynamics, stable one-cycle dynamics and dominant lineage dynamics shift with changing c 1 but maintain their qualitative relationship. Numerical examination of behaviour for c 0 > 0 confirmed that the qualitative nature of the effect of c 0 is similar to that of c 1. See Appendix 2 for analytical details.
Figure 3a shows a numerically computed bifurcation diagram for adult hosts with inter-lineage transmission. The bifurcation branches in Fig. 3a predict the equilibrium proportion of dominance as a function of η for c i = 0. Dividing the equilibrium abundance of the non-dominant line by that of the dominant line yields the “equivalence ratio,” which varies with η. Thus, viewed with line dominance in mind, the bifurcation branches give the equilibrium dominance relationship of the lineages as a function of the bifurcation parameter η. Figure 3b shows the equivalence ratio computed for adult hosts. Movement from the “stable” region into “dominance” in η rapidly increases dominance, shown by the decreasing equivalence ratio plotted in Fig. 3b.
Line dominance arises through a period-doubling bifurcation. Bifurcation in system (Eq. 2) for adult hosts in η for r = 1.2, c 0 = 0, c 1 = 0 (a) shows single period doubling with increasing η, (η = 2.5 for this value of r), and period-two dynamics for a large range of η > 2.5. The period doubling occurs in the ηr plane for η = 2.5 along the black dashed line of Fig. 2a. Model-predicted equivalence ratio as a function of η (b), computed by dividing lower branch by upper branch. The ratio is 1.0 for η < 2.5; intermediate equivalence ratios occur only for a small range of η
Furthermore, the relationships between host density, parasite abundance and density dependence permit quantitative descriptions of how strong these interactions must be to induce line dominance in the non-dimensionalized version of Eq. 1. When dominance does occur in host–parasite systems governed by Eq. 1, the more abundant lineage experiences proportionally less mortality due to inter-lineage negative density dependence (whether mediated by parasites or not) than does the less-abundant lineage. See Appendix 3 for details.
Host–parasite dynamics with farms
The introduction of farm hosts, acting as disease reservoirs, causes changes in system dynamics from the model given in Eq. 2 to that given by Eq. 5. The qualitative nature of the change depends on the relationship of farm infections P f to wild hosts and their parasites, i.e. dynamical variables J, A and P w . Farm infections are influenced by prior-year infections of wild adults. Infection status the next year, however, is dependent on management of infections on farms that arise from parasites of wild salmon. Using Eq. 5, we examined two cases: where parasites on the farm are controlled to a constant abundance ϕ > 0, η f = 0, and where parasites abundance on the farm is linearly proportional to previous-year wild infections ϕ = 0, η f > 0. Through numerical bifurcation analysis we examined the changes induced by farm hosts in terms of shifts in the boundary between the stable and dominance regions, i.e. the onset of period-doubling, which without farms corresponds to the dashed line in Fig. 2a.
Figure 4 summarizes the effect of constant and proportional management of infection on the location of the onset of period-doubling and resulting line dominance relationships relative to the transmission parameter η. Figure 4a gives the numerically computed continuation of the period-doubling curve in the ϕη plane with constant farm input ϕ. For fixed η, farm input moves the system further into the period-doubling region, increasing line dominance. Numerically computed bifurcations and resulting line dominance profiles shown in Fig. 4b confirms the suggestion of Fig. 4a that constant input from farms increases dominance at equilibrium.
Constant (row 1) and proportional (row 2) management of infection of farms have opposite effects on dominance. Stability planes for system (Eq. 5) giving changes in the onset of period-doubling (dashed lines) in η-space for constant management (a), i.e. changing farm input ϕ and proportional management (c), i.e. changing farm-mediated transmission η f . Equivalence ratio as function of η computed for r = r * = 1.2, c 0 = 0 and c 1 = 1 and assuming a w = a f with constant management (b) for various values given in legend of constant input ϕ, and proportional management and d for various values given in legend of farm-mediated transmission η f . For constant management (a, b), the locations in parameter space where period-doubling in η causes line dominance for different ϕ are labelled (a) and (b). For proportional management (c, d), locations where period-doubling in η causes line dominance for different η f are labelled (c) and (d)
Under proportional management a farm acts as a transmission route within a lineage. This has an effect opposite of constant farm input. Figure 4c shows the numerically calculated continuation of the period-doubling point in η f η plane with farm-mediated transmission η f . For fixed η, increased farm-mediated transmission moves dynamics away from the period-doubling region, decreasing line dominance. By recomputing bifurcations in adult numbers for various values of η f we numerically computed the effect of farm-mediated transmission on the relationship between η and dominance, as shown in Fig. 4d for values of η f given in legend. This computation confirms the suggestion of Fig. 4c that a farm under proportional management decreases dominance at equilibrium.
Intuition suggests that the negative effect of increased parasite load on juvenile hosts means that increases in ϕ will decrease equilibrium host abundance. Structural stability of Eq. 5 permits analysis with ϕ as a bifurcation parameter. Numerical bifurcations in ϕ for values of r < 2 revealed that increased ϕ drives down equilibrium host abundance. Above a critical level, which depends on η, constant farm input results in host extirpation (equilibrium abundance of 0) for the deterministic model analysed.
Discussion
The effect of salmon aquaculture sites as reservoirs for sea lice have long been recognized (Tully and Whelan 1993; Costelloe et al. 1996). Empirical studies have demonstrated that declines in wild salmon populations are associated with aquaculture (Krkošek et al. 2007a; Ford and Myers 2008). Recently, Frazer (2009) introduced an equilibrium theory for effects of a farmed hosts on sympatric wild hosts via a directly-transmitted parasite, demonstrating that increased farm host density and infections of wild juveniles can combine to explain observed declines. Such infections of juveniles arise when farms act as reservoirs and break the allopatric barrier to parasite transmission that is formed by the migratory life history of pink salmon under natural conditions (Krkošek et al. 2007b). Though these infections are a consequence of migration, the analysis of Frazer (2009) did not include salmon population dynamics, so the inferred effect of reservoirs was limited to a decline in equilibrium abundance. Other analyses have coupled lice infections to models of population dynamics (Krkošek et al. 2007a, b, Krkošek 2010), but have not combined these with models for louse transmission. Here, we developed a host–parasite model that couples population dynamics of pink salmon with a simple transmission model incorporating temporal heterogeneity in transmission driven by migratory allopatry. We found that, in addition to declines in average population abundance, spillover and spillback with farms can alter patterns in population dynamics, either increasing or decreasing line dominance.
The direction of the change in line dominance depends on how farms respond to wild-origin infections. When infections on farms are independent of wild infections, and farms provide a constant infection pressure on wild hosts, this increases dominance; on the other hand, when infections on farms depend on wild-origin infection, farms provide an intra-lineage transmission route that decreases dominance. Under the assumption that farm stocking levels are constant, these situations correspond to two management scenarios. In the first, lice on farms are managed to a constant abundance. In the second, lice on farms are managed to an abundance proportional to the abundance of lice on prior-year wild hosts, i.e. the infection pressure on farms from wild-hosted lice.
The mechanism by which the first scenario (“constant” management) increases dominance is that the farm always hosts the same number of lice, which results in a constant infection pressure on wild fish. This constant input has a proportionally larger effect on the less-abundant line. This is a depensatory effect and is thus similar to a number of additional hypotheses proposed by Ricker (1962) that related dominance to other mechanisms that can have depensatory effects, including fishing and predation. Constant infection pressure results from managing for constant average abundance, i.e. γ 1 because of the assumption that the number of hosts on the farm, i.e. the stocking level N, is constant.
The second scenario (“proportional” management) decreases dominance because the abundant parasites of the dominant lineage have a negative effect on juvenile survival within that lineage. This result demonstrates the potential, when wild hosts display migratory allopatry, of introduced farm hosts to change the structure of density dependence governing wild host population dynamics. This farm-mediated intra-lineage transmission alters the “process order” of density dependence in the population. Turchin (2003) defines process order as the number of population densities at earlier times needed to adequately describe fluctuations in the focal population. Populations governed by different structures of density dependence generally display different patterns of population fluctuations, e.g. period and amplitude (Turchin 2003). Thus, in a more general context, changes to density-dependent interactions of the type demonstrated here might be expected to alter patterns of population fluctuations.
Under either management scenario (constant versus proportional response to wild-origin infection), equilibrium wild host abundance, averaged over both lineages, decreases. This result is consistent with empirical observations in wild salmon populations potentially affected by disease spillover from aquaculture (Gargan et al. 2003; Krkošek et al. 2007a; Ford and Myers 2008; Costello 2009). In the case of constant input, when dominance increases the abundance of the non-dominant lineage goes to zero while the dominant lineage increases slightly in abundance. In the second case, when dominance decreases both lineages decrease in abundance but the dominant lineage decreases more than the non-dominant lineage. Recently published data on farm infections in Pacific Canada indicates that, over the past 10 years, lice levels on farms in spring are proportional to prior year returns (Marty et al. 2010). This is our “proportional” management scenario. In this context, the work presented here provides a prediction: that line dominance in Canadian pink salmon exposed to farm-origin infections should have decreased. Testing whether this prediction is borne out by stock-recruitment data is subject to ongoing research.
Connections to epidemiological theory
The reservoir effects of farms studied here have parallels in epidemiological theory. Under the management scenario of constant input, farm-origin infection can be viewed as a deterministic, periodic forcing of the host–parasite system. Forcing affects behaviour of a variety of dynamical disease models (Hastings et al. 1993). Perhaps the most common epidemiological application of forced models is to express seasonality, which has broad importance across human and wildlife disease systems (Altizer et al. 2006). In the context of seasonally forced disease models, the shape of continuous time forcing has a strong influence on observed dynamics (Earn et al. 2000). Though our study examined only one type of constant forcing, based on management of parasites to a constant threshold, future studies might benefit from considering a variety of forcing functions based on different management scenarios.
On the other hand, the scenario of proportional management results in farm-mediated transmission. This situation has conceptual connections to epidemiology of multi-host parasites and indirect transmission. Farm hosts can be viewed as a new introduced species that increases the number of parasites in coastal waters. This accords with the theory of multi-species epidemics for pathogens transmitted by free-living infective stages, where host species diversity can amplify epidemic outbreaks (Dobson 2004). Because parasites on farm hosts are managed, however, farm hosts could also be viewed as a type of indirect or environmental transmission with the functional form of transmission depending on management actions. Different functions representing a variety of management response to infections could result in different dynamics. Rohani et al. (2009) showed that for a stochastic model of disease outbreaks in migratory hosts, neglecting the role of environmental transmission can underestimate the probability of outbreak. Though we did not include stochastic effects in the deterministic system studied here, transmission through farms plays a similar role, increasing the average intensity of infection in wild juveniles in the coastal region of the farm. In the case, we treat the regular migrations of wild hosts and the static location of the farm mean that the farm primarily mediates intra-lineage transmission.
Assumptions and implications
The analysis presented here rests on a great many assumptions that should be kept in mind when interpreting our results. Transmission poses a difficult modelling problem (McCallum et al. 2001). We assumed that transmission occurs through mass action between well-mixed infective parasites and wild juvenile hosts. We applied this assumption to infection both from wild adult hosts and from farm hosts. In British Columbia, farm-to-wild infections occur in fjords (Morton et al. 2004), while wild-to-wild infections occur during a period of summer sympatry in neritic waters (Beamish et al. 2007). Because these two types of transmission occur in different hydrodynamic environments, our approximate transmission function may not apply equally to both processes. The mass action assumption, however, is perhaps better justified in these marine environments than in many places where it has been applied. The difference between the transmission environments for farm-to-wild and wild-to-wild infections would be expected to result in lower transmission probability in the more dispersive neritic environment. This, however, does not address the potential for a qualitative difference in transmission between the fjord and the neritic zone. To address this possibility, one could build approximations based on more detailed models of transmission developed by Krkošek et al. (2005) for farm-to-wild transmission.
In addition, we focused on larvae in our transmission derivation. For sea lice, however, some evidence indicates that motile adult stages can play a role in transmission (Ritchie 1997; Krkošek et al. 2007b; Connors et al. 2008, 2011). In general, very little is known about motile transmission (Costello 2009). Despite this, our mass action transmission function could be adapted to describe motile transmission. The “infective parasites” attaching to juvenile hosts (Appendix 1) would then be motile adults, this would reduce the proportionality k between infective parasites and adults, but could increase the attachment probability β w . Because motile adults swim actively, unlike naupliar stages, the assumption that fish and infective parasites are well-mixed may be less justified for motile transmission. In addition, spatial scale for motile transmission may also differ from that of larval transmission. The differences in transmission between larval and motile transmission indicate that a single equation of the simple single mass action type used here may be inadequate to describe both processes. To consider multiple modes of transmission using mass action, an extended model using multiple transmission equations could be developed. Alternatively, a single equation that is spatially explicit might capture both types of transmission.
When farm hosts are present, our transmission function assumes that parasites from farms and the wild additively contribute to total parasites on juveniles. Contributions may be additive when parasite abundance is low, but when there are very many lice attaching to juveniles this likely breaks down. Thus, during high intensity infections observed in salmon farming regions (Morton and Williams 2003; Morton et al. 2004; Krkošek et al. 2006), the equations used here may overestimate the role of wild–wild transmission in host–parasite dynamics.
Additionally, our transmission function uses an approximation that is best when the number of juvenile hosts is small relative to the inverse probability of transmission. Thus, the approximation is better when the probability of transmission is lower. As discussed above, the probability of transmission is possibly higher in farm-to-wild transmission than in wild-to-wild transmission. Furthermore, farm-to-wild transmission occurs earlier in time and space (Krkošek et al. 2005), when populations of juvenile hosts are larger (Groot and Margolis 1991). These two facts mean that the transmission function is likely less valid for farm-to-wild transmission than for wild-to-wild transmission. This is an additional reason that future work should look to bridge between the simple transmission model used here and more detailed models for farm-to-wild transmission (Krkošek et al. 2005).
Another consequence of our transmission function is that more lice on a farm result in more lice on juvenile hosts, proportionally. This linearity is the reason that a constant farm input acts in a depensatory manner where the less-abundant line suffers higher average infections from the farm. The increase in line dominance seen when farm status is constant is due to this depensatory effect. Because this theoretical increase in line dominance is clearly sensitive to assumptions on transmission, further work is needed to better understand whether management of farms to constant infection pressures would be expected to increase line dominance.
One fundamental assumption in our model is that the populations of salmon and sea lice are closed. This violates biological reality, as during the high-seas phase of life, salmon populations may exchange sea lice with one another (Beamish et al. 2007). If this exchange equilibrates sea lice across salmon populations, this could decrease the strength of the lice-mediated interactions considered here.
Environmental stochasticity is thought to play an important role in pink salmon population dynamics (Myers et al. 1999). Here, we focused solely on deterministic results, but future studies should examine the role of reservoirs in host–parasite systems in the presence of stochasticity. When noise is considered, the transient behaviour of the system is likely to be more important than the asymptotic equilibria (Hastings 2004). The particular values of parameters pointed out here as resulting in dominance are based on asymptotic analysis of Eq. 1. When transient behaviour of Eq. 1 is considered, the region of parameter space in which transient two cycles, and thus line dominance, occurs may expand. Preliminary analysis and simulation of a related model (Krkošek et al. 2010) indicates that when noise is included and statistical two cycles are considered, dominance occurs over a large region of parameter space.
Significance and future directions
Our results suggest that when spillover and spillback occur with wild migratory hosts, the way in which managers of farms respond to wild-origin infections will determine the effect on wild host population dynamics. We were able to study interaction of wild host migration, farm hosts, and parasites by substituting temporal heterogeneity in transmission for an explicit spatial model. Temporal heterogeneity is common in epidemiological interactions and has been a focus of intensive study (Anderson and May 1992; Altizer et al. 2006). The importance of space and host movement have been studied extensively in human disease systems (see, e.g., Grenfell et al. 2001), and recognized in wildlife-farm interactions (Morgan et al. 2004). The model we formulate here combines these ideas, permitting us to study the effect of host movement through its connection to temporal changes in transmission processes. Though this type of space-time substitution may prove fruitful in other contexts, there are also reasons to develop explicit models of the spatial and continuous time processes at work in the salmon–sea lice system. The difference between constant farm status and farm-mediated transmission is essentially one of forcing a dynamical system versus altering its dynamical structure. Future efforts to understand how infection management in farms, and other reservoirs, can interact with spillover and spillback to alter wildlife disease dynamics could examine a number of different functions defining either management response to wild infection or changing farm status over the time infections occur. Such research, however, might benefit from modelling in continuous time. Further, as discussed above, the spatial dynamics of lice transmission may differ between farm–wild and wild–wild transmission, and between motile and larval transmission. Considering the full richness of dynamics involved in these processes may require a spatially explicit host–parasite model.
More broadly, we expect the processes of wild host migration, spillover, spillback and management of farms to result in changes to wild host population dynamics in the large variety of avian, aquatic and terrestrial systems where wild hosts display migratory behaviour and potentially interact with domesticated animals. Our model is specific to the system of sea lice and pink salmon, however, and the interaction of these processes should be explored in other system-specific models, as well as more generally, e.g. in the setting of theoretical epidemiological models.
References
Altizer S, Dobson AP, Hosseini P, Hudson P, Pascual M, Rohani P (2006) Seasonality and the dynamics of infectious diseases. Ecol Lett 9(4):467–484. doi:10.1111/j.1461-0248.2005.00879.x
Anderson R, May RM (1978) Regulation and stability of host–parasite population interactions: I. Regulatory processes. J Anim Ecol 47:219–247
Anderson R, May RM (1992) Infectious diseases of humans: dynamics and control. Oxford University Press, Oxford
Beamish R, Neville C, Sweeting R, Jones S (2007) A proposed life history strategy for the salmon louse, Lepeophtheirus salmonis in the subarctic Pacific. Aquaculture 264:428–440. doi:10.1016/j.aquaculture.2006.12.039
Bengis R, Kock R, Fischer J (2002) Infectious animal diseases: the wildlife/livestock interface. Rev Sci Tech-Off Int Epizoot 21(1):53–65
Cain JW (2007) Criterion for stable reentry in a ring of cardiac tissue. J Math Biol 55(3):433–448. doi:10.1007/s00285-007-0100-z
Cheville NF, McCullough DR, Paulson LR (1998) Brucellosis in the Greater Yellowstone Area. National Academy of Sciences, Washington
Connors BM, Krkošek M, Dill LM (2008) Sea lice escape predation on their host. Biol Lett 4(5):455–457. doi:10.1098/rsbl.2008.0276
Connors BM, Lagasse C, Dill LM (2011) What’s love got to do with it? Ontogenetic changes in drivers of dispersal in a marine ectoparasite (in press)
Corless RM, Gonnet GH, Hare DEG, Jeffrey DJ, Knuth DE (1996) On the Lambert W function. Adv Comput Math 5:329–359. doi:10.1007/BF02124750
Costello M (2006) Ecology of sea lice parasitic on farmed and wild fish. Trends Parasitol 22:475–483. doi:10.1016/j.pt.2006.08.006
Costello MJ (2009) How sea lice from salmon farms may cause wild salmonid declines in Europe and North America and be a threat to fishes elsewhere. Proc R Soc Lond B, Biol Sci 276(1672):3385–3394. doi:10.1098/rspb.2009.0771
Costelloe M, Costelloe J, Roche N (1996) Planktonic dispersion of larval salmon lice, Lepeophtheirus salmonis, associated with cultured salmon, Salmo salar, in western Ireland. J Mar Biol Assoc UK 76:141–149. do10.1017/S0025315400029064
Daszak P, Cunningham A, Hyatt A (2000) Emerging infectious diseases of wildlife—threats to biodiversity and human health. Science 287(5452):443–449. doi:10.1126/science.287.5452.443
Dhooge A, Govaerts W, Kuznetsov YA, Mestrom W, Riet AM (2003) Cl_matcont: a continuation toolbox in Matlab. In: SAC ’03: Proceedings of the 2003 ACM symposium on applied computing. ACM, New York, pp 161–166. doi:10.1145/952532.952567
Dobson AP (2004) Population dynamics of pathogens with multiple host species. Am Nat 164(5):S64–S78. doi:10.1086/424681
Dorner B, Peterman RM, Haeseker SL (2008) Historical trends in productivity of 120 Pacific pink, chum, and sockeye salmon stocks reconstructed by using a Kalman filter. Can J Fish Aquat Sci 65(9):1842–1866. doi:10.1139/F08-094
Earn DJD, Rohani P, Bolker BM, Grenfell BT (2000) A simple model for complex dynamical transitions in epidemics. Science 287(5453):667–670. doi:10.1126/science.287.5453.667
Ford JS, Myers RA (2008) A global assessment of salmon aquaculture impacts on wild salmonids. PLoS Biol 6(2):e33. doi:10.1371/journal.pbio.0060033
Frazer LN (2008) Sea-lice infection models for fishes. J Math Biol 57(4):595–611. doi:10.1007/s00285-008-0181-3
Frazer LN (2009) Sea-cage aquaculture, sea lice, and declines of wild fish. Conserv Biol 23(3):599–607. doi:10.1111/j.1523-1739.2008.01128.x
Gargan PO, Tully O, Poole WR (2003) The relationship between sea lice infestation, sea lice production and sea trout survival in Ireland, 1992–2001. In: Mills D (ed) Salmon at the edge. Blackwell, Oxford, pp 119–135
Gilbert M, Chaitaweesub P, Parakamawongsa T, Premashthira S, Tiensin T, Kalpravidh W, Wagner H, Slingenbergh J (2006) Free-grazing ducks and highly pathogenic avian influenza, Thailand. Emerg Infect Dis 12(2):227–234
Grenfell BT, Bjørnstad ON, Kappey J (2001) Travelling waves and spatial hierarchies in measles epidemics. Nature 414(6865):716–723. doi:10.1038/414716a
Groot C, Margolis L (1991) Pacific salmon life histories. UBC, Vancouver
Hale JK, Kocak H (1991) Dynamics and bifurcations. Texts in applied mathematics, vol 3. Springer, New York
Hastings A (2004) Transients: the key to long-term ecological understanding? Trends Ecol Evol 19(1):39–45. doi:10.1016/j.tree.2003.09.007
Hastings A, Hom CL, Ellner S, Turchin P, Godfray HCJ (1993) Chaos in ecology: is mother nature a strange attractor? Annu Rev Ecol Syst 24(1):1–33. doi:10.1146/annurev.es.24.110193.000245
Hudson PJ, Dobson AP (1995) Macroparasites: observed patterns in naturally fluctuating animal populations. In: Grenfell BT, Dobson AP (eds) Ecology of infectious diseases in natural populations. Publications of the Newton Institute, Cambridge University Press, Cambridge
Iooss G (1979) Bifurcation of maps and applications. North-Holland, Amsterdam
Johnson SC, Albright LJ (1991) Development, growth, and survival of Lepeophtheirus salmonis (Kroyer, 1837) (Copepoda: Caligidae) under laboratory conditions. J Mar Biol Assoc UK 71(2):425–436. doi:10.1017/S0025315400051687
Kilpatrick AM, Chmura AA, Gibbons DW, Fleischer RC, Marra PP, Daszak P (2006) Predicting the global spread of H5N1 avian influenza. Proc Natl Acad Sci USA 103:19368–19373. doi:10.1073/pnas.0609227103
Krkošek M (2010) Sea lice and salmon in Pacific Canada: ecology and policy. Front Ecol Environ 8(4):201–209. doi:10.1890/080097 http://www.esajournals.org/doi/pdf/10.1890/080097
Krkošek M, Lewis MA, Volpe JP (2005) Transmission dynamics of parasitic sea lice from farm to wild salmon. Proc R Soc Lond B, Biol Sci 272(1564):689–696. doi:10.1098/rspb.2004.3027
Krkošek M, Lewis MA, Volpe JP, Morton A (2006) Fish farms and sea lice infestations of wild juvenile salmon in the Broughton Archipelago—a rebuttal to Brooks (2005). Rev Fish Sci 14(1–2):1–11. doi:10.1080/10641260500433531
Krkošek M, Ford JS, Morton A, Lele S, Myers RA, Lewis MA (2007a) Declining wild salmon populations in relation to parasites from farm salmon. Science 318(5857):1772–1775. doi:10.1126/science.1148744
Krkošek M, Gottesfeld A, Proctor B, Rolston D, Carr-Harris C, Lewis MA (2007b) Effects of host migration, diversity and aquaculture on sea lice threats to Pacific salmon populations. Proc R Soc Lond B, Biol Sci 274(1629):3141–3149. doi:10.1098/rspb.2007.1122
Krkošek M, Hilborn R, Peterman R, Quinn TP (2010) Cycles, stochasticity, and density dependence in pink salmon population dynamics. Proc R Soc Lond B, Biol Sci. doi:10.1098/rspb.2010.2335
Kuznetsov YA (2004) Elements of applied bifurcation theory. Springer, New York
May RM, Oster G (1976) Bifurcations and dynamic complexity in simple ecological models. Am Nat 110:553. doi:10.1086/283092
Marty GD, Saksida SM, Quinn TJ (2010) Relationship of farm salmon, sea lice, and wild salmon populations. Proc Natl Acad Sci USA. doi:10.1073/pnas.1009573108
McCallum HI, Barlow N, Hone J (2001) How should pathogen transmission be modelled? Trends Evol Ecol 16(6):295–300. doi:10.1016/S0169-5347(01)02144-9
Morgan E, Medley G, Torgerson P, Shaikenov B, Milner-Gulland E (2007) Parasite transmission in a migratory multiple host system. Ecol Model 200:511–520. doi:10.1016/j.ecolmodel.2006.09.002
Morgan ER, Milner-Gulland EJ, Torgerson PR, Medley GF (2004) Ruminating on complexity: macroparasites of wildlife and livestock. Trends Evol Ecol 19(4):181–188. doi:10.1016/j.tree.2004.01.011
Morgan ER, Shaikenov B, Torgerson PR, Medley GF, Milner-Gulland EJ (2005) Helminths of saiga antelope in Kazakhstan: implications for conservation and livestock production. J Wildl Dis 41(1):149–162
Morton A, Williams R (2003) First report of a sea louse, Lepeophtheirus salmonis, infestation on juvenile Pink Salmon, Oncorhynchus gorbuscha, in nearshore habitat. Can Field-Nat 117(4):634–641
Morton A, Routledge R, Peet C, Ladwig A (2004) Sea lice (Lepeophtheirus salmonis) infection rates on juvenile pink (Oncorhynchus gorbuscha) and chum (Oncorhynchus keta) salmon in the nearshore marine environment of British Columbia, Canada. Can J Fish Aquat Sci 61(2):147–157. doi:10.1139/f04-016
Muzaffar SB, Ydenberg RC, Jones IL (2006) Avian influenza: an ecological and evolutionary perspective for waterbird scientists. Waterbirds 29(3):243–257. doi:10.1675/1524-4695(2006)29[243:AIAEAE]2.0.CO;2
Myers RA, Bowen KG, Barrowman NJ (1999) Maximum reproductive rate of fish at low population sizes. Can J Fish Aquat Sci 56(12):2404–2419. doi:10.1139/cjfas-56-12-2404
Revie C, Robbins C, Gettinby G, Kelly L (2005) A mathematical model of the growth of sea lice, Lepeophtheirus salmonis, populations on farmed Atlantic salmon, Salmo salar L., in Scotland and its use in the assessment of treatment strategies. J Fish Dis 28:603—613. doi:10.1111/j.1365-2761.2005.00665.x
Ricker WE (1954) Stock and recruitment. J Fish Res Board Can 11:559–663
Ricker WE (1962) Regulation of the abundance of pink salmon populations. In: Wilimovsky NJ (ed) Symposium on pink salmon. H.R. MacMillan lectures in fisheries. Institute of Fisheries, University of British Columbia, Vancouver
Ritchie G (1997) The host transfer ability of Lepeophtheirus salmonis (Copepoda: Caligidae) from farmed Atlantic salmon, Salmo salar L. J Fish Dis 20(2):153–157. doi:10.1046/j.1365-2761.1997.00285.x
Rohani P, Breban R, Stallknecht D, Drake J (2009) Environmental transmission of low pathogenicity avian influenza viruses and its implications for pathogen invasion. Proc Natl Acad Sci USA 106(25):10365–10369. doi:10.1073/pnas.0809026106
Stien A, Bjorn P, Heuch P, Elston D (2005) Population dynamics of salmon lice Lepeophtheirus salmonis on Atlantic salmon and sea trout. Mar Ecol Prog Ser 290:263–275. doi:10.3354/meps290263
Tully O, Whelan KF (1993) Production of nauplii of Lepeophtheirus salmonis (Krøyer) (Copepoda, Caligidae) from farmed and wild salmon and its relation to the infestation of wild sea-trout (Salmo trutta L) off the westcoast of Ireland in 1991. Fish Res 17:187–200. doi:10.1016/0165-7836(93)90018-3
Turchin P (2003) Complex population dynamics: a theoretical/emprical synthesis. Princeton University Press, Princeton
Acknowledgements
JA was supported by a Pacific Institute of Mathematical Sciences IGTC fellowship. MK was supported by a NSERC Postdoctoral Fellowship. MAL gratefully acknowledges support from an NSERC Discovery Grant and a Canada Research Chair. The authors are grateful to N Frazer and an anonymous reviewer for detailed comments that improved the manuscript. Comments from M Auger-Methe, D Coltman, D Lyons, T Hillen, M Pineda-Krch, C Strasser and M Wonham improved earlier drafts.
Author information
Authors and Affiliations
Corresponding author
Appendices
Open Access This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Appendix 1
Derivation of the parasite map
In this appendix, we suppress the w subscripts. The map governing average parasite per juvenile dynamics, P(t + 1) = βΔkλ(1 − Δ)P(t) A(t + 1), represents two processes, growth and transmission. For sea lice, problems of transmission (Krkošek et al. 2005; Frazer 2008) and growth (Stien et al. 2005; Revie et al. 2005; Krkošek 2010; Frazer 2009) have been studied in detail; however, the transmission models are spatially explicit descriptions of dynamics occurring in fjordic habitats over small time scales, and the growth models consider details of parasite age structure. We neglect the details of these formulations in favour of generality, assuming only that transmission results from low-probability infection events occurring in a well-mixed environment. Here, we derive the map used above to approximate a mass action process in a well-mixed environment that is valid when transmission is based on low-probability attachment events. Additionally, we assume that parasites grow without density dependence and have no age structure.
Each year includes a short infection window Δ, the period of wild adult and juvenile summer sympatry. During the remainder of the year, the maturation period, (1 − Δ), juveniles J(t) become adults A(t + 1) and parasite population growth occurs. The total number of adult-associated parasites at the end of the maturation period, which we denote \({\mathcal {P}}_{\rm adult}\) using a calligraphic “P” to differentiate from the variables for average parasite abundance used elsewhere, is reduced by host death due to parasitism and other factors, and increased by parasite reproduction and growth. Assuming the parasites are uniformly distributed on hosts, decline in host population from juvenile to adults due to parasites (\(1 - e^{-P_w}\)) affects the parasite population proportionally. Parasite population increase is expressed as a geometric growth in the average parasites per host at rate λ over the time (1 − Δ). Then, the number of adult-associated parasites at the end of maturation and the onset of transmission is given by
We consider transmission during the infection window Δ in continuous time τ. Specifically, we consider the process of infective parasites, ψ, attaching to juvenile fish, F, during an infection window of length Δ. Because Δ is short, we treat number of juveniles F as constant and ignore production or immigration of new infective parasites ψ, of which we assume there are an initial quantity proportional to the number of adult-associated parasites at the beginning of transmission,
which relates back to model (Eq. 1) through the definition of \({\cal P}_{\rm adult}\) in Eq. 8. We further assume that infective parasites ψ become attached parasites \({\cal P}\) independently from one another at a constant rate β. Finally, for consistency with Eq. 1, where the units of P are motile parasites per fish, we track \(P = {\cal P}/F\) the average attached parasites per fish. This gives the following equations for τ ∈ (0, Δ),
The equation for the change in parasites per fish, \(\dot P\), comes from dividing the equation for total attached parasites \(\dot {\cal P}\) by F. Note that attachment rate β implicitly includes mortality of infective parasites. This is similar to equations underlying the macroparasite model of Anderson and May (1978), but here considered only over a short time scale.
With a constant number of juveniles F, we have \(\psi(\tau) = \psi_{0}e^{-\beta F \tau}\) and \(P(\tau) = \beta \psi_{0}\int_{0}^{\tau}e^{-\beta F s}{\rm d} s\) on τ ∈ (0, Δ). This expresses average parasites per fish at the end of the infection window as a function of juveniles, initial infective parasites, the transmission rate, and the length of the window: \(P(\Delta) = \frac{\psi_{0}}{F}[1-e^{-\beta \Delta F}]\). If βΔF ≪ 1 a first-order Taylor approximation yields P (Δ) ≈ βΔψ 0. For \(F < \frac{1}{\beta\Delta}\), the error in this approximation is bounded by \(\frac{\psi_0 \beta \Delta}{e}\) (where e is Euler’s constant). Using Eqs. 8 and 9 to relate this approximation back to the variables in Eq. 1,
we also note that the relevant quantity of juveniles is J(t + 1). We use this equation under the assumption that the number of juveniles falls below a threshold \(J(t+1) < \frac{1}{\beta \Delta}\), which is an inverse measure of the strength of inter-lineage transmission. When inter-lineage transmission is very weak, β is very low and \(\frac{1}{\beta \Delta}\) is very large.
Appendix 2
Analysis of farm-free system
Using both analytical techniques from dynamical systems and numerical bifurcation analysis we find regions where line dominance occurs in the two-dimensional space of parameters governing (1) negative density-dependent interactions between host lineages and (2) host productivity. Line dominance corresponds to mathematical two cycles and arises from stable equilibria through period-doubling so we focus on defining boundaries of the region where period-doubling occurs in parameter space. In the results of the main text, we report how these boundaries shift with the introduction of farm hosts.
Recall that we treat the low-juvenile case, where \(N_0 \le \frac{1}{\beta_w\Delta_f}\). We introduce a scaling of Eq. 1 to obtain the non-dimensional equations,
where non-dimensional parameters \(\tilde c_0 = \frac{c_0}{s_1 b}\), \(\tilde c_1 = \frac{c_1}{b}\) relate to inter-cohort density dependence. Dynamical variables are N 0 = b s 1 J, N 1 = b A, and P = a w P w . Host growth rate is \(e^r = s_0s_1s_2 f\). The non-dimensional parameter for parasite-mediated density dependence is \(\eta = \frac{\beta_w \Delta_f k\lambda(1-\Delta_f)}{b}\). For the remainder of the appendix we suppress tildes on \(\tilde c_i\). The model (Eq. 12) exhibits positive invariance to \(\mathbb R^3_+\). To see this, define N ( t) as \(\left(N_0 (t), N_1(t), P(t)\right)\) then take N( t 0 ) > 0 as initial data at time t 0. Applying Eq. 12 once, N ( t 0 + 1) > 0 and repeated application of Eq. 12 results in N( t) > 0 for all t > t 0.
We assume that parameters r and η are positive thereby restricting attention to cases where wild adult–juvenile transmission occurs. Furthermore, we focus attention on changes in parameters governing negative density-dependent inter-lineage interactions that result in two cycles in Eq. 12. Mathematically, these are period-doubling bifurcations of stable equilibria.
Standard linearized stability analysis requires solving Eq. 12 for equilibria. The analytical tractability of Eq. 12 depends on the values of the parameters describing general negative density-dependent interactions c i . We assume c i are non-negative and treat several cases. In two of these, one parameter is zero and at least some analytical treatment is possible: (1) when c 0 = 0 but c 1 > 0 and maturation range inter-lineage interactions are possible, and (2) when c 0 > 0 but c 1 = 0. In case (3) where both maturation range and nursery range inter-lineage interactions are possible, i.e. c i > 0, but the fixed points of Eq. 12 are not expressible in terms of elementary functions. We do not consider this case further. Biologically, this means that we treat cases where negative density-dependent interactions occur between lineages either in ocean habitat (c 1) or in breeding habitat (c 0), but not in both.
Equilibria
Bifurcations of equilibria from fixed points to two cycles through period-doubling occur from both parasite-free N PFE and coexistence N * equilibria. The cases treated here differ in their potential for period-doubling bifurcations from these two types of equilibria. For cases (1) and (2), parasite-free equilibria are given in Table 3. Only for case (1) can the coexistence equilibria be obtained analytically in terms of elementary functions; given in Table 3.
In case (2), when c 0 > 0 and c 1 = 0, the coexistence equilibria of Eq. 12 are defined by transcendental equations. Specifically, let \(\mathbf N^{(2)}_{*} := (N^*_0, N^*_1, P^*)\) denote the equilibrium in this case. Dividing Eq. 12c through by P *, we see \(1 = \eta N^*_0 e^{-P^*}\). Substituting this relation into Eq. 12b,
By substituting into Eq. 12a, we see that
a transcendental equation for \(N^*_0\). This equation does have a unique solution, which expressible in terms of the Lambert W function (see, e.g., Corless et al. 1996), and is given in Table 3.
Stability
Standard linearized stability also requires linearizing the system (Eq. 12). The linearization is expressed through the Jacobian matrix of the system:
We use standard local stability analysis of dynamical systems. For discrete-time systems, linear stability requires that each eigenvalue of the Jacobian matrix (Eq. 13) evaluated at an equilibrium lies within the unit circle in the complex plane. If the linearized system at a particular equilibria satisfies this requirement, then it is stable. For analysis of the parasite-free equilibrium, N PFE we are able to analytically compute the eigenvalues of Eq. 13 evaluated at the equilibrium and thus verify stability. For the coexistence equilibrium, N * , we use Jury’s criteria, which provide necessary and sufficient conditions on the characteristic polynomial of the Jacobian for stability. We do not focus on the stability of equilibria per se, but instead on the location in parameter space where stability is lost, through bifurcation. Thus, results of our stability analysis are described below in our bifurcation analysis.
Bifurcations
Throughout we focus on behaviour for moderate values of host reproduction, i.e. r < 2, that correspond to the situation of biological interest. This eliminates possible period-doubling bifucations due to the host reproduction parameter r. Such bifurcations occur in the classical Ricker model, as part of a period doubling cascade to chaos as outlined in May and Oster (1976). Because our concern is line dominance, we focus on period-doubling bifurcations that occur with changes in parameters governing negative density-dependent inter-lineage interactions, including general interactions c i and parasite-mediated interactions governed by the inter-lineage transmission term η.
Period-doubling (PD) bifurcations of maps must satisfy two criteria (Iooss 1979, p. 12):
Theorem 1
Consider the map \((\mu, X_{i}) \!\mapsto\! f_\mu (X_i): \mathbb R^4 \to\) \( \mathbb R^3\) where \(X_{i} \in \mathbb R^3\) are dynamical variables and \(\mu \in \mathbb R\) is a parameter. If f μ is of class C k for k ≥ 2 near a fixed point X * , then a period doubling bifurcation exists at μ = μ * if the following conditions are satisfied:
-
(PD1)
Eigenvalue location The Jacobian \(D f_\mu (X^*)\) has an eigenvalue λ 0(μ) with \(\lambda_0(\mu^*) = -1\) and \(|\lambda_i(\mu^*)|<1\) for i = 1,2; and
-
(PD2)
Transversal \(\frac{d |\lambda(\mu^*)|}{d\mu} < 0\).
Specifically, there exists a unique one-sided bifurcated branch of fixed points of order 2, (μ(s), X j (s), j = 1, 2) for f μ such that μ(X *) = X * , μ( − s) = μ(s), X 1( − s) = X 2(s),\(\frac{d_{X_1}}{ds}(0) = 1\),\(X_j(0) = X^*\),\(f_\mu (X_j) = X_{j^{\prime;}}, j \ne j^{\prime}\). The functions μ and X j are C k − 1.
Bifurcation from parasite-free equilibrium
For the parasite-free equilibria N PFE , we characterized period-doubling bifurcations for both case (1) and case (2).
In case (1), c 0 = 0 the Jacobian (Eq. 13) evaluated at N PFE from Table 3 is given by
The characteristic equation of Eq. 14 is
The polynomial on the right hand side of Eq. 15 can be factored,
To find potential curves in parameter space where period-doubling occurs, we set one root of the characteristic equation (Eq. 15) to negative unity. The resulting curve is c 1 = 1. Along this curve, one eigenvalue of Eq. 14, i.e. root of Eq. 15, is negative unity. The eigenvalue of Eq. 14
evaluates to negative unity when c 1 = 1. The other roots of Eq. 15 have absolute value less than unity when conditions on η and r are satisfied: the root \(\frac{\eta r}{1+c_0}\), has absolute value less than unity when η is sufficiently small, i.e. \(\eta < \frac{2}{r} = \frac{1+c_1}{r}\); the other root is the complex conjugate of Eq. 16, and has absolute value less than unity for values of r considered here, i.e. r < 2. Thus the eigenvalue location (PD1) criterion is satisfied for r < 2 and sufficiently small values of η. For this eigenvalue,
thus satisfying the transversal (PD2) criterion for values of r considered here, i.e. r < 2.
In case (2), c 1 = 0, the Jacobian (Eq. 13) evaluated at N PFE from Table 3 is given by
The characteristic equation of Eq. 17 is
The polynomial on the right hand side of Eq. 17 can be factored,
To find potential curves in parameter space where period-doubling occurs, we set one root of the characteristic equation (Eq. 18) to negative unity. The resulting curve is c 0 = 1. Along this curve, one eigenvalue of Eq. 17, i.e. root of Eq. 18, is negative unity. The eigenvalue of Eq. 17
evaluates to negative unity when c 0 = 1. The other roots of Eq. 18 have absolute value less than unity when conditions on η and r are satisfied: the root \(\frac{\eta r}{1+c_0}\), has absolute value less than unity when η is sufficiently small, i.e. \(\eta < \frac{2}{r} = \frac{1+c_0}{r}\); the other root is the complex conjugate of Eq. 19, and has absolute value less than unity for values of r considered here, i.e. r < 2. Thus the eigenvalue location (PD1) criterion is satisfied for r < 2 and sufficiently small values of η.
For this eigenvalue,
thus satisfying the transversal (PD2) criterion for values of r considered here, i.e. r < 2.
Bifurcation from coexistence equilibrium
For the coexistence equilibrium, N * , in case (1), the Jacobian (Eq. 13) evaluated at N * from Table 3 is given by
The characteristic equation of Eq. 20 is
To find potential curves in parameter space where period-doubling occurs, we set one root of the characteristic polynomial (Eq. 21) to negative unity. The resulting curve is \(r = \frac{3 - c_1}{\eta}\). Along this curve, one eigenvalue of Eq. 20 is negative unity and thus part of the eigenvalue location (PD1) criterion is satisfied. The roots of Eq. 21 are obtainable through the formula for the roots of a cubic. The formulae that result from these roots, however, are very long and would be tedious to treat analytically. We use Jury’s criteria, which provide necessary and sufficient conditions on the characteristic polynomial of the Jacobian for stability, to verify that the remaining eigenvalues fall within the unit circle. We state Jury’s stability criteria from (Cain 2007):
Theorem 2
(Jury stability test) All roots of the polynomial
lie in the open disc in the complex plane if and only if
-
(J1)
a m q(1) > 0,
-
(J2)
\((-1)^m a_m q(-1) > 0\) , and
-
(J3.j)
|r j | < 1 for j = 1, 2, ...m, where r j are given by the following iterative procedure. First, set b j = a m − j for j = 0, 1, ...m and define r m = b m /a m . Then, define \(a^{\rm new}_{j-1} = a_j - {\rm r}_m b_j\) for j = 1, 2, ...m. This gives the coefficients a m − 1, a m − 2 ...a 0 for the next iteration.
The characteristic polynomial of Eq. 20 is given by the left-hand side of the characteristic equation (Eq. 21). To apply Theorem 2 to the linearization (Eq. 20), we identify coefficients of the polynomial from Eq. 21 with coefficients a j of Eq. 22:
The full set of Jury’s criteria from Theorem 2 for N * in case (1) are given in Table 4. Equality in condition J2 of Table 4 corresponds to the curve \(r = \frac{3-c_1}{\eta}\). Condition J1 is satisfied along this curve for c 1 < 1, and condition J3.1 is satisfied for \(\eta > \frac{1}{2}\). Thus, along the curve \(r = \frac{3-c_1}{\eta}\), for r < 2, \(\eta > \frac{1}{2}\), and c 1 < 1, when criteria J3.2 and J3.2 are also met, the full eigenvalue location criterion (PD1) is satisfied.
Because we did not explicitly compute the eigenvalues of Eq. 21, we could not verify the transversal condition analytically. Using the numerical continuation tool Cl_matcontM (Dhooge et al. 2003), however, we verified that the system undergoes a period-doubling bifurcation along the dashed line of Fig. 2a. This tool, like many software packages for numerical analysis of bifurcations, solves equations that define a bifurcation type, e.g. period-doubling, and computes corresponding normal forms to identify the bifurcation (Dhooge et al. 2003; Kuznetsov 2004).
Thus, equality in the conditions of Table 5 defines boundaries between regions in which the coexistence and parasite-free equilibria are stable and those in which two cycles occur. For c i < 1 period-doubling bifurcations from a stable coexistence equilibrium are possible. The dashed lines in Fig. 2 represent curves where the eigenvalue location (PD1) criterion is satisfied for the coexistence equilibrium N * . Numerical computations using Cl_matcontM (Dhooge et al. 2003) confirm these curves represent the location of period-doubling bifurcations with increasing η. In this case, the dynamics undergo a qualitative transition from stable endemic equilibrium to dominance through period doubling with increase in either η or c 1.
The ηr stability plane, i.e. Fig. 2a in the main text, shows curves based on the applying Jury’s criteria to N * for case (1), i.e. Table 4, and results from numerical continuation. The structure shown in this figure indicate that the governing of dynamics by r is also typical for η > 0. For fixed r, e.g. r = r * = 1.2 the empirical estimate for pink salmon (Myers et al. 1999), as η becomes very large, a bifurcation across the dotted line of Fig. 2a to higher-order cycles is possible. This line corresponds to Neimark–Sacker bifurcation, i.e. a Hopf bifurcation for maps (Hale and Kocak 1991). Bifurcation in η is shown in Fig. 3a. The character of the bifurcation in η is a single period doubling. In contrast to the “cascade to chaos” familiar from the Ricker model (May and Oster 1976), the period-two regime is present for a large range, η ≈ 2.5 to η ≥ 100 (not shown).
Appendix 3
Differential mortality between lines when dominance occurs
If dominance occurs in Eq. 1, the less-abundant lineage experiences 40% mortality (or greater) due to negative density-dependent inter-lineage interactions, while the dominant lineage experiences less mortality. Figure 5a shows the equilibrium mortality of juvenile hosts due to general negative density dependence and parasitism at the edge of the dominance region, i.e. dashed lines in Fig. 2. The degree of overall mortality due to both factors decreases slightly as the general negative density dependent , c 1/b, interaction strength is increased. The figure was computed for a system with where negative density-dependent effects occur between lineages only based on adult abundance (c 1 > 0, c 0 = 0). In the “dominance” region of Fig. 2a, mortality for the more-abundant lineage falls below the curves given, while mortality for the less-abundant lineage is above the curve.
Bounds on mortality of “dominant” and “non-dominant” lineage juveniles at equilibrium of system (Eq. 2) for a parasite-mediated and general negative density dependence between lineages, and b parasite-mediated interactions only. The curves are computed for various values of r, given in legend, and c 0 = 0 at the boundary of the dominance region, i.e. at onset of period-doubling induced by parameter c 1. For a given value of r, mortality of the dominant lineage has a value below the curve while mortality of the non-dominant lineage has a value above the curve
As the strength of general negative density-dependent interactions is increased, the amount of parasite-mediated negative density-dependent mortality needed to maintain dominance decreases. Figure 5b shows this effect, plotting the mortality due to parasite-mediated effects alone that is needed to maintain line dominance plotted against the strength of general negative density-dependent inter-lineage interactions c 1/b.
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Ashander, J., Krkošek, M. & Lewis, M.A. Aquaculture-induced changes to dynamics of a migratory host and specialist parasite: a case study of pink salmon and sea lice. Theor Ecol 5, 231–252 (2012). https://doi.org/10.1007/s12080-011-0122-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12080-011-0122-4