Population persistence in the face of advection

Abstract

Many populations live in ‘advective’ media, such as rivers, where flow is biased in one direction. In these environments, populations face the possibility of extinction by being washed out of the system, even if the net reproductive rate (R) is greater than one. We propose a formal condition for population persistence in advective systems: a population can persist at any location in a homogeneous habitat if and only if it can invade upstream. This leads to a remarkably simple recipe for calculating the minimal value for the net reproductive rate for population persistence. We apply this criterion to discrete-time models of a semelparous population where dispersal is characterized by a mechanistically derived kernel. We demonstrate that persistence depends strongly on the form of the kernel’s ‘tail’, a result consistent with previous literature on the speed of spread of invasions. We apply our theory to models of stream invertebrates with a biphasic life cycle, and relate our results to the ‘colonization cycle’ hypothesis where bias in downstream drift is offset by upstream bias in adult dispersal. In the absence of bias in adult dispersal, variability in the duration of the larval stage and in oviposition sites have a large effect of the persistence condition. The minimization calculations required in our approach are very straightforward, indicating the feasibility of future applications to life history theory.

Introduction

Individuals in a wide variety of environments are faced with unidirectional drift (advection) that threatens their populations with extinction by being washed out of the system. Examples include the chemostat (Smith and Waltman 1995), gut-dwelling bacteria (Ballyk and Smith 1999), phytoplankton (Huisman et al. 2002), benthic marine species along coastlines with dominant long-shore currents (Byers and Pringle 2006), and even terrestrial species under the influence of climate change (Potapov and Lewis 2004). Arguably, the most famous example, however, are invertebrates living in streams and rivers where they are subject to downstream drift due to water movement. The question of how their populations can persist in the same location over large temporal scales has first been raised and studied by Müller (1954) and is now known as the ‘drift paradox’ (Hershey et al. 1993). Ecologists have since hypothesized several mechanisms that could lead to population persistence; and many field studies aim to quantify dispersal of invertebrates in streams.

Müller (1954) proposed the ‘colonization cycle’ hypothesis, by which stream insects at the adult stage preferentially fly upstream for oviposition and thereby replenish the larval population in the next generation that then drifts downstream. Downstream drift of larvae (on average) is well documented in many species; it ranges from several meters to kilometers, depending on stream and species (e.g., Elliott 2003; Hershey et al. 1993; Macneale et al. 2005; Müller 1954, 1982; Turner and Williams 2000; Waters 1972; Williams and Hynes 1976). The question of whether adult insects show a bias for upstream movement is much less clear. Several authors found such a bias (e.g., Hershey et al. 1993; Müller 1982) whereas others did not (e.g., Williams and Williams 1993) and yet some authors found upstream bias depended on species (Bird and Hynes 1981) or gender (Flecker and Allan 1988), see Waters (1972) and Macneale et al. (2004) for a literature overview. Individual-based simulations demonstrated that an upstream bias in adult flight is not necessary for species persistence (Anholt 1995; Kopp et al. 2001).

Whether or not upstream flight of adults is biased, it is clear that Müller’s hypothesis applies only to species that do have winged adult stages. Waters (1961) with his ‘production hypothesis’ suggested that the probability of an individual to enter the drift is density dependent: only individuals produced in excess of the (benthic) carrying capacity enter the drift and may be carried downstream. Experimental support for this hypothesis comes from studies finding a positive relationship between population densities in the drift and several indices of productivity (e.g., Waters 1961; Müller 1970), or from removal studies (Dimond 1967). Such a relationship, however, is not uniform across species (Pearson 1970). Bishop and Hynes (1969) found that hydrological effects dominate production effects in determining drift density. We are not aware of individual-based simulations for the production hypothesis, but some of the analytic results by Pachepsky et al. (2005) and Lutscher et al. (2005) can be interpreted to support this hypothesis, as we explain below.

While much of the experimental literature is focused on whether there is an upstream bias for adult movement and whether there is density dependence, simulation-based modeling explored the question of whether either or both are necessary or sufficient to explain the drift paradox. Anholt (1995) found that an upstream bias is neither necessary nor sufficient, but that density dependence together with some upstream bias would resolve the paradox. The interpretation of his results in the present context is complicated by two facts. Anholt considered not only the question of how a population manages to prevent extinction but also of what limits a population from growing without bound. It is the second aspect that requires density-dependent population regulation (which is different from the density-dependent drift rate as postulated in the production hypothesis). Anholt’s way of implementing density-dependent production, however, can lead to confusion in that strong density dependence and/or high carrying capacity in his model imply high per capita growth rates at low density. In an extreme case, a single individual can, in one generation, produce as many surviving offspring as a quarter to one half of the carrying capacity, see the criticism in Speirs and Gurney (2001). Re-interpreting the same individual-based model as Anholt’s (1995), Humphries and Ruxton (2002) claim that there might not even be a drift paradox if considered at the correct spatial and temporal scales. Their results, however, are based on increasing the carrying capacity in Anholt’s model and hence are subject to the same criticism. Kopp et al. (2001) use a modified version of Anholt’s model that avoids the original difficulties, and they show that upstream bias is not necessary for population persistence, unless the maximal per capita growth rate is small.

A fundamentally different approach to the drift paradox originated from the work of Speirs and Gurney (2001). Their ‘diffusion hypothesis’ states that small-scale random movement of individuals can lead to population persistence at a given location. Humphries and Ruxton (2002) come to a similar conclusion. There is ample evidence that benthic invertebrates exhibit such small-scale movements (e.g., Elliott 1971). More importantly, Speirs and Gurney (2001) use an analytically tractable model not only to establish the qualitative plausibility of their argument but rather to find precise quantitative parameter relationships that allow for persistence. Such quantitative relationships are hard, if not impossible, to obtain from individual-based simulations. The work of Speirs and Gurney (2001) has been extended to explicitly include a benthic compartment (Pachepsky et al. 2005; Lutscher et al. 2005) and strong spatial heterogeneity (Lutscher et al. 2006). One of the results by Pachepsky et al. (2005) is that if the production rate on the benthos exceeds the rate at which individuals enter the drift at low population density, then the population can persist, independent of any small- or large-scale movement. This finding formalized Waters’ (1961) production hypothesis.

All of the above mentioned models exploring the diffusion hypothesis considered one life history scenario: continuously growing populations. However, invertebrates living in streams often have winged adult stages and discrete generations. Moreover, as discussed above, much of the experimental studies focused on whether upstream bias of flight at the adult stage compensates for downstream movement of larvae. The goal of the present work is to apply the modeling insights and analytical tools from the aforementioned diffusion models to describe the growth and movement dynamics of stream insects with separate larval and winged adult stages and to quantify their persistence conditions in terms of movement mechanisms. In the next section, we present our model, which has the form of an integrodifference equation (Kot and Schaffer 1986) where a ‘dispersal kernel’ (Neubert et al. 1995) accounts for movement of individuals. We give exact and approximate persistence conditions. In the following section, based on assumptions about individual movement mechanisms, we derive several dispersal kernels from partial differential equation models and investigate their effect on population persistence. We then show how approximations can be applied to a model with individual movement separated into the movement during the larval and adult stages. We apply these results to quantify how much upstream movement of adults is necessary to compensate downstream movement of larvae.

Model

We consider a single semelparous population with distinct, non-overlapping reproductive and dispersal phases. For simplicity of exposition, we assume one generation per year and consider models that describe the year-to-year changes in the population distribution on one date (e.g., immediately after reproduction is completed). We denote by N _t (x) the population density on that date at location x in a homogeneous, one-dimensional habitat, e.g., a river that is much longer than wide. We describe dispersal of individuals by a redistribution kernel, K(z), which is the probability density function of the location of an individual after dispersal (Neubert et al. 1995), i.e., if an individual is located at a point x in one year, K(z)dz is the proportion of its surviving offspring that are located in the infinitesimal range x+z to $x + z + dz$, the following year. We denote by R the net reproductive rate (Caswell 2001) of the population, i.e., the mean number of individuals by which an individual present at the census date in one year is replaced on the corresponding date the following year, and assume that R takes a constant value independent of population density and spatial location. With these assumptions, we arrive at the following linear integrodifference equation for the dynamics between generations (e.g., Kot and Schaffer 1986),

$$ {N_{t + 1}}(x) = R\int\limits_{ - \infty }^\infty {K\left( {x - y} \right){N_t}(y)dy.} $$

(1)

In deriving Eq. 1, we made several simplifying assumptions, e.g., linearity, infinitely long river. We will consider each of these assumptions and their impact in the “Discussion”.

Population persistence at a location and spreading speed

The total population, defined by ${\overline N_t} = \int\limits_{ - \infty }^\infty {{N_t}(x)dx}$, satisfies the equation ${\overline N_{t + 1}} = R{\overline N_t},$ since the redistribution kernel (by definition) integrates to unity. The persistence condition for the total population defined this way is therefore formally R ≥ 1. This result, though mathematically correct, is ecologically misleading as it does not imply that the population persists at any specified point in space. Indeed, in the presence of advection this condition is not sufficient for the population to persist at any particular location because movement bias transports the population away faster than it can reproduce locally. This is the basis of the drift paradox discussed in the “Introduction”; see Byers and Pringle (2006) for application to a particular case of our model.

The calculation of persistence conditions at a location might appear to require an explicit solution of Eq. 1, which is only available in a few special cases and almost never in nonlinear models. Instead, we make use of recent analytical results (Pachepsky et al. 2005; Lutscher et al. 2005) and characterize persistence at a location in terms of spreading speeds.

The spreading speed of a population is defined as the (asymptotic) velocity with which it expands its range in a homogeneous habitat when introduced locally (Aronson and Weinberger 1975; Kot et al. 1996). This speed is arguably the single most important quantity for invasion processes, and considerable progress has been made in calculating this quantity for various types of models, see Hastings et al. (2005) and references therein. In most previously studied cases, the dispersal process is assumed to be unbiased, so that the spreading speed is independent of direction (but see Medlock and Kot (2003)). When individual movement is biased, the spreading speed in the direction of the bias (downstream) is larger than the speed against the bias (upstream). Based on this observation we propose to characterize the persistence conditions as follows. A population can persist at any location in a homogeneous habitat if and only if its upstream speed is positive. In Appendix A, we prove this condition to be correct in an arbitrarily long river for a particular dispersal kernel, and we demonstrate that the persistence condition for a finite river is only slightly more stringent. We consider the limitations of our persistence condition in detail in the “Discussion”.

Following the above characterization, the critical condition between persistence and extinction is given when the upstream speed is zero (Pachepsky et al. 2005; Lutscher et al. 2005). The advantage of this characterization is that the critical condition can often be calculated relatively easily even when an explicit solution of the full model Eq. 1 is not available.

Calculation of the persistence condition

In order to calculate the spreading speed for Eq. 1, we make the assumption that the dispersal kernel has exponentially bounded tails (Kot et al. 1996). This restriction only excludes consideration of a few forms of passive long-range dispersal, e.g., seeds carried long distances by birds (Clark et al. 2001). Mathematically, this implies that a powerful tool, the moment generating function,

$$ M(s) = M\left( {s;K} \right) = \int\limits_{ - \infty }^\infty {K(z)\exp \left( {sz} \right)dz,} $$

(2)

of the redistribution kernel exists for all s in some interval about zero (Kot et al. 1996). This in turn ensures that Eq. 1 has a finite spreading speed and constant-speed traveling-wave solutions (Weinberger 1982). We derive several redistribution kernels for larvae and adult stages of stream insects from mechanistic movement models below, and all of these have exponentially bounded tails. If this condition is not satisfied, the model may exhibit accelerating waves (Kot et al. 1996). We return to this aspect in the “Discussion”.

The characteristic equation for the speed, c, of a traveling-wave solution is given by exp(sc) = RM(s) (Kot et al. 1996, Eq. A6). A speed of zero occurs when RM(s) = 1. The smallest value of M(s) gives the critical threshold R ^* for which the upstream speed is zero as

$$ {R^*} = \frac{1}{{{{\min }_s}\left\{ {M(s)} \right\}}} = \frac{1}{{M\left( {{s^*}} \right)}}, $$

(3)

where s ^* is the value at which the minimum occurs, see Appendix A for an alternative, more detailed derivation. Our central result is that a population can persist at any location in the face of advection if and only if R ≥ R ^*. If movement is biased, then R ^* > 1; as the bias decreases to zero, R ^* decreases to unity. Pringle et al. (2009) recently presented an extension of this argument to structured populations. In the remainder of this paper, we use this result to derive persistence conditions for a range of ecological situations.

Explicit examples and an approximation

In the case of Gaussian dispersal, Eq. 1 can be solved explicitly, which allows us to demonstrate that the explicit approach and our upstream speed characterization Eq. 3 agree. We compare and contrast this situation with two variants of the Laplace kernel for which only the new approach is available. Our findings establish the importance of higher moments of the dispersal kernel. Recognizing that reconstruction of redistribution kernels from ecological data makes severe data requirements, we propose and evaluate an approximation that takes account of skewness and kurtosis in the dispersal kernel, but does not require full reconstruction of the kernel.

Gaussian kernel

We assume that individuals are initially concentrated at x = 0 and disperse according to the Gaussian kernel with mean μ and variance σ ²,

$$ G\left( {z;\mu, {\sigma^2}} \right) = \frac{1}{{\sqrt {{2\pi {\sigma^2}}} }}\exp \left( { - \frac{{{{\left| {z - \mu } \right|}^2}}}{{2{\sigma^2}}}} \right), $$

(4)

The explicit solution of Eq. 1 is given by N _t (x) = R ^t G (x; tμ,tσ ²). At x = 0, we obtain

$$ {N_t}(0) = \frac{{{{\left( {R\exp \left\{ { - {\mu^2}/\left( {2{\sigma^2}} \right)} \right\}} \right)}^t}}}{{\sqrt {{2\pi {\sigma^2}t}} }}. $$

(5)

If R > exp{μ ²/(2σ ²)} then the numerator grows faster than the denominator in time so that the population can persist at x = 0, otherwise the numerator decreases in time, and the population cannot persist at x = 0 (Byers and Pringle 2006).

The moment generating function of the Gaussian kernel is given by

$$ M\left( {s;G} \right) = \exp \left( {\mu s + \frac{{{\sigma^2}{s^2}}}{2}} \right). $$

(6)

Its minimum is attained at s ^* = −μ/σ ², so that the critical threshold, calculated from the recipe in the preceding section,

$$ {R^*} = \exp \left( {\frac{{{\mu^2}}}{{2{\sigma^2}}}} \right), $$

(7)

is precisely the persistence condition found by Byers and Pringle (2006).

Laplace kernel

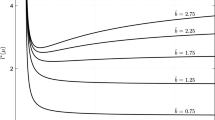
Dispersal data are often leptokurtic rather than normally distributed (Kot et al. 1996). The Laplace kernel that is frequently used to describe this situation has the additional advantage that it can be derived from a mechanistic dispersal model (Neubert et al. 1995). To incorporate movement bias into a Laplace kernel one can simply shift the symmetric Laplace kernel to some nonzero mean, or one can include bias into the dispersal model and derive an asymmetric Laplace kernel (Lutscher et al. 2005). In both cases, the critical value R ^* can be expressed as a function of the single non-dimensional variable μ ²/σ ², which is the squared inverse of the coefficient of variation (CV). Details are given in Appendix B. The respective kernels and resulting R ^* are plotted in Fig. 1, which shows that the threshold sensitively depends on the precise dispersal mechanisms that lead to the redistribution kernel, a finding consistent with previous work (Lutscher 2007). Thus, knowledge of the CV or even mean and variance of the dispersal kernel is not sufficient for determining the persistence condition, and we now give an approximate persistence condition that incorporates higher moments of the redistribution kernel.

Fig. 1

Comparison of three kernels and persistence conditions for identical mean and variance. a The three kernels, Gauss, shifted Laplace, and asymmetric Laplace with mean μ = 2/3 and variance σ ² = 10/9. b The critical threshold R ^* for persistence as a function of the non-dimensional variable μ ²/σ ². c The true and approximate persistence condition for the asymmetric Laplace kernel and, for comparison, the values for the Gaussian kernel, i.e., the values that result from taking the mean and variance only

Approximate persistence conditions

In the case of symmetric dispersal, previous workers have derived an approximate formula for persistence that takes the excess kurtosis, γ ₂, of the kernel into account (van den Bosch et al. 1992; Lutscher 2007). Redistribution kernels in advective environments can have significant skewness, γ ₁, as we saw above. We now extend the above approximate persistence condition to take skewness into account.

The Gaussian kernel has ${\gamma_1} = {\gamma_2} = 0$, and the critical value for its moment generating function is s ^* = −μ/σ ² (see above). In general, when ${\gamma_1} \ne 0 \ne {\gamma_2}$, we write ${s^*} = - \mu /{\sigma^2} + \varepsilon$ and derive a first order approximation for ε in terms of the mean, variance, skewness, and kurtosis of the kernel to arrive at the approximate persistence condition

$$ {R^*} \approx \frac{1}{{M\left( { - \mu /{\sigma^2} + \varepsilon } \right)}},{\hbox{with}}\;\varepsilon = \frac{{{\mu^2}}}{{6{\sigma^2}}}\frac{{{\gamma_2}\mu - 3{\gamma_1}\sigma }}{{\left( {{\sigma^2} - {\gamma_1}\mu \sigma + {\gamma_2}{\mu^4}/2} \right)}}, $$

(8)

as long as the denominator is not zero, see Appendix A for details. The results for the asymmetric Laplace kernel, plotted in Fig. 1, show that the approximation has limited value for kernels with strong skewness. One likely reason for this is that consideration of two further central moments does still not capture the effects of the tail of the distribution.

Dispersal mechanisms and redistribution kernels for stream insects

From one generation to the next, many stream insects undergo dispersal in two life stages, namely as waterborne larvae and as airborne adults. To find the dispersal kernel from one generation to the next, we therefore follow an individual that first dispersed as larva through its dispersal as adult. Mathematically, if we denote by K _L and K _A the respective kernels for larvae and adults, then the combined kernel between generations is given by the convolution

$$ K(z) = {K_{\rm{A}}}*{K_{\rm{L}}}(z) = :\int\limits_{ - \infty }^\infty {{K_{\rm{A}}}\left( {z - w} \right){K_{\rm{L}}}(w)dw} . $$

(9)

Since moment generating functions simply multiply under convolution, i.e., M(s;K) = M(s;K _A)M(s;K _L), the persistence condition Eq. 3 is easily computed once the two separate kernels or their moment generating functions are known. Similarly, the approximate condition Eq. 8 is easily computed for the convolution of two kernels since moments are additive under convolutions and skewness and kurtosis of K can be computed as weighted averages of these quantities for K _L and K _A, see Appendix A for details.

We derive the redistribution kernel for the larval stage from a mechanistic description of the dispersal process, using physically measurable quantities (Neubert et al. 1995). We assume that larvae experience random diffusion, d, and advection with effective speed v, which can be significantly smaller than the average stream flow due to boundary layers (Speirs and Gurney 2001) and time spent on the benthos (Pachepsky et al. 2005). We consider three alternative descriptions of larval emergence times. Emergence can be after a certain fixed maturation time, τ, (FE), or at a constant rate, a, (CE), or at a constant rate, a, after a delay of τ time units, (DE). The different redistribution kernels, K _L1 –K _L6, resulting from these assumptions, are summarized in Table 1. Details of the derivation are given in Appendix C.

Table 1 Redistribution kernels for larval dispersal mechanisms

We proceed in a similar fashion to derive kernels for adult dispersal, where we denote diffusive flight by D, and potential upstream bias by V, with v and V having opposite sign. We only consider the two cases that oviposition happens at a fixed time, T, after emergence (FP), or continuously with rate A, (CP). The resulting kernels, K _A1 –K _A5, are summarized in Table 2.

Table 2 Redistribution kernels for adult dispersal mechanisms

Application of the main formula to the drift paradox

We now use condition (3) together with the mechanistic movement descriptions above to find the precise quantitative relationships between larval dispersal downstream, adult upstream bias, net reproductive rate, and persistence.

We start with the baseline case that larvae exhibit no random upstream movement (d = 0) and that adults have no upstream bias in their flight (V = 0). We consider fixed time or continuous emergence for larvae and fixed time or continuous oviposition for adults. Hence, we consider the four cases FE/FP, FE/CP, CE/FP, and CE/CP according to Tables 1 and 2. We choose parameters such that the two different kernels for the larval stage have the same mean, and the two kernels for adult dispersal have the same variance. We plot the resulting threshold R ^* as a function of advection velocity, v, in Fig. 2. (Explicit calculations are relegated to Appendix D.) The kernels K _L4 *K _A1 (FE/FP) and K _L4 *K _A2 (FE/CP) are identical in mean and variance, but differ in the tails. The resulting threshold R ^* is higher when the tails of the kernel decay faster. This result was to be expected since the spreading speed is determined by the weight in the tails of a distribution (Kot et al. 1996). The other two kernels K _L5 *K _A1 (CE/FP) and K _L5 *K _A2 (CE/CP) are also identical in mean and variance, but have a larger variance than the former ones. Consequently, the threshold R ^* is even lower for these kernels.

Fig. 2

The critical threshold R ^* for population persistence for four different kernels, as described in Tables 1 and 2. Parameter values are d = 0, τ = 1, and a = 1, so that the mean for the kernels describing larval dispersal are the same (μ = 1/λ). Similarly, since V = 0, T = 1, and A = 1, the variances of the kernels for adult dispersal are identical (σ ² = 2/α ²)

Next, we consider the role of upstream bias in adult flight, using the same four combinations of dispersal mechanisms as above. We fix the downstream drift velocity of the larvae, v > 0, and vary the upstream speed of adults, V < 0, so that the bias is in the opposite direction of larval drift. At V = 0 the upstream bias is zero, for V < 0 the upstream bias increases. We plot the critical threshold R ^* as a function of the probability that an adult moves upstream from where it emerges (Fig. 3). As upstream bias increases, the critical threshold decreases. This decrease is stronger for the two combinations that involve the (asymmetric) Laplace kernel (FE/CP and CE/CP) than for the Gaussian kernels (FE/FP and CE/FP), again demonstrating the importance of the tails of the distribution. The critical upstream moving probability that exactly balances downstream drift (so that R ^*  = 1) is lower for the former two cases than for the latter.

Fig. 3

The critical threshold R ^* for population persistence for four different kernels, as described in Tables 1 and 2. Parameter values are d = 0, τ = 1, v = 2, and a = 1, for the kernels describing larval dispersal. Adult dispersal is biased upstream with speed V ranging between 0 and −2. The other parameters are T = 1 and A = 1. For a more detailed explanation, see text

When the mean dispersal distance downstream equals the mean dispersal distance upstream then the critical threshold for persistence is R ^*  = 1, independent of the shape of the two kernels. This can be seen as follows. The moment generating function, M(s), of the convolution of the adult and larvae dispersal kernels satisfies M′(0) = 0, since its slope at zero is the sum of the slopes of the moment generating functions of the individual kernels, which, in turn, are the respective means. Furthermore, M(s) is convex. Therefore, the unique minimum of M is at zero, and since M(0) = 1, we have R ^*  = 1. Hence, a single species where the mean upstream distance exactly balances the mean downstream drift requires the least possible R ^* for persistence. Kopp et al. (2001) showed that this exact balance is indeed an evolutionary stable strategy in the presence of competition.

When the mean downstream drift is larger than the mean upstream movement, then the critical threshold R ^* sensitively depends on the movement mechanisms. We explore this relationship in Fig. 4. We vary the advection speed for larvae and choose the upstream flight speed for adults in such a way that the total mean displacement remains constant. In the case FE/FP, the resulting Gaussian kernel is independent of the advection speed, and hence the critical threshold is constant. In all other cases, however, the critical threshold is a decreasing function of the advection speed. In other words, faster upstream flight more than compensates for faster downstream drift even though the average displacement is constant.

Fig. 4

The critical threshold R ^* for population persistence for four different kernels, as described in Tables 1 and 2. Parameter values are d = 0, τ = 1, and a = 1, for the kernels describing larval dispersal. Adult dispersal is biased upstream in such a way that the combined effect of larval and adult dispersal is a downstream mean dispersal distance of one. The other parameters are T = 1 and A = 1. For a more detailed explanation, see text

We now consider the case that larvae show random movement, i.e., d > 0. Such small-scale random movements can be active (larvae crawling on the stream benthos, see Townsend and Hildrew (1976)) or passive (non-laminar flow and eddies during drift, see Svendsen et al. (2004)). As d increases, the critical threshold R ^* will decrease, independent of the detailed movement assumptions. As an example, we consider the case that larval and adult movement occurs for a fixed time period (FE/FP, see Tables 1 and 2). Then the resulting kernels for larval and adult dispersal are Gaussian with means μ _L, μ _A, and variances $\sigma_{\rm{L}}^2,\sigma_{\rm{A}}^2$, respectively. The combined redistribution kernel between generations is again Gaussian with means and variances added. Hence, the critical R ^* is given by Eq. 7. The elasticity of R ^* with respect to $\sigma_{\rm{L}}^2 = 2d\tau$ is

$$ \frac{1}{{{R^*}}}\frac{{d{R^*}}}{{d\sigma_{\rm{L}}^2}} = - \frac{{{{\left( {{\mu_{\rm{L}}} + {\mu_{\rm{A}}}} \right)}^2}}}{{4{{\left( {\sigma_{\rm{L}}^2 + \sigma_{\rm{A}}^2} \right)}^2}}} < 0. $$

(10)

The parameter R in model (1) denotes the average number of offspring recruited from a single adult individual. For many stream invertebrates, a major source of mortality is predation in the drift, so that predation and dispersal are intimately linked. We can incorporate predation in the drift into the mechanistic dispersal models by adding a removal term with death rate m into the diffusion equation in Appendix C. Assuming that all individuals drift for a fixed period of time, τ, the resulting kernel is the Gaussian kernel K _L1, scaled by the factor exp(−mτ). On the other hand, if we assume that individuals settle at a constant rate a, then the resulting kernel is the asymmetric Laplace kernel K _L2, scaled by a/(a + m). Assuming that the average time in the drift is the same in both cases (τ = 1/a), we see that the fraction of larvae surviving drift mortality is larger for constant settling than for fixed time settling. Hence, the dispersal mechanism influences the necessary number of larvae produced by a single adult individual.

Our formalism can, of course, also be applied to study the precise persistence conditions for the ‘diffusion hypothesis’ (e.g., Speirs and Gurney 2001), i.e., the possibility of small-scale random movements of benthic organisms with no winged adult stage being the sole mechanism for persistence. We simply consider the redistribution kernel between generations to be the kernel for the larvae (K = K _L), as described in Appendix C and Table 1. The general formula and the approximate conditions still apply.

Discussion

The research reported here starts by proposing a formal condition for population persistence in advective systems: a population can persist at any location in a homogeneous habitat if and only if it can invade upstream. This condition leads to a recipe Eq. 3 that defines the minimal value for the net reproductive rate for population persistence. Besides its intuitive appeal, our recipe also has computational advantages. The required minimization can be carried out numerically relatively easily. The alternative way of determining persistence conditions via dominant eigenvalues of certain differential or integral operators on bounded domains is much more laborious (see Speirs and Gurney 2001; Pachepsky et al. 2005. Lutscher et al. 2005).

Most of our findings can be related to insights derived from the large, and growing, body of literature on the speed of spread of invasions. In particular, while persistence conditions in the absence of advection are insensitive to long-distance movements (Lockwood et al. 2002), invasion speeds are strongly influenced by the form of the tails of dispersal kernels (e.g., Kot et al. 1996); similar sensitivity is illustrated by our demonstration that different kernels with the same coefficient of variation may lead to very different persistence conditions (Fig. 1b). The ‘upstream’ tail of the kernel appears to be particularly important, with the persistence condition being especially stringent when this tail decays rapidly (Fig. 1c). This critical role played by the kernel’s tail presents challenges for ecologists as the form of tails are notoriously hard to estimate from data with corresponding challenges for estimating invasion speeds (Clark et al. 2003). However, Clark et al. suggest that invasion speed calculations “remain valuable for comparing spread potential among species and for identifying potential for invasion”. A similar argument holds for the theory developed in this paper.

We assumed that the tails of the dispersal kernels are exponentially bounded so that the moment generating functions exist. All the kernels that we derived from partial differential equation models satisfy this assumption (Table 1 and 2). When the tails of the dispersal kernels are not exponentially bounded, invasions may accelerate (Kot et al. 1996) so that no spreading speed can be defined and our recipe does not apply. Lutscher et al. (2005) numerically found that populations with fat-tailed redistribution kernels can persist in bounded domains even for very high advection speeds. It is tempting to conjecture that when invasions accelerate without bound, populations may persist in the face of arbitrarily fast advection. However, since extreme dispersal events are crucial for accelerating invasions, there could be a significant discrepancy between persistence on bounded and invasion in unbounded domains (see below). The theories developed by Clark et al. (2001) or Kot et al. (2004) might be helpful to explore this question further.

Faced with the difficulty of estimating dispersal kernels, it is tempting to invoke “rules of thumb” to determine the likelihood of population persistence. For the systems considered here, the natural choice would be that of Byers and Pringle (2006) that assumes a Gaussian dispersal kernel—our Eq. 7. Absent information other than mean and variance, this is an obvious starting point. However, our analysis shows that the validity of such an approximation strongly depends on the particular modeling assumptions. The persistence condition derived from Gaussian dispersal may crudely underestimate the true persistence condition (Fig. 1b,c) or considerably overestimate the true condition (Figs. 2, 3 and 4). The obvious statement that different mechanistic assumptions lead to different persistence conditions seems to be excarbarated by the presence of unidirectional flow.

Four important mathematical simplifications were involved in this work: (1) a one-dimensional river; (2) an infinitely long river; (3) a linear model; and (4) no spatial heterogeneity in rates. We now discuss each of these.

• One-dimensional river. Almost all mechanistically based theory for population dynamics all comes from 1-D models. This is not a requirement for our persistence condition (possibility of upstream invasion) to be reasonable, nor for our remarks on the importance of tails of distributions to remain valid. For rivers that are much longer than wide, a 1-D model seems reasonably appropriate. However, adding even one extra space dimension may substantively change the form of any mechanistically derived 1-D approximation to the dispersal kernel through the inclusion of back-eddies and other aspects of turbulent flow. One of us (RMN), with collaborators, is currently exploring this question using a previously parameterized 2-D hydraulic model for a section of river in central California. Whether some or all of this theory applies to one-dimensional transects in oceans, e.g., coastlines with long-shore currents, is a more difficult question that requires additional investigation. For example, the dispersal of larvae in the coastal ocean may be influenced by large-scale eddies. This may produce dynamics for which our use of the dispersal kernel is inappropriate as all larvae originating at a particular location in a given year may travel together to another location (Siegel et al. 2008).

• Infinitely long river. For mathematical tractability, we set the limits of integration in the master Eq. 1 to be ±∞. Persistence conditions derived for an infinite system are those for which the “critical domain size” is infinity Lutscher et al. 2005; Pachepsky et al. 2005. In principle, this leaves open the question of whether our theory can be applied to a real stream or river, which of course has finite length. Calculations in Appendix A.4 demonstrate that the critical domain size decreases rapidly with increasing growth rate (see Figure in Appendix A), i.e., the critical conditions for infinitely long rivers are only slightly less stringent for a large range of finite length rivers. For management applications, one would in any case require the growth rate to exceed the critical R^*, simply to minimize the effects of demographic or environmental stochasticity.

• We considered a linear model since persistence conditions are determined by the linearization at zero, as long as there is no Allee effect. When population growth is monotone, then the linear model (1) has the same invasion speed as the nonlinear model (Weinberger 1982). Even for a large class of overcompensatory growth functions, the invasion speed is still given by the linearization at zero (Hsu and Zhao 2008). Density dependence in movement, rather than population dynamics, can lead to novel qualitative behavior (Cantrell and Cosner 2006; Lutscher 2008). However, rather than speculating on general effects, we suggest that our framework can be used to explore the effects of particular mechanisms when modeled properly. Interaction with other species, competitors or predators alike, certainly affects population dynamics, but not necessarily persistence conditions since, following invasion analysis, linearization at low densities renders the equation for the focal species independent of the others.

• No spatial heterogeneity. This is probably the greatest limitation of the theory. Previous work by Lutscher et al. (2006) provides some pointers to possible consequences. These authors studied continuous time models with alternating ‘good’ and ‘bad’ patches, but with no downstream ‘trend’ in model parameters. They concluded: “If the advection speed in good patches is larger than the critical speed, then the population cannot persist nor invade upstream, if it is smaller, then there are parameter values such that the population can persist and invade upstream”. Clearly spatial heterogeneity at some spatial scales will impact the conclusions in the present paper, but the nature of these changes is a subject requiring future research.

Many organisms that have to adapt to advective media have synchronized reproduction and biphasic life histories. Our approach offers a particularly powerful theoretical tool for modeling populations of these organisms. The dispersal kernel involves a convolution Eq. 9, but the moment generating function is simply the product of the moment generating functions for the individual stages. This opens the way to relatively straightforward investigations of the effects on persistence of life history changes in the individual stages, as exemplified by the examples considered here. Our result on the minimization of R ^* points the way to other applications in life history theory.

Appendices

Appendix A: Analytical results and derivations

A.1 Derivation of the main formula

For the linear integrodifference Eq. 1 Kot et al. (1996) gave the relationship between the population growth rate, its movement behavior, and the spreading speed, c, in parametric form

$$ \begin{array}{*{20}{c}} {c = \frac{{M \prime (s)}}{{M(s)}},} & {R = \frac{{\exp \left\{ {sM \prime (s)/M(s)} \right\}}}{{M(s)}}} \\\end{array}, $$

(A1)

where s is related to the steepness of the population density at the advancing edge of its range. The speed is zero only if M′(s) = 0, which, since M is a convex function (see below), implies that M(s) is at its minimum, s ^*. Therefore, the speed is zero precisely at the critical value R ^* = 1/M(s ^*). By definition, M(0) = 1. Furthermore, if there is movement bias to the right then

$$ M \prime (0) = \int\limits_{ - \infty }^\infty {xK(x)dx > 0}, $$

which implies that M(s) < 1 for some s < 0, and hence R ^* > 1. The second derivative

$$ M \prime \prime (s) = \int\limits_{ - \infty }^\infty {{x^2}K(x)\exp \left( {sx} \right)dx > 0}, $$

is positive since all functions under the integral sign are positive. Therefore, M is convex.

A.2 The approximate persistence condition

To derive the approximate persistence condition, we work with the cumulant generating function, which is the logarithm of the moment generating function, C(s) = ln{M(s)}. Since the logarithm is a monotone function, the unique minimum of M(s) gives rise to a unique minimum of C(s) for the same critical value s ^*. The first four terms of the Taylor series of the cumulant generating function are given in terms of the mean, variance, skewness, and excess kurtosis as

$$ C(s) = \mu s + \frac{{{\sigma^2}{s^2}}}{2} + \frac{{{\gamma_1}{\sigma^3}{s^3}}}{6} + \frac{{{\gamma_2}{\sigma^4}{s^4}}}{{24}}. $$

(A2)

For the Gauss kernel, we have ${\gamma_1} = 0 = {\gamma_2}$, and the minimum of C(s) occurs at s ^* = −μ/σ ². If we assume that γ ₁, γ ₂ are close to zero, we expect the minimum to occur near that same value. Therefore, we differentiate C(s), set ${s^*} = - \mu /{\sigma^2} + \varepsilon$, and arrange by powers of ε. This gives

$$ C \prime \left( {{s^*}} \right) = \frac{{{\gamma_1}{\mu^2}}}{{2\sigma }} - \frac{{{\gamma_2}{\mu^3}}}{{6{\sigma^2}}} + \varepsilon \left( {{\sigma^2} - {\gamma_1}\mu \sigma + \frac{{{\gamma_2}{\mu^4}}}{2}} \right) + O\left( {{\varepsilon^2}} \right). $$

(A3)

In the first order approximation, i.e., discarding higher powers of ε, the minimum occurs at C′(s ^*) = 0 if

$$ \varepsilon = \frac{{{\mu^2}}}{{6{\sigma^2}}}\frac{{{\gamma_2}\mu - 3{\gamma_1}\sigma }}{{\left( {{\sigma^2} - {\gamma_1}\mu \sigma + {\gamma_2}{\mu^4}/2} \right)}}. $$

(A4)

Then the critical threshold R ^* is given by

$$ {R^*} = \frac{1}{{M\left( {{s^*}} \right)}} = \exp \left( { - C\left( {{s^*}} \right)} \right) = \exp \left( { - C\left( {\varepsilon - \mu /{\sigma^2}} \right)} \right). $$

(A5)

A.3 The approximate condition for convolutions of kernels

The approximate formula (A5) is particularly useful for kernels that arise as a convolution of two kernels (see Eq. 9) since the cumulants of a distribution simply add under convolution. More precisely, if K _A, K _L are two kernels with moment generating functions M _A, M _L and means μ _A, μ _L, variances σ ² _A, σ ² _L, skewness γ _1A, γ _1L, and excess kurtosis γ _2A, γ _2L, then the convolution kernel K = K _A*K _L has the cumulant-generating function

$$ C(s) = \ln \left( {M(s)} \right) = \ln \left( {{M_{\rm{A}}}(s){M_{\rm{L}}}(s)} \right) = \ln \left( {{M_{\rm{A}}}(s)} \right) + \ln \left( {{M_{\rm{L}}}(s)} \right) = {C_{\rm{A}}}(s) + {C_{\rm{L}}}(s), $$

and therefore, the characteristic quantities of the kernel K are given by

$$ \begin{array}{*{20}{c}} {\mu = {\mu_{\rm{A}}} + {\mu_{\rm{L}}},} & {{\sigma^2} = \sigma_{\rm{A}}^2 + \sigma_{\rm{L}}^2,} & {{\gamma_1} = \frac{{\sigma_{\rm{A}}^3{\gamma_{1{\rm{A}}}} + \sigma_{\rm{L}}^3{\gamma_{1{\rm{L}}}}}}{{{\sigma^3}}},} & {{\gamma_2} = \frac{{\sigma_{\rm{A}}^4{\gamma_{2{\rm{A}}}} + \sigma_{\rm{L}}^4{\gamma_{2{\rm{L}}}}}}{{{\sigma^4}}}.} \\\end{array} $$

Formulas (A4) and (A5) then give the approximate persistence condition for the convolution of the two kernels.

A.4 Proof of the persistence condition and sensitivity for finite rivers

For a particular choice of dispersal kernel, we show that a population can persist on an arbitrarily long bounded river if and only if it can invade upstream. We then demonstrate that the length of a river required to sustain a population decreases very rapidly as a function of the population growth rate.

Population dynamics on a finite river of length L, represented by the interval [0, L], are given by the integrodifference equation

$$ {N_{t + 1}}(x) = R\int_0^L {K\left( {x - y} \right){N_t}(y)dy,} $$

where we assume that individuals who disperse outside of [0, L] are lost from the population. In particular, we assume that individual behavior does not change at the boundaries. In the more general case when we wish to include particular behavior at the boundary, we write K(x,y), see for example van Kirk and Lewis (1999). We look for the dominant eigenvalue of the operator on the right hand side, i.e., we set N _t + 1 = λN _t . The population can persist on the domain if λ > 1. Alternatively, the population can persist if the dominant eigenvalue of

$$ v\phi (x) = \int_0^L {K\left( {x - y} \right)\phi (y)dy,} $$

(A6)

is greater than 1/R. It can be shown that v is increasing from 0 to 1 as L increases from 0 to infinity (Lutscher and Lewis 2004). Given R, the critical domain size is then the value of L for which v = 1/R. In general, the dominant eigenvalue or even the critical domain size cannot be calculated explicitly. For the special case that K is the asymmetric Laplace kernel (Appendix B, B5), however, progress can be made by converting the integral equation into a second-order differential equation (see Lutscher et al 2005). Given $0 < v < 1$, one can calculate the critical domain size L above which the population described by (A6) can persist from

$$ L = \frac{{4\arctan \left( {1/\sqrt {{\frac{{4\alpha \beta }}{{v{{\left( {\alpha + \beta } \right)}^2}}} - 1}} } \right)}}{{\left( {\alpha + \beta } \right)\sqrt {{\frac{{4\alpha \beta }}{{v{{\left( {\alpha + \beta } \right)}^2}}} - 1}} }}. $$

(A7)

As a function of v, the critical domain size approaches infinity as v approaches $\frac{{4\alpha \beta }}{{{{\left( {\alpha + \beta } \right)}^2}}}$.

The persistence threshold R ^* for the asymmetric Laplace kernel according to our recipe (3) is

$$ {R^*} = \frac{{{{\left( {\alpha + \beta } \right)}^2}}}{{4\alpha \beta }}, $$

see (B8), i.e., the persistence condition is valid in the limiting case for an arbitrarily long river. In other words: For every R > R ^* the upstream speed is positive, hence recipe (3) predicts persistence. At the same time, for every R > R ^*, expression (A7) gives the finite, but potentially large, domain size L, above which the population can persist in the bounded river.

To demonstrate how rapidly the critical domain size drops for values R > R ^* we choose R = ρR ^*for some ρ > 1, then the critical domain length becomes

$$ L = \frac{{4\arctan \left( {1/\sqrt {{\rho - 1}} } \right)}}{{\left( {\alpha + \beta } \right)\sqrt {{\rho - 1}} }}. $$

The plot in Figure (A) shows that the critical domain size is a rapidly decreasing function near ρ = 1, so that our persistence condition (3), while strictly speaking only true for infinitely long rivers, is a very good approximation for considerably shorter finite rivers.

Note that the integral operator in Eq. A6 is a non-negative operator. If we assume that the kernel is positive everywhere, then the eigenfunction corresponding to the dominant eigenvalue is also positive everywhere. Due to that fact, it is irrelevant for population persistence where in the domain the population is introduced. The location of introduction does, however, influence the time it takes for the total population to reach a certain density after introduction. Hence, in a stochastic rather than deterministic model, the location of population introduction could strongly influence its probability of persistence.

Fig. A

The critical length of a river for population persistence decreases rapidly as a function of ρ, see text. The parameter values are $\alpha + \beta = 1$

Appendix B: The two variants of the Laplace kernel

B.1 The shifted Laplace kernel

We take the symmetric Laplace kernel (back-to-back exponential) and shift it to some nonzero mean, analogously to the Gaussian kernel (4). The resulting kernel is

$$ K(z) = \sqrt {{\frac{1}{{2{\sigma^2}}}}} \exp \left( { - \frac{{\left| {z - \mu } \right|}}{{\sqrt {{{\sigma^2}/2}} }}} \right), $$

(B1)

with mean μ and variance σ ². The minimum of the moment generating function,

$$ \begin{array}{*{20}{c}} {M(s) = \frac{{\exp \left( {\mu s} \right)}}{{1 - {\sigma^2}{s^2}/2}},} & {{s^2} < 2/{\sigma^2}} \\\end{array}, $$

(B2)

occurs at

$$ {s^*} = \frac{1}{\mu }\left( {1 - \sqrt {{1 + \frac{{2{\mu^2}}}{{{\sigma^2}}}}} } \right), $$

(B3)

which gives a persistence threshold of

$$ {R^*} = \frac{{{\sigma^2}}}{{{\mu^2}}}\left( {\sqrt {{1 + \frac{{2{\mu^2}}}{{{\sigma^2}}}}} - 1} \right)\exp \left\{ {\sqrt {{1 + \frac{{2{\mu^2}}}{{{\sigma^2}}}}} - 1} \right\}. $$

(B4)

B.2 The asymmetric Laplace kernel

The symmetric Laplace kernel can be derived from a mechanistic movement model, assuming individuals move randomly without bias and settle at a constant rate (Neubert et al. 1995). Assuming that individual movement is biased, one arrives at the asymmetric Laplace kernel (Lutscher et al. 2005), see Appendix C. It is given by

$$ L\left( {z;\alpha, \beta } \right) = \left\{ {\begin{array}{*{20}{c}} {\phi \exp \left( {\alpha z} \right),} & {z \leqslant 0,} \\{\phi \exp \left( { - \beta z} \right),} & {z \geqslant 0,} \\\end{array} } \right. $$

(B5)

with normalizing constant $\phi = \alpha \beta /\left( {\alpha + \beta } \right)$, α, β > 0. The mean and variance of this kernel are $\mu = 1/\alpha - 1/\beta$ and ${\sigma^2} = 1/{\alpha^2} + 1/{\beta^2}$, respectively. The skewness and kurtosis are given by

$$ \begin{array}{*{20}{c}} {{\gamma_1} = 2\frac{{{\beta^3} - {\alpha^3}}}{{{{\left( {{\alpha^2} + {\beta^2}} \right)}^{3/2}}}},} & {{\gamma_2} = 6} \\\end{array} \frac{{{\beta^4} + {\alpha^4}}}{{{{\left( {{\alpha^2} + {\beta^2}} \right)}^2}}}. $$

The minimum of the moment generating function

$$ \begin{array}{*{20}{c}} {M(s) = \frac{{\alpha \beta }}{{\left( {\alpha - s} \right)\left( {\beta + s} \right)}},} & { - \beta < s < \alpha } \\\end{array}, $$

(B6)

occurs at

$$ {s^*} = \frac{{\alpha - \beta }}{2}, $$

(B7)

which gives a persistence threshold of

$$ {R^*} = \frac{{{{\left( {\alpha + \beta } \right)}^2}}}{{4\alpha \beta }} = \frac{{1 - \frac{{{\mu^2}}}{{2{\sigma^2}}}}}{{1 - \frac{{{\mu^2}}}{{{\sigma^2}}}}}. $$

(B8)

Note that for the asymmetric Laplace kernel, we always have μ ²  < σ ², since

$$ {\mu^2} = {\left( {\frac{1}{\alpha } - \frac{1}{\beta }} \right)^2} = \frac{1}{{{\alpha^2}}} - \frac{2}{{\alpha \beta }} + \frac{1}{{{\beta^2}}} < \frac{1}{{{\alpha^2}}} + \frac{1}{{{\beta^2}}} = {\sigma^2}. $$

Now we can understand why the critical R ^* goes to infinity as μ ²→σ ². In this limit, the term 1/αβ has to approach zero, which implies that either 1/α or 1/β approach zero. But then, the asymmetric Laplace kernel approaches the one-sided exponential distribution, which allows no upstream movement at all, so that the population cannot persist, no matter how large R ^*.

Appendix C: Derivation of kernels from PDEs

Assuming that an individual performs a potentially biased random walk for a certain time and stops at a certain rate, the probability density function u(t,x) of the location of the individual satisfies the partial differential equation

$$ \begin{array}{*{20}{c}} {\frac{{\partial u}}{{\partial t}} = d\frac{{{\partial^2}u}}{{\partial {x^2}}} - v\frac{{\partial u}}{{\partial x}} - a(t)u,} & {u\left( {0,x} \right) = \delta (x)} \\\end{array} $$

where d is the diffusion coefficient, v is the drift speed, and a(t) is the rate at which the individual stops. The dispersal kernel results as the density of the locations where the individual stops, i.e.,

$$ K(x) = \int\limits_0^\infty {a\left( \tau \right)u\left( {\tau, x} \right)d\tau }, $$

see Neubert et al. (1995) or Lutscher et al. (2005).

If the random walk occurs for a fixed period of time, τ, then the settling rate becomes a delta distribution $a(t) = \delta \left( {t - \tau } \right)$ and the resulting kernel K(x) = u(τ,x) is simply a Gaussian kernel with mean μ = vτ and variance σ ² = 2dτ.

If instead we assume that the stopping times are exponentially distributed with mean 1/a, then the settling rate is a constant a(t) = a, and the asymmetric Laplace kernel results with parameters

$$ \begin{array}{*{20}{c}} {\alpha = \frac{{v + \sqrt {{{v^2} + 4ad}} }}{{2d}},} & {\beta = \left| {\frac{{v - \sqrt {{{v^2} + 4ad}} }}{{2d}}} \right|,} \\\end{array} $$

(C1)

In terms of the random walk parameters, the mean of the asymmetric Laplace kernel is μ = v/a and the variance is ${\sigma^2} = 2d/a + {v^2}/{a^2}$. For v = 0, we obtain the symmetric Laplace kernel (see Neubert et al. 1995).

Appendix D: Kernels for stream insects: explicit examples

D.1: FE/FP

Larval emergence and oviposition occur after a fixed period of time. The resulting kernel for larveae is a delta distribution (K _L4), for adults a Gaussian kernel results (K _A1). The convolution is Gaussian with the means and variances added. The calculations for the critical R ^* are as in the first example in the main text.

D.2: FE/CP

When larvae emerge at a fixed time and oviposition occurs at a constant rate, we obtain a delta distribution (K _L4) convolved with a Laplace kernel (K _A2). The result is the shifted Laplace kernel. All the calculations are as presented in Appendix B.

D.3: CE/FP

Larvae emerging at a constant rate give rise to an exponential kernel (K _L5), whereas oviposition is described by a Gaussian kernel (K _A1). The convolution of these two does not have a simple closed-form representation of the kernel, but the moment generating function is

$$ \begin{array}{*{20}{c}} {M(s) = \frac{\lambda }{{\lambda - s}}\exp \left( {{\sigma^2}{s^2}/2} \right),} & {s < \lambda } \\\end{array} . $$

(D1)

Differentiating and setting M′(s) = 0 to zero gives

$$ \frac{\lambda }{{\lambda - s}} + \lambda {\sigma^2}s = 0. $$

The resulting quadratic polynomial in s has one admissible root, namely

$$ {s^*} = \frac{\lambda }{2} - \sqrt {{\frac{{{\lambda^2}}}{4} + \frac{1}{{{\sigma^2}}}}}, $$

(D2)

which then gives the threshold value as R ^* = 1/M(s ^*).

D.4: CE/CP

When larval emergence and oviposition both happen at a constant rate, the resulting kernels are the exponential (K _L5) and the Laplace kernel (K _A2). It is tedious but possible to calculate their convolution explicitly. However, the relevant moment generating function simply is

$$ \begin{array}{*{20}{c}} {M(s) = \frac{\lambda }{{\lambda - s}}\frac{{{\alpha^2}}}{{{\alpha^2} - {s^2}}},} & { - \alpha < s < \min \left\{ {\alpha, \lambda } \right\}.} \\\end{array} $$

(D3)

Again, the critical value for M(s) is given by the solution of M′(s) = 0 or

$$ \frac{\lambda }{{\lambda - s}} + \frac{{2s}}{{{\alpha^2} - {s^2}}} = 0. $$

The resulting quadratic equation for s has the solution

$$ {s^*} = \frac{\lambda }{3} - \sqrt {{\frac{{{\lambda^2}}}{9} + \frac{{{\alpha^2}}}{3}}}, $$

(D4)

and the critical threshold follows from that.