Introduction

Hodgkin (1948) found that various squid axon preparations responded in qualitatively different ways to applied currents. Some preparations gave a frequency of firing which rose smoothly from zero as the current increased whereas others manifested the sudden appearance of a train of spikes at a particular input current. Cells that responded in the first manner were called Class 1 (which we refer to as Type 1) whereas cells with a discontinuous frequency-current curve were called Class 2 (Type 2). More recently (Tateno et al. 2004) it has been found that regular spiking and fast spiking neurons in the rat somatosensory cortex exhibit Type 1 and Type 2 firing behaviours, respectively. Mathematical explanations for the two types are found in the bifurcation which accompanies the transition from rest state to a periodic firing mode. For Type 1 behaviour, a resting potential vanishes via a saddle-node bifurcation whereas for Type 2 behaviour the instability of the rest point is due to an Andronov-Hopf bifurcation; see Rinzel and Ermentrout (1989).

Stochastic effects in the firing behaviour of neurons have been widely reported, discussed and analyzed since their discovery in the 1940s. One of the first reports for the central nervous system was by Frank and Fuortes (1955) for cat spinal neurons. Although there have been many single neuron studies, the effect of noise on systems of coupled neurons has not been extensively investigated. Some preliminary studies are those of Gutkin et al. (2004) and Casado and Baltanás 2003.

The quadratic integrate and fire model

A relatively simple neural model which exhibits Type 1 firing behaviour is the quadratic integrate and fire (QIF) model. We couple two model neurons in the following manner (Gutkin et al. 2004).

Let {X 1(t), X 2(t), t ≥ 0} be the depolarizations of neurons 1 and 2, where t is the time index. Then the model equations are, for subthreshold states of two identical neurons,

$$ {\rm d}X_1=[(X_1-x_R)^2 + \beta + g_{s}S_1]\,{\rm d}t + \sigma\,{\rm d}W_1 $$
(1)
$$ {\rm d}X_2=[(X_2-x_R)^2 + \beta + g_{s}S_2]{\rm d}t + \sigma {\rm d}W_2 $$
(2)
$$ {\rm d}S_1=\left(-{\frac{S_1}{\tau}} + F(X_2)\right){\rm d}t $$
(3)
$$ {\rm d}S_2=\left(-{\frac{S_2}{\tau}} + F(X_1)\right){\rm d}t $$
(4)

where S 1 is the synaptic input to neuron 1 from neuron 2 and S 2 is the synaptic input to neuron 2 from neuron 1. The quantity x R is a resting value. g s is the coupling strength. β is the mean background input. W 1 and W 2 are independent standard Wiener processes which enter with strength σ. This term may model variations in nonspecific inputs to the circuit as well as possibly intrinsic membrane and channel noise. By construction, we take this term to be much weaker than the mutual coupling between the cells in our circuit. The function F is given by

$$F(x)= 1 + \tanh (\alpha(x-\theta))$$

where θ characterizes the threshold effect of synaptic activation. Since when a QIF neuron is excited and it receives no inhibition, its potential reaches an infinite value in a finite time, for numerical simulations a cutoff value x max is introduced so that the above model equations for the potential apply only if X 1 or X 2 are below x max. To complete a “spike” in any neuron, taken as occurring when its potential reaches x max, its potential is instantaneously reset to some value x reset which may be taken as −x max. At the bifurcation point \(g_s = g_s^\ast,\) two heteroclinic orbits between unstable rest points turn into a periodic orbit of antiphase oscillations.

Results and theory

In the numerical work, the following constants are employed throughout. x R  = 0, x max = 20, θ = 10, α = 1, β = −1, g s  = 100 and τ = 0.25. The initial values of the neural potentials are X 1(0) = 1.1, X 2(0) = 0 and the initial values of the synaptic variables are S 1(0) = S 2(0) = 0.

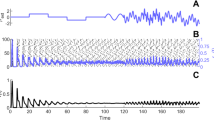
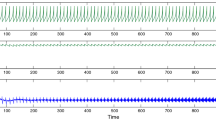
When there is no noise, σ = 0, the results of Fig. 1 are obtained, showing the spike trains of the two coupled neurons and their synaptic inputs. The firing settles down to be quite regular and the periodic orbit is shown in Fig. 2. Here the patch marked P is the location of the region explored in detail below.

Fig. 1
figure 1

Solutions of Eqs. (1)–(4) without noise for two coupled quadratic integrate-and-fire model neurons with the standard parameters. X 1 and X 2 are the potential variables of neurons 1 and 2 and S 1 and S 2 are the inputs to neurons 1 and 2, respectively

Full size image
Fig. 2
figure 2

The periodic orbit of the system without noise in the (x 1,x 2)-plane. The square marked P was explored in detail in reference to the extent of the basin of attraction of the periodic orbit

Full size image

The effects of a small amount of noise are shown in Fig. 3. The neural excitation variables are shown on the left and the corresponding trajectories in the (x 1,x 2)-plane are shown on the right. In the top portion an example of the trajectory for σ = 0.1 is shown. Here three spikes arise in neuron 1 and two in neuron 2, but the time between spikes increases and eventually the orbit collapses away from the periodic orbit. In the example (lower part) for σ = 0.2 there are no spikes in either neuron. In ten trials, the average numbers of spikes obtained for the pair of neurons were (2.5,2.2) for σ = 0.1, (1.4,1.1) for σ = 0.2 and (1.3,0.9) for σ = 0.3; these may be compared with (5,5) for zero noise. In addition, we explored the properties of the last-spike time random variable, T L. The smaller this quantity, the greater the diminution of firing. Figure 4 shows the distributions, based on 500 trials, of the last-spike time for the two values of the noise parameter, σ = 0.1 and σ = 0.45. Here it is clear that the spiking stops after approximately an integer multiple of the first spike time. Furthermore, as σ increases, the number of occasions on which no spike was generated increases.

Fig. 3
figure 3

On the left are shown examples of the neuronal potentials for neurons 1 and 2 (quadratic integrate-and-fire model) for two values of the noise, σ = 0.1 and σ = 0.2. On the right are shown the trajectories corresponding to the results on the left, showing how noise pushes or keeps the trajectories out of the basin of attraction of the periodic orbit, which is also shown in red

Full size image
Fig. 4
figure 4

The distributions (histograms) for the time of last spike for small noise σ = 0.1 and larger noise σ = 0.45. These are based on 500 trials with an initial value on the periodic orbit for the standard parameter set

Full size image

Exit-time and orbit stability

If a basin of attraction for a periodic orbit can be found, then the probability that the process with noise escapes from the region of attraction gives the probability, in the present context, that spiking will cease. Since the system (1)–(4) is Markovian, we may apply standard first-exit time theory (Tuckwell 1989). Letting \({{\mathcal{A}}}\) be a set in R 4 and letting \({{\mathbf{x}}}= (x_1,x_2,s_1,s_2) \in {{\mathcal{A}}} \) be a value of (X 1, X 2, S 1, S 2) at some given time, the probability p(x 1, x 2, s 1, s 2) that the process ever escapes from \({{\mathcal{A}}}\) is given by

$$ \begin{aligned} {{\mathcal{L}}}p\ \equiv\ & {\frac{\sigma^2}{2}} {\frac {\partial^2p}{\partial x_1^2}} + {\frac{\sigma^2}{2}} {\frac {\partial^2p}{\partial x_2^2}} \\ & \quad + [(x_1-x_R)^2 + \beta + g{_{s}}x_3]{\frac{\partial p}{\partial x_1}} + [(x_2-x_R)^2 + \beta + {g_s}{x_4}]{\frac{\partial p}{\partial x_2}} \\ &\quad + \left(F(x_2)- {\frac{s_1}{\tau}}\right){\frac{\partial p}{\partial s_1}} + \left(F(x_1)- {\frac{s_2}{\tau}}\right){\frac{\partial p}{\partial s_2}} = 0, \quad {{\mathbf{x}}} \in {{\mathcal{A}}}, \end{aligned} $$
(5)

with boundary condition that p = 1 on the boundary of \({{\mathcal{A}}}\) (since the process is continuous). If one also adds an arbitrarily small amount of noise for S 1 (s 1) and S 2 (s 2) (or considers those solutions of Eq. (5) that arise from the limit of vanishing noise for S 1,S 2), the solution of the linear elliptic partial differential equation (5) is unique and ≡ 1, that is, the process will eventually escape from \({{\mathcal{A}}}\) with probability 1. Hence, the expected time f(x) of exit of the process from \({{\mathcal{A}}}\) satisfies \({{\mathcal{L}}}f =-1, {{\mathbf{x}}} \in {{\mathcal{A}}} \) with boundary condition f = 0 on the boundary of \({{\mathcal{A}}}.\) In fact, for small noise, the logarithm of the expected exit time from \({{\mathcal{A}}},\) that is, the time at which firing stops, behaves like the inverse of the square of the noise amplitude (Freidlin and Wentzell 1998; Dembo and Zeitouni 1998).

These linear partial differential equations can be solved numerically, for example by Monte-Carlo techniques. The basin of attraction \({{\mathcal{A}}}\) must be found in order to identify the domain of Eq. (5). We have done this approximately for the square P in Fig. 1. The effects of perturbations of the periodic orbit S within P on the spiking activity were found by solving Eqs. (1)–(4) with various initial conditions in the absence of noise. The values of x 1 were from −0.43 to 1.57 in steps of 0.2 and the values of x 2 were from −4 to 2 also in steps of 0.2. For this particular region, as expected from geometrical considerations, the system responded sensitively to variations in x 1 but not x 2. For example, to the left of S there tended to be no spiking activity whereas just to the right there was a full complement of spikes and further to the right (but still inside P) one spike.

Coupled Hodgkin–Huxley neurons

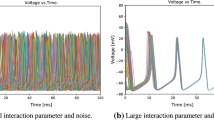
As an example of a Type 2 neuron, we use the standard Hodgkin–Huxley (HH) model augmented with synaptic input variables as in the model for coupled QIF neurons given by Eqs. (3) and (4), but with different parameter values. It has been long known that additive noise has a facilitative effect on single HH neurons (Yu and Lewis 1989). Coupled pairs of HH neurons have been employed with a different approach using conductance noise in order to analyze synchronization properties (e.g. Casado and Baltánas 2003). For the present approach, with X 1 and X 2 as the depolarizations of the two cells, we put,

$${\rm d}X_i={\frac{1}{C}}[ \beta + \overline{g}_Kn_i^4(V_K-X_i) + \overline{g}_{Na}m_i^3h_i(V_{Na}-X_i) + g_l(V_l-X_i)]{\rm d}t + g_{s}S_i{\rm d}t + \sigma {\rm d}W_i, $$

where i = 1,2. The equations for S1 and S 2 are again as in Eqs. (3) and (4). The equations for the auxiliary variables h i ,m i and n i are standard and all parameters associated with the Hodgkin–Huxley equations were assigned the standard values (Hodgkin and Huxley 1952).

When each cell is in the oscillatory regime, synaptic connections can modulate the spike rate, and noise can speed it up. In the bistable regime, when each cell has a stable rest point as well as a stable periodic spiking orbit, synapses can initiate or augment joint oscillatory spiking, but noise can stop it. This can be seen in simulations and deduced from the qualitative theory of dynamical systems. We note here that in general the ten-component coupled Hodgkin–Huxley model has a much more complex behavior then the QIF model considered in the previous section. Hence, in principle noise may lead to effects that are more nuanced and subtle in the HH model.

Length constraints preclude us from a detailed discussion. Here it suffices to note that each of the HH cells may either be excitable (at rest unless perturbed), bistable (as above: with a coexistent limit cycle as well as a stable steady state), oscillatory or in depolarization block (where only a single transient spike is emitted followed by a decaying oscillation to a depolarised steady state). In the first case, noise may pump the inherent subthreshold oscillations of the membrane and lead to the well discussed stochastic resonance effect for spiking (Lee and Kim 1999). In the latter case, the noise again may lead to subthreshold oscillation, and perhaps even partially relieve the block extending the upper limit of repetitive spiking. In the bistable case, even in a single cell, noise can induce transitions between the oscillatory and rest states. In fact this has been demonstrated for Type II neurons in the cortex (Tateno et al. 2004). Hence for our case, the synaptic coupling is strictly speaking, necessary only to initiate the sustained firing in each of the bistable HH neurons and is not required for the subsequent firing. Thus, a noise dependent transition of one of the cells into the lower steady state does not necessarily imply that the whole circuit will turn off: the second cell may remain in the “upper” oscillatory state. Yet if the synapses are strong enough (to fire either of the neurons), a transition of one of the cells into the oscillatory state from the “lower” rest state will always lead to sustained activity for the whole circuit. These effects remain an active research topic and we will report further on our investigations of them elsewhere.

Discussion

We have studied the effect of noise in systems of two coupled neurons of Type 1 and Type 2. In Type 1, we found a generic effect, because QIF neurons represent a generic model. That effect is that while coupling can cause asynchronous oscillatory activity in excitable neurons, noise can terminate that sustained spiking (near to the bifurcation point where the asynchronous periodic orbit emerges). This circuit model is a stochastic analogue of the deterministic case previously studied by Gutkin et al. (2001) where it was found that transient synchronization can terminate sustained activity. For Type 2 neurons, we have investigated coupled Hodgkin–Huxley neurons and found that in the bistable regime, noise can again terminate sustained spiking activity initiated by synaptic connections. We have investigated a minimal circuit model of sustained neural activity. Such sustained activity in the prefrontal cortex has been proposed as a neural correlate of working memory (Fuster and Alexander 1971).