Abstract
We measure the empirical distribution of the accuracy of projected population in sub-national areas of England, developing the concept of ‘shelf life’: the furthest horizon for which the subsequent best estimate of population is within 10% of the forecast, for at least 80% of areas projected. Since local government reorganisation in 1974, the official statistics agency has projected the population of each local government area in England: for 108 areas in nine forecasts up to the 1993-based, and for over 300 areas in 10 forecasts from the 1996-based to the 2014-based forecasts. By comparing the published forecast (we use this term rather than projection) with the post-census population estimates, the empirical distribution of errors has been described. It is particularly dependent on the forecast horizon and the type of local authority. For 10-year forecasts the median absolute percentage error has been 7% for London Boroughs and 3% for Shire Districts. Users of forecasts tend to have in mind a horizon and a required accuracy that is of relevance to their application. A shelf life of 10 years is not sufficient if the user required that accuracy of a forecast 15 years ahead. The relevant effective shelf life deducts the user’s horizon. We explore the empirical performance of official sub-national forecasts in this light. A five-year forecast for London Boroughs requiring 10% accuracy is already beyond its effective shelf life by the time it is published. Collaboration between forecasters and users of forecasts can develop information on uncertainty that is useful to planning.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Are population forecasts acceptably accurate for those who make decisions based on them? A simple answer would take the continued reliance of decision-makers on population forecasts as an indication of their acceptance. A more considered answer demands information about the benefits of forecasts and the costs of their inaccuracies that are only dimly understood. The answer is likely to vary for each application: the requirements for managing an individual school and for allowing the expansion of housing land involve significant but different resources.
This study focuses on the empirical measurement of the accuracy of past population forecasts of sub-national areas in England made by the national statistics agency (Office for National Statistics [ONS]) across 40 years between 1974 and 2014. It uses the results to provide confidence intervals around 2016-based forecasts, and uses the concept of ‘shelf-life’ (Wilson et al. 2018) to provide an answer to the question of the forecasts’ quality. These official forecasts are cohort component forecasts with age and sex disaggregation; in this paper we look only at the accuracy of the forecast of total population.
This introduction summarises the state of the art for evaluation of sub-national population forecasting, and finishes by setting out the structure of the rest of the paper. We use the term ‘forecasting’ in spite of official agencies’ preference for naming their product as ‘projections’, because most users of the projections take official outputs as the most likely future, on which plans can be based. In the official projections considered here the assumptions are framed as “the continuation of recent demographic trends” (ONS 2016: 4), rather than less likely scenarios. Later in the paper we describe the official methods and here we acknowledge that the official production is based on the past 5 years’ local experience of fertility, mortality, and migration, albeit shaped somewhat by national assumptions for long-term future trends of fertility, mortality and international migration. There is no attempt to forecast local developments that might differ from what has happened in the past 5 years. We also use the term jump-off year to be synonymous with ‘launch year’ in some other literature, and ‘base year’ in ONS reports, referring to the latest year in the forecast for which data are estimated from direct evidence of population or population change. ‘Base year’ is elsewhere usefully used for the year from which past data are gathered to inform a forecast (Rayer et al. 2009), which is 5 years earlier than the jump-off year in the forecasts studied here.
We should also acknowledge the useful variety of analyses of variation between forecasts, in order to clarify our own aims. One approach measures reliability, referring to variation in how recent demographic trends might be projected forward, without reference to their closeness to actual future population (explored for London by Greater London Authority 2015, Appendix A). Another is the comparison of scenarios that explore the impact of specific factors on future local population, such as the UK exit from the EU, or a proposed housing development. We take a third approach in this paper, focussing on inaccuracy and prediction error by comparing past forecasts with the eventual population outcome. Our approach is one of ‘error analysis’ in the classification of evaluation methods by Rees et al. (2018, Table 1).
The variation between scenarios indicates different demographic outcomes, but is not a quantification of the uncertainty surrounding each scenario. The planner needs both approaches: the most likely implications of alternative plans, and the uncertainty around each outcome. This was recognised in the earliest of public administration texts (e.g. Baker 1972: 119–126).
Tayman (2011) and Wilson et al. (2018) list reasons for studying the accuracy of forecasts and summarise the results most generally found. Information on accuracy can identify problems that when rectified improve future forecasts, manage users’ expectations about size of errors, indicate the most reliable results which should be emphasised in publication, distinguish between producers, help planners design contingency plans, and be used to quantify error in current forecasts (Wilson et al. 2018: 148).
Based on extensive investigations of sub-national forecasts in the USA, Jeff Tayman summarises their accuracy as follows:
-
1.
Forecast error generally decreases with population size; although once a certain size threshold is reached the error level tends to stabilize;
-
2.
Forecast error is lowest for places with stable population or slow rates of change and highest for growth rates that deviate from these levels; that is, the error increases in areas with increasing rates of population change (either positive or negative);
-
3.
Average forecast error generally grows linearly with the horizon length;
-
4.
No single method of projection has consistently larger errors than any other. Put another way, more complex methods do not outperform simpler methods in terms of their forecast error; and
-
5.
No general conclusions can be drawn regarding the direction of forecast error or bias. There is no way to know in advance whether a particular forecast (or set of forecasts) will be too high or too low. Over time positive and negative errors seem roughly in balance. In these sense (sic), most population forecast methods are likely to be unbiased.” (Tayman 2011: 782)
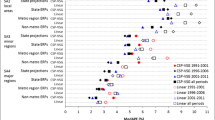
Tayman characterises the impact of two main factors, horizon and population size, summarising for the USA that the mean absolute percentage error (MAPE) ranges from 3% for State forecasts (average population several million) to 9% for Census Tract forecasts (population 2500 to 8000) 5 years ahead, and from 18% to 54% for forecasts with horizon 30 years ahead. Forecasts for small areas in Australia showed the same association with horizon and population size, and a stabilising of error in populations over 20 thousand. The MAPE was rather less than in the USA, for 5 years ahead averaging 4.5% for areas with population size mainly smaller than 10 thousand. In a study of Japan and a comparative review, Yamauchi et al. (2017) found a still lower MAPE of 0.8% to 2.3% for a horizon of 5 years across Japan, USA and European countries. The variety of results suggests that there are several characteristics that affect forecast accuracy, including but not limited to size of population.
For England, the evaluation by ONS (2015) of its four forecasts based in the 2000s against the 2011 Census showed a similar pattern of results for horizon and population size, as had its earlier assessment of forecasts based between 1996 and 2004 (ONS 2008). Forecasts 5 years ahead of local authority populations, ranging up to 1 million but mostly between 20 and 200 thousand, had a root mean square error (RMSE) of 6.6%. The RMSE emphasises large errors and is therefore higher than the MAPE, suggesting a lower error than the USA and more in line with the experience of Australia. The better accuracy than the USA for the UK and Australia may be explained by Australia’s advantage of five-yearly censuses, and England’s advantage of annual age-specific demographic information from its national health service from which sub-national migration flows are derived. ONS (2015) compared the accuracy of only four forecasts, contrasting the overall average for local authorities and for the much larger regions of England. The UK water industry has extrapolated from this ONS analysis of four forecasts, providing confidence intervals for total population for horizons of 5 to 30 years ahead (UKWIR 2015). We have been surprised to find no other evaluation of past official sub-national forecasts in the UK, although the accuracy of a longer run of national forecasts has been studied by ONS itself (Shaw 2007). The current paper is able to look back over nineteen forecasts and examine the influence of population size, horizon and other factors.
There are strong indications from these past studies that particular types of local areas will lead to greater uncertainty in population forecasts. Higher error of forecasts was found in areas of population change in the USA, in mining areas and areas with majority Indigenous populations in Australia (Wilson and Rowe 2011), and in London in England, suggesting that error is associated with irregular and occasionally intense levels of migration, whether internal or international. The association of types of area with different levels of uncertainty guides users towards a more precise expectation of accuracy for specific areas.
Forecasts are never entirely accurate, but are they accurate enough? An average error is not so useful in this context, since an indication of the error to be expected approximately half the time is a low threshold for users, who would prefer to know the range within which the forecast will more usually be correct. A distribution of uncertainty is required. Directly probabilistic methods of forecasting which could yield prediction intervals are rarely attempted at sub-national scale. This paper instead follows the strategy of Wilson et al. (2018): “Empirical prediction intervals are much simpler and easier to handle at the local scale. They can also simply be ‘added on’ to existing local area forecasts without requiring any change to forecasting methods and processes” (140). Empirical prediction intervals are derived by comparing past forecasts with a subsequently estimated ‘truth’: the best estimate of population that has become available after censuses and demographic monitoring of births, deaths and migration.
A target is set of the truth being within 10% of the forecast 80% of the time. Remembering that forecasts with longer horizons are less accurate, the ‘shelf life’ of a forecast in Wilson et al. (2018) is the furthest horizon with which a forecast can expect to still meet that target. Note that we have adjusted the definition since Wilson et al. (2018) where the forecast had to be within 10% of the truth: the truth is unknown to the user when a forecast is made and the user’s interest is in the distance of the truth from the forecast rather than the reverse. It is a slight adjustment but one we think is in accord with the user’s perspective.
In this paper we extend the concept of shelf life to consider the user whose interest is accurate forecasts N years ahead. That user needs the shelf life of a forecast to be at least N years. Indeed, the effective shelf life for that user must deduct N years from the shelf life defined by Wilson et al. Figure 1 shows the relationship between shelf life and effective shelf life for a user.
For example, local ‘district plans’ in England often look 15 years ahead to set the release of land for housing (Simpson 2016). If the planner expects to have 80% confidence that the actual outcome will be within 10% of the forecast, then s/he needs to know this will be the case for forecasts with horizon of at least 15 years ahead. If our study showed this confidence can be had for forecasts 20 years ahead, then for this user the forecasts have an effective shelf life of 5 years after their jump-off year.
This paper is structured as follows. The data are described, involving matching past forecasts to subsequent population estimates. We note differences in the nature of the evidence from Australia and England. The measures of accuracy are described in a section on methods. The results are presented in three parts (sections 4 to 6 below). The first and longest part summarises the average accuracy from past forecasts with jump-off years 1974 to 2014, and associates it with horizon, population size, and type of local authority area. Known variations in data quality are explored and found to have limited effect on uncertainty. The second part of the results derives a probability distribution from the past forecasts and applies it to the latest 2016-based forecasts. In the third part, the shelf-life of forecasts of local authorities in England is calculated. A discussion of the significance of the results and opportunities for further research concludes the paper.
Data
The nineteen official forecasts with jump-off years 1974 to 2014 for local authority areas in England have been collated from outputs of the Office for National Statistics (ONS) and its predecessor the Office for Population Censuses and Surveys (OPCS). All sub-national forecasts employed a standard cohort component projection methodology with single years of age, using a prior forecast for England to control the sum of sub-national forecasts for each of births, deaths, internal migration and international migration.
The main methodological changes over time have been the sources for migration data. In the 1990s estimation of internal migration within the UK switched from a mix of census, health records and electoral analysis to inference only from health-based administrative data. International migration has relied on the International Passenger Survey, combined with a variety of indicators for its distribution within the UK. For each component of change, future assumptions are generally set to repeat the local experience of the 5 years prior to the jump-off year, relative to the national experience. Representative methodological descriptions are contained in OPCS (1977-1995), ONS (1999), and ONS (2016).
In 1974, local authorities were reorganised and given more strategic powers. 1974 is the first year from which official sub-national projections were made: for 36 Metropolitan Districts, for 39 Shire Counties, and for London as a whole. From 1977, the 33 London Boroughs were projected individually. From 1996 the districts within the Shire Counties were projected, as well as the Unitary Authorities, a new category of local authority created in that year from some of the Shire Districts, usually amalgamating whole districts into new authorities (see Table 1).
Forecasts from years up to 1993 were transcribed from printed reports (OPCS 1977-1995) that give results for selected years rounded to the nearest 100. Forecasts from 1996 were available as spreadsheet files for each year of the forecast and unrounded except for the 2010–2014 projections which were again rounded to the nearest 100. In total, the 19 sets of projections included 4362 area projections. The transcription of forecasts from printed reports was subject to internal consistency checks which revealed one discrepancy within the reports; for the jump-off year population of the 1983 forecast, the sum of areas in the South East region including London is 6900 lower than the jump-off population provided for the region as a whole. No correction has been found for the discrepancy but it can have only a minor effect on the analysis.
Each forecast has been matched to the latest official estimate for the year projected, which we take as our ‘truth’. The estimates are also a product from ONS, rounded to the nearest 100 from 1974 to 1980 and unrounded for all subsequent years up to the most recent, for 2017. The matching process was complicated because sometimes a forecast extended across the periods of local authority reorganisation indicated in Table 1. Area boundaries are also subject to regular review which occasionally results in movements of boundary that affect the population, though usually these are minor. In the great majority of cases there is a one-to-one match between forecast and estimate, but where necessary we have aggregated the forecast areas or the estimate areas to provide the closest match possible, using a variety of Geographical Conversion Tables for 1-to-1 and many-to-1 matches (Simpson 2002; Rees et al. 2004).
The resulting dataset has 40,729 pairs of a forecast with corresponding estimate. These include the forecast for the jump-off year itself, which is the estimate for that year at the time of the projection. In our dataset this is also compared with the revised estimate after a subsequent census. The forecast horizons in the dataset are from 1 up to 23 years. Recent forecasts have horizon up to 25 years but the final years are beyond the official demographic estimates, at the time of analysis. A proportional Geographical Conversion Table between local authorities of 1981, 1991 and 2001 was used to indicate the percentage of addresses which had changed between those years for local authorities which were superficially the same. Such changes affected 6% of forecast-estimate data points, but in all but twenty five data points the impact was of less than 1% of the population.
The dataset allows for the first time an assessment of the accuracy of sub-national population forecasts made over four decades within England. It contains the projected and observed total population at jump-off year and forecast year, the horizon (the difference in years between jump-off and forecast year), and the five types of local authority referred to in Table 1. Further work could include the age structure which has been recorded in each forecast but not transcribed, and area characteristics which can be matched from censuses.
In order to maintain more than a thousand forecast points in the categories for which results are given, some analyses group the horizon of each forecast into 0–2 years, 3–7 years, 8–12 years, 13–17 years and 18–23 years. The mid-points of 1 year, 5 years, 10 years 15, years, and 20 years make possible convenient comparisons with other studies. The jump-off population size is that estimated for the jump-off (base) year of each forecast, and is grouped into categories to ensure more than a thousand forecast points in each category except the smallest. The largest jump-off population category is 0.5 m to 1.5 m, including the very largest metropolitan districts such as Birmingham, and the largest shire counties such as Essex that were forecast up to the 1993-based release. The smallest population category contains only the Isles of Scilly and the City of London, both with jump-off populations always under 10,000, while all other areas have jump-off populations always more than 20,000. This smallest category provides 237 forecast points.
Three significant differences exist between this dataset and that obtained for Australia in our previous work. First, the areas considered for England are generally larger than those in Wilson et al. (2018), which had a median population size of about 10,000 with only 5% of populations exceeding 135,000. Second, the areas considered for England are those which raise direct taxes, receive financial contributions from central government, and are responsible for town planning and providing many local services. This gives the forecasts a semi-legal status within the English planning system. Third, the horizon of each data point varies from 0 (the jump-off population) to 23, with values between; in Australia the practice of forecasting from quinquennial censuses naturally gave rise to horizons of 5, 10, 15 and 20 years, so that there is a structural difference between the datasets.
Methods
The forecast error of each forecast for an individual local area was measured by the percentage error (PE):
where F denotes the forecast as published, t a year in the future, and E represents the estimated resident population. Positive values of PE indicate forecasts which were too high; negative values are obtained for forecasts which proved too low.
ONS ‘rebases’ the estimated resident populations after each census, updating its best estimate for each of the years since the previous census to be consistent with the new evidence from the latest census. This results in discrepancies between jump-off populations in the forecast datasets and the rebased estimates for the same year. We therefore decided to include a second measure of error which removes jump-off discrepancies for all forecasts to remove the effect of the initial discrepancy:
where 0 refers to the jump-off year.
A third measure has been calculated, to remove the impact of the national forecast for the same jump-off year, to which the sum of area forecasts is constrained. This third measure is:
The first measure is used in most of this paper, because it reflects the error actually encountered. The second measure is most suitable for comparing forecasts with different jump-off years. The third measure is most suitable for comparing the performance of these forecasts with other forecasts that might be made for a local area; it also relates well to the distribution of resources to local authorities.
When calculating a prediction interval for forecasts and their shelf life, we measure the percentage deviation of the estimated truth from the forecast, requiring a slight adjustment so that the forecast is the denominator:
In much of the paper, absolute percentage error (APE), the unsigned value of PE, is used. Average absolute errors are reported with median absolute percentage error, the middle value of a set of ranked errors. Average signed errors are measured with median percentage error. Table 2 gives the median and mean for APE and PE, for each of three measures defined above, and of the percentage deviation (PD) and its absolute value (APD). The forecasts as published have little bias and very close to 2% median absolute error. The mean APE is larger than the median, reflecting a considerably skewed distribution with a long tail of few extremely large errors. A substantial portion of the error is accounted for by error in the population estimated for jump-off year. When further constraining each forecast to the independently-forecast national total, some large errors are reduced and bias nearly eliminated, but the median APE is not improved. The use of the forecast as denominator, PD rather than PE, makes little difference to the summary distributions: the sign of the percentage is reversed, and the absolute averages are very similar.
Previous authors (in demography, Rayer et al. 2009) have based empirical prediction intervals for forecasts on the distribution of absolute percentage error. Since the user is interested in how far the truth will be from a forecast, we believe that it is the distribution of absolute percentage deviation that is more relevant when providing advice to users, APD as defined above rather than APE. We have examined the results from both approaches and they differ in small ways rather than in the pattern or the general conclusions, but we believe that our use of APD for our results on error distribution and shelf life give more direct answers to the user’s question ‘How far is the truth likely to be from this forecast?’
Both the forecast and the estimate are affected by errors when estimating population between census years. As the jump-off year is up to 9 years later than the previous census year, the forecast might be expected to be increasingly in error not only in its jump-off population but for all horizons. The estimate itself can be expected to be increasingly in error even after correction following a census, as it refers to 0 to 5 years away from that census. For example a forecast with jump-off year just before a census year is likely to be in greatest error, while the estimate for that year will be good because estimates are corrected after each census. These measures of distance from census of the jump-off year and estimate year were calculated to test their impact on the measured accuracy of each forecast point.
Finally, the impact of different factors was assessed against each other using linear regression models of the absolute percentage error, APE, after a suitable transformation to make it approximately normal in distribution.
Results: The Accuracy of Past Forecasts
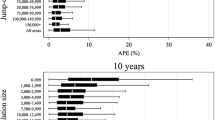
Population Size
Figure 2 shows that there is little relationship between population size and the size of forecast errors, for English local authorities with population over 20 thousand. There are only two areas under this threshold, the Isles of Scilly and the City of London, both of which have had a population estimated and projected under 10 thousand throughout the period under consideration. The Isles of Scilly resident population varies with season, while the City of London’s population is affected by the unpredictable changing use of its inner-city buildings. It is difficult to say when development of a specific small area may take place, whereas larger areas are more predictable.
Among the bulk of areas with population between 20 thousand and 300 thousand the absolute error shows little pattern. The fewer observations for very large areas have rather lower absolute percentage error. The median APE appears to reduce slightly for populations over 275 thousand, but in general there is little relationship between population size and error for larger populations.
On the other hand, forecasts do degrade over time, with larger errors for longer horizons, at every population size. Forecasts just 0–2 years ahead have a median error of under 2%, while forecasts 8–12 years ahead can be expected to have about 5% error, and 18–23 years ahead are often nearer 10% error than 5%. The population sizes and horizons are grouped in Fig. 2 to ensure several hundred and usually more than one thousand data points in each category. An appendix provides fuller results and numbers of areas in each category.
Type of Local Authority
Figure 3 confirms that forecasts for London Boroughs during the period under study suffered from the greatest uncertainty, more than double the median error for each of the other types of local authority. London can largely be considered as one labour and housing market, so that movements of population between its Boroughs are relatively frequent. Changes in the nature of areas related to gentrification, to entry points for immigration, and to student living, mean that areas may house many more people or fewer people in the same housing stock over a period, in ways that are not forecast well. Inner (and many outer) Boroughs have little scope for building on new sites, which is more typical of other types of local authority in satisfying forecast demand. Areas outside London are more self-contained. Unitary authorities often contain a large city and are in that sense similar to many of the Metropolitan Districts.
Median APE, according to type of local authority and horizon. Notes. Horizon is grouped in categories centred on the values shown on the axis: 0-2 yrs., 3–7 yrs., 8–12 yrs., 13–17 yrs., and 18–23 yrs. the values of median APE are added for London boroughs and for Shire counties only, to avoid clutter (values for all categories shown in the appendix). Isles of Scilly and City of London excluded
Shire Counties provide a useful contrast to the Shire Districts that are contained within them. The Counties show considerably less error. In this dataset an official forecast was made for either all Shire Counties (up to 1993-based forecasts) or all Shire Districts (forecasts from 1996), and so the averages in Fig. 3 refer to different forecasts. But it is reasonable to suppose that the lower errors for Shire Counties are a result of their larger size, since errors for smaller areas will tend to cancel out when added to larger areas. This suggests that the overall lack of association between population size and error found in this and other studies of relatively large localities may be an artefact of the nature of the larger areas.
Focusing now on the greatest percentage errors recorded at a fixed 10 years horizon, these were for the small City of London and other London Boroughs. The largest percentage error outside the City of London was an over-estimate of 45% made for Kensington & Chelsea from 2003 to 2013. In Westminster and Kensington & Chelsea a population growth of more than 10% during 1998–2003 had led to forecasts made during that period that suggested further growth, when in fact the population stabilised shortly afterwards. Additionally the 2000-based forecast suffered from a considerable over-estimate in the starting population that was corrected after the 2001 census. The over-forecasts of between 30 and 47% (Fig. 4) were due to short-lived population growth in inner-urban areas, probably from international migration which then dispersed to other areas in secondary moves that were not monitored well by the existing estimates methodology. This tendency to keep immigration too long in inner London Boroughs, and insufficiently distribute it to outer London Boroughs, was much reduced by ONS in its estimates and projections from the mid-2000s (ONS 2012).
Outside London, the greatest errors were experienced by Forest Heath shire district in Suffolk. It is home to the largest US Air Force base in the UK, whose residents are included in population estimates and which are consequently subject to irregular change.
Data Quality
Kensington and Chelsea’s error in the jump-off population shortly before the decennial census raises the possibility of associating error with the jump-off year. Figures 5 and 6 explore this and other indicators of data quality. In Fig. 5, there is a slight association with the distance from the previous census to the jump-off year, so that forecasts made in the years before the next census tend to have larger errors, but the association is neither linear nor large. One might separately expect the post-census population estimates that we have used as the ‘truth’ to be least accurate in the years furthest from a census, i.e. mid-decade, and for this to show in the assessment of forecast error, but this is not the case. These raw comparisons may be misleading, because only one forecast was based in census year and only one forecast was based in the year after a census. The latter was the 2012-based which contributes data points only with low horizons up to the latest estimate for 2017 and could be expected to therefore have low errors. The black bars in Fig. 5 therefore divide the values of APE by the horizon, when the horizon is more than 1. This gives some recognition that absolute error is approximately linearly related to horizon. The pattern of errors with distance from the census year is more in line with that expected, but the relationships are not strong.
The major influence on error from data quality in Fig. 5 is among the 25 cases where the forecast area could not be matched very closely with an estimate for the same area. These are too few cases to influence the patterns found above for horizon and population size.
Figure 6a shows the association of jump-off year with median error. Again, the latest forecasts can be compared only with estimates for their shortest horizons; their low errors are to be expected and are not a fair comparison with earlier forecasts. Figure 6b corrects for this in two ways. First, the error at jump-off year, known for each area from the estimates which have been revised with successive censuses, has been deducted from all the forecasts of that jump-off year (see Methods section above). Secondly, each forecast’s error has been divided by its horizon, for horizons more than 1.
From 1996, the forecasts included all Shire Districts rather than the larger Shire Counties, which may account for the slightly larger errors seen in Fig. 6b for jump-off years 1996 through to 2006. Improved measures of internal and international migration were developed from the late 1990s, and may be visible in the slightly lower median errors in the latest forecasts. However, this will also be partly due to our inability to correct for jump-off error in the last two forecasts, which awaits the rebasing of population estimates after the 2021 Census. We were not able to retrieve the unrebased population estimates from previous decades, which would have enabled a like-for-like comparison for the accuracy of these latest forecasts.
Regression analysis has been used to test the hypothesis that population size may be associated with reduced error once the impact of district type has been taken into account. The two smallest districts were omitted, as were the twenty-five data points where boundaries of forecasts and estimates could not be closely matched. Following the approach of Marshall et al. (2017), a log transform to the absolute percentage error provided a near-normal dependent variable. Independent variables were horizon and its interaction with the five district types as in Fig. 3. Jump-off population size was additionally statistically significant; allowing for different slopes for each district type provides coefficients varying between −0.20 to +0.05 per hundred thousand difference in jump-off population. These are smaller than the impact of different types of district or the length of horizons of the forecast. The model details are provided in the appendix.
Comparison with a Constant Forecast
One result from previous studies, and confirmed by the discussion of large errors above, is that rapid population change is unlikely to be sustained and will therefore be associated with large errors in forecasts. One might worry that all forecasts which are based on recent change will suffer from this unpredictability. Figure 7 reassures somewhat. It shows that the errors for an alternative that assumes no change at all performs considerably worse than the official forecast, for all horizons after the jump-off year.
Bias
Any overall bias would be mostly induced by the national forecasts to which sub-national forecasts are constrained. Figure 8 confirms previous studies for other countries that there is no clear bias to official English sub-national forecasts: one cannot say that there has been a tendency to produce over-forecasts or under-forecasts, although under-forecasts have been more often experienced. These under-forecasts are most pronounced within London, due to a growing net impact of international migration in the 2000s.
Results: A Probability Distribution Applied to 2016-Based Forecasts
We calculated empirical prediction intervals for the total population in local areas using distributions of the absolute percentage deviation (APD) of the estimated truth from the forecast. The 80th percentile of past APD distributions (Table 3) can be interpreted as an 80% prediction interval for a current population forecast. This interpretation assumes that (i) future errors will have the same median size and distribution as in the past, and (ii) local areas will experience the same errors as others in their district type category.
In Fig. 9, the 80th percentiles of the probability distribution for each type of district are plotted, interpolating and extrapolating linearly to provide values for each horizon of zero up to 25 years. The jump-off year has zero horizon: the error is that of the estimated population at the time the forecast is made.
80th percentile of absolute percentage deviation, according to type of area. Notes: Interpolated and extrapolated from adjacent values in Table 3
The 80% prediction interval may be calculated for a local area population forecast as:
where the 80th percentile APD refers to the values in Table 3, interpolated and extrapolated for horizons from 0 to 25.
These prediction intervals are approximate. They are symmetrical only because they are calculated from the absolute percentage deviation applied either side of the forecast. Intervals could be refined by incorporating asymmetry, which would tend to indicate less uncertainty below than above the main forecast. But the intervals calculated as above do provide appropriate guides to the uncertainty intrinsic to local area population forecasts and allow them to be visualised with minimal data inputs.
Forecast producers can use prediction intervals calculated in this way to provide users with measures of uncertainty. They should stress that they are conditional in nature, and note their weaknesses and strengths. They represent the likely range of error in a current set of population forecasts, providing that the error distributions of the past also apply in the future. This assumption will not hold if there have been or are in the future major changes in demographic trends, if local planning creates or demolishes substantial developments, if an area’s main employer closes, or if there are major disasters. Even without shocks such as these, the 80% interval does not indicate a maximum–minimum range. An estimated 20% of population outcomes will lie outside the 80% interval. There are usually some local areas that experience large errors due to specific local factors.
This approach to empirical prediction intervals has been implemented for all English official forecasts, and is illustrated in Fig. 10 for selected sub-national areas forecast by ONS with 2016 jump-off (ONS 2018).
2016-based forecasts for four districts, with 80% confidence interval. Notes. The thick lines show the ONS estimated population from 2001 to 2016 and its 2016-based forecast of total population for each area and the estimated population. The dotted lines show a symmetrical 80% confidence interval around each forecast. MD = Metropolitan District; LB = London borough; UA = unitary authority; CD = County District
Each forecast suggests growth over 25 years, with greatest growth for the London Borough of Tower Hamlets. In each District, however, there is a not insignificant chance that the population will grow either minimally or not at all. In Liverpool the re-attainment of half a million population after decrease in the twentieth century is by no means certain, but is likely. Following the empirical evidence of higher past errors in London Boroughs, the 80% confidence interval after 10 years amounts to 14.9% of the forecast for Tower Hamlets, or 53 thousand residents either side of the forecast of 355 thousand.
The four districts have been chosen because they are currently engaged in consultation on local plans, which depend heavily on the evidence of demographic change in the ONS forecasts and the household forecasts that will be derived from them. The plans usually aim to attract housing projects to meet the forecast of demand exactly, although the London-wide plan adopts Borough housing targets according to land availability. The past evidence suggests that the future demand in each district will not be as suggested in the forecast, even if the forecast is the most likely future. A higher or lower outcome may result in crowded or under-utilised properties. Forecast errors may in part be due to migration responding to over or under-provision, reminding us that the housing market and the population adapt to each other.
Results: The Shelf Life of a Forecast
If the past errors calculated for this paper prove a guide to the magnitude of errors in the future, then ‘shelf life’ estimates for current local area forecasts can be calculated on the basis of users’ demand for levels of accuracy. Following Wilson et al. (2018) the shelf life can be defined as the number of years ahead that 80% of estimated populations for local areas remain within 10% of their forecast. Taking 80% as the cut-off covers the majority of forecasts but excludes the more volatile tail-end of the error distribution (Lutz et al. 2004). The analysis of the 80th percentile of absolute percentage deviation given in Table 3 and Fig. 9 provides the shelf life in Table 4, for which 80% of forecasts for local areas remain within 10% APE.
It is clear from Table 4 that the accuracy of forecasts for London Boroughs is much less than for other sub-national areas, in the sense that it dips below 10% for 80% of areas within 6 years, while forecast for other types of area remain with that accuracy for 18 years or longer.
Now we extend the interpretation of Wilson et al. (2018) to include the user’s horizon of interest to establish the effective shelf life, which is always less than the shelf life as defined here. A user who requires 10% accuracy in a forecast N years ahead, must deduct N from the shelf life. For example, if a user requires 10% accuracy with 80% certainty for a forecast 15 years ahead, and a forecast is within that accuracy up to 18 years ahead (that is its shelf life), then for this user’s purpose the forecast has an effective shelf life of just 3 years from its jump-off year.
Demographic forecasts in England are used with a variety of perspectives. They are a strategic guide for at least 15 years ahead. The forecasts for London Boroughs are not fit for this purpose if it is desired that their uncertainty does not exceed 10% in 80% of cases. For Unitary Authorities and Shire Districts the forecasts’ effective shelf life expires 3 or 5 years after their jump-off year. Only for Metropolitan Districts, or aggregates of other areas, do the forecasts last longer.
The forecasts are also used to set land-release for the following 5 years. If 10% is again set as the permissible error, the forecasts for London Boroughs have an effective shelf life of only 1 year after the jump-off year, which has usually expired before their publication due to the time taken in assembling relevant data. Other types of area have less uncertainty in their forecasts.
Of course, these effective shelf life estimates contain several limitations. They are only approximate indicators of the longevity of forecasts. They apply error distributions from large numbers of past forecasts to individual areas based on smooth lines fitted to fairly noisy original data, and they do so simply on the basis of five types of area and not any other characteristics. Nonetheless, they provide a simple indication of how far into the future a forecast is likely to remain usable and when it has reached its ‘use by’ date. Forecasts beyond the recommended effective shelf life should be disregarded by users in the majority of situations. Forecast producers could consult shelf lives to decide how much of their forecasts to report. If they applied the shelf life concept as a cut-off for publication, it would result in much shorter forecast horizons being published than the 20–30 years commonly found today.
Discussion
We have extended knowledge about the accuracy of sub-national forecasts by comparing 40 years of official forecasts in England with the subsequent best population estimates. We confirm that forecasts degrade with the distance of the horizon to which they look ahead, in a close to linear relationship. The accuracy is not the same for all areas, and in particular forecasts for Boroughs in London – the only city in the UK which is divided up into many areas for official forecasts – are considerably more uncertain than those for other areas, such that one cannot be 80% sure that the true total population more than 6 years ahead will be within 10% of the population that has been forecast.
The study of past forecasts has allowed a probability distribution to be suggested for current forecasts, which helps users to understand the potential risks of decisions made using the forecasts.
The size of population at the start of a forecast was not closely related to forecast error, apart from the larger errors associated with the two smallest local authorities. This is consistent with the small gradient found in other studies for larger populations. Since there is insignificant bias in the forecasts there will be both over-forecasts and under-forecasts within any aggregate area, which will cancel out and leads one to expect a smaller percentage error for larger areas. That this isn’t the case supports the likelihood that error is also associated with many other characteristics that are confounded with and possibly more important than population size, as for example we found with the type of local authority.
There is therefore considerable potential to develop this and previous studies in order to develop appropriate prediction intervals around forecasts for individual areas, that take into account more characteristics of the area. Prediction intervals in which planners can have confidence will help them to develop contingency plans for outcomes different from the forecast and to avoid some of the social and monetary costs associated with forecast errors.
In England’s official forecasts as elsewhere the future assumptions continue the experience of the previous period. It is likely that change is over-predicted and that areas with volatile past migration patterns can be expected to suffer greater forecast error. The speed of population change in the previous years will be one useful indicator of likely future error.
Beyond the association of area characteristics with forecast errors, the past performance of forecasts in each area should be a guide to future performance. A combined analysis of performance conditional on area characteristics and on past individual area performance may give the best guide to future prediction intervals. Such analysis is feasible using multilevel modelling (eg. Marshall et al. 2017) but would be original in the analysis of demographic forecasts.
Considerable use is made of forecast changes in the age-composition of the population, to foresee needs of an ageing population and a changing workforce. Age-specific forecasts will have their own characteristic uncertainty and shelf life, which is informative to those users and can be the subject of future study.
Smaller areas than the local authorities considered in this paper are also forecast in Britain. Although small area forecasts are not regular or official, they have a long-standing place within service planning and neighbourhood development (Rhodes and Naccache 1977; Simpson and Snowling 2011; NRS 2016), and a thorough evaluation is likely to be fruitful.
In the technical development of post-hoc error distributions of this sort, there are various other potential improvements: an asymmetric distribution using the signed percentage error may give smaller lower interval and larger upper bounds; the data on individual years of horizon are more variable than the grouped categories used here but give extra information.
Our adoption of 10% as the point beyond which errors would become embarrassing is not without evidence but there are many other aspects which specific users may be more interested in. Further research with users could validate and develop practical rules of thumb for forecast shelf lives. This paper assumes that a user should specify the percentage error that would be embarrassing or difficult if it occurred 80% of the time, but in our experience this is not a question that is easily answered with confidence. Focus groups among British local authorities found that “Errors of 10% … could still be regarded as acceptable depending on whether any major capital or revenue commitments were made as a result. However there would begin to be some loss of credibility in the methodology and sources of data.” (Tye 1994: 13). In a recent survey of Australian forecast users, Wilson and Shalley found that:
“After guided discussion, participants collectively arrived at 3% to 5% for large population area estimates and 5% to 10% for areas with smaller populations. This was consistent across the three focus groups. For one participant, it was the accuracy of forecast population change rather than the accuracy of population stock forecasts that was important: “If the movement is accurate then I can live with 40%.” Discussion also suggested users expected higher levels of accuracy over the short term and that they accepted regular adjustment as more information about the population becomes available.” (Wilson and Shalley 2019: 384)
If users require greater accuracy over the short term, then the empirical confirmation of greater accuracy with shorter horizons is reassuring. Sometimes there may be regulatory regimes in which certain targets or units are more important than others. In school planning the error might be best expressed as numbers of surplus or crowded classrooms. What are the units of risk when forecasts are used for housing, employment, transport plans, or health care (Buchan et al. 2019)?
All this underlines the importance for forecasters to understand the risks taken by planners when using population forecasts, together with the feasible ways of expressing risk from population forecasts.
For some users, the forecast is not used as a prediction but as a scenario, perhaps even one that planners will act to escape. There is an epistemological problem when discussing the accuracy of a forecast whose worth may have been precisely to help change the future to avoid its outcome. It is fair to remind users that what we have called the official forecast is avowedly a projection that continues current local demographic rates averaged over the past 5 years, modified in a minor way by a national projection of future trends. It is therefore unsurprising that it is usually wrong as a prediction, and particularly wrong as a prediction when the local impact of migration is unstable. Users beware!
Forecasts are used very often to make plans and decisions that allocate resources. The understanding of what is most certain and what is uncertain, can give more responsibility to the decision-makers, though they may not thank the forecasters for it. Apart from the official forecast, planners will seek other scenarios to explore the impact of housing or major policy developments, which also carry uncertainty around their conditional predictions. Effective forecasting requires careful collaboration between producers and users.
References
Baker, R. J. S. (1972). Administrative theory and public administration. London: Hutchinson University Library.
Buchan J, Norman P, Shickle D, Cassels-Brown A, MacEwen C (2019) Failing to plan and planning to fail. Can we predict the future growth of demand on UK Eye Care Services? Eye https://www.nature.com/articles/s41433-019-0383-5
Greater London Authority. (2015). GLA 2014 round of trend-based population projections - Methodology, GLA intelligence update 04–2015. London: GLA.
Lutz, W., Sanderson, W. C., & Scherbov, S. (2004). The end of world population growth. In W. Lutz, W. C. Sanderson, & S. Scherbov (Eds.), The end of world population growth in the 21st century (pp. 17–83). London: Earthscan.
Marshall, A., Christison, S., & Simpson, L. (2017). Error in official age-specific population estimates over place and time. Statistical Journal of the IAOS, 33, 683–700.
NRS (2016). Population and household projections for Scottish sub-council areas (2012-based), National Records of Scotland. Website: https://www.nrscotland.gov.uk/statistics-and-data/statistics/statistics-by-theme/population/population-projections/population-and-household-sub-council-area-projections
ONS. (1999). Subnational population projections (series PP3, number 10). London: Office for National Statistics.
ONS. (2008). Subnational population projections accuracy report. Titchfield: Office for National Statistics http://www.ons.gov.uk/ons/rel/snpp/sub-national-population-projections/2006-based-projections/subnational-population-projections%2D%2Daccuracy-report.pdf.
ONS. (2012). Migration statistics improvement Programme final report. Titchfield: Office for National Statistics.
ONS (2015). Subnational population projections accuracy report. Titchfield, Office for National Statistics. https://www.ons.gov.uk/file?uri=/peoplepopulationandcommunity/populationandmigration/populationprojections/methodologies/subnationalpopulationprojectionsaccuracyreport/snppaccuracyreportfinaltcm774144461.pdf
ONS (2016). Methodology used to produce the 2014-based subnational population projections for England, Office for National Statistics, Titchfield. https://www.ons.gov.uk/peoplepopulationandcommunity/populationandmigration/populationprojections/methodologies/methodologyusedtoproducethesubnationalpopulationprojectionsforengland
ONS. (2018). Subnational population projections for England: 2016-based. Titchfield: Office for National Statistics.
OPCS. (1977-1995). Population Projections, Area (series PP3, numbers 1-9). In Office of population censuses and surveys. London Digital copies available from the authors of this paper.
Rayer, S., Smith, S. K., & Tayman, J. (2009). Empirical prediction intervals for county population forecasts. Population Research and Policy Review, 28, 773–793.
Rees, P., Norman, P., & Brown, D. (2004). A framework for progressively improving small area population estimates. Journal of the Royal Statistical Society: Series A (Statistics in Society), 167, 5–36.
Rees, P., Clark, S., Wohland, P., & Kalamandeen, M. (2018). Evaluation of sub-national population projections: A case study for London and the Thames Valley. Applied Spatial Analysis and Policy, online 31Aug2018.
Rhodes, T., & Naccache, J. A. (1977). Population forecasting in Oxfordshire. Population Trends, 7, 2–6.
Shaw, C. (2007). Fifty years of United Kingdom national population projections: How accurate have they been? Population Trends, 128, 8–23.
Simpson, L. (2002). Geography conversion tables: A framework for conversion of data between geographical units. International Journal of Population Geography, 8(1), 69–82.
Simpson, L. (2016). Integrated local demographic forecasts constrained by the supply of housing or jobs: Practice in the UK. In D. A. Swanson (Ed.), The Frontiers of applied demography (pp. 329–350). New York: Springer.
Simpson, L., & Snowling, H. (2011). Estimation of local demographic variation in a flexible framework for population projections. Journal of Population Research, 28, 109–127.
Tayman, J. (2011). Assessing uncertainty in small area forecasts: State of the practice and implementation strategy. Population Research and Policy Review, 30(5), 781–800.
Tye, R. (1994). Local Authority Estimates and Projections: How are they used and how accurate do they have to be? Estimating with confidence: Making small area population estimates in Britain, working paper 9. Southampton: University of Southampton.
UKWIR. (2015). WRMP19 Methods - Population, household, property and occupancy forecasting Supplementary Report; report ref. no. 15/WR/02/8, UK water industry research ltd. London.
Wilson, T., & Rowe, F. (2011). The forecast accuracy of local government area population projections: A case study of Queensland. Australasian Journal of Regional Studies, 17(2), 204–243.
Wilson, T., & Shalley, F. (2019). Subnational population forecasts: Do users want to know about uncertainty? Demographic Research, 41(13), 367–392. https://doi.org/10.4054/DemRes.2019.41.13.
Wilson, T., Brokensha, H., Rowe, F., & Simpson, L. (2018). Insights from the evaluation of past local area population forecasts. Population Research and Policy Review, 37(1), 137–155.
Yamauchi, M., Koike, S., & Kamata, K. (2017). How accurate are Japan’s official subnational projections? Comparative analysis of projections in Japan, English-speaking countries and the EU. In D. A. Swanson (Ed.), The frontiers of applied demography (pp. 305–328). Dordrecht: Springer.
Acknowledgements
Paul Norman for advice and materials to complete a set of local authority mid-year population estimates appropriate as the benchmark, and the 1981-1991-2001 Geographical Conversion Table. Brian Parry, Tim Pateman and others at the Office for National Statistics for providing access to past population forecasts and estimates. John Hollis, Ben Corr, and Andrew Nash and an anonymous reviewer for pertinent critical comments which allowed us to improve our draft. Data entry and the presentation of an early draft of this study were supported financially by the Australian Research Council (Discovery Project DP150103343).
Funding
Data entry and the presentation of an early draft of this study were supported financially by the Australian Research Council (Discovery Project DP150103343).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Simpson, L., Wilson, T. & Shalley, F. The Shelf Life of Official Sub-National Population Forecasts in England. Appl. Spatial Analysis 13, 715–737 (2020). https://doi.org/10.1007/s12061-019-09325-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12061-019-09325-3