Abstract
In this paper, we examine the effects of unemployment, immigration and emigration on fertility variation during the Great Recession in Spain, while taking account of trans-spatial relationships. Using a spatial Durbin approach and panel data with observations from 50 Spanish provinces, we investigate the impact of an increase in unemployment on fertility and ask whether, and to what extent, fertility has been affected by reduced immigration and increased emigration following the economic crisis of 2008. Our results suggest that unemployment has had a strong negative impact on fertility during the recession, and that the impact of the total unemployment rate was primarily confined to the province where the unemployment occured, although with significant spillover effects from female unemployment. Further, although female immigration was reduced during the recession, it nevertheless continued to have a positive impact on fertility, and its impact seems to matter both directly (own-province) and indirectly (spillover). Finally, our results show that increased emigration had a negative and indirect (spillover) impact on fertility. These findings contribute to the debate on the relationship between unemployment and fertility during the Great Recession, and demonstrate that both international immigration and emigration have affected province-level fertility and should therefore be given serious consideration in any analysis of fertility during the current long recessionary period.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Several recent studies have provided evidence of fertility reductions due to high levels of unemployment and economic insecurity in a number of countries following the economic crisis of 2008 (Cherlin et al. 2013; Comolli 2017; Goldstein et al. 2013; Matysiak et al. 2018; Schneider 2015; Sobotka et al. 2011). However, far less is known about whether, and to what extent, international migration, both immigration and emigration, have affected fertility during the current long recessionary period. As migration appears to have responded to changes in relative economic opportunities during this ‘Great Recession’, particularly in low fertility countries within Europe (IOM 2010; Roos and Zaun 2016), we argue that it is important to assess the roles of immigration and emigration in such contexts to further understand fertility variation post-2008.
Although some migrants certainly move for non-economic reasons, a large body of research highlights that the labour-related migration of individuals and families constitutes an important mechanism for coping with employment declines, lower incomes and economic insecurity (Borjas 1999; Dustmann and Weiss 2007; Martin 2009; Massey et al. 1993; Harris and Todaro 1970). Therefore, how migration and fertility intersect following an economic downturn seems to be of some consequence, particularly in crisis-stricken countries which have experienced both considerable international migration and remarkable upturns and reversals in total fertility rates in recent years. Indeed, as noted by Sobotka (2017: 25) in relation to current low and unstable fertility levels, “one broad force that deserves to be explored more is the influence of migration, which has been gradually reshaping the ethnic and social composition of many highly developed countries”.
Recent work by Cherlin et al. (2013) and Villarreal (2014) indicates that the fall in fertility in the US during the economic crisis was partly attributable to a drop in immigration, and that the recession had an effect on fertility by discouraging immigrants from entering, or remaining in, the country. In Europe, despite economic and migration-related factors frequently being advanced to explain short-term changes in fertility, including fertility rebounds prior to the economic crisis (Coleman 2006; Goldstein et al. 2009; Sobotka 2008), evidence is still lacking on the extent to which immigration may have affected fertility following the Great Recession. Another line of research (albeit less prominent) suggests that emigration can also have profound implications for changes in population composition and thus contribute to fertility decline (Ebanks et al. 1975; Lerch 2009; Prieto 2016). In this respect, the interaction between the numerical size of the emigrant population and their relatively young age structure (migration typically occurs at younger ages) implies that an increase in international emigration following the economic crisis may have had a negative impact on fertility in areas most affected. Migration must therefore be considered as a possible response to the economic recession, along with postponing partnership and/or births, or revising fertility intentions downwards (Testa and Gietel-Basten 2014).
Yet there have been few investigations of relationships between international immigration, emigration and fertility in Europe following the economic recession. One reason for the dearth of research may be that most of the economic recessions in the past have been of a relatively short duration, and their impact on fertility rates is assumed to be temporary and thus less important than secular demographic trends (Lee 1990; Sobotka et al. 2011). Most research on fertility and the economic crisis centres on the short-term impact of rising unemployment levels or other measures of economic uncertainty, even if a portion of fertility declines may be attributable to migration-related factors (Graham et al. 2016). Our study addresses this important knowledge gap by investigating whether fertility has responded to the effects of immigration and emigration during the Great Recession in Spain.
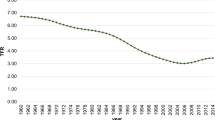
We focus on Spain as a European country badly hit by the economic recession, where period fertility rates (TFRs) have exhibited a pattern of sharp decline (from 1.39 in 2008 to 1.24 in 2013, to 1.29 in 2015). Thus, fertility has returned to lowest-low levels following the economic downturn, and economic conditions, particularly unemployment rates, have been offered as the main explanation for fertility variation (Comolli 2017; Goldstein et al. 2013; Matysiak et al. 2018; Sobotka et al. 2011). However, given the substantial migration response following the crisis (with Spain now recording net emigration, for the first time since the 1970s, and with net outflows estimated at around 70 thousand since 2012), the question insufficiently addressed by previous research is: has fertility in Spain been affected by reduced immigration and increased emigration following the economic recession and, if so, to what extent? To answer this question, we use rich panel data with observations from 50 Spanish provinces and employ a dynamic spatial Durbin approach that accommodates spatial dependenceFootnote 1 and dynamic effectsFootnote 2 (Elhorst 2014). This approach is important, as we later demonstrate, because the total fertility rate of a certain province may be influenced not only by its own characteristics but also by the characteristics of neighbouring provinces, and such influences could persist for the short or longer term. Further, unemployment and migration are inherently spatial phenomena, with local and regional forces of supply-push and demand-pull reflecting disparities across areas that may also be characterised by temporal correlations.
To date, nearly all studies on the recession and fertility in Europe have investigated associations between time trends in fertility and economic conditions at a national scale or, alternatively, have pooled data for different countries or regions in cross-national analyses (Comolli 2017; Goldstein et al. 2013; Matysiak et al. 2018; Sobotka et al. 2011). Existing studies at a sub-national scale are predominantly focused on the US experience of fertility variation during the recession, and have examined the effect of area-level economic conditions on state-level fertility trends (Cherlin et al. 2013; Schneider 2015; Schneider and Gemmill 2016). Although the latter is an important step, to our knowledge there has been no area-based fertility research investigating the effects of the economic recession that has considered both the sub-national spatial structure and the serial dynamics among its spatial units. In addition to this novel contribution to the literature, we also consider a longer period than the official recession years of 2009–2010 and 2012, and analyse the effects of unemployment and migration on fertility both in the short and the longer term. The latter is seen as especially relevant in the Spanish case where unemployment rates have remained high despite some signs of economic recovery and the effects of recession on immigration and emigration have spanned a much longer period (Izquierdo et al. 2016).
The rest of the paper is organised as follows: "The Spanish Context and Hypotheses" discusses the Spanish context and the hypotheses that guide the empirical analysis; "Data" describes the data and "Methodology" provides the main model specification and the analytical approach; "Results" presents the results on the effects of unemployment, immigration and emigration on total fertility rates (TFR); and "Discussion and Conclusions" summarises our main findings and comments briefly on their wider implications.
The Spanish Context and Hypotheses
Spain is well known as having experienced lowest-low fertility in the late 1990s (Kohler et al. 2002). While national fertility levels appeared to be recuperating in the 2000s, with many provinces recording TFR above 1.3 children per woman, the onset of the economic crisis brought new declines in fertility with TFR below or at 1.3. In this context, a number of studies have shown that high unemployment prior to the economic recession had a particularly strong effect in reducing fertility (Gutiérrez-Domènech 2008; Adserà 2011), and that income and job insecurity largely discouraged family formation (De la Rica and Iza 2005). Beyond structural labour market conditions, the so-called ‘postponement transition’ (Sobotka 2017) has also been an important factor explaining the emergence of very low period fertility during recent decades in Spain due to a general trend of progressive postponement of major family events. More specifically, the growth in higher education and women entering the labour market in record numbers, with female labour force participation at age 30–34 almost tripling from below 30% in 1980 to 85% in 2012 (OECD 2016), are considered to be important changes affecting the tempo of fertility. Lesthaeghe and Lopez-Gay (2013) showed that this is reflected in the spatial pattern of fertility postponement in Spain prior to the economic crisis, with a strong spatial correlation between parenthood postponement and female higher education and labour force participation.
The Great Recession in Spain seems to have interrupted the diminishing pace of fertility postponement and the moderate fertility recuperation that began around the turn of the century (Esping-Andersen 2013). Indeed, the intensity with which the economic crisis impacted on the Spanish labour market has been remarkable: from start (third quarter of 2007) to peak (first quarter of 2014), employment fell by 18.3%, while the unemployment rate reached a maximum of 26.9% in the first quarter of 2013. Thus, unsurprisingly, cross-national evidence from Europe suggests that the reversal in positive fertility trends in Spain is associated with high unemployment rates and the precarious position of many of those in employment, both representing major obstacles to childbearing at all ages (Goldstein et al. 2013; Matysiak et al. 2018; Sobotka et al. 2011). Although it remains unknown whether the fertility decline will be temporary or might have more lasting effects, sustained economic hardship coupled with economic policy uncertainty, government financial risk, and lower consumer confidence seems to favour the more pessimistic outcome (Comolli 2017).
Spain also represents a telling example of change in international migration. Before the crisis, it experienced some of the largest increases in immigration relative to population size in Europe (Sobotka 2008). In the period between 2000 and 2007, the share of foreign-born rose from 2% to 12%. After centuries of sustained emigration, Spain not only became a country of immigration in the 2000s but a prominent destination among the ‘new immigration countries’ of the European Union (Arango 2013). This turnaround grew particularly intense in the mid-2000s, when a third of all arrivals to Europe went to Spain, making it the most important destination on the continent for international migrants and the second largest worldwide, behind only the USA (Domingo et al. 2015). However, the economic crisis that began in 2008 has drastically reduced immigration, producing migration-diversion effects as migrants divert to other destination countries with better economic prospects (Bertoli et al. 2016). At the same time, the Spanish government has adopted various measures of migration protectionism to restrict the arrival of new immigrants, including the reduction of work permit quotas and residence permits (Domínguez-Mujica et al. 2014), and a programme of voluntary returns to provide assistance to immigrants originating from countries with which Spain has social security agreements. As a consequence, immigration started to reduce slowly and the onward migration of resident immigrants rose markedly (Mas Giralt 2017). Loss of the native population is also likely to have impacted on fertility in Spain. Native emigration, both as part of a globalising labour force and as a negative result of the economic crisis, has contributed to the increase in international emigration (Lafleur et al. 2017).
Overall, more than 400,000 exits have been recorded since 2010, which is in absolute and relative terms the highest level of emigration in Spanish history (Izquierdo et al. 2016). In particular, the last decade has seen increased emigration towards Latin America (Recaño et al. 2015) and the rest of Europe (Bermudez and Brey 2017), where the United Kingdom, Scandinavia and Germany are the main destination countries (OECD 2013, 2014, 2015).Footnote 3 This suggests that international emigration has become a key adjustment factor and mechanism for coping with the long-term financial instability brought about by the economic crisis (Beyer and Smets 2015; Jauer et al. 2014). Moreover, the scale of emigration and the relatively young age profile of emigrants (51% and 46% of Spanish-born and foreign-born, respectively, are aged 30–44)Footnote 4 supports our contention that, in addition to the effect of high unemployment, the migration response must be considered in any explanation of the impact of economic recession on fertility.
In this study, we hypothesise that a rise in unemployment has a negative impact on total fertility rates across provinces in Spain (H1). In addition, we expect that high unemployment may produce migration-diversion effects, diminishing the generally positive impact of immigration on fertility. However, since the consolidation of transnational networks appears to be less sensitive to the effects of economic conditions, any continued immigration could still be expected to have a positive impact on fertility. To test the relationship between immigration and fertility, we hypothesise that the relationship between immigration and total fertility rates across provinces in Spain remains positive despite the economic crisis (H2). Finally, we expect the significant increase of international emigration to reduce the size of cohorts in reproductive ages as migration typically occurs at younger ages. Thus lastly, we hypothesise that the relationship between emigration and total fertility rates across provinces in Spain is negative following the economic crisis (H3). In the next section, the unique aggregate data for provinces across Spain and the analytical methods used to investigate our three hypotheses are described in detail.
Data
Fertility Data
For this study we assembled a panel of province-level fertility data with observations from 50 Spanish provinces over the period 2008–2015. The province constitutes the lowest administrative level in Spain for which data on fertility rates are readily available from the statistical office (INE) (data and documentation are accessible at http://ine.es/). In our analyses, we use province-level total period fertility rates (TFR) as our main dependent variable, computed as the sum of the age-specific fertility rates per women within a province in a given calendar year. Although this synthetic fertility measure may not predict completed life-time fertility, as age-specific fertility rates are subject to future change, the TFR is a useful summary of current fertility levels in a population.
Key Covariates
In order to analyse the impact of economic conditions on fertility and the role of migration in fertility variation, we use the following independent macro-correlates in each province for the years 2008–2015: unemployment rate and rates of immigration and emigration. Since the worsening of economic structural conditions during the economic recession is captured not only by total unemployment rates (as in Goldstein et al. 2013) but also by female unemployment rates (as in Comolli 2017), we employ both measures in the analyses, as well as rates of immigration and emigration for the total and female population. The specific analyses provided here focus on the overall impact of total and female immigration and emigration on province-level fertility for the study period, including both native and foreign-born populations of reproductive age (defined as ages 16 to 49). All covariate information was also obtained from INE, and general definitions of these covariates are elaborated below.
Unemployment Rate
The unemployment rate is measured as the number of people (either total or women) aged 16–49 looking for work in a given province divided by the number of people in the labour force of the same age in that province. The rate is expressed as a percentage. Since business cycles affect households mainly through unemployment (Ahn and Mira 2002; Sobotka et al. 2011), we therefore follow the great majority of recent studies that examine links between fertility decline and economic recession by using the unemployment rate as the main economic indicator. As Goldstein et al. (2013) point out, the unemployment rate constitutes a more tangible and direct indicator of people’s economic circumstances, particularly of women of reproductive age.
Rates of Immigration and Emigration
Data on international immigration and emigration are obtained from the new Migration Statistics (Estadística de Migraciones) provided by INE since 2008. The latter overcomes some of the drawbacks of previous official statistics on international migration from the Residential Variation Statistics (Estadística de Variaciones Residenciales), including allowances for registration delays and a better estimation of emigration (for a detailed description of the new Migration Statistics, see http://www.ine.es/en/metodologia/t20/t2030277_en.pdf). Despite these advances, both immigration and emigration flows are likely to reflect lower bounds, given that the inflows might not capture some seasonal workers who come to Spain for a short spell, while outflows of temporary emigrants might be under-stated because some people do not de-register despite being legally obliged to. Therefore, our data mainly reflect long-term moves to and from Spain, given that the system of entry-exit registration only counts migrants who register and de-register.
In our analysis, the immigration rate is measured as the number of people aged 16–49 (either total or women) who have entered the country and established their regular residence in a given province, divided by the number of inhabitants of the same age in that province. The emigration rate is measured as the number of people aged 16–49 (either total or women) who have left the country and established their regular residence abroad, divided by the number of inhabitants of the same age in the province of origin prior to the emigration. Both rates are expressed as a percentage.
In addition, the Gross Domestic Product (GDP) per capita is included as a time-varying control variable to indicate the level of provincial wealth. GDP at current prices is expressed in Euros per inhabitant, thus representing the value of all final goods and services produced within each province in a given year, divided by the province’s population for the same year. We expect that higher levels of GDP per capita will correspond with increased fertility. This is because higher levels of wealth tend to bring higher standards of living that are associated with increased fertility (Fox et al. 2015; Lacalle-Calderon et al. 2017).
Finally, we also adjust our models for two time-varying measures of province-level demographic composition that distinguish between Spanish-born and foreign-born using the population size of each group of women aged 16–49 who were resident in a given province. The latter information can also be considered as a proxy for urbanisation given that larger populations are located in urban areas. Data are derived from the new Population Figures time series of INE, which includes full consistency of results with those provided in the Vital Statistics and the Migration Statistics (for a detailed description of the new Population Figures, see http://www.ine.es/en/inebaseDYN/cp30321/docs/meto_cifras_pobla_en.pdf).
All variables were log-transformed prior to analysis to allow us to interpret the estimates as elasticity. Using balanced panel data for the period 2008–2015, our final analytical sample consists of 400 observations (8 years * 50 provinces).
Methodology
The Advantages of the Spatial Durbin Model
Recent fertility studies (Cherlin et al. 2013; Schneider 2015; Schneider and Gemmill 2016) have included state and year fixed effects to account for unobserved time-invariant characteristics of the state and for unobserved period characteristics that are stable across states, but it is increasingly recognised that a spatial perspective is needed in macro-level fertility research as macro-level demography is inherently a spatial science (Voss 2007). Due to the spatial nature of our data (Spanish provinces) there is a strong likelihood that the observations are not independent of one another, thus implying that there is spatial dependency within the data. This spatial dependency usually originates from a variety of sources, with the existence of arbitrary political boundaries (that split or aggregate spatial units without regard to socioeconomic variables) and spatial interaction as the more fundamental ones. Crucially, this spatial dependency violates the assumption made by ordinary regression methods that each observation is independent of other observations, which not only has the potential to render inefficient standard errors but also introduces modelling uncertainty because the nature of spatial interaction effects is unknown.
In modelling terms, three different types of interaction effects can be distinguished (Manski 1993; Elhorst 2010): (1) an endogenous interaction relationship, which indicates that the outcome for a spatial unit is dependent on the outcomes for other spatial units; (2) a correlated relationship that refers to the situation where unobserved factors lead to similar outcomes across spatial units (i.e. interaction effects among the error terms); and (3) an exogenous interaction relationship that suggests that the outcome for a spatial unit is associated with the determinants of the outcome in other spatial units. Traditionally, spatial lag and spatial error models have focused on the endogenous interaction and correlated relationship (Anselin 1988). However, since explanatory variables also show a spatial pattern and these may be captured as local and global spillover effects (Elhorst 2010), a spatial Durbin model that includes both a spatially lagged dependent variable and spatially lagged explanatory variables is preferred (LeSage and Pace 2009). The advantage of the spatial Durbin model is that it allows researchers to separate the direct (within a province) impact of an independent variable on the dependent variable from the indirect (to/from neighbouring provinces) impact (LeSage and Pace 2009; Fischer 2011). Another advantage of the spatial Durbin approach is that it is considered the only means of producing unbiased coefficient estimates, regardless of the true spatial processes underlying the observed data (Elhorst 2010).
While the main focus of fertility research using spatial econometrics was originally on one type of interaction effect such as the spatial lag (Goldstein and Klüsener 2014; Waldorf and Franklin 2002), recently models with more than one type of interaction effect, as well as extensions to panel data and to marginal effects (i.e. direct and indirect effects) of the explanatory variables are gradually gaining traction. For instance, recent contributions using a spatial Durbin model show the importance of taking into account spatial dependence in province-level fertility. Studying the process of fertility diffusion, Vitali and Billari (2017) demonstrated that fertility in a given area depends not only on the economic, institutional and cultural characteristics of that area but also on the characteristics of neighbouring areas. Using the same spatial approach, Vitali et al. (2015) documented how the spread of childbearing within cohabitation in a given municipality in Norway was influenced by the characteristics of neighbouring municipalities. These studies show the power of the spatial Durbin specification in not only capturing the spatial dependency in the data but also the impact of a change in a given independent variable on fertility, taking into account both own-province and spatial spillover effects.
Specification of the Spatial Durbin Model
We employ a spatial Durbin model in this study to examine whether the total fertility rate in one province is additionally related to the characteristics of neighbouring provinces and, if so, how they are associated. For this purpose, the specification of our model include lags of the dependent variable (TFR) and of the independent variables (unemployment, immigration and emigration) in both space and time to quantify the magnitude of direct and indirect effects both in the short and longer term. A full model with all types of interaction effects reads, in vector form, as
where Yt denotes an N × 1 vector that consists of one observation of the dependent variable for every province (i = 1, ..., N) in the sample at time t (t = 1, ..., T), which for this study is the total fertility rate; and Xt is an N × K matrix of exogenous explanatory variables (unemployment rate and rates of immigration and emigration), observed at the start of each observation period. A vector or matrix with subscript t–1 in Eq. (1) denotes its time lagged value, whereas a vector or matrix pre-multiplied by W denotes the spatially lagged value. The N × N matrix W is a spatial connectivity matrix that defines the geographical extent of province spillovers.Footnote 5
The parameters τ, δ, and η are the response parameters of, respectively, the dependent variable lagged in time Yt-1, the dependent variable lagged in space WYt, and the dependent variable lagged in both space and time WYt-1. The symbols β and θ represent K × 1 vectors of the response parameters of the exogenous explanatory variables. The N × 1 vector μ = (μ1, …, μN)T that contains spatial specific effects μi and is used to control for all spatial-specific, time-invariant variables whose omission could bias the estimates in a typical cross-sectional study (Baltagi et al. 2014); and time-specific effects λt (t = 1, …, T), where ιN is a N × 1 vector of ones, to control for all time-specific, unit-invariant variables whose omission could bias the estimates in a typical time-series study. Such spatial- and time period–specific effects generally can be treated as fixed or random effects, but as Elhorst (2014) notes, a random effects model in the cross-sectional domain might not be an appropriate specification if observations of adjacent units in an unbroken study area are being used and the whole population is sampled.Footnote 6
Direct interpretation of the coefficients in the dynamic spatial Durbin model is difficult, because they do not represent true partial derivatives (LeSage and Pace 2009). However, Debarsy et al. (2012) and Elhorst (2014) have shown that the matrix of (true) partial derivatives of the expected value of the dependent variable with respect to the kth independent variable for i = 1, …, N in year t for the short-term is given by.
The expression in Eq. 2 is the total (short-term) effect and it can be broken down into direct (own-province) and indirect (spillover) effects (LeSage and Pace 2009). The direct effect captures the impact within a particular province of the unit change in explanatory variable, thus reflecting the impact on the dependent variable that results from a change in the kth regressor xk in province i in the short-term; the direct effect stems from the own-partial derivatives along the diagonal in the matrix presented in Eq (2) and can be expressed as (I − δW)−1[βkIN]. The indirect effect, known as spatial spillover, is reported as the average of the row sums of non-diagonal elements of the matrix (I − δW)−1[θkW]. As the discussion on portioning the direct and indirect impacts is beyond the scope of this study, we refer readers to the works by Elhorst (2014) and LeSage and Pace (2009) for further details.
Given that both direct and indirect effects may persist for a long time, an analysis of their stability and relevance over the longer term is seen as important. While for the short-term effects we ignore the parameters τ and η, and these can be interpreted as mainly pure spatial feedback effects, the longer term effects contain space-time feedbacks passing from one province to another, thus capturing potential impacts that go beyond a short-term or temporary shock. To obtain the longer term effects, we assume that Yt = Yt − 1 = Y∗ and WYt = WYt − 1 = WY∗. From Elhorst (Elhorst 2014), the longer term marginal effects can be expressed as.
Therefore, by examining the relationship between total fertility rates and its macro-correlates (unemployment, immigration and emigration) using the decompositions in Eqs. (2) and (3), we can disentangle direct and indirect effects into short and longer term effects. Since we leave aside the spatial interaction effects among the error terms, our specification is consistent with a dynamic spatial Durbin model (SDM).Footnote 7 As LeSage and Pace (2009) note, the cost of ignoring spatial dependence in the dependent and/or independent variables is relatively high, because if one or more relevant explanatory variable gets omitted from a regression equation, the estimator of the coefficients for the remaining variables is inherently biased and inconsistent. In contrast, ignoring spatial dependence in the error term, if present, only leads to a loss of efficiency.
Analytical Strategy
Analysing the impact of unemployment, immigration and emigration on fertility variation involves taking into account both the effect of each explanatory variable on the dependent variable and the potential impact of inter-relationships among the independent variables under consideration (see Fig. 1). Previous research has shown that the total fertility rate tends to reflect the level of unemployment, with rises in fertility accompanying lower unemployment (Currie and Schwandt 2014), and vice versa (Karaman Örsal and Goldstein 2018). In this study, we argue that, as migration appears to have responded to changes in relative economic opportunities during this ‘Great Recession’ in Spain, it is also important to assess the role of immigration and emigration to understand fertility variation post-2008.
However, it appears difficult to estimate the combined impact of unemployment and international migration as these explanatory variables are not necessarily independent from each other. In the human capital framework, immigrants perceive areas with low unemployment rates as attractive and areas with high unemployment as unattractive (Massey et al. 1993). At the same time, economic theory suggests that those who are unemployed or dissatisfied with their jobs are more likely to migrate than the employed or those who are not searching for a different job (DaVanzo 1978). Further, the unemployment-migration relationship may also go in the opposite direction. The entry of immigrants may impact host labour markets although, in terms of overall unemployment, the absence of a noticeable effect has been documented (see Okkerse 2008 for a review). Finally, emigration may be encouraged and used as a buffer to absorb the ‘conjunctural shocks’ that produce high unemployment (Beets and Willekens 2009). Thus, because the potential existence of such inter-relationships could lead to confounding the regression parameters and hence their interpretation, even when independent variables are only relatively weakly correlated, we run two separate final models in this study: one with unemployment (Model 1), and one with immigration and emigration (Model 2), including in each model GDP per capita and demographic composition as time-varying control measures.
Using the analytical strategy outlined above, we reviewed various model specifications to assess the performance of the spatial Durbin model compared to the other models (Belotti et al. 2016). The results provide a strong justification for the implementation of SDM in this study. For brevity we show only the conventional results of the non-spatial OLS and the spatial dynamic SDM here (see Appendix 1 and 2) as model testing confirmed that the latter model fits the data better than any other model.Footnote 8 The results of all dynamic SDM models (for the total and female populations) clearly indicate that there are strong spatial interactions between provinces. The spatial lag effects (Rho in Appendices) demonstrate that the endogenous interaction relationship accounts for the fertility variation across Spanish provinces,Footnote 9 meaning that the use of a non-spatial OLS model is likely to produce biased estimates. Although we assume that the models do not provide a comprehensive analysis of all the factors influencing fertility, the focus on key variables covers a substantial part of the variance and captures the main drivers of fertility in a period of economic recession. The within R2 statistics for the non-spatial OLS and dynamic SDM indicate that all models account for a relatively large proportion of fertility variation over time. Importantly, the correlated relationships caused by omitted variables in the spatial error can be explained by the lagged covariates included in the spatial Durbin model specification (LeSage and Pace 2009).
Results
In the first part of this section, we conduct an exploratory analysis of the province-level data for the period 2008–2015 to gain a basic understanding of the dataset. We then examine the decomposition of the marginal effects into direct (own-province) and indirect (spillover) effects, and whether these effects differ in the short and longer term. Finally, we analyse the direct and indirect effects by different definitions (or orders) of 'neighbouring' among the provinces to discuss evidence for spatial feedback.
Descriptive Analysis
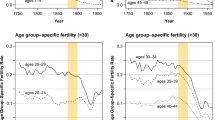
Descriptive statistics for the dependent variable and covariates are summarised in Table 1. They show a significant temporal variation in province-level fertility as revealed by the mean total fertility rate (see also Fig. 2), which decreased sharply in 2009, from 1.39 to 1.33 children per woman, and remained low through 2015 (1.29). During the whole 2008–2015 period, total fertility rates in Spanish provinces range from 0.96 to 1.71 children per woman, indicating that there is substantial geographic variation over the study period. However, it is also clear that during the years following the economic crisis the amount of dispersion (SD) in province-level fertility decreased from 2008 (0.19) to 2015 (0.15), suggesting that fertility trends across Spanish provinces since the crisis of 2008 have become less heterogeneous over time.
Table 1 also indicates that there is significant temporal variation in unemployment rates and rates of immigration and emigration. As expected, the total unemployment rate follows the business cycle, rising around the start of the economic recession (between 2008 and 2009) and falling slightly at the end of the study period (between 2014 and 2015). These descriptive results also show that female unemployment has stayed consistently above that of total unemployment throughout the study period, although the latter has clearly risen at a faster rate since 2008 due to a process of convergence of unemployment rates between males and females. This is because the Great Recession in Spain, as elsewhere, has had a greater negative effect on working men compared to working women (De la Rica and Rebollo-Sanz 2017), which is consistent with the notion that males are disproportionally represented in highly cyclical sectors, such as construction, whereas females are disproportionately represented in noncyclical sectors, such as services (e.g. education and health care).
The descriptive statistics from Table 1 also show that international migration has responded to changes in economic conditions, with rates of immigration decreasing and rates of emigration increasing for the total and female populations. This preliminary evidence links to the initial question of whether both or either have affected total fertility rates following the economic recession. As shown in Fig. 3, where the distribution of province-level fertility relative to the average of all provinces is plotted, the probability density of total fertility rates has gradually increased since 2008, suggesting that the relationship between explanatory factors and fertility might have changed over time. Regarding control variables, the evolution of GDP per capita indicates a reduction from 2008 onwards, although with a slight recovery at the end of the study period. It seems that the economic recession has also increased economic disparities between provinces as the amount of dispersion (SD) in terms of provincial wealth increased from 2008 (4438) to 2015 (4716). For demographic composition, the standard deviations are much larger than the mean values, which implies that the distribution of Spanish-born and foreign-born women aged 16–49 varies greatly across provinces.
The results of all dynamic SDM models (for the total and female populations) clearly indicate that there are strong spatial interactions between provinces. A common way to illustrate the existence of spatial dependence for the dependent and independent variables under study is to examine the evolution of Moran’s I statistic, which is a summary measure of spatial correlation assessing the degree of similarity or dissimilarity of values of neighbouring provinces.Footnote 10 Table 2 shows the estimated Moran’s I statistic and its associated z-scores (standard deviations) for the dependent variable and its covariates for the period 2008–2015.Footnote 11 Results indicate high/moderate positive spatial correlation for all variables (with the exception of demographic composition), implying that provinces with relative high (low) fertility, unemployment, immigration, emigration and provincial wealth are located close to other provinces with similar high (low) values. Thus, we can argue that while provinces had different levels of fertility, unemployment, immigration and emigration from the national average, they had very similar outcomes to those of their neighbours. Importantly, the results also provide evidence that the geographic distribution of fertility, unemployment, immigration and emigration has remained relatively concentrated over time, albeit with a tendency towards both moderate clustering (e.g. fertility, immigration and emigration) and high clustering (e.g. total and female unemployment).
Direct and Indirect Effects on Fertility
We now turn to the results from the implementation of the dynamic SDM. As estimates from these models cannot be interpreted as partial derivatives in typical regression model fashion, the signs and magnitudes arising from changes in the explanatory variables are reported as summary measures of total, direct and indirect effects both in the short and longer term. Tables 3 and 4 summarise the key findings for the total and female populations respectively.
Table 3 displays the decomposition of estimates from the SDM using the total population. The results from Model 1 show that the total effects of unemployment and GDP per capita are significantly different from zero, both in the short and longer term. While total unemployment rates are negatively related to TFRs at province level, GDP per capita is positively related to province-level fertility. The results also indicate that the evolution of the sizes of the Spanish and foreign-born female populations are positively related to the TFR at province level, albeit the average total effect from these two controls is not significantly different from zero.
After controlling for provincial wealth (GDP per capita) and the sizes of the Spanish and foreign-born female populations, we observe that unemployment exerts a negative effect: a one-unit increase is associated with a 10.7% decrease in province-level fertility both in the short and longer term. As noted above, some effects are pure spatial feedback effects (short-term) whereas others include space-time feedback effects (longer term). The fact that the magnitude of these effects is the same may be interpreted as evidence that the initial shock of the economic crisis has not diminished since 2008, with feedback effects passing from one province to another over time.
The results from the separate Model 2 in Table 3 indicate that the total effect of emigration is also significantly different from zero, both in the short and longer term. As with total unemployment, the effect of emigration is negative: a one-unit increase is associated with a 8.6% (short-term) and 10.2% (long-term) decrease in province-level fertility. The latter constitutes evidence that as the impact of the crisis persisted, the effect of emigration on province-level fertility increased, giving an indication of the sizeable negative effects of (young) people leaving the country on fertility.
Although inference in the context of dynamic spatial panels is based on the total simulated effect, one of the advantages of decomposing the marginal effects into direct (own-province) and indirect (spillover) effects is that it is possible to examine which one matters more for the total effect. The results from Models 1 and 2 show that, while the total impact of unemployment is predominantly a direct effect, the total impact of emigration is mostly an indirect effect. With respect to the total effect of unemployment, the results also show that over a half (59%) of the average total effects of unemployment in the short-term are comprised of direct effects, while the rest (41%) are due to indirect effects. In other words, the impact of unemployment on fertility is primarily confined to the province where it occurs, although it seems that there may be additional impacts on the fertility rate of neighbouring provinces due to spillover effects. Nonetheless, for the longer term, the average total effects of unemployment are almost entirely due to direct effects, with marginal impact from indirect effects.
In contrast, Model 2 shows that, the average total effect of emigration on the fertility rate is mostly due to a large spillover impact (around 86% of the short- and longer-term effects are indirect). Since the latter refers to a contagion or diffusion effect, it may be defined in two (non-exclusive) ways (Elhorst 2010). First, from a to-a-unit perspective, the indirect effect could be interpreted as showing how changes in emigration in all Spanish provinces affect fertility in a particular province. Second, from a from-a-unit perspective, the indirect effect could be interpreted as how changes in the emigration rate in a given province influence fertility in other provinces across Spain. Given that international migration rarely occurs from, or to, all Spanish provinces, the from-a-unit perspective is seen as particularly important in this case. However, both perspectives are plausible, not least because the large indirect effect may well be capturing a contagion effect whereby there is an overall increase in emigration (i.e. from all neighbouring provinces) in the context of a more general economic recession.
Table 4 shows the decomposition of estimates from the spatial Durbin model using the female population only. The results from Model 1 reveal the expected negative sign from female unemployment: a one-unit increase is associated with 15.5 (short-term) and 15.1 (longer term) percent decreases in province-level fertility. These estimates display some differences compared to the model with the total population. First, more than three quarters (76%) of the average total effects of unemployment in the short-term are comprised of indirect effects, while the rest (24%) are due to direct effects, suggesting that, unlike total unemployment, the impact of female unemployment on fertility is not predominantly confined within a province. Second, although the results for the longer term signal a reduction in the weight of the spillover effects from female unemployment, more than two thirds (66%) of the average total effects of female unemployment remain as indirect effects. Such a finding can be explained by the large multipliers associated with the location of female employment in predominantly urban provinces and supports the findings of Overman and Puga (2002) where the industry mix had a relevant effect on the spatial distribution of unemployment. Given that the estimates from female unemployment suggest a high level of interdependence between provinces, these results may also be viewed as the outcome of a chain reaction with prolongued regional adjustments to shocks (Bande and Karanassou 2009), where the induced changes in female unemployment in neighbouring provinces may spillover again to include the province where the effect originated.
Moreover, the results from Model 2 in Table 4 reveal that the total effect of female immigration is positive and significantly different from zero in this model, with a one-unit increase associated with a 8.4% (short-term) and 9.9% (long-term) increase in fertility. While the total effect of female immigration in the short-term consists of two thirds (66%) indirect effects and one third (34%) direct effects, almost equal parts of direct and indirect impact are found in the longer term, indicating that the impact of people entering the country on fertility is greater over time, particularly locally (own-province). These findings suggest that while immigration has reduced in importance since the economic recession in 2008, it still has a positive impact on fertility both in the short and longer term, thus supporting our argument that the consolidation of transnational networks through chain migration processes deserves more attention when considering fertility change in times of recession.
Finally, the total impact of female emigration provides evidence for a large spillover effect which influences fertility negatively in neighbouring provinces. More specifically, a one-unit increase in female emigration is associated with a 3.4% (short-term) and 3.9% (long-term) reduction in province-level fertility. The presence of a small direct effect from female emigration appears to play a (modest) role in reducing fertility in a particular province, but the indirect effect is clearly of greater magnitude (86%) both in the short and longer term. Given that spatial spillover effects due to female emigration have not been studied in the fertility literature, these findings can be seen as particularly important, not least because female emigration constitutes an important driver of the relationship under consideration during times of economic distress. Since these results are structurally similar to the impact of female unemployment on fertility, it is reasonable to assume that unemployment and emigration dynamics may be linked, not only in a given province, but also across nearby provinces due to the interdependencies brought about by general equilibrium-disequilibrium effects.
Because the total unemployment rate reflects the share of individuals in the labour force who are currently unemployed and actively seeking work, it may be argued that this indicator fails to capture the number of individuals who are not actively seeking work but are still affected by the economic recession. For instance, those individuals who have become discouraged and stopped looking for work are not accounted for in the total unemployment measure. To address this issue, we carried out a sensitivity test using the total employment-to-population ratio, which is broadly defined as the ratio of the number of employed individuals in a province in a given year to the total population of the province. The results are similarly robust compared to the results using total unemployment rate (see Appendix 3 for the conventional estimation results and Appendix 4 for the decomposition of estimates). As expected, they display a positive impact of labour force participation on fertility in the total effect. Further, unlike the total effect of unemployment, the impact of the employment-to-population ratio is predominantly driven by spillover effects in neighbouring provinces. While this analysis provides valuable information, several factors beyond the impact of the economic recession can affect labour force participation. For instance, the retirement of large cohorts would result in some downward pressure on the overall labour force participation rate, while younger adults’ decisions to extend education would affect participation rates at the other end of the age spectrum. Therefore, the use of the unemployment rate makes the findings easier to interpret and is to be preferred in an analysis where the purpose is to capture how the recession has affected the economic circumstances of women of reproductive age.
Partitioning the Direct and Indirect Effects on Fertility
The spatial Durbin model produces coefficient estimates that incorporate simultaneous feedback between regions located in space. However, the decomposition estimates of direct and indirect effects do not indicate the relative importance of effects from close and distant neighbours for province-level fertility. For this purpose, we employ partitioning techniques to compute the coefficient estimates by different neighbouring orders in the short-term, as shown by LeSage and Pace (2009). The results from this exercise convey three important messages. First, they provide evidence that the impact of the zero-order neighbouring (W0) is most relevant in the direct effects for the total population (see Table 5) and for the female population (see Table 6), demonstrating that the direct impacts of unemployment (Model 1), and immigration as well as emigration (Model 2) come primarily from within a province itself.
Second, the partitioned direct effects provide a clearer picture of the spatial feedback effects (Elhorst 2014), with significant direct impacts beyond the zero-order neighbouring, (W1- W5). In other words, a change in a given province, for instance in terms of unemployment or immigration, also affects fertility in neighbouring provinces through the spatial lags, as each province is considered its neighbours’ neighbour. Thus, the average effect of each order takes into account feedback loops between neighbouring provinces which, in our model, are essentially the elements of the diagonal matrix (LeSage and Pace 2009; Elhorst 2014).
Finally, with respect to the indirect effects, the partitioning results indicate that spillover effects may originate from both immediate and further neighbouring relationships. For instance, the results for the total population (see Table 5) show that the spillover impact of emigration may come from the fourth and fifth orders. The partitioning of the indirect effects of emigration also provide evidence of significant spillover effects in both zero-order estimates.Footnote 12 These results highlight that indirect effects from immediate and distant neighbours matter, and that the existence of various provinces that experience immigration or emigration may exert a significant impact on the fertility of all provinces.
Discussion and Conclusions
The present analysis has used Spain as a case study to examine the effects of unemployment, immigration and emigration on fertility variation while recognising the trans-spatial relationships between provinces during the Great Recession. The results demonstrate that Spain is a highly appropriate test case for investigating our research question of whether, and to what extent, fertility has been affected by reduced immigration and increased emigration following the economic recession. As our study shows, both international immigration and emigration have affected fertility levels in Spain and should therefore be given serious consideration in any analysis of fertility during the current long recessionary period.
First, we examined whether a rise in unemployment has a negative impact on total fertility rates across provinces in Spain (H1). In line with previous studies (Cherlin et al. 2013; Comolli 2017; Goldstein et al. 2013; Matysiak et al. 2018; Schneider 2015; Sobotka et al. 2011), our findings suggest that the increase in total unemployment, and especially in female unemployment, had a strong negative impact on fertility following the economic crisis, thus confirming our first hypothesis. Further, we demonstrate that, while the impact of total unemployment on province-level fertility is primarily confined to the province where it occurs, the impact of female unemployment on province-level fertility is mostly the result of spillover effects. These results are consistent with those of Overman and Puga (2002) for European regions and make it clear that the industry mix in both own and neighbouring provinces has a relevant effect on the spatial distribution of unemployment. The findings thus confirm the fact that spatial effects are relevant factors when interpreting provincial disparities in unemployment rates in Spain. As Rios (2017) suggests, given the direct and indirect impact of unemployment, the implementation of labour market policies, should be coordinated and take into account both own and neighbours’ effects due to the interdependence of unemployment between provinces.
Second, we analysed whether the relationship between immigration and total fertility rates across provinces in Spain remains positive despite the economic crisis (H2). Our findings indicate that, although immigration declined during the economic recession, female immigration still had a positive impact on fertility in Spain following the 2008 crisis, with a large spillover effect in the short-term and similar direct and indirect impacts in the longer term. This confirms our second hypothesis and suggests that female immigration has a positive impact on fertility both in the short and longer term, not least because female immigrants tend to be young adults and most new migrants are of the age to start families. The latter aspect appears to be particularly important given that the Great Recession has not only seen a decrease in the total fertility rate coupled with rising unemployment, but also substantially modified the trends that had previously characterised recent international immigration. Despite the reduced number of immigrants entering the country during the economic recession, their effect on fertility nevertheless remains positive, indicating that in the absence of immigration total fertility rates would probably have decreased even further. The existence of a cumulative migration process (such as family reunification), which is not necessarily linked to the effects of economic conditions (Massey et al. 1993), along with the availability of extensive networks following unprecedented immigration and settlement prior to 2008, appear to have played a significant role in sustaining immigration in Spain (Izquierdo et al. 2016).
Finally, we tested whether the relationship between emigration and total fertility rates across provinces in Spain is negative following the economic crisis (H3). Our analyses provide suppport for our third hypothesis, as they demonstrate that increased levels of both total and female emigration had a negative impact on province-level fertility in Spain following the economic crisis. The negative impact of total and female emigration on fertility is primarily indirect, suggesting that emigration from one province set in motion a sequence of adjustments in all provinces with the effect of generally reducing fertility rates. Thus, the overall picture that emerges is one of diffusion of the economic shock of the Great Recession, where changes in emigration from a given province influences fertility in other provinces across Spain. Indeed, this constitutes a novel finding and bolsters the proposition that if a province experiences a sustained increase in emigration, fertility may not only be reduced in that province but also in neighbouring provinces. This spatial spillover effect seems to be responsible for the overall negative marginal effect of emigration on fertility variation during the study period, suggesting that the emigration context and feedback effects between neighbouring provinces extending to the whole territory can play an important role in the fertility response to an economic shock. Because the age selectivity of emigration has structural impacts on overall population size and composition, some cohorts in reproductive ages can become smaller and, as a result, may reduce the number of children born per woman. Recognising these changes due to emigration appears to be important in understanding fertility change in the context of the economic recession.
The use of a spatial Durbin approach represents a parsimonious way to model the structured dependence of province-level fertility and a number of key correlates during the study period. More specifically, this approach has allowed us to demonstrate that examining only the relationships between fertility rates and the characteristics of a particular province is insufficient for capturing the complex influences of unemployment and international immigration and emigration on fertility variation during economic recession. The existence of spatial multipliers through direct and indirect (spillover) effects confirms the shortcomings of traditional ecological approaches for fertility research. As previously noted, some effects are pure spatial feedback effects (short-term) whereas others include space-time feedback effects (longer term). Results of this study provide evidence that the initial shock of the economic crisis has not diminished since 2008, particularly with regard to unemployment and emigration, with feedback effects passing from one province to another over time.
Although it is seldom possible to obtain all the desired variables to analyse fertility at the macro-level, according to LeSage and Pace (2009) there is a strong motivation for a spatial Durbin approach when the omitted variables are spatially autocorrelated. Given that the main explanatory variables (unemployment, immigration and emigration) are viewed as simultaneously determined, we have separately modelled their spatial effects working through a set of conditioning variables (provincial wealth and the sizes of the Spanish and foreign-born female populations). Thus, although the models presented in this study are robust, the results should be interpreted as indicating a predictive relationship as opposed to a causative one. Further, although by using a 8-year period panel data set we are effectively able to control for unobserved provincial heterogeneity, the panel is too short to say much about how the impact of unemployment, immigration and emigration is likely to extend beyond the study period 2008–2015, which could usefully be addressed by future research.
In conclusion, this study highlights the importance of considering international immigration and emigration in current debates about fertility in Europe as these capture important structural changes that are not measured by unemployment alone. It remains unknown whether fertility decline in Spain will be more or less temporary or might have more lasting effects, but both increased economic hardship and increased economic uncertainty, coupled with decreased immigration and increased emigration, would favour the more pessimistic outcome (Lesthaeghe and Permanyer 2014). The economic impacts of the Great Recession in Spain have clearly had an effect on province-level fertility but some of this effect works through the impact of economic recession on migration. More research is needed to understand the multiple socioeconomic pathways from economic recession to childbearing. This study moves beyond the first-order question of whether and how unemployment has affected fertility to shed light on the negative effect of emigration, as well as the role of immigration in mitigating fertility decline. However, further work remains to be done. In particular, more policy attention needs to be given to the fertility consequences of both the decline in immigration and the acceleration of emigration in low fertility contexts severely hit by economic recession. A continuing shift to low and unstable fertility levels (Sobotka 2017) coupled with more dynamic and complex international migration in Europe (Trenz and Triandafyllidou 2017) clearly signal some of the new developments and challenges ahead.
Notes
Spatial dependence measures the correlation of a variable with itself through space, and can be positive or negative. The former refers to when similar values occur near one another, whereas the latter refers to when dissimilar values occur near one another.
Dynamic effects measure the serial correlation on each spatial unit over time.
The example of Germany, one of the largest recipients of these migrants, illustrates this well. In the first half of 2013, new registered immigrations of citizens from Spain and Italy to Germany increased by about 40% compared with the first half of 2012.
It is also worth noting that foreign-born emigrants are generally older than foreign immigrants, whereas the group of Spanish-born who emigrate is much younger than returning migrants. This could be because a large proportion of foreign-born emigrants are return migrants, whereas Spanish-born emigrants are (mostly) migrating to another country for the first time.
For this study, we repeated the analysis with several specifications of the neighbourhood matrix, in particular an inverse distance matrix and q-nearest neighbours matrices. Comparison of neighbourhood matrices showed that the worst performing spatial matrix is the inverse distance matrix, whereas the q-nearest neighbours matrix for q = 5 showed the best performance. While the specification of W has been a source of significant debate within the spatial econometrics literature, LeSage and Pace (2014) highlight that good fitting models using different forms of W are not likely to produce estimates and inferences that materially differ.
In fact, a random effects model would only make sense if a limited number of provinces were being drawn randomly from Spain, albeit in that case the elements of the neighborhood matrix could not be defined, and the impact of spatial interaction effects could not be estimated consistently. Only when neighboring units are part of the sample is it possible to measure the impact of neighboring units.
The estimator used in the dynamic SDM is the bias-corrected quasi-maximum likelihood (BCQML) estimator developed by Lee and Yu (2010), which yields consistent parameter estimates provided that the model is stable.
The summary table with all spatial models includes the following regression models: OLS, spatial lag (SAR), dynamic spatial lag (dynamic SAR), spatial Durbin (SDM), dynamic spatial Durbin (dynamic SDM), spatial error (SEM) and spatial lag error (SAC) is available on request.
Using the results from our models as an illustration, this means that if the average fertility rate of neighbouring provinces increases by 1%, the fertility rate of a particular province increases by around 0.3% (Model 1) and 0.1% (Model 2).
Moran’s I statistic is defined as: I = ε′Wcε/ε′ε. Where ε represents the residuals from regressing each variable on a constant (i.e. yi = ι + εi), and Wc is the spatial weight matrix. Moran’s I is bounded by −1.0 and 1.0, with values close to 0 suggesting a random spatial pattern and values 1 or − 1 indicating perfect positive or negative spatial autocorrelation respectively.
All values are significant at the 1% level. Only values referring to demographic composition are not statistically significant.
As noted by Jensen and Lacombe (2012), the estimates at zero order in the spatial Durbin model do not equal zero and can be greater than those at higher orders due to the sophisticated spatial dynamics and significant spatially lagged independent covariates across spatial units.
References
Adserà, A. (2011). The interplay of employment uncertainty and education in explaining second births in Europe. Demographic Research, 25(16), 513–544.
Ahn, N., & Mira, P. (2002). A note on the changing relationship between fertility and female employment rates in developed countries. Journal of Population Economics, 15(4), 667–682.
Anselin, L. (1988). Spatial econometrics: Methods and models. Dordrecht: Kluwer Academic Publishers.
Arango, J. (2013). Exceptional in Europe? Spain’s experience with immigration and integration, Migration Policy Institute Report at https://www.migrationpolicy.org/research/exceptional-europe-spains-experience-immigration-and-integration, Accessed 20 October 2017.
Baltagi, B. H., Fingleton, B., & Pirotte, A. (2014). Estimating and forecasting with a dynamic spatial panel data model. Oxford Bulletin of Economics and Statistics, 76(1), 112–138.
Bande, R., & Karanassou, M. (2009). Labour market flexibility and regional unemployment rate dynamics: Spain 1980-1995. Papers in regional science, 88(1), 181–207.
Beets, G., & Willekens, F. (2009). The global economic crisis and international migration: An uncertain outlook. Vienna Yearbook of Population Research, 19-37.
Belotti, F., Hughes, G., & Mortari, A. P. (2016). Spatial panel data models using Stata. CEIS tor Vergata research paper series, 14(5), No. 373), 1–38.
Bermudez, A., & Brey, E. (2017). Is Spain becoming a country of emigration again? Data evidence and public responses. In South-North Migration of EU Citizens in Times of Crisis (pp. 83-98). Springer International Publishing.
Bertoli, S., Brücker, H., & Moraga, J. F. H. (2016). The European crisis and migration to Germany. Regional Science and Urban Economics, 60, 61–72.
Beyer, R. C., & Smets, F. (2015). Labour market adjustments and migration in Europe and the United States: How different? Economic Policy, 30(84), 643–682.
Borjas, G. J. (1999). Economic research on the determinants of immigration: Lessons for the European Union (Vol. 438). Washington, D.C.: World Bank Publications.
Cherlin, A., Cumberworth, E., Morgan, S. P., & Wimer, C. (2013). The effects of the great recession on family structure and fertility. The Annals of the American Academy of Political and Social Science, 650(1), 214–231.
Coleman, D. (2006). Immigration and ethnic change in low-fertility countries: A third demographic transition. Population and Development Review, 32(3), 401–446.
Comolli, C. L. (2017). The fertility response to the great recession in Europe and the United States: Structural economic conditions and perceived economic uncertainty. Demographic Research, 36, 1549–1600.
Currie, J., & Schwandt, H. (2014). Short-and long-term effects of unemployment on fertility. Proceedings of the National Academy of Sciences, 111(41), 14734–14739.
DaVanzo, J. (1978). Does unemployment affect migration? Evidence from micro data. The Review of Economics and Statistics, 60(4), 504–514.
De la Rica, S., & Iza, A. (2005). Career planning in Spain: Do fixed-term contracts delay marriage and parenthood? Review of Economics of the Household, 3(1), 49–73.
De la Rica, S., & Rebollo-Sanz, Y. F. (2017). Gender differentials in unemployment ins and outs during the great recession in Spain. De Economist, 165(1), 67–99.
Debarsy, N., Ertur, C., & LeSage, J. P. (2012). Interpreting dynamic space-time panel data models. Statistical Methodology, 9(1–2), 158–171.
Domingo, A., Sabater, A., & Verdugo, R. R. (eds.). (2015). Demographic analysis of Latin American immigrants in Spain: From boom to bust. Applied Demographic Series, vol. 5. Springer.
Domínguez-Mujica, J., Guerra-Talavera, R., & Parreño-Castellano, J. M. (2014). Migration at a time of global economic crisis: The situation in Spain. International Migration, 52(6), 113–127.
Dustmann, C., & Weiss, Y. (2007). Return migration: Theory and empirical evidence from the UK. British Journal of Industrial Relations, 45(2), 236–256.
Ebanks, G. E., George, P. M., & Nobbe, C. E. (1975). Emigration and fertility decline: The case of Barbados. Demography, 12(3), 431–445.
Elhorst, J. P. (2010). Applied spatial econometrics: Raising the bar. Spatial Economic Analysis, 5(1), 9–28.
Elhorst, J. P. (2014). Spatial panel models, In Handbook of regional science (pp. 1637–1652). Berlin Heidelberg: Springer.
Esping-Andersen, G. (ed.) (2013). The Fertility Gap in Europe: Singularities of the Spanish Case. Barcelona: Obra Social Fundació “La Caixa”.
Fischer, M. M. (2011). A spatial Mankiw–Romer–Weil model: Theory and evidence. The Annals of Regional Science, 47(2), 419–436.
Fox, J., Klüsener, S., & Myrskylä, M. (2015). Is a positive relationship between fertility and economic development emerging at the sub-national regional level? Theoretical considerations and evidence from Europe. Max Planck Institute for Demographic Research Working Paper, 6. Available from https://www.demogr.mpg.de/papers/working/wp-2015-006.pdf Accessed 28 February 2018.
Goldstein, J. R., & Klüsener, S. (2014). Spatial analysis of the causes of fertility decline in Prussia. Population and Development Review, 40(3), 497–525.
Goldstein, J., Kreyenfeld, M., Jasilioniene, A., & Örsal, D. D. K. (2013). Fertility reactions to the" great recession" in Europe: Recent evidence from order-specific data. Demographic Research, 29, 85–104.
Goldstein, J. R., Sobotka, T., & Jasilioniene, A. (2009). The end of “lowest-low” fertility? Population and Development Review, 35(4), 663–699.
Graham, E., Sabater, A., & Fiori, F. (2016). Fertility change in the context of economic recession in Italy and Spain. ESRC Centre for Population Change, Briefing 36.
Gutiérrez-Domènech, M. (2008). The impact of the labour market on the timing of marriage and births in Spain. Journal of Population Economics, 21(1), 83–110.
Harris, J. R., & Todaro, M. P. (1970). Migration, unemployment and development: A two-sector analysis. The American Economic Review, 60(1), 126–142.
International Organization for Migration. (2010). Migration and the economic crisis in the European Union: Implications for policy. Brussels: IOM.
Izquierdo, M., Jimeno, J. F., & Lacuesta, A. (2016). Spain: From massive immigration to vast emigration? IZA Journal of Migration, 5(1), 10.
Jauer, J., Liebig, T., Martin, J. P., & Puhani, P. A. (2014). Migration as an adjustment mechanism in the crisis? A comparison of Europe and the United States. Institute for the Study of labor, IZA discussion paper no. 7921. Available at SSRN: https://ssrn.com/abstract=2389289
Karaman Örsal, D. D., & Goldstein, J. R. (2018). The changing relationship between unemployment and total fertility. Population Studies, 72(1), 109–121.
Kohler, H. P., Billari, F. C., & Ortega, J. A. (2002). The emergence of lowest‐low fertility in Europe during the 1990s. Population and Development Review, 28(4), 641–680.
Lacalle-Calderon, M., Perez-Trujillo, M., & Neira, I. (2017). Fertility and economic development: Quantile regression evidence on the inverse J-shaped pattern. European Journal of Population, 33(1), 1–31.
Lafleur, J. M., Stanek, M., & Veira, A. (2017). South-north labour migration within the crisis-affected European Union: New patterns, new contexts and new challenges. In South-North Migration of EU Citizens in Times of Crisis (pp. 193-214). Springer International Publishing.
Lee, R. (1990). The demographic response to economic crisis in historical and contemporary populations. New York: Population Bulletin of the United Nations, 29, 1–15.
Lee, L. F., & Yu, J. (2010). Estimation of spatial autoregressive panel data models with fixed effects. Journal of Econometrics, 154(2), 165–185.
Lerch, M. (2009). The impact of migration on fertility in post-communist Albania. Southeast European and Black Sea Studies, 9(4), 519–537.
LeSage, J. P., & Pace, R. K. (2009). Introduction to spatial econometrics. Boca Raton: Taylor & Francis.
LeSage, J. P., & Pace, R. K. (2014). The biggest myth in spatial econometrics. Econometrics, 2(4), 217–249.
Lesthaeghe, R., & Lopez-Gay, A. (2013). Spatial continuities and discontinuities in two successive demographic transitions: Spain and Belgium, 1880-2010. Demographic Research, 28, 77–136.
Lesthaeghe, R., & Permanyer, I. (2014). European sub-replacement fertility: Trapped or recovering? (pp. 14–822). Population Studies Center Research Report: University of Michigan.
Manski, C. F. (1993). Identification of endogenous social effects: The reflection problem. The Review of Economic Studies, 60(3), 531–542.
Martin, P. (2009). Recession and migration: A new era for labor migration? International Migration Review, 43(3), 671–691.
Mas Giralt, R. (2017). Onward migration as a coping strategy? Latin Americans moving from Spain to the UK Post-2008. Population, Space and Place, 23(3), https://doi.org/10.1002/psp.2017.
Massey, D. S., Arango, J., Hugo, G., Kouaouci, A., Pellegrino, A., & Taylor, J. E. (1993). Theories of international migration: A review and appraisal. Population and Development Review, 19(3), 431–466.
Matysiak, A., Sobotka, T. & Vignoli, D. (2018). The Great Recession and Fertility in Europe: A Sub-National Analysis. Vienna Institute of Demography Working Papers 02/2018.
OECD. (2013). International migration outlook 2013. Paris: OECD Publishing.
OECD. (2014). International migration outlook 2014. Paris: OECD Publishing.
OECD. (2015). International migration outlook 2015. Paris: OECD Publishing.
OECD (2016). Labour force indicators by sex and age. OECD.Stat at http://stats.oecd.org/viewhtml.aspx?datasetcode=LFS_SEXAGE_I_R&lang=en, Accessed 20 October 2017.
Okkerse, L. (2008). How to measure labour market effects of immigration: A review. Journal of Economic Surveys, 22(1), 1–30.
Overman, H. G., & Puga, D. (2002). Unemployment clusters across Europe's regions and countries. Economic Policy, 17(34), 115–148.
Prieto, V. (2016). Lost toys. Uruguayan births lost by migration in the period 1996-2010. Revista Latinoamericana de Población, 10(18), 63–81.
Recaño, J., Roig, M., & De Miguel, V. (2015). Spain: A new gravity centre for Latin American migration. In Demographic Analysis of Latin American Immigrants in Spain (pp. 181–209). Springer International Publishing.
Rios, V. (2017). What drives unemployment disparities in European regions? A dynamic spatial panel approach. Regional Studies, 51(11), 1599–1611.
Roos, C., & Zaun, N. (2016). The global economic crisis as a critical juncture? The crisis’s impact on migration movements and policies in Europe and the US. Journal of Ethnic and Migration Studies, 42(10), 1579–1589.
Schneider, D. (2015). The great recession, fertility, and uncertainty: Evidence from the United States. Journal of Marriage and Family, 77(5), 1144–1156.
Schneider, D., & Gemmill, A. (2016). The surprising decline in the non-marital fertility rate in the United States. Population and Development Review, 42(4), 627–649.
Sobotka, T. (2008). The rising importance of migrants for childbearing in Europe. Demographic Research, 19(9), 225–248.
Sobotka, T. (2017). Post-transitional fertility: childbearing postponement and the shift to low and unstable fertility levels (no. 01/2017). Vienna Institute of Demography Working Papers.
Sobotka, T., Skirbekk, V., & Philipov, D. (2011). Economic recession and fertility in the developed world. Population and Development Review, 37(2), 267–306.
Testa, M. R., & Gietel-Basten, S. (2014). Certainty of meeting fertility intentions declines in Europe during the'Great Recession'. Demographic Research, 31, 687–734.
Trenz, H. J., & Triandafyllidou, A. (2017). Complex and dynamic integration processes in Europe: Intra EU mobility and international migration in times of recession. Journal of Ethnic and Migration Studies, 43(4), 546–559.
Villarreal, A. (2014). Explaining the decline in Mexico-US migration: The effect of the great recession. Demography, 51(6), 2203–2228.
Vitali, A., Aassve, A., & Lappegård, T. (2015). Diffusion of childbearing within cohabitation. Demography, 52(2), 355–377.
Vitali, A., & Billari, F. C. (2017). Changing determinants of low fertility and diffusion: A spatial analysis for Italy. Population, Space and Place, 23(2), https://doi.org/10.1002/psp.1998.
Voss, P. R. (2007). Demography as a spatial social science. Population Research and Policy Review, 26(5–6), 457–476.
Waldorf, B., & Franklin, R. (2002). Spatial dimensions of the Easterlin hypothesis: Fertility variations in Italy. Journal of Regional Science, 42(3), 549–578.
Funding
As members of the ESRC Centre of Population Change, we receive funding from the Economic and Social Research Council (ES/K007394/1).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The Authors have no conflict of interest to declare.
Appendices
Appendix 1
Appendix 2
Appendix 3
Appendix 4
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sabater, A., Graham, E. International Migration and Fertility Variation in Spain during the Economic Recession: A Spatial Durbin Approach. Appl. Spatial Analysis 12, 515–546 (2019). https://doi.org/10.1007/s12061-018-9255-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12061-018-9255-9