Introduction

The aviation industry has developed rapidly with improved living standards and increased economic trade between regions. The global passenger turnover (RPK) is expected to increase from 8.68 trillion in 2019 to 20 trillion in 2050, growing at 3.0% yearly. International air cargo demand increased by 9.6% in 2019. But the issue of aviation carbon emissions has attracted more and more societal attention. The transportation industry is an energy-intensive industry globally (Chang et al., 2013), emitting more greenhouse gas than any other sector except the chemical industry. Meanwhile, energy consumption in the aviation industry is increasing by 6% a year. With the growth in energy consumption, there has been a massive rise in environmental pollution. Data published by the International Air Transport Association (IATA) show that the carbon emission of the airline industrial sector accounts for 2.4% of the total 37.5 billion tons in 2018, which caused environmental destruction. Based on the International Civil Aviation Organization (ICAO) forecast, aviation carbon emissions in 2050 will be 4–6 times that of 2010. To alleviate the situation, many strategies of international guidelines have been implemented. For example, ICAO proposed the Carbon Neutral Growth strategy (CNG2020) in 2016, which requires the global aviation sector to offset carbon dioxide emissions to achieve carbon–neutral growth by 2021. The motions above have a significant impact on the airlines. Therefore, it is essential to explore the environmental efficiency of airlines so that countermeasures can be put forward.

Air transportation usually consists of passenger and freight services. Passenger transportation accounts for a large proportion of most companies, and its revenue is far more significant than freight revenue. However, the air cargo industry generates 70 billion US dollars in economic value each year, accounting for about 15% of the total business of the air transportation industry. Air cargo is growing 1.5 to 2 times faster than GDP, around 3%, even faster than air passenger transportation. According to the IATA report, the freight revenue of the international aviation industry has shown a growing trend in 2020, affected by COVID-19, an increase of 15% compared to 2019. Many airlines have changed cabins to cargo cabins to increase revenue, such as United Airlines and Lufthansa. Moreover, empirical data proves that air cargo is significantly and positively correlated with national GDP and air cargo provides approximately 57 million jobs worldwide annually. Therefore, airfreight is becoming an important indicator to determine the status of a company with its rapid development. Consequently, it is necessary to consider it. About 55% of air transport items are placed in the passenger plane, so passenger and freight systems are mixed in daily operations. As is shown in Table 1, the top ten mixed passenger/freight airlines are listed based on AirlineRatings.com (an internationally renowned aviation professional website) in 2019 (AirlineRatings, 2021). Freight revenue accounts for over 11%, much smaller than passenger transportation. Six out of ten airlines lie in Asia, and others in Oceania. Table 1 shows that the sum of passenger and cargo revenue accounts for a substantial proportion of total payment. Passenger transport and freight transport are the main business income items, but the sum of the two is not equal to 100%. Airlines have other revenue-generating subsystems, such as airplane rental business, advertising services, and fleet maintenance services. However, these subsystems have a deficient proportion of revenue and are not the primary source of income for airlines, so we do not consider these subsystems.

Table 1 Top ten mixed passenger/freight airlines in 2019
Full size table

Unlike the entirety of previous studies, this paper divides airline transportation into two subsystems. Then, decompose the efficiency of two relatively independent departments and provide information on inefficiency by comparison. Some unique inputs and outputs belong to one subsystem: flight attendant, passenger volume, and passenger turnover in passenger transportation, while freight volume and loading costs in the other. However, some inputs and outputs are shared evidently, such as operating costs. Different operating costs are allocated to each subsystem to realize the company’s normal operation. Meanwhile, for the same subsystem, different companies have different ratios of operating costs, which are closely related to actual production conditions. So previous papers may be unreasonable, setting the operating costs as input of the passenger transportation. On the other hand, it is more important to measure whether the current allocation ratio is reasonable to achieve optimal environmental efficiency. How can we get the optimal percentage of shared operating costs if not? The above questions will be answered in the “Case study” section. The results of an empirical study can provide helpful advice for airline managers from theoretical and practical perspectives.

Many studies measure the energy and environmental efficiency (EEP) of the system using the stochastic frontier analysis (SFA) approach and data envelopment analysis (DEA) (Coelli et al., 1999; Sickles et al., 2002; Zou et al., 2014). The former is a usual parametric method with apparent disadvantages. The basic assumptions of the stochastic frontier analysis model are more complex, and the specific form of the production function needs to be considered, so the requirements for input–output data are higher. Suppose the input–output data does not meet the basic assumptions. In that case, the skewness problem is prone to occur, resulting in the technical efficiency values of each decision-making unit being very close to 1. Furthermore, the probability density distribution of the index affects the results, and there is no theoretical proof that the index obeys any distribution. Moreover, the improvement by adjusting the input and output types or increasing the sample size has no apparent effect. DEA, proposed by Charnes et al. (1978), can overcome the above. Recently, papers have applied the DEA to evaluate homogeneous industries, such as the economic industry (Iftikhar et al., 2018), the banking industry (Ebrahimnejad et al., 2014), and the aviation industry (Li et al., 2016a, b; Rajbhandari & Zhang, 2018). This paper studies the environmental efficiency of major international airlines and proposes a novel input–output shared range adjusted measure (RAM) model to analyze the internal network structure. By eliminating inefficiencies under the reasonable assumption, the strong monotonicity of parallel range adjusted measure (PRAM) can provide clear priorities between decision-making units (DMUs).

Existing literature focuses on applying the RAM model to airline efficiency evaluation to improve the accuracy of the overall efficiency measure. The focus is on a single system, which is generally analyzed in multiple stages of operation, ignoring other revenue-generating subsystems, such as freight transport. Air cargo is a robust sunrise industry, less affected by economic development fluctuations than air passenger transport. This paper fills the research gap on air cargo, emphasizes the position of cargo in the company’s overall strategy, optimizes the allocation of shared resources, and enriches the research connotation on the environmental efficiency of airlines.

The following is a summary of the structure of this paper. “Literature review” section presents a literature review. “Methodology” section presents a methodology to measure the performance of parallel systems considering possible shared inputs, desirable outputs, and undesirable outputs. “Case study” section applies the proposed approach to the 18 airlines worldwide and analyzes the obtained efficiency values and distribution ratios. Finally, “Conclusion” section summarizes the conclusions and limitations.

Literature review

The data envelopment analysis on airlines

Recently, the issue of airline environmental efficiency evaluation has attracted the attention of many scholars, who mainly use the ratio of outputs divided by inputs to measure whether it meets transportation needs and environmental protection requirements. However, from a methodological point of view, many papers mainly apply DEA and its deformation modes.

In 1993, Schefczyk (1993) began to use standard DEA model technology to conduct a comparative analysis of the energy performance of 15 airlines. Traditional DEA models (CCR and BCC models) are usually applied to evaluate the airline’s technical and scale efficiency. Arjomandi and Seufert (2014) used DEA models with a bootstrapped method to examine 48 airlines of the significant full-service carriers and low-cost carriers from 2007 to 2010. Jain and Natarajan (2015) investigated the efficiency of all airlines in India with the DEA and input efficiency profiling (IEP) model from 2006 to 2010. Then a combination of DEA models and other methods has long been the most popular. Since Distexhe and Perelman (1994) combined the standard DEA and Malmquist index to analyze the production rate of 33 American and European airlines. Hu et al. (2017) applied the bootstrapped DEA method to calculate input efficiency and returns to the scale of 15 ASEAN airlines. Other main methods combined with DEA are Fisher productivity index (Zofío & Prieto, 2006), Tobit regression (Fethi et al., 2000), balanced score card (Wu & Liao, 2014), and so on. With the deepening of research, scholars have developed variously extended and improved DEA models under complex circumstances. Tavassoli et al. (2014) applied the SBM network DEA model to evaluate the operating efficiency of air passenger and cargo transportation services. Cui and Li (2015) innovatively combined the virtual frontier benevolent DEA with cross efficiency to assess airlines’ efficiency and identified capital efficiency as the determinant. And in 2018, Cui and Li used a dynamic RAM model with natural and managerial disposability to evaluate the dynamic efficiency of 29 airlines. Soltanzadeh and Omrani (2018) applied the fuzzy dynamic network DEA to calculate the efficiencies of Iranian airlines’ systems and processes. Chen et al. (2021) introduced the network SBM approach to explore Chinese airlines’ two-stage and undesirable output efficiency. Cui and Arjomandi (2021) utilized an epsilon-based measure (EBM) model to analyze the efficiency of major airlines worldwide.

The data envelopment analysis from the perspective of “black boxes” ignores the internal structure of airline operations and cannot effectively measure production efficiency. Throughout the existing research, if we want to consider the internal structure of the airline fully, what needs to be done is to analyze the affiliation relationship between the internal subsystems: parallel, chained, or a combination of the two, and analyze whether there are shared inputs and outputs between sub-processes. For example, in addition to exclusive inputs and outputs, there are shared resources between the passenger and freight subsystems.

Scholars have early paid attention to the complex efficiency measurement of the parallel subsystems with sharing resources, and the established model system is relatively mature. Beasley (1995) proposed a discriminant method based upon data envelopment analysis to apportion shared resources between different activities with the same discipline. Cook et al. (2000) constructed one DEA framework that can get the optimal ratio of resource allocation when inputs are shared among functions. Jahanshahloo et al. (2004) used the dynamic DEA model that considers the effect of time with shared inputs and outputs. Cook and Zhu (2005) extended the previous method and provided a concrete method to achieve fair cost distribution. Chen et al. (2010) presented an additive model for measuring the efficiency of the DMUs that have inseparable inputs. Rogge and De Jaeger (2012) proposed an adjusted “shared-input” version to measure the efficiency of waste collection and processing performances in settings where waste costs are shared. Moreno et al. (2015) introduced two network DEA models, relational and additive approaches to assess the efficiency of electricity distribution companies, whose operating costs are shared between the stages. Li et al. (2016a, b) extended the centralized model to evaluate 17 city branches of banks sharing the same inputs and outputs in Anhui Province. Chao et al. (2018) applied a DEA deformation model decomposing the sharing of standard inputs between the two processes of 13 major global container shipping companies. Zhu et al. (2019) analyzed the efficiency of a randomly generated data set by allocating the fixed costs between two phases. Song et al. (2020) established a stochastic DEA model of shared inputs and unexpected output to assess the bank’s performance. Cheng et al. (2020) indicated that relational decomposition and additive network models show better discriminating power. Nguyen and Yu (2020) adopted a network DEA approach to examine the operational efficiency of the top cruise lines when sharing inputs. The prominent features of these studies are that the shared undesirable output is not considered, and applied DEA models are traditional radial models in most papers. Omrani et al. (2022) combined DEA models and the TOPSIS approach to evaluate airlines’ technical, social, environmental, and sustainable efficiencies, but the model was also a radial model.

This paper follows the direction of the above articles and applies the RAM model to deal with the issue. The non-radial RAM model proposed by Aida et al. (1998) and Cooper et al. (1999) has recently been used in airline efficiency evaluation. Compared with the standard DEA model, the RAM model can also simultaneously process multiple reference sets and the negative data of input or output. Wanke and Barros (2016) used the virtual frontier dynamic RAM model to evaluate the Latin American airlines, revealing that the influence of fleet size and ownership nature cannot be ignored. Li and Cui (2018) used the network RAM model to study the performance of 29 global airlines from 2008 to 2015 when setting the number of employees as a stage-sharing input to achieve optimal employee allocation. The results showed that most airlines’ maximum number of employees should be allocated to the sales stage. Heydari et al. (2020) introduced an utterly fuzzy network DEA-RAM model for evaluating the overall efficiency of Iranian airlines and extended it to an utterly fuzzy setting. However, relatively few papers use the RAM model to evaluate airline parallel systems’ efficiency.

The research gap

In the current research, there is little research on the parallel subsystem of airlines. Most discuss the chain structure (such as operations, services, and sales stage). At the same time, they also ignore the sharing of undesirable output. As a result, they cannot distinguish the role from undesirable production among subsystems, resulting in an inaccurate quantitative evaluation of efficiency. Furthermore, few papers evaluate the efficiency of parallel airline systems, and existing models cannot handle shared input and outputs simultaneously.

This paper fills the gap in the efficiency research of air passenger transport and freight transport parallel subsystem and provides a reference for airlines’ recovery in the post-epidemic era. This paper innovatively proposes a theoretical framework that includes airline passenger and cargo transportation. This method of efficiency decomposition can help identify the real reason for inefficiency and obtain an accurate efficiency evaluation. This paper proposes a parallel RAM model with shared inputs and outputs to analyze the airline environmental efficiency, which can compute the overall efficiency and the subsystem efficiency. The results also confirm the robustness and reliability of our model. Finally, our case study shows how the proposed model works and presents key findings that are helpful to decision-makers.

Methodology

Data envelopment analysis is now widely used to calculate environmental efficiency in aviation industry. When considering the undesirable outputs, the production set is:

$$T=\left\{\left(X,Y,Z\right):X\text{ can produce }(Y,Z)\right\}$$
(1)

In Eq. (1), \(X={\left\{{x}_{mk}\right\}}^{M\times K}\) stands for the \(M\times K\) matrix of the inputs, \(Y={\left\{{y}_{nk}\right\}}^{N\times K}\) stands for the \(N\times K\) matrix of the desirable outputs, and \(Z={\left\{{z}_{lk}\right\}}^{L\times K}\) stands for the \(L\times K\) matrix of the undesirable output. \(K\) is the number of the DMUs and \(M,N,K\) denotes the number of the inputs, the desirable outputs, and the undesirable output, respectively.

Usually, there are five main disposability approaches to handle the undesirable outputs: weak disposability (Wu et al., 2013), strong disposability (Yang & Pollitt, 2010), natural and managerial disposability (Cui & Li, 2018b), by-production disposability (Murty et al., 2012), and weak G-disposability (Dakpo et al., 2014). A detailed comparison of five methods can get from Cui (2020).

One popular way is strong disposability which beliefs in the environment’s capacity to handle a predetermined amount of undesirable outputs. Namely, the undesirable outputs are treated as inputs. Both methods have been studied in academic papers, while the results from Cui et al. (2018) indicate that strong disposability is more reasonable when dealing with undesired outputs. So, we introduce a RAM model with strong disposability to reasonably compare a parallel system’s efficiency.

First, we introduce the RAM model, whose modifications have been used far and wide recently, such as weak disposability in the virtual frontier network RAM model (Li and Cui, 2016); natural and managerial disposability in the network RAM model.

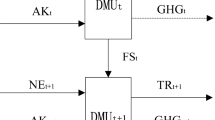
The network RAM model (NRAM) is firstly proposed by Avkiran and McCrystal (2012):

$$\begin{array}{c}\theta =1-{\text{max}}\sum\limits_{j=1}^{J}\frac{1}{{m}_{j}+{n}_{j}+{l}_{j}}\left(\sum\limits_{m=1}^{M}\frac{{s}_{m}^{j-}}{{R}_{m}^{-}}+\sum\limits_{n=1}^{N}\frac{{s}_{n}^{j+}}{{R}_{n}^{+}}+\sum\limits_{l=1}^{L}\frac{{s}_{l}^{j-}}{{R}_{l}^{-}}\right)\\ s.\mathrm{t}.\left\{\begin{array}{c}\begin{array}{c}{x}_{m0}^{j}=\sum_{j=1}^{J}{\lambda }_{k}^{j}{x}_{mk}^{j}+{s}_{m}^{j-}\\ {y}_{m0}^{j}=\sum_{j=1}^{J}{\lambda }_{k}^{j}{y}_{nk}^{j}-{s}_{n}^{j+}\\ {z}_{l0}^{j}=\sum_{j=1}^{J}{\lambda }_{k}^{j}{z}_{lk}^{j}+{s}_{l}^{j-}\end{array}\\ \sum_{k=1}^{K}{\lambda }_{k}=1\\ {\lambda }_{k}, { s}_{m0}^{j-},{ s}_{n0}^{j+},{ s}_{l0}^{j-}\ge 0\end{array}\right.\end{array}$$
(2)

\({x}_{mk}, {y}_{nk}, {z}_{lk}\) denote the \(m\) th input, the \(n\) th desirable output, and the \(l\) th undesirable output of \({DMU}_{k}, k=\mathrm{1,2},\cdots ,K\). \({R}_{m}=\mathrm{max}\left({x}_{mk}\right)-\mathrm{min}\left({x}_{mk}\right), {R}_{n}=\mathrm{max}\left({y}_{nk}\right)-\mathrm{min}\left({y}_{nk}\right), {R}_{z}=\mathrm{max}\left({y}_{zk}\right)-\mathrm{min}\left({y}_{zk}\right), k=\mathrm{1,2},\cdots ,K\) are the ranges of the inputs, desirable output, and undesirable outputs. \({s}_{m}^{-}, {s}_{n}^{+}, {s}_{z}^{-}\) stand for the slacks. \(\lambda\) is the weight. \(j\) is the number of the subsystems.

Then we apply the model (2) to a parallel system of two subsystems with shared inputs, desirable outputs, and the undesirable outputs. Referring, we set the allocative factors as \(\alpha ,\beta ,\gamma\) and then the RAM model with strong disposability is:

$$\begin{array}{c}\theta =1-{\text{max}}\sum_{j=1}^{J}\frac{1}{{m}_{j}+{n}_{j}+{l}_{j}}\left(\sum_{m=1}^{M}\frac{{s}_{m}^{j\alpha -}}{{\alpha }^{j}*{R}_{m}^{-}}+\sum_{n=1}^{N}\frac{{s}_{n}^{j\beta +}}{{{\beta }^{j}*R}_{n}^{+}}+\sum_{l=1}^{L}\frac{{s}_{l}^{j\gamma -}}{{{\gamma }^{j}*R}_{l}^{-}}\right)\\ \mathrm{s}.\mathrm{t}.\left\{\begin{array}{c}\begin{array}{c}{{\alpha }^{j}x}_{m0}^{j}=\sum_{j=1}^{J}{\alpha }^{j}{\lambda }_{k}^{j}{x}_{mk}^{j}+{s}_{m}^{j\alpha -}\\ {{\beta }^{j}y}_{n0}^{j}=\sum_{j=1}^{J}{\beta }^{j}{\lambda }_{k}^{j}{y}_{nk}^{j}-{s}_{n}^{j\beta +}\\ {\gamma }^{j}{z}_{l0}^{j}=\sum_{j=1}^{J}{{\gamma }^{j}\lambda }_{k}^{j}{z}_{lk}^{j}+{s}_{l}^{j\gamma -}\end{array}\\ \sum_{k=1}^{K}{\lambda }_{k}^{j}=1\\ \lambda , {s}^{-},{s}^{+}\ge 0\\ 0\le \alpha ,\beta ,\gamma \le 1\end{array}\right.\end{array}$$
(3)

In model (3), when the value of \(\alpha ,\beta ,\gamma\) equals to 0 or 1, it means that the input or output is not a shared one but is completely used by a certain subsystem. \(\alpha {x}_{mk}\) is the input of the subsystem of the \({DMU}_{k}\); \(\beta {y}_{nk}\) is the desirable output of the subsystem of the \({DMU}_{k}\); and \(\gamma {z}_{lk}\) is the undesirable output of the subsystem of the \({DMU}_{k}\). In the objective function, \({R}_{\alpha {x}_{m0}}^{-}=\alpha *{R}_{{x}_{m0}}^{-}\) means the range of the allocated inputs in the subsystem, others are the same as model (2).

The optimal results of model (3) and the values of the allocative factors: \(\alpha ,\beta ,\gamma\) can be obtained by programming solution.

The subsystem efficiency of subsystem \(j\) is:

$${\theta }_{j}=1-\frac{1}{{m}_{j}+{n}_{j}+{l}_{j}}\left({\sum}_{m=1}^{M}\frac{{s}_{m}^{j\alpha -}}{{\alpha }^{j}*{R}_{m}^{-}}+{\sum}_{n=1}^{N}\frac{{s}_{n}^{j\beta +}}{{{\beta }^{j}*R}_{n}^{+}}+{\sum}_{l=1}^{L}\frac{{s}_{l}^{j\gamma -}}{{{\gamma }^{j}*R}_{l}^{-}}\right)$$
(4)

Case study

One of the most forward-looking applications of DEA is efficiency evaluation on airlines. Therefore, a case study is presented in this section to illustrate the reliability and rationality of our proposed PRAM model.

The efficiency models

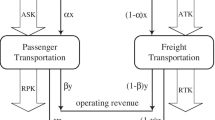
Based on previous academic research and the daily operation process of the airline, we select the inputs and outputs of airlines and construct a new airline internal structure system, as shown in Fig. 1.

Fig. 1
figure 1

A parallel system comprised of two transportation subsystems

Full size image

Three measurable variables are selected as the inputs: available seat kilometers (ASK), available ton kilometers (ATK), and operating costs (OC). As stated by, passenger transportation needs to fully use the human and material resources to increase its passenger delivery capacity, which can be reflected by available seat kilometers (ASK). This index reflects the most significant economic benefit that an airline can generate. The larger the ASK value, the more routes and capacity resources the airline has. Similarly, we choose the available ton kilometers (ATK) to embody the cargo-carrying capacity of freight transportation. Operating cost is obvious to be a shared input in daily operations. For the same subsystem, different airlines have different operating costs. For example, in 2019, the operating costs proportions of Air China were 0.936 and 0.043. The corresponding ratios of Singapore Airlines were 0.798 and 0.149. Compared with the direct input—operating costs, employees, and other indicators allocation may affect the quickness, satisfaction, repeat business, and profitability. As a result, we select the direct shared inputs in our model.

Correspondingly, four variables are selected as the outputs: revenue passenger kilometers (RPK), revenue ton kilometers (RTK), operating revenue (OR), and greenhouse gas emission (GHG). Among them, the GHG is an undesirable output that includes \({\text{CO}}_{2}\text{, }{\text{HO}}_{2}\text{, }{\text{NO}}_{\text{x}}\text{, }{\text{SO}}_{\text{x}}\), and soot, of which \({\text{CO}}_{2}\) is the most important greenhouse gas (Sausen et al., 2005). Therefore, we use carbon dioxide emissions to represent the greenhouse gas. RPK and RTK are comprehensive indicators to measure passenger and freight traffic. Operating revenue (OR) is another shared resource.

In Fig. 1, OC is the shared input that some is responsible for passenger subsystem and freight subsystem. What we do is to use \({\alpha }_{t}\) denoting the proportion of the operating cost in subsystem \(j\), while \({\alpha }_{t}\ne 0\) and \(\sum_{j=1}^{J}{\alpha }_{t}=1\). Only in the process of overall optimization efficiency can the optimal value of unknown variable \({\alpha }_{t}\) be solved. The same is true for unknown variables \({\beta }_{t}\) and \({\gamma }_{t}\).

The data

This paper will use the data from 6 years for empirical research from 2014 to 2019. Due to the relative importance of the freight business, the data of the freight department in some airlines is incomplete. After careful filtering, the empirical data are obtained from 18 global airlines: Aeroflot, Air China, All Nippon Airways, British Airways, Cathay Pacific Airways, China Airlines, China Eastern, China Southern Airlines, Emirates, Eva Air, Hainan, KLM Royal Dutch Airlines, Korean Air, Lufthansa, Scandinavian Airlines, Singapore Airlines, Spring Airlines, and Thai Airways. Among the above airlines, five airlines (All Nippon Airways, Cathay Pacific Airways, Emirates, Eva Air, and Singapore Airlines) ranked top 10 all over the world in 2019, announced to Airline Ratings.com.

The data on available seat kilometers, available ton kilometers, operating costs, revenue passenger kilometers, revenue ton kilometers, and operating revenues are extracted from the annual reports of the 18 airlines. The data on carbon dioxide emissions is taken from the sustainability, environment, and corporate social responsibility reports.

Descriptive statistics of the inputs and outputs are provided in Table 2.

Table 2 Descriptive statistics of the inputs and outputs during 2014–2019
Full size table

Table 2 shows the mean value, the standard deviation, the minimum value, and the maximum value in the transportation sector of 18 global airlines. The data of operating cost and operating revenue has a big difference, the former of which ranges from 819.21 to 26,280.32. And the standard deviation is 6440.75. The latter ranges from 1007.57 to 33,764.46, and the standard deviation is 7316.13. This means that passenger and freight transportation in different airlines have different levels of development. Nevertheless, the data of ASK, ATK, RPK, and RTK are in line with reality. The range of carbon dioxide emissions is from 1.02 to 36.94, and the reason is that the development modes of airlines are diverse. For example, airlines represented by Lufthansa and Scandinavian Airlines focus on consuming clean energy to produce less pollution, while some airlines use their income to offset environmental pollution. Therefore, considering the undesirable outputs in energy efficiency assessment is of greater significance.

Table 3 shows this paper’s Pearson correlation coefficients between the inputs and outputs. Again, most coefficients are positive and close to 1, indicating a strong correlation between input and output. Therefore, the selection of indicators is reasonable.

Table 3 Input–output correlations
Full size table

The overall and subsystem efficiencies

The weight ratio of two subsystems is set as [1/2,1/2]. We apply the 1st Opt software to compute the model (2) and the results are listed in Table 4. Then, we apply the RAM model (8) to calculate the overall efficiency of the airlines in Table 5.

Table 4 Overall efficiency of RAM model during 2014–2019
Full size table
Table 5 Overall efficiency of input–output-shared RAM model during 2014–2019
Full size table

In Table 4, columns 2–7 show the overall systems’ efficiency scores of 18 airlines between 2014 and 2019, while the last column represents the average efficiency scores. The numbers in Table 5 are the same meaning as Table 4. The yearly efficiency of some airlines is 1 indicating the efficient airline. Comparing the two tables, we can find that shared resources can significantly improve overall efficiency. There are five efficient airlines in Table 4, while four efficient ones are in Table 5. However, the minimum values of yearly efficiency in Table 5 are 0.9200, 0.9090, 0.9115, 0.9163, 0.9106, and 0.9285 and the values in Table 4 are 0.7829, 0.7815, 0.8079, 0.8196, 0.8249, and 0.7834, showing that the former are significantly higher. The mean values and standard error values also verify this situation. Operating costs, revenues, and greenhouse gasses are optimally allocated between the two subsystems, which promotes overall efficiency. The efficiency in the last column of Table 5 shows that the average efficiency difference of the 18 airlines is insignificant. In addition, there are some airlines with relatively low overall efficiency, such as British Airways (0.92905), Thai Airways (0.94669), and China Southern Airlines (0.96914), and the majority are in Asia. This result shows that airlines face the problem of relatively low transportation system efficiency in the current real situation.

In Table 5, the annual average efficiency value from 2014 to 2019 increased and decreased but showed an upward trend from 0.9836 in 2014 to 0.9901 in 2019. The development prospect of airlines is good. Compared with the values in Table 4, the average efficiency value of each airline in Table 5 is higher, which inspires managers to reasonably allocate shared input and output indicators. The subsystem efficiency values in Tables 6 and 7 provide ideas. For example, the efficiency value of the passenger transport subsystem of Russian Airlines in 2014–2019 is 1.0000, while the freight subsystem is inefficient. Therefore, improving freight efficiency is the direction of improvement. Aeroflot Airlines generally uses the belly compartment of the passenger plane to transport cargo, with a share of about 1.8% in the global air cargo market. In 2019, Aeroflot joined the Digital Transportation and Logistics Association, created and developed a single multimodal digital transportation and logistics environment in all parts of Russia, and launched an automated system of cargo air based on big data to predict the cargo and mail capacity on Aeroflot passenger flights. Aeroflot Airlines also needs to make more active exploration to develop freight subsystems.

Table 6 Subsystem efficiency of input–output-shared RAM model during 2014–2016
Full size table
Table 7 Subsystem efficiency of input–output-shared RAM model during 2017–2019
Full size table

All Nippon Airways, Emirates, Lufthansa, and Spring Airlines have the maximum overall efficiency during 2014–2019 in Table 5, so they are benchmarking airlines among 18. Inefficient years, four airlines’ subsystem efficiencies are all equal to 1. Take Emirates as an example. Emirates’ overall revenue has maintained growth through active capacity adjustment and potential flight route development. During these years, Emirates has developed new service types and established partnerships with Indian airlines to improve convenience. The intelligent combination of customer needs and actual operations successfully implements dynamic scheduling. Moreover, Emirates has ordered 50 Airbus A350 XWBs and 30 Boeing 787 airplanes in 2019. These new aircraft will increase fleet mix and keep the average fleet age of 5.7 years, well below the industry. As a result, fuel efficiency improved with the retirement of older aircraft and the introduction of new aircraft. Besides, Emirates supports the development of a supply and demand network for sustainable aviation kerosene and uses operational procedures to reduce aircraft noise. Emirates is trying to realize emissions by reducing the adverse global influence of greenhouse gas emissions and establishing a positive image as a sustainable and green corporation. The above measures significantly improve Emirates’ overall and subsystem efficiency and provide a reference for other airlines.

Then we pay attention to airlines with an ineffective system whose efficiency is not equal to 1. It means there is room for further improvement that other airlines should focus on. The overall efficiency of the entire system is decomposed into the efficiency of the two subsystems, and the results are listed in Tables 6 and 7 from 2014 to 2019. The passenger transport system is more efficient, which can be seen from the results that, except for 2014, the average efficiency of the passenger transport system from 2015 to 2019 is higher than that of the freight system. The number of airlines whose passenger subsystem is efficient is 12, 13, 14, 11, 10, and 14, while the number of freight subsystems is 13, 12, 11, 12, 9, and 13. Volatility in the price of petroleum products and the significant level of ATC strikes in Europe over the summer of 2018 can significantly impact the airlines’ operating results. The maximum average passenger and freight transportation subsystem efficiencies are 0.9811 and 0.9708, respectively, showing that the efficiency of the passenger subsystem is more decisive for overall efficiency than the freight subsystem, and the latter is a breakthrough for the rapid development of most airlines.

Combined with subsystem efficiency, airlines can clarify specific measures to improve efficiency. British Airways performed poorly among the 18 airlines, with the lowest average efficiency score of 0.9290. Analyzing the subsystem efficiency is always inefficient from 2014 to 2019, except for the passenger subsystem in 2016 and 2019. Therefore, freight efficiency is the main direction to improve overall efficiency. The inputs and outputs of the freight subsystem are OC, ATK, RTK, OR, and GHG in the model (10), and the slacks of these indices are adjustment directions. After calculation, the proportion of slacks are 0.2589 (OC), 1.2727 (OR), 5.6647 (GHG), − 1.42559E − 16 (ATK), and 1.91E − 16 (RTK). Among them, the slack of GHG has the largest value, so British Airways should focus on reducing greenhouse gas emissions. In strong disposability, the undesirable outputs are treated as inputs, while the slacks mean input redundancy. Thence British Airways should lead aviation action on climate change and step up its commitment with a package of new measures to reduce its carbon footprint. British Airways is the first UK airline to announce it would offset carbon emissions on its domestic flights from 2020 and lead the way in sustainable fuel development. However, there is more to do, and change takes time. Similarly, the operating costs invested in the passenger transport system must be reduced. The analysis process is the same for other inefficient airlines.

The optimal allocation ratios

The optimal allocation values of α, β, and γ during 2014–2019 are enumerated in Tables 8 and 9. The comprehensive efficiency decomposition method proposed in this paper can obtain the optimal rates of shared resources between passenger and freight subsystems. And then, each airline can understand how to choose the optimal division of shared resources. Take China Southern Airlines, for example. The optimal proportions of OC, OR, and GHG for the passenger subsystem were 0.6516, 0.3320, and 0.5193, respectively, in 2017. In other words, the optimal proportions for the freight subsystem are 0.34844, 0.6680, and 0.4807. The allocation ratios of operating costs and greenhouse gas are relatively high in the passenger subsystem. Comparing these data with the actual percentage of China Southern Airlines’ passenger and cargo operating costs (93.25% and 6.75%), it should increase resources in the passenger subsystem to reduce carbon dioxide emissions in 2017. It can be seen from Tables 8 and 9 that there is a big difference in the optimal allocation of operating costs, operating revenues, and CO2 emissions. Indeed, the distribution ratio in different years is also different for the same company. Just like China Southern Airlines, the optimal ratios in 2019 are 0.3676, 0.5300, and 0.3211, which is contrary to the situation in 2017. The more significant operation cost allocation proportion occurs in the freight subsystem. The results are in line with reality because COVID-19 has greatly affected tourism and business visits in the aviation industry, and the status of freight transportation has begun to rise.

Table 8 Three optimal allocation ratios during 2014–2016
Full size table
Table 9 Three optimal allocation ratios during 2017–2019
Full size table

Comparing the optimal distribution ratios of 18 airlines in Tables 8 and 9, we can find some interesting conclusions. First, the passenger subsystem has a relatively smaller proportion of operating costs. The numbers are 7 (2014), 7 (2015), 6 (2016), 8 (2017), 9 (2018), and 6 (2019), respectively. It means that the importance of the freight transport system is higher, so more cost needs to be invested into it in pursuit of optimal efficiency. The relatively significant gap between the two subsystems in Tables 6 and 7 supports this view. The accurate values of each year guided us to dynamically adjust the operating costs, which are formed by the production and operation of an airline. It mainly includes direct materials, direct labor, and manufacturing costs. Specifically, airlines make decisions by adjusting employees’ salaries, bonuses and allowances, aviation fuel consumption, passenger and cargo cabin service fees, aviation material consumption, and so on. As an airline’s cost expenditure items, operating time and aircraft fuel costs are the bulk of the airline’s expenses. For some companies, the above two costs account for more than 50% of the main business cost. Reducing investment targets can be reduced by managing flight time and fuel consumption. The rapid development of cross-border e-commerce business has promoted the recovery of the air cargo market and accelerated process modernization to a certain extent. While entering the next financial year, 2020–2021, the full-scale outbreak of COVID-19 has brought an unprecedented crisis to airlines. The closure of country borders has brought air passenger traffic to a standstill, while cargo traffic has increased slowly. Take Hainan Airlines as an example. It uses its extensive airline network and efficient services to actively respond to the Civil Aviation Administration’s calls. It replaces passenger aircraft with cargo charter services to facilitate the rapid turnover of supplies.

Then, we pay attention to the allocation value of outputs in Tables 8 and 9. As shown by data, the number of airlines with higher operating income distribution is 9 (2014), 10 (2015), 9 (2016), 7 (2017), 11 (2018), and 10 (2019), which indicates that the passenger transport system generates more operating revenue. This situation is consistent with reality, as shown in Table 1. According to the forecast of IATA, the average annual growth rate of air passenger turnover (RPK) will be 4.4–4.7%, which is still in a relatively fast growth range in the next 20 years. Increasing demand means more competition for airline passenger transportation. Then comes the issue of greenhouse gas reduction. The number of airlines whose distribution ratio of greenhouse gasses in Tables 8 and 9 is higher than 0.5000 is 12 (2014), 14 (2015), 14 (2016), 13 (2017), 9 (2018), and 12 (2019). Therefore, the passenger subsystem may emit more greenhouse gasses, and the airlines should take measures according to the situation. The overall efficiency value of Lufthansa in Tables 5 and 6 is 1, indicating that it can be used as a benchmarking airline. For many years, the Lufthansa Group has taken steps to minimize the environmental impact of its business operations. Current examples are developing innovative cleaning processes, applying coatings to make aircraft more aerodynamic, and so on.

Some optimal allocation ratios of greenhouse gas are an extreme value of 0.1000 in Table 9, such as the Hainan Airlines and Lufthansa in 2018. The result shows that to achieve the optimal overall efficiency of airlines in 2018, the reduction requirements for passenger subsystem are minimal. The result is not in line with other years because of the relatively turbulent economic situation. Combined with the actual operating conditions of Hainan Airlines in 2018, the slacks of inputs and outputs are 7.5173E − 15 (OC), 5.71769E − 15 (OR), and 4.6121E − 15 (GHG). Among them, the adjustment ratios of operation cost and operating revenue are more prominent so that the passenger transportation system can emit few greenhouse gasses when pursuing optimal overall efficiency. So there exists the extreme distribution value of 0.1000.

The ideal value and actual value

Due to the lack of some data, we compare the optimal ratio of operating costs with the actual ratio of Hainan Airlines during 2014–2019, as shown in Table 10.

Table 10 Comparison between ideal value and actual value of Hainan Airlines’ operation cost
Full size table

We can find that despite the slight increase, the proportion of operating costs allocated to the freight subsystem has indeed increased in recent years, from 2.76% in 2014 to 3.71% in 2019. But the actual distribution values are much different from the ideal ones. In essential operation, the passenger transport system investment is higher than 95%, while the freight transport system only accounts for a little. The optimal allocation ratio is around 50%, and the passenger transportation system accounts for a little bit higher. The results show that the specific direction of improvement is to increase the operation cost of the freight subsystem and play the critical role of cargo subsystems in daily operations. The same efficiency analysis is proper for other airlines.

The efficiency comparison between European airlines and Asian airlines

Due to the feature of the samples, 18 airlines are mainly located in Europe and Asia, and the specific distribution is shown in Table 11. Calculate and analyze the average annual efficiency of each continent in Table 12. Figure 2 shows that the yearly efficiencies of Asian airlines are higher than those in Europe. The overall average efficiency score in Asia is 0.9863, and that in Europe is 0.9820 from 2014 to 2019, and the efficiency difference is not apparent. Asia’s economic and transportation competitiveness has improved in recent years. IATA states Asia is one of the world’s central air travel regions. In 2016, 35% of global travelers chose to fly with airlines in the Asia–Pacific region, and the aviation market share in Asia is also increasing yearly. We can also find that compared with European airlines, the efficiency of Asian airlines is higher in the whole parallel system and each subsystem.

Table 11 Geographical distribution of 18 airlines
Full size table
Table 12 The average annual efficiency of each continent
Full size table
Fig. 2
figure 2

The average annual efficiency of each continent

Full size image

In addition, we know that the overall efficiency in Table 4 and the efficiency of the passenger and freight subsystem are relatively low compared with efficiencies after the optimal allocation. This shows that airlines are focusing on the development of transportation but not on solving the consequent air pollution problems. Therefore, all airlines should consider adopting emission reduction measures, strengthening pollution prevention, and saving energy. Finally, there is a big difference in efficiency between passenger and freight subsystems, and airlines should coordinate and balance the development.

Through calculation, we get the optimal allocation proportion of shared input and output indicators. We draw some interesting conclusions after discussing operating costs, income, and carbon dioxide allocation values. In daily operations, airlines should first increase the cost investment of the freight subsystems. The operating cost of airlines is mainly composed of aviation fuel and operating costs, which account for even more than 50%. Aviation fuel is also the leading cause of carbon dioxide production. Achieving the goal of “carbon neutrality” is the consensus of international airlines, which requires them to use clean energy, update the green fleet, and reduce operating costs and carbon dioxide emissions. The business model realizes the increase or decrease of operating income, and the relaxation value of each input and output index provides a specific solution.

The sensitivity analysis

We performed a sensitivity analysis to test the empirical results’ accuracy. Then, taking 2019 as an example, the initial weights of passenger transport and freight transport [1/2,1/2] were changed to [3/4,1/4] and [1/4,3/4], respectively, and the efficiency scores and optimal allocation ratios of the PRAM model were calculated again, as shown in Tables 13, 14, and 15.

Table 13 The efficiency scores and optimal allocation ratios with the weight [1/2,1/2]
Full size table
Table 14 The efficiency scores and optimal allocation ratios with the weight [3/4,1/4]
Full size table
Table 15 The efficiency scores and optimal allocation ratios with the weight [1/4,3/4]
Full size table

The above three tables list the efficiency values and the optimal allocation ratio under three different ratios. Comparing the efficiency values of 18 airlines, we can find that the rankings of efficiencies remain the same, except for British Airlines and Cathay Pacific Airlines in Table 15. The results indicate that the weights of passenger and freight subsystems do not affect airlines’ efficiency values, and the PRAM model results are robust. In 2019, due to trade tensions between China and the USA, air cargo demand remained sluggish throughout the year, resulting in a disconnect between supply and demand. But in the second half of 2019, the traditional peak season improved Cathay Pacific Airlines’ cargo performance, with new consumer goods and specialist air cargo volumes increasing, while British Airways did not. This also explains the rise of Cathay Pacific’s efficiency ranking after the increase in the proportion of its cargo subsystem.

Conclusion

In this paper, we evaluate the efficiency of the passenger and freight subsystems. Based on the empirical research, the proposed model can provide a ranking that genuinely reflects the environmental efficiency of 18 airlines. The implications of this paper are drawn following.

  1. (1)

    From a macro perspective, an airline’s overall environmental efficiency level is determined by its subsystems. The empirical results show that the different proportional allocation of shared resources will change the efficiency of the two subsystems. Therefore, our study provides directions for future resource allocation and improvement measures. Over the past several years, the development level of the freight system has been relatively low. However, it can be seen from the empirical results that too much investment in the passenger transport subsystem will slow down the overall efficiency improvement. On the other hand, increasing inputs in the freight subsystem will improve the overall efficiency and bring more significant benefits to investors. Therefore, airline executives should keep each subsystem in line. The direction of improvement is this paper’s distribution ratio of operation cost, operating revenue, and carbon dioxide emissions. Different airlines have operating conditions, including geographical location, environmental resources, economic level, etc. Therefore, each company must use these characteristics to take specific measures.

  2. (2)

    Theoretically, we innovatively proposed a PRAM model based on shared inputs, shared desirable outputs, and shared undesirable outputs. The model can compute the system efficiency, the subsystem efficiency, and the optimal allocation ratios of shared resources. We apply the proposed model to assess the performance of 18 global airlines from 2014 to 2019. And the purpose of efficiency measurement is to find weak areas so that appropriate actions can be implemented to achieve optimum performance. Moreover, ASK and RPK is the specialized input and output in the passenger-transportation subsystem. In the freight-transportation subsystem, ATK is the input to obtain the RTK. Through decomposition, decision-makers can better distinguish between these two subsystems’ weaknesses to be more effectively committed to improving the overall efficiency. The results also provide improvement directions for non-benchmark airlines.

From the results of the empirical study, we can conclude some exciting findings from the results. First, All Nippon Airways, Emirates, Lufthansa, and Spring Airlines have the highest overall efficiency among these 18 airlines, which is closely related to the excellent performance in both passenger and freight transportation subsystems. Therefore, it can be regarded as a benchmark company. Second, the shared inputs and outputs can significantly improve overall efficiency. In contrast, the optimal distribution ratio is shown in Table 9. Third, by comparison, the passenger transportation system is more important. However, we can see that airlines with higher cargo system efficiency have higher overall efficiency in Table 5. Only by eagerly developing the freight transportation networks, updating the fleet size, and so on can the efficiency of the freight system improve. Fourth, overall, the efficiencies of the 18 airlines are not very high in Table 4, and actual operating conditions need to be improved. Finally, the efficiency scores of Asian airlines are higher than airlines in Europe. Still, the gap between the two is not very big, indicating that the Asian aviation market has great potential in the future.

We propose the following transformational business models. First, change the business model. In this paper, the research on the input and output indicators provides a new idea for the management of airlines. By finding the weak links in the process of improving the efficiency of airlines, they can make up for their deficiencies and improve their competitiveness. Second, focus on freight systems. This paper proves the importance of the cargo subsystem. As COVID-19 continues to ferment, the demand for new cargo airports and passenger-cargo planes continues to increase, and investors are increasingly confident in the cargo market. International airlines should seize the opportunity to enhance cargo capacity, improve the service chain, and improve the level of specialization in cargo. Third, focus on the aviation market in the Asia–Pacific region. The rapid rise of the Asia–Pacific region proves its vast development potential. In the next 20 years, the passenger traffic in the Asia–Pacific region will maintain an average annual growth rate of 5.6%. Governments worldwide are making continuous efforts to support the sustainable development of the air transport industry. For example, China has invested heavily in green aviation initiatives, and Singapore has established a cross-industry international aviation advisory group. Therefore, international airlines must deepen their efforts in Asia–Pacific and expand their territories.

Meanwhile, this paper also has some limitations. First, subjective factors have a noticeable influence on the proposed model. Also, the parameters in the model are influenced by external factors such as economic level, consumer confidence, market structure, and so on. The second limitation occurs in the weights of the two subsystems. We default that the two subsystems are equally important. This is not the case for some airlines. Finally, the evident limitation is the number of sample airlines. Considering the data on freight systems is challenging to obtain, we select 18 airlines and ignore their types—LCC (low-cost carrier) or FSC (full-service carrier), which may influence empirical results.

Correspondingly, we propose the directions for future research. One suggestion for improvement is to have an overall view, including the external factors. Another advice is to analyze the weights of the two subsystems, which can help us conclude whether the consequences influence airlines’ efficiency. The third topic is considering the difference between low-cost and full-service carriers. Furthermore, we can apply other modified models to airlines, such as the RAM model with managerial disposability, dynamic RAM, and the epsilon-based measure (EBM) model. By adding time dimensions, airlines’ efficiency can be more accurately evaluated. In addition, our model does not consider the intermediate outputs, which is also a point for improvement.