Abstract
By introducing doors on refrigerated display cabinets, the energy demand is substantially decreased. However, there exist significant discrepancies in temperature readings between visually identical refrigerated display cabinets equipped with doors. This study explores the cause and consequences of these differences. The exploratory methodology used within the study has used CFD simulations combined with laboratory experiments to conclude that there exists a thermal gradient in the area of the return air temperature sensor causing these discrepancies to occur. Thus, the temperature sensors position within the thermal gradient affects the perceived temperature of the control system and thereby the refrigeration strategy adopted by it. To follow up on the consequences of this observed issue, two field studies were performed to investigate the effects and occurrence of temperature sensors within the thermal gradient. Through this, it was concluded that by moving the return air sensors away from the thermal gradient, the refrigerated display cabinets were performing more uniformly as well as with a reduced heat extraction demand. Additionally, from the field study investigating the occurrence, it was found that 80.5% of the 221 reviewed refrigerated display cabinets had sensors placed in a zone where a thermal gradient exists.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
On the national level of Sweden, the UK and Germany, 3% of the national electricity is used by supermarkets (Arias 2005; Tassou et al. 2010; Månsson 2019) where off about 50% origins from the refrigeration system (Little 1996; Tahir and Bansal 2005; Statens Energimyndighet 1990, 2010). Thus supermarket refrigeration represents approximately 1.5% of the nation’s electrical energy demand, making it a very interesting sector to approach for energy efficiency measures on a national level.
Studies have shown energy savings ranging between 50 and 82% when implementing doors on refrigerated display cabinets (RDCs) (Schmidt et al. 2017; Faramarzi et al. 2002). Hence, with the observed trend of open RDCs being replaced with doored RDCs, it would be likely that the energy demand for refrigeration in supermarkets would be on a decline.
However, from a comparison of two subsequent studies by the Swedish Energy Department made in 1990 and 2009, increased energy demand for refrigeration was observed (Statens Energimyndighet 1990; 2010). This indicates a significant increase in the share of refrigerated goods as the efficiency of the refrigerated display cabinets has drastically increased during the same time period.
With a current global trend forecasting a continued increase of refrigerated goods (Goodburn 2014; PreparedFood 2018; Research 2015), it is increasingly important to ensure that the RDCs are operated at an optimal level. Both with regards to energy efficiency and to ensure adequate temperature levels with regards to food preservation and safety.
In a study performed during 2014 on open RDCs, it was found that about 50% of the investigated RDCs were violating the temperature regulations (Lundén et al. 2014). Any violations of the temperature regulations do jeopardise food safety and could result in significant economic losses as a consequence of the damaged food. Wasted food is in addition to a great economic loss, also known to be a substantial global environmental problem (SAVE FOOD 2018).
By investing in modern RDCs equipped with doors, the supermarkets can in addition to the energy savings also reduce the risk of temperature violations dramatically. In Faramarzi et al. (2002), Evans et al. (2007, 2014), Fricke and Becker (2010), and Atilio de Frias et al. (2015), it is concluded that doored RDCs do provide a more even temperature distribution both spatial and temporal and thereby an increased food safety (Atilio de Frias et al. 2015; Laguerre et al. 2011).
Along with implementing high-performing hardware such as doored RDCs, the accuracy of the temperature control system regulating the heat extrac tion rate (\(\dot {Q}_{HE}\)) becomes increasingly important. This is because the overall heat transfer coefficient UEnv and infiltration flow rate \(\dot {m}_{Inf}\) of the RDC as described in Eq. 1 decrease in magnitude; therefore, the heat extraction rate must be more delicately controlled to avoid temperature fluctuation.
The control system of RDCs most commonly estimate the internal air temperature (TRDC,Est) as shown in Eq. 2, i.e. by the weighted average between return (RA) and discharge air (DA) temperature, where the weights for doored RDCs is most commonly given as w1 = w2 = 1.
To keep TRDC,Est at the targeted setpoint temperature TRDC,Set, the control system adapts the heat extraction rate to achieve an adequate heat balance. Consequently, TDA is adjusted so that TRDC,Est is kept within its limits, meaning that if TRA is perceived higher, TDA is decreased proportionally. It is important to notice that the estimated value of TRDC,Est is not necessarily equal to the actual temperature of the RDC, TRDC,Act, but only an approximation based on TRA and TDA. Thus, when the difference between the approximation and actual value is too large, this becomes an issue as the RDC then will perform inadequately based on false assumptions of internal temperature.
This article presents novel findings on how the spatial position of the return air temperature sensor causes such mismatch between estimated and actual temperature of the RDC. The study has been performed in an exploratory way where the issue was found based on a hypothesis, then further investigated, confirmed and later amended. As a consequence of the exploratory research methodology, this article will be presented in chronological order.
Indications of inadequate temperature readings
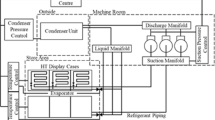
A data set with hourly average temperatures (TRA and TDA) for medium temperature RDCs in an operational supermarket outside of Hamburg in Germany was reviewed in 2016. The 12 RDC modules assemble three inline connected cabinets with a total of 61 doors. In Table 1, a summary of the RDCs content, connections, number of doors and their individual temperature setpoints are listed. RDC1 − 4 were located along the wall after passing the produce area by the entrance of the supermarket. RDC5 − 7 were positioned further into the store along the same wall but separated from RDC1 − 4 by and emergency exit. Both of these lines were facing shelves with dry goods, separated from the RDCs by a wide aisle. RDC8 − 12 followed the wall perpendicular to the line of RDC1 − 4 and RDC5 − 7, and faced the short side of the shelves with dry goods. At the site visit, neither of the RDC lines was found to be exposed to any external heat sources which could have significantly affected their thermal performance. Thus, there were no RDCs with an incorporated condensing unit, heated cabinets or air supply units in proximity of either of the lines.
The collected temperature data set was originally generated from the local monitoring system of the store with the purpose to benchmark the RDCs energy performance. Although, in this process, the authors found an unexpected pattern in temperature readings, indicating that the temperature control system was operating inadequately.
To get an indication of the energy performance of the RDCs, the sensible heat extraction rate was investigated and estimated by the the relation:
During opening hours, the operational patterns differed between the RDCs as a consequence of variations in customer interactions. Consequently, the temperatures (TRA and TDA) and, therefore, the heat extraction rate varied similarly. In contrary to weekdays, from Saturdays at 22:00 until Mondays at 7:00 the store was closed with no maintenance work or re-stocking of products. Hence, the ambient conditions were constant, the interactions were nil, and, therefore, the performance was expected to be almost identical for RDCs with similar configurations (Fig. 1).
In Fig. 2, the average return air and discharge air temperature for four Sundays (10, 17, 24, 31/1—2016) is presented. As can be seen, the variations among the RDCs are significant, even for RDCs connected in the same line. For example, RDC2 had a 0.64 ∘C higher difference between TRA and TDA than RDC3, even though they were directly connected (See Fig. 1). This difference corresponds to a 32% higher sensible heat extraction rate in RDC2, which is dubious for two connected RDCs of the same brand and design, exposed to the same ambient condition and at times of no interaction. There were, however, some minor differences between RDC2 and RDC3. The right side of RDC2 was openly connected to RDC1 whereas there was an intermediate division wall between RDC3 and the neighbouring meat RDC, RDC4. From the pictures shown in Fig. 1 it can be seen that the products are not identical, but the occupied volume is similar.
Mean TDA and TRA for the 12 RDCs in the supermarket during four Sundays (10, 17, 24, 31/1—2016). Significant differences between RDCs can be noticed. Special notice for RDC1,2,3 which are internally connected and would thereby be expected to show readings of same magnitude. Note: The temperature of RDC4 is set to 2 ∘C as it mainly contains meat products
The temperature readings presented in Fig. 3 show that RDC2 was operating with a lower TDA and yet reporting a higher TRA than RDC3. During Friday and Saturday, this anomaly could be addressed to the differences in customer interactions with these RDCs. However, the same trend continued during Sunday, even though the supermarket was closed. In theory, identical RDCs exposed to the same ambient conditions should maintain equal TRA and TDA. The small differences in the RDCs’ setup are rather unlikely to cause the 32% increase in heat extraction. Therefore, it was concluded that the anomaly might be a result of inadequately measured temperatures as explained in the next section.
Hypothesis
From a site visit to the supermarket, it could be confirmed that the RDCs mentioned in Section 1 were visually identical, i.e. no visible external differences such as damaged doors and uneven gaps between doors. Additionally, as mentioned above, no external factors that could have affected the thermal performance of the RDCs such as heated cabinets, ovens and air intakes were identified in the close proximity of the RDCs. However, it was noticed that the placement of the RA temperature sensors varied among the RDCs. Some had sensors placed closer to the front and others further back towards the evaporator. Also, a variation in heights above the cabinet floor was noticed. (Data on location of sensor placement will be presented in Section 1.)
A hypothesis was formed around that the return air temperature sensor was located in the area where a thermal gradient exists. Consequently, the temperature readings depended largely on the position of the sensor. The hypothesis states that a heated air layer is formed along the interior side of the glass doors of the RDC. This heated air layer then follows the path of the airflow through the return air grille, creating a thermal gradient in the area of the RA temperature sensor as visualised in Fig. 4. As a result, a RA temperature sensor that is placed at a low height above the RDC floor would falsely indicate higher temperatures due to the warmer air layer.
The discharge air passing the glass door is heated by heat gains through the door. The thermal gradient created thereby continues along the entire path of the discharge airflow, through the return air grille towards the front of the heat exchanger further back. This results in a warmer air layer close to the floor of the RDC in the area of the RA temperature sensor
From other studies based on CFD modelling on open RDCs it is shown that a heterogeneous temperature field is occurring in and around the return air grille area. A substantial literature review presenting the methods and references for the mentioned work can be found in Smale et al. (2006). In analogy with Axell (2002), Lindberg et al. (2008), Foster et al. (2005), and Hadawey et al. (2012), which all present studies on air curtains in open RDCs, it can be seen that a heated air layer is formed following the streamlines of the airflow towards the evaporator in the rear part of the air return. Such a temperature gradient along the bottom of the return air duct is visible in the results of CFD simulations on doored RDCs too, as presented in D’Agaro et al. (2006) and Orlandi et al. (2013). However, this phenomenon was not the primary focus of the referenced articles and thus neither discussed nor explored.
Evaluation of hypothesis by CFD and experiment
The hypothesis on the existence of a thermal gradient in the proximity of the RA temperature sensor was investigated further by means of numerical simulations and laboratory experiments. As for the former, two CFD models representing the geometries of a Carrier Monaxis 63 C3.DL RDC and KMW VSST were developed, as shown in Fig. 5. These two models were chosen solely for their similarities with the RDCs investigated in the field study and presented in Section 1, without any intention of comparing their performances. The laboratory experiments were performed for the purpose of validating the CFD simulations.
The created CFD models are based on the non-isothermal turbulent flow (K − 𝜖) module in COMSOL 5.2 (AB 2013), which is used to model temperatures and energy transports in fluid flows. The module solves the Navier-Stokes equations for incompressible flow coupled with an energy balance, which considers heat fluxes by convection, conduction and radiation. The CFD models were not intended to depict the RDCs with high accuracy, but rather to investigate if the above stated hypothesis was feasible. Thus, both CFD models were reduced to two-dimensional (2D) spatial domains and run in steady-state mode to limit the computational time. Furthermore, the CFD validation was limited to the area of interest, i.e. in close proximity to the air return grille area. Three-dimensional effects coming from, e.g., lights and gaps between the doors were neglected. The mentioned neglected parameters would have affected the temperature field to be more heterogeneous if taken into consideration. Therefore, the numerical models and the results of simulations are considered as conservative.
Governing equations
The equations solved by the turbulent non-isothermal fluid flow module are the Reynolds-averaged Navier-Stokes (RANS) equations for the conservation of momentum and the continuity equation for conservation of mass, as shown in Eqs. 4–6. As mentioned above, the air inside the RDC is considered incompressible to decrease computational time.
The turbulence is modelled using the standard two-equation k − 𝜖 model with realisability constraints and the flow in the near-wall region is modelled using wall functions. The standard closure coefficients: Cμ = 0.09, C𝜖1 = 1.44, C𝜖2 = 1.92, σk = 1.0 and σ𝜖 = 1.3, are used.
By evaluation of the Richardson number, as described in Eq. 7, values << 0.1 were obtained for the air return, meaning that the influence of natural convection could be neglected. This is valid by assuming the velocity in the return air duct (URA) to be > 0.4ms− 1, the cold reference temperature (TRef,Cold) to be equal to the air discharge temperature of 5 ∘C, and the warm reference temperature (TRef,Hot) to be 7 ∘C.
The transport of turbulent kinematic energy, k, and turbulent dissipation, 𝜖, is modelled as shown in Eqs. 8 and 9.
While the turbulent viscosity reads
Boundary conditions
The inlet boundary conditions for the air discharge in the top and perforated back panel in the rear (see Fig. 5) are described in Eq. 11 with a reference velocity in the opposite direction of the normal to the boundary. The inlet turbulent kinetic energy and dissipation rate are calculated as shown in Eqs. 12 and 13, where the length scale and turbulent intensity were estimated as in Eqs. 14 and 15, in accordance with the recommendation in (AB 2013).
The air discharge inlet velocity is defined by multiplying the highest velocity with a ramp function, f(s), to account for variations over the inlet, as shown in Eq. 16
where f is defined, as shown in Eq. 17, on the normalised boundary coordinate system s along the inlet boundary.
The perforated back panel is modelled as an open inlet, i.e. the influence on turbulence by the grille is not considered. To justify this approach, a separate study was conducted where velocity profiles after a fully open inlet and a perforated panel with 27 scattered inlets were compared. As it can be seen in Fig. 6, the velocity magnitude over the full height of the cavity are rather close. Hence, as the distance affected by the boundary conditions is limited to the rear area of the cavity between the shelves, and the area of interest within this study is located significantly further downstream, we have chosen to simplify to maintain a balance of necessary accuracy and computational effort. Thus, the airflow along the inside of the glass door is not affected by the simplification. This simplification can be further justified as the quote between turbulent kinematic energy and dissipation at the inlet as well as in the middle of the shelf indicated that the turbulent disturbances from the inlet would only affect the air contained in-between the shelves. Specifically, k/𝜖 ≈ 7 (s) and the velocity was approximately 0.02–0.03 m s− 1, i.e. the affected length after the inlet is only approximately 0.15 m. Hence, the inlet boundary conditions does not affect the area of interest around the return air grille further downstream.
The inlet velocity at the rear grille, URear, is defined as a fixed ratio of the discharge air velocity UDA,0, as shown in Eq. 18. The used factor was derived from an empirical study in the laboratory where the volumetric flow ratio between the air discharge and rear grille was measured and found to be approximately 11:6.
The inlet temperature for both the air discharge grille and the rear grille is set to 5 ∘C in the model, in conformity with the measured hourly averages presented in Fig. 3.
The outlet representing the heat exchanger front downstream of the return air grille is modelled with a relative pressure set to 0 Pa and with no viscous stresses to suppress back-flow.
As the model is stationary, the density and heat capacity of materials can be neglected. Therefore, thermal contact between solids and the air can be modelled as Neuman boundary conditions as shown in Eq. 19. The door facing the ambient is assigned a heat transfer coefficient h = 2.67 (W/m2 K), representing the thermal conductance of the door including the outside convective surface resistance (8 W/m2K).
For effects of radiation inside the RDC, the presented model is using a simplified approach. Along the floor of the RDC, a boundary condition which assumes radiation towards an infinite fictitious surface with a temperature equivalent to the inlet temperature is applied, i.e. the view factor is assumed to be 1 and the effects of the radiation on the floor can be expressed as shown in Eq. 20.
This assumption gives a good indication of how the radiation affects the warmer areas such as the area around the return air temperature sensor.
For the RDC, an emissivity of 𝜖 = 0.9 was assumed, representing the emissivity of commonly used paints for coating metal sheets.
Boundary conditions and model details used in the validation experiments are listed in Tables 2 and 3.
Validation
The validation experiment was performed with the Carrier Monaxis 63 C3.DL RDC connected to a Silensys SIL4524Z R404A remote compressor. The RDC was filled with 120 canisters containing 5 litres of water each to resemble a thermal mass of products. In total, 624 kg was added. The canisters were placed in the left and right section of the RDC, leaving the section used of the validation measurements behind the two middle doors of the RDC empty, i.e. undisturbed flow along the shelves . The ambient room temperature was elevated and kept at 27–28 ∘C during the experiment to cause an increased thermal load and, therefore, a more profound thermal gradient in the area of the air return.
The vertical temperature profile of the return air duct was measured with 5-s intervals by a datalogger (HIOKI LR8431-20) connected to 7 K-type thermocouples mounted on a bracket at a height of 2, 5, 10, 15, 20, 30 and 40 mm, as shown in Fig. 8. The bracket was installed so that the thermocouples measured the temperature profile 100 mm from the front of the RDC, at a position indicated by line C1 in Fig. 9. Prior to the experiment, the thermocouples were calibrated using a 4-wire platinum probe (FisherbrandTM Traceable Platinum Ultra-Accurate Digital Thermometer) with a specified accuracy of ± 0.05 ∘C as reference. The calibration was conducted in a thermally controlled bath, comprising a dry-block cylindrical calibrator of aluminium. The resulting accuracy ± 0.1 ∘C of the thermocouples refers to the calibration temperatures at 0, 2, 5, 7, 10, 15 and 20 ∘C, applying thus to the entire temperature range in the conducted experiments.
Before the experiment was performed, the RDC was running for over 200 h to ensure that a quasi steady-state was reached. In Fig. 7 the transient temperature profile of the inlet air during the experiment is shown. During the intervals of 455 s between the compressor cycles, the inlet temperature varied between 2.2 and 7.10 ∘C. This periodic behaviour affected the development of the heated air layer in the air return, causing its magnitude to vary in time, which consequently caused an offset between the simulated steady-state results and the measured temperatures.
Therefore, to validate the steady-state simulation with the transient experiment, the relative temperature differences are compared rather than absolute values. A temperature (measured or simulated) at 2 mm distance from the floor is used as reference, while the results are presented as offsets to the reference value. For the measured temperatures, the offset temperatures vary a lot over time due to the variation in discharge air temperature. To visualise the measured temperature profile, the corresponding offsets are presented as box-plots at each respective height as shown in Fig. 8.
Left: Photo of thermocouples fixed at 2, 5, 10, 15, 20, 30 and 40 mm on a steel bracket. Right: The box-plot shows the measured temperature offset for the validation experiment. The black lines show the calculated temperature offset with varying inlet velocity and emissivity. The shown data represents the temperatures along the line C1 from Fig. 9
In the same figure, the black lines show the offset results from the CFD model where the inlet velocity was varied by ± 50% and emissivity between 𝜖 = 0 − 1. The variation in velocity was made to investigate the impact of of RDC loading of food, i.e. packaging blocking the flow in certain areas which consequently would increase velocity in other areas. As can be seen in Fig. 8, the velocity has a negligible effect in relation to the spatial variations of the air temperature in the considered area. As the actual emissivity of the floor surface was unknown, this parameter was varied between the extremes, 0–1, to evaluate the impact range. Also here, the effects were of negligible magnitude compared to the spatial variations in temperature.
The validation experiment confirms that the CFD model is sufficiently accurate for approximating the spatial distribution of the thermal gradient in the area of the return air grille. The simulated band of results differs by up to 0.2 ∘C from the measured values, and falls within the 25–75th percentiles.
Results from CFD assessment
A larger temperature overview of the middle sections of the full RDCs was generated from the CFD models, as shown in Fig. 9. In this overview, the formation of the heated air layer along the interior side of the glass door can be seen. It develops from the air discharge in the top along the glass door towards the return air grille, and later all the way to the front of the heat exchanger in the rear bottom of the RDC.
This larger temperature overview additionally supports the hypothesis on the formation of the heated air layer along the glass door. Thus, the collected data from the validation experiment further confirmed the hypothesis of a thermal gradient to exist in the area of the RA temperature sensor (see Fig. 8).
The actual height and temperature profile of the heated air layer varies quite significantly in time due to the cyclic operation of the refrigeration system. The temperature inside the RDC varies between 4 and 8 ∘C during the on and off cycles. As the CFD model is a steady-state model, these transient effects are not considered. However, the results clearly indicate the existence of a heated air layer and its magnitude.
For the scenario presented in the validation simulation, the average temperature calculated over the full height of the return air duct at the position C1 was found to be 5.36 ∘C whereas the temperature at the floor was 6.25 ∘C. The coldest position, measuring 5.19 ∘C was found at 35 mm above the floor. The temperature then gradually increased to 5.3 ∘C until a height of approximately 50 mm where it plateaued.
These values do, however, not take into consideration that the velocity profile of the air varied significantly over the height of the duct too, which affects the heat extraction demand of the RDC. The velocity at 15mm above the floor was found to be 2.92 ms− 1, then decreased rapidly and plateaued at 0.2–0.3 ms− 1 at a height of 55 mm. Over the height of the return air duct, the velocity weighted average temperature was found to be 5.45 ∘C.
In Fig. 10, a zoomed-in view of the area around the return air grille is shown for the two RDC geometries. In the flat-floored RDC (left) it can be observed that there is a larger area of stagnant air in the front than in the case with slanted floor (right). As can be seen (see bottom right corner), this stagnant air leads to the larger extent of the heated air layer in the front. Apart from that front area, there are no significant differences in the air mixing and extent of the heated air layer between the two studied RDC models. For both cases, a heated air layer with a thickness of approximately 50 mm follows the vertical front wall and then transitions into a 20-mm-thick layer following the horizontal floor. Consequently, placing sensors within proximity of this layer would result in inadequate temperature readings.
For RDCs in operating conditions in supermarkets, the path of the airflow may be altered due to products blocking its way. Products that have fallen on to the return air grille or that is stocked in a way that it blocks the airflow on the shelves are rather common and should be taken into consideration. Also the accumulation of dust and dirt on internal surfaces might influence the radiative heat exchange within the RDC. However, from CFD simulations where these effects were replicated by varying the inlet velocity ± 50% and emissivity of interior surfaces between 0 and 1, it was found to be of negligible magnitude as they only affect the heated air layer slightly, see the range of temperature profiles in Fig. 8. The operation of doors do impact the air flow and mixing significantly as large turbulent vortexes are created when the door is opened. However, the induced mixing and turbulence decrease the magnitude of the thermal gradient as it counteracts the separation causing the thermal gradient to occur. Thus, the investigated issue of a thermal gradient is less present at times of higher opening frequencies.
Field study 1—Effects on temperature measurements
To investigate the impact of how the heated air layer affect the RA temperature sensor readings, a field study was conducted in a supermarket in the greater Hamburg area in Germany. The study was conducted in two steps, first the position of the return air temperature sensors was measured and thereafter the RA temperature sensor was relocated to a position approximately 150 mm from the front and 65 mm above the RDC floor. Data from the supermarkets’ temperature monitoring system was collected continuously from 33 days before the re-positioning until 28 days after. In Fig. 11, a photo of the RA temperature sensors of RDC2 is shown before and after the re-positioning.
In total, 12 RA temperature sensors were re-positioned in this supermarket. In Fig. 15, the original position is marked with red in the graph and in Fig. 12 the effect on the measured temperature of the relocation can be seen. The presented graphs in Fig. 12 are showing the measured daily average temperature for the return and discharge air. Here the relocation of the return air temperature sensors occurred on the 33rd day. This is clearly visible as a step-change in both TRA and TDA. The increase of TDA is a consequence of the control system responding to the perceived decreased RA temperature, which is interpreted by the control system as decreased heat gains to the RDC. Hence a decreased temperature difference between TDA and TRA, which indicates a lowered heat extraction rate. However, it should be explicitly stated that the TRA prior to the re-positioning of the sensor does not represent the actual return air temperature but rather the temperature of the heated air layer.
Temperature data for one month before and after the relocation of the return air temperature sensor in a supermarket outside of Hamburg. The relocation occurred on day 33. The second graph on the top row (RDC2) shows temperature data for the sensor in Fig. 11. Notice: RDC4 is used for meat and therefore has a lower temperature
For comparison with Fig. 3, the hourly temperature readings for RDC2 and RDC3 after the sensor re-positioning are presented in Fig. 13. Here it can be seen that the discrepancies have reduced both within and outside of the supermarkets opening hours. Although different thermal performance of the RDCs or unsynchronised control and operation of the EEVs would hypothetically cause similar discrepancies in the temperatures as shown in Fig. 3, we feel confident that the spatial position of the temperature sensor is the only significant cause of the perceived error as these differences are no longer present after the re-positioning. Differences in thermal performance or differently operating EEVs would continue to affect the operation of the RDCs in the same manner, i.e. with the same effects on both DA and RA readings.
Showing the return and discharge air temperature of RDC2 and 3 after the re-positioning of the return air sensor. A significant decrease in discrepancies between the two RDCs compared to the data visualised in Fig. 3
Further, it can also be seen that the difference between TRA and TDA has decreased significantly, indicating decreased heat extraction. Thus, instead of keeping the products below the specified temperature levels, due to inadequate temperature readings, the control system can now balance the temperature at the desired levels.
Similar general trend of decreased differences is observed for all RDCs in the supermarket as can be seen in Fig. 14. Here, the average TDA and TRA for the four Sundays following the date of temperature sensor re-positioning is presented.
Additionally, the individual opening times of the valves supplying the RDCs with refrigerant was monitored as an indicative measurement of heat extraction demand. For the same period as presented in Fig. 12 the opening time was lowered from 37.48 to 35.38% after the re-positioning, i.e. a relative decrease in valve opening time by 5.6%. Worth mentioning is that the average indoor temperature for the period before the re-positioning was 19.65 ∘C and for the period after 19.63 ∘C, i.e. this should be of negligible influence.
Field study 2—Return air temperature sensor positions
As could be seen in Fig. 12 the re-positioning has a significant effect on the temperature readings. Therefore, to investigate if the occurrence of sensors in the heated air layer is a common phenomenon or if it was coincident that the majority of the sensors in the visited market were misplaced, the authors initiated a field study to measure the location of 221 return air temperature sensors in supermarkets around Hamburg, Germany. The generated data was then assembled to a scattered plot as shown in Fig. 15 to visualise the actual positions. Figure 15 should be interpreted as the distance from the front along the face of the floor and vertical as the distance perpendicular to the face of the floor, i.e. height above the floor. Here it can be seen that a majority (80.5%) of the return air temperature sensors are located in a zone where a thermal gradient exists. There are 42 RA sensors located in the front area marked with red and additional 136 sensors in the yellow area, which both represents areas of thermal gradients.
Scattered plot showing the position of return air temperature sensors in 221 refrigerated display cabinets in supermarkets around Hamburg. The light red area indicates the warmest zone of the heated air layer and the yellow indicates the outline. The red asterisk indicates the position of the RA temperature sensors from field study 1 (4 sensors are not represented in the figure as they were placed at heights between 100 and 120 mm)
Discussion
The presented study is limited to 221 RDCs from two different brands and located in the greater Hamburg area in Germany. As the vast majority (80.5%) of the investigated return air temperature sensors were located within the thermal gradient, one may extrapolate the results and assume that this misplacement is a common phenomenon within modern doored RDCs. Consequently, with the current strive for increasingly energy efficient RDCs it is advisable for supermarkets to inspect the return air temperature sensor position in conjunction with periodic cleaning or maintenance work, allowing them to adjust the position if found inadequate.
In the scenario of a RA temperature sensor being located in the warmer air layer, it will consequently indicate a higher temperature than the true average RA temperature. Thus, the control system will lower the temperature of the RDC accordingly until the set point temperature is perceived to have been reached. However, as the control system is fed with “false” readings, the actual temperature will be below the setpoint temperature once the cooling cycle is finished.
This sub-cooling implies a multifaceted problem for the supermarket. At first, the heat gains to the RDC increases with the increased temperature difference between interior and ambient temperatures, i.e. the refrigeration system must extract larger quantities of energy. This causes an increased electrical energy demand by the compressors for in the refrigeration system. Following the increased heat extraction that is needed by the RDC, the supermarket HVAC system must compensate for this heat sink by supplying additional heat to the indoors. Creating a secondary effect that increases the supermarkets’ energy demand for heating and thereby its energy bills are increased. These effects are however complicated to measure as the energy demand is also dependent on weather, maintenance levels, the number of customers and their behaviour etc.
Within the presented study, the authors choose to focus solely on investigating the thermal effect and limit the study to temperature readings. Data on refrigerant supply valve opening times was presented to indicate the magnitude of heat extraction reduction. However, to evaluate the actual energy savings the study must be expanded to include parameters for the ambient conditions, customer interactions etc.
Additionally, this study has only evaluated the thermal gradient in doored RDCs. However, from previous CFD studies made on open RDCs it can be seen that there is a formation of a similar thermal gradient along the streamlines of the air curtain. Hence, the issue of inadequate temperature readings by the return air sensors is likely to occur in these types of RDCs too.
Conclusion
This study concludes through CFD calculations, laboratory experiments and field studies that there exists a thermal gradient in the proximity of the air return grille of doored refrigerated display cabinets. Consequently, the position of the return air temperature sensor significantly affects its measured temperature and thereby the response of the control system. For return air temperature sensors located within this gradient there is a risk of inefficient temperature control of the RDC as a consequence of inadequate temperature readings. Extrapolated from the investigated supermarkets within this study it is likely that the unfavourably located return air temperature sensors are commonly existing in modern supermarkets.
Abbreviations
- β :
-
-Volumetric thermal expansion coefficient (-)
- C p :
-
-Specific thermal capacity (J/kg K)
- CFD :
-
-Computational fluid dynamics
- 𝜖 :
-
-Emissivity (-)
- 𝜖 :
-
-Turbulence dissipation rate (m2/s3)
- h :
-
-Heat transfer coefficient (W/m2 K)
- \(\bar {I}\) :
-
-The unit matrix (-)
- γ :
-
-Heat capacity ratio (-)
- I :
-
-Intensity (-)
- k :
-
- Turbulent kinematic energy (m2/s2)
- L :
-
-Length (m)
- λ :
-
-Thermal conductivity (W/m K)
- \(\dot {m}\) :
-
-Mass flow rate (kg s− 1)
- μ :
-
-Dynamic viscosity (Pa S)
- \(\hat {n}\) :
-
-Normal vector (-)
- p :
-
-Pressure (Pa)
- \(\dot {Q}\) :
-
-Power (W)
- \(\bar {q}\) :
-
-Heat flux vector (W/m)
- ρ :
-
-Density (kg/m3)
- RDC :
-
-Refrigerated display cabinet
- R e :
-
-Reynolds number (-)
- R i :
-
-Richardson number (-)
- σ :
-
-Stefan-Boltzmann constant (W/m2 K4)
- T :
-
-Temperature (∘C)
- \(\bar {u}\) :
-
-Velocity vector (m s− 1)
- w :
-
-Constant (-)
- U :
-
-Speed (ms− 1)
- A c t :
-
-Actual
- A m b :
-
-Ambient
- C o n v :
-
-Convection
- D A :
-
-Discharge air
- E n v :
-
-Envelope
- E s t :
-
-Estimated
- E v a p :
-
-Evaporator
- H E :
-
-Heat exchanger
- I n f :
-
-Infiltration
- I n t :
-
-Internal
- R A :
-
-Return air
- R a d :
-
-Radiation
- T :
-
-Turbulent
- R e f :
-
-Reference
References
AB, C. (2013). The Heat Transfer Module User’s Guide, 2nd edn. Stockholm: COMSOL AB.
Arias, J. (2005). Energy Usage in Supermarkets - Modelling and Field Measurements. Ph.D. Thesis, Royal Institute of Technology.
Atilio de Frias, J., Luo, Y., Kou, L., Zhou, B., & Wang, Q. (2015). Improving spinach quality and reducing energy costs by retrofitting retail open refrigerated cases with doors. Postharvest Biology and Technology, 110, 114–120. https://doi.org/10.1016/j.postharvbio.2015.06.016.
Axell, M. (2002). Vertical display cabinets in supermarkets - Energy efficiency and the influence of air flows. Doctoral Thesis, Chalmers University of Technology.
D’Agaro, P., Croce, G., & Cortella, G. (2006). Numerical simulation of glass doors fogging and defogging in refrigerated display cabinets. Applied Thermal Engineering, 26, 1927–1934. https://doi.org/10.1016/j.applthermaleng.2006.01.014.
Evans, J.A., Scarcelli, S., & Swain, M.V.L. (2007). Temperature and energy performance of refrigerated retail display and commercial catering cabinets under test conditions. International Journal of Refrigeration, 30(3), 398–408. https://doi.org/10.1016/j.ijrefrig.2006.10.006.
Evans, J. (2014). Are doors on fridges the best environmental solution for the retail sector ? Technical report 2009, Faculty of Engineering, Science and the Built Environment: Bristol.
Faramarzi, R.T., Coburn, B.A., & Sarhadian, R. (2002). Performance and energy impact of installing glass doors on an open vertical deli/dairy display case. ASHRAE Transactions, 108 PART 1, 673–679.
Foster, A.M.M., Madge, M., & Evans, J.A.A. (2005). The use of CFD to improve the performance of a chilled multi-deck retail display cabinet. International Journal of Refrigeration, 28(5), 698–705. https://doi.org/10.1016/j.ijrefrig.2004.12.009.
Fricke, B., & Becker, B. (2010). In Refrigeration And Air Conditioning (pp. 1–8). West Lafayette: Purdue e-Pubs. http://docs.lib.purdue.edu/cgi/viewcontent.cgi?article=2153{%&}context=%iracc.
Goodburn, K. (2014). Chilled Food Association - Market Data. http://www.chilledfood.org/Resources/ChilledFoodAssociation/kantar-market-data-2006-2014-jan-2012-onwards-revised-basis-uploaded-10-3-14.pdf.
Hadawey, A.F., Jaber, T.J., Ghaffar, W.A., & Dhabi, A. (2012). Air Curtain Design Optimization of Refrigerated Vertical Display Cabinet using CFD. International Journal of Scientific Engineering and Technology, 1 (4), 76– 88.
Laguerre, O., Hoang, M., Alvarez, G., & Flick, D. (2011). Influence of room temperature on food safety in refrigerated display cabinet. In 11th International Congress on Engineering and Food (pp. 3).
Lindberg, U., Axell, M., Fahlén, P, & Fransson, N. (2008). Supermarket, indoor climate and energy efficiency field measurements before and after installation of doors on refrigerated cases. In Refrigeration And Air Conditioning (pp. 2–7).
Little, A.D. (1996). Energy Savings Potential for Commercial Refrigeration Equipment. Cambridge: U.S. Department of Energy.
Lundén, J., Vanhanen, V., Myllymäki, T., Laamanen, E., Kotilainen, K., & Hemminki, K. (2014). Temperature control efficacy of retail refrigeration equipment. Food Control, 45, 109–114. https://doi.org/10.1016/j.foodcont.2014.04.041.
Månsson, T. (2019). Potential of Supermarket Refrigeration Systems for Grid Balancing by Demand Response. In Proceedings of the 8th International Conference on Smart Cities and Green ICT Systems: Heraklion.
Orlandi, M., Visconti, F.M., & Zampini, S. (2013). In 2nd IIR International Conference on sustainability and the cold chain. Paris: International Institure of Refrigeration (vol. 2, pp. 1–8).
PreparedFood. (2018). Chilled and Deli Foods Market to Reach $988.7 Billion by 2021. https://www.preparedfoods.com/articles/117545-chilled-and-deli-foods-market-to-reach-9887-billion-by-2021.
Research, G.V. (2015). Chilled and Deli Food Market Analysis, Market Size, Application Analysis, Regional Outlook, Competitive Strategies and Forecasts, 2015 To 2022. Technical report, Grand View Research, N/A. https://www.grandviewresearch.com/industry-analysis/chilled-deli-food-market.
SAVE FOOD. (2018). Global Initiative on Food Loss and Waste Reduction. http://www.fao.org/save-food/resources/infographic/en/.
Schmidt, O., Hawkes, A., Gambhir, A., & Staffell, I. (2017). The future cost of electrical energy storage based on experience rates. Nature Energy, 6(July), 17110. https://doi.org/10.1038/nenergy.2017.110. http://www.nature.com/articles/nenergy2017110.
Smale, N. J., Moureh, J., & Cortella, G. (2006). A review of numerical models of airflow in refrigerated food applications. International Journal of Refrigeration, 29(6), 911–930. https://doi.org/10.1016/j.ijrefrig.2006.03.019. http://www.sciencedirect.com/science/article/pii/S0140700706000971.
Statens Energimyndighet. (1990). STIL - Energianvändning i handelslokaler. Technical Report, Energimyndigheten, Stockholm.
Statens Energimyndighet. (2010). STIL 2 - Energianvändning i handelslokaler. Technical Report, Energimyndigheten, Stockholm.
Tahir, A., & Bansal, P.K. (2005). MEPR versus EEPR valves in open supermarket refrigerated display cabinets. Applied Thermal Engineering, 25(2-3), 191–203. https://doi.org/10.1016/j.applthermaleng.2004.06.008. http://www.sciencedirect.com/science/article/pii/S1359431104001632.
Tassou, S.A.A., Lewis, J.S.S., Ge, Y.T.T., Hadawey, A., & Chaer, I. (2010). A review of emerging technologies for food refrigeration applications. Applied Thermal Engineering, 30 (4), 263–276.
Acknowledgements
The authors would like to acknowledge and thank the REWE Group and especially the energy management of the REWE region north for their patience and support in executing and enabling this study. The authors would like to thank the main funding body, Climate-KIC, that provided not just the necessary funds but an invaluable network and inspirational community.
Funding
Open Access funding provided by Chalmers University of Technology
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Månsson, T., Ostermeyer, Y. & Kalagasidis, A.S. Exploratory investigation of return air temperature sensor measurement errors in refrigerated display cabinets. Energy Efficiency 14, 11 (2021). https://doi.org/10.1007/s12053-020-09912-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12053-020-09912-1