Design of optimal controller for static compensator via Hamiltonian formalism for the multimachine system

Abstract

This article introduces a novel strategy for devising an optimal Static Synchronous Compensator (STATCOM) controller via Hamiltonian function method in mitigating the transient stability of a multimachine power system. The STATCOM, a second generation shunt type FACTS device, is popularly employed for power system control. To test the applicability of the Hamiltonian function approach, an IEEE Type WSCC 9-bus system is taken under study. An appropriate Hamiltonian functional has been framed using the parameters of the test system, which is applied to optimize the preferred performance index. The performance of the proposed nonlinear controller is judged against a regular state feedback based STATCOM controller. The parameters of this traditional controller are computed via dynamical Games of the Nash Equilibrium method. The proposed method is beneficial in terms of mathematical complexity as needed in estimating relative degree and coordinate transformation in the feedback linearization method. A detailed investigation of the results reveals that the proposed controller is effective and efficient to a greater degree than the traditional STATCOM controller in a multimachine system, even at some point in serve eventualities like earth fault scenarios.

Appendix 1

1.1 Detailed derivation of IEEE-9 bus system

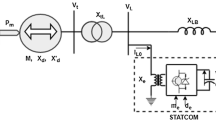
The standard swing equations of ith machine of the 3-machine 9-bus system (figure 1) shown in (22)–(23) are given by

$$ \dot{\omega }_{i} = \frac{{\omega_{0} }}{{H_{i} }}\left( {P_{{M_{i} }} - \frac{{D_{i} }}{{\omega_{0} }}\left( {\omega_{i} - \omega_{0} } \right) - E^{\prime}_{{q_{i} }} V_{{s_{i} }} \left( {B_{{s_{i} }} \sin \delta_{i} + G_{{s_{i} }} \cos \delta_{i} } \right)} \right. $$

$$ + \left. {\sum\limits_{\begin{subarray}{l} i = 1 \\ j \ne i \end{subarray} }^{n} {E^{\prime}_{{q_{i} }} E^{\prime}_{{q_{j} }} \left( {B_{ij} \sin \delta_{ij} + G_{ij} \cos \delta_{ij} } \right)} } \right) $$

(a.1)

$$ \dot{\delta }_{i} (t) = \left( {\omega - \omega_{0} } \right) $$

(a.2)

To find out the Hamiltonian $H_{{m_{i} }}$ for i^th machinethe dynamics (a.1)–(a.2) are expressed first as a standard plant model which is given by;

$$ \dot{X}_{i} = f_{i} \left( {X_{i} (t),u_{i} (t),t} \right); $$

where, $X_{i} (t_{0} ) = \left[ {\begin{array}{*{20}c} {\omega_{0} } & {\delta_{0} } \\ \end{array} } \right]$ and $f_{i} = \left[ {\begin{array}{*{20}c} {f_{{i_{1} }} } & {f_{{i_{2} }} } \\ \end{array} } \right]^{T}$ for which

$$f_{{i_{1} }} = \frac{{\omega_{0} }}{{H_{i} }}\left( {P_{{m_{i} }} - \frac{{D_{i} }}{{\omega_{0} }}\left( {\omega_{i} - \omega_{0} } \right) - \left\{ {V_{{s_{i} }} E^{\prime}_{{q_{i} }} \left( {G_{{s_{i} }} \cos \delta_{i} + B_{{s_{i} }} \sin \delta_{i} } \right)} \right.} \right. + \sum\limits_{\begin{subarray}{l} i = 1 \\ j \ne i \end{subarray} }^{n} {\left. {\left. {E^{\prime}_{{q_{i} }} E^{\prime}_{{q_{j} }} \left( {G_{ij} \cos \delta_{ij} + B_{ij} \sin \delta_{ij} } \right)} \right\}} \right)} $$

(a.3)

and

$$ f_{{i_{2} }} = \left( {\omega_{i} - \omega_{0} } \right) $$

(a.4)

Now, putting $i = 1, \cdots ,3$ for the 3-generator buses and considering all the load buses which are directly affected by the generator buses (i.e., neglecting the buses which are not directly affected by the generator buses), the expression (a.3)–(a.4) can be written as-

$$ f_{{1_{1} }} = \frac{{\omega_{0} }}{{H_{1} }}\left( {P_{{m_{1} }} - \frac{{D_{1} }}{{\omega_{0} }}\left( {\omega_{1} - \omega_{0} } \right) - V_{{s_{1} }} E^{\prime}_{{q_{1} }} \left( {G_{{s_{1} }} \cos \delta_{1} + B_{{s_{1} }} \sin \delta_{1} } \right) + \left( {E^{\prime}_{{q_{1} }} E^{\prime}_{{q_{2} }} \left( {B_{12} \sin \delta_{12} + G_{12} \cos \delta_{12} } \right) + E^{\prime}_{{q_{1} }} E^{\prime}_{{q_{3} }} \left( {B_{13} \sin \delta_{13} + G_{13} \cos \delta_{13} } \right)} \right)} \right) $$

(a.5)

$$ f_{{2_{1} }} = \frac{{\omega_{0} }}{{H_{2} }}\left( {P_{{m_{2} }} - \frac{{D_{2} }}{{\omega_{0} }}\left( {\omega_{2} - \omega_{0} } \right) - V_{{s_{2} }} E^{\prime}_{{q_{2} }} \left( {G_{{s_{2} }} \cos \delta_{2} + B_{{s_{2} }} \sin \delta_{2} } \right) + \left( {E^{\prime}_{{q_{2} }} E^{\prime}_{{q_{3} }} \left( {B_{23} \sin \delta_{23} + G_{23} \cos \delta_{23} } \right) + E^{\prime}_{{q_{2} }} E^{\prime}_{{q_{1} }} \left( {B_{21} \sin \delta_{21} + G_{21} \cos \delta_{21} } \right)} \right)} \right) $$

(a.6)

$$ f_{{3_{1} }} = \frac{{\omega_{0} }}{{H_{3} }}\left( {P_{{m_{3} }} - \frac{{D_{3} }}{{\omega_{0} }}\left( {\omega_{3} - \omega_{0} } \right) - V_{{s_{3} }} E^{\prime}_{{q_{3} }} \left( {G_{{s_{3} }} \cos \delta_{3} + B_{{s_{3} }} \sin \delta_{3} } \right) + \left( {E^{\prime}_{{q_{3} }} E^{\prime}_{{q_{1} }} \left( {B_{31} \sin \delta_{31} + G_{31} \cos \delta_{31} } \right) + E^{\prime}_{{q_{3} }} E^{\prime}_{{q_{2} }} \left( {B_{32} \sin \delta_{32} + G_{32} \cos \delta_{32} } \right)} \right)} \right) $$

(a.7)

$$ f_{{1_{2} }} = \left( {\omega_{1} - \omega_{0} } \right) $$

(a.8)

$$ f_{{2_{2} }} = \left( {\omega_{2} - \omega_{0} } \right) $$

(a.9)

$$ f_{{3_{2} }} = \left( {\omega_{3} - \omega_{0} } \right) $$

(a.10)

Now, using Hamiltonian formalism the nonlinear control law, $V_{{s_{1} }}$, $V_{{s_{2} }}$ and $V_{{s_{3} }}$(shown in (a.5)–(a.7)) have been derived as shown in the expression (21) in the main text.

The control laws (35) & (46) for the conventional controllers have also been derived in the similar way as follows;

The swing equations of ith machine of the 3-machine 9-bus system (figure 1) shown in (22)–(23) are rewritten as

$$\dot{\omega }_{i} = \frac{{\omega_{0} }}{{H_{i} }}\left( {P_{{M_{i} }} - \frac{{D_{i} }}{{\omega_{0} }}\left( {\omega_{i} - \omega_{0} } \right) - E^{\prime}_{{q_{i} }} V_{{s_{i} }} \left( {B_{{s_{i} }} \sin \delta_{i} + G_{{s_{i} }} \cos \delta_{i} } \right)} \right. + \left. {\sum\limits_{\begin{subarray}{l} i = 1 \\ j \ne i \end{subarray} }^{n} {E^{\prime}_{{q_{i} }} E^{\prime}_{{q_{j} }} \left( {B_{ij} \sin \delta_{ij} + G_{ij} \cos \delta_{ij} } \right)} } \right) $$

(a.11)

$$ \dot{\delta }_{i} (t) = \left( {\omega - \omega_{0} } \right) $$

(a.12)

The affine form of WSCC type IEEE-9 bus system can be written as

$$ \dot{X} = f\left( X \right) + \sum\limits_{i = 1}^{m} {g_{i} \left( X \right)u_{i} };\quad{text{for}},\; i =1,\ldots,3$$

(a.13)

$$ y_{i} \left( t \right) = h_{i} \left( X \right) = \delta_{i} $$

(a.14)

where

$$ f(X) = \left[ {\begin{array}{*{20}c} {\frac{{\omega_{0} }}{{H_{1} }}\left( {P_{{m_{1} }} - \frac{{D_{1} }}{{\omega_{0} }}\left( {\omega_{1} - \omega_{0} } \right) + \left( {E^{\prime}_{{q_{1} }} E^{\prime}_{{q_{2} }} \left( {B_{12} \sin \delta_{12} + G_{12} \cos \delta_{12} } \right) + E^{\prime}_{{q_{1} }} E^{\prime}_{{q_{3} }} \left( {B_{13} \sin \delta_{13} + G_{13} \cos \delta_{13} } \right)} \right)} \right)} \\ {\frac{{\omega_{0} }}{{H_{2} }}\left( {P_{{m_{2} }} - \frac{{D_{2} }}{{\omega_{0} }}\left( {\omega_{2} - \omega_{0} } \right) + \left( {E^{\prime}_{{q_{2} }} E^{\prime}_{{q_{3} }} \left( {B_{23} \sin \delta_{23} + G_{23} \cos \delta_{23} } \right) + E^{\prime}_{{q_{2} }} E^{\prime}_{{q_{1} }} \left( {B_{21} \sin \delta_{21} + G_{21} \cos \delta_{21} } \right)} \right)} \right)} \\ {\frac{{\omega_{0} }}{{H_{3} }}\left( {P_{{m_{3} }} - \frac{{D_{3} }}{{\omega_{0} }}\left( {\omega_{3} - \omega_{0} } \right) + \left( {E^{\prime}_{{q_{3} }} E^{\prime}_{{q_{1} }} \left( {B_{31} \sin \delta_{31} + G_{31} \cos \delta_{31} } \right) + E^{\prime}_{{q_{3} }} E^{\prime}_{{q_{2} }} \left( {B_{32} \sin \delta_{32} + G_{32} \cos \delta_{32} } \right)} \right)} \right)} \\ {\left( {\omega_{1} - \omega_{0} } \right)} \\ {\left( {\omega_{2} - \omega_{0} } \right)} \\ {\left( {\omega_{3} - \omega_{0} } \right)} \\ \end{array} } \right] $$

$g_{1} (X)\left[ {\begin{array}{*{20}c} { - \frac{{\omega_{0} }}{{H_{1} }}E^{\prime}_{{q_{1} }} \left( {G_{{s_{1} }} \cos \delta_{1} + B_{{s_{1} }} \sin \delta_{1} } \right)} \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]$; $g_{2} (X)\left[ {\begin{array}{*{20}c} 0 \\ { - \frac{{\omega_{0} }}{{H_{2} }}E^{\prime}_{{q_{2} }} \left( {G_{{s_{2} }} \cos \delta_{2} + B_{{s_{2} }} \sin \delta_{2} } \right)} \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]$; $g_{3} (X)\left[ {\begin{array}{*{20}c} 0 \\ 0 \\ { - \frac{{\omega_{0} }}{{H_{3} }}E^{\prime}_{{q_{3} }} \left( {G_{{s_{3} }} \cos \delta_{3} + B_{{s_{3} }} \sin \delta_{3} } \right)} \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]$

Now, employing $f(X)$ and $g_{i} (X)$, state feedback control law (35) becomes

$$ \left. {\begin{array}{*{20}c} {u_{1} = \frac{{\left[ {\left( {P_{{M_{1} }} - \frac{{D_{1} \left( {\omega_{1} - \omega_{0} } \right)}}{{\omega_{0} }} - \left( {E^{\prime}_{{q_{1} }} E^{\prime}_{{q_{2} }} \left( {B_{12} \sin \delta_{12} + G_{12} \cos \delta_{12} } \right) + E^{\prime}_{{q_{1} }} E^{\prime}_{{q_{3} }} \left( {B_{13} \sin \delta_{13} + G_{13} \cos \delta_{13} } \right)} \right)} \right) - 1} \right]}}{{E_{{q_{1} }}^{\prime} \left( {G_{{s_{1} }} \cos \delta_{1} + B_{{s_{1} }} \sin \delta_{1} } \right)}}\gamma_{1} } \\ {u_{2} = \frac{{\left[ {\left( {P_{{M_{2} }} - \frac{{D_{2} \left( {\omega_{2} - \omega_{0} } \right)}}{{\omega_{0} }} - \left( {E^{\prime}_{{q_{2} }} E^{\prime}_{{q_{3} }} \left( {B_{23} \sin \delta_{23} + G_{23} \cos \delta_{23} } \right) + E^{\prime}_{{q_{2} }} E^{\prime}_{{q_{1} }} \left( {B_{21} \sin \delta_{21} + G_{21} \cos \delta_{21} } \right)} \right)} \right) - 1} \right]}}{{E_{{q_{2} }}^{\prime} \left( {G_{{s_{2} }} \cos \delta_{2} + B_{{s_{2} }} \sin \delta_{2} } \right)}}\gamma_{2} } \\ {u_{3} = \frac{{\left[ {\left( {P_{{M_{3} }} - \frac{{D_{3} \left( {\omega_{3} - \omega_{0} } \right)}}{{\omega_{0} }} - \left( {E^{\prime}_{{q_{3} }} E^{\prime}_{{q_{1} }} \left( {B_{31} \sin \delta_{31} + G_{31} \cos \delta_{31} } \right) + E^{\prime}_{{q_{3} }} E^{\prime}_{{q_{2} }} \left( {B_{32} \sin \delta_{32} + G_{32} \cos \delta_{32} } \right)} \right)} \right) - 1} \right]}}{{E_{{q_{3} }}^{\prime} \left( {G_{{s_{3} }} \cos \delta_{3} + B_{{s_{3} }} \sin \delta_{3} } \right)}}\gamma_{3} } \\ \end{array} } \right\} $$

(a.15)

Finally, the fictitious inputs ($\gamma_{1}$, $\gamma_{2}$ and $\gamma_{3}$) of the expression (a.15) are derived using game theory and the control law for the conventional control law (46) is derived as

$$ \left. {\begin{array}{*{20}c} {u_{1} = \frac{{\left[ {\left( {P_{{M_{1} }} - \frac{{D_{1} \left( {\omega_{1} - \omega_{0} } \right)}}{{\omega_{0} }} - \left( {E^{\prime}_{{q_{1} }} E^{\prime}_{{q_{2} }} \left( {B_{12} \sin \delta_{12} + G_{12} \cos \delta_{12} } \right) + E^{\prime}_{{q_{1} }} E^{\prime}_{{q_{3} }} \left( {B_{13} \sin \delta_{13} + G_{13} \cos \delta_{13} } \right)} \right)} \right) - 1} \right]}}{{E_{{q_{1} }}^{\prime} \left( {G_{{s_{1} }} \cos \delta_{1} + B_{{s_{1} }} \sin \delta_{1} } \right)}}\left[ { - \left( {\delta_{1} \left( t \right) - \delta_{0} } \right) - 1.7325\left( {\omega_{1} \left( t \right) - \omega_{0} } \right)} \right]} \\ {u_{2} = \frac{{\left[ {\left( {P_{{M_{2} }} - \frac{{D_{2} \left( {\omega_{2} - \omega_{0} } \right)}}{{\omega_{0} }} - \left( {E^{\prime}_{{q_{2} }} E^{\prime}_{{q_{3} }} \left( {B_{23} \sin \delta_{23} + G_{23} \cos \delta_{23} } \right) + E^{\prime}_{{q_{2} }} E^{\prime}_{{q_{1} }} \left( {B_{21} \sin \delta_{21} + G_{21} \cos \delta_{21} } \right)} \right)} \right) - 1} \right]}}{{E_{{q_{2} }}^{\prime} \left( {G_{{s_{2} }} \cos \delta_{2} + B_{{s_{2} }} \sin \delta_{2} } \right)}}\left[ { - \left( {\delta_{2} \left( t \right) - \delta_{0} } \right) - 1.7325\left( {\omega_{2} \left( t \right) - \omega_{0} } \right)} \right]} \\ {u_{3} = \frac{{\left[ {\left( {P_{{M_{3} }} - \frac{{D_{3} \left( {\omega_{3} - \omega_{0} } \right)}}{{\omega_{0} }} - \left( {E^{\prime}_{{q_{3} }} E^{\prime}_{{q_{1} }} \left( {B_{31} \sin \delta_{31} + G_{31} \cos \delta_{31} } \right) + E^{\prime}_{{q_{3} }} E^{\prime}_{{q_{2} }} \left( {B_{32} \sin \delta_{32} + G_{32} \cos \delta_{32} } \right)} \right)} \right) - 1} \right]}}{{E_{{q_{3} }}^{\prime} \left( {G_{{s_{3} }} \cos \delta_{3} + B_{{s_{3} }} \sin \delta_{3} } \right)}}\left[ { - \left( {\delta_{3} \left( t \right) - \delta_{0} } \right) - 1.7325\left( {\omega_{3} \left( t \right) - \omega_{0} } \right)} \right]} \\ \end{array} } \right\} $$

(a.16)