Abstract
This paper presents computation of swing modes of a large power system that could be significantly affected by power swing damping controllers in FACTS or HVDC devices at a given location. Modal controllability is a suitable measure to isolate these modes for analysis. Computation of the controllable swing mode spectrum is useful, especially in situations where the controller structure and feedback signals are not frozen (e.g., at the planning stage). This paper proposes two important steps that allow us to map the problem of finding highly controllable swing modes to the problem of finding the swing modes that have high transfer function residues (for which efficient algorithms are available). The steps are: (a) normalization of the eigenvectors corresponding to different modes and (b) identification of specific feedback signals for each type of FACTS/HVDC device such that the modal observability and modal controllability are tightly coupled. Once the mapping is done, a computationally efficient method like the Subspace Accelerated Dominant Pole Algorithm [16] (SADPA) can be adapted to find the highly controllable swing modes. The effectiveness of this approach is demonstrated by case studies of FACTS and HVDC devices in a 16-machine system and the Indian power grid.








Similar content being viewed by others
Notes
For complex poles, the complex–conjugate pair is considered as one mode.
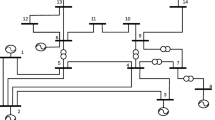
G(s) is calculated using Eq. (16) for a frequency range of 1.26–19 rad/s in steps of 0.01 rad/s.
References
Padiyar K R 2007 FACTS controllers in power transmission and distribution. New Delhi: New Age International(P) Ltd
Padiyar K R 2012 HVDC power transmission systems, 2nd ed. New Delhi: New Age International(P) Ltd
Martins N, Lima L T G and Pinto H J C P 1996 Computing dominant poles of power system transfer functions. IEEE Trans. Power Syst. 11(1): 162–167
Uchida N and Nagao T 1988 A new eigen-analysis method of steady-state stability studies for large power systems: Smatrix method. IEEE Trans. Power Syst. 3(2): 2085–2092
Semlyen A and Wang L 1988 Sequential computation of the complete eigen system for the study zone in small signal stability analysis of large power systems. IEEE Trans. Power Syst. 3(2): 715–725
Wang L and Semlyen A 1989 Application of sparse eigenvalue techniques to the small signal stability analysis of large power systems. In: Proceedings of the Power Industry Computer Application Conference, pp. 358–365
Angelidis G and Semlyen A 1995 Efficient calculation of critical eigenvalue clusters in the small signal stability analysis of large power systems. IEEE Trans. Power Syst. 10(1): 427–432
Yang D and Ajjarapu V 2007 Critical eigenvalues tracing for power system analysis via continuation of invariant subspaces and projected Arnoldi method. IEEE Trans. Power Syst. 22(1): 324–332
Li Y, Geng G and Jiang Q 2016 An efficient parallel Krylov–Schur method for eigen-analysis of large-scale power system. IEEE Trans. Power Syst. 31(2): 920–930
Rommes J and Martins N 2008 Computing large-scale system eigenvalues most sensitive to parameter changes, with applications to power system small-signal stability. IEEE Trans. Power Syst. 23(2): 434–442
Chung C Y and Dai B 2013 A combined TSA–SPA algorithm for computing most sensitive eigenvalues in large-scale power systems. IEEE Trans. Power Syst. 28(1): 149–157
Chung C Y and Dai B 2015 A generalized approach for computing most sensitive eigenvalues with respect to system parameter changes in large-scale power systems. IEEE Trans. Power Syst. pp. 1–11, https://doi.org/10.1109/TPWRS.2015.2445792
Byerly R T, Bennon R J and Sherman D E 1982 Eigenvalue analysis of synchronizing power flow oscillations in large electric-power systems. IEEE Trans. Power Appl. Syst. PAS-101: 235–243
Wong D Y, Rogers G J, Porretta B and Kundur P 1988 Eigenvalue analysis of very large power systems. IEEE Trans. Power Syst. 3(2): 472–480
Martins N 1997 The dominant pole spectrum eigensolver. IEEE Trans. Power Syst. 12(1): 245–254
Rommes J and Martins N 2006 Efficient computation of transfer function dominant poles using subspace acceleration. IEEE Trans. Power Syst. 21(3): 1471–1483
Mhaskar U P and Kulkarni A M 2006 Power oscillation damping using FACTS devices: modal controllability, observability in local signals, and location of transfer function zeros. IEEE Trans. Power Syst. 21(1): 285–294
Rogers G 2000 Power system oscillations. Norwell, MA: Kluwer
Rommes J 2007 Methods for eigenvalue problems with applications in model order reduction. PhD Thesis, Utrecht University, Utrecht, http://dspace.library.uu.nl/handle/1874/21787 [Accessed 28 October 2016]
Shubhanga K N and Anatholla Y 2000 Manual for a multi-machine small-signal stability programme (Version 1.0). Department of Electrical Engineering, NITK Surathkal, Karnataka, India, p 54
EIGS. http://www.mathworks.com/help/matlab/ref/eigs.html [Accessed 28 October 2016]
Latorre H F, Ghandhari M and Soder L 2008 Active and reactive power control of VSC-HVDC. Electr. Power Syst. Res. 78: 1756–1763
Power System Operation Corporation Ltd. POC data, https://posoco.in/transmission-pricing/poc-data [Accessed 28 October 2016]
Central Electricity Authority manual on transmission line planning criteria, http://cea.nic.in [Accessed 28 October 2016]
Kundur P 1994 Power systems stability and control. New York: McGraw-Hill
Acknowledgements
The authors gratefully acknowledge the contributions of Mr Abishek R S and Mr A Sinkar in preparation of the small signal model of the Indian Power System. Both of them have received their Master’s degrees from the Department of Electrical Engineering, IIT Bombay.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix I. Derivation of constraint in Eq. (12)
Following a perturbation, the energy in the disturbance can be expressed as sum of potential and kinetic energy as follows:
It is constant for the unforced system (i.e., \(u = 0\)). If the \(i{\hbox {th}}\) mode only is excited, then from Eq. (5) we have
Using Eq. (A2) in Eq. (A1), it can be shown that
From Eqs. (3) and (4), it can be shown that
and therefore
where \(E_i\) denotes the energy when only the \(i{\hbox {th}}\) mode is excited. It can be shown that when several modes are excited, the disturbance energy is given by the sum of all modal energies, i.e, \(E = \sum _{i = 1}^{(n_g-1)} E_i\). Note that \(E_i\) is also a constant and does not depend on scaling of the eigenvectors.
The strength of the modal signal \(y = v_i^Tz = z_{m_i}\) is given by its amplitude, which is equal to \(|z_{m_i}|\). When only one mode is excited at a time, with the same disturbance energy \(E_i\), strength of the modal signal being equal across modes implies \((x_{\delta _i}^{H}A_rx_{\delta _i}+x_{\omega _i}^{H}Mx_{\omega _i})\) is the same across all modes (as seen from Eq. (A6)). Without loss of generality, we assign its value to be 1 and obtain the following condition:
Using the initial assumption of \(x_{\delta _i}\) being real, we obtain the result of Eq. (12).
Appendix II. Example of dominant pole at infinity
Let us consider the state-space matrices \(E = \begin{bmatrix} I&0\\0&0 \end{bmatrix},\; A = \begin{bmatrix} \alpha&0\\ 0&\alpha \end{bmatrix} {\text {where}}\; \alpha = \begin{bmatrix} 0.1&0.2\\ -\,0.2&0.3 \end{bmatrix}\) and \(b = c = [0.1\;0.1\;1.0\;1.0]^T\). Generalized eigenvalue analysis of this system yields a mode \(0.2 \pm 0.17321i\) with residue of 0.01 and two poles at infinity with residue of \(\infty \).
Trajectories of the eigenvalue estimate over iterations, when SADPA is applied on this system with \(|\rho _i|\) (or \(|\rho _i||\lambda _i|\)) (case (a)), and \(|\rho _i|/|\lambda _i|\) (case (b)) as selection criteria separately are shown in the following table. It is clearly seen that the selection criterion in case (b) avoids convergence to the dominant pole at \(\infty \).
Iteration | Eigen-estimate | |
|---|---|---|
Case (a) | Case (b) | |
0 | 0 +j 0.1700 | 0 +j 0.1700 |
1 | 25.2768 –j 5.1847 | 25.2768 –j 5.1847 |
2 | (2.72 +j 3.50)\(\times 10^5\) | 0.2944 +j 0.1997 |
3 | \(\infty \) | 0.2000 –j 0.1732 |
- A, b, c, d:
-
state-space matrices
- z :
-
state variables
- \(\delta , \omega \) :
-
rotor angle (rad), speed (rad/s)
- \(n_g\) :
-
number of generators
- \(\Omega _i\) :
-
frequency of the \(i{\hbox {th}}\) swing mode (rad/s)
- \(x_{\delta _i}, x_{\omega _i}\) :
-
components of right eigenvector corresponding to rotor angle and speed, respectively
- \(v_{\delta _i}, v_{\omega _i}\) :
-
components of left eigenvector corresponding to rotor angle and speed, respectively
- Re(.):
-
real part of a complex number
- \((.)^*\) :
-
element-wise conjugate of a complex vector
- \((.)^T\) :
-
transpose
- \((.)^H\) :
-
conjugate-transpose of a vector
- G(s):
-
SISO transfer function
- SSPF:
-
sum of slip participation factors
Rights and permissions
About this article
Cite this article
Pradhan, V., Kulkarni, A.M. & Khaparde, S.A. Computation of the controllable swing mode spectrum of FACTS and HVDC in large power systems. Sādhanā 43, 176 (2018). https://doi.org/10.1007/s12046-018-0960-5
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12046-018-0960-5