Coherent nonlinear electromagnetic response in twisted bilayer and few-layer graphene

Abstract

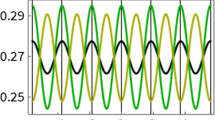
The phenomenon of Rabi oscillations far from resonance is described in bilayer and few-layer graphene. These oscillations in the population and polarization at the Dirac point in n-layer graphene are seen in the nth harmonic term in the external driving frequency. The underlying reason behind these oscillations is attributable to the pseudospin degree of freedom possessed by all these systems. Conventional Rabi oscillations, which occur only near resonance, are seen in multiple harmonics in multilayer graphene. However, the experimentally measurable current density exhibits anomalous behaviour only in the first harmonic in all the graphene systems. A fully numerical solution of the optical Bloch equations is in complete agreement with the analytical results, thereby justifying the approximation schemes used in the latter. The same phenomena are also described in twisted bilayer graphene with and without an electric potential difference between the layers. It is found that the anomalous Rabi frequency is strongly dependent on twist angle for weak applied fields – a feature absent in single-layer graphene, whereas the conventional Rabi frequency is relatively independent of the twist angle.

Appendices

Appendix A

In this section, we present the solution of Bloch equations at resonance for multilayer graphene. The general Bloch equations for n-layer graphene are

$$\begin{array}{@{}rcl@{}} i\partial_{t} {N}(t) &=& 2 \lambda \left[ (k_{-} - A_{c}^{\ast}(t))^{n} \pi(t) - (k_{+} - A_{c}(t))^{n} \pi^{\ast}(t)\right], \\ i\partial_{t} {\pi}(t) &=& \lambda \left(k_{+} - A_{c}(t)\right)^{n} N(t),\quad i\partial_{t} {\pi^{\ast}}(t) = -\lambda \left(k_{-} - A_{c}^{\ast}(t)\right)^{n} N(t), \\ A_{c}(t) &=& \frac{e}{c} \left( A_{x}(0) + i A_{y}(0) \right)\mathrm{e}^{- i \omega t} = A_{c}(0) \,\,\,\mathrm{e}^{- i \omega t},\qquad\lambda = \frac{{v_{0}^{n}}}{(-\gamma_{1})^{n - 1}}. \end{array} $$

The above equations exhibit what may be termed as ‘harmonic resonances’. Their description is as follows. First, we diagonalize a time-independent matrix formed by the Bloch equations, when the external field is absent, and that may be diagonalized by making the substitution,

$$\left( \begin{array}{clcr} N \\ \pi \\ \pi^{\ast} \end{array} \right) = \left( \begin{array}{clcr} 0 & 2 \frac{|k|^{n}}{k_{-}^{n}} & -2 \frac{|k|^{n}}{k_{-}^{n}} \\ \frac{|k|^{2n}}{k_{-}^{2n}} & - \frac{|k|^{2n}}{k_{-}^{2n}} & - \frac{|k|^{2n}}{k_{-}^{2n}} \\ 1 & 1 & 1 \end{array}\right) \left( \begin{array}{clcr} \tilde {N} \\ \tilde {\pi} \\ \tilde {\pi}^{\ast} \end{array} \right). $$

Now, the full Bloch equations may be written in a matrix form as follows:

$$\begin{array}{@{}rcl@{}} i\partial_{t} \left( \begin{array}{clcr} N \\ \pi \\ \pi^{\ast} \end{array} \right)& =& \left(\begin{array}{cccr} 0 & 2 \lambda k_{-}^{n} & - 2 \lambda k_{+}^{n} \\ \lambda k_{+}^{n} & 0 &0 \\ -\lambda k_{-}^{n} & 0 & 0 \end{array}\right) \left( \begin{array}{clcr} N \\ \pi \\ \pi^{\ast} \end{array} \right) \\ &&+ {\sum}_{m=1}^{n}{C^{n}_{m}}\left(\begin{array}{clcr} 0 & 2 (b_{1})_{12} & - 2 (b_{1})_{12}^{*} \\ (b_{1})_{12}^{*} & {\kern1pc}0 & 0 \\ - (b_{1})_{12} & {\kern1pc}0 & 0 \end{array}\right) \left( \begin{array}{clcr} N \\ \pi \\ \pi^{\ast} \end{array} \right), \end{array} $$

where

$$(b_{1})_{12} = \lambda k^{n-m}_{-} (-A_{c}^{*}(t))^{m} ~~~\textnormal{and}~~~ {C^{n}_{m}} = \frac{ n! }{ (n-m)! m! } $$

are combinatorial factors. Now, we transform to the new variables.

In this case, we retain only one value of m in the above equation, denoted by m=ν, anticipating that the resonance will occur for that particular value of ν for which ν ω=2λ|k|ⁿ. The other values of ν are far from resonance for the value of |k| obeying this equation. In such a situation we may write

$$\begin{array}{@{}rcl@{}} i\partial_{t}\tilde{N}(t) &=& C^{n}_{\nu} (-)^{\nu} (-a {\tilde{\pi}(t)} + a {\tilde{\pi}}^{*}(t)), \\ i\partial_{t}\tilde {\pi}(t) &=& -2 \lambda |k|^{n}\quad\tilde {\pi}(t) + C^{n}_{\nu} (-)^{\nu}\left(\frac{1}{2}a {\tilde{N}(t)} - b \quad {\tilde{\pi}}(t)\right), \\ i\partial_{t}\tilde {\pi}^{*}(t) &=& 2 \lambda |k|^{n}\quad\tilde {\pi}^{*}(t) + C^{n}_{\nu} (-)^{\nu} \left(-\frac{1}{2}a {\tilde{N}}(t) + b \quad {\tilde{\pi}}^{*}(t)\right), \end{array} $$

where

$$a \equiv |k|^{n} \lambda (-k_{+}^{-\nu} (A_{c}(t))^{\nu} + k_{-}^{-\nu} (A_{c}^{*}(t))^{\nu}) $$

$$b = |k|^{n} \lambda (k_{+}^{-\nu} (A_{c}(t))^{\nu} + k_{-}^{-\nu} (A_{c}^{*}(t))^{\nu}). $$

Rotating wave approximation involves using $\tilde {\pi }({\vec {k}},t) = \mathrm {e}^{2 i t \lambda |k|^{n} }\quad \tilde {\pi }^{\prime }({\vec {k}},t)$ and using ν ω−2λ|k|ⁿ≡Δ≪ν ω so that

$$\begin{array}{@{}rcl@{}} &&i\partial_{t}\tilde{\pi}^{\prime}(t) = C^{n}_{\nu} (-)^{\nu}\left(\frac{1}{2}|k|^{n} \lambda (k_{-}^{-\nu} (A^{*}_{c})^{\nu} \textnormal{e}^{i {\Delta} t }) {\tilde{N}} (t)\right), \\ &&i\partial_{t}\tilde{N}(t) = C^{n}_{\nu} (-)^{\nu} |k|^{n} \lambda(k_{+}^{-\nu} (A_{c})^{\nu} \textnormal{e}^{- i {\Delta} t }~\tilde{\pi}^{\prime}(t) + \textnormal{h.c.} ), \\ &&\tilde{\pi}^{\prime}({\bf{k}},t) = \textnormal{e}^{i {\Delta} t } {\Pi}({\mathbf{k}},t), \\ &&i\partial_{t} {\Pi}(t) - {\Delta}\mbox{ }\!\! {\Pi}(t) = C^{n}_{\nu} (-)^{\nu}\,\,\,\frac{1}{2}|k|^{n} \lambda k_{-}^{-\nu} (A^{*}_{c})^{\nu} {\tilde{N}}(t), \\ &&i\partial_{t}\tilde{N} (t)= C^{n}_{\nu} (-)^{\nu} (-|k|^{n} \lambda (-k_{+}^{-\nu} (A_{c})^{\nu} ) \mbox{ }\!\!{\Pi}(t) + \textnormal{h.c.} ), \\ &&{\Pi}({\mathbf{k}},t) = \frac{\mathrm{e}^{i \pi \nu } |k|^{n} k_{-}^{-\nu} \lambda {\tilde{N}}({\mathbf{k}},0) C^{n}_{\nu } {\Delta}(-1 + \text{cos}({\Omega} t ) - i {\Omega} ~\text{sin}({\Omega} t ) ) (A_{c}^{*})^{\nu} }{ 2 {\Omega}^{2} }, \\ &&{\tilde{N}}({\mathbf{k}},t) = {\tilde{N}}({\mathbf{k}},0) \frac{ {\Delta}^{2} + ({\Omega}^{2} - {\Delta}^{2})~\text{cos}({\Omega} t) }{ {\Omega}^{2} }, \\ &&{\Omega}^{\text{NLG}} = \sqrt{ {\Delta}^{2} + {\omega_{\textnormal{R}}^{2}} }, \quad\omega_{\textnormal{R}} = \lambda C^{n}_{\nu } |A_{c}(0)|^{\nu} |k|^{(n-\nu)}. \end{array} $$

Appendix B

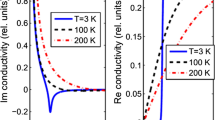
In this section, we describe the analytical expressions used for generating the central result of our work, viz. figure 2. All the three parts of figure 2 are obtained through a numerical solution of the nonlinear equation for the eigenfrequency (see our earlier work [11]). In our earlier work, we showed that the plots are equally well represented by a simple smooth interpolation of subplots applicable in different regimes, where analytical expressions are possible (the last four equations on p. 4606 of that work). Here too, we adopt the same strategy to obtain:

(a) For single-layer graphene:

$$\begin{array}{@{}rcl@{}} {\Omega}_{\text{SLG}}\left(v_{F}|k| < \frac{ \omega }{4}\right) &=& 2 \sqrt{{\left(v_{\mathrm{F}} |k|\right)^{2}} + \frac{\omega_{\mathrm{R}}^{4}}{\omega^{2}}}, \\ {\Omega}_{\text{SLG}}\left(\frac{ \omega }{4} < v_{\mathrm{F}}|k|\right) &=& \sqrt{\left( \omega - 2 v_{\mathrm{F}} |k| \right)^{2} + \omega_{\mathrm{R}}^{2} }. \end{array} $$

The conventional Rabi frequency is related to the fields in single-layer graphene through, $\omega _{\mathrm {R}} = v_{\mathrm {F}}|\frac {e}{c} {\vec {\sigma }}_{\text {BA}}\cdot {\vec {A}}(0)|$.

(b) For BLG:

$$\begin{array}{@{}rcl@{}} {\Omega}_{\text{BLG}}\left(\frac{|k|^{2}}{2 m} < \frac{ \omega }{4}\right) &=& 2 \sqrt{{\left(\frac{|k|^{2}}{2 m}\right)^{2}} + \frac{\left( {\omega_{R}^{2}} + 8 \frac{|k|^{2} \omega_{\mathrm{R}}}{2 m}\right)^{2}}{4 \omega^{2}}}, \\ {\Omega}_{\text{BLG}}\left(\frac{ \omega }{4} < \frac{|k|^{2}}{2 m} < \frac{ 3\omega }{4}\right) &=& \sqrt{\left( \omega - 2 \frac{|k|^{2}}{2 m} \right)^{2} + 4 \frac{|k|^{2} \omega_{\mathrm{R}}}{2 m}}, \\ {\Omega}_{\text{BLG}}\left(\frac{ 3\omega }{4} < \frac{|k|^{2}}{2 m}\right) &=& \sqrt{\left( 2 \omega - 2 \frac{|k|^{2}}{2 m} \right)^{2} + {\omega_{R}^{2}}},\mbox{ }\quad \omega_{\mathrm{R}} = \frac{ |A_{c}(0)|^{2} }{2m}. \end{array} $$

(c) for trilayer graphene:

$$\begin{array}{@{}rcl@{}} && {\Omega}_{\text{TLG}}\left( \alpha |k|^{3} < \frac{ \omega }{4}\right) = 2 \frac{\sqrt{\left( \omega_{\mathrm{R}}^{\prime} \right)^{2} + \alpha^{2}|k^{3}|^{2} \omega^{2}}}{\omega}, \\ && \omega_{\mathrm{R}}^{\prime} = \left( 9 \alpha^{2} |k|^{4}\left( \frac{\omega_{\mathrm{R}}}{\alpha}\right)^{2/3} + \frac{9}{2} \alpha^{2} |k|^{2} \left( \frac{\omega_{\mathrm{R}}}{\alpha}\right)^{4/3} + \frac{1}{3} {\omega_{R}^{2}} \right), \\ && {\Omega}_{\text{TLG}}\left(\frac{ \omega }{4} < \alpha |k|^{3} < \frac{ 3\omega }{4} \right) = \sqrt{{\Delta}^{2} + 9 \omega_{\mathrm{R}}^{2/3} \left( \alpha |k|^{3} \right)^{4/3} }, \\ && {\Omega}_{\text{TLG}}\left(\frac{ 3\omega }{4} < \alpha |k|^{3} < \frac{ 5\omega }{4} \right) = \sqrt{{\Delta}^{2} + 9 \omega_{\mathrm{R}}^{4/3} \left( \alpha |k|^{3}\right)^{2/3}}, \\ && {\Omega}_{\text{TLG}}\left(\frac{ 5\omega }{4} < \alpha |k|^{3} \right) = \sqrt{{\Delta}^{2} + \omega_{\mathrm{R}}^{2} },\qquad \omega_{\mathrm{R}} = \frac{{v_{0}^{3}}}{{\gamma_{1}^{2}}} \quad |A_{c}(0)|^{3}. \end{array} $$

where Δ=(ν ω−2α|k|³). ν=1,2,3 for first, second and third harmonic resonances, respectively. These formulae clearly show the harmonic resonances associated with conventional Rabi oscillations.