1 Introduction

Over the past decade, wireless communications have experienced significant advancements and progress. As a result, an increasing number of devices are utilizing the electromagnetic spectrum, leading to a substantial volume of mobile data being transmitted daily. This has consequently placed significant strain on limited radio spectrum sources (Rabnawaz et al. 2023). Several technologies have been developed to improve electromagnetic spectrum efficiency, including code division multiple access (CDMA), orthogonal frequency division multiplexing (OFDM), and multi-input multioutput (MIMO). The Shannon limit is closely related to both the channel capacity and spectrum utilization. Enhancing the channel capacity beyond its current limitations proves to be a challenging task when relying on the conventional modulation techniques of amplitude, phase, frequency, and polarization. Recently, the concept of orbital angular momentum (OAM) has been proposed to increase spectrum efficiency. Orthogonality guarantees that the mode can be effectively multiplexed at the transmitter, propagated in a spatially coherent manner, and then demultiplexed at the receiver while minimizing any interference between different modes. It is widely recognized that an electromagnetic wave can transport both linear and angular momentum, which can be simply expressed as L = r xmv, where r is the position from the origin, mv is the linear momentum, and x is the cross product (Yao and Padgett 2011). There are two distinct forms of angular momentum: the first one, known as spin angular momentum (SAM), is linked to the polarization of the field, while the second form, referred to as orbital angular momentum, relies on the spatial distribution of the field. The OAM vortex beam possesses a wide range of potential applications in the fields of optics, radio communication, and antenna technology. This beam could enhance the communication capacity without the need to expand the bandwidth. Vortex beams travel in a parallel manner along the axis of the beam and spread out in the radial direction. In (Poynting 1901), the earliest study by J. H. Poynting made a prediction regarding the existence of angular momentum in electromagnetic waves. In (Beth 1936), R.A. Beth and colleagues demonstrated a device specifically designed to detect and quantify the angular momentum of light. Building upon this work, L. Allen and his team acknowledged that orbital angular momentum is a natural property of all helically phased beams (Allen et al. 1992). The concept of OAM was proposed for radio communications. In (Thide et al. 2007), Bo Thide et al. introduced the OAM from an optical frequency to a radio band. To generate radio beams with OAM properties, a phased array can be employed, and alternatively, a time-switched array (TSA) can also serve this purpose (Bai et al. 2013; Tennant and Allen 2012). Notably, F. Tamburini et al. conducted pioneering experimental validation of vortex beams within the radio frequency spectrum (Tamburini et al. 2011; Tamburini et al. 2012). These waves have garnered attention in fields such as communication systems, superresolution imaging, optical communications, and quantum state manipulation. A notable contribution in this area is the design of a vortex beam generation lens by J. Yi et al. (2019).

Metamaterials possess unique electromagnetic properties that are not present in natural substances or conventional materials due to their artificially engineered sub-wavelength structure. Dielectric metamaterials and metal-based metamaterials are the two primary categories into which electromagnetic metamaterials are commonly classified. The fundamental concept behind the metal-based metamaterial involves utilizing metal to construct an array composed of periodic or quasi-periodic unit structures with a specific shape. Several publications have focused on the examination of metamaterials for different purposes in the microwave, infrared, and THz frequency band, and in the optical range of light (Ng et al. 2009, Schurig et al. 2006, Zhang et al. 2018, Grady et al. 2013). Metasurfaces possess unique capabilities for effectively controlling the amplitude, phase, and polarization of incident electromagnetic waves. Initially, the metasurface was used to generate optical vortices by applying the fundamental principles of reflection and refraction (Huang and Li 2019). In a subsequent study, the concept of generating optical orbital angular momentum (OAM) at visible wavelengths through a plasmonic metasurface was introduced (Li et al. 2021). Additionally, the investigation involved the observation of a surface plasmon vortex that carries OAM within a gold metasurface when subjected to linearly polarized optical excitation (Avramov-Zamurovic et al. 2023). Reconfigurable metasurface can change their electromagnetic properties dynamically. This means that they can be tuned or reconfigured to manipulate the behavior of electromagnetic waves in real-time. This reconfigurability is typically achieved through the use of semiconductor-based controlling elements (e.g., PN diodes and varactor diodes), which are difficult to implement in the high-frequency spectrum of terahertz waves (Bharathidevi and Kumar 2023), or the use of materials with tunable properties, such as liquid metal (Yan et al. 2018), phase-change materials (Lin et al. 2022), or graphene (Malaht er al. 2021) which are suitable for use in terahertz wave applications. By changing the configuration of the metasurface, it is possible to control the reflection, refraction, absorption, and polarization of electromagnetic waves, making reconfigurable metasurfaces promising for applications in communication systems, imaging, sensing, and beam steering. Graphene consists of carbon atoms arranged in a 2D-hexagonal lattice structure. It exhibits great potential as a material for the implementation of compact resonant terahertz antennas. Graphene possesses appealing physical characteristics, including excellent conductivity, favorable transparency, and nonlinearity. Moreover, it facilitates the existence of surface plasmon polaritons in the terahertz range, which can be extensively adjusted by modifying graphene’s conductivity through chemical doping, applying a magnetic field, or utilizing electrostatic gating. Extensive research has been conducted on the conductivity of graphene, encompassing both DC and RF frequencies spanning from the terahertz band (0.1–10 THz) to the visible region. In (Zainud-Deen et al. 2018), a novel design for a tunable graphene transmitarray was proposed. This study focuses on the development of a graphene-based plasmonic nanoantenna specifically designed for terahertz band communication.

In this paper, an arrangement of metasurface elements based on the reconfigurable conductivity of a graphene material is introduced. The proposed graphene metasurface unit-cell at 1.2 THz is investigated and optimized. The manipulation of metasurface elements to scatter vortex beams in different directions has been investigated. The radiation characteristics of graphene metasurface for two/four beams are studied. Two excitation techniques, plane wave illumination and focused feed using horn antenna are considered. A full-wave simulation using a CST-MWS electromagnetic simulator is used and verified using Ansys HFSS CAD tools.

2 Geometry, results and discussions

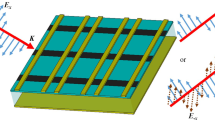
A graphene metasurface composed of 20 × 20 unit-cell elements with interelement spacing of dx = dy = 75 μm (≈ 0.3 λo at f = 1.2 THz) is considered. Figure 1 shows the construction of the proposed unit-cell. It is made of a graphene ring with an inner radius Ri = 26.4 μm and an outer radius Ro= 31.4 μm with a thickness of 0.2 μm. The ring is connected to 4 arms, each with a width of 5 μm, and is printed on 25 μm thick grounded quartz dielectric substrate with εr = 3.75 and tanδ = 0.0184. A polysilicon line with a width 2 μm, and was printed at a depth of 100 nm in the substrate below the graphene ring to apply the DC biasing voltage. The optimized structure parameters of the metasurface geometric unit cell are presented in Table (I). The complex conductivity of graphene\(\sigma\) can be represented by modeling it as an extremely thin surface, and it is represented by (Gusynin et al. 2006):

$$\sigma \left(\omega \right)={\sigma }_{intra}\left(\omega \right)+{\sigma }_{inter}\left(\omega \right)$$
(1)

where

$${\sigma }_{intra}\left(\omega \right)\approx -j \frac{{q}_{e}^{2}{k}_{B}T}{\pi \hslash (\omega -j2{\Gamma })}\left[\frac{{\mu }_{c}}{{k}_{B}T}+2 \text{l}\text{n}({e}^{-\frac{{\mu }_{c}}{{k}_{B}T}}+1)\right]$$
(2)
$${\sigma }_{inter}\left(\omega \right)\approx -j \frac{{q}_{e}^{2}}{4\pi \hslash } ln\left[\frac{2\left|{\mu }_{c}\right|-(\omega -j{\tau }^{-1})\hslash }{2\left|{\mu }_{c}\right|+(\omega -j{\tau }^{-1})\hslash }\right]$$
(3)

and

$${\epsilon }_{r}\left(\omega \right)=1+\frac{\sigma \left(\omega \right)}{{\epsilon }_{o}\omega \varDelta }$$
(4)

where \({\sigma }_{intra}\left(\omega \right)\) and \({\sigma }_{inter}\left(\omega \right)\) are the intraband and interband graphene conductivities, respectively. qe, \(\hslash =h/2\pi\) and KB are the electron charge, reduced Planck’s constant, and the Boltzman’s constant, respectively. \(\tau\) is the transport relaxation time, T is the temperature in Kelvin, \(\omega\)is the angular frequency, \({\Gamma }=1/2\tau\) is the scattering rate, and µc is the chemical potential. The latter parameter µc is affected by the externally applied DC biasing voltage. εo is the permittivity in free space, and ∆ denotes the graphene thickness. The \({\sigma }_{intra}\left(\omega \right)\) conductivity dominates in the frequency range below 8 THz and \({\sigma }_{inter}\left(\omega \right)\) is neglected. Figure 2a and b show the real and imaginary parts of the surface conductivity of graphene versus frequency at \(\tau\) =5 ps, T = 300 K and different values of µc. At a fixed biasing chemical potential, the graphene conductivity decreases gradually with increasing the operating frequency while the losses increase slightly. For the same operating frequency, increasing the chemical potential improves the graphene conductivity with reduced metallic losses. Figure 2c shows the graphene complex conductivity frequency response at µc = 0.7 eV, and T = 300 K for different relaxation times \(\tau .\) Increasing the relaxation time reduces both the graphene conductivity and loss. The graphene conductivity independent of temperature from 100 K to 400 K, as shown in Fig. 2d.

Fig. 1
figure 1

The configuration of the proposed graphene unit-cell of the metasurface. (a). 3D- view (b). Top viw (c). Side view

Full size image
Table 1 The graphene unit-cell dimensions in (µm)
Full size table
Fig. 2
figure 2

The variation in the graphene complex conductivity under different operating conditions determined using Eq. (1). (a). Real part of the conductivity at different µc (b). Imaginary part of the conductivity at different µc (c). Conductivity at different τ values d. Conductivity at T

Full size image

The reflection coefficient of a unit-cell element is determined by employing a waveguide simulator in CST MWS electromagnetic simulator. Image theory is employed, and a perfect electric conductor (PEC) and a perfect magnetic conductor (PMC) are applied to the ± x-axis and ± y axis of the unit-cell respectively, to simulate an infinite array of identical elements. The limitations of infinite array approach are as follows: first, the properties of all graphene elements are indistinguishable, which is not realistic. Second, the simulator does not consider the edges effects, such as diffraction, as the array itself has a finite extent. A normal incident plane wave was employed for unit-cell excitation. Figure 3 shows the reflection coefficient, magnitude and phase, versus frequency at \(\tau\) =5 ps, and T = 300 K for different values of µc under normal incidence. The µc variation from 0.25 eV to 1.6 eV shifts the reflection coefficient to higher frequencies and changes the reflection coefficient magnitude from − 6.2 dB to -1.8 dB with a phase variation of 360 degrees to 240 degrees over the frequency band from 0.8 THz to 1.5 THz. The effect of the graphene relaxation time from 0.3 ps to 10 ps on the reflection coefficient at µc = 0.7 eV, and T = 300 K was investigated as shown in Fig. 4. A High relaxation time reduces the reflection coefficient magnitude with nearly the same phase response which improves the unit-cell performance. At an operating frequency of 1.2 THz, the variations in the reflection coefficient magnitude and phase versus µc are plotted in Fig. 5a. The reflection magnitude is varied from − 2.1 dB to -0.8 dB with 350 degrees phase variation for µc ranging from 0.25 eV to 1.6 eV at \(\tau\) =5 ps, and T = 300 K. Figure 5b shows he reflection magnitude is varied from − 16 dB to -2 dB with a 110 degrees phase variation when \(\tau\) changes from 0.3 ps to 10 ps at µc = 0.7 eV, and T = 300 K.

Fig. 3
figure 3

The reflection coefficient, magnitude, and phase, versus frequency of the proposed graphene unit-cell of the metasurface at \(\tau\) =5 ps, T = 300 K and different values of µc

Full size image
Fig. 4
figure 4

The reflection coefficient, magnitude, and phase, versus frequency of the proposed graphene unit-cell of the metasurface at µc = 0.7 eV, T = 300 K and different values of \(\tau\)

Full size image
Fig. 5
figure 5

The reflection coefficient, magnitude, and phase at 1.2 THz versus (a) chemical potential, and (b) relaxation time of the unit-cel

Full size image

Figure 6 shows the frequency response of the reflection coefficient, magnitude, and phase, at µc1 = 0.36, and µc2 = 0.51 eV. The magnitude of the reflection coefficient reaches − 3.6 dB for µc1 = 0.36 eV and − 2.2 at µc2 = 0.51 eV. It can be clearly observed that the phase of the reflection coefficient is 330o degrees for µc1 = 0.36 eV and exceed 280o degrees for µc2 = 0.51 eV. The results are compared with those calculated by using the HFSS package. Good agreement between the two techniques is shown. In this paper, two distinct sources of incidents are considered: the first one is the plane-wave incidence, while the second is the focused-wave incidence, which involves the utilization of a feeding horn antenna for higher radiated fields.

Fig. 6
figure 6

The reflection coefficient, magnitude, and phase, versus frequency of the proposed graphene unit-cell of the metasurface

Full size image

2.1 Plane-wave incidence

The graphene metasurface is illuminated by a normally x-polarized incident plane wave. The direction of the scattered beam is controlled by adjusting the reflection phase of each element. To generate the vortex beam, a phase shift that resembles a spiral is introduced to the metasurface individual elements as follows:

$$\varnothing \left({x}_{ij},{y}_{ij}\right)=l \phi = l. {tan}^{-1} \left(\frac{{y}_{ij}}{{x}_{ij}}\right)$$
(5)

where \(\phi\) denotes the azimuth angle of the (xij, yij) element and \(l\) is the topological charge (the mode number of the phase singularity). The phase delay for\(l\) =1 is calculated as shown in Fig. 7a. It consists of eight sectors, with a phase step of ± 45o, i.e. the phase variation within a complete circle is 360o. Figure 7b shows the normalized 3D scattering pattern in uv-plane (u = sinϴ cosφ, v = sinϴ sinφ). The center of the beam has a deep null region and is about 12 dB lower than the annular high-intensity region (doughnut like main beam). The scattered pattern in y-z plane is shown in Fig. 7c. To investigate the influence of topological charge \(l\), the normalized scattered patterns at f = 1.2 THz for \(l\) =3 and \(l\) =5 are shown in Figs. 8 and 9. It is obvious that performance deteriorates with the increase in both the phase distributions and the scattered patterns. Mode purity is an important reference for the quality of the OAM, which determines.

the performance of OV in various applications. Low mode purity means frequency spectrum expansion, which increases the difficulty of signal detection in radar applications. In the field of micro-manipulation, high mode purity is more conducive to the use of superposed OVs to achieve static capture of targets (Wang et al. 2022). The calculated mode purity of single beam at different modes components are shown in Fig. 10. The modes are investigated from − 8 to 8 modes with approximately 94% of the radiated power concentrated in the designed modes which are mode 1 in Fig. 10a, mode 3 in Fig. 10b and mode 5 in Fig. 10c.

Fig. 7
figure 7

Normalized scattering patterns at f = 1.2 THz for \(l\) =1. (a). Phase distribution, (b). 3-D pattern, (c). Scattering pattern in the y-z plane

Full size image
Fig. 8
figure 8

Normalized scattering patterns at f = 1.2 THz for \(l\) =3. (a). Phase distribution, (b). 3-D pattern, (c). Scattering pattern in the y-z plane

Full size image
Fig. 9
figure 9

Normalized scattering patterns at f = 1.2 THz for \(l\) =5. (a). Phase distribution, (b). 3-D pattern, (c). Scattering pattern in the y-z plane

Full size image
Fig. 10
figure 10

Mode purity of a single beam for different mode components. (a). \(l\) =1 (b). \(l\) =3 (c). \(l\) =5

Full size image

The scanning performance of array antennas is one of the most crucial characteristics. Figures 11, 12, and 13 depict the phase distribution, 3D normalized scattering patterns and the normalized scattering pattern in y-z plane when the main beam points to θ = 30°, 50°, 70°, respectively, for \(l\) =1. The main lobe still carries OAM when steered to the offset direction. The two peaks of the main lobe (Figs. 11c, 12c, and 13c) become unbalanced when the beam is steered to a certain angle, which is caused by the element pattern in the corresponding direction.

Fig. 11
figure 11

Normalized scattering patterns at f = 1.2 THz after beam steering with a steering angle (30o,90o) for \(l\) =1. (a). Phase distribution, (b). 3-D pattern, (c). Scattering pattern in y-z plane

Full size image
Fig. 12
figure 12

Normalized scattering patterns at f = 1.2 THz after beam steering with a steering angle (50o,90o) for \(l\) =1. (a). Phase distribution, (b). 3-D pattern, (c). Scattering pattern in y-z plane

Full size image
Fig. 13
figure 13

Normalized scattering patterns at f = 1.2 THz after beam steering with a steering angle (70o,90o) for \(l\) =1. (a). Phase distribution, (b). 3-D pattern, (c). Scattering pattern in y-z plane

Full size image

Multiple vortex beams are being examined because they are emitted in various directions from the metasurface. To achieve the generation of two or four vortex beams, the square metasurface is divided into two or four equal regions. This division enables the independent manipulation and control of the modes associated with each of the two or four vortex beams. Vortex beams with different orbital angular momentum modes can be independently generated in each channel by dividing the square metasurface into two or four equivalent sections. As a result, a single metasurface can produce two or four vortex beams, each with unique topological modes and inclination angles. According to the superposition method, Fig. 14 shows the normalized scattering patterns at f = 1.2 THz for 2-beams at (25o, 0o) and (25o, 90o) under an x-polarization normal incident. The phase distribution, 3D normalized scattering pattern and 2D contour pattern are displayed. The beams have a doughnut-shaped magnitude distribution. A Four-beam metasurface is considered in Fig. 15. The beams point at (θ1 = 30o, θ2 = 25o, θ3 = 45o, θ4 = 35o, \({\phi }_{1}={0}^{o}\)\({\phi }_{2}={100}^{o}\),\({\phi }_{3}={200}^{o}\), \({\phi }_{4}={280}^{o}\)) for \(l\) =1.

Fig. 14
figure 14

Normalized scattering patterns at f = 1.2 THz for 2-beams at (25o,0o) and (25o,90o) for \(l\) =1. (a). Phase distribution, (b). 3-D pattern, (c). 2-D contour pattern

Full size image
Fig. 15
figure 15

Normalized scattering patterns at f = 1.2 THz for 4-beams at (30o,0o), (25o,100o), (45o,200o) and(35o,280o) for \(l\) =1. (a). Phase distribution, (b). 3-D pattern, (c). 2-D contour pattern

Full size image

2.2 Focused- wave incidence

In the preceding section, the generation of OAM by a metasurface under the incidence of a plane wave was discussed. However, exciting a plane wave is not a straightforward task. Conversely, the implementation of a focused feed metasurface proves to be more viable in practical applications for higher radiated fields. In this case, the phase distribution of such a focused vortex beam on the metasurface can be expressed as

$${\phi }_{OAM}=l. {tan}^{-1}\left(\frac{{y}_{ij}}{{x}_{ij}}\right)+k\left(\sqrt{{{x}^{2}}_{ij}+{{y}^{2}}_{ij}+{F}^{2}}- \left|F\right|\right)$$
(6)

where F is the focal length. A linearly polarized circular horn is used as the feed as shown in Fig. 16a. It has a radius RH=352 μm, length LH= 640 μm and thickness tH =32 μm. The 3D radiation pattern of the horn at 1.2 THz is shown in Fig. 16b. The horn antenna gain is 16.4 dBi and the 3-dB beamwidth is 25.2odegrees. The focal length-to-diameter ratio F/D for the metasurface is optimized for lowest side lobe level (SLL) and highest gain, where D is the length of the metasurface plate. The F/D = 0.7 is chosen. The 3D radiation pattern at 1.2 THz is depicted in Fig. 17. The peak gain is 18.7 dBi. The vortex beam propagates along the beam axis and spreads along the radius direction. The 3D radiation pattern at 1.2 THz for \(l\) =3 is shown in Fig. 18. The peak gain is 15.6 dBi.

Fig. 16
figure 16

(a). The detailed construction of the feeding horn. (b). The 3-D gain radiation pattern at f = 1.2 THz

Full size image
Fig. 17
figure 17

3-D radiation pattern at f = 1.2THz and \(l\) =1. (a). 3-D pattern, (b). 2-D contour pattern (c). Gain pattern in y-z plane

Full size image
Fig. 18
figure 18

3-D radiation pattern at f = 1.2THz and \(l\) =3. (a). 3-D pattern, (b). 2-D contour pattern (c). Gain pattern in y-z plane

Full size image

3 Conclusion

This paper focuses on studying the radiation characteristics of orbital angular momentum in terahertz band produced by a reflective graphene metasurface. Two types of incidence sources, plane-wave excitation and focused-wave excitation are considered. The conductivity of graphene is varied by changing the chemical potential by adjusting the applied DC biasing voltage. A single vortex beam with different OAM modes can be flexibly obtained in various orientations. The impact of various topological charges on radiation is thoroughly examined. The scanning performance from the graphene metasurface is obtained. Multiple vortex beams are examined. Two/four vortex beams in different directions are demonstrated. They are achieved by dividing the square metasurface into two/four equal regions. A Focused feed metasurface using horn at 1.2 THz is investigated. This multifunctional vortex beam generator has many applications in wireless communication systems, radar, and target detection.