Effect of pore connectivity on reflection amplitudes of an inhomogeneous wave in a composite porous solid saturated by two immiscible fluids

Abstract

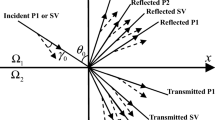
Present paper aims to study the phenomenon of reflection and transmission when an inhomogeneous wave strikes some discontinuity in a composite porous medium saturated by two immiscible viscous fluids. The incident wave splits into six reflected and six transmitted waves at the interface. All reflected and transmitted waves are inhomogeneous in nature with different directions of propagation vector and attenuation vector. A dimensionless parameter $\varsigma \in [0, 1]$ is introduced to represent the extent of connection among the pores at the interface. Expression of Umov–Poynting vector is derived to obtain energy flux vector. Continuity of energy flux vector at the interface gives the required boundary conditions for the system. Connecting parameter $\varsigma$ is also employed in boundary conditions to model the partial connection of pores at the interstices of two media. For numerical discussion we consider a porous medium composed of sandstone and ice, saturated with oil and water. The effect of parameter $\varsigma$ and angle of incidence is determined numerically on the amplitude and the energy ratios of reflected and transmitted waves.

Appendices

Appendix 1

(a) The elements of matrices appearing in equation (2) are given below.

$$\begin{aligned} {[}\sigma {]}= & {} [\sigma ^{s_1}_{xx}~ \sigma ^{s_1}_{yy}~ \sigma ^{s_1}_{zz}~ \sigma ^{s_1}_{xy}~ \sigma ^{s_1}_{xz}~ \sigma ^{s_1}_{yz}\\&\quad \sigma ^{1}~ \sigma ^{2}~ \sigma ^{s_2}_{xx}~ \sigma ^{s_2}_{yy}~\sigma ^{s_2}_{zz}~ \sigma ^{s_2}_{xy}~ \sigma ^{s_2}_{xz}~ \sigma ^{s_2}_{yz}]^T.\\ {[}\epsilon {]}= & {} [\epsilon ^{s_1}_{xx}~ \epsilon ^{s_1}_{yy}~ \epsilon ^{s_1}_{zz}~ \epsilon ^{s_1}_{xy}~ \epsilon ^{s_1}_{xz}\\&\quad \epsilon ^{s_1}_{yz}~ \vartheta _{1}~ \vartheta _{2}~ \epsilon ^{s_2}_{xx}~ \epsilon ^{s_2}_{yy}~ \epsilon ^{s_2}_{zz}~ \epsilon ^{s_2}_{xy}~ \epsilon ^{s_2}_{xz}~ \epsilon ^{s_2}_{yz}]^T. \end{aligned}$$

Non-zero elements of symmetric matrix $[\mathcal {L}]$ are

$$\begin{aligned}&\mathcal {L}_{1, 1}=\mathcal {L}_{2, 2}=\mathcal {L}_{3, 3}= \bar{a}_{11},\\&\mathcal {L}_{1, 2}=\mathcal {L}_{1, 3}=\mathcal {L}_{2, 3}= \breve{a}_{11},\\&\mathcal {L}_{1, 7}=\mathcal {L}_{2, 7}=\mathcal {L}_{3, 7}=a_{12}, ~\\&\mathcal {L}_{1, 8}=\mathcal {L}_{2, 8}=\mathcal {L}_{3, 8}=a_{13},\\&\mathcal {L}_{1, 9}=\mathcal {L}_{2, 9}= \mathcal {L}_{3, 9}=a_{14}, \\&\mathcal {L}_{1, 10}=\mathcal {L}_{2, 10}= \mathcal {L}_{3, 10}=a_{14},\\&\mathcal {L}_{1, 11}=\mathcal {L}_{2, 11}= \mathcal {L}_{3, 11}=a_{14}, \\&\mathcal {L}_{4, 4} =\mathcal {L}_{5, 5}=\mathcal {L}_{6, 6}=G_{s_1}, \\&\mathcal {L}_{7, 7}=a_{22}, \mathcal {L}_{7, 8}=a_{23}, ~\\&\mathcal {L}_{7, 9}=\mathcal {L}_{7, 10}=\mathcal {L}_{7, 11}=a_{24},\\&\mathcal {L}_{8, 8}=a_{33}, \mathcal {L}_{8,9}=~\mathcal {L}_{8, 10}=~\mathcal {L}_{8, 11}=a_{34}, \\&\mathcal {L}_{9, 9}=\mathcal {L}_{10, 10}=\mathcal {L}_{11, 11}= \bar{a}_{44},\\&\mathcal {L}_{9, 10}=\mathcal {L}_{9, 11}=\mathcal {L}_{10, 11}=\breve{a}_{44}, \\&\mathcal {L}_{12, 12}=\mathcal {L}_{13, 13}=\mathcal {L}_{14, 14}=G_{s_2}, \end{aligned}$$

where

$$\begin{aligned}&\vartheta _\mathfrak {{f}}=\nabla \cdot {\varvec{u}_{\mathfrak {f}}}, \breve{a}_{11}=a_{11}-\frac{2}{3}G_{s_1}, \breve{a}_{44}=a_{44}-\frac{2}{3}G_{s_2} ,\\&a_{11}= K_{s_1} S_{s_1}(-\delta _{s_1}+\theta _s),~~ a_{12}= -K_{s_1} S_{s_1}\delta _1,\\&a_{13}= -K_{s_1} S_{s_1}\delta _2,~~ a_{34}= -K_{s_2} S_{s_2}\delta _2, \\&a_{14} =-K_{s_1} S_{s_1}\delta _{s_2}=-K_{s_2} S_{s_2}\delta _{s_1},\\&a_{22}=\displaystyle \frac{-1}{M_1}\Big [M_3\delta _1+\frac{K_1K_2S_1f}{1-S_1}\frac{d S_1}{d p_c}+K_1f S_1\Big ],\\&a_{23}=\displaystyle \frac{-1}{M_1}\Big [\frac{\delta _1 \delta _2M_1(K_{s_1}S_{s_1}+K_{s_2}S_{s_2})}{\delta _{s_1}+\delta _{s_2}}\\&\qquad \quad +K_1K_2f\frac{d S_1}{d p_c}\Big ],\\&a_{24} = -K_{s_2} S_{s_2}\delta _1,\\&a_{33} =\displaystyle \frac{-1}{M_1}\Big [M_4\delta _2+\frac{K_1K_2(1-S_1)f}{S_1}\frac{d S_1}{d p_c}\\&\qquad \quad +K_2(1-S_1)f\Big ],~~\\&a_{44} = K_{s_2} S_{s_2}(-\delta _{s_2}+\theta _s),\\&\delta _1=\frac{M_3}{M_1\left( K_{s_1}S_{s_1}+K_{s_2}S_{s_2}\right) }\left( \delta _{s_1}+\delta _{s_2}\right) ,\\&M_1 =-\left( 1+\displaystyle \frac{K_2}{1-S_1}\frac{dS_1}{dp_c}+\frac{K_1}{S_1}\frac{dS_1}{dp_c}\right) ,\\&\delta _2=\frac{M_4}{M_1\left( K_{s_1}S_{s_1}+K_{s_2}S_{s_2}\right) }\left( \delta _{s_1}+\delta _{s_2}\right) ,\\&M_2 =\displaystyle \frac{K_1 K_2}{f S_1(1-S_1)}\frac{d S_1}{d p_c} +\frac{K_1S_1}{f}+\frac{K_2(1-S_1)}{f},\\&M_3 =\displaystyle \frac{K_1K_2S_1}{1-S_1}\frac{d S_1}{d p_c} +K_1S_1 +K_1K_2\frac{d S_1}{d p_c},\\&M_4=K_1K_2\displaystyle \frac{d S_1}{d p_c}+K_2\left( \frac{K_1}{S_1}\frac{d S_1}{d p_c}+1\right) (1-S_1),\\&\delta _{s_\mathfrak {f}}=K_{s_\mathfrak {f}}\left( \frac{-1}{K_{s_\mathfrak {f}}}{+}\frac{\theta _{s_\mathfrak {f}}}{K'_{s_\mathfrak {f}}}\right) \left[ \mathcal {B}{+}\frac{M_2\Big (1-\frac{{K_{s_\mathfrak {f}}\theta _{s_\mathfrak {f}}}}{{K'_{s_\mathfrak {f}}}}\Big )}{M_1K_{s_\mathfrak {f}}S_{s_\mathfrak {f}}}\right] ^{-1},\\&\mathcal {B}=\Big (\displaystyle \frac{K_{s_1}\theta _{s_1}}{K'_{s_1}}+\displaystyle \frac{K_{s_2}\theta _{s_2}}{K'_{s_2}}\Big )\frac{1}{1-f}\!. \end{aligned}$$

(b) Expressions of coefficients appearing due to inertial and viscous drag

$$\begin{aligned}&A_{11}= S_{s_1}(\rho _1 \theta _1 - q_1 f^2),\\&A_{22}= S_{s_1}(\rho _2 \theta _2 - q_2 f^2),\\&~B_{11} = S_{s_2}(\rho _1 \theta _1 - {q_1}' f^2),\\&B_{22}= S_{s_2}(\rho _2 \theta _2 - {q_2}' f^2),\quad A_{12}= -0.1\sqrt{q_1 {q_2}'},\\&R_{11}=\displaystyle \frac{-\theta _1^2 \eta _1}{\mathbb {K}_s\mathbb {K}_{r1}},~~R_{22}=\displaystyle \frac{-\theta _2^2 \eta _2}{\mathbb {K}_s\mathbb {K}_{r2}},\\&R_{12}=0,~ q_\mathfrak {f} =\displaystyle \frac{\mathfrak {T}_{s_1} \rho _\mathfrak {f} S_\mathfrak {f}}{f},~ {q_\mathfrak {f}}' =\displaystyle \frac{\mathfrak {T}_{s_2} \rho _\mathfrak {f} S_\mathfrak {f}}{f},\\&\mathbb {K}_s= S_{s_1}\mathbb {K}_{s_1}+S_{s_2}\mathbb {K}_{s_2},\\&\mathbb {K}_{r1}(S_2)=(1-S_2)^\eta [1-(S_2)^\frac{1}{\mathfrak {g}}]^{2\mathfrak {g}},\\&\mathbb {K}_{r2}(S_2)=(S_2)^\eta [(1-(1-(S_2)^\frac{1}{\mathfrak {g}}))^\mathfrak {g}]^2,\\&\displaystyle \frac{dp_c}{dS_1}=\frac{1}{\mathfrak {g}\mathfrak {h}\mathfrak {i}}[(1-S_1)^\frac{-\mathfrak {h}}{\mathfrak {h}-1}-1]^\frac{1-\mathfrak {h}}{\mathfrak {h}}(1-S_1)^\frac{-(2\mathfrak {h}-1)}{\mathfrak {h}-1}, \end{aligned}$$

where $K_{\alpha }$ represents bulk modulus of each phase. $\mathbb {K}_{s_1}$ and $\mathbb {K}_{s_2}$ represent permeability of first and second solid, respectively whereas $\eta _\mathfrak {f}$ corresponds to viscosity of fluid phases. The symbols $\mathfrak {T}_{s_1}$, $\mathfrak {T}_{s_2}$ correspond to the tortuosity of the solids, which depends upon porosity. For numerical purpose their values are obtained from the relation $\mathfrak {T}_{s_1}= \mathfrak {T}_{s_2} = \displaystyle \frac{1}{2}\left( 1+({1}/{f})\right)$. The symbols $S_\mathfrak {f}=\displaystyle {\theta _\mathfrak {f}}/{f}$ and $S_{s_\mathfrak {f}}=\displaystyle {\theta _{s_\mathfrak {f}}}/{\theta _s},~~~(\theta _s=\theta _{s_1}+\theta _{s_2})$ correspond to saturation of fluid phases and solid fraction in composite matrix, respectively. Pore space is considered to be completely filled by fluids. Mathematically, this can be written as $S_1+S_2=1$. Dry bulk modulus and shear modulus of each solid is depicted by $K^d_{s_\mathfrak {f}}$, $G_{s_\mathfrak {f}}$. The term $p_c$ signifies the pressure difference between fluid phases. For numerical example we consider $\mathfrak {i}=25\times 10^{-5}$. The symbols $\mathfrak {g}=1-({1}/{\mathfrak {h}})$, $\mathfrak {h}$ and $\mathfrak {i}$ correspond to fitting parameters involved in understanding the soil water content in Van ganuchten model (1980). The values of these independent parameters may be obtained by finding the best fit of soil water retention curve to experimental data. In most of cases the method of least squares is used to find the value of these parameters. The parameter $\eta$ is also a fitting parameter, which is employed to find the relative permeability of wetting and non-wetting fluids as a function of water saturation.

Appendix 2

The expressions of coupling coefficients

$$\begin{aligned}&\kappa _1=\mathrm{Det}[X_4~X_2~X_3],~\kappa _2=\mathrm{Det}[X_1~X_4~X_3],\\&\kappa _3=\mathrm{Det}[X_1~X_4~X_3] ,~\kappa _4=\mathrm{Det}[X_1~X_2~X_3] ,\\&\epsilon _1=\mathrm{Det}[X_8~X_6~X_7] ,~\epsilon _2=\mathrm{Det}[X_5~X_8~X_7],\\&\epsilon _3=\mathrm{Det}[X_5~X_6~X_8] ,~\epsilon _4=\mathrm{Det}[X_5~X_6~X_7], \end{aligned}$$

where Det is employed to symbolize the determinant of a matrix. Also,

$$\begin{aligned}&X_1=[a_{22}{Y} +\eta _{11}~~a_{23}{Y} +\eta _{12}~~a_{24}{Y} +\eta _{01}]^T,\\&X_2=[a_{23}{Y} +\eta _{12}~~a_{33}{Y} +\eta _{23}~~a_{34}{Y} +\eta _{02}]^T,\\&X_3=[a_{24}{Y} +\eta _{01}~~a_{34}{Y} +\eta _{02}~~\bar{a}_{44}{Y} +\eta _{44}]^T,\\&X_4=-[a_{12}{Y} +\eta _{01}~~a_{13}{Y} +\eta _{02}~~a_{14}{Y} +\eta _{03}]^T,\\&X_5=[\eta _{11}~~\eta _{12}~~\eta _{01}]^T,~X_6= [\eta _{12}~~\eta _{23}~~\eta _{02}]^T,\\&X_7=[\eta _{01}~~\eta _{02}~~G_{s_2}{Y}+\eta _{44}]^T,\\&X_8= -[\eta _{01}~~\eta _{02}~~\eta _{03}]^T,\\&\lambda ^\beta _{s_1}=1,~\lambda ^\beta _{1}=\displaystyle \frac{\kappa _1}{\kappa _4},~~\lambda ^\beta _{2}=\displaystyle \frac{\kappa _2}{\kappa _4},~~ \lambda ^\beta _{s_2}=\displaystyle \frac{\kappa _3}{\kappa _4}, {Y}=\displaystyle \frac{-1}{v^2_\beta },\\&\lambda ^l_{s_1}=1,~\lambda ^l_{1}=\displaystyle \frac{\epsilon _1}{\epsilon _4},~~\lambda ^l_{2}=\displaystyle \frac{\epsilon _2}{\epsilon _4},~~ \lambda ^l_{s_2}=\displaystyle \frac{\epsilon _3}{\epsilon _4},~~{Y}=\displaystyle \frac{-1}{v^2_l}. \end{aligned}$$

Appendix 3

The explicit expressions of elements of matrix given in equation (40) are

$$\begin{aligned}&b_{1,\beta }=-\left( J_\beta +(2G_{s_1}+J_\beta ){d_\beta }^2\right) ,~~~\\&b_{1,l}=2 G_{s_1}d_l,~~~b^{\prime }_{1,\beta }=J^{\prime }_\beta + (2G_{s_1}^\prime +{J^{\prime }_\beta }){d^{\prime }_\beta }^2,\\&b^{\prime }_{1,l}=2 G_{s_1}^{\prime }d^{\prime }_l,\\&b_{2,\beta }=-\left( M_\beta +(2G_{s_2}\lambda ^\beta _{s_2}+M_\beta \right) {d_\beta }^2),\\&b_{2,l} =2\lambda ^l_{s_2} G_{s_2}d_l,\\&b^{\prime }_{2,\beta }=M^{\prime }_\beta +(2G_{s_2}^\prime {\lambda ^\beta _{s_2}}^\prime +{M^{\prime }_\beta }){d^{\prime }_\beta }^2,\\&b^\prime _{2,l} =2{\lambda ^l}^\prime _{s_2} G_{s_2}^\prime d^\prime _l,~~~b_{3,\beta }=2G_{s_1}d_\beta ,\\&b_{3,l}=G_{s_1}(-1+d_l^2),~~~b^\prime _{3,\beta }=2G_{s_1}^\prime d^\prime _\beta ,\\&b^\prime _{3,l} =-{G^\prime _{s_1}}(-1+{d^\prime _l}^2),\\&b_{4,\beta }= 2G_{s_2}\lambda ^\beta _{s_2} d_\beta ,~~~b_{4,l}= G_{s_2}(-1+d_l^2)\lambda ^l_{s_2},\\&b^\prime _{4,\beta }=2G_{s_2}^\prime {\lambda ^\beta _{s_2}}^\prime d^\prime _\beta ,\\&b^\prime _{4,l}= -G_{s_2}^\prime (-1+d{^\prime }_l^2){\lambda ^l}^\prime _{s_2},~~~b_{5,\beta }=1,\\&b_{5,l} =d_l,~~~b^\prime _{5,\beta }=-1,~~~b^\prime _{5,l}=d_l^\prime ,\\&b_{6,\beta }=\lambda ^\beta _{s_2} ,~~~ b_{6,l}=\lambda ^l_{s_2} d_l,~~~b^\prime _{6,\beta }=-{\lambda ^\beta _{s_2}}^\prime ,\\&b^\prime _{6,l} ={\lambda _{s_2}^l}^\prime d^\prime _l,~~~b_{7,\beta }=-d_\beta ,\\&b_{7,l}=1,~~~ b^\prime _{7,\beta }=-d^\prime _\beta ,~~~b^\prime _{7,l}=-1,\\&b_{8,\beta } =-{\lambda ^\beta _{s_2}}d_\beta ,~~~b_{8,l}=\lambda ^l_{s_2},\\&b^\prime _{8,\beta }= -{\lambda ^\beta }^\prime _{s_2} d^\prime _\beta ,~~~b^\prime _{8,l}=-{\lambda ^l}^\prime _{s_2},\\&b_{9,\beta } =-\varsigma (\delta _\beta -\xi _\beta \theta _1+d_\beta ^2\{\delta _\beta -(H_\beta +\xi _\beta )\theta _1\}),\\&b_{9,l}=-\varsigma d_l S_l \theta _1,\\&b^\prime _{9,\beta }=(1-\varsigma )d^\prime _\beta T_1 ({\lambda ^\beta _{1}}^\prime -\theta ^\prime _{s_1}-{\lambda ^\beta _{s_2}}^\prime \theta ^\prime _{s_2})\Upsilon ,\\&b^\prime _{9,l} ={(1-\varsigma )T_1 ({\lambda ^l}^\prime _{1}-\theta ^\prime _{s_1}-{\lambda ^l}^\prime _{s_2} \theta ^\prime _{s_2})\Upsilon },\\&b_{10,\beta }=-(1-\varsigma )T_1(\lambda ^\beta _{1}-\theta _{s_1}-\lambda ^\beta _{s_2}\theta _{s_2})\Upsilon ,\\&b_{10,l} =(1-\varsigma )T_1(\lambda ^l_{1}-\theta _{s_1}-\lambda ^l_{s_2}\theta _{s_2})\Upsilon ,\\&b^\prime _{10,\beta }= -\varsigma \left( \delta ^\prime _\beta -\xi ^\prime _\beta \theta ^\prime _1+{d^\prime _\beta }^2\Big \{\delta ^\prime _\beta -(H^\prime _\beta +\xi ^\prime _\beta )\theta ^\prime _1\Big \}\right) ,\\&b^\prime _{10,l} =\varsigma d^\prime _l S^\prime _l \theta ^\prime _1,~~~b_{11,l}=-\varsigma d_lS_l\theta _2,\\&b_{11,\beta }=-\varsigma \left( \zeta _\beta -\xi _\beta \theta _2+d_\beta ^2\{\zeta _\beta -(H_\beta +\xi _\beta )\theta _2\}\right) ,~~~\\&b^\prime _{11,\beta }=(1-\varsigma )d^\prime _\beta T_2 ({\lambda ^\beta _{2}}^\prime -\theta ^\prime _{s_1}-{\lambda ^\beta _{s_2}}^\prime \theta ^\prime _{s_2})\Upsilon ,\\&b^\prime _{11,l}={(1-\varsigma )T_2 ({\lambda ^l}^\prime _{2}-\theta ^\prime _{s_1}-{\lambda ^l}^\prime _{s_2} \theta ^\prime _{s_2})\Upsilon },\\&b_{12,\beta }=-(1-\varsigma )T_2 (\lambda ^\beta _{2}-\theta _{s_1}-\lambda ^\beta _{s_2}\theta _{s_2})\Upsilon ,\\&b_{12,l}= (1-\varsigma )T_2(\lambda ^l_{2}-\theta _{s_1}-\lambda ^l_{s_2}\theta _{s_2})\Upsilon ,\\&b^\prime _{12,\beta } =-\varsigma \left( \zeta ^\prime _\beta -\xi ^\prime _\beta \theta ^\prime _2+{d^\prime _\beta }^2 \{\zeta ^\prime _\beta -(H^\prime _\beta +\xi ^\prime _\beta )\theta ^\prime _2\}\right) ,\\&b^\prime _{12,l}= \varsigma d^\prime _l S^\prime _l\theta ^\prime _2, \end{aligned}$$

Elements of matrix $\mathcal C$ if P waves are incident.

$$\begin{aligned}&c_{1,1}=-b_{1,\beta },~~~c_{2,1}=-b_{2,\beta },~~~c_{3,1}=b_{3,\beta },\\&c_{4,1}=b_{4,\beta },~~~c_{5,1}=-b_{5,\beta },~~~c_{6,1}=-b_{6,\beta },\\&c_{7,1}=b_{7,\beta },~~c_{8,1}=b_{8,\beta },~~~c_{9,1}= -b_{9,\beta },\\&c_{10,1}=b_{10,\beta },~~~c_{11,1}= -b_{11,\beta },~~c_{12,1}=b_{12,\beta }. \end{aligned}$$

Also,

$J_\beta =(a_{11}-\frac{2}{3}G_{s_1}+a_{12}\lambda ^\beta _1+a_{13}\lambda ^\beta _2+a_{14}\lambda ^\beta _{s_2})$, $M_\beta =a_{14}+a_{24}\lambda ^\beta _1+a_{34}\lambda ^\beta _2+(a_{44}-\frac{2}{3}G_{s_2})\lambda ^\beta _{s_2}$,

$$\begin{aligned}&\delta _\beta =a_{12}+\lambda ^\beta _1a_{22}+\lambda ^\beta _2 a_{23}+\lambda ^\beta _{s_2} a_{24},\\&\zeta _\beta =a_{13}+\lambda ^\beta _1 a_{23}+\lambda ^\beta _2 a_{33}+\lambda ^\beta _{s_2} a_{34},\\&J=a_{11}-\frac{2}{3}G_{s_1}+a_{12}+a_{13}+a_{14},\\&K_1 =a_{12}+a_{22}+a_{23}+a_{24},\\&L_1=a_{13}+a_{23}+a_{33}+a_{34},\\&N_1 =a_{14}+a_{24}+a_{34}+(a_{44}-\frac{2}{3}G_{s_2}),\\&\xi _\beta =J+K_1 \lambda ^\beta _1+L_1\lambda ^\beta _2+N_1 \lambda ^\beta _{s_2},\\&H_\beta =2G_{s_1}+2G_{s_2}\lambda ^\beta _{s_2},\\&S_l =2G_{s_1}+2G_{s_2}\lambda ^l_{s_2},\\&d_m=s_{mz}/s,~~~\Upsilon =\omega /s, \end{aligned}$$

where $s_{mz}$ corresponds to vertical slowness of all propagating waves.