Abstract
We study first-order symmetrizable hyperbolic \(N\times N\) systems in a spacetime cylinder whose lateral boundary is totally characteristic. In local coordinates near the boundary at \(x=0\), these systems take the form
where \({{\mathcal {A}}}(t,x,y,xD_x,D_y)\) is a first-order differential operator with coefficients smooth up to \(x=0\) and the derivative with respect to x appears in the combination \(xD_x\). No boundary conditions are required in such a situation and corresponding initial-boundary value problems are effectively Cauchy problems. We introduce a certain scale of Sobolev spaces with asymptotics and show that the Cauchy problem for the operator \(\partial _t + {{\mathcal {A}}}(t,x,y,xD_x,D_y)\) is well-posed in that scale. More specifically, solutions u exhibit formal asymptotic expansions of the form
where \((p,k)\in {{\mathbb {C}}}\times {{\mathbb {N}}}_0\) and \(\Re p\rightarrow -\infty \) as \(|p|\rightarrow \infty \), provided that the right-hand side f and the initial data \(u|_{t=0}\) admit asymptotic expansions as \(x \rightarrow +0\) of a similar form, with the singular exponents p and their multiplicities unchanged. In fact, the coefficients \(u_{pk}\) are, in general, not regular enough to write the terms appearing in the asymptotic expansions as tensor products. This circumstance requires an additional analysis of the function spaces. In addition, we demonstrate that the coefficients \(u_{pk}\) solve certain explicitly known first-order symmetrizable hyperbolic systems in the lateral boundary. Especially, it follows that the Cauchy problem for the operator \(\partial _t+{{\mathcal {A}}}(t,x,y,xD_x,D_y)\) is well-posed in the scale of standard Sobolev spaces \(H^s((0,T)\times {{\mathbb {R}}}_+^{1+d})\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Due to their importance in the physical and engineering sciences, the investigation of hyperbolic initial-boundary problems has a long-standing history. Depending on the hyperbolic differential operators under study, the main questions concern the correct number and kind of boundary conditions to be imposed and well-posedness of the resulting initial-boundary problems in suitable scales of function spaces. See Benzoni-Gavage and Serre [1] for a recent account. In case of a non-characteristic boundary, it is known that the weak Lopatinskii condition is necessary for well-posedness, while the uniform Lopatinskii condition has been shown by Lopatinskii [13], Kreiss [10], and Sakamoto [20] to be necessary and sufficient in order to obtain the strongest possible regularity results, comparable to those one has for the pure Cauchy problem. See also Chazarain and Piriou [3]. The understanding of the characteristic case is considerably less complete. There are many works contributing to the uniformly characteristic case, especially for first-order systems when the differential operators under study are symmetric hyperbolic, see e.g. Majda and Osher [14], Ohkubo [17], Rauch [18], or Secchi [24]. In these results, one often has more regularity in directions tangent to the boundary than in directions transverse to it. By contrast, for a totally characteristic boundary, one has the same regularity in all directions, as observed already by Sakamoto [21].
This observation was our point of departure. We investigate symmetrizable hyperbolic first-order differential systems in space-time cylinders \((0,T)\times \Omega \), where \(\Omega \subseteq {{\mathbb {R}}}^n\) is a \({{\mathscr {C}}}^\infty \) domain (or, more general, \({\overline{\Omega }}\) is a \({{\mathscr {C}}}^\infty \) manifold with non-empty boundary) and where the lateral boundary \((0,T)\times \partial \Omega \) is totally characteristic. The main technical innovation is to regard the differential operators under study as cone-degenerate with respect to the spatial variables, which in turn is possible due to the totally characteristic boundary. As a consequence, using a suitable calculus for cone-degenerate pseudodifferential operators (detailed below), we construct symmetrizers for the systems under consideration and, as a result of the symmetrization process, are able to establish well-posedness in so-called Sobolev spaces \(H_{P,\theta }^{s,\delta }({\overline{\Omega }})\) with asymptotics (also detailed below). Here, the asymptotics alluded to are discrete conormal asymptotics, given by an asymptotic type P. Special cases include the standard Sobolev spaces \(H^s(\Omega )\) and \(H_0^s({\overline{\Omega }})\). Another relevant case is when the function spaces carry no asymptotic information at all, i.e., when \(\theta =0\). Then the asymptotic type P is redundant and \(H_{P,0}^{s,\delta }({\overline{\Omega }}) = {{\mathscr {K}}}^{s,\delta }(\Omega )\) is a weighted Sobolev space.
It turns out that in the situation considered no boundary conditions are required. One main contribution of this paper is the revelation that the boundary traces of the solutions themselves satisfy hyperbolic differential equations in the lateral boundary \((0,T)\times \partial \Omega \). In particular, these boundary traces can be determined ahead of determining the solutions.
There is a long-running program of investigating conormal asymptotic expansions of solutions to elliptic partial differential equations as an integral part of the structure, initiated by different people, see e.g. Melrose [15] or Rempel and Schulze [19]. Recently, there have been attempts to extend this program to include hyperbolic partial differential equations, see e.g. Hintz and Vasy [6]. This paper can also be seen as a contribution in this direction.
1.1 Formulation of the problem and main results
In this paper, we investigate well-posedness of the Cauchy problem for first-order hyperbolic systems with totally characteristic boundary. More specifically, we consider the Cauchy problem for \(N\times N\) systems
where \({{\mathcal {A}}}\in {{\mathscr {C}}}^\infty ([0,T];{\text {Diff}}^1({\overline{\Omega }}; {{\mathbb {C}}}^N))\), \({\overline{\Omega }}\) is \({{\mathscr {C}}}^\infty \) manifold with non-empty boundary \(\partial \Omega \), and \(\Omega ={\overline{\Omega }}{\setminus }\partial \Omega \). Our standing assumptions are that the differential operator

and that the lateral boundary

The latter condition means that \(\sigma _\psi ^1({{\mathcal {A}}})(t,\varpi ,\nu (\varpi ))=0\) for \((t,\varpi )\in [0,T]\times \partial \Omega \), where \(\sigma _\psi ^1({{\mathcal {A}}})\) is the principal symbol of \({{\mathcal {A}}}\) and \(\nu (\varpi ) \in T_\varpi ^* {\overline{\Omega }}\) is conormal with respect to the boundary \(\partial \Omega \) (i.e., \(\nu (\varpi )\bigr |_{T_\varpi (\partial \Omega )}=0\)). A first observation is that the characteristic curves of \({{\mathscr {L}}}\) stay inside the lateral boundary when they started out there. In particular, they are tangent to the boundary. Consequently, no boundary conditions are required in order to solve Eq. (1.1). Besides, there is no need for a Lopatinskii condition or an replacement of it in one or the other form.
1.1.1 The result for standard Sobolev spaces
We begin with describing the result for the standard Sobolev spaces \(H^s(\Omega )\), where \(\Omega \subseteq {{\mathbb {R}}}^n\) is a \({{\mathscr {C}}}^\infty \) domain and \(s\ge 0\). This case deserves special attention for two reasons: firstly, the proof here is considerably simpler than in the general case, secondly, it helps to develop some additional intuition for the problems studied later.
Theorem 1.1
Suppose that the differential operator \(\partial _t+{{\mathcal {A}}}\) in Eq. (1.1) has coefficients in \({{\mathscr {C}}}_b^\infty ([0,T]\times {\overline{\Omega }}; {\text {Mat}}_{N\times N}({{\mathbb {C}}}))\) and that it is symmetrizable hyperbolic uniformly in \((t,\varpi )\in [0,T]\times {\overline{\Omega }}\). Let \(u_0\in H^{s+\sigma }(\Omega ;{{\mathbb {C}}}^N)\) and \(f\in \bigcap _{r=0}^\sigma W^{r,1}((0,T);\) \(H^{s-r+\sigma }(\Omega ;{{\mathbb {C}}}^N))\) for some \(s\ge 0\), \(\sigma \in {{\mathbb {N}}}_0\). Then Eq. (1.1) possesses a unique solution
In addition, the boundary traces
for \(\ell \in {{\mathbb {N}}}_0\), \(\ell <s+\sigma -1/2\) (defined by extending \(\nu \) to a \({{\mathscr {C}}}^\infty \) vector field in a neighborhood of \(\partial \Omega \)) are uniquely determined as solutions to certain hyperbolic Cauchy problems in \((0,T)\times \partial \Omega \).
See (1.5), (2.1) for the explicit form of the hyperbolic Cauchy problems in \((0,T)\times \partial \Omega \) governing the boundary traces \(\gamma _\ell u\). Especially, when \(\gamma _\ell u_0=0\) and \(\gamma _\ell f=0\) for \(\ell \in {{\mathbb {N}}}_0\), \(\ell <s+\sigma -1/2\), then it follows that \(\gamma _\ell u=0\) for all those \(\ell \). Consequently, Theorem 1.1 remains valid when the Sobolev spaces \(H^s(\Omega )\), where \(s\ge 0\), are replaced with \(H_0^s({\overline{\Omega }})\).
Remark
The latter observation is actually one of the guiding principles in what follows. Start with the standard Sobolev spaces \(H^s(\Omega )\), remove the asymptotic terms arising from a Taylor series expansion at the boundary \(\partial \Omega \) to arrive at the spaces \(H_0^s({\overline{\Omega }})\), then adjust the reference conormal order from 0 to \(\delta \) (see, e.g., Lemma 3.10) and affix asymptotic terms once again, now possibly of a different asymptotic type P. This yields the function spaces \(H_{P,\theta }^{s,\delta }({\overline{\Omega }})\) in which well-posedness for Eq. (1.1) will be shown to hold as well.
Remark
The regularity of the boundary traces \(\gamma _\ell u\) results from the trace theorems for the standard Sobolev spaces. It is a half an order less than what is obtained in case of a non-characteristic boundary when the uniform Lopatinskii condition hold and the usual compatibility conditions between initial and boundary data are satisfied.
1.1.2 The local problem
Most of the effort in this paper is put into the local situation, where \({\overline{\Omega }}={\overline{{{\mathbb {R}}}}}_+^{\,n}\) is a closed half-space. We state the result in this situation next.
We assume that the coefficients of the differential operator \({{\mathcal {A}}}\) belong to \({{\mathscr {C}}}_b^\infty ([0,T]\times \overline{{{\mathbb {R}}}}_+^{\,n};\) \({\text {Mat}}_{N\times N}({{\mathbb {C}}}))\). We further set \(n=1+d\) and write the spatial coordinates as \((x,y)\in {\overline{{{\mathbb {R}}}}}_+\times {{\mathbb {R}}}^d\). Then the Cauchy problem to be investigated becomes
where \((t,x,y)\in (0,T)\times {{\mathbb {R}}}_+^{1+d}\). Here, \(\partial _j=\partial /\partial y_j\), \(xA,A_j,B\in {{\mathscr {C}}}_b^\infty ([0,T]\times {\overline{{{\mathbb {R}}}}}_+^{1+d};{\text {Mat}}_{N\times N}({{\mathbb {C}}}))\), and A is \({{\mathscr {C}}}^\infty \) up to \(x=0\). Further, we assume that the linear differential operator \({{\mathscr {L}}}=\partial _t + xA\partial _x + \sum _{j=1}^d A_j\partial _j +B\) is symmetrizable hyperbolic uniformly in \((t,x,y)\in [0,T]\times {\overline{{{\mathbb {R}}}}}_+^{1+d}\).
Having concrete applications in mind, apart from asymptotics resulting from a Taylor series expansion at \(x=0\) as in Theorem 1.1,
we consider more general asymptotics of the form
where \((p,k) \in {{\mathbb {C}}}\times {{\mathbb {N}}}_0\) with \(\Re p\rightarrow -\infty \) as \(|p|\rightarrow \infty \). (The precise conditions are stated in Definition 3.1.) Such asymptotics arise in many applications, both linear and nonlinear. The choice of the exponent \(-p\) (in place of p) and the appearance of the factor \((-1)^k/k!\) is related to the normalization of the Mellin transform (see “Appendix A.1”) and simplifies certain formulas later on, especially (1.8), (1.10). We shall denote the uniquely determined coefficients \(u_{pk}\) in those asymptotic expansions by \(\gamma _{pk}u\) and regard these coefficients as boundary traces as before.
Incorporating the asymptotic information provided by (1.4) into function spaces \(H_{P,\theta }^{s,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d})\) (neglecting the dependence on t at this point, see Sect. 3.2.3), the main result of this paper is as follows:
Theorem 1.2
Let \(s\in {{\mathbb {R}}}\), \(\sigma \in {{\mathbb {N}}}_0\), \(P\in \underline{As }^\delta \), and \(\theta _0\ge \dotsc \ge \theta _\sigma \ge 0\). Under the assumptions stated above, given \(u_0\in H_{P,\theta _0}^{s+\sigma ,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {C}}}^N)\) and \(f\in \bigcap _{r=0}^\sigma W^{r,1}((0,T);\) \(H_{P,\theta _r}^{s-r+\sigma ,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {C}}}^N))\), Eq.(1.1) possesses a unique solution
In addition, for all \((p,k)\in P\) with \(\Re p>1/2-\delta -\theta _0\), \(\gamma _{pk}u\) solves the Cauchy problem
where the expression \(R_{pk}[u]\) appearing in the right-hand side of (1.5) stands for a term that depends linearly on \(\gamma _{ql}u\) for \(q - p\in {{\mathbb {N}}}_0\) and \(l>k\) if \(q=p\).
Notice that Eq. (1.5) is a hyperbolic Cauchy problem for \(\gamma _{pk}u\) in \((0,T)\times {{\mathbb {R}}}^d\). It follows that the coefficients \(\gamma _{pk}u\) in the asymptotic expansion (1.4) can be successively computed and are uniquely determined by the corresponding coefficients of the initial data \(u_0\) and the right-hand side f.
Remark
Theorem 1.1 is a special case of Theorem 1.2 when \(\Omega ={{\mathbb {R}}}_+^{1+d}\). Here, \(s\ge 0\), \(\delta =0\), \(P=P_0\), and \(\theta _r=s-r+\sigma \) for \(0\le r\le \sigma \) (see the example after Definition 3.1).
Remark
Strictly speaking, we only deal with constant discrete asymptotics. It is likely that similar results also hold for continuous asymptotics as well as for variable discrete asymptotics (see, e.g., [5, 9, 19] for elliptic problems).
1.1.3 Further results
The situation described in Sect. 1.1.2 is invariant under coordinate changes for manifolds with boundary. A proof will appear in [11]. Hence, one also has the function spaces \(H_{P,\theta ,{\text {loc}}}^{s,\delta }({\overline{\Omega }})\) when \({\overline{\Omega }}\) is a \({{\mathscr {C}}}^\infty \) manifold with boundary. In local coordinates, elements of \(H_{P,\theta ,{\text {loc}}}^{s,\delta }({\overline{\Omega }})\) belong (locally) either to \(H^s({{\mathbb {R}}}^n)\) for inner charts or to \(H_{P,\theta }^{s,\delta }({\overline{{{\mathbb {R}}}}}_+^n)\) for boundary charts.
Theorem 1.3
Let \(s\ge 0\), \(\sigma \in {{\mathbb {N}}}_0\), \(P\in \underline{As }^\delta \), and \(\theta _0\ge \dotsc \ge \theta _\sigma \ge 0\). Furthermore, let \(u_0\in H_{P,\theta _0,{\text {loc}}}^{s+\sigma ,\delta }({\overline{\Omega }};{{\mathbb {C}}}^n)\) and \(f\in \bigcap _{r=0}^\sigma W^{r,1}((0,T);H_{P,\theta _r,{\text {loc}}}^{s-r+\sigma ,\delta }({\overline{\Omega }};{{\mathbb {C}}}^n))\). Then Eq. (1.1) possesses a unique solution
Moreover, the boundary traces \(\gamma _{pk}u\) for \((p,k)\in P\) with \(\Re p>1/2-\delta -\theta _0\) can be successively computed as before by solving hyperbolic Cauchy problems in the lateral boundary \((0,T)\times \partial \Omega \).
1.2 Outline of the argument
In the sequel, we fix a \(\delta \in {{\mathbb {R}}}\) as reference conormal order. The weighted \(L^2\) space \({{\mathscr {K}}}^{0,\delta }({{\mathbb {R}}}_+^{1+d})\) (see Definition 3.4) will be our basic Hilbert space, replacing the space \(L^2({{\mathbb {R}}}_+^{1+d})={{\mathscr {K}}}^{0,0}({{\mathbb {R}}}_+^{1+d})\). Denote by \(\Vert \;\Vert \) the norm and by \(\langle ,\,\rangle \) the inner product in \({{\mathscr {K}}}^{0,\delta }({{\mathbb {R}}}_+^{1+d})\).
One basic problem is to define the asymptotic terms appearing in asymptotic expansions like
appropriately (see (1.4)). The asymptotic expansion (1.6) is with respect to an increasing flatness as \(x\rightarrow +0\), where the term \((-1)^k/k!\,x^{-p}\log ^k\!x\, v_{pk}(y)\) has conormal order \(1/2-\Re p-0\). For \(v\in H_{P,\theta }^{s,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d})\), this asymptotic expansion breaks off at conormal order \(\delta +\theta \) so that effectively only finitely many terms in the right-hand side of (1.6) have to be taken into account. Nonetheless, as \(v\in H_{P,\theta }^{s,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d})\) implies that both \(\Re p<1/2-\delta \) and \(v_{pk} \in H^{s+\Re p+\delta -1/2,\langle k\rangle }({{\mathbb {R}}}^d)\), as a rule we have that \((-1)^k/k!\,x^{-p}\log ^k\!x\, v_{pk}(y)\notin H_{P,\theta }^{s,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d})\) near \(x=0\). The correct form of the asymptotic term is given by \(\Gamma _{pk}v_{pk}\), where
and \(\varphi \) is a cut-off function. (See Sect. 1.4 for the notation used.) Especially, \(\Gamma _{pk}w\in {{\mathscr {C}}}^\infty ({{\mathbb {R}}}_+^{1+d})\) for \(w\in {{\mathscr {S}}}'({{\mathbb {R}}}^d)\), \(\Gamma _{pk}w\bigr |_{x=0} = w\), and \(\Gamma _{pk}w\) is supported for \(x\lesssim 1\). The decisive property which makes the approach work, however, is
provided that \(w\in H^{s,\langle k\rangle }({{\mathbb {R}}}^d)\) (see Lemma 3.6).
We construct a calculus \(\Psi _{\text {c}}^\infty ({\overline{{{\mathbb {R}}}}}_+^{1+d}) = \bigcup _{\mu \in {{\mathbb {R}}}} \Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\) of cone-degenerate pseudodifferential operators on the half-space \({{\mathbb {R}}}_+^{1+d}\), where \(\Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\subset \Psi _{\text {cl}}^\mu ({{\mathbb {R}}}_+^{1+d})\) and the pseudodifferential operators contained exhibit a prearranged behavior as \(x\rightarrow +0\). The basic idea is taken from Schulze [22, 23]. In particular, near \(x=0\), the operators \(A\in \Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\) are to the leading order of the form
where \(h(z) = h(y,z,D_y)\) is an entire family of pseudodifferential operators in \(\Psi _{\text {cl}}^\mu ({{\mathbb {R}}}^d)\) subject to further conditions, \({\text {op}}_M(h) = M_{z\rightarrow x}^{-1} h(z) M\) with M being the Mellin transform, and \(\varphi ,\varphi _0\) are cut-off functions. Compared to the cone calculus of Schulze, where the coefficients \(v_{pk}\) would be in \({{\mathscr {S}}}({{\mathbb {R}}}^d)\) in the situation considered here, we now had to show that operators \(A\in \Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\) act in an appropriate way on the asymptotic terms given by (1.7). Indeed, it holds that
provided that \(w\in H^{s,\langle k\rangle }({{\mathbb {R}}}^d)\).
The operator \({{\mathcal {A}}}(t,x,y,xD_x,D_y)\) from Eq. (1.2) belongs to \({{\mathscr {C}}}^\infty ([0,T];\Psi _{\text {c}}^1({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {C}}}^N))\). Furthermore, a symbolic symmetrizer for the hyperbolic operator \({{\mathscr {L}}}= \partial _t + {{\mathcal {A}}}(t,x,y,xD_x,D_y)\) is indeed a symmetrizer \(b(t,x,y,{\tilde{\xi }},\eta )\) for the compressed principal symbol \({\tilde{\sigma }}_\psi ^1({{\mathcal {A}}})(t,x,y,{\tilde{\xi }},\eta )\) of \({{\mathcal {A}}}\). Using Gårding’s inequality in a routine way yields an operator \({{\mathcal {B}}}\in {{\mathscr {C}}}^\infty ([0,T];\Psi _{\text {c}}^0({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {C}}}^N))\) with \({\tilde{\sigma }}_\psi ^0({{\mathcal {B}}})=b\) such that
-
\({{\mathcal {B}}}= {{\mathcal {B}}}^*\ge cI \) for some \(c>0\),
-
\(\Re ({{\mathcal {B}}}{{\mathcal {A}}}) \in {{\mathscr {C}}}^\infty ([0,T];\Psi _{\text {c}}^0({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {C}}}^N))\), i.e., \(\Re {\tilde{\sigma }}_\psi ^1({{\mathcal {B}}}{{\mathcal {A}}})=0\).
Together with the fact that integration by parts produces no boundary terms, i.e.,
-
\(\left\langle {{\mathcal {B}}}{{\mathcal {A}}}u,v\right\rangle = \left\langle u,({{\mathcal {B}}}{{\mathcal {A}}})^*v\right\rangle \) holds for \(u,v\in {{\mathscr {C}}}([0,T];{{\mathscr {K}}}^{1,\delta }({{\mathbb {R}}}_+^{1+d}))\),
one produces, for \(u\in {{\mathscr {C}}}^0([0,T];{{\mathscr {K}}}^{1,\delta }({{\mathbb {R}}}_+^{1+d})) \cap {{\mathscr {C}}}^1([0,T];{{\mathscr {K}}}^{0,\delta }({{\mathbb {R}}}_+^{1+d}))\), the basic energy inequality
in a standard manner. Once the calculus of cone-degenerate pseudodifferential operators mentioned above is established, this essentially means that one can treat the Cauchy problem (1.2) in \((0,T)\times {{\mathbb {R}}}_+^{1+d}\) like a Cauchy problem in free space \((0,T)\times {{\mathbb {R}}}^{1+d}\).
From estimate (1.9), one obtains well-posedness of Eq. (1.2) in the basic Hilbert space \({{\mathscr {K}}}^{0,\delta }({{\mathbb {R}}}_+^{1+d})\), i.e., the first part of Theorem 1.2 for \(s=0\), \(\sigma =0\), and \(\theta _0=0\). Well-posedness in the weighted Sobolev spaces \({{\mathscr {K}}}^{s,\delta }({{\mathbb {R}}}_+^{1+d})\), i.e., the first part of Theorem 1.2 in all other cases with \(\theta _0=0\), then likewise follows using order reductions that exist in the pseudodifferential calculus considered.
To establish the well-posedness results in the Sobolev spaces \(H_{P,\theta }^{s,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d})\) with asymptotics is a considerably more involved task. The crucial observation is that the boundary traces \(\gamma _{pk}u\) solve hyperbolic Cauchy problems in the lateral boundary. To see this, one needs to know that, besides the compressed principal symbol \({\tilde{\sigma }}_\psi ^\mu (A)\), operators \(A\in \Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\) possess also a sequence \(\left( \sigma _{\text {c}}^{-j}(A)\right) _{j\in {{\mathbb {N}}}_0}\) of so-called conormal symbols. Like the function \(h(z)=h(y,z,D_y)\) above, these are entire functions of \(z\in {{\mathbb {C}}}\) taking values in \(\Psi _{\text {cl}}^\mu ({{\mathbb {R}}}^d)\), and they determine the manner in which asymptotics are mapped by A. More precisely, it holds that
where the finite sum in the right-hand side is over those \((j,\ell ,r)\) such that \(\Re p+j<1/2-\delta \). Thus, applying \(\gamma _{pk}\) to both sides of the equation in (1.1) results in an equation for \(\gamma _{pk}u\),
where the term \(R_{pk}[u]\) has a similar meaning as in (1.5). In fact, a compatibility condition between \(\sigma _\psi ^1(\sigma _{\text {c}}^0({{\mathcal {A}}}(t)))\) and \(\tilde{\sigma }_\psi ^1({{\mathcal {A}}}(t))\) ensures that the operator \(\partial _t +\sigma _{\text {c}}^0({{\mathcal {A}}}(t))\) is symmetrizable hyperbolic.
Hence, one obtains existence, uniqueness, and higher regularity for the boundary traces \(\gamma _{pk}\) in the correct regularity classes. Subtracting the boundary terms from the prospective solution u, one ends up in weighted Sobolev spaces \({{\mathscr {K}}}^{s-\theta _0,\delta +\theta _0}({{\mathbb {R}}}_+^{1+d})\), in which well-posedness has been shown before. Note that at this place it is crucial that the cone-degenerate pseudodifferential operators in \(\Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\) have holomorphic conormal symbols (as opposed to finitely meromorphic ones, one usually sees in a cone pseudodifferential calculus), which implies that the action of \(A\in \Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\) on \({{\mathscr {K}}}^{s,\gamma }({{\mathbb {R}}}_+^{1+d})\) is the same for any conormal order \(\gamma \in {{\mathbb {R}}}\) (in the sense that it agrees on \({{\mathscr {K}}}^{s,\gamma }({{\mathbb {R}}}_+^{1+d})\cap {{\mathscr {K}}}^{s+\mu ,\gamma '}({{\mathbb {R}}}_+^{1+d})\) independently of whether this intersection is seen as a subspace of \({{\mathscr {K}}}^{s,\gamma }({{\mathbb {R}}}_+^{1+d})\) or \({{\mathscr {K}}}^{s,\gamma '}({{\mathbb {R}}}_+^{1+d})\)). Hence, the argument provided for well-posedness in function spaces with conormal order \(\delta \) works for any other conormal order just the same.
1.3 Comparison with other results and open problems
One of the big open problems in the field is to provide satisfactory answers concerning well-posedness for hyperbolic boundary problems with a uniformly characteristic boundary. There only exist several partial results in the literature, see e.g. [1, 2, 14, 18, 24].
Totally characteristic hyperbolic boundary problems (for higher-order scalar equations) were treated by Sakamoto [21]. She obtained results comparable to ours by showing (in our own notation) well-posedness in the scales \(H_{P,\theta }^{s,\delta }({\overline{\Omega }})\), where \(P= T^\delta P_0\), with \(P_0\) being the type for Taylor asymptotics, and \(\theta =s\ge 0\). Our results are slightly more general in that respect that we now allow general asymptotic types P, general weight intervals given by \(\theta \ge 0\), and also negative Sobolev orders s. In addition, we show that the boundary traces are given as solutions to hyperbolic Cauchy problems in the lateral boundary. This later result appears to be new.
Sakamoto [21] used pseudodifferential techniques to establish her results, albeit in a different manner. Our approach might have the advantage that it yields a symmetrizer also in the uniformly characteristic case, upon further developing an adapted pseudodifferential calculus. It seems to be evident that this calculus has to be some sort of an edge calculus, as in Schulze [23]. On the level handled in this paper the difference between an edge calculus and a cone calculus is rather marginal: In the latter one first performs the Fourier transform \({\mathcal {F}}_{y\rightarrow \eta }\) with respect to the y-variables and then the Mellin transform \(M_{x\rightarrow z}\) with respect to the x-variable, while in the former these transforms are performed in the opposite order. As both operations commute, \(M_{x\rightarrow z} \mathcal F_{y\rightarrow \eta } = {\mathcal {F}}_{y\rightarrow \eta } M_{x\rightarrow z}\), it is possible to recast the cone calculus utilized here in the form of an edge calculus, up to some technical details. Note that the form of the asymptotic terms as given in (1.7) is already typical of edge problems.
1.4 Notation
We shall use freely standard notation from microlocal analysis (see [7]). For singular analysis, we closely follow the notation used in [23].
Throughout the paper, we shall especially employ the following notation:
-
\(\delta \in {{\mathbb {R}}}\) denotes the reference conormal order, which is fixed once and for all.
-
For the Mellin covariable \(z\in {{\mathbb {C}}}\), we write \(z=\beta +i \tau \) with \(\beta ,\,\tau \in {{\mathbb {R}}}\).
-
For \(\beta \in {{\mathbb {R}}}\), we introduce the weight line \(\Gamma _\beta =\{z\in {{\mathbb {C}}}\mid \Re z=\beta \}\). The weight line that corresponds to the reference conormal order \(\delta \) is \(\Gamma _{1/2-\delta }\).
-
\(\varphi \in {{\mathscr {C}}}^\infty ({\overline{{{\mathbb {R}}}}}_+;{{\mathbb {R}}})\) is a cutoff function, i.e., \(0\le \varphi \le 1\), \(\varphi (x)= 1\) for \(|x|\lesssim 1\), and \(\varphi (x)=0\) for \(|x|\gtrsim 1\). Likewise, \(\varphi _0,\varphi _1\) are also cutoff functions satisfying, in addition, \(\varphi \varphi _0=\varphi \) and \(\varphi \varphi _1=\varphi _1\) (i.e., \((1-\varphi )(1-\varphi _1)=1-\varphi \)).
-
\(\psi \in {{\mathscr {C}}}^\infty (\overline{{{\mathbb {R}}}}_+;{{\mathbb {R}}})\) denotes a non-decreasing function such that \(\psi (x) = x\) for \(0\le x\le 1/2\) and \(\psi (x)=1\) for \(x\ge 1\). Furthermore, \(\psi ^\varrho \) for \(\varrho \in {{\mathbb {R}}}\) is the \(\varrho \)th power of \(\psi \).
-
\(\langle \eta \rangle = (4+ |\eta |^2)^{1/2}\) for \(\eta \in {{\mathbb {R}}}^d\). Hence, \(\langle \eta \rangle \ge 2\) and \(\log \langle \eta \rangle >0\).
-
The Mellin transform of u with respect to \(x\in {{\mathbb {R}}}_+\) is \({\widetilde{u}}(z) = Mu(z) = \int _0^\infty x^{z-1} u(x)\,d x\) for \(z\in {{\mathbb {C}}}\). The inverse Mellin transform is \(M^{-1}v(x) = \frac{1}{2\pi i } \int _{\Gamma _\beta } x^{-z}v(z)\,d z\) for a suitable \(\beta \in {{\mathbb {R}}}\) depending on the situation under consideration.
-
The Fourier transform of w with respect to \(y\in {{\mathbb {R}}}^d\) is \({{\hat{w}}}(\eta ) = {\mathcal {F}} w(\eta ) = \int _{{{\mathbb {R}}}^d}e ^{-i y\cdot \eta }w(y)\,d y\) for \(\eta \in {{\mathbb {R}}}^d\). The inverse Fourier transform is
 , where
, where  .
. -
The space \(H^{s,\langle k\rangle }({{\mathbb {R}}}^d)\) for \((s,k)\in {{\mathbb {R}}}\times {{\mathbb {Z}}}\), consists of all w such that \(\langle \eta \rangle ^s \log ^k \langle \eta \rangle {{\hat{w}}}(\eta )\in L^2({{\mathbb {R}}}^d)\). In particular, \(H^s({{\mathbb {R}}}^d)= H^{s,\langle 0\rangle }({{\mathbb {R}}}^d)\).
-
In the closed half-space \({\overline{{{\mathbb {R}}}}}_+^{1+d}\), we use coordinates (x, y) with \(x\ge 0\) and \(y\in {{\mathbb {R}}}^d\).
-
The weighted Sobolev spaces \({{\mathscr {K}}}^{s,\gamma }({{\mathbb {R}}}_+^{1+d})\) are introduced in Definition 3.4 and the Sobolev spaces \(H_{P,\theta }^{s,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d})\) with asymptotics in Definition 3.8.
-
\(\gamma _{pk}\) for \((p,k)\in P\), where P is an asymptotic type, is a trace operator. Similarly, \(\Gamma _{pk}\) for \((p,k)\in P\) is a potential operator.
-
\({\mathcal {M}}^\mu ({{\mathbb {R}}}^d)\) denotes the space of holomorphic Mellin symbols \(h(z) = h(y,z,D_y)\).
-
The Mellin quantization of an amplitude function \(h\in {{\mathscr {C}}}^\infty ({\overline{{{\mathbb {R}}}}}_+;{\mathcal {M}}^\mu ({{\mathbb {R}}}^d))\) is
$$\begin{aligned} ({\text {op}}_M(h)u)(x,y) = \frac{1}{2\pi i }\int _{\Gamma _{1/2-\delta }} \, x^{-z}\, h(x,y,z,D_y){\tilde{u}}(z,y)\,d z. \end{aligned}$$\({\text {op}}_M(h)\) acts on suitable distributions \(u=u(x,y)\).
-
The Fourier quantization of an amplitude function \(a\in S_{\text {cl}}^\mu ({{\mathbb {R}}}^d\times {{\mathbb {R}}}^d)\) is \(a(y,D_y)={\text {op}}_\psi (a)\) with

The principal symbol of \(A=A(y,D_y)\) is denoted by \(\sigma _\psi ^\mu (A)\).
-
\(\Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\) is the class of cone-degenerate pseudodifferential operators, of order \(\mu \in {{\mathbb {R}}}\), utilized here. Elements of this space are symbolically written as \(\mathcal A(x,y,xD_x,D_y)\).
-
\({\widetilde{T}}^*{\overline{{{\mathbb {R}}}}}_+^{1+d}\) denotes the compressed cotangent bundle over \({\overline{{{\mathbb {R}}}}}_+^{1+d}\).
2 Well-posedness in standard Sobolev spaces
We start with proving Theorem 1.1. Notice that it is enough to treat the case \(\sigma =0\). Cases with \(\sigma \ge 1\) then follow by differentiating the equation \(\sigma \) times with respect to t, as in the proof of Proposition 4.5 below.
Proposition 2.1
Let \(u_0\in H^s(\Omega ;{{\mathbb {C}}}^N)\), \(f\in L^1((0,T);H^s(\Omega ;{{\mathbb {C}}}^N))\) for some \(s\ge 0\). Then Eq. (1.1) possesses a unique solution \(u\in {{\mathscr {C}}}([0,T]; H^s(\Omega ;{{\mathbb {C}}}^N))\). In addition, for \(\ell <s-1/2\), one has that \(\gamma _\ell u\in {{\mathscr {C}}}([0,T];H^{s-\ell -1/2}(\partial \Omega ;{{\mathbb {C}}}^N))\) is uniquely determined as the solution to the hyperbolic Cauchy problem
Here, the term \(R_\ell [u]\) is zero for \(\ell =0\) and linear in \(\gamma _0u,\dotsc ,\gamma _{\ell -1}u\) for \(\ell \ge 1\).
The precise form of the term \(R_\ell [u]\) will be given in (4.7) below.
Proof
Extend the matrix-valued coefficients \(A, A_j, B\) in Eq. (1.1) to matrix-valued functions \(A, A_j, B\in {{\mathscr {C}}}^\infty ([0,T]\times {{\mathbb {R}}}^{n};M_{N\times N}({{\mathbb {C}}}))\) so as to obtain a uniformly symmetrizable hyperbolic system \(\partial _t+xA\partial _x + \sum _{j=1}^d A_j\partial _j +B\) on \((0,T)\times {{\mathbb {R}}}^{n}\) (keeping the notation from above). Then consider the hyperbolic Cauchy problem
where \(U_0\in H^s({{\mathbb {R}}}^{n};{{\mathbb {C}}}^N)\), \(U_0\bigr |_{\Omega }=u_0\), \(F\in L^1((0,T);H^s({{\mathbb {R}}}^{n};{{\mathbb {C}}}^N))\), and \(F\bigr |_{(0,T)\times \Omega }=f\). Because this system is on whole space, Eq. (2.2) possesses a unique solution \(U\in {{\mathscr {C}}}([0,T]; H^s({{\mathbb {R}}}^{n};{{\mathbb {C}}}^N))\). As characteristics of this system are tangent to the hypersurface \((0,T)\times \partial \Omega \), it follows that whatever starts out in the region \((0,T)\times ({{\mathbb {R}}}^n{\setminus }\Omega )\) stays in that region for all times. Therefore, \(u=U\bigr |_{(0,T)\times \Omega }\) only depends on \(u_0\), f, in particular, u is independent of all the extensions chosen. We conclude that u is the unique solution to the original problem (1.2).
Differentiating (2.2) a number of times with respect to x and setting \(x=0\) yields (2.1). \(\square \)
3 Cone-degenerate pseudodifferential operators
The main technical tool to prove the result in Theorem 1.2 is a calculus for a certain class of cone-degenerate pseudodifferential operators on \({{\mathbb {R}}}_+^{1+d}\). Here we briefly introduce this pseudodifferential calculus. Calculi for cone-degenerate pseudodifferential operators have been developed by Schulze [22, 23], see also [4]. We closely follow his approach and refer to the said references for details. An equivalent calculus is the b-calculus of Melrose and Mendoza [15, 16]. For our purposes, Schulze’s cone calculus is preferable as it is more analytic in flavor and, therefore, easier to adapt to our needs.
Compared to [22, 23], there are a few differences. First of all, the base of the cone is \({{\mathbb {R}}}^d\) which is a non-compact manifold. This non-compactness introduces no additional difficulties, as we are not interested in the Fredholm property of elliptic operators, but solely in the construction of a symmetrizer. Secondly, the coefficients \(u_{pk}\) in the asymptotic expansions (1.4) do not belong to finite-dimensional subspaces of \({{\mathscr {C}}}^\infty ({{\mathbb {R}}}^d;{{\mathbb {C}}}^N)\), but instead can be any functions from the space \(H^{s+\Re p+\delta -1/2,\langle k\rangle }({{\mathbb {R}}}^d;{{\mathbb {C}}}^N)\), see Definition 3.8 and Proposition 3.9 for details. This then requires a special treatment of the asymptotic terms, see Definition 3.7. In fact, the function spaces \(H_{p,\theta }^{s,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {C}}}^N)\) employed below are modeled after the edge Sobolev spaces of Schulze (see [11] for a discussion of this point). Lastly, the cone-degenerate pseudodifferential operators we utilize do not produce any further asymptotic information, but instead preserve the given one. This is in the sense that the given asymptotic type, P, which collects the (p, k) appearing in (1.4), is preserved, while certainly the coefficients \(u_{pk}\) are, in general, altered when applying an operator A belonging to the calculus to u (see Proposition 3.26 for the way in which this happens). Accordingly, the conormal symbols \(\sigma _{\text {c}}^{-j}(A)\) of operators A in the calculus (see Definition 3.20) are holomorphic functions of the Mellin covariable \(z\in {{\mathbb {C}}}\), while for general cone pseudodifferential calculi these conormal symbols are finitely meromorphic functions of \(z\in {{\mathbb {C}}}\). Again, our choice is justified by the fact that we do not have to construct parametrices for elliptic cone-degenerate pseudodifferential operators (with the exception of Proposition 3.28 where we establish the existence of order reductions).
3.1 Asymptotic types
The functional-analytic approach of handling the asymptotic expansions (1.6) starts with collecting the data (p, k) appearing in (1.6) into so-called asymptotic types. Recall that we fix a \(\delta \in {{\mathbb {R}}}\) as a reference conormal order.
Definition 3.1
The set \(\underline{{\text {As}}}^\delta \) of asymptotic types associated with the conormal order \(\delta \in {{\mathbb {R}}}\) consists of discrete subsets \(P\subset {{\mathbb {C}}}\times {{\mathbb {N}}}_0\) with the following properties:
-
(i)
\(\Re p<1/2-\delta \) for \((p,k)\in P\),
-
(ii)
\(\Re p\rightarrow -\infty \) as \((p,k)\in P\), \(|p|\rightarrow \infty \),
-
(iii)
\((p,k-1)\in P\) if \((p,k)\in P\) and \(k>0\),
-
(iv)
\((p-1,k)\in P\) if \((p,k)\in P\).
Remark
Property (iv) is needed to guarantee the coordinate invariance of the constructions.
We set \(\pi _{{\mathbb {C}}}P =\bigl \{p\in {{\mathbb {C}}}\mid (p,k)\in P\text { for some} k\in {{\mathbb {N}}}_0\bigr \}\) and \(m_p=\max \{k+1\mid (p,k)\in P\}\) with the convention that \(m_p=0\) if \(p\notin \pi _{{\mathbb {C}}}P\). An asymptotic type P is then completely determined by the \(m_p\). In this sense, P can be thought of as a non-negative divisor (in the sense of complex analysis) having additional properties. Still, regarding P as a discrete subset of \({{\mathbb {C}}}\times {{\mathbb {N}}}_0\) comes in handy in the notation employed below.
Example
-
(i)
The asymptotic type governing (1.3) is \(P_0=\{(-\ell ,0)\mid \ell \in {{\mathbb {N}}}_0\}\). We refer to it as Taylor asymptotics.
-
(ii)
As a subset of \({{\mathbb {C}}}\times {{\mathbb {N}}}_0\), the empty asymptotic type \({\mathcal {O}}\) is given by \({\mathcal {O}}=\emptyset \).
Let \(P\in \underline{{\text {As}}}^\delta \), \(\varrho \in {{\mathbb {R}}}\). Then we define \(T^\varrho P\in \underline{{\text {As}}}^{\delta +\varrho }\) to consists of all \((p,k)\in {{\mathbb {C}}}\times {{\mathbb {N}}}_0\) such that \((p+\varrho ,k)\in P\).
3.2 Function spaces
Next we introduce suitable weighted Sobolev spaces and Sobolev spaces with asymptotics. These are the function spaces in which we will establish the energy inequalities.
3.2.1 Weighted Sobolev spaces
Definition 3.2
Let \(\gamma \in {{\mathbb {R}}}\). For \(s\in {{\mathbb {N}}}_0\), the weighted Sobolev space \({{\mathscr {H}}}^{s,\gamma }({{\mathbb {R}}}_+^{1+d})\) is defined to consist of all functions \(u=u(x,y)\) such that
For general \(s\in {{\mathbb {R}}}\), the spaces \({{\mathscr {H}}}^{s,\gamma }({{\mathbb {R}}}_+^{1+d})\) are then introduced by complex interpolation and duality.
We can characterize the space \({{\mathscr {H}}}^{s,\gamma }({{\mathbb {R}}}_+^{1+d})\) via the Mellin transform (see Sect. A.1).
Lemma 3.3
Let \(s\ge 0\), \(\gamma \in {{\mathbb {R}}}\). Then \(u\in {{\mathscr {H}}}^{s,\gamma }({{\mathbb {R}}}_+^{1+d})\) if and only if
where \({\tilde{u}}(z, \cdot )\) is the Mellin transform of \(u(x, \cdot )\) with respect to x.
As said in the introduction, we are mostly interested in the behavior of solutions to Eq. (1.2) near \(x=0\). Hence, we make a generic choice for their possible behavior near \(x=\infty \) (also compare with Eq. (4.8)). Note that \(u \in {{\mathscr {H}}}^{s,\gamma }({{\mathbb {R}}}_+^{1+d})\) implies that \(\varphi u \in {{\mathscr {H}}}^{s,\gamma }({{\mathbb {R}}}_+^{1+d})\).
Definition 3.4
For \(s,\gamma \in {{\mathbb {R}}}\), we set
In view of \({{\mathscr {H}}}^{s,\gamma }({{\mathbb {R}}}_+^{1+d}) \subset H^s_{\text {loc}}({{\mathbb {R}}}_+^{1+d})\), the space \(\mathcal K^{s,\gamma }({{\mathbb {R}}}_+^{1+d})\) is independent of the choice of the cut-off function \(\varphi \). Moreover, \(\mathcal K^{s,\gamma }({{\mathbb {R}}}_+^{1+d})\) is a Hilbert space in a natural way.
Now fix \(\delta \in {{\mathbb {R}}}\). In the sequel,
Write \(\langle , \,\rangle \) for the inner product and \(\Vert \;\Vert \) for the norm in \({\mathscr {K}}^{0,\delta }({{\mathbb {R}}}_+^{1+d})\).
3.2.2 The asymptotic terms
The next two lemmas prepare for introducing the terms occurring in the asymptotic expansions (1.6). Recall that the asymptotic expansions (1.6) are formal in the sense that, in general, we do not have enough regularity for the coefficients \(v_{pk}\) to write the asymptotic terms as tensor products.
Lemma 3.5
Let \((p,k)\in {{\mathbb {C}}}\times {{\mathbb {N}}}_0\) and \(w\in H^s({{\mathbb {R}}}^d)\) for some \(s\in {{\mathbb {R}}}\). Then the function v defined by
belongs to \(\bigcap _{\epsilon >0} {{\mathscr {K}}}^{s+\Re p+\epsilon ,1/2-\Re p-\epsilon }({{\mathbb {R}}}_+^{1+d})\). Moreover,
where \(v'\in \bigcap _{\epsilon >0} {{\mathscr {K}}}^{s+\Re p-\epsilon ,1/2-\Re p+\epsilon }({{\mathbb {R}}}_+^{1+d})\).
Proof
Let m(z) denote the Mellin transform of \(\varphi (x)x^{-p}\log ^k\!x\). Then m(z) is meromorphic in \({{\mathbb {C}}}\) with a single pole of order \(k+1\) at \(z=p\). In addition, \(m(z) = (-1)^k k! \left( z-p\right) ^{-(k+1)} + O(1)\) as \(z\rightarrow p\) and \((\chi m)(z)\in {{\mathscr {C}}}^\infty ({{\mathbb {R}}}_\beta ;{\mathcal {S}}({{\mathbb {R}}}_ \tau ))\), where \(\chi \in {{\mathscr {C}}}^\infty ({{\mathbb {C}}})\), \(\chi (z)=0\) for \(|z-p|\le 1/2\), and \(\chi (z)=1\) for \(|z-p|\ge 1\) (see Lemma A.1). Recall that we have written \(z=\beta +i \tau \) with \(\beta ,\,\tau \in {{\mathbb {R}}}\).
Direct calculations show that
In particular, \({\tilde{v}}(z,\cdot )\) is meromorphic in \(z\in {{\mathbb {C}}}\) taking values in \(H^{-\infty }({{\mathbb {R}}}^d)\) with a single pole of order \(k+1\) at \(z=p\) and
in view of \(\langle \eta \rangle ^{-z} = \sum _{r=0}^k \frac{(-1)^r}{r!}\,\langle \eta \rangle ^{-p}\log ^r\langle \eta \rangle \,(z-p)^r + O((z-p)^{k+1})\) as \(z\rightarrow p\).
For all \(t\in {{\mathbb {R}}}\) and \(\epsilon >0\),

This implies that \(v\in {{\mathscr {H}}}^{s+\Re p+\epsilon ,1/2-\Re p-\epsilon }({{\mathbb {R}}}_+^{1+d})\) for \(s+\Re p+\epsilon \ge 0\) by Lemma 3.3 and then for \(s+\Re p+\epsilon <0\) by duality.
Denote \(v''(x,y) = (2\pi i )^{-1}\int _{\Gamma _{\Re p-\epsilon '}}x^{-z} {\tilde{v}}(z,y)\,d z\), where \(\epsilon '>0\) is arbitrary. Repeating the argument just given, one finds that \(v''\in \bigcap _{\epsilon >0} {{\mathscr {H}}}^{s+\Re p-\epsilon ,1/2-\Re p+\epsilon }({{\mathbb {R}}}_+^{1+d})\). Furthermore, by (3.2) and Cauchy’s integral theorem,
One obtains (3.1) by multiplying the last equation by \(\varphi (x)\) and taking into account that \(\varphi (x)\varphi (x\langle \eta \rangle )= \varphi (x\langle \eta \rangle )\) for all \(\eta \in {{\mathbb {R}}}^d\). \(\square \)
Lemma 3.6
Let \((p,k)\in {{\mathbb {C}}}\times {{\mathbb {N}}}_0\). Suppose that \(w\in H^{s,\langle k\rangle }({{\mathbb {R}}}^d)\) for some \(s\in {{\mathbb {R}}}\). Then
and
Proof
We set \(w_0 = {\mathcal {F}}^{-1} \{\langle \eta \rangle ^p{\hat{w}}(\eta )\}\in H^{s-\Re p, \langle k\rangle }({{\mathbb {R}}}^d)\) and proceed by induction on k.
For \(k=0\), one has
and
by Lemma 3.5.
For \(k\ge 1\), we set \(w_r = {\mathcal {F}}^{-1}_{\eta \rightarrow y} \{ \log ^r\langle \eta \rangle \, {\hat{w}}(\eta )\}\in H^{s,\langle k-r\rangle }({{\mathbb {R}}}^d)\) for \(1\le r\le k\). Then, by Lemma 3.5 and the induction hypothesis,
as well as
This finishes the proof. \(\square \)
We are now ready to introduce potential operators.
Definition 3.7
For \((p,k)\in {{\mathbb {C}}}\times {{\mathbb {N}}}_0\), the potential operator \(\Gamma _{pk}\) acting on functions \(w=w(y)\) is given by
The role played by the normalizing factor \((-1)^k/k!\) becomes apparent from Lemma A.2 in conjunction with (3.7). Based on Lemma 3.6, we have that, for any \(s\in {{\mathbb {R}}}\),
3.2.3 Sobolev spaces with asymptotics
The definition of the Sobolev spaces with asymptotics postulates an improvement of the conormal order up to \(\delta +\theta \) upon subtracting finitely many asymptotic terms. This works as long as no singular exponent p from the asymptotic type P comes to lay on the weight line \(\Gamma _{1/2-\delta -\theta }\). This leaves out a discrete set of values for \(\theta >0\). The general case is then handled by complex interpolation.
Definition 3.8
Let \(s\in {{\mathbb {R}}}\), \(P\in \underline{As }^\delta \), and \(\theta \ge 0\).
(i) For \(\pi _{{\mathbb {C}}}P\cap \Gamma _{1/2-\delta -\theta }=\emptyset \), the space \(H_{P,\theta }^{s,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d})\) consists of all \(v\in {\mathscr {K}}^{s,\delta }({{\mathbb {R}}}_+^{1+d})\) for which there are functions \(v_{pk} \in H^{s+\Re p+\delta -1/2,\langle k\rangle }({{\mathbb {R}}}^d)\) for \((p,k)\in P\), \(\Re p>1/2-\delta -\theta \) such that
(ii) For general \(\theta \ge 0\), the space \(H_{P,\theta }^{s,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d})\) is then defined by complex interpolation with respect to the parameter \(\theta \).
For \(s\ge 0\), we also write \(H_P^{s,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d})=H_{P,s}^{s,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d})\).
Example
The spaces \(H_{P,\theta }^{s,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d})\) constitute a natural generalization of the standard Sobolev spaces in view of the following two facts:
(i) For \(s \ge 0\), \(H^s({{\mathbb {R}}}_+^{1+d}) = H_{P_0}^{s,0}(\overline{{{\mathbb {R}}}}_+^{1+d})\), where \(P_0\) is the type for Taylor asymptotics.
(ii) For \(s\ge 0\), \(H_0^s(\overline{{{\mathbb {R}}}}_+^{1+d}) = H_{\mathcal O}^{s,0}(\overline{{{\mathbb {R}}}}_+^{1+d})\), where \({\mathcal {O}}\) is the empty asymptotic type.
It is not hard to see that the coefficients \(v_{pk}\) in (3.4) are uniquely determined. We then introduce, for \((p,k)\in P\) with \(\Re p>1/2-\delta -\theta \), the trace operators
Essentially by definition, we have the following trace theorem.
Proposition 3.9
Let \(s\in {{\mathbb {R}}}\), \(P\in \underline{As }^\delta \), \(\theta \ge 0\), and \(\pi _{{\mathbb {C}}}P\cap \Gamma _{1/2-\delta -\theta }=\emptyset \). Then the short sequence
is split exact.
The next result tells us that, for theoretical purposes, one can adjust the reference conormal order \(\delta \) to be any given real number.
Lemma 3.10
Let \(s\in {{\mathbb {R}}}\), \(P\in \underline{As }^\delta \), \(\theta \ge 0\), and \(\varrho \in {{\mathbb {R}}}\). Then multiplication by \(\psi ^\varrho (x)\) realizes an isomorphism between \(H_{P,\theta }^{s,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d})\) and \(H_{T^\varrho P,\theta }^{s,\delta +\varrho }({\overline{{{\mathbb {R}}}}}_+^{1+d})\).
Proof
A straightforward verification. \(\square \)
3.2.4 The Schwartz class with asymptotics of type P
At last, we introduce a replacement for the space \({{\mathscr {S}}}({\overline{{{\mathbb {R}}}}}_+^{1+d})= \bigl \{v |_{\,{{\mathbb {R}}}_+^{1+d}}\bigm | v\in {{\mathscr {S}}}({{\mathbb {R}}}^{1+d})\bigr \}\). First we let \({{\mathscr {S}}}_0({\overline{{{\mathbb {R}}}}}_+^{1+d})\) be the space of all \(u\in {{\mathscr {S}}}({\overline{{{\mathbb {R}}}}}_+^{1+d})\) that vanish to infinite order at \(x=0\).
Definition 3.11
For \(P\in \underline{As }^\delta \), the space \({{\mathscr {S}}}_P({\overline{{{\mathbb {R}}}}}_+^{1+d})\) consists of all v for which there are sequences \((v_{pk})_{(p,k)\in P} \subset {{\mathscr {S}}}({{\mathbb {R}}}^d)\) and \((c_p)_{p\in \pi _{{\mathbb {C}}}P}\subset {{\mathbb {R}}}_+\) with \(c_p\rightarrow \infty \) as \(\Re p\rightarrow -\infty \) sufficiently fast such that
The space \({{\mathscr {S}}}_P({\overline{{{\mathbb {R}}}}}_+^{1+d})\) is a nuclear Fréchet space in a natural way. Furthermore, upon an appropriate choice of \((c_p)\) depending on \((v_{pk})\), the series in the left-hand side of (3.6) converges absolutely in \({{\mathscr {S}}}_P({\overline{{{\mathbb {R}}}}}_+^{1+d})\). Moreover, \({{\mathscr {S}}}_P({\overline{{{\mathbb {R}}}}}_+^{1+d})\subseteq H_{P,\theta }^{s,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d})\) for any \(s,\theta \) and, for v as in (3.6) and \((p,k)\in P\), we have \(\gamma _{pk}v=v_{pk}\). Indeed, the short sequence
is exact.
Example
One has \({{\mathscr {S}}}_{P_0}({\overline{{{\mathbb {R}}}}}_+^{1+d})={{\mathscr {S}}}({\overline{{{\mathbb {R}}}}}_+^{1+d})\) and \({{\mathscr {S}}}_{\mathcal O}({\overline{{{\mathbb {R}}}}}_+^{1+d})={{\mathscr {S}}}_0({\overline{{{\mathbb {R}}}}}_+^{1+d})\).
Lemma 3.12
The space \({{\mathscr {S}}}_P({\overline{{{\mathbb {R}}}}}_+^{1+d})\) is dense in \(H_{P,\theta }^{s,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d})\).
Proof
By complex interpolation, we can assume that \(\pi _{{\mathbb {C}}}P\cap \Gamma _{1/2-\delta -\theta }=\emptyset \). It is known that \({{\mathscr {S}}}_0({\overline{{{\mathbb {R}}}}}_+^{1+d})\) is dense in \({{\mathscr {K}}}^{s-\theta ,\delta +\theta }({{\mathbb {R}}}_+^{1+d})\). In view of (3.4) and as \({{\mathscr {S}}}({{\mathbb {R}}}^d)\) is dense in \(H^{r,\langle l\rangle }({{\mathbb {R}}}^d)\) for any \((r,l)\in {{\mathbb {R}}}\times {{\mathbb {N}}}_0\), it is enough to show that \(\Gamma _{pk}w\in {{\mathscr {S}}}_P({\overline{{{\mathbb {R}}}}}_+^{1+d})\) for \((p,k)\in P\) and \(w\in {{\mathscr {S}}}({{\mathbb {R}}}^d)\). The latter, in turn, will follow from the relation
which, however, is apparently true. \(\square \)
3.3 Calculus of cone-degenerate pseudodifferential operators
We now introduce the class \(\Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\) of cone-degenerate pseudodifferential operators on the half-space \({{\mathbb {R}}}_+^{1+d}\) mentioned in the introduction. To make connection to the theory of cone-degenerate pseudodifferential operators, note that the closed half-space \({\overline{{{\mathbb {R}}}}}_+^{1+d}\) is considered as a blowup of the cone \((\overline{{{\mathbb {R}}}}_+\times {{\mathbb {R}}}^d)/(\{0\}\times {{\mathbb {R}}}^d)\). We do not provide proofs for results that can be found in the literature in the form as stated or in a similar form (then with no essential changes in the proofs). Notable exceptions are Propositions 3.25 through 3.29. For other results, we refer to the literature, e.g., Harutyunyan and Schulze [4] or Schulze [23].
3.3.1 Parameter-dependent pseudodifferential operators
We start with parameter-dependent pseudodifferential operators.
Definition 3.13
For \(\mu \in {{\mathbb {R}}}\), the class \(\Psi _{\text {cl}}^\mu ({{\mathbb {R}}}^d;{{\mathbb {R}}})\) of classical parameter-dependent pseudodifferential operators on \({{\mathbb {R}}}^d\), with parameter \(\tau \in {{\mathbb {R}}}\), consists of all families \(A=\left( A(\tau )\right) _{\tau \in {{\mathbb {R}}}}\subset \Psi _{\text {cl}}^\mu ({{\mathbb {R}}}^d)\) such that

where \(a\in S_{\text {cl}}^\mu ({{\mathbb {R}}}_y^d\times {{\mathbb {R}}}_{(\eta ,\tau )}^{d+1})\).
Note that any \(A\in \Psi _{\text {cl}}^\mu ({{\mathbb {R}}}^d;{{\mathbb {R}}})\) admits a parameter-dependent principal symbol \(\sigma _\psi ^\mu (A) \in S^{(\mu )}({{\mathbb {R}}}^d\times ({{\mathbb {R}}}^{d+1}{\setminus }0))\). Then A is parameter-dependent elliptic if \(\sigma _\psi ^\mu (A)\) is nowhere vanishing. In the elliptic case, A admits a parametrix, i.e., there exists a \(B\in \Psi _{\text {cl}}^{-\mu }({{\mathbb {R}}}^d;{{\mathbb {R}}})\) such that \(AB-I ,BA-I \in \mathcal S({{\mathbb {R}}}_\tau ;\Psi ^{-\infty }({{\mathbb {R}}}^d))\). This parametrix B is essentially unique, i.e., it is unique modulo \(\mathcal S({{\mathbb {R}}};\Psi ^{-\infty }({{\mathbb {R}}}^d))\). Moreover, \(A(\tau )\) is invertible for \(|\tau |\) large and B can be chosen to satisfy \(B(\tau ) = A(\tau )^{-1}\) for \(|\tau |\) large. Note also that \(\Psi _{\text {cl}}^\mu ({{\mathbb {R}}}^d;{{\mathbb {R}}})\) equipped with its canonical system of seminorms is a nuclear Fréchet space.
Example
\(A= -\Delta _y+\tau ^2+\tau \in \Psi _{\text {cl}}^2({{\mathbb {R}}}^d;{{\mathbb {R}}})\) has principal symbol \(\sigma _\psi ^2(A)(y,\eta ,\tau ) = |\eta |^2+\tau ^2\) and is parameter-dependent elliptic.
3.3.2 Holomorphic Mellin symbols
Recall that we write \(z\in {{\mathbb {C}}}\) as \(z=\beta +i \tau \) with \(\beta ,\tau \in {{\mathbb {R}}}\).
Definition 3.14
For \(\mu \in {{\mathbb {R}}}\), we define
as the set of holomorphic Mellin symbols of order \(\mu \).
These Mellin symbols are entire functions of \(z=\beta +i\tau \) taking values in the nuclear Fréchet space \(\Psi _{\text {cl}}^\mu ({{\mathbb {R}}}^d)\) and are also smooth functions of \(\beta \) taking values in \(\Psi _{\text {cl}}^\mu ({{\mathbb {R}}}^d;{{\mathbb {R}}}_\tau )\). Note that, as a consequence of the Cauchy–Riemann equations, the principal symbol \(\sigma _\psi ^\mu (h)(y,\eta ,\tau )\) of \(h\bigr |_{\Re z=\beta }\in \Psi _{\text {cl}}^\mu ({{\mathbb {R}}}^d;{{\mathbb {R}}}_\tau )\) for \(h\in {\mathcal {M}}^\mu ({{\mathbb {R}}}^d)\) is independent of \(\beta \in {{\mathbb {R}}}\).
Proposition 3.15
Let \(a\in S^{(\mu )}({{\mathbb {R}}}^d\times ({{\mathbb {R}}}^{d+1}{\setminus }0))\) be elliptic. Then there exists a \(h\in {\mathcal {M}}^\mu ({{\mathbb {R}}}^d)\) with \(\sigma _\psi ^\mu (h)=a\) such that \(h^{-1}\in \mathcal {M}^{-\mu }({{\mathbb {R}}}^d)\)
Proof
This is proven as in Witt [25]. \(\square \)
The following result provides a means to control the action of \({\text {op}}_M(h)\) for \(h\in {\mathcal {M}}^\mu ({{\mathbb {R}}}^d)\) on asymptotic terms. Recall that \(h^{(r)}(p)=\partial _z^r h(p) \in \Psi _{\text {cl}}^\mu ({{\mathbb {R}}}^d)\) for \(p\in {{\mathbb {C}}}\).
Proposition 3.16
Let \(h\in {\mathcal {M}}^\mu ({{\mathbb {R}}}^d)\), \((p,k)\in {{\mathbb {C}}}\times {{\mathbb {N}}}_0\), and \(w\in H^{s+\mu ,\langle k\rangle }({{\mathbb {R}}}^d)\) for some \(s\in {{\mathbb {R}}}\). Then
Proof
Let m(z) be the Mellin transform of \(\varphi (x) x^{-p}\). Then the Mellin transform of \(\varphi (x) x^{-p} \log ^{k-r}\!x\) for \(0\le r\le k\) equals \(m^{(k-r)}(z)\). Doing the computations modulo \(\bigcap _{\epsilon >0} {{\mathscr {K}}}^{s-\epsilon ,1/2-\Re p +\epsilon }({{\mathbb {R}}}_+^{1+d})\), we find that (see Lemma 3.6)
where we have used that \( (z-p)^{k+1} m^{(k)}(z) \in {\mathcal {H}}({{\mathbb {C}}}) \cap {{\mathscr {C}}}^\infty ({{\mathbb {R}}}_\beta ;{{\mathbb {R}}}_\tau )\) and also that
for \(0\le r\le k\). \(\square \)
3.3.3 Cone-degenerate pseudodifferential operators
In order to introduce cone-degenerate pseudodifferential operators, we choose cut-off functions \(\varphi ,\varphi _0,\varphi _1\in {{\mathscr {C}}}_{\text {c}}^\infty ({\overline{{{\mathbb {R}}}}}_+)\) that localize near \(x=0\) and satisfy \(\varphi \varphi _0=\varphi \), \(\varphi \varphi _1=\varphi _1\).
Definition 3.17
For \(\mu \in {{\mathbb {R}}}\), the class \(\Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\) of cone-degenerate pseudodifferential operators on \({{\mathbb {R}}}_+^{1+d}\) consists of all pseudodifferential operators A on \({{\mathbb {R}}}_+^{1+d}\) which are of the form
where
-
(i)
\(A_M = \varphi {\text {op}}_M(h) \varphi _0\) for some \(h=h(x,z,y,D_y)\in {{\mathscr {C}}}^\infty ({\overline{{{\mathbb {R}}}}}_+;{\mathcal {M}}^\mu ({{\mathbb {R}}}^d))\),
-
(ii)
\(A_\psi = (1-\varphi ){\text {op}}_\psi (a)(1-\varphi _1)\) for some \(a\in S_{\text {cl}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d}\times {{\mathbb {R}}}^{1+d})\).
-
(iii)
\(A_{r}\) has integral kernel in \(\mathscr {S}_0({\overline{{{\mathbb {R}}}}}_+^{1+d}){\hat{\otimes }} \mathscr {S}_0({\overline{{{\mathbb {R}}}}}_+^{1+d})\) (with respect to the measure \(\psi ^{-2\delta }(x)\,d x d y\) attached to the right factor).
Notice that any operator A of the form in (3.8) is a pseudodifferential operator on \({{\mathbb {R}}}_+^{1+d}\). The point of this definition is to enforce control on the behavior as \(x\rightarrow +0\) in a specific way (see, e.g., the mapping properties in Proposition 3.25 below).
Remark
Although the weight factor \(\psi ^{-2\delta }(x)\) appears explicitly in the definition of the residual class \(\Psi _{\text {c}}^{-\infty }({\overline{{{\mathbb {R}}}}}_+^{1+d})\) consisting of the operators \(A_r\) in (3.8), the classes \(\Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\) and \(\Psi _{\text {c}}^{-\infty }({\overline{{{\mathbb {R}}}}}_+^{1+d})\) are in fact independent of \(\delta \in {{\mathbb {R}}}\).
3.3.4 Symbolic structure
For the rest of this section, we develop certain elements of the calculus of pseudodifferential operators in \(\Psi _{\text {c}}^\infty ({\overline{{{\mathbb {R}}}}}_+^{1+d}) = \bigcup _{\mu \in {{\mathbb {R}}}}\Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\). We start with the symbolic structure.
First note that the vector fields \(a(x,y)x\partial _x + \sum _{j=1}^d a_j(x,y)\partial _j\) tangent to \(\partial {\overline{{{\mathbb {R}}}}}_+^{1+d}\), where \(a,a_j\in {{\mathscr {C}}}^\infty ({\overline{{{\mathbb {R}}}}}_+^{1+d})\), are the \({{\mathscr {C}}}^\infty \) sections of a vector bundle over \({\overline{{{\mathbb {R}}}}}_+^{1+d}\) that we denote by \({\widetilde{T}}^*{\overline{{{\mathbb {R}}}}}_+^{1+d}\) and call it the compressed cotangent bundle (see, e.g., Melrose [15]). Indeed, the covariable to \((x,y)\in {\overline{{{\mathbb {R}}}}}_+^{1+d}\) in \({\widetilde{T}}^*{\overline{{{\mathbb {R}}}}}_+^{1+d}\) can be taken to be \(({\tilde{\xi }},\eta )\) with \({\tilde{\xi }}=\psi (x)\xi \).
Definition 3.18
The compressed principle symbol \({\tilde{\sigma }}_\psi ^\mu (A) \in S^{(\mu )}({\widetilde{T}}^*{\overline{{{\mathbb {R}}}}}_+^{1+d}{\setminus }0)\) of an operator \(A\in \Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\) is defined as
Here, \(\sigma _\psi ^\mu (h)\) is the parameter-dependent principal symbol of \(h = h(x,y,z,D_y)\).
Proposition 3.19
The short sequence
is split exact.
Consequently, the compressed principal symbol \({\tilde{\sigma }}_\psi ^\mu (A)\) provides control on operators in \(\Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\) up to lower-order perturbations.
Still, control of the asymptotic behavior as \(x\rightarrow +0\) is achieved with the help of the full sequence \(\left( \sigma _{\text {c}}^{-j}(A)\right) _{j\in {{\mathbb {N}}}_0}\) of conormal symbols.
Definition 3.20
For \(A\in \Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\) written as in (3.8), the conormal symbol \(\sigma _{\text {c}}^{-j}(A)\) of conormal order \(-j\) for \(j\in {{\mathbb {N}}}_0\) is defined as
Lemma 3.21
There is a compatibility condition between \(\tilde{\sigma }_\psi ^\mu (A)\) and \(\sigma _{\text {c}}^0(A)\), namely
It is this compatibility condition which later will guarantee that the governing equations for the coefficents \(\gamma _{pk}u\) are symmetrizable hyperbolic.
Remark
In order to provide a heuristic explanation of how control on the asymptotic behavior as \(x\rightarrow +0\) is achieved by the sequence \(\left( \sigma _{\text {c}}^{-j}(A)\right) _{j\in {{\mathbb {N}}}_0}\) notice that, informally, we have that
upon performing a Taylor series expansion of \(A_M\) at \(x=0\). (See also Proposition 3.26.)
Example
The first-order differential operator
where \(a, a_j, b \in {{\mathscr {C}}}^\infty _b({\overline{{{\mathbb {R}}}}}_+^{1+d})\), belongs to \(\Psi _{\text {c}}^1({\overline{{{\mathbb {R}}}}}_+^{1+d})\). Then it is readily checked that
-
(i)
\({\tilde{\sigma }}_\psi ^1(A)(x,y,{\tilde{\xi }},\eta ) = a(x,y){\tilde{\xi }} + \sum _{j=1}^d a_j(x,y)\eta _j\).
-
(ii)
\(\sigma _{\text {c}}^0(A)(z) = i a(0,y) z + \sum _{j=1}^d a_j(0,y)D_j+b(0,y)\).
-
(iii)
\(\sigma _\psi ^1(\sigma _{\text {c}}^0(A))(y,\eta ,\tau ) = -\,a(0,y)\tau + \sum _{j=1}^d a_j(0,y)\eta _j\).
3.3.5 Compositions and adjoints
Now we get into the calculus of cone-degenerate pseudodifferential operators. First consider their formal adjoints. Let \(A^*\) be formal adjoint operator of \(A \in \Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\), i.e.,
Proposition 3.22
The class \(\Psi _{\text {c}}^\infty ({\overline{{{\mathbb {R}}}}}_+^{1+d})\) of cone-degenerate pseudodifferential operators is closed under taking adjoints in the sense that whenever \(A\in \Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\), then \(A^* \in \Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\). Moreover,
-
(i)
\({\tilde{\sigma }}_\psi ^\mu (A^*) = {\tilde{\sigma }}_\psi ^\mu (A)^*\)
-
(ii)
\(\sigma _{\text {c}}^0(A^*)(z) = \sigma _{\text {c}}^0(A)(1-2\delta -{\bar{z}})^*\).
Another result is that cone-degenerate pseudodifferential operators are closed under compositions.
Proposition 3.23
The class \(\Psi _{\text {c}}^\infty ({\overline{{{\mathbb {R}}}}}_+^{1+d})\) of cone-degenerate pseudodifferential operators is closed under compositions in the sense that whenever \(A\in \Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\) and \(B\in \Psi _{\text {c}}^\nu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\), then their composition \(A\circ B\) belongs to \( \Psi _{\text {c}}^{\mu +\nu }({\overline{{{\mathbb {R}}}}}_+^{1+d})\). Moreover,
-
(i)
\({\tilde{\sigma }}_\psi ^{\mu +\nu }(A\circ B)= {\tilde{\sigma }}_\psi ^\mu (A) \, {\tilde{\sigma }}_\psi ^\nu (B)\),
-
(ii)
\(\sigma _{\text {c}}^{-\ell }(A\circ B)(z) = \sum _{j+k=\ell } \sigma _{\text {c}}^{-j}(A)( z-k) \, \sigma _{\text {c}}^{-k}(B)(z)\) for \(\ell \in {{\mathbb {N}}}_0\).
3.3.6 Mapping properties
Cone-degenerate pseudodifferential operators act continuously in the scale of Sobolev spaces with asymptotics. To see this, we start with the following result:
Lemma 3.24
For each \(\mu \in {{\mathbb {R}}}\), \(\Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\subset \bigcap _P{\mathcal {L}}({\mathscr {S}}_P({\overline{{{\mathbb {R}}}}}_+^{1+d}))\), where the intersection is over all asymptotic types P.
Proof
This is a standard result in the theory of cone-degenerate pseudodifferential operators. In particular, it relies on the fact that the conormal symbols are assumed to be holomorphic. \(\square \)
Proposition 3.25
For \(\mu \in {{\mathbb {R}}}\),
where intersection is over all \(s\in {{\mathbb {R}}}\), \(P\in \underline{{\text {As}}}^\delta \), and \(\theta \ge 0\).
Proof
It is well-known that \(\Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\subset \bigcap _{s,\gamma } {{\mathscr {L}}}\bigl ({{\mathscr {K}}}^{s+\mu ,\gamma }({{\mathbb {R}}}_+^{1+d}), {{\mathscr {K}}}^{s,\gamma }({{\mathbb {R}}}_+^{1+d})\bigr )\). That this holds for all \(\gamma \in {{\mathbb {R}}}\) is again a consequence of the holomorphy of the conormal symbols.
By the closed graph theorem and complex interpolation, it is enough to show that
whenever \((p,k)\in P\), \(w\in H^{s+\mu +\Re p+\delta -1/2,\langle k\rangle }({{\mathbb {R}}}^d)\), \(1/2-\delta -\theta < \Re p\), \(\Re p-(1/2-\delta -\theta ) \notin {{\mathbb {N}}}\), and \(h\in {{\mathscr {C}}}^\infty ({\overline{{{\mathbb {R}}}}}_+;{\mathcal {M}}^\mu ({{\mathbb {R}}}^d))\), where \(\Gamma _{pk}w\) is given in (3.3). Let \(\kappa \) be the smallest integer such that \(\Re p-\kappa <1/2-\delta -\theta \). Writing \(h(x,z) = \sum _{0\le j<\kappa } x^j h_j(z) + x^\kappa h'(x,z)\), where \(h_j\in {\mathcal {M}}^\mu ({{\mathbb {R}}}^d)\) for \(0\le j<\kappa \) and \(h'\in {{\mathscr {C}}}^\infty ({\overline{{{\mathbb {R}}}}}_+;{\mathcal {M}}^\mu ({{\mathbb {R}}}^d))\), one has
where \(v_j\in {{\mathscr {K}}}^{s-\theta +j,\delta +\theta }({{\mathbb {R}}}_+^{1+d})\), and
Altogether, (3.11) follows. This completes the proof. \(\square \)
As a consequence, \(\gamma _{pk}(Au)\) for \(u\in H_{P,\theta }^{s+\mu ,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d})\) is computable in terms of \(\{\sigma _{\text {c}}^{-j}(A)\}_{j\ge 0}\).
Proposition 3.26
Let \(A\in \Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\), \(u\in H_{P,\theta }^{s+\mu ,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d})\), and \((p,k)\in P\), where \(\Re p>1/2-\delta -\theta \). Then
The sum in the right-hand side is over those \((j,\ell ,r)\), where \(\Re p+j<1/2-\delta \) and \(0\le \ell <m_{p+j}\). In particular, this sum is finite.
Proof
By Lemma 3.12 and continuity of the trace maps according to Proposition 3.9, it is enough to verify (3.12) when \(u\in {{\mathscr {S}}}_P({\overline{{{\mathbb {R}}}}}_+^{1+d})\). In this case, (3.12) follows from (3.6), (3.10), (A.1), (A.2). (See [12] for such explicit calculations.) \(\square \)
3.3.7 Further results
Here we collect several results about the calculus for cone-degenerate pseudodifferential operators that we will need later, e.g., when constructing a symmetrizer.
It is crucial that an integration by parts produces no boundary terms. It is precisely this property which allows us to treat the initial-boundary value problem Eq. (1.1) as a Cauchy problem.
Lemma 3.27
For \(A\in \Psi _{\text {c}}^1({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {C}}}^N)\) and \(u,v\in {{\mathscr {K}}}^{1,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N)\), it holds that
Proof
Property (3.13) holds whenever \(u,v\!\in \!{{\mathscr {C}}}_{\text {c}}^\infty ({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N)\). Because \({{\mathscr {C}}}_{\text {c}}^\infty ({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N)\) is dense in \({{\mathscr {K}}}^{1,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N)\), the result follows. \(\square \)
The existence of so-called order reductions is assured next.
Proposition 3.28
Let \(\mu \in {{\mathbb {R}}}\). Then there exists a selfadjoint, positive definite operator \(\Lambda ^\mu \in \Psi _{\text {c}}^\mu ({\overline{{{\mathbb {R}}}}}_+^{1+d})\) such that \(\Lambda ^{-\mu }=(\Lambda ^\mu )^{-1}\in \Psi _{\text {c}}^{-\mu }({\overline{{{\mathbb {R}}}}}_+^{1+d})\). In particular,
is an isomorphism for all \(s\in {{\mathbb {R}}}\), \(P\in \underline{As }^\delta \), and \(\theta \ge 0\).
Proof
One way to prove the result is to start with a parameter-dependent version \(\Psi _{\text {c}}^{\mu /2}({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {R}}})\) of the class \(\Psi _{\text {c}}^{\mu /2}({\overline{{{\mathbb {R}}}}}_+^{1+d})\) consisting of families \(A= \left( A(\lambda )\right) _{\lambda \in {{\mathbb {R}}}}\subset \Psi _{\text {c}}^{\mu /2}({\overline{{{\mathbb {R}}}}}_+^{1+d})\), as in Sect. 3.3.1. Choose a parameter-elliptic family \(A\in \Psi _{\text {c}}^{\mu /2}({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {R}}})\) with compressed principal symbol \({\tilde{\sigma }}_\psi ^{\mu /2}(A) = ({\tilde{\xi }}^2 + |\eta |^2 + \lambda ^2)^{\mu /4}\) and leading conormal symbol \(\sigma _{\text {c}}^0(A) = \sigma _{\text {c}}^0(A)(z,\lambda )\in \mathcal M^{\mu /2}({{\mathbb {R}}}^d;{{\mathbb {R}}})\) such that \(\sigma _{\text {c}}^0(A)^{-1}\in \mathcal M^{-\mu /2}({{\mathbb {R}}}^d;{{\mathbb {R}}})\) (see Proposition 3.15). Then \(A(\lambda ) \in \Psi _{\text {c}}^{\mu /2}({\overline{{{\mathbb {R}}}}}_+^{1+d})\) is invertible for \(|\lambda | \gtrsim 1\), with \(A(\lambda )^{-1} \in \Psi _{\text {c}}^{-\mu /2}({\overline{{{\mathbb {R}}}}}_+^{1+d})\). Now pick a \(\lambda \in {{\mathbb {R}}}\) with \(|\lambda |\) large and set \(\Lambda ^\mu = A(\lambda )^*A(\lambda )\). \(\square \)
We have the following form of Gårding’s inequality.
Proposition 3.29
Let \(\mu \ge 0\). Suppose that \(A \in \Psi _{\text {c}}^{\mu }({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {C}}}^N)\) has a positive definite compressed principle symbol satisfying \({\tilde{\sigma }}_\psi ^\mu (A)(x,y,{\tilde{\xi }},\eta )\gtrsim ({\tilde{\xi }}^{\,2}+|\eta |^2)^{\mu /2}\,I _{N}\). Then there exists a \(C=C^* \in \Psi _{\text {c}}^{\mu -1}({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {C}}}^N)\) and a constant \(c>0\) such that
for all \(u\in {{\mathscr {K}}}^{\mu ,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N)\).
Proof
Writing \(u = \Lambda ^{-\mu /2}v\) with \(v\in {{\mathscr {K}}}^{\mu /2,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N)\), we can assume that \(\mu =0\). Then \({\tilde{\sigma }}_\psi ^0(A)(x,y,{\tilde{\xi }},\eta )\ge 2c\, I _{N}\) for some constant \(c>0\). Choose \(B\in \Psi _{\text {c}}^0({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {C}}}^N)\) such that \({\tilde{\sigma }}_\psi ^0(B) = \bigl ({\tilde{\sigma }}_\psi ^0(A) - c\, I _{N}\bigr )^{1/2}\). By construction, \(C= B^*B -\Re A + c \in \Psi _{\text {c}}^{-1}({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {C}}}^N)\). We obtain
for \(u\in {{\mathscr {K}}}^{0,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N)\). \(\square \)
4 Proof of the main results
In this section, we establish our main results. In fact, it suffices to prove Theorem 1.2. Theorem 1.1 is a special case of Theorem 1.2, where \(s\ge 0\), \(\delta =0\), \(P=P_0\), and \(\theta _r = s-r+\sigma \) for \(0\le r\le \sigma \). Besides, Theorem 1.1 has been proven independently in Sect. 2. Theorem 1.3 follows from Theorem 1.2 in the usual way using coordinate invariance (see [11]) and finite propagation speed. An alternative argument retraces the steps of the proof of Theorem 1.2 displayed below and uses cone-degenerate pseudodifferential operators from a class \(\Psi _{\text {c}}^\mu (\overline{\Omega };{{\mathbb {C}}}^N)\), where now operators in this class are additionally assumed to be properly supported.
We consider the Cauchy problem
where
We assume that the operator \(\partial _t + {{\mathcal {A}}}(t,x,y,xD_x,D_y)\) is hyperbolic in the sense that \({{\mathcal {A}}}\) admits a symbolic symmetrizer. This means that there exists a \(b \in {{\mathscr {C}}}^\infty \bigl ([0,T];S^{(0)}(\widetilde{T}^*{\overline{{{\mathbb {R}}}}}_+^{1+d}{\setminus }0;M_{N\times N}({{\mathbb {C}}}))\bigr )\) such that
-
(i)
\(b(t,x,y,{\tilde{\xi }},\eta )=b(t,x,y,{\tilde{\xi }},\eta )^* \ge c\,{\text {I}}_{N}\) for some constant \(c>0\),
-
(ii)
\(b(t, x, y, {\tilde{\xi }},\eta ) {\tilde{\sigma }}_\psi ^1(\mathcal A)(t,x,y,{\tilde{\xi }},\eta )\) is skew-Hermitian for all \((t, x, y, {\tilde{\xi }}, \eta )\).
Example
The operator \({{\mathcal {A}}}(t,x,y,xD_x,D_y) = x A(t,x,y)\partial _x + \sum _{j=1}^d A_j(t,x,y)\partial _j + B(t,x,y)\) from Eq. (1.2) was assumed to satisfy these assumptions.
4.1 Well-posedness in weighted Sobolev spaces
Employing the symbolic symmetrizer, b, we first construct a genuine symmetrizer, \({{\mathcal {B}}}\).
Lemma 4.1
Let \(b\in {{\mathscr {C}}}^\infty \bigl ([0,T];S^{(0)}(\widetilde{T}^*{\overline{{{\mathbb {R}}}}}_+^{1+d}{\setminus }0;\) \(M_{N\times N}({{\mathbb {C}}}))\bigr )\) be a symbolic symmetrizer for \({{\mathcal {A}}}\). Then there exists a \({\mathcal {B}}\in {{\mathscr {C}}}^\infty \bigl ([0,T];\Psi _{\text {c}}^0({\overline{{{\mathbb {R}}}}}_+^{1+d}; {{\mathbb {C}}}^N)\bigr )\) such that
for some \(c>0\) and all \(t \in [0, T]\).
Proof
We pick a \({{\mathcal {B}}}_1\in {{\mathscr {C}}}^\infty \bigl ([0,T]; \Psi _{\text {c}}^0({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {C}}}^N)\bigr )\) with \({\tilde{\sigma }}_\psi ^0({{\mathcal {B}}}_1(t))=b(t)\) for \(t \in [0, T]\) and set \({{\mathcal {B}}}_0 =\left( {{\mathcal {B}}}_1+{{\mathcal {B}}}_1^*\right) /2\). Then \({\tilde{\sigma }}_\psi ^0({{\mathcal {B}}}_0(t))=b(t)\) for \(t \in [0,T]\). By Proposition 3.29, there exists a \({\mathcal {C}}\in {{\mathscr {C}}}^\infty \bigl ([0,T];\) \(\Psi _{\text {c}}^{-1}({\overline{{{\mathbb {R}}}}}_+^{1+d}; {{\mathbb {C}}}^N)\bigr )\) with \({\mathcal {C}}(t)={\mathcal {C}}(t)^*\) for \(t\in [0,T]\) such that, for any \(u \in {{\mathscr {C}}}^\infty _c({{\mathbb {R}}}^{1+d}_+;{{\mathbb {C}}}^N)\) and \(t \in [0, T]\),
It follows that the operator \({{\mathcal {B}}}={{\mathcal {B}}}_0 + {\mathcal {C}}\) has the desired properties. \(\square \)
Next we derive energy estimates for Eq. (4.1) in the weighted Sobolev spaces \({{\mathscr {K}}}^{s,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N)\).
We start with the case \(s=0\). As usual, the proof of the next proposition relies on the following facts (as was already mentioned in the introduction):
-
\(\langle {{\mathcal {B}}}(t) u, u\rangle \) is equivalent to \(\Vert u\Vert ^2\) uniformly in \(t\in [0,T]\),
-
Integration by parts produces no boundary terms (see Lemma 3.27),
-
\({{\mathcal {B}}}{{\mathcal {A}}}+({{\mathcal {B}}}{{\mathcal {A}}})^* \in {{\mathscr {C}}}^\infty ([0,T];\Psi _{\text {c}}^0({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {C}}}^N))\).
Proposition 4.2
Let \(u\in {{\mathscr {C}}}([0,T];{\mathscr {K}}^{1,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N)) \cap {{\mathscr {C}}}^1([0,T];{\mathscr {K}}^{0,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N)) \). Then
Proof
Let \(u(0)=u_0\), \(\partial _t u -{{\mathcal {A}}}u=f\). By construction, there exists a constant \(C>0\) such that
Then
Setting \(K=\sup _{t\in [0,T]}\langle {{\mathcal {B}}}(t)u(t),u(t)\rangle ^{1/2}e ^{-C t}\), the Cauchy–Schwarz inequality implies that
i.e.,
It follows that
Because the norm \(v\mapsto \langle {{\mathcal {B}}}(t)v,v\rangle ^{1/2}e ^{-C t}\) is equivalent to \(\Vert v\Vert \) uniformly in \(t\in [0,T]\), this finishes the proof. \(\square \)
As an immediate consequence we have the next result.
Proposition 4.3
Let \(u\!\in \! {{\mathscr {C}}}([0,T];{\mathscr {K}}^{s+1,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N)) \cap {{\mathscr {C}}}^1(([0,T];{\mathscr {K}}^{s,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N))\) for some \(s\in {{\mathbb {R}}}\). Then
Proof
Let again \(u(0)=u_0\), \(\partial _t u(t) - {{\mathcal {A}}}u=f\). Let \(\Lambda ^s\in \Psi _{\text {c}}^s({\overline{{{\mathbb {R}}}}}_+^{1+d})\) be a scalar invertible operator such that \((\Lambda ^s)^{-1}\in \Psi _{\text {c}}^{-s}({\overline{{{\mathbb {R}}}}}_+^{1+d})\), as constructed in Lemma 3.28. Then, \(\Lambda ^s u\) solves the system
Notice that \(\Lambda ^s {{\mathcal {A}}}\,\Lambda ^{-s} \in {{\mathscr {C}}}^\infty ([0,T]; \Psi _{\text {c}}^1({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {C}}}^N))\) and \(\tilde{\sigma }_\psi ^1(\Lambda ^s{{\mathcal {A}}}\Lambda ^{-s})= {\tilde{\sigma }}_\psi ^1({{\mathcal {A}}})\). Hence, system (4.4) is symmetrizable hyperbolic. Applying Proposition 4.2 yields
As \(\Vert \Lambda ^s\cdot \Vert \) is an equivalent norm on \(\mathscr {K}^{s,\delta }\), we obtain estimate (4.3). \(\square \)
Proposition 4.4
Let \(u_0\in {\mathscr {K}}^{s,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N)\) and \(f\in L^1((0,T); {\mathscr {K}}^{s,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N))\) for some \(s\in {{\mathbb {R}}}\). Then Eq. (4.1) possesses a unique solution \(u\!\in \!{{\mathscr {C}}}([0,T]; {\mathscr {K}}^{s,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N))\). Moreover, the energy inequality
holds.
Proof
Uniqueness. Let \(u_0=0\), \(f=0\). Then \({{\mathcal {A}}}(t)u \in {{\mathscr {C}}}([0,T]; {\mathscr {K}}^{s-1,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N))\) and, consequently, we obtain \(\partial _t u \in {{\mathscr {C}}}([0,T]; \mathscr {K}^{s-1,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N))\) from the equation. Hence, estimate (4.3) (with s replaced with \(s-1\)) yields \(u=0\).
Existence. We argue by duality. Set \({\mathcal {Y}}=\{v\in {{\mathscr {C}}}([0,T];{{\mathscr {S}}}({{\mathbb {R}}}^d;{{\mathbb {C}}}^N))\mid v(T)=0\}\). The operator \(\partial _t + {{\mathcal {A}}}(T-t)^*\) is symmetrizable hyperbolic. Hence, estimate (4.3) implies (after the change of variables \(t\mapsto T-t\))
We now consider the functional
on the space \(\left( -\partial _t + {{\mathcal {A}}}(t)^*\right) {\mathcal {Y}}\), where \(g = -\partial _t v + {{\mathcal {A}}}(t)^* v\), \(v\in {\mathcal {Y}}\). We have the estimate
By the Hahn–Banach theorem, the functional in (4.5) extends to a bounded functional on the space \(L^1((0,T); {{\mathscr {K}}}^{-s,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N))\). By duality, such an extension is given as \(g \mapsto \int _0^T \langle u(t),g(t)\rangle \,d t\) for some uniquely determined \(u\in L^\infty ((0,T);{{\mathscr {K}}}^{s,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N))\). We obtain that
Taking \(v\in {{\mathscr {C}}}_{\text {c}}^\infty ((0,T)\times {{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N)\) demonstrates that u is a weak solution to \(\partial _t u +{\mathcal {A}}(t) u = f(t)\) on \((0,T)\times {{\mathbb {R}}}_+^{1+d}\).
If \(f\in L^1((0,T);{{\mathscr {K}}}^{s+1,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N))\), then \(u\in L^\infty ((0,T);{{\mathscr {K}}}^{s+1,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N))\) and, moreover, \(u \in {{\mathscr {C}}}([0,T];{{\mathscr {K}}}^{s,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N))\) from the equation. Indeed, u is absolutely continuous with values in \({{\mathscr {K}}}^{s,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N)\). In addition, it follows from (4.6) that \(u(0)=u_0\). In the general case, we choose sequences \((u_{0\,m})\subset {{\mathscr {K}}}^{s+1,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N)\) and \((f_m) \subset {{\mathscr {C}}}([0,T];{{\mathscr {K}}}^{s+2,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N))\) such that
Let \((u_m)\subset {{\mathscr {C}}}([0,T];{{\mathscr {K}}}^{s+1,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N)) \cap {{\mathscr {C}}}^1([0,T];{{\mathscr {K}}}^{s,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N))\) be the sequence of solutions to Eq. (4.1), with the data \((u_0,f)\) replaced with \((u_{0m},f_m)\). By Proposition 4.3, \((u_m)\) is a Cauchy sequence in \({{\mathscr {C}}}([0,T];{{\mathscr {K}}}^{s,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N))\). It is readily seen that its limit u is the desired solution. \(\square \)
Eventually, we discuss higher regularity with respect to t.
Proposition 4.5
Let \(u_0\in {{\mathscr {K}}}^{s+\sigma ,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N)\), \(f\in \bigcap _{r=0}^\sigma W^{r,1}((0,T);{{\mathscr {K}}}^{s-r+\sigma }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N))\) for some \(s\in {{\mathbb {R}}}\), \(\sigma \in {{\mathbb {N}}}_0\). Then the unique solution u to Eq. (4.1) belongs to the space \(\bigcap _{r=0}^\sigma {{\mathscr {C}}}^r([0,T];\) \({{\mathscr {K}}}^{s-r+\sigma }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N))\). Moreover, the energy inequality
holds.ccccqwaaw
Proof
We proceed by induction on \(\sigma \).
The base case \(\sigma =0\) was treated in Proposition 4.4.
For the induction step \(\sigma \rightarrow \sigma +1\), suppose that \(u_0\in {{\mathscr {K}}}^{s+\sigma +1,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N)\), \(f\in \bigcap _{r=0}^\sigma W^{r,1}((0,T);\) \({{\mathscr {K}}}^{s-r+\sigma +1}({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N))\). By induction hypothesis, \(u \in \bigcap _{r=0}^\sigma {{\mathscr {C}}}^r([0,T];\) \({{\mathscr {K}}}^{s-r+\sigma +1}({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N))\) (upon replacing s with \(s+1\)). Moreover, \(u_t = \partial _t u\) solves the equation
where \(f(0)-{{\mathcal {A}}}(0) u_0\in {{\mathscr {K}}}^{s+\sigma ,\delta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N)\), \(\partial _t f - (\partial _t{{\mathcal {A}}}) u\in \bigcap _{r=0}^\sigma W^{r,1}((0,T);{{\mathscr {K}}}^{s-r+\sigma }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N))\). Again by induction hypothesis, we conclude that \(\partial _t u\in \bigcap _{r=0}^\sigma {{\mathscr {C}}}^r([0,T];{{\mathscr {K}}}^{s-r+\sigma }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N))\). Altogether, we obtain that \(u\in \bigcap _{r=0}^\sigma {{\mathscr {C}}}^r([0,T];{{\mathscr {K}}}^{s-r+\sigma +1}({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N))\) as required. \(\square \)
4.2 Well-posedness in Sobolev spaces with asymptotics
Here we establish Theorem 1.2 in full generality. In fact, we only derive the fundamental energy inequality. Then the rest of the proof is completely analogous to the proof in the previous section, and it is omitted.
Proposition 4.6
Let \(u\!\in \! {{\mathscr {C}}}([0,T];H_{P,\theta }^{s+1,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d}; {{\mathbb {C}}}^N))\cap {{\mathscr {C}}}^1([0,T];H_{P,\theta }^{s,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d}; {{\mathbb {C}}}^N))\) for some \(P\in \underline{As }^\delta \), \(s\in {{\mathbb {R}}}\), and \(\theta \ge 0\). Then
Proof
As before, we set \(u_0=u(0)\), \(f= \partial _t u +{{\mathcal {A}}}(t)u\). By interpolation, we may assume that \(\pi _{{\mathbb {C}}}P\cap \Gamma _{1/2-\delta -\theta }=\emptyset \). We then proceed in three steps.
Step 1 By Proposition 3.26, taking traces one has
This is a Cauchy problem for an \(N\times N\) first-order hyperbolic system in \((0,T)\times {{\mathbb {R}}}^d\). Hyperbolicity follows from
Solving these systems successively using Proposition A.2, one finds
for \((p,k)\in P\), \(\Re p>1/2-\delta +\theta \).
Step 2 Set \(v_0 = u_0 - \sum _{\begin{array}{c} (p,k)\in P,\\ \Re p>1/2-\delta -\theta \end{array}} \Gamma _{pk}( \gamma _{pk}u_0)\in \mathcal K^{s-\theta +1,\delta +\theta }({{\mathbb {R}}}_+^{1+d};{{\mathbb {C}}}^N)\),
Now we solve the hyperbolic system
Then, by Proposition 4.4,
Step 3 Because of \(u=v + \sum _{\begin{array}{c} (p,k)\in P,\\ \Re p>1/2-\delta -\theta \end{array}} \Gamma _{pk} (\gamma _{pk}u)\), it follows that
This completes the proof. \(\square \)
Remark
By the arguments above, one can show that the Cauchy problem (4.1) is well-posed in the Sobolev spaces \(H_{P,\theta }^{s,(\delta ,\rho )}({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {C}}}^N)\), where
for \(s,\rho \in {{\mathbb {R}}}\), \(P\in \underline{As }^\delta \), and \(\theta \ge 0\). In view of
this immediately leads to the well-posedness of the Cauchy problem (4.1) in \({{\mathscr {S}}}_P({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {C}}}^N)\). More precisely, Eq. (4.1) has a unique solution \(u \in {{\mathscr {C}}}^\infty ([0,T];{{\mathscr {S}}}_P({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {C}}}^N))\) provided that \(u_0\in \) \({{\mathscr {S}}}_P({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {C}}}^N)\), \(f\!\in \!{{\mathscr {C}}}^\infty ([0,T];{{\mathscr {S}}}_P({\overline{{{\mathbb {R}}}}}_+^{1+d};{{\mathbb {C}}}^N))\).
References
Benzoni-Gavage, S., Serre, D.: Multidimensional Hyperbolic Partial Differential Equations: First-Order Systems and Applications. Oxford Math. Monogr., Clarendon Press, Oxford (2007)
Casella, E., Secchi, P., Trebeschi, P.: Non-homogeneous linear symmetric hyperbolic systems with characteristic boundary. Differ. Integral Equ. 19, 51–74 (2006)
Chazarain, J., Piriou, A.: Introduction to the Theory of Linear Partial Differential Equations. Stud. Math. Appl., vol. 14. North-Holland, Amsterdam (1982)
Harutyunyan, G., Schulze, B.-W.: Elliptic Mixed, Transmission and Singular Crack Problems. EMS Tracts Math, vol. 4. Eur. Math. Soc., Zürich (2008)
Hedayat Mahmoudi, M., Schulze, B.-W., Tepoyan, L.: Continuous and variable branching asymptotics. J. Pseudo-Differ. Oper. Appl. 6, 69–112 (2015)
Hintz, P., Vasy, A.: Stability of Minkowski space and polyhomogeneity of the metric. Ann. PDE 6, 146 (2020)
Hörmander, L.: The Analysis of Linear Partial Differential Operators. III. Pseudo-Differential Operators, Classics Math. Springer, Berlin, Reprint of the 1994 edition (2007)
Kapanadze, D., Schulze, B.-W., Witt, I.: Coordinate invariance of the cone algebra with asymptotics. In: Albeverio, S., Demuth, M., Schrohe, E., Schulze, B.-W. (eds.) Parabolicity, Volterra calculus, and Conical Singularities, Oper. Theory Adv. Appl., vol. 138, pp. , 307–358. Birkhäuser, Basel (2002)
Krainer, T., Mendoza, G.A.: Boundary value problems for first order elliptic wedge operators. Am. J. Math. 138, 585–656 (2016)
Kreiss, H.-O.: Initial boundary value problems for hyperbolic systems. Commun. Pure Appl. Math. 23, 277–298 (1970)
Liu, X.-C., Ruan, Z.-P., Witt, I.: Elliptic boundary problems for edge-degenerate pseudodifferential operators. I: The general calculus. II: Coordinate invariance (Forthcoming)
Liu, X.-C., Witt, I.: Asymptotic expansions for bounded solutions to semilinear Fuchsian equations. Doc. Math. 9, 207–250 (2004)
Lopatinskii, Y.B.: The mixed Cauchy–Dirichlet type problem for equations of hyperbolic type. Dopovidi Akad. Nauk Ukrain. RSR Ser. A 668, 592–594 (1970). (Ukrainian)
Majda, A., Osher, S.: Initial-boundary value problems for hyperbolic equations with uniformly characteristic boundary. Commun. Pure Appl. Math. 28, 607–675 (1975)
Melrose, R.: The Atiyah–Patodi–Singer Index Theorem, Res. Notes Math, vol. 4. A K Peters, Wellesley, MA (1993)
Melrose, R., Mendoza, G.: Elliptic Operators of Totally Characteristic Type. MSRI Prepint (1983)
Ohkubo, T.: Regularity of solutions to hyperbolic mixed problems with uniformly characteristic boundary. Hokkaido Math. J. 10, 93–123 (1981)
Rauch, J.: Symmetric positive systems with boundary characteristic of constant multiplicity. Trans. Am. Math. Soc. 291, 167–187 (1985)
Rempel, S., Schulze, B.-W.: Asymptotics for Elliptic Mixed Boundary Problems. Pseudo-Differential and Mellin Operators in Spaces with Conormal Singularity, Math. Res., vol. 50. Akademie Verlag, Berlin (1989)
Sakamoto, R.: Hyperbolic Boundary Value Problems. Cambridge University Press, Cambridge (1982)
Sakamoto, R.: Hyperbolic Cauchy problems in a region with a characteristic boundary of full multiplicity. J. Math. Kyoto Univ. 29, 283–308 (1989)
Schulze, B.-W.: Pseudo-Differential Operators on Manifolds with Singularities. Stud. Math. Appl., p. 24. North-Holland, Amsterdam (1991)
Schulze, B.-W.: Boundary Value Problems and Singular Pseudo-Differential Operators, Pure Appl. Math. (N. Y.). J. Wiley, Chichester (1998)
Secchi, P.: The initial-boundary value problem for linear symmetric hyperbolic systems with characteristic boundary of constant multiplicity. Differ. Integral Equ. 9, 671–700 (1996)
Witt, I.: On the factorization of meromorphic Mellin symbols. In: Albeverio, S., Schrohe, E., Demuth, M., Schulze, B.-W. (eds.) Parabolicity, Volterra Calculus, and Conical Singularities. Oper. Theory Adv. Appl., vol. 138, pp. 279–306. Birkhäuser, Basel (2002)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The first author was supported by NSFC Grant 11771206. Part of the work was done while she was visiting the University of Göttingen.
Some basic material
Some basic material
For the reader’s convenience, we collect here a few basic facts that are used in the main body of the paper without further reference. (See Sect. 1.4 for the notation used.)
1.1 The Mellin transform
The Mellin transform M is defined by
for \(u \in {{\mathscr {C}}}_{\text {c}}^\infty ({{\mathbb {R}}}_+)\). It is then suitably extended to other spaces of (generalized) functions. The inverse transform is given by \(M^{-1}v(x) = \frac{1}{2\pi i } \int _{\Gamma _\beta } x^{-z}v(z)\,d z\) for a suitable \(\beta \in {{\mathbb {R}}}\) depending on the situation under consideration.
Among others, the Mellin transform has the following properties:
-
(a)
\(\{-\,x \partial _x u\}\,\tilde{}\,(z) = z\,\tilde{u}(z)\),
-
(b)
\(\{x^{-\gamma } u\}\,\tilde{}\,(z) = {\tilde{u}}(z-\gamma )\) for \(\gamma \in {{\mathbb {R}}}\),
-
(c)
\(\{\log x\, u\}\,\tilde{}\,(z) = \partial _z {\tilde{u}}(z)\),
-
(d)
\(M:L^2({{\mathbb {R}}}_+,x^{-2\gamma }\,d x)\rightarrow L^2\bigl (\Gamma _{1/2-\gamma }, (2\pi i )^{-1}d z\bigr )\) is unitary for \(\gamma \in {{\mathbb {R}}}\).
In particular, for \(h\in {\mathcal {M}}^\mu ({{\mathbb {R}}}^d)\), \(u\in {{\mathscr {H}}}^{s,\gamma }({{\mathbb {R}}}_+^{1+d})\), one has that
and then that \({\text {op}}_M(h) :{{\mathscr {H}}}^{s+\mu ,\gamma }({{\mathbb {R}}}_+^{1+d}) \rightarrow {{\mathscr {H}}}^{s,\gamma }({{\mathbb {R}}}_+^{1+d})\) is continuous.
Lemma A.1
Let \(v\in {{\mathscr {S}}}_P({\overline{{{\mathbb {R}}}}}_+^{1+d})\) for some asymptotic type P. Then \(\tilde{v}(z,\cdot )\) is a meromorphic function of \(z\in {{\mathbb {C}}}\) with values in \({{\mathscr {S}}}({{\mathbb {R}}}^d)\) having poles at most at points \(z=p\) for \(p\in \pi _{{\mathbb {C}}}P\). Moreover, for v as given in (3.6),
where \(v_{p0},\dotsc ,v_{p,m_p-1}\in {{\mathscr {S}}}({{\mathbb {R}}}^d)\). In addition, if \(\chi \in {{\mathscr {C}}}^\infty ({{\mathbb {C}}})\) satisfies \(\chi (z)=0\) for \({\text {dist}}(z,\pi _{{\mathbb {C}}}P)\le 1/2\) and \(\chi (z)=1\) for \({\text {dist}}(z,\pi _{{\mathbb {C}}}P)\ge 1\), then \(\chi {\tilde{v}}\in {{\mathscr {C}}}^\infty \bigl ({{\mathbb {R}}}_\beta ;{{\mathscr {S}}}({{\mathbb {R}}}_{(y,\tau )}^{d+1})\bigr )\).
Similar statements hold for \((\varphi v)\,\tilde{}\,(z,\cdot )\) when \(v \in H_{P,\theta }^{s,\delta }({\overline{{{\mathbb {R}}}}}_+^{1+d})\), where now, however, \((\varphi v)\,\tilde{}\,(z,\cdot )\) is holomorphic in the half-space \(\{z\in {{\mathbb {C}}}\mid \Re z\ge 1/2-\delta \}\) and meromorphic in the open half-space \(\{z\in {{\mathbb {C}}}\mid \Re z>1/2-\delta - \theta \}\). As these statements are more involved in their formulation and we do not make use of them, we refrain from making these statements explicit. (See, e.g., [19, 22].)
1.2 The hyperbolic Cauchy problem
For the sake of completeness, we state a result about the well-posedness of the hyperbolic Cauchy problem in the spaces \(H^{s,\langle k\rangle }({{\mathbb {R}}}^d;{{\mathbb {C}}}^N)\) for \((s,k)\in {{\mathbb {R}}}\times {{\mathbb {Z}}}\). For \(k=0\), this is a standard result, but for \(k\ne 0\) we were not able to locate it in the literature.
Let \({{\mathcal {B}}}\in {{\mathscr {C}}}^\infty ([0,T];\Psi ^1({{\mathbb {R}}}^d;{{\mathbb {C}}}^N))\) and assume that the operator \(\partial _t +{{\mathcal {B}}}(t,y,D_y)\) is symmetrizable hyperbolic uniformly in \((t,y)\in [0,T]\times {{\mathbb {R}}}^d\) in the sense that there is a \(b \in S^{(0)}([0,T]\times {{\mathbb {R}}}^d\,\times \) \(({{\mathbb {R}}}^d{\setminus }0);{\text {Mat}}_{N\times N}({{\mathbb {C}}}))\) such that
-
(i)
\(b(t,y,\eta ) = b(t,y,\eta )^*\ge c\,I _{N}\) for some constant \(c>0\),
-
(ii)
\(b(t,y,\eta )\,\sigma _\psi ^1({{\mathcal {B}}})(t,y,\eta )\) is skew-Hermitian for all \((t,y,\eta )\in [0,T]\times {{\mathbb {R}}}^d\times ({{\mathbb {R}}}^d{\setminus }0)\).
We consider the Cauchy problem
Proposition A.2
Let \(u_0\in H^{s+\sigma ,\langle k\rangle }({{\mathbb {R}}}^d;{{\mathbb {C}}}^N)\), \(f\in \bigcap _{r=0}^\sigma W^{r,1}((0,T);H^{s-r+\sigma ,\langle k\rangle }({{\mathbb {R}}}^d;{{\mathbb {C}}}^N))\) for some \((s,k)\in {{\mathbb {R}}}\times {{\mathbb {Z}}}\), \(\sigma \in {{\mathbb {N}}}_0\). Then Eq. (A.3) possesses a unique solution
Proof
We introduce the operator \(M=\log ^k \langle D_y\rangle \) and set \(v = M u\), \(v_0= Mu_0\), and \(g=Mf\). Then \(v_0\in H^{s+\sigma }({{\mathbb {R}}}^d;{{\mathbb {C}}}^N)\), \(g\in \bigcap _{r=0}^\sigma W^{r,1}((0,T);H^{s-r+\sigma }({{\mathbb {R}}}^d;{{\mathbb {C}}}^N))\), and \(u\in \bigcap _{r=0}^\sigma {{\mathscr {C}}}^r([0,T];\) \(H^{s-r+\sigma ,\langle k\rangle }({{\mathbb {R}}}^d;{{\mathbb {C}}}^N))\) is equivalent to \(v\in \bigcap _{r=0}^\sigma {{\mathscr {C}}}^r([0,T];H^{s-r+\sigma }({{\mathbb {R}}}^d;{{\mathbb {C}}}^N))\). Furthermore, v solves the Cauchy problem
Now, \({{\mathcal {B}}}+ [M,{{\mathcal {B}}}]M^{-1}\in {{\mathscr {C}}}^\infty ([0,T];\Psi ^1({{\mathbb {R}}}^d;{{\mathbb {C}}}^N)+\bigcap _{\epsilon >0}\Psi _{1,0}^\epsilon ({{\mathbb {R}}}^d;{{\mathbb {C}}}^N))\), while \(\sigma _\psi ^1({{\mathcal {B}}}+ \left[ M,{{\mathcal {B}}}\right] M^{-1}) = \sigma _\psi ^1(B)\). Then standard hyperbolic theory yields that Eq. (A.4) possesses a unique solution \(v\in \bigcap _{r=0}^\sigma {{\mathscr {C}}}^r([0,T];\) \(H^{s-r+\sigma }({{\mathbb {R}}}^d;{{\mathbb {C}}}^N))\). \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ruan, Z., Witt, I. Hyperbolic problems with totally characteristic boundary. J. Pseudo-Differ. Oper. Appl. 15, 29 (2024). https://doi.org/10.1007/s11868-024-00599-x
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11868-024-00599-x
Keywords
- First-order hyperbolic systems
- Totally characteristic boundary
- Asymptotic expansions of conormal type
- Discrete asymptotic types
- Sobolev spaces with asymptotics
- Calculus of cone-degenerate pseudo-differential operators
- Holomorphic conormal symbols
- Singular analysis



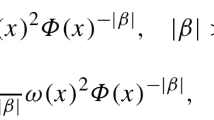
 , where
, where  .
.