1 Introduction

As a 21st-century skill, creativity has attracted increasing attention in mathematics education. Much of the early research on mathematical creativity examined the relationship between creativity and either mathematical ability (Kattou et al., 2013) or academic achievement (Mann, 2009), with a focus on gifted students (Leikin et al., 2009). Different definitions of creativity are emerging (Joklitschke et al., 2022), and research on creativity in mathematics education has expanded to address aspects such as students’ creativity in problem posing (Van Harpen & Sriraman, 2013), teachers’ perception of creativity (Bolden et al., 2010; Leikin et al., 2013; Lev-Zamir & Leikin, 2013), and creativity in teaching practices (Mhlolo, 2017). However, regarding creativity as a learning outcome in digital mathematical activities (Weng et al., 2022b), few studies have examined the development of creativity with mathematical and computational thinking, specifically the emergence and merging of mathematical concepts and programming skills when individuals engage in creative programming tasks.

Although creativity in mathematics can be problem-oriented, as in being inventive in problem-solving situations, it is far more than that. For example, students’ creativity development in the context of mathematical problem-based digital making—a form of constructionist learning which emphasizes the creation of digital or tangible artifacts via programming during mathematical problem-solving (Ng & Cui, 2021)—could be understood in terms of creative exploration, creative solution, or creative expression (Weng et al., 2022a, b). While such characterizations offer new insights into different forms of creativity in mathematical activities, limited empirical evidence of them exists beyond snapshots of student work, and we lack understanding of the actions of creative exploration in constructing mathematical and programming concepts. As Leikin and Elgrably (2022) point out, the “relationship between creative process and creative products in mathematics has barely been explored systematically” (p. 36). Extending this argument, we suggest that studies linking creative actions (as processes) and creative artefacts (as products) in the context of programming-based mathematical activities are urgently required, given the recent rise of child-friendly programming language and emerging research on the integration of programming activities in mathematics education (see a review in Ye et al., 2023a).

Moreover, more studies consider student creativity than teacher creativity: Only six of 49 empirical studies on creativity in mathematics education published between 2010 and 2021 investigated teachers’ creativity-related conceptions and competencies (Leikin & Sriraman, 2022). Among them, five investigated pre-service or in-service teachers’ conceptions of creativity (Bolden et al., 2010; Leikin et al., 2013; Lev-Zamir & Leikin, 2013), the development of creativity awareness (Shriki, 2010) and creativity-noticing professional knowledge (Hoth et al., 2017) through questionnaires, interviews and analysis of teachers’ engagement in mathematics activities or teaching practices. In addition, Zazkis (2017) explored lesson play tasks as a fruitful avenue for displaying and supporting teachers’ creativity. As the work of Kynigos and Diamantidis (2022) has evidenced that appropriate tools and discursive environments may offer space for actions with creative potential for students, we suggest teachers’ engagement in programming-based mathematical activities may also serve as significant professional development opportunities, giving rise to their new mathematical thinking and supporting their creativity-noticing. Furthermore, teachers’ situated knowledge, experiences, and practices play an important role in fostering students’ creativity (Lu & Kaiser, 2022; Pitta-Pantazi et al., 2018). Thus, this study aimed to illuminate the creative actions exhibited by school mathematics teachers during programming-based mathematical activities as part of their professional development. Specifically, we focused on the creative actions demonstrated by mathematics teachers in using the block-based programming tool, Scratch, to create geometric shapes, and we explored how their creative actions were mediated by their mathematical and programming concepts, as well as the programming tool used, which in turn provided new possibilities for doing mathematics. Therefore, this study seeks to address the following research questions (RQs):

  1. (1)

    What creative actions do mathematics teachers exhibit during programming-based mathematical activities?

  2. (2)

    How might creative actions serve as objects-to-think-with to engender new possibilities for mathematics teachers to do mathematics in a programming context?

2 Theoretical background

In this section, we first review the literature around creativity and introduce the framework of creative mathematical action (Riling, 2020). We then describe the theory of constructionism, which underpins the design of this study, and discuss our conceptualization of Scratch as an “object-to-think-with” during programming-based mathematical activities under the framework of creative mathematical action.

2.1 Creativity and creative mathematical action

Creativity, defined as the generation of novel and useful ideas or products (Amabile, 1996), has received widespread attention in K-12 education. Research about creativity in mathematics education often deals with the construct of “mathematical creativity”, though its notion in empirical studies is diverse. Joklitschke et al. (2022) conducted a systematic review and identified five predominant notions of creativity in mathematics education research. That is, creativity is defined as (1) flexibility, fluency, and/or other characteristics; (2) divergent thinking; (3) a sequence of stages; (4) creative mathematical reasoning; and (5) person-, product-, process-, and/or behavior-based notion. In addition, creativity can be also grouped into dimensions of creativity-as-talent, creativity-as-product, and creativity-as-process. Creativity-as-talent focuses on personal characteristics, such as the relationship between students’ creativity and mathematical abilities (Kattou et al., 2013), while creativity-as-product examines the novelty and usefulness of students’ artefacts as learning outcomes (Weng et al., 2022b). As for creativity-as-process, attention is paid to personal creativity that occurs during the learning process, which relates to what Beghetto and Kaufman (2007) term mini-c creativity—“the novel and personally meaningful interpretation of experiences, actions, and events” (p.73). Other scholars also highlight the cognitive aspect of creativity-as-process, or the process of creative thinking (Schoevers et al., 2019) during learning activities.

Considering the interplay among person, product and process in mathematical creativity rather than addressing a particular level of creativity, Riling (2020) proposed the creative mathematical action framework (CMAF) which defines creative mathematical action as “one that transitions a given mathematical context into a new version of mathematics by creating ways of doing or thinking about mathematics that were previously not possible for a particular community of mathematicians” (p. 17). Noteworthy, the mathematician mentioned refers to any individual who engages in doing mathematics rather than only those who are mathematical experts. Specifically, the CMAF emphasizes four important components of action, context, new possibilities and community:

  1. 1.

    Mathematical context: creativity is not the sudden, random endeavor of individuals, but is inevitably influenced by the mathematical concepts and practices existing in the community.

  2. 2.

    New mathematical possibilities: the set of mathematical concepts and practices of any community is not pre-ordained; rather, it will vary according to the creative acts performed.

  3. 3.

    Mathematical community: how and what mathematicians (everyone in the community) create will depend on their identities, their relationship with one another and their relative engagement with privilege and oppression.

  4. 4.

    Creative action: since each action has its roots in one’s community, creative acts inside one community may or may not lead to new mathematical possibilities in another.

The CMAF highlights the interactions between the four components, and we thus also see the possibility of creative actions in programming-based mathematical activities. Concerning creativity, Kafai (2006) explains that constructionist learning is a form of creative experiment in which learners construct, examine, and revise connections between pre-existing and new knowledge gained from the real world. This idea has important implications for mathematics education, as it implies that learning is tangible and experimental. Furthermore, constructionist learning is highly relevant to doing mathematics by means of programming (Feurzeig et al., 2011; Kynigos et al., 2014; Papert, 1980). Thus, we see the potential to investigate mathematics teachers’ creative actions in a programming-based mathematical context as a form of professional development. We will detail the concept of constructionist learning and the relationship between creative mathematical actions in the next section.

2.2 Constructionism and “Object-to-think-with”

This research is underpinned by Seymour Papert’s constructionism (Papert & Harel, 1991) which was influenced by Jean Piaget’s constructivist learning theory. While both constructivism and constructionism are premised on students’ active construction of knowledge, constructionism highlights that the most productive learning happens when learners create a personal and shareable artefact. Therefore, the meaning of “construction” has two levels: learners create artefacts in the physical world (first-level construction) which serves as an “object-to-think-with” to facilitate them to build coherent and cognitive structures about the learning content (second-level construction), that is, “learning-by-making”. Thus, whereas constructivism suggests that learners move progressively from concrete objects to mental symbolic objects and can increasingly extract rules from empirical regularities, constructionism emphasizes knowledge construction in situ, in the sense that learners should be situated to become “one” with the environment instead of “looking at a distance” (Ackermann, 2001).

Papert (1980) identified his Logo programming as an “object-to-think-with,” namely a physical or digital or even mental object that becomes a cognitive artefact in which “there is an intersection of cultural presence, embedded knowledge, and the possibility for personal identification” (p. 11) during the thinking and learning process (e.g., a formula in a computer program can be seen as a digital object-to-think-with). As captured by Sinclair et al. (2013) making a square in Logo can be seen as a creative act or an example of “potential inventive moments in which the human-technology interaction gives rise to new ways of thinking and moving” (p. 242), which exemplifies Logo programming as engagement with intellectual tools and affording thinking about concepts and strategies that are grounded in intuitive knowledge (Noss & Hoyles, 2017). Thus, an object-to-think-with can serve as “a cognitive tool that thinkers can observe, manipulate, or probe, and in doing so test and explore complex phenomena or ideas with which they are unfamiliar” (Holbert & Wilensky, 2019, p. 36).

While Papert’s Logo was, in the early 1990s, a high-tech and active computational expressive medium, the emergence of forthcoming digital technologies (e.g., block-based programming, geometrized programming, tangible programming; Ye et al., 2023a) demands the need to reconceptualize constructionist learning with current programming tools. To this end, the work of Ng and colleagues (Ng & Cui, 2021; Ng et al., 2021) has provided insight into “digital making” as a form of constructionist learning afforded by block-based programming environments, where students actively engage in constructing digital artefacts in the form of programming solutions to mathematical problems. In these studies, it was shown that Scratch was instrumented as a creative environment in which mathematics can not only be read numerically but also heard and visually and dynamically represented.

From the perspective of creative mathematical actions, learners and their more-knowledgeable-others establish a community that occasions the creation of ideas and artefacts in the programming-based mathematical context. Within this shared community, learners will be expected to leverage pre-existing programming and mathematical knowledge to engage in creative activities in which programming artefacts serve as an object-to-think-with to yield new experiences of doing mathematics. Therefore, this study conceptualizes Scratch as an object-to-think-with that facilitates mathematical actions with creative potential, and we designed programming tasks to inspire new ways to think about geometry in the given constructionist learning context. From this, the overall objective of this study was to investigate what creative actions mathematics teachers exhibit while engaging in geometrical constructions in a programming context, and how these actions facilitated them to develop mathematical and computational concepts, thus experiencing new possibilities for doing mathematics as part of their professional development.

3 Methodology

This study is situated in a series of Scratch professional development workshops which aim to facilitate in-service mathematics teachers’ learning in a programming-based mathematical context. The following subsections detail the methods undertaken.

3.1 Participants and context

A 10-h, five-week professional development workshop series in Scratch programming was delivered online (one two-hour session per week) to six in-service secondary school mathematics teachers, recruited through the network of the first author (hereafter, “the researcher”) in Mainland China. Inclusion criteria of participants were: (1) having a range (1 to 5 years) of teaching experience; (2) having no prior experience of Scratch programming; and (3) showing a strong interest in programming-based mathematical activities as professional development. Four female and two male teachers, aged from 20 to 30, were divided into three pairs, and each pair attended the workshops separately to maintain an optimal researcher: participant ratio of 1:2 for in-depth analysis. Most of the sessions are completed by two participants working together throughout; but as the session chosen for this study aims to examine the creativity of each individual, the two participants first worked together to familiarize themselves with some basic functionality by solving a geometry task, and then worked independently with Scratch to create geometric figures. Only when the participants encountered difficulties would the researcher briefly pause their work and lead a discussion between the two participants.

3.2 Task design

We chose a task used during the third session as the focus of our investigation because it offered flexibility for participants to express and create their figures through tinkering with different aspects of rotational symmetry, namely, what figure to be rotated and how to rotate it. From a programming perspective, the task may prompt the use of loops when making a figure with congruent sides and congruent interior angles, and of subroutines (“My Block” in Scratch) when creating duplicates of a figure. During the session, we initially invited the teachers to draw some geometrical figures utilizing concepts such as angle of turn and interior angles of regular polygons. Then, they were given a sample figure made up of six identical pentagons differing by a 60-degree turn at one of the vertices of the pentagon (Fig. 1) and asked to work collaboratively to replicate it in Scratch. This was intended to familiarize the teachers with the drawing functions (“Pen up,” “Pen down,” “erase all”) and some transformation functions (“turn,” “move,” “rotate”). Following that, they were given 30 min to engage in the exploratory drawing task, working individually to create any figures that they wished according to their imagination.

Fig. 1
figure 1

Sample figure of rotational symmetry

Full size image

3.3 Data collection and analysis

Given that “we may not, and probably cannot, account for students’ [or others’] mathematics using our own mathematical concepts and operations” (Steffe & Thompson, 2000, p. 268), we collected data through task-based semi-structured interviews during participants’ geometry figure construction process. Task-based semi-structured interview is suitable for this qualitative and in-depth study, as we could interpret the participants’ task performance to look for evidence of creative actions from their discourse. To maximize discourse opportunities, we used open questions to prompt the participants to express their thought processes (e.g., What did you do? Why did you do this? How did you achieve this drawing? Is there anything else you would like to draw?) By asking a series of what, why and how questions, we aimed to interpret the participants’ thinking processes from a discursive approach while triangulating with their programming activities as captured by screen-recording. Since an important characteristic of the qualitative research methodology is the collection and analysis of data from multiple sources, we collected observation data and the programming artefacts during the task. In summary, the qualitative data emanated from several sources: video-recorded construction sessions which captured the participants’ interviews and computer screens on which they were working; the participants’ final programming codes and working notes; and the researcher’s field notes.

Under the framework of creative mathematical actions, our analysis of the teachers’ creative actions while engaging in their geometric creations was twofold in response to the two RQs posed. To answer RQ1, our data analysis focused on identifying the creative actions demonstrated by the participants during the task, particularly novelty as an attribute of creativity. As we see opportunities for our designed programming-based geometry task to be a medium for expression by extending and recreating the initial drawing in novel ways, we focus our attention on the creative process—“the sequence of thoughts and actions that leads to a novel, adaptive production” (Lubart, 2001, p. 295)—rather than just the creative product. Thus, we attended to the actions taken with the programming tool (as context) upon which there emerged new ways to interpret teachers’ construction mathematically or computationally during the task from the perspective of CMAF. In terms of RQ2, we adopted thematic analysis to examine how creative actions provide new possibilities for doing mathematics by the teacher participants. Specifically, we look for evidence of how teachers both develop and integrate mathematical and programming concepts when they demonstrate creative actions during the construction.

We conducted thematic analysis coupled with deductive and inductive coding to analyze moments that participants demonstrated creative actions or (re-)shaped their mathematical and programming concepts in their ongoing geometric creation, and we undertook iterative comparisons to verify the findings obtained. In Phase 1, we conducted attribute coding, that is, to organize the data by their attributes (i.e., type of observation, type of data collection method, which participant). We then carried out topic coding, another deductive analysis, to sort the data into categories that are relevant to the respective research questions in Phase 2. From there, open coding was applied to identify emerging ideas in the data, which generated inductive codes: “changing values”, “remixing and reusing”, respectively under RQ 1, and “recognizing difference between counter- concepts”, “experiencing connections between family concepts”, “exploring particular concepts at multiple levels”, “algorithmic thinking”, “iterative thinking” under RQ 2 in Phase 3. Finally, based on the open codes, we developed themes that included two kinds of creative actions (i.e., testing and iterating practices) and two forms of new possibilities for doing mathematics (i.e., new ways to engage in mathematical processes and understand mathematics from a computational perspective). The thematic analysis is supported by the lens of CMAF, which informs the relations among the creative actions, tools, and new possibilities for doing mathematics.

4 Results

In this section, we respond to the RQs by analyzing two participants’ creative mathematical actions during the geometric construction and detail the new possibilities of doing mathematics in the programming context. They were chosen because they were more expressive during the interview process, which allowed us to gain a clear understanding of their actions. Furthermore, although the other participants evidenced discussions and results similar to those evidenced by these two cases, the creation process of these two teachers encompassed the commonality and distinctiveness observed in this case study.

4.1 Case 1

We characterized Teacher 1’s (T1) construction as encompassing three kinds of approach: initial intentional creation related to rotations of regular polygons; accidental or unplanned creation with rotations of non-regular polygons and purposeful new creation based on translation.

4.1.1 Intentional creation: rotations of regular polygons

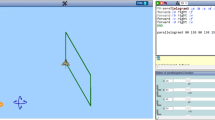
In the given mathematical context to draw a sample figure, T1 first defined a My Block named “regular pentagon” and recalled the subroutine in the main program (Fig. 2) to draw several rotated pentagons. Then, T1 associated her drawing with another polygon by connecting the properties of hexagons with her programming codes. That is, she changed the number of sides from 5 to 6, and the angle of the rotation from 72 to 60 degrees in her original subroutine to draw the repeated hexagon six times. Figure 3a shows her initial explorative drawing upon her enactment of the existing mathematics concepts and programming skills in the programming-based mathematical learning context.

Fig. 2
figure 2

Teacher 1’s programming codes for the sample figure

Full size image
Fig. 3
figure 3

Some figures created by Teacher 1: (a) initial explorative drawing; (b) a trapezoidal rotation figure; (c) a non-enclosed figure; (d) an enclosed trapezoid; (e) a figure formed by the rotation of a triangle. Note. The red arrows indicate the final position and direction of the pen

Full size image

4.1.2 Unplanned creation: rotations of non-enclosed polygons

Subsequently, the action of T1 to change the values of different parameters triggered some unplanned creative works that just opened new possibilities for doing mathematics. At first, T1 offered to draw a new figure with a triangle as the base figure (Episode 1, [25:16]), to be rotated six times. However, when she changed the number of sides of the figure from six to three, she neglected to change the turn angle, thus inadvertently drawing three sides of a regular hexagon. Finding that the drawing resembled a trapezoidal rotation shape (Fig. 3b), T1 realized that the [turn clockwise 60°] block in the subroutine had made a different interior angle from that anticipated. Here, her mathematical knowledge of interior angles of regular polygons in the programming context of turning the Pen supported her new experience of drawing geometric figures while debugging the program. The following episode illustrates this new experience of doing mathematics brought by T1’s creative actions.

Episode 1. Teacher 1 questioned why she had created a trapezoid instead of a triangle.

What was said

What was done

[25:16] T1: I wanted to change it to a triangle

[T1 changed the “side_number” parameter from 6 to 3 in My Block, and a trapezoid was created (Fig. 3d)]

[25:31] T1: It became a trapezoid

 

[25:35] R: Why does it draw this shape? Why is it not a triangle?

 

[25:57] T1: Why? …

[T1 inserted a “[wait 1 s]” block in the subroutine to slow down the drawing steps and observe the drawing process]

[28:04] T1: I see, I have set this [turn clockwise 60°] wrong, it should be 120 degrees

[T1 successfully drew the target figure after modifying the program (Fig. 3e)]

[28:41] R: Can you see what happened to the 60 degrees just now? Why is it drawn like that?

 

[29:25] T1: I see. Because I’ve defined the starting point as (0,0) every time here! So according to this code, first, it takes 40 steps from the starting point… then turns clockwise 60 degrees. Okay, then the second side. Then the Pen continues to turn clockwise 60 degrees and takes 40 steps, at which point it has reached my requirement that the number of sides equals three. The loop is over. Okay, and then what? When we repeat it, the point moves to (0,0), and it draws the next step again

[T1 ran the program and kept watching]

  1. T1 represents Teacher 1, R represents researcher

As shown above, T1 identified that she had created a non-enclosed figure upon the loop executed three times, each creating a line and performing a 60-degree rotation of the Pen direction (Fig. 3c). Furthermore, when the next subroutine was called in the main program, the Pen would be initialized to move back to (0,0) each time it was in a “Pen down” position, hence forming a line connecting the current position and (0,0), resulting in an enclosed trapezoid (Fig. 3d). With her programming knowledge, she modelled the codes with the properties of triangles and reflected that it was incorrect to make the Pen turn by 60 degrees (instead, the turn should be by 120°). Upon her change of codes at [28:04], the final figure which was made up of six triangles and with a rotational symmetry of degree six was formed (Fig. 3e).

Thus far, we see that T1’s creation is caused by changing two parameters, namely the number of line segments to be formed and the turn angle between each line, which would determine the shape of the base figure. Interestingly, by figuring out a bug in the program, T1 realized that even if she had made three segments, the base shape would not necessarily be a triangle if coupled with an incorrect turn angle, which would produce a non-enclosed figure [29:25]. Such a new experience of drawing provided opportunities for T1 to recognize the relationship between regular and non-regular, enclosed and non-enclosed figures which was illustrated in Episode 2.

Episode 2. Teacher 1’s exploration of base shapes evidencing her creative actions.

What was said

What was done

[34:43] R: Now [the base shape] isn’t a quadrilateral, is it?

[T1 created a shape as shown in Table 1, Figure c)

[34:46] T1: This isn’t a quadrilateral

[T1 changed the angle turn in the subroutine to 90° and obtained a figure with rotational symmetry of degree 6 by drawing 6 squares (Table 1, Figure d).]

[34:51] T1: Because it must be turned by 90 degrees to be a quadrilateral

[35:01] R: Okay. What do you need to change if you want to draw a regular octagon?

[T1 changed the number of sides to 8, the angle turn in the main program to 30° and the number of repetition to 12; however, the angle turn in the subroutine remains 90 o.]

[35:19] R: Would this draw a regular octagon?

 

[35:23] T1: Not now. I must do the calculations… 45 degrees

[T1 changed the angle turn in the subroutine from 90 o to 45°]

[35:49] T1: This is drawn with the regular octagon as the base figure…

(Table 1, Figure g)

[40:47] T1: Like the triangle that we just did, if I rotate it here by an angle other than its exterior angle, it ends up going three times, and after it’s done three times, it doesn’t go back to the origin point, but we set it up to move back to the (0,0), so it creates an extra side. Thus, the triangle becomes a quadrilateral

 

As depicted above, T1 has identified the underlying processes in the generation of regular and non-regular polygons which implicated new possibilities for doing mathematics upon the creative actions. Specifically, when drawing an interior angle (αo) of an n-sided regular polygon in Scratch, one needs to turn the Pen by its exterior angle (180- αo) because of the way Scratch interprets an angle by the turning of a Pen, as opposed to the angle formed by turning an array at a vertex. In other words, to create a regular octagon, one would need to make eight turns, each equaling the exterior angle of that regular octagon (i.e., 360/n = 360/8 = 45°; see [35:23]). Meanwhile, as in the case of making a trapezoid by forming three segments in the subroutine, T1 also generalized that when making n line segments and n turns that do not total 360°, the shape formed would be non-enclosed. Therefore, a non-regular polygon with n + 1 sides would be created due to the Pen moving back to (0,0) as programmed. Upon this discovery, T1 used the subroutine to create n-sided regular polygons and (n + 1)-sided non-regular polygonal base shapes, as well as tested different parameters in the main program that served to control the angle and number of rotations of the base shapes, thus producing the series of novel figures shown in Table 1.

Table 1 Teacher 1’s series of creations generated by changing values of different variables
Full size table

In summary, the creation of non-regular and regular shapes in Table 1 featured T1’s creative actions as afforded by the programming environment—she randomly changed the parameters inherited in the program (number of loops and exterior angle of the figure in the subroutine; the degrees and number of rotations in the main program) and explored how they generated different kinds of polygons with and without rotational symmetry. This indicates that T1 could flexibly create novel and esthetic graphics by integrating her mathematical concepts about regular polygons and rotational symmetry with her programming knowledge about loops and subroutines, which she developed from testing the value of different parameters in the program as a kind of creative mathematical action. The mathematical and programming concepts (emerged in the programming process) and artefacts (geometrical shapes created) developed contributed to T1’s creative actions uniquely within a programming-based mathematical context.

4.1.3 Purposeful new creation: translation of regular polygons

After experiencing new construction to explore the relationship between non-regular polygons and regular polygons, T1 proposed to produce some novel shapes by translating the base figure rather than rotating it at a point. As translating a figure was a different transformation from rotating it, she faced various challenges throughout the creation process and had to integrate her existing mathematical concepts of transformation and programming skills (a new block [change x by XX] which would translate the x-coordinate of the Pen) to achieve her creation. Initially, T1 placed the [change x by 10] block in the subroutine loop (Fig. 4a), resulting in a shape that did not match her imagining (Fig. 4b and c).

Fig. 4
figure 4

a Teacher 1’s initial subroutine for figure translation; b a shape created by the subroutine of (a); c the overall shape created when executing the codes as shown in (a)

Full size image

By reflecting on the difference between the translation process (in the mathematical sense) and the code sequence (in the programming sense), T1 found a bug in that the Pen position was changed after each side was drawn rather than after each figure was drawn, which relates to the computational concept of “sequence”. She then repositioned the block [change x by 10] (related to translation) in the main program loop (Fig. 5a) but had not expected that the program would cause the graphic to be rotated while simultaneously being translated to the right (Fig. 5b, i-ii), which provided opportunities for T1 to experience the connection of translations and rotations. Referred to the properties of translations and rotations, T1 successfully debugged the code by removing the [turn clockwise XX degrees] block (related to rotation) from the loop and produced her imagined figure (Fig. 5b, iii), which indicates that the computational concept of sequence is important to achieve a mathematical process. This episode also evidenced the role of the unexpected programming artefact as an object-to-think-with in inquiring about geometrical properties and reflecting on the program as T1 integrated a combination of mathematical and programming knowledge to facilitate her creative actions.

Fig. 5
figure 5

a Teacher 1 repositioned the block [change x by 10] in the main program loop; b some shapes created during the reflecting process

Full size image

4.2 Case 2

Unlike T1’s parameterless subroutine, Teacher 2’s (T2) figure construction began with a parameterized subroutine, which led to a series of progressive constructions related to the same mathematical concept: rotational symmetry of single figure, rotational symmetry of composite figures, and rotational symmetry of figures with rotational symmetry.

4.2.1 Rotational symmetry of single figure

In the pre-construction stage, by connecting the existing mathematical concepts of rotational symmetry and programming skills (loop and subroutines etc.) to investigate the method of creating regular pentagons with rotations, T2 designed a My Block (subroutine) with one parameter (“side_length,” Fig. 6a) which could take on different values of side lengths to change the overall size of the base shape. When the researcher proposed drawing another polygon (e.g. a regular hexagon) as the base figure, T2 soon added a second parameter, “exterior_angle,” in her My Block (Fig. 6b). Episode 3 illustrates T2’s sharing of her thinking with Teacher 3 (T3), which also depicts how she imagined her existing approach to solving the problem.

Fig. 6
figure 6

a A My Block with one parameter; b A My Block with two parameters; c a non-enclosed “hexagon” with one side missing

Full size image

Episode 3. Teacher 2’s sharing with Teacher 3 on her imagined approach.

What was said

[35:00] T3: I am wondering if we could make a My Block that could draw any n-sided shapes

[35:52] R: T2, can you share your thoughts on the My Block with T3? Because I noticed that your My Block has an extra parameter now

[36:03] T2: The [move 50 steps] in the code corresponds to the length of each side of the polygon, which is taken as a parameter. Then 72 in [Turn clockwise 72 degrees] is the degree of turn to create an exterior angle, which is also taken as a parameter. As soon as you change this (pointing to the “exterior_angle” parameter), it becomes a different polygon, so two parameters are enough

[36:28] R: Are two parameters enough to change the shape of a polygon? T3, what do you think?

[36:34] T3: Yes, I agree

As can be seen from the episode above, T2 stated that her subroutine with two parameters, “side_length” and “exterior_angle,” was sufficient to draw different regular polygons as long as the parameters were changed [36:03]. Therefore, she quickly changed the parameter in the subroutine—exterior angle—from 72 degrees of the regular pentagon (Fig. 6b) to 60 degrees of the regular hexagon. However, the code only produced a non-enclosed “hexagon” with one side missing (Fig. 6c). This was because the subroutine did not contain a loop that would control repeatedly drawing n sides of a n-sided regular polygon, but instead included five [move XX steps] blocks to fix the number of sides to five (Fig. 6b).

T3 then proposed to simplify the program by using a loop to avoid reusing multiple [move XX steps, turn clockwise YY degrees] blocks, where the number of loops, n, corresponded to the number of sides (and angles) in a regular n-sided polygon. By observing T3 used a repeat block and created a My Block with three parameters (“side_length,” “exterior_angle,” “number_of_sides,” Fig. 7a), T2 then successfully debugged her subroutine differently, that is, T2 did not set a third parameter in the subroutine but made the second parameter “number_ of_sides” instead of “exterior_angle” (Fig. 7b), suggesting that she optimized the My Block with only two parameters to the same effect. We infer that T2 had integrated her programming and mathematical thinking by relating the two parameters in a multiplicative relationship: The second parameter (“exterior_angle”, x) could be deduced from the third parameter (“number_of_sides”, n) in the sense that x = 360/n. Thus, the My Block only requires two parameters to control its shape (“number_of_sides”) and size (“side_length”) respectively.

Fig. 7
figure 7

a Teacher 3’s My Block with three parameters; b Teacher 2’s My Block with two parameters

Full size image

T2’s debugging of the subroutine that could change the shape and size of regular polygons prepared for her subsequent creations in significant ways. Like T1, she first constructed some regular polygonal base shapes by changing the different parameters (Method 1). This creation process was much simpler and more accurate than T1’s parameterless subroutine which had occasioned unplanned drawings, since T2 only needed to input the values of “side_length” and “number_of_sides,” upon which the size of the exterior angle and number of loops could be computed automatically without any data mismatch resulting in non-regular polygonal shapes. Thus, the process of developing a subroutine with key parameters aligned with geometrical properties generated new ways for T2 to do mathematics from a computational perspective.

4.2.2 Rotational symmetry of multiple figures

After a few attempts at changing the number of sides and loops to form the rotational symmetry of a single polygon (Method 1), T2 tried a second round of creation built on Method 1. That is, she innovated to create a new base shape by using “a combination of pentagon and hexagon”. Converting to the programming context, T2 replicated her My Block (subroutine) named “polygon” to create two regular polygons with different parameters. In programming terms, she was remixing her polygon creation by calling the subroutine twice (3-sided, 30 steps; 6-sided, 50 steps) within the main program (Fig. 8a). She then kept trying different values of the two parameters in each subroutine and the number of rotations in the main program to create different composite base shapes consisting of multiple polygons varying in shape and size for her rotational symmetrical figure (see Table 2). She also added a third subroutine to the main program (Fig. 8b) to perform rotation of a base shape composed of three different-sized and shaped regular polygons (Table 2, Figure c-d). Thus far, T2’s creative actions were demonstrated in remixing and reusing subroutines several times by connecting properties of polygons to generate shapes that were personally meaningful. Importantly, she did so by integrating her geometrical knowledge about the parameters of regular polygons (size and shape) and programming concepts of subroutines, which provided a new way to achieve the drawings with rotational symmetry.

Fig. 8
figure 8

Teacher 2 remixed her polygon creation by calling the My Block (a) twice; (b) three times

Full size image
Table 2 Examples of Teacher 2’s creations formed by adopting Method 1 and Method 2
Full size table

4.2.3 Rotational symmetry of figures with rotational symmetry

Thus far, T2’s creations have extended from a base shape made of a single polygon to composite shapes made of several polygons by reusing multiple My Blocks. Having inquired into the mathematical concept of composite figures and the codes used in Method 1, T2 derived a third method of creation—using Method 1 to create a rotational symmetrical figure formed by rotating an equilateral triangle three times as the new composite figure (Fig. 9a), then rotating the base figure again to form the symmetrical figure (Fig. 9b). We analyze her actions in detail below.

Fig. 9
figure 9

a A base shape created by using Method 1; b the final symmetrical figure

Full size image

Before finalizing the figure shown in Fig. 9b, T2 experienced challenges while inquiring how she could rotate her composite base figure. To do so, she decomposed the problem and tried the [go to random position] block to check if the composite base figure would appear in random positions. Initially, T2 was confused as to how to rotate the base shapes while changing their positions, as she placed the [go to random position] block after the first loop in the main program (to draw the first composite figure) (Fig. 10a). Thus, even though the loops were able to draw multiple composite shapes, the position could only be changed once because the position-changing block was not placed inside the loop. Upon reflecting on the relationship between codes and artefacts, she realized the problem and placed the [move to random position] block after creating each composite figure, successfully drawing several composite shapes in random positions (Fig. 10b). Here, the programming artefact as an object-to-think-with related to the programming concept of sequence supported her reflection. Having figured out this process, T2 then replaced the [move to random position] block with [move XX steps] and [turn right YY degrees] by referring to mathematical concepts of rotational symmetry. Through several times of debugging, T2 eventually succeeded in drawing a rotational symmetric figure of a composite base shape that was formed by rotating an equilateral triangle three times (Fig. 9b). Overall, this case supported the view that T2 regarded an artefact as an object-to-think-with by drawing upon mathematical properties (rotational symmetry) and programming concepts (sequences, loops) in her iterative creative action, which not only contributes to her understanding of rotational symmetry at multiple levels but also facilitated T2’s experience of the rotational process from a computational perspective.

Fig. 10
figure 10

a Initial codes that only changed the position of composite shape once; b several composite shapes were drawn in random positions

Full size image

5 Discussion

Prior studies have noted the importance of regarding programming as an object-to-think-with to learn mathematics (Papert, 1980), which is also an expressive medium for exploring personal ideas supported by existing mathematical concepts (Kynigos, 1995; Lewis, 2017). Linking mathematical creativity and programming as constructionist learning, we set out to investigate the characteristics of creative mathematical actions exhibited by mathematics teachers during programming-based mathematical activities. In the following, we will discuss the findings that responded to the two RQs (Table 3) and some further implications.

Table 3 Summary of the creative actions and new possibilities for doing mathematics in programming contexts
Full size table

5.1 Two kinds of creative actions in a programming-based mathematical context

We have described and analyzed the creative process of the two cases in detail in the results section, from which we noted that the teachers went through different creation processes. In the first case, T1 produced a series of unstructured, independent creations related to different mathematical concepts, whereas in the second case, T2 showed a progressive, structured creation rooted in the same concept of rotational symmetry. Despite the difference in the creative process between the two cases, the results indicate two kinds of creative mathematical actions inspired by the programming-based mathematical context.

5.1.1 Unstructured creative action by testing: Changing the value of different parameters (variables)

The testing practices demonstrated by the teacher participants were seen as one kind of important creative action. As shown in Table 1, T1 tested various combinations of parameters by changing their values in the subroutine (“side_number” and “turn_angle”) and main program (“turn_angle” and “rotation_times”) to explore different rotational symmetry or asymmetrical shapes that were made of regular or non-regular polygons. Although these may seem like random actions of trial and error, the practice of changing the value of several parameters in the programming-based mathematical activity did provide a rich opportunity for creative actions. That is, the programmer could proceed to a new round of reflection-based exploration and creation relying on the programming artefacts by trial and error as an object-to-think-with, which engendered new possibilities for doing mathematics in their community. These random testing practices to create new geometrical figures, despite producing unstructured results, were indeed an important source of new experience for doing mathematics.

5.1.2 Structured creative action by iterating: reusing and remixing codes

Another significant creative action shown in this study was the iterative practice of reusing and remixing codes as exhibited by T2. In the case of T2, we notice a gradual and sustained development from her initial figure (adopting Method 1) to the final figure (adopting Method 3) through an iterative creative process. That is, T2 created three levels of rotational symmetry, starting from the single polygon as the base figure to multiple polygons by reusing several subroutines, and finally derived a rotational symmetric figure with the base figure also having rotational symmetry. This was achieved by remixing codes related to drawing rotational symmetric figures. Hence, T2 was advancing her knowledge about rotational symmetry and loops in her creative actions, finally generating a nested loop which performed one level of rotation inside another. Simultaneously, she was working with each level of the base figure as an object-to-think-with in an increasingly sophisticated manner. Thus, we regard such iterative practices of reusing and remixing codes as a kind of structured creative action underlying the programming-based mathematical context.

5.2 New possibilities for doing mathematics engendered by creative actions

In this study, we were also interested in what and how new mathematics possibilities may be engendered by creative actions for mathematics teachers in a programming context. From the results of the study, we suggest that new realizations and interpretations of mathematics may be engendered by creative actions. First, we evidence T1’s new realization of mathematics through her unstructured creative actions. As argued by previous studies (Cui & Ng, 2021), given there exists a mismatch between mathematical and programming languages, new realizations may emerge when participants need to transform mathematical processes into a programming language (Ye et al., 2023b). Likewise, while exploring the series of non-regular polygons and regular polygons, T1’s unexpected creation led her to a new interpretation of making n-sided regular polygons and non-regular polygons with n + 1 sides using a combination of n line segments and n angle turns as part of her creative actions, which generated a new opportunity for T1 to experience geometric figures different from a paper-and-pencil context. From this and together with T2’s iterative creation of rotational symmetry, we infer that programming artefacts generated by testing and iterating creative actions served as an object-to-think-with, yielding three different opportunities for teacher participants to make sense of mathematics in a new context: (a) recognizing the difference between counter-concepts (e.g., non-regular and regular polygons; symmetry and asymmetry); (b) experiencing connections between family concepts (e.g., transformation concepts of translations and rotations); and (c) exploring particular concepts at multiple levels (e.g., rotation symmetry). These findings may help us to better understand the kinds of new mathematical experiences elicited by creative actions in the programming-based mathematical context.

Secondly, the results suggest that the practices of algorithmic thinking and iterative thinking, which are highly relevant to computational thinking (Wing, 2006), could facilitate new interpretations of mathematics from a computational perspective (Ye et al., 2023a). Taking the case of T1, she manipulated her code sequences and used nested loops to repeatedly (re-)interpret her geometric transformations. From the perspective of computational thinking, sequences determine the order of events, while loops control the number of times an event occurs, and nested loops imply that a certain cyclic process is repeated. Hence, T1’s algorithmic thinking was interacting with her interpretations of mathematics in a mutual and complementary way.

Regarding iterative thinking, in the case of T2, we notice two different ways of reusing codes, namely repetition and iteration. As illustrated in Method 2 (Sect. 4.2.2), T2 realized her idea of rotating a composite figure as the base shape by repeatedly calling a subroutine to draw multiple regular polygons of different shapes and sizes within the rotation loop. That is, the composite figure was generated by reusing the same subroutines several times but with different parameters. Furthermore, in Method 3, although T2 did not directly call a subroutine with the function to draw a figure of rotational symmetry, she remixed codes related to rotational symmetry that was used in Method 1 to form the base shape and then nested the codes in another level of rotation, demonstrating that her concept of rotational symmetry evolved from an iterative perspective. Taken together, these findings suggest that creative action in a programming environment is supportive of new realizations and interpretations of mathematics from a computational perspective.

5.3 An adapted framework for investigating creative actions in a programming-based mathematical context

Overall, by adopting the framework of creative mathematical action (Riling, 2020), this study provides qualitative evidence of the creative actions taking place in a programming-based mathematical context, which has significant implications for understanding creativity in K-12 mathematics education. The teachers’ creative actions highlight the potential affordances of Scratch as a creative learning environment (Weng et al., 2022b) and an object-to-think-with that facilitates participants’ mathematics learning and programming practices. Not only does Scratch’s block-based programming environment support a dynamic visualization of the geometry drawing process; but its open-ended, free-form coding provides opportunities for flexible understanding and application of participants’ geometry concepts and programming skills. Unlike traditional curriculum where geometry knowledge is applied to solving a specific type of geometry problem, the free creation of geometric shapes in Scratch can inspire connections between various geometry concepts. Thus, concerning the context of programming-based mathematical activities, we propose an adapted framework (Fig. 11) which would be helpful for future research in identifying creative mathematical actions in domain-specific ways by drawing close connections with concepts from mathematics and computer science. Specifically, we emphasize the creative actions in the programming context, and thus extend the given mathematical context to a programming-based mathematical context which includes the programming tool as a constructionist learning environment. Furthermore, we highlight the role of the programming artefact as an “object-to-think-with” to inspire creative actions that bring new possibilities for doing mathematics in a cyclical way.

Fig. 11
figure 11

Framework adapted from the CMAF (Riling, 2020) for programming-based mathematical learning context

Full size image

Nevertheless, it is important to realize that creativity should be seen as a dynamic process of interaction between participant, task and situation (Tromp & Sternberg, 2022), which are important components of a mathematical community. Thus, rather than seeing creativity as an end in itself, we should see it as a means to other ends (Beghetto & Kaufman, 2014).

6 Conclusion

In conclusion, this study provided evidence that testing and iterative practices of reusing and remixing are two kinds of creative actions afforded by the programming environment, which offered new possibilities for doing mathematics in the sense of generating new ways to engage in mathematical processes and to understand mathematics from a computational perspective. The findings of this study contribute to our understanding of creative mathematical actions and new possibilities in mathematics inspired by a programming-based mathematical context, particularly the role of mathematics and programming concepts and their interplay, in developing teachers’ creative mathematical actions. The results also support the idea that Scratch can be a creative learning environment and an object-to-think-with to facilitate mathematics teachers’ experience of doing mathematics, which informs future research on task design to support teacher professional development. Furthermore, our adapted framework for creative actions in the context of programming-based mathematical activities is worthy of future research and can be practical for supporting teachers in identifying students’ mathematical creativity from the perspective of creative actions during classroom teaching. However, as our design of the study only focuses on one sample task related to rotational symmetry in Scratch, these findings may be somewhat limited by the task design and participants’ programming experience. Thus, future work is needed to shed light on different creative mathematical actions in different programming contexts with various tasks.