1 Introduction

Solving arithmetic word problems is a fundamental mathematical competence advocated in the curricula of various countries (e.g., National Council of Teachers of Mathematics, 2000; LOMLOE, 2022). For that reason, recent studies have focused on teaching mathematical problem-solving to students with moderate and severe disabilities (Bowman et al., 2019), including those with autism spectrum disorder (ASD).

ASD is a chronic neurobiological disorder characterized by difficulties in social interaction and communication and a restricted range of interests and behaviours (DSM-5; American Psychiatric Association, 2013). Although the manifestation of these symptoms varies widely among individuals with ASD, they often exhibit challenges in attention and executive functioning (Ozonoff & Schetter, 2007), as well as in language comprehension and theory of mind (e.g. the individual’s ability to recognize and infer the mental states of self and others; Baron-Cohen et al., 2000; Whalon & Cox, 2020). The characteristics associated with ASD often impact mathematical learning (Bullen et al., 2022), resulting in gaps in learning trajectories and slower progress compared to other disabilities as students progressed through grade levels (Fernández-Cobos & Polo-Blanco, 2024; Wei et al., 2013).

In this work, we consider verbal arithmetic problems as situations presented within an academic setting that involve questions solvable through mathematical operations (Verschaffel et al., 2020). Students with ASD have been noted to demonstrate poorer problem-solving performance in comparison to their typically-developing (TD) peers. This has been attributed to difficulties in domains like language, executive functions and theory of mind (e.g., Chen et al., 2019; Polo-Blanco et al., 2024; Root et al., 2021). Furthermore, previous studies have delved into the problem-solving strategies employed in arithmetic word problems, revealing that students with ASD tend to utilize less efficient approaches compared to their TD peers (e.g. Bae, 2013; Polo-Blanco et al., 2024). This discrepancy in strategy use has been associated with difficulties in inhibition, cognitive flexibility and theory of mind (Polo-Blanco et al., 2024). On the other hand, students with autism often benefit from a form of visual thinking, which, as described by Grandin (1995), is the ability to think and reason through images and visual systems. This type of thinking may often manifest through the use of drawings, which serves as a crucial mode of expression, especially given challenges in communication inherent to the disorder (Di Renzo et al., 2017). In the domain of problem-solving, this has been manifested through the frequent use of drawing-based strategies in students with autism when solving algebraic tasks (Goñi-Cervera et al., 2022) and word problems (Goñi-Cervera et al., 2023).

The use of visual representations has also been proposed as a potent instructional tool for teaching problem solving, not only in TD students (Rellensmann et al., 2017) but also in students with learning disabilities (Jitendra et al., 2002) and those with ASD (Root et al., 2021). Some instructional methodologies, such as schema-based instruction (SBI; Jitendra et al., 2002) and the conceptual model problem-solving approach (COMPS; Xin, 2012), incorporate visual representations and schemas to further enhance conceptual comprehension of the problem-solving process. In this work, we focus on the latter, which has been successfully employed to improve the arithmetic problem-solving skills of students with learning difficulties (Xin et al., 2008, 2020) and with ASD (García-Moya et al., 2022; Polo-Blanco et al., 2022).

In the present paper, we complement the case study presented in Polo-Blanco et al. (2022) employing a qualitative methodology to describe and analyze the strategies used by a student with ASD and intellectual disabilities when solving multiplicative word problems in the context of a COMPS approach. Multiplicative problems are those requiring multiplication or division, which are often categorized into three groups (see Table 1): (1) equal-groups (EG), (2) multiplicative comparison (MC), and (3) Cartesian product (CP) problems (Nesher, 1992). These specific types of problems have received limited attention in previous research involving students with ASD (Polo-Blanco et al., 2019).

Table 1 Types of Multiplicative Problems, Conceptual Model Diagrams, and Visual Representations
Full size table

We specifically address the following research questions:

  1. 1)

    Which strategies did the student with ASD and intellectual disabilities employ when solving multiplication problems of the three types (EG, MC, and CP) while following a COMPS approach

  2. 2)

    What characteristics related to ASD might influence the above strategies?

  3. 3)

    What elements of the COMPS approach played a role in improving conceptual understanding across the three problem types for a student with ASD and intellectual disabilities, especially in terms of transitioning to more formal strategies?

2 Theoretical background

2.1 Literature review

Solving arithmetic word problems involves the integration of various processes that blend procedural and conceptual knowledge and may pose significant challenges, especially for students with learning disabilities (Griffin & Jitendra, 2009) and those with ASD (Bullen et al., 2022; Polo-Blanco et al., 2022). Conceptual knowledge involves understanding interconnected facts and properties, while procedural knowledge encompasses familiarity with written symbols and the set of rules and algorithms employed for solving mathematical problems (Hiebert, 1986). Part of conceptual understanding in problem-solving involves aspects related to comprehending the problem statement, forming a mental representation of the situation, and subsequently connecting it with the mathematical operations necessary for its resolution. Procedural knowledge, on the other hand, pertains to the execution processes of these operations. Although the sequence in which conceptual understanding or procedural fluency develops remains uncertain, conceptual understanding may lay the foundation for procedural fluency (Burns et al., 2015). A student's conceptual understanding expands, for example, when they acknowledge the interconnection between two operations, such as addition and subtraction or multiplication and division. Moreover, this conceptual knowledge is applied when the student understands how to use these operations to solve a situation presented in a problem-solving context (Miller & Hudson, 2007). On the other hand, a student's problem-solving strategies may be rooted either in the procedures linked to the problem or a creative approach derived from a solid conceptual grasp of the problem at hand (Burns et al., 2015).

2.2 Theoretical framework

2.2.1 Multiplicative problem-solving strategies

In light of the above, the examination of strategies becomes particularly relevant when teaching word problem-solving to students facing difficulties. Some authors have provided detailed classifications of the strategies used by TD students when solving multiplicative problems (Mulligan, 1992). These classifications are based on two criteria: the degree of abstraction of the procedure used to calculate and the way in which the elements specific to the problem statement are used during the resolution process. Combining these criteria, the following types of strategies are described by Mulligan (1992), presented in order from the lowest to the highest level of abstraction,

  1. (1)

    Direct modeling with counting (modeling, in short): The student employs concrete objects or drawings to depict the action described in the problem and utilizes various counting techniques. For instance, to determine the total number of apples in 5 trees, each having 4 apples, the student draws five trees and places four apples in each, subsequently counting the total number of apples drawn.

  2. (2)

    Counting without modeling (counting, in short): At this level, students employ mental counting, addition, or subtraction without the use of objects or drawings. Strategies include rhythmic ascending or descending counts, as demonstrated in the previous problem where the student finds the answer by expressing, “4–8-12–16-20.”

  3. (3)

    Known or derived numerical facts (operation, in short): addition and multiplication facts are used to reach the result. For example, in the previous problem, the student argues that “4 × 4 is 16, and 4 more is 20”.

Research with typically developing children indicates a progression from informal strategies, such as modeling and counting, to more formal strategies like resorting to numerical facts, whereas studies suggest that students with learning disabilities face challenges in transitioning to advanced strategies, and exhibit less flexibility in their strategy use compared to their typically developing peers (Geary et al., 2004; Mulligan, 1992; Siegler, 2007). In the case of students with autism, some recent studies in the last decade have analyzed problem-solving strategies (Bae, 2013; Goñi-Cervera et al., 2023; Polo-Blanco et al., 2019, 2024). For instance, Polo-Blanco et al. (2019) showed a preference for modeling strategies when providing material support to a student with ASD and intellectual disabilities while solving EG division problems. Subsequently, Polo-Blanco et al. (2024) examined the multiplication problem-solving strategies of 26 students diagnosed with ASD without intellectual disabilities, comparing them to a matched group of 26 students without ASD in terms of sex, age, and school (grade and classroom). Results revealed a higher proportion of poorer performers in the ASD group, who exhibited lower strategy abstraction compared to the other ASD peers, with no such distinctions noted in the non-ASD group. Additionally, Goñi-Cervera et al. (2023) analyzed the strategies utilized by 10 students with ASD, some with intellectual disabilities, aged 8 to 13, when solving EG problems. The majority of students relied on low-level strategies, such as counting, with little use of formal multiplication and division. Bae's (2013) study, comparing 40 fourth and fifth graders, revealed that typically developing students outperformed those with ASDs in word problem-solving. In students with ASD, this performance significantly correlated with sentence comprehension, math vocabulary, computation, and everyday math knowledge. However, the use of drawing strategies was limited in both groups.

2.2.2 Conceptual model-based approach COMPS

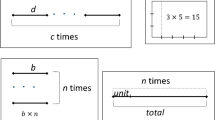
The design of methodologies that foster conceptual understanding in the problem-solving process becomes especially relevant for students with learning difficulties (Jitendra et al., 2002). One common instructional methodology is COMPS (Xin, 2012), which incorporates conceptual diagrams, explicit instruction, heuristics, and metacognitive approaches. In particular, COMPS is presented as a comprehensive approach that facilitates connections between different problem types by utilizing a conceptual diagram model to determine the arithmetic operations for solving a specific problem (Xin et al., 2020). In this context, a model refers to a mathematical representation of the problem, typically expressed as an expression that provide a pathway to finding the solution (e.g., “Part1 + Part2 = Whole” for group additive problems, or “Group Rate x Number of Groups = Product” for EG problems). Table 1 displays conceptual model diagrams for the three types of multiplication problems considered in this study (EG, MC, and CP), along with visual representations used to further aid in the understanding of the problems.

The typical teaching sequence using a COMPS approach shows how to identify the type of model diagram associated with the problem and represent the quantities and relationships on it. The teacher prompts the student with a series of connected questions to direct their attention to the three quantities involved in the problem. For example, in the case of EG problems, the questions could include “Which part of the problem provides information about the value of each group?”, “which part provides information about the number of groups?”, or “which part refers to the total or product?” (see Table 1). The student is prompted to recognize and complete the model diagram representing the problem situation, which depicts a multiplicative expression 'AxB = C.' The accompanying words under the boxes aim to help the student associate the meaning of each number in the problem statement with its role in the operation. This is crucial for determining whether the solution involves multiplication or division. If C is the unknown, the operation is multiplication, while if A or B is the unknown, the operation is division. At this stage, the student relies on visual representations of the problem to connect with the corresponding conceptual model diagram in order to transform the data in it into the problem-solving operation (see Table 1).

The use of COMPS to teach multiplication problem-solving skills to students with learning difficulties has yielded positive outcomes. Xin et al. (2008) investigated the effects of teaching problem stories to five fourth- and fifth-grade students with mathematics disabilities or those at risk. The results indicated that the instructional intervention not only enhanced problem-solving abilities for both additive (group and compare) and multiplication (EG and MC) problems. More recently, Xin et al. (2020) supplemented a COMPS approach with a computer tutoring system and achieved significant performance improvement in solving EG and MC problems in three third- and fourth-grade students with learning disabilities.

In the context of Autism Spectrum Disorder, the use of diagrams and visual aids in the COMPS approach is expected to enhance conceptual understanding of problem-solving. Individuals with ASD often excel in visual processing (Grandin, 1995), and visual support can alleviate cognitive demands related to verbal comprehension and potential working memory limitations (Ozonoff & Schetter, 2007). Garcia-Moya et al. (2022) demonstrated the success of COMPS in improving the problem-solving skills of three 8-year-old students with ASD without intellectual disabilities. Similarly, Polo-Blanco et al. (2022) found positive outcomes in teaching a 14-year-old student with ASD and intellectual disabilities various multiplication problem types using the COMPS approach, leading to improved performance and generalization of skills.

3 Methodology

This study adopted an exploratory approach (Yin, 2017) on the strategies employed when solving multiplicative word problems by a student with ASD and intellectual disabilities through the analysis of written problems and video recordings of student–teacher interactions during the instructional process. All sessions, including instruction and test administration, were recorded on video. A qualitative methodology approach was employed to offer a descriptive analysis of the specific characteristics of problem-solving strategies and a COMPS approach, with an emphasis on the ASD characteristics of the student.

3.1 Participant

Peter (pseudonym) is a 14-year-old male diagnosed with ASD at the age of 6 through clinical evaluations based on DSM-4 diagnostic criteria. Peter attends a special education center since age 10, and displays stereotyped behaviors, exhibits particular interests, and shows a positive response to established routines, according to the center's guidance team report. He has been diagnosed with intellectual disabilities, with an IQ score of 54 (WISC-V; Wechsler, 2014). In mathematics, Peter follows an adapted curriculum dedicating four hours per week to the subject. He possesses good reading comprehension skills, although he encounters difficulties comprehending certain words. A characteristic of Peter that was emphasized by his teachers is his fondness and inclination for creating drawings as a means of expressing his desires and fears, as well as for completing school tasks, particularly for solving mathematical problems. Prior to the study, Peter had worked on additive structure problems, showing the ability to identify the operation (addition or subtraction) and solve it using number facts. Regarding multiplicative structure, he had received instruction through EG problems, which he was able to solve drawing equal groups for multiplication and performing partitioning strategies for division. He had neither memorized the multiplication tables nor received formal instruction on multiplication or division algorithms. Consequently, it was deemed an opportune moment for Peter to expand his comprehension of multiplication and division.

3.2 COMPS instructional approach

Instructional sessions were conducted individually in a distraction-free environment. The instructor had prior experience in teaching mathematics to the participant. Worksheets were provided to the student (see Fig. 1) to cover the four steps proposed in the DOTS list (Xin, 2012). The detailed sequence for each problem was as follows:

  1. (1)

    Problem statement and multiplicative model diagram (detect and organize): The student read the problem independently and was guided to place the quantities into the multiplicative model diagram. A visual representation was also used to help understand the meaning of the data.

  2. (2)

    Transform: The student was asked to write the operation that solved the problem based on the data from the model diagram.

  3. (3)

    Solve: The student explicitly wrote the expression of the operation to be performed and solved it.

Fig. 1
figure 1

Worksheet Following the DOTS Steps

Full size image

Taking into account previous research on problem difficulty in TD students (Nesher, 1992), our instruction sequentially introduced EG, MC and CP problems. For each problem type, multiplication problems (with the total quantity unknown) were introduced first, followed by division ones (with the unknown in the other positions), and finally, mixed problems involving either multiplication or division. The problem statements for each type responded to contexts close to the student. The numbers used in the problem statements implied that the total amount should not exceed 30, since the student had not memorized the multiplication tables and thus could approach them with informal strategies. The problem data did not contain double factors to differentiate whether the participant discerned the meaning of each one at the moment in which he incorporated them in the model (for instance, “how many”, “how many each” or “total”).

The instructional sessions with problems followed a model-lead-test sequence. They began with an explanation from the instructor in the model phase, initially using a visual representation (see Table 1) to illustrate the problem and then placing the quantities on the conceptual model diagram. In the lead phase, the student solved various problems through interaction with the teacher, and in the test phase, he independently solved problems without the instructor's assistance, serving as assessment tests for the respective session.

3.3 Design and data collection

Table 2 summarizes the sequence of all tests conducted during the course of the study, indicating in parentheses the number of problems for each one. These tests evaluate problem-solving skills: prior to the beginning of the instruction (Baseline tests, Bx-type), during instruction (Training tests, Tx-type), right after the end of instruction (Post Training tests, PTx-type) and five weeks after the end of the instruction (Maintenance tests, M-type). In particular, during baseline, post-training and maintenance tests, a multiplication problem and a division problem were posed for each problem type. During each training test, the student solved four problems of the same type and operation(s) as the problems addressed during model and lead phases of the corresponding training session.

Table 2 Tests Administered During the Study
Full size table

The study commenced with the administration of baseline tests for the three types of problems (B1-EG to B4-EG, B1-MC to B4-MC, and B1-CP to B4-CP). After four baseline sessions, the student initiated the training sessions for EG problems. Tests T1-EG to T4-EG were conducted at the end of these sessions. After that, performance with all types of problems was evaluated again: with EG problems (post-training tests PT1-EG to PT3-EG) and the remaining types of problems during baseline (B5-MC to B7-MC and B5-CP to B7-MC). This was done to observe whether the instruction of EG problems had an impact on the performance on MC and CP problems. The next type of problem (MC problems) was then introduced in the instruction and assessed at the conclusion of each instructional session with tests T5-MC to T9-MC. After those sessions, the improvement in the two types of problems already addressed was confirmed with post-training tests (PT4-EG, PT5-EG, PT4-MC, and PT5-MC), and CP problems continued to be evaluated during baseline (B8-CP and B9-CP). Subsequently, instructional sessions of CP problems were conducted, assessed with training probes T10-CP to T13-CP. After completing this instruction phase, the three types of problems were reassessed through post-training tests (PT6-EG, PT7-EG, PT6-MC, PT7-MC, PT6-CP, and PT7-CP). Finally, a maintenance test was conducted for the three problem types to observe the retention of the learned skills (M-EG, M-MC and M-CP). Due to the nature of this methodology, the number of training sessions conducted for each type of problem varied. For instance, four sessions were necessary for EG and CP problems, while MC problems required five sessions because the student experienced more difficulties.

The analysis of the problem-solving process in the tests involved examining the student's written responses and the video recording transcriptions. This examination focused on understanding the sequential steps undertaken by the student leading up to his final answer. The evaluation encompassed both the student’s success and the strategies employed during tests, which were systematically coded. Additionally, the transcriptions of instructional sessions and tests served as a means to track the instructional process. In the analysis for the strategies employed for each problem, we considered the following categories: (1) Success in problem-solving: a problem was considered correct when both the operation (multiplication or division) was correctly identified, and the solution was successfully obtained. Errors related to division notation, such as the expression “2/8 = 4” instead of the correct “8/2 = 4,” were not categorized as incorrect; (2) Strategies employed, which included Modeling, Counting, Operation, and Others (responses without a reasonable explanation). The use of these strategies may result in incorrect solutions, and there could be combinations of strategy operations in conjunction with either modeling or counting (categorized as Modeling/Operation and Counting/Operation).

4 Results

In this section, Table 3, 4, and 5 present the types of strategy employed by the student during tests for each of the three types of problems (EG, MC, and CP, respectively). For better visualization, zero is omitted in the count of incorrect or correct strategies in these tables.

Table 3 Number of Problems, Success and Strategies for EG Problems
Full size table
Table 4 Number of Problems, Success and Strategies for MC Problems
Full size table
Table 5 Number of Problems, Success and Strategies for CP Problems
Full size table

4.1 Equal group problems

The results for EG problems are summarized in Table 3. Below is a detailed description of the results in each type of test.

Baseline test of EG problems

Peter demonstrated partial knowledge of the EG problems in the baseline tests (B1-EG to B4-EG). The problems that were answered correctly were the four multiplication problems, using a modeling strategy. In Fig. 2, two examples are shown, where the student modeled through drawings, subsequently counting (in B1-EG), and through mental calculation (in B3-EG).

Fig. 2
figure 2

Correct Resolution of EG Problems in Baseline Tests

Full size image

Peter also employed incorrect modeling strategies in the four division problems, treating them as multiplication or subtraction problems. This is evident in the case of the problem shown in the left panel of Fig. 3, where he used a multiplicative strategy by drawing 24 candies in each of the 4 bags and then counting them. The great size of the collections led to error in the number of candies drawn in one of the bags and in the overall count. In the case of the problem shown in the right panel of Fig. 3, Peter incorrectly modeled it as a subtraction problem, crossing out 6 objects out of the 24 drawn, as seen in the vertical line he traced on the toys on the right.

Fig. 3
figure 3

Incorrect Resolution of Division EG Problems in Baseline Tests

Full size image

The baseline responses revealed the use of elaborate drawing-based modeling strategies, a pattern commonly observed in individuals with ASD (Polo-Blanco et al., 2019, 2024) and notably distinctive in the study participant. He successfully solved multiplication problems without explicitly identifying the operation, but exhibited deficiencies in conceptual understanding regarding division problems, suggesting challenges in comprehending the given situations. This might have been influenced by vocabulary related to equal distribution (e.g., “repartir por igual” in Spanish, which translates to “distributed equally among”). As mentioned before, individuals with ASD often face challenges associated with language comprehension (American Psychiatric Association, 2013), which, in this instance, might have led Peter to incorrectly rely on his prior knowledge of addition or multiplication.

Training on EG problems

During the training sessions on multiplication problems, the instructor guided Peter in connecting the visual representation with the model diagram and identifying the multiplication operation. Peter sometimes correctly solved multiplication problems using the diagram model and the operation and then proceeded to create drawings of the situation, which supports his liking for drawings even if he did not use them for the resolution. To address division problems, the instructor paid special attention to ensure that Peter understood the vocabulary associated with division problems, such as “in each” (“en cada” in Spanish) and “distributed equally” (“repartido por igual” in Spanish). Subsequently, the focus shifted to Peter filling in the model diagram, aligning both numbers from the statement with the corresponding sections in the model diagram to determine the result (e.g., “how many” and “total” to find “how many in each”), helping identify the division operation as the inverse of multiplication, and drawing on his prior knowledge of multiplication. At this point, he was told to write the word “division” in the operation section and show the solution in fraction form in the solution section. This notation was chosen for its simplicity, although xcessive emphasis was not placed on this formal aspect.

In the training tests (T1-EG and T4-EG), Peter correctly solved all the multiplication problems except one, where he used an additive strategy (left panel of Fig. 4). In T1-EG test, he employed mixed strategies, modeling/operation and counting/operation, to arrive at the solutions. In T4-EG, he abandoned the modeling strategies in favor of stating the operation. In one problem, he wrote down the result directly (the right panel of Fig. 4) and in another, he followed a counting approach, as we observed him moving the pencil over his fingers. It was difficult to identify the specific strategy he used in those movements to reach the result.

Fig. 4
figure 4

Incorrect and Correct Resolution of EG Problems in Training Tests

Full size image

Peter correctly solved all the EG problems involving division during the training tests (T2-EG to T4-EG). He used a correct modeling/operation strategy only once (Fig. 5) to find the number of passengers in each train car. Specifically, he placed the given data from the problem statement in the diagram (21 and 3), then drew the train cars and placed the passengers using a trial-and-error process, erasing and adding passengers until reaching the solution. Afterwards, he wrote “7” in the circle, and from the representation in the diagram, he identified that the operation that solved the problem was the 21/3 division. Once again, the participant's preference for drawing is observed, as he created a visual representation that was coherent with the problem situation. He relied on this representation to find the value of the unknown factor, demonstrating a conceptual understanding of the problem.

Fig. 5
figure 5

Correct Resolution of an EG Problem in Training Tests

Full size image

To solve the remaining division problems, Peter wrote the division operation based on the model diagram, reaching the correct result either directly or through counting strategies, as indicated by his finger movements. Although it is challenging to ascertain with certainty due to the quickness of his counting and the absence of verbalization, we infer from his prior knowledge that in these latter instances, he would likely employ multiplicative strategies, adding the divisor until reaching the dividend.

Post-training tests and maintenance test of eg problems

During the sessions dedicated to the post-training tests of EG problems (PT1-EG to PT7-EG), Peter correctly solved 13 out of 14 problems. To arrive at the solution, he applied operation strategies, sometimes in combination with modeling in multiplication problems (Fig. 6) and other times with counting. The response collected in Fig. 6 shows how he had integrated the features of the followed instruction, the generation of a visual representation, the model diagram (drawn by himself), and the decision of the operation that solved the problem.

Fig. 6
figure 6

Correct Resolution of EG Problems in Post Training Tests

Full size image

Peter successfully solved the two EG problems in the maintenance session, employing a modeling strategy for one multiplication problem and an approach combining operation and counting for the division problem.

In summary, Peter completed the EG problem sessions with accurate solutions to multiplication and division problems. While incorporating the operational strategy, he did not entirely abandon the modeling strategy in either multiplication or division problems, though it was more frequently observed in the former. Peter achieved a proper conceptual understanding in these problems with appropriate strategies, including modeling (with detailed drawings in most cases) and operational approaches. The results also demonstrated his assimilation of common vocabulary in division problems.

4.2 Multiplicative comparison problems

The results for MC problems are summarized in Table 4.

Baseline test of MC problems

Peter struggled to understand the statements of the MC problems during the baseline tests, leading to incorrect answers for 13 out of the 14 problems. He employed the same strategies for both multiplication and division problems. In the first four baseline tests (B1-MC to B4-MC), Peter employed a modeling strategy, but he interpreted the comparison factor as adding the given quantity (sometimes more than once). This shows a lack of conceptual understanding regarding this type of problem, which is evident both in the modeling he performed and in the operations he proposed. As shown in the left panel of Fig. 7, Peter depicted the quantity of Carla’s candies in the left hand of a character, while in the right hand, he drew the comparison factor three times, i.e., 3 + 3 + 3 candies. Then, his counting resulted in an incorrect result of 13 candies. In the subsequent tests (B5-MC to B7-MC), conducted after completing instruction on EG problems, Peter persisted with the same strategy but introduced an incorrect additive operation. In the example shown in the right panel of Fig. 7, he added the given quantity, 14, to the comparison factor of 2, resulting in the incorrect answer “16 candies.” Note that, in Spanish, as in English, additive and multiplicative comparatives are similar: “dos más” means “two more,” and “dos veces más” means “twice as many.”

Fig. 7
figure 7

Incorrect MC Problems in Baseline Tests

Full size image

Training on MC problems

To facilitate the understanding of the comparative vocabulary (“times as many”), the instructor used modeling and emphasized the quantities “the one with more” and “the one with less” in the model diagram. Occasionally, he substituted these with terms such as “double” or “triple” to enhance comprehension. Initially, he relied on the visual representation indicated in Table 1 for this type of problem. Subsequently, the instructor guided Peter to connect this representation with the model diagram by underlining the words below the boxes. However, Peter did not seem to integrate the visual representation and, from the beginning, skipped this step, moving directly to the model diagram.

Results from the training tests (T5-MC to T9-MC) demonstrated Peter's ability to connect the problems with multiplication or division operations through the model diagram without relying on visual representations. He successfully solved 17 out of the 20 problems, employing a strategy of operation, with and without numerical counting (see left panel of Fig. 8). In two of them, the error was attributed to a misinterpretation of the comparison factor using an additive strategy. For instance, in the problem shown in Fig. 8 (right panel), Peter interpreted “5 times more” as adding 5 + 5, resulting in writing 10 in the “how many times” box of the diagram. The third incorrect problem was due to a calculation error (8 × 2 = 14), the solution to which was obtained by counting fingers.

Fig. 8
figure 8

Correct (Left) and Incorrect (Right) Resolution of MC Problems in Training Tests

Full size image

Post-training tests and maintenance test of MC problems

In the post-training sessions, Peter solved all the MC problems using operation strategy and mixed strategies of counting and operation. He arrived at the correct solution in 7 out of the 8 problems. Peter correctly solved the two MC problems in the maintenance session using a mixed strategy of counting and operation.

In summary, Peter demonstrated the acquisition of skills in solving this type of problems, although the occasional difficulties observed might still indicate a lack of conceptual understanding regarding MC problems, as already observed in the baseline tests, which might be attributable to some difficulties inherent to the disorder, like language comprehension.

4.3 Cartesian product problems

The results for CP problems are summarized in Table 5.

Baseline tests of CP problems

Peter answered all the problems in the baseline tests incorrectly. He encountered difficulties understanding the problem statements, as he provided responses using one of the numbers given in the problem or wrote text related to the problem situation, showing a clear lack of conceptual understanding for these problems. For instance, in B4-CP (left panel of Fig. 9), he responded with all possible clothing combinations, mentioning items such as “pants, shirts, socks, and underwear.” On two occasions, he employed an additive strategy by adding the numbers given in the problem statement. One of these instances involved modeling, as shown in the right panel of Fig. 9 (B1-CP), where he represented 6 dishes and then added 3 more dishes before counting all them. In the remaining cases, he did not answer. We interpret that he did not understand the scenarios outlined in CP problems and tried to address them by either elucidating contextual non-mathematical aspects, or relying on his prior additive knowledge.

Fig. 9
figure 9

Incorrect Resolution of CP Problems in Baseline Tests

Full size image

Training on CP problems

For this type of problems, the instructor began by using the visual representation from Table 1 for CP problems, depicting the two given sets with arrows to establish pair combinations, to later help Peter connect it with the model diagram where the expression “total combinations” appears. The visual representations motivated the student, although occasional instructor intervention was needed during the initial training sessions to correct the diagrams.

As evident from the results in Table 5 (T10-CP to T13-CP), the instruction was effective, and Peter demonstrated the use of correct strategies from the first evaluation session. Figure 10 shows a correct solution from the T13-CP test. After reading the statement, Peter sketched the letters and added directional arrows. Next, he inscribed the numbers “4” and “2” onto the diagram before returning to count the arrows. He finally wrote “multiplication” and, just beneath it, the correct solution. We interpret that his representation of the combinations allowed him to understand the situation, obtain the result, and ultimately discern the operation from the model diagram. This exhibits his grasp of the problem at a conceptual level.

Fig. 10
figure 10

Correct Resolution of an MC Problem in Training Tests

Full size image

Peter employed the modeling strategy in 12 out of the 16 problems corresponding to the training phase, along with utilizing the model diagram and setting up the operation for both multiplication and division problems. He rarely deviated from the modeling approach, except in the two problems of the T11-CP session, where multiplication was involved (5 × 4 = 20; 7 × 2 = 14), and in two problems of the T12-CP session, that required division (10/2 = 5; 6/2 = 3). The process Peter followed in solving the division problems showed his understanding. For example, in the problem depicted in Fig. 11, Peter read the statement, wrote an 8 in the “total combinations” box, and a 2 in the “how many of” box of the model diagram. Subsequently, he drew representations of the two types of ice cream. Positioning himself to the left of the ice creams, he drew two arrows towards them. He repeated this process from three other points until he stopped, presumably because he had already counted 8 arrows. Then, he circled the four marked points to represent the ice cream flavours. Peter completed the model diagram by filling in the number 4 and wrote the operation and the correct solution (8/2 = 4). On this occasion, we could observe Peter's effective interpretation of the problem statement, as he employed drawings to depict the situation, which in turn assisted him in establishing a meaningful connection with the necessary operation.

Fig. 11
figure 11

Correct Resolution of a CP Problem in Training Tests

Full size image

Post-training tests and maintenance test of CP problems

In the four CP problems presented during the post-training test sessions (PT6-CP and PT7-CP), the student demonstrated success by employing a mixed modeling and operation strategy. In the subsequent maintenance test session (M-CP), Peter showed his sustained problem-solving ability while consistently employing modeling techniques, although he made a mistake in identifying the operation by writing “multiplication” in a division problem.

In summary, the instruction on the use of visual representation as well as the model diagram led to success for Peter in the case of CP problems. The use of this representation was noteworthy, likely because he could establish the relationship between the two sets of data, and the arrows helped him find the solution. The modeling strategy he employed in division problems demonstrates a high level of conceptual understanding of the problems.

5 Discussion and conclusions

We conducted an analysis of an instructional process based on the COMPS approach for multiplicative problems (EG, MC and CP) in a student with ASD and intellectual disabilities. The first research question aimed to describe the student's problem-solving strategies while following a COMPS approach, based on Mulligan's classification (1992). Different performances across the three problem types were observed in the student's responses at the beginning of the study. In EG problems, he demonstrated a certain level of understanding through the application of modeling strategies and counting, while significant comprehension difficulties were evident in the MC and CP problems. After completing the COMPS approach, the student successfully solved all three types of problems, but the strategies employed varied depending on the type of problem. In EG problems, he demonstrated a conceptual understanding by connecting modeling and operations. A notable improvement was his capacity to discern and write the operation, both for multiplication and for division problems. MC problems posed the greatest challenge for the student during instruction.

The student’s performance could be related to some of the characteristics of people with ASD, in answer to the second research question. On one hand, challenges in understanding key terms, such as "three times as many" (often interpreted as an additive comparison, i.e., "three more"), may have impeded the comprehension of the situation, aligning with suggestions from previous studies involving students with ASD (Bae, 2013; Polo-Blanco et al., 2019). On the other hand, the inherent complexity of these problems, which requires students to adopt different perspectives by placing themselves in the position of two distinct individuals when comparing quantities, may present challenges related to theory of mind—a common characteristic in individuals with autism (Baron-Cohen et al., 2000). This trait has been previously linked to problem-solving abilities in individuals with the disorder (Polo-Blanco et al., 2024; Whalon & Cox, 2020). Furthermore, in the case of students who express themselves through drawings, like the participant in the study, the observation of informal strategies might shed light on their progression through instruction. As pointed out by Di Renzo et al. (2017), for students facing challenges in verbal communication the use of drawings serves as a crucial mode of expression. Previous studies including students with ASD with intellectual disabilities like the participant of this study (Goñi-Cervera et al., 2023) and others involving students with ASD without intellectual disabilities (Polo-Blanco et al., 2024), have also indicated a preference for modeling strategies, which contrasts with findings from studies involving TD students, suggesting a transition away from modeling towards strategies based on numerical facts around the age of 8–9 (Ivars & Fernández, 2016; Mulligan, 1992).

The third research question investigated the elements of the COMPS approach that contributed to enhancing conceptual understanding across three problem types for a student with ASD and intellectual disabilities, particularly in transitioning to more formal strategies. The results show that COMPS has adapted well to the specific characteristics of the student. In particular, it addresses potential deficits in planning (a type of executive function) by guiding the problem resolution in steps and helps overcome verbal comprehension difficulties by relying on visual representations and the model diagram. For EG and CP problems (despite incorporating unfamiliar terminology for Peter in the latter, such as 'combinations'), the visual representation effectively facilitated his comprehension of the situation from the beginning, both for multiplication and division problems. This was evident in the way he connected this representation with the model diagram, writing the corresponding data in the diagram, and relying on that to identify the operation and the solution. Particularly impressive was his use of drawings with arrows in CP division problems to derive the results. Previous work has already shown the effectiveness of the COMPS approach for teaching CP problems to students with ASD without intellectual disabilities (García-Moya et al., 2022). In the case of MC problems, the visual representation used by the instructor might not have been suitable for illustrating the context of the MC problems for Peter, leading him to rely exclusively on the model diagram from the beginning and use fewer drawing-based strategies.

In summary, our study suggests that the COMPS approach allows for flexibility, considering individual challenges and the specific profile of each learner, particularly for students with ASD. While our observations emerge from the participant in our study, we believe that this adaptability may be extended to other students with ASD, which is crucial when integrating them into mainstream classrooms and addressing diverse educational needs. Although extensive research has delved into problem-solving abilities among TD students, there exists still a notable gap in our understanding regarding students with intellectual disabilities and/or ASD. Moreover, as emphasized by Bowman et al. (2019), it is essential to broaden the scope of mathematics skills imparted to students with intellectual disabilities, which is generally centered on basic mathematical skills. This paper directly addresses this need by focusing on multiplicative problem-solving. Finally, given that research concerning instructional experiences for students with disabilities relies on case studies, it is imperative to conduct this type of research across various profiles and settings to broaden our understanding of students’ capabilities and challenges.

EG: Equal Group; MC: Multiplicative Comparison; CP: Cartesian Product; (x): Number of Problems