1 Introduction

In his famous work, Hattie (2008) analyses the effects of “what actually works in schools to improve learning”. He highlights that one of the most powerful impact factors of successful teaching is FA. Therefore, within recent years researchers investigated how to implement FA into teaching (of mathematics) best and how to support teachers in doing so successfully (Boström & Palm, 2023; Johnson et al., 2019; Schütze et al., 2017). A key result of these efforts is that understanding effects of FA at school implies not only analyzing the quality of implementation of this specific teaching practice itself but considering “global factors of high quality teaching and quality components of specific teaching practices” (Decristan et al., 2015, p. 1153) simultaneously. This is in line with theoretical and empirical work about the impact of learning processes in classroom (Good et al., 2009; Patrick et al., 2012; Seidel & Shavelson, 2007) as well as about the characteristics and influences of teachers’ competences (Blömeke et al., 2015; Kunter et al., 2013) on students’ development: It is the (generic and subject-specific) instructional quality being an important mediator between teachers’ expertise and learning outcomes (Muijs et al., 2014; Roehring et al., 2012). Based on this, some very first studies have analyzed (interaction) effects of GIQ and FA on students’ learning simultaneously (Decristan et al., 2015; Pinger et al., 2018), but studies considering both GIQ and SSIQ when investigating the quality of implementation of FA are not known to the authors. Starting from this desideratum the present exploratory study analyses the added value of considering (interaction) effects of GIQ and SSIQ on students’ learning when implementing FA. Therefore, the paper is structured as follows: Within the theoretical part, central considerations about FA (Sect. 2) as well as about (FA in the context of) instructional quality (both GIQ and SSIQ) are outlined (Sect. 3). Within the empirical part, research question and hypotheses are given (Sect. 4) and methods (Sect. 5) as well as results (Sect. 6) are described. Finally, implications and limitations (Sect. 7) are discussed by pointing out the added value of considering GIQ and SSIQ in empirical educational research.

2 Formative assessment (in mathematics education)

Black and Wiliam (1998, p. 7) define FA as “all those activities undertaken by teachers, and/or by their students which provide information to be used as feedback to modify the teaching and learning activities” (see also Black & Wiliam, 2009). “All those activities” subsume different kinds of assessment (like teacher-directed assessment, peer-assessment or self-assessment) ranging on a scale from a informal, unplanned on-the-fly assessment to a formal, planned embedded assessment (Shavelson et al., 2008). In line with these ideas, Andrade (2010, p. 344) stresses that main purposes of FA are “(1) providing information about students’ learning to teachers and administrators in order to guide them in designing instruction; and (2) providing feedback to students about their progress in order to help them determine how to close any gaps between their performance and the targeted learning goals”. Consequently, feedback is considered being a central element of FA, which is proven being a powerful tool for supporting learning if it addresses the questions “Where am I going?”, “How am I going?”, and “Where to next?” (Hattie & Timperley, 2007). In their prominent works, Bennett (2011) and Hattie (2008) highlight that implementing FA into teaching can have significant effects on students’ learning. That’s why FA is described being the “next best hope” (Cizek, 2010, p. 2) or a “powerful tool” (Wylie et al., 2012, p. 121) in educational research and policy.

Based on this research, recently several studies have analyzed ways of implementing FA into mathematics education and of supporting mathematics teachers in doing so. Dalby and Swan (2019) underpin that using iPads can support teachers’ implementation of FA in mathematics education, but that harking back to technology can cause uncertain roles of teachers, students and technology in classrooms. Rakoczy et al. (2019) point out that effects of FA on achievement and interest are not direct but indirect ones and that students’ support by FA in mathematics education depends on students’ perceived usefulness. In the study of Boström and Palm (2023), mathematics teachers took part in a professional development program (PDP) on FA and implemented FA into mathematics teaching afterwards. Effects on students’ learning cannot be found, the authors explain this finding by a big variance of quality of implementation of FA into teaching. On the contrary, Andersson and Palm (2017) find effects of a teacher PDP on FA on students’ achievement in a control trial (d = 0.66), but particular effects on students’ specific mathematical processes do not exist. And Schütze et al. (2017) demonstrate that teachers’ taking part in PDP can have indirect effects on teachers’ feedback generation, but not on instructional practice in mathematics education.

Those results stress that implementing FA into teaching (of mathematics) is challenging both teachers and students and that teacher PDPs are necessary but not sufficient. This is also reported by reviews on implementation of FA highlighting the complex mechanisms of FA in classroom: Yan et al. (2021) review 52 studies exploring teachers’ role in FA and point out that both contextual and personal factors influence teachers’ intention and implementation regarding FA. Heitink et al. (2016) review 25 studies on implementing assessment for learning and derive a complex model of prerequisites of teachers, students and assessment all influencing each other. And Kingston and Nash (2011, p. 33) highlight in their often cited meta-analysis “that there is wide variation in the type and impact of formative assessment. Moderator analysis showed content area had the greatest impact on mean effects with mathematics”.

In summary, although FA is “next best hope” in the beginning 2010, research results about ways of implementing FA and ways of supporting teachers in doing so are struggling and empirical effects are partly inconsistent.

3 Instructional quality of teaching (in mathematics education)

Starting from these inconsistent results and based on the idea that considering (instructional) quality of teaching is crucial when thinking about how to improve students’ learning (Muijs et al., 2014; Roehring et al., 2012), some very first studies consider instructional quality of teaching for better understanding effects of the implementation of FA into teaching. Decristan et al. (2015) analyze the interplay of curriculum-embedded FA (categorized as a “specific teaching practice” by the authors) on the one hand and GIQ (categorized as a “global factor”) on the other hand. They report (interaction) effects of GIQ and FA on students’ science learning. These findings are partly confirmed by Pinger et al. (2018) for mathematics education, reporting interaction effects of some aspects of GIQ (cognitive activation, classroom management) and the implementation of FA as well. By these results, both studies highlight that considering instructional quality of teaching can have an added value for better understanding effects of FA on students’ learning. However, studies analyzing the added value of (interaction) effects of both GIQ and SSIQ as well as of the implementation of FA on students’ (mathematics) achievement simultaneously are not known to the authors.

The current exploratory study harks back to this desideratum and analyzes the added value of considering both GIQ and SSIQ for understanding effects of the implementation of FA into teaching. GIQ and SSIQ are based on already existing (and prominent) work on instructional quality of teaching (in mathematics education) – both frameworks will be presented briefly for preparing empirical work (for further frameworks see e.g. Learning Mathematics for Teaching Project, 2011; Pianta & Hamre, 2009; Schoenfeld, 2013): (1) In line with previous work of Decristan et al. (2015) and Pinger et al. (2018) on GIQ and FA, GIQ refers to the model of “Three Basic Dimensions” (TBD; for current discussions see Praetorius et al., 2020; Praetorius & Charalambous, 2018). It is a model of GIQ being prominent (not only) in German speaking countries, being published first based on empirical findings in the context of TIMSS (Klieme et al., 2001) and being discussed in the international context theoretically based on a Swiss-German video study on teaching of Pythagoras’ theorem (Klieme et al., 2009; Lipowsky et al., 2009). The model comprises three basic dimensions of GIQ (Praetorius & Charalambous, 2018, pp. 409–410): Classroom management, that is “identifying and strengthening desirable student behaviors, and preventing undesirable ones”; cognitive activation, saying that “teachers should explore and build on students’ prior knowledge” and that “challenging problems and questions […] should be used to stimulate cognitive conflicts, engage students in higher-level thinking processes, and support metacognition”; and student support, which “primarily deals with the shared perception of the quality of social interactions”. The later one is sometimes theoretically and empirically separated into cognitive support on the one hand and motivational support on the other hand (Kleickmann et al., 2020). Although studies on GIQ in mathematics education prove effects of (several) dimensions of this model on students’ mathematics learning (Decristan et al., 2015; Kunter et al., 2013; Pinger et al., 2018), empirical results about the impact on students’ achievement in general are inconsistent – and in many cases no effects can be reported (Praetorius & Charalambous, 2018). (2) Since the model of TBD can be discussed critically concerning the lack of subject-specifics (Praetorius & Charalambous, 2018; Schlesinger & Jentsch, 2016), based on a systematic literature survey Schlesinger et al. (2018) expand this model by two subject-specific dimensions for mathematics education. First added dimension is subject-related quality, e.g. comprising the mathematical depths of a lesson (“the teacher provides generalizations, mathematical connections and possibilities to structure the mathematical content”) and the support of mathematical competencies (“the teacher provides the opportunity to deal with mathematical processes such as problem-solving, modelling or reasoning and proof”). Second added dimension is teaching-related quality, e.g. comprising the use of multiple representations and the use of mathematical examples in classroom. Both quantitative and qualitative analyses point out that this framework offers additional possibilities for understanding mathematics education as well as “the opportunity to present a more extensive and complete picture of instructional quality” (Schlesinger et al., 2018, p. 487). However, significant empirical evidence is still missing.

Despite this theoretical conceptualization and empirical verification of GIQ and SSIQ (not only of those two frameworks presented here), it must be stated (independently of the idea of understanding the implementation of FA): Effects of GIQ are inconsistent as well (Praetorius et al., 2020) and the role of SSIQ for understanding effective teaching remains complex (Charalambous & Praetorius, 2018). This is the more problematic, since subject-specific perspectives on instructional quality of teaching are claimed offering additional insights into mathematical learning processes at school (Brunner, 2018; Lindmeier & Heinze, 2020). It is imperative that further work on the added value of considering both GIQ and SSIQ when analyzing specific teaching practices (not only but also in the context of implementation of FA) is needed for a better understanding of effective teaching.

4 Research question and hypotheses

Based on those considerations – that is: (1) FA is a promising specific teaching practice (in mathematics education) (Bennett, 2011; Hattie, 2008), but effects of implementation are inconsistent (Kingston & Nash, 2011); (2) considering GIQ and SSIQ can have added values for understanding these inconsistent effects of implementation of FA into (mathematics) teaching (Decristan et al., 2015; Pinger et al., 2018), but effects of GIQ and SSIQ itself are inconsistent/complex as well (Charalambous & Praetorius, 2018; Praetorius et al., 2020); (3) SSIQ should be considered explicitly in further empirical research (Brunner, 2018) –, the present exploratory study addresses the following research question:

Research Question (RQ). Does considering (interaction) effects of GIQ and/or SSIQ of teaching mathematics have an added value for understanding students’ learning when implementing FA into mathematics education instead of solely looking at the implementation of FA itself?

Hypotheses can only be formulated unambiguously to a limited extent: On the one hand, Decristan et al. (2015) report (interaction) effects of dimensions of GIQ (and FA) on students’ achievement, on the other hand, Pinger et al. (2018) cannot confirm these findings completely. Additionally, on the one hand empirical studies highlight the importance of considering SSIQ of teaching mathematics at least from a theoretical perspective (Charalambous & Praetorius, 2018), on the other hand, empirical evidence is rare (Lindmeier & Heinze, 2020). And empirical studies analyzing the effect of implementation of FA and SSIQ on students’ learning simultaneously are not known to the authors.

5 Method

The current exploratory study re-analyzed data of the research project Conditions and Consequences of Classroom AssessmentFootnote 1 (Co2CA), which was funded by the German Research Foundation (GRF) within the priority program Competence Models for Assessing Individual Learning Outcomes and Evaluating Processes. The project lasted for six years (2007–2013) and was conducted by the German Institute for International Educational Research and the Universities of Kassel and Lueneburg. Study work finished in 2018 by the publication of Pinger et al. (2018) about an intervention study in mathematics education (lasting from October 2010 to March 2011), reporting interaction effects of GIQ (assessed by students’ perception) and the implementation of FA on students’ mathematics achievement. SSIQ is not considered in this or any former publication.

The study presented here reports on this intervention study as well, re-analyzing the effect of GIQ and SSIQ on students’ achievement when implementing FA into every-day teaching of mathematics (focusing on the topic of Pythagoras’ theorem and the competence of mathematical modelling exemplarily; see below). This is done by using newly created data both on GIQ and SSIQ being based on analyzing videotaped lessons for the first time. Students’ achievements were assessed before and after the intervention. Reported information on participants, design, measures, and data analyses only refer to this special intervention.Footnote 2

5.1 Participants

39 mathematics teachers/classes from 25 German middle schools (grade 9; so called “Realschule”) in Hessian participated in the intervention study. All participating schools, teachers and students (as well as their parents) had been informed about the purpose of the study as well as the collection and use of data before starting the study. Written permission for videotaping classroom lessons twice during the intervention (videotaped situation 1 and 2; see below) was asked for additionally. All participants (teachers as well as students) took part in the study voluntarily, no compensation was paid.

Participating teachers/classes were assigned either to a control group (CG) or an experimental group (EG) by random. While there are videos from all 39 participating classes for the first videotaped situation, there are only 33 videos for the second videotaped situation (caused by illnesses or unexpected disruptions to the daily routine at school).

Students’ outcomes at the end of the intervention are central for analyses given below. In total, 856 students participated in the achievement-test at the end of the intervention. 353 of those were female, 405 were male, 98 did not make any indication. Before starting the intervention, those students were in average 14.59 years old.

Additional information on descriptive data concerning intervention groups is given in Table 1.

Table 1 Descriptive data concerning intervention groups
Full size table

5.2 Design

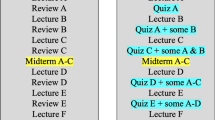
The intervention covered 13 consecutive lessons (each lasting for 45 min), introducing into Pythagoras’ theorem (lessons 1 to 5) and focusing on mathematical modelling in lessons 6 to 13 exemplarilyFootnote 3. Pythagoras’ theorem had not been taught in participating classes before. All participating teachers from CG and EG were told to implement a unit structure of teaching consisting of four phases (see Fig. 1): (Phase 1) Introduction of Pythagoras’ theorem including at least one proof and some technical tasks for training, focusing primarily on building up a general understanding of central elements of Pythagoras’ theorem (in line with Drollinger-Vetter, 2011). (Phase 2) Students had to work on embedded word problems (Maaß, 2010) for making them to use Pythagoras’ theorem in simple real world situations. (Phase 3) More realistic (but not necessarily authentic) mathematical modelling problems covering the whole modelling cycle (Blum & Leiss, 2007; Kaiser, 2020) were implemented into mathematics teaching for supporting students in building up modelling competencies when dealing with Pythagoras’ theorem. (Phase 4) Additional lessons were used for consolidating former learning processes and for offering the opportunity to reflect ones’ own competencies. A concrete schedule, some possible proofs as well as mandatory and voluntary tasks had been given to the teachers before starting intervention. A sample proof and some sample tasks are given in Fig. 2.

Fig. 1
figure 1

Design of the intervention study (adapted from Pinger et al., 2016)

Full size image
Fig. 2
figure 2

Sample proof and sample tasks (technical tasks, embedded word problem, realistic modelling problem)

Full size image

All teachers from CG and EG had to participate in a first teacher training before starting the intervention (for details see Besser et al., 2015). The teachers were informed about content and processes of the study, teaching material was discussed, and the predesigned teaching unit was recapitalized. Additionally, those teachers from EG had to join a second teacher training before starting the intervention. Based on ideas about FA (Black & Wiliam, 2009; Hattie & Timperley, 2007), those teachers were trained implementing a diagnostic tool assessing students’ performances regularly (at the end of lesson 5, 8 and 11) and giving task-related, process-oriented, individual written feedback to each student at the beginning of the next lesson (beginning of lessons 6, 9 and 12). This diagnostic tool (see Fig. 3 for an example) consisted of one or two tasks students had to work on and some feedback about personal strengths (processes that had been mastered), weaknesses (processes that need further improvements) as well as hints/strategies on how to continue (for more details see Pinger et al., 2016).

Fig. 3
figure 3

Example of the diagnostic tool at the end of lesson 8; embedded word problem on the left, teachers’ feedback on the right (see also Pinger et al., 2016)

Full size image

Assessments of students’ mathematics achievement took place immediately before and after the teaching unit. GIQ and SSIQ is based on videotapes recording lesson 1 and 2 (videotaped situation 1; dealing with an introduction and a proof of Pythagoras’ theorem) as well as lesson 9 and 10 (videotaped situation 2; dealing with mathematical modelling problems). Those lessons were held as double lessons.

5.3 Measures

Achievement (A1 and A2; student level). Students’ achievement was assessed by a pretest before starting the intervention (achievement 1; A1) and by a posttest at the end of the intervention (achievement 2; A2). Since students worked on Pythagoras’ theorem in the intervention for the first time, the pretest asked for students’ prior knowledge and consisted of 19 items dealing with mathematical content being necessary for handling Pythagoras’ theorem (e.g.: using variables and simplifying terms, extracting the square root of numbers, identifying a right angle and right-angled triangles and different sides of a triangle). The posttest consisted of 17 items and assessed students’ capability to use Pythagoras’ theorem successfully when working on tasks focusing on technical problems, embedded word problems and realistic modelling problems. Both tests lasted for 45 min. Items were administered as a paper-pencil-test, item formats were single choice response or open response (sample items are given in Fig. 4). All items were coded dichotomously (0 = incorrect; 1 = correct) by three trained raters, interrater-reliability was very good (about 10% of students’ answers were double-coded by all raters; two-way mixed (absolute) intraclass correlation (ICC(3,3)) was calculated both for pretest and posttest; see Table 2). Students’ test-scores were one-dimensional Rasch-scaled. Since all items had been analyzed previously in a scaling study (N = 1570, Harks et al., 2014), item-parameters were fixed on those study results for scaling. Weighted likelihood estimators were used as students’ achievement scores for pretest (A1) and posttest (A2). EAP/PV-Reliability was 0.66 for the pretest and 0.74 for the posttest. ICC(1) indicating the proportion of total variance which can be attributed to between-differences is 0.15 for pretest and 0.09 for posttest.

Fig. 4
figure 4

Sample items of pretest and posttest

Full size image

Implementation of FA (FA; class level). For controlling for potential differences due to the group allocation, the implementation of FA is assessed by a dummy-coded variable, either indicating that students/classes are assigned to CG (FA = 0) or to EG (FA = 1).

Generic instructional quality (GIQ 1a-c and GIQ 2a-c; class level). Based on the model of Three Basic Dimensions (Praetorius et al., 2020), all videos from the videotaped situations 1 and 2 were analyzed regarding GIQ by using high-inference ratings for describing classroom management, cognitive activation and cognitive support: The rating scale for classroom management (GIQ 1a and GIQ 2a) consisted of seven items, e.g. asking for classroom disruptions, the teacher’s monitoring and clarity of rules. The rating scale for cognitive activation (GIQ 1b and GIQ 2b) consisted of eight items, e.g. asking for the insistence on reasons and explanations, the support for cognitive autonomy and the implementation of challenging problems. Student support (GIC 1c and GIQ 2c) was assessed by cognitive support (and not motivational support; see above), since empirical evidence indicates effects of cognitive support (and not of motivational support) on students’ achievement (Kleickmann et al., 2020). The rating scale consisted of nine items, e.g. asking for the clarity of goals, the coherence of teaching and the supportive use of feedback. All scales had already been used in previous studies (Lotz et al., 2013) and have only been adapted for study use slightly.

Three trained raters (university pre-service teacher students; trainings lasted for several days using sample video material) analyzed the generic quality of teaching (ICC(3,3) is good to very good, see Table 2), the rating of the items ranged from 1 (appearing nearly never) to 4 (appearing extremely often), the mean score of all items was the scale score. The mean scores of all three raters were used as scores for GIQ of classroom management, cognitive activation, and student support – separated for videotaped situation 1 (GIQ 1a-c) and videotaped situation 2 (GIQ 2a-c).

Subject-specific instructional quality (SSIQ 1 and SSIQ 2; class level). Based on the work of Schlesinger et al. (2018), GIQ is extended by elements of SSIQ by assessing mathematical depth and support of mathematical competence as part of subject-related quality. In lesson 1 and 2 (videotaped situation 1), students were introduced to Pythagoras’ theorem by working on a proof and some technical tasks. It was analyzed, whether “the teacher provided generalizations, mathematical connections and possibilities to structure the mathematical content” by an appropriate thematization of so called “elements of understanding of Pythagoras’ theorem” (SSIQ 1). The scale was adapted from Drollinger-Vetter and Lipowsky (2006) and Drollinger-Vetter (2011) and consisted of twelve items, e.g. asking for the thematization of different types of triangular sides in rectangular triangles as well as the thematization and combination of algebraic and/or geometric formulations of Pythagoras’ theorem. In lesson 9 and 10 (videotaped situation 2), students worked on realistic modelling problems which can be solved by using Pythagoras’ theorem in real world contexts. It was analyzed, whether “the teacher provided the opportunity to deal with mathematical processes” (SSIQ 2) by demanding students to conduct central steps of mathematical modelling (Kaiser, 2020). The scale covered those processes of mathematical modelling which are being described by a well-established modelling cycle (Blum & Leiss, 2007), which are justified by a activity-theoretical analysis of mathematical modelling (Böhm, 2013), and which are already being used by many empirical case studies to analyze the quality of implementation of mathematical modelling into teaching (for an overview see Vorhölter et al., 2019). The scale consisted of ten items, e.g. asking for the appropriate implementation of having to understand given information, of having to make assumptions, of having to work on the modelling problem mathematically as well as of having to interpret and to validate mathematical results.

Items of both scales were scored dichotomously (0 = no thematization in classroom; 1 = appropriate thematization in classroom) by three trained raters (ICC(3,3) is good to very good, see Table 2). For scoring 1, the content covered by an item had to be thematized substantially for mor than just a few seconds (as beeing standard in many subject-specific frameworks, see e.g. Learning Mathematics for Teaching Project, 2011). Scale-score was the sum of item-scores, normed on a range from zero to one (for an easier interpretation; scores indicate the percentage of thematized content). For describing SSIQ, the mean score of all three raters was used.

An overview of measures is given in Table 2, additional information on instruments assessing GIQ and SSIQ is given in an electronic supplement (ES01). Since measures of achievement are used both on the student and the class level within analyses (see below), those measures are listed as “student/class level”.

Table 2 Overview of measures
Full size table

5.4 Data analysis

Data analyses for the preparation of descriptive data were conducted by using SPSS 27. For doing so, student data (A1 and A2) was aggregated on a class level, while class level data was used as given in Table 2.

Data analyses focusing on the research question were conducted by using Mplus 7 (Muthén & Muthén, 2012). Achievement 1 (A1) and Achievement 2 (A2) were z-standardized on the student level (level 1; within), variables assessing instructional quality (GIQ and SSIQ) were z-standardized on the class level (level 2, between). The implementation of FA (FA) was implemented as dummy (0 = CG; 1 = EG) on the class level. Multilevel regression analyses were conducted, several models were compared: In all models, students’ achievement in the posttest (A2) was dependent variable, students’ achievement in the pretest (A1; both on student and class level) and the implementation of FA (FA; on class level) were independent variables. In selected models, instructional quality of teaching (GIQ and SSIQ) as well as interactions of FA and instructional quality (FA*GIQ and FA*SSIQ) were additional independent variables.

Caused by relatively few cases on the class level, missing data was dealt with by listwise exclusion of cases.

6 Results

Descriptive statistics including sample size, mean scores, standard deviations, and correlations are given in the electronical supplement (ES02). It can be summarized: Firstly, the implementation of FA (FA), that is belonging to CG or EG, is not correlated with any measure of instructional quality. Instructional quality is neither systematically better nor worse if teachers/classes are advised to FA. Secondly, sub-dimensions of GIQ correlate significantly among each other (0.34 < r <.76) on a medium level. Additionally, GIQ of videotaped situation 1 (GIQ 1a-c) does not correlate with SSIQ of videotaped situation 1 (SSIQ 1), but GIQ of videotaped situation 2 (GIC 2a-c) correlates with SSIQ of videotaped situation 2 (SSIQ 2) significantly.

Regarding the research question, selected standardized model results are given in Table 3 and 4 (only models with interaction effects are reported here; all models are given in an electronic supplement (ES03)). Firstly, across different models it can be stated that it is mainly students’ achievement in the pretest (A1) predicting students’ achievement in the posttest, whereas effects of implementation of FA (FA) cannot be found. Secondly, effects of GIQ (β = 0.78) as well as interaction effects (β=-0.71) reducing the main effect can be found for classroom management in videotaped situation 1 (GIQ 1a; model 10), but not in videotaped situation 2 (GIQ 2a; model 13). Thirdly, some effects of SSIQ are given (model 08, 09, 16 and 17). SSIQ 1 (Pythagoras’ theorem in videotaped situation 1) is predicting students’ achievement in the posttest positively (β = 0.28; model 08), the effect even becomes bigger when considering the interaction effect of FA and SSIQ 1 (β = 1.06; model 16). Interaction effect in this model is negative, that is high quality of SSIQ reduces the influence of FA on students’ achievement. Additionally, and on the contrary, SSIQ 2 (mathematical modelling in videotaped situation 2) is predicting students’ achievement in the posttest negatively (β=-0.41 and β=-0.60; model 09 and model 17).

Table 3 Multilevel regression analyses predicting students’ achievement in the posttest (A2) – part 1 (all models are given in ES03)
Full size table
Table 4 Multilevel regression analyses predicting students’ achievement in the posttest (A2) – part 2 (all models are given in ES03)
Full size table

7 Discussion

The present exploratory study aims at analyzing the added value of considering (interaction) effects of GIQ and SSIQ on students’ mathematics achievement when implementing FA into mathematics teaching. Results reveal some important findings: Firstly, there are no direct effects of implementation of FA on students’ learning. It can be stated once again (see also Pinger et al., 2018) that changing classroom teaching (by implementing FA) does not have to imply improving classroom teaching immediately. Although teachers of the current study were trained to implement FA explicitly, effective implementation of FA is challenging. This is in line with research on teachers’ professional development, pointing out that changing teaching practices successfully needs supporting teachers in doing so over a long period of time (Darling-Hammond et al., 2017). Secondly, these interpretations are additionally underpinned by (interaction) effects of GIQ 1a (concretely: classroom management), which are given immediately after starting to implement FA into teaching mathematics (model 10) but are disappearing a few lessons later (model 13), although correlations of GIQ 1a and GIQ 1b are at least medium ones (r =.67). Positive effects of classroom management (β = 0.78), which had also been found by Lipowsky et al. (2009), are counterbalanced by negative interaction effects with FA (β = -0.71), so classroom management has nearly a zero effect size in EG (β = 0.78–0.71 = 0.07). Or in other words: Implementing FA is extremely complex (Kingston & Nash, 2011; Yan et al., 2021), teachers’ routines seem to break down. Thirdly, referring to negative effects of SSIQ on students’ learning (models 09 and 17), it is imperative to understand that changing teachers’ way of teaching mathematics on a content level by implementing a specific teaching practices (here: FA) also might cause negative effects on students’ learning, at least in the short term (which is in line with theory about teachers’ expertise and about deliberate practice, see e.g. Berliner, 1995; Ericsson et al., 1993). In this special case, teachers had to implement mathematical modelling into teaching mathematics – it is well known, that this is challenging for teachers (Blum, 2015).

All those findings stress the added value of considering GIQ and SSIQ when analyzing the impact of implementation of FA on learning, However, implications for research must be discussed carefully in the context of the operationalization of GIQ and SSIQ and its interplay with FA: According to Decristan et al. (2015), in the present study GIQ and SSIQ are operationalized being “global factors of instructional quality”, while FA is operationalized being a “specific teaching practice” (see also Good et al., 2009). However, GIQ/SSIQ on the one hand and FA on the other hand are not necessarily disjoint constructs, on the contrary “formative assessment may be closely related to global factors” (Decristan et al., 2015, p. 1138). This is obvious for GIQ immediately (e. g.: “exploring and building on students’ prior knowledge” is a key concept of FA as well), but also relevant for conceptualizations of SSIQ: For example the subject specific framework “TRU Math” (Schoenfeld, 2013, 2014) comprises the “use of assessment” (“building on students’ ideas”) being an inherent component of high quality of teaching mathematics. Future studies should focus this interplay of (subject specific) instructional quality of teaching (mathematics) and specific teaching practices for further improving understanding effective teaching.

Some design-based and methodological limitations must be addressed when interpreting the results: (a) Design. As has already been mentioned, the teacher training for implementing FA into teaching Pythagoras’ theorem only lasted for several hours. This is caused by careful and conscious considerations about supporting teachers to implement central elements of teaching on the one hand and about not making teachers to overtime while taking part in the study on the other hand. However, effective teacher PDPs should at best last for several weeks/months, not for several hours (Darling-Hammond et al., 2017). (b) Measures I. GIQ and SSIQ are assessed by using instruments having been slightly adapted from prior empirical studies (Drollinger-Vetter & Lipowsky, 2006 (SSIQ 1); Lotz et al., 2013 (GIQ)) or having been newly developed based on theoretical considerations and empirical work of many case studies (Vorhölter et al., 2019 (SSIQ 2). For GIQ, this decision is based on the empirically-based idea of assessing students’ support by cognitive support and not by motivational support (Kleickmann et al., 2020). For SSIQ, this has been done because the framework offered by Schlesinger et al. (2018) is conceptualized for on-the-fly assessment of nine different sub-dimensions of SSIQ, not allowing deeper analyses of single subject-specific sub-dimensions (here: mathematical depth of the lesson; support of mathematical competencies) of quality of instruction. Since implementation of “elements of understanding concerning Pythagoras’ theorem” and the implementation of “mathematical modelling” is focused, those conceptualizations are used. (c) Measures II. Assessments of GIQ and SSIQ are based on videotaped classroom observations of external (trained) observers. Although those ratings are usually much more objective than those from students or teachers, open questions of validity (of scoring, generalization, extrapolation and implication) must be thought about consciously (Bell et al., 2012; Praetorius et al., 2014). However, in general validity of those external observations is high (for a brief discussion see Schlesinger & Jentsch, 2016). (d) Measures III. SSIQ is assessed by low-inference ratings. While low-inference ratings are generally more reliable than high-inference ratings, those ratings are quite often used to describe the quantity/frequency of events, not its quality. However, in this special case SSIQ is operationalized by analyzing whether “the teacher provides a specific opportunity to learn”, which is in line with theory (see above) and which is also done by prominent studies describing mathematics instructional quality (Learning Mathematics for Teaching Project, 2011; National Center for Education Statistics, 2003). (e) Data analyses. Since data analyses are based on measures of instructional quality on the class level, the sample size consists of only 39 or 33 classes on level 2 respectively. This is unproblematic for interpreting both regression coefficients and variance components, but standard errors might be estimated too small in some cases (Maas & Hox, 2005). Furthermore, since participating classes are distributed equally between CG and EG (concerning age, gender), only prior knowledge is used as independent variable on the student level, results must be interpreted with this limitation. (g) Topicality of the study. Data being used is based on an intervention study from 2010/2011. Analyses possibly do not describe the “current state of teaching in German mathematics classroom”– which is of course not intended by this study. But based on design, measures, and analyses, reported results support understanding the complexity of implementing FA into teaching mathematics by considering both GIQ and SSIQ.