Abstract
The integration of dynamic visualisations, feedback formats and digital tools is characteristic of state-of-the-art digital mathematics textbooks. Although there already is evidence that students can benefit from these technology-based features in their learning, the direct comparison between the use of a comparable digital and printed resource has not yet been sufficiently investigated. We address this research gap by contrasting the use of an enriched digital textbook that includes these features and comparable printed materials without them. To do so, we investigate the achievement of 314 students in a pretest-posttest control group design in a five-hour series of lessons on conditional probability. Using the Rasch model and mixed ANOVA, the results indicate that students can benefit from digital textbook features, especially compared to the use of comparable printed materials. In line with other studies on mathematical achievement and the use of digital resources, our study also shows differences between boys and girls. It seems that particularly girls benefit from the use of the digital textbook, whereas, for the boys, it does not seem to make a difference what kind of resources they use. The group and gender differences are discussed against the background of other studies considering that, especially in Bayesian situations, the way statistical situations are visualised can be decisive for a student’s performance.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Current digital mathematics textbooks provide potential for learning and teaching mathematics (Pepin et al., 2015; Rezat et al., 2021; Yerushalmy, 2015). This potential is particularly grounded in the digitally enriched features of digital textbooks, such as the integration of dynamic mathematical tools (Hillmayr et al., 2020), computer-based and adaptive feedback (Van der Kleij et al., 2015), and dynamic visualizations (Berney & Bétrancourt, 2016; Castro-Alonso et al., 2019). While there is already evidence that these individual features can have a positive impact on student performance (Hillmayr et al., 2020), the direct comparison between such a diversely digitally enriched resource and content-equivalent and comparable printed material has hardly been studied so far (but consider, e.g., Kaplar et al., 2022; Reinhold et al., 2020). This is particularly relevant considering that the textbook can be of outstanding importance for everyday school routines (Fan et al., 2013; Rezat et al., 2021).
The present study compares the use of a digital mathematics textbook with dynamic visualisations and feedback options to the use of adapted, printed materials in the subject area of conditional probability. A special approach of this study is that each participating teacher conducted a five-hour series of lessons in both research groups based on predefined lesson plans, once with printed and once with digital materials (see Sample and procedure). In addition, the study is part of a larger project (KomNetMath), so the teachers and their students were already familiar with the structure and use of the materials at the time the study was held. The focus is on the topic of conditional probabilities, where the type of visualisation can be of decisive importance for the students’ achievement (Binder et al., 2015; Böcherer-Linder & Eichler, 2019; McDowell & Jacobs, 2017; Spiegelhalter et al., 2011). Thereby, it is still unclear in this domain whether a dynamic visualisation is to be preferred to a static visualisation (Büchter et al., 2022). Moreover, as achievement differences in the area of data and chance can be found in favour of boys (Schipolowski et al., 2019; Stanat et al., 2019), but at the same time there are indications that girls can particularly benefit from digital curriculum resources (e.g., Kaplar et al., 2022; Reinhold et al., 2020), the present study investigates this interaction between this subject area and such resource use, which has hardly been examined so far, and focuses on possible gender differences.
2 Theoretical and empirical background
2.1 Digital mathematics textbooks
The textbook is considered a key resource for mathematics teaching and learning (Fan et al., 2013; Rezat et al., 2021). Teachers and students may draw on different curriculum resources in the mathematics classroom, where curriculum resources can be generalised as „all the material resources that are developed and used by teachers and students in their interaction with mathematics in/for teaching and learning, inside and outside the classroom” (Pepin & Gueudet, 2018, pp. 1–2). Among the curriculum resources, the textbook is considered to be of outstanding importance. This is attributed to the fact that it has a mediating function between the intended and the implemented curriculum, that is, the actions of teachers and students as well as the processes that take place in the classroom (Cai & Howson, 2013; Fan et al., 2013). Thus, the textbook can be considered to have an influence on the “what”, that is, what content is covered in class, and on the “how”, that is, in what way the content is covered in class (Chazan & Yerushalmy, 2014; Pepin et al., 2015). These views on the importance of the textbook can be applied to both printed and digital textbooks (Rezat et al., 2021).
One plausible distinction between digital textbooks and printed textbooks is the appearance of dynamic structural elements in digital textbooks (Pohl & Schacht, 2019), for example, animations or drag-and-drop tasks. Moreover, multimedia elements and interactivity, as well as assessment and feedback options, are seen as potentials of digital textbooks, along with ecological factors (Choppin et al., 2014; Wijaya et al., 2022). We define second-generation digital textbooks, which are not just a digitised version of printed textbooks (Pepin et al., 2015), accordingly as follows:
A digital mathematics textbook is a technology-based curriculum resource for learning and teaching mathematics. It provides enhancement features, such as interactive and multimedia elements, feedback options, adaptivity, and customisation features that distinguish it from a printed textbook.
In particular, the integration of dynamic visualisations and computer-based feedback can be seen as key differentiators between digital and printed materials that have a relevant impact on student learning (see, e.g., Berney & Bétrancourt, 2016; Castro-Alonso et al., 2019; Van der Kleij et al., 2015).
Dynamic visualisations can be used in mathematics lessons to illustrate dynamic processes, for example, concerning covariation, that is, how the change of one parameter affects other parameters, which can be relevant when examining conditional probabilities (Büchter et al., 2022). In printed textbooks, dynamic processes are represented with the help of single or multiple static visualisations, which cannot represent any change over time and can only describe one state of an object (Rolfes et al., 2020). In contrast, dynamic visualisations can be integrated into a digital textbook. These are differentiated in terms of whether they are designed to be linear dynamic or interactive dynamic. Linear dynamic visualisations represent a dynamic process, but cannot be manipulated by the learner, for example, watching a video. In contrast, interactive dynamic visualisations can be manipulated by the learner, for example, a GeoGebra app with sliders (Rolfes et al., 2020). Meta-studies in instructional psychology suggest that learners benefit more from dynamic visualisations than from static visualisations (Berney & Bétrancourt, 2016; Castro-Alonso et al., 2019). This could be attributed to the implication that dynamic visualisations provide more information than static visualisations (Tversky et al., 2002) or that they facilitate the cognitive demands of complex tasks in particular (Schnotz & Rasch, 2008).
Feedback is perceived as one of the potentially most influential factors on the learning process, with computer-based feedback, in particular, being considered one of the most effective types of feedback (Hattie, 2015; Hattie & Timperley, 2007; Shute, 2008; Van der Kleij et al., 2015). Feedback is “conceptualized as information provided by an agent (e.g., teacher, peer, book, parent, self, experience) regarding aspects of one’s performance or understanding” (Hattie & Timperley, 2007, p. 81). However, the effectiveness of feedback depends on the design of the feedback, especially the information provided and the timing of the feedback (Hattie & Timperley, 2007; Shute, 2008; Van der Kleij et al., 2015). For textbooks, it is relevant to consider task-specific feedback provided during or after the completion of a task (Shute, 2008). In digital textbooks, feedback can be provided immediately due to the computer-based implementation. Immediate feedback is considered to be more effective when working on more complex tasks and for low-achieving students, while delayed feedback can be more helpful when working on simpler tasks and for high-achieving students (Shute, 2008). How students deal with feedback depends in turn on the implementation of the specific feedback (Jonsson & Panadero, 2018; Panadero & Lipnevich, 2022). For example, a computer-based implementation of feedback can include the possibility of resubmission and thus differ from a printed implementation of feedback (Panadero & Lipnevich, 2022). Consequently, the content of the feedback message is determined by the respective source (e.g., a digital textbook). For this reason, the source of the feedback can be considered a crucial factor when studying a feedback process (Jonsson & Panadero, 2018; Panadero & Lipnevich, 2022; Van der Kleij & Lipnevich, 2021). The source influences the way feedback is given and how it is perceived by the students. If students perceive feedback in a visual as well as supportive way, so that they use it, feedback can enhance the learning process (Van der Kleij & Lipnevich, 2021).
Such features of digital mathematics textbooks, as computer-based feedback and dynamic visualisations, are intended to support learning (Yerushalmy, 2015). The effectiveness of interactive digital curriculum resources with such integrated tools is highlighted by Hillmayr et al. (2020) who analysed studies with a pre-post control group design with secondary school students. Initial study results explicitly comparing digital and printed materials in mathematics education point to the effectiveness of digital textbooks and their integrated tools (e.g., Kaplar et al., 2022; Reinhold et al., 2020). Thus, in a study on the learning of fractions with sixth graders, it could be shown that especially low-achieving students could benefit from the use of digital materials with integrated scaffolds and feedback compared to the use of an analogue printed adaptation or the use of a traditional printed textbook regarding their achievement. Kaplar et al. (2022) observed positive effects on students’ performance in mathematical reasoning tasks in geometry for the same age group using interactive materials with integrated feedback compared to using printed textbooks. These results are in line with Jang et al. (2016), where the use of digital textbooks showed a positive influence on learning outcomes.
2.2 Gender differences in mathematical achievement
The first studies on the use of digital textbooks were able to identify a different influence on achievement (e.g., Brnic & Greefrath, 2022a; Kaplar et al., 2022; Reinhold et al., 2020) and a different usage behaviour between boys and girls (e.g., Hoch, 2020; Reinhold et al., 2020). The study by Kaplar et al. (2022) indicates that female students were better than boys at solving certain tasks after using the interactive materials. Reinhold et al. (2020) presented comparable results, as girls developed better initial fraction concepts among high-achieving students (in their study meaning students from the highest school track—German Gymnasium). One possible reason could be that girls and boys engage with the digital textbook differently, that is, girls use the digital textbook more conscientiously, for example by spending longer on interactive tasks (Hoch, 2020) and boys are more likely to be distracted—and start ‘gaming the system’—while girls tend to show higher cognitive and behavioural engagement (Reinhold et al., 2020).
In addition, the ICILS study shows in an international comparison that girls have higher computer skills on average (Fraillon et al., 2020), which can be especially important when dealing with digital curriculum resources. Preliminary results of our project also indicated gender differences, for example, that girls are particularly good at using digital materials (Brnic & Greefrath, 2022a). Collectively, these studies indicate that students’ gender is of interest when investigating the use of digital curriculum resources in mathematics.
Large-scale studies such as PISA often document a significant difference in favour of boys in terms of mathematical achievement in international comparisons (OECD, 2019; Stoet & Geary, 2013). Reasons for gender differences in mathematical achievement are attributed mainly to environmental social and cultural factors, such as prejudices that maths is a male domain (Kaiser & Zhu, 2022). This is supported by the inconsistency in gender differences across countries when looked at more deeply (OECD, 2019; Stoet & Geary, 2013). For example, in Germany, where we conducted the study reported here, significant differences are found in the PISA 2018 results and boys show higher mathematical competencies on average than girls (OECD, 2019).
It is noteworthy, that in The Second National Assessment of Mathematics and Science Proficiencies at the End of Ninth Grade (IQB Bildungstrend) 2018 in Germany, the largest differences between boys and girls were found in the core theme of data and chance, which includes dealing with Bayesian situations (Schipolowski et al., 2019; Stanat et al., 2019); since we focus on conditional probabilities in this study, the findings that boys showed higher skills in this area than girls in a national comparison are of particular relevance.
2.3 Conditional probability
Dealing with Bayesian situations corresponds to a field of application that students not only encounter in mathematics lessons but is of actual relevance for professions such as doctors or lawyers (Binder et al., 2015) or school teachers (Leuders & Loibl, 2020). Here, it is necessary to conclude from a binary information (e.g., test negative or positive) to a binary hypothesis (e.g., ill or not ill) (Büchter et al., 2022; Zhu & Gigerenzer, 2006). In Bayesian tasks the base rate (frequency of disease), the true-positive rate P(test positive|disease) and the false-positive rate P(test positive|no disease) are typically given, whereby posterior probabilities, such as the conditional probability P(disease|test positive) or P(disease|test negative) for a judgement are calculated. Since the posterior probabilities depend on the base rate, which is usually low in medical contexts, the posterior probabilities are often underestimated (Cosmides & Tooby, 1996; Gigerenzer & Hoffrage, 1995). The posterior probabilities can be calculated with the help of Bayes’ theorem or with the help of appropriate visualisations, such as the tree diagram or 2 × 2 tables (e.g., see Binder et al., 2015; Böcherer-Linder & Eichler, 2017).
The use of visualisations is a strategy that can increase the solution rate on Bayesian tasks; McDowell and Jacobs (2017) found an increase in the solution rate of 23%. However, which type of visualisation is most promising is debated in current studies (e.g., Binder et al., 2015, 2020; Böcherer-Linder & Eichler, 2019; Spiegelhalter et al., 2011). The extent to which the set-subset relation is made comprehensible through the visualisation can have a performance-enhancing function for the students’ achievement (McDowell & Jacobs, 2017). In this context, it also matters to what extent a visualisation provides sufficient information, for example, further graphical or numerical information, for the student (Khan et al., 2015). We assume that when static and dynamic visualisations are compared, the type of information differs because interactivity can generate more information. However, the results on whether interactive visualisations actually help in conditional probability tasks are still limited and contradictory (Büchter et al., 2022).
3 The present study
The integration of additional interactive elements, such as dynamic visualisations and feedback opportunities, in a digital textbook aims to provide additional support for the teaching and learning of mathematics (Rezat et al., 2021; Yerushalmy, 2015). To investigate this influence, we designed a study that contrasts the use of printed and digital materials and investigates the impact on students’ achievement. So far, the relationship between achievement and textbook use has been investigated in only a few studies, as direct comparison presents methodological challenges, such as the equitable comparison of printed and digital materials in terms of content and visual comparison (Castro-Alonso et al., 2016; Fan et al., 2013; Rezat et al., 2021). To be able to distinguish effects between a digital textbook, which is enriched with dynamic visualisations and feedback options, and a printed material, we have developed a paper-based textbook with the same content that is visually comparable. The study focuses on the topic of conditional probabilities, as especially in Bayesian situations, the visualisation of the statistical situations through the representation of the set-subset relation can be decisive for a student’s performance (Binder et al., 2015; Böcherer-Linder & Eichler, 2019). Consequently, we ask the following research question:
-
1.
What are the effects of dynamic visualisations, feedback formats and digital tools used in a digital textbook on students’ mathematics achievement in a series of lessons on conditional probability?
These effects are examined in a comparison to the use of analogue, printed materials. We assume that the use of the digital textbook has a greater positive effect on student performance than the use of the printed textbook, because of the integration of computer-based feedback and dynamic visualisations (Berney & Bétrancourt, 2016; Castro-Alonso et al., 2019; Hattie, 2015; Van der Kleij et al., 2015). In addition, particularly the use of visualisations in conditional probabilities is a strategy that promotes learning (McDowell & Jacobs, 2017), and we assume that the interactive elements provide additional helpful information (Khan et al., 2015).
As previous studies on the use of digital curriculum resources give first indications that boys and girls use digital textbooks differently and that this can result in achievement differences between boys and girls (Hoch, 2020; Kaplar et al., 2022; Reinhold et al., 2020; Reinhold et al., 2020), and large-scale studies in Germany in particular have found gender-specific achievement differences (OECD, 2012; Schipolowski et al., 2019; Stanat et al., 2019), the research question is extended to question whether there is a difference between boys’ and girls’ achievement when working with digital or printed resources.
-
2.
What are the effects of dynamic visualisations, feedback formats and digital tools used in a digital textbook on students’ mathematics achievement, especially considering gender, in a series of lessons on conditional probability?
The extension of the research question thus addresses the research gap of how the combination of digital curriculum resources and dealing with content from the field of data and chance affects the performance of boys and girls. Based on the previous evidence on the usage behaviour of digital textbooks, such as working more conscientiously with the digital supplementary elements (Hoch, 2020; Reinhold et al., 2020), we assume that girls can benefit more from the digital textbook in our setting. Such effects may occur especially when dealing with conditional probabilities, as we suspect that the affordances of the digital textbook may be of particular relevance in the case of conditional probabilities. Since the participating students have already used the digital textbook before the study, the advantages in favour of boys found in large-scale achievement studies should not be present at the beginning of our study.
4 Method
4.1 Sample and procedure
The study presented here from the school years 2020/21 and 2021/22 is part of the project KomNetMath, which investigates the use of the digital textbook Net-Mathebuch in mathematics lessons (see Brnic, in preparation). For this purpose, 22 teachers and their students from Germany were provided with this digital textbook for a complete school year so that they could use it regularly in class. The teachers voluntarily participated in the project KomNetMath. In the study presented here, the focus is on the impact of working with a digital textbook on student achievement.
The sample consists of a total of 314 students from Germany who participated in all parts of this study (154 female, Mage = 15.62, SDage = 0.77). Of these students, 180 were in grade 10 of the Gymnasium and 134 students were in grade 11 of the Gesamtschule (comprehensive school). In each case, this is the first year of the upper secondary school, so these grades can be classified as equivalent. Two of these students did not indicate their gender and four of these students identify themselves as non-binary, so no group comparisons are possible with these students.
To answer the research question, an already existing chapter of the digital textbook Net-Mathebuch on conditional probabilities was redeveloped together with the authors of the digital textbook, who are experienced mathematics teachers, and a five-hour (à 45 min) lesson series was developed based on this chapter. The series of lessons builds on previous knowledge of the 2 × 2 table and the tree diagram. These two visualisations were mainly used at all project schools. The series of lessons introduces the concept of conditional probability and aims to build an understanding of how conditional probabilities can be calculated using 2 × 2 tables and tree diagrams. In addition, the lessons are characterised by the students working out how to deal with conditional probabilities using authentic examples of applications such as the HIV test, DNA analysis or a diabetes test; there is a special focus on how to vary the types of representations and feedback.
Before and after the series of lessons, an achievement test on conditional probabilities was conducted (see Instrument and statistical analyses). Based on the results of the pretest and taking into account an equal gender distribution, the students from each mathematics class were divided into two comparably achieving groups. One half of the class then formed the digital group and worked with the Net-Mathebuch in the lesson series. The other half of the class worked with a printed adaptation of the Net-Mathebuch in the lesson series. This group will be referred to as the printed group in the following. The digital group consisted of 154 students (74 female, Mage = 15.59, SDage = 0.77) while the printed group included 160 students (80 female, Mage = 15.62, SDage = 0.74).
The digital and printed groups were taught in separate rooms by their teacher for the series of lessons. The same teacher taught the same lessons to both groups, once with the digital textbook and once with printed materials, based on predefined lesson plans (see Fig. 1). All students have thus worked on the same tasks in the lesson series.
In lessons II and IV, which were held without the teacher, the students continued to work independently. During this time, they were accompanied by a research assistant. The students were given exercises that were related to the lesson with the teacher and whose solutions they could check on their own with the digital or printed textbook. But even in the lessons with the teacher, the students should work as independently as possible to minimise the teacher’s influence. The design sequence was varied so that lesson t1 took place first in the digital group in 12 courses, as shown in Fig. 1, and in the printed group in 11 courses so that sequence effects in this respect can be excluded.
4.2 Material
The digital mathematics textbook Net-Mathebuch (NET-Schulbuch.DE gUG, 2021) is an exclusively digitally developed textbook. It covers the complete content for the upper secondary level in Germany to achieve the highest school-leaving certificate, the Abitur. The digital textbook is characterised by the fact that it has integrated not only static but also dynamic structural elements (see Pohl & Schacht, 2019). Thus, it offers many of the potentials of digital textbooks, such as feedback options and interactivity (Choppin et al., 2014). As GeoGebra is integrated as a digital tool in the textbook, the interactive tasks and visualisations were partly implemented with this software. Examples of how selected potentials have been implemented in the Net-Mathebuch are shown in Table 1.
The newly developed chapter on conditional probabilities from the Net-Mathebuch that is relevant for this study was transformed into an analogue printed version that the printed group worked with when conducting the study. As the comparison of static and dynamic representations presents methodological challenges and can generate a bias towards one of the representations (Castro-Alonso et al., 2016), care was taken in the development of the printed adaptation to ensure that it matched the digital model. The idea was that the printed material should cover identical content but without digital features. In the adaptation, it was ensured that, in addition to copying the same tasks, the colour scheme, the same illustrations and comparable proportions were adopted, and that the structure of the digital Net-Mathebuch was reflected in the printed version (see Castro-Alonso et al., 2016; Reinhold et al., 2020).
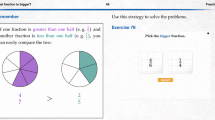
Key differentiators between the digital and printed versions concern the use of the medium, the possibilities for interaction and the way feedback is provided (see Fig. 2). The digital textbook is opened via the browser and can thus be used on the laptop or tablet, for example. The adaptation is a printed version on paper, which was compiled in a binder. In addition, dynamic visualisations were transferred to static visualisations. For example, for a GeoGebra app in which different values can be set using sliders, several static images of the app were shown on paper, which show differently set states (see Fig. 3).
In the digital textbook, students can have their solutions checked immediately for correctness or incorrectness by entering them in corresponding solution fields (see Fig. 4). In addition, students can call up hints for the solution process immediately. In contrast, in the printed material, corresponding hints and solution pages are integrated, which can be opened separately by the students in the binder.
4.3 Implementation check
Teacher training can be a crucial part of the successful implementation of digital curriculum resources (Hillmayr et al., 2020). Such teacher training was offered to the teachers to support the use of the Net-Mathebuch in the classroom, where they learned about the design and use of the digital textbook. These training sessions took place at the beginning, middle and end of the school year and were conducted by the authors of the textbook. The students and their mathematics teachers had already been using the digital textbook for at least one month at the time of the intervention.
Due to the analogue visual design and comparable structure, we assume that the printed adaptation also looked familiar to the students and teachers, especially as they should have broad experience in working with printed materials through their previous school careers. In summary, this should mean that they do not have to learn how to use the printed or digital materials during the intervention.
However, there were no guidelines on how the teachers should use the Net-Mathebuch with their students previously in class. Such specifications were only made for the intervention presented here. Through the additional supervision by a research assistant during the series of lessons, it was at least possible to monitor the use of the materials in the independent work lessons. In addition, the students were given a checklist in which they could tick off the tasks completed in the lesson series. These checklists could be provided to the research team by the students voluntarily. On average, 87% (Median 95%) of all tasks were completed.
4.4 Instrument and statistical analyses
In a pretest-posttest design, the achievement of the students is measured before and after the series of lessons on conditional probabilities. The pretest and posttest were previously piloted and then further developed for this study. Both tests consist of 13 items each, whereby the pretest and the posttest are linked with the help of five anchor items. Therefore, in the first step, we analyse the data using item response theory, specifically with the Rasch model, so that the results of the pretest and posttest can be represented on one scale (see Bond & Fox, 2015; Rasch, 1960). In the second step, the data are analysed using classical test theory (see Döring, 2023).
The pretest and the postest were each compiled in two different versions as a paper-pencil test, in which only the order of the items differs. The content of the test is designed to test the content of the lesson series. In the pretest, there are more items on the students’ previous knowledge of constructing tree diagrams and 2 × 2 tables, and in the posttest there are mainly items in which dealing with conditional probabilities is required.Footnote 1 The items are in single-choice or short answer format and were coded dichotomously with one exception. One more complex item was polytomously coded with an intermediate level (0, 1, 2). For this item, students were asked to transfer percentages from a 2 × 2 table to a tree diagram and calculate the missing conditional probabilities (see Fig. 5). The correct transfer was scored with code 1, and the additional correct calculation of the conditional probabilities with code 2.
Using the partial credit Rasch model (Rasch, 1960), the data are scaled using the software ACER ConQuest 5. In the first step, the item parameters were estimated to check the fit of the individual items and to test unidimensionality, meaning whether all items test the same latent construct. For this purpose, the weighted mean square (wMNSQ) was analysed, which describes whether the individual item fits the model well, that is, whether the observed value for a solution fits the expected response probability. In addition, the item-total correlation was considered as an index for discriminatory power. The wMNSQ should have values between 0.8 and 1.2 and the discriminatory power should be above 0.2 (OECD, 2012). As one item did not meet these criteria, it is excluded from the model. All other items are assumed to measure the same latent construct (performance on conditional probabilities) (Bond & Fox, 2015).
In the next step, the partial credit Rasch model was used to estimate an ability parameter representing achievement in the tests for each person. The EAP/PV reliability, which compares the estimated variance with the actual variance, is 0.54, which is sufficient for group comparisons (Lienert & Raatz, 1998, p. 14). The estimated abilities are used for further analyses and group comparisons using classical test theory. To determine the group differences concerning the two measurement time points pretest and posttest, a mixed ANOVA was performed, taking into account the factors of gender and group. The software JASP was used for this purpose.
5 Results
We questioned to what extent using a digital textbook with integrated dynamic visualisations and feedback formats compared to using a printed mathematics textbook, influences the students’ achievement. For this purpose, we had students take a test before and after a series of lessons on conditional probability.
5.1 Mathematical achievement in the digital and printed group
We expected that the students in the digital group would make greater achievement gains due to the additional digitally enriched features of the digital textbook. As Table 2 and a mixed ANOVA reveal, the students in the digital group, in fact, were able to show higher achievement compared to the printed group in the posttest. Thus, the mixed ANOVA shows a significant small effect for the corresponding interaction between group and measurement time points, F(1, 310) = 5.59, p =.02, partial η2 = 0.02. In addition, there is a significant main effect of time, F(1, 310) = 52.20, p <.001, partial η2 = 0.02, and a non-significant main effect of the group, F(1, 310) = 1.48, p =.26, partial η2 < 0.01. The hypothesis that working on conditional probabilities with the digital textbook and its integrated features leads to higher achievement than working with a printed textbook with the same content can thus be confirmed and is discussed below.
Post hoc tests using the Holm-Boferroni correction show that from the first to the second time point the printed group (t(159) = -3.47, p <.01, d = 0.23) and the digital group improved significantly (t(153) = -6.71, p <.001, d = 0.45) meaning that in both groups the students acquired additional competencies in dealing with conditional probabilities with a small effect.
5.2 Mathematical achievement of boys and girls
Furthermore, we asked to what extent it makes a difference for boys and girls whether they use the printed or digital textbook. At the time of the pretest before conducting the series of lessons, there are no significant differences between boys and girls, t(313) = -1.13, p =.52, d = 0.13. However, the choice of the respective materials has an influential effect on the achievement gain between the genders. The mixed ANOVA shows that there is a significant interaction with a small effect between the factors time, gender and group, F(1, 310) = 4.09, p =.04, partial η2 = 0.01. The interaction between the measurement points and gender is not significant, F(1, 310) = 0.05, p =.83, partial η2 < 0.001.
Post hoc tests using the Holm-Bonferroni correction to the trajectories shown in Fig. 6, show that boys improved significantly in the digital group, t(79) = -3.71, p <.01, d = 0.34, and in the printed group, t(79) = -3.37, p =.02, d = 0.31, with a small effect. In contrast, the girls improved only in the digital group, t(73) = -5.74, p <.001, d = 0.55, with a medium effect. In the printed group, the girls did not improve significantly, t(79) = -0.09, p = 1.00, d = 0.14.
Pretest and posttest results of girls and boys in both intervention groups
Note. Error bars in Fig. 6 show 95% confidence intervals
6 Discussion
State-of-the-art digital mathematics textbooks are characterised by the integration of digitally enriched features, such as interactive elements and feedback options (Choppin et al., 2014; Wijaya et al., 2022). Our study aimed to investigate to what extent the use of such features has an impact on student achievement compared to the use of one-to-one adapted, printed materials—with an additional focus on gender differences. This was investigated in the context of a series of lessons on conditional probabilities, since in this content area, in particular, the type of visualisation, which can be enriched in digital form by additional information, can have a decisive influence on the students’ understanding (see Binder et al., 2015; Böcherer-Linder & Eichler, 2019; Khan et al., 2015; McDowell & Jacobs, 2017).
6.1 Digital textbook or printed materials
The results indicate that the students in both groups were able to increase their achievement in dealing with conditional probabilities. Thus, the lesson series and the design can be classified as functional for working on conditional probabilities. The overall low estimated abilities, which were already present in the pretest, indicate the students’ difficulties in dealing with stochastic situations and conditional probabilities (Cosmides & Tooby, 1996; Gigerenzer & Hoffrage, 1995; McDowell & Jacobs, 2017). This assumption is also supported by the rather small effects found in this study.
Nevertheless, the results of this study show empirical evidence that students could additionally benefit from the additional elements of a digital textbook, such as dynamic visualisations and computer-based feedback. The fact that there are several features in one digital learning environment is also the distinctive feature of a digital textbook. This suggests that the effectiveness of these individual features (such as dynamic visualisations or computer-based feedback), which have each been investigated in meta-studies (Berney & Bétrancourt, 2016; Castro-Alonso et al., 2019; Van der Kleij et al., 2015), can also function in interaction. The findings of this study thus join the initial evidence on the effectiveness of digital textbooks in other content areas (Jang et al., 2016; Kaplar et al., 2022; Reinhold et al., 2020) or the more general assumption that digital curriculum resources that share those potentially helpful digital features are effective for learning (Hillmayr et al., 2020).
A decisive factor here could also be the previous experiences of the students, who were already familiar with the use of digital feedback and dynamic visualisations at the time of the survey and thus already were aware of the possibilities and limitations of these features. These are also the two main distinguishing features between the compared materials. The digital textbook presents feedback immediately on a computer basis and has integrated dynamic visualisations, which are mostly characterised by interactivity, whereas in the printed materials feedback could only be looked up with a time delay and the students dealt with static visualisations. However, immediate feedback is considered to be more effective for learning, especially with more complex tasks (Shute, 2008). In addition, the higher degree of information of an interactive visualisation, which may have a crucial role especially when considering visualisations on conditional probabilities (Büchter et al., 2022; Khan et al., 2015), may have influenced students‘ performance by facilitating the cognitive processing of the task (Schnotz & Rasch, 2008). This is particularly relevant because the topic of conditional probabilities is considered challenging for students.
6.2 Differences between boys and girls
The results also show that the difference between the two groups is due to the achievement of the girls in particular. For the girls, using the digital features of a digital textbook was essential for improving their achievement, whereas, for the boys, it does not seem to make a difference what kind of resources they use. It is also worth noting that the girls in the digital group improved from the lowest to the highest average estimated abilities. The fact that girls can work particularly well with a digital textbook is also in line with the first indications in this direction in comparable studies (Hoch, 2020; Kaplar et al., 2022; Reinhold et al., 2020; Reinhold et al., 2020).
In summary, the choice of material made a crucial difference for the girls. Reasons for them being proficient with the digital textbook could be, for example, a greater engagement with the digital textbook and its features. The assumption is that boys are more likely to be distracted by digital resources, while girls use them meaningfully for their work (see Hoch, 2020; Reinhold et al., 2020).
Future research could focus on the elements in which digital and printed materials differ. For example, concerning boys and girls, it could be investigated how dynamic visualisations are used and how often feedback is used, for example, by analysing process data. However, why girls could only achieve such low performance with the printed materials remains an open question. This is particularly noteworthy because the textbook, and here the printed textbook so far, is the central key resource in mathematics classrooms (Fan et al., 2013; Pepin & Gueudet, 2018; Rezat et al., 2021). Since achievement differences in favour of boys can be found in the German context, especially in the subject area of data and chance (Schipolowski et al., 2019; Stanat et al., 2019), the use of the digital textbook could be a way to minimise these differences.
6.3 Limitations
Due to the specificity of the digital textbook that different dynamic elements or features occur together and are used in the study, the differences in effects cannot be attributed to individual structural elements. While a textbook is developed with a specific intention by the designers and editors, how it is actually used depends on the individual students and their prior experiences and beliefs (Pepin & Gueudet, 2018; Rezat et al., 2021). Although the pre-post design can show differences between working with digital and printed materials, no statements can be made about how the learning processes differ. It can only be assumed that the students learnt differently due to the digital textbook and its integrated features. This can be followed up by further research that investigates the actual use, for example through a qualitative approach to the learning process or process data. Such an approach could also be used to investigate how exactly girls and boys differ in their use of the digital textbook and whether working independently in the lessons works well under the supervision of a research assistant. Furthermore, effects of the teacher cannot be completely excluded, even though each teacher taught in both the digital and the printed group. Moreover, the results are limited to conditional probabilities only and for the age group studied. The extent to which the results can be transferred to other subject areas and age groups must be investigated in future studies.
7 Conclusion
Overall, the results indicate that students can benefit from the potentials of digital textbooks in the area of conditional probabilities, especially compared to working with analogue, printed materials. This also contributes to enriching the still limited picture of whether dynamic visualisations are to be preferred over static visualisations in conditional probabilities. The results should be considered in particular from the perspective that a printed and a digital group were each taught by their usual teacher and in both groups the lessons were carried out according to predefined course plans, meaning that the teacher’s influence should be as minimal as possible.
Thereby, it seems to make a difference, especially for girls, whether they use digital materials enriched with dynamic visualisations and computer-based feedback or printed materials. It should also be noted that the additional support for girls does not disadvantage boys. Due to the often outstanding importance of the textbook as a guiding resource for teachers (Fan et al., 2013; Rezat et al., 2021), these are crucial indications to conduct further studies that explain why these gender differences occur in comparison of printed and digitally enriched learning settings, and whether these are a persistent phenomenon. This is particularly relevant for the further development of printed and digital textbooks and materials. Through the potential integration of further features, such as the integration of augmented reality and virtual reality, or the consideration of digital accessibility, the digital textbook can distinguish itself from the printed model through even more aspects in the future.
Notes
An overview of the tasks of the tests and further sample tasks can be found in supplementary material A1 and A2.
The logit unit represents a transformation of the test scores, whereby the estimated abilities can take on values between (-∞, ∞).
References
Berney, S., & Bétrancourt, M. (2016). Does animation enhance learning? A meta-analysis. Computers & Education, 101, 150–167. https://doi.org/10.1016/j.compedu.2016.06.005
Binder, K., Krauss, S., & Bruckmaier, G. (2015). Effects of visualizing statistical information– an empirical study on tree diagrams and 2 × 2 tables. Frontiers in Psychology, 6, 1186. https://doi.org/10.3389/fpsyg.2015.01186
Binder, K., Krauss, S., & Wiesner, P. (2020). A new visualization for probabilistic situations containing two binary events: The frequency net. Frontiers in Psychology, 11, 750. https://doi.org/10.3389/fpsyg.2020.00750
Böcherer-Linder, K., & Eichler, A. (2017). The Impact of Visualizing Nested Sets. An Empirical Study on Tree Diagrams and Unit Squares. Frontiers in Psychology, 7:2026. https://doi.org/10.3389/fpsyg.2016.02026
Böcherer-Linder, K., & Eichler, A. (2019). How to improve performance in bayesian inference tasks: A comparison of five visualizations. Frontiers in Psychology, 10, 267. https://doi.org/10.3389/fpsyg.2019.00267
Bond, T. G., & Fox, C. M. (2015). Applying the Rasch model: Fundamental measurement in the human sciences, 3rd ed (pp. xxi, 383). Routledge/Taylor & Francis Group.
Brnic, M. (in preparation). Lernen mit einem digitalen Mathematikschulbuch und dessen digitalen Werkzeugen [Learning with a digital mathematics textbook and its digital tools] [Doctoral dissertation]. University of Münster.
Brnic, M., & Greefrath, G. (2022a). Does the gender matter? The use of a digital textbook compared to printed materials. In U. T. Jankvist, R. Elicer, A. Clark-Wilson, H.-G. Weigand, & M. Thomsen (Eds.), Proceedings of the 15th International Conference on Technology in Mathematics Teaching (ICTMT 15) (pp. 128–135). Danish School of Education, Aarhus University. https://doi.org/10.7146/aul.452
Brnic, M., & Greefrath, G. (2022b). Distance learning versus face-to-face classroom learning: Student achievement in conditional probability when using a digital textbook with integrated digital tools. Proceeding of the Twelfth Congress of the European Society for Research in Mathematics Education. CERME 12, Bozen-Bolzano, Italia. https://hal.science/hal-03748202/
Büchter, T., Steib, N., Böcherer-Linder, K., Eichler, A., Krauss, S., Binder, K., & Vogel, M. (2022). Designing visualisations for bayesian problems according to Multimedia principles. Education Sciences, 12(11), 739. https://doi.org/10.3390/educsci12110739
Büchter, T., Eichler, A., Steib, N., Binder, K., Böcherer-Linder, K., Krauss, S., & Vogel, M. (2022). How to train novices in bayesian reasoning. Mathematics, 10(9). https://doi.org/10.3390/math10091558. Article 9.
Cai, J., & Howson, G. (2013). Toward an International Mathematics Curriculum. In M. A. (Ken) Clements, A. J. Bishop, C. Keitel, J. Kilpatrick, & F. K. S. Leung (Eds.), Third International Handbook of Mathematics Education (pp. 949–974). Springer. https://doi.org/10.1007/978-1-4614-4684-2_29
Castro-Alonso, J. C., Ayres, P., & Paas, F. (2016). Comparing apples and oranges? A critical look at research on learning from statics versus animations. Computers & Education, 102, 234–243. https://doi.org/10.1016/j.compedu.2016.09.004
Castro-Alonso, J. C., Wong, M., Adesope, O. O., Ayres, P., & Paas, F. (2019). Gender imbalance in Instructional Dynamic Versus static visualizations: A Meta-analysis. Educational Psychology Review, 31(2), 361–387. https://doi.org/10.1007/s10648-019-09469-1
Chazan, D., & Yerushalmy, M. (2014). The Future of Textbooks: Ramifications of Technological Change for Curricular Research in Mathematics Education. Media and Education in the Digital Age. Concepts, Assessments, Subversions, 63–76.
Choppin, J., Carson, C., Borys, Z., Cerosaletti, C., & Gillis, R. (2014). A typology for analyzing digital curricula in mathematics education. International Journal of Education in Mathematics Science and Technology, 2(1), 11–25.
Cosmides, L., & Tooby, J. (1996). Are humans good intuitive statisticians after all? Rethinking some conclusions from the literature on judgment under uncertainty. Cognition, 58(1), 1–73. https://doi.org/10.1016/0010-0277(95)00664-8
Döring, N. (2023). Forschungsmethoden und evaluation in den Sozial- Und Humanwissenschaften [Research methods and evaluation in the social and human sciences]. Springer. https://doi.org/10.1007/978-3-662-64762-2
Fan, L., Zhu, Y., & Miao, Z. (2013). Textbook research in mathematics education: Development status and directions. ZDM– The International Journal on Mathematics Education, 45(5), 633–646. https://doi.org/10.1007/s11858-013-0539-x
Fraillon, J., Ainley, J., Schulz, W., Friedman, T., & Duckworth, D. (2020). Preparing for life in a Digital World: IEA International Computer and Information Literacy study 2018 International Report. Springer International Publishing. https://doi.org/10.1007/978-3-030-38781-5
Gigerenzer, G., & Hoffrage, U. (1995). How to improve bayesian reasoning without instruction: Frequency formats. Psychological Review, 102, 684–704. https://doi.org/10.1037/0033-295X.102.4.684
Hattie, J. (2015). The applicability of visible learning to higher education. Scholarship of Teaching and Learning in Psychology, 1(1), 79–91. https://doi.org/10.1037/stl0000021
Hattie, J., & Timperley, H. (2007). The power of feedback. Review of Educational Research, 77(1), 81–112. https://doi.org/10.3102/003465430298487
Hillmayr, D., Ziernwald, L., Reinhold, F., Hofer, S. I., & Reiss, K. M. (2020). The potential of digital tools to enhance mathematics and science learning in secondary schools: A context-specific meta-analysis. Computers & Education, 153, 103897. https://doi.org/10.1016/j.compedu.2020.103897
Hoch, S. (2020). Prozessdaten aus digitalen Schulbüchern als Instrument der mathematikdidaktischen Forschung [Process data from digital textbooks as an instrument for mathematics education research] [Doctoral dissertation, Technische Universität München]. https://nbn-resolving.de/urn/resolver.pl?urn:nbn:de:bvb:91-diss-20201218-1554567-1-1
Jang, D. H., Yi, P., & Shin, I. S. (2016). Examining the effectiveness of Digital Textbook use on students’ learning outcomes in South Korea: A Meta-analysis. The Asia-Pacific Education Researcher, 25(1), 57–68. https://doi.org/10.1007/s40299-015-0232-7
Jonsson, A., & Panadero, E. (2018). Facilitating Students’ Active Engagement with Feedback. In A. A. Lipnevich & J. K. Smith (Eds.), The Cambridge Handbook of Instructional Feedback (1st ed., pp. 531–553). Cambridge University Press. https://doi.org/10.1017/9781316832134.026
Kaiser, G., & Zhu, Y. (2022). Gender differences in mathematics achievement: A secondary analysis of Programme for International Student Assessment data from Shanghai. Asian Journal for Mathematics Education, 1(1), 115–130. https://doi.org/10.1177/27527263221091373
Kaplar, M., Radović, S., Veljković, K., Simić-Muller, K., & Marić, M. (2022). The influence of interactive learning materials on solving tasks that require different types of Mathematical reasoning. International Journal of Science and Mathematics Education, 20(2), 411–433. https://doi.org/10.1007/s10763-021-10151-8
Khan, A., Breslav, S., Glueck, M., & Hornbæk, K. (2015). Benefits of visualization in the Mammography Problem. International Journal of Human-Computer Studies, 83, 94–113. https://doi.org/10.1016/j.ijhcs.2015.07.001
Leuders, T., & Loibl, K. (2020). Processing Probability Information in Nonnumerical Settings– Teachers’ Bayesian and Non-bayesian Strategies During Diagnostic Judgment. Frontiers in Psychology, 11:678. https://doi.org/10.3389/fpsyg.2020.00678
Lienert, G. A., & Raatz, U. (1998). Testaufbau und testanalyse [Test design and test analysis] (6th ed.). Beltz, Psychologie Verlags Union.
McDowell, M., & Jacobs, P. (2017). Meta-analysis of the effect of natural frequencies on bayesian reasoning. Psychological Bulletin, 143(12), 1273–1312. https://doi.org/10.1037/bul0000126
NET-Schulbuch.DE gUG (Eds.). (2021). Net-Mathebuch. https://m2.net-schulbuch.de
OECD. (2012). PISA 2009 Technical Report. OECD.https://doi.org/10.1787/9789264167872-en
OECD. (2019).PISA 2018 Results (Volume II): Where All Students Can Succeed. OECDPublishing. https://doi.org/10.1787/b5fd1b8f-en
Panadero, E., & Lipnevich, A. A. (2022). A review of feedback models and typologies: Towards an integrative model of feedback elements. Educational Research Review, 35, 100416. https://doi.org/10.1016/j.edurev.2021.100416
Pepin, B., & Gueudet, G. (2018). Curriculum Resources and Textbooks in Mathematics Education. In S. Lerman (Ed.), Encyclopedia of Mathematics Education (pp. 1–5). Springer International Publishing. https://doi.org/10.1007/978-3-319-77487-9_40-7
Pepin, B., Gueudet, G., Yerushalmy, M., Trouche, L., & Chazan, D. (2015). E-textbooks in/for teaching and learning mathematics: A disruptive and potentially transformative educational technology. In L. D. English & D. Kirshner (Eds.), Handbook of International Research in Mathematics Education. Third edition (pp. 636–661). Routledge. https://hal.archives-ouvertes.fr/hal-01207678
Pohl, M., & Schacht, F. (2019). How do students use digital textbooks? In S. Rezat, L. Fan, M. Hattermann, & H. Wuschke (Eds.), Proceedings of the Third International Conference on Mathematics Textbook Research and Development (pp. 39–44). Universitätsbibliothek Paderborn. https://doi.org/10.17619/UNIPB/1-768
Rasch, G. (1960). Studies in mathematical psychology: I. probabilistic models for some intelligence and attainment tests (pp. xiii, 184). Nielsen & Lydiche.
Reinhold, F., Hoch, S., Werner, B., Richter-Gebert, J., & Reiss, K. (2020). Learning fractions with and without educational technology: What matters for high-achieving and low-achieving students? Learning and Instruction, 65, 101264. https://doi.org/10.1016/j.learninstruc.2019.101264
Reinhold, F., Strohmaier, A., Hoch, S., Reiss, K., Böheim, R., & Seidel, T. (2020). Process data from electronic textbooks indicate students’ classroom engagement. Learning and Individual Differences, 83–84, 101934. https://doi.org/10.1016/j.lindif.2020.101934
Rezat, S., Fan, L., & Pepin, B. (2021). Mathematics textbooks and curriculum resources as instruments for change. ZDM– Mathematics Education, 53(6), 1189–1206. https://doi.org/10.1007/s11858-021-01309-3
Rolfes, T., Roth, J., & Schnotz, W. (2020). Learning the Concept of function with dynamic visualizations. Frontiers in Psychology, 11, 693. https://doi.org/10.3389/fpsyg.2020.00693
Schipolowski, S., Wittig, J., Mahler, N., & Stanat, P. (2019). Geschlechtsbezogene Disparitäten [Gender disparities]. In P. Stanat, S. Schipolowski, N. Mahler, S. Weirich, & S. Henschel (Eds.), IQB-Bildungstrend 2018 (pp. 237–264). Waxmann.
Schnotz, W., & Rasch, T. (2008). Functions of animation in comprehension and learning. Learning with animation: Research implications for design (pp. 92–113). Cambridge University Press.
Shute, V. J. (2008). Focus on formative feedback. Review of Educational Research, 78(1), 153–189. https://doi.org/10.3102/0034654307313795
Spiegelhalter, D., Pearson, M., & Short, I. (2011). Visualizing uncertainty about the future. Science, 333(6048), 1393–1400. https://doi.org/10.1126/science.1191181
Stanat, P., Schipolowski, S., Mahler, N., Weirich, S., & Henschel, S. (Eds.). (2019). IQB trends in Student Achievement 2018. The Second National Assessment of mathematics and Science Proficiencies at the end of Ninth Grade. Waxmann.
Stoet, G., & Geary, D. C. (2013). Sex differences in Mathematics and Reading Achievement are inversely related: Within- and across-Nation Assessment of 10 years of PISA Data. Plos One, 8(3), e57988. https://doi.org/10.1371/journal.pone.0057988
Tversky, B., Morrison, J. B., & Betrancourt, M. (2002). Animation: Can it facilitate? International Journal of Human-Computer Studies, 57(4), 247–262. https://doi.org/10.1006/ijhc.2002.1017
Van der Kleij, F. M., & Lipnevich, A. A. (2021). Student perceptions of assessment feedback: A critical scoping review and call for research. Educational Assessment Evaluation and Accountability, 33(2), 345–373. https://doi.org/10.1007/s11092-020-09331-x
Van der Kleij, F. M., Feskens, R. C. W., & Eggen, T. J. H. M. (2015). Effects of Feedback in a computer-based learning environment on students’ learning outcomes: A Meta-analysis. Review of Educational Research, 85(4), 475–511. https://doi.org/10.3102/0034654314564881
Wijaya, T. T., Zhou, Y., Houghton, T., Weinhandl, R., Lavicza, Z., & Yusop, F. D. (2022). Factors affecting the Use of Digital Mathematics textbooks in Indonesia. Mathematics, 10(11), 1808. https://doi.org/10.3390/math10111808
Yerushalmy, M. (2015). E-textbooks for mathematical guided inquiry: Design of tasks and task sequences. Task Design in Mathematics Education (pp. 229–247). Springer.
Zhu, L., & Gigerenzer, G. (2006). Children can solve bayesian problems: The role of representation in mental computation. Cognition, 98(3), 287–308. https://doi.org/10.1016/j.cognition.2004.12.003
Funding
This work is part of the project KomNetMath, which is funded by Medienberatung NRW. The Medienberatung NRW did not provide support for the preparation of the article, in study design, in the collection, analysis and interpretation of data, in the writing of the report and in the decision to submit the article publication.
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors of the digital textbook are not involved in the design of the study, the collection, analysis and interpretation of data and not involved in the writing and submission of this article. The authors of the digital textbook were only involved in the development of the chapter and the series of lessons on conditional probabilities.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic Supplementary Material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Brnic, M., Greefrath, G. & Reinhold, F. Working with digital textbooks or printed materials: A study with boys and girls on conditional probability. ZDM Mathematics Education (2024). https://doi.org/10.1007/s11858-023-01543-x
Accepted:
Published:
DOI: https://doi.org/10.1007/s11858-023-01543-x