1 Introduction

In the university education of preservice teachers (PSTs), subject-specific professionalization has traditionally been a major challenge. There is an ongoing discussion among teachers, researchers, and learners about the appropriateness of the current study programs. A key point of debate is the design of mathematics courses, which often lack an explicit connection to future mathematics teaching (e.g., Even, 2022). This problem is often called second discontinuity, which goes back to mathematician Felix Klein, who introduced it as one part of the so-called double discontinuity (Klein, 2016, p. 1). The first discontinuity refers to the transition from school to university and is not the focus of this paper. We are concerned with the second discontinuity, which refers to the transition from academic studies (as a PST) to working as a mathematics teacher. Klein formulates the problem from the perspective of a young teacher who “suddenly finds himself expected to teach the traditional elementary mathematics according to school practice; and, since he will be scarcely able, unaided, to discern any connection between this task and his university mathematics, he will soon fell in with the time honored way of teaching, and his university studies remain only a more or less pleasant memory which has no influence upon his teaching” (Klein, 2016, p. 1). Here, the insertion of “unaided” is crucial: Klein considers his books an essential “tool” for prospective teachers to acquire some kind of knowledge and skills to make these linkages.

In this paper, we aim to investigate how appropriate innovations in mathematics courses can contribute to overcoming the second discontinuity by taking up Klein’s basic approach of supporting PSTs in making connections through specific learning opportunities. We focus on a geometry course that was developed, implemented, and studied in the first author’s PhD project (Hoffmann, 2022). In this course, we chose and arranged content and teaching/learning methods in an explicitly profession-oriented way. Two weeks of the course (lectures and tutorials), the so-called interface weeks, are specifically designed to connect the course content to future teaching at school. There is also a so-called interface ePortfolio, on which the PSTs worked the whole semester. For the conceptual classification of these innovations, we theoretically clarify what we understand by the design principle of profession orientation and the extent to which its implementation can help overcome the second discontinuity. After that, we present the results of a qualitative study of the reflection texts that PSTs wrote. Through this, we investigate the extent to which the implemented innovations are suitable for overcoming the second discontinuity from the PSTs’ perspectives.

2 Theoretical background

2.1 Two facets of Klein’s second discontinuity

Research and practice widely indicate that many teachers feel what Klein describes in the quote mentioned in the introduction (e.g., Even, 2022). However, apart from practice reports (e.g., Hefendehl-Hebeker and Schuster, 2006), only a few empirical studies have examined the perspectives of practicing mathematics teachers (e.g., Wasserman et al., 2018; Zazkis and Leikin, 2010).

Zaskis and Leikin (2010, p. 279) observed that teachers’ perceptions of how often they use academic mathematics in everyday teaching vary widely. Although many teachers ascribe a general value to academic mathematical content knowledge (CK), the research results show clear difficulties in specifying this in terms of particular problems and situations that have occurred when teaching secondary mathematics. The authors considered this to be evidence of the gap we described as second discontinuity (p. 280) and called for “identifying explicit content-based connections” and “an explicit awareness of these connections”.

Wasserman et al. (2018) surveyed practicing teachers (and PSTs) related to aspects of real analysis at the academic level that they saw as relevant to teaching secondary mathematics. The researchers identified the rationale of the so-called transport model. By this, they mean the assessment of the usefulness of a content (e.g., proof) of academic mathematics according to the extent to which it is suitable (in as unchanged a form as possible) to be transferred to the classroom. As an alternative to simply accepting this rationale, the authors suggest developing innovations that help PSTs see the benefits of academic mathematics for teaching secondary mathematics beyond the transport model.

In their concluding discussions, both papers refer to innovations in the PSTs’ study program. This fits in with the fact that also PSTs often perceive university mathematics courses a priori (without having worked as teachers) as not useful or irrelevant for their (future) teaching. This may already negatively affect how motivated and deeply they learn academic mathematics during their studies. Again, there is much anecdotal evidence for this but only a fragmentary situation of empirical studies.

A recent contribution to this discussion is provided by Eichler and Isaev (2022), who, in a questionnaire study, investigated, among other things, the beliefs of PSTs (first and third semesters) about the relevance of the mathematical content learned for their later job in a pre-post control group design. The experimental group was treated with so-called teacher-oriented tasks that drew relations to future teaching. A decrease in perceptions of relevance was observed in the control group, showing that positive expectations of the relevance of university mathematics decreased after the first encounter. This decrease did not occur in the experimental group.

We coined the term subjective facet of the second discontinuity (cf. Hoffmann, 2022) for the subjective attitudes of PSTs and teachers that appeared in these previous studies. The subjective facet refers to the perception that their acquired CK is not relevant or helpful to job-related issues, regardless of the objective accuracy of this judgment. This perception can lead to a lack of motivation to learn, resulting in future mathematics courses being perceived as irrelevant, although objectively, that knowledge might be useful. In future teaching situations, this attitude may persist and prevent teachers from using their academic CK as a resource, although their knowledge may have this potential.

Felix Klein argued for aiding PSTs in using their academic CK as a resource for teaching, seemingly without considering whether the relevant CK had already been learned. However, the situation can be worse because PSTs may objectively lack the helpful mathematical knowledge and skills necessary for their work as teachers. We refer to this second aspect as the objective facet, for which there are several possible reasons: PSTs may have never seen a particular school-relevant concept from an academic perspective; they may have built up CK at the beginning of their time at university but then forgotten it; or the required CK may exist, but there is no clarity about how to relate it to school mathematics (in the sense of “elementary mathematics from an advanced standpoint,” e.g., Buchholtz et al., 2013).

The objective facet is a real problem supported by theoretical analyses (e.g., Winsløw and Grønbæk, 2014; Wu, 2011) and empirical investigations (e.g., Buchholtz et al., 2013; Darling-Hammond, 2011; Hoth et al., 2020). Furthermore, in the discussion on the structure of mathematics teacher’s professional knowledge (Neubrand, 2018), there have been suggestions for additional and mediating profession-specific knowledge categories (e.g., Ball et al., 2002; Dreher et al., 2018) to characterize specific linking-knowledge and skills. This need is also supported by discussions that refute the intellectual trickle-down theory (by learning academic mathematics as relevant to mathematics students, PSTs automatically acquire the mathematical competencies they need for teaching) (Hoth et al., 2020; Wu, 2011).

A distinction between the two facets of the second discontinuity is relevant for research and development; it is needed to address PSTs’ attitudes as well as their skills and knowledge.

2.2 Existing ideas for overcoming the second discontinuity

In recent years, two main ways to address the second discontinuity have emerged in various projects: Enriching mathematics courses with additional design elements (e.g., Bauer, 2013; Eichler and Isaev, 2022; Suzuka et al., 2009) and the development of entirely new types of mathematics courses (e.g., Barquero and Winsløw, 2022; Beutelsbacher et al., 2011; Fukawa-Connelly et al., 2020; Hoffmann, 2022; Loe & Rezac, 2006). Other approaches include explicating linkages to academic mathematics in courses on the didactics of mathematics (Biehler & Hoffmann, 2022) or offering advanced university courses for experienced teachers (Even, 2011). However, most of these projects are situated at the beginning of a study program and often do not distinguish between the first and second discontinuity.

Regarding additional design elements, the term interface tasks (orig.: Schnittstellenaufgaben) has become established in German-speaking countries. It refers to tasks used in a mathematics course to create opportunities for linking school mathematics and academic mathematics (matching, e.g., Wasserman’s (2018) and Zaskis and Leikin’s (2010) calls described in Section 2.1). In Germany, the use of such tasks has increased significantly in recent years, with a high variety of task types (Weber & Lindmeier, 2022). Although some research findings suggest that such types of activities succeed in mitigating at least some aspects of the second discontinuity (e.g., Eichler and Isaev, 2022; Weber et al., 2022), the overall research situation is still fragmentary.

A key design element of most of the innovations mentioned above is that mathematical knowledge and skills are used in the context of “school-related situations” in some sense. A concept that brings more clarity into the discussion is the notion of job tasks (Ball & Bass, 2002; Prediger, 2013). Teachers’ professional expertise is seen as related to solving job tasks, identified as the results of empirical classroom observations. In the context of innovations to overcome the second discontinuity, job tasks in which academic mathematical competencies are a relevant resource are of particular interest. These include, for example, analyzing and evaluating approaches (e.g., in textbooks), examining students’ contributions and mistakes, and reacting to them in a way conducive to their learning.

Using the job task notion, interface tasks can be seen as learning opportunities whose design is based on identified job tasks with the following objectives: first, to enhance the probability that PST will use their academic CK and skills in future teaching situations and second, to change the attitude that their academic CK and skills are relevant by broadening and deepening PSTs’ views on future typical requirements. This theoretical background was used, for example, by Eichler and Isaev (2022) in designing interface tasks.

An often unstated underlying assumption in approaches such as interface tasks is that the academic mathematics covered in a course is linkable in the first place (both objectively and from the PSTs’ perspective).

One aspect we have hardly found in the existing literature is the integration of interface tasks or activities into course exams. According to the principle of constructive alignment (Biggs, 1996), there is a risk that PSTs will concentrate on the “exam-relevant” parts of a course and not on the interface activities. When we conducted our first practical tests on using interface activities in the context of an analysis course a few years ago, we experienced this effect. Not for PSTs but for engineering students, an empirical study reported that their engagement and attitudes toward interface tasks decreased when it became clear that the tasks were irrelevant to the exam (Wolf, 2017, p. 480).

2.3 Defining profession orientation as a design principle for mathematics courses

In this section, we propose profession orientation as a design principle for mathematics courses for PSTs. We build on the approaches described in Section 2.2 but explicitly consider both facets of the second discontinuity (Section 2.1) as well as the principle of constructive alignment.

By profession orientation, we mean the design of learning opportunities in a way that connects mathematical knowledge and skills to mathematics-containing job tasks. Thus, we take up the idea of interface tasks but broaden the view to more complex learning opportunities. We differentiate between two sub-principles:

1. Principle of implicit profession orientation: Whenever there are several similarly suitable options (e.g., for an axiom system, a definition, or a proof), the one that best establishes a connection to the future teaching situation should be chosen.

2. Principle of explicit profession orientation: Special interface-learning opportunities should be implemented: PSTs should use their mathematical knowledge and skills in situations related to future job tasks and then reflect on their use. In the spirit of constructive alignment, such activities should also be part of the course exam in some form.

Regarding the second discontinuity, implicit profession orientation can help address the objective facet (but not necessarily the subjective facet) and focuses primarily on the academic CK learned being essentially “linkable.” This first sub-principle is complemented by the explicit profession orientation, which includes fostering linking knowledge and skills and reflecting on the job-related usefulness of the mathematics learned. Overall, the design principle of profession orientation addresses the problems of the second discontinuity identified in Section 2.1, considering the existing innovation approaches described in Section. 2.2.

However, implementing profession orientation in mathematics courses is not a magic bullet that will automatically improve PSTs’ later teaching. This becomes clear when looking at teachers’ professional competence from the perspective of the established continuum modeling of Blömeke et al. (2015). In this view, professional competence has different components: Situation-specific skills mediate between dispositions and performance. Typical implementations of explicit profession orientation in a mathematics course, for example, using interface tasks, do not even yield situation-specific skills because in the context of a task in a mathematics course, real situations that require, for example, teacher noticing under time pressure are not included. Instead, we are at an intermediate point that is not captured explicitly in the continuum model, since how exactly mathematical knowledge and skills must be acquired to be useful as dispositions and resources for the requirement of situation-specific skills is not modeled. Our approach provides a preliminary step, namely to examine and process a fictitious situation designed based on a typical job task without time pressure and from a dominant mathematical perspective. This preliminary stage can be built upon in subsequent didactics courses or in-service training.

3 The course “Geometry for PSTs”

We have been exploring ways to implement profession orientation in a 6th -semester course called “Geometry for PSTs,” which we introduce in this section, beginning with a brief discussion of the country-specific conditions of teacher education in Germany. Here, the university-based part of teacher education (e.g., Tatto et al., 2012, p. 70) consists of three course pillars: academic mathematics, didactics of mathematics, and general pedagogics. During their university studies, in addition to short internships, there is a “practice semester” in which PSTs spend half a year in schools gaining and reflecting on practical experiences. A second stage of education follows the university part: 18 months of guided teaching in schools, partly independent, partly supervised, and with so-called practice-related theoretical blocks at special centers for teacher education (“Referendariat”).

There are different study programs for future primary teachers (grades 1 to 4), future secondary teachers (grades 5 to 10), and future gymnasium teachers (grades 5 to 13). The gymnasium is the “highest level” school, ultimately leading to the Abitur, a final exam that must be taken to enter university studies in any subject. As a rule, future gymnasium teachers take mathematics courses with students majoring in mathematics. However, the course we designed and studied is for future gymnasium teachers only because Euclidean plane geometry is not considered relevant for mathematics majors. The existence of this course is a certain concession that PSTs have special mathematical needs.

In addition to this course, there are two other compulsory courses with references to school geometry. In their first and second semesters, PSTs enroll in a linear algebra course designed for mathematics majors. In the second semester, there is a course called Didactics of Geometry. It discusses standard didactic issues (curricula, learning objectives, problem-solving, proving and reasoning, etc.) in the context of (synthetic) geometry at the lower secondary level.

The course is only taken by PSTs, thus making it well-suited for exploring ways to implement profession orientation. We have realized various innovations, such as designing the course content (see App. 1, supp. material) so that many definitions and proofs can be elementarized to the level of school geometry. Further, the two major parts of the course correspond to the different types of geometry teaching in German schools: upper secondary analytic geometry and lower secondary elementary (synthetic) geometry. The course is, therefore, implicitly profession oriented. Explicit profession orientation is realized by devoting two weeks of the semester to interface weeks and by asking the PSTs to work on interface tasks and document them in the interface ePortfolio (Sections 4).

The main content foci of the interface weeks were congruence and symmetry. For both topics, the essential characteristics of their rigorous mathematical treatment were first detached from the particular axiomatic approach of the lecture. This is done by explicating so-called interface aspects (Biehler & Hoffmann, 2022; Hoffmann & Biehler, 2022) resulting from inductive subject-specific-didactical analyses. Based on these interface aspects, typical elements of the treatment of concepts in school are discussed from a mathematical point of view. In the associated interface tasks, PSTs must apply both the interface weeks’ content and the geometry learned in the course.

4 Interface-ePortfolios

Portfolio work provides a natural method for documenting and combining tasks with reflection processes (Paulson et al., 1991). We adapted the concept of a course-accompanying ePortfolio from Siebenhaar et al. (2013), with a particular focus on profession orientation, mainly in the form of interface tasks, hence the term interface ePortfolio.

4.1 Integration of the interface-ePortfolio in the course

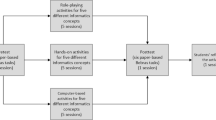
The PSTs collected their learning products digitally in a cloud, creating their electronic portfolios (“ePortfolio”). These learning products were not graded but checked for completeness, and the PSTs received feedback on their work from a tutor. The individual portfolios were only available in pseudonymized form for the lecturer to promote the honesty of reflections. Figure 1 provides an overview of all the tasks we used. We realized constructive alignment, as the ePortfolio was relevant for the final assessment and grading of the PSTs in the following way: the final oral exam started with presenting (under certain conditions) self-selected parts of the PSTs’ ePortfolios; thus, polishing and recapitulating the ePortfolio was required as an essential part of the preparation for the final exam.

Fig. 1
figure 1

Overview of all interface ePortfolio tasks. Connected tasks relate to each other; tasks in braces refer to one of the two interface weeks: those with a gray background were used during the interface week itself, and the others occurred in the weeks before (PRE refers to such tasks that are used again in the interface week). REFLECT stands for tasks with an additional reflection subtask and DGS stands for tasks where PSTs worked with a dynamic geometry system

Full size image

4.2 Different types of ePortfolio tasks

In the ePortfolio, we pursue the following four objectives with different types of tasks (in italics):

  1. 1.

    Linking academic CK with school geometry (interface tasks, fact sheets).

  2. 2.

    Using academic CK as a resource for tackling typical job tasks (interface tasks).

  3. 3.

    Initiating reflection processes (competence grids, reflection tasks).

  4. 4.

    Restructuring and deepening the academic CK (fact sheets).

The difference between the related Objectives 1 and 2 lies in the degree of situating: Objective 1 aims at establishing content links between the geometry course and school geometry (Example: “Draw the house of quadrilaterals ordered by symmetry properties and formally state the respective symmetry groups” [ePF15]), whereas Objective 2 explicitly focuses on job tasks such as responding to a student statement.

4.2.1 Competence grids for self-assessment

We followed Siebenhaar et al. (2013) and integrated competence grids for self-assessment in the ePortfolio (ePF1, ePF2; example: App. 2, supp. material). With these grids, PSTs had to self-assess their knowledge of the mathematical backgrounds of school geometry concepts and theorems, as well as their skills in dealing with mathematics-containing job tasks.

4.2.2 Interface tasks

In our approach, interface tasks are central to the ePortfolio work. They relate to the topics of the interface weeks, congruence (ePF2, ePF5–ePF10), and symmetry (ePF13, ePF15–ePF18), as well as the overarching topic of isometries (ePF11, ePF12). As described in Section 2.2, all interface tasks are based on typical mathematics-containing job tasks. Examples include analyzing textbook approaches to the concept of symmetry (ePF16) or mathematically clarifying and answering a student’s question about congruence theorems (ePF7). A translated and annotated example of an interface task on congruence can be found in Appendix 3 (supp. material).

4.2.3 Reflection tasks

In the ePortfolio, reflection tasks are provided on various levels. In some cases, interface tasks are used twice, and PSTs must reflect on how the competencies acquired in the course influence their work on these tasks (ePF7, ePF9, ePF17). There are also occasions for reflection on one’s prior knowledge of the topics of congruence and symmetry (ePF2, ePF13). The third type of reflection activity generally refers to how PSTs see geometry as relevant content in school mathematics and self-perceptions about their ability to teach geometry (ePF3, ePF14, ePF20). We will examine ePF3 and ePF20 in detail in the following sections. (Regarding the focus of this paper, ePF14 is not relevant to our study because its reflection relates primarily to a school-oriented review of the course content and less to a reflection on one’s professionalization.)

4.2.4 Fact sheets for geometric mappings

During the semester, PSTs study different geometric mappings (reflections, rotations, …). In the fourth type of task, fact sheets for geometric mappings (ePF4, ePF19), PSTs summarize their knowledge of geometric mappings in a pre-structured way. This consists of a formal definition, an explanation of all possible variants of the formalization, and a detailed written example calculation.

5 Investigating PST’s perspectives – study design

5.1 Objectives of the study

We aim to explore how PSTs perceive the contribution of the profession-oriented innovations presented in Sects. 3 and 4 to their professionalization. With this focus, we primarily address the second discontinuity’s subjective facet. From the PSTs’ perspective, this research interest involves two questions: How prepared do the PSTs feel to teach geometry? What contribution has the course Geometry for PSTs made to this? Thus, the focus is on PSTs’ judgment of their ability to teach geometry in the future, which can be understood as self-efficacy (Bandura, 1977; Bjerke & Solomon, 2020). The following refined research questions guided our empirical investigations:

RQ.1. How do the PSTs perceive the benefits of using interface ePortfolios to enhance their professionalization, and how do these perceptions align with the broader objectives of implementing a profession-oriented approach characteristic of this course, as well as the specific objectives of the four interface task types used in the course?

RQ.2. What do PSTs report regarding their self-efficacy in teaching geometry before and after the course, and what changes occurred?

For RQ2, two sub-aspects were explored. The PSTs’ self-efficacy is influenced first (RQ2.1) by their self-assessment of mathematical knowledge and skills that they assumed to be relevant for their future teaching, and second (RQ2.2) by their perceived ability to manage those job tasks that they find typical for their future teaching. We describe the operationalization of the research questions and related analyses in the Sections 6.1.1 and 6.2.1, respectively.

5.2 Data and method of analysis

Our data are PSTs’ texts from the reflection tasks ePF3 and ePF20. As such, the interface ePortfolio was a research instrument (for collecting data), and the completed interface ePortfolios were the research objects (data). For the study, we concentrated on the text passages that refer to the guiding questions listed in Table 1, as these fit our research interests best. A complete set of all guiding questions can be found in Appendix 4 (supp. material).

Question ePF20-3 provides the basis for answering RQ1. Self-efficacy for teaching geometry in the pre/post comparison (RQ2) was examined based on the PSTs’ texts on ePF3-3 and ePF20-2.

Table 1 Guiding questions from ePF3 and ePF20 used in the study
Full size table

Pseudonymized data were available from 40 (ePF3) and 34 (ePF20) PSTs. For each PST, we linked the two texts and comparatively analyzed the beginning and end of the semester using qualitative content analysis (QCA; Mayring, 2014). We deductively defined category systems based on our theoretical background and research interests. We then analyzed the data using these categories and inductively formed further categories. Lastly, we coded the texts again using these new categories. We describe the initial categories and results of the QCA in the following section, sorted by the research questions.

6 Results

6.1 PSTs’ evaluation of the interface-ePortfolio

6.1.1 Method of analysis

To answer RQ1, we analyzed the PSTs’ reflections on ePF20-3 (Table 1). Regarding this RQ, it is necessary to relate the PSTs’ perceived benefits of the interface ePortfolio (henceforth “ePortfolio”) to the types of tasks mentioned in their texts. To analyze these benefits, we defined four categories corresponding to the objectives described in Section 4.2 and an additional category for further statements beyond these categories. This allows for aligning the PSTs’ statements to our course objectives while remaining open to statements beyond them. Therefore, our initial categories cover PST’s statements on the usefulness of the ePortfolio regarding:

  1. (1)

    tackling job tasks.

  2. (2)

    linking school mathematics and academic mathematics.

  3. (3)

    restructuring and deepening mathematical knowledge.

  4. (4)

    initiating reflections.

  5. (5)

    other benefits.

To answer the second part of RQ1, we assigned more categories to the text passages that explicitly referred to a specific task type: (A) competence grids, (B) interface tasks, (C) reflection tasks, and (D) fact sheets. We also used one category, (E) ePF in general, for coding text passages in which a task type was not explicitly mentioned. For the analysis, we crossed the two main categories. We are interested in the frequency of their occurrence and in how PSTs express their thoughts. The anchor examples for the crossed categories also served this purpose.

Table 2 Category system for the QCA regarding RQ1. The numbers in the cells must be interpreted as the < number of coded text passages> (< number of different PSTs>). (N = 34)
Full size table

6.1.2 Results for RQ1: PSTs’ evaluation of the interface ePortfolio

The QCA led to the categorization in Table 2. All of the intended objectives of the ePortfolio (Cat. 1–4) can be found in the PSTs’ texts; no further benefit (Cat. 5) was indicated. The different objectives (rows in Table 2) will now be discussed in detail: Practicing mathematical knowledge and skills as a resource for coping with job tasks is a major objective of the ePortfolio concept, which is addressed in the interface tasks (Sections 4.2.2). The analysis shows that most PSTs see benefits in this regard (Cat. 1) and, as expected, refer mainly to the interface tasks (Cat. 1B). As job tasks do not play an explicit role in the other types of tasks, the statements in the category tackling job tasks in which interface tasks are not explicitly mentioned (Cat. 1E), nevertheless, can be assigned to them. In addressing RQ2 (Sections 6.2), we will explain the job tasks that PSTs explicitly mention and how they relate to the job tasks examined in the interface tasks.

Making connections between the academic mathematics learned and the mathematics taught in school is an essential prerequisite for using mathematical knowledge and skills as resources for tackling job tasks. Many PSTs explicitly mentioned that the ePortfolio contributed to their making such connections (Cat. 2). However, most PSTs did not explicitly connect their assessments to a specific task type. For nearly all text passages coded in this category, the nature of this linkage was not further elaborated upon (see Justus, Table 2). Nevertheless, in terms of the subjective facet of the second discontinuity, many PSTs stated that they considered the contents of a university mathematics course to be connectable to the school mathematics they would be teaching. This difference is particularly clear in Florian’s quote.

“The ePortfolio has accompanied my learning process in that I have reflected on the content I have learned and have thus related it back to the school situation. This is essential for me and is missing at every other point in the mathematics study program.” (Florian)

Florian contended that the mere act of establishing connections between university and school mathematics was a distinctive benefit of this course, distinguishing it from other mathematics courses that may not prioritize this aspect. The quote also provides an example for Category 4 (initiate reflections), which will be discussed later.

The results for Category 3 (restructuring and deepening mathematical knowledge) showed that most PSTs perceived the benefit of the ePortfolio in increasing their understanding of the mathematical content. Many coded text passages (see Johannes, Table 2) explicitly referred to the fact sheets (Cat. 3D). This is expected, given the design of this task type. However, it is remarkable that there were also text passages with categories related to the interface tasks (Cat. 3B, see Maxim below) or the ePortfolio in general (Cat. 3E).

“But also, in the tasks in which we were supposed to respond to learner comments or pick out a suitable textbook task on certain interface aspects, I often studied the previously covered contents of the lecture very closely.” (Maxim)

Initiating and supporting reflection processes are at the core of any portfolio. In the QCA, there were corresponding text passages (Cat. 4) for nine PSTs, with reference to the reflection tasks (Cat. 4 C; see Judith, Table 2) and the ePortfolio in general (Cat. 4E; see Florian, above). However, the analysis method we used only captured the responses of PSTs who explicitly stated that they had reflected through the ePortfolio. Further, although the analysis did not identify them, there were PSTs who reflected in a differentiated way in their texts without making this explicit at the meta-level. This includes, for example, Angelina (Table 2).

Examining the results from Table 2 in the context of the different task types (i.e., column by column), no text passages were found for Subcategory A (competence grids). One possible explanation for this is that this task type was perceived as less relevant by the PSTs in retrospect and in comparison to the other activities, due to it encompassing a small portion of the overall ePortfolio. For the other three task types, the assignment to the usefulness categories 1–3 corresponded to the respective intentions (Sections 4.2) of these types.

Overall, concerning RQ1, the analysis yielded three key findings:

1. In response to the guiding question (ePF20-3, Table 2), PSTs described the benefits of the interface ePortfolio exactly as intended: making connections between academic mathematics and the mathematics, they would later teach (Cat. 2) to use academic mathematics as a resource for tackling job tasks (Cat. 1). Further, restructuring and deepening of content knowledge took place (Cat. 3), and reflection processes were initiated (Cat. 4).

2. The categorizations also reflect the different emphases within the task types, although competence grids are not explicitly mentioned. The most task-specific statements were made for the interface tasks and the fact sheets.

3. Overall, we were surprised that the ePortfolio’s benefits for understanding academic mathematics were emphasized similarly to its benefits for professionalization in a narrower sense.

Category 3 especially indicates the possible potential of interface ePortfolio: To support students’ (not only PSTs’) learning of academic CK, it could be beneficial to examine the content of a mathematics course from other perspectives detached from rigorous embedding in the “definitions-theorem-proof” structure (as done in our ePortfolio concept).

6.2 PSTs’ reported self-efficacy in teaching geometry (pre/post)

6.2.1 Method of analysis

To answer RQ2, we analyzed the PSTs’ reflections on ePF3-3 (“pre-texts”) and ePF20-2 (“post-texts”). We structured our analysis along the two sub-aspects (RQ2.1/2) we distinguished at the end of Section 5.1. In Section 6.2.2, we present the results of the QCA on the pre-post comparison of the PSTs’ statements regarding the elements of knowledge they refer to when assessing their self-efficacy in teaching geometry. We used the three main categories of professional teacher knowledge and distinguished between mathematical content knowledge, pedagogical content knowledge, and pedagogical knowledge. We also formed further categories inductively. We then distinguished whether the knowledge was “regarded as available” or “regarded as not available” in the coded text passages. For the post-texts, we also analyzed what contribution PSTs attribute to the course Geometry for PSTs. Lastly, we compared the pre- and post-texts along each category by assessing the code frequencies and striking points that deviate from our theoretical and design-related background.

Section 6.2.3 addresses RQ 2 by focusing on job tasks that PSTs mention in their reflections on their self-efficacy in teaching geometry. Since two job tasks were explicitly addressed in the interface tasks (analyze and evaluate approaches (e.g., in textbooks), analyze students’ contributions and mistakes, and react to them in a way conducive to learning), we expected these to be mentioned in the post-texts. Accordingly, we initially defined two categories, which we also used for coding the pre-texts for comparison purposes. All other categories were created inductively from the job tasks mentioned by the PSTs. An interesting aspect of the analysis is the job tasks the PSTs mentioned before and after the intervention and what changes occurred. Further, with a focus on the RQ, we analyzed how the PSTs assessed their abilities to tackle the respective job tasks by defining corresponding subcategories. The core of the analysis is a comparison of the code frequencies and exposing interesting PSTs opinions.

6.2.2 Results for RQ2 – part 1: PSTs’ knowledge

We present key findings from the QCA on the knowledge that the PSTs referred to in their self-assessments for teaching geometry. First, the initial category of pedagogical knowledge was not coded, meaning that the PSTs referred exclusively to their mathematics-specific knowledge (content/pedagogical content knowledge). We start with the first-named category, for which we inductively found three subcategories (Table 3).

Table 3 Category system for the QCA regarding the mathematical content knowledge PSTs mentioned when reflecting on their self-efficacy in teaching geometry
Full size table

Subcategory 1.1 refers to PSTs’ statements about their school geometry knowledge. This category was identified primarily in the pre-texts. The PSTs who referred to existing school geometry knowledge (Cat. 1.1.+, pre) mentioned the course Didactics of Geometry or giving private lessons as acquisition contexts (see Valentina, Table 3). Some PSTs explicitly limited their knowledge to lower secondary geometry. Fittingly, most PSTs who described a lack of school geometry knowledge (Cat. 1.1.-, pre) referred to upper secondary analytical geometry (see Tom, Table 3). In this context, some PSTs mentioned that this topic area did not play a role in the previous course, especially not in the course on Linear Algebra (see Tim), and by design, it was not part of the course Didactics of Geometry.

“I had the impression that the lecture Linear Algebra (1 + 2) stopped exactly where one would begin with geometry and school mathematics (position relations of straight lines and planes, e.g.).” (Tim)

Isabell further stated that due to the lack of treatment of school content, the courses even contribute to forgetting it.

“The fact that little or no attention is paid to the school content in my studies gives me the impression that I will have to learn all the content again after graduation. In my opinion, these studies do not prepare me for teaching geometry or any other topic. The longer the studies take, the more you forget what was covered in school, and the more difficulty you have remembering it.” (Isabell)

In the post-texts, this category is essentially non-existent. One possible explanation is that in the post-text, PSTs tended to argue more regarding the academic mathematics covered in the course as background to school geometry and less regarding available school knowledge alone. Corresponding text passages fall into Category 1.2 (academic background knowledge). Most of the deficits mentioned by PSTs regarding mathematical knowledge fall into this category. The PSTs often, although not exclusively, referred to upper secondary geometry (see Mattis, Table 3). These deficits were explicitly framed as a relevant gap in their self-efficacy in teaching geometry (see Timon).

“I have not really received further and deeper insight into the subject area of geometry than from the school itself. Thus, I do not have much more than the school knowledge of geometry. However, I think a teacher should have a much deeper knowledge of the subject area than the teacher teaches in order to be able to give clear and precise answers to the various student questions.” (Timon)

This category’s strikingly high coding frequency in the post-texts (Cat. 1.2.+, post) shows that the PSTs felt that the course made a significant contribution. We inductively defined further subcategories for a more detailed analysis. Most of the text passages coded in this category (30 (20)) generally spoke about mathematical background and school geometry (see Isabell) without mentioning a specific topic.

“I currently feel quite well prepared to teach geometry in school. In contrast to other areas of mathematics, I have dealt with school content and its background in this course and thus developed a deeper understanding.” (Isabell)

A comparison of Isabell’s statement to the quote from her pre-text shows that she perceived that this geometry course succeeded in helping her make the links to school mathematics that she otherwise found to be lacking in university courses. The second most frequently (12 (11)) coded text passages were those in which the PSTs explicitly referred to the interface activities (particularly the interface aspects) of congruence and symmetry (see Leandro, Table 3.). The other coded text passages were distributed among statements on the notion that the mathematical background made it easier to make connections between individual school mathematics topics (7 (8)) and that the background of particular theorems and proofs of school geometry was better understood (7 (7)). The PSTs (e.g., Henning, Table 3) who still saw gaps in the mathematical background (Cat. 1.2.-, post) related them exclusively to individual concepts.

The last mathematics-related category (Cat 1.3) captures references to academic CK without a school reference. This category appears only in the post-texts and only in the way that PSTs (e.g., Timon, Table 3) highlighted that their mathematical understanding of geometry has deepened. However, since they use these statements as arguments in assessing their self-efficacy to teach geometry, it can be assumed that they also see this deeper understanding as useful.

We found no interesting results regarding the pedagogical content knowledge for this paper’s focus, so we will not discuss it here. Appendix 5 (supp. material) contains an overview of the categories identified.

In summary, this part of the analysis shows that, from the perspective of most PSTs, the course succeeded in providing mathematical content knowledge relevant to later teaching in the form of a deeper understanding of school geometry linked to an academic mathematics background. This becomes particularly clear in the pre–post comparison. In their pre-texts, the PSTs exclusively stated a lack of relevant academic background knowledge, whereas the analysis of the post-texts showed a clear increase in availability in this category, which the PSTs explicitly attribute to the course. The PSTs mentioned that the course elements introduced to implement explicit profession orientation, such as interface weeks, interface aspects, and interface tasks, were beneficial to their professionalization.

6.2.3 Results for RQ2 – part 2: job tasks

The second part of the analysis on RQ2 examines the job tasks that PSTs mention in their reflections and how prepared they feel to accomplish them (Table 4). We used different subcategories for the pre- and post-texts (columns in Table 4). We distinguished them in the pre-texts whether the PSTs felt rather well prepared or rather unprepared to cope with a job task. Since the post-texts focus on the contribution of the course, we distinguish whether the PSTs felt better prepared for tackling a job task due to the course or whether they had reflected a job task as challenging and needed further professionalization. Further, there were job tasks that were only mentioned.

Table 4 Category system for job tasks mentioned by the PSTs in their texts when reflecting on their self-efficacy in teaching geometry
Full size table

Category 1 hardly ever occurred in the pre-texts; in the passages coded in the post-texts, the corresponding learning opportunities of the course were mentioned as contributing to better preparation.

The PSTs who felt rather prepared in Category 2 justified this assessment either by attending the course or by having given private tutoring. Those who felt rather unprepared referred to their lack of either mathematical or didactic knowledge. Many PSTs felt better prepared in the post-texts and explicitly referred to the interface tasks as having affected this. Matching the mathematical focus of the course, the PSTs described the added value mainly in their ability to clarify student statements mathematically.

Some PSTs who mentioned dealing with student statements in their post-texts explicitly indicated that the challenges inherent in this job task had become apparent through working on the interface activities:

“In the process [working on an interface task with a fictitious student statement], I first became aware that breaking it down can be very difficult because you want to convey all of the relevant mathematical information, but you can’t do it in too complex a way, or it could become too complicated for the students.” (Angelina)

The most common category for job tasks we found in the pre-texts included general statements about explaining and teaching mathematical content (Cat. 3). Here, many PSTs had an instructional perspective on the teaching secondary mathematics (see Amy). In the post-texts, this category did not occur.

“In my eyes, the art of a math teacher is teaching the content to the weakest and explaining it vividly.” (Amy)

The results support the assumption that the course design (particularly the interface ePortfolio) can lead PSTs to develop a more differentiated idea of future job tasks. This includes a shift away from the instructional idea of “explaining reduced academic mathematics” (Cat. 3).

In summary, in their reflection texts, PSTs named different job tasks. It is essential to consider that the guiding questions did not ask them to elaborate on job tasks, meaning that their choice to make statements on this topic was a not-prompted decision. The analysis shows that the PSTs commented more frequently and in a more differentiated manner on job tasks at the end of the semester. The job tasks explicitly mentioned in the interface tasks (Cat. 1, 2) were dominant. Many PSTs stated that they felt better prepared to cope with them due to the course and referred, in particular, to use their mathematical knowledge as a helpful resource (cf. RQ2.1). Thus, the self-efficacy to teach geometry—at least related to these aspects—was increased by our innovations. This includes the fact that the PSTs considered the job tasks presented in the course relevant to their future teaching practice. That was our assumption. However, many courses operate with the assumption of presenting content relevant to PSTs, an assumption that the PSTs do not share. Thus, our course was successfully different.

Further, for some PSTs, engagement with the job tasks encouraged more substantial reflections on the requirements for their professionalization. This can be seen in the subcategory reflected as challenging (Table 4) and in statements such as Florian’s:

“Before the course, I often carelessly claimed that I could teach geometry in school. I had a good geometry class in school, which gave me a lot of background understanding of geometry. In attending this course, many things became more difficult for me. The topic of congruence and the proofs of congruence theorems particularly aroused my interest in understanding the background in detail. [...]” (Florian)

7 Discussion

We addressed the topical and relevant question of how to counteract the second discontinuity through appropriate innovations in university mathematics courses. The focus of this article is on interface tasks embedded in an interface ePortfolio, through which the design principle of profession orientation formulated by us is implemented in a geometry course for PSTs. We qualitatively investigated the PSTs’ perspectives on this innovation.

An important limitation of our study is that the results cannot be solely attributed to the course design, as the instructor’s role also played a role. However, the pseudonymization of the texts and their indirect relevance to the final exam minimized the likelihood of socially desirable reflections.

Our study shows that the design of the course Geometry for PSTs in general and the innovation of the interface-ePortfolio in particular succeeded in making almost all the PSTs feel more prepared to teach geometry after the course. They attributed this primarily to acquiring relevant and profession-oriented linked mathematical knowledge and to learning opportunities in which they could practically apply their mathematical knowledge in fictitious situations constructed based on the requirements of typical job tasks. Thereby, the PSTs evaluated the benefits of the different task types (especially the interface tasks) in the intended sense. We were pleasantly surprised to find that many PSTs attributed the restructuring and deepening of their academic CK to the ePortfolio, despite it being designed to link to future school teaching rather than to enhance their mathematical understanding. This unexpected finding highlights a potential strength of the course approach that justifies further investigation.

The fact that PSTs self-assessed their academic background knowledge as relatively weak at the start of the course is consistent with the findings of Buchholtz et al. (2013) regarding insufficient professional knowledge of elementary mathematics from an advanced standpoint. The substantially improved assessment of self-efficacy to teach geometry at the end of the course aligns with the positive changes in beliefs observed by Eichler and Isaev (2022) through the use of interface tasks. A particular strength of our approach appears to be in providing the PSTs with a better view of relevant future job tasks through our ePortfolio activities. This is evidenced by numerous PSTs explicitly mentioning the job tasks addressed in our tasks when assessing their self-efficacy in teaching geometry.

Overall, the course concept succeeded in counteracting the subjective facet of the second discontinuity for many PSTs, as it helped them perceive their acquired academic CK as transferable to job-related issues. This supports the results of an initial questionnaire study conducted to evaluate the innovations in Hoffmann (2022). The PSTs worked on typical job tasks in the ePortfolio and perceived themselves to be more successful at the end of the course than at the beginning. Since their assessments are not only based on assumptions but also on real experiences (the processing of interface tasks), a contribution to counteracting the objective facet is also apparent.

With reference to the existing literature, profession orientation and its implementation in the geometry course is exactly the kind of innovation that Zaskis and Leikin (2010) and Wasserman (2018) call for. That many of our students are now more sophisticated in reflecting on their mathematical knowledge and skills in relation to potential job tasks can be interpreted as contributing to overcoming the transport model-rationale.

Since, in practice, PSTs often take courses together with mathematics majors, the question arises about whether our innovations can be applied to those courses as well. We believe that using the ePortfolio concept is also possible in this case: While the PSTs work on the interface tasks, the other students can be asked to work on relevant tasks for their study focus (e.g., examples that show links to the advanced courses they will attend in the future). Nevertheless, the initial development of suitable ePortfolio tasks requires close collaboration between mathematics and the didactics of mathematics. Once designed, the concept can then be used in the long term. For the interface weeks, it could be an option to produce self-learning materials that can be used by instructors who are not professionalized in mathematics didactics. To maintain constructive alignment, it is necessary that the differentiation between PSTs and other students also takes place in the exams. Nevertheless, we assume that successful implementation always requires instructors who are convinced that it makes sense to provide PST-specific innovation space in their mathematics courses.

Clearly, implementing profession orientation in mathematics courses through the use of the interface-ePortfolio is an innovative and promising approach. To gain further insights into its impact on the objective facet of the second discontinuity, the next step will be to evaluate the PSTs’ solutions to individual interface tasks in detail.