1 Introduction

In mathematics, a discipline dealing with mostly abstract objects (e.g., numbers, chance, change), the importance of visualization as a medium in mathematical thinking and learning and its benefits and boundaries to student learning was suggested decades ago (e.g., Bishop, 1973; Presmeg, 1986). The historical discourse on visualization in mathematics education went through different phases (for an overview see Presmeg, 2006): In the 1980 s, research aimed at understanding benefits and boundaries of learning and teaching with visualization for individual learners (e.g., Presmeg, 1986). To gain insights into the thinking and learning processes, research relied predominantly on qualitative methods including interviews and classroom observations. A new emerging topic in the 1990 s was curriculum development (e.g., Ginsburg, 2002) along with further research on individual differences in visualization preferences (e.g., Kozhevnikov et al., 2002) and visualization skills (e.g., Stylianou & Silver, 2004). In addition, research interest in learning with computer technology emerged (e.g., dynamic geometry software; Yerushalmi & Chazan, 1990). Since the 2000 s, research on visualization in mathematics education further diffused (Presmeg, 2006). One research focus lies on the effectiveness of visualizations to promote learning of specific topics and processes (e.g., arithmetic problem solving, Booth & Thomas, 1999) and the role of gestures in forming and communicating understanding (e.g., Radford, 2003). Research designs include qualitative methods, quantitative methods, and mixed methods designs depending on the research aims.

To our knowledge, Presmeg (1986), Bishop (1989), and Presmeg (2006) have provided the only reviews on visualization specific to mathematics learning and teaching. More recent reviews focused specific types of external visualizations (e.g., concept maps, Schroeder et al., 2018), specific samples (e.g., elementary education, Sokolowski, 2018), or STEM learning (e.g., Wu & Rau, 2019). As research on visualization in mathematics education has diffused, we aim to systematically identify empirical studies published in the last 5 year to explore how external visualization is characterized and how it has been addressed in most recent mathematics education research. Findings will indicate how recent research continues the historical discourse on external visualization, structure the state-of-the-art of research, and provide common ground for future research on external visualization in the learning and teaching of mathematics.

2 Characterizing external visualization in mathematics education

External visualization is a wide and complex research field, as studies reference different theoretical frameworks (Fagnant & Vlassis, 2013; Wu & Rau, 2019) and use alternative terminology. For example, the terms visual representation (e.g., van Garderen et al., 2021), visual image (e.g., Aydin & Monaghan, 2018), diagram (e.g., Haj-Yahya, 2021), drawing (Rellensmann et al., 2022), sketch (e.g., Widder et al., 2019), or specific types of external visualizations (e.g., bar graph, Sankey diagram, tree diagram) have been used to refer to external visualization.

We use Arcavi’s (2003) influential definition of visualization as a starting point from which to synthesize recent research on external visualization in mathematics education: Visualization is “the process and the product of creation, interpretation, use of and reflection upon pictures, images, diagrams, in our minds, on paper or with technological tools, with the purpose of depicting and communicating information, thinking about and developing previously unknown ideas and advancing understandings” (p. 217). In this review, we focus external visualizations as objects of mathematics education research. In contrast to internal visual representations, which are a person’s mental, cognitive concepts or configurations, external visualizations are physically embodied and observable from the outside (Goldin & Kaput, 1996). Because of their accessibility, choosing, constructing, using, and interpreting external visualizations is a central goal of mathematics education (OECD, 2019), and an important object of mathematics education research. Still, when interacting with an external visualization, important two-way interaction processes between internal and external representations take place(Goldin & Kaput, 1996) and may be subject of research on external visualization: As one example, external representations can be converted into internal representations and stored in long-term memory contributing to students’ conceptual understanding. As another example, self-generated external representations rely on a students’ internal representations (e.g., self-generated drawing), thereby providing insights into students’ understanding.

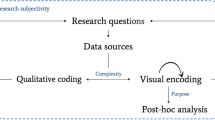
According to Arcavi’s (2003) definition, external visualizations have four important dimensions (Fig. 1): product and process component, type of visualization, media, and purpose. We will elaborate on the four dimensions and related theoretical and empirical works in the following subsections.

Fig. 1
figure 1

Four dimensions of external visualization

Full size image

2.1 Process and product components

Process and product component have long been the focus of research on external visualization in mathematics education. The process component of external visualization includes processes and activities associated with choosing, constructing, using, and interpreting an external visualization in mathematics teaching and learning (Arcavi, 2003; Bishop, 1989). As one example, Presmeg (1986) categorized the teaching styles of 13 teachers within one High school year according to their use of visual methods. As another example, Schoenherr (née Rellensmann) and colleagues observed dyads of ninth graders and analyzed their reasoning when evaluating the accuracy of their drawings for geometry real-world problems (Rellensmann et al., 2020). The product component of external visualization refers to the resulting visual depiction (Arcavi, 2003; Bishop, 1989), including, for example, research on the effects of different external visualization types (Elia et al., 2007) or accuracy of learner-generated external visualizations (van Essen & Hamaker, 1990) on solution accuracy. In this review, we analyze the extent to which recent research captures the process and product components of external visualization.

2.2 Types of external visualizations

Previous research provided several classifications of external representations. Popular classifications include concrete, pattern, kinesthetic, and dynamic imagery (Presmeg, 1986); dramatic, physical, pictorial, verbal, and symbolic representations (Verschaffel & Corte, 1997); pictorial and schematic representations (Hegarty & Kozhevnikov, 1999); pictures, images, and diagrams (Arcavi, 2003). These classifications build amongst others on two visualization characteristics: mode and resemblance (Finesilver, 2022; Schnotz, 2005). Mode describes the means of mean making (Finesilver, 2022), which applies to external visualization as follows: External visualizations can be classified as depictions that rely on icons to make meaning of a concept or object, as opposed to descriptions (e.g., word and symbols). Next, resemblance describes by what means the representation resembles the original. Two types of external visualizations can be identified according to their type of resemblance: The first type relies on physical resemblance with the represented concept or object; the second type relies on structural resemblance with the represented concept or object. Physical resemblance exists if spatial characteristics of the visualization represent spatial characteristics of the represented concept or object (Schnotz, 2005). An example for an external visualization with physical resemblance is representational drawing (van Meter & Garner, 2005): In a drawing for a modelling problem, for example, the height of a house is represented by the length of a vertical line (Rellensmann et al., 2020). Resemblance in external visualizations relying on physical resemblance can range from high resemblance (i.e., concrete/pictorial visualizations) to low resemblance (i.e., abstract/schematic visualizations; c.f., Finesilver, 2022). Structural resemblance exists if spatial characteristics of the visualization represent abstract, structural characteristics of the represented concept or object (Schnotz, 2005). The heights of bars in a bar graph, for example, can stand for the numbers of shoes four workers produced in 2 weeks (Ludewig et al., 2020). As another example, the arrangement of number in a table indicates relationships between characteristic levels.

In this review, we analyze external visualization in recent mathematics education research according to their type and degree of resemblance to explore the types of visualizations that have been addressed in recent research.

2.3 Media

As external visualization is physically embodied (Goldin & Kaput, 1996), learners and teachers need make use of media (i.e., means of production, Finesilver, 2022) to construct and use external visualization. Media refers to any instrument or device that students or teachers use to construct, use, or interpret external visualizations. Arcavi (2003) broadly distinguishes between analogous and digital media for creating and using external visualization. Analogous media include hand-drawn external visualizations with paper and pencil (Hegarty & Kozhevnikov, 1999), gestures or body movements (Presmeg, 1991; Radford, 2003), and hands-on objects (Anderson, 1957; Presmeg, 1991). Digital media include use of dynamic geometry software (Yerushalmi & Chazan, 1990), spreadsheets (Ainley, 1996), and handheld graphing technologies (Rivera & Becker, 2004), for example. In this review, we explore the media used in recent research on visualization in mathematics education.

2.4 Purposes

From preschool education to university education, visualization plays a role at every educational level in learning and teaching (van Meter & Garner, 2005). The purposes of using external visualization in mathematics learning and teaching usually refer to achieving learning goals, which include mastering mathematical processes (e.g., understanding or problem solving) in specific content domains (e.g., arithmetic or calculus). Geometry learning is referred to as an obviously visual domain; still, visualization can be useful in other domains, including analysis, algebra, and probability (Arcavi, 2003; Presmeg, 2006). Processes that are to be promoted by visualization can be diverse (Arcavi, 2003): communicating information, supporting reasoning, and advancing understanding. In this study, we analyzed the content domains and processes that are to be promoted by external visualization in recent mathematics education research.

3 Research aim

We systematically reviewed empirical studies on external visualization in mathematics education published in the last five years. Our aim was to provide an overview on the most recent discourse on external visualization in mathematics education research and describe the extents to which the dimensions of external visualization (product and process components, types of visual representations, media, and purposes) are addressed.

4 The present review

4.1 Search strategy and selection criteria

We followed the Preferred Reporting Items for Systematic reviews and Meta-Analyses extension for Scoping Reviews (PRISMA-ScR) guidelines (Tricco et al., 2018) to structure our scoping review study. Figure 2 presents the manuscript selection procedure. For the selection phase, we conducted a systematic data base search on 26 April 2022. To identify the relevant studies, we searched for diagram*, draw*, visual*, image*, sketch*, representation*, or graph* in the Title, and math* in the whole text. We restricted our search to peer-reviewed reports published between 2018 and 2022 in English (Table 1). The screening phase began with the removal of duplicates before the Titles, Abstracts, and Keywords of the remaining reports were manually screened for inclusion and exclusion criteria (Table 1). The remaining 340 reports were then screened for full-text eligibility, and full texts were screened for inclusion and exclusion criteria again. The remaining 130 studies were included in this review (see the Electronic Appendix for the list of included articles).

Table 1 Inclusion and exclusion criteria
Full size table
Fig. 2
figure 2

Article selection process

Full size image

4.2 Data analysis

To systematically analyze the identified studies, we applied a qualitative content analysis to the full text reports. Category systems refer to (a) general characteristics of the studies and (b) the four dimensions of external visualization in mathematics education: product and process components, type of external representation, media, and purposes.

4.3 General characteristics

To extract information about the general characteristics of the studies, we applied a slightly modified version of an established category system by Cevikbas et al. (2022). As one example, we added preschool children as a sample category because we found studies on preschool children’s reasoning with external visualization in the reviewed studies (e.g., Björklund & Palmér, 2020). The final coding scheme is included in the Electronic Appendix.

4.4 Visualization dimensions

To systematically describe the four visualization dimensions, we began with a deductively built coding scheme based on Arcavi’s (2003) definition and previous theoretical and empirical works on visualization in mathematics education (Fig. 1). Then we elaborated on it inductively to depict the diversity of recent research on visualization in mathematics education.

Regarding the process and product components of external visualization, we coded whether a study focused on visualization product, visualization process, or both or whether the information was not available. As one example, a focus on the visualization product was coded if student-generated drawings were analyzed (e.g., Mejia-Ramos & Weber, 2019). A focus on the visualization process was coded if students’ or teachers’ interactions with an external visualization were being studied (e.g., Bullock et al., 2021; Martinovic & Manizade, 2020).

To explore the types of external visualizations addressed in recent research on visualization in mathematics education, we assigned the identified visualizations according to their type of resemblance to external visualizations with physical resemblance and structural resemblance, respectively (Schnotz, 2005). By examining differences between the visualizations, we inductively arrived at external visualizations ranging from high physical resemblance (pictorial visualizations) to low physical resemblance (abstract visualizations) and three subtypes of external visualizations with structural resemblance (see Fig. 5 and description in Section 5).

Regarding the media dimension, we applied the deductively built categories paper-pencil, technology, hands-on objects (e.g., Presmeg, 1991), gestures (e.g., Radfort, 2003), and not applicable. As a borderline example, using technology as a display only to provide students with information within computer-based data collection was not coded as technology use (e.g., Adams & Maki, 2020). Technology use was applied if participants constructed, manipulated, or interacted with the technology-based external visualization.

To explore the purposes related to visualization in the reviewed studies, we applied a deductive-inductive procedure to develop the mathematical content domains numbers and operations, algebra, analysis, geometry, stochastic and data analysis, logic and set theory, and not available. Additionally, we inductively developed categories of process-related purposes, including understanding, problem solving, modelling, arguing and proofing, teaching, and not available.

To determine the reliability of the coding, 19 % of the reports (n = 25) were double-coded by an external coder. Each characteristic was dichotomously coded, as more than one characteristic of a dimension could apply to the same study, and coders were asked to identify whether a certain characteristic applied to a given study or not. For example, some studies focused on the product and process components of visualization, or several types of visualization were investigated in the same study. For this reason, the coding frequencies in the 5 section might exceed the sum of 130. Intercoder reliability was satisfactory overall with an average Cohen’s κ of 0.83 (SD = 0.18, κmin = 0.5, κmax = 1). Discrepancies were resolved by consensus between coders.

5 Results

5.1 Study characteristics

The 130 empirical studies included in our review consisted of 127 journal articles and three conference proceedings. Of the 127 journal articles, 61 studies were published in mathematics education journals, 32 in journals for education and educational psychology, 24 in interdisciplinary journals for STEM learning, and 10 in journals focusing on special educational needs.

Concerning publication years, the reviewed studies appeared between 2018 and 26 April 2022. As Fig. 3 illustrates, there is a substantial number of peer-reviewed empirical studies on external visualization in mathematics education published in English, with new studies emerging every year from 2018 to 2022.

Fig. 3
figure 3

Accumulated number of studies on visualization in mathematics education published between 2018 and 2022

Full size image

This review includes studies by authors affiliated with 30 different countries. The distribution across continents shows that studies came from Africa (n = 9), Asia (n = 17), Australia (n = 6), Europe (n = 41), North America (n = 55), and South America (n = 2). The geographical distribution of studies suggests that external visualization is a research topic in mathematics education all over the world.

Half of the reviewed studies used qualitative research methods (n = 65), the most prominent being task-based interviews, analyses of student productions, and observations of students or classroom situations. A total of 35 % of studies applied quantitative research methods (n = 45), using mainly performance or knowledge tests and questionnaires with closed or open-ended questions, whereas 15 % of studies combined qualitative and quantitative data collection and analysis methods (n = 20).

The coding of participants’ educational levels (Fig. 4) showed that external visualization in mathematics learning was investigated from preschool to university, with the largest proportion of studies conducted in secondary schools. A total of 14 % and 15 % of studies investigated external visualization with preservice or inservice mathematics teachers. The majority of reviewed studies had 50 or fewer participants (61 %, n = 79). One study had between 201 and 500 participants, and three studies were large-scale studies with more than 1,000 participants. Four studies that conducted document analyses were coded as not applicable, as they did not rely on a sample of human participants.

Fig. 4
figure 4

Participants’ educational levels

Full size image

5.2 Process and product components of visualization

About one third of the studies (n = 43, 33 %) focused primarily on the visualization process, 12 % of the studies (n = 16) focused on the product component of visualization, and 19 % (n = 25) considered both the process and product components of external visualization. A notable proportion of 35 % of the studies (n = 46) explicitly considered neither the process nor the product component of external visualization. For example, these studies investigated the effect of providing an external visualization (e.g., Hoogland et al., 2018) or examined preconditions for visualization use and abilities (e.g., Tikhomirova et al., 2019).

5.3 Types of visualizations

We identified about 20 different external visualizations in the 130 studies that were reviewed. Our categorization (Fig. 5) resulted in two visualization types based on physical or structural resemblance (Schnotz, 2005). External visualizations with physical resemblance use spatial characteristics (e.g., length and arrangement of objects) to represent the spatial characteristics of the represented concept or object. We differentiated external visualizations with physical resemblance further according to their degree of resemblance ranging from high resemblance (pictorial visualizations, n = 34), including virtual reality, photographs, and pictorial illustrations; to lower resemblance (abstract visualizations, n = 44), including figures, three-dimensional shapes, and pattern series. As one example, we consider a situational drawing for a geometry modelling problem, i.e., a drawing depicting objects pictorially according to their physical appearance, an external visualization with high physical resemblance. A mathematical drawing for the same modelling problem depicts only mathematical objects like lines and angles, having low physical resemblance. Within external visualizations with structural mode, we identified three categories based on the visualization’s characteristic creating the structural resemblance: length visualization (n = 15), including number lines, bar graphs, and line graphs; area visualization (n = 23), including pie charts, tape diagrams, and Venn diagrams; and relational visualization (n = 51), including tables, tree diagrams, function graphs, state-transition diagrams, net diagrams, concept maps, vectors, arrays, and Sankey diagrams. Length, area, and relational visualizations use length, area, and relationships, respectively, to represent the structural characteristics of the represented concept or object. For example, a bar graph displaying the numbers of shoes produced by workers uses the length of a bar to represent the number of shoes (Ludewig et al., 2020). A pie chart uses parts of a circle to represent partial values of a whole. And a tree diagram uses relationships, which are established by branches, to display relationships. The visualization types are not free from overlap: For example, the structural characteristic in a bar chart with percentage labeling is represented by the height of the bar and the proportionate area. A notable proportion of the reviewed studies (n = 16) did not mention specific visualizations explicitly.

Fig. 5
figure 5

Classification of external visualizations

Full size image

5.4 Media

Our review revealed that in 81 of the reviewed studies (62 %), visualizations were constructed, used, or interpreted with paper and pencil. In 36 studies (28 %), technological tools were applied. Exemplary technological tools used in the reviewed studies were dynamic geometry software GeoGebra (e.g., Bullock et al., 2021), the applet Calculus Integral Sketc.h (e.g., Swidan & Naftaliev, 2019), the Visual Basic Application for Excel (e.g., Bernard & Senjayawati, 2019), Augmented reality (e.g., Bhagat et al., 2021; Chen, 2019), and digital math games (e.g., Moyer-Packenham et al., 2022). In nine studies, hands-on objects were used for visualization, among other things. For example, Flores et al. (2020) used plastic base 10 blocks that represented ones, tens, and hundreds to teach fourth and fifth graders the partial products algorithm. Four studies investigated visualization generated by gestures. For example, Okumus and Hollebrands (2019) analyzed students’ gestures for forming three-dimensional objects in addition to the technological tool Cabri 3D or hands-on objects.

5.5 Purposes

In the reviewed studies, visualization was investigated in relation to a variety of mathematical content domains (Fig. 6). Most studies investigated visualization in the domain of geometry (n = 38, 29 %), followed by numbers and operations (n = 31, 24 %). In the domain of numbers and operations, nine studies focused on visualization in fraction learning (e.g., Soni & Okamoto, 2020). A total of 27 and 23 studies (21 % and 18 %) were related to the learning of algebra and analysis, respectively. In the domain of analysis, visualization in learning calculus was a predominant topic (e.g., Mejia-Ramos & Weber, 2019; Swidan & Naftaliev, 2019). Only a few studies investigated visualization when learning about probability and data analysis (n = 5, 4 %) or logic and set theory (n = 2, 2 %). As one example, Lee et al. (2018) investigated students’ performance in solving probability word problems after learning about state transition graphs or tables. In 18 studies (14 %), no mathematical content domain was explicitly mentioned.

Fig. 6
figure 6

Content-related purposes of visualization

Full size image

Regarding process-related purposes, visualization was investigated for the purposes of understanding mathematical concepts (n = 55), solving or posing mathematical problems (n = 38), solving modelling problems specifically (n = 6), developing an argumentation or a proof (n = 9), or as a tool for teaching, including promoting and assessing students’ competencies (n = 16; e.g., Borji & Sánchez, 2019; Hollebrands & Okumuş, 2018; Mavani et al., 2018). In six studies, no process-related purpose of visualization was clearly mentioned.

6 Discussion, future directions, and limitations

This review of 130 recent empirical studies on external visualization in mathematics education indicates worldwide interest in this topic. On the basis of the review’s findings, we describe visualization in most recent mathematics education research and offer directions for future research.

6.1 Expanding the characterization of visualization in mathematics education research

We used Arcavi’s (2003) definition of visualization as a starting point and inductively identified key characteristics of external visualization in recent mathematics education research: (a) External visualization comprises the processes and products of constructing, using, and interpreting depictive external representations. (b) External visualizations include visualizations ranging from high physical resemblance (i.e., pictorial visualization) to low physical resemblance (i.e., abstract visualization) and visualizations with structural resemblance including length, area, and relational visualizations. (c) External visualization can be provided or developed on paper, with hands-on objects, gestures, or technology. (d) The purposes of external visualization include understanding mathematical concepts, solving or posing mathematical problems, developing an argumentation or a proof, or teaching in various mathematical content domains, ranging from geometry and analysis to algebra, probability, and logic.

An important contribution of this review is our attempt to classify different types of external visualizations, building on previous classifications (e.g., Arcavi, 2003; Finesilver, 2022; Presmeg, 1986). We distinguish between external visualizations with physical resemblance ranging from high resemblance (i.e., pictorial visualizations) to low resemblance (i.e., abstract visualizations). In addition, we found three subtypes of visualizations relying on structural resemblance: length, area, and relational visualizations. Subtypes of visualizations relying on structural resemblance might overlap: for example, the unit square, which uses different areas within a square to represent relationships between two dichotomous variables, is a mixed form of area and relational visualization.

6.2 Methodological implications

Regarding research methodology, our review showed that visualization was still predominantly investigated with qualitative research approaches, using, amongst others, task-based interviews and observations of small samples (see Presmeg, 2006). As these research methods allow visualization processes to be captured, they were often aimed at analyzing students’ or teachers’ interactions with visualizations during learning or teaching, respectively (e.g., Gallagher & Infante, 2021; Hollebrands & Okumuş, 2018). In addition to qualitative research approaches that examine visualization in depth, quantitative and mixed methods approaches can help validate theoretical considerations, e.g., theory of self-generated drawing (Van Meter & Garner, 2005), or contribute to collecting evidence on the effectiveness of visualization trainings on visualization use and learning outcomes (e.g., Rellensmann et al., 2021). Visualizations can be used universally and can support learning at different educational levels (Van Meter, 2005). Most of the recent research on external visualization in mathematics education has been conducted in secondary schools. As prior research indicates that learners of different ages have somewhat different problems with visualization (e.g., Guncaga & Zilkova, 2019), research with learners in preschool, elementary school, or university must not be neglected. Also, the use of visualization by (preservice) mathematics teachers is a practically important yet understudied area in recent research. Future studies should build on both pioneering and recent research that have examined teachers’ knowledge (e.g., Friesen & Kuntze, 2020) and beliefs (e.g., Sunzuma et al., 2020; van Garderen et al., 2018) about visualization, teachers’ ways to effectively integrate visualization in the classroom discourse (e.g., Ding et al., 2019; Presmeg, 1986), and developed (preservice) teacher intervention programs on visualization (e.g., van Garderen et al., 2021).

6.3 Process and product components, types, media, and purposes of visualization

The product and process components of visualization have continued to play roles in recent research on visualization in mathematics education. As one example, Jones (2018) focused on the product component by describing the appearance of prototype images of the definite integral in students’, teachers’, and textbook visualizations. Kobiela and Lehrer (2019) focused on the process component by examining how students’ understanding of area developed with an intervention in which students had to “sweep” paint across a ceramic tile with squeegees. Although product and process are important for visualization, 36 % of studies did not focus on the product or process of external visualization. Many of these studies investigated effects of learning with visualization without explicitly examining the visualization’s products or processes. As product and process are by definition important components of visualization, measures of product or process should be considered in research on visualization. As one example, Rellensmann et al. (2021) measured accuracy in student-generated drawings, which helped them explain the null effect of drawing training on modelling performance. As another example, Bhagat et al. (2021) used eye-tracking measures to investigate whether visual attention patterns helped explain achievement when learning about geometry with an augmented reality application.

Our review revealed a large number of different visualizations, which we assigned to subtypes of external visualizations (Fig. 5). We identified visualizations, which use physical resemblance to represent mathematical concept or objects, ranging from pictorial visualizations with high resemblance (e.g., illustrations, augmented reality) to abstract visualizations with low physical resemblance (e.g., figures and shapes). These correspond to the categories of concrete and pattern imagery (Presmeg, 1986) and pictures and images (Arcavi, 2003) in previous classifications. In line with previous research (Ainsworth, 2022; Finesilver, 2022; Rellensmann et al., 2022), we noted a continuum of the degree of physical resemblance with pictorial and abstract visualizations forming the opposite poles. Visualizations with structural resemblance were diverse: Length, area, and relational visualizations differ in the representational means used to represent mathematical objects or relationships. They focus on specific information, thus rendering them particularly powerful if the visualization matches the intended purpose. Still, the diversity of representations and the different representational means pose high affordances to students and teachers in selecting, understanding, interpreting, and using these external visualizations. As one example, students often misinterpret the area of the box in boxplots as representing numbers or proportions of observations (e.g., Lem et al., 2013). Although benefits and boundaries of visualization in mathematics education is a research trend since the 1980 s (Presmeg, 2006), more research is needed on the effects of different types of visualizations and the benefits and hurdles they offer to learners at different educational levels.

Regarding visualization media, we found that visualization media mentioned in early works are still of interest in recent research, i.e., paper-pencil, hands-on objects, gestures, and technology (Presmeg, 1986). Although the emergence of technology, recent research in mathematics education has mostly investigated visualizations that were constructed or provided in a paper-and-pencil format. Still, a notable number of studies made use of technological tools (e.g., dynamic geometry software, calculus applets, spreadsheet applications, augmented reality applets, and digital math games). Since the beginning interest in technology-based visualization (e.g., Yerushalmi & Chazan, 1990), new forms of technology-based visualizations have expanded previous research. For example, augmented reality and digital math games have been in the interest of recent research on visualization in mathematical learning and teaching (e.g., Bhagat et al., 2021; Moyer-Packenham et al., 2022). Recent research on technology use continues previous research by examining, for example, how visualization with technology helps or hinders students’ mathematics learning (e.g., Bullock et al., 2021), and whether technology-based learning is more effective or more motivating than traditional learning (e.g., Chen, 2019). As technological tools continue to evolve, on-going research is needed on the opportunities and challenges of technology-based visualization. In addition, visualization literature considers gestures and hands-on objects as promising visualization media. For example, Earnest (2022) derived from case studies that different kinds of hands-on clocks interacted with elementary students’ reasoning about time. Visualization by gestures and hands-on objects indicates an overlap between research on external visualization and other topics, such as embodied cognition (e.g., Sinclair & Freitas, 2019) and manipulatives (e.g., Bartolini & Martignone, 2014). Thus, expanding the characterization of external visualization in mathematics education can open discussions across different theoretical approaches with the aim of creating inclusive common research ground.

Our review confirmed that recent research investigates external visualization for various purposes in the teaching and learning of mathematics, going beyond understanding and problem solving in the domain of geometry. As the effectiveness of visualizations might depend on the specific task (e.g., Uesaka & Manalo, 2012), future research needs to continue investigating which external visualization is helpful for whom to achieve the intended process- and content-related purpose.

6.4 Limitations

One limitation of this scoping review involves the search strategy and selection criteria: First, we synthesized the research literature on external visualization in mathematics education. Further reviews should include, for example, theoretical papers, textbooks, and teacher journals to describe the visualization dimensions addressed in educational practice. Second, although we applied extensive search strategies and a standardized study selection procedure in high-ranking databases to identify relevant empirical studies, important studies that focus indirectly on visualization in mathematics education or rely on different theoretical frameworks (e.g., manipulatives and schema-based instruction) might have been missed. Third, the extensive literature on external visualization in languages other than English was not included in this review. Thus, additional key characteristics of external visualization in mathematics education may be obscured.

Another limitation concerns the coding strategy, which relied mostly on the information provided by the authors of the studies. For example, if the authors named the process-related purpose problem solving, the study’s purpose was coded as problem solving, without further investigation of whether the term was coherently used across studies.

The aim of this scoping review was to synthesize recent studies to characterize external visualization in recent research on visualization in mathematics education. Due to the diversity of visualizations, tools, and domains of application, this approach has limitations. Future reviews should focus on specific visualizations to inform research and practice in depth (e.g., see a review on learner-generated drawing in STEM education; Fiorella & Zhang, 2018). Further, purely mental visualization has been excluded from this review, but this type of visualization merits further investigation in future research.