Teachers’ practices and resources in the Hungarian “Guided Discovery” approach to teaching mathematics: presenting and representing “series of problems”

Abstract

In the Hungarian “Guided Discovery” approach to teaching mathematics, teachers’ planning work plays a crucial role. Teachers following the approach develop teaching trajectories based on “series of problems”. This work includes the choice, creation, transformation, organization and networking of problems with regard to various teaching objectives. However, most of this planning work remains implicit; the structure and rationale of the teaching trajectories are often inaccessible for an external observer (including, for example, student teachers). An ongoing project based on teacher–researcher collaboration aims to reveal the hidden characteristics and principles of teachers’ work with series of problems through the creation of innovative resources for teachers. In this paper, we present the design of this collaborative work, a process we designate “reverse engineering”, and analyse the development process of resources, focusing particularly on the emergence of new vocabulary and representation tools serving as mediators in the communication between teachers and researchers.

1 Introduction

Several recent research projects have questioned the cultural embedding of teachers’ ways of interacting with resources and the role of language in these processes (Adler et al., 2022; Trouche, 2020). They orient attention to, among other things, teachers’ language and naming systems, and raise questions such as, ‘what do researchers learn when they take teachers’ language(s) into account?’ or ‘how might analysis of teachers’ naming systems shed light on their resource and activity systems?’

In our paper, we address similar questions from a specific point of view: we focus on the problem of lack of convenient resources in a particular cultural context of mathematics education, the so-called Guided Discovery (GD) approach to teaching mathematics in Hungary. We suggest that this problem goes back to the lack of convenient language and communication tools. We describe a project based on teacher–researcher collaboration, designed for a combined development of new resources and analysis of teachers’ work. We will analyse how the project’s design favours the emergence of new communication tools related to the specific context, and how these tools contribute to the achievement of the project’s dual objective.

Guided Discovery, or “felfedeztető matematikaoktatás”, is an approach to mathematics education through problem solving and mathematical inquiry, developed in the Hungarian mathematical and mathematics educational context during the twentieth century, which can be considered one of several international approaches to Inquiry-Based Mathematics Education (IBME) (Artigue et al., 2020a; Gosztonyi, 2020). The reform movement of T. Varga, in the 1960s and 1970s, shaped GD as a basis of general mathematics education and a guiding principle of the official curriculum for primary and lower secondary school (Halmos & Varga, 1978). The approach is still recognized by Hungarian specialists of mathematics education as relevant and consistent with modern educational trends (see Sect. 2.2). At the same time, it is practised in ordinary classes only by a narrow circle of teachers, and its dissemination, i.e. the initiation of novice teachers into GD, poses problems. Furthermore, the approach exists only ‘in act’, while its theoretical description has not been developed. Although Varga actively participated in the international discourse on mathematics education in the 1960s and 1970s, and developed his conception at the same time as Brousseau (1998) or Freudenthal (1991),¹ his publications focused more on experimentation and curriculum development, and less on the theoretical description of the underlying conception. This missing description results in a lack of appropriate language to communicate the approach to both the larger community of Hungarian mathematics teachers and to the international mathematics educational research community. Although important developments were made in recent years (Artigue et al., 2020b), understanding the rationale of expert teachers’ work in GD² and communicating it necessitates further improvement.

One of the specificities of the GD approach identified in preliminary research of the first author (Gosztonyi, 2020) is that long and complex teaching trajectories³ based on “series of problems” are used and developed by teachers. The term “series of problems” (SoP) itself was originally introduced in the frame of an interdisciplinary history of science project as a more or less undetermined methodological tool to analyse the structure of historical texts in different periods and cultures (Bernard, 2015). In the specific Hungarian context, Gosztonyi used the term SoP as a list of problems with a consciously chosen ordering which is relevant for one or several educational purposes. The term appeared to be productive in analysing twentieth century resources related to GD (Gosztonyi, 2015). It also provoked vivid reactions from expert teachers following the approach nowadays, who recognised a crucial, albeit rarely discussed, aspect of their practice which this term echoed.

Nevertheless, the exact meaning of SoP for these teachers remained somewhat obscure. Identifying and describing SoP, understanding related educational purposes, and describing and analysing the often long and complex teaching trajectories these SoP build is a challenging task because of the many implicit elements in existing resources and in teachers’ work. To better understand the role of SoP in the work of expert teachers, we need new communication tools which better explicate these aspects.

We thus address the following questions in this paper:

• 1. What kind of language and communication tools could be developed to facilitate teachers’ explication of their work with SoP (what is their structure and role in teaching through GD)?

• 2. What kind of procedures could foster the emergence of such a language and communication tools?

We use here the term “language” in a restricted sense of verbal communication, while we talk about “communication tools” in a broader sense than “language”. As we will see below, the development of communication about SoP includes linguistic elements, especially the emergence of new vocabulary, but also other elements such as visual representations of the structure of SoP and related coding systems. We present below the design of a collaborative project including researchers and expert teachers of GD, and analyse how this design fosters the development of communication about SoP.

This ongoing project aims, on one hand, to analyse expert teachers’ practices related to SoP, and on the other to develop new, innovative resources for teachers, supporting the dissemination of GD in the Hungarian mathematics educational community. We developed a methodology called reverse engineering (Gosztonyi, 2019) that allows us to lean on the development process of resources in order to access to the implicit aspects of the participating teachers’ work. In this paper, we will analyse this development process, focusing on the role of communication tools, namely the emergence of new vocabulary and visual representations, and their role in the elucidation of teachers’ working principles related to SoP.

First (Sect. 2), we provide some elements of context: elements of the analysis of historical resources on GD, explaining the role of SoP in GD and the challenges of the analysis of SoP (Sect. 2.1), and elements of context of GD in current Hungarian mathematics education (Sect. 2.2). In Sect. 3, we present the design of our project discussing theoretical and methodological considerations. In Sect. 4, we present and analyse the development process of resources in three examples issued from our group work (Sects. 4.1–4.3), and we discuss the emerging vocabulary and representation tools (Sect. 4.4). Finally, in Sect. 5, we discuss perspectives in teacher education by presenting a pilot teacher education project and a master thesis developed in this frame.

2 Preliminaries and context of the research

2.1 Analysis of GD and SoP based on historical resources

The first step for a theoretical reconstruction of GD was to go back to its origins in the frame of a comparative study between Varga’s reform and the contemporary French “Mathématiques modernes” reform, and to carry out their combined historical, epistemological and didactical analysis based on written sources (Gosztonyi, 2015).

This analysis helped to identify some main characteristics of GD. In the background of Varga’s reform project, a quite coherent “heuristic” epistemology of mathematics and mathematics education can be outlined in the twentieth century’s Hungarian mathematical culture (Gosztonyi, 2016), represented by mathematicians living in Hungary, as well as by Pólya and Lakatos (Lakatos, 1976; Péter, 1961; Pólya, 1954).

This epistemology deeply influenced Varga’s “Complex Mathematics Education Reform” conception. The analysis of resources associated with the reform helped to identify some of its main principles, concerting New Math principles with the heuristic epistemology developed in Hungary (Gosztonyi, 2020):

• Development and implementation of rich tasks (problem-situations)⁴

  • Allowing students to make sense of mathematical notions

  • Allowing students’ active contribution to the construction of mathematical knowledge

  • Linking several mathematical domains

  • Open to different solution strategies

• Conceiving collective rediscovery processes of mathematics, based on

  • Long, complex teaching trajectories structured by series of problems

  • Classroom dialogues

• Complexity of the curriculum

  • Diversity of the domains treated in parallel

  • Spiral and flexible structure

• Diversity of tools and representations

• Emphasis on the playful and aesthetic character of mathematics

• Respect and valuing of students’ diversity

The idea of conceiving inquiry-based teaching processes based on complex series of problems appeared to be crucial for the implementation of the approach, and one of the important requirements for teachers. Furthermore, teachers’ handbooks related to the reform insist on the importance of teachers’ autonomy in conceiving their own teaching trajectories adapted to their classes. At the same time, there are only partial examples and very limited commentaries on the principles of conceiving teaching processes by SoP, dispersed in the books and rarely generalized (Gosztonyi, 2015).

Gosztonyi (2015) developed analyses of different resources to identify SoP and describe their structuring principles. Several texts of mathematicians representing the “heuristic” epistemology were analysed, especially R. Péter’s book popularizing mathematics, Playing with Infinity (Péter, 1961), written as an interesting inquiry story where one question invites the next. In this case, a representation of the structure of an extract, in the form of a graph, supported the analysis. Extracts of Varga’s textbooks and teacher’s guides were also identified and analysed, presenting coherent successions of problems, and containing enough commentary to understand the logic and the purpose of their construction. One of the most developed examples concerns the teaching of combinatorics in primary school described in a chapter of the first grade teachers’ guide: in this case, subseries were identified, generated by systematic variation of problems and leading to progressive generalization of mathematical knowledge.

In summary, the analysis of written documents representing the heritage of GD confirms the importance of SoP in the approach, identifies some key principles concerning the role and the structure of SoP, and highlights tools to analyse and represent SoP (e.g. by graphical representations or structuring by main and subseries).

We remind the reader that the term “series of problems” was originally a methodological tool introduced by an international history of sciences project. It appeared to be efficient at capturing important aspects of GD which have not been discussed in an explicit and systematic way in the Hungarian context.

The terms problem (“probléma”) and problem solving (“problémamegoldás”) themselves appear regularly in meta-discourse about mathematics education—in books of Hungarian mathematicians as well as in teachers’ guides describing teaching objectives and strategies. Nevertheless, it is not a technical term applied in resources for students. What is given to students in textbooks or by teachers is generally called a task (“feladat”). “Problem” means a task which represents a challenge for the solver because the method of solution is not directly available and needs to be discovered. In this sense, the same task can represent a problem for some and an exercise (“gyakorlat”) for others who are in possession of the solution method.⁵ We can thus understand an SoP as a series of tasks where each step represents a new challenge for (most of) the students to whom the SoP is addressed.

2.2 GD in current mathematics education in Hungary

Varga’s reform and the GD approach are recognized to this day as relevant by various influential actors and communities related to Hungarian mathematics education, authors of curricula, teacher educators,⁶ and associations of mathematics education (Gosztonyi, 2015; Pálfalvi, 2019). Varga’s importance is recognized by institutions such as the Tamás Varga Competition (a national competition for lower secondary school students),⁷ and the Tamás Varga Days (mathematics teachers’ yearly conference), co-organized by the Tamás Varga Foundation⁸ and the country’s biggest mathematics teacher education centre at the Eötvös Loránd University of Budapest. To this day, mathematics curricula follow the structure established by Varga with only slight modifications. National teacher education curricula explicitly insist on the relevance of Varga’s heritage and on the importance of familiarizing future teachers with GD.

Nevertheless, there is a general agreement among promoters of GD that, despite the efforts in curricula development, textbook production and teacher education, most teachers have difficulty comprehending, acquiring and implementing the approach.

Concerning resources, the textbooks and teachers’ guides developed for Varga’s reform in the 1970s appeared to be difficult to use for teachers without specific training or collaboration with the designers of the reform (Gosztonyi, 2015). In 1985, with a “correction” of the reform, they were replaced by another textbook series not reflecting the GD approach. In the 1990s, with the liberalisation of the educational system and of textbook production,⁹ authors of GD-related series renewed the textbooks of the 1970s: successive, modernized versions of these series are still available for primary and lower secondary schools today. In the 1990s and 2000s, several other textbook series were developed, some of which at least partially attempted to implement GD principles. The most popular textbook series of the 2000s, Sokszínű matematika,¹⁰ has not been in official use since 2013, but many teachers still use it as a resource. Two of the authors of these series—József and Klára—participate in the collaborative project described below. They insisted on following GD principles while conceiving tasks and series of tasks for these books—nevertheless, these principles are not explained in the published resources.

Published resources do not seem sufficient for a successful implementation of GD. Most of the teachers who apply GD (who consider themselves and/or are considered by the community as followers of GD) learned it through personal experience as students or as disciples of expert teachers of the approach. Expert teachers often consider transmission through master–disciple relationship and long-term observation as crucial, but also see that this allows very limited transmission. This problem is the main motivation for teacher participants of our research project: to find new, more efficient ways to share their knowledge with non-expert colleagues and students.

3 Design of the project: theoretical and methodological considerations

3.1 Theoretical considerations

As we explained above, the problem we want to address is that of missing communication tools necessary to elucidate teachers’ work on SoP, and also to communicate with expert teachers on their own work and transmit the approach to non-expert teachers. Although some main principles of GD could be reconstructed on the basis of historical sources, a better understanding of teachers’ work is necessary to further elucidate the approach.

We make the hypothesis that behind expert teachers’ work there lies a ‘theory-in-act’ specific to GD. These teachers (who mutually recognise themselves and each other as representatives of GD, see below) have strong and complex ideas about the structuring of their teaching processes and the related teaching goals, ideas which seem to be shared among them, but are rarely formulated explicitly.

We seek to understand and describe the operational knowledge and shared principles behind these teachers’ work. We rely on Vergnaud’s Theory of Conceptual Fields (2009), which offers tools to explore connections between operational and predicative forms of knowledge. Vergnaud uses the notion of scheme as a stable organization of activity for a certain class of situations, but which is also adaptable to new situations: “they assimilate new situations by accommodating to them” (p. 88). A scheme is composed of a goal or several goals of the activity; rules to generate activity; operational invariants, namely concepts-in-action and theorems-in-action (their main function is to pick up and select the relevant information and infer goals and rules from it); and possibilities of inference.

Trouche et al. (2020) adapt this notion to the analysis of teachers’ work in the framework of the Documentational Approach to Didactics (DAD).

We retain particularly the notion of operational invariants, the component of schemes describing principles behind the actors’ actions. We expect that by analysing the expert teachers’ work and identifying operational invariants, we can elucidate the (shared) principles of their work and how they drive these teachers’ choices while developing their SoP.

Beyond the idea of adapting Vergnaud’s notion of scheme to the analysis of teachers’ work, the DAD offered further inspiration to our work in the following aspects:

• Focusing on teachers’ documentation work: work outside the classroom, the planning of teaching processes

• Elements of the methodology of reflective investigation (Gueudet & Trouche, 2012), especially the idea of relying on visual representations of teachers’ resource systems as tools of mediation in the discussion between teacher and researcher. (Resource system means the set of resources used by a teacher.)

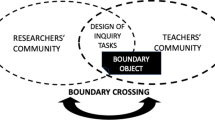
The DAD inspired a modelling of Hungarian expert teachers’ documentational genesis and of their possible analyses (Fig. 1) (Gosztonyi, 2019).

Fig. 1

Analysis of series of problems (the visible elements are marked with bold, the hidden ones with broken outline)

Nevertheless, while we focus on the development process of the documents and the related schemes, we are less interested (at least at this stage of the research) in the original resources used by teachers. This is for several reasons.

First, there is the very long documentational genesis of SoP. Expert teachers participating in our project state that their SoP were developed over decades, and they do not necessarily recall the original (often oral) sources of their designs. They also insist on their autonomy and claim that most of their teaching design is their own development. Even if they found inspiration in various sources, they usually adopt small elements, often with their own variations, to fill gaps in a structure of an SoP they already have in mind. Finally, several of our participants have very specific statuses concerning published resources: they are themselves authors of nationally widespread textbook series or direct disciples of textbook authors.

Another important observation is that, in the specific context of GD, basic elements of teachers’ resource systems seem to be problems. Written documents from these expert teachers typically contain a list of problems, with or without solutions. But the documents are only a skeleton of their planned teaching process. Essential elements remain implicit: the main teaching goals, the organization of classroom work, the planned discussions, and choices and adaptations they consider making ‘on the spot’, depending on the students’ reactions (e.g. change of order, omission of some problems or introduction of new ones). Furthermore, these projects are conceived as long-term developments, even for several years,¹¹ and only parts of them appear in written documents. Expert teachers confirm having a complex network of problems in mind that they can mobilize in order to create problem series and adapt them to their aims and to the students’ needs or interests, during preparation or in the classroom.

Understanding teachers’ work with SoP thus necessitates understanding the choice, variation and development of problems, the construction of ‘networks’ based on logical links between problems, and the choices of ordering in reaching various teaching goals.

Gaining access to the implicit logic of SoP’s design and to the underlying principles shared by these teachers required development of a specific methodology which we present in the following section.

3.2 Design of the project and the reverse engineering methodology

In 2016, in the frame of the Complex Mathematics Education Research Project¹² financed by the Hungarian Academy of Sciences, we created a mixed group involving researchers, teacher educators and expert teachers of GD. The aim was to (1) further elucidate the main principles of GD, focusing especially on the teachers’ role by analysing expert teachers’ work with SoP; and (2) develop resources and later teacher education modules contributing to the dissemination of GD.

We show in the following how the design of this project supported the emergence of new language and communication tools on SoP.

The group has had between six and eight participants over the years, most of them participating continuously from the beginning. Each participant has a well-defined relationship to GD (family member of T. Varga or of other agents of Varga’s reform; student of an experimental class; disciple of one of the agents of the reform, etc.), and they recognise GD’s importance for their professional identities. They also mutually recognise each other as experts of GD.

The leading researcher of the group is K. Gosztonyi, the first author of this paper. The other participants mostly consist of (lower or upper secondary school) teachers or (primary or secondary school) teacher educators. Nevertheless, many of the participants have multiple identities. E. Varga, for example, the second author of this paper, joined the group as an expert teacher but started a PhD (related to SoP) in the meantime and progressively moved into the role of researcher (without completely abandoning the teacher attitude). Several of the participants are teacher educators with important secondary school teaching experience.

One important challenge of the project comes from this diversity of profiles and professional identities. Complex negotiations were necessary to meet the interests and expectations of each participant. While from a researcher perspective, focusing on the analysis of teachers’ practices (objective 1) appeared to be a necessary first step, this was not relevant enough for most of the participating teachers. They were instead motivated to share their practices with other, non-expert teachers (objective 2). The solution which emerged was to work on these objectives in parallel.

We decided to develop a collection of commented examples of SoP. The purpose of this collection (currently being prepared) is not to offer ready-made resources for teaching, but generic examples which introduce the reader into the practice of using and preparing SoP.

In addition, preparing commented examples also serves the project’s research aim: for teachers to explicate their teaching goals and principles of structuring SoP. We rely on teachers’ designs of SoP and the development process of resources to reconstruct the hidden aims and operational invariants driving the teachers’ choices. We named this procedure reverse engineering.¹³ The specificity of our approach is that we are not only looking for teachers’ individual documentational schemes but for the (at least partially) shared principles.

The principle of reverse engineering is implemented in our group work in the following way:

In the first step, teachers were asked to provide examples from their own practice of what they consider SoP. The examples we received were of varying nature (e.g. SoP of short- and long-term sequences, SoP to introduce new mathematical notions, SoP to explore heuristic strategies, SoP to serve diagnostic purposes). Confronting the new and previously analysed examples led to discussion on various questions: classification of purposes, different structuring principles, possibilities of representation. The discussions evoked new examples.

In the next step, teachers were asked to write commentaries to their SoP, addressing colleagues unfamiliar with the GD approach, focusing on the didactical aims of their trajectories and on explaining the SoP structure. For the elucidation of these structures, different representation tools were developed (see below).

According to the original idea, one example consists of the SoP itself (a list of problems); a document containing the solutions; a representation of the SoP’s structure; and a commentary explaining the didactical aims, the structure, elements of implementation, and ideas about potential variations and adaptations of the SoP. Participants, however, furnished resources of slightly different composition, according to what they felt was applicable to their example.

Each commented SoP was discussed in group meetings. Many questions of clarification were raised, and representations appeared to be crucial support for these clarifications, also shaping the language used in the group work. Furthermore, considering the examples as resources for non-expert teachers led to discussions on how they may (or may not) help to mediate principles of GD. This also fostered the explanation of the principles represented by each example.

Following the discussions, commented examples were developed further by their authors: for most of the examples, several successive versions were prepared. Again, the development of representations appeared to be a crucial driving force in this process.

In the following, we analyse the development of three commented SoP, underlying how the process contributed to the elucidation of teachers’ operational invariants, and to the emergence of new language and communication tools about SoP (Sects. 4.1–4.3). We will summarize some initial results in Sect. 4.4.

We rely on the following data: successive versions of SoP, their commentaries and their representations; notes about group discussions; recordings of some group discussions; interviews with the authors of examples.

Commented SoP were analysed by the two co-authors: we looked for indicators of operational invariants, especially the appearance of new vocabulary, and the choices emphasised by commentaries and representations. The analysis of interviews allowed us to complete the process and reinforce our interpretations. The analysis process crossed different expertise of the authors: while Gosztonyi relied on her earlier analyses of GD in identifying and interpreting potential operational invariants, Varga, who was herself a practising teacher and author of one of the SoP, emphasised recurrent choices between the different examples. These comparative aspects (with other GD-related documents and among different SoP of the group) are particularly relevant as we look for shared principles of GD beyond the individual choices of the teachers.

The current analysis is considered an intermediate phase of the process: the results will be resubmitted to the group for further discussion, allowing the development of both the didactical analyses and the commentaries addressed to non-expert teachers.

4 Development of new resources: analysis of examples

The three examples below represent different kinds of SoP:¹⁴ shorter and longer ones, about different topics, and different school levels. They allow us to show the emergence of different representations, and also that confrontation of examples from different authors helped to increase consciousness about teachers’ choices during group work.

4.1 Eszter: a long-term problem-network in geometry, with graph representation

Eszter, one of the authors of this paper, brought to the group an example of a long-term SoP in the field of geometry. This was a result of the initial discussions: the first examples consisted of short sequences since this was easier to document for teachers; but during the discussions, they all agreed on the importance of long-term planning. Eszter thus looked for a long trajectory from her practice which covered several school years.

The first version of her example contained a linear list of problems. The aims and the logic of construction were not immediately clear for the group members and necessitated explanation. As Eszter explained, the overall structure focuses on the concept of distance, while also dealing with several related concepts such as loci of points or geometrical transformations. It is built around a “core” problem: finding the equidistant points of three different lines in the plane. Although some notable theorems of higher-level mathematics appear in the series (in a problematized form), the main aim of the SoP is not to learn these theorems but to familiarize students with the aforementioned concepts, related mathematical techniques, and problem-solving skills through the exploration of interesting geometrical questions.¹⁵

Fig. 2

Eszter’s graph

The term “core” used by Eszter indicates a logic of construction: a problem or short SoP which generates the rest of the structure. The development of this SoP started with a “core” series of four problems, for ninth or tenth grade students, with increasing complexity about the loci of points (C1–C4). In this “core subseries”, the order of the problems is strict. This order is intended to make the later, more difficult problems progressively accessible for students. Several other subseries are conceived on the basis of this core, exploring different mathematical themes such as space analogies, angles, similarities or combinatorics.

As she explained in the interview, the frustration of incomprehension and the importance she accorded to the non-linearity of the structure led Eszter to propose a graph representation of the SoP (Fig. 2). For her, it helped to express important principles, or theorems-in-act: that the order of problems should be flexible and adaptable to students; and that in a ‘rich’ SoP links between problems are dense.¹⁶

The idea of representation in graph form had already appeared in Gosztonyi’s preliminary research, namely in the analysis of Péter’s book (Gosztonyi, 2015), but Eszter was not aware of this when she proposed a graph. The graph representation was later recognized as a natural form of representation for SoP’s structure by several participants of our group.

In Eszter’s graph, the arrows show complex mathematical or didactical interdependencies between the problems, but also illustrate the flexibility of the structure which is not visible in the simple numerated list of problems. Some problems or subseries are sequential, while for other problems the order is more flexible.

The first version contained the “core” and problems following the core, issued from Eszter’s high school practice. After a first discussion, we agreed that it would be useful to complete this SoP with a preparatory part which dealt with the middle school level prerequisites. Thus, Eszter added a new part to her graph (P1–P10, above the core). As she explained, the problems in this part serve for diagnostic purposes in her high school work. They also fill possible gaps in students’ knowledge. The problems presented illustrate different types of tasks which have to be explored in order to prepare students for the core. More tasks can be inserted depending on the students’ needs.

To make this typology more accessible, Eszter added a new coding system to the graph. Some subgroups of problems are related to some of these codes, but many problems have multiple codes. We can infer here another theorem-in-act: ‘good’ problems not only target one piece of mathematical content but also allow work on multiple things in parallel. This makes the network denser. The network of problems is less hierarchic here than in other parts, leaving more flexibility to the teacher. However, the discussion also revealed some further hidden interdependencies of the ordering. Another iterative process of discussions and the development of representations is necessary to clarify these choices.

4.2 József: a short SoP leading to a new theorem

József is an experienced secondary school teacher educator with notable high school teaching experience, especially in talent-nurturing programs. He is one of the leading authors of the aforementioned Sokszínű matematika textbook series.

He provided the group with several short SoP illustrating different teaching objectives. One of them is in the field of elementary geometry for grade 7–9 students, containing six problems in immediate succession.

According to his commentary, the didactical problem he wants to address is that students seldom figure out the classical, traditional proof of a certain theorem (the existence of the centroid of a triangle) on their own, even with hints and leading questions. Thus, neither the theorem nor the elements of proof turn into operative mathematical knowledge. József’s SoP creates a bypass using only rudimentary prior knowledge (area of triangles). It is constructed backwards from a “target problem”, identifying an entry point (“initial problem”) accessible for students that is based on the mathematical knowledge they already possess. The new notions are named and the statement is formulated as a theorem after Problem 6, at the end of the process, once students have discovered the properties and proofs.

During group discussions, the terms “target-given” or “culminant” SoP emerged to describe this structure. “Culminant SoP” refers to an SoP leading students step by step towards a “target problem” which might be too difficult and inaccessible without preparation. The target problem might serve, for example, as a problematised theorem, a key for a new mathematical notion, or a synthesis of different elements of mathematical knowledge. These terms lead back to a theorem-in-act: that a difficult piece of mathematical knowledge can be made accessible to students by an appropriate SoP guiding them to this knowledge. This structure was reminiscent of the internal structure of Eszter’s “core” series, leading to the acknowledgment of the importance of this strategy, and the stabilisation of the terms “target problem” and “culminant SoP” in the group’s vocabulary. Also, the distinction between the roles of “core” and “target” problems was discussed (although both can generate an SoP, the “core” is not necessarily at the end).

In József’s example, the SoP leads to a target theorem. But in earlier versions, the theorem itself was not formulated in József’s document: it only appeared in the SoP ‘disguised’ as a problem. For group members, it was considered self-evident that the theorem should be stated during classroom implementation at the end of the process. Discussions about the aims of József’s SoP and about the transparency of his resources for non-expert teachers led to the completion of the document with the statement of the theorem. These discussions revealed another theorem-in-act of teachers: students can discover mathematical theorems if they appear in a problematised form, making the ideas of the proof emerge before the statement of the proposition.

József did not propose a representation in his first version. As explained in his interview, he first considered his SoP linear and did not see the purpose of a representation. Nevertheless, others’ graph representations inspired him to think about this and recognize more complex links between his problems. His graph (Fig. 3) manifests these reflections. During further discussions, the possibility of adding the target theorem to the graph was brought up, in line with the issue of explication of objectives explained above.

Fig. 3

Graph for József’s SoP

4.3 Klára: “word tasks” for primary and middle school—a new representation by table

Klára is an experienced primary school teacher educator, particularly interested in transition from primary to secondary level. She is an author of the same textbook series as József. She provided an example covering long-term teaching trajectories for grade 1–6 students concerning “word tasks” (Pintér, 2021).

“Word task” (“szöveges feladat”, “task with text” in literal translation) is a widely used expression in Hungarian mathematics education (in curricula, resources and by teachers), which refers to mathematical tasks formulated in a non-mathematical context: thus, the interpretation of the text, identification of relevant information and transformation into a mathematical task is required for their solution.¹⁷ “Word tasks” are present in curricula from the end of primary school to high school and their solution usually poses significant difficulty for students at every age.

The didactical challenge Klára wants to address, as she explained orally and in her written commentary, is that many teachers classify “word tasks” according to the context evoked, and not according to the nature of the (mathematical or interpretational) challenges these problems raise. With her SoP, she wants to show a more didactically meaningful classification to teachers, helping them conceive teaching trajectories which equip students with efficient and transferable solution strategies for these problems.

These considerations rely on implicit theorems-in-act. ‘Categorisation of tasks by mathematical content helps the teacher conceive teaching processes more consciously.’ Similar ideas led Eszter to introduce a coding system into her graph. They both implied that in a ‘good’ task, the mathematical content at stake can be complex, and is not necessarily obvious at first glance. This is in line with Varga’s principles described above, namely that ‘rich’ tasks might deal with multiple pieces of mathematical content at the same time, and that mathematical content should be frequented recurrently through various problems and over a long time for progressive construction of mathematical knowledge.

Klára partially organized her SoP into a table. This representation form (Fig. 4) allows a visualisation of various criteria regarding mathematical and linguistic complexity, and an arrangement of the problems of her SoP into progressive scales according to these criteria. The idea of the design is to nurture the different aspects of students’ problem-solving capacity by a systematic variation of problems, both by gradually moving forward at each scale and by crossing between the scales.

Fig. 4

Extract from Klára’s table

This structuring is reminiscent of Varga’s work on combinatorics analysed in preliminary research, and also appears locally in subseries of Eszter’s graph. It relies on several theorems-in-act, particularly the principle that ‘mathematical abstraction can be developed by progressive generalization’ (Gosztonyi, 2015).

The table representation proposed by Klára allows a visualisation of this kind of structuring, presenting the systematic variations according to different criteria identified. Problems in the table are examples representing a category of problems. Different teaching trajectories can be conceived by different “walks” through this table (although they are more difficult to visualize than on a graph representation).

It is interesting to point out that the first version of Klára’s written commentaries focused almost exclusively on solutions of individual problems, and on the systematic elaboration of a representation tool for these solutions based on Cuisenaire rods. No explicit discussion of the SoP’s structure was included: the presentation of this structure relied entirely on the table representation. This issue was raised by other participants during discussions who suggested completing the commentaries with a more explicit discussion of the SoP’s structure.

Also, in her first attempt, Klára struggled to include every problem into her table. Thus, the first version of her SoP is a mix of an ordered list of problems and a table of problems. The group discussion led towards the development of a new, three-level table, which necessitated the revision and more systematic explication of Klára’s categorisation criteria.

4.4 Emergence of language and representations through the development of new resources

The examples presented above illustrate how the development process of new resources containing commented SoP contributed to the development of communication about SoP inside the working group and the elucidation of teachers’ underlying principles. Numerous operational invariants which guided teachers’ choices in the structuring of their SoP were revealed through group discussions, especially around the representations and through the emerging new vocabulary.

In the SoP discussed above, recurrent choices and strategies could be identified as “culminant” SoP or progressively increasing linguistic and mathematical complexity. The emerging new vocabulary reflects the recognition of these recurrences and helps to identify operational invariants shared by expert teachers, which can thus be considered shared principles of GD.

At the same time, the three examples above also represent apparent differences between SoP. This is partly a difference of scales: some examples focus more on the microstructure, while other long-term examples present larger steps of a teaching trajectory which might be distributed over several school years. Beyond that, in our group discussions, we identified different individual preferences (some teachers develop more linear SoP while others insist more on the flexibility of structure), and we also make the hypothesis that structural choices might depend on mathematical domains and school level. Although we consider GD a coherent approach, the group work also leads to exploration of its boundaries and the variations it allows.

The visual representations and the discussions about them played a crucial role in the emergence of new vocabulary (such as “core” or “target problem”). The development of vocabulary also concerns the SoP themselves, in close relationship with the development of representations. The term “series of problems”, although calling for the Hungarian community of GD, generated debates in our group, especially because of the linearity the term “series” suggests, hiding the underlying complexity and flexibility of SoP structures. The term “network” appeared during group discussions expressing these characteristics. When we talk about the hidden structure of SoP as a “network of problems” (cf. Fig. 1), the term reflects the idea of seeing the structure of an SoP as a graph. The graph representation allows us to emphasise the non-linearity of SoP and the diverse, rich connections between the problems.

Although graphs seemed at first to be well adapted to represent structures of SoP, they did not appear to be appropriate for every example proposed by group participants. For example, as we have seen in Sect. 4.3, Klára came up with a table representation. In other cases, there was no obviously convenient representation at first glance. Coding systems also appeared as complementary solutions to clarify structures. These reflections on representation made us reconsider the general validity of the term “network of problems”. We are currently thinking about introducing even more general terms, for example “problem systems”, in addition to earlier expressions.

Visual representations play a key role in our process: they help us understand the structure of SoP and the elucidation of teachers’ working principles, and they generate the development of new language for SoP. We use them as mediators in an iterative development process: representations contribute to the understanding and interpretation of the designers’ choices, and the analysis of SoP contributes to the development of representations.

Beyond the mediator role, representations become integral components of commented SoP, expressing characteristics of the structures themselves and completing written commentaries. We also consider the possibility of using these representations as design tools which could help non-expert teachers develop their design capacity in line with the principles of GD (see below).

The collective nature of our process plays an important role, not only through questions and remarks of the participants in each SoP but also through the mutual inspiration participants give each other in the elaboration of examples and the development of commentaries and representations, slowly leading to the development of a common language about SoP.

5 Perspectives for teacher education: a pilot experiment

In later phases of this project, the team plans to conduct pre- and in-service teacher education experiments to see how the developed resources can support non-expert teachers’ professional development. We expect that familiarization with our examples can help them better understand GD principles, especially those related to the design of teaching trajectories by SoP, and to develop their own designs inspired by our examples.

This part of the project is in its preliminary stage: we conducted several pilot experiments which could serve in defining the design of further teacher training sessions and to the methodology of analysis of non-expert teachers’ professional development. We briefly describe here the conception of one of these pilot experiments and illustrate the potential outcomes through the example of a master’s thesis.

The experiment was carried out by E. Varga on the basis of her SoP presented in Sect. 4.1, once as a workshop with non-expert colleagues in GD, and once as a university course for student teachers. In both cases, participants were first given the SoP without commentaries or graph, and were asked to solve the problems, then analyse and illustrate links between them in the form of a graph. Eszter’s graph was then shared and discussed with participants. Subsequently, participants were asked to develop, in groups, their own SoP on a chosen topic, using the graph representation as a tool. The participants’ products were presented and discussed.

A master’s student, Dorottya, who participated in the pilot experiment, prepared her master’s thesis following this experience under the supervision of Gosztonyi. She presents (Bonyai, 2021) how she implemented the problem graph representation as a tool for her planning work in her teaching practice as a beginner teacher.

She explains that discovering SoP and their graph representation helped her develop her design capacity, more clearly see connections between problems and mathematical content, and make more conscious choices about organisation of teaching trajectories in connection with various teaching goals. She presents several graphs on which the influence of Eszter’s graph is obvious. We can see not only a general implementation of the idea of problem graphs but also several of Eszter’s specificities, such as the coding system or the circles distinguishing smaller groups of problems. At the same time, Dorottya also made adaptations of the representation tool.

One of the examples she dealt with concerns teaching the properties of special quadrilaterals in high school (Fig. 5). In this topic, she needs to explicitly cover several definitions, and the problems of her SoP are closely related to these definitions. In Eszter’s example, mathematical notions were developed in a more implicit way, integrated with the discussions of problem solutions (this is represented in her coding system); however, in Dorottya’s example, definitions have a more autonomous role, and therefore she preferred to introduce these elements into her graph (orange elements). She also worked on the interpretation of the meaning of arrows which was not explicitly laid out in Eszter’s example.¹⁸

Fig. 5

Dorottya’s graph about properties of quadrilaterals

Although this was an informal pilot experience, and the analysis of Dorottya’s work cannot be interpreted as a solid research result, it is nonetheless promising and shows the potential of our approach. Dorottya’s thesis illustrates that our resources and the related teacher education sessions helped her understand and conceive long and relatively complex teaching trajectories based on SoP. She applied the representation tools efficiently for her planning work, and she adapted and developed the graph representation according to her own personal interpretation of teaching trajectories and the specificities of the topic she was teaching.

6 Conclusion and perspectives

In this paper, we addressed the problem of lack of convenient resources and, behind this, the lack of convenient language and communication tools concerning teaching with SoP in the Hungarian context of the GD approach. We raised the questions as to what kind of language and communication tools could be developed to facilitate teachers’ explication of their work with SoP, and how the emergence of such language and communication tools could be fostered.

We presented a methodology named reverse engineering, based on the collaborative work of expert teachers and researchers, which was designed to analyse expert teachers’ work through the creation process of new resources for non-expert teachers. Instead of relying on an a priori theory of teachers’ design work, the reverse engineering allows us to reveal teachers’ implicit working principles, specific, in our case, to the context of GD.

The creation and the analysis of new resources is an iterative process: Vergnaud’s Theory of Conceptual Fields, especially the notion of operational invariants and the component of schemes connecting operational and predicative knowledge, appeared to be a fruitful tool for our analyses. We analysed how teachers’ operational invariants manifest themselves through the creation of new resources on SoP and through group discussions about these resources. We focused particularly on the emergence of new language and communication tools during group work which facilitated teachers’ explication of their working principles.

During the process, new vocabulary emerged which helped describe teaching goals and operational invariants guiding expert teachers’ choices in designing SoP. New representation tools (graph, table, coding system) were also developed, facilitating communication on SoP. They are constitutive parts of our resources, bearing complementary meaning to written commentaries. They also play a crucial mediator role in the group discussion about SoP. Finally, we expect that they could serve as new design tools supporting non-expert teachers’ professional development.

We are planning several new activities in our group in order to gain better access to expert teachers’ teaching goals and operational invariants. First, we will analyse the participating teachers’ work while they implement their SoP in their classrooms. Second, we will collectively develop a long-term SoP about one topic going from the end of primary school to high school. We expect to gain better access to the documentational genesis (the process of development) of SoP and its underlying principles through the discussion of participants’ choices during the collective work.

Although the development of teacher education modules on SoP is still in an early stage of pilot experiments, our project attained an important outcome on this subject. In the frame of the ongoing national reform of teacher education, the notion of SoP was introduced in the national requirements of mathematics teacher education and, more generally, GD obtained further emphasis in the requirements. This will take effect over the following 5 years, and hopefully our experimentation will contribute to the efficient integration of this topic into Hungarian teacher education.

Dialogue between international research and specific educational context appears in our project on several levels.

As we explained in Sect. 3.1, DAD offered important inspiration for the design of our research project. At the same time, it is not a simple application of DAD. As the DAD-Multilingual project (Trouche, 2020) highlighted, the implementation of a didactical theory in different languages and cultural contexts can often raise difficulties and necessitate adaptations. Our participation in the DAD-Multilingual project helped us raise consciousness about the specificities of the Hungarian context and to reflect on possible adaptations of the approach. We showed in this article how we relied on DAD to develop a project adapted to the Hungarian context and to our specific research problems.

The development of new communication tools about SoP contributes to the reconstruction of the hidden theory of GD as one possible approach to IBME. Among the principles emerging in our research process, some are reminiscent of well-established didactical theories, such as the systematic variation of problems according to different criteria. A comparison between SoP in GD, didactical variables in Brousseau’s approach and the Chinese variation method was launched to explore these apparent similarities and their limits (Gosztonyi et al., 2020). Other aspects, such as the mathematical complexity of problems, seem to be rather specific to GD.

The understanding of teachers’ design work in the specific context of GD can provide elements, more generally, for a better understanding of teachers’ work in IBME. A new project¹⁹ aims to reinvest in the idea of “problem networks” as a modelling and design tool for teachers beyond the Hungarian context and analyse teachers’ design work in France and Hungary.