Abstract
During the last decades, the study of how learners and teachers of mathematics use the resource of language has contributed to our understanding of mathematics teaching and learning in a variety of classrooms and cultures. Developmental work with mathematics teachers on the particular resource of mathematics teaching talk is more recent. In order to explore responses related to the importance of this talk, in this paper we consider three sites of practice in mathematics education—research, professional development and teaching—and illustrations of data from or about them, including studies from the literature, and work with secondary school mathematics teachers in Catalonia-Spain and Malawi around the teaching of angles. We argue that tensions permeate these sites of practice when a focus is placed on word use, specifically the practices of naming and explaining, in mathematics teaching talk. We conclude that the importance of mathematics teaching talk is construed through tensions with other resources in language and teaching. Tensions specifically appear in the realisation of mathematics teaching talk as mediational in the work with mathematics teachers on their classroom teaching.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we draw on two projects with secondary school mathematics teachers, namely, one with Núria as researcher and teacher educator in Catalonia-Spain, and the other with Jill as researcher and Lisnet as researcher and teacher educator in Malawi. In the paper by Essien et al. (2016), challenges of mathematics teacher education were explored across these countries. In this collaboration, the focus is on mathematics teaching talk. We share a concern regarding the importance of mathematics teaching talk as a resource for learners’ learning, and those aspects that matter for teacher learning. In Malawi, it is common to find teacher-centred pedagogies in which the mathematics teacher assumes the responsibility for the teaching of mathematical knowledge in a large classroom. Learner participation lies in answering the teacher’s questions in whole class instruction, working with a partner on a textbook task and coming up to the chalkboard to share a solution—typically in writing, without accompanying explanations. All of these activities are authorised by the teacher and implemented through teaching talk. In Catalonia, it is common to find learner-centred pedagogies in which group work and problem-based methods guide classroom practice. The principle that learners must be active in knowledge construction is then interpreted to imply a diminishing direct role of the teacher and of teaching talk in learners’ learning. We claim that our concern is relevant for mathematics teaching and learning with consequences of opening and closing opportunities for mathematics learning through mathematics teaching talk, be it very present or residual in classrooms and thus within and beyond our cultural contexts. We bring mathematics teaching talk into the foreground in this special issue since, as we show, it recedes into the background in recent studies related to language and mathematics teaching and learning, including in multilingual classrooms (e.g., Turner et al., 2019; Zahner et al., 2021). Wilkinson’s (2018) analysis of what research tells us teachers need to know and do with respect to teaching the language of mathematics includes that teachers “model the use of the mathematics register when they talk about mathematical problem solving and mathematical ideas” (p. 174). Emphasis on establishing classroom norms and mathematical discourse practices—moves with which we agree—tend to mask this step, and all that ‘modelling’ the use of the mathematics register entails.
The aim of this paper is to examine and so bring into view, the importance of mathematics teaching talk. By this we mean the mathematical talk of the teacher with her learners in classroom teaching. While our focus is on the mathematical aspects of the talk of the teacher, this talk in the classroom is, of course, in the context of pedagogy and therefore intertwined with pedagogical aspects. Despite the many challenges around the articulation between pedagogical and mathematical aspects, in the context of teaching and thus language-in-use, we do not construct a strict divide between them. We think of mathematics teaching talk in three sites of practice in mathematics education, namely, research, developmental work, and teaching. In so doing, we confront mathematics teaching talk crossing languages and cultures. Linguistic diversity is a feature of the contexts in which we work. Whereas the choice of multilingual countries is not especially intended, we expect that it will impact the data collected. Teachers in Catalonia and Malawi respectively teach mathematics and participate in developmental sessions through Catalan—the language of instruction in that part of Spain—and English—the colonial and now official language in Malawi—, which may not be home languages of participants. So, even if we, as researchers and teacher educators, do not pay attention in this collaboration to multilingual issues around mathematics teaching talk, teachers’ comments and practices will raise these issues occasionally or frequently.
With the above as context and introduction, we move on to summarize our sociocultural approach to word use in mathematics teaching talk (Sect. 2), and thus our theoretical grounding. In the following sections, we dig into tensions concerning mathematics teaching talk. Adopting a Vygotskian lens (Vygotsky, 1978; Wertsch, 2007), we refer to tensions as dialectical (Williams & Ryan, 2020) to imply dynamic relationships and dialogue between conflicting values such as the importance or non-importance of research on mathematics teaching talk, and of work on mathematics teaching talk in professional development, or in classroom teaching. We examine meanings of this talk in research and ask the following question: What tensions does mathematics education research suggest concerning the study of mathematics teaching talk? (Sect. 3, Question 1). We then examine meanings of this talk in two contexts of professional development, one in Malawi and one in Catalonia, and question further: What tensions does professional development with mathematics teachers suggest concerning the work on mathematics teaching talk? (Sect. 4, Question 2); What tensions does classroom teaching—as reported by teachers in the developmental sessions—suggest concerning the use of mathematics teaching talk? (Sect. 5, Question 3). From answers to Questions 1, 2 and 3, we conclude with reflections for the mathematics education community across languages and cultures (Sect. 6).
The exploration of Questions 1, 2 and 3 is sociocultural (Holstein & Gubrium, 2008). Methodologically, we draw on the role of the participants in the respective sites of mathematics education practice, as mediating the understanding of, and actions around mathematics teaching talk. The empirical base for the site of research in mathematics education includes studies taken from the research literature i.e., the studies themselves are the focus on our analyses. These studies are viewed as expressions of circulating discourses in the research domain. The empirical bases for the sites of professional development and mathematics teaching are professional development discussions, teachers’ lesson plans, and oral reports about teaching (Questions 2 and 3); thus, the participants in this part of our research collaboration are the two groups of teachers and the teacher educators singled out by means of noticing workshops in Catalonia, and Lesson Study in Malawi, both of which included deliberate work on mathematics teaching talk. It is not our intention to identify tensions in teaching by means of data from teaching, but from the mathematics teachers’ talk about their teaching plans and their teaching during the developmental sessions. This talk about their mathematical talk with learners in classroom teaching constructs mathematics teaching talk as a type of meta-talk reflectively mediated by the site of professional development. Further methodological details follow below. Overall, we make tensions visible through analysis across different data forms by documenting insights from the research literature, and the teachers in interaction with the teacher educators, and these insights mediate our response to the purpose of mathematics teaching talk.
2 Our sociocultural approach to mathematics teaching talk
We have selected a focus on mathematics teaching talk in order to gain clarity on the nature of word use for mathematical meaning making in talk with learners. Learning to talk mathematics, and teaching for this learning, are not about the learning and teaching of words and grammar, but, in Halliday (1985) terms—and highlighted by Wilkinson (2018)—of the words and grammar of the mathematical register in use across practices. We therefore argue that mathematics teaching talk matters in that it can open up or close opportunities for participating in the mathematical discourse for school learners who have little to no experience with making specialised word use function in order to discuss and reason mathematically. Here mathematics teaching talk is a means to teach the mathematical discourse and to promote participation in this discourse, understood as the language and the communication aspects of practices such as mathematical reasoning, arguing, proving or conjecturing. Furthermore, we argue for using a sociocultural approach (Vygotsky, 1978; Wertsch, 2007), which allows us to emphasize participation in our work with teachers and to highlight mathematics teaching talk as mediational in the learners’ participation in the mathematical discourse.
In Vygotskian terms, mathematics teaching talk is a tool, with the potential to mediate the learners’ participation in the mathematical discourse by means of creating situations of mathematical interaction with others. Working from Systemic Functional Linguistics (SFL) (Halliday, 1985) in the first instance, and in conjunction with the Mathematics Discourse in Instruction (MDI)/Mathematics Teaching Framework (MTF) (Adler, 2021), we zoom in on the layered structure of word use in talk and focus on two layers or tools within the tool of talk, i.e., naming and explaining. We choose these tools because naming and explaining together function to communicate what people can mean, and as encoding for and originating many (though not all) further layers of meaning making through the processes of language (Halliday, 1968; Schleppegrell, 2014; Wells, 1994). SFL and MDI/MTF underscore the importance of teachers’ knowledge of mathematical-linguistic forms for the learning of the mathematical meanings of the forms in use, as stated by Pimm (1987) and by Wilkinson (2018); names and explanations are hence viewed as lexical units related to the teaching practices of naming and explaining that require lexical knowledge. In mathematics teaching talk in a lesson, the teacher can add names and explanations to the discussion of an object of learning, so that extended opportunities of participation in the mathematical discussion can be created for learners. These teacher contributions are visible in domain studies related to language and learning (e.g., Moschkovich, 2008), but typically not problematised. As we have shown in prior research on which we now build, naming and explaining are part of what is entailed in word use within explanatory communication (Adler et al., 2022), and interpreted by Planas (2021), concerning how words can be lexicalised to encode meanings and relations amongst meanings.
Before continuing with further details of SFL, we turn briefly to elaborate the MDI/MTF and so locate the construct of explanatory communication, and our use of this through this paper. As discussed by Adler et al. (2022), the MDI was developed as an analytic tool to enable systematic description of elements of mathematics teaching across lessons, and for use in a research and professional development project in South Africa. MDI was redescribed for developmental work with teachers, this form being named the MTF, and with shifts from descriptive constructs to more prescriptive teaching practices. MDI and MTF have the same structure and theoretical roots. For ease of reference, we refer to the MDI/MTF framework. The MDI/MTF is rooted in sociocultural theory and structured around three recognisable and inter-connected teaching practices as key mediational means in mathematics classroom instruction, as follows: exemplification (examples, tasks, and their representational forms), explanatory communication (word use and justifying) and learner participation (what learners are invited to do, say and write). These instructional, and ultimately cultural tools work together to open (or close) opportunities for learning related to an object of learning in a lesson. Critical literature on exemplification with variation in mathematics and mathematics education (e.g., Watson & Mason, 2006) and language as a resource in mathematics teaching and learning with emphasis on lexicalisation (naming and explaining) on the one hand (Planas, 2019), and explicit criteria for mathematical explanations on the other (Prediger, 2019), was networked into the framework. As has been argued (Adler, 2021), their salience in the MDI framework, and interpretation for teaching in the MTF, were their resonance with on the ground practices, and thus with possibilities for connections with teachers. Within the South African project, and now the Malawi LS in focus in this paper, the MDI/MTF operates as a boundary object, flexing to meet the different practices of research and professional development.
Following the early distinction in Halliday (1968) between the linguistic representation of the class-naming principle inherent in word nouns and the meaning representation of naming processes in language use, we refer to naming—instead of vocabulary or technical register—because it brings in the teaching practice of communicating mathematical meaning or lexical knowledge encoded in names. Naming is specifically considered at the level of words, which can be nouns, noun phrases or phrases in general. In the MDI/MTF, naming is included to emphasize learners’ encounters with mathematical objects through how these are named. The naming practices are then defined to mean “the use of words to refer to other words, symbols, images, procedures or relationships” (Adler & Ronda, 2015, p. 5). From a Hallidayan perspective and noting how little attention is generally paid to the study of names and naming in mathematics education research—a seminal exception is the work of Pimm (1987)—Planas (2021) highlighted the complexity of the naming practices that support the learning of meanings for already-known words such as ‘equivalence’ or for combinations of already-known words such as ‘equivalence of expressions’ in the algebra of equations. These naming practices and names function to communicate mathematical meanings encoded for those names and for the eventual connections to one another in the mathematical practice. Even if the linguistic forms are familiar, the newer meanings are not predictable and cannot be assumed to be known by the learners before their lexicalisation in teaching. How ‘equivalence’ and ‘equivalence of expressions’ are lexicalised in mathematics teaching talk, or become mathematical names, i.e., names with meaning encoded in the mathematical register, in this talk, is again more important than the linguistic knowledge of the words themselves.
A distinction can also be made between the linguistic representation of the explaining principle inherent in some forms of grammar (Halliday, 1968, 1978) and the meaning representation of explaining processes in language use. Like naming, explaining is an important language-responsive teaching practice that entails word use and new lexical elaboration of sentences that include rationales or justifications. More broadly, by language-responsive teaching we refer to the teaching that is planned and developed with explicit attention, in the interaction with the learners, to the nuances of word meaning in relation to the plurality of forms of word use in any discourse organization. Adler et al. (2022) illustrated explaining practices in communicating the geometric meaning of the exterior angle of a triangle and the moves between the visual, the verbal and the diagrammatic. Planas (2021) focused on the verbal mode of the explaining practices, as we do in this paper. not without acknowledging the other modes involved in explanatory communication and teaching. That pilot study involved the case of two secondary school mathematics teachers who tended to do most of the mathematical naming in their lessons on the algebra of equations, but hardly offered mathematical explanations of the names and concepts to the learners during their teaching talk. In the developmental sessions with the teachers, explaining was approached by means of relatively short sentences, starting with or including mathematical names, and lexicalising explanatory relationships between, for example, the solutions of two algebraic equations and the equivalence of the equations: “… a sequence of equivalent equations, or equations with the same solutions” (p. 283). Discussion with teachers illuminated how naming and explaining—alongside the resulting names and explanations—function in mathematics teaching talk to produce participation by making available, and enabling learners’ use of mathematics. In this way, the value of naming and explaining in mathematics teaching talk was associated with the facilitation of naming and explaining done by the learners. This valuing, nevertheless, appears to bring with it tensions across sites of practice.
3 What tensions does mathematics education research suggest concerning the study of mathematics teaching talk?
The site of practice addressed in Question 1 is mathematics education research, and the studies from the research literature are the ‘participants’ with which we interact. A focus on mathematics teaching talk led to progress in the early field on language when researchers such as Pimm (1987) began to look at aspects of mathematics teaching including words and sentences that had not previously been considered important. Lampert (1998) was also influential in illuminating productive communication in the mathematics classroom in the context of curriculum reform in the USA. In a lesson on the wooden pieces of a tangram, “Can two of them be joined to make a hexagon?” (p. 1), was an illustration of word use in mathematics teaching talk leading to talk about whether the angles in one of the figures proposed should be measured with respect to the “inside” or the “outside” of the figure (p. 3). The teacher talked about angle types, related this teaching talk to whether the result was or was not a hexagon, “Does every figure that has six sides also have six angles?” (p. 4), and highlighted the relationship, “So the fact that a hexagon has six sides that you started out saying there, and the relationship between these shapes…” (p. 2). Mathematics teaching talk was approached from the intertwined perspectives of ‘modelling’ word use and reasoning.
Our first step in our focused review of research was to recall the early studies above, emerging from examining mathematics education with a language lens. Equally important was to recall early work in teaching and learning mathematics in multilingual classrooms that paid explicit research attention to mathematics teaching talk. An argument by Adler (1999), for example, was that teaching talk is a resource for mathematics learning, whose use in the classroom needs to be alternatively visible, so that attention can be focused on the use of the language aspects of the mathematical discourse, and invisible, so that attention can be focused on the wider practice of the mathematical discourse. Adler discussed tensions likely to be experienced by mathematics teachers, particularly if they are teaching in multilingual classrooms, and these were illustrated through moves of focusing in and out of technical names in mathematical talk with a goal of inducing learners’ participation in that talk.
Our second step was to move from that early time through a swathe of studies where these tensions were discussed by others in research that assumed and concluded that the focused study of mathematics teaching talk is important (e.g., Barwell & Pimm, 2016; Morgan et al., 2021; Robertson & Graven, 2018; Sherin, 2002; Turner et al., 2019). Confirming these tensions as a continuing feature in current teaching practices, Turner et al. (2019) addressed language understandings and teaching in classrooms and pointed to tensions faced by teachers when wanting to draw attention to mathematical language and, at the same time, being concerned with interrupting the learners’ reasoning, and hence seeing their mathematical talk as an obstacle to learners’ participation in mathematics. The question that then arises is whether and how recent research that has brought significant attention to the what and how of language-responsive teaching practices (Prediger, 2019) engages what appears to be an enduring and perhaps inherent tension related to mathematics teaching talk as a resource for supporting learners’ participation in that talk, and thus also in mathematics practice.
We turned in a third and final step in exploring mathematics education research related to mathematics teaching talk, to a meta view of current research as reflected in two survey papers, one in ZDM 2021 and thus in mathematics education (Erath et al., 2021), and one in linguistics and education with a focus on mathematics (Wilkinson, 2019). Wilkinson (2019) reviewed published research on the relationship between language and mathematics in the journal Linguistics and Education over three decades. In the concluding discussion about implications for instruction, she argued that “the mathematics register should be modelled by teachers and encouraged with students as their schooling proceeds” (p. 94). There is some coherence with this argument in the overview of “the roles that teacher moves play in enhancing students’ language in mathematics classrooms” in Erath et al. (2021, p. 252). In addition to probes and questioning, moves include revoicing student offerings (in specialised language in the sense of language that functions to communicate mathematical meaning), choosing language that represents a mathematical idea more transparently, providing vocabulary and syntactical structures, and acting as a language model, which is acknowledged as a highly challenging pedagogic practice for mathematics teachers, “necessitating planning and preparing” (p. 255).
The studies covered by these surveys (e.g., Ernst-Slavit & Mason, 2011; Götze & Baiker, 2021) have made considerable advances in our learning about language-responsive content teaching. We would add, however, that in both these surveys, the inherent tensions in the work around ‘modelling the mathematics register’ or ‘acting as a language model’ in mathematics teaching talk are underscored, and we suggest that this is a function of what is prioritised and focused on across the articles reviewed. As Erath et al. (2021) stated, articles in the ZDM special issue are largely centred around “the role of language in collective meaning-making processes” (p. 258). From our perspective, while the authors of these studies recognize research on mathematics teaching talk to be important, it mostly appears subordinated to research on mathematical discourse practices. As such, this talk is not given direct attention, or it is just explored for how it contributes to the enhancement of learners’ participation in these practices (e.g., Zahner et al., 2021). Despite mathematics teaching talk being valued, a consequence of subsuming it into, or backgrounding it in the study of discourse practices is that it is not examined in depth—since it is not the primary object of the research—and its impact on mathematics learning can be underestimated.
As a result of our step-wise literature review, we posit a tension within the research community because of the existing subordination of the study of mathematics teaching talk to the study of discourse practices. The discourse focus has been fruitful for describing mathematics learning as moving from exposition to participation in mathematical discourse. However, there are typically unintended consequences to developments or interventions, and a tensional way of constructing the relation between discourse practices and teaching talk is produced, with teaching talk often lacking an autonomous research profile, tacitly encoded as dispensable, and represented in the perspective of the discourse practices. Notwithstanding an emphasis on mathematics teaching talk, just focusing on it can suggest in the research community that the research concern is not entirely with mathematics learning or learners’ participation and talk. Any primary focus on mathematics teaching talk can provoke the response that, whether intended or not, views of teaching and learning mathematics that reflect transmission teaching are encouraged, and so result in a backwards movement in the field of mathematics education. Furthermore, focusing on the word and sentence levels as one important aspect of mathematics teaching talk can suggest that research and developmental concerns are not with argumentation or reasoning, aspects that in the field tend to be equated with discourse practices. Again, a primary focus on words and sentences can provoke the response that narrow views of discourse are encouraged, and thus revert backwards in the field. Theoretical emphases on mathematical discourse practices, which suggest subordination rather than correspondence between connected aspects of language-responsive mathematics teaching, may thus be limiting the understanding of discourse practices as made of word use and reasoning in equal measure.
4 What tensions does professional development with mathematics teachers suggest concerning the work on mathematics teaching talk?
The site addressed in Question 2 is mathematics teacher professional development. The group of six secondary school teachers and Núria in Catalonia, together with the group of ten secondary school teachers and Lisnet in Malawi, are the participants. The data were not collected for the purposes of this paper, but rather the issues emerged in the discussion of the two projects in which work with these groups was embedded. The projects are methodologically different in many respects. In Catalonia, the project aimed at promoting processes of professional noticing (Mason, 2002) in mathematically-varying workshops supported by components of the MDI/MTF (Adler, 2021) and the naming and explaining practices piloted in Planas (2021). All teachers were new to practices of noticing and of lexicalising mathematical meanings and explanations in relatively short sentences. The workshop on angles, and consequently the involvement of the six teachers there, was chosen to share the topic at play in Malawi. Workshop data included the written and oral work from two three-people assignments on pedagogical tasks and follow-up reflective joint discussion. In Malawi, the project aimed at introducing Lesson Study (LS) (Huang et al., 2019), focused on lower secondary geometry supported by the MDI/MTF focus on explanatory communication in mathematics teaching talk. The ten teachers were learning ideas about geometry teaching, those embedded in the MDI/MTF, and the LS practice. Data included lesson plans, transcripts of video-recordings of lesson planning, teaching, and post-teaching reflective discussions. To respond to Question 2, we drew on transcripts of the reflective discussions in Catalonia and in the initial LS planning in Malawi. We analysed utterances in which participants were expressing conflicting values concerning the importance of pedagogical work with a focus on mathematics teaching talk.
More than twenty years ago, Ball and Cohen (1999) brought up the agenda of developing theories and practices of professional learning for the support of work with mathematics teachers on the multiple ways of thinking about student work, classroom discussions, and content representations (p. 28). Much relevant research on mathematics teachers’ professional development and learning has occurred since then (Sztajn et al., 2017), but what is entailed in pedagogic practices involving mathematics teaching talk remains uncommon. Recent design research on language-responsive mathematics teaching and professional development (Prediger, 2019) includes the talk of the teacher but it is typically out of focus because the study of this teaching tends to emphasise the products of the learners resulting from their participation in mathematical discourse practices. Interestingly, in design research, attention to mathematical language is primarily in the materials. That this is in the materials reflects the significance of lexical elaborations for learning and learners’ developing of mathematical discourse practices, but relegates the mediation to the materials without simultaneous attention to their mediation by the teacher through her talk in teaching. In our developmental sessions, as we show in the subsections below, when mathematics teaching talk (as a means to teach the mathematical discourse) was made visible and presented as the object of discussion with the teachers, an opposite version of the same tension seemed to be created. Teaching talk and learner participation in mathematical discourse practices were perceived as mutually exclusive, hence inhibiting rather than enhancing the understanding of mathematics teaching talk as a resource for promoting content learning. Exclusionary values attached to teaching talk and learner participation emerged during the involvement in the professional tasks centred on mathematics teaching talk. Unexpectedly, the attention to words and sentences in teaching talk was merged with arguments in favour of the ubiquity of this talk, and perceived as contradicting teaching that encourages learner participation in the mathematical discourse.
4.1 The angle workshop with the teachers in Catalonia
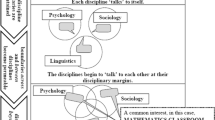
In the workshop on angles, the importance of mathematics teaching talk was raised through professional tasks of identifying, interpreting and deciding on practices (van Es & Sherin, 2021) of naming and explaining, with the potential to communicate angle-specific meanings. The naming and explaining in teaching talk were introduced as complementing other resources such as lesson work involving mathematically rich problems, and hence autonomous participation of learners in mathematical discourse. The workshop consisted of two parts. In the first part, Núria presented learning challenges commonly faced by many secondary school learners as reported in the specialised literature (e.g., the static angle bias, Mitchelmore & White, 2000), and then offered written responses to mathematical tasks of learners seemingly experiencing some of these challenges (selected from prior local projects, see Planas, 2018). In the second part, the teachers discussed problem-based professional tasks with lesson transcripts of mathematics teaching talk and questions for discussion of that talk with respect to angle learning challenges. Figure 1 shows an English version of one of the tasks,Footnote 1 with A1 and A2 representing mathematics teaching talk of a real and a fictional teacher. Núria commented on the lesson from which the situation in Fig. 1 was drawn, where the angle concept had not been named in the teaching talk, which mostly happened in the final discussion of the problem following learners’ work.
In the analysis of the reflective discussion following work on the task in Fig. 1, we see evidence of the focus on teaching talk being first interpreted as an expression of ‘antiquated’ transmission pedagogies, contradicting the focus on learning and learner participation. Mathematics teaching talk was associated with the amount of time of direct instruction, and this was in turn associated with less time for the learners’ participation in the mathematical discourse. Part of this reasoning is illustrated in the turn of a teacher who said that time in a lesson is limited, and “we cannot really increase teaching time much, and still have time for problem solving.” Teaching time, including mathematics teaching talk, was thought of as separate from learner participation in problem solving. The experience of this tension is not surprising in light of the institutional local discourses on what learner-centred practices are and what they imply for meaning making and learning. In the guidelines for teachers in the secondary school mathematics curriculum, the aspects that account for the learning outcomes are the nature of the tasks (i.e., mathematically rich problems) and the time-on-task (i.e., group work that involves talk among learners for exploration of mathematical ideas). Moreover, teachers are called to empower learners to become more active and integral to their learning processes. “Flipped teaching” methods, in which learners are provided with written materials and videoclips with definitions of mathematical vocabulary and content summaries to be studied in the home, have become a common interpretation of the curricular guidelines. In this context, the teachers argued that their learners “already have the materials with the theory of the mathematics to be learned.” They also argued that teaching talk cannot anticipate every single learning challenge, no matter how much it was improved, and thus how much dialogue to insert between this talk of important mathematical names, and ensuing explanations. One reason was however raised in favour of naming and explaining in teaching when a teacher referred to multilingual mathematics classrooms:
Teacher 1: You recommend talking about the intersection of two half-planes, not just about the region. This makes sense, but will this way of talking work in the classroom? We do not know the particular challenges of the learners.
Núria: Isn’t this way of talking angles powerful for all classrooms and learners?
Teacher 1: It may be already clear and not always so important.
Teacher 2: (…) What about learners who struggle with Catalan? We may need to explain how an angle around a point is an angle rotated around a point, and different from the angle at a point.
Núria: Isn’t this explanation important for all learners and classrooms?
This intervention of Teacher 2 suggests a remedial approach to professional work on mathematics teaching talk. The value of naming and explaining in teaching seems to be seen as relative and limited to some learners and classrooms, and hence linked to professional demands specific to teachers who teach in these classrooms. All the six teachers worked in public secondary schools within low socio-economic urban areas with high percentages of migrant families, which suggests a reason why they said they found the workshops useful even though they experienced tensions with the curricular and pedagogic discourses. In fact, the question posed by Núria at the end of the above dialogue started a discussion which led to acknowledging the importance, for all learners and thus for all their teachers, of being exposed to and using mathematics teaching talk in order to understand and explain the definitions of angles and of the concave and convex classes of angles given in the written materials and talked about in the videoclips as well. In those materials and videoclips, the prepositional phrases ‘at/around a point’ (en/al voltant d’un punt in the original) and ‘on/around a segment line’ (sobre/al voltant d’un segment in the original) were indistinctly used for defining the plane angle despite the suggested lexicalisation of the plane angle through ‘at/around a point’ and of the spatial angle through ‘on/around a segment line.’ The vivid discussion of these phrases and of some explanations in the written materials and in the videoclips contributed to raising the issue of precise naming and explaining for the teaching of plane angles for all learners, including those for whom Catalan was their home language. In this way, there was some closure to the more general tension perceived by these teachers between a focus on mathematics teaching talk and a focus on all learners’ participation in the mathematical discourse.
4.2 The lesson study with the teachers in Malawi
In Malawi, the Lesson Study (LS) aimed at enhancing the teaching and learning of geometry, which is recognised as a challenge by the Ministry of Education Science and Technology (MoEST, 2020). There was an initial two-day workshop with ten teachers from two secondary schools in order to promote their geometric thinking and introduce them to the process of Lesson Study and its developmental cycle. In contrast to the context in Catalonia where attention to challenges for teaching were research-informed and presented as common across educational systems and mathematics classrooms, in the Malawian LS, the starting point was localised through teachers’ expressed concerns about Grades 8 and 9 learning challenges in geometry. Learners could identify properties related to angles when they were given numerical measures in simple geometric figures such as those involving two intersecting lines. However, when given complex figures, or algebraically expressed angle measures, they either confused or misapplied the properties, suggesting a fragile understanding of these geometric objects, their definitions and properties.
Consequently, in the initial workshop, the teachers were introduced to research-informed ideas about teaching and learning geometric reasoning, and linked with the mediational means foregrounded in the MDI/MTF, including explanatory communication. Tasks included geometric figures with deliberate varying of complexity and orientation, with attention to how these can make visible and/or obscure geometric properties (Huang & Leung, 2017). Discussion on explanatory communication included attention to the demands in geometry of linking properties expressed in words or symbolic forms to figures (e.g., Duval, 2006), and then planning for mediation through mathematics teaching talk, i.e., word use (how we use words to name and identify mathematical objects and their properties), and justifications (how we explain and justify the words to communicate meanings of definitions and properties). It was during these initial sessions that teachers’ tensions became apparent, between their experiences and interpretations of activities related to mathematics teaching talk, and their desire for enacting learner-centred pedagogies. They interpreted practices focused on mathematics teaching talk as giving pedagogic value to ‘spoon feeding’, similarly to the teachers in Catalonia and their concerns with direct instruction and transmission pedagogies. When they were encouraged to ensure that they consider planning about mathematics teaching talk by thinking about names that they and their learners would use and how they would explain and justify those names, one teacher raised the following concern:
In the previous in-service training workshops that we have attended, they have emphasised much on learner centred teaching practice. Now with what we are now getting about MTF today is putting me in a dilemma to say now what should I do. Should I emphasise on learner centred approaches that we have been learning before or I should be doing spoon feeding. I mean how do I marry these things, planning for mathematical language and then doing learner centred education practices?
While mathematics teaching talk and learner centred teaching as opposing poles was articulated by one teacher, the other teachers concurred with his view. That this was a dilemma for these teachers is unsurprising given this continuing tension in the field of practice as discussed by Pimm (1987) and Turner et al. (2019) referenced above. Yet, there are complex specificities in the Malawian education context, with implications for dialogue with teachers in professional development and over time. In Malawi, ‘spoon feeding’ equates with the teacher explaining while learners listen passively. For example, to introduce the notion of an exterior angle of a triangle (the concept and theorem in focus in the LS in one school), the teacher would write out the definition on the chalkboard and express it in words; she would then provide examples of exterior angles, write out the proof of the relationship between the exterior and two opposite interior angles, and do an example to illustrate how to apply the property. Only after that would learners be given an exercise. For the teachers, drawing attention to mathematical language implied only paying attention to their talk, hence limiting learner participation in the lessons. Mathematics teaching talk became merged with arguments in favour of more time for direct instruction and transmission models of learning. Yet, neither in Catalonia, nor in Malawi, was it direct instruction or spoon feeding as such, nor the amount of time for this, that were in focus, but mathematics teaching talk that supported access to and participation in mathematical discourse. All these tensions may remain unnoticed by mathematics teacher educators, in the same way that we were surprised when noticing them. It was difficult to think of our focus on mathematics teaching talk as competing with the mathematical pedagogies we believe in, or as serving only for multilingual mathematics teaching. In both contexts of professional development, we were thus challenged to explain our understanding of mathematics teaching talk for induction of learner participation in mathematics. As we show in the next section, as the LS unfolded, the Malawi teachers in the school where the exterior angle was in focus took steps towards working with and reflecting on this tension.Footnote 2
5 What tensions does classroom teaching, as reported by the teachers, suggest concerning the use of mathematics teaching talk?
In the approach to the data for responding Question 3, we draw on evidence of teachers in the two contexts explicitly connecting the focus on mathematics teaching talk in the professional tasks with their uses of this talk in their teaching. The site of practice addressed in this question is now mathematics teaching, and the groups of teachers in Catalonia and Malawi are the participants that report on their teaching during the time of the developmental sessions. Access to the practice of mathematics teaching is therefore through the teachers’ mentions of their teaching over the time of the workshops in Catalonia and the teachers’ planning and reflections on their teaching in the LS. We drew on the same transcripts of the reflective discussions in Catalonia and across data in Malawi, but now searched for evidence in dialogues of teachers expressing tensions between their use of mathematics teaching talk in the classroom and their expectations of learners’ participation in the mathematical discourse.
The tensions that teachers suggested point to the experience of a gap between participating in the mathematical discourse and listening to/hearing mathematics teaching talk, with the expectation that the naming and explaining would rest with the teacher and not be extended to the learner. At the basis of these tensions there is once more the representation of the schism between teaching and learning, which nowadays seems to be increased by the representation of teaching talk as detrimental to learner participation in discourse practices. The mathematics teaching challenges coming from the experiences of these tensions were manifold, as the teachers in Catalonia and Malawi reported. Yet, in neither context was explicit language-responsive teaching visible. In Catalonia, while mathematical problems demanded and elicited learner mathematical language during participation in group activity, this was not extended except for a few minutes at the end of the lessons following the group work and the expression of reasoning on the sheets given. Naming and explaining were residual in that they were left for the time in which the learners had discussed the problem and written their resolutions. In spite of this gap, moments of naming and explaining were reported, such as the following: “When you say angle you do not mean a number, there is no need to assign a measure or a number to an angle”, in response to a learner talking about el número angle, “the number angle.” In Malawi, most classroom tasks did not demand discourse practices from learners that went beyond single words and short phrase answers to questions in the first instance, and so a critical step was to extend this practice. With this came the challenge of time, as well as how to work with what is subsequently needed from the perspective of mathematics teaching talk.
5.1 The final workshop with the teachers in Catalonia
A teacher in the angle workshop reported “the difficulty of finding time for more explanations” in her teaching of angles. In the final workshop that took place eight months later (there had been four more mathematically-specific workshops in-between as well as much classroom teaching), four teachers brought up experiences of tensions regarding the quantity of their mathematics teaching talk. Here too, the well-known tension from Adler (1999) between learner participation and teaching persisted. They had introduced naming concepts and explaining names and concepts in their teaching, and expressed their concerns about not interrupting learner participation by doing so and finding the appropriate moments, which for them was not easy. As Sherin (2002) showed, teachers engaging in productive dialogue that builds learners’ mathematical discourse is not trivial. They did not view their mathematical talk as a form of supporting the progressive transition of their learners into the mathematical discourse by learning how to name and explain themselves. They rather seemed to relate their mathematics teaching talk to learners listening to and hearing specialised mathematical talk, and less on learners beginning to use this talk so as to become full participants in the mathematical discourse. The teachers recognised the importance of the words and names the learners use as they describe objects and processes and reason about these, but at the same time they did not seem to connect the mathematical naming and explaining in their teaching with the creation of opportunities for learners to participate in the mathematical discourse. This continued to be equated to doing, saying and writing during engagement in problem solving practices of reasoning and argumentation. In her reflection on a lesson on angles, a teacher raised this tension as follows:
In the small groups I heard a lot of talk about doors opening and other everyday situations for making meaning of angles. I did not hear them talking about rotations, turns, quantities of rotation… They were so engaged in talk that I did not want to interrupt. Then I remembered our discussions on explaining mathematical meanings for angle. I made time at the end of the lesson to associate rotations to angles, and to talk.
We discussed the learning opportunities created for learners in their lessons when listening to mathematics teaching talk in terms of the facilitation of the mathematical discourse, and the fact that these opportunities could not be created equally in the small groups if learners did not go beyond everyday meanings for angle, or if they all stayed tied to the static thinking concerning the concept. This focus on mathematics teaching talk raised the question of how to know at what specific point too much time for naming and explaining has no impact, or perhaps detrimental impact, on the creation of opportunities for autonomous participation of learners in the mathematical discourse. The discussion emerged in connection with the amount of mathematics teaching talk that is appropriate so as to make the mathematical discourse intelligible to the learners, and around ‘too much’ and ‘too formal’ talk as opposed to ‘everyday’ talk. While they valued and had been attentive to the naming and explaining in their teaching, they were concerned with having provoked unintended interruptions in learners’ participation. One of the teachers referred to the risks of “too much of good mathematical talk” as follows:
You cannot talk as if they were mathematicians. They will not participate if everything is too formal. You can talk about the centre of the rotation angle, but you will not strengthen their participation if you then go on with the measure of the amount that a figure is rotated. You better talk about the measure of the angle, and let them think about the task. Too much of good mathematical talk is not so good.
5.2 The Lesson Study with the teachers in Malawi
After the two-day workshop in Malawi, the teachers began a lesson study cycle in their schools. The initial lesson plan was followed by teaching, reflection and then lesson plan 2, which was again followed by teaching and reflection. As noted, in one school, the focus was on the property of the exterior angle of a triangle being equal to the sum of its interior opposite angles. The teachers collaboratively discussed and wrote the first lesson plan, with input from the researcher. Figure 2 shows how the teachers planned to introduce the lesson, with attention to teacher and learner activities, in relation to the learning points (this follows lesson plan templates in use in Malawi). To illustrate tensions concerning mathematics teaching talk, we focus first on the introduction, as tensions emerged here.
The intention was for learners to express their meanings of an exterior angle in words, and ‘demonstrate/identify’ these. The teachers expected the everyday word ‘outside’ to be used, and that the teacher might need to extend this meaning to include how the angle was formed. In the lesson, three learners were successively invited to the board. The first drew a triangle and marked one reflex angle as the exterior angle. The second simply drew an arrow pointing outside the triangle. The third learner illustrated an appropriate exterior angle. In their reflection on the lesson, the teachers initially expressed “shock” that learners’ interpretation of an exterior angle was expressed as “outside”. However, this was the word used initially by the teacher in the lesson to contrast interior angles as inside the triangle. What is interesting here, and in contrast to the Catalonian teachers, is that word use was not the tension experienced by the teachers. They spent time discussing how important it was to include “extending a side”—previously referred to as an angle—and describing the angle formed as the one “adjacent to the interior angle” where the side was extended, and thus not the 180-degree angle also formed:
Teacher 3: The other part is to do with language, anyway. Why do we put this, this adjacent angle to the interior angle? Just to appear …
Teacher 2: … to be exact.
Teacher 3: Okay, aaah yes! Okay, why can’t we say ‘adjacent angle formed outside a triangle, after extending any of the sides of the triangle’? Adjacent, okay, adjacent angle formed.
Teacher 1: We are saying that it’s an angle formed outside a triangle.
Teacher 2: Seems like I heard something in addition to that, some research has been done here, what did you say?
Teacher 3: Okay, I was saying that an adjacent angle formed outside a triangle after extending any of the sides of the triangle.
Teacher 1: Yeah, it’s making sense.
Teacher 3: It’s the adjacent angle part that needs modification so that it should be clearly understood.
The tension for the teachers was the time it takes to have learners come to the chalkboard to illustrate and talk about their meanings so that the teaching can build on these. Their reflection focused on how to save time, by, for example, asking only one learner to the board to indicate and talk about all exterior angles on one triangle, or whether the teachers should bring pre-drawn ‘charts’ showing all exterior angles as shown in the figure for the second lesson plan (see Fig. 3).
Throughout the discussion of the planning for the second lesson. the teachers were concerned with the time it would take for learner activities. The transcript of the discussion is littered with “too much time”, “minimising time” in relation to planned activities, be these learners coming to the board, or doing tasks on pre-given charts. That the teachers’ concerns were not about language use, but about time for learner participation is reflected in the extract below from the summary presented to the teachers in the other school at the end of the planning session.
We’re also intending to, uhm, to, to change the definition of the exterior angle, … we’re going to add the word adjacent, adjacent angle so that the definition of an exterior angle should be ‘an adjacent angle that is formed outside a tringle after extending any of the sides of the triangle.’ So, the key word there that has been, uhm, added is the adjacent angle. Previously, it wasn’t there, so, it was a bit confusing for the learners. … And we’re also going to use charts, this time around, … even, uhm, the examples, we’re also going to write on the charts so that we try to … maximise the little time that we have.
What is also visible here is that with respect to teaching talk, the teachers were more focused on the specialised language expected of the teacher and not of the learners. Participation by learners in the lesson included some coming to the board to illustrate where the exterior angle was in the first lesson, or drawing on a pre-given chart. Learners describing this angle type in words themselves was by-passed. Initially we wondered whether this might be a function of learners’ fluency in English and this being the language in the public classroom channel of talk. Recent evidence of learners’ explanations of exterior angles in a task preceding the start of the second lesson study cycle suggests that many are able to write out verbal reasoning. Across 40 learner descriptions and diagrams of an exterior angle, all marked the exterior angle on a diagram of a triangle with an extended side, although the verbal description did not include reference to the adjacent angle.
6 What, then, is mathematics teaching talk for?
Our response, based on three sites of practice in mathematics education, to the question of what mathematics teaching talk is for, is permeated by the visibility of the following three tensions, each in different ways: subordination of mathematics teaching talk to mathematical discourse practices in research; association of mathematics teaching talk with transmission teaching in professional development; and association of teacher naming and explaining with less learner participation in classroom teaching. These are different kinds of tensions—hence the fluidity in how we work with these—but there are common threads. A consistent theme running across these tensions is the position that mathematical talk and more generally language has for the learners and their participation in mathematical discourse and discourse practices, in the forms of doing, talking and writing. We agree with this position, which for us does not compete with the deliberate use of mathematics teaching talk to “model” the mathematical talk (Erath et al., 2021; Wilkinson, 2018). Our discussion of tensions concerning mathematics teaching talk as permeating research and developmental practice, and not only teaching, and through illustrations across contexts is not about this being ‘new’ but rather that its continued presence in classrooms is now reflected in our research and professional development practices. As the field of mathematics education has developed, and as our understanding of the tensions in teaching has fostered further research and then more attention in teacher education and professional development, other related tensions to those documented in teaching have arisen. Thus there is all the more reason for making this visible, and arguing for the place for mathematics teaching talk with discourse practices in language-responsive mathematics teaching, and highlighting that developing learner mathematical talk is related to the emergence of this talk in dialogue with the teacher.
Using the example of the teaching of angles, we have discussed tensions and challenges regarding mathematics teaching talk, as well as how some conflicting values in the sites of research, professional development and teaching can inhibit us from embracing this talk as a resource for language-responsive mathematics classrooms across linguistically diverse cultural contexts. While some distinctions between the participation of the teacher and of the learners in the mathematical discourse, and more generally between teaching and learning, can be useful, these distinctions can limit the full realisation of mathematics teaching talk that is supportive of learners’ participation in the mathematical discourse. In their processes of understanding and participating in this discourse, learners are expected to use multiple resources. We are arguing that there are important learning and pedagogic reasons for one of these resources being mathematics teaching talk. Lampert’s teaching talk (1998), discussed earlier in the paper, illustrates why materials in the form of textbooks, worksheets, or videoclips to be watched in the home—for learners with life conditions to do so—cannot replace this resource. Our thinking about mathematics teaching at the word and sentence levels of talk does not merely consist of technical names and phrases, but of naming and explaining, and it is not especially adequate or more adequate for multilingual learners, a context that was not specific to Lampert’s study. That said, the complexity of naming and explaining in the multilingual teacher education and teaching sites cannot be overlooked—and of the naming and explaining in our own multilingual research collaboration—happening in the dominant language. While there are many instances of Chichewa-English and Spanish-Catalan translanguaging in our multilingual sites, we did not dig into the issues of translanguaging in our collaboration, in our developmental sessions, nor in how these issues manifest in teaching practices. Further study of mathematics teaching talk needs additional focus on issues of translanguaging.
Finally, an idea that we have intended to communicate is the mathematical specificity of mathematics teaching talk. Mitchelmore and White (2000) reported challenges experienced by many school learners in their learning of angles, including exclusively static thinking concerning angles, or thinking of the concept of angles through their measurable parts only. In the workshops in Catalonia, the resources of naming and explaining in mathematics teaching talk guided the professional tasks around the communication of mathematical meanings for supporting learners’ participation in the mathematical discourse concerning the angle. During the engagement of the teachers in the task of Fig. 1, and rather than no teaching talk during learners’ participation in the resolution of the mathematical problem, the use in teaching talk of “rotation”, “turn amount”, and “the turn amount between two lines around their common point makes an angle”, was considered for supporting learners’ participation in the mathematical discourse of angles. In the LS in Malawi, the resource of word use in mathematics teaching talk was a focus in different moments, and gave rise to geometric approaches to angles beyond the measuring of the angle amplitude. The dialogue around the adjacent angle of a triangle exemplifies professional talk on the teaching of angles that is language-responsive. In this respect, the use of mathematics teaching talk in classrooms, and the work on it in professional development can be further pursued in the community of mathematics education, and especially further studied and valued on its own in the research within this community.
Data availability
The data that support the findings published in this paper is protected within the Universitat Autònoma de Barcelona and the University of the Witwatersrand repositories, and available from the authors upon reasonable request, when not containing information that could compromise research participants.
Notes
An English version is necessary for the linguistic medium of the journal. Although we do not discuss in the current paper what is gained and lost in this translation, we want to highlight that the analysis of this data for the purpose of Question 2 was conducted in Catalan by Núria, and then shared and discussed with Jill and Lisnet in English.
Since writing this paper, and in the next LS cycle with the teachers, they worked on this particular tension with interesting learning potentialities for them and their students (see Mwadzaangati & Adler, in preparation).
References
Adler, J. (1999). The dilemma of transparency: Seeing and seeing through talk in the mathematics classroom. Journal for Research in Mathematics Education, 30(1), 47–64.
Adler, J. (2021). Content and context specificity matter in the ‘how’ of language-responsive mathematics teacher professional development. In N. Planas, C. Morgan, & M. Schütte (Eds.), Classroom research on mathematics and language: Seeing learners and teachers differently (pp. 77–100). Routledge.
Adler, J., Mwadzaangati, L., & Takker, S. (2022). From defining as assertion to defining as explaining meaning: Teachers’ learning through theory-informed lesson study. International Journal for Lesson & Learning Studies. https://doi.org/10.1108/IJLLS-02-2022-0029
Adler, J., & Ronda, E. (2015). A framework for describing mathematics discourse in instruction and interpreting differences in teaching. African Journal of Research in Mathematics, Science and Technology Education, 19(3), 1–18. https://doi.org/10.1080/10288457.2015.1089677
Ball, D. L., & Cohen, D. K. (1999). Developing practice, developing practitioners: Toward a practice-based theory of professional education. In G. Sykes & L. Darling-Hammond (Eds.), Teaching as the learning profession: Handbook of policy and practice (pp. 3–32). Jossey Bass.
Barwell, R., & Pimm, D. (2016). Bakhtin and some dilemmas of mathematics—language. In M. Phakeng & S. Lerman (Eds.), Mathematics education in a context of inequity, poverty and language diversity: Giving direction and advancing the field (pp. 7–18). Springer.
Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics, 61, 103–131. https://doi.org/10.1007/s10649-006-0400-z
Erath, K., Ingram, J., Moschkovich, J., & Prediger, S. (2021). Designing and enacting instruction that enhances language for mathematics learning: a review of the state of development and research. ZDM - Mathematics Education, 53(2), 245–262. https://doi.org/10.1007/s11858-020-01213-2
Ernst-Slavit, G., & Mason, M. (2011). “Words that hold us up”: Teacher talk and academic language in five upper elementary classrooms. Linguistics and Education, 18, 430–440. https://doi.org/10.1016/j.linged.2011.04.004
Essien, A., Chitera, N., & Planas, N., et al. (2016). Language diversity in mathematics teacher education: Challenges across three countries. In R. Barwell et al. (Eds.), Mathematics education and language diversity. The 21st ICMI Study (pp. 103–119). Springer.
Götze, D., & Baiker, A. (2021). Language-responsive support for multiplicative thinking as unitizing: Results of an intervention study in the second grade. ZDM - Mathematics Education, 53(2), 263–275. https://doi.org/10.1007/s11858-020-01206-1
Halliday, M. A. K. (1968). Language and experience. Educational Review, 20(2), 95–106. https://doi.org/10.1080/0013191680200203
Halliday, M. A. K. (1978). Language as social semiotic: The social interpretation of language and meaning. Edward Arnold.
Halliday, M. A. K. (1985). An introduction to functional grammar. Edward Arnold.
Holstein, J. A., & Gubrium, J. F. (2008). Interpretive practice and social action. In Y. Lincoln & E. Guba (Eds.), Strategies of qualitative inquiry (pp. 173–202). Sage.
Huang, R., & Leung, F. (2017). Teaching geometry concepts through variation. In R. Huang & Y. Li (Eds.), Teaching and learning mathematics through variation (pp. 151–168). Sense Publishers.
Huang, R., Takahashi, A., & da Ponte, J. (Eds.). (2019). Theory and practice of lesson study in mathematics. Springer.
Lampert, M. (1998). Introduction. In M. Lampert & M. L. Blunk (Eds.), Talking mathematics in school: Studies of teaching and learning (pp. 1–14). Cambridge University Press.
Mason, J. (2002). Researching your own practice. Routledge.
Mitchelmore, M. C., & White, P. (2000). Development of angle concepts by progressive abstraction and generalisation. Educational Studies in Mathematics, 41, 209–238. https://doi.org/10.1023/A:1003927811079
MoEST (2020). National education sector investment plan: Education Sector Analysis. Ministry of Education.
Morgan, C., Planas, N., & Schütte, M. (2021). Developing a perspective on multiplicity in the study of language in mathematics classrooms. In N. Planas, C. Morgan, & M. Schütte (Eds.), Classroom research on mathematics and language: Seeing learners and teachers differently (pp. 3–21). Routledge.
Moschkovich, J. N. (2008). “I went by twos, he went by one”: Multiple interpretations of inscriptions as resources for mathematical discussions. Journal of the Learning Sciences, 17, 551–587. https://doi.org/10.1080/10508400802395077
Pimm, D. (1987). Speaking mathematically: Communication in mathematics classrooms. Routledge.
Planas, N. (2018). Language as resource: A key notion for understanding the complexity of mathematics learning. Educational Studies in Mathematics, 98(3), 215–229. https://doi.org/10.1007/s10649-018-9810-y
Planas, N. (2019). Transition zones in mathematics education research for the development of language as resource. In M. Graven, H. Venkat, A. Essien, & P. Vale (Eds.), Proceedings of the 43th Conference of the International Group for the Psychology of Mathematics Education (Vol. 1, pp. 17–31). PME.
Planas, N. (2021). How specific can language as resource become for the teaching of algebraic concepts? ZDM - Mathematics Education, 53(2), 277–288. https://doi.org/10.1007/s11858-020-01190-6
Prediger, S. (2019). Investigating and promoting teachers’ expertise for language-responsive mathematics teaching. Mathematics Education Research Journal, 31(4), 367–392. https://doi.org/10.1007/s13394-019-00258-1
Robertson, S.-A., & Graven, M. (2018). Using a transdisciplinary framework to examine mathematics classroom talk taking place in and through a second language. ZDM - Mathematics Education, 50(6), 1013–1027. https://doi.org/10.1007/s11858-018-0952-2
Schleppegrell, M. (2014). Purposeful grammar. For the Learning of Mathematics, 34(2), 44–45.
Sherin, M. G. (2002). A balancing act: Developing a discourse community in a mathematics classroom. Journal of Mathematics Teacher Education, 5, 205–233. https://doi.org/10.1023/A:1020134209073
Sztajn, P., Borko, H., & Smith, T. (2017). Research on mathematics professional development. In J. Cai (Ed.), Compendium for research in mathematics education (pp. 793–823). NCTM.
Turner, E., McDuffie, A. R., Sugimoto, A., Aguirre, J., Bartell, T. G., Drake, C., Foote, M., Stoehr, K., & Witters, A. (2019). A study of early career teachers’ practices related to language and language diversity during mathematics instruction. Mathematical Thinking and Learning, 21(1), 1–27. https://doi.org/10.1080/10986065.2019.1564967
van Es, E. A., & Sherin, M. G. (2021). Expanding on prior conceptualizations of teacher noticing. ZDM - Mathematics Education, 53(1), 17–27. https://doi.org/10.1007/s11858-020-01211-4
Vygotsky, L. S. (1978). Mind in society: The development of higher psychological processes. Harvard University Press.
Watson, A., & Mason, J. (2006). Seeing an exercise as a single mathematical object: Using variation to structure sense-making. Mathematical Thinking and Learning, 8(2), 91–111. https://doi.org/10.1207/s15327833mtl0802_1
Wells, G. (1994). The complementary contributions of Halliday and Vygotsky to a “language-based theory of learning.” Linguistics and Education, 6(1), 41–90. https://doi.org/10.1016/0898-5898(94)90021-3
Wertsch, J. (2007). Mediation. In H. Daniels, M. Cole, & J. Wertsch (Eds.), The Cambridge companion to Vygotsky (pp. 178–192). Cambridge University Press.
Wilkinson, L. C. (2018). Teaching the language of mathematics: What the research tells us teachers need to know and do. The Journal of Mathematical Behavior, 51, 167–174. https://doi.org/10.1016/j.jmathb.2018.05.001
Wilkinson, L. C. (2019). Learning language and mathematics: A perspective from Linguistics and Education. Linguistics and Education, 49, 86–95. https://doi.org/10.1016/j.linged.2018.03.005
Williams, J., & Ryan, J. (2020). On the compatibility of dialogism and dialectics: The case of mathematics education and professional development. Mind, Culture, and Activity, 27(1), 70–85. https://doi.org/10.1080/10749039.2019.1686026
Zahner, W., Calleros, E. D., & Pelaez, K. (2021). Designing learning environments to promote academic literacy in mathematics in multilingual secondary mathematics classrooms. ZDM - Mathematics Education, 53(2), 359–373. https://doi.org/10.1007/s11858-021-01239-0
Funding
Open Access Funding provided by Universitat Autonoma de Barcelona. This collaboration work was supported by: the PID2019-104964 GB-100 of the Spanish Government; the 2017SGR-101 Grant to the GIPEAM Research Group of the Catalan Government; the South African Research Chairs Initiative of the Department of Science and Technology and the National Research Foundation, Grant no. 71218 at the University of the Witwatersrand; and the School of Education, University of Malawi.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Planas, N., Adler, J. & Mwadzaangati, L. What is mathematics teaching talk for? A response based on three sites of practice in mathematics education. ZDM Mathematics Education 55, 521–534 (2023). https://doi.org/10.1007/s11858-022-01452-5
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11858-022-01452-5