1 Introduction

In recent decades, there has been steep growth in research on motivation interventions in educational psychology. These interventions target specific psychological processes that are important sources of motivation and can have surprisingly strong and long-lasting effects on students’ motivation and performance (Lazowski & Hulleman, 2016; Yeager & Walton, 2011). One particular type of motivation intervention that has aroused great interest consists of relevance interventions, which help students see the relevance of what they are learning in school for their current and future lives (Hulleman & Harackiewicz, 2021).

However, motivation interventions are not implemented in a vacuum but in a particular instructional context that has its own motivational affordances or constraints. For instance, teachers might already support students’ perceptions of relevance to different degrees (Parrisius et al., 2020). Recently, Walton and Yeager (2020) argued that psychological interventions can work only in contexts that afford the way of thinking that is offered by the intervention—like a seed that can grow only in fertile soil. Moreover, a change in context might sometimes be necessary to yield positive effects (Walton & Yeager, 2020). When interventions are implemented in the classroom context and teachers are exposed to the intervention materials and the underlying theory, this might actually change the context through affecting teachers’ teaching beliefs and practices. Specifically, relevance interventions—though aimed at the students—might affect the teachers’ efforts to support students’ perceived relevance. Students might also interpret the context differently after participating in the intervention, regardless of actual changes in the teachers’ behavior. Such changes in students’ perceptions of their teacher might ultimately facilitate an intervention’s effects on students’ motivation.

In this study, we examined the interplay between a relevance intervention implemented in mathematics classrooms and the motivational teaching practices applied before and after the intervention in regular classes. To this end, we used data from a cluster-randomized trial with 79 mathematics classes that tested the effectiveness of a 90-min relevance intervention, which was implemented by the regular mathematics teacher or a master’s student after training (Gaspard et al., 2021). Specifically, we investigated whether perceived relevance support before and after the intervention moderated the effects of the intervention on students’ utility value, whether students’ perceptions of relevance support changed after the intervention, and whether such changes mediated effects of the intervention on students’ utility value.

1.1 Motivation interventions as a means to foster students’ motivation

Motivation interventions have received much attention in recent years. One type of intervention that has been implemented successfully in mathematics classrooms consists of relevance interventions. Relevance interventions are often grounded in Eccles et al.’s expectancy-value theory (Eccles et al., 1983), which has recently been renamed as situated expectancy-value theory (SEVT) to emphasize the situative nature of motivation (Eccles & Wigfield, 2020). SEVT posits that the most proximal predictors of students’ academic choices are their expectancies of how well they will do on specific tasks and the value they ascribe to these tasks. Eccles et al. (1983) distinguished different components that positively influence students’ subjective valuing of a given task, including its intrinsic value (enjoyment of the task), attainment value (personal importance of doing well on the task), and utility value (perceived usefulness of the task for achieving one’s goals). A large body of research has supported the basic assumptions of SEVT, showing that students’ expectancies and values in a particular domain (e.g., mathematics) are important predictors of their engagement, achievement, and academic choices in this domain (e.g., Marsh et al., 2005; Watt et al., 2012).

Intervention research drawing on SEVT has focused on utility value because it is assumed to be to be the most malleable value component (Gaspard et al., 2015a; Hulleman et al., 2010). Compared with attainment and intrinsic value, utility value is more extrinsic in nature (Eccles & Wigfield, 2020) and seems to be more easily influenced from the outside. By fostering perceived utility value, these interventions should also enhance students’ engagement and interest in the domain and, thus, ultimately lead to higher performance (Hulleman et al., 2010). Indeed, interventions targeting utility value have been shown to positively affect intrinsic and attainment value, interest, and achievement (Brisson et al., 2017; Gaspard et al., 2015a; Hulleman et al., 2010). Even though these interventions mainly target utility value, we use the term relevance intervention here to denote that they rely on mechanisms that include not only utility but also target relevance as “a personally meaningful connection to the individual” (Priniski et al., 2018, p. 12) more broadly and can lead to effects on motivational outcomes beyond utility value (see Hulleman & Harackiewicz, 2021).

The Motivation in Mathematics (MoMa) intervention is a relevance intervention that was developed for ninth-grade mathematics classes. It consists of a 90-min lesson on the relevance of mathematics as a domain, including an instructor-led psychoeducational presentation and writing tasks for individual students. We have conducted two large cluster-randomized trials to test this intervention so far. In MoMa 1, researchers who were involved in developing the intervention implemented it in the classroom. With this first trial, we found positive effects of the intervention versus a waitlist control condition on students’ values (including their utility value), expectancies, teacher-rated effort, and standardized achievement scores (Brisson et al., 2017; Gaspard et al., 2015a). To test its effectiveness under more realistic conditions for scaling up, the regular mathematics teachers or master’s students implemented the intervention in MoMa 2 after training. Both intervention conditions again showed positive effects on utility value compared with a waitlist control condition until 3 months after the intervention (d = 0.09–0.18; Gaspard et al., 2021). However, these effects were somewhat smaller compared with MoMa 1 and did not extend to all of the outcomes for which positive effects were observed in the first trial. Only small differences in the effectiveness of the intervention were observed between the teachers and master’s students, with the effects of the master’s student condition extending to some more outcomes, but no differences between the two intervention conditions were found in the effects on utility value. Although teachers and master’s students both showed a high level of implementation fidelity as indicated by the adherence rated through observers, master’s students showed an even higher level of adherence.

1.2 Motivational teaching practices in regular mathematics classes

Teachers also apply a variety of teaching practices to foster their students’ motivation in regular mathematics classes. Making what students learn in class relevant to their lives, in particular, has been discussed as a strategy for fostering students’ motivation in several theoretical frameworks in educational psychology and in mathematics education. According to self-determination theory, providing meaningful rationales and thus speaking to the relevance of a task is one possible way to support students’ need for autonomy (Su & Reeve, 2011). Indeed, research has shown that teachers’ general level of relevance support and their lesson-specific provision of relevance support are linked with different components of students’ motivation, including their utility value (Flunger et al., 2022; Parrisius et al., 2020, 2022).

In mathematics didactics, making mathematics useful has been discussed among the concepts of realistic mathematics education (van den Heuvel-Panhuizen & Drijvers, 2014) and mathematical modeling (Blum & Niss, 1991). Although increasing students’ motivation is often mentioned as one goal of these instructional approaches, they are also aimed at increasing students’ understanding and mathematical competences (Blum & Niss, 1991; Freudenthal, 1968). Indeed, a qualitative study by Pierce and Stacey (2006) revealed that teachers place high priority on students’ attitudes and therefore use real-world problems to foster students’ engagement. However, they also noted that although this strategy can make learning more enjoyable for students, it may be at the cost of more substantive learning goals. Moreover, whereas modeling problems are often used to increase student motivation, Krawitz and Schukajlow (2018) showed that students actually report lower self-efficacy and task value for modeling problems compared with other types of mathematical problems (see also Schukajlow et al., 2012). Furthermore, Rellensmann and Schukajlow (2017) found that pre-service teachers overestimate students’ interest in solving real-world problems. However, Schukajlow et al. (2012) showed that students’ self-efficacy and interest can be increased when students are taught using modeling problems for a while, particularly if student-centered teaching methods are applied.

1.3 Seed-and-soil hypothesis: interactions between motivation interventions and the motivational affordances of the broader educational context

The effects of motivation interventions on students’ academic outcomes have been found to vary (Lazowski & Hulleman, 2016; Rosenzweig & Wigfield, 2016). These interventions are assumed to trigger recursive processes in students as they engage in a particular educational context, which can then lead to long-term effects of the interventions (Harackiewicz & Priniski, 2018; Yeager & Walton, 2011). However, as detailed above, educational contexts have their own motivational affordances. Therefore, motivation interventions are viewed as context-dependent (Harackiewicz & Priniski, 2018; Yeager & Walton, 2011). Recently, Walton and Yeager (2020) proposed that such interventions work only in contexts that afford the way of thinking offered by the intervention—like a seed that grows only in fertile soil. Alternatively, it might also be plausible to expect that interventions are not needed in contexts in which students’ motivation is already supported (Rosenzweig & Wigfield, 2016) and thus would be more effective in contexts in which students’ motivation is not fostered (“parched soil”). However, the recursive changes in students’ beliefs that should be triggered through educational-psychological interventions might not be possible if the educational context does not provide opportunities for the relevant changes, which is why Walton and Yeager (2020) assume that a supportive context is needed. Although the seed-and-soil metaphor clearly has its limitations (including the implied passivity of the context), it has received much attention in intervention research and can be fruitful in understanding heterogeneity of intervention effects. Current research points towards positive interactions in line with the seed-and-soil hypothesis. For example, Yeager et al. provided support for the moderation of the effects of a growth mindset intervention through the broader school context as well as teachers’ beliefs in a large study. First, they found that the intervention worked better in schools with peer norms that supported the intervention message (i.e., support for challenge seeking; Yeager et al., 2019). Second, the intervention was also shown to work only in mathematics classrooms in which teachers endorsed a growth mindset and were therefore supportive of the intervention’s message (Yeager et al., 2022). Another study found that a purpose intervention that taught the lay theory that school is a place to develop general skills that can help oneself and others later in life increased students’ performance only when students also received a purpose-affording note from a teacher (Reeves et al., 2021).

Similarly, relevance interventions might work only in classes where the students perceive that the teacher supports their perceptions of relevance of the materials, and thus cares about their reasons for engaging with them. By contrast, if teachers undermine the intervention’s message that mathematics is useful outside of school (e.g., by explicitly stating the contrary or by not caring about students’ concerns in this regard), this might reduce the possible effect that a one-time intervention in the classroom can have on students’ beliefs in the long term. Using the data from the MoMa 1 study described above, Parrisius et al. (2021) examined whether the effects of the intervention were moderated by several motivational teaching practices (i.e., daily life examples, learning support, enthusiastic teaching). They found only a few significant moderation effects and a mixed pattern of results in terms of the direction of effects. It is not clear whether the motivational teaching practices investigated in their study matched the intervention message sufficiently to investigate the seed-and-soil hypothesis. However, before relevance interventions are implemented at scale, it is important to know in which educational contexts they work.

Furthermore, it may be necessary to complement student-targeted interventions with changes in the educational context (Walton & Yeager, 2020). Although relevance interventions are targeted at students, it is possible that teachers also change their beliefs and practices and try to support students’ perceptions of relevance more after learning about the usefulness of such an approach, thus also leading to a change in the context. Prior research has shown that teachers can successfully apply autonomy-supportive practices (e.g., providing rationales) after brief training in a specific physics teaching unit (Flunger et al., 2019). Furthermore, teachers can be trained to endorse autonomy-supportive practices more strongly and to enact these practices in their regular classes through a more extensive program that focuses on their teaching beliefs and practices more generally (Reeve & Cheon, 2021). However, prior research has not investigated whether teachers may also change their teaching practices after a one-time intervention in their classroom, such as the MoMa intervention. It is plausible that teachers might relate material back to the intervention in subsequent lessons and try to foster students’ perceptions of relevance during their teaching more generally after being exposed to exemplary methods for applying this strategy through the intervention materials. This seems particularly likely when the teachers get to deliver the intervention themselves and to participate in relevant training. Moreover, a one-time relevance intervention delivered by the teacher might already lead the students more strongly to see that the teacher cares about students’ perceptions of the relevance of the learning materials and cares to make connections with their lives. Relatedly, a values-affirmation intervention, in which students are asked to write about their broader personal values, has been found to lead students to perceive their teacher as being more interested in their out-of-school lives and as providing more care and support when the same intervention was provided by their teacher versus a researcher (Smith et al., 2021).

1.4 The present study

In this study, we wanted to examine the interplay between a one-time relevance intervention implemented in mathematics classrooms (provided by either the regular teacher or a master’s student) and students’ perceptions of the relevance support provided by their teacher in their regular classes before and after the intervention. We used both lesson-specific and general measures of relevance support to enable us to investigate the immediate changes in students’ perceptions across the lessons following the intervention as well as changes in students’ more general perceptions. More specifically, we asked the following research questions:

  1. 1.

    Do the effects of a one-time relevance intervention vary between mathematics classes in which students perceive different levels of relevance support? To be able to understand interactions with the context better, we considered whether the teacher was perceived to support relevance already before the intervention (thus providing a ‘fertile soil’ for the intervention seed) as well as after the intervention (thus carrying forward the message planted through the intervention). We also tested whether such interactions depended on whether the intervention was delivered through the teacher or an external person.

  2. 2.

    Are students’ perceptions of general and lesson-specific relevance support in mathematics class affected by a one-time relevance intervention, and if so, do these perceptions mediate the effects of the intervention on utility value? We expected such changes in perceived relevance support particularly if the intervention was delivered through the teacher.

2 Method

2.1 Sample and procedure

The data stemmed from the MoMa 2 study, which was conducted within ninth-grade classes in academic track schools in the German state of Baden-Württemberg from October 2017 to March 2018 (for more information about the study design, see Gaspard et al., 2021). The Ministry of Education and Cultural Affairs in Baden-Württemberg approved the study and the collection of the data. The Ethics Committee for Psychological Research at the University of Tübingen confirmed that the procedures were in line with ethical standards of research with human subjects.

A total of 70 teachers (44.2% women; age M = 38.7, SD = 9.8; years of teaching experience M = 10.4, SD = 8.5) from 28 schools participated in the study with their 78 classes (one to five classes per school). In one of the schools, one of the participating classes, which was usually comprised of the same group of students in each subject, was divided into two learning groups for mathematics that were taught by different teachers. We treated these two learning groups as separate classes in our analyses because of our focus on the teachers’ relevance support, resulting in a sample of 79 classes. Within each school, participating teachers and their classes were randomly assigned to one of two intervention conditions (intervention delivered by the mathematics teacher or a master’s student) or to a waitlist control condition, in which the intervention was implemented after the last wave of data collection.

Students’ participation was voluntary and nonincentivized, and parents and students had to provide written consent. Overall, 1744 students participated in the study (88.7% participation rate). Students’ mean age was 14.63 years (SD = 0.48) at the beginning of the study. In line with the typical composition of academic track schools, 31.7% of the students had a migration background (i.e., the student or one of their parents was not born in Germany), 72.9% had at least one parent who had obtained a general university entrance qualification, and the average socioeconomic status was relatively high (highest international socio-economic index of occupational status [HISEI] was M = 64.7 on a scale from 16 to 90).

The study consisted of several waves of data collection. Students were administered questionnaires by trained research assistants before the intervention (pretest = T1), an average of 4 weeks after the intervention (posttest = T2), and an average of 3 months after the intervention (follow-up = T3). Additionally, students’ lesson-specific perceptions were assessed during the five mathematics lessons following the intervention. These brief repeated questionnaires were administered by the teachers at the end of each lesson. In one of the classes, the allocation of individual questionnaires was not implemented correctly because the teacher failed to hand the questionnaires out to the students as indicated by a post-it note on the questionnaire, and this incorrect allocation could not be resolved later. Thus, the data from this class are missing for the lesson-specific questionnaires.

2.2 MoMa relevance intervention in the classroom

The intervention was a 90-min lesson on the relevance of mathematics, which consisted of an instructor-led psychoeducational presentation for the whole class (~ 45 min) and a relevance-inducing task that the students worked on individually (~ 40 min; for more information, see Gaspard et al., 2021). The presentation included various examples of the utility of mathematics for future education, career opportunities in different fields, and leisure time activities. In the individual task, students were asked to read and evaluate interview quotations of young adults describing situations in which mathematics was useful to them. Although some of the examples referred to specific content, the intervention as a whole was targeted to the relevance of mathematics as a broader domain.

The master’s students and teachers who implemented the intervention in the classroom received all intervention materials from the research team and these materials did not differ between conditions (for more information about the training in both conditions, see Gaspard et al., 2021).

A total of six master’s students (five women and one man; age M = 24.7, SD = 1.5) delivered the intervention in the master’s student condition (four to five classes per student). They were trained for this purpose as part of a two-semester class on motivation interventions in the master’s program Education Sciences and Psychology at the University of Tübingen.

The teachers (n = 24; 45.8% women; age M = 40.2, SD = 9.8; years of teaching experience M = 11.8, SD = 8.9) assigned to the teacher condition were asked to participate in a 3-h workshop in small groups to prepare for the intervention implementation. One teacher in this condition declined to participate in the workshop and thus did not deliver the intervention. We followed the intention-to-treat approach in our analyses and included this class in the teacher condition so that the random assignment was kept intact. In the workshops, the teachers were provided with brief information about the theoretical background of the intervention, the importance of conducting randomized experiments, and the results of the MoMa 1 trial. The teachers were then walked through the intervention, followed by a discussion about potential challenges when delivering the intervention in the classroom.

Two trained observers attended each intervention and rated the degree of implementation fidelity. Overall, the intervention was implemented as planned in both intervention conditions, with the observers noting only very few severe deviations from the script. All predefined intervention phases were implemented in all classes. Moreover, adherence was rated to be high in both conditions (M = 7.29 and 9.05 in the teacher and master’s student conditions, respectively, on a scale from 1 to 10).

2.3 Instruments

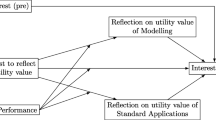
All items were rated on a 4-point Likert scale ranging from 1 (completely disagree) to 4 (completely agree). The mean scores for the respective scales were used in the analyses. An overview of the instruments is shown in Fig. 1.

Fig. 1
figure 1

Overview of the measurement time points and instruments of the study

Full size image

2.3.1 Utility value

Mathematics utility value was the primary outcome of the intervention and was assessed at T1, T2, and T3. For the purpose of this study, we slightly adapted a scale developed by Gaspard et al. (2015b) and further improved by Gaspard et al. (2017). A total of 12 items tapping general utility (e.g., “Math is very useful to me”), utility for job (e.g., “A good knowledge of math will help me in my future job”), utility for daily life (e.g., “Knowing about the subject of math brings me many advantages in my daily life”), and utility for school (e.g., “Being good at math will help me in the remaining school years”) were used. In this study, we were interested in the overall level of utility value and thus combined all items into one mean score (see Gaspard et al., 2021, for effects of the intervention conditions on the different subscales). The scale had high internal consistency at all time points (α = .88–.89).

2.3.2 Relevance support

Students were asked to report their general perceptions of relevance support from their mathematics teacher with five items at T1 and T2 (e.g., “I feel that in general in our math lessons, we are shown how the learning content is personally relevant to us”). These items were partly taken from a scale measuring the provision of meaningful rationales (Flunger et al., 2019) and partly newly developed to refer to the usefulness of mathematics in everyday and future life specifically. The scale’s internal consistency was high at both time points (α = .82 and .87). Furthermore, students were asked to rate their perceived lesson-specific relevance support during the five lessons following the intervention with two items (e.g., “Our teacher explained to us why the topic of today’s lesson can be relevant to us”). Considering the low number of items, the internal consistency of this scale was acceptable across time points (α = .68–.74).

2.3.3 Covariates

Similarly to the analyses performed by Gaspard et al. (2021), we used several covariates assessed at pretest in our analyses. These included students’ gender and previous mathematics grades based on information provided by the schools. Furthermore, we considered students’ self-reported intrinsic value, cost, self-concept, self-efficacy, and effort in mathematics. A brief, standardized mathematics test measured students’ fluency in solving typical mathematical operations (taken from Schmidt et al., 2013). Finally, teachers rated each individual students’ effort in mathematics on two items. More information about these scales can be accessed at https://osf.io/tr8cw/.

2.4 Statistical analyses

We conducted multilevel moderation and mediation analyses in Mplus 8.4 (Muthén & Muthén, 1998–2017) to address our research questions. All analyses considered the student and class levels. Moreover, the analyses including relevance support as assessed during the five lessons following the intervention considered this variation across time points within students at the lowest level, resulting in a three-level model. However, we focused on the student and class levels, which were set up in parallel with the two-level analyses. All continuous variables were standardized before we ran the analyses so that the regression coefficients could be understood as standardized effects with respect to the total variance in the outcome variables (Marsh et al., 2009). Because of the high sampling ratio, manifest aggregation was used for all predictor variables (Marsh et al., 2009). We used grand-mean centering to be able to estimate the cross-level mediation paths (Pituch & Stapleton, 2012). To deal with missing data, we used the full information maximum likelihood method, which considers all available information.

2.4.1 Multilevel moderation analyses

Multilevel regression analyses were conducted to test whether the effects of the intervention on utility value at T2 and T3 were moderated by the teachers’ relevance support before and after the intervention (RQ1). In these analyses, we controlled for utility value at T1 and a set of covariates at the student and class levels to yield more precise estimates of the intervention effects (Raudenbush, 1997). In line with the guidelines proposed by the What Works Clearinghouse (2020), we included those variables for which we found small differences between the experimental conditions before the intervention (0.05 < d < 0.20) in our analyses in addition to the pretest score (i.e., gender, grade, intrinsic value, cost, self-concept, self-efficacy, effort, achievement score, and teacher-rated effort; see Gaspard et al., 2021, for the pretest differences). At the class level, the two intervention conditions were included as dummy variables. Additionally, as predictors, we included students’ relevance support at the student and class levels and two product terms indicating the interactions between relevance support and the two intervention conditions at the class level.

2.4.2 Multilevel mediation analyses

We specified cross-level mediation models (Pituch & Stapleton, 2012) to investigate the links between the intervention implemented at the class level and utility value as a student level outcome as mediated by relevance support measured at the student level (RQ2). In contrast to class-level-only mediation approaches, cross-level mediation models consider both the individual and shared perceptions of students when testing for mediational associations. Such models thereby provide information about (a) whether the class-level predictor has an indirect effect on the student-level outcome through a student-level mediator (cross-level indirect effect) and (b) whether there is an additional indirect effect of the class-level predictor on the outcome over and above the indirect effect via the student-level mediator (unique class-level indirect effect). We thus tested whether the two intervention conditions affected students’ relevance support at the class level and whether there were indirect effects of the two intervention conditions on utility value through relevance support at both the student level (cross-level indirect effect) and the class level (unique class-level indirect effect, see Fig. 2). The total indirect effect was then computed as the sum of the cross-level and the unique class-level indirect effects. We included relevance support and utility value at T1 as predictors on the student and class levels to investigate changes in these variables, and additionally controlled for the set of covariates described above. In line with the moderation analyses, we also included potential interactions between relevance support at pretest and the two intervention conditions.

Fig. 2
figure 2

Cross-level mediation model testing the association between the intervention implemented at the class level and utility value at the student level mediated by relevance support. Note. Agg. = aggregated. Subscripts: 1 = master’s student condition; 2 = teacher condition; S = student-level path; cont = contextual effect. Apostrophe: mediated direct paths between intervention conditions and utility value. The grey cross-level path is not explicitly modeled but is equal to the class-level effect of the intervention conditions on the mediator (see Pituch & Stapleton, 2012)

Full size image

3 Results

3.1 Descriptive statistics

Descriptive statistics for the major study variables are presented in Table 1. Correlations between all study variables can be found at https://osf.io/tr8cw/.

Table 1 Descriptive statistics for all study variables by experimental condition
Full size table

3.2 Moderation analyses for testing relevance support as a moderator of the intervention effects on utility value

We tested a total of six moderation models involving utility value as the outcome assessed at T2 or T3 and relevance support as the moderator assessed at T1, at T2, or during the five lessons after the intervention. The main results are reported in Table 2; full models including all covariates and the variance components at both levels can be found online (https://osf.io/tr8cw/). Across all models, relevance support showed positive effects on utility value at the student level. Because we used grand-mean centering, the effects of relevance support at the class level represent additional effects of the class composition beyond student-level effects. Controlling for students’ individual perceptions of relevance support, there was a tendency for a negative effect of being in a class with high shared perceptions of relevance support.

Table 2 Moderation analyses for testing relevance support at T1, at T2, and during the five lessons after the intervention as moderators of the intervention effects on utility value at T2 and T3
Full size table

Concerning relevance support at T1 as a moderator, we found a significant, positive interaction between the teacher condition and relevance support for utility value at T2 as an outcome. That is, larger effects of the intervention were observed for classes in which the students had already perceived high relevance support before the intervention.

For relevance support at T2 as the moderator, we found a marginally significant positive interaction with the master’s student condition for utility value at T2 and a significant positive interaction with the master’s student condition for utility value at T3. Both interactions can be interpreted to mean that the intervention was more effective in classrooms in which students also generally perceived higher relevance support from their teacher after the intervention. Finally, for relevance support during the five mathematics lessons following the intervention, we again observed a significant positive interaction with the master’s student condition but only at T3.

3.3 Mediation models for testing indirect effects of the intervention on utility value through relevance support

We tested two mediation models, namely, (a) relevance support at T2 as a mediator of intervention effects on utility value at T3 (see Table 3), and (b) relevance support during the five lessons after the intervention as a mediator of intervention effects on utility value at T2 (see Table 4, for the full models with all covariates and variance components see https://osf.io/tr8cw/). With respect to relevance support at T2, we found that—compared with the control condition—the teacher condition had a positive effect on students’ relevance support at T2, which, in turn, positively predicted utility value at T3 at the student level. No further contextual effect of relevance support (i.e., an effect of students’ shared perceptions of relevance support when controlling for their individual perceptions) on utility value was found. These paths resulted in a significant cross-level indirect effect and a marginally significant total indirect effect of the teacher condition. For the master’s student condition, we observed only a marginally significant direct effect of the intervention (vs. the control condition) on students’ utility value but no effects involving relevance support. These mediated paths were not moderated by relevance support at T1.

Table 3 Mediation analyses for testing relevance support at T2 as a mediator of the intervention effects on utility value at T3
Full size table
Table 4 Mediation analyses for testing relevance support during the five lessons after the intervention as a mediator of the intervention effects on utility value at T2
Full size table

For relevance support during the five lessons after the intervention, there were no significant effects of the two intervention conditions on relevance support. However, relevance support during these lessons predicted utility value at T2 at the student level. The model also showed significant effects of both intervention conditions on utility value at T2, which could not be explained by relevance support during the five lessons after the intervention. Thus, no significant indirect effects could be observed.

4 Discussion

In the present study we examined whether the effects of a one-time relevance intervention were moderated by perceived relevance support before and after the intervention and whether the intervention had indirect effects on students’ utility value through their perceived relevance support. Data stemmed from a large cluster-randomized effectiveness trial in which the intervention was implemented by either the regular mathematics teacher or a master’s student. Interactions between the two intervention conditions and relevance support before and after the intervention provided support for the seed-and-soil hypothesis (Walton & Yeager, 2020): Larger intervention effects tended to be found in classes where students perceived stronger relevance support from their teachers during regular classes and, thus, where the teachers afforded the intervention’s message. We also found some support for indirect effects of the relevance intervention on utility value through students’ perceptions of relevance support after the intervention, but only if the intervention was provided by their own teacher, which sheds light on the mechanisms at work in this condition.

4.1 Relevance support as a contextual moderator of intervention effects

We found some evidence for our assumption that intervention effects would be moderated by students’ perceived relevance support in the classroom in line with the seed-and-soil hypothesis (Walton & Yeager, 2020). These effects varied between intervention conditions and the time at which the moderator was measured. In the master’s student condition, interactions were mostly found for relevance support after the intervention, with similar patterns for general perceptions at T2 and lesson-specific perceptions during the lessons following the intervention. When the intervention was delivered by an external person, the intervention was thus more effective if its message was reinforced (and not undermined) by the teacher afterwards. These findings are similar to results of prior research that reported that computerized motivation interventions are effective only when their message is afforded later by the teacher (Reeves et al., 2021). For the teacher condition, we found a significant positive interaction only for perceived relevance support before the intervention. Here, it thus seemed to matter more whether the teacher had already provided a fertile soil before the intervention, which might have resulted in a more authentic delivery of the intervention message through the teacher. In contrast to our study, Parrisius et al. (2021) found only a few moderation effects in the MoMa 1 study, where the intervention was delivered by researchers, which is closer to the master’s student condition in our study. However, the motivational practices considered as moderators in their study might not have been close enough to the intervention message, whereas the moderator considered here (i.e., perceived relevance support) is arguably a direct assessment of the psychological affordance of the intervention message through the instructional context. Moreover, they only considered students’ perceptions of motivational practices prior to the intervention in their study.

In general, all interaction terms found in the current study were positive, in line with the seed-and-soil hypothesis. Under some circumstances, negative interactions indicating that interventions are most effective in contexts in which students’ motivation is not supported already (‘parched soil’) might also be found. However, it seems that a negative development such as a decline in utility value in mathematics during secondary school (Gaspard et al., 2017) can best be prevented through the combination of a targeted intervention and a supportive instructional context. These varying effects across contexts are also important to consider when implementing student-targeted interventions in educational practice. The intervention approach might have to be changed in instructional contexts in which teachers do not successfully support students’ perceptions of relevance during regular lessons. Some educational contexts might be too ‘parched’ to afford positive motivational development and might require other types of interventions focused on changing the context (e.g., targeting teachers’ beliefs and practices).

4.2 Relevance support as an intervention mechanism in the teacher condition

Students in classes in which the intervention was implemented by their teacher reported higher relevance support at posttest, which could partly explain the positive effects of the teacher condition on utility value at follow-up. This result is interesting insofar as similar effects of the two intervention conditions were observed although the master’s students showed a higher adherence to the script when delivering the intervention (Gaspard et al., 2021). It thus seems that teachers achieved the same end through different means. Our findings are similar to those of Smith et al. (2021), who found that students perceived that their teacher provided more care and support when they received a teacher-provided (vs. a researcher-provided) values-affirmation intervention. Two explanations for higher perceived relevance support at posttest are possible. Teachers could have tried to relate the material back to the intervention message in the lessons after the intervention and would thereby have supported students’ perceived relevance to a greater extent. Alternatively, the one-time delivery of the intervention, which was quite different from a regular mathematics lesson, might have already been enough to change students’ perceptions of relevance support from their teacher. The items assessing perceived relevance support at posttest were formulated in a general way, which makes the first explanation more plausible. However, although the regression coefficient for the intervention effect on relevance support during the five lessons that followed the intervention was also positive, it was not statistically significant, so that there was no difference in lesson-specific relevance support between the teacher and the control conditions. This finding instead supports the second explanation. More research is thus needed to examine whether a brief training session and the delivery of a scripted intervention are enough to trigger actual changes in teachers’ teaching beliefs and practices during regular classes following this intervention. Still, our findings speak to the potential power of having teachers deliver motivation interventions in educational practice as this may positively affect students’ perceptions of their teacher. To maximize effects of motivation interventions, it might be necessary not only to target students’ motivation but also to involve teachers in the intervention approach and change their teaching beliefs and practices in ways that support students’ motivation (Reeve & Cheon, 2021). Our study, however, applied a more minimal approach in that teachers participated only in a short workshop focused on delivering a one-time relevance intervention rather than changing their teaching beliefs and practices more generally. When it comes to developing interventions targeted at teachers, it might also be important to consider individual teachers’ beliefs and practices—some might need different intervention techniques than others.

4.3 Limitations

Although we used data from a large cluster-randomized trial in which the intervention was delivered under conditions that were close to educational practice, our study also has several limitations that need to be considered when interpreting its findings. First, our sample was limited to ninth-grade students in the academic track in one region in Germany. Future research therefore needs to examine whether our findings generalize across grade levels, school types, and regions. Second, when interpreting the effects of the intervention, we referred to effects in comparison with the control condition. However, these results are not necessarily aligned with the mean-level trajectory over time within the conditions. In terms of this trajectory, we observed a decline in utility value in the control condition, as has been found in previous research (e.g., Gaspard et al., 2015a). Instead of lifting utility value overall, the intervention thus functioned as a buffer against this negative development. The effects that we found were furthermore small relying on conventional standards, but can be judged as medium to large when using the benchmarks proposed for educational interventions and considering the low cost of the intervention (Kraft, 2020). Third, whereas the study was adequately powered to detect small (and realistic) main effects (δ = 0.20; see Gaspard et al., 2021), the power to detect effects of cluster-level moderators, such as the ones examined in our study, was likely lower (Parrisius et al., 2021; Spybrook et al., 2016). It is therefore unclear whether the effects we found capture all true moderation effects or whether they overestimate the true effects. A replication with more classes is necessary to be able to reliably detect small moderation effects. Fourth, we focused on utility value as the primary outcome of the intervention, but future research should also investigate whether similar interactions can be found for more distal outcomes such as academic choices and achievement. Finally, we considered relevance support only as perceived by the students. Although the students’ perspective is arguably most important for the psychological affordance of the instructional context, this prevented us from coming to a clear conclusion about whether teachers changed their teaching beliefs and practices after the intervention or whether students just perceived them differently. It would be necessary to incorporate teacher and potentially observer ratings to fully answer this question.

5 Conclusions

The present study sheds light on the interactions between a one-time relevance intervention implemented in the classroom and teachers’ continuing instructional practices to support perceived relevance. Our study has two main conclusions. First, if the interventions are delivered by external individuals, they are more beneficial for students’ motivation if the teachers also afford the intervention message afterwards. Second, when teachers deliver the interventions in the classroom, this can promote students’ perceptions of their teachers’ relevance support, which further helps explain effects on students’ valuing of mathematics later in the school year. Our findings thus contribute to knowledge about the conditions in which such interventions work and how such interventions can be implemented more effectively in practice. Future research will need to continue examining motivation interventions in diverse contexts using adequate research designs to be able to test the robustness and generalizability of these findings.