1 Introduction

Mathematics learning in the initial stage of schooling (i.e., primary or elementary school) provides children with the functional numerical skills required throughout adult life and provides the foundation for more advanced learning in secondary education and beyond. In England, for example, where schools follow a prescribed National Curriculum, children learn numerical functions (i.e., addition, subtraction, multiplication, and division), fractions, geometry, and measurement, in the first six years of schooling. Unfortunately, many children struggle to learn these basic mathematics skills. In 2019, 21% of children, aged 11, left primary school in England without meeting the minimum expected standards of learning in mathematics (Department for Education, 2019). The impact of poor numeracy skills in adult life is profound resulting in a greater likelihood of unemployment or low paid work, physical illness, poor mental health, and engaging in criminal activity (Windisch, 2015). For society, the costs of poor numeracy skills in adulthood for lost revenue, increased taxes, and reduced global economic competitiveness are huge; the cost to the United Kingdom economy was estimated in 2014 at £20 billion per year (National Numeracy, 2014).

Accordingly, educational researchers have sought to understand the causes and reasons for poor mathematics learning and achievement. One area of interest has concerned children’s attitudes towards mathematics and mathematics leaning to broadly encompass their beliefs, emotions, motivations, and values (e.g., Goldin et al., 2016). In particular, the fear provoked by mathematics has been identified as a source of avoidance, low or maladaptive motivation, and low achievement (Ramirez et al., 2018). Based on Control-Value Theory (CVT: Pekrun, 2006, 2018), studies have examined how appraisals of control over, and the subjective value ascribed to, learning or learning outcomes, can predict mathematics-related anxiety. Few studies have examined another key proposition of CVT, however, that control-value appraisals and anxiety are related in a reciprocal fashion (e.g., Ahmed et al., 2012). That is, mathematics-related anxiety could also predict control-value appraisals.

Understanding this reciprocal link could assist teachers, parents, and others involved in a child’s learning, to identify key points of intervention; how negative self-reinforcing cycles of control-value appraisals and anxiety, that are damaging to learning, can be prevented or minimised. In the present study we examine how control-value appraisals are reciprocally related to anxiety in the mathematics classroom using a sample of students in their penultimate year of primary education (in England this is Year 5). In addition, we explore relations to a subsequent mathematics test to examine another somewhat understudied element of CVT, the indirect relations from control-value appraisals to subsequent achievement, mediated by anxiety in the mathematics classroom.

1.1 Achievement emotions

Achievement emotions refer to the affective experiences that occur in relation to achievement-related activities or outcomes (Pekrun, 2006). Such emotions are commonly encountered during the course of routine schooling in the classroom, in tests, and when completing homework or self-study (Lichenfeld et al., 2012). A student could, for instance, find a mathematics lesson boring or be anxious about a forthcoming test. The focus of achievement emotions on an activity or outcome enables a distinction from other affective experiences that may also occur in achievement-related settings such as moods which do not typically have a specific referent.

1.2 Anxiety in control value theory

In CVT (Pekrun, 2006, 2018) achievement emotions are categorised along dimensions of valence (pleasant vs. unpleasant emotions), activation (activating vs. deactivating emotions), and object focus (activity- vs. outcome-focused emotions). Anxiety is conceptualised to be an unpleasant, outcome-focused, activating emotion. Achievement-related mathematics anxiety can be experienced in relation to different aforementioned situations (homework, self-study, testing, and classroom learning), and is detrimental to learning, achievement, and wellbeing (e.g., Putwain et al., 2021; Putwain et al., 2021). Furthermore, in these achievement situations, a student may experience momentary instances of anxiety, or have a tendency to become anxious more frequently (Goetz et al., 2013). In the present study we define classroom-related anxiety as being a situation-specific general tendency; that is, a student’s tendency to become anxious when learning mathematics in the classroom.

Classroom-related anxiety conceptually overlaps with that of mathematics anxiety, (Ashcraft, 2002). Mathematics anxiety, however, is not limited to achievement settings and could be experienced in many areas of one’s life (e.g., when managing daily finances). In contrast, classroom-related anxiety is focused on a specific achievement setting and, in keeping with CVT, on learning outcomes in mathematics. We concentrated specifically on classroom-related anxiety partly as this has not been widely studied (in comparison to math or test anxiety, for example; see Putwain et al., 2021), and partly as the sample in the present study was comprised of students aged 9–10 years in their penultimate year of primary schooling. As this age group of students typically experience less self-study, homework, and testing, than older students, we reasoned that of the various achievement settings, classrooms settings were the most applicable to the study of student emotion.

1.3 Control-value antecedents of classroom-related anxiety

Anxiety, along with other discrete emotions, is theorised in CVT to arise from proximal control and value appraisals (Pekrun, 2006, 2018). Control appraisals can be forward-looking in the form of action-control beliefs (or self-efficacy; Bandura, 1997). These are expectations that one will be able to successfully perform the actions required for achievement activities (e.g., the steps required to solve an algebraic equation) and outcomes (e.g., to successfully solve that algebraic equation). Control can also be backward-looking in the form of retrospective attributions over the cause of success or failure (see Graham & Taylor, 2014). Achievement activities and outcomes can be valued to a greater or lesser extent for their intrinsic qualities, such as interest and enjoyment, or for their extrinsic usefulness in contributing to one’s goals. Together, the intrinsic and extrinsic values represent the outcome value (Pekrun, 2006). In order to ensure good coverage of value, we included items corresponding to intrinsic and extrinsic values (the utility of mathematics for one’s goals, and the value of achievement for one’s identity). These were combined into an omnibus measure of outcome value primarily as we did not theorise differences between intrinsic and extrinsic values in their relations with anxiety.

Anxiety in the mathematics classroom has not been widely researched and there are few empirical studies for the control-value appraisals that underlie classroom-related anxiety specifically. We review three notable exceptions next. In a sample of North American elementary school students (aged 8–12 years), Lichtenfeld et al. (2012) found anxiety in the mathematics classroom to negatively correlate with control (measured using competence beliefs as a proxy; rs = − 0.52 and − 0.53 for 2nd and 3rd Grade students respectively) and value (using a single item measuring the perceived importance of mathematics; rs = − 0.29 and − 0.27 for 2nd and 3rd Grade students respectively). In Portuguese secondary school students aged 11–16 years, Peixoto et al. (2016) found negative correlations between anxiety in the mathematics classroom and control (measured using competence beliefs as a proxy; r = − 0.32), and intrinsic value (r = − 0.07). Furthermore, Putwain et al. (2021) found, in a sample of English primary school students (mean age 9 years) that control over, and value (intrinsic, attainment, utility) of, mathematics, were negatively related to class-related anxiety (rs = − 0.17 to − 0.36). The finding that all three facets of value correlated negatively with class-related anxiety partly informed the decision in the present study to use a combined measure of outcome value.

In addition, two related studies used an aggregate of class, learning, and test-related anxiety, in mathematics. Frenzel et al. (2007) showed in a sample of German secondary school students (with a mean age of 11 years) that anxiety was negatively related to control (measured using competence beliefs as a proxy; β = − 0.39) and the domain value of mathematics (β = − 0.15), but positively related to achievement value (β = 0.22). Luo et al. (2016) found, in a sample of Singaoporian secondary school students (mean age 13 years), that mathematics self-efficacy (a proxy for control; β = − 0.57) was negatively, and utility value (a form of extrinsic value that focuses on the usefulness of mathematics; β = 0.34) was positively, related to anxiety.

The aforementioned studies show that lower appraisals of control are consistently related to higher anxiety in the mathematics classroom. Relations with value, however, are equivocal. This may be partly an artefact of the different approaches to measuring perceived value and considering anxiety in different settings. Furthermore, the aforementioned studies used cross-sectional designs that limit inferences of directionality. Relations between control-value appraisals and anxiety in the mathematics classroom could have reflected the control-value appraisals as following, as much as preceding, anxiety.

1.4 Reciprocal relations between control-value appraisals and anxiety

In CVT a feedback loop is proposed between control-value appraisals and achievement-related anxiety (Forsblom et al., 2022; Pekrun, 2006, 2018). Not only will control-value appraisals influence subsequent classroom-related anxiety but anxiety will influence subsequent control-value appraisals. That is, relations between control-value appraisals and anxiety are conceptualised as being reciprocal. Higher classroom-related anxiety could emphasise the anticipation of failure to the student and therefore reinforce the belief that control over success was uncertain. We might therefore expect anxiety to be negatively related to subsequent control appraisals.

In addition, it may be difficult to value an achievement outcome that causes anxiety. Mathematics-related anxiety is aversive and often associated with the behavioural and cognitive avoidance of mathematical tasks and activities (e.g., Haase et al., 2019; Ramirez et al., 2018). From an emotional regulation perspective, these avoidance strategies are cognitive and behavioural methods of down-regulating anxiety, albeit ones that are damaging to learning and achievement (Harley et al., 2019). The distance created by the use of avoidance strategies, however, can reduce value. Thus, persons who experience high levels of classroom-related anxiety come to lower the extent to which mathematics activities or achievement is valued as a form of self-protection against anxiety (also see Loose et al., 2012). Higher anxiety in the mathematics classroom, therefore, would be negatively related to subsequent value appraisals.

At present there is limited evidence for how anxiety relates to subsequent control-value appraisals or for reciprocal relations between control-value appraisals and anxiety. Reciprocal relations between academic self-concept (a proxy for control) and an achievement-related anxiety for mathematics have been shown in Dutch secondary school students (Ahmed et al., 2012; βs = − 0.06 and − 0.07 from anxiety to academic self-concept; βs = − 0.15 and − 0.14 from academic self-concept to anxiety) and Finnish students transitioning from primary to secondary school (Clem et al., 2021; βs = − 0.08 to − 0.10 from anxiety to academic self-concept; βs = − 0.10 to − 0.13 from academic self-concept to anxiety). In a related study, also using an aggregated measure of class-, homework-, and test-related anxiety for mathematics, Sutter-Brandenberger et al. (2018) examined relations between anxiety and intrinsic motivation (similar to intrinsic value) and identified motivation (similar to extrinsic valueFootnote 1) over three waves in a sample of Swiss secondary school students. From the first to second waves of data collection, anxiety was negatively related to subsequent intrinsic (β = − 0.11) and identified motivation (β = − 0.18), but intrinsic and extrinsic motivation was unrelated to subsequent anxiety (βs = − 0.03). From the second to third waves of data collection there were no statistically significant relations between anxiety and intrinsic or identified motivation (βs = 0.00 to − 0.13).

There is insufficient empirical evidence, on the basis of existing empirical studies, to definitely judge whether relations from control-value appraisals to subsequent anxiety are stronger than those from anxiety to subsequent control-value appraisals. Negative self-knowledge beliefs show a pervasive and ubiquitous role in higher anxiety (Cassady, 2010) whereas anxiety is just one of several influences on control beliefs (Bandura, 1997; Graham & Taylor, 2014). All things being equal, therefore, we would expect relations from control appraisals to subsequent anxiety to be stronger. The parallel question for value appraisals will likely depend on the type of value in question. Where the value of positive outcomes is measured (as in the present study) the need to lower value in order to regulate anxiety may outweigh the outcome value of mathematics; hence relations from anxiety to subsequent value appraisals would the stronger. If the negative values were measured (fear of failure or effort cost) relations may be more equally balanced.

1.5 Class-related anxiety and achievement in mathematics

There is a well-established negative relation between achievement and anxiety in mathematics (e.g., Hembree, 1990; for other emotions see Camacho-Morles et al., 2021) that is often attributed to anxiety interfering with working memory function and capacity (Eysenck et al., 2007; Ramirez et al., 2013) or a confounding variable such as low mathematics competence (Maloney, 2016). The evidence linking achievement anxiety in the mathematics classroom, specifically, is more limited. Lichtenfeld et al. (2012) showed that mathematics class-related anxiety was negatively related to mathematics test scores (rs = − 0.37 and − 0.29 for 2nd and 3rd Grade students respectively) and teacher-assessed mathematics grades (rs = − 0.31 and − 0.32 for 2nd and 3rd Grade students respectively). Raccanello et al. (2019) showed showed that class-related anxiety was negatively related to teacher-assessed mathematics grades (r = − 0.28) in a sample of Italian primary school students (mean age 7 years). Putwain et al. (2021) found classroom-related anxiety to negatively correlate (r = − 0.31) with test performance in a sample of English primary school students (mean age 9 years).

As with other forms of anxiety, anxiety in the mathematics classroom also would appear to correlate negatively with achievement. In the present study we add to this nascent body of work and examine relations between class-related anxiety and achievement on a low-stakes class test. By virtue of measuring control-value appraisals and anxiety simultaneously over two waves we are also able to examine relations between T1 control-value antecedents and T3 mathematics achievement mediated by T2 anxiety. While several studies have shown how academic self-concept (which underpins control beliefs) and value predict mathematics achievement (Guo et al., 2016; Trautwein et al., 2012), the role of emotions in mediating relations between control-value and achievement has not been widely studied.

In the aforementioned study by Luo et al. (2016) indirect relations were shown between control-value appraisals and homework effort/distraction, mediated by anxiety. In addition, Putwain et al. (2021) showed that control-value appraisals were positively related to mathematics achievement, mediated by lower class-related anxiety. Control-value appraisals and anxiety, however, were measured concurrently in Putwain et al. (2021) thereby limiting understanding of directionality in control-value and anxiety relations. In the present study, we address this limitation by including a temporal gap between the measurement of control-value appraisals and subsequent class-related anxiety. There is theoretical and practical virtue in establishing if relations from control-value appraisals to achievement are mediated by anxiety. Theoretically, this helps to understand whether anxiety (and other achievement emotions) is an outcome of personal judgements, such as control-value appraisals, that is incidental to achievement, or whether emotions are more centrally implicated. Practically, interventions to strengthen control-value appraisals may show downstream benefits in both reducing classroom-related anxiety and boosting subsequent achievement.

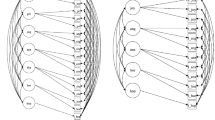
Based on CVT theorising, we would anticipate that all things being equal, T1 control appraisals would show a positive indirect relation, and T1 value appraisals would show a negative indirect relation, with T3 mathematics achievement mediated by T2 anxiety. The inclusion of un-lagged, cross-lagged, and auto-lagged, paths in the fully-forward analytic model (see Fig. 1) makes this a particularly robust test of mediation and, somewhat unusually in the canon of CVT studies, models anxiety as a predictor of achievement alongside control-value antecedents.

Fig. 1
figure 1

The hypothesized model of reciprocal relations between anxiety, control, and value, and relations with subsequent mathematics achievement. Paths for gender and age are not depicted

Full size image

1.6 Aims of the present study

The aims of the present study are twofold. First, was to examine reciprocal relations between control-value appraisals and class-related anxiety over two waves of measurement. Previous studies have used cross-sectional designs to examine relations between control-value appraisals and classroom-related anxiety (e.g., Lichtenfeld et al., 2012; Peixoto et al., 2016). The present study, addresses this limitation, and makes a novel contribution to the literature, by testing reciprocal relations between control-value appraisals and anxiety in the mathematics classroom over two waves of measurement. Second, was to examine whether T2 class-related anxiety mediated relations between T1 control-value antecedents and T3 mathematics achievement. As female students typically report higher mathematics anxiety, lower mathematics competence beliefs (and expectations for success), and mathematics related anxiety increases over the primary years (e.g., Geary et al., 2019; Goetz et al., 2013) we included gender and age as covariates in all analyses. The following hypotheses were tested:

Hypothesis 1

T1 control will be negatively, and T1 value will be positively, related to T2 anxiety in the mathematics classroom.

Hypothesis 2

T1 anxiety in the mathematics classroom will be negatively related to T2 control and T2 value.

Hypothesis 3

T1 control will be positively and indirectly related to T3 mathematics achievement mediated by class-related anxiety.

Hypothesis 4

T1 value will be negatively and indirectly related to T3 mathematics achievement mediated by class-related anxiety.

2 Methods

2.1 Participants and procedure

The participants in this study were 1242 year 5 students from 24 English primary schools (45 different classes). There were 633 males and 609 females with a mean age of 9.3 years (SD = 0.49). Year 5 is the penultimate year of primary schooling in England. The ethnic heritage of participants was as follows: Asian = 246 (19.8%), Black = 58 (4.7%), white = 876 (70.5), Chinese = 11 (0.9%), other = 22 (1.8%), and mixed background = 29 (2.3%).

Data were collected over three waves in students’ classrooms by their regular teacher following a script in the 2018–2019 school year. The project was approved by an institutional research ethics committee (19/EHC/001) and written consent was provided by the Head Teachers of participating schools and students’ parents or carers. In addition, students provided verbal assent at each wave of data collection. Self-reported anxiety, Control, and Value were collected at T1 and T2 with a seven-month interval. These data were collected using an online survey tool that prompted participants if they had missed an item in order to reduce missing data. Mathematics achievement was collected at T3, from a class test (also hosted online) one week after T2 data were collected. Anonymous data were linked by a student generated code.

In common with other longitudinal studies there was attrition at T2 (n = 863) and T3 (n = 734) arising from students being absent from school, having moved school, or through choosing not to participate. An omnibus Little’s test showed that for missing completely at random (MCAR) could not be assumed. A series of follow-up t tests showed that participants missing at T3 were more likely to report lower T1 control, t(1240) = 3.07, p = 0.001, lower T1 value, t(1240) = 3.01, p = 0.001, lower T2 control, t(881) = 3.10, p < 0.001, lower T2 value, t(881) = 3.42, p < 0.001, and higher T2 anxiety: t(855) = − 1.78, p = 0.04. Data can be treated as missing at random (MAR), and handled using full-information-maximum-likelihood (FIML) estimation, when the cause of missingness can be identified and included in subsequent models (Nicholson et al., 2017).

2.2 Analytic plan

A latent variable modelling approach was adopted for analyses using the Mplus v.8 software (Muthén & Muthén, 2017). First, latent bivariate correlations were estimated using confirmatory factor analysis (CFA). Second, longitudinal measurement invariance was checked using CFA. Third, hypothesised relations between control, value, anxiety, and mathematics achievement, were estimated using a structural equation model (SEM). Latent models were assessed using the following goodness-of-fit statistics: root mean error of approximation (RMSEA), standardized root mean residual (SRMR), confirmatory fit index (CFI), and Tucker-Lewis index (TLI). Good fitting models have RMSEA ≈ 0.05, SRMR ≈ 0.06, and CFI and TLI ≈ 0.95 (Hu & Bentler, 1999). Flexibility in the interpretation of these cut-points is encouraged when applied to complex models that use naturalistic data (Heene et al., 2011). All latent models were estimated using maximum-likelihood with robust standard errors (MLR), to account for the small deviations from normal distribution of data, and the ‘type = complex’ command to account for the clustering of data within schools.

2.3 Measures

2.3.1 Anxiety

Anxiety was measured using the four-item class-related anxiety scale from the Achievement Emotions Questionnaire-Elementary School (Lichtenfeld et al., 2012). Item wording was modified to fit with the English context (e.g., ‘maths’ and ‘lessons’ rather than ‘math’ and ‘class’). Participants responded to items (e.g., “When I think about maths lessons, I get nervous”) on a five-point scale (1 = strongly disagree, 3 = neither agree nor disagree, and 5 = strongly agree), thus a higher score represented higher anxiety. This scale has shown excellent psychometric properties in previous studies (Lichtenfeld et al., 2012; Raccanello et al., 2019) and in the present study the internal consistency was excellent (see Table 1).

Table 1 Descriptive statistics and item factor loadings
Full size table

2.3.2 Control

Control was measured using four items from the Self-Description Questionnaire II (SDQII: Marsh, 1990) modified partly to reflect the parlance of English education (e.g., referring to mathematics as ‘maths’) and to ensure that items represented control over one’s learning (e.g., “Work in maths is easy for me”). Participants responded to items on a five-point scale (1 = strongly disagree, 3 = neither agree nor disagree, and 5 = strongly agree) such that a higher score indicates greater control. The original SDQII, as well as Putwain et al.’s (2018) adapted control scale, have shown excellent construct validity and internal consistency (e.g., Putwain et al., 2018). Internal consistency was high in the present study at T1 and T2 (see Table 1).

2.3.3 Value

Value was measured using a twelve item scale adapted from Eccles et al.’s (2005) Michigan Study of Adolescent Life Transitions scales (see Putwain et al., 2018). Four items each corresponded to intrinsic value (e.g., “I find doing maths interesting”), attainment value (e.g., “I want to get good marks in maths”), and utility value (e.g., “Maths can help with things in everyday life”). As the focus in the present study was on outcome value, rather than the specific differences between the different aspects of value, these were combined into a single scale. Participants responded to items on a five-point scale (1 = strongly disagree, 3 = neither agree nor disagree, and 5 = strongly agree). Previous research has evidenced strong internal consistency and construct validity for these scales (e.g., Putwain et al., 2016, 2018) and in the present study the internal consistency was also good at T1 and T2 (see Table 1).

2.4 Mathematics achievement

Mathematics achievement was measured using a 40-min classroom test based on the curriculum studied in Years 4 and 5 of primary school (measurement, geometry, fractions and statistics, ratio and proportion, and simple algebra; see Department for Education, 2019). The test comprised of eighteen questions (e.g., “A book has 276 pages. Amina has read 1/3 of the book. How many pages are left for Amina to read?”) worth 20 marks in total. Marks were awarded for a correct answer only and no marks were provided for correct reasoning accompanied with an incorrect answer. Test items were randomly selected from a pool created from questions taken from the 2016, 2017, and 2018, Key Stage 2 National Curriculum Tests (NCTs) for mathematical reasoning. NCTs are taken at the end of Primary schooling in England (Year 6). Accordingly, items corresponding to curriculum content covered in Year 6 were disregarded. Two primary mathematics learning specialists who were unconnected to this study confirmed the appropriateness of items for students in Year 5. In the present study, internal reliability was also high (see Table 1).

3 Results

3.1 Descriptive statistics and latent bivariate correlations

Descriptive statistics are shown in Table 1. T1 and T2 anxiety scores were relatively low and T1 and T2 value and control relatively high. T2 value also showed a negatively skewed and leptokurtic distribution. The internal consistency of all measures (established via Cronbach’s α and McDonalds ω) were all strong (≥ 0.78) and factor loading (from the measurement model described next) were good (λ ≥ 0.4). The proportion of variance occurring between schools was lower for T1 and T2 anxiety, value and control (ρIs ≤ 0.06) and larger for T3 mathematics test performance (ρI = 0.15).

A measurement model was built that included four indicators each for T1 and T2 anxiety and control and twelve indicators for T1 and T2 value, T3 mathematics test performance as a single item latent variable. Residual variance was allowed to correlate for the value indicators referring to intrinsic, achievement, or utility value. This measurement model was examined using confirmatory factor analysis and showed a reasonable fit to the data, χ2(772) = 1866.18, p < 0.001, RMSEA = 0.031, SRMR = 0.049, CFI = 0.938, and TLI = 0.928, so we proceeded to inspect correlation coefficients (see Table 2). At T1 and T2, control and value appraisals were negatively correlated with anxiety. At T1 and T2, control and value were positively correlated. Mathematics achievement was positively correlated with T1 and T2 control and value, and negatively correlated with T1 and T2 anxiety. Female students reported higher anxiety, and lower control and value at, T1 and T2. Age positively correlated with mathematics achievement.

Table 2 Correlations between the study variables
Full size table

3.2 Longitudinal measurement invariance and structural equation modeling

A precondition of longitudinal structural equation modeling (SEM) is that construct indicators show invariance of factor intercepts on the different occasions they were measured (Widaman et al., 2010). First a model was that examined with an identical factor structure at T1 and T2 (configural invariance). Second, item factor loadings were constrained to be identical at T1 and T2 (metric invariance). Third, item factor intercepts were constrained to be identical at T1 and T2 (scalar invariance). Fourth, item residual variances were constrained to be identical at T1 and T2 (residual invariance). Longitudinal invariance is indicated by no substantive deterioration of model fit as successive constraints are applied (ΔRMSEA < 0.15, and ΔCFI; TLT of < 0.1; Chen, 2007). Invariance tests are reported in Table 3. Anxiety, control, and value, showed residual longitudinal invariance.

Table 3 Tests of measurement invariance for anxiety, control, and value
Full size table

A SEM was tested to estimate the hypothesised paths shown in Fig. 1. This SEM showed a reasonable fit to the data: χ2(771) = 1768.24, p < 0.001, RMSEA = 0.032, SRMR = 0.048, CFI = 0.939, and TLI = 0.928. Standardised path coefficients are reported in Table 4 and diagrammed in Fig. 2.

Table 4 Standardized path coefficients for the SEM to examine reciprocal relations between anxiety, control, and value, and relations with subsequent mathematics achievement
Full size table
Fig. 2
figure 2

Statistically significant relations (standardised path coefficients) between T1 and T2 anxiety, control, and value, and T3 mathematics achievement. Paths for gender and age are not depicted. Dashed lines represent correlations and straight lines represent structural paths

Full size image

3.2.1 Relations from T1 anxiety, T1 control, and T1 value, to T2 anxiety

T2 Anxiety was predicted by T1 Control (β = − 0.181) beyond the autoregressive relation with T1 Anxiety (β = 0.439). T1 Value was not a statistically significant predictor of T2 Anxiety (β = − 0.020).

3.2.2 Relations from T1 anxiety, T1 control, and T1 value, to T2 control

T2 Control was predicted by T1 Anxiety (β = − 0.138) beyond the autoregressive relation with T1 Control (β = 0.619). T1 Value was not a statistically significant predictor of T2 Control (β = 0.037).

3.2.3 Relations from T1 anxiety, T1 control, and T1 value, to T2 value

T2 Value was predicted by T1 Anxiety (β = − 0.077) beyond the autoregressive relation with T1 Value (β = 0.695). T1 Control was not a statistically significant predictor of T2 Value (β = − 0.040).

3.2.4 Relations from T1 and T2 anxiety, control, and value, to T3 mathematics achievement

T3 Mathematics Achievement was predicted by T1 Anxiety (β = − 0.146) and T2 Anxiety (β = − 0.246). T1 Value (β = 0.096), T2 Value (β = − 0.201), T1 Control (β = − 0.028), and T2 Control, were not statistically significant predictors of T3 Mathematics Achievement.

3.2.5 Demographic covariates

Female students reported higher T1 Anxiety (β = 0.119) and lower T1 Control (β = − 0.167) and T1 Value (β = − 0.131). Older students showed higher T3 Mathematics Achievement (β = 0.098). All other relations were not statistically significant.

3.2.6 Indirect relations from T1 anxiety, T1 control, and T1 value, to T3 mathematics achievement mediated by T2 anxiety

Indirect relations were assessed by creating 95% confidence intervals (CIs) around the point estimate of the indirect effect. CIs that do not cross zero are statistically significant at p < 0.05. T1 Anxiety was negatively related to T3 Mathematics Achievement mediated by T2 Anxiety: β = − 0.116, SE = 0.036, 95% CIs [− 0.057, − 0.176]. T1 Control was positively related to T3 Mathematics Achievement mediated by T2 Control, β = 0.193, SE = 0.093, 95% CIs [0.040, 0.346] and T2 Anxiety, β = 0.048, SE = 0.021, 95% CIs [0.013, 0.083]. All other indirect relations were not statistically significant (95% CIs cross zero).

4 Discussion

Based on CVT (Pekrun, 2006, 2018), the aim of the present study was to examine: (1) the reciprocal relations between control-value appraisals and class-related anxiety, and (2) the indirect relations from control-value appraisals to mathematics achievement, mediated by class-related anxiety. In partial support of Hypothesis 1, T1 control was negatively related, but T1 value unrelated, to T2 anxiety in the mathematics classroom. In support of Hypothesis 2, Higher T2 anxiety in the mathematics classroom was negatively related to T2 control and T2 value. In support of Hypothesis 3, T1 control was positively related to T3 mathematics achievement mediated by T2 anxiety in the mathematics classroom. We did not find support for Hypothesis 4; T1 value was unrelated to T3 mathematics achievement.

CVT proposes that relations between control-value appraisals and anxiety and are reciprocal (Pekrun, 2006, 2018). Evidence for these relations, however, is scarce especially for classroom-related anxiety in particular. We found evidence for negative reciprocal relations between control appraisals and classroom-related anxiety. That is, when participants believed they would succeed in their mathematics lessons they experienced less anxiety. In addition, participants who experienced less anxiety in mathematics classes subsequently developed a greater belief in their capacity to perform the activities in their mathematics lessons. This finding provides strong support for the propositions of CVT, namely that lower control leads to higher anxiety, but also that higher anxiety can reinforce a belief in lower control.

Previous studies have shown lower control (or a proxy) to be negatively related to anxiety in the mathematics classroom (Frenzel et al., 2007; Lichtenfeld et al., 2012; Peixoto et al., 2016) or mathematics anxiety (Meece et al., 1990). Moreover, only two studies have shown negative reciprocal relations between academic self-concept (a proxy for control) and achievement-related anxiety for mathematics (Ahmed et al., 2012; Clem et al., 2021). Our finding, is consistent with this body of work and the first to demonstrate the reciprocal relation specifically for anxiety in the mathematics classroom while also including a measure of value. We reasoned that the path from control to anxiety would be stronger than from anxiety to control. Findings did support this proposition (β = − 0.18 vs. β = − 0.14) but the different was not large.

We did not, however, find evidence for a reciprocal relation between value and classroom-related anxiety; anxiety was negatively related to subsequent value, but value was not related to subsequent anxiety. As we noted in the introduction, the extant research has shown inconsistent findings for relations between value and anxiety in the mathematics classroom. Relations have been positive (Frenzel et al., 2007; Luo et al., 2016) and negative (Lichtenfeld et al., 2012; Peixoto et al., 2016; Putwain et al., 2021). In the present study, the bivariate correlation between T1 value and T2 anxiety was negative (r = − 0.28; see Table 2) and concurrent relations in the SEM between value and anxiety were also negative (T1: r = − 0.35; T2: r = − 0.39; see Fig. 2). This would suggest that the small and non-statistically significant path from T1 value to T2 anxiety was artefact of the shared variance with control (T1: r = 0.79; see Fig. 2) leaving insufficient remaining variance for T1 value to predict T2 anxiety. In addition, the negative value-anxiety relations aligned with other studies measuring value through the perceived importance of mathematics as a subject domain (Lichtenfeld et al., 2012; Peixoto et al., 2016; Putwain et al., 2021).

It may be the case that students find it difficult to maintain higher value in mathematics if they do not expect to succeed. Reducing the value of mathematics offers a degree of self-protection against failure (somewhat similar to the mechanism we proposed for anxiety). Put simply, the cost of maintaining high value is potentially too damaging to one’s self-worth (see Gaspard et al., 2020; Jiang et al., 2018, 2020). From this perspective, both anxiety and value are outcomes of control appraisals, hence the path from T1 value to T2 anxiety was small and not statistically significant. We reasoned that the path from anxiety to value would be stronger than from value to anxiety and findings supported this proposition (β = − 0.08 vs. β = − 0.02).

As theorised, however, we did find that T1 anxiety was negatively related to T2 value. This finding is similar to that of Sutter-Brandenberger et al. (2018) who found across the first two waves of measurement in their study that higher anxiety in the mathematics classroom was negatively related to subsequent lower intrinsic and identified forms of motivation (which, as we noted earlier, are similar to intrinsic and extrinsic task value respectively). It seems likely that students lower the value of mathematics tasks and activities, when they experience a high degree of anxiety as a form of self-protection. This discounting or de-valuing of mathematics (Loose et al., 2012) may help to manage anxiety (Harley et al., 2019), but ultimately is damaging to students’ learning and progression in mathematics. Unless this cycle is broken, the eventual outcome could be disaffection and disengagement from learning in mathematics (Martin et al., 2012).

In keeping with previous findings (e.g., Hembree, 1990) negative relations were shown between anxiety in the mathematics classroom and subsequent performance in a mathematics class test. The finding that T2 control was only marginally related, and T2 value was unrelated, to subsequent test performance accords with CVT; relations between control-value appraisals and achievement are mediated through emotions (in this case anxiety). Following this theorising we expected to find positive indirect relations from T1 control, and negative indirect relations from T1 value, to subsequent test performance. T2 anxiety in the mathematics classroom was shown to mediate relations between T1 control and T3 test performance. T2 anxiety, however, did not mediate relations from T1 value to T3 test performance as a result of non-statistically path from T1 value to T2 anxiety. This finding builds on those previous showing relations between control-value appraisals and homework behaviour in mathematics are mediated by anxiety (Luo et al., 2016).

4.1 Limitations and recommendations for future research

There are five limitations we would like to highlight. First, we were not able to include a measure of prior mathematics learning; students in English primary schools are not provided with grade cards to summarise achievement and so even a self-reported measure of achievement was not possible. Prior mathematics achievement would have been expected to account for variance in control-value appraisals and anxiety. Relations between, control-value appraisals, anxiety, and subsequent mathematics test performance may, therefore, be somewhat larger than if a prior measure of achievement was included. Where possible, future studies examining relations between control-value appraisals, emotions, and subsequent achievement, should strive to include, where it is practical and feasible to do so, a prior measure of achievement.

Second, while a two-wave study is sufficient to examine reciprocal relations, it is cannot establish unfolding feedback loops of control-value appraisals and emotions over time. Ideally, designs should include four waves of data collection to enable at three tests of temporally separated reciprocal relations; from the second wave onwards, tests will be particularly stringent after controlling for prior control-value appraisals and emotions. Third, our study focused on one classroom-related emotion, namely anxiety. There is little research on the emotions experienced in the mathematics classroom specifically (rather than in tests or when learning or studying) and it would be beneficial for future studies to include other achievement emotions such as pride, hope, enjoyment, and boredom. Fourth, the research questions and materials for this study were registered after data were collected and analysed. Future studies should ensure that studies are pre-registered in order to ensure maximum openness and transparency.

Fifth, although we rely on conceptualisations of self-protection as explanations for the relations between value and anxiety we did not measure self-protection (avoidance, discounting, devaluing, and ego-cost) directly. It would be a useful direction for future studies to examine these processes as mediating the relations between value and anxiety. In addition, while not being a limitation, per se, as the present study focused on mathematics only, it is not clear the extent to which findings are specific to mathematics or would generalise to other subjects. While studies have shown that students can, and do, experience high levels of anxiety in subjects other than mathematics (e.g., Raccanello et al., 2019), some subjects (notably mathematics and second language learning; Ramirez et al., 2018; Teimouri et al., 2019) do seem to prompt fears in a way that other subjects do not. Accordingly, future studies could compare relations between control-value appraisals and emotions in different school subjects (see Clem et al., 2021).

4.2 Implications for educational practice

Our findings show that low control and high anxiety in the mathematics classroom predict lower test performance. Although our study did not directly measure forms of self-protection, such avoidance, de-valuing or discounting mathematics, or ego cost and threat, the implication is that low control and high anxiety could keep a student locked into a cyclical pattern of low control and high anxiety. Eventually, without intervention, this could result in a more profound and damaging disengagement from learning. Interventions could be educational in nature, incorporated into routine teaching and learning, and focus principally on building control. Individualised learning, where the difficulty level of mathematics activities, tasks, and lesson, can be matched to the student, in order to optimise the challenge level, have been shown to be effective in teaching children mathematics (e.g., Nurmi et al., 2012). Such strategies may be difficult to incorporate into whole class teaching, especially in mixed ability groups. Where resources permit, the difficulties associated with individual instruction in whole class teaching can be overcome with intensive one-to-one tutoring (Wu, 2019) or incorporating technology to enable students to work through activities matched to their level of progress on a tablet (Outhwaite et al., 2017). Instructional interventions can also incorporate the principles of growth mind-set based to encourage effort and persistence in the face of difficult or challenging learning, and that failure is a normal part of learning (Lin-Siegler et al., 2016).

Interventions could also be more psychological in nature and focus principally on reducing anxiety, as has been the case with the implementation of Social and Emotional Learning (SEL) schemes designed to facilitate improvement in social and emotional well-being, as well as initiatives, such as ‘Building Learning Power’ (Claxton, 2002), that focus on resilience building within school-based topics. Cognitive-based approaches, such as reappraisal (Jamieson et al., 2016) and worry-regulation through therapeutic expressive writing (Park et al., 2014), are effective anxiety management approaches for secondary school and undergraduate students. Similarly, cognitive-behavioural interventions effective in reducing test anxiety (Putwain & von der Embse, 2021) could be adapted for use with mathematics in adolescent, and older, students. Reappraisal and the more complex aspects of cognitive restructuring used in cognitive-behavioural interventions (e.g., identifying and challenging biased thoughts) might be less appropriate for younger, primary or elementary school aged, students (Kingery et al., 2006). Expressive writing and the less complex aspects of cognitive-behavioural interventions (e.g., relaxation and calming self-task; see Yeo et al., 2016), however would be appropriate for use with younger students.

5 Conclusion

We found evidence for negative bidirectional relations between control appraisals and anxiety in the mathematics classroom. Relations between value appraisals and anxiety in the mathematics classroom were, however, unidirectional; anxiety negatively predicted subsequent value, but not vice versa. Furthermore, control appraisal was positively and indirectly related to performance on subsequent mathematics test, mediated by anxiety in the mathematics classroom. These findings add to the limited body of work that examines anxiety specifically in the classroom rather than generically, or in relation to tests or learning. The findings for control appraisals (relations with anxiety and achievement) support CVT (Pekrun, 2006, 2018). The findings for value appraisals indicate the need for more research into value appraisal and anxiety relations; different forms of self-protection (avoidance, discounting, devaluing, and ego-cost) could be one possible avenue. In order to ensure that students do not become locked into a cyclical pattern of low control and high anxiety, leading to disengagement from learning, intervention may be necessary. Interventions could be instructional (e.g., individualised learning) or psychological in nature (e.g., therapeutic expressive writing, cognitive-behavioural interventions).