The centrality of student-generated representation in investigating generalizations about the operations

Abstract

This article addresses the nature of student-generated representations that support students’ early algebraic reasoning in the realm of generalized arithmetic. We analyzed representations created by students for the following qualities: representations that distinguish the behavior of one operation from another, that support an explanation of a specific case of a generalization, and that support justification of a generalization. One key finding is that representations in the form of pictures, diagrams, arrangements of manipulatives, or story contexts that embody the meaning of the operation(s) allow students to distinguish between operations. Such representations can be used by young students to illustrate relationships conveyed in specific instances of a general claim. Further, extending these representations to class of numbers is a mechanism for proving a general claim.

1 Introduction

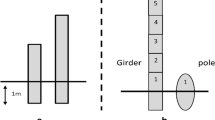
As part of her start-of-the-day routine, fourth-grade teacher Monica Royce¹ gave her class a few quick subtraction problems, among them 145 − 100 and 145 − 98. Students solved the problems correctly except 145 − 98, for which the class had two answers: 47 and 43. They listened intently as their classmates presented different strategies for solving the problem, and all became convinced the correct answer was 47, but some were still mystified. Since 98 is 2 less than 100, shouldn’t 145 − 98 be 2 less than 145 − 100? Why wasn’t that working? After some discussion, Brian got up to draw a picture (Fig. 1), explaining, “It’s like you’ve got this big thing to take away, and then you have a littler thing to take away, so you have more.”

Fig. 1

A representation of the result of subtracting less

Rebecca said, “It’s like you have this big hunk of bread, and you can take a tiny bite or a bigger bite. If you take away smaller, you end up with bigger,” and Max declared, “Yeah, the less you subtract, the more you end up with and, in fact, the thing you end up with is exactly as much larger as the amount less that you subtracted.”²

This episode illustrates a key aspect of early algebraic reasoning: exploring generalizations in the context of arithmetic and quantitative reasoning (Kaput, 2006). Starting with a question that arose from a routine subtraction problem, Brian, Rebecca, and Max broadened their thinking from specific numbers to examine the behavior of subtraction. Based on Brian’s drawing and Rebecca’s story context, Max formulated a generalization that could be translated into algebraic notation: a − (b − c) = (a − b) + c, where a, b, and c are positive numbers and a > b > c. In the example of 145 − 98, if a = 145, b = 100, and c = 2, the problem can be thought of as 145 − (100 − 2) = (145 − 100) + 2.

Ms. Royce reported this episode as part of a multi-year collaboration between researchers, including the authors, and groups of teachers to investigate algebraic thinking at ages 5–12. As we collected classroom cases from participating teachers, we found that drawings, such as that offered by Brian, and story contexts, like Rebecca’s, provided the means for students to recognize and articulate generalizations about the operations and gain insight into why they must be true.

This article addresses the strand of our early algebra research that involves noticing, articulating, exploring, and justifying generalizations about the operations. Specifically, we consider the question, what characterizes images like Brian’s and story contexts like Rebecca’s that help students make sense of the regularities they notice in arithmetic calculations?

Deep understanding of generalizations about operations—including but not exclusive to the commutative, associative, and distributive properties; the identity elements; the inverse relationship of addition and subtraction, and that of multiplication and division—provides an important foundation for students as they enter the study of algebra in older grades. As we discuss later, in addition to establishing a set of mathematical dispositions such as looking for structure and constructing mathematical arguments, experience with generalizations about the operations may help students interpret the same ideas expressed in algebraic notation and become fluent with algebraic symbol manipulation.

2 Related research

Much study of representation in early algebra focuses on the use of algebraic notation in the content of functions or generalized arithmetic, sometimes combined with natural language (Blanton et al., 2019; Brizuela & Earnest, 2008; Ramírez et al., 2020). In contrast, our focus is on images and models already familiar to young students: drawings, arrangements of physical objects, and story contexts. Our interest is on how children can use such tools to explore the regularities they notice in their work on calculation and to understand why the generalizations they formulate work as they do. For the purposes of this paper, we define representations as pictures, diagrams, arrangements of physical objects, or story contexts created by students to illustrate such regularities.

Multiple representation of mathematical operations, relations, and structures has been described as key in early mathematics learning (e.g., Bruner, 1966; Hiebert et al., 1997; National Council of Teachers of Mathematics, 2000, 2014; National Research Council, 2001). The power of mathematical representations is in moving between representations and in linking physical models and visual representations with mental images (Lesh et al., 1987). In comparing representations for the same mathematical situation, students learn to abstract the common underlying structure (Khoury & Behr, 1982; Lesh, 1979). Representation in mathematics learning is essentially bi-directional, “an interaction of internalization of external representations and externalization of mental images” (Pape & Tchoshanov, 2001, p. 119).

In the context of early algebra involving functions and covariation, several researchers have converged on this aspect of the role of multiple representations. Radford (2011) comments: “The awareness of these structures and their coordination entail a complex relationship between speech, forms of visualization and imagination, gesture, and activity on signs (e.g., number and proto-algebraic notations)” (p. 23). Moss and London McNab (2011) theorize that “the merging of the numerical and the visual provides the students with a new set of powerful insights that can underpin not only the early learning of a new mathematical domain but subsequent learning as well” (p. 280).

In the context of generalized arithmetic, Warren and Cooper (2009) used balances to convey the meaning of the equal sign and number lines to build students’ understanding of the inverse relationship of addition and subtraction. They hypothesize that “abstraction is facilitated by comparing different representations of the same mental model to identify commonalities that encompass the kernel of the mental model” (p. 90).

The research and curriculum development of Dougherty and Slovin (2004), based on Davydov’s (1975) emphasis on generalized representational tools (using length, area, volume, or mass to represent “how much”), indicates that students are capable of early abstraction through moving between different representations of a situation, using “an approach that consistently and simultaneously links the physical model, intermediate representations, and symbolizations within each lesson, and not in a sequential manner” (p. 301). Within the first few weeks of school, the fundamental properties of equality—reflexive, symmetric, and transitive—are introduced, and “because the children are modeling the properties with physical quantities, they can clearly see and describe how these properties work” (Dougherty, 2008, p. 393). From these experiences, a variety of number and operation concepts emerge. For example, given two unequal lengths, students explain there are two ways to make them equal: add a quantity to the shorter length or subtract the same quantity from the longer length.

Ding and Li (2014) considered word problems as a form of representation in their study of the treatment of the distributive property in a Chinese textbook series. Their analysis points to the potential power of story problem contexts which are often ignored in favor of physical models or diagrams as a tool for connecting the concrete and abstract. They note that while word problems are often used as applications, they are rarely seen as tools for the development of knowledge about mathematics, such as the properties of operations, examples of which we saw in the elementary classrooms we studied.

3 Research methods and questions

In this article, we report on data collected from collaborating teachers across five projects conducted from 1993 to 2022. (See Appendix A.) In addition to classroom field notes and video recordings, our data included what we call “episode writing,” for which collaborating teachers recorded classroom lessons. Based on the transcription, they selected an episode from the lesson and wrote a narrative that included samples of student work and discussion of their goals, reasoning behind their on-the-spot decisions, reflections on what transpired, and questions about student thinking. Early in our first project, we noted that, once classrooms opened up to students’ ideas, students frequently commented on regularities in the number system. We asked teachers to focus lessons on such student observations and to ask, “Will this always work?” and “How do you know?” Thus, our extended inquiry into early algebraic reasoning began. In subsequent projects, we refined our questions and continued to collect from collaborating teachers between 80 and 220 episodes per year. We also documented more than 200 lessons with field notes and video recording.

As our research program developed, collaborating teachers enacted lessons in which students noticed, expressed, and proved generalizations about the operations. Recognizing the complexity of this content for young students, we created a teaching model to help students and teachers focus on key aspects of this process. The model emerged from close analysis of K-6 students’ written and oral expression and of collaborating teachers’ developing practices. Through an iterative process of delineating the model, we identified and elaborated five phases of activity (Schifter & Russell, 2020):

• 1. Noticing regularities in the study of number and operations.

• 2. Articulating conjectures based on what students notice.

• 3. Representing examples with diagrams, pictures, physical models, and story contexts in order to understand the mathematical structure of their conjectures.

• 4. Constructing representation-based arguments for a class of numbers.

• 5. Comparing and contrasting operations by investigating analogous generalizations for another operation, moving again through phases 1–4.

This paper addresses the part of our analysis focused on drawings, diagrams, arrangements of manipulatives, and story contexts—referred to in this paper as representations—created by students in the process of investigating a generalization. For phases 3 and 4 of the model, we examined students’ representations to consider which contributed to insight about the generalization under study and which did not. Our research questions about student-generated representations are:

• 1. What characterizes a representation that allows students to distinguish one operation from another?

• 2. What characterizes a representation that supports students’ insight into an instance of a generalization relating two equations (e.g., 145 − 100 = 45 and 145 − 98 = 47)?

• 3. What characterizes a representation that supports students’ arguments for a generalization about an operation?

The representations used as data for the study were produced by students of teacher collaborators who voluntarily participated in the projects for their own professional development. Professional development activities focused on three broad areas: teachers explored mathematical concepts that underlie the elementary curriculum (i.e. mathematics content for teachers themselves), analyzed cases of student thinking related to this content, and investigated their own students’ thinking through episode writing.

In our data analysis, we considered representations in three categories: (1) representations of a single number sentence, (2) representations of specific instances of a generalization, and (3) representations of the generalization. For each category, we sorted representations into those that could ultimately support a general argument for a generalization and those that could not, and we described the representations. We periodically discussed our findings with collaborating teachers, who used our descriptions to consider selection of student representations to bring to classroom discussions and guide their focus in those discussions. Through an iterative process, we examined new classroom episodes until our description of each category stabilized.

Although our analyses included representations created across multiple projects, the examples that follow, chosen to illustrate representations in each category, are drawn from classrooms using lesson sequences written by project researchers in 2012 (Russell et al., 2017). These lesson sequences were produced for grades 1–5 based on our teaching model, each sequence addressing a set of related generalizations in 20–25 20-min sessions (see Appendix B for generalizations addressed in each sequence). From 2013 to 2020, participants in our projects taught two lesson sequences each year, in addition to their regular mathematics curriculum; lessons were documented through field notes, teacher episodes, video, and photographs.

4 Results

4.1 Representation of a number sentence

Research Question 1: What characterizes a representation of a number sentence that allows students to distinguish one operation from another?

Characterization: Effective representations are pictures, diagrams, arrangements of manipulatives or story contexts that embody the meaning of the operation(s). They show the relationship between the operands and the result of the operation.

In extant practice, especially in higher grades, diagrams, pictures, and manipulatives are usually dropped as students work with calculation procedures on larger or different kinds of numbers, and students frequently lose touch with the meaning of the operation. When working with numerical expressions and equations, students may focus exclusively on number patterns, and the operations lose salience (Kieran, 1989, 2018; Subramaniam & Banerjee, 2011). Some of the most persistent errors in arithmetic calculation are based on the assumption that regularities noticed in addition apply to other operations as well. In our classroom documentation, we found that, even when a class conjecture specified the operation of addition, many students assumed the same regularity would occur for subtraction or multiplication. For this reason, we sought a mechanism to return students to the very meaning of the operations.

In the introductory example, Ms. Royce’s fourth graders knew that, given an addition equation, if a term decreases by some amount, the sum decreases by the same amount, and some students expected the same to happen when subtracting. It took Brian’s representation to bring students back to a meaning of subtraction—removing one part from a whole—to recognize that subtraction behaves differently than addition: If the subtrahend (the second term) decreases, the difference increases. Key to Brian’s representation is that it shows the relationship between three quantities—the whole, the amount removed, and the amount that remains—under the action of subtraction.

Our analysis found that representations that allowed students to distinguish between operations were pictures, diagrams, arrangements of manipulatives, or story contexts that embody the meaning of the operation(s) and quantities involved. That is, the representation demonstrates the relationship between two operands and the result of the operation. A representation of an addition equation might show the joining of two quantities which, together, comprise the sum, whereas a representation of a subtraction equation might show one quantity being removed from another, leaving the difference. Kanika, a first grader who created the work shown in Fig. 2, drew two representations for 7 + 5 = 12: (1) 7 balloons held by one child and 5 balloons held by another, totaling 12 balloons, and (2) 7 lines labeled 1 to 7 and 5 lines labeled 8 to 12, making a total of 12 lines. Kanika’s representation of 12 − 5 = 7 shows 12 balloons, with 5 crossed out, leaving 7 balloons.

Fig. 2

Kanika’s representations of 7 + 5 = 12 and 12 − 5 = 7

Because a static drawing or model cannot convey intended dynamic characteristics of the representation, students’ gestures and natural language explanations that accompany their representations are often essential parts of the representation. Kanika’s classmate, Jan, working with the same problems, built a stack of 7 cubes of one color and a stack of 5 cubes of another color. To show addition, she put the stacks together to make a single stack of 12 cubes. To show subtraction, she started with the stack of 12 and removed the 5 cubes of one color, leaving 7 cubes of the other color (see Fig. 3.)

Fig. 3

Jan put together two stacks of cubes to show addition and removed one stack to show subtraction

A representation of multiplication or division might show a collection of equal-sized groups. Third grader Jude drew the representation in Fig. 4 for 7 × 5 = 35, along with a story context, “There are 7 tables with 5 kids at each table. There are 35 kids in all.”

Fig. 4

Jude’s representation of 7 × 5 = 35

As students create their own representations, they also become familiar with and begin to use conventional representations—initially encountered in their regular mathematics curriculum—such as number lines, as shown in Fig. 5. To represent 12 − 5 = 7, second grader Emma started at 12, took five steps to the left, and landed on 7.

Fig. 5

Emma’s number line representation of 12 − 5 = 7

Similarly, as students come to understand the structure of arrays by identifying correspondences between arrays, multiplicative contexts, and images of equal groups, such as Jude’s in Fig. 4, they may include this conventional representation in their repertoire.

We have identified three types of representation created by students that do not embody the operation. First, when asked to represent a story problem about subtraction, for example, that 12 birds were sitting on a wire and 5 birds flew away, very young students may simply draw a picture of birds. They have drawn a scene, not a representation of the quantities and their relationships. Unlike Kanika’s representations of the balloons, they don’t specify the initial quantities, the action of the operation, and the result of that action.

Second, students may show each quantity separately, connecting them with the symbols they have learned in school as shown in Fig. 6a for the story problem about birds on the wire. This kind of pseudo-equation, like an equation using mathematical symbols, is not an image of how the initial amount and the subtracted amount are related to the difference. In fact, the student could just as easily draw the quantities incorrectly, as in Fig. 6b. Because the three quantities are drawn independently of each other, there is nothing in the drawing itself that requires that it be correct. Contrast this to Kanika’s representation. Although she could, perhaps, count incorrectly as she created or explained her representation of balloons, her pictures and descriptions embody the actions of addition and subtraction. Once the correct quantities of the numerical expression 7 + 5 or 12 − 5 are depicted and either joined or crossed out, the result will be the correct sum or difference.

Fig. 6

a Mimicking the equation format is not a useful representation. b Such a format can just as easily mimic an untrue number sentence

A third common student response before having experience with representation is like Fig. 6a: some students used cubes to recreate the equation itself, as shown in Fig. 7. This representation neither reveals the meaning of subtraction nor the relationship between the terms and the difference.

Fig. 7

A cube construction of 12 − 5 = 7

In collaborating teachers’ classrooms, students learned how to create a variety of representations not only by having opportunities to produce their own images but through whole group discussion in which the class analyzed a selection of representations produced by their classmates.

4.2 Representation of an instance of a generalization

Research Question 2: What characterizes a representation that supports students’ insight into a generalization that relates two equations (e.g., 145 − 100 = 45 and 145 − 98 = 47)?

Characterization: A representation of an instance of a generalization embodies the meaning of the operation(s) and shows how one equation can be transformed into the other. If the generalization is stated in if–then format, the representation shows how the premise of the generalization leads to the conclusion.

At the start of lesson sequences written by project researchers, students are presented with sets of related expressions, equations, and/or story problems that illustrate a particular behavior of an operation to engage students in noticing patterns and articulating conjectures. A teacher might start the class’s investigation of a structure of multiplication by posting these pairs of equations and asking students what they notice:

$$\left. {\begin{array}{*{20}c} {3 \times 5 = 15} \\ {4 \times 5 = 20} \\ \end{array} } \right|\begin{array}{*{20}c} {3 \times 5 = 15} \\ {3 \times 6 = 18} \\ \end{array}$$

After seeing a regularity across multiple sets of equations, and after working together to formulate a conjecture based on that regularity, students create representations of specific instances of their conjecture.

In Maisie Schmidt’s fourth-grade class, students articulated the conjecture: When you add 1 to the first or second factor, the product goes up by the factor that does not change. Individuals and pairs created representations for specific instances of the claim, first the two equations 3 × 5 = 15 and 4 × 5 = 20, then the equations 3 × 5 = 15 and 3 × 6 = 18. After reviewing the class’s work, Ms. Schmidt selected several representations to discuss with the class (Fig. 8), including some that would need editing.

Fig. 8

A selection of representations to illustrate a conjecture about multiplication

³

For each representation, Ms. Schmidt asked the following questions.

• How does this representation show multiplication?

• How does it show changing one of the factors by 1?

• How does it show the change in the product?

• Does this show an example of our conjecture?

The teacher’s questions about each of the representations—which we call core questions—focus the students on the operations and how the two equations are related. By applying the same questions to a variety of representations and looking for correspondences across representations, students make explicit the aspects that reveal mathematical structure.

To address the fourth question—Does this show an example of our conjecture?—students in Ms. Schmidt’s class discussed, for each representation in Fig. 8, whether it shows why the premise, 1 is added to a factor, leads to the conclusion, the product increases by the factor that doesn’t change. They explained that the bag of apples Jeff’s Mom bought was the 1 bag added to 3 bags (the first factor), increasing the total number of apples, the product, by 5 (the second factor). They identified how the story relates to the four squares, each with five circles inside—the fourth square (orange in the original) could be Jeff’s Mom’s bag, showing the product increasing by 5. Similarly, Jeff’s Mom’s bag and the fourth square containing 5 dots correspond to the bottom row of the array of squares (red in the original).

When students are first learning to represent examples of a conjecture, some students create a representation for each equation but do not show how the equations are related. In selecting representations to discuss, Ms. Schmidt intentionally chose a few that raised this issue. For example, consider the story problems created for 3 × 5 = 15 (Jeff bought 3 bags of apples with 5 apples in each) and 3 × 6 = 18 (Jeffy, Jeff’s twin brother, bought 3 bags of apples with 6 apples in each). Both story problems match their corresponding equation, but they don’t show what changes when the first is transformed into the second. The second story, as written, does not show 1 added to 5 nor 3 added to 15. In contrast, the context for the first pair of equations embeds the story for 3 × 5 = 15 in the story for 4 × 5 = 20: Jeff bought 3 bags of apples with 5 in each. Jeff’s Mom bought 1 more bag with 5 in it.

As the class began to discuss the second set of representations, the author of the story recognized the issue and asked to revise his story: Starting with the same story for 3 × 5 = 15, his revision stated, “Jeffy, Jeff’s twin brother, bought 3 apples, adding 1 to each of Jeff’s three bags.” The 1 apple Jeffy added to each bag corresponds to the 1 added to 5 (the second factor in the first equation), and the 3 apples Jeffy bought correspond to the 3 (the first factor) added to 15 (the product in the first equation).

The same issue arose for the set of three squares, each containing six dots. Although the representation correctly shows 3 × 6 = 18, it does not explicitly demonstrate how it relates to 3 × 5 = 15. To correct this, students suggested showing one dot in each square in a different color to indicate the 1 apple Jeffy added to the 5 apples already in each bag (see Fig. 9).

Fig. 9

Using a different color for 1 dot in each square, students embedded a representation of 3 × 5 = 15 in the representation of 3 × 6 = 18

As the discussion in Ms. Schmidt’s class demonstrates, representing an instance of a conjecture involves more than simply creating separate representations of the two equations. Rather, one must demonstrate how the representation of one equation is related to and can be transformed into the representation of the other. Keeping their conjecture in mind, the students revised the representations to show, in each instance, a factor increasing by 1 and how the conclusion of the conjecture—that the product increases by the amount of the other factor—follows from the composition of the representation.

4.3 A representation that supports a general argument

Research Question 3: What characterizes a representation that supports students’ arguments for a generalization about an operation?

Characterization: To support an argument for a generalization, a representation must meet three criteria.

• 1. The meaning of the operation(s) involved is represented in diagrams, manipulatives, or story contexts.

• 2. The representation shows how the conclusion of the generalization follows from the premise.

• 3. The representation can accommodate a class of instances, for example, all whole numbers.

Young children bring to formal schooling a natural inclination to prove, to convince, and to be convinced (Stylianou et al., 2009). Early in our research into early algebraic thinking, building on that inclination, we suggested to collaborating teachers that, when students notice a pattern or state a generalization, they ask, “Does that work for other numbers?” “What other numbers does that work for?” “How do you know?” In response, students often turned to representations. For example, on the topic of changing the order of addends, first graders would hold up two stacks of cubes and show that when they change the positions of the stacks, “Nothing got taken away and nothing more was added in, so it’s the same.” Although some young students might be thinking only of the specific number of cubes in the two stacks, others indicated, by their wording and gestures, that they understood that changing the order of addends does not change the sum, no matter how many cubes are in the stacks.

Another example that arose early in our study was what we referred to as “Brian’s blob,” the representation produced by Ms. Royce’s student. Although the class was specifically talking about 145 − 100 and 145 − 98, some students saw in it the demonstration of a general claim, in Max’s words, “The less you subtract, the more you end up with and, in fact, the thing you end up with is exactly as much larger as the amount less that you subtracted.”

The teachers’ written classroom episodes offered evidence that representations that illustrate the meaning of the operations serve as touchstones, or starting points, for conviction, an analog to a mathematician’s axioms. As we analyzed students’ explanations, we referred to them as representation-based arguments, for which we identified the three criteria stated above (Russell et al., 2011). The first two of these criteria are satisfied by representations that illustrate specific instances of a generalization, discussed in the previous section. Now the challenge to students is to think of the representations in general terms.

Marla Gonzales’s fifth graders formulated the conjecture, For a multiplication expression, if you divide one factor by 2 and multiply the other factor by 2, the product is the same. They represented specific instances such as 3 × 10 = 6 × 5 and 8 × 6 = 4 × 12 by cutting arrays into two parts and rearranging those parts (see Fig. 10).⁴

Fig. 10

Representations of specific instances of a conjecture about multiplication

These representations satisfy the first two criteria: (1) The meaning of the operation(s) involved is represented in diagrams, manipulatives, or story contexts. The first factor of a multiplication expression is represented as the number of rows in an array; the second factor is the number of squares in each row; the product, the result of multiplication, is the total number of squares. (2) The conclusion of the claim follows from the structure of the representation. Each of the representations shows that by moving half the array, the number of rows is halved (or doubled) and the number of squares in each row is doubled (or halved), creating a new array with the same number of squares. While the dimensions of the arrays (the factors) change, the number of unit squares (the product) does not.

With that insight, students realized that they could imagine rectangles with unspecified dimensions (see Fig. 11).

Fig. 11

A representation of the generalization for all positive factors

The two-colored rectangle on the left represents an initial equation. No matter what the length and width representing the two factors, the area represents the product of those factors. By cutting the rectangle in half and realigning the two parts, a second rectangle is created. In this second rectangle, one dimension (one factor) is half the corresponding dimension of the first rectangle, the other dimension (the other factor) is double that of the corresponding dimension of the first rectangle, and the area (the product) is conserved. This representation-based argument can accommodate any positive values for the factors, thus satisfying the third criterion.

For another example, consider the representations offered by Jill Bujak’s third graders⁵⁶ after they articulated the conjecture: If you have two addends, and you take some amount from an addend and add that same amount to the other addend, it should equal the same sum. Maria created a story context: “There are two parties. At one party, there are some people. At the other there are some. When an amount of people leave the party and go to the other, you will always get the same amount of people you started with, if you’re adding the two parties.” In Maria’s representation, adding an amount to or subtracting it from an addend is represented by some number of people joining or leaving a party, and the sum is represented by the total number of people attending the two parties (Criterion 1). The premise of the conjecture is represented as some number of people leaving one party and joining the other. The conclusion—that the sum is the same—follows from the fact that the same set of people are distributed between the two parties (Criterion 2). Any whole number of people can attend the parties and any number of people up to the size of a party can leave that party to join the other (Criterion 3).

Even when students work with representations that necessarily contain a fixed number of elements, such as stacks of cubes, they might describe them in such a way as to have them stand for a class of instances, what Mason (1996) calls “seeing the general through the particular.” Maria’s classmate, Melody, justifying the same conjecture, presented a long stick of red cubes and a long stick of blue cubes for her two addends: “Our model shows that we don’t know how many cubes are on the stick. We don’t, actually! And if we take this many,” removing some red cubes, “and put it onto there,” adding them to the blue stick, “it would be the same thing. The red one got smaller and the blue one got bigger, and it’s the same.”

Through representation-based arguments, young students take on the question, how can you know a statement is true when you can’t test every instance? Even when students’ images show a finite number of items such as cubes or squares, the drawing or model together with students’ words and actions, can stand for a representation that applies to the general case.

5 Discussion

In our early algebra research, we sought a mechanism to address the fact that many students tended to think that regularities they noticed in their calculations were about numbers rather than about a specific operation. We found that representations in the form of pictures, diagrams, arrangements of manipulatives, or story contexts could be employed to address this concern. Project researchers analyzed student-generated representations in three categories—representation of a number sentence, representation of a pair of related equations that illustrate a specific instance of a generalization, and representation of a generalization—and characterized those that could eventually prove fruitful as students work to understand what a given generalization says and why it is true. Our findings indicate that pictures, diagrams, arrangements of manipulatives, or story contexts that embody the meaning of the operation(s)—that is, those that show the relationship between the operands and the result of the operation—served as touchstones, analogous to a mathematician’s axioms, for reasoning about operations. To reason about a specific instance of a generalization illustrated by two related equations, students used such representations to show how one equation can be transformed into the other. An argument in support of the generalization itself extends such representations to accommodate a class of numbers.

The purpose of the teaching model we created, as well as the lesson sequences we wrote to enact it, was to engage students in the practices of noticing, articulating, investigating, and justifying generalizations about the operations. Creating representations and analyzing classmates’ representations allowed students to deepen their understanding of mathematical structure (Kieran, 2018) and to encounter the activity of justifying mathematical generalizations. The goal was not necessarily that each student individually construct representation-based arguments. While we have observed some students coming up with representation-based arguments on their own, most of the work on conjecture and argument we have documented in elementary grades occurs in the social context, through discussions among students (Cobb et al., 1992; Seeger, 1998).

Collaborating teachers reported to us that, when the class turned to lessons on generalizations about the operations, greater numbers of students participated in discussions than in their regular mathematics lessons. When focused on representations, all students could participate in the discussions while attending to what they needed to work on. Some students took on the challenge of deductive reasoning, other students were building networks of connections across representations and specific examples to solidify their conception of the generalization, and yet other students continued to build their understanding of what the operations are and how to represent them. Even though different students focused on different aspects of the investigation, the variety of comments moved the discussion forward.

We believe student engagement has to do with the variety of representations presented for the same conjecture. Consistent with the studies described above in the literature review, the variation across representations triggers the act of abstraction, even for those students who are not as fluent with symbolic manipulation. Making sense of and comparing a variety of representations may be precisely what allows students to recognize what those representations share—the generalization they represent. Apprehending commonalities across representations, alongside verbal statements of the generalization and arithmetic symbols illustrating specific instances, is an important pathway for students in making the critical connection between the concrete and the abstract. In this way, students develop “structure sense” and “symbol sense,” both in the early grades and in their later study of formal algebra (Arcavi, 1994; Hoch & Dreyfus, 2004, 2006; Mason et al., 2009; Tabach & Fridlander, 2008).

6 Limitations of the study

There are two broad areas in which future research could build on the findings described in this paper. First, in almost all our data, students were working in the domain of whole numbers, and their representations generally accommodated whole numbers, although occasionally students created representations that accommodated all positive numbers. We have not studied what happens if students have opportunities to investigate related structures as they are introduced to new kinds of number—fractions, integers, etc. What questions might arise as they revisit the generalizations they have established for whole numbers? What forms of representation can they use to justify conjectures about integers or rational numbers?

Second, this project did not produce instruments for scoring student-created representations to assess performance in the aggregate. Such an instrument could provide data on how the nature of students’ representations develop by grade or through the year and to what extent students’ production of different categories of representation correlate with other measures of their understanding of a generalization.

7 Establishing new dispositions and implications for later grades

In the classrooms of our collaborating teachers, as students noticed, expressed, and proved generalizations about the operations, they moved back and forth between physical models, drawings, diagrams, gestures, story contexts, arithmetic symbols, and verbal statements. In this way, they developed an elaborate network of connections and deepened their understanding of the generalization under investigation. Working through the five phases of the teaching model nurtured a set of dispositions we characterize with the following points:

• 1. Through their study of generalizations about operations, students develop the habit of looking for regularity to identify structure.

• 2. As they construct and analyze their representations, students develop a deeper understanding of how the operations behave, recognizing that a regularity they have identified for one operation doesn’t necessarily hold for others. Operations attain greater salience and are recognized as objects, each with a unique set of properties, rather than exclusively as a set of steps to perform calculations (Kieran, 1989; Sfard, 1991; Slavit, 1999).

• 3. Using representations, students explain to themselves and to others why their conjectures are true, initially showing how the conclusion follows from the premise for specific instances. Representation-based argument provides a mechanism for generalizing their representations to justify a claim for a class of numbers.

• 4. Students recognize applications of their generalizations when decomposing and recomposing numbers to calculate. As reported by teachers and documented on video, when discussing a new computational strategy, students would comment, “It’s just like our conjecture.”

These points have direct application for later mathematical studies and address common difficulties students encounter in formal algebra courses. If students develop the habit of looking across representations to find correspondences and explain why mathematical relationships hold—including geometric representations (Banchoff, 2008) and story contexts (Ding & Li, 2014; Tabach & Fridlander, 2008)—they are creating a repertoire of tools they can use to understand algebraic concepts. The disposition to explain why establishes a foundation for understanding proof. In this early work on representation of general claims, students encounter the distinction between proving a claim for an infinite set and relying on empirical verification, a distinction that often eludes high school students (Chazan, 1993; Healy & Hoyles, 2000).

With greater salience of the operations, students are better positioned to interpret the language of algebra, for example, recognizing that ab = ba is not a statement about a and b, but a statement about multiplication. Furthermore, deeper understanding of the laws of arithmetic can support greater fluency with algebraic manipulation. Experiences like those in Ms. Royce’s class when discussing 145 − 100 and 145 − 98 may provide students with a foundation for thinking through, for example, why

$$\begin{gathered} a + \left( {b + c} \right) = \left( {a + b} \right) + c,{\text{but}} \hfill \\ a{-}\left( {b{-}c} \right) \ne \left( {a{-}b} \right){-}c. \hfill \\ \end{gathered}$$

Finally, the experience of recognizing structure in their study of number systems and applying this structural understanding to strategically decompose and recompose numbers as they solve computation problems, may provide both the disposition and tools for students to look for application of structure in solving problems in algebra (Kieran, 2018).

As we hypothesize how students in their algebra studies might draw on their activity of generalizing in early grades, we must acknowledge that bridging these two realms effectively will depend on many factors, including teachers who encourage students to access and build on their earlier experiences.

8 Conclusion

Over the years and across projects, we have worked with teachers in a wide variety of schools: in urban, suburban, and rural settings; in communities with majority white populations and those with mostly Black and brown students; and in schools with a range of income levels, including those in which the majority of students qualify for reduced-price meals. Our most recent project was based in a school assigned the status of “turn around” for its low performance on standardized tests. In all these settings, given support and experience, students succeeded in constructing, analyzing, and comparing representations for understanding the behavior of the operations. Collaborating teachers consistently reported that discussions based on representations engaged students who tended to struggle with calculation as well as those for whom calculation came easily. These reports were confirmed by field observations and analysis of videotaped class sessions. Not captured in transcripts, but evident in video, is that near the end of many of the lessons, the majority of students are still eagerly raising their hands to contribute.

Across our projects, teachers had opportunities to learn about generalized arithmetic, representation-based arguments, and how students reason about such content. Without professional development that introduces elementary teachers to what generalizing about the operations looks like at these grades, and to the centrality of representation in the development of mathematical arguments, they may have no images of how students engage in this crucial practice. LeMay (2017) found in his study of K-5 educators’ conceptions of mathematical argument that they saw arguments about generalized arithmetic as “products of prose … bereft of representations” (p. 35), and that, even when representations were used, they were considered as intermediate steps that were then “sidelined” and not presented as part of final work.

From observations across many classrooms, we conclude that, once teachers know how to bring this content to their teaching, students are deeply interested in the behavior of operations and how they are represented. The focus of discussion is not on finding an individual sum, difference, product, or quotient; the “answers” are known to the students before discussions begin. Rather, the discussion emphasizes the foundations of the number system—it provides a challenge to students’ reasoning and requires hard work in articulating that reasoning. Noticing, representing, and generalizing about the behavior of the operations is at the core of what elementary students are learning, and they are eager to learn it.

Appendices

Appendix A

Our research into early algebra was conducted in the context of five projects that each had a professional development component for teachers and educational leaders, as well as a materials development component.

• Teaching to the Big Ideas (TBI)

• Teaching to the Big Ideas of Early Algebra (TBI-EA)

• Foundations of Algebra in the Elementary and Middle Grades: Supporting Students to Make, Represent, and Justify General Claims about the Operations (FOA)

• Using Routines as an Instructional Tool for Developing Students' Conceptions of Proof (Routines)

• Mathematical Argument and Student Agency and Identity (MASAI)

	Years	Number of teachers in each cohort	Professional development contact hours	Grade levels	Funder
TBI	1993–1997	36	355	K-6	National Science Foundation (NSF)
TBI-EA	2003–2008	30/80/150	108/24/24	K-8	NSF
FOA	2006–2012	9/11/85/20	72/48/54/54	1–8	NSF
Routines	2010–2016	7/13	84/42	2–5	NSF
MASAI	2018–2022	6	20	1–4	Internal support from TERC and Boston Teacher Residency

Teaching to the Big Ideas was a multi-year collaboration to investigate key conceptual themes of K-6 mathematics, documenting how such themes arise in different contexts and tracking how they develop through the grades. In this context, we began to explore generalizations students notice in their study of number and operations. Teacher collaborators wrote “episodes,” described in the text of this paper, both as a source of research data (in addition to field notes and video recordings) and as a professional development exercise. Episode writing, field notes, and video continued to be a feature of subsequent projects.

Teaching to the Big Ideas of Early Algebra narrowed the mathematical focus from K-6 mathematics in general to two branches of early algebra: generalized arithmetic and functions. As part of our investigation of generalized arithmetic, we defined representation-based argument and began to delineate characteristics of student-generated representations. As subsequent projects brought in more samples of student work, we periodically reviewed, revised, and refined our criteria for assessing students’ representations.

Foundations of Algebra developed a book and online course to support teachers in learning how elementary and middle school students come to recognize, verbalize, represent, and justify general claims about operations, and to help teachers make the critical and difficult leap from their own learning to sustained, coherent implementation of these ideas with students. We created teacher and student assessments for which we developed reliable coding rubrics in order to understand what course participants and their students learned in contrast to a comparison group.

The Routines project iteratively created and refined a teaching model for incorporating mathematical argument into elementary classroom instruction. Eight lesson sequences based on the teaching model were produced, each sequence investigating a small set of related generalizations. In addition to classroom documentation, Routines included individual student interviews using the assessment developed in the FOA project. Analysis of students’ articulations of conjectures in the interviews led to a theoretical framework of four dimensions (Higgins et al., 2022, in press). Student-interview data was also used in our continuing analysis of student-generated representations.

Mathematical Argument and Student Agency and Identity collected video from the classrooms of teachers who implemented lesson sequences created in the Routines project. Video analysis, currently underway, examines how the mathematical integrity of a lesson is interwoven with equitable student participation.

Many teacher collaborators worked with us as core participants across multiple projects. In TBI-EA, FOA, and Routines, we pilot-tested professional-development materials with an additional cohort of teachers with whom we had not worked in prior projects. The third cohort of TBI-EA and the fourth cohort of FOA participated in field tests of our materials taught by other educators throughout the United States.

Most participants taught in public schools in urban, suburban, and rural settings, with a few who taught in independent schools. In the Mathematical Argument project, we worked exclusively with teachers who taught in a large urban school system. The teachers were new to us, but were graduates from a master’s program in which they took two math courses taught by faculty who had, when they themselves were K-6 teachers, participated in our projects.

Materials produced in these projects include four modules of the professional development curriculum, Developing Mathematical Ideas, one of which focuses on generalized arithmetic (Schifter et al., 2018); the book titled Connecting Arithmetic to Algebra: Strategies for Building Algebraic Thinking in the Elementary Grades (Russell et al., 2011); an on-line course based on that book; and the resource, But Why Does It Work?: Mathematical Argument in the Elementary Classroom (Russell et al., 2017), which includes a book, the lesson sequences described in this paper, and video examples.

Appendix B

2.1 Claims investigated in eight lesson sequences

SEQUENCE 1: Core ideas of addition and subtraction (whole numbers)

• Changing the order of the addends in an addition expression does not change their sum. Includes work with two and three addends.

• Changing the order of the numbers in a subtraction expression changes the difference, except when the two numbers are the same.

• Addition and subtraction are inversely related.

SEQUENCE 2: Changing a number in addition or subtraction (whole numbers)

• In an addition expression, if 1 (or some amount) is added to an addend, the sum increases by 1 (or that amount).

• In a subtraction expression, if 1 is added to the starting amount, the difference increases by 1.

• In a subtraction expression, if 1 is added to the amount taken away, the difference decreases by 1.

SEQUENCE 3: Same sum, same difference (whole numbers)

• In an addition expression, if you add an amount to one addend and subtract the same amount from another addend, their sum remains the same.

• In a subtraction expression, if you increase (or decrease) both numbers by the same amount, their difference remains the same.

SEQUENCE 4: Core ideas of multiplication and division (whole numbers)

• Changing the order of the factors in a multiplication expression does not change the product. Includes work with two and three factors.

• Changing the order of the numbers in a division expression changes the quotient, except when the two numbers are the same.

• Multiplication and division are inversely related.

SEQUENCE 5: Changing a number in addition or multiplication (whole numbers)

• In an addition expression, if you add some amount to an addend, the sum increases by that amount.

• In a multiplication expression with two factors, if you add 1 to a factor, the product increases by the other factor.

• In a multiplication expression with two factors, if you add some amount to a factor, the product increases by the other factor multiplied by that amount.

SEQUENCE 6: Factors, products, and fractions (whole numbers and fractions)

• In an addition expression, if you add some amount to an addend, the sum increases by that amount.

• In a multiplication expression with two factors:

  • If the factors are both greater than 1, their product is greater than both factors.

  • If one factor is equal to 1, the product is equal to the other factor.

  • If one factor is equal to 0, the product is equal to 0.

  • If one factor is between 0 and 1, the product is less than the other factor.

• In a whole-number multiplication expression with two factors, if you add a fraction to one of the factors, the product increases by the other factor multiplied by the fraction.

SEQUENCE 7: Same product, same quotient (whole numbers)

• In a multiplication expression, if you multiply one factor by an amount (not equal to 0) and divide the other factor by the same amount, their product remains the same.

• In a division expression, if you multiply (or divide) the dividend and divisor by the same amount (not equal to 0), their quotient remains the same.

SEQUENCE 8: Multiplication, division, and powers of ten (whole numbers and decimals)

• When a number is multiplied by 10, every digit moves one place to the left.

• When a number is divided by 10, every digit moves one place to the right.

• If you multiply a number by a multiple of 10, for example 20 or 30, you multiply that number by the number of tens, for example 2 for 20 or 3 or 30, then move all the digits one place.