Abstract
A significant distinguishing characteristic of the International Classroom Lexicon Project was the documentation of classroom pedagogical practices of mathematics teachers in the original languages of ten communities. These lexicons provide us with an opportunity to compare identified teacher practices within these communities. In this paper, we explore the challenges of conducting a cross-lexicon comparison to explore the possibility of moving towards an international lexicon by focusing on the Australian, Chilean, Czech and French lexicons. We focus on two clusters of terms, namely, those related to assessment and those related to mathematics. Inspired by theories and studies related to networking and boundary crossing, strategies were conceived and tested in order to accomplish the following objectives: to support a meticulous and comprehensive comparison of the lexical items; to classify the complexity of similarity of lexical items; and to reveal connections amongst the four lexicons in a bid towards developing an international lexicon. This analysis has the potential to contribute significantly to the study and promotion of mathematics teachers’ reflective practice and highlights the cultural underpinning of the way classroom practices are perceived.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 The International Classroom Lexicon Project
The International Classroom Lexicon Project (hereafter ‘the Lexicon Project’) was amongst the more recent international projects conceived by David Clarke to contribute to our understanding of the complexity of classroom practice. Research teams from ten international communities (situated in Australia, Chile, China, Czech Republic, Finland, France, Germany, Japan, Korea, and the United States) with different educational traditions and pedagogical histories, committed to documenting the professional language of their middle-school mathematics teachers. Documentation of these lexicons put into practice a ‘negotiative’ methodology (Clarke, 2012; Mesiti et al., 2021a) whereby a diversity of community members including academics, teachers, and teacher educators negotiated the terms that constituted teachers’ professional vocabulary. The emphasis on the teacher’s voice was a distinguishing characteristic, and a significant intention of the project was to contribute to reducing the teacher/researcher gap (McIntyre, 2005).
The interest in professional vocabulary, describing the phenomena of the classroom, began with the recognition that practices of the classroom named by one community are not necessarily named by another. Professional lexicons from different cultural communities vary, and these differences and absences in vocabulary influence and indicate a diversity of teachers' worldviews about the classroom (Mesiti et al., 2021a). In most contexts, the teaching profession still lacks the documented professional language characteristic of established professions. For example, researchers agree that a technical or professional language to describe and analyse practice in teaching is underdeveloped among professional lexicons expressed in English (Grossman et al., 2009; Lampert, 2000).
The standardised use of English for international communication in educational research has made it difficult to develop a comprehensive and accurate view of the potential richness of professional lexicons in languages other than English. Accordingly, the initial aim of the Lexicon Project involved documenting the pedagogical-didactical terminology reasonably shared by mathematics teachers representing a rich diversity of educational cultures and languages. This first aim has been accomplished with the publication of a book detailing the ten lexicons (Mesiti et al., 2021a). These lexicons include a version in the original language and an English translation and constitute a set of objects available for further questioning and research.
In this paper, we explore the challenges of conducting a cross-lexicon comparison to investigate the possibility of moving towards an international lexicon. We focus on the Australian, Chilean, Czech and French lexicons, benefitting from the fact that the four co-authors have been tightly involved in the elaboration of these lexicons. These lexicons reflect differences in educational culture and pedagogical history and use some of the most commonly spoken languages in the world (see Sect. 4). We begin by outlining our theoretical background and propose an approach that involves re-imagining the terms as clustered around a related construct. The results that follow are analysed in consideration of the four national lexicons, the following research questions, and the aim of moving towards an international lexicon:
-
(i)
How might we identify and highlight productive connections across lexicons?
-
(ii)
What can we learn about the language of assessment when comparing lexicons?
-
(iii)
What can we learn about the language of mathematics when comparing lexicons?
Our analyses of these clusters have the potential to contribute significantly to the study and promotion of reflective practice for teachers of mathematics, as constructs found in other communities, and which are otherwise absent from one’s own, may operate as tools for reflection about one's practice.
2 Theoretical background
The theoretical background for this paper combines the theoretical framework adopted for the documentation of lexicons, that is, the role of language, with the theoretical elements regarding the characteristics of teachers’ professional discourse and comparative studies in mathematics education. This combination of theory supported our work in moving towards an international lexicon and is discussed below.
2.1 The role of language and the characteristics of teachers’ professional discourse
The theoretical position adopted for the Lexicon Project is that of linguistic relativity (Boroditsky, 2001; Casasanto, 2008; Levinson, 2003), which is a recognition that differences amongst languages may influence our thinking, our behaviour, and hence our lived experience. The notion that language shapes thought has been much debated and this weaker interpretation of the Sapir-Whorf hypothesis (Sapir, 1949), has been favoured ahead of other interpretations.
The researchers involved in this project recognised that the ten lexicons differ with respect to vocabulary, grammatical structure, and organisational categories. For example, the English language includes the gerund, composite words are a defining characteristic of Finnish and German lexicons, whilst the French, German, Spanish and Czech languages include grammatical genders. These structural differences in language affect people’s evaluation of similarity between objects, thus influencing the speaker to attend to certain aspects of language (Boroditsky et al., 2003).
Another major source of difference is the state of development of teachers’ professional discourse. The ten lexicons differ in the professional acts they name, and how these are named: these are sometimes reified into a single word, at other times expressed in both shorter and longer phrases. The benefit of a 'named' activity is that it can be readily observed and recognised within a classroom setting. This allows us to ask how well the activity is performed and how it might be improved. A classroom activity that cannot be named is less likely to be observed and less visible for reflective analysis. These differences must be considered in our attempt to move towards an international lexicon. However, this move must also be respectful of the cultural basis of each lexicon. For this purpose, we rely on constructs and views coming from comparative studies in mathematics education regarding classroom research and the way they are synthesised (Clarke, 2017).
2.2 Comparative studies in mathematics education
2.2.1 Complementary accounts
The experience provided by the Learner’s Perspective Study (LPS) (Clarke, 2006) emphasised the importance of approaching comparison in terms of complementarity rather than in terms of consensus and convergence. This approach resulted in the importance given in the LPS to the generation of “complementary accounts” (Clarke, 1997) of classroom practice by researchers from different cultures. The generation of such complementary accounts, the investigation of their commonalities, differences, and silences, act as a theoretical and methodological acknowledgement of the multiple potential meanings of the situations under study, of a complexity that no single account can capture. International comparison necessarily constructs boundaries (Akkerman & Bakker, 2011) and the act of comparison also constitutes an act of boundary crossing. Therefore, international comparative research should create and destabilise boundaries in ways that enhance our ability to benefit from other practices (Clarke, 2017).
The different lexicons documented for the Lexicon Project can be viewed as elemental for the generation of complementary accounts of classroom mathematical lessons. Moving towards internationalisation could be viewed as looking for connections likely to support the expression of this complementarity, and as looking for boundary objects likely to support the boundary crossing inherent in comparative studies.
2.2.2 Networking studies
The networking of theories enterprise shares with the Lexicon Project the conviction that diversity is a potential source of richness for the field of mathematics education. Differences amongst lexicons require systematic investigation. One essential idea from research on networking of theories is the diversity of possible networking strategies. The Scale of Networking Strategies (Prediger et al., 2008) organises these along a continuum between two extreme positions: ignoring other theories and unifying globally (Fig. 1).
Scale of networking strategies (Prediger et al., 2008)
Strategies are organised in pairs and not all strategies have similar ambitions. The strategies combining, and coordinating are generally used to make sense of empirical data, whilst integrating locally and synthesizing are strategies used for “putting together a small number of theories or theoretical approaches into a new framework" (p. 173). Not all strategies require the same level of compatibility between theories; coordinating, “a conceptual framework is built by well fitting elements from different theories,” (p. 172) requires complementarity of theories while combining purports that theoretical approaches are juxtaposed and may involve theories with conflicting basic principles. The Lexicon Project is not about theories; however, the Scale of Networking Strategies and the reflection it supports provided a source of inspiration for this study.
3 The International Classroom Lexicon Project: Research Design
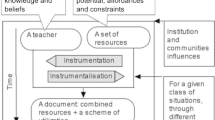
In the original international project, research teams followed a three-phase project-wide research design to document national lexicons. The main phases included a phase of identification, an iterative phase of validation, and a final phase of clarity check (see Fig. 2). This involved putting into practice a ‘negotiative methodology’ (Clarke, 2012; Mesiti et al., 2021a). The content of the lexicon was incrementally negotiated. Initially, the negotiation was conducted amongst the research team members, subsequently, this was expanded to include local, followed by national, mathematics community members. Research teams were stipulated to include junior and senior researchers as well as experienced middle-school mathematics teachers.
Main phases for the documentation of national lexicons (Mesiti et al., 2021a, p. 7)
In Phase One a stimulus package was assembled to include video material and time-stamped transcripts of a middle-school mathematics lesson from each community. This package of a variety of classroom settings and instructional approaches functioned as stimulus material to support the research teams’ responses to the prompt: “What do you see that you can name?” (Mesiti et al., 2021a, p. 8). Proposed names were recorded as candidate terms for the lexicon and additionally helped call to mind related terms that could also be considered for inclusion in the lexicon. Excluded from the lexicon were terms that referred to mathematical domains (e.g., algebra), mathematical tools (e.g., protractor) and mathematical objects (e.g., functions). Each term was operationalised with a description and illustrated with examples (and non-examples) from the classroom.
In Phase Two the draft lexicon underwent a validation process whereby opinions of relevant communities were sought to determine the extent to which the draft lexicon was seen as reasonable. The question was: “Do different communities within a country, who might employ such a lexicon, see its content and structure as reasonable?” (Mesiti et al., 2021a, p. 8). Validation processes were iterative and collaborative and included local interviews with mathematics education researchers and national surveys of mathematics teachers.
The final phase, Phase Three, involved a clarity check of the terms and their operational definitions (description and illustrative examples from the classroom). Each lexicon was checked by another team and problematic descriptions were identified for review by the originating team. This process ensured that the final lexicons were clear and understandable and free from ambiguity.
With the adoption of the three-phase project-wide methodology the original study has some limitations within which the national lexicons should be interpreted. The video stimulus included only nine lessons; one from each community. This material, coupled with the prompt, helped to stimulate thinking about candidate terms. Although a variety of classroom settings and activities were represented across the videos, not all possible classroom practices were captured. To address this limitation serious efforts were made by the research teams to complement this approach with free-association (where the identification of one term led to the identification of another related term). This process resulted in the inclusion of practices that were not visible in the original package of video material but were deemed necessary to include.
Additionally, only the members of the research team drafted the first versions of the lexicons. As such, we acknowledge their influence on the inclusion of candidate terms. The various and complex validation processes were designed to address this limitation. Educators were invited to comment on the familiarity, suitability and clarity of each of the terms in a variety of contexts. The contexts varied from community to community, however, various forums were adopted to document the opinions of educators. Each community’s validation processes have been detailed elsewhere (Mesiti et al., 2021a).
The objective of the larger, international project was to identify and document a professional lexicon of middle school mathematics teachers. The researchers recognised that a definitive lexicon, one that would hold for all in a teaching community in an individual country, was neither plausible nor realistic. As an alternative, the researchers aimed to document a lexicon that is a reasonable representation of language in use by mathematics teachers when speaking about the mathematics classroom. These national lexicons were validated as reasonable by local and national educators whose opinions we were able to access.
4 National lexicons: Australia, Chile, Czech Republic and France
National lexicons from Australia, Chile, Czech Republic, and France, as documented for the Lexicon Project, reflect differences in context, community, educational culture, and pedagogical history (Mesiti et al., 2021a). Three of the four teaching communities use the most commonly spoken languages in the world. English is spoken by 1.132 billion people (379 million native speakers), Spanish (the official language of Chile) is spoken by 534 million people (460 million native speakers), and French is spoken by 280 million people (77 million native speakers) (Ghosh, 2020). Middle school mathematics classrooms in these four countries share many common features, yet the professional language available to mathematics teachers is different in content and structure (Table 1).
The Australian Lexicon consists of 61 terms considered familiar to lower secondary school teachers of mathematics, organised across five teacher-informed categories. Distinguishing features of the Australian Lexicon include the following:
-
terms are generally expressed as gerunds and participles; this grammatical structure lends to the lexicon a distinct flexible and dynamic quality;
-
terms not only name general pedagogical practices but also reflect more than one pedagogical intention;
-
more terms identify classroom activities involving teacher actions than student actions, nevertheless, student voice and participation remain significant characteristics; and,
-
almost all terms are highly familiar to teachers, however, the frequency of their use in conversation varies.
The Chilean Lexicon contains 74 items, predominantly short phrases that are grouped in five categories with some terms belonging to more than one category. Distinguishing features of the Chilean Lexicon include the following:
-
the lexicon features predominantly short phrases as opposed to single word terms;
-
classroom phenomena are referred to in a passive form;
-
most of the terms that involve agency are actions performed by teachers; and
-
the lexicon is in the main a generalist one.
The 57 terms of the Czech Lexicon are organised across 11 categories. Distinguishing features of the Czech Lexicon include the following:
-
terms focus mainly on pupils’ and teachers’ observable activities;
-
terms can be used about lessons in any subject;
-
teachers tend to use everyday language rather than pedagogical terminology; and
-
there is a prevalence of student-oriented terms that reflect the importance attached to the teacher-student relationship.
The 116 terms of the French Lexicon are distributed across six categories and are highly influenced by the French educational context and culture. Distinguishing features include the following:
-
the lexicon’s mathematical orientation reflects the importance attached to the disciplines in this culture;
-
its didactic orientation reflects the existence of a strong didactic tradition in mathematics distinct from pedagogy;
-
its technical terms from didactic research illustrate the connection of this tradition to school practice; and
-
the small number of terms related to an affective dimension of teaching and learning processes reflects the limitations of French didactic research in this area.
4.1 Notable similarities and differences
The content of the four lexicons, including descriptive material and illustrative examples concerning each term, was shared amongst the researchers and reviewed to allow critical distinctions in meanings to emerge. The following differences were noted:
-
i.
The number of terms The French Lexicon has considerably more terms than the others and more of these relate to didactics of mathematics.
-
ii.
Lesson structure Terms related to the structure of the lesson (e.g., beginning, closure) are present in the Chilean, Czech, and French lexicons but absent from the Australian one.
-
iii.
Teaching strategies. Terms related to teaching strategies in the Czech and French lexicons are detailed and complex, and take more words to be described, than in the Chilean and Australian lexicons.
-
iv.
Mathematical terms The Australian and Czech lexicons do not include a category for terms related to mathematics.
-
v.
Affect-related terms The Czech and French lexicons have fewer terms and examples related to socio-emotional motivators, in comparison with the Chilean and Australian lexicons.
-
vi.
Pedagogical vs didactical lexicons The Australian, Czech and Chilean lexicons are more pedagogical than didactical (even though the Chilean Lexicon includes a category devoted to subject-matter didactics). This contrasts with the French Lexicon, in which historical influences impact its didactical nature (Blum et al., 2018).
It is important to note that if a term does not have an equivalent in another lexicon this does not necessarily mean that this classroom practice does not exist in that community. For example, the use of humour is included in the Chilean Lexicon but was not named in the other three. The use of humour in mathematics classrooms has been identified as a technique for creating a joyful, creative and positive classroom environment (Shmakov & Hannula, 2009). Our lexicons do not capture all the things that teachers name; however, exploring and reflecting on the lexicons of other communities allows us to recognise practices that were not included (for which a name does exist) as well as practices for which we have no name. This cross-lexicon comparative analysis has the potential to contribute significantly to the study and promotion of teachers’ practice, support their reflection on that practice, and highlight the cultural and historical underpinnings of the way the classroom is perceived.
5 In search of an international lexicon
From the commencement of the research project, of interest was the possibility of developing an ‘international lexicon’ of classroom-related terms. The first lexicon drafts helped clarify that building an international lexicon and conceptualising the form it could take was challenging. Terms that were considered similar or related were expressed differently. For instance, similar terms differed concerning the following:
-
i.
Detail Where the Australian Lexicon identifies the phenomenon of questioning the Chilean Lexicon has four questioning-related terms (pregunta por información, contra-preguntar, pregunta metacognitiva, pregunta por elaboración).
-
ii.
Actor A pairing of terms for student support differed by actor. The Australian term, peer support, refers to the student activity of peers assisting each other; the Chilean term, promover apoyo entre pares, refers to the teacher promoting such student activity.
Nonetheless, attempts to find commonalities between lexicons began early. They mainly took the form of comparisons between two lexicons (Artigue et al., 2017; Mesiti & Clarke, 2018; Mesiti et al., 2017, 2019) and illustrated diversity amongst the lexicons. They differed in the following aspects:
-
(a)
Content: number of terms, nature, ways in which they are defined and associated with examples and non-examples;
-
(b)
Organisational structure: number and names of categories, content of categories with similar names; and,
-
(c)
Status given to specificities of the mathematics discipline.
The educational and pedagogical history of each community is encrypted in each lexicon and the understanding of similarities and differences necessitates reflecting on this history (Artigue et al., 2017; Clarke et al., 2017).
Earlier comparative work across the three Australian, Chilean and Czech lexicons identified five triplet terms identically expressed in all three lexicons (Mesiti et al., 2020): formative assessment, disciplining, group work, student (individual) work and monitoring. Such comparisons seeking identical terms amongst the lexicons confirmed that this avenue offered little to explore concerning mathematics lessons. We needed to consider how productive connections can be developed among the different lexicons, allowing for enrichment of these while preserving their individual identity and coherence (see Research Question 1). Given the challenges, the experience gained in the enterprise of networking of theories (Bikner-Ahsbahs & Prediger, 2014) and the theoretical perspective of boundary crossing (Akkerman & Bakker, 2011; Bakker, 2016) helped us establish connections across defined borders.
6 Clusters as a unit of comparison
Few lexical terms are identically matched; the cultural diversity reflected in these lexicons, coupled with known limitations of the mathematics teachers’ technical professional language, have contributed to this phenomenon. For many lexical items, short phrases are used to capture teacher professional practice, which limits the possibility of one-to-one correspondence. Terms across lexicons are more likely to be interrelated, that is, belonging to similar categories denoting properties in common. Recognition of this attribute allowed us to reflect on the lexicons with open minds, re-imagining a more generous interpretation of what the terms, coupled with descriptions and examples, genuinely capture.
Given the structural diversity shown by the first comparative studies (Artigue et al., 2017; Mesiti & Clarke, 2018; Mesiti et al., 2017, 2019), we decided to move the boundaries created by these structures and identify significant clusters of neighbouring terms. Two clusters emerged as of particular interest:
-
(i)
An assessment cluster Our interest in an assessment cluster was motivated by the recognition that Assessment was a common category across the lexicons and all lexicons included assessment-related terms.
-
(ii)
A mathematics cluster The research project began with mathematics teachers and their classrooms, yet mathematical terms populate some of the lexicons and not others. Not only are general pedagogical practices of interest to the community, but so too is the pedagogical content knowledge for the teaching of mathematics.
The intention of working within clusters was to create meaningful and valid connections, offering the potential for enrichment of local professional terminologies. In a move towards internationalisation, we purposefully repositioned, and at times dissolved, the boundaries created by the categories developed locally in each community. The processes by which these were found are discussed in Sects. 7 and 8.
7 The assessment cluster
Networking studies have identified a diversity of strategies that can be employed in seeking connection (Bikner-Ahsbahs & Prediger, 2014). Some of the strategies have already been used in analyses related to the pairing of lexicons: these include making understandable, comparing, and contrasting. However, in a move towards an international lexicon more advanced forms of networking were required. We adopted the strategies of coordinating, synthesizing and integrating locally, adapting these to our specific purpose.
7.1 Establishing the cluster
We began with the entire data set, 308 terms in the four lexicons, which was examined and reduced to include a constellation of terms centred around the construct of assessment. This initial step was a move that resembled a form of coordination amongst the lexicons; its purpose was to gather terms similar in name and meaning. It soon became clear that although terms were complementary, they held subtle differences in meaning.
Researchers have argued that assessment practices take place continually in the classroom to help determine the gap between what students know and what is expected (Shavelson, 2006) and to provide informative feedback (assessment for learning) to support student learning (Black & Wiliam, 1998). Shavelson et al. (2008) proposed a continuum, with three distinct anchor points, to capture the range of forms of formative assessment: these range from the informal, unplanned, on-the-fly formative assessments at one end, to those planned-for-interaction assessment practices in the middle, to formal, planned, embedded assessments at the other end of the continuum. “Where a particular practice falls on the continuum depends on the amount of planning involved, its formality, the nature and quality of the data sought, and the nature of the feedback given to students by the teacher” (p. 300).
To share a nuanced understanding of the terms, we found the use of a continuum, extended from Shavelson et al. (2008), a useful tool for helping to distinguish and interpret our collection of assessment-related practices. A model was devised to represent features of the collection of assessment-related terms (Fig. 3) and to integrate the terms of the four lexicons in one display (Fig. 4). Using this model, we were able to accommodate the following practices.
-
(a)
Formal and informal assessment-related practices.
We identified the formal (and informal) assessment-related practices by identifying those that were planned for, usually ahead of time, that occurred regularly, and whose forms were recognisable and consistent.
-
(b)
The assessment-related practices that were on the periphery.
The assessment-related practices were situated on a continuum, with anchor points regulation at one end and evaluation at the other, to capture the range of forms of practices that were found in the lexicon. We extended the boundary of assessment beyond the sphere of evaluation to include practices of regulation, that is, those practices that are informal, in the moment, incidental, and either student or teacher-driven. In this way, we can capture those strategies that extend our cross-lexicon understanding of the function and form of assessment-related terms.
-
(c)
The assessment-related practices in which responsibility is given to students.
The participation of students in their learning is highlighted in the identification of those assessment-related practices that were intended to be student-led.
Our model (Fig. 3) was used to integrate the terms in the assessment cluster, from the four lexicons, in one display (Fig. 4). A quantitative summary of the findings is given in Table 2.
7.2 Assessment cluster by lexicon
7.2.1 Australia
This cluster of assessment-related terms includes 19 instances in total: these include 15 unique terms and four that appear in more than one location (Fig. 4 and Table 2). Eleven of these were originally part of the Assessment category locally defined by the Australian Lexicon Project research team: assessment, correcting, elicit understanding, feedback, formative assessment, marking, monitoring, reviewing, student responses, summative assessment, and test/testing. Four of these were neighbouring terms, originally not associated with an assessment category: checking, differentiation, giving praise, and reflecting.
A significant characteristic of the Australian Lexicon is the flexibility of meaning and intention within context (Mesiti et al., 2021b, 2021c); this flexibility is evidenced here by the number of terms that appear in more than one location on the graphical representation (checking, correcting, reviewing, and reflecting). This flexibility is also evidenced by the fact that almost all of the unique 15 terms, (except summative assessment and test/testing) are found in one or more other locally defined categories, namely, Administration (2 terms); Classroom Management (2); Learning Strategies (5); and, Teaching Strategies (11).
Fourteen of the 19 terms are considered teacher-led; four of these are quite formal in nature. Five of the terms are student-led (and all considered informal). Of interest is that the terms populate all points along the continuum giving insight into the complexity of practice concerning formative assessments. However, distribution along this continuum indicates a greater number of terms to describe teacher-led, evaluative activities.
7.2.2 Chile
Ten terms from the Chilean Lexicon relate to assessment (Fig. 4 and Table 2). They are equally distributed concerning formal and informal modes of assessment. Formal terms are located towards the evaluation end of the continuum whilst informal terms are more closely related to regulation. In the original organisation of terms in the Chilean Lexicon, these ten terms did not belong to the same category. They belonged to the following categories: General Pedagogies, Teaching Interactions, and Classroom Climate. A category named ‘evaluation’ or ‘assessment’ was not present in the Chilean Lexicon.
There are significantly fewer terms than in the other three lexicons. At first, this seems surprising as in Chile there is a culture of evaluation. However, commonly used terms such as testing, summative assessment, diagnostic assessment, and correcting are absent. This might be a consequence of the protocol used to create the lexicon within the Chilean team, in which the terms were significantly based on the phenomena directly observed in the stimulus package (see also Sect. 3). Activities such as testing or diagnostic assessment were not present in the video material, however, such activities are widely used by Chilean teachers (Calcagni et al., 2021).
7.2.3 Czech Republic
The assessment-related cluster in the Czech Lexicon includes 13 instances in total, 12 unique terms, one of which appears in more than one location (Fig. 4 and Table 2). The 12 terms are found in three different organisational categories, at times in more than one. Seven of these were originally part of the Assessment category locally defined by the Czech Lexicon Project research team, as follows: assessment general, assessment non-directed, commendation, self-assessment, summative assessment, formative assessment, and peer-assessment. Five of these were neighbouring terms, originally not associated with an assessment category, namely, checking homework, checking individual work, correcting of the didactical test, monitoring pupils’ work, and oral exam. Almost all the terms are featured on the evaluation end of the continuum and just over half of the terms are formal. In the Czech Republic there is a strong culture of evaluation (Slavík, 1999).
7.2.4 France
This cluster of assessment-related terms includes 28 instances in total, 23 unique terms, five of which appear in more than one location (Fig. 4 and Table 2). Seventeen of the 28 terms in this cluster are part of the category Pedagogical and Didactical Management of the Classroom and six terms belong to other categories. The terms correction, institutionalisation, kneading-up, and summary/synthesis belong to the category Lesson Phases, verifying belongs to the category Mathematical Activities, and narrative of research, which labels a task that requires a reflective stance, belongs to the category Nature of Tasks/Activities. Assessment is also one of the six study moments, a term belonging to the category General Terms (Artigue et al., 2021). We also found the following results:
-
some terms appear twice on the graphical display: formative assessment can be a formal activity (when anticipated) or an informal activity (when decided in the moment);
-
three terms denote activities whose responsibility can be given to both students and teachers, namely, commenting, comparing/ranking productions, validating/invalidating productions; and verifying denotes a mathematical activity that is also expected from students.
Most terms refer to activities led by teachers (21). Informal activities (17) are more numerous than formal activities (11). Many of the informal terms are situated on the regulation end of the continuum and these capture situations when these activities are not fully anticipated. The distribution across the continuum is rather balanced and all points are populated.
7.3 What can we learn about the language of assessment when comparing lexicons?
7.3.1 The synthesis of terms in the assessment cluster
The model for representing and integrating the terms in the assessment cluster (Fig. 3) has expanded our understanding of assessment and its neighbouring terms. Individual elements are situated concerning the following three dimensions: along a continuum from regulation to evaluation; whether student-led or teacher-led; and, whether formal or informal. The display supports our understanding of the clusters in helping us recognise the following results:
-
the number of terms in each cluster ranges from 10 to 28 (with terms appearing in more than one location);
-
there are more than twice as many teacher-led actions as student-led actions;
-
there are more informal terms than formal terms, and most of the formal terms are located on the evaluation end of the continuum;
-
the distribution of formal terms is similar across the Australian, Chilean, and Czech clusters, whereas the French teachers, on the other hand, have additionally identified the terms summary, institutionalisation, narrative of research, and differentiating as formal, practices anticipated ahead of the lesson;
-
the French and Chilean clusters identify peer-assessment and self-evaluation/self-evaluation as formal activities, the Czech and Australian clusters indicate that student-led activity is not formal, even if at the evaluation end of the continuum;
-
feedback is present only in the Australian cluster, however, it is increasing in use in other communities particularly as the interest and research in formative assessment grows; and,
-
monitoring was identified as an assessment-related term for the Australian, Chilean and Czech lexicons, and it was positioned as an informal teacher-led action closer to regulation than evaluation.
7.3.2 Productive connections in the assessment cluster
The French cluster was the most populated. One might hypothesise that this cluster captures all the terms within the other lexicons, nonetheless, several terms including test/testing, assessment (general and non-directed), student notices teacher’s mistake, monitoring and marking were absent. Of interest is that similar terms were positioned differently along the continuum (monitoring, formative assessment). Investigating these might assist our understanding of the difference in form and intention; and this might help us better understand our teaching culture and its approach to assessment-related practices.
Our work within this cluster, along three different dimensions, supported our intention to create meaningful and productive connections. This window into our own and others’ lexicons has offered us an opportunity to enrich local professional terminology. In this move towards internationalisation, we were able to position each community's practice by considering the notions of regulation and evaluation, formal and informal, student-led and teacher-led. This analysis moved our work beyond a one-dimensional comparison, where absence and presence are the only key features, to an integrated approach that revealed degrees of commonalities and relationships amongst the terms.
8 The mathematics cluster
The national lexicons were developed to identify the pedagogical-didactical teacher discourse, not the mathematical discourse. From the beginning, it was decided that terms referring to mathematical domains, such as algebra or geometry, or concepts such as rational number, were excluded. However, there was general agreement not to exclude a priori mathematically-related terms, denoting mathematical activities such as calculating, reasoning, or proving, or actions from teachers and students more specific to a mathematics classroom. The presence of such terms in the four lexicons is highly variable. For instance, the Australian Lexicon could be used in other disciplines (Mesiti et al., 2021b, 2021c), which is not at all the case for the French Lexicon, certainly the most mathematical of the ten lexicons. In this lexicon, there is a category named Mathematical Activities with 19 terms. All these terms express actions, 16 with a single word, a verb in the infinitive form, and the lexicon makes explicit that these actions can be performed both by teacher and by students. The Chilean Lexicon includes a category named Subject Matter Didactics with 22 terms. Terms in this category are more diverse. Some of them denote mathematical actions but many of them denote types of tasks or didactic practices of the teacher.
The Czech Lexicon, like the Australian one, does not have a mathematical category, however, some of the terms are specific to mathematics, such as counting on calculator, use of models and visualisation, found mainly in the category Use of Didactical Means. The Australian and Czech lexicons are not the only lexicons in the Lexicon Project not to include a category specific to mathematical terms. The aim of the project was to document a pedagogic vocabulary that was negotiated by and within national teams and with the larger mathematics community. The members of the French national team reported that their teachers requested a category devoted to mathematical forms of activities and this was seen as compatible with the focus on teachers’ pedagogical-didactic vocabulary.
8.1 Establishing the cluster
The following strategy was developed to identify the mathematics cluster. Starting with the two lexicons that contain a category specific to mathematics, the Chilean and French lexicons, we listed the mathematical terms within these and invited each co-author, after seeking expert advice, to classify the terms in one of the following four ways:
-
(i)
present the mathematical term is present in the lexicon
-
(ii)
close term the mathematical term is absent from the lexicon, but a close term exists in the lexicon
-
(iii)
candidate term the mathematical term is absent from the lexicon, but a candidate term exists
-
(iv)
absent the mathematical term is absent from the lexicon, there is neither a close nor candidate term.
A term was considered ‘present’ when a term exact in name and intention was identified. When considering whether there was an eligible ‘close term’ in the lexicon this involved consideration of the lexical items in relation to agency, form, breadth, and mathematical content. The researchers supported their analyses with discussions centred around exploring the ‘fullness’ of the definition—deciding which characteristics were crucial in understanding the meaning of the term and what action, activity or cognitive activity was being represented. This analysis was supported with readings and re-readings of the operational definitions of the term. The terms of the lexicon were identified as ‘close’ when they conveyed a similar idea but were not identical. These terms differed, for example, by containment (where one term was a subset of another term) and inter-relatedness (terms with properties in common but, for example, the agent differed). When an exact or close term in the lexicon could not be found the responsible co-author and up to six experts discussed the possibility of ‘candidate’ terms or synonyms in their language that capture the meaning of the mathematical term. The experts included members of the research team, teachers of mathematics, and mathematics educators. Where a candidate term could not be agreed upon, the mathematical term proposed from the Chilean or French lexicons was considered ‘absent’ from the lexicon and the community’s mathematical discourse.
There are 19 and 16 mathematical terms in the French and Chilean lexicons respectively. Table 3 lists these mathematical terms in the first column and the corresponding terms from the other lexicons are listed in the adjacent three columns. A quantitative summary of the findings is given in Table 4.
8.2 What can we learn about the language of mathematics when comparing lexicons?
The results in Tables 3 and 4 indicate that five of the original 35 mathematical terms are associated with present codes, 21 terms with close codes, 23 terms with candidate codes, and 11 terms with absent codes. Most of the terms (22 out of 35) have mixed associations, that is, the term is associated with more than one code. For example, the French term mathématiser (mathematical modelling) is present in the Australian Lexicon, a close term exists in the Czech Lexicon, but the term is absent from the Chilean Lexicon.
8.2.1 Term association: present, close and candidate terms
The majority of the mathematical terms (24 out of 35) are associated with present or close terms. If we consider the lexicons as they currently stand and expand the boundary of the mathematics cluster to include close terms, the count of present and close terms is as follows: French, 28; Chilean, 18; Czech, 14; and, Australian, 11 (see Tables 3 and 4). The French Lexicon remains more highly mathematical than the others and the Australian Lexicon remains the least mathematical even with the adoption of this generous re-interpretation of associations. Some of the close terms differed concerning containment; for example, the Chilean mathematical activity of solving a mathematical task together is matched against the Australian term whole class discussion which includes the activity described by the Chilean term as well as any “activity in which the teacher and students have the opportunity to engage in dialogue about the learning” (Mesiti et al., 2021b, 2021c, p. 51).
In the absence of close terms, we considered whether there were synonyms in our language that captured the meaning of the mathematical term. At times, the candidate term was a translation of the original term; consider the French mathematical terms estimating and generalising. At other times this was not possible nor sensible. However, it was of note to find that so many of the remaining mathematical terms were familiar and understandable to the community.
8.2.2 Term association: absent terms
Of the 11 terms associated with absent codes, eight were absent in more than one lexicon. The terms from the French Lexicon reflect the influence of French didactic research on teachers’ professional discourse (Blum et al., 2018). These three terms offer the possibility of enrichment:
-
(a)
changing the register of representation
Teachers are recognising the importance of using several semiotic representations to approach mathematical concepts, often with the support of calculators and mathematics digital tools.
-
(b)
problematizing
Increasingly emphasis is being paid to inquiry-based practices and the association of mathematical questions to a given context that this entails.
-
(c)
changing the setting
Increasing attention is being paid to the learning potential offered by connections.
The term, didactic variables (also present in the French Lexicon) originated with the Theory of Didactic Situations (TDS) (Blum et al., 2018). The remaining four terms, systematisation, valuing procedures, developing content within a problem, and formalising procedures, from the Chilean Lexicon, describe teacher practices not necessarily named in other communities but recognisable upon reading of the definition.
8.3 Productive connections in the mathematics cluster
This analysis revealed that the French mathematical terms captured, overall, mathematical activity that by its very nature has a universal quality to it. It can be performed by both teachers and students, in fact, by anyone doing mathematics, and the definition of the mathematical term focuses on the precise nature of this mathematical activity. In contrast, the Chilean mathematical terms were more didactical, capturing the variety of teaching activities that are present in the classroom to support the learning of mathematics.
The results confirm that most of the terms, even when absent, are considered familiar to teachers in the four countries. This familiarity indicates that the absence of terms in the currently documented national lexicons does not impede the move towards internationalisation. A way forward might involve enriching the current descriptions with comments and examples that capture the original forms of terms in other communities as well as the candidate terms.
9 Towards an international lexicon
The methodological practices advocated by ‘networking of theories’ has been a source of inspiration for our work and has supported us to think beyond mere comparison to other more advanced forms of connection. Earlier comparative studies of different lexicons, in consideration of the networking scale, made clear that the strategies used in these analyses did not move beyond the comparing/contrasting strategies. They were useful and effective strategies for providing evidence for the diversity of lexicons involved in the International Classroom Lexicon Project, but we needed to look beyond these in our move towards an international lexicon.
The strategies of coordinating, synthesizing and integrating locally helped us develop strategies unique to each cluster that highlight productive connections across the different lexicons. These approaches have supported our consideration of each lexicon as a system that can be explored and investigated beyond the single term-by-term comparison. We dissolved the boundaries formed by the existing categorical structures to move towards the adoption of clusters as an alternative unit of comparison; clusters can be envisaged as a collection of central and neighbouring terms connected across one or more dimensions. This is an original strategy specifically adapted to the aims of this study and its specific context.
The two quite different clusters at the centre of our analyses were the assessment cluster and the mathematics cluster. Creating a cluster was the first step. To coordinate, synthesize and integrate the terms within a cluster, development of strategies that helped identify meaningful and purposeful connections appropriate to the cluster were required. Due to differing characteristics of these clusters (their number, nature, and distribution of terms across differing categories), specific connecting strategies were created unique to the assessment and mathematics clusters.
The assessment cluster is centred around the notions of regulation and evaluation, and its terminology is not limited to the field of mathematics education. This cluster included terms from all the lexicons, and some were common, and others were not. However, even if the term was identical in its English translation there were differences in the visions conveyed by the descriptions and examples (it is worth noting that this also applied to the mathematics cluster). These differences were made more apparent with the adoption of a continuum within a three-dimensional model. This required a form of coordination and integration, in which terms similar in name and meaning were gathered and represented in a singular display. In the move towards internationalisation a significant feature of this visual synthesis is the positioning of terms with respect to three dimensions; this positioning highlighted relationships amongst the clusters yet preserved their cultural specificities.
The mathematics cluster is concerned with the language that considers mathematical specificity when speaking about the phenomena of the mathematics classroom. This language was categorised in two of the four lexicons, namely, the Chilean and the French ones, and even amongst these lexicons there were differences in the terms that were identified for inclusion in this category. In the French case, the terms describe forms of mathematical activity that can be performed by the student or teacher. In the Chilean case, the terms identify didactic practices of the teacher. Although categories of mathematical terminology do not exist in the two other documented lexicons (Australian and Czech lexicons), the description of most of the French and Chilean terms were understandable to the experienced teachers and teacher educators who took part in the research analysis. Indeed, many of the mathematical terms correspond to recognised practices; some are already named and when absent generally there are candidate terms to identify these.
Returning to our original research questions, where we aimed to identify and highlight productive connections amongst the four lexicons, we have developed methods and strategies that can be used to reveal meaningful connections amongst the lexicons concerning the language of assessment and practice. However, this study also has its limitations. Firstly, we involved only four of the ten documented lexicons identified in International Classroom Lexicon Project, and it would be of interest to test the results obtained with other lexicons. Secondly, only two different clusters have been studied. In the move towards an international lexicon, this study represents a first leap. As shown by the analysis of the assessment cluster, investigating degrees of commonality along three dimensions, amongst terms that were not always distinguishable by form and intention alone, reveals productive connections. Whilst the study of the mathematics cluster suggests that such a move towards an international lexicon could benefit from considering the already published lexicons as provisional entities, an international lexicon could result from the enrichment of these entities with new terms, comments or examples, facilitating connections that the collection of the original state of the different lexicons is unable to convey.
The lexicons have varied in content and in structure, and comparison until now has been constrained by the differing lexical organisational systems. The adoption of clusters as a unit of analysis has offered complementary insights in the move towards internationalisation. The analytical steps we have taken in this paper have confirmed that it is possible to progress from a one-dimensional strategy for comparison to a more advanced form of synthesis that recognises the complexity of classroom practice and the many cultural contexts in which mathematics is performed. The professional discourse of teachers in different communities appears more developed than the categories in the original lexicons captured. The move towards an international lexicon is not a move towards a single lexicon, but rather a move towards an integration of a collection of local lexicons, centred around clusters, evolving with each additional analysis.
References
Akkerman, S. F., & Bakker, A. (2011). Boundary crossing and boundary objects. Review of Educational Research, 81, 132–169.
Artigue, M., Grugeon-Allys, B., Horoks, J., & Pilet, J. (2021). Identifying the professional lexicon of middle-school mathematics teachers: The French case. In C. Mesiti, M. Artigue, H. Hollingsworth, Y. Cao, & D. J. Clarke (Eds.), Teachers talking about their classrooms: Learning from the professional lexicons of mathematics teachers around the world (pp. 179–192). Routledge.
Artigue, M., Novotná, J., Grugeon-Allys, B., Horoks, J., Hošpesová, A., Moraová, H., Pilet, J., & Žlábková, I. (2017). Comparing the professional lexicons of Czech and French mathematics teachers. In B. Kaur, W. K. Ho, T. L. Toh & B.H. Choy (Eds.), Proceedings of the 41st annual meeting of the international group for the psychology of mathematics education (Vol. 2, pp. 113–120). PME.
Bakker, A. (2016). Networking theories as an example of boundary crossing. Educational Studies in Mathematics, 93(2), 265–273.
Bikner-Ahsbahs, A., & Prediger, S. (Eds.). (2014). Networking of theories as a research practice in mathematics education. Springer.
Black, P., & Wiliam, D. (1998). Assessment and classroom learning. Assessment in Education: Principles, Policy and Practice, 5(1), 7–74.
Blum, W., Artigue, M., Mariotti, M. A., Strässer, R., & Van den Huevel-Panhuizen, M. (Eds.). (2018). European traditions in didactics of mathematics. Springer.
Boroditsky, L. (2001). Does language shape thought?: Mandarin and English speakers’ conception of time. Cognitive Psychology, 43, 1–22.
Boroditsky, L., Schmidt, L. A., & Phillips, W. (2003). Sex, syntax and semantics. In D. Gentner & S. Goldin-Meadow (Eds.), Language in mind: Advances in the study of language and thought (pp. 61–79). MIT Press.
Calcagni, E., Grau, V., Cortez, M., & Gómez, D. (2021). What we can name in the classroom: A Chilean Lexicon of middle-school mathematics teachers. In C. Mesiti, M. Artigue, H. Hollingsworth, Y. Cao, & D. J. Clarke (Eds.), Teachers talking about their classrooms: Learning from the professional lexicons of mathematics teachers around the world (pp. 55–70). Routledge.
Casasanto, D. (2008). Who’s afraid of the big bad Whorf? Crosslinguistic differences in temporal language and thought. Language Learning, 58(1), 63–79.
Clarke, D. J. (1997). Studying the classroom negotiation of meaning: Complementary accounts methodology. Journal for Research in Mathematics Education, Monograph No., 9, 98–111.
Clarke, D. J. (2006). The LPS research design. In D. Clarke, C. Keitel, & Y. Shimizu (Eds.), Mathematics classrooms in twelve countries: The insider’s perspective (pp. 15–37). Sense Publishers.
Clarke, D. J. (2012). Constructing and concealing difference in international comparative educational research [Keynote]. 2012 Finnish Educational Research Association (FERA) Conference on Education, Helsinki, Finland.
Clarke, D. J. (2017). Using cross-cultural comparison to interrogate the logic of classroom research in mathematics education. In B. Kaur, W.K. Ho, T. L Toh, & B. H Choy (Eds.), Proceedings of the 41st annual meeting of the international group for the psychology of mathematics education (Vol. 1, pp. 13–28). PME.
Clarke, D. J., Mesiti, C., Cao, Y., & Novotná, J. (2017). The lexicon project: Examining the consequences for international comparative research of pedagogical naming systems from different cultures. In T. Dooley, & G. Gueudet (Eds.), Proceedings of the tenth congress of the european society for research in mathematics education (pp. 1610–1617). ERME.
Ghosh, I. (2020). Ranked: The 100 most spoken languages around the world. Visual Capitalist. https://www.visualcapitalist.com/100-most-spoken-languages
Grossman, P., Compton, C., Igra, D., Ronfeldt, M., Shahan, E., & Williamson, P. W. (2009). Teaching practice: A cross-professional perspective. Teachers College Record, 111(9), 2055–2100.
Lampert, M. (2000). Knowing teaching: The intersection of research on teaching and qualitative research. Harvard Educational Review, 70(1), 86–99.
Levinson, S. C. (2003). Space in language and cognition: Explorations in cognitive diversity. Cambridge University Press.
McIntyre, D. (2005). Bridging the gap between research and practice. Cambridge Journal of Education, 35(3), 357–382.
Mesiti, C., Artigue, M., Hollingsworth, H., Cao, Y., & Clarke, D. J. (Eds.). (2021a). Teachers talking about their classrooms: Learning from the professional lexicons of mathematics teachers around the world. Routledge.
Mesiti, C., & Clarke, D. J. (2018). The professional, pedagogical language of mathematics teachers: A cultural artefact of significant value to the mathematics community. In E. Bergqvist, M. Österholm, C. Granberg, & L. Sumpter (Eds.), Proceedings of the 42nd conference of the international group for the psychology of mathematics education (Vol. 3, pp. 379–386). PME.
Mesiti, C., Clarke, D. J., Dobie, T., White, S., & Sherin, M. (2017). “What do you see that you can name?” Documenting the language teachers use to describe phenomena in middle school mathematics classrooms in Australia and the USA. In B. Kaur, W.K. Ho, T. L Toh, & B. H Choy (Eds.), Proceedings of the 41st annual meeting of the international group for the psychology of mathematics education (Vol. 2, pp. 241–248). PME.
Mesiti C., Grau, V., & Novotná, J. (2020). Exploring teachers’ professional language in three different communities: Detailing the early development of an international lexicon [Paper presentation]. ECER 2020—Educational Research (Re)connecting Communities, Glasgow, Scotland. Retrieved from https://eera-ecer.de/previous-ecers/ecer-2020-glasgow (Conference cancelled)
Mesiti, C., Novotná, J., Clarke, D. J., Hošpesová, A., & Hollingsworth, H. (2019). Speaking about the mathematics classroom: A comparison of the professional lexicons of teachers in Australia and the Czech Republic. In M. Graven, H. Venkat, A. Essien, & P. Vale (Eds.), Proceedings of the 43rd conference of the international group for the psychology of mathematics education (Vol. 3, pp. 89–96). PME.
Mesiti, C., Hollingsworth, H., & Clarke, D. J. (2021b). Naming aspects of teaching practice: Describing and analysing a lexicon of mathematics teachers in Australia. In C. Mesiti, M. Artigue, H. Hollingsworth, Y. Cao, & D. J. Clarke (Eds.), Teachers talking about their classrooms: Learning from the professional lexicons of mathematics teachers around the world (pp. 17–38). Routledge.
Mesiti, C., Hollingsworth, H., Clarke, D. J., Reed, A. S., & Roan, K. (2021c). Australian Lexicon. In C. Mesiti, M. Artigue, H. Hollingsworth, Y. Cao, & D. J. Clarke (Eds.), Teachers talking about their classrooms: Learning from the professional lexicons of mathematics teachers around the world (pp. 39–54). Routledge.
Prediger, S., Bikner-Ahsbahs, A., & Arzarello, F. (2008). Networking strategies and methods for connecting theoretical approaches—First steps towards a conceptual framework. ZDM—the International Journal on Mathematics Education, 40(2), 165–178.
Sapir, E. (1949). Selected writings on language, culture and personality. University of California Press.
Shavelson, R. J. (2006). On the integration of formative assessment in teaching and learning: Implications for new pathways in teacher education. In F. Oser, F. Achtenhagen, & U. Renold (Eds.), Competence-oriented teacher training: Old research demands and new pathways (pp. 63–78). Sense Publishers.
Shavelson, R. J., Young, D. B., Ayala, C. C., Brandon, P. R., Furtak, E. M., Ruiz-Primo, M. A., Tomita, M. K., & Yin, Y. (2008). On the impact of curriculum-embedded formative assessment on learning: A collaboration between curriculum and assessment developers. Applied Measurement in Education, 21(4), 295–314.
Shmakov, P., & Hannula, M. S. (2009). Humour as means to make mathematics enjoyable. In V. Durand-Guerrier, S. Soury-Lavergne & F. Arzarello (Eds.), Proceedings of the Sixth congress of the European society for research in mathematics education (pp. 144–153). ERME.
Slavík, J. (1999). Hodnocení v současné škole. Východiska a nové metody pro praxi. [Contemporary school assessment and evaluation. Starting points and new methods for practice.] Portál.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mesiti, C., Artigue, M., Grau, V. et al. Towards an international lexicon. ZDM Mathematics Education 54, 239–255 (2022). https://doi.org/10.1007/s11858-022-01349-3
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11858-022-01349-3