Abstract
Levering change is hard, and an incremental process. In the education process it requires an interaction between teachers, resources and learners. Levering change with human resources—teachers themselves, is a long term, time-intensive process requiring investment and commitment. The teacher–resources relationship is complex and not always optimal, particularly in disadvantaged educational environments where resources are constrained, and the education system is centralized and highly regulated. This article posits a mathematics teaching framework developed in a low-income educational context to make more transparent the relationship between teachers and resources to the benefit of learning both of teachers and of learners.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The complex and dialectic relationship between mathematics teachers and the resources in their practice has been elaborated through extensive research over the past two decades (Choppin et al., 2018; Fan et al., 2018; Gueudet & Trouche, 2009; Leshota, 2020; Pepin et al., 2013; Remillard, 2005; Remillard & Kim, 2020; Rezat & Strasser, 2012; Trouche et al., 2019). Frameworks conceptualising resources in teacher education (Adler, 2000) and as levers of educational change (Venkat & Graven, 2017) have extended how we think about each arm of the teacher–resource relationship. On the one hand, the what, why and how of a wide range of material and digital curriculum resources, artefacts and social and cultural resources including teacher communities (Arcavi, 2020), language and time (Adler, 2021; Venkat & Graven, 2017) have come in to view, with principles for the their educative design (Davis et al., 2017). On the other, we have learned a great deal about teachers’ themselves as they interact with resources, their knowledge bases, their learning and developing mathematics teaching identities (e.g. Ntow & Adler, 2019), their documentation practices (Trouche et al., 2019), their pedagogical design capacity and how this is distributed across teachers and their resources (Remillard, 2018).
Out of view and under-explored across this expansive body of work are ideational resources,Footnote 1 particularly frameworks that foreground key elements of mathematics teaching. In this paper I bring the why, what and how of such an ideational resource into view and build an argument as to the contributory role it can play in levering educational change.
Methodologically, I follow Davis et al., (2017) who synthesised results and findings from a science project on educative curriculum materials to move from earlier heuristics of their design research to the description of more substantive design principles for such materials (p. 293). In this paper I synthesise results and findings in previously published qualitative and quantitative studies in a research and professional development project to support an argument for the contributory role of an ideational resource such as a teaching framework in levering educational change. I organise the findings around key research questions:
-
1.
What evidence do we have of teachers’ learning and their learners’ attainments following teachers’ participation in the professional development project?
-
2.
What evidence do we have of teachers’ take-up and educative use of ideas from the teaching framework as they interacted with other curriculum related resources?
-
3.
How do the findings from 1 and 2 combine to illuminate the contribution of a teaching framework to levering change and how can this be explained?
I begin by locating the paper in the wider literature on the teacher–resources relationship with a specific focus on the inevitable design tensions in educative curriculum materials, and how these speak to ideational resources and teachers’ use of these in levering change. I then theorise this relationship through the notion of transparency (see below). Together these provide the framing for the description of the overall professional development project and the what, why and how of its teaching framework. A description and synthesis of the project’s inter-related research, methodologies, findings and results follows. By bringing a teaching framework into view and evidencing and theorising its role in levering improved teaching and learning, I hope to extend the literature on the teacher–resources relationship by offering ideational resources as contributory change levers, particularly in the context of mathematics teacher professional development.
2 The teacher–resources relationship and transparency of materials design
As noted, ideational resources are out of view in the wider literature on the teacher–resources relationship, with no apparent specific literature base focused on such a resource. Indeed, Pepin and Gueudet (2018) explicitly exclude conceptual frameworks, what they call “cognitive resources”, in their Mathematics Education Encyclopaedia entry on curriculum resources and textbooks. Pertinent to this paper, nevertheless, is literature on curriculum resources as levers for instructional change stretching back over two decades.
Ball and Cohen (1996), and others who have followed, emphasised that if curriculum materials were to be levers for instructional change, they needed to be ‘educative’ i.e. enabling teachers’ learning from these through their use (see also Davis & Krajcik, 2005). In the swathe of research on educative curriculum materials, the materials have ranged from designed curriculum packages and increasingly expanded mathematics textbooks and teacher guides produced to support mathematics curriculum reform and inquiry-based teaching in highly resourced educational contexts (e.g. Remillard & Kim, 2020); to scripted lessons plans also produced to support curriculum change, here in resource-constrained contexts where traditional teaching modes were the norm (Shalem et al., 2018). Within this body of work is a common argument that if materials are to be educative (i.e. also enable teacher learning) they need to be designed with greater transparency, to be more explicit to the teacher. In Remillard’s (2005) terms, they need to communicate “to” rather than “through” the teacher (see also Remillard & Kim, 2020). Principles to guide the design of materials to this end include the need for materials to be more explicit particularly with respect to subject specific i.e., mathematical demands and rationales for these. At the same time calls for greater transparency point to ‘design tensions’ in curriculum materials (Dietiker & Riling, 2018), and the need for “balance”: between “adequate support and too much, and … between prescription and teacher autonomy” (Davis et al., 2017, p. 302).
To give further substance to issues and tensions related to resource transparency and explicitness with regard to subject-specific demands, and to focus a review of literature pertinent this paper, I purposefully select and discuss in some detail three studies on the relationship between educative curriculum materials and teachers’ enactment. Two of the studies were conducted in the United States on curriculum reform materials, and teachers’ educative use of these. One was in science education (Davis et al., 2017), the other in mathematics (Remillard & Kim, 2020). The third similarly focused study was conducted in South Africa (Shalem et al., 2018). The South African materials were scripted lesson plans (SLPs) and thus more directive. All three were extensive, providing systematic descriptions of the designed curriculum materials or the SLPs in focus, and analyses of the relationship between these and observation of teachers’ enactments. Each study was located in a substantive, and overlapping, review of the field that I do not revisit here. More significantly, in their differences, produced in part by their differing theoretical orientations,Footnote 2 they offer an expanded view into the complexity of being explicit in the design of curriculum materials, and teachers’ use of these, across educational contexts. I draw from findings from these studies to reinforce the need for further reflection and research related to how greater transparency can be accomplished and how this shapes the teacher–resources relationship and so the motivation for, and hence location of, this paper.
Remillard and Kim (2020), and Shalem et al., (2018) found that authors’ ideas (both mathematical and instructional) were encodedFootnote 3 into and spread across different features of the materials without always being made explicit. As such they were more or less accessible. Remillard and Kim studied five sets of elementary mathematics curriculum materials, and teachers’ use of these. Shalem et al. studied mandated English language and mathematics scripted lesson plans and their daily use by elementary teachers across selected schools in one province in South Africa. Both studies found that the materials were clear on actions, on what teachers needed to do, but they did not make available the design rationales behind the foci and selections in the materials and the steps to follow in their enactment. Remillard and Kim (2020, p. 261) described this as a “tendency for curriculum authors to communicate through directing action as opposed to communicating to teachers”. In Wenger’s (1998) terms, the materials had procedural, but not cultural transparency, and I elaborate on this below.
Davis et al (2017, pp. 300–301) reached a similar conclusion. The science materials required new scientific practices. They found limited take-up by teachers of scientific argument and explanation. These were more opaque to teachers than some of the actions to be carried out. Hence the argument that the materials needed to be more ‘educative’ particularly in relation to scientific knowledge and ways of knowing and doing science. They described four general design principles of educative materials (materials needed to suggest adaptations; be situated and grounded in teachers’ practices; take multiple forms to highlight important content ideas and meet a range of teachers’ needs), adding two related to content specific demands on teachers. Principle 5 is that educative features should purposefully support teachers in the what, how and why of scientific explanation and its instruction. This needs to link with Design Principle 6: “connect to teachers’ existing teaching practice to create leverage points”. They argued further that designers needed to embrace developmental change, with more “straightforward practices” as entry points. Entry level scientific practices which were closer to teachers’ existing repertoires of teaching would be a developmental route to lever change.
Remillard and Kim (2020) also found that teacher directed materials were “more straightforward” for teachers to enact. They did not advocate these as necessary entry points but pointed to the greater difficulties teachers faced with inquiry-based activities that were reliant on eliciting learner contributions and their more complex co-ordination by the teacher towards the intended mathematical point of the lesson. They argued for materials to communicate more explicitly or transparently the key elements of content and pedagogic content knowledge aimed at, and their rationales. They found that while aspects of these knowledge elements could be made visible and so were part of the “objective conditions” of the materials, choices for these and their rationales, or design intentions in Choppin et al.’s (2018) terms, were driven by more invisible entailments.
In the South African study, the SLPs were largely organized around teacher directed instruction. Shalem et al. (2016) showed that SLPs were ‘thin’ on explicating key content ideas. These similarly specified actions to be followed but did not provide explicit elaborations of the content in focus, its key ideas and their rationales. This required teachers to bring “strong subject matter knowledge to transmit the conceptual relations that underly the teaching routines of the lesson plan” (p. 13). The irony here are consequences for equity: it is well known that high quality teachers are typically not found in schools serving learners from disadvantaged communities (OECD, 2013).
Shalem (2018, p. 184) goes further to help us understand that explicit communication of ideas and values related to knowledge and practice is easier said than done. She argues that “the most difficult task of teaching, and the one which has been shown to matter the most for closing the gap between middle- and working-class learners, is the transmission of evaluative criteria”. Communicating clear evaluative criteria for worthwhile knowledge and ways of knowing is conceptually demanding and distinguishes teaching as “specialised conceptual work”. She reinforces Davis et al.’s (2017) epistemic Design Principles 5 and 6. Designing SLPs to be more ‘educative’ and thus explicit about knowledge assumptions or expectations entails providing clear evaluative criteria. At the same time, Shalem reminds us curriculum materials cannot compensate for the know-how of teachers.
Collectively these studies show the need for educative materials to be more explicit particularly with key content ideas and their evaluative criteria, as well as the designers’ rationales. Across the materials, procedural transparency—what to do—was evident. Less explicit were the epistemological underpinnings of the materials and design rationales, reflecting inherent tensions in the design of materials to support curriculum reform. Davis et al. (2017, p. 302) called for further research related to these tensions, as well as more specifically focused studies that disaggregated key design principles. Like Shalem (2018), they argued further that materials themselves are not a panacea and called for empirical research to “investigate how professional development and educative curriculum materials work together to support teacher learning” and lever change. The investigation in this paper is a response and contribution to this call.
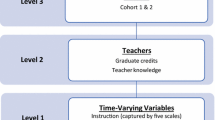
However, a question remains. What accounts for the limits to curriculum materials? Why do epistemic elements and their rationales remain implicit—accessible to some, and opaque and perhaps alienating to others? What is it that resides in the teacher-resource relation that can help us to theorise further its complexity, and move towards understanding and producing developmental materials as change levers? In their initiating work on educative resources Ball and Cohen (1996) described the teacher–resource relationship with a third arm—the context in which this occurs. Shalem et al. (2018) show how authority relations in the wider social context can support or thwart teachers’ use of materials. Extending this line of thinking, and developing my earlier work, I propose the notion of “relational transparency” as a theoretical means for understanding the inevitable gap between resources and their users, a gap that is profoundly shaped by socio-cultural practices and hence in the realm of the invisible, with suggestions for possible contributions to bridging this in particular settings.
3 Theorising transparency
In Adler (2000), I posited that access to resources was not only a function of what they were and how they were used but also their “transparency”. I drew on Lave and Wenger’s (1991) theory of situated learning that increasing participation in any social practice was a function of access to resources in the practice, and that these could be more or less transparent. What this signalled was that in addition to what was made available through resources were questions of how, as well as for whom?
For Lave and Wenger, (1991, pp. 102–103), “transparency in its simplest form may just imply that the inner workings of an artifact are available for the [user’s] inspection”. However, the knowledge and practices of the community, with all its history, are “encoded” in the resource, creating a “cultural organization of access”. Depending on how these resources are being used, by whom and in what kinds of social practices, the “inner workings” will be more or less transparent and so more or less accessible to newcomers and participants more broadly in the practice. Lave & Wenger elaborated their notion of “transparency” as combining “invisibility and visibility: invisibility in the form of unproblematic interpretation and integration into activity, and visibility in the form of extended access to information”. Extended information in the context of curriculum materials would include particular activities, or explanations of mathematical ideas, i.e. what Remillard and Kim (2020) referred to as visible objective conditions. However, interpretation and hence integration into the activity in the practice is a function of the ideas and values encoded into the materials, and hence at the level of the invisible.
From this dual perspective of visibility/invisibility, transparency is not a feature of the resource in itself. For Lave and Wenger it is “a process that involves specific forms of participation in which the technology fulfils a mediating function”. While the ‘technology’ (and for our purposes curriculum materials) fulfils a ‘mediating function’, its use and so its mediating potential is a process of participation. Transparency lies in the use of the resource in a socio-cultural context, and thus in the relationship between the user and the resource in practice. Transparency is relational. Access to a practice through access to its resources requires more than materials, illuminating Davis et al.’s (2017) point of materials not being a panacea. Additional forms of participation with the materials are needed.
In Fig. 1 above, I illustrate relational transparency, adding in the useful distinction made by Wenger (1998) between procedural and cultural transparency, a distinction emerging from his analysis of how insurance claims processors learned with and through the resources in their practice. He draws our attention to a worksheet that was procedurally clear to the processors following their training in its use. They were able to carry out all the steps required to complete the worksheet. It was transparent with respect to what to “do”, what actions to carry out. However, the rationales for these, and how they came to be what they were, and thus their significance in the practice were not. The claims processors were unable to respond to questions about how and why from claimants. The cultural practices that supported “unproblematic integration” of the technologies into their work were opaque, tied to the history, cultural and social practices in which they had been and now needed to function. The distinction between procedural and cultural transparency is useful as it extends how we think about the complex socio-cultural relation between teachers and their resources, together with interacting forms of participation.
Curriculum materials design is clearly complex, and more so with an eye on concerns for equity. It is one thing to know that the materials need to be explicit about the valued content and how to steer instruction so that this can be learned. The materials also need to connect with teachers, which entails an appreciation of the inevitable gap between what teachers bring, the nature of intended change, and how these will interact in the socio-cultural contexts in which they will function. The latter points to the importance of attention to key design principles and participation with these that could support the interaction between teachers and their curriculum resources developmentally and over time.
These understandings, while not as clearly articulated at the outset, informed the choices made in designing a professional development intervention for a selection of lower secondary mathematics teachers in South Africa, an intervention that included the development and mediation of a mathematics teaching framework.
4 The wits Maths Connect Secondary Project and the what, why and how of its mathematics teaching framework
The Wits Maths Connect Secondary Project (WMCS) project was a 10-year longitudinal research linked professional development (PD) aimed at improving the quality of teaching, and through this, learners’ opportunities to learn mathematics. The project began in 2010, and over time, worked with 180 mathematics teachers teaching Grades 8–10 across 80 schools that drew their learners from low-income communities. The focus on teaching quality and improved learning outcomes is critical in the South African education context which continues to be characterised by deep inequality, enduring high poverty levels, and related poor educational outcomes for students, particularly in such schools. These, typically, are over-crowded, with constrained human and material resources to name just two conditions shaping teachers’ work.
The details of the project and its intervention have been described elsewhere (Adler, 2017; Adler & Pillay, 2017a, 2017b). Briefly, we knew that any potential success of our intervention would depend on whether and how the project connected with teachers in their schools and classrooms, and this included their current practices and the materials with which they were required to work. South Africa has a national curriculum, strongly regulated by official annual teaching plans. During our work in the project, these were supplemented with daily lesson plans. Of concern to us was that despite prescription of what was to be taught when and how, lessons observed were mathematically incoherent. The mathematical object of learning was out of focus. Despite an announced topic, frequently there was no apparent mathematical story linking what learners were to know and be able to do. There were disconnects between the exemplification of the object and the accompanying explanatory talk (Venkat & Adler, 2012). Moreover, our collaboration with schools soon confirmed that while many teachers of learners in the lower secondary grades were “qualified”, this did not necessarily equate with them being “mathematically” prepared for teaching in these grades. Many had received poor quality pre-service education. There were also out-of-field teachers, some trained as primary teachers, others qualified in different subjects. All this underscored a key dimension of inequality that shaped our work. As with schools in low-income communities elsewhere, learners, particularly in Grades 8 and 9, had poor access to a suitably qualified mathematics teacher with appropriate depth of mathematical knowledge and professional experience (CDE, 2010).
With our underlying equity agenda, our major intervention was a 16-day course spread over an academic year and called Transition Maths 1 (TM1). We were clear that we needed to work first and foremost with the human resources in the schools, and specifically the teachers’ mathematical knowledge base. We also understood the extent to which the curriculum materials supporting teachers’ work were fixed and regulated by the education department. We needed to support teachers’ work with these. We described the course as a mathematics for teaching (mft) course as it included both subject matter (SMK) and pedagogical content knowledge (PCK) in Shulman’s (1987) terms, as well as specialised content knowledge (SCK) in Ball et al.’s (2008) terms. As we have argued elsewhere, the boundary between these professional knowledge categories blur, particularly in the practice of mathematics teacher education and so we work with the notion of “mathematics-for-teaching” (mft) (Adler & Davis, 2006) as an amalgam of mathematical and mathematics teaching knowledge.
Roughly two thirds of the TM1 course provided opportunities for teachers to strengthen their mathematical knowledge for the grades they were teaching and beyond, as well as their underlying relationship with mathematics as disciplinary knowledge (see Pournara & Barmby, 2019; Pournara et al., 2015). Our working hypothesis was that with a stronger base in mathematics, and a guiding teaching framework, available curriculum material resources could be used in educative ways. In the remaining third of the course, we mediated particular instructional practices, reified in the framework. In terms of the literature, our intervention in the teacher–resources relationship was to strengthen subjective conditions as depicted in Fig. 1 i.e., teachers’ mft with structured opportunities in the course sessions for teachers to participate with mathematics and the framework to which I now turn.
5 The what, how and why of the WMCS mathematics teaching framework
Over its ten years of professional development work, the WMCS developed and refined a ‘living’ teaching framework that has operated as a boundary object (Akkerman & Bakker, 2011) adjusting to meet the different practices we moved between: the practices of teacher educationFootnote 4 and the practices of mathematics teaching on the one hand, and the practices of researchFootnote 5 on the other (Adler, 2017). The mathematics teaching framework (MTF) is the teaching version, and it was developed as a resource for teachers’ use in their interaction with other resources as they went about their work of teaching. Prieur (in Wang, 2019) would call the MTF a “meta-resource” as its raison d’être is its use in supporting a reflective attitude of teachers in their design and use of other resources. I refer to the MTF as an ideational resource to foreground it as a reified set of ideas about mathematics and mathematics teaching in general, and ideas in a mathematics lesson in particular. It was designed to make visible the valued mathematics and mathematics teaching rationales of the project overall, and through this to serve as a support for teachers in their teaching and learning about their mathematics teaching and to contribute to levering change.
The overall project and its interventions, including the MTF, were grounded in the contextual realities in which teachers were working, and simultaneously informed by our overall socio-cultural orientation to knowledge and practice and key tenets of socio-cultural theory, as well as research in mathematics education. Briefly, these tenets included an orientation to mathematics as coherent and connected scientific knowledge (Vygotsky, 1978); to mathematics teaching and learning as goal directed with mediation towards learners’ appropriation of the increasingly sophisticated and increasingly general ways of thinking that constitute progression in the discipline. Critically, teaching was always about something (Alexander, 2000) and the coherent mediation of that ‘something’ was understood as the teacher’s work.
These tenets have been interpreted into the WMCS MTF presented in Fig. 2 above. If teaching is always about ‘something’, a first step in coherent mathematics teaching is being able to articulate the object of learning in a lesson: that which students are to come to know and be able to do. The heuristic signified in the “Lesson Goal” box in Fig. 2 is for the teacher to articulate her lesson goals in this way. While such as a step is in many ways obvious to any teacher, its enactment towards coherent teaching is not trivial. Moreover, SLPs typically have explicit lesson objectives. It is how these connect with what follows that is critical. The MTF focuses on three recognisable teaching practices as key mediational means in mathematics classroom instruction: exemplification (examples, tasks, and their representational forms), explanatory communication (word use and justifications) and learner participation (what learnersFootnote 6 are invited to do, say and write). These instructional, and ultimately cultural tools were informed by the literature on exemplification in mathematics and mathematics education (Bills et al., 2006) and language as a resource in mathematics teaching and learning with emphasis on lexicalisation on the one hand (Planas, 2020), and explicit criteria for mathematical explanations on the other (Prediger, 2019). Their salience in the framework, and the PD, was their resonance with on the ground practices, and thus with possibilities for connection with teachers—and design principle 5 highlighted in the literature above.
The left hand side of Fig. 2 presents the objective and visible ideas in the framework. We refer to the representation of the framework on the left of the figure as the first level of reification of the ideas of the MTF. The ideas are named (examples, word use etc.), and also linked to desired and named end-goals: building generality, and substantiating mathematics with full explanations. These complex ideas and values related to both mathematics and teaching are encoded into the component boxes in the framework. The framework has been elaborated to a second level with the MTF now a five-page document. The left side of Fig. 2 is the first page of the document. Page 2 extends description of the object of learning or lesson goal and includes curriculum and mathematical analysis of the object of learning. Page 3 extends exemplification, making visible the importance of variation amidst invariance in building generality (Watson & Mason, 2006). On page 4, the extension of learner participation includes extended description of learners’ mathematical actions and whether and how they use mathematical language and have opportunity to articulate their reasoning and justify their thinking. On page 5, the extension of explanatory communication includes extended descriptions of board use, word use and justification. The extension of justification into different kinds of evaluative criteria is illustrated in a box on the right side of Fig. 2.
The MTF and its extended components were explicitly mediated in the TM1 teaching sessions. Teachers worked with a printed hard copy of the 5-page MTF alongside related curriculum materials (prescribed textbooks, departmental lesson plans, and additional materials selected by the project). For example, in a session on exemplification, teachers studied the example set in a prescribed lesson plan on the multiplication and division rules of exponents. Their task in the session was to use their experience, their prescribed textbooks and TM1 course materials, to consider the quality of the selected examples and their sequencing; and using principles of variation (as elaborated in the MTF on page 3), refine the lesson plan with particular attention to exemplification. The MTF itself is thus a cultural resource in that it encodes valued ideas of mathematics and mathematics teaching. Its productive and educative use by teachers, both its parts, and as a whole, as they plan/reflect on their lessons and the curriculum resources used, depends on what sense teachers make of the ideas and values encoded into the framework and its underlying rationale.
Research on educative curriculum materials revealed the complexities in written texts of making underlying rationales, ideas, and values explicit. So too, as we have learned, is this a non-trivial task even in direct interaction with teachers. Indeed, there was a great deal of refining of the MTF in successive iterations of the TM1 course. Our mediation of exemplification and explanatory communication, their rationales, ideas and values have been elaborated in Adler and Pournara (2020), and Adler (2021) respectively. In each of these articles we locate these elements of the framework in the literature, and articulate and illustrate the principles that guided this work with data from our course sessions. Working from the overarching principle that modelling teaching practices did not equate with their explicit mediation, three further principles of practice structured the design and development of tasks to support the mediation of the components of the MTF. These are listed in Table 1.
Reflecting back to the Davis et al.’s (2017) design principles, the MTF embodies their four general principles (noted in Sect. 2 above). The MTF is situated and grounded in practice, close enough to teachers’ work to be “entry points” towards more coherent teaching. As a framework for planning and reflection on teaching, it encourages and supports teachers’ adaptation of the materials they have. The MTF supports teachers’ educative use of the mandated curriculum materials. By disaggregating practice into key components such as exemplification, explanatory communication, and learner participation, it supports diverse possibilities for take up, and thus diversity across teachers. The MTF provides explicit evaluative criteria for exemplification (systematic variation in example sets) and explanatory communication (mathematical justification, appropriate use of mathematical language).
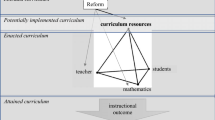
At the same time, in the MTF itself, there is no topic specific elaboration of generality, properties, definitions and so on to justify mathematical claims. The ideas were about mathematics or metamathematical, and not mathematical ideas per se. Opportunities to engage with these ideas relevant to specific mathematical content, linked to the curriculum materials teachers had, were provided in mathematics teaching focused course sessions through content specific tasks designed to mediate the MTF and its elements (themselves mediational means). The MTF was thus an object of learning for the teachers in the TM1 course, as well as a resource for educative use of curriculum materials in the context of their teaching, as illustrated in Fig. 3 above.
I now turn to answering the research questions on p. 2. These structure the presentation of the findings from multiple studies in the next section.
6 WMCS research studies, their methods and outcomes
The evidence presented below shows significant impact on participating teachers’ mft (our direct point of intervention); and diverse, uneven teacher learning and take-up of exemplification and explanatory communication teaching practices. Evidence is also presented of the modest, relatively small but significant increments in the mathematics attainment of the learners of participating teachers’ (indirect effects). Together the studies discussed below point to the contributory role of the MTF in levering change. The complexities of conducting rigorous research that links an intervention, be this through curriculum materials, and/or professional development, to improved teaching quality that is in turn related to increases in student attainment are well known (Davis & Krajcik, 2005, p. 10). I thus also point to the methodologies used and literature base of the various studies and their findings.
-
The quasi-experimental learning gains study: research question 1
Questions about the impact of professional development on learner attainment prevail, world over. A review of studies of professional development relating to school mathematics, showed that very few of the initiatives which met acceptable standards of rigor also led to positive effects on learner attainment. Moreover, effect sizes reported on learner attainment for teachers who had attended two courses in a PD intervention were relatively small (e.g., 0.20 Hedge’s g) (See Gersten et al. (2014), and Sample-McMeeking et al., (2012) respectively, cited in Pournara and Barmby (2019)).
Cognisant of the methodological difficulties in such studies and building from our experience in 2013 with a small pilot study of “learning gains” (Pournara et al., 2015), in 2018 we carried out a quasi-experimental study of learning gains (Pournara & Barmby, 2019). The sample comprised 31 intervention teachers, 16 from the 2016 and 15 from the 2017 TM1 cohorts and 1587 of their Grade 9 or 10 learners; and 23 comparison teachers with 1531 Grade 9 or 10 learners. The pre/post learner test was developed, piloted, and revised in 2017. A repeated measures ANOVA analysis was carried out to see whether the interaction between pre/post gains in the learner assessment and the learners’ group (control vs TM1) was statistically significant. As we wished to investigate whether improved teachers’ mathematical knowledge led to gains in their learners’ achievement, the study design included analysis of assessments of teachers’ mathematical knowledge at the start and end of the course. A repeated sample t-test was conducted on teachers’ scores for TM1 to determine whether gains were statistically significant. All results and tables below are extracted from Pournara and Barmby, with the first showing significant improvement in the teachers’ mathematic test-scores in both 2016 and 2017 (Table 2).
Pournara and Barmby concluded that not only did these results indicate that the course had a significant impact on teachers’ mft, but that the statistics under-reported the impact because the post-course test was substantially harder. It also covered more topics than the pre-test.
The results of the learner test scores for the pre- and post-tests are presented in Table 3. Mean scores for the comparison group and the TM1 learners were compared. A repeated measures ANOVA analysis showed significant interaction between pre/post-test and learner group (F = 9.321, df = 1, p < 0.001). The effect size between the comparison and the combined TM1 group in the pre-test was of the order of 0.3. In the post-test, this was reduced to 0.1. So, a change in the effect size of 0.2 took place in favor of the TM1 group, an effect size similar to that reported by Sample-McMeeking et al. (op cit).
Pournara and Barmby (2019, p. 222) concluded that there was a statistically significant difference in the gains in the learner test scores pre to post between the comparison group and the TM1 group. In addition, a disaggregation of the TM1 learners taught by teachers in the 2016 cohort of the TM1 course and those in the 2017 cohort of TM1 (Table 4) showed that that the gains made by the learners taught by the TM1 2016 cohort of teachers were considerably bigger than those taught by the 2017 cohort, arguing that this finding was “in line with our expectations and the literature … that there is a delayed effect of professional development on learner attainment”.
I have presented some detail here as the learning gains study showed that improving teachers’ subject knowledge leads to improved access to mathematics for their learners. While the gains were small, they were not out of line. Levering such change is typically incremental, and crucially important in a context where poor attainment in mathematics appeared intractable.
Of course, impact studies while critical for determining end point goals of student learning cannot provide insights into the mechanisms which enable or constrain the desired change. I turn to a set of small qualitative studies to explore whether and how teachers’ use of the MTF contributed to these results.
-
Qualitative studies on teaching and teachers’ use of the MTF: research question 2
-
Teachers’ algebra knowledge and opportunities made available to learn
Early in the project we set out to study the opportunities made available to learn mathematics in participating teachers’ mathematics teaching pre and post their participation in the 2012 TM1 course. We collected video records of teaching from all participating teachers at the start of the TM1 course, and then post completion of the course in early 2013. We described opportunities made available to learn in terms of our goals for more coherent lessons, where example sets and accompanying explanatory talk cohered with the object of learning, and learners were invited to participate in doing and talking mathematically, of course in relation to the object of learning. The alignment here with the MTF is apparent and a first task was to construct an analytic frameworkFootnote 7 for the video-data to enable description and interpretation of differences in teaching and the mathematics made available to learn. We named this the mathematics discourse in instruction (MDI) framework where each of the constructs of exemplification, explanatory talk and learner participation were defined and operationalized (see Adler & Ronda, 2015). I return later to discuss this pre-post video study.
I start instead with a sub study reported in Ronda and Adler (2019) of the relationship between teachers’ subject knowledge and the quality of their teaching. Within the above video-data were algebra lessons of seven 2012 TM1 teachers after completing the MT1 course. We had data on the teachers’ scores on the algebra items in their end of course test, scores that conveniently ranged across the cohort. Using the MDI framework, we were able to relate the teachers’ algebra knowledge to the algebra they made available to learn. Analysis of their lessons focused on how they exemplified and explained algebra and by inference the coherence of their lessons. We found a correlation between the measure we had of teachers’ algebra knowledge, and the features of the example sets in their lessons that were critical to the object of learning and its generalisation. In addition, teachers with higher algebra test scores offered more complete justifications in their explanatory communication with learners.
This study was small and focused on limited content. We make no hard claims for what has been argued elsewhere: that teachers content knowledge matters for the quality of their mathematics teaching. I report this study as it highlights correlations between higher test scores, and better quality teaching in terms of the ideas and values encoded into the MTF. These findings, however limited, reinforced our intervention strategy. Of course, the specific role of the MTF contributing to the results of learning gains remains backgrounded. Further qualitative studies point in this direction.
-
The teacher–textbook relationship
A qualitative study on teachers’ mobilisation of the affordances of the textbook informed the intervention and MTF use (Leshota, 2020). The study was motivated by our observations of incoherent teaching coupled with a sense that teachers were working haphazardly rather than deliberately with the prescribed textbooks available in their schools. Seven teachers across three schools were observed teaching the topic of functions in Grade 10, with data collected in 2011, prior to teachers’ participation in TM1 in 2012. As anticipated, teachers adapted the contents and activities in the textbook, with injections (elements of the lesson that were not available in the textbook) as well as omissions (elements that were available in the textbook that did not appear in their lessons). Critically, there were “detractive omissions” i.e., key conceptual ideas and related activities available in their textbook were omitted by some of the teachers in their lessons. There were also productive injections, but in some cases, these introduced error. The overarching findings pointed to “generally tacit use of the textbook” (Leshota, 2020, p. 1) and a “need to “strengthen teachers’ capacity to perceive the affordances (and constraints) of the prescribed textbook” (p. 10). These results supported the project’s starting assumption that teachers could benefit from participation in activities that promoted their deliberate and more productive use of their mandated curriculum resources, activities supported by an ideational resource like the MTF.
-
Teachers learning to use the MTF through participation in lesson study
Between 2014 and 2016, we carried out a series of lesson study cycles in three different school clusters (see Adler & Alshwaikh, 2019). Project team members worked with a group of teachers in a cluster to plan, teach and reflect on lessons, deliberately using the MTF as a guide. One of the goals of this small side project alongside the TM1 course was to explore with teachers in their school contexts, the contributory role of a resource like the MTF for working on teaching. Thembi, one of the teachers, captures key findings from this work:
What I have learned … is not only about my teaching and the strategies I use, but it is about giving them [learners] the mathematics that is behind each and every topic so that they understand what we are doing. The reflection has helped a lot. We can reflect on what language are the learners using … And most of all looking at the examples, that is one where we have grown a lot, what examples we use and why we use such examples. (Thembi Ndlovu,Footnote 8 TM1 2013, Seminar, June 2016).
Thembi’s self-report on learning about word use and exemplification, and particularly example sets, was echoed in evaluation self-reports completed by each cohort of MT1 teachers at the end of the course.
The way I prepare my lessons has changed … I do not take a textbook and give learners examples and activities; but I do the work first, then look for cohesion my examples have towards the attainment of my lesson goals. (Mary Mdluli, TM1 2016)
Mary, and many others, explicitly pointed to more deliberate use of her textbook, particularly with selection of examples, and thus of using it in more educative ways supported by the MTF. This evidences greater relational transparency between the teachers and their available resources, and an improvement of the teacher–curriculum resources relationship found by Leshota (2020). A further contributory role of the MTF as expressed by both Thembi and Mary was towards lesson coherence. Thembi spoke of having informed rationales (being able to say why) for her choice of examples, and Mary actively sought coherence between the examples she chose and her lesson goals, reflecting the importance of the connective elements of the MTF.
Evidence of take-up, or in other words of learning and more educative use of other material resources by teachers, needs to extend beyond self-reports. In 2016 we systematically studied the evolution of a lesson, its preparation, enactments and reflection, during a lesson study cycle focused on ‘brackets’ and the distributive law, a topic chosen by the participating teachers. Data included the evolving lesson plan, and video-records in all planning and reflective discussions. The initial planning session in the cycle focused on examining curriculum texts (curriculum guidelines, mandated lesson plans and textbooks) that combined with teachers’ own experience in their teaching, and in the project, to refine an object of learning, and produce a first lesson plan. In Adler and Alshwaikh (2019) we focused in on teachers’ take-up of exemplification and careful use of words in their lesson, and how this evolved through the lesson study cycle. We examined the evolving lesson plan and the discussions following its enactments that produced successive changes. With respect to the example sets and how these changed through three iterations of the lesson planning, there was clear evidence of teachers’ attention to “variation amidst invariance so as to bring generality, structure and strategy into focus with learners” (p. 338). We reported challenges teachers faced enacting increased task demands and mediating the justification of key mathematics ideas in interaction with learners.
That teachers used and reflected on elements of the MTF was to be expected within the lesson study work. The MTF was an explicit structuring resource in the collaborative planning and reflection during the lesson study cycle. For the project, however, that teachers were able to explicitly use the components of the MTF as they engaged with available curriculum materials, planned and reflected on their lessons, together with their self-reports, confirmed its value as an ideational resource designed to support teaching and the teacher–resources relationship. But what then of teachers’ take-up of the MTF in their day-to-day teaching, without the collaborative support of a lesson study?
-
Teachers take up of the MTF: a study of practice-linked identity resources
In 2016–2017 we studied five purposefully selected TM1 2016 teachers’ take-up from their participation in MT1 course, including their use of the MTF. In Ntow and Adler (2019), we used Nazir and Cook’s (2009) framework of “practice-linked identity resources” to explore, in depth, the learning of two contrasting teachers. We confirmed the complexity of their developing identities as reported in much research elsewhere be this on take-up from PD programs in general or those linked with educative curriculum materials and discussed earlier in this article. Both teachers exhibited purposeful teaching towards an articulated object of learning, thus reflecting take-up of key a component of the MTF, and ultimately teaching coherent lessons. Their enactments were different, a consequence of a complex array of factors including different backgrounds and initial motivations for joining the TM1 course, that in turn influenced their selective interaction with the MTF.
Patricia identified strongly with exemplifying in the MTF as she could control her selections. She constructed example sets from available curriculum texts deliberately inserting additional and pertinent variations—productive insertions in Leshota’s (2020) terms. As Patricia selected ordered pairs for points on the Cartesian plane, and asked learners about the quadrants in which they were located, she included points on the axes. She struggled to interact with interesting learner responses that she had intentionally provoked. She commented that she did not have time to go into a discussion on these specific points, reflecting her commitment to the mandated Annual Teaching Plan and its specified pacing in daily lesson plans. Thulela’s strong identification, in contrast, was with learner participation. In her lesson on linear functions she invested in interaction with learners so they would see the equation and graph as different representations of the same set of points. She too struggled. In Ntow and Adler we associate these differences with the range of factors mentioned above. The point here is not their different foci, nor how and why these emerged. Rather, the MTF played a contributory role in levering change in both teachers’ teaching though in different ways, and not without difficulties. This study further reinforces the notion of relational transparency as residing between the teacher, what she brings, and the functioning of an ideational resource like the MTF in its socio-cultural context.
-
The pre and post video study of teachers in the 2012 TM1 course
As noted above, we embarked on pre and post video study over 2012 and 2013 meeting significant methodological challenges—first at the level of the data gathered, and then in the analysis of the lessons and interpretation of this. I mention this study here despite not publishing its results beyond project reports and descriptive presentations of the project (see Adler, 2017). Limitations included: obtaining only one lesson per teacher in each year; a number of teachers were not teaching similar content or grades in the 2 years, let alone the same lesson topic. We nevertheless used the research version of the framework (Adler & Ronda, 2015) to study the opportunities to learn made available in pre and post lessons ultimately of only nine teachers that were comparable. This is a small number and so with limits on making claims about observable patterns in their practices. We nevertheless interpreted differences in the quality of the example sets in the lessons of all nine teachers after completing the course. On reflection and with findings from later studies, this data appears to confirm the easier take-up and learning of and from this component of the framework. Given that teachers were working with SLPs and prescribed textbooks, it is possible that through their participation in the TM1 course, and the mediation of the MTF, their use of curriculum materials, particularly textbooks, was more deliberate.
-
7 Accumulating findings and explaining the contributory role of the MTF in levering change: research question 3
The qualitative studies presented above influenced and/or confirmed the choices made in the WMCS to first and foremost strengthen the subjective conditions in the teachers–resources relationship through teachers’ participation in TM1 mft course. The studies that followed pointed to teachers’ take up and educative use of the elements of the MTF—a socio-cultural mathematics teaching framework, grounded in contextual realities of teaching and informed by relevant research in mathematics education. As each study included a small purposeful selection of TM1 teachers I am not suggesting the findings refer to all TM1 teachers. This broader view into the range of participating teachers comes with the juxtaposition of the qualitative findings with the results from the learning gains study. Evidence there was of, firstly, significantly improved mft of a relatively large group of teachers across the 2016 and 2017 TM1 cohorts. Secondly, there were modest but significant gains made by their learners over 1 year of teaching. The design of the study enabled the linking of these results and the conclusion that the teachers’ participation in the TM1 course impacted their students’ mathematics learning, where the course included the mediation of the elements of the MTF. In the accumulation of these studies’ different foci, findings and results, an overarching story emerges of a contributory role of an ideational resource such as the MTF in the teachers’ teaching, and by inference improved coherence and so opportunities for their learners to learn mathematics.
8 Concluding comments
This paper began with a review of research, across educational contexts, that made visible inevitable tensions in the design of educative curriculum materials. The line between increasing cultural transparency, explicit elaboration needed particularly for subject specific elements in the materials and their rationales, and prescription is delicate and no doubt situational. Procedural transparency appears less complex. In addition, curriculum materials are not a panacea. They cannot compensate for weaknesses in the subjective conditions in the teacher–resources relationship. Davis et al. (2017) called for more research on how materials function together with their mediated use in professional development. At the same time, and this is the theoretical point of this paper, transparency, the unproblematic integration of new resources into cultural practices, does not lie in the resource itself. Socio-cultural practices profoundly shape the teacher–resources relationship.
To make the case for the contributory role of an ideational resource like the MTF, I described the TM1 course in the WMCS project and the what, why and how of the MTF within it so as to illuminate the project’s context and socio-cultural practices in which the above findings and story emerged. In so doing I positioned a practical example of a teaching framework as an ideational resource functioning with an explicit elaboration of valued mathematics and mathematics teaching practice between curriculum resources and teachers in their socio-cultural context and as a contributory change lever.
At a theoretical level I have posited the teaching framework as a linking resource to deal with the inevitable gap interpreted in the literature between curriculum materials and teachers. And as has been shown, specific attention needs to be given to design and transparency, including that of the ideational resource if it is to function in the gap and lever change. In the South African context, and by implication other contexts of educational disadvantage, the improvement of teachers’ knowledge, their own educative use of material resources, and the consequent positive impact on learners, has a major implication for dealing with inequality and levering change.
Notes
I use ideational in the dictionary sense of “pertaining to ideas” (https://www.merriam-webster.com/dictionary/ideational). I discuss this naming and the meaning attached to it later in the paper.
The US studies were, broadly, located in socio-cultural theoretical approaches. The SA study drew on the Bernstein’s (2000) sociological theory of pedagogic discourse. The detail of these is beyond the scope of this paper and not necessary for the developing story.
In the project we also use the framework to support our own teaching.
The research framework was named the Mathematics Discourse in Instruction (MDI) framework and not detailed here. See Adler and Ronda (2015).
In South Africa, school students are referred to as learners. In the chapter I use learner and student interchangeably.
Elsewhere (Venkat & Adler, 2021)we have argued why available frameworks describing quality mathematics teaching would under-describe mathematics teaching in traditional teaching contexts like South Africa, and the salience therefore of MDI.
This is a pseudonym, as are the names of other WMCS teachers in the paper.
References
Adler, J. (2000). Conceptualising resources as a theme for mathematics teacher education. The Journal of Mathematics Teacher Education, 3(3), 205–224. https://doi.org/10.1023/A:1009903206236
Adler, J. (2017). Mathematics discourse in instruction (MDI): a discursive resource as boundary object across practices. In G. Kaiser (Ed.), 13th International Congress on Mathematical Education, ICME-13 (Vol. Proceedings of the Monographs, pp. 125–143). Springer.
Adler, J. (2021). Content and context specificity matter in the ‘how’ of language responsive mathematics teacher professional development. In N. Planas, C. Morgan, & M. Schütte (Eds.), Classroom research on mathematics and language: seeing learners and teachers differently. (pp. 77–1000). Routledge. https://doi.org/10.4324/9780429260889
Adler, J., & Alshwaikh, J. (2019). A case of lesson study in South Africa. In R. Huang, A. Takahashi, & J. da Ponte (Eds.), Theory and practices of lesson study in mathematics: an international perspective. (pp. 317–342). Springer. https://doi.org/10.1007/978-3-030-04031-4
Adler, J., & Davis, Z. (2006). Opening another black box: researching mathematics for teaching in mathematics teacher education. Journal for Research in Mathematics Education, 37(4), 270–296. https://doi.org/10.2307/30034851
Adler, J., & Pillay, V. (2017a). Mathematics education in South Africa. In J. Adler & A. Sfard (Eds.), Research for educational change: transforming researchers’ insights into improvement in mathematics teaching and learning. (pp. 9–24). Routledge.
Adler, J., & Pillay, V. (2017b). Setting the scene. In J. Adler & A. Sfard (Eds.), Research for educational change: transforming researchers’ insights into improvement in mathematics teaching and learning. (pp. 25–37). Routledge.
Adler, J., & Pournara, C. (2020). Exemplifying with variation and its development in mathematics teacher education. In D. Potari & O. Chapman (Eds.), International handbook of mathematics teacher education: volume 1. Knowledge, beliefs, and identity in mathematics teaching and teaching development. (pp. 329–353). Sense.
Adler, J., & Ronda, E. (2015). A framework for describing mathematics discourse in instruction and interpreting differences in teaching. African Journal of Research in Mathematics, Science and Technology Education. https://doi.org/10.1080/10288457.2015.1089677
Akkerman, S. F., & Bakker, A. (2011). Boundary crossing and boundary objects. Review of Educational Research, 81(2), 132–169. https://doi.org/10.3102/0034654311404435
Alexander, R. (2000). Culture and pedagogy: international comparisons in primary education. Blackwell.
Arcavi, A. (2020). From tools to resources in the professional development of teachers: general perspectives and cross-cutting issues. In D. Potari & O. Chapman (Eds.), International handbook of mathematics teacher education: volume 1. Knowledge, beliefs, and identity in mathematics teaching and teaching development.Sense.
Ball, D., & Cohen, D. (1996). Reform by the book: what is: or might be: the role of curriculum materials in teacher learning and instructional reform? Educational Researcher, 25(9), 6–14. https://doi.org/10.2307/1177151
Ball, D., Thames, M., & Phelps, G. (2008). Content knowledge for teaching: what makes it special? Journal of Teacher Education, 59, 389–407. https://doi.org/10.1177/0022487108324554
Bernstein, B. (2000). Pedagogy, symbolic control and identity: theory. Rowman & Littlefield.
Bills, L., Dreyfus, T., Mason, J., Tsamir, P., Watson, A., & Zaslavsky, O. (2006). Exemplification in mathematics education. Prague, Czech Republic: PME. In J. Novotna (Ed.), Proceedings of the 30th Conference of the International Group for the Psychology of Mathematics Education. Prague: PME.
CDE (2010). The maths and science performance of South Africa’s public schools: some lessons from the past decade. https://www.cde.org.za/reports. Accessed 20 Feb 2011
Choppin, J., McDuffie, A., Drake, C., & Davis, J. (2018). Curriculum ergonomics: conceptualizing the interactions between curriculum design and use. International Journal of Educational Research, 92, 75–85. https://doi.org/10.1016/j.ijer.2018.09.015
Davis, E., & Krajcik, J. (2005). Designing educative curriculum materials to promote teacher learning. Educational Researcher, 34(3), 3–14. https://doi.org/10.3102/0013189X034003003
Davis, E., Palincsar, A., Smith, S., Arias, A. M., & Kademian, S. (2017). Educative curriculum materials: uptake, impact, and implications for research and design. Educational Researcher, 46(6), 293–304. https://doi.org/10.3102/0013189X17727502
Dietiker, L., & Riling, M. (2018). Design (in)tensions in mathematics curriculum. International Journal of Educational Research, 92, 43–52. https://doi.org/10.1016/j.ijer.2018.09.001
Fan, L., Trouche, L., Chunxia, Q., Rezat, S., & Visnovska, J. (Eds.). (2018). Research on mathematics textbooks and teachers’ resources. Springer
Gersten, R., Taylor, M.J., Keys, T.D., Rolfhus, E., Newman-Gonchar, R. (2014). Summary of research on the effectiveness of math professional development approaches. Washington, DC: U.S. Department of Education, Institute of Education Sciences, National Center for Education Evaluation and Regional Assistance, Regional Educational Laboratory Southeast
Gueudet, G., & Trouche, L. (2009). Towards new documentation systems for mathematics teachers? Educational Studies in Mathematics, 71(3), 199–218. https://doi.org/10.1007/s10649-008-9159-8
Lave, J., & Wenger, E. (1991). Situated learning: legitimate peripheral participation. Cambridge University Press.
Leshota, M. (2020). Teacher–textbook telationships in mathematics in contexts of limited resources. African Journal of Research in Mathematics, Science and Technology Education. https://doi.org/10.1080/18117295.2020.1847833
Nasir, N. S., & Cooks, J. (2009). Becoming a hurdler: how learning settings afford identities. Anthropology & Education Quarterly, 40(1), 41–61. https://doi.org/10.1111/j.1548-1492.2009.01027.x
Ntow, F., & Adler, J. (2019). Identity resources and mathematics teaching identity: an exploratory study. ZDM, 51, 419–432. https://doi.org/10.1007/s11858-019-01025-z
OECD. (2013). OECD economic surveys: South Africa 2013. https://doi.org/10.1787/eco_surveys-zaf-2013-en.
Pepin, B., & Gueudet, G. (2018). Curriculum resources and textbooks in mathematics education. In S. Lerman (Ed.), Encyclopedia of mathematics education.Springer.
Pepin, B., Gueudet, G., & Trouche, L. (2013). Resourcing teachers’ work and interactions: a collective perspective on their resources, their use and transformation. ZDM, 45(7), 929–944. https://doi.org/10.1007/s11858-013-0534-2
Planas, N. (2020). How specific can language as resource become for the teaching of algebraic concepts? ZDM Mathematics Education. https://doi.org/10.1007/s11858-020-01190-6
Pournara, C., & Barmby, P. (2019). No significant impact on learner attainment - really? A quasi-experimental impact study of a professional development course for secondary mathematics teachers. In M. Graven, H. Venkat, A. Essien, & P. Vale (Eds.), Proceedings of the 43rd Conference of the International Group for the Psychology of Mathematics Education (Vol. 3, pp. 86–98). Pretoria: PME.
Pournara, C., Hodgen, J., Adler, J., & Pillay, V. (2015). Can improving teachers’ knowledge of mathematics lead to gains in learners’ attainment in mathematics? South African Journal of Education. https://doi.org/10.15700/SAJE.V35N3A1083
Prediger, S. (2019). Investigating and promoting teachers’ expertise for language-responsive mathematics teaching. Mathematics Education Research Journal, 31, 367–392. https://doi.org/10.1007/s13394-019-00258-1
Remillard, J. (2005). Examining key concepts in research on teachers’ use of mathematics curricula. Review of Educational Research, 75(2), 211–246. https://doi.org/10.3102/00346543075002211
Remillard, J. (2018). Examining teachers’ interactions with curriculum resources to uncover pedagogical design capacity. In L. Fan, L. Trouche, C. Qi, S. Rezat, & J. Visnovska (Eds.), Research on mathematics textbooks and teachers’ resources: advances and issues. (pp. 69–88). Springer.
Remillard, J., & Kim, O.-K. (2020). Elementary mathematics curriculum materials: designs for student learning and teacher enactment. Springer.
Rezat, S., & Strasser, R. (2012). From the didactical triangle to the socio-didactical tetrahedron: artifacts as fundamental constituents of the didactical situation. ZDM - Mathematics Education, 44(5), 641–651. https://doi.org/10.1007/s11858-012-0448-4
Ronda, E., & Adler, J. (2019). Subject matter knowledge and the quality of mathematics made available to learn: some hypotheses. In M. Graven, H. Venkat, A. Essien, & P. Vale (Eds.), International group for the psychology of mathematics education. (Vol. 3, pp. 257–264). PME
Sample-McMeeking, L.B., Orsi, R., Cobb, R.B. (2012). Effects of a teacher professional development program on the mathematics achievement of middle school students. Journal for Research in Mathematics Education, 43, 159–181
Shalem, Y. (2018). Scripted lesson plans. In B. Barrett, U. Hoadley, & J. Morgan (Eds.), Knowledge, curriculum and equity: social realist perspectives. (pp. 183–198). Routledge.
Shalem, Y., De Clercq, F., Steinberg, C., & Koornhof, H. (2018). Teacher autonomy in times of standardised lesson plans: the case of a primary school language and mathematics intervention in south Africa. Journal of Educational Change, 19, 205–222. https://doi.org/10.1007/s10833-018-9318-3
Shalem, Y., Steinberg, C., Koornhof, H., & De Clercq, F. (2016). The what and how in scripted lesson plans: the case of the gauteng primary langage and mathematics strategy. Journal of Education, 66, 13–36. https://doi.org/10.17159/2520-9868/i66a01
Shulman, L. (1987). Knowledge and teaching: foundations of a new reform. Harvard Educational Review, 57(1), 1–22. https://doi.org/10.17763/haer.57.1.j463w79r56455411
Trouche, L., Gueudet, G., & Pepin, B. (Eds.). (2019). The ‘resources’ approach to mathematics education. Springer.
Venkat, H., & Adler, J. (2012). Coherence and connections in teachers’ mathematical discourses in instruction. Pythagoras. https://doi.org/10.4102/pythagoras.v33i3.188
Venkat, H., & Adler, J. (2021). Mediating mathematics in instruction: trajectories towards generality in “traditional” teaching. In S. Zehetmeier, D. Potari, & M. Ribeiro (Eds.), Professional development and knowledge of mathematics teachers. (pp. 5–23). Routledge.
Venkat, H., & Graven, M. (2017). Changing teaching through a resources approach. In H. Venkat & M. Graven (Eds.), Improving primary mathematics education, teaching and learning: research for development in resource-constrained contexts. (pp. 163–178). Palgrave.
Vygotsky, L. S. (1978). Mind in society: the development of higher psychological processes. Harvard University Press.
Wang, C. (2019). An investigation of mathematics teachers’ documentation expertise and its devel-opment in collectives: two contrasting cases in China and France. Université de Lyon, East China normal university.
Watson, A., & Mason, J. (2006). Seeing an exercise as a single mathematical object: using variation to structure sense-making. Mathematical Thinking and Learning, 8(2), 91–111. https://doi.org/10.1207/s15327833mtl0802_1
Wenger, E. (1998). Communities of practice: learning, meaning, and identity. Cambridge University Press.
Acknowledgements
This work is based on the research supported by the South African Chairs Initiative of the Department of Science and Technology, and National Research Foundation of South Africa (Grant No. 71218). Any opinion, finding and conclusion or recommendation expressed in this material is that of the authors and the National Research Foundation does not accept any liability in this regard. I thank reviewers for critical comments towards the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
While I am the author of this paper, it is ultimately a collective product as it rests on the work by the WMCS research team whose work is included in the discussion of accumulating results.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Adler, J. Levering change: the contributory role of a mathematics teaching framework. ZDM Mathematics Education 53, 1207–1220 (2021). https://doi.org/10.1007/s11858-021-01273-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11858-021-01273-y