Abstract
Teachers’ confidence and facility with strategies that position and support students who are English learners (ELs) as active participants in middle grades mathematics classrooms are key to facilitating ELs’ mathematics learning. The Visual Access to Mathematics (VAM) project developed and studied teacher professional development (PD) focused on linguistically-responsive teaching to facilitate ELs’ mathematical problem solving and discourse. This study examines whether VAM PD has a positive impact on teachers’ self-efficacy in supporting ELs in mathematics and how components of the PD may have influenced teacher outcomes. Results from a field test involving a cluster randomized trial of 101 teacher participants from 47 schools showed that VAM PD had a positive impact on participants’ self-efficacy related to teaching ELs in mathematics, based on pre/post self-efficacy survey responses. An analysis of participants’ written reflections suggests that supported implementation of language strategies with ELs in their mathematics teaching contexts was a key PD component that contributed to teacher self-efficacy outcomes. Findings offer implications for mathematics teacher PD and for facilitating ELs’ learning in mathematics.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Mathematics educators in the US face an urgent need to strengthen mathematics instruction for English language learners (ELs).Footnote 1 For decades, ELs, defined as students whose home language is other than English and who are eligible for language support services based on the results of an English language proficiency assessment, have persistently scored below native English speakers by 20 or more points on National Assessment of Educational Progress (NAEP) mathematics assessments (McFarland et al., 2019). To facilitate ELs’ mathematics learning, mathematics teachers must attend to students’ English language learning as English is the main language of instruction in the US. Integrating support for language and communication during mathematics instruction is critical given the language and literacy demands embedded in US Common Core State Standards of Mathematics for all students, including ELs (Bunch, 2013). Best instructional practices for ELs must “go beyond what many call ‘good teaching’” (Celedón-Pattichis & Ramirez, 2012, p. 1) and specifically address ELs’ language strengths and needs and facilitate their listening, speaking, reading, and writing skills while they learn mathematics. Addressing language needs for students who are not fluent in the language of instruction can lead to increased mathematical learning opportunities (e.g., August et al., 2005; Prediger & Wessel, 2013; Secada & de la Cruz, 1996). Specifically, teachers must facilitate access to the language of each lesson and scaffold language production because language should be practiced by ELs “not only as a communicative tool but also as a cognitive tool for interacting with the teacher, with one another, and with content knowledge itself” (Lyster, 2007, p. 22). Regular participation in “explaining solution processes, describing conjectures, proving conclusions and presenting arguments” is imperative for ELs’ learning in mathematics (Moschkovich, 1999, p. 11).
With growing numbers of ELs in schools, many US mathematics teachers are teaching ELs for the first time or in larger numbers but are neither well-equipped nor confident in how to integrate strategies to facilitate ELs’ mathematics learning (de Araujo et al., 2018; Lucas & Villegas, 2013). Few pre-service teaching programs support participants to learn about effective mathematics instruction for ELs; recommendations for teacher preparation do not consistently specify strategies that mathematics teachers can use to teach ELs (de Jong & Harper, 2005). Even after completing coursework focused on ELs, in-service teachers stress that they need more specific and extensive training to support ELs’ language and mathematics learning. In surveys, US teachers have emphasized how they “do not have the resources or training to do these students justice” (Petit, 2013, p.10), emphasizing the need for intensive support rather than short, one-time workshops. Without focused training, teachers may underestimate students’ abilities and engage in practices that reduce ELs’ opportunities to thrive in their mathematics learning. Differences in language and cultural norms of communication can create “cultural distance between teachers and students” (NASEM, 2018). When confronted by these differences, teachers may adopt deficit perspectives about ELs, focusing on what their students cannot do in mathematics rather than on what they can do and achieve (Turner et al., 2013) and limiting ELs’ classroom participation (Yoon, 2008).
2 Linguistically responsive teaching (LRT)
To provide ELs with equitable mathematics learning opportunities, researchers suggest that mathematics teachers must develop capacities for and self-efficacy with linguistically responsive teaching (LRT). LRT involves recognizing, addressing, and capitalizing on students’ individual sociocultural, linguistic, cognitive, and academic strengths and needs. LRT requires specific orientations, such as a view that language, culture, and identity are interconnected; an appreciation for linguistic diversity; and an inclination to advocate for ELs (Lucas & Villegas, 2013). It also involves a set of pedagogical skills, including the abilities to (A) learn about ELs’ linguistic and academic backgrounds; (B) identify the language demands of classroom tasks; and (C) scaffold instruction for ELs. While broad and not specific to core content, these orientations and skills comprise a framework that aligns with research recommendations for facilitating ELs’ language access and production in content- and context-specific ways (Bunch, 2013; Aquino-Sterling et al., 2016). Mathematics teachers who demonstrate LRT make efforts to learn about the backgrounds and cultural knowledge that ELs bring to the classroom (Turner et al., 2013; Varley Gutiérrez et al., 2011); identify the language demands of mathematics tasks and content; and implement strategies and scaffolds to facilitate mathematics learning in light of ELs’ strengths and needs (e.g., Aquino-Sterling et al., 2016; Prediger, 2019).
To enact LRT, mathematics teachers must develop specific knowledge and skills as well as self-efficacy in conducting LRT with their ELs. Bandura (1997) defined self-efficacy as the belief in one’s abilities to carry out activities required to achieve specific outcomes. Attention to teacher self-efficacy is important because even when middle grades mathematics teachers have had opportunities to learn about strategies for teaching ELs, many lack self-efficacy and confidenceFootnote 2 in implementing them in their classrooms (e.g., Petit, 2013). Promoting teacher self-efficacy with LRT may support teachers to enact practices consistent with LRT in mathematics instruction. Teachers with stronger self-efficacy are likely to use more student-centered instruction; encourage student autonomy; pay attention to student needs; praise students for their successes; and persist in supporting struggling learners (Bandura, 1997; Goddard et al., 2004; Tschannen-Moran et al., 1998). Teacher self-efficacy also predicts student achievement, likely because it is associated with more productive teacher attitudes and practices (Goddard et al., 2004). Professional development (PD) that builds mathematics teachers’ self-efficacy in LRT has the potential to increase the numbers of teachers who will incorporate LRT into their practice and to improve the mathematics learning of the ELs they serve.
3 Teacher PD related to LRT in mathematics
Current theory and research suggest that to promote capacity for and self-efficacy with LRT in mathematics classrooms, mathematics teachers need well-designed PD experiences with activities that complement and build on each other. First, teachers need to experience mathematics tasks and language strategies as learners themselves (Lampert et al., 2013). Such opportunities have been shown to support teacher knowledge and use of language strategies in mathematics classrooms (Neumayer DePiper et al., 2013). Immersion in student activities as learners can alter teachers’ views of themselves and their students: One study found that teacher self-efficacy in meeting ELs’ needs increased after teachers participated in a learning experience in which they did not know the language of instruction (Wright-Maley & Green, 2015). Second, PD programs need to include opportunities for teachers to plan mathematics tasks that incorporate strategies for addressing students’ language needs and to discuss these strategies with other teachers. Detailed planning can help teachers develop insights into ELs’ language strengths and needs and prepare them to implement strategies to support ELs’ language access and production (e.g., Hansen-Thomas et al., 2018).
A third important PD component is support for teachers to implement new strategies and practices in their classrooms. Teachers can develop understandings of ELs’ needs and how to facilitate more equitable classroom participation when they plan and implement new instructional approaches with support (Michaels & O’Connor, 2015; Takeuchi & Esmonde, 2011). Repeated opportunities to test and refine new strategies with students may help teachers gain the mastery experiences they need to develop confidence and self-efficacy with new approaches (Bandura, 1997). Fourth, research on mathematics teacher learning suggests analyzing student work is another key PD component. Analysis of student work can encourage teacher reflection on their own practice and student thinking (Goldsmith & Seago, 2011). As teachers gain insight into their students’ understandings, they can more effectively tailor their mathematics instruction to target specific concepts and skills (e.g., Ball & Cohen, 1999). Building skills and routines for analyzing student work may help teachers develop insights into ELs’ language needs and mathematical understandings and inform their next steps to advance ELs’ learning.
Theory also suggests that effective PD for LRT in mathematics needs to integrate PD components in mutually supportive and coherent ways (e.g., Silver et al., 2006; Solano-Campos et al., 2019). For example, a PD program may begin by having participants experience and build knowledge of specific language support strategies, then plan and test new strategies with students during mathematics instruction, and finally reflect on implementation and student responses. When accompanied by expert feedback and regular group discussion, this sequence may provide participants with opportunities to witness student success and develop a sense of mastery with new strategies, which in turn may promote self-efficacy (Bandura, 1997).
Although there has been significant theorizing about the components and activities that may be needed for developing LRT, there is little empirical evidence about the efficacy of specific PD activities for promoting LRT among mathematics teachers (de Araujo et al., 2018). This study aims to contribute to the research base by describing a PD program that was designed to promote mathematics teachers’ LRT and its impacts on teachers’ self-efficacy outcomes.
4 Mathematics Teacher PD to support ELs: VAM PD
The Visual Access to Mathematics (VAM) PD is a 60-hour blended, face-to-face and online course to build teachers’ knowledge of and self-efficacy in LRT strategies to strengthen ELs’ mathematical problem solving and discourse in the middle grades. A four-day face-to-face summer institute is followed by eight two-week long asynchronous online sessions, two face-to-face workshops, and four synchronous online meetings. VAM PD’s design builds on evidence-based teacher PD strategies both in general and in mathematics by focusing heavily on content; engaging in active and job-embedded learning; supporting teacher collaboration; modeling effective practice; providing coaching and expert support; and offering ongoing opportunities for feedback and reflection (Darling-Hammond et al., 2017). Incorporating language strategies and visual representations such as tape diagrams and double number lines, VAM PD focuses on supporting ELs’ learning of proportional reasoning content, which has been called the "the most difficult to teach, the most mathematically complex, the most cognitively challenging, [and] the most essential to success in higher mathematics and science" (Lamon, 2007, p. 629). The PD includes the following four key components as well as their integration, which align with activities that researchers have theorized are important for supporting LRT in mathematics (Lucas & Villegas, 2013).
4.1 Engaging in language strategy experiences
To support ELs’ mathematical learning, teachers need to know and deploy multiple strategies to facilitate ELs’ access to language (reading and listening, or receptive language) and production of language (speaking and writing) (Chval & Chávez, 2011; Prediger & Wessel, 2013). VAM PD highlights different functions of language and raises awareness that strategies that support access to the language of a mathematics task may not be sufficient to support student communication of their mathematical ideas. VAM PD supports teachers to learn the theory behind multiple language strategies (Driscoll et al. 2016; see Fig. 1 for examples) and to experience their application in mathematical learning contexts. PD facilitators model these strategies while teachers solve and discuss mathematical tasks; teachers then debrief their experiences with the strategies. Having expert, yet relatable, facilitators model the use of language strategies with mathematics tasks may help to build participants’ self-efficacy in using the strategies themselves (Bandura, 1997), and may provide teachers with immersive experiences as language learners, thereby raising their sensitivity to ELs’ challenges and needs in mathematics classrooms (Wright-Maley & Green, 2015).
4.2 Lesson planning that incorporates language objectives and strategies
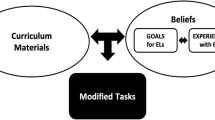
During VAM PD, teachers gain experience planning lessons that engage ELs in mathematical problem solving and integrate language objectives and strategies (e.g., Driscoll et al. 2016). Teachers select focus ELs from among their students, situate the language strengths and needs of these students relative to the specific mathematics content and objectives of the lesson, and plan strategy implementation that will help their focus students meet language and mathematics goals. The use of focus students grounds planning and student work analysis and encourages specificity in planning (Driscoll et al. 2016). For example, a planning activity focused on the Co-Constructed Word Bank (CCWB) strategy includes identifying a mathematics task; describing when the CCWB will be used during the lesson; and anticipating words that will be part of it. An example prompt is: “What words or phrases, if any, will you ask your focus students to use in written or oral responses? Consider their English language proficiency levels and the math and language objectives.” Planning protocols support teachers to identify key elements of a language strategy, make instructional moves visible, and detail how use strategies to meet varying language needs. By anticipating how they will use a strategy and how students might respond, teachers can deepen their understandings of and build mastery with the strategy.
4.3 Implementing and reflecting on strategies
VAM PD asks teachers to try using language strategies in classroom instruction, then reflect on how and why the strategy supported ELs’ mathematics learning. Teachers write their individual reflections in private online VAM PD “notebooks,” which prompt them regularly to “reflect on their own learning.” Ongoing opportunities to incorporate, test, and reflect on the results of language strategies with students during mathematics instruction are designed to build teachers’ mastery of and self-efficacy with these strategies. PD facilitators regularly respond to participants’ notebook reflections with feedback and encouragement to further support teachers’ self-efficacy with these strategies.
4.4 Analyzing ELs’ work
During VAM PD, teachers review student work on mathematical tasks from their own ELs and from example work. Explicit attention to ELs’ mathematical thinking can expand teachers’ understanding of ELs’ strengths and needs in mathematics, deepen teachers’ awareness of language issues, prompt greater use of language support strategies, and thereby increase ELs’ learning opportunities (Turner et al., 2013). Teachers reflect on ELs’ strengths, even when student work includes incorrect responses, to identify how to build on students' initial productive thinking. Analysis of student work provides teachers with formative feedback on their own teaching, which can help them refine their practice. PD facilitators support analysis by sharing student work samples that were captured using screencasts, which are digital video recordings of the students’ verbal cues, written notations, and the visual representations that students produce while solving a task on a tablet or computer screen. Teacher use and analysis of student screencasts support deeper understanding of student thinking (Roschelle & Leinwand, 2011). Teachers also analyze work from the focus students they select as part of lesson planning during the PD.
4.5 Integrating components
In VAM PD, participants experience each language strategy, learn about the strategy’s implementation characteristics, plan use of the strategy, and then analyze and reflect on their implementation. This intentional integration of activities has been found to support teacher learning (Silver et al., 2006), particularly if teachers witness student success and learn to anticipate and overcome possible instructional challenges. Detailed lesson planning with attention to tasks and students can facilitate teachers’ classroom implementation of new strategies; subsequent analyses of student work guides teacher reflection on instruction (e.g., Ball & Cohen, 1999). Tools such as the Focus Student Language Strategies Review and Planning template (Fig. 2) helps teachers integrate attention to ELs, planning, and mathematics instruction in context. Coordinating activities provides multiple opportunities to build teacher self-efficacy with new instructional practices. Furthermore, VAM PD supports teachers across the school year as they plan and implement new strategies, analyze student work, and reflect on their practice, aligning with research that suggests that diverse sources of information, experiences, and guidance support developing self-efficacy with new skills (Bandura, 1999).
5 Research questions
This study examines whether VAM PD has a positive impact on teachers’ self-efficacy in supporting ELs in mathematics. Under the hypothesis that VAM PD impacts might be greater for participants with less prior training and lower initial levels of self-efficacy, the study also examines whether the effect of VAM PD depends on participants’ initial self-efficacy levels. In addition, the study explores how VAM PD may contribute to growth in teachers’ self-efficacy by investigating the connections participants made between the components of VAM PD (detailed in Sect. 4) with positive changes in their self-efficacy. These efforts respond to a call for research that examines not only the efficacy of specific interventions but also how interventions, their components, and their contexts may interact to influence teacher change (Opfer & Pedder, 2011). To address these issues, this study explored two research questions:
-
RQ1.
Does VAM PD improve teachers’ self-efficacy in supporting ELs in mathematics, and do impacts vary depending on teachers’ initial levels of self-efficacy?
-
RQ2.
In what ways do VAM PD components contribute to growth in teacher self-efficacy, as suggested by participants?
6 Methods
To address the impact of VAM PD on teacher self-efficacy (RQ1), a cluster randomized control trial (RCT) of VAM PD was performed with 101 middles grades teachers working in 47 schools in New England. This design supports causal inferences about the effect of VAM PD on teacher outcomes (Holland, 1986; Shadish et al., 2002). Then, to investigate the ways in which VAM PD may have contributed to teacher growth in self-efficacy in support ELs in mathematics (RQ2), we examined treatment teachers’ written responses to online notebook prompts over the 10 months of VAM PD to identify how they connected their growth in self-efficacy to specific VAM PD components. Research efforts were led by the first two authors, who served as the project’s researchers with no involvement in the development or facilitation of the PD, and supported by the remaining authors, who were VAM PD developers and facilitators and who provided input on the study findings and implications.
6.1 Sample
In the spring of 2017, districts with the largest EL populations in Massachusetts (the site of the VAM PD face-to-face components) and in some surrounding states (Maine, New Hampshire, Connecticut, and Rhode Island) were identified using publicly available data. The project team reached out to mathematics and EL leads from these districts, who shared the opportunity to participate in the study with educators with responsibilities for Grades 6–8 mathematics instruction for ELs.
In late spring of 2017, 101 teachers from five statesFootnote 3 agreed to participate in the pilot study. Using a balanced design and stratified by state, the teachers’ 47 schools were randomly assigned to treatment (23 schools; 53 teachers) or control (24 schools; 48 teachers). The final analytic sample for RQ1 reflected low attrition rates, with 23 schools (52 teachers) in the treatment and 23 schools (46 teachers) in the control.Footnote 4 Over half (52%) of schools in the control and close to half (43%) of schools in the treatment had one teacher participant; the remaining schools each had 2–4 teacher participants, except one treatment school with 8 teacher participants. Based on responses to a background survey, participants had been teaching for an average of 14.7 years, 70% had a teaching certificate in mathematics, and 58% reported an endorsement in English as a second language or in Sheltered English Immersion. Most participants were female (90%) and spoke English as their first language (93%). About two-thirds of participants (67%) taught mathematics only or with another subject, while 13% were math coaches or curriculum directors. Remaining participants were EL specialists, special education teachers, or other specialists. The analytic sample for RQ2 (n = 50) included only treatment teachers who completed the pre- and post-self-efficacy instruments and had completed at least two written online notebook reflections.
6.2 RQ1 data source
Teacher self-efficacy in mathematics instruction for ELs was measured with an instrument composed of nine items adapted from existing self-efficacy scales (Ross, 2014; Siwatu, 2007; Wright-Maley & Green, 2015). The instrument was administered twice: pre-VAM PD in July 2017, and post-VAM PD in April 2018. Table 1 shows how the nine items align with two categories of pedagogical skills that may be fundamental to LRT as described by Lucas and Villegas (2013).Footnote 5 Exploratory factor analysis yielded a single “self-efficacy-EL” scale (α = 0.98; possible total score from 9 to 63, with each item on a 7-point Likert-type rating scale from Strongly Disagree to Strongly Agree) addressing self-efficacy in teaching ELs in mathematics.
6.3 RQ1 analysis
The effect of VAM PD on participants’ scores on the self-efficacy-EL scale was estimated with two-level hierarchical linear models using HLM 7.03 software (Raudenbush et al., 2017). A multi-level modeling approach was used because study participants were clustered within schools, and disaggregated estimation approaches that do not account for clustering (even when cluster sizes are small) underestimate standard errors and raise the likelihood of Type I errors (Clarke, 2008; Hedges & Hedberg, 2007; Hox, 2002). The team first examined baseline equivalence between treatment and control groups by estimating a two-level model with pretest score as the outcome and treatment status entered at Level 2. Mean treatment and control group pretest scores differed by an effect size of Hedges’ g =|0.19|, which suggests baseline equivalence when acceptable statistical adjustments are included in analyses (WWC, 2020). Project researchers then fit a sequence of models to the data to predict self-efficacy-EL posttest scores. An unconditional model estimated the variability at each level (Model 1); a second model included pretest scores (a statistical adjustment, grand-mean centered) at Level 1 (Model 2); a third model added treatment status at Level 2 as a predictor of mean outcome scores (Model 3); and a fourth model tested for a cross-level interaction effect between treatment status and pretest scores (Model 4). Models estimated randomly varying intercepts and fixed slopes. Fixed and random effects were estimated using restricted maximum likelihood and model fit statistics were estimated using full maximum likelihood. The final model was specified as follows:
Level-1 Model
Level-2 Model
6.4 RQ2 data source
To complement the analysis of scores on the self-efficacy-EL scale and to respond to RQ2, project researchers analyzed treatment participants’ written notebook responses from VAM PD to examine how participants described their own growth in self-efficacy related to teaching ELs and the VAM PD components to which they attributed this growth. After the summer institute and after each of the eight 2-week asynchronous online sessions, participants were asked to respond to two open-ended prompts in personal online notebooks to synthesize their learning. One prompt was about content from the session and one prompt asked them to “reflect on your own learning.” Fifty participants responded to at least one of the 18 prompts, yielding 819 total responses for analysis. Responses ranged from one sentence to multiple paragraphs in length. Although the online notebooks were designed as a PD activity to support teacher learning and not as a research instrument, participants’ responses offer insights into how participants made sense of their learning, how they viewed their PD experiences, and how VAM PD components may have built their self-efficacy in supporting ELs in mathematics.
6.5 RQ2 analysis
Analysis of teachers' online notebook responses in which they reflect on their own growth in self-efficacy responds to a call for research that explores patterns and theories of teacher change as well as quantitative measures of such change (Opfer & Pedder, 2011). All online notebook responses were input into MAXQDA coding software for analysis. Coding was conducted in two major stages. In the first stage, the two primary researchers read through all the notebook responses and assigned a set of a priori codes to statements in which a participant described an increase in their own self-efficacy in supporting the mathematics learning of ELs. The a priori codes were drawn from the nine self-efficacy-EL scale items and the categories of LRT described in Table 1. Sample codes include when participants described an increase in self-efficacy in describing language access challenges; an increase in self-efficacy in implementing language production strategies; and greater recognition of the importance of understanding ELs’ backgrounds. Statements were defined as a sentence or sets of sentences; a single notebook response could contain multiple statements. Statements indicating an increase in self-efficacy included descriptions of improved confidence in, comfort with, knowledge of, or ability in the specific area. The project’s researchers coded all notebook responses independently and then through discussion arrived at consensus in identifying all relevant statements and appropriate codes. Coded statements were grouped into three sets of self-efficacy outcomes, each aligned with a category of LRT drawn from the framework of Lucas and Villegas (2013) in Sect. 2: (A) learning about ELs’ linguistic and academic backgrounds; (B) identifying the language demands of classroom tasks and practices; and (C) applying language support and differentiation strategies based on ELs’ needs and abilities.
A second stage of coding was then conducted to identify statements in which participants described not only a positive change in their self-efficacy, but also a VAM PD component that contributed to this change. The two primary researchers reviewed the full set of participant statements that had been coded for an increase in self-efficacy in a specific LRT category and independently applied a code to indicate which, if any, of the four primary VAM PD components the participants cited as contributing to their self-efficacy outcome. The four primary VAM PD components, described in Sect. 4, are: (1) engaging participants as learners in language strategy experiences; (2) supporting participants’ lesson planning with language objectives and strategies; (3) supporting participants’ implementation of and reflection on language strategies with students in their own classrooms; and (4) analyzing ELs’ work. Statements that received both a code indicating an increase in self-efficacy in LRT as well as a code attributing that growth to a VAM PD component were labeled as “link statements.” A sample link statement, drawn from a participant’s notebook reflection at the end of Session 8, is the following:
I have incorporated the Three Reads strategy in at least half of my units… By using [this and other strategies] in my classroom, I have become more confident and willing to try more of them more often and am excited to continue using them next year and hopefully make them better and/or use in more units than this year.
This statement was given a code indicating growth self-efficacy in LRT category C (i.e., applying language support and differentiation strategies based on ELs’ needs and abilities) as well as a code for VAM PD component 3 (i.e., supporting participants’ implementation of and reflection on language strategies with students in their own classrooms).
Differences in coding between the researchers were discussed and reconciled to arrive at consensus in identifying all link statements. The number and types of link statements were summarized to identify quantitative patterns in ways that participants connected VAM PD components to self-efficacy outcomes. Researchers also identified patterns in responses that mentioned two VAM PD components as contributing to a self-efficacy outcome. Link statements were reviewed to identify illustrative examples of how a particular VAM PD component may have helped to promote teachers’ self-efficacy in a specific LRT category.
7 RQ1 results: impacts of VAM PD on teacher self-efficacy
Table 2 displays basic descriptive statistics summarizing participants’ pre- and post-VAM PD self-efficacy-EL scores, unadjusted for cluster effects and covariates. These statistics show a positive effect of VAM PD on participants’ self-efficacy-EL scores: mean scores grew 0.6 points for the control group (from 43.6 to 44.2 points) while they grew 9.2 points for the treatment group (from 45.4 to 54.6 points).
HLM model estimates, which adjust for cluster effects as well as covariates, also show positive impacts of VAM PD participation on participants’ post-VAM PD self-efficacy-EL scores (Table 3). Based on estimates from Model 1, about 22% of total variance in these scores is between schools and 78% is between participants. Results from Model 2 indicate that pretest scores explain about 45% of between-participant variation and contribute to a slight increase in between-school variation, while estimates from Model 3 show that the VAM PD treatment explains an additional 4% of the variation between participants and an additional 88% of the variation between schools. Controlling for pretest scores, the mean post-self-efficacy-EL score for the control group was 44.7 points out of a possible total of 63 points, while the mean score for the treatment group was almost 9.5 points higher (Model 3). This difference is statistically significant at p < 0.001 and represents an effect size of Hedges’ g = 1.14. Model 4 reveals that VAM PD also had a statistically significant moderating effect on the relationship between pre- and post-self-efficacy-EL scores. For the control group, a point increase in pretest scores was associated with a 0.77 increase in posttest scores. In contrast, the associated posttest score increase was only 0.33 points for treatment group members. VAM PD appears to have raised treatment group members’ mean post-self-efficacy-EL scores over those of control group members, and it also appears to have blunted the positive effect of pretest scores on posttest scores. Based on χ2 difference tests involving each model’s deviance statistics, the full model that includes treatment and cross-level interaction effects (Model 4) fits the data better and is favored over the other models.
8 RQ2 results: VAM PD components and links to teachers’ self-efficacy
Based on analysis of the online notebook responses, there are 174 link statements where a participant wrote that a primary VAM PD component contributed to a self-efficacy outcome. Table 4 provides a summary of the frequencies in which participants suggested that one of four VAM PD components (in rows 1–4, henceforth VAM PD 1–4) contributed to self-efficacy in one of three LRT categories (in columns A-C, henceforth LRT A-C). The last column of the table shows that participants linked a self-efficacy outcome to engaging as a learner with language strategies in 14 statements (8%); to lesson planning with language objectives and strategies in 49 statements (28%); to implementation of and reflection on language strategies in 79 statements (45%); and to analysis of ELs’ work in 32 statements (18%).
8.1 The important role of implementing and reflecting on language strategies
Opportunities to implement and reflect on language strategies in their own classrooms (VAM PD component 3) was the most frequently cited contributor to participants’ growth in self-efficacy outcomes, both overall and in two out of three LRT categories. Almost half of the link statements that connected a VAM PD component to growth in participants’ self-efficacy in using language strategies (LRT C) mentioned implementation and reflection opportunities during PD as a contributing factor (52 out of 110 responses, or 47%). Over half of all link statements that connected a VAM PD component to greater self-efficacy in identifying the language demands of mathematics tasks and practices (LRT B) linked experiences implementing and reflecting on language strategies to this outcome (18 out of 34 responses, or 53%). Implementing language strategies also appears to have played an important role in promoting participants’ self-efficacy in learning about ELs’ linguistic and academic backgrounds (LRT A); almost a third of link statements that described how VAM PD contributed to this outcome cited opportunities to implement and reflect on language strategies as helpful (9 out of 30 responses, or 30%).
For some participants, opportunities to practice with students what they had read about or experienced as learners appeared to promote their self-efficacy in applying language strategies in their classrooms. At the end of Session 8, Lydia Footnote 6wrote:
I have incorporated the Three Reads strategy in at least half of my units… By using [this and other strategies] in my classroom, I have become more confident and willing to try more of them more often and am excited to continue using them next year and hopefully make them better and/or use in more units than this year.
Similarly, Gwen explained in an end-of-course notebook response that she had previously learned about language strategies in the Massachusetts state’s Rethinking Equity in Teaching English Language Learners (RETELL) course, which helps teachers earn the required Sheltered English Immersion (SEI) endorsement. RETELL did not provide her with supported opportunities to explore language strategies in her classroom, but VAM PD’s emphasis on applying language strategies in her mathematics instruction significantly enhanced her self-efficacy in using these strategies:
I had heard about many of the language strategies when taking my RETELL course a few years ago, but there really wasn’t much application during RETELL to actually use the strategies—more about learning what they are. Through this course, we’ve been challenged to apply the various strategies in different ways in our classroom. I find myself stopping and clarifying vocabulary a lot more.… I have a lot more strategies for assessing students and providing supports in class for them after working through this course and learning more about the actual real-life application of these strategies in class. (Session 8 response)
VAM PD’s frequent opportunities for teachers to test language strategies with their students led some to realize that the strategies were not difficult to implement and could produce positive learning outcomes for students. Observations of their own abilities to implement the strategies and of student successes contributed to stronger self-efficacy in supporting ELs and all students. After trying out the CCWB strategy, Jenny shared: “I found that my students used the CCWB to identify information that was important to solve, but also terms that were necessary for true understanding. I also really enjoyed that students were able to explain the terms to each other in most cases. CCWBs are a simple tool that I feel I can implement immediately” (Session 5 response). Tracy also echoed these sentiments: “I found that incorporating the Three Reads, Acting Out & Realia, Sentence Starters/Frames and the co-constructed word bank supported all of my students. I will continue to use them all” (Session 8 response).
Having multiple opportunities to try a variety of language strategies with students can help build teachers’ understandings of the strengths and needs of their ELs (LRT A) as well as the language demands of mathematics tasks and practices (LRT B). After using the CCWB with her students, Ariana wrote at the end of the PD:
One thing I want to continue to try is the CCWB. I think it is very important to provide students with the time to identify words/vocabulary that they may not understand. Often, we as teachers can assume or neglect vocabulary words that students know and do not know… Before the activity, I neglected to reflect on how important names are and how it makes an impact on understanding the problem. It also allowed me to reflect on other components of word problems that students may not have prior knowledge/personal connections. (Session 8 response).
Ariana states that by using the CCWB with her students, she gained more awareness of the terms, proper nouns, and cultural references that she had previously assumed her ELs would understand but were in fact foreign to them. She realized that using the CCWB could grant her greater insight into what students “know and do not know” and the specific language in a task that may be challenging for students.
8.2 The role of other VAM PD components on self-efficacy
Analysis also identified the role of other VAM PD components on teacher self-efficacy outcomes. For example, when reflecting on their increased understanding and application of language strategies (LRT C), Melody noted the role of lesson planning (VAM PD 2): “It’s all about the intentional planning” (Session 8). Another emphasized the importance of “tak[ing] the time before the lesson to plan the questions that would be asked to certain students” (Bethany, Session 4 response). Planning helped participants feel better prepared for their instruction, and as Callie noted, the strategies “are much more effective tools for my students when I pre-plan and the learning experience is richer for them” (Session 5 response).
Teacher analysis of student work (VAM PD 4) also supported participants’ self-efficacy in multiple LRT categories. For example, Danielle felt that analysis of student work increased her self-efficacy in implementing strategies, such as the Three Reads strategy, because she was able to see how effective the strategy was for her students’ access to the task. She wrote: “Comparing the student work helped to show how effective the instruction of the Three Reads strategy has been in the classroom.…Keeping the student experience as a focus for the course helped motivate me and encourage use of the strategies” (Session 2 response). Analyzing student work helped Danielle learn about her students (LRT A); focusing on her students and how effective the strategies have been for them have supported her confidence in implementing new strategies (LRT C).
Although fewer participants linked engaging as a learner in language strategy experiences (VAM PD 1) to greater self-efficacy, it did play an important role for some participants. Tracy explained:
Prior to taking the course, I was aware that I knew very few strategies that support EL students… During the course I have not only learned of many others, but have also gotten the opportunity to try them out myself at workshops and with my students. What I have found to be most beneficial is trying these strategies myself before trying them with my students. Had I simply read about them I most likely would not have the same level of understanding. At this point, I feel comfortable with utilizing many of the language access and production strategies we have learned about. (Session 8 response).
Tracy felt that engaging in the strategy as a learner— “trying them herself”—increased her understanding and increased her confidence in using the strategies in her classroom (LRT C).
8.3 Multiple VAM PD components working together to support self-efficacy
Of the 94 responses that mentioned at least one VAM PD component and at least one self-efficacy outcome, 17 described how two VAM PD components worked together or interacted to promote a self-efficacy outcome. Student work analysis was the most common VAM PD component that was cited in combination with another PD component (in 11 of the 17 responses, 65%), and lesson planning was the second most common (referenced in 10 of the 17 responses, 58%).
Different combinations of VAM PD components worked together to support teacher self-efficacy outcomes. For example, one structured activity (see Fig. 2) combined analysis of student work (VAM PD 4) and planning for instruction (VAM PD 2) to support participants’ self-efficacy in identifying language demands of classroom tasks (LRT B) and understanding ELs’ needs and how to address them (LRT A). Gwen found that analysis of student work helped her understand her student’s linguistic and academic background and their strengths and needs in mathematics. These understandings then supported her planning:
My experience with the [template in Fig. 2] stood out for my learning because it forced me to look at what my focus student is producing, look at her strengths and weaknesses and then determine what the best next steps are in order to keep her moving forward in both her math learning and her language usage. It's not that I don't already think about these things, but typically it's all anecdotal and informal. Writing it all down in the graphic organizer made me connect her weaknesses to goals that I can set, as well as connect her strengths to starting points for conversations with her. Overall, I've found that it's made me more aware of what she is or isn't accessing during class and put her at the forefront of my mind when I am planning lessons or interventions, in order to make sure that I'm meeting her needs specifically to help her make progress. (Session 6 response).
Teachers also noted that an iterative process of planning for instruction and implementing tasks with students (VAM PD 2 and 3) supported their self-efficacy in identifying language demands and implementing strategies (LRT B and C). For example, Jewel described how the planning process helped her to adapt the Three Reads strategy to fit her grade-level content and tasks, but then when implementing the Three Reads with the tasks, she found students were still not able to get started on them. She engaged in more detailed planning, revising the Three Reads prompts to better support ELs’ writing, and then found, “Students started having success understanding how to use the strategy. Now I use it as much as possible” (Session 4 response). The cycle of planning, implementing, reflecting, revising, planning, and implementing led her to identify ELs’ struggles and develop her confidence with new strategies in ways that planning or implementing alone may not have supported.
9 Discussion
In response to RQ1, results of a cluster RCT indicate that VAM PD had a positive impact on participants’ self-efficacy in supporting ELs in mathematics. As measured by the project’s self-efficacy-EL scale, participants gained confidence in multiple categories of LRT. VAM PD’s impacts differed depending on teachers’ baseline self-efficacy levels: self-efficacy-EL scores grew more for teachers with lower initial scores than for teachers with higher initial scores. This differential impact may have arisen if teachers who began the PD with higher scores simply had less room to grow on the self-efficacy-EL scale. Relatively high mean pre-scores and left-skewed pre- and post- score distributions (not shown but available upon request) provide evidence for a possible ceiling effect. The differential impact could also indicate that VAM PD is a particularly powerful intervention for teachers who begin with lower self-efficacy-EL. Although prior research has found that many teachers lack confidence and skills in supporting ELs in mathematics (de Araujo et al., 2018; Lucas & Villegas, 2013), this study suggests that it is possible to design and implement PD to improve teachers’ self-efficacy in this arena. Future work is needed to examine whether VAM PD’s positive impacts can be replicated with broader populations of teachers and with alternate measures of self-efficacy, and whether VAM PD can affect other important outcomes such as teacher knowledge and practice.
In response to RQ2, participants’ written reflections provide insights into how VAM PD components may have helped to promote self-efficacy in LRT. Based on responses to open-ended prompts about their learning, participants drew many links between specific sets of activities within VAM PD and ways in which their self-efficacy grew. While these components may not be the only components that contributed to participant growth in self-efficacy, participant reflections suggest that having opportunities to implement language strategies with their own students during mathematics instruction, and having time to reflect on and learn from their efforts during PD, may play an important role in boosting teachers’ self-efficacy in incorporating these strategies more regularly into their instructional practice. Their reflections also highlight the importance of integrating PD components to promote teachers’ self-efficacy. For example, asking participants to connect lesson planning with structured analyses of ELs’ work may help teachers develop more holistic understandings of individual ELs’ strengths and needs and greater insights into productive next steps to advance ELs’ mathematics learning. Ensuring that PD activities intersect and interrelate is consistent with prior research on how to structure mathematics teacher professional learning (Silver et al., 2006).
Because the online notebook was designed primarily as a tool to support teachers’ professional learning rather than as a research instrument, findings from the analysis of notebook responses are exploratory and preliminary. Interestingly, the connections that participants described between VAM PD components and self-efficacy outcomes arose without explicit prompting or probing for causal connections and can serve as groundwork for further research. Future studies could examine the relative import of VAM PD components through structured participant surveys or through experimental studies that measure the impacts of individual PD components on teacher self-efficacy or on other important outcomes such as teacher knowledge or practice. In-depth interviews with future participants could also probe further the mechanisms and processes by which VAM PD activities may support teachers’ self-efficacy with ELs in mathematics.
10 Conclusion
This study responds to the call for more research on whether and how teacher PD that integrates language and mathematics teaching can lead to teacher change (Erath et al., 2021). Given the critical need to support ELs in mathematics, future work can continue to build on these findings to broaden the ranks of mathematics educators with the self-efficacy in LRT that is required to serve ELs effectively.
Availability of data and material
Available upon request.
Notes
In this article, we use the phrases students who are English learners and English language learners and the term ELs. We appreciate a focus on students’ strengths inherent in phrases such as emergent multilingual or bilingual, but we use ELs because of its alignment with the ways in which students who are eligible for language support services are labeled in US schools, where English is the language of instruction.
We use the concepts of “confidence” and “comfort” as indicators of self-efficacy, in line with other research on teacher self-efficacy related to LRT (e.g., Wright-Maley & Green, 2015).
About 63% of teachers in the final analytic sample were from Massachusetts; 26% were from Maine; and the remaining 11% were from Connecticut, New Hampshire, or Rhode Island.
The final analytic sample includes only those participants who provided both pre- and post-tests for project outcome measures. Teachers were remunerated to complete both pre- and posttests.
Items in the self-efficacy-EL scale align with two categories of pedagogical skills that Lucas and Villegas (2013) suggest are critical for LRT. The scale does not include items that align with another important LRT category: the ability to learn about ELs’ linguistic and academic backgrounds. All three categories are explored in greater depth later in this article in analyses of participants’ online notebook responses, which were conducted to address RQ2.
All names are pseudonyms
References
Aquino-Sterling, C., Rodríguez-Valls, F., & Zahner, W. (2016). Fostering a culture of discourse in secondary mathematics classrooms: Equity approaches in teaching and teacher education for emergent bilingual students. Revista Internacional de Educación para la Justicia Social (RIEJS), 5(2), 87–107.
August, D., Carlo, M., Dressler, C., & Snow, C. (2005). The critical role of vocabulary development for English language learners. Learning Disabilities Research & Practice, 20(1), 50–57.
Ball, D. L., & Cohen, D. K. (1999). Developing practice, developing practitioners: Toward a practice-based theory of professional education. In L. Darling-Hammond & G. Sykes (Eds.), Teaching as the learning profession: Handbook of policy and practice (pp. 3–32). Jossey-Bass.
Bandura, A. (1997). Self-efficacy: The exercise of control. Hoboken: W.H. Freeman and Company.
Bandura, A. (1999). Social cognitive theory: An agentic perspective. Asian Journal of Social Psychology, 2, 21–41.
Bunch, G. C. (2013). Pedagogical language knowledge: Preparing mainstream teachers for English learners in the new standards era. Review of Research in Education, 37, 298–341.
Celedón-Pattichis, S., & Ramirez, N. G. (Eds.). (2012). Beyond good teaching: Advancing mathematics education for ELLs. National Council of Teachers of Mathematics.
Chval, K. B., & Chávez, O. (2011). Designing math lessons for English language learners. Mathematics Teaching in the Middle School, 17(5), 261–265.
Clarke, P. (2008). When can group level clustering be ignored? Multilevel models versus single-level models with sparse data. Journal of Epidemiology and Community Health, 62, 752–758.
Darling-Hammond, L., Hyler, M. E., & Gardner, M. (2017). Effective Teacher Professional Development. Learning Policy Institute.
de Araujo, Z., Roberts, S. A., Wiley, C., & Zahner, W. (2018). English learners in K–12 mathematics education: A review of the literature. Review of Educational Research, 88(6), 1–41.
De Jong, E. J., & Harper, C. A. (2005). Preparing mainstream teachers for English language learners: Is being a good teacher good enough? Teacher Education Quarterly, 32(2), 101–124.
Driscoll, M., Nikula, J., & Neumayer DePiper, J. (2016). Mathematical Thinking and Communication: Access for English Learners. Heinemann.
Erath, K., Ingram, J., Moschkovich, J., & Prediger, S. (2021). Designing and enacting teaching that enhances language in mathematics classrooms. ZDM, 53, 2.
Goddard, R. D., Hoy, W. K., & Hoy, A. W. (2004). Collective efficacy beliefs: Theoretical developments, empirical evidence, and future directions. Educational Researcher, 33(3), 3–13.
Goldsmith, L.T., & Seago, N. (2011). Using classroom artifacts to focus teachers’ noticing: Affordances and opportunities. In M.G. Sherin, V.R. Jacobs, & R.A. Philipp (Eds.), Mathematics teacher noticing: Seeing through teachers’ eyes (pp. 169–187). Routledge.
Hansen-Thomas, H., Langman, J., & Sokoloski, T. F. (2018). The role of language objectives: Strengthening math and science teachers’ language awareness with emergent bilinguals in secondary classrooms. Latin American Journal of Content and Language Integrated Learning, 11(2), 193–214.
Hedges, L. V., & Hedberg, E. C. (2007). Intraclass correlation values for planning group-randomized trials in education. Educational Evaluation and Policy Analysis, 29(1), 60–87.
Holland, P. (1986). Statistics and causal inference. Journal of the American Statistical Association, 81(396), 945–960.
Hox, J. (2002). Multilevel analysis: Techniques and Applications. New Jersey: Lawrence Erlbaum Associates.
Lamon, S. J. (2007). Rational numbers and proportional reasoning. In F. K. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 629–667). Information Age Publishing.
Lampert, M., Franke, M. L., Kazemi, E., Ghousseini, H., Turrou, A. C., Beasley, H., et al. (2013). Keeping it complex: Using rehearsals to support novice teacher learning of ambitious teaching. Journal of Teacher Education, 64(3), 226–243.
Lucas, T., & Villegas, A. M. (2013). Preparing linguistically responsive teachers: Laying the foundation in preservice teacher education. Theory into Practice, 52(2), 98–109.
Lyster, R. (2007). Learning and teaching languages through content: A counterbalanced approach. Amsterdam: John Benjamins.
McFarland, J., Hussar, B., Zhang, J., Wang, X., Wang, K., Hein, S., Diliberti, M., Forrest Cataldi, E., Bullock Mann, F., & Barmer, A. (2019). The Condition of Education 2019 (NCES 2019–144). National Center for Education Statistics.
Michaels, S., & O’Connor, C. (2015). Conceptualizing talk moves as tools: Professional development approaches for academically productive discussions. In L. B. Resnick, C. S. C. Asterhan, & S. N. Clarke (Eds.), Socializing Intelligence Through Academic Talk and Dialogue (pp. 347–362). American Educational Research Association.
Moschkovich, J. (1999). Supporting the participation of English language learners in mathematical discussions. For the Learning of Mathematics, 19(1), 11–19.
National Academies of Sciences, Engineering, and Medicine (NASEM). (2018). English learners in STEM subjects: Transforming classrooms, schools, and lives. The National Academies Press.
Neumayer DePiper, J., Nikula, J., & Wing DiMatteo, R. (2013). Examining integrated professional development to support mathematics teachers of English learners. In M. Martinez, & A. Castro Superfine (Eds.), Proceedings of the 35th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (p. 947). University of Illinois-Chicago.
Opfer, V. D., & Pedder, D. (2011). Conceptualizing teacher professional learning. Review of Educational Research, 81(3), 376–407.
Petit, S. K. (2013). Teachers’ and students’ beliefs about ELLs in mainstream mathematics classrooms. Journal of Contemporary Research in Education, 1(3), 130–143.
Prediger, S. (2019). Investigating and promoting teachers’ expertise for language responsive mathematics teaching. Mathematics Education Research Journal, 31(1), 367–392.
Prediger, S., & Wessel, L. (2013). Fostering German language learners’ constructions of meanings for fractions – Design and effects of a language- and mathematics-integrated intervention. Mathematics Education Research Journal, 25(3), 435–456.
Raudenbush, S. W., Bryk, A. S., & Congdon, R. (2017). HLM 7.03 for Windows [Computer software]. Scientific Software International, Inc.
Roschelle, J., & Leinwand, S. (2011). Improving student achievement by systematically integrating effective technology. NCSM Journal, 13(22), 3–11.
Ross, K. E. L. (2014). Professional development for practicing mathematics teachers: A critical connection to English language learner students in mainstream USA classrooms. Journal of Mathematics Teacher Education, 17, 85–100.
Secada, W.G., & De La Cruz, Y. (1996). Teaching mathematics for understanding to bilingual students. In J.L. Flores (Ed.), Children of la frontera: Binational efforts to serve Mexican migrant and immigrant students (pp. 3–25). ERIC Clearinghouse on Rural Education and Small Schools.
Shadish, W. R., Cook, T. D., & Campbell, D. T. (2002). Experimental and quasi-experimental designs for generalized causal inference. Boston: Houghton Mifflin Company.
Silver, E. A., Mills, V., Castro, A., & Ghousseini, H. (2006). Blending elements of lesson study with case analysis and discussion: A promising professional development synergy. In K. Lynch-Davis & R. L. Rider (Eds.), The work of mathematics teacher educators: Continuing the conversation (pp. 117–132). San Diego: Association of Mathematics Teacher Educators.
Siwatu, K. O. (2007). Preservice teachers’ culturally responsive teaching self-efficacy and outcome expectancy beliefs. Teaching and Teacher Education, 23, 1086–1101.
Solano-Campos, A., Hopkins, M., & Quaynor, L. (2019). Linguistically responsive teaching in preservice teacher education: A review of the literature through the lens of cultural-historical activity theory. Journal of Teacher Education, 71(2), 203–217.
Takeuchi, M., & Esmonde, I. (2011). Professional development as discourse change: Teaching mathematics to English learners. Pedagogies: An International Journal, 6(4), 331–346.
Tschannen-Moran, M., Hoy, A. W., & Hoy, W. K. (1998). Teacher efficacy: Its meaning and measure. Review of Educational research, 68(2), 202–248.
Turner, E., Dominguez, H., Maldonado, L., & Empson, S. (2013). English Learners’ participation in mathematical discussion: Shifting positionings and dynamic identities. Journal for Research in Mathematics Education, 44(1), 199–234.
What Works Clearinghouse (WWC). (2020). Procedures Handbook, Version 4.1. U.S. Department of Education, Institute of Education Sciences, National Center for Education Evaluation and Regional Assistance.
Wright-Maley, C., & Green, J. (2015). Experiencing the needs and challenges of ELLs: Improving knowledge and efficacy of pre-service teachers through the use of a language immersion simulation. Cogent Education, 2, 1–17.
Yoon, B. (2008). Uninvited guests: The influence of teachers’ roles and pedagogies on the positioning of English language learners in the regular classroom. American Educational Research Journal, 45, 495–522.
Funding
The Visual Access to Mathematics: Professional Development for Teachers of English Learners project is supported by the National Science Foundation (NSF) under Grant no. DRL 1503057. Any opinions, findings, and conclusions or recommendations expressed are those of the authors and do not necessarily reflect the views of the NSF.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
All author(s) declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Neumayer DePiper, J., Louie, J., Nikula, J. et al. Promoting teacher self-efficacy for supporting English learners in mathematics: effects of the Visual Access to Mathematics professional development. ZDM Mathematics Education 53, 489–502 (2021). https://doi.org/10.1007/s11858-021-01227-4
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11858-021-01227-4