1 Introduction

Mathematics education for young children has a long history. Its beginning is found already in the first half of the seventeenth century (Saracho and Spodek 2009). Nevertheless, it was only in 2000 that the National Council of Teachers of Mathematics (NCTM 2000) first included this age group in their standards for mathematics education. Since then, much awareness has grown that young learners’ future understanding of mathematics requires an early foundation based on a high-quality, challenging, and accessible mathematics education (NCTM 2013). Necessary for developing this education is a good understanding of what mathematics we want beginning learners of mathematics to get acquainted with and need to teach them. To feed this understanding, in this study we focus on the early number strand and unravel its components, their relations and their generality for kindergartners in different countries.

2 Theoretical background

2.1 The focus on early number and its structure

Although the domain of number has always been considered a cornerstone of mathematics and the complete school curriculum for mathematics is strongly grounded in number (NCTM 2000), only recently have studies shown that “early math concepts as knowledge of numbers and ordinality were the most powerful predictors of later learning” (Duncan et al. 2007, p. 1443) and that “early quantitative competencies […] uniquely contribute to mathematics learning” (Geary 2011, p. 1539). Similarly, it was brought to light that these competencies highly predict mathematics performance in later grades (e.g., Bruce et al. 2016; Claessens and Engel 2011), and that they are even found to be an influence on adults’ functional numeracy (Geary et al. 2013).

Another revelation from these and earlier studies on young children’s learning of number is the large variety in how early number competencies are conceptualized and assessed. For example, Geary (2011) found in previous studies that they were measured by focusing on children’s understanding of numerical magnitude (Starkey et al. 1990), on their knowledge of the rules for counting (Briars and Siegler 1984; Gelman and Gallistel 1978), on their awareness that adding or subtracting an object means an increase or decrease of the quantity (Levine et al. 1992), and on their ability to subitize (Starkey and Cooper 1980; Wynn et al. 2002) and represent the approximate magnitude of larger collections of objects (Halberda and Feigenson 2008; Xu and Spelke 2000).

Several authors (Berch 2005; Howell and Kemp 2010; Torbeyns et al. 2012; Verschaffel et al. 2007) underline that there are many ways to define the concept ‘number sense’. In fact, Berch (2005) found over 30 different definitions or features of number sense in early mathematics literature. Another complicating factor in its definition is that this early understanding of number displayed by children before they go to grade classes where they receive explicit lessons in mathematics—viewed as a prerequisite for success in school-based mathematics—is labelled very differently. While it is often named ‘number sense’, terms such as ‘numerosity’, ‘number competence’, ‘numerical proficiency’ and ‘mathematical proficiency’ are also used (Howell and Kemp 2010).

To establish consensus on the skills that should be considered essential components of early number sense and how best to assess them in young children, Howell and Kemp (2010) carried out two Delphi studies and a review of number sense literature. This resulted in a list of 18 number sense components, with 11 components related to counting, 3 to number principles, and 4 to number magnitude. All components were measured by a number of items used to establish what percentage of children in preschools and childcare centres demonstrated the skills identified as essential components of early number sense.

A study by Purpura and Lonigan (2013) went further. Their aim was to investigate the structure of preschool children’s early number competence. According to them, there is a need to synthesize the informal numeracy knowledge base and identify and validate these constructs through statistical and methodological techniques. By applying confirmatory factor analysis (CFA), they tested and compared one-, two-, and three-factor models based on the threefold distinction of the early number domain suggested by the National Research Council Committee on Early Childhood Mathematics (NRC 2009). The committee grouped the major concepts of early number into three core areas: number (i.e., giving a number to the numerosity of a set), relations (i.e., dealing with relations such as ‘less than’, ‘greater than’, and ‘equal to’), and arithmetic operations (i.e., carrying out the operations of addition, subtraction, multiplication, and division). Although in the study of Purpura and Lonigan (2013) all factor models fitted the data well, it was clear that the best model was that with the three components highlighted by the NRC committee (2009). This however means that the results from Purpura and Lonigan (2013) contrasted with earlier studies that investigated the structure of early number. Particularly, the study of Jordan et al. (2006) arrived at a fitting two-factor model including number and arithmetic operations as suggested in the standards of the NCTM (2000) and the study of Clements et al. (2008) ended up with a one-factor model for early mathematical skills.

2.2 Further research on the structure of early quantitative competence

The study by Purpura and Lonigan (2013) offered relevant information for understanding the underlying structure of the nature of informal numeracy skills. Nevertheless, even the authors themselves concluded that for the purpose of developing teaching–learning trajectories and constructing assessments, more research was needed, in particular on how different early number components are connected and develop.

Our study was set up in line with this recommendation. Our goal is to contribute to gaining more knowledge about the components of early quantitative competence and the relations among them. We see this study as our first attempt to unravel the structure of quantitative competence of kindergartners. Therefore, we decided to focus on a simple competence model with two constituent parts, each with two components (see Fig. 1).

Fig. 1
figure 1

Model of quantitative competence

Full size image

The two constituent parts of the model, the ability to connect a number to a given collection of objects (quantification) and the ability to think and work with quantities to solve problems (quantitative reasoning), correspond with the division into two components (number and arithmetic operations) identified by Jordan et al. (2006) and suggested in the NCTM standards (2000). Yet, this division contrasts with the three-way split in the NRC (2009) report and the study of Purpura and Lonigan (2013), both of which include the component of relations. Along with simplifying our model by leaving out this component, there was another reason to not include relations. The understanding of quantitative relations is difficult to distinguish from the two other components, because it can be considered essential to both quantification and quantitative reasoning. This may also be why even in the NRC (2009) report the relations and operations core are often taken together. Moreover, further support for having a model with two constituent parts is that Purpura and Lonigan (2013) measured the relations component by using tasks such as number order, sequencing, set reproduction, and number comparison, which can easily be assigned to either quantification or quantitative reasoning. What is new in our model compared to those of Jordan et al. (2006) and Purpura and Lonigan (2013) is that we extended the quantitative reasoning part of the model with multiplicative reasoning. In the next section, we elaborate on the four investigated components of quantitative competence.

2.3 Components of early quantitative competence

2.3.1 Quantification

In its most simple conceptualization, quantification stands for “a process by which one assigns numerical values to qualities” (Thompson 2011, p. 35). As Thompson (1990, p. 5) clarified, this covers a broad range of processes: “Young children’s counting can be a quantification process (to measure numerosity) just as can a nutritionist’s attempts to quantify the energy required to dispose of complex sugars.”

In general, for children’s competence to connect a number to a given collection of objects, a division is made into two quantification components, namely, counting and subitizing (e.g., NRC 2009).

2.3.1.1 Counting

Counting, as the process of determining the number of elements of a set of objects or events by making use of the number list (NRC 2009), is considered a key component in the development of the concept of number (Baroody and Wilkins 1999; Sarama and Clements 2008). By using counting in everyday experiences, children construct basic knowledge about numbers resulting in being able to find the numerosity of a collection of objects. To succeed in this task, children have to acquire the ability of oral counting (knowing the sequence of number words), the one-to-one correspondence between the set of objects and the number words, the ability to keep track of counted objects and objects that have not yet been counted, and they have to understand the cardinality principle (the realization that the numerosity of the set of objects is indicated by the last number word of the counting process) (Baroody and Wilkins 1999; Frye et al. 2013; Kilpatrick et al. 2001). Mou et al. (2018, p. 121) measured this counting competence in two directions, each reflecting a different aspect of number understanding. In one task, the give-a-number task, children were presented with a number of items and had to give a particular number of them by counting aloud, while in the other task, the what’s-on-this-card task, they had to identify the cardinal value of a set of items.

2.3.1.2 Subitizing

The other way to determine the numerosity of a collection of items is subitizing. It is a perceptual process implying children can instantly recognize the quantity of small sets (Baroody and Wilkins 1999; Clements 1999; NRC 2009). In the words of Conderman et al. (2014), subitizing “refers to the child’s ability to quickly and accurately identify how many items are contained in a small set of objects or in a small visual quantity, such as a picture of a group of objects, without actually counting each item” (p. 20). Although counting aloud one-by-one by pointing at the counted objects is often considered the primary start of the concept of number with subitizing as a later development (Silverman and Rose 1980), there is substantial evidence that the development of the competence of subitizing occurs even before children have learned to count objects using the number list (Baroody 2004; Clements et al. 2019; Sophian 2008). This view is in line with the hypothesized model of Klahr and Wallace (1976, cited by Silverman and Rose 1980) that the onset of subitizing precedes that of counting. Clements et al. (2019) also emphasize this by calling subitizing “the neglected quantifier” (p. 13). According to them, subitizing deserves more instructional attention because it appears to be fundamental to all number learning.

Based on the different mechanisms underlying the process of identifying the cardinality of a collection of objects through subitizing, Clements (1999) distinguished between perceptual subitizing and conceptual subitizing. Perceptual subitizing best fits the general meaning of subitizing. It means a quick visual recognition of how many objects there are in a small collection of objects without a conscious effort of counting (NRC 2009; Sarama and Clements 2008). Conceptual subitizing is quickly figuring out the numerosity of a larger collection of objects (usually more than five) by viewing it as being composed of smaller groups of objects (Clements 1999). By making use of the structure in which objects are presented, children can repeatedly subitize perceptually and quickly unitize the numbers. This decomposing and composing of numbers helps them to develop generalized part-whole relations (Clements et al. 2019).

To measure children’s subitizing competence it is important that the quantification tasks allow and trigger children to subitize. This requires either including a very small number of objects that can be recognized directly, or presenting the children with a larger collection of objects in such a structured way that the numerosity of the collection can be derived by conceptual subitizing.

2.3.2 Quantitative reasoning

In general, quantitative reasoning is regarded as understanding and using relations between quantities to solve problems. This focus on relations means quantitative reasoning cannot be seen simply as the application of procedures learned to solve arithmetic computations (Nunes et al. 2015). This view is clearly reflected by Thompson (1990) for whom quantitative reasoning means “the analysis of a situation into a quantitative structure—a network of quantities and quantitative relationships” (p. 12). Like quantification, quantitative reasoning can take place at several mathematical levels. It can serve as a foundation for arithmetic and algebra but can also play a central role in students’ learning of calculus and differential equations (Thompson 2011).

Nunes et al. (2015) found that preschool children and children in the first year of primary school can already reason quite successfully about quantitative relationships. The conceptual framework that Nunes and her colleagues developed to measure this reasoning included problems in which the children had to combine their counting competence both with their intuitive models for addition and subtraction and with their intuitive models for multiplication and division. As a result, this conceptualization of quantitative reasoning was broader than that used by Jordan et al. (2006) and Purpura and Lonigan (2013), who measured the ability to think and work with quantities only with tasks related to addition and subtraction. In Nunes et al.’s study (2015) quantitative reasoning comprised not only working with additive relations but also with multiplicative relations. These two types of reasoning are based on different schemas of action. Additive reasoning is based on part–whole situations and multiplicative reasoning on one-to-many situations, which means these two types of reasoning constitute different ways of establishing relations between quantities (Nunes and Bryant 1996, 2015).

2.3.2.1 Additive reasoning

Children’s early experiences with counting (Eisenhardt et al. 2014) and subitizing (Clements 1999) are the basis for additive reasoning involving addition and subtraction. This process starts at a young age. Most preschoolers can understand and solve simple additions and subtractions when they are three years old, often by using real objects to model the tasks and find how many objects there are in total (or are left) by touching the objects to count them (Kilpatrick et al. 2001). Playing with collections of objects can lead to comprehending that adding something to a collection means having something more and that taking away means having something less (Baroody and Wilkins 1999). A further step in children’s understanding of additive relations occurs when they develop a basic understanding of part-whole relations. As Sophian and McCorgay (1994) have shown, children are already able to reason about part-whole relations before they have reached first grade. Being able to do this signifies they have at least a notion of the additive composition of numbers, meaning they understand that any number can be seen as the sum of two other numbers (Nunes 2012). Since the quantitative relations involved in additive reasoning are all part-whole relations (Nunes et al. 2015), this understanding of part-whole relations forms the basis of additive reasoning. In total, three types of situations with part-whole relations can be distinguished: transformations with increase or decrease, compositions of two quantities, and comparisons of two quantities (Nunes et al. 2015; Vergnaud 1983).

2.3.2.2 Multiplicative reasoning

Multiplicative reasoning is clearly distinct from additive reasoning (e.g., Clark and Kamii 1996; Vergnaud 1983). Like additive reasoning, it is about understanding relational meanings of numbers and quantities, but the relations are multiplicative, not additive. This means they can involve (i) a direct ratio between two quantities, (ii) an inverse multiplicative relation between two quantities, (iii) a third quantity formed by a multiplication or division of two quantities, and (iv) a quantity that proportionally is related to more than one other quantity (Nunes et al. 2015). Nunes et al. (2015) view “the hallmark of multiplicative reasoning […] the ability to make inferences about quantities by establishing one-to-many correspondences between the quantities” (pp. 184–185). They used “[t]he simplest type of multiplicative reasoning problem [involving] two quantities connected by a fixed ratio” to assess young children’s multiplicative reasoning, and used multiplication problems such as the following: “In each of the 4 houses in this street live 3 dogs; how many dogs live in this street?” Division problems such as the following were included: “There are 20 sweets and 4 children; how many sweets will each child receive?” (partitive division) and “I have 8 carrots, and I am going to give two carrots to each of the rabbits in my rabbit hutch; how many rabbits do I have?” (quotative division) (see also Bakker et al. 2014).

Multiplicative reasoning is found to be more complex than additive reasoning because the former requires keeping track of the iterations of the composite unit (Ulrich 2015) or, in other words, asks for “coordinated counting” (Tzur et al. 2012); in the problem about the dogs one has to follow two integrated counting traces: the number of groups of dogs and the number of dogs. Despite this difficulty, evidence has been found that when the opportunity is there to use the right sorts of representation, young children, even in preschool and in the first year of primary school, can solve multiplicative reasoning problems before they have been taught anything about the operations of multiplication and division (Nunes and Bryant 2015). Obviously, the schemas of action that are necessary for multiplicative reasoning may develop intuitively in children (Bakker et al. 2014; Mulligan and Mitchelmore 1997). In addition, indications were found (Bakker et al. 2014; Mulligan and Mitchelmore 1997) that for children who have not received explicit instruction on multiplicative reasoning, multiplication and division are equally difficult. This finding may reflect children’s intuitive understanding of the connections between the two operations.

3 Research questions

The aim of this study was to investigate the early number skills of children before they have had explicit instruction in numbers and operations. Drawing on the study of Purpura and Lonigan (2013) we took on board their recommendations that for the development of teaching–learning trajectories and the construction of assessments, more knowledge should be gathered about the underlying structure of the nature of informal numeracy skills. In line with this, our goal was to unravel young children’s quantitative competence and test whether it can be considered a multidimensional construct containing a number of empirically distinguishable components. Based on the reviewed studies concerning early number skills, we focused on the components counting, subitizing, additive reasoning and multiplicative reasoning, and examined how they are connected and develop (sequentially or concurrently). As we also wanted to explore the generality of the structure, we carried out the study in two countries.

The above led to the following research questions:

R1. Can early quantitative competence be modelled as a four-factor structure containing the components counting, subitizing, additive reasoning and multiplicative reasoning? Is this a general structure that applies to kindergartners in different countries?

R2. What does the performance of kindergartners show concerning early quantitative competence and does this performance differ according to children’s kindergarten year, gender, and country?

R3. What are the relations among items assessing components of early quantitative competence? Are these relations different for kindergartners in different countries?

4 Method

To know more about the structure of children’s quantitative competence before they have been formally taught numbers and operations, we set up a study in the Netherlands and Cyprus assessing kindergartners’ early number skills by administering a paper-and-pencil test consisting of two booklets with items about counting, subitizing, additive reasoning and multiplicative reasoning.

4.1 Participants

4.1.1 Netherlands sample

In the Netherlands, children from 18 kindergarten classes in 18 primary schools in the province of Utrecht took part in the study. The sample of children was drawn from regular schools. This means that schools with specific teaching methods, such as Montessori schools, were excluded from participation. The composition of the included schools was mixed with respect to school size, socio-economic background of the children and the urbanisation level of the school’s location. All kindergarten classes included both first-year (K1) and second-year kindergartners (K2). To teach mathematics in kindergarten, schools and teachers in the Netherlands can choose from various source materials and textbook parts for young children. There is no prescribed programme at the national level. The mathematics programme mostly consists of playful activities about number and shape and space. This general picture also applied to the schools from which the sample was drawn.

The sample included at first 384 kindergartners, but after excluding those who did not do both test booklets from the analyses, we ended up with a final sample of 334 kindergartners; 123 children in K1 (average age = 4.67) and 211 children in K2 (average age = 5.69), with a total of 176 girls and 158 boys (see Table 1).

Table 1 Sample composition
Full size table

4.1.2 Cyprus sample

In Cyprus, 10 primary schools with kindergarten classes in the province of Nicosia were recruited. All these schools used the regular curriculum provided by the Cyprus Ministry of Education and Culture. The kindergarten classes in four schools included both first-year (K1) and second-year kindergartners (K2), while in six schools K1 children and K2 children were in separate classes. In Cyprus, the majority of schools involve separate classes for K1 and K2 children, thus it was not feasible to have more schools with integrated classes. Consequently, the sample in Cyprus involved schools with both types of classes.

Another difference from the sample in the Netherlands was that more than one class from each school participated in the study. The sample initially was drawn from 23 kindergarten classes with 364 children. After removing the children who did not complete both test booklets, the final sample contained 304 children; 86 children (average age = 4.67) in K1 and 218 children (average age = 5.61) in K2, with a total of 163 girls and 141 boys (see Table 1).

4.2 Instrument

The kindergartners’ quantitative competence was assessed in a whole-class setting with a set of paper-and-pencil items originally developed for the PICO project (PIcture books and COncept development mathematics) (Van den Heuvel-Panhuizen et al. 2016). We chose this format because of the large sample size and because our focus was on whether the students could solve the problems instead of on the strategies they used. The set includes two items about counting, three items referring to subitizing, three items involving additive reasoning and three items referring to multiplicative reasoning (see Table 2; four sample items are shown in Fig. 2). Each item covers one page with a picture illustrating the problem situation. The instruction with the question to be answered is given to the children orally. Each page contains some pictures depicting possible answers to questions. The children indicate their answers by underlining or circling the picture they think conveys the correct answer. Of the 11 items, eight have a multiple-choice format and three have an open-response format. The items do not contain number symbols and no number words are used in the oral instruction.

Table 2 Overview of test items
Full size table
Fig. 2
figure 2

Examples of items: Lollipops (counting), Sweets (subitizing), Candleholder (additive reasoning), Mittens (multiplicative reasoning)

Full size image

The items were piloted before the data collection took place. This led to a revision of some items to clarify the wording and illustrations. The final versions of the items were divided into two booklets, which were administered on different days with a one-week interval. Data collection in the Netherlands and in Cyprus was carried out by trained test administrators. Correct responses were coded as 1, and incorrect ones as 0.

For the Netherlands sample, the Cronbach’s alpha reliability of the items was α = 0.72, and for the Cyprus sample it was α = 0.49. The reliability for the Cyprus sample is below the often-used minimal criterion of 0.70. This may indicate that for the latter children, the competences assessed by the items do not have much in common.

4.3 Analysis

To answer our first research question a confirmatory factor analysis (CFA) was applied, using MPLUS (Muthén and Muthén 1998–2010). In this analysis, we investigated in the two samples whether confirmation could be found of the hypothesized structure of kindergartners’ early quantitative competence. Three fit indices were computed (Marcoulides and Schumacker 1996) to evaluate model fit: the chi-square to its degree of freedom ratio (χ2/df should be less than 2); the comparative fit index (CFI should be higher than 0.90); and the root mean-square error of approximation (RMSEA should be close to or lower than 0.08). To answer the second research question, we computed the children’s performance concerning their early quantitative competence. To compare elements of performance, we planned to carry out analyses of variance (ANOVA) in order to identify the effects of country, kindergarten year and gender on performance. Finally, for the third research question, we delved deeper into the structure of kindergartners’ early quantitative competence by zooming in at item level and investigating for each country the implicative relations between the used items by means of CHIC (Classification Hiérarchique, Implicative et Cohésitive) software (Bodin et al. 2000). This statistical implicative analysis can reveal whether an item implies another item, which means that if a subject successfully solved an earlier item in the implicative chain, this same subject generally had success in a later item in this chain.

5 Results

5.1 Components of early quantitative competence

A series of CFA models were explored for each country’s sample. Based on our hypothesized model of early quantitative competence, the first CFA model that was tested included the four first-order factors counting, subitizing, additive reasoning and multiplicative reasoning. For the Netherlands sample, the used items loaded adequately on each of these four factors. The model reflected the empirical data quite well, as the descriptive-fit measures indicated support for the hypothesized model (χ2 = 40.59, df = 38, χ2/df = 1.07, CFI = 0.997 and RMSEA = 0.01). All factor loadings were statistically significant and most of them were rather large; their total range being from 0.31 to 0.87. The interrelations between the factors were significant and considerably strong, ranging from 0.65 to 0.92. So, in the Netherlands, the hypothesized structure of early quantitative competence consisting of the distinct but closely related components counting, subitizing, additive reasoning and multiplicative reasoning was largely confirmed. For the Cyprus sample, testing the four-factor model led to correlations between factors which were greater than 1. In other words, the hypothesized four-factor structure did not make sense for the empirical data on the early quantitative competence of the kindergartners in Cyprus.

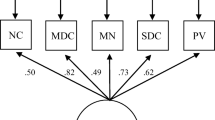
To investigate whether early quantitative competence is a unidimensional construct, a simpler model with only one first-order factor connected with all of the items was tested. For the Netherlands’ sample, the fit of this model (χ2 = 51.37, df = 44, χ2/df = 1.17, CFI = 0.99 and RMSEA = 0.02) was not as good as the four-dimensional one. This result provides evidence for the multidimensional structure of early quantitative competence. For the Cyprus sample, the fit of this model was inadequate (χ2 = 68.29, df = 44, χ2/df = 1.55, CFI = 0.88 and RMSEA = 0.04). Furthermore, the factor loadings of three items, namely, Marbles, Shoeboxes, and Building Blocks, were not statistically significant. Eliminating these three items from this model, resulting in a better fit (χ2 = 39.49, df = 20, χ2/df = 1.97, CFI = 0.90 and RMSEA = 0.06), made the model acceptable (see Fig. 3).

Fig. 3
figure 3

CFA model for early quantitative competence in Cyprus

Full size image

This means that in the Cyprus sample although the hypothesized four-factor structure could not be confirmed, a unidimensional structure for the major part of the items (8 out of 11) assessing quantitative competence could be found. Not finding the underlying quantitative skills in the kindergartners in the Cyprus sample may indicate that the early quantitative competence is not as differentiated as in the Netherlands sample.

For the Netherlands sample, considering the high correlations between the first-order factor of the former model, as a next step a higher- order model was tested, which involves four first-order factors and a second-order factor on which all the first-order factors are regressed. The second-order factor stands for the general quantitative competence underlying the solution of items involving counting, subitizing, additive and multiplicative reasoning. The fit of this model was slightly better than the former model (χ2 = 42.40, df = 40, χ2/df = 1.06, CFI = 0.997 and RMSEA = 0.01) (see Fig. 4).

Fig. 4
figure 4

CFA model for early quantitative competence in the Netherlands

Full size image

Comparably to the first four-factor model, all factor loadings were statistically significant and most of them were rather large; their total range was from 0.31 to 0.87. The relations between the first-order factors and the second-order factor were significant and considerably strong, ranging from 0.81 to 0.98. This model suggests that a higher–order construct, namely quantitative competence, underlies the components represented by the four first-order factors. In light of the above, we kept this latter model as our final solution for the Netherlands sample.

5.2 Early quantitative competence and effect of kindergarten year, gender and country

For the Netherlands sample, a repeated-measures analysis of variance (ANOVA) with kindergarten year and gender as between-subjects factors and with the components of early quantitative competence as within-subjects factors showed a strong and significant main effect of kindergarten year (F(1, 330) = 72.44, p < 0.001, η2 = 0.18), indicating that K2 children outperformed K1 children. For the components of early quantitative competence a strong and significant main effect was also found (F(3, 990) = 59.01, p < 0.001, η2 = 0.15). Table 3 shows mean performances for the Netherlands kindergartners’ component-specific and overall quantitative performance per kindergarten year.

Table 3 Mean performance in the component-specific and overall quantitative performance of kindergartners in the Netherlands per kindergarten year
Full size table

However, the interaction between kindergarten year and the components of early quantitative competence was significant (F(3, 990) = 4.42, p < 0.01, η2 = 0.01), indicating that the differences between the components varied between K1 and K2 children (see Fig. 5).

Fig. 5
figure 5

Mean performance in the Netherlands sample as a function of component of early quantitative competence and kindergarten year

Full size image

As is shown in Table 3, in K1 the performance in subitizing was significantly better than that in additive reasoning (p < 0.01) and in K2 the performance in counting was significantly better than the performance in subitizing (p < 0.01) and in additive reasoning (p < 0.01). For both kindergarten years though, children exhibited higher performance in counting, subitizing and additive reasoning than in multiplicative reasoning (p < 0.001). Finally, the effect of gender was not significant (F(1, 330) = 0.06, p < 0.81, η2 = 0.00).

When analysing in the Cyprus sample the effect of kindergarten year and gender on the quantitative performance, using an ANOVA, we found a significant main effect of kindergarten year (F(1, 300) = 48.56, p < 0.001), with K2 children (M = 0.52, SD = 0.21) outperforming K1 children (M = 0.33, SD = 0.21). The effect of gender was not significant (F(1, 300) = 0.02, p = 0.88).

Since the structure of early quantitative competence was modelled differently between the samples of the two countries, it was not possible to compare kindergartners’ performances in the components of early quantitative competence between the two countries (see Research Question 2). However, to investigate the effect of country on kindergartners’ performance we continued with a comparison on item level, based on the 11 test items and using independent samples t tests. Table 4 shows mean performances for the Netherlands and Cyprus kindergartners and the statistical significance of the different scores in the two samples.

Table 4 Mean performance and differences in the test items by kindergartners in the Netherlands and Cyprus
Full size table

Kindergartners in the Netherlands significantly outperformed kindergartners in Cyprus in six items, three subitizing items (Hand, Sweets and Building Blocks), two additive reasoning items (Cake and Apples) and one multiplicative reasoning item (Mittens). In the Marbles item, which refers to multiplicative reasoning, particularly partitive division, the kindergartners in Cyprus demonstrated significantly higher performance than the kindergartners in the Netherlands. In fact, this difference is the largest one among the items between the two countries. In the rest of the items, that is, Lollipops and Sausages, which refer to counting, Candleholder and Shoebox about additive and multiplicative reasoning respectively, kindergartners in both countries exhibited similar levels of performance.

5.3 Implicative relations between the early quantitative competence items

The diagrams in Fig. 6 graphically show the implicative relations we found between the early quantitative competence items in the Netherlands (on the left) and Cyprus (on the right). The relations are based on the children’s answers and the arrows specify the directions of the relations. We included only implicative relations that have at least an 85% probability of being identified correctly. The proportions of correct answers ranged from 0.82 to 0.12, with the most difficult items on top of the implicative chains. In both diagrams there are direct and indirect implicative relations, which are either between items belonging to the same early quantitative component or between items belonging to different components.

Fig. 6
figure 6

Implicative diagram of the early quantitative competence items based on the responses of the kindergartners in the Netherlands (left) and Cyprus (right). aM = Proportion correct answers. bProbability of a correctly identified implicative relations; ºp > 0.85, ^p > 0.90, *p > 0.95, **p > 0.99. cConditional probability; for example, 0.57 means: of the 33% children who answered Building Blocks correctly 57% answered Mittens correctly

Full size image

5.3.1 Implicative relations found in the Netherlands sample

In the Netherlands sample, direct implicative relations were found within the multiplicative and the additive reasoning items. A strong relation was obtained between the multiplicative reasoning items Shoeboxes and Mittens, indicating that children who were successful in the Shoeboxes item, figuring out how many pairs of shoes can be made by ten shoes (quotative division), must have been successful also in the Mittens item where they had to figure out the total number of mittens needed for three children (multiplication). No implicative relation was identified with the third multiplicative reasoning item Marbles, which is about equally partitioning nine marbles between three children to figure out how many marbles each child will get (partitive division).

Regarding the three additive reasoning items, the analysis revealed that the children who succeeded in the Apples or the Candleholder item must have succeeded in the Cake item as well. These additive reasoning items all involve understanding the part-whole structure of numbers. In the Apples item, children had to figure out the quantity of a subset to complete the total set, and in the Cake and Candleholder items a given larger set had to be composed from smaller sets.

For the conceptual subitizing items Building Blocks and Sweets, in which the kindergartners had to deal with a relatively large, but structured, number of objects, only an indirect implicative relation was found with the perceptual subitizing item Hand. The small number involved in this latter item can be recognized directly by view. The indirect implicative relations we found between the subitizing items indicate that children who were successful in the conceptual subitizing must have succeeded in perceptual subitizing also.

Overall, the left diagram shows that in the Netherlands the multiplicative reasoning component is on the top of the chain, underscoring that the items of this component were more complex than most other items. Children who succeeded in these multiplicative items did this also on the counting and additive reasoning items. Two other items that got a rather high position in the chain are the two conceptual subitizing items. This indicates that success in these items led to positive results in two of the additive reasoning items and one of the multiplicative reasoning items.

5.3.2 Implicative relations found in the Cyprus sample

The implicative diagram for the Cyprus sample shows that for nine out of eleven items implicative relations were identified. No implications could be identified for the multiplicative reasoning items Marbles and Shoeboxes. It is noteworthy that these items were excluded from the CFA structure that was confirmed for the Cyprus sample. Furthermore, the probabilities of the correctly identified implicative relations were lower in the Cyprus sample than in the Netherlands, which indicates that in Cyprus the implicative relations are less strong.

Similarly to the Netherlands results, the conceptual subitizing item Building Blocks (which also was excluded from the CFA structure in the Cyprus sample) and the multiplicative reasoning item Mittens are on the top of the implicative chain, meaning that in Cyprus the children who succeeded in these items must have been successful as well in most of the other items. This particularly applies to the additive reasoning items.

In accordance with the findings in the Netherlands, the perceptual subitizing item Hand and the counting item Lollipops are also placed at the lower end of the implicative chain, but unlike the results in the Netherlands, the relation between these two items is in the reverse direction. In the Cyprus sample, the perceptual subitizing item implies the counting item. This may indicate that in Cyprus the Hand item was solved by one-by-one counting the number of fingers, not prompt recognition of the number. This counting approach is also suggested by the direct implicative relation between the counting item Sausages and the Hand and the Lollipops item. From the perspective of the size of the numbers, this result underlines that the children who succeeded in detecting ten dogs and ten sausages, must have been successful in identifying a hand with five fingers and in circling five objects out of a larger collection of objects spread irregularly on a page. Another difference from the Netherlands results is that the counting item Sausages was found to imply two additive reasoning items, while in Cyprus the reverse was the case. The kindergartners who succeeded in these two additive reasoning items were inclined to perform well in the Sausages item.

6 Conclusions and discussion

For the kindergartners in the Netherlands sample our hypothesized model with a four-factor structure of kindergartners’ quantitative competence consisting of the components counting, subitizing, additive reasoning and multiplicative reasoning could be confirmed. Compared to earlier research this model is in line with the division of number competence into two constituent parts (number and arithmetic operations) as identified by Jordan et al. (2006), and at the same time it extends previous models (see Jordan et al. 2006; Purpura and Lonigan 2013) with multiplicative reasoning. For the children in Cyprus, who were about the same age as the children in the Netherlands, this structure with four distinct, but closely related components could not be identified. Instead, a unidimensional structure of early quantitative competence consisting of a major part of the items assessing this competence was found. In general terms, this unidimensional structure is in agreement with the study of Clements et al. (2008) which ended up with a one-factor model for early mathematical skills. Thus, no support was found for the generality of the hypothesized multidimensional early quantitative competence structure over the two countries. Obviously, the quantitative competence repertoire of the children in the Cyprus sample, as measured with the items in our study, was not as differentiated as the repertoire of the children in the Netherlands sample. Furthermore, for the Cyprus sample, three of the items were excluded from the confirmed unidimensional structure. Two of these items deal with multiplicative reasoning and the other item involves conceptual subitizing. A possible reason for this finding could be the inadequate attention given to activities providing opportunities for multiplicative reasoning or conceptual subitizing in Cyprus kindergarten classes, which probably resulted in making the solution of items involving these aspects of quantitative thinking isolated from solving other quantitative competence items, i.e., including counting and additive reasoning. Overall, the above findings challenge the generalizability of the models about the underlying structure of the nature of informal numeracy skills that were found in earlier research carried out in only one country.

As it was expected, in the samples of both countries there was a significant improvement of early quantitative competence with kindergarten year. A component-specific investigation of performance for the Netherlands sample revealed similar as well as different patterns between K1 and K2 children. For both kindergarten years, children’s performance in multiplicative reasoning was lower than their performance in the other quantitative competence components. This finding is in line with previous research providing evidence for the complex nature of the quantitative relations involved in multiplicative reasoning (e.g., Tzur et al. 2012).

With respect to counting versus subitizing, we found that in K1 the performance in subitizing was significantly higher than for the other components (only for counting this difference was not significant), while in K2 the performance in counting was significantly higher than in all the three other components. This latter finding may indicate that the development of the competence of subitizing takes place before counting, which was already suggested by other researchers (Baroody 2004; Clements et al. 2019; Sophian 2008).

At item level, the implicative analysis revealed that in both samples the multiplicative reasoning and conceptual subitizing items were found at the top of the chain and the counting and perceptual subitizing items at its end. In both samples, the three additive reasoning items are in the middle of the chain. These results suggest that fostering children’s multiplicative reasoning and conceptual subitizing performance may support getting a higher score in additive reasoning but also that being better in additive reasoning means being better in counting and perceptual reasoning. In this way, both implicative chains by and large reflect trajectories identified in previous research for counting (Eisenhardt et al. 2014), subitizing (Clements 1999) and additive reasoning, as well as for additive and multiplicative reasoning (Ulrich 2015). They also reflect the sequential steps mostly followed in teaching kindergartners early number, namely, starting with counting and subitizing, then additive reasoning and finally multiplicative reasoning. Of course, this is not a linear pathway with only one single step-by-step track. The implicative chains show that even for this small collection of items there are many parallel processes and cross-connections between components.

When comparing the findings in the two samples, we found that the kindergartners in the Netherlands outperformed those in Cyprus in the majority of the quantitative competence items. However, it was intriguing that for some items the implicative relation was in the reverse direction, such as between the Sausage item and the additive reasoning items, and between the Lollipops and the Hand item. It might be tempting to view these anomalies as evidence for the very complex and at times messy process of young children’s development of quantitative competence, but it is also appropriate to look critically at the items used to capture children’s quantitative competence. Items may work out differently in different countries for all sorts of (unforeseen) reasons. This is illustrated by the difference in position of the Cake item. In the Netherlands, this item is below the Apples and Candleholder item, while in Cyprus the Cake item is above these two items. All three items are additive reasoning items and are about part-whole relations, but in the Cake item more than one correct answer is possible. This makes the item more challenging for the Cyprus kindergartners, probably because such open-ended problems are uncommon in kindergarten activities in Cyprus. In addition, other features of the items, such as size of the numbers and the used contexts, but also the class-administered setting in which the data were collected could have biased our findings. It is therefore important to handle the results of our study with prudence. Moreover, it is also necessary to take into account that we did not cover all aspects of quantitative competence, that we had only a small number of items, and that the kindergartners involved in our study cannot be considered a representative sample of the Netherlands and Cyprus kindergarten population. However, despite these shortcomings, we think our study, in which we tried to unravel the components of children’s quantitative competence, has added some new knowledge about these components, their relations and the generality of the structure of early quantitative competence over different countries, but to further investigate the deep structure of young children’s quantitative competence and conceptualize a robust map of it, more research is necessary.