Abstract
This papers comments on the contributions of ZDM Mathematics Education dedicated to the theme “Perception, interpretation and decision making: understanding the missing link between competence and performance”. The papers within this issue are brought together under the perspective of the stated aims of this issue, and then questions are raised about assumptions underlying methods of the studies and the overall enterprise. It becomes clear that teacher competence is a shining example of how in mathematics education both researchers and teachers need to develop a shared approach to negotiating meaning of terms used partly technically so that the use of the same terms for different things and different terms for essentially the same thing is reduced. The commentary aims to contribute to a joint understanding of the concepts used, so that researchers can communicate effectively with each other and so that their findings can support teacher development.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Stated aims of this issue
The challenge for research on teacher competence is to come close to real classroom situations in terms of performance on the one hand, and on the other hand, to include assessments of the dispositional base in terms of cognition, affect and motivation-volition as resources. Most current teacher research relies either on traditional paper-and-pencil assessments of the different dispositional facets or on holistic performance assessments. Only rarely are both perspectives are combined or are the connecting processes examined. There is an urgent need for methodologically innovative studies that examine competent teaching under controlled conditions and with sample sizes sufficient for multivariate and multidimensional analyses. Such laboratory-like data could provide important information on the internal structure of teacher competence and the many steps mediating the transformation of competence into performance.
The four research questions intended to guide the papers in this special issue are as follows
-
Q1. How do teachers who possess all of the resources belonging to professional competence integrate these, such that the underlying competence emerges in performance?
-
Q2. What is the internal structure of teacher competence? Is it organized into domain-specific components or are there other organizing principles governing its structure?
-
Q3. How do the different facets of teacher competence play out in the classroom? Do the teacher’s observable acts relate differently to the cognitive, affective, or motivational-volitional characteristics?
-
Q4. Is teacher competence directly predictive of student achievement? Or are other processes and context-conditions mediating the transformation of competence into performance so that an indirect model is better suited to depict the relationship?
I begin by considering the contributions of the papers to addressing these questions, in their own terms. I then consider some underlying assumptions, both to the original questions and to the research reported in the papers, which leads me to address the connection between researchers’ distinctions and teachers’ actions, from a qualitative, even phenomenological perspective.
2 What do the papers contribute to the original questions?
Looking at the papers in the light of research questions, I begin with Q2 about components of teacher competencies before considering Q1 on integration of different competencies, then Q3 on how these play out in the classroom, and finally Q4 concerning prediction of student achievement from observed competencies.
2.1 Q2. What is the internal structure of teacher competence? Is it organized into domain-specific components or are there other organizing principles governing its structure?
All of the papers refer directly or indirectly to Shulman-based distinctions between Mathematics Content Knowledge (MCK), Mathematics Pedagogical Content Knowledge (MPCK) and General Pedagogical Knowledge (GPK), even though these are, as several authors point out, not as well-specified as is needed for the kind of research evidence sought in the aims of this issue.
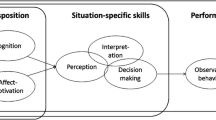
In their attempts to identify and even measure teacher competence, many of the papers make either explicit or implicit use of a triadic distinction between perceiving, interpreting, and decision-making using Blömeke et al. (2015). Individual papers make use of dyadic distinctions between instructional norms and professional obligations (Herbst et al. 2016); and between mathematical and pedagogical resources (Dunekacke et al. 2016). Hoth et al. (2016a) follow Weinert et al. (1990) in distinguishing diagnostic competence in addition to instructional competence, subject-matter knowledge, and classroom management. Hoth et al. (2016a) also draw upon a continuum comprising disposition, situation-specific skills, and performance again based on Blömeke et al. (2015). König & Kramer (2016) distinguish between structure (knowledge of structuring lessons); motivation and classroom management; adaptivity (dealing with heterogeneous learning groups); and assessment. Dyer & Sherin (2016) identify three forms of teacher reasoning about student behavior, involving connecting specific moments of student thinking; linking the mathematics of student thinking and the structure of a mathematical task; and probing student thinking.Pankow et al. (2016) correlated reaction time and appropriateness of response of teachers asked to anticipate possible student errors in different topics. Bruckmaier et al. (2016) develop the construct of situated reaction competency, showing it to comprise both pedagogic action cometency and subject-specific competency, through analysis of teachers interpretation of and responses to classroom video episodes. These, together with specific pedagogic actions comprising them, offer some finer detail concerning perceiving and interpreting, providing a range of actions from which to make choices. None of the papers address (at least explicitly and directly) the issue of contingency raised in the distinctions used by Rowland & Turner (2007) in the knowledge quartet.
All of these distinctions could be considered to be organizing principles, but as I will suggest later in more detail, they constitute observer-constructed distinctions or principles, not inherent structure. But then this is partly due to the fact that teacher competence itself is not well-specified, and is indeed highly context dependent, influenced by both observer and situation, as two of the papers note (Schlesinger & Jentsch 2016; Hoth et al. 2016b).
The papers report little in the way of surprising results as seen from a teacher’s practical perspective, but they do serve to show consistency between organizing distinctions and what was observed. For example, we learn that teachers with a strong mathematical background tended to notice content-based issues, whereas teachers with a strong pedagogic background tended to notice pedagogic issues (Hoth et al. 2016a). In other words, people notice what they are attuned to notice. Although not part of that study, it is obvious that the nature of recent significant experience can influence the sorts of things that are noticed. This is addressed in Herbst et al. (2016) who were able to discern and distinguish between influence from instructional norms and influence from professional obligations on teacher’s choices of pedagogical strategies. Others of the papers found confirmation that the distinctions they had chosen to make were indeed discernible in their data, and that there were correlations along expected lines in most cases.
2.2 Q1. How do teachers who possess all of the resources belonging to professional competence integrate these, such that the underlying competence emerges in performance?
Although not addressed directly by authors, there are some implications from the papers in response to this question. For example Dunekacke et al. (2016) found that some pre-school teachers needed a combination of mathematical and pedagogical resources in order to perceive and plan effective classroom interaction. Their study was based on the assumption that “only when teachers’ knowledge and beliefs fit together can teachers be expected to draw on their knowledge and be able to successfully master the demands of the classroom”. Having been oriented by their assumptions, it is perhaps not surprising that they found what they expected to find. Again perception, interpretation and decision-making are seen as skills to be acquired, based on alignment of beliefs and orientations.
Put another way, ‘competencies having been displayed in the past’ are not necessary conditions, nor are they sufficient conditions for them to be enacted in-the-moment in classrooms (or even during lesson preparation). Rather, actions need to be available to be enacted, and aligns with findings in others of the papers. For example:
Santagata & Yeh (2016) found support for the complexity of teacher actions in classrooms, noting that sometimes the institutional norms and requirements (as perceived by teachers) play a dominant role, while at other times, especially as the teachers they studied became more experienced, teachers enact actions that are more in alignment with their own espoused beliefs (ideals and propensities). They found that their interpretation of teachers’ perceiving, interpreting and decision-making increased in sophistication over time. They also acknowledge that at any specific moment, teachers may not act in accordance with or be informed by ‘knowledge’ that tests have shown them to ‘possess’. Their results align with those of Herbst et al. (2016) who suggest that integration of competencies, or at least choices of action, are significantly affected by teacher perceptions of instructional norms and professional obligations. Anyone who has been involved with teacher education will recognise the tension that novice and newly accredited teachers experience between what they encounter at university and what they experience in their school placement. Even though many schools look for newly qualified teachers to ginger the department, the inherent inertia of an established community of practice can be over whelming (Wenger 1998).
König & Kramer (2016) developed a video-based instrument for measuring instructional behaviour to address structural relations, expert-novice differences and the predictive validity of classroom management expertise and general pedagogical knowledge. Statistically, they conclude that pedagogical knowledge and classroom management are different constructs, but this could be an indication of the specific behaviours that were attributed to one or other category, because some pre-service teachers with a year’s experience statistically performed indistinguishably from pre-service teachers without that experience. Predictive validity was evaluated by comparing pre-service teacher behaviour with student comments on the instructional quality of the teaching. But these general claims turn out to be specifically about a rather limited scope of classroom management and pedagogical content knowledge, namely whether the students were clear about classroom ‘rules’ and how they expressed their sense of the teacher’s ‘with-it-ness’.
Kersting et al. (2016) present evidence for a functioning knowledge system that they believe can be tested systematically on large numbers of teachers, based on scores assigned to teachers’ responses to video clips of teaching of a range of topics. Curiously, aggregation of the scores appears to be more stable than the range of variation associated with individual clips. They conclude that usable knowledge requires both individual knowledge components, and an overarching ability to access and apply those components that are most relevant to a particular teaching episode (always? under what conditions?) and that teachers often do not call upon the wide range of actions that they have shown they ‘know’. However perception and interpretation of classroom incidents involving other teachers is a far cry from acting in-the-moment in a classroom.
What we are reminded of in several of these papers, but in different discourses, is that actions and perceptions need to be linked, and these, I suggest, involve sensitivity to the whole of the human psyche: cognition, affect, enaction, attention, witness and will. In other words, teacher attention has to include access to actions associated with mathematical thinking, with attention, with pedagogy (both topic specific and more general), and with their own dispositions and propensities, in order to be sensitive to the whole of learners’ psyche. This includes their own mathematical thinking; their own likes and dislikes; their own mathematical and epistemic attention; and their own mathematical actions (both enacted and suppressed).
A shift from the rather loose distinctions offered by PCK and its relatives to thinking in terms of resources (e.g. Dunekacke et al. 2016) is to be welcomed, as it signals appreciation of a more fully rounded image of human beings and how actions are enacted].
2.3 Q3. How do the different facets of teacher competence play out in the classroom? Do the teacher’s observable acts relate differently to the cognitive, affective, or motivational-volitional characteristics?
Dyer & Sherin (2016) report some stability in the three kinds of reasoning they identified in teachers known to be responsive to students: making connections between specific moments of student thinking; considering relationships between the mathematics of student thinking and the structure of the mathematical task; and testing student thinking. They further propose that these forms of reasoning (foci of attention while teaching) support, even enable responsive teaching.
Lande & Mesa (2016) uncovered differences in experienced and expressed agency between full-time and part-time teachers. This they cast in terms of professional obligations, though they could well have included personal commitment and personal survival as associated factors. The more agentively their teachers spoke, and the more flexibly they expressed what they observed, the more likely they were to diverge from institutional and other professional norms.
Jacobs & Empson (2016) focus on categories of teacher actions (‘moves’) in one-to-one situations as the teacher is circulating around the classroom and ‘teaching-between-desks’ (kikan-shidō). They noticed that these categories mostly aligned with actions with the whole class, but that it was their categories rather than specific behaviours that were in common. They conclude that ‘between-desks-teaching’ is more than simply ‘circulating’ to pick up on what students are doing, but rather, present real opportunities to develop and enrich students’ thinking. Of course interacting effectively one-to-one is no easy matter, as students often do not seem to take up advice they receive. The authors note that the classroom ethos, the trust built up between students and teacher, the relationships between teacher and student, and of course between teacher and mathematics, play a vital role in the possibility of between-desks-teaching to be effective. Teaching mathematics is a caring profession, but a balance is needed between caring for the students and caring for the mathematics. Detecting this through questionnaires and short videos of classroom may prove to be a challenge.
2.4 Q4. Is teacher competence directly predictive of student achievement? Or are other processes and context-conditions mediating the transformation of competence into performance so that an indirect model is better suited to depict the relationship?
In claiming that certain professional competencies necessarily contribute to student achievement, or even that they are often (sometimes?) correlated with student achievement, it will be necessary to study classrooms where student achievement is high (to see whether claimed teacher competencies are being enacted) and classrooms where student achievement is not high (to see whether claimed competencies are not being enacted, and to consider whether some actions being enacted are working against goals). It will also be necessary to propose some causal connection between them. It might be the case that in delineating professional competencies, what might be lost are the subtle relationships that make up human interaction: relationships between teacher and mathematics, learners and teachers, learners and mathematics, and between these and perceived conditions of the milieu (including perceived institutional demands, professional demands, and personal desires).
An enactivist stance would suggest that “knowing is acting”, that despite having displayed actions in the past associated with mathematical thinking, pedagogic strategies, the didactics of particular mathematical topics, and socio-cultural sensitivities, what matters ultimately is behaviour and the ethos in which it is enacted. Whereas a potter can be judged by the pots produced, people often do not appreciate the actions of their teachers, sometimes until many years later. Judging teacher professionality, teacher artistry, is even more complex than is perhaps commonly recognised. Developing and working with the discipline of noticing (Mason 2002) has led me to value a programme of on-going development of myself as teacher. Rather than trying to change other people, a process which is highly problematic and notably ineffective, I prefer to engage others to work with me. Thus instead of classifying and judging teacher competencies, I would prefer to use the insights gained in these papers and in others as part of an on-going development process in which all teachers, educators and researchers are together engaged.
3 Overall issues and concerns
Hoth et al. (2016b) encountered wide variation in the judgements of a range of experts when viewing video recordings of mathematics classrooms, and Kersting et al. (2016) encountered considerable variation in the way that teachers perceived and interpreted what they saw in video clips of teaching across a range of mathematical topics. More subtly, variation was larger when more inferences being called upon, rather than simply on direct observation. This gives support to the discipline of making specific non-judgemental brief-but-vivid accounts of incidents that others can identify, rather than mixing observation and assumption-based opinion (Mason 2002).
Schlesinger & Jentsch (2016) conclude that there is huge variation and no common agreement as to what constitutes quality instruction in mathematics. They also found issues concerning reliability and validity in the reports of observations that they studied.
Two quite similar studies report on the development of particular video-based instruments for evaluating teaching. Herbst et al. (2016) report on the development of a collection of instruments which use video-recordings of classroom incidents and constructed scenarios with questionnaires, as the basis for judging both instructional decisions and teacher recognition of the basis for those decisions. Their contention is that their instruments avoid assumptions about teacher rationality in making choices. But this conjecture seems itself to depend on a rationalist stance concerning teacher epistemology and choice making. Kersting et al. (2016) made use of a particular form of teaching evaluation from video-recordings of some lessons, together with a collection of questions to be addressed by teachers. Their statistical studies did not permit them to assert that teachers’ scores on their instrument actually measure useable knowledge as a functional system. The answer to this dilemma will, I suspect, lie not in statistics, but in the appropriateness of underlying assumptions about how human beings actually function.
Of course what transforms the various artefacts comprising researchers’ instruments into data are researcher interpretations of what they see and comprehend of teacher responses. Perceiving and interpreting as actions, indeed as foci of attention, apply to researchers as well as to teachers, and this is what I tried to get at when talking about three levels of awareness (Mason 1998).
4 Underpinning assumptions
The reification of teacher competence as a ‘thing’ with internal structure and hence presumably multiple components is an assumption that itself may need to be questioned. After all, the artistry and effectiveness of the potter and the painter whose work is admired do not consist solely of a collection of competencies, structured or unstructured. Indeed, many might question the notion of component competencies at all in the arts. And teaching must be considered an art, at least in part. A more fruitful version of question 1 might be “What distinctions in the observed competent actions of teachers might be fruitful for informing future practice and for inclusion in teacher education programmes?”, rather than assuming that there is some implicit structure to be located.
In order to obtain practical and effective results that can be proposed to others, it is vital to be clear concerning assumptions being made about human psyche during the validation process. As mentioned, many of the papers are based on perceiving, interpreting and deciding, quoting Blömeke, Gustafsson, & Shavelson (2015), and these seem to be taken as unproblematic. For example, is correctness an attribute of an interpretation, or might appropriateness depend on being able to be justify or to provide warrants? Is there a single interpretation or might there be many? If someone else’s perceptions are different to mine, then I would expect our interpretations to differ, but even when our perceptions are in alignment, our interpretations may differ. We may read the situation differently. And since we are likely to have different backgrounds, the possible actions which occur to us are very likely to differ. Furthermore, even if the same or similar actions occur to us, we may enact and manifest them differently, due to our personal propensities, values, and relationships with mathematics and with students. Surely this is the artistry of teaching mathematics.
A dominant assumption in these papers concerning the human psyche seems to be that human beings possess knowledge, that they act rationally after consideration and interpretation of a situation that strikes them as being problematic or ambiguous, drawing upon their knowledge of mathematics, of how people learn mathematics, and of how people learn more generally. When people teach they make conscious, even considered choices as to what to say and do next, informed or guided by beliefs and ideals, by assumed social pressures and norms. Furthermore, this view includes the assumption that by watching someone teach, one can gauge their competence as a teacher according to various scales. The thrust of associated research is to develop instruments which enable error-free measurement of that competence. Presumably this is then intended to inform teacher education: you train people to enact actions that have been deemed maximally effective. It certainly leads to a sense of a gap between perceived competence and performance.
An alternative view is that human beings are mainly habit-driven organisms with the potential to consider possible internalised actions, informed by past experience and by theoretical constructs, ideals, aims and intentions. Sometimes choices are made in the moment, but often those choices have been made in the past, and follow a line of greatest immediacy (or least resistance). Choice making is more like participating in a brief moment, momentarily poised on a knife edge and then sliding down one side or the other, than it is like making a rational choice by listing all the known pros and cons and maximising benefit (to the teacher, to the learners, to the institution, …). From this perspective, watching someone teach brings to mind actions in the observer’s repertoire based on their interpretation of the situation from an observer’s perspective, which may be in stark contrast to the teacher’s experience. If those actions are not then enacted, the teacher may not be considered to be competent. But a different observer might see things differently.
A useful way to envision this alternative perspective is to consider a human being as occupying one or a few of a variety of states, in which emotional energy has characteristic flows associated with characteristic ways of acting, thinking and feeling. Some people go so far as to think of these as separate selves, using constructs such as ‘frames of mind’ (Hudson 1968; Minsky 1975) which is in alignment with the notion of polyphrenia, otherwise known as ‘multiple selves’ (Bennett 1964) and ‘micro-identities’ (Varela 1999). Others wish to retain the integrity of personhood, preferring to think in terms of ‘adherences and coordinations’ (Mason & Metz 2016) between cognition, affect, enaction, attention, will and witness.
When someone responds to a probe, whether a questionnaire or a video-clip, can it be assumed that what the person says and does forms a considered response, or might it be unconsidered immediate reactions? It must surely matter when analysing what people say and do! Kahneman (2012) introduced the language of System 1 and System 2 to distinguish between automatic, habit-based reactions and cognitively considered responses. This brings to the surface what has been known for a long time in eastern psychology and reiterated in different terms (Ouspensky 1950; Norretranders 1998), namely that, as Swift (1726) satirically proposes in Gulliver’s Travels, human beings are not so much rational animals, as animals capable of reason. A real issue then is how might an observer distinguish between habitual reactions and considered responses? Pankow et al. (2016) cleverly exploited differences in response times. They found that teachers who reacted quickly often overlooked possible errors that students might make, or even anticipated them incorrectly, whereas teachers who took time responding to the probes tended to have more complex and appropriate proposals.
In order to act freshly (not out of habit) it is necessary to notice an opportunity while at the same time having one or more possible actions come to mind (not just to body so that they are enacted automatically), and then participating in a choice of whether to act and in what way. The language of decision-making implies assumptions about the rationality of human behaviour which are not in alignment with ancient psychology or with detailed observation of oneself.
Concerning quality of teaching, was nothing learned from Zen and the Art of Motorcycle Maintenance (Pirsig 1974)? Quality is not measurable on a linear or other scale. It is not an interval quantity. It is not a quantity at all. Was nothing learned from the study of tailors in Liberia and other contexts (Lave 1988)? Being in the presence of an expert (even a relative expert viz Vygotsky’s zone of proximal development) can be sufficient, without being tested, without being instructed directly. The problem, from my way of thinking, is that because education is seen as important by politicians, policy makers try to engineer education, as if it were a machine in which tinkering with components can make the whole more or less effective and productive. The result is that education systems are treated as production lines. Just as time-and-motion studies tried to make assembly-line workers (and office workers) more efficient, so too educational institutions are being forced to mimic the now robotic assembly line. Time and motion studies failed because they did not take into account the full psyche of human beings, with all their foibles and automaticities, their habits and desires, their emotions, behaviours and thoughts, not to say their attention and will. Attempts to engineer the teaching of mathematics, and the teaching of how to teach mathematics, will, I suggest, likewise fail. The trouble is that it means several generations of children being abused by an inappropriate regime of measure-driven behaviour, and because future generations operate from the basis of their own experience, there is enormous inertia so it takes a long time to turn such a behemoth around.
There is also a lurking issue concerning distinguishing between the researcher and the researched. Might we not be learning as much or more about the sensitivities of the observers as about the situations being observed? After all, other observers, arriving with different frameworks of distinctions, and proceeding on the basis of different assumptions, might observe different things. We notice what we are sensitised to notice, so that we learn as much about a researcher’s sensitivity to notice as we learn about the situation being observed. This ‘Heisenbergian’ invariance (ratio of precision of detail concerning the researcher to precision of detail in the researched) applies whether the data consists of observations or responses to interviews or to questionnaires (Mason 2002).
The trouble is, knowing some mathematics, thinking mathematically, is pretty important for effective teaching. The abiding issue is how to make this claim more precise, and if really necessary, to justify it. But there are well known examples of teachers whose mathematics was weak but who nevertheless taught at least some children effectively. My own secondary mathematics teacher was a case in point. It is not so much the actual mathematics studied previously, as the being of the teacher (Mason & Davis 2013). This is why I refer to the mathematical being of a teacher, a collection of qualities that do not respond well to measuring. It is Heidegger’s notion of Being, crossed out so as not be mistaken for a ‘thing’. It is the totality of the person’s relationship with mathematics and with students together with their awareness (access to actions) and sensitivity in-the-moment to the situation (as they perceive it). So part of their Being includes the breadth and scope of their reading of a situation.
Teaching is unlike any other profession in that an ‘expert’ finds them selves enacting actions to initiate and carry through actions in the moment-by-moment flow of a lesson which in retrospect and with hindsight they might have chosen differently. Put another way, there is no, in my view, ‘best way to teach’, nor even a ‘best action to choose with particular learners at a particular time and place’. Teaching is not a manufacturing process in which raw materials are shaped according to some prearranged plan. Using statistical evidence which is necessarily aggregated, as the basis for making choices in particular situations requires a close fit between all the situational details of the study and of the particular situation. Making a decision on the basis of statistical correlations is as sensible in mathematics education as it is in medicine (where the particularities of the individual rarely align with the particularities of the statistical sample) or as it is in gauging your life expectancy by looking at actuarial tables. Teaching is an interaction between cognising, habit-enacting, emotion-driven, potentially-agentive human beings.
5 Summary
It is evident that different research communities use different terms for somewhat the same ideas, and sometimes the same term for rather different ideas. Furthermore, as others take up and use the same terms, meanings shift, sometimes subtly, sometimes significantly. MPK, MCPK and GCPK are cases in point, joining a long list which includes ZPD, discovery learning, scaffolding, assimilation and accommodation, and many others. Indeed, one of the forces leading us as a community to invent new terms for what seem like fresh distinctions could be that terms already in use have become ambiguous. They no longer signify a distinction that we, through our lived experience, wish to make.
Even comparing frameworks is problematic. How for example, are we to inter-relate the knowledge quartet (Rowland & Turner 2007) and the perceiving-interpreting-deciding trio? What can we bring forward from earlier research such as the making of ‘in-flight’ choices (McNair 1978a, b)? If it is necessary or useful to report on quality of curriculum teaching, then it is necessary to reach agreed definitions so that teachers and researchers can be confident that they are noticing the same things when they use the same labels. Then and only then will it make sense to pass on recommendations to policy makers. The mathematics education research community needs to take a lead, otherwise policy makers will determine the parameters.
One thing that I have learned from trying to provide a philosophically foundation for working on one’s own practices as a valid research tool through becoming aware of noticing and shifts of attention (Mason 2002), has been that making distinctions is one thing; testing out whether others can make a similar distinction is another, and whether it then informs future practice to good effect is quite another. Believing that my distinctions are structural, that is, in some sense ‘already present’ is always dangerous, which is why I stress the need for a conjecturing atmosphere in which ‘results’ are announced. In an uncertain world I am wary of the confidently asserted which brooks no alternatives. I fully acknowledge that there is a need to validate distinctions, but I am myself less convinced by statistical studies than I am through seeking resonance amongst new communities of students, teachers and mathematics educators and researchers. The lived experience of a phenomenological stance is for me, more convincing than correlation.
Furthermore, any sort of cause-and-effect relationships between actions I observe someone making and judgments I might want to make, are for me problematic at the very best. Although cause-and-effect is a mechanism that enables people to make accurate predictions about the functioning of machines, it simply does not work for me as a mechanism when human beings are involved. Skinner and other behaviourists were very effective in charting the mechanical aspects of human functioning, but there is much more to human beings than their automaticities. It is precisely when the vagaries of the functioning of attention, especially intentionally, come into play that prediction requires a different underlying metaphor. The best I have found is that of a complex chemical reaction is in which there is always flux between the combining and splitting of different compounds, and no clear indication of which forces are dominant. The presence of intention and will (partially considered under the heading of ‘agency’) and links between cognition, affect, enaction, attention, will, and witness, confound any mechanistic explanation. This is what the discipline of noticing offers: a way of researching the complexities of the human psyche, in any caring profession including mathematics education.
There is a plethora of reports contributing to specifying the underlying assumptions of the questions posed in this issue, namely what constitutes professional competence. Some readers will be in sympathy with the value, indeed for some the necessity of defining professional competencies, while others may be dubious about the possibility. Others yet may, like me, fear that in trying to be cause-and-effect-precise about such competencies, the complexity of the human psyche may be overlooked, and the professionality, including the artistry of teaching, may be lost, may wither on the vine as policy makers turn specifications of competencies into checklists.
There is indeed, as it says in the aim of this issue, an urgent need for methodologically innovative studies that examine competent teaching under controlled conditions and with sample sizes sufficient for multivariate and multidimensional analyses. But there is also an urgent need for phenomenologically based studies that provide teachers access to enriching both their repertoire of pedagogic actions and the discourse they use to justify those actions. There is certainly still a great deal to be done to appreciate and comprehend how teacher’s dispositions and propensities guide or restrict the possible pedagogical actions that teachers have access to, whether during lesson planning or in-the-moment.
References
Bennett, J. (1964). Energies: material, vital, cosmic. London: Coombe Springs Press.
Blömeke, S., Gustafsson, J.-E., & Shavelson, R. (2015). Beyond dichotomies: Competence viewed as a continuum. Zeitschrift für Psychologie, 223, 3–13.
Bruckmaier, G., Krauss, S., Blum, W., & Leiss, D. (2016). Measuring mathematical teachers’ professional competence by using video clips (COACTIV video). ZDM Mathematics Education, 48(1) (this issue).
Dunekacke, S., Jenßen, L., Eilerts, K., & Blömeke, S. (2016). Epistemological beliefs of prospective preschool teachers and their relation to knowledge, perception, and planning abilities in the field of mathematics: a process model. ZDM Mathematics Education, 48(1). doi:10.1007/s11858-015-0711-6 (this issue).
Dyer, E. B., & Gamoran Sherin, M. (2016). Instructional reasoning about interpretations of student thinking that supports responsive teaching in secondary mathematics. ZDM Mathematics Education, 48(1). doi:10.1007/s11858-015-0740-1 (this issue).
Herbst, P., Chazan, D., Kosko, K. W., Dimmel, J., & Erickson, A. (2016). Using multimedia questionnaires to study influences on the decisions mathematics teachers make in instructional situations. ZDM Mathematics Education, 48(1). doi:10.1007/s11858-015-0727-y (this issue).
Hoth, J., Döhrmann, M., Kaiser, G., Busse, A., König, J., & Blömeke, S. (2016a). Diagnostic competence of primary school mathematics teachers during classroom situations. ZDM Mathematics Education, 48(1) (this issue).
Hoth, J., Schwarz, B., Kaiser, G., Busse, A., König, J., & Blömeke, S. (2016b). Uncovering predictors of disagreement: Ensuring the quality of expert ratings. ZDM Mathematics Education, 48(1) (this issue).
Hudson, L. (1968). Frames of Mind. London: Methuen.
Jacobs, V. R., & Empson, S. B. (2016). Responding to children’s mathematical thinking in the moment: an emerging framework of teaching moves. ZDM Mathematics Education, 48(1). doi:10.1007/s11858-015-0717-0 (this issue).
Kahneman, D. (2012). Thinking fast, thinking slow. London: Penguin.
Kersting, N. B., Sutton, T., Kalinec-Craig, C., Jablon Stoehr, K., Heshmati, S., Lozano, G., & Stigler, J. W. (2016). Further exploration of the classroom video analysis (CVA) instrument as a measure of usable knowledge for teaching mathematics: Taking a knowledge system perspective. ZDM Mathematics Education, 48(1). doi: 10.1007/s11858-015-0733-0 (this issue).
König, J., & Kramer, C. (2016). Teacher professional knowledge and classroom management: on the relation of general pedagogical knowledge (GPK) and classroom management expertise (CME). ZDM Mathematics Education, 48(1). doi:10.1007/s11858-015-0705-4 (this issue).
Lande, E., & Mesa, V. (2016). Instructional decision making and agency of community college mathematics faculty. ZDM Mathematics Education, 48(1). doi:10.1007/s11858-015-0736-x (this issue).
Lave, J. (1988). Cognition in practice: Mind, mathematics, and culture in everyday life. Cambridge: Cambridge University Press.
Mason, J. (1998). Enabling teachers to be real teachers: Necessary levels of awareness and structure of attention. Journal of Mathematics Teacher Education, 1(3), 243–267.
Mason, J. (2002). Researching your own practice: The discipline of noticing. London: RoutledgeFalmer.
Mason, J., & Davis, B. (2013). The importance of teachers’ mathematical awareness for in-the-moment pedagogy. CJSMTE, 13(2), 182–197.
Mason, J., & Metz, M. (2016). Digging beneath dual systems theory and the bicameral brain: Abductions about the human psyche from experience in mathematical problem solving. In U. Uxe & X. Eligio (Eds.) Understanding emotions in mathematical thinking and learning (submitted).
McNair, K. (1978a). Thought and action, a frozen section. Educational Research Quarterly, 3(4), 16–25.
McNair, K. (1978b). Capturing inflight decisions: Thoughts while teaching. Educational Research Quarterly., 3(4), 26–42.
Minsky, M. (1975). A Framework For Representing Knowledge. In P. Winston (Ed.), The Psychology of Computer Vision (pp. 211–280). New York, USA: McGraw Hill.
Norretranders, T. (1998). (J. Sydenham Trans.). The user illusion: Cutting consciousness down to size. London: Allen Lane.
Ouspensky, P. (1950). In search of the miraculous: Fragments of an unknown teaching. London: Routledge & Kegan Paul.
Pankow, L., Kaiser, G., Busse, A., König, J., Hoth, J., Döhrmann, M., & Blömeke, S. (2016). Early career teachers’ ability to focus on typical students errors in relation to the complexity of a mathematical topic. ZDM Mathematics Education, 48(1) (this issue).
Pirsig, R. (1974). Zen and the art of motorcycle maintenance: An inquiry into values. New York: Morrow.
Rowland, T., & Turner, F. (2007). Developing and using the ‘knowledge quartet’: A framework for the observation of mathematics teaching. The Mathematics Educator., 10(1), 107–124.
Santagata, R., & Yeh, C. (2016). The role of perception, interpretation, and decision making in the development of beginning teachers’ competence. ZDM Mathematics Education, 48(1). doi:10.1007/s11858-015-0737-9 (this issue).
Schlesinger, L., & Jentsch, A. (2016). Theoretical and methodological challenges in measuring instructional quality in mathematics education using classroom observations. ZDM Mathematics Education, 48(1) (this issue).
Swift, J. (1726). (Ed. H. Davis). Gulliver’s travels (vol. XI, p. 267). Oxford: Blackwell.
Varela, F. (1999). Ethical Know-How: action, wisdom, and cognition. Stanford: Stanford University press.
Weinert, F. E., Schrader, F. W., & Helmke, A. (1990). Educational expertise. Closing the gap between educational research and classroom practice. School Psychology International., 11, 163–180.
Wenger, E. (1998). Communities of practice: Learning, meaning and identity. Cambridge: Cambridge University Press.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Mason, J. Perception, interpretation and decision making: understanding gaps between competence and performance—a commentary. ZDM Mathematics Education 48, 219–226 (2016). https://doi.org/10.1007/s11858-016-0764-1
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11858-016-0764-1