Abstract
Lesson Study is rapidly becoming one of the most adopted models of teacher professional development worldwide. In this paper, we examine the teachers’ discussions that are an integral part of the Lesson Study research cycle. In particular, we investigate the ‘dialogic mechanisms’ that enable teachers’ pedagogical intentions to be developed within the context of discussions that stem from observations of students as they address mathematical problems. In so doing we hypothesize about the nature of the ‘dialogic space’ that is created and how this allows teachers to move from the collaborative analysis of student outcomes to an enhanced understanding of pedagogical intentions in mathematics. Data for this paper derive from a large research project taking place in Camden, London. This project aims to implement Lesson Study in the context of the introduction of a New National Curriculum for Mathematics in England. It involves a large cohort of mathematics teachers across primary and secondary schools. Quantitative analysis of video-recorded Lesson Study discussions is reviewed and one illustrative case study is included to contextualise the quantitative data. Findings suggest that a focus on student outcomes enables teachers to collaborate effectively on developing pedagogical intentions to directly address student need. Further, it seems that particular features of dialogue are evident where teachers move to an agreed perspective on pedagogic change; and evidence of ‘supportive moves’ in interactions suggest that a form of dialogic space is necessary if all teachers in a Lesson Study group are to learn from shared understandings about future teaching and learning needs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper draws on data from a large-scale LS research project carried out with primary and secondary mathematics teachers by a leading UK University and schools in a London borough (district). Within the body of research on how teachers learn, Lesson Study (hereafter ‘LS’) is widely acknowledged as an effective means of pursuing professional development (Borko, Jacobs and Koellner, 2010); and it is now firmly established within the UK (Dudley, 2012). By enabling teachers to work together within an established professional community, LS offers the opportunity to gain a more profound understanding of both student learning and their own pedagogical approaches. Further, it enables the sharing of these insights with colleagues, either within their own schools or across schools in a district. This may be of particular importance in a time of curricular change (Chen and Yang, 2013; Lewis and Takahashi, 2013; Lewis and Tsuchida, 1998), so it is worth noting that the project that underpins this paper was a specific response to the introduction of a new National Curriculum for Mathematics in the UK from 2013/2014.
The interim report for the project indicates substantial developments for both teachers and learners that seem to correlate with immersion in LS (Ylonen, Dudley and Lang, 2014). A survey focused on confidence in teaching mathematics within the new National Curriculum highlighted that, for 32 identified areas of mathematics teaching, teacher confidence pre-project reached a figure of 70 % in only 7 areas, whilst the figure was above 70 % in 24 areas by mid-way through the project. A generic teacher mathematics confidence survey revealed that, of 38 areas of mathematics examined, there was only one where over 75 % of teachers were very confident or expert prior to the LS project; mid-way through the project there was a 21 % increase in the number of teachers who were either very confident or had expertise in the 38 areas examined. The statistical indicators about student progress in mathematics in the project schools compared to other schools, both in the borough and nationally, were also very encouraging. There was a 3 % increase in pupils attaining Level 5Footnote 1 or above in mathematics in the participating schools, whilst in the borough overall and nationally the increase was only 1 % during the same time period.
In the UK at least, teacher professional development programmes have historically rarely been assessed on outcomes (Opfer & Peddar, 2011) and the impact of such programmes has often been significantly under-evaluated (Harris, Day, Goodall, Lindsay & Muijs, 2006). The evaluated findings of outcomes for this project are therefore not only encouraging; they support the view that higher levels of evaluation consider participants’ use of new knowledge and skills, together with students’ learning outcomes (Guskey, 2002). Interestingly, LS does seem to provide more studies that consider these higher levels of evaluation than those concerned with other forms of teacher professional development (Cheung and Wong, 2014; Dudley, 2012; Kullberg 2012; Murata, Bofferding, Pothen and Taylor, 2012).
The intention of the paper is to examine the specific dialogic mechanisms that enable teacher learning to take place in the context of LS. LS seems to make a positive difference to both teacher and student learning, but what are the ‘internal mechanisms’ of LS discussions?
2 Theoretical framework
Research on Lesson Study echoes many of the themes found within the broader literature on teachers’ learning (Bakkenes, Vermunt and Wubbels, 2010) and in work on the interaction of teachers within a professional community (Lieberman and Miller, 2008; McLaughlin and Talbert, 2006). The idea of intervention models that support professional development, explicitly by creating a context for professional interaction, is of particular relevance here, since it fits within a wider framework of teacher learning. Building on the work of Vermunt and Endedijk (2011), which considers patterns in teacher learning, we see LS as a ‘contextual factor’ that may lead to the creation of positive learning patterns, in turn resulting in teacher learning. Thus, we would broaden Vermunt and Endedijk’s model of teacher learning in the following way in the context of LS (Fig. 1).
Some features of LS mirror successful elements of other professional learning activities. For example, Kwakman (2003) emphasises the importance of reflecting and cooperating, whilst in other studies on how experienced teachers learn from their professional practice (Bakkenes, Vermunt and Wubbels, 2010; Tynjälä, 2008) collaboration in teams, and cooperating and interacting with colleagues are seen as vital components of professional learning.
Thus interaction, the sharing of ideas, and collaboration and cooperation with colleagues, seem central to the learning activities that are likely to lead to positive learning outcomes for teachers. Yet what makes the nature of interactions that occur in teacher discussions more or less “conducive to learning and improvement” (Horn and Little 2010, p. 183) is generally unclear, even within the relatively structured expectations of LS. Our research is designed to clarify this. It focuses on mathematics education and is one of relatively limited number of studies that consider specific ways in which teachers talk together about students’ performance and subsequently link this to their practical understanding of teaching and learning (Dudley, 2013; Suzuki, 2012; Tepylo and Moss 2011).
We focus explicitly on how shared information about student performance can act as a mediating artefact for the development of common knowledge amongst teachers (Engstrom, 2003; Edwards, 2012; Edwards and Mercer, 1987). We also focus on the nature of the professional learning outcomes, evident as developed pedagogic intentions that arise from teachers using information about student performance. We thus take a sociocultural perspective, built from the original work of Vygotsky (1978; see also Daniels, 2001), who proposed a special relationship between language use and thinking. His concern was with interactions between adults and children for promoting children’s cognitive development; but here we are concerned with the use of language by peers in the pursuit of common goals (as are Littleton and Mercer, 2013). By combining their intellectual resources, members of a group are able to address a shared problem and pursue a common goal more effectively than they could alone. In using language to make joint sense of their experience, those people may create new understandings which each individual could not have achieved. It is this capacity which makes the relationship between language and thinking so special, and so distinctively human. The term ‘interthinking’ (Littleton and Mercer, 2013) was coined to convey the meaning that people cannot only act together (interact), they can think together (interthink). We extend this idea to suggest that teachers’ interthinking may help to develop the kind of Pedagogical Content Knowledge (Schulman, 1986) identified by Ball, Thames & Phelps (2008) as Knowledge of Content and Students (KCS)—“knowledge that combines knowing about students and knowing about mathematics” (p. 401).
Whilst the “established body of literature (on interactions in formal instructional contexts) looks at student-to-student and teacher-to-student interactions” (Liu, 2013, p. 196), in this paper we consider the relevance of such ideas to the specific circumstances of LS reflective discussions between teachers. Where teachers are collaborating it seems likely that they will have “a co-ordinated joint commitment to a shared goal, reciprocity, mutuality and the continual (re)negotiation of meaning” (Mercer and Littleton, 2007, p. 25). Thus, one or more perspectives may be held in tension as a ‘dialogic space’ is created in which teachers can “engage with each other and, in a sense, learn to see the task through each other’s eyes” (Wegerif, 2007, p. 4). This idea of “thinking … in dialogues” (Wegerif, 2007, p. 116) seems highly pertinent in the context of LS discussions.
Our hypothesis here might be presented as follows (Fig. 2):
Here, the nature of the learning activity around the mediating artefact of reported student performance is given greater definition, whilst the nature of the learning outcomes is also defined; it relates to future teaching intentions and implies pedagogical development. At the centre of the dialogic space is genuine collaborative endeavour, an extrapolation of more generalised understanding of student learning in mathematics and “a continued attempt is made by those involved to construct and maintain a shared conception of the problems they are solving” (Ferguson, 2009, p. 39).
In their work on the relevance of the Japanese LS model to other cultural contexts, Doig and Groves (2011, p. 87) point to the importance of this sharing of professional perspectives in communities of inquiry through LS, where types of knowledge are made visible and frameworks for analysis of practice are developed (Lewis, Perry and Hurd 2009). Numerous recent studies echo the idea that the central driver of teacher learning within LS is interaction within a professional community of practice (Cajkler, Wood, Norton and Pedder, 2013; Chichibu and Kihara, 2013; Davies and Dunhill 2008; Hart and Carriere, 2011). Doig and Groves (2011), for example, cite the work of Catherine Lewis and her collaborators in stating the importance of teachers seeing LS as an opportunity to learn to ‘see’ students through systematic data gathering and through the sharing of ideas in teacher discussions. Other studies add detail about the nature of teacher interactions in LS groups. Suzuki (2012), for example, analyses modes of discourse used in LS and suggests six discursive modes that are conventionally employed. And Fernandez (2010), in linking LS discussions to Schön’s (1983) notion of reflection in action, indicates the importance of teachers feeling comfortable with contributing ideas, raising alternative perspectives and supporting views with evidence.
A logic of expected improvement drives LS (Lewis, Fischman, Riggs and Wasserman, 2013) and it is the purpose of this paper to consider what is happening in LS dialogic spaces where just a positive correlation between teacher and student outcomes is occurring. Are there particular environmental conditions that might lead to more or less productive interaction amongst LS teacher groups? Certainly, Perry and Lewis (2009) have a cautionary tale to tell: In examining what might constitute successful adaptation of LS to the US, they show how a lack of guidance for teachers in the initial phases of a lesson study cycle meant that teacher outcomes “varied substantially in their lesson study approaches and in the learning that resulted from their work” (p. 372). In the project that forms the basis of this paper great care was consequently taken to ensure the provision of clear procedures for teacher groups working independently on LS research. This was done in three ways: through LS conference days, where all of the teachers in the project had the opportunity to share experiences of LS on a termly basis; through the provision of a common LS workbook that guided key elements of the planning, teaching and reflection cycle; and, building on our own work on ground rules for dialogue (e.g. Littleton and Mercer 2013; Mercer 2013; Mercer and Littleton 2007; Warwick, Mercer, Kershner and Kleine Staarman, 2010), designed to raise teachers’ awareness of the features of group talk that are usually present where a dialogic space for learning is evident.
Given, then, that it has been suggested that professional development practices based on professional dialogue about teaching and learning are the most valuable in enhancing teachers’ instructional practices (Warwick, Rivers & Aggleston 2004), this paper will present and analyse examples of teachers’ lesson discussions where the performance of individual students in mathematics is the focus. It will address the problem of how the specific components of dialogue can be evidenced, and which are essential in helping teachers collectively move their pedagogy forward. The paper thus addresses two research questions:
-
1.
How does the joint analysis of students’ behaviours in LS research lessons help teachers to develop their pedagogical intentions in mathematics?
-
2.
Are there dialogic mechanisms in LS groups that promote agreement around developed pedagogic intentions?
3 Methodology
3.1 Project aims
The wider, two-year research project (September 2013–August 2015), within which the analysis for this paper took place, sought to investigate whether LS had an influence on both the learning and regulation activities teachers undertake and on teachers’ mathematical subject knowledge, pedagogical content knowledge, mathematical teaching practices, motivation, and conceptions of learning and teaching. More specifically, the project aimed to:
-
Identify more or less powerful components of teacher discussions taking place in Lesson Study sessions that can support and foster teacher learning;
-
Understand how and why Lesson Study teacher discussions may impact upon teacher learning;
-
Contribute to theory development about understanding and improving teacher learning in the context of educational innovation.
3.2 Data collection
In the first year of the project, Mathematics teachers from 22 primaryFootnote 2 and secondary schools in the area of Camden, London, participated in the project. This number increased to 56 schools (15 continuing and 41 new schools) across London in the second year of the project. Teachers who taught mathematics within each school were required to form small groups, normally consisting of 3 to 4 teachers, and conduct one Lesson Study every term. The project lasted for six terms over the 2 years, so teachers from schools that entered the project on the first year (Cohort 1) had the opportunity to participate in all six Lesson Studies, while teachers from schools that entered the project on the second year (Cohort 2) had the opportunity to participate in the three latter Lesson Studies (see Fig. 3).
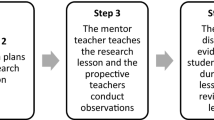
As proposed by Dudley (2013), one Lesson Study consisted of 3 research lessons, all preceded by a planning meeting and followed by a reflective meeting (Fig. 4 below). In the planning meetings, teachers collaboratively considered the aims of the research lesson, selected three case students that they would monitor closely and created a thorough lesson plan for each research lesson. An additional element in this LS process was the use of interviews with case pupils, which took place after the research lessons and served to provide teachers with more in-depth data of student progress. In the reflective meetings, teachers reflected on the research lesson by evaluating the progress of each case pupil in relation to the pre-determined success criteria, considering the interview data, evaluating the teaching in relation to student learning, and considering what aspects of their teaching could be adjusted to improve the progress of case pupils, and consequently that of the whole class.
The Lesson Study process (Dudley, 2013: 108)
Data for the project comes from two main sources:
-
1.
Video-recordings of the LS planning and reflective sessions conducted in each school, roughly ranging from 20 min to 1 h in terms of length. Teachers acted as co-researchers throughout the project, video-recording their LS meetings using school equipment; sending their video data to the research team; and engaging with the findings of the project during project events. In these events, the research team provided feedback on the progress of the teachers in the LS context and teachers were actively involved in interpreting some of the data by sharing their views and reflecting on their experience. The video data were accompanied by the LS workbooks mentioned above. The workbooks assisted teachers’ discussions by directing them to provide information on the lesson objectives of the LS cycle, lesson plans, success criteria set for each case pupil, and lesson observation information. These were completed by the teachers during their LS meetings.
-
2.
Survey data were collected at three different time points during the project and aimed to examine teacher learning over time.
For the present paper, data is drawn from the first source and from a single data collection phase only, as the focus is on teachers’ discussions in LS meetings. The survey data will be presented in a separate paper.
3.3 Development of a coding scheme
A significant part of the overall project concerned the production and development of a protocol for analysing teacher learning in the context of LS. It seems important to provide information here about the overall development of the protocol, in order to contextualise the specific use of protocol elements in the work carried out for this paper; the detailed development of the protocol is in the focus of a coming paper.
The methodology for the protocol construction was built upon that of studies that detail the use of digital video as a key tool in capturing the complexity of teaching and learning processes (Powell, Francisco and Maher, 2003; Sorenson, Newton and Harrison, 2006). The protocol (Appendix) is comprised of three sections, with features arrived at through methods associated with Sociocultural Discourse Analysis (SDCA: Mercer, 2004; Mercer, Littleton and Wegerif, 2004); this focuses on “the use of language as a social mode of thinking – a tool for teaching-and-learning, constructing knowledge, creating joint understanding and tackling problems collaboratively” (p. 137).
As Mercer (2004) points out, “[t]alk which mediates joint intellectual activity poses a considerable methodological challenge for a discourse analyst because of its reflexivity” (p. 140). SDCA attempts to capture the constructed meaning of talk for participants, placing more emphasis on the developing common knowledge that emerges through the interaction and the social and cultural context of the talk than, say, Conversational Analysis (Heritage and Clayman, 2010), with its focus on the structure of the interaction. It is essentially an agglomeration of methods, both qualitative and quantitative.
In light of the literature and using SCDA in the manner described below, a collaborative video and document analysis by members of the research team led to a detailed characterisation of three elements in these LS discussions:
-
1.
the characteristics of the discourse;
-
2.
the content of discussion and;
-
3.
the nature of teacher learning.
Having established these initial working protocol categories at each of the six phases of the project, new videos from LS meetings were analysed. On the initial analysis phases, a team of researchers adopted a qualitative approach to the analysis of the videos and tried to identify features that characterized the three elements above. For the discourse column, the researchers noted down anything that seemed to be answering the question of what makes a productive discussion; for the content column, how and what do teachers are discussing; and for the learning outcomes column, they noted statements that suggested teacher learning. The result of this process was three lists of features that, as the project progressed, needed to be simplified for the purposes of reliability. The protocol was therefore iteratively developed through each analysis phase, until a more simplified and reliable version was created through the comparison of researcher coding of specific videos (the details of this process will be described in a separate paper).
After building and testing the protocol through the re-visiting of numerous video-recordings of different LS discussions, the version of the protocol used for the analysis undertaken in this paper was eventually agreed (see “Appendix”).Footnote 3 This consists of three major categories: (1) Discourse-related Features detail important elements of talk that contribute to a collaborative and productive learning environment; (2) Content-related Features points to teachers’ mental processes in relation to specific content; and (3) Learning Points identify types of teacher learning from LS discussions, with direct reference to teaching mathematics, understanding students’ learning and learning about the subject of mathematics. Therefore, the protocol reflects the combination of two different theoretical frameworks, which seem to be crucial in understanding how teacher learning occurs in the LS context. First, the discourse element of the protocol represents how social interaction is best achieved; from a sociocultural perspective this is central to individual learning. Second, Vermunt and Endedijk’s model of teacher learning (see Fig. 1), which represents the relationship between teacher learning processes and learning outcomes, constitutes a second central foundation for the protocol. In particular, the discourse-related features and content-related features reflect ways in which learning processes can be enabled. The outcome of those processes is represented by the ‘learning points’ column.
The version of the protocol presented in Appendix 1, then, was used for quantitative coding of the videos considered for this paper. All videos were segmented into 4-min episodes, a grain size determined by taking into account issues such as pace of activity, nature of coding categories and cognitive load of the coder (Angelillo, Rogoff & Chavajay, 2007); NVivo, a software package for qualitative analysis, was used to capture coding outcomes. Raters coded each 4-min episode by determining whether or not a code from the protocol could be observed in the discussion.
3.4 Sampling video data
Video data for this paper came from the LS meetings of Cohort 1 teachers on the third phase of the project (Summer Term 2014), the Cross-Phase round. In this round, the teacher groups included both primary and secondary school teachers; secondary school teachers joined teachers of primary schools to plan lessons for the latter’s selected class, and vice versa. We were particularly interested in examining the dynamic of the dialogue in cross-phase work, partly to examine whether there was a ‘power dynamic’ at play in the dialogue between specialists and non-specialists. As shown in Table 1 below, data come from four different LS groups taking place at four different schools; two primary and two secondary schools.
In identifying video episodes which illustrate our proposed diagram (Fig. 2), episodes beginning with an analysis of an individual’s performance and ending with teacher learning development (in terms of stated pedagogic intentions) were selected; we only considered in details those post-lesson reflective meetings where this was evident in an initial analysis. The exact number of reflective meetings analysed in this phase of the project is given in the table below.
In order to identify relevant episodes from these videos, the protocol codes, and in particular codes P3 and PCK2 (Appendix) were used as start and end points. As shown on the protocol, code P3 was used when teachers evaluated students’ performances. This student evaluation comes after the behaviour and progress of case pupils have been very closely monitored by the observing teachers. Code PCK2 pointed to some kind of pedagogical change in teachers’ understanding and, as we have explained above, the linking of P3 and PCK2 seems to us to indicate “knowledge that combines knowing about students and knowing about mathematics” (Ball, Thames & Phelps, 2008, p. 401). This could either be an incremental change at the level of teaching strategies or a broader understanding of pedagogy. Relating PCK2 and P3 (P3 either in the same or the previous episode) thus provided the basis for selecting episode for closer examination in relation to dialogic processes, which are the central focus of this paper. As shown in Table 1 above, this type of coding gave a total of 9 episodes.
3.5 Analysis
For the analysis of the nine episodes, a more in-depth analysis was required so a qualitative design was chosen to attain the grounded insights from the observed dialogues between the involved teachers (Cresswell, 2007). Transcriptions of the nine episodes were first analysed using open coding. More specifically, each turn in the transcriptions was coded based on the protocol developed as part of the larger project.
The open coding process revealed a variety of dialogic moves, which were reconsidered and organised according to the themes that emerged from the data in a following phase of axial coding. This resulted in 5 moves that were considered most important for the efficacy of the dialogue. In Table 2, an overview is provided of the extent to which these moves were represented in the 9 episodes.
These codes are might be seen as ‘essential elements’ of the 5 codes for discourse-features of the protocol. The first move, questioning, is reflected in the first code of the protocol, which refers to requesting information, opinion or clarifications (D1). This behaviour could include negotiating meaning and questioning. The next two moves, building on each other’s ideas and coming to some agreement, are reflected in the third protocol code. This code refers to expressing shared ideas and agreement (D3); importantly here, the co-construction of knowledge takes place when participants in dialogue make contributions that build on each other and where participants work towards a dialogic resolution (Howe, 2010). The fourth identified move, providing evidence or reasoning, is again reflected in the fourth protocol code, which is used whenever teachers illustrated their arguments. Finally, challenging each other is reflected in the fifth protocol code, which accounts for challenging ideas or re-focusing talk (D5), in the form of positive professional critique. By evaluating the quality of talk based on these codes, all 9 episodes were considered to be highly dialogic.
By scrutinizing the data with open coding, however, it became clear that there were qualitative differences in the coding. In particular, two levels of dialogic features could be observed: ‘dialogic moves’ and ‘supportive moves’. Dialogic moves were reflected in contributions that brought the conversation further to a collaborative learning experience, such as those presented in Table 2. Apart from the dialogic moves however, it became clear that certain interactional cues were crucial for the creation of dialogic space, in which the teachers felt supported in expressing their views. Specifically, these supportive contributions could be found either physically (e.g. nodding) or verbally (e.g. minimal responses), in teachers being non-disputational, and creating a friendly and relaxing environment. These ‘supportive moves’ are reflected in the second protocol code (D2). The interaction of the dialogic moves and the supportive moves played a key role in creating a productive learning environment; or in other words, in developing a dialogic space for teacher learning.
Although determining the quality of analysis is a requirement for all kinds of studies, in this case it is a specific matter of attention, since the process of analysis involves many interpretations and iterations, which makes it impossible to use standard procedures. Akkerman, Admiraal, Brekelmans & Oost (2008) describe how it is possible to ensure the quality of findings by evaluating the extent to which the results is visibly grounded in the data, by evaluating the comprehensibility of the results with respect to the field of teacher learning, and by evaluating the acceptability of the results one is able to ensure the quality of the findings. Accordingly, meetings with the research group were held to discuss the quality of the findings of this analysis in respect to these aspects.
4 Findings
To give a flavour of both the data and the analysis, we present one case study from Table 2; it is seen as representative of the kinds of reflective discussions that led to changed pedagogical intentions amongst the teachers involved. It should be noted, however, that it is not necessarily representative of the content of each discussion, as this was determined by the observations made of the focus students analysed by each teacher group.
4.1 Case study
This case study is from a primary school where the teachers’ concerns are focused on students who are not lower ability groupings in a mixed-ability class. There is a clear concern with the clarity of language used in mathematics classrooms. The research lesson was the first in a series of three carried out at Oakwood Primary school with a Year 5 class (aged 9–10 years); it is LS Group 4, Episode 7 in Table 2 above. The focus was on improving students’ mathematical reasoning, expressed through the ways in which they discuss and explain their mathematical ideas. These intentions are in line with the new Mathematics National Curriculum in England which states that ‘students should make connections across mathematical ideas to develop fluency, mathematical reasoning and competence in solving increasingly sophisticated problems’ (Department for Education, 2013: 3).
The class teacher (T) and observing teacher 1 (OT1) were from the primary school. Observing teacher 2 (OT2) was from another primary school and observing teacher 3 (OT3) was a maths specialist from a secondary school. Following the first planning meeting, the teachers prepared a lesson plan for the first research lesson, which was divided into four main stages. At Stage 1 children, working in small groups, were given a percentage, a fraction and decimals. They were asked to put those in order of size and to demonstrate how they know this was the correct order by using examples with numbers, symbols, drawing and other equipment. At Stage 2 children were shown the statement ‘A fraction is a small piece of a whole’ and were given 5 min to think how they could prove or disprove that statement. Stage 3 was similar to Stage 2 in that the same activity of proving or disproving a given statement was conducted in groups. Finally, Stage 4 involved students feeding back on their discussion on the statement by using the interactive whiteboard.
In the subsequent reflective meeting, although the discussion started with an articulation of the performance of a specified observed student (‘him’ in turn 8 below) and returned to consider another individual (turn 16), it extrapolates from these individuals to consider the wider groups within which they were working (see Fig. 2 above). The transcript segments additionally illustrate the problem-solving nature of interactions within a dialogic space.
The lesson involved placing fractions, decimals and percentages in order; considering statements about smaller and larger fractions; and providing mathematical proofs for comparative statements about fractions. The first student identified for observation (turn 8) was predicted to ‘want to explain and demonstrate how he has proved/disproved’. The second student identified for observation (turn 16) was predicted to ‘lack some of the mathematical vocabulary’ required for these tasks. The second student was therefore seen as being less secure in his ability to reason mathematically.
Turns | Dialogue moves | Supportive moves | |
|---|---|---|---|
1 | OT2: One of the things I noticed was a maths vocabulary. That isn’t […] on the children who are talking among themselves. They weren’t necessarily using the appropriate maths vocabulary… | Raising an issue | |
2 | OT1 + T: Yeah | √ | |
3 | OT2: …and maybe that’s one thing that we could look at in terms of the children and the vocabulary | Building on ideas (D3) | |
4 | OT1: Sometimes I find they couldn’t even articulate themselves so… | Building on ideas (D3) | |
5 | OT2: No. Hm | √ | |
6 | OT1: So they actually call ‘there’s a big piece’… | Providing evidence (D4) | |
7 | OT2: Hmm | √ | |
8 | OT1: I was like ‘ok what do you mean?’ But when T stepped into try and help him he couldn’t make it any clearer either. So you’re definitely right. That is missing | Providing evidence (D4) | |
9 | All: Hmm | √ | |
10 | T: They think if they just throw a few numbers there, then they’re talking in maths language… | Building on ideas (D3) | |
11 | OT2: Hmm | √ | |
12 | T: But it’s using the precise language that they need to explain themselves | Building on ideas (D3) | |
13 | OT1: And they know that you know what they mean as well so I think they’re too used to saying some things. ‘Oh you get what I mean’. I was like ‘I do understand what you mean…’ | Building on ideas (D3) | |
14 | All: Hmm [nodding] | √ | |
15 | OT1: ‘…but still it’s not very mathematical’ | (continuing from turn 14) |
At the start of this extract, which follows from the detailing of the performance of the observed students a common issue is identified for discussion. The teachers identify, once again, the centrality of appropriate mathematical language to mathematical reasoning, in line with the lesson intentions (Ball and Bass 2000). The first student, though predicted as being likely to want to ‘explain and demonstrate’ his understanding, was nevertheless fairly imprecise in his use of mathematical language. The teachers identify a wider problem whereby students are using everyday language to express mathematical concepts and ‘just throw[ing] a few numbers [in]’ (turn 10), rather than focusing on the precise terminology that enables collective understanding in the domain of mathematics. This does not necessarily mean that the students do not understand the concepts that they are addressing, but the teachers are concerned that they need to develop the ability to communicate mathematics by using universally understood terms. What the observed students are doing is, in the words of OT1, ‘not very mathematical’ (turn 15).
This understanding is shared within a dialogic space, where again we see supportive moves throughout, but also certain dialogic moves to be very prominent. After one teacher raises an issue, the others build on the initial idea but also illustrate their observations. These moves allow the cumulative building on the ideas which lead towards agreement on pedagogic development.
Turns | Dialogue moves | Supportive moves | |
|---|---|---|---|
16 | T2: So maybe even having…I’m thinking of the child that was on my table. He was very reluctant to speak. Maybe he would benefit from some sentence openers… | Making a suggestion | |
17 | OT1: Yeah | √ | |
18 | OT2: And you know specific maths vocabulary related to the topic. Umm and then hopefully they’ll have a starting point to, you know, to use the appropriate maths vocabulary | Building on ideas (D3) | |
19 | OT3: Well, if you challenge non-specific language that came through examples, it forces them to be more specific [other teachers nod in agreement]. So ‘it’s a big piece’. You could maybe you know give them something which is almost a half but which isn’t. I’m struggling to find an example of that but em…just challenge the words and things that fit their definition but which […] | Building on ideas (D3) | √ (nodding) |
20 | OT1: I mean that could be quite interesting to start off tomorrow’s lesson, couldn’t it? [all nod]. So I mean almost quoting statements that we’ve heard and then say, talk to them in various ways it could be interpreted | Questioning, Building on ideas (D3) | √ (nodding) |
21 | OT2: Hmm | √ | |
22 | OT1: Yeah that’s a good idea | √ | |
23 | OT2: Yeah I think definitely the next lesson’s focus should be around building on maths vocab. Looking, looking at…because they were using those […] you could see what they were trying to say… | Coming to some agreement, Providing reasoning (D4) | |
24 | OT1&T: Yeah. | √ | |
25 | But you’re right. It wasn’t very articulate. Because I’m just thinking, had the children were expected […] improved. I know we didn’t get them to do that because that wasn’t the point but I think that the children on my table, the boy in particular was struggling | Building on ideas (D3) | |
26 | OT1: Yeah | √ |
This passage initially revealed that the second student was more hesitant than the first in expressing his thinking at all. This finding chimes with the predicted outcome for this student, that they would be unsure in using mathematical language appropriately. The discussion widens out to consider ways in which all students, at least in the groups associated with the targeted students, might be encouraged to be more specific in their use of mathematical vocabulary. This includes suggestions from the primary teachers about sentence starters and the ways in which subsequent lesson introductions focus on being articulate and precise in discussing mathematical concepts. Interestingly, OT3 (secondary school maths teacher) raises the issue of challenging the children directly to use more precise vocabulary, whereas the primary teachers suggest what might be seen as ‘softer’ approaches.
In terms of continuing to develop the interactions within this dialogic space, we see evidence of the teachers building on one another’s ideas (D3) throughout (lines 18, 19, 20 and 25) and providing reasoning (line 23). As in previous examples, supportive moves are prominent verbally and physically (lines, 17. 19, 20, 21, 22, 24 and 26) and play a key role in creating a dialogic space. All of this indicates genuine engagement in a community of peers seeking agreement in developing future teaching approaches.
4.2 The issue of challenge
All 5 most-frequently occurring dialogic moves appear in the case study, apart from one: challenging each other. In order to illustrate what we mean by challenging, we present a short extract from another of the nine episodes.
Turns | Dialogic moves | Supportive moves | |
|---|---|---|---|
1 | OT1: It’s the, it’s the, the feedback cycle. So it’s the same thing that affected Germaine really affects them all in one way or another. It’s, it’s about how do we do the feedback cycle well | Building on ideas (D3) | |
2 | T: Yeah | √ | |
3 | OT1: And that’s our next big step | Coming to some agreement (D3) | |
4 | T: Yeah, but in the first lesson did we not feel like that we shared too much? Remember when we said that we would put up some results on the board that, for discussion, and… | Challenging (D5) | |
5 | OT1: Oh that, yeah, that doesn’t necessarily imply sharing… If you let them stare and do it in their own work and thinking, oh one example for four lines is not enough | Backing up (D4) |
The above exchange takes place between the teachers of the Holt secondary school. OT1 builds on an idea that was previously expressed and explains what he thinks affects students’ progress. With T’s supportive move on turn 2, OT1 takes this a step further by suggesting that this should be their next big step in planning lessons. However, on turn 4 T challenges his suggestion by reminding OT1 of a previous conversation they had. So here we see how challenging ideas as a dialogic move has a direct effect on the course of the dialogue. Where challenge occurred in the data set of nine dialogues, it always moved the dialogue forward positively towards collective or individual learning. Thus, though challenge only occurs 8 times across the nine episodes (as compared for example, to 59 cases of building on each other’s ideas) we identify it as particularly significant in the development of teacher learning.
5 Discussion and conclusions
Although the usefulness of the LS model in teacher development is acknowledged in a growing number of countries, evidence demonstrating how and what teachers learn through Lesson Study is still very scarce. In this paper, we have presented a unique analysis of teachers’ reflective discussions that illustrates how they use information about students’ learning or difficulties in mathematics to develop their professional and pedagogical intentions. In reviewing the research questions, it is worth noting that in the episodes examined we found no particular ‘power dynamic’ evident in the discussions between the generalist primary teachers and their secondary mathematics specialist colleagues (see Sect. 3.4).
In addressing the first research question, we identified nine episodes from teacher reflective discussions in one phase of the overall project’s six phases. Using relevant codes within our LS analysis protocol, we revealed those parts of the dialogue that began with an analysis of student learning strategies (or, in some cases, outcomes) and concluded with agreement on future pedagogical intentions. It is certainly true to say that these episodes formed only a small part of the total content of the teachers’ discussions in their reflective sessions, but we would argue strongly for their significance in the overall pattern of those discussions, since they led to teacher learning. Given their significance to teacher learning, teachers should consider how to maximise the number of instances of such discussions so that practice can be improved.
Considering the second research question, teachers were seen to be engaging in dialogic interactions that involved such features as requesting information, giving reasons, providing evidence, making supportive comments and articulating shared ideas. This is not a coincidence; unlike the teachers observed by Perry and Lewis (2009), these teachers were trained in the productive use of dialogue and professional interactions. This allowed them to quickly and effectively open up a dialogic space for interaction in which each member of the group was able to make relevant contributions, receive both support and appropriately phrased challenge from their peers and work towards agreed adaptations to their future pedagogical approach. Using LS as a “joint enterprise” that binds community members together, they used dialogues to develop a “shared repertoire” of understanding (Wenger 1998, p. 73). Such dialogue might be contrasted with the kinds of discussions where individuals might take a dominant role, or where power relationships within the group might prevent those participating from expressing their own perspectives or feeling a part of a collective solution.
However, what seems most significant in the analysis presented here is the power of particular dialogue moves in effecting progress in the dialogue. Questioning (including negotiating meaning), building on each other’s ideas, coming to some agreement, providing evidence or reasoning and challenging seem to be dialogue moves that forward productive professional dialogues. The experienced teachers that were the focus of this research were already at the centre of a community of teachers of mathematics with a shared interest in using LS to open up the “pedagogic black box” (Cajkler et al., 2013, p. 550) of mathematics teaching. Here we see that a focus on specific dialogic moves in group interactions can considerably assist this process.
Further, two levels of dialogic features were found in the data; we called these ‘dialogic moves’ and ‘supportive moves’. Dialogic moves are accepted within groups because they were accompanied by supportive interactional cues that seem crucial for the creation of a supportive dialogic space—a space of “reciprocity, mutuality (allowing) the continual (re)negotiation of meaning” (Mercer and Littleton, 2007, p. 25). It is specifically the interaction of the dialogic moves and the supportive moves that seem to create a productive learning environment.
This paper set out specifically to examine teachers’ pedagogical intentions in the context of LS discussions. However, in exploring this issue we became interested in discovering how the teachers themselves perceived their practice as having changed in response to their LS discussions. After completing the research for this paper, therefore, we worked with 18 primary and secondary teachers from the original cohort of schools. We asked them to note three things that changed in terms of their classroom practice as a result of their participation in LS. We found ample evidence of stated change, including:
-
a more targeted use of practical resources for modelling concepts;
-
changing lesson structure, particularly to give students the time to articulate their thinking and reasoning, and to give scope for groups to interact more effectively;
-
a strong focus on developing the language of mathematics, with a focus on, amongst other things, sentence starters and challenging pupils to use terms appropriately;
-
the presentation of tasks as problem-solving challenges.
Though these are self-reported findings, the teachers spoke clearly about how the experience of LS discussions had given them the collective confidence to make changes to their practice that stemmed from the pedagogical intentions stated in their discussions.
Though not specifically related to our research questions, one issue emerged from our analysis that requires comment; this concerns the link between conceptual understanding in mathematics and the ways in which teachers develop the use of precise mathematical vocabulary with students. In the presented case study it was the issue of the links between vocabulary and conceptual understanding that was a strong focus, in different ways, of the teacher LS dialogue. This is hardly surprising, given that “[m]athematical language is crucial to reasoning - to the construction of mathematical knowledge - for it provides the medium in which claims are developed, made, and justified” (Ball and Bass, 2000, p. 205). But the fact that this connection is an interesting and repeated theme in the data set analysed for this paper seems to illustrate that it deserves further attention, despite the work of many mathematics educators over the decades to suggest ways in which students can be helped to engage with definitions and vocabulary of mathematics (Watson and Mason, 2008).
With respect to themes for future research, an issue that we have discussed above concerns the whole question of pedagogical intentions being translated into pedagogical outcomes. The nature of the data that was analysed for this paper means that only teacher discussions were analysed and it was therefore only pedagogical intentions that were evidenced. We did not observe subsequent lessons to see what the teachers actually did in relation to their conclusions from discussion; and whilst the use of workbooks to guide both the planning and review elements of teacher discussions proved an invaluable prompting mechanism for teachers and record for researchers, these did not require the teachers to review whether changes to their practice from one research lesson to another. This is clearly an area that requires further attention from academics. It should be noted that papers from our own research will include an in-depth analysis of the LS protocol (Appendix 1) and a consideration of teacher learning across the length of the project.
Notes
At present, National Curriculum attainment in the UK is measured in ‘Levels’. Level 5 represents a good level of attainment for pupils leaving primary schools.
It should be noted that the primary teachers involved were not teachers purely of mathematics but had responsibility for teaching a full curriculum to their classes.
It should be noted that the process of protocol development continues through the analysis of further data and through dialogue with the teachers as ‘co-researchers’ on this research and development project. Further work by the research team will provide a more detailed account of the construction of the protocol.
References
Akkerman, S., Admiraal, W., Brekelmans, M., & Oost, H. (2008). Auditing quality of research in social sciences. Quality & Quantity, 42(2), 257–274.
Angelillo, C., Rogoff, B., & Chavajay, P. (2007). Examining shared endeavours by extracting video coding schemes with fidelity to cases. In R. Goldman, R. Pea, B. Barron, & S. J. Derry (Eds.), Video research in the learning sciences (pp. 189–206). Mahwah: Erlbaum.
Bakkenes, I., Vermunt, J. D., & Wubbels, T. (2010). Teacher learning in the context of educational innovation: Learning activities and learning outcomes of experienced teachers. Learning and Instruction, 20(6), 533–548.
Ball, D. L., & Bass, H. (2000). Making believe: The collective construction of public mathematical knowledge in the elementary classroom. In D. Phillips (Ed.), Yearbook of the National Society for the Study of Education, Constructivism in Education (pp. 193–224). Chicago: University of Chicago Press.
Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching what makes it special? Journal of Teacher Education, 59(5), 389–407.
Borko, H., Jacobs, J., & Koellner, K. (2010). Contemporary approaches to teacher professional development. In E. Baker, B. McGaw, & P. Peterson (Eds.), International encyclopedia of education (part 7) (3rd ed., pp. 548–555). Oxford: Elsevier Scientific Publishers.
Cajkler, W., Wood, P., Norton, J., & Pedder, D. (2013). Lesson study: Towards a collaborative approach to learning in initial teacher education? Cambridge Journal of Education, 43(4), 537–554.
Chen, X., & Yang, F. (2013). Chinese teachers’ reconstruction of the curriculum reform through lesson study. International Journal for Lesson and Learning Studies, 2(3), 218–236.
Cheung, W. M., & Wong, W. Y. (2014). Does lesson study work? A systematic review on the effects of lesson study and learning study on teachers and students. International Journal for Lesson and Learning Studies, 3(2), 137–149.
Chichibu, T., & Kihara, T. (2013). How Japanese schools build a professional learning community by lesson study. International Journal for Lesson and Learning Studies, 2(1), 12–25.
Cresswell, J. (2007). Qualitative enquiry and research design: Choosing among five approaches (2nd ed.). Thousand Oaks: Sage.
Daniels, H. (2001). Vygotsky and pedagogy. London: Routledge/Falmer.
Davies, P., & Dunnill, R. (2008). ‘Learning Study’ as a model of collaborative practice in initial teacher education. Journal of Education for Teaching, 34(1), 3–16.
Department for Education (2013). Mathematics programmes of study: key stage 1 and 2: National curriculum in England.
Doig, B., & Groves, S. (2011). Japanese lesson study: Teacher professional development through communities of inquiry. Mathematics Teacher Education & Development, 13(1), 77–93.
Dudley, P. (2012). Lesson Study development in England: from school networks to national policy. International Journal for Lesson and Learning Studies, 1(1), 85–100.
Dudley, P. (2013). Teacher learning in Lesson Study: What interaction-level discourse analysis revealed about how teachers utilised imagination, tacit knowledge of teaching and fresh evidence of students learning, to develop practice knowledge and so enhance their students’ learning. Teaching and Teacher Education, 34, 107–121.
Edwards, A. (2012). The role of common knowledge in achieving collaboration across practices. Learning, Culture and Social Interaction, 1(1), 22–32.
Edwards, D., & Mercer, N. (1987). Common knowledge: The development of understanding. London: Methuen.
Engstrom, Y. (2003). Activity theory and individual and social transformation. In Y. Engstrom, R. Miettinen, & R. L. Punamaki (Eds.), Perspectives on activity theory. Cambridge: Cambridge University Press.
Ferguson, R. (2009). The construction of shared knowledge through asynchronous dialogue. PhD thesis, The Open University. Available online at: http://oro.open.ac.uk/19908/1/RFerguson_Thesis.pdf. Accessed 10 Nov 2014.
Fernandez, M. L. (2010). Investigating how and what prospective teachers learn through microteaching lesson study. Teaching and Teacher Education, 26(2), 351–362.
Guskey, T. (2002). Does it make a difference? Evaluating professional development. Educational Leadership, 59(6), 45–51.
Harris, A., Day, C., Goodall, J., Lindsay, G., & Muijs, D. (2006). What difference does it make? Evaluating the impact of continuing professional development in schools. Scottish Educational Review, 37, 90–98.
Hart, L. C., & Carriere, J. (2011). Developing the habits of mind for a successful lesson study community. In L. C. Hart, A. S. Alston, & A. Murata (Eds.), Lesson study research and practice in mathematics education (pp. 27–38). Netherlands: Springer.
Heritage, J., & Clayman, S. (2010). Conversation analysis: Some theoretical background. In J. Heritage & S. Clayman (Eds.), Talk in action: Interactions, identities, and institutions. Chichester: Wiley-Blackwell.
Horn, I., & Little, J. (2010). Attending to problems of practice: routines and resources for professional learning in teachers’ workplace interactions. American Educational Research Journal, 47(1), 181–217.
Howe, C. (2010). Peer dialogue and cognitive development: a two-way relationship? In K. Littleton & C. Howe (Eds.), Educational dialogues: Understanding and promoting productive interaction. Abingdon: Routledge.
Kullberg, A. (2012). Can findings from learning studies be shared by others? International Journal for Lesson and Learning Studies, 1(3), 232–244.
Kwakman, K. (2003). Factors affecting teachers’ participation in professional learning activities. Teaching and Teacher Education, 19(2), 149–170.
Lewis, J. M., Fischman, D., Riggs, I., & Wasserman, K. (2013). Teacher learning in lesson study. Montana Mathematics Enthusiast, 10(3), 583-620.
Lewis, C. C., Perry, R. R., & Hurd, J. (2009). Improving mathematics instruction through lesson study: A theoretical model and North American case. Journal of Mathematics Teacher Education, 12(4), 285–304.
Lewis, C., & Takahashi, A. (2013). Facilitating curriculum reforms through lesson study. International Journal for Lesson and Learning Studies, 2(3), 207–217.
Lewis, C., & Tsuchida, I. (1998). A lesson is like a swiftly flowing river: Research lessons and the improvement of Japanese education. American Educator, (Winter), 14–17 and 50–52.
Lieberman, A., & Miller, L. (2008). Teacher in professional communities. New York: Teachers College Press.
Littleton, K., & Mercer, N. (2013). Interthinking: Putting talk to work. Abingdon: Routledge.
Liu, Y. (2013). The social organisation of talk-in-interaction at work in a language teacher professional community. Learning, Culture and Social Interaction, 2(3), 195–207.
McLaughlin, M., & Talbert, J. (2006). Building school-based teacher learning communities: Professional strategies to improve student achievement. New York: Teachers College Press.
Mercer, N. (2004). Sociocultural discourse analysis: analysing classroom talk as a social mode of thinking. Journal of Applied linguistics and Professional Practice, 1(2), 137–168.
Mercer, N. (2013). The social brain, language, and goal-directed collective thinking: A social conception of cognition and its implications for understanding how we think, teach, and learn. Educational Psychologist, 48(3), 148–168.
Mercer, N., & Littleton, K. (2007). Dialogue and the development of children’s thinking: A sociocultural approach. London: Routledge.
Mercer, N., Littleton, K., & Wegerif, R. (2004). Methods for studying the processes of interaction and collaborative activity in computer-based educational activities. Technology, Pedagogy and Education, 13(2), 193–209.
Murata, A., Bofferding, L., Pothen, B. E., & Taylor, M. W. (2012). Making connections among student learning, content, and teaching: Teacher talk paths in elementary mathematics lesson study. Journal for Research in Mathematics Education, 43(5), 616–650.
Opfer, V. D., & Pedder, D. (2011). The lost promise of teacher professional development in England. European Journal of Teacher Education, 34(1), 3–24.
Perry, R., & Lewis, C. (2009). What is successful adaptation of Lesson Study in the US? Journal of Educational Change, 10(4), 365–391.
Powell, A., Francisco, J., & Maher, C. (2003). An analytical model for studying the development of learners’ mathematical ideas and reasoning using videotape data. Journal of Mathematical Behaviour, 22(4), 405–435.
Schön, D. A. (1983). The reflective practitioner: How professionals think in action. London: Maurice Temple Smith.
Schulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4–14.
Sorenson, P. D., Newton, L. R., & Harrison, C. (2006). The professional development of teachers through interaction with digital video. Paper presented at the BERA Annual Conference 2006, September 2006.
Suzuki, Y. (2012). Teachers’ professional discourse in a Japanese lesson study. International Journal for Lesson and Learning Studies, 1(3), 216–231.
Tepylo, D. H., & Moss, J. (2011). Examining change in teacher mathematical knowledge through lesson study. In L. C. Hart, A. S. Alston, & A. Murata (Eds.), Lesson study research and practice in mathematics education (pp. 59–77). Netherlands: Springer.
Tynjälä, P. (2008). Perspectives into learning at the workplace. Educational Research Review, 3(2), 130–154.
Vermunt, J. D., & Endedijk, M. D. (2011). Patterns in teacher learning in different phases of the professional career. Learning and Individual Differences, 21(3), 294–302.
Vygotsky, L. S. (1978). Mind in society: The development of higher psychological processes. Cambridge: Harvard University Press.
Warwick, P., Mercer, N., Kershner, R., & Kleine Staarman, J. (2010). In the mind and in the technology: The vicarious presence of the teacher in pupil’s learning of science in collaborative group activity at the interactive whiteboard. Computers & Education, 55(1), 350–362.
Warwick, I., Rivers, K., & Aggleston, P. (2004). Developing a programme of continuing professional development (CPD) in citizenship. Research briefing. London: Department for Education and Skills.
Watson, A., & Mason, J. (2008). Mathematics as a constructive activity: Learners generating examples. Mahwah: Erlbaum.
Wegerif, R. (2007). Dialogic education and technology: Expanding the space for learning. New York: Springer.
Wenger, E. (1998). Communities of practice: Learning, meaning, and identity. Cambridge: Cambridge University Press.
Ylonen, A., Dudley, P., & Lang, J. (2014). London schools excellence fund: interim report. Prepared for the LSEF on behalf of Camden Borough Council; details available through educationprogramme@london.gov.uk.
Acknowledgments
We would like to thank the teachers and Local Authority staff who were engaged in the Camden LS project for their collaboration. The research was funded from the Office of the Lord Mayor of London.
Author information
Authors and Affiliations
Corresponding author
Appendix: Video-analysis protocol used in this study
Appendix: Video-analysis protocol used in this study

Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Warwick, P., Vrikki, M., Vermunt, J.D. et al. Connecting observations of student and teacher learning: an examination of dialogic processes in Lesson Study discussions in mathematics. ZDM Mathematics Education 48, 555–569 (2016). https://doi.org/10.1007/s11858-015-0750-z
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11858-015-0750-z