Introduction

Additive manufacturing (AM) enables the layer-by-layer fabrication of three-dimensional geometry directly from CAD data, which provides significant advantages over conventional manufacturing.1 AM can fabricate complex geometry as a single structure, for instance a unitized medical implant, whereas conventional manufacturing constrains designs by the need for tool access.2 Furthermore, AM is compatible with topology optimization, thereby enabling mass reduction. Despite these advantages, the AM process is subject to a series of potential technical challenges, including limited production rate, thermal stresses, potentially high material cost and availability, and uncertainties in as-manufactured geometry.3

Metal Additive Manufacturing

Metal additive manufacturing (MAM) refers to a category of AM processes that melt metal feed stock layer-by-layer to fabricate novel, lightweight, and high-value components such as medical implants or optimized aerospace components. In this research, lattice structures were fabricated using laser-based powder bed fusion (LB-PBF), a MAM method recognized for its high-resolution features and dimensional control.4

MAM Defects Associated with LB-PBF

Manufacturing defects are inherent to all manufacturing processes. For LB-PBF, the magnitude and frequency of these defects is influenced by the many process parameters involved, such as laser power, scan speed, hatch spacing, material thermal properties, powder size, and layer thickness.5 Echeta et al.6 classified the defects produced by LB-PBF into three main categories: porosity and lack of fusion, residual stress, and surface texture.

Zhang et al.5 defined porosity as spheroidal voids of up to approximately 100 µm diameter within the solid material. Porosity is formed due to high cooling rates during the solidification process, leading to gas that cannot escape from the melt pool. Additionally, lack of fusion refers to an internal fusion defect that occurs due to insufficient input energy. Residual stress is formed during PBF processes due to localized rapid heating and cooling rates.7,8 Furthermore, shrinkage occurs as the fused powder begins to cool, leading to part distortion and, in severe cases, surface cracking. Surface texture is defined as the geometric variation between the as-designed and as-manufactured structure. This texture is due to a range of phenomena at various length scales,9 including: stair-step phenomena10; thermal interaction of melt pool with supporting powder bed11 and adherence of particles12 ; interaction of neighboring tracks and melt-pool phenomena, including recoil pressure effects13; and Marangoni convection.14 For lattice structures, surface texture effects are clearly observed in strut elements, and are exacerbated with increasingly acute inclination to the build platen.15 The effects of surface texture are highly relevant to the mechanical16 and biological response17 of lattice strut elements.

Since AM products might be implemented in high-value applications, it is crucial to have an accurate method to measure the MAM defects. Echeta et al.7 comprehensively reviewed and discussed the most relevant measurement methods for MAM defects. These methods include x-ray computed tomography (XCT), scanning electron microscope (SEM), vernier calipers, optical microscopy, and the Archimedes method. Each of these methods may be applied to the characterization of surface texture (although with distinct capabilities). Of these methods, x-ray computed tomography has been employed in this research due to its capacity for high-resolution data acquisition, and its compatibility with non-destructive testing and emerging methods that have been developed to determine the associated MAM defects of lattice struts.

MAM Lattice Defects Associated with LB-PBF

Although MAM technologies enable the fabrication of complex structures that can be optimized for complex mechanical loading, the effect of these potential MAM defects must be quantified and accommodated. The criticality of these potential defects is highly sensitive to the mechanical failure mode of relevance. For example, local geometric defects can substantially compromise fatigue resistance18; and bulk geometric defects, as occur due to inclination of lattice strut elements, influence the observed buckling response.7

The available literature that provides insight into the effect of MAM defects is relatively limited; however, the following research is of particular interest for the design of MAM lattice structures:

  • Wauthle et al.19 studied the effect of build orientation and heat treatment on the mechanical response of Ti-6AI-4V lattice microstructure fabricated by LB-PBF. A significant reduction of the structural strength was observed with diagonally oriented strut elements. Hot isostatic pressing (HIP) was observed to achieve a slight ductility increase.

  • Yavari et al. studied the fatigue performance on various lattice unit cell types of Ti-6AI-4V lattice structure fabricated by LB-PBF.20 Cube, diamond, and truncated cuboctahedron are the three types of unit cells investigated in this study. The cube unit cell’s fatigue-life was found to exceed that of the other lattice types assessed, due to fewer manufacturing defects.

  • Lozanovski et al.21 developed an efficient non-destructive approach to quantify node response uncertainty on a Ti-6AI-4V FCCZ-lattice structure manufactured by LB-PBF. Micro-computed tomography (µCT) data was used to generate a digital model of the physical lattice. A custom algorithm was then implemented to automatically extract digital data for each node element, and numerical simulation was then applied to determine the structural impact of manufacturing defects. The outcome of the non-destructive approach came up with a realistic numerical response of as-manufactured nodes compared with the physical response, which emphasizes that this method can be certified as a non-destructive method in high-value AM applications. However, this method was only implemented on lattice nodes and, in this research, the method is developed to be utilized in strut elements.

  • Alghamdi et al.16 conducted a comprehensive study of titanium (Ti-6Al-4V) lattice strut elements under compressive loading. The critical buckling load was predicted analytically, numerically, and experimentally. It was found that neither the analytical nor the numerical prediction based on idealized geometry were sufficient to precisely quantify the critical buckling load. However, non-linear numerical simulation (including displacement control and Riks) of the µCT reconstruction of the as-manufactured geometry was shown to provide a robust estimate of the experimental response. This observation enables confidence in the numerical simulation methodology applied in this research (Sect. 1.2.2).

  • Alghamdi et al.15 investigated the effect of polygon order (triangle, square, octagon, and circle) on the geometry of as-manufactured lattice strut elements fabricated with LB-PBF in aluminum and titanium. They observed the tendency for nominally triangular and square cross sections to become circular upon fabrication (as quantified by the isoperimetric quotient). This observation was particularly strong for aluminum material (as opposed to titanium) and for small cross-sectional area. Triangular cross sections observe greater manufacturability when the triangular apex faces downward.

Mechanical Response of AM Lattice Structure and Strut Element

Standards used in the literature for testing the mechanical response of metal AM lattices include general compression testing for metallic materials,22 where elastic modulus and yield response are important. Other standards are more specific to porous materials23,24 which provide recommendations on the test specimen sizes, testing procedures, and additional mechanical properties specific to cellular and lattice structures.

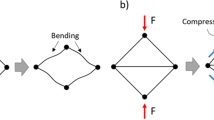
Gibson-Ashby describe a lattice’s mechanical response as being dependent on three main factors: bulk mechanical properties of the lattice structure material, the lattice topology which is defined by connectivity of lattice strut elements, and the relative lattice density that is influenced by both topology and local geometry of strut and node elements.25,26 The influence of the lattice topologies on the mechanical response depends on whether they are classified as being either bending-dominated or stretch-dominated. The mechanical behavior of stretch-dominated topologies is associated with high strength and low compliance, while bending-dominated mechanical behavior is associated with relatively low strength and high compliance.27 In bending-dominated structures, the deformation of unit cells occurs via the action of bending moments at the node elements, resulting in elastic deformation and, with increasing load, plastic-hinge deformation.7 Stretch-dominated lattice structures deform due to tensile or compression loads within the strut elements, resulting in local yield or buckling followed by catastrophic failure.

Buckling is a phenomenon that predominantly affects slender strut elements under compression, but can combine with yielding to also influence shorter struts under compression.16,28 When buckling occurs, an individual strut element’s ability to carry load is reduced. Within the lattice, as a strut element buckles, load paths through the structure can change, thereby distributing additional load to other strut elements, potentially leading to a cascade of buckled strut elements and associated lattice collapse, typically along a compressive or shear plane.2 The load at which buckling occurs, the critical buckling load, is related to the strut element geometry, material properties, and associated end fixity.

Analytical Buckling Prediction

The critical buckling load, \({P}_{cr}\), can be predicted analytically using the Euler buckling formula based on the modulus of elasticity, \(E\); moment of inertia, \(I\); strut length, \({L}_{s}\); and the effective length factor, \(K\) [(1)]. It is assumed the load is applied in the center of the column member, and the material is linear, homogeneous, and elastic. The slenderness ratio classifies the column as either short, intermediate, or slender. The other consideration is the boundary conditions which depend on applied end-fixity. Combinations of fixed and free boundary conditions are generally considered to be within the range of effective length, \(0.5<K<2\).29

$${P}_{\mathrm{cr}}= \frac{EI{\pi }^{2}}{{(K{L}_{\mathrm{s}})}^{2}}$$
(1)

Numerical Buckling Prediction

Numerical simulation was implemented and compared with analytical predictions of the critical buckling load. The eigenvalue buckling analysis is an effective method for estimating the critical buckling loads and to capture the buckling behavior associated with different buckling modes.30 The critical load of stiff structures can be obtained by solving the general eigenvalue buckling problem (Eq. 2), where the model stiffness matrix becomes singular, thereby providing nontrivial solutions.31 Under applied loads,\({K}_{0}^{\mathrm{NM}}\) represents the stiffness matrix due to the base state, while preloads, \({K}_{\Delta }^{\mathrm{NM}},\) represent the change in the stiffness matrix due to the incremental load beyond the base state, and \({\lambda }_{i}\) and \({v}_{i}^{M}\) are the ith eigenvalue and eigenvector, respectively, which represent the critical buckling loads and associated buckling modes.

$$\left({K}_{0}^{NM}+ {\lambda }_{i}{K}_{\Delta }^{NM}\right){v}_{i}^{M}=0$$
(2)

Comprehensive analysis of the applicability of this methodology by Alghamdi et al.16 provides confidence for their application to quantify the buckling response of as-manufactured LB-PBF lattice strut elements in this research (Sect. 3.1).

Digital Twins and Certification

As simulation tools become more reliable and accurate, a new virtual design concept known as the digital twin (DT) is being developed. The DT was proposed by Gaaessegen and Stargel in 2012 to have interactions between the digital and physical worlds. The DT contains three main elements: the physical product, the virtual product, and the associated linkage between the physical and virtual products.32 The DT concept contributes to the quantification and documentation of MAM manufacturing variability, thus enabling deep insight into the causal nature of these defects and providing a robust basis for the certification of high-value MAM components such as medical implants and safety-critical structural applications.

The geometric uncertainties that arise in the simulation of AM lattice response due to AM process induced defects and dimensional inaccuracies are difficult to predict. The exact deviation from design via process simulation is highly challenging due to the complexity of the underlying physical phenomena as well as the disparate spatial and temporal scales of the LB-PBF process.33 Alternatively, defects and dimensional inaccuracies produced in AM lattices can be viewed as random or stochastic occurrences.34 Characterization and study of manufactured parts has produced data which can be utilized with formal uncertainty quantification (UQ) methods to enable a probabilistic approach to the design and simulation of AM lattices. Uncertainties can be categorized as either aleatory or epistemic, in which the former refers to intrinsic uncertainties in the model’s predictive capability, such as variability in geometric parameters due to AM. The latter usually refers to uncertainties which cannot be reduced by the acquisition of more data, because the fundamental knowledge and physics of the system being modeled is not fully understood.35

Forward uncertainty propagation, that is the analysis of uncertainty in system’s outputs via propagation of input uncertainties, is a common objective of UQ studies. It gives the ability to solve problems such as ‘reliability’ or ‘certification’ where outcomes involve determining the probability of failure given a predetermined or identified failure set.36

Proposed Method and Expected Outcome

This research proposes a novel non-destructive methodology for quantifying the influence of surface defects on the functional response of individual strut geometries (and associated statistical distributions) from x-ray micro-computed tomography (µCT) data for as-manufactured AM lattice structures. This methodology is non-destructive, as is required for the pre-production certification of high-value lattice structures. A novel, two-stage registration is proposed to map between the µCT and idealized geometry, thereby allowing a digital twin with direct mapping to the idealized geometric data. This mapping allows algorithmic extraction and quantification of functional elements from the digital twin, allowing numerical analysis of specific lattice elements and the reporting of the statistical response of each element within the entire lattice system. This capability can be applied directly for the algebraic certification of high-value lattice structures, as well as aiding in the optimization of design and processing variables for intended mechanical response.

This proposed methodology is demonstrated by a digital twin of over 2000 strut elements within a Ti-6AI-4V lattice fabricated by LB-PBF. For this lattice, the critical buckling load is compared and verified between the as-designed lattice struts and over 2000 as-manufactured unique strut elements using experimentally validated numerical simulation methods for acquiring the column buckling response of MAM strut elements.16 This outcome allows formal verification that the as-manufactured strut geometry matches the intended functional response and thereby aids in the certification and optimization of high-value lattice structures.

Method

In the current literature, there exist significant challenges for the non-destructive qualification of AM lattice structures. This research proposes a comprehensive digital-twin methodology for geometrically registering the as-manufactured lattice structure to allow for direct mapping and analysis based on the idealized lattice geometry. This methodology enables functional (not just geometric) data to be extracted.

The generalized procedure for the proposed digital-twin methodology (Fig. 1) consists of: lattice design and manufacture (Sect. 2.1), micro-computed tomography and reconstruction (Sect. 2.2), global and subsequent local point registration (Sect. 2.3), automated volume of interest (VOI) extraction (Sect. 2.4), VOI processing to generate strut specimen models (Sect. 2.5), image-based FEM of digital twin response (Sect. 3.1), and statistical analysis (Sect. 3.2).

Fig. 1
figure 1

Schematic overview of the proposed digital-twin methodology for the extraction and analysis of the functional response of as-manufactured lattice strut elements.

Full size image

Lattice Design and Manufacture

Image-based FEM is used in this research to study the variation in buckling response of as-manufactured struts within a lattice digital twin. The proposed methodology is demonstrated for periodic lattice structures with FCC and FCCZ unit cell topologies and an overall cubic geometry. The lattice CAD models are generated programmatically using the method detailed by McMillan et al.37 (Fig. 2).

Fig. 2
figure 2

FCC and FCCZ experimental lattice design used in this research to quantify buckling response of lattice strut elements within complex lattice structures.

Full size image

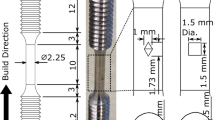
The experimental lattice structures used in this research are designed with a constant strut diameter and contain two unique strut inclination angles relative to the build platform. The strut geometries for each lattice are detailed in Table I, including their idealized lengths measured from the node element centroid.

Table I Overview of struts within the lattice design used in this research (Fig. 2).
Full size table

The methodology proposed in this research is independent of any AM technology, machine, or process category. However, to demonstrate the method’s ability, the experimental lattice designs were manufactured via LB-PBF from titanium alloy Ti6Al4V (powder volumetric measurement parameters: Dv10 = 35.1 µm, Dv50 = 48.9 µm, Dv90 = 86.7 µm). Both lattices were manufactured in an SLM250HL machine with processing parameters as per Table II. Each lattice was fabricated with block type support structures which were manually removed post-manufacture.

Table II LB-PBF process parameters used to fabricate the two sample lattice structures.
Full size table

X-ray Micro-Computed Tomography and Reconstruction

The geometry of the as-manufactured lattices was obtained via a Bruker Skyscan 1275 x-ray µCT. The energy source was operated at 90 kV with an intensity of 100 µA, and with a 1-mm Cu filter. A voxel size of approximately 10 µm was achieved during scanning of the as-manufactured lattice structures (Fig. 2), and the energy source parameters produced a minimum and maximum attenuation of 10% and ~90%, respectively. The scan data was then converted to a 3D volumetric data set via commercial reconstruction software (N-Recon, Micro Photonics Inc.) with beam hardening and ring artefact corrections ignored. Post-processing of the grayscale cross-sectional images included binarization via global thresholding to identify lattice material. Figure 3 displays the 3D volume rendering of as-manufactured lattice structures, plus µCT scan parameters and post-processing threshold values.

Fig. 3
figure 3

Overview of µCT scan parameters and post-processing.

Full size image

Global and Local Point Cloud Registration

A novel two-stage, global and local registration process was applied to enable robust geometric mapping between the centroid of each node element in the idealized and as-manufactured geometries. This mapping enabled strut elements to be extracted directly from the digital twin strut VOI, thereby enabling a functional digital twin.

The global method for locating each node centroid utilized the iterative closest point (ICP) algorithm for the registration of a moving point cloud to one which is fixed via a rigid transformation.38,39 In this research, the stationary point cloud is associated with the as-manufactured geometry as defined by the µCT voxel centroids (obtained from image row/column data and µCT slice number). The moving point cloud is associated with the idealized lattice geometry as defined by a discrete set of nodal locations connected by points interpolated along the strut axisFootnote 1. Prior to registration, the CT point cloud was uniformly down-sampled as required to reduce noise and assist in registration while reducing computational costFootnote 2. Additionally, the idealized lattice point cloud was dilated to match a voxel scale and was rotated so its principal axes matched those of the CT voxel point cloud. The global point cloud registration was performed for the FCC lattice (Fig. 3) as shown in Fig. 4, with the CT point cloud shown as translucent for clarity. This global registration introduces a visible registration error between the idealized and as-manufactured lattice at the node centroid (Fig. 5).

Fig. 4
figure 4

Global registration of moving idealized lattice point cloud to CT-derived as-manufactured lattice point cloud.

Full size image
Fig. 5
figure 5

Local nodal geometry displaying results from global point cloud registration. A registration error is visible between the local ideal lattice surface point cloud and local CT point cloud. This error is due to local geometric deviation in the as-manufactured lattice structure and is corrected by a local registration process (Fig. 6).

Full size image

Following the global registration, a local registration method was implemented to refine the local position of each nodal centroid (Fig. 5) to accommodate local geometric deviation of as-manufactured node elements. This local registration involved extracting the µCT data within a bounding box centered at the ‘globally’ registered nodal centroidFootnote 3. This data was then compared with an equivalent region of the idealized lattice point cloud (Fig. 5). Local registration then involved the movement of the idealized point cloud to the as-manufactured point cloud by the ICP method to achieve local registration. The increase in accuracy from applying the local node registration is visible in Fig. 6.

Fig. 6
figure 6

Local registration of nodal geometries, displaying the increased accuracy of the local registration step, i.e., local registration node centroid closer to (dashed) geometric centerlines than global registration centroid, and overcoming the registration error observed in Fig. 5.

Full size image

Strut VOI Extraction

The proposed global and local point cloud registration method allows registration of as-manufactured geometry while maintaining robust mapping between idealized and as-manufactured node positions. This outcome would not be achievable with traditional best-fit registration methods that have been applied for AM component certification,40 and allows automated extraction of the as-manufactured geometry based on the idealized geometry. This capability enables a functional digital twin where each of the functional elements (in this case strut elements) can be individually characterized for their intended function.

In this case, the locally registered nodal centroids are then used to extract volumes of interest (VOI) from the as-manufactured lattice CT dataset. Firstly, a cylindrical VOIFootnote 4 is extracted with its axis connecting the nodal centroids for the strut of interest. Secondly, the extracted VOI is prepared for image-based FEM by cropping extraneous geometry at the node region (Fig. 7).

Fig. 7
figure 7

Wireframe representation of extracted strut element location (red) in lattice structure (left) and volume rendering of initial strut VOI (middle). Final strut model geometry (right), is used for subsequent image-based FEM analysis of strut buckling response. Also displayed are the cropped and uncropped regions of the final strut VOI (red and blue, respectively) (Color figure online).

Full size image

Results and Discussion

Critical Buckling Prediction of Ideal Cases and As-Manufactured Strut Elements

The prediction of critical buckling load, \({P}_{cr}\), of as-designed struts is obtained analytically using the Euler buckling formula, and numerically using Eigenvalue modes. The applied boundary conditions of these strut elements are fixed-free, although the method is compatible with any boundary condition of interest. The material used is titanium alloy Ti6Al4V and its modulus of elasticity, \(E\), is 113.8 GPa.41 Since the as-manufactured mesh size is 0.01 mm, it is implemented in the numerical simulation for the idealized case, which reflects similar results.

To explore the contribution of the thickened node regions to the critical buckling load of the strut elements, three idealized geometries were considered and their numerical buckling load predictions were compared with those of the as-manufactured geometry (Fig. 8). The first case is an idealized cylindrical column which takes the dimensions of the ideal strut geometry based on the node-to-node distance and the as-designed diameter (Ls 2 mm, Ds 0.3 mm). For this case, the Euler and numerical critical buckling load agree, with 27.9 N and 27.5 N, respectively. The second case approximates the additional material in the node regions using idealized cylindrical nodes; similar to the extracted nodes, their diameters are twice the ideal strut diameter, while their heights are set to half of the ideal strut diameter, representing a T-intersection at the node. The critical load of this case 29.1 N which is slightly higher than predicted for an ideal cylindrical column, indicating a potential increase of critical buckling load with the presence of additional material at the nodes. These first two cases provide results that align with the simulations in16 where idealized strut simulations included small spherical nodes which reproduced the Euler prediction for a perfect cylinder. The third case creates an idealized node that better matches the node size of the extracted as-manufactured strut. The height of the nodes was determined by measuring the node height from the cross section of the extracted as-manufactured strut. The results of case 3 and the extracted strut simulation (case 4) differ by 1.4% which confirms the importance of the contribution of the expanded node region in the simulation of the extracted strut.

Fig. 8
figure 8

Critical buckling prediction of idealized (as-designed) and as-manufactured strut elements.

Full size image

Statistical Distribution Buckling Response and Color Map of Extracted Struts

Once the as-designed and as-manufactured analytical and numerical results are verified in Section 3.1, the developed methodology was implemented to automatically extract geometries, build the model, and execute the numerical simulation for all individual strut elements. The simulations were successfully executed computationally without requiring manual intervention.

Figure 9 shows the histograms indicating the distribution of predicted critical buckling loads alongside color maps of as-manufactured buckling responses of both FCCZ and FCC lattice structures. The critical buckling load of vertical FCCZ ranges from 37 N to 58 N with an average predicted load of just under 50 N and standard deviation of 3.7 N. Alternatively, the 45° struts within the FCCZ lattice are shorter than the vertical struts, and their buckling load ranges from 61 N to 121 N. Within the FCC lattice, the 45° diagonals are slightly longer than in the FCCZ, and their critical buckling ranges from 60 N to 107 N, with an average of 66 N and standard deviation of 9.52 N.

Fig. 9
figure 9

Buckling response of individual struts of FCC and FCCZ lattice structures. Histogram and associated colour map, for FCCZ 90° (a and b), FCCZ 45° (c and d), and FCC (e and f) (Color figure online).

Full size image

Figure 9 visualizes the buckling response of individual struts in the FCCZ and FCC lattice geometries. This visualization tool indicates a variety of different functional responses within the lattice structure, including strut elements with lower-than-average critical buckling loads. This visualization highlights how the proposed methodology can be used as a non-destructive technique to certify lattice response for a specified expected performance.

As-Manufactured Average Diameter Effectiveness on Buckling Response

As well as characterizing the variability in functional response of the as-manufactured struts (in this case the critical buckling load), the proposed digital-twin methodology can be applied to characterize variation in geometry. Furthermore, this capability can be applied conditionally. For example, the specimens in Table III were conditionally extracted from the set of vertical FCCZ strut elements to show the geometric data for the strut elements with upper, median, and lower Pcr values. In this case geometric data included the strut length, volume, average cross section area and material volume, although the method is compatible with any geometric data of interest. This example demonstrates the flexibility for the proposed digital-twin methodology to provide rich data on both the functional response and the causal geometry as is required for the robust certification of complex lattice strut elements.

Table III Average diameter of vertical as-manufactured extracted strut elements from the FCCZ lattice.
Full size table

Conclusion

In this research, a novel methodology for generating and quantifying a lattice structure digital twin is presented. This methodology is developed in response to an identified limitation for non-destructive, algorithmic extraction of both the functional and geometric properties of individual as-manufactured strut elements, as is required for certification and optimization of high-value lattice structures. Specific conclusions of relevance are:

  • Micro-computed tomography (µCT) can provide a robust basis for the acquisition of both geometric data as well as functional response of individual as-manufactured specimens. This data is non-destructive and is therefore compatible with the requirements for high-value lattice structure certification. This data is fundamentally limited by the resolution of the µCT data obtained.

  • µCT data can provide a useful digital twin for as-manufactured lattice structure certification and optimization; however, traditional registration algorithms such as iterative closest point (ICP) fail to register individual strut elements in such a way that mapping between the idealized and as-manufactured strut elements is maintained. This limitation stymies the use of digital twins for functional response of as-manufactured strut elements.

  • A local and global point cloud registration is proposed in this research that allows extraction of individual strut geometries from µCT scans while revealing local geometric deviation of as-manufactured node elements. This robust method maintains geometric mapping between idealized and as-manufactured geometry, thereby enabling systematic generation of a digital twin of individual strut elements, even for geometrically complex lattices with numerous strut elements.

  • The proposed registration methodology allows both the geometry and functional response of each strut element to be characterized using previously validated numerical methods, providing insight into the individual strut response as well as the statistical distribution of responses within the lattice structure, as well as associated statistical data as is required for non-destructive certification of high-value lattice structures (such as medical implants and aerospace structures) according to a pre-determined allowable distribution.

  • This proposed digital-twin methodology is demonstrated on two topologies of lattice structures, FCCZ and FCC, fabricated from Ti6Al4V material using the LB-PBF process. The methodology is implemented algorithmically as is required for product certification. Furthermore, the statistical distributions obtained for sample lattice systems provides input data for uncertainty quantification lattice design methods, as well as providing a systematic basis for design and process optimization of lattice structural efficiency.

The presented methodology demonstrates the fundamental steps for the non-destructive acquisition and analysis of as-manufactured lattice strut elements to algorithmically generate a digital twin. This methodology has been applied to characterize the buckling response and geometric strut attributes of each strut element and associated statistical distributions. This methodology can be readily extended to perform further studies such as fatigue analysis, non-linear plasticity analysis, and thermal and dynamic mechanical behaviors of stochastic lattice structures.