Introduction

Third-generation advanced high-strength steels (3GAHSS) demonstrate excellent mechanical combinations of properties, such as ductility and strength, by leveraging multiple deformation mechanisms. In quenched and partitioned (Q&P) steels, deformation is accommodated by dislocation slip in ferrite, martensite, and austenite, as well as by volume expansion and distortion associated with the transformation-induced plasticity (TRIP) effect in austenite. The TRIP effect is activated upon the transformation of metastable austenite to martensite during plastic deformation. The TRIP effect enhances the strain hardening rate by increasing the dislocation density in the untransformed austenite, while simultaneously increasing the volume fraction of the strong martensite. The balance of dislocation slip versus TRIP is controlled by characteristics of the microstructure (such as crystallographic texture, grain size, morphology, dislocation content, and alloy content), as well as by the imposed deformation conditions (such as the strain state, strain rate, and temperature).1,2

During deformation in processing (e.g., sheet forming) and service (e.g., automobile crashes), the strain rates imposed upon Q&P steels can vary from quasistatic (~10−4 s−1) to dynamic (~103 s−1). For high-strain-rate deformation, there is an increased number of shear band intersections in austenite, which correspondingly increases the number of possible martensite nucleation sites.3,4 Concurrently, as strain rates increase, the heat generated during plastic deformation is allowed less time to dissipate from the steel; at high enough strain rates, sheet temperatures rise adiabatically.5 Rising temperatures decrease the chemical driving force for the martensitic transformation and thus the likelihood that martensite will nucleate.6,7 Strain partitioning between the phases within a Q&P steel may also be strain rate sensitive; because short-range barriers to dislocation motion are more difficult to overcome in body-centered cubic (BCC) versus face-centered cubic (FCC) crystals,8 it is expected that the flow stresses of martensite and ferrite will increase as strain rates increase, leading to enhanced plasticity in austenite.

We showed previously that increasing the strain rate from 10−4 s−1 to 10−1 s−1 deleteriously decreased the strain hardening rate and ductility of a Q&P steel.9 It was hypothesized that a ductility trough existed at intermediate strain rates (approximately 10−1 s−1), which was caused by the competing effects of adiabatic heating and strain rate on the deformation-induced martensitic transformation. That experiment was limited in two ways. First, no interrupted tests were performed, so it was difficult to resolve the extent of the martensitic transformation as a function of the imposed true strain (ɛ). Second, temperature and strain rate are intrinsically physically coupled, so it was difficult to determine whether temperature, strain rate, or a convolution of both variables affected the work hardening behavior of the Q&P steel.

In most high-strain-rate experiments, temperature is viewed as a response variable that is impossible to decouple from strain rate. However, several methods have been implemented to decouple the effects, including isothermal bath testing, strain rate jump testing, and thermal–mechanical simulation. Rana et al. performed tensile tests of a medium-Mn steel at various strain rates in cooled-ethanol and heated-oil baths.10 The heated and cooled baths accelerated the heat transfer between the tensile specimen and the environment, thereby reducing the effects of deformation-induced heating on the mechanical properties. However, the temperature change could not be fully eliminated for the strain rates and temperatures of interest in the study, so strain rate and temperature effects were not fully decoupled. Isakov et al. performed strain rate jump tests to evaluate the strain rate sensitivity of the martensitic transformation in a metastable austenitic stainless steel.11 By deforming the steel to a predetermined strain at a quasistatic rate, then rapidly increasing the strain rate, the strain rate dependence of the martensitic transformation was evaluated without a significant temperature rise; in this case, measurements of the martensite fraction suggested that increasing the strain rate partially suppressed the martensitic transformation. One drawback was that the influence of strain rate history, and thus any strain-rate-dependent microstructure evolution, was not resolved.

Thermal–mechanical simulation has emerged as a more promising approach; by simulating the adiabatic heat rise during quasistatic testing, temperature conditions can be held equivalent between tests with drastically different strain rates. Using this approach, Vázquez-Fernández et al. removed the influence of heat accumulation and showed that the martensitic transformation rates decreased under increasing strain rates for a metastable austenitic stainless steel.12 Strain rate and temperature effects have yet to be decoupled for 3GAHSS with lean alloy additions. In the work described herein, thermal–mechanical simulations were implemented to decouple the roles of temperature and strain rate in dictating the balance of dislocation slip and TRIP in a Q&P steel. The thermal–mechanical simulations and complementary microstructure characterization provide insights into tailoring the stability of retained austenite for enhanced performance over a range of strain rates.

Experimental Procedures

A commercially produced 1.4-mm-thick 0.2C-1.9Mn-1.6Si (wt.%) steel was intercritically annealed followed by Q&P processing. In a previous study using scanning electron microscopy (SEM), the microstructure was revealed to contain ~ 20 vol.% ferrite formed by intercritical annealing, ~70 vol.% martensite, and ~ 10 vol.% retained austenite.2 During deformation under uniaxial tension at a quasistatic strain rate of 10−4 s−1, the steel achieved an ultimate tensile strength greater than 980 MPa and a uniform elongation of 19%. Accordingly, the steel is referred to as “QP980” hereafter. QP980 was revealed to exhibit strain rate-sensitive ductility and strain hardening; as the strain rate was increased to 10−1 s−1, the uniform elongation decreased to 14%.9 To investigate the strain rate-sensitive ductility, this study uses the same QP980 steel.

Tensile specimens with gauge length of 25.4 mm and width of 12.7 mm were machined parallel to the rolling direction of the sheet. Thermal–mechanical simulation was performed in a Dynamic Systems, Inc. Gleeble 3500 equipped with closed-loop control direct resistance heating and servohydraulic actuation. Temperature was monitored using a K-type thermocouple welded to the center of each sample, while actuator displacement was used to compute strain. The springs-in-series reciprocal addition relationship was used to correct for the elastic compliance of the hydraulic actuator. The compliance correction was based on the theoretical elastic modulus of the steel samples (200 GPa), the initial dimensions of the tensile samples, and the assumption that the actuator and samples initially deformed elastically in accordance with Hooke’s law.

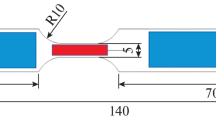
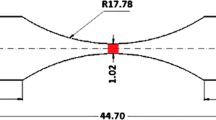
Three thermal–mechanical conditions were investigated for the samples that were monotonically loaded until fracture. Two conditions were tested without external heating at strain rates of 10−4 s−1 and 10−1 s−1. The third condition was tested with external heating at 10−4 s−1, where the thermal profile as a function of strain was programed to mimic the deformation-induced heat rise of the 10−1 s−1 condition; a schematic of a tensile specimen subjected to the resistance heating is shown in Fig. 1a. The test conditions are referred to by their strain rate and thermal condition: 10−4 s−1 (isothermal), 10−1 s−1 (adiabatic), and 10−4 s−1 (resistance heated). Comparing the 10−4 s−1 (isothermal) and 10−4 s−1 (resistance heated) samples will give an indication of the effect of temperature rise on TRIP. Meanwhile, comparing the 10−4 s−1 (resistance heated) and 10−1 s−1 (adiabatic) samples will isolate the effect of strain rate rise on TRIP, while maintaining comparable temperature. Note that for the adiabatic and external resistive heating test specimens, thermal gradients likely existed as a result of specimen geometry and contact with the grip fixtures. However, for both tests, gradients along the length of the specimens were measured to be no greater than 5°C. For the monotonic tests to fracture, two replicates were tested for each thermal–mechanical condition, with no significant variability in the mechanical response being observed between the replicates.

Fig. 1
figure 1

(a) Schematic of tensile specimen used for thermal–mechanical simulations. Some specimens deformed at 10−4 s−1 were resistance heated, to emulate the adiabatic temperature rise at 10−1 s−1. (b) Surface temperature, (c) true stress, and (d) strain hardening exponent (ni) plotted as functions of true strain for two representative tests from each thermal–mechanical condition.

Full size image

To complement the complete tensile tests, where specimens were deformed until fracture, single specimens were interrupted in ɛ increments of approximately 0.02 to evaluate the (untransformed) austenite volume fraction and microstructure evolution as functions of ɛ. On interrupted specimens, metallographic polishing to 1 μm was performed prior to x-ray diffraction (XRD) scans on the normal plane. Scans intended to determine the bulk austenite content were performed using a PANalytical X’Pert diffractometer equipped with a copper source over the 2θ range from 40° to 146°. Because seven to ten interrupted specimens were characterized at sequential ɛ increments for each thermal–mechanical condition, the data presented resolve the variability in the measurement of austenite phase volume fraction as a function of the thermal–mechanical condition and ɛ. After XRD, selected samples were vibratory-polished to 0.05 μm prior to SEM electron backscatter diffraction (EBSD) mapping of the microstructure. EBSD maps were collected in a JOEL JSM7000F field-emission SEM with step size of 0.1 μm. Kernel average misorientation (KAM) analysis was performed for fifth-order neighbors with a threshold of 10° using MTEX to provide insight into the lattice rotation and microstructure as a function of ɛ and the thermal–mechanical condition.13

Results and Discussion

The three thermal–mechanical conditions are represented with temperature versus ɛ plots in Fig. 1b. The 10−4 s−1 (isothermal) specimen exhibited a temperature rise of less than 2°C above room temperature, because the test duration (~ 40 min) was sufficient to allow for nearly complete heat dissipation to the environment. For the 10−1 s−1 (adiabatic) specimen, the surface temperature increased as a function of ɛ, up to approximately 40°C above room temperature at the end of uniform elongation. Based on previous work by the authors,9 it is assumed that the strain rate of 10−1 s−1 is ostensibly greater than the adiabatic threshold strain rate for QP980. The thermal profile of the 10−4 s−1 (resistance heated) samples was chosen empirically, based on the temperature of the 10−1 s−1 (adiabatic) specimen. The temperature profiles of the 10−1 s−1 (adiabatic) and 10−4 s−1 (resistance heated) specimens were within 2°C for the duration of the tests.

The tensile mechanical responses for each condition are shown with ɛ versus true stress (σ) and instantaneous strain hardening exponent (ni) plots in Fig. 1c and d, respectively. To eliminate the influence of the load cell noise on ni, σ and ε were smoothed by adjacent values. ni was calculated after Dieter:14

$$ n_{{\text{i}}} = \frac{{{\text{d}}\left( {{\text{ln}} \sigma } \right)}}{{{\text{d}}\left( {{\text{ln }}\varepsilon } \right)}} $$
(1)

Each thermal–mechanical condition exhibited similar initial yielding behavior without any clear strain rate sensitivity. However, significant differences in the work hardening behavior (manifested by ni) were apparent after the onset of plastic deformation. Comparing the two test conditions deformed at 10−4 s−1, the isothermal specimens exhibited much higher work hardening rates at all stages of plastic deformation. Meanwhile, comparing the 10−4 s−1 (resistance heated) and 10−1 s−1 (adiabatic) specimens, the higher-strain-rate samples exhibited higher work hardening rates at intermediate tensile strains, then the work hardening rates for both conditions converged at ɛ = 0.15. Each sample necked in accordance with the tensile instability criterion (ni = ɛ). Thus, the specimen deformed isothermally at 10−4 s−1 exhibited the highest ductility because it had the highest work hardening rate at ɛ > 0.12. Serrations in the strain hardening exponent curves were observed for specimens deformed at 10−4 s−1 for both thermal conditions; these are attributed to dynamic strain aging in ferrite and secondary martensite.9,15,16 It is known that the diffusivity of carbon within the BCC matrix increases with increasing temperature. However, between the isothermal and resistance heated specimens, no difference in the severity of the serrations was observed. Meanwhile, no serrations were present in the specimen deformed adiabatically at 10−1 s−1, presumably because the carbon diffusion kinetics were insufficient to facilitate DSA for the higher average dislocation velocities associated with higher strain rates.

To measure the extent of TRIP, XRD characterization was performed. Representative XRD scans of QP980 prior to deformation and after 17% tensile strain are shown in Fig. 2a. Four FCC peaks ({111}, {002}, {112}, and {022}) and six BCC peaks ({011}, {002}, {112}, {022}, {013}, and {222}) were indexed. After tensile deformation, the relative height of FCC peaks diminished significantly, indicating that the deformation-induced transformation of austenite to martensite occurred. The progression of the martensitic phase transformation suggests that the TRIP effect influenced the deformation response. Figure 2b shows the austenite content in the interrupted test specimens as a function of ɛ. The austenite fractions reported in Fig. 2b were measured by comparisons of the integrated intensities of BCC and FCC peaks after Cullity.17 Taken as a measure of the TRIP effect, the exponential decay of the austenite fraction in each test condition supports the strain hardening data. That is, higher work hardening rates were correlated to more extensive decreases in the austenite fraction. For instance, samples deformed adiabatically at 10–1 s–1 exhibited the highest work hardening rates and decreases in the austenite content during the initial stages of plastic deformation, suggesting that the TRIP effect was exceedingly active in rapidly strained specimens. Conversely, the extent of the deformation-induced martensitic transformation was reduced in samples deformed (isothermally) at a strain rate of 10−4 s−1. For the deformation condition employing a strain rate of 10−4 s−1 along with resistance heating, the TRIP effect was further suppressed. Therefore, based on both the tensile data and the associated XRD characterization, strain rate and temperature independently influence the TRIP effect in Q&P alloys. Variations of up to 1 vol.% were observed between the exponential decay functions and the experimentally measured austenite fraction. This variability is perhaps due to a combination of uncertainty in the XRD measurements, as well as local variations in austenite stability and volume fraction due to strain and chemical inhomogeneity.

Fig. 2
figure 2

(a) XRD scans before deformation (ε = 0) and after deformation (ε = 0.17) at a strain rate of 10−4 s−1 under isothermal conditions. During tensile deformation under this condition, the austenite content decreased from 11.9 vol.% to 3.8 vol.%. (b) Evolution of retained austenite versus true plastic strain for each thermal–mechanical condition. Plotted lines are exponential decay fits with R2 values of 0.87, 0.93, and 0.90, for the 10−1 s−1 (adiabatic), 10−4 s−1 (isothermal), and 10−4 s−1 (resistance heated) test conditions, respectively. The star symbols in (b) indicate specimens subsequently characterized using EBSD.

Full size image

Specimens labeled with star symbols in Fig. 2b were selected for further characterization by EBSD. In Fig. 3a, image quality maps overlaid with phase maps indicate the presence of austenite (FCC), ferrite (BCC without substructure), and martensite (BCC with blocky substructure) prior to deformation and after deformation at a strain rate of 10−4 s−1 under isothermal conditions. The austenite phase in both maps is mostly visible in a blocky morphology and is generally located adjacent to ferrite grain boundaries. Film-morphology austenite also exists between martensite laths. However, it was not fully resolved because the interaction volume of the backscattered electrons was larger than the lath thickness. The EBSD and XRD scans of the undeformed QP980 agree well; the XRD scan measured a slightly greater amount of austenite (12 vol.% versus 10 vol.%), suggesting the presence of several volume percent of film-morphology austenite. Secondary martensite in the deformed samples, assumed to have transformed from austenite because of the tensile deformation, is labeled with the black oval in Fig. 3a. This feature was distinguished from the primary martensite and ferrite based upon its darker contrast in the EBSD image quality maps and high local misorientation in the KAM maps. Note that the (secondary) martensite in the deformed Q&P microstructure has a greater carbon content and dislocation density compared with primary martensite in undeformed specimens; both of these factors lead to observable contrast differences in the EBSD image quality and KAM maps.

Fig. 3
figure 3

(a) EBSD image quality + phase maps, kernel average misorientation (KAM) maps of BCC phases, and KAM maps of FCC phases, prior to deformation and after deformation at a strain rate of 10−4 s−1 under isothermal conditions. The black oval in the IQ + phase map and KAM in BCC map emphasizes a region of the microstructure that was suspected of containing secondary martensite that formed by the transformation of austenite as a result of tensile deformation. (b) KAM distributions of BCC and FCC phases, respectively, for each thermal–mechanical condition.

Full size image

Short-range rotation of the BCC and FCC lattices, caused by the presence of geometrically necessary dislocations, is revealed with KAM maps in Fig. 3a. Prior to deformation, the local misorientation was uneven in the BCC lattice; KAM was low in the ferrite and high in the martensite. After deformation at 10−4 s−1 under isothermal conditions, KAM became more homogeneous in the BCC map. This suggests that ferrite accommodated a relatively large amount of strain with dislocation slip, relative to martensite. This makes sense because ferrite is known to exhibit a comparatively lower flow strength, due to its lower initial dislocation density and depleted alloy content (e.g., by carbon and manganese partitioning to austenite during intercritical annealing). KAM also increased in the austenite during deformation. This was attributed to dislocation slip in the austenite, as well as dislocation generation due to the TRIP effect.18

KAM distributions of the undeformed QP980 are plotted for the BCC and FCC phases in Fig. 3b. The inhomogeneous KAM within the BCC phases prior to deformation is evident, where the undeformed (ɛ = 0) profile contains a broad martensite shoulder at a KAM above 0.7°. Comparing the undeformed BCC and FCC spectra, it appeared that austenite exhibited an initial KAM that was greater than ferrite and less than martensite. It is sensible that KAM was relatively high in the austenite; the volume expansion associated with the martensitic phase transformation likely imposed significant compressive stresses on the surrounding austenite during the initial quenching step of the Q&P process. These stresses necessitate dislocation slip in austenite to maintain plastic compatibility at austenite–martensite interfaces.

After plastic deformation under every thermal–mechanical condition, the KAM distributions evolved similarly (variations in the distributions were within the estimated uncertainty associated with the EBSD scan size). This suggested that the extent of dislocation slip was ostensibly similar for each thermal–mechanical condition. This is rational because the strain hardening rates of ferrite–martensite dual-phase steels, whose microstructures are like QP980 that lacks austenite, are reportedly indistinguishable from 10−3 s−1 to 10−1 s−1.19 Since the dislocation slip behavior was similar for each thermal–mechanical condition, it is concluded that the dissonant strain hardening responses shown in Fig. 1d are solely due to variations in the potency of the TRIP effect.

Conclusion

The data presented here quantify the independent effects of strain rate and deformation-induced temperature rises on the martensitic phase transformation. By externally heating without increasing the strain rate, it was shown that deformation-induced temperature rises greatly impede the martensitic transformation and reduce the strain hardening contribution of the TRIP effect. Meanwhile, by comparing samples deformed at 10−4 s−1 and 10−1 s−1 that were heated externally and adiabatically, increasing the strain rate appears to accelerate the martensitic transformation and enhance the work hardening. This result clarifies the root cause of the ductility and martensitic transformation trough that was reported for 3GAHSS previously;9 because the temperatures reached by deformation-induced heating saturate at the adiabatic threshold strain rate, adiabatic temperature rise no longer causes shifts in the TRIP effect for strain rate variations above approximately 10−1 s−1. Rather, for strain rate shifts at dynamic rates, e.g., for a shift from 1 s−1 to 1000 s−1, the martensitic transformation kinetics are controlled by an increase in the number of martensite nucleation sites and an increased mechanical driving force.20,21

This revelation was quite challenging to reach using conventional tensile tests. Thus, thermal–mechanical simulation is a promising method to decouple the influences of temperature and strain rate on the deformation behavior of structural metals; the technique will be useful for tailoring the microstructures of 3GAHSS, and other alloy classes that take advantage of the TRIP or twinning-induced plasticity (TWIP) effects for strain accommodation and strengthening.