The Effect of Loading Inclination and Eccentricity on the Bearing Capacity of Shallow Foundations: A Review

Abstract

This paper provides a comprehensive review on the effect of load inclination and eccentricity on the bearing capacity of shallow foundations. Regarding load eccentricity, Meyerhof’s intuitive formula ${B}{\prime}=B-2{e}_{b}$ aligns well with finite element analyses, though it is slightly conservative. Analysis using finite element results revealed the more accurate formula $B-1.9{e}_{b}$. Concerning load inclination factors, numerous such factors exist in the literature. However, most are either intuitive or derived from small-scale experimental results, rendering them unreliable due to the significant impact of model scale on the bearing capacity of footings. Based on numerical results, it is proposed that all inclination factors (namely ${i}_{c}$, ${i}_{\gamma }$ and ${i}_{q}$) can be reliably expressed by a formula of the form ${\left(1-{f}_{1}\cdot {\tan }\left({f}_{3}\delta \right)\right)}^{{f}_{2}}$, where $\delta$ is the inclination angle of the loading with respect to the vertical, ${f}_{1}$ and ${f}_{3}$ are coefficients and ${f}_{2}=3$. The latter ensures smooth transition from the bearing capacity failure to the sliding failure as $\delta$ increases. It is also observed that many $i-$ factors in the literature and various design standards employ an impermissible combination of sliding resistance at the footing-soil interface and Mohr–Coulomb bearing capacity failure under the footing. Moreover, it is shown that only the ${i}_{c}$ factor depends on the angle of internal friction of soil. Finally, Vesic’s 1975 “m” interpolation formula largely falls short in accurately representing the effect of the direction of the horizontal loading.

1 Introduction

The bearing capacity of shallow foundations is influenced by various factors, such as embedment depth, loading eccentricity and inclination, ground, and base inclination. These factors are integrated into Terzaghi's fundamental equation, which traditionally employs three $N$- factors and is expressed as follows:

$${q}_{u}=c{N}_{c}{d}_{c}{i}_{c}{s}_{c}{g}_{c}{b}_{c}+\frac{1}{2}\gamma B^{\prime}{N}_{\gamma }{d}_{\gamma }{i}_{\gamma }{s}_{\gamma }{g}_{\gamma }{b}_{\gamma }+\gamma {D}_{f}{N}_{q}{d}_{q}{i}_{q}{s}_{q}{g}_{q}{b}_{q}$$

(1)

${N}_{c}$, ${N}_{\gamma }$ and ${N}_{q}$ represent the bearing capacity factors related to cohesion, unit weight of soil and lateral surcharge, respectively. Depth factors are denoted as ${d}_{c}$, ${d}_{\gamma }$ and ${d}_{q}$, load inclination factors as ${i}_{c}$, ${i}_{\gamma }$ and ${i}_{q}$, footing shape factors as ${s}_{c}$, ${s}_{\gamma }$ and ${s}_{q}$, ground inclination factors ${g}_{c}$, ${g}_{\gamma }$ and ${g}_{q}$ and base inclination factors as ${b}_{c}$, ${b}_{\gamma }$ and ${b}_{q}$. $\gamma$ is the unit weight of the soil, while ${D}_{f}$ is the embedment depth of the footing. $B^{\prime}$ is the effective depth of the footing, traditionally taken equal to $B-2{e}_{B}$, following Meyerhof’s recommendation. Expressing the effect of footing eccentricity as a factor (i.e., ${e}_{\gamma }=B^{\prime}/B$), Eq. 1 can be rewritten as follows:

$${q}_{u}=c{N}_{c}{d}_{c}{i}_{c}{s}_{c}{g}_{c}{b}_{c}+\frac{1}{2}\gamma B{N}_{\gamma }{{e}_{\gamma }d}_{\gamma }{i}_{\gamma }{s}_{\gamma }{g}_{\gamma }{b}_{\gamma }+\gamma {D}_{f}{N}_{q}{d}_{q}{i}_{q}{s}_{q}{g}_{q}{b}_{q}$$

(2)

${e}_{\gamma }$ is the footing eccentricity factor. The latter is equal to $1-2{e}_{B}/B$ if Meyerhof’s recommendation of 1953 [43] is adopted. Since 1953, alternative expressions for ${e}_{\gamma }$ have been suggested in the literature based on experimental results, analytical modeling, or numerical modeling.

Considering that both loading inclination and loading eccentricity are related to the vector of loading acting on the footing, their joint consideration in this paper seems appropriate. Besides, both factors influence the contact pressure beneath the footing. The literature review below will encompass the loading inclination factors for the case of shallow foundations over a single-layer medium of great depth, highlighting a multitude of such factors and a general disagreement among them.

The effect of loading inclination on the bearing capacity of footings over stratified media has been studied, among others, by Meyerhof and Hanna [1], Panwar and Dutta [2,3,4], Dutta et al. [5], Rao et al. [6], Singh and Roy [7, 8], Femmam et al. [9] and Yuan et al. [44]. Sharma and Kumar studied [10] the behavior of ring footings resting on reinforced sand subjected to eccentric-inclined loading. However, the review of special cases has been reserved for future work.

This paper explores the effects of load inclination and eccentricity on the bearing capacity of shallow foundations from a critical point of view of the existing literature, while it employs finite element analyses to assess and refine existing formulas for effective footing width and inclination factors. The research introduces more accurate expressions for these factors, validated against numerical results, enhancing reliability and precision in foundation design. Additionally, it corrects common misconceptions in the application of load inclination factors, thereby improving the understanding of soil-structure interaction under complex loading conditions. These advancements not only elevate the theoretical understanding of bearing capacity but also have practical implications for safer and more efficient foundation design in civil engineering.

In this study, the symbols $c$ and $\varphi$ represent the cohesion and friction angle of soil, respectively. Depending on the context, these symbols may refer to shear strength parameters under either drained or undrained conditions.

2 Loading Eccentricity and Effective Width of Footings

When a foundation carries eccentric load, it tilts toward the side of the eccentricity. This inevitably affects the contact pressure below the base and, in turn, the bearing capacity of the footing. Meyerhof first addressed this issue, assuming central load action on a foundation with an effective contact width $B^\prime =B-2{e}_{b}$. Meyerhof’s assertion was that ignoring the remaining width (that is, the $B-B^{\prime}$) results in plastic equilibrium zones in the material on the side of the eccentricity side, similar to those in a centrally loaded foundation. Meyerhof considered his intuitive formula $B^\prime =B-2{e}_{b}$ somewhat conservative. The validity of this formula and statement are also under investigation in this paper.

Following Meyerhof's formula, various researchers proposed alternative formulas for effective footing width. These new approaches drew from methodologies like small-scale laboratory tests [11,12,13,14,15,16], analytical modeling [17], and numerical analyses [18, 19]. These formulas are listed in Table 1. For consistency, these expressions are presented as loading eccentricity factor ${e}_{\gamma }=B^{\prime}/B$. Thus, the soil unit weight term in the basic bearing capacity equation will be modified as follows:

$${q}_{u} ={1/2}\cdot \gamma \cdot B^{\prime} \cdot {N}_{\gamma }={1/2}\cdot \gamma \cdot B \cdot {e}_{\gamma }\cdot {N}_{\gamma }$$

(3)

$e/B$ versus ${e}_{\gamma }$ charts are given in Figs. 1 and 2 for comparison. These figures demonstrate that the effective width formulas derived from experimental results (Figs. 1b and 2) are more conservative than Meyerhof’s effective width. On the other hand, the numerical results are only slightly higher than Meyerhof’s ones. Analytically, Michalowski [17] found that Meyerhof’s $B^\prime =B-2{e}_{b}$ applies to smooth footings, whereas for footings without separation, the impact of eccentricity is significantly reduced.

Table 1 ${e}_{\gamma }$ factors suggested by various scientists

Fig. 1

${e}_{\gamma }$ versus $e/B$ charts for ${e}_{\gamma }$ factors derived a) numerically or analytically and b) experimentally

Fig. 2

${e}_{\gamma }$ versus $e/B$ chart for the Patra et al. [14, 15] and Ganesh et al. [16] methods

Numerically, Loukidis et al. [18] suggested two expressions for $B^\prime$ (the second derived from their ${i}_{\gamma }$ factor for $\delta =0$), yielding results similar to Meyerhof’s $B^\prime =B-2{e}_{b}$, particularly when ${e}_{\rm B}<1/3$. Pham et al. [19] conducted numerical analyses considering both rough and smooth footings, concluding that $B^\prime =B-1.85{e}_{b}$ in all cases, closely aligning with Meyerhof’s intuitive formula.

Regarding experimental results [11,12,13,14,15,16], it is important to be noted that the tests carried out by Purkayastha and Char [11], Ingra and Baecher [12], Georgiadis and Butterfield [13], Patra et al. [14, 15] and Ganesh et al. [16] were small scale. Small-scale tests in bearing capacity analysis are known to be unreliable, as bearing capacity inversely correlates with increasing footing size [20,21,22,23, 45, 46]. Centrifuge tests by Kimura et al. [23] revealed a scale effect in the bearing capacity factor ${N}_{\gamma q}$, diminishing at approximately 80 cm or higher, depending on the relative density of sand. Yamaguchi et al. [22] suggested a minimum $B$ value of approximately 80 cm also based on centrifuge test results.

Thus, it is deduced that Meyerhof’s [43] $B^\prime =B-2{e}_{b}$ intuitive formula is not only a reliable but also slightly conservative.

3 The Loading Inclination Factors: Literature Review

Schultze [25] suggested $N-$ factors for all terms in the basic bearing capacity equation, considering the influence of load inclination. However, this 1953 analytical solution did not gain significant attention. Instead, simpler $i-$ correction $-$ factors for existing $N-$ factors (for $\delta =0$) were favored. Subsequently, many researchers attempted to quantify the effect of load inclination by incorporating relevant factors into the bearing capacity equation, rather than introducing new $N-$ factors. Table 2 lists $i-$ factors suggested by various researchers and included in different design standards. Not all design standards in Table 2 are currently active, but they provide valuable insights into the evolution of the three inclination factors.

Table 2 Inclination factors appearing in various sources

The $i-$ factors are usually expressed as a function of ${\tan }{\delta }_{x}$, i.e.:

$$i={\left(1-{f}_{1}\cdot {\tan }{\delta }_{x}\right)}^{{f}_{2}}$$

(4)

where ${f}_{1}$ and ${f}_{2}$ are real numbers, while ${\tan }{\delta }_{x}$ takes one of the following forms:

$${\tan }\delta =H/V$$

(5)

$${{\tan }\delta }_{{c}_{u}}=\frac{H}{{B}^{{{\prime}}}{L}^{{{\prime}}}{c}_{u}}$$

(6)

$${\tan }{\delta }_{c}=\frac{H}{V+{B}^{{{\prime}}}{L}^{{{\prime}}}c{\text{ cot}}\varphi }$$

(7)

Given that many design standards have adopted the formulations of Eqs. 6 and 7, the authors deem it appropriate to comment on how these equations were found in the prominence. Starting from Eq. 5, this form was introduced by Hansen in 1955 [26], and it clearly represents the inclination of the loading with respect to the vertical. The expressions presented in Eqs. 6 and 7 were also introduced by Hansen in 1959 [47] and 1961 [27] for total and effective stress analysis, respectively. More specifically, Eq. 6 first appeared in:

$${i}_{c}=1-0.5\cdot {{\tan }\delta }_{{c}_{u}}$$

(8)

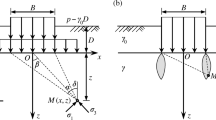
However, Hansen [27] deemed the latter “too inaccurate”. The proposal of ${{\tan }\delta }_{{c}_{u}}$ for total stress analysis (Eq. 6) was not straightforward. Hansen first made the assumption that the correct angle of the soil wedge, $a$, beneath a strip footing on the opposite side of the failure is a function of both $\delta$ and $\varphi$ (Fig. 3). That is:

Fig. 3

The angle ${{\delta}}$ of the loading (with respect to the vertical) and the angle ${{a}}$ in the soil wedge beneath the footing

$${\tan }\left(a-\varphi /2\right)=\frac{\sqrt{1-{\left({\tan }\delta \cdot {\text{cot}}\varphi \right)}^{2}}-{\tan }\delta }{1+{\tan }\delta /{\text{sin}}\varphi }$$

(9)

Subsequently, Eq. 9 led to an ${i}_{q}$ factor that is a function of $a$ and thus, of $\delta$ and $\varphi$ (see Table 2). Regarding Eq. 9, although the validity of this equation is not checked herein, it is well known that $a$ depends on $\delta$ and $\varphi$.

For the special case of $\varphi =0$, Hansen assumed that the angle $a$ also depends on the shear strength of soil, but this time on cohesion:

$${{\cos}}2a=\frac{H}{B\cdot c}$$

(10)

The ratio of the horizontal loading, $H$, over the peak shear force resisting sliding, $B\cdot c$ (per meter length), represents the mobilized shear resistance at the base of the footing; if $H> B\cdot c$, the footing slides. Indeed, when $H=$ $B\cdot c$, $a$ is $0^\circ$, indicating limit equilibrium against sliding of footing, and when $H=$ $0$, $a$ becomes $45^\circ$, which is the angle of the soil wedge beneath the footing in the undrained soil condition. However, it appears that Hansen was misled by these extreme cases. As previously mentioned, it is well-known that the shape of the soil wedge beneath the footing depends on the friction angle of the soil as well as on the inclination of the load and not on cohesion and on the degree of mobilization of the shear strength on the foundation surface. From a rational perspective, if cohesion influences the angle $a$ in the undrained state of the soil, it should likely have a similar effect in the drained state. Van Baars [28] also refers to “a disallowed mixture of the Coulomb failure of the interface and the Mohr–Coulomb bearing capacity failure of the half-space below the interface”. Therefore, Eq. 10 represents an incorrect assumption made by Hansen.

Hansen used the angle $a$ defined in Eq. 10 in the following inclination factor:

$${i}_{c}=\frac{1}{2}+\frac{2a+{\text{sin}}2a}{\pi +2}$$

(11)

Although Hansen [27] did not provide any reference for Eq. 11, this expression, which was derived analytically, belongs to Green [29], with ${{\cos}}2a$ being equal to ${\tan }\delta$ (see Table 2).

Hansen [27] proposed the following formula as a better fit for Eq. 11, describing it as "a somewhat simpler formula, yielding approximately the same results":

$${i}_{c}=\frac{1}{2}+\frac{1}{2}\sqrt{1-{{\tan }\delta }_{{c}_{u}}}$$

(12)

This proposal involves the a posteriori substitution of ${\tan }\delta$ with ${{\tan }\delta }_{{c}_{u}}$. It is also mentioned that Hansen’s expression from 1961 (Eq. 12) does not differ from his ${i}_{c}=0.5-0.5\sqrt{1-{{\tan }\delta }_{{c}_{u}}}$ expression from 1970 [30]; Hansen merely felt that it is “theoretically more correct (for the $\varphi =0$ case) to introduce additive constants instead of factors”. That is,

$${q}_{u}=\left(\pi +2\right){c}_{u}\left(1+{s}_{c}+{d}_{c}-{i}_{c}-{g}_{c}-{b}_{c}\right)$$

(13)

However, the scientific community has not accepted the concept of additive constants.

Regarding effective stress analysis and the derivation of the expression ${{i}_{q}=\left(1-{\tan }{\delta }_{c}\right)}^{2}$ (also refer to Eq. 7), Hansen [27] assumed two forces, namely, ${\rm H}_{1}$ and ${V}_{1}$, corresponding to the special case where $\gamma =0$, $q=1$ and $c=0$. Hansen suggested that for the more general case of $\gamma =0$, $q>0$ and $c>0$, the values of $H$ and $V$ should be:

$$\left\{\begin{array}{c}H=\left(q+c\cdot {\text{cot}}\varphi \right){\rm H}_{1}\\ V=\left(q+c\cdot {\text{cot}}\varphi \right){V}_{1}-A\cdot c\cdot cot\varphi \end{array}\right.$$

(14)

Hence, the ratio determining the inclination factors is:

$$\frac{{\rm H}_{1}}{{V}_{1}}=\frac{H}{V+Ac{\text{ cot}}\varphi }={\tan }{\delta }_{c}$$

(15)

Equation 14 is not only a major and unjustified assumption, but it also incorrectly states that the forces ${\rm H}_{1}$ and ${V}_{1}$ have units of area, which is not correct.

Hansen’s ${{\tan }\delta }_{cu}$ and ${\tan }{\delta }_{c}$ approaches (Eqs. 6 and 7, respectively) were later incorporated into the $i-$ factors suggested by Vesic [46]. The $i-$ factors, proposed by both Hansen and Vesic, have subsequently been adopted by several standards, including EN1997-1:2004 [31], DIN4017:1979–02 [48], DIN4017:1996-04 [49], API [50], GEO [32], DIN4017:2006–03 [51] and AASHTO [52]. The recent draft standard prEN1997-3:2023 [53] has moved away from using ${i}_{\gamma }$ and ${i}_{q}$ factors based on the peak shear strength of the footing—soil interface. However, Hansen’s ${i}_{c}=0.5+0.5\sqrt{1-{{\tan }\delta }_{{c}_{u}}}$ from 1961 [27] has been retained for the undrained state of soil.

Another inclination factor proposed by Hansen [27] and later adopted by many others, involves the ${i}_{c}$ expression in relation to ${i}_{q}$ and ${N}_{q}$, that is:

$${i}_{c}={i}_{q}-\frac{1-{i}_{q}}{{N}_{q}-1}$$

(16)

Indeed, Hansen proposed that equations analogous to this one are also applicable to depth and shape factors (${d}_{c}$ and ${s}_{c}$, respectively). Hansen developed this equation based on the rule of corresponding states. This rule suggests that by adding a hydrostatic stress of $c\cdot cot\phi$ to the stresses, one can derive a solution for a limit-state problem in cohesive-frictional soil from the solution for granular soil. However, Michalowski [33] points out that adding the hydrostatic stress $c\cdot cot\phi$ to any limit stress field in granular soil alters the primary stress directions. Consequently, when this rule is applied to a base solution for frictional soil to derive a solution for cohesive-frictional soil, the resulting solution pertains to a scenario with different boundary conditions (traction inclination) from the original problem. Working with weightless material and based on Prandl’s [34] and Reissner’s [54] works, Terzaghi [35] found the following:

$${N}_{c}=\left({N}_{q}-1\right){\text{cot}}\varphi$$

(17)

Schultze [25] analytically calculated the ${N}_{q}$ and ${N}_{\gamma }$ factors for the $\delta >0$ case. Equation 17 was adopted for ${N}_{c}$. Below are the ${N}_{q}$ and ${N}_{\gamma }$ factors as determined by Schultze:

$${N}_{q}=\frac{{{\tan }}^{2}\alpha }{{\tan }\left(\alpha +\beta \right)\cdot {{{\cos}}}^{2}\delta \cdot \left({\tan }\left(\alpha -\beta \right)-{\tan }\delta \right)}$$

(18)

$${N}_{\gamma }={\left(\frac{{\tan }\beta }{{\tan }\alpha }\right)}^{2}\frac{{N}_{q}}{\left(1-{{\tan }}^{2}\alpha \cdot {{\tan }}^{2}\beta \right)\cdot {\tan }\left(\alpha +\beta \right)}$$

(19)

where $\alpha =\pi /4+\varphi /2$, $\beta ={\text{Arctan}}\left({\mu }_{\alpha }+\sqrt{{\mu }_{\alpha }^{2}+{\lambda }_{\alpha }}\right)$, ${\lambda }_{\alpha }={{\text{cot}}}^{2}\alpha$ and ${\mu }_{\alpha }=\left(1-{\lambda }_{\alpha }\right)/\left(2\cdot {\tan }\delta \right)$.

The three $i-$ factors can be extracted by the $N-$ factors as follows:

$${i}_{q}=\frac{{N}_{q}}{{N}_{q}\left(\delta =0\right)}=\frac{{\text{sin}}\left({\alpha }-\upbeta \right)}{{\text{sin}}\left({\alpha }-\upbeta -\updelta \right)\cdot {{\cos}}\delta }$$

(20)

$${i}_{\gamma }=\frac{{N}_{\gamma }}{{N}_{\gamma }\left(\delta =0\right)}=\frac{{\text{sin}}\left({\alpha }-\upbeta \right)}{{\text{sin}}\left({\alpha }-\upbeta -\updelta \right)\cdot {{\cos}}\delta }={i}_{q}$$

(21)

$${i}_{c}=\frac{{N}_{c}}{{N}_{c}\left(\delta =0\right)}={i}_{q}-\frac{1-{i}_{q}}{{N}_{q}-1}$$

(22)

Two observations can be made here. According to Schultze, ${i}_{\gamma }$ is equal to ${i}_{q}$, and ${i}_{c}$ is equal to $(1-{i}_{q})/({N}_{q}-1)$ (refer to Eq. 16). The latter finding is not surprising, as in deriving Eq. 21, it is based on Eq. 17, and this aligns with what was previously mentioned about the corresponding states (see also [33]).

The interrelation between ${i}_{c}$ and ${i}_{q}$ in Eq. 21 has been adopted by Vesic [46] and subsequently by many design standards (refer to Table 2). Generally, in the literature, it is not uncommon to find that various $i-$ factors are interrelated (see Table 2); these $i-$ factors may be equal to, approximately equal to, or a function of other $i-$ factors. Regrettably, the interrelations between the various $i-$ factors presented in Table 2 have been proposed “as they are”, without further elaboration.

Another interesting point is that some $i-$ factors appear to depend on $e/B$ or $\varphi$. For example, Loukidis et al. [18] suggested two ${i}_{\gamma }$ expressions, one involving $\delta$ and $e/B$ and one involving $\delta$ and $\varphi$. However, since both expressions show strong relational characteristics, the influence of the second factor (i.e., $e/B$ or $\varphi$) is relatively weak and should be disregarded. This will be further examined in the next section.

Finally, according to the FHWA [55], the simultaneous application of both shape and load inclination factors can lead to an overly conservative design. Therefore, the inclination factors are omitted from the calculation of the bearing capacity. Additionally, the FHWA recommends evaluating the bearing capacity using effective footing dimensions. The validity of these statements will also be examined in the following section.

4 The ${{{i}}}_{{{\gamma}}}$ Factor Load Inclination Factor

4.1 Horizontal Load Acting Along the Short Side of the Footing

4.1.1 The ${{B}}/{{L}}=0$ Case

Figures 4 and 5 depict ${V}_{u,FE,(\delta >0)}$ versus ${V}_{u,FE,(\delta =0)}\cdot {i}_{\gamma }$ charts for $\psi =\varphi$ and $\psi =0$, respectively. ${V}_{u,FE,(\delta >0)}$ represents the finite element analysis value of the ultimate vertical loading force that the footing can withstand, considering the loading inclination, $\delta$. ${V}_{u,FE,(\delta =0)}$ denotes the corresponding load for $\delta =0$. The ${i}_{\gamma }-$ factors list is provided in Table 2. When an ${i}_{\gamma }-$ factor includes the shear strength at the footing–soil interface in its formula, the ${\tan }{\delta }_{{c}_{u}}$ or the ${\tan }{\delta }_{c}$ term is replaced by the more logical ${\tan }\delta$, at least for evaluating the general form of these ${i}_{\gamma }-$ factors. The numerical procedure and results for all example cases are detailed in Loukidis et al. [18]. There are 54 example cases for each $\psi$ value (i.e., $\psi =0$ and $\psi =\varphi$). The examples for $\delta =0$ are excluded from the charts for evident reasons. Additionally, if an ${i}_{\gamma }$ factor is specifically intended for positive $\delta$ values, it is applied only to these values.

Fig. 4

${V}_{u,FE,(\delta >0)}$ versus ${V}_{u,FE,(\delta =0)}\cdot {i}_{\gamma }$ charts for $\psi =\varphi$ for various ${i}_{\gamma }$ factors

Fig. 5

${V}_{u,FE,(\delta >0)}$ versus ${V}_{u,FE,(\delta =0)}\cdot {i}_{\gamma }$ charts for $\psi =0$ for various ${i}_{\gamma }$ factors

${V}_{u,FE,(\delta >0)}$ versus ${V}_{u,FE,(\delta =0)}\cdot {i}_{\gamma }$ charts using Schultze’s [25] method, but with the ${i}_{\gamma }-$ factor from Eq. 21 instead of his ${N}_{\gamma }-$ factor (Eq. 19), are illustrated in Fig. 6.

Fig. 6

${V}_{u,FE,(\delta >0)}$ versus ${V}_{u,FE,(\delta =0)}\cdot {i}_{\gamma }$ charts for a) $\psi =\varphi$ and b) $\psi =0$ for Schultze’s ${i}_{\gamma }$

In the same context, the authors conducted regression analysis on the aforementioned finite element analysis examples [18], deriving new expressions for both the ${i}_{\gamma }$ and ${e}_{\gamma }$ factors. The authors found that the equation best describing ${V}_{u}$ is:

$${V}_{u} ={1/2}\cdot \gamma \cdot B^2 \cdot {e}_{\gamma }^{2}\cdot {N}_{\gamma \left(\delta =0\right)}\cdot {i}_{\gamma }$$

(23)

with

$${e}_{\gamma }=1-1.9\frac{e}{B}$$

(24)

and

$${i}_{\gamma }={\alpha }_{\psi }{\left(1-{\tan }\left|\delta \right|\right)}^{3}=\left\{\begin{array}{c}{\alpha }_{\psi }=1, 0^\circ \le \delta \le 45^\circ\quad and\quad any\quad \psi\, value\\ {\alpha }_{\psi }=1.46, -45^\circ \le \delta \le 0^\circ \quad and \quad \psi =\varphi \\ {\alpha }_{\psi }=1.36, -45^\circ \le \delta \le 0^\circ\quad and\quad \psi =0\end{array}\right.$$

(25)

The relevant ${V}_{u,FE(\delta >0)}$ versus ${V}_{u}$ charts are presented in Fig. 7, where the ${N}_{\gamma ,FE}$ value is used.

Fig. 7

${V}_{u,FE,(\delta >0)}$ versus the proposed ${V}_{u} = 1/2\cdot \gamma \cdot B^{2} \cdot {e}_{\gamma }^{2}\cdot {N}_{\gamma \left(\delta =0\right)}\cdot {i}_{\gamma }$ (with ${B}{\prime}=1-1.9\frac{e}{B}$ and ${i}_{\gamma }=\alpha {\left(1-tan\left|\delta \right|\right)}^{3}$) charts for a) $\psi =\varphi$ and b) $\psi =0$

At first glance, it appears that proposing a new ${i}_{\gamma }$ factor (as per Eq. 25) was unnecessary, given that the factor by Loukidis et al.’s [18] is equally effective. However, Eq. 25 is significantly simpler; it clearly demonstrates that ${i}_{\gamma }$ depends only on $\delta$ (and $\psi$ for negative $\delta$ values), whereas users are generally more familiar with expressions like that in Eq. 4. Additionally, Eq. 25 supports the choice of the prEN1997-3:2023 draft standard. It is also noted to be slightly more accurate than the factor by Loukidis et al.’s [18]. Furthermore, Fig. 4, 5, 6, and 7 provide qualitative assessment of the discrepancies in values, based on simple visual observation. A quantitative assessment is conducted through the mean bias deviation (MBD), the mean absolute error (MAE), and the regression line parameters: slope ($a$) and $y-$ intercept ($b$), which are included in the charts. The MAE is a valuable measure for understanding the average magnitude of prediction errors, regardless of their direction. On the other hand, a negative MBD suggests that predictions tend to be on the unsafe side. The ideal values for MBD, MAE, and $b$ are zero, while the ideal value for $a$ is one. The extent of conservatism or non-conservatism in predictions can also be inferred from the value of $a$. Specifically, if $a<1$, then the predictions tend to be conservative and vice versa.

As demonstrated in the same figures, the coefficient of determination $({R}^{2})$ is consistently very high in each case, which reduces its usefulness for this comparison. Besides, a high ${R}^{2}$ value does not necessarily mean that the model is accurately predicting the data, especially if there is a significant scatter in the values. If the scatter of the values is great but symmetrically aligned around the regression line, it means that, despite the variability, the average trend described by the model is still strong. To facilitate comparison, MBD, MAE, $a$ and $b$ are summarized in Table 3.

Table 3 MBD, MAE, a and b indices for the various ${i}_{\gamma }$ factors

Both the visual interpretation of Figs. 4, 5, 6, and 7 and the values of the four indices presented in Table 3 clearly indicate that the proposed approach (Eqs. 23–25), Vesic’s [46] approach (modified to use ${\tan }\delta$ instead of ${{\tan }\delta }_{c}$), Loukidis et al.’s [18] rigorous formula and Schultze’s [25] analytical approach (Eq. 19) are significantly more reliable. It is emphasized that Loukidis et al.’s ${i}_{\gamma }$ factor and the proposed ${i}_{\gamma }$ factor were derived from finite element results, Schultze’s factor was purely analytical, and Vesic’s [46] empirical ${i}_{\gamma }$ factor was not used in its original form. Regarding the other ${i}_{\gamma }$ factors listed in Table 2, they were proposed based on either limited small-scale experimental results or intuition.

More specifically, concerning Schultze’s ${i}_{\gamma }-$ factor (Eq. 21), comparing this factor with finite elements analysis shows excellent agreement for $\left(\beta -\alpha \right)/\left(\beta -\alpha +\delta \right)>0.35$ (error less than 10%). In other cases (ratio < 0.35), which correspond to high friction angles ($\varphi >35$ ^ο), combined with high $\delta$ angles ($\delta >15$ ^ο), the error increases as the $\left(\beta -\alpha \right)/\left(\beta -\alpha +\delta \right)$ ratio decreases.

Finally, the authors conducted their own finite element analysis to investigate the validity of the ${i}_{\gamma }={\left(1-{\tan }\delta \right)}^{3}$ formula. The software used was Rocscience’s RS2, and the model used is shown in Fig. 8. The results are presented in Fig. 9. The chart considers parameters such as $c^\prime =$ 20 kPa and 10 kPa, $\varphi =$ 30°, $\gamma =$ 17 kN/m, $\psi =\varphi$, $B=$ 2 m and no lateral surcharge, with the footing being rigid and infinitely length. As shown, the new finite element results align closely with those obtained using the ${i}_{\gamma }={\left(1-{\tan }\delta \right)}^{3}$ formula.

Fig. 8

The finite element analysis model used in the present paper

Fig. 9

Evaluation of the ${i}_{\gamma }={\left(1-tan\delta \right)}^{3}$ formula against finite element analysis result

4.1.2 The $0\le {{B}}/{{L}}\le 1$ General Case

Muhs and Weiss [57] performed tests with a 1.0 m wide and 3.0 m long footing but with inclined loads applied in the direction of the short side of the footing. For this $L/B=3$ footing, they concluded that:

$${i}_{\gamma } = {\left(1-{\tan }\delta \right)}^{2}$$

(26)

Theoretically, when $\delta$ equals 90° (indicating purely horizontal loading), the bearing capacity becomes infinite. On the other hand, the minimum value of ${i}_{\gamma }$ should correspond to a $\delta$ angle that falls within the range of 0° to 90°. However, in practical scenarios, $\delta$ does not usually (and should not) take great values, let alone $45^\circ$ or even greater, avoiding the risk of sliding. The empirical function ${i}_{\gamma }={\alpha }_{\psi }{\left(1-{\tan }\left|\delta \right|\right)}^{3}$ (referred to as Eq. 25), effectively describes the relationship between the bearing capacity factor ${i}_{\gamma }$ and $\delta$ for angles ranging from 0° to $45^\circ$. This function shows that as $\delta$ approaches $45^\circ$, ${i}_{\gamma }$ smoothly approaches zero, indicating a sharp decrease for small $\delta$ values. It is important to be noted that the primary concern when $\delta$ exceeds 45° is not the soil's inability to bear the vertical component of the load, but rather the lack of adequate sliding resistance provided by the foundation surface against the horizontal component of the load. This behavior is commonly observed in finite element analysis.

The function ${i}_{\gamma }={\left(1-{\tan }\delta \right)}^{3}$ for $0^\circ \le \delta \le 45^\circ$ has been drawn in Fig. 10a alongside a hypothetical function ${i}_{\gamma }={f}_{3}{\left(\left( \delta -90^\circ \right)\pi /180^\circ \right)}^{-2}+{f}_{4}$ for $45^\circ \le \delta \le 90^\circ$, where ${f}_{3}$ and ${f}_{4}$ are real numbers. In Fig. 10a, ${f}_{3}=0.05$ and ${f}_{4}=-0.081$. The hypothetical curve has been drawn with the criteria of smooth and logical continuity between the left and right segments of the chart, ensuring no sliding risk, while satisfying the condition of infinite bearing capacity at $\delta =90^\circ$. From Fig. 10b it is evident that small values of ${f}_{2}$ do not meet the criterion for a smooth transition between the two segments on an $i-$ factor versus $\delta$ chart. Although a value of ${f}_{2}=2$ could be a suitable choice, the ${f}_{2}=1$ value, as proposed by Hansen [26, 47, 56] and ${\text{Vesic}}$ [46], is certainly not. The coefficient ${f}_{1}$ in Eq. 4 controls the boundary $\delta$ value between the descending and ascending branches in an $i-$ factor versus $\delta$ chart (as shown in Fig. 10c). For $\delta >45^\circ$ the failure mode is purely translational, which in a graph could be represented by setting ${f}_{3}={f}_{4}=0$. For $\delta =0^\circ$ the movement of the footing is purely vertical. For intermediate $\delta$ values, the movement is a combination of vertical and horizonal movement.

Fig. 10

a ${{\text{i}}}_{\upgamma }$ versus $\updelta$ chart using ${{\text{i}}}_{\upgamma }={\left(1-{\tan\delta }\right)}^{3}$ for $0^\circ \le\updelta \le 45^\circ$ and a hypothetical function ${{\text{i}}}_{\upgamma }=\upkappa {\left(\left(\updelta -{90}^{*}\right)\uppi /{180}^{*}\right)}^{-2}+\uplambda$ for $45^\circ \le\updelta \le 90^\circ$ ($\upkappa$ and $\uplambda$ are natural numbers), b ${\text{i}}-$ factor versus $\updelta$ chart assuming various functions for the $0^\circ \le\updelta \le 45^\circ$ part of the chart and that the minimum value for the ${\text{i}}-$ factor is at $\updelta =45^\circ$, c Example chart showing the effect of the ${{\text{f}}}_{1}$ coefficient in Eq. 4, d Muhs and Weiss’ [57] ${\left(1-{\tan\delta }\right)}^{2}$ (Eq. 26) rewritten in the ${\left(1-{{\text{f}}}_{1}\cdot {\tan\delta }\right)}^{3}$ form

In this regard, Eq. 26 from Muhs and Weiss’ [57], as illustrated in Fig. 10d, can be rewritten in the form of ${\left(1-{f}_{1}\cdot {\tan }\delta \right)}^{3}$. Thus, it becomes:

$${i}_{\gamma } = {\left(1-0.75{\tan }\delta \right)}^{3}$$

(27)

The value of ${f}_{1}$ is known for two $B/L$ values, specifically $B/L=0$ and 1/3. To establish a relationship between ${f}_{1}$ and $B/L$,it is necessary to obtain at least one more value for ${f}_{1}$, preferably within the range of $1/3<B/L\le 1$. Since, to the best of the authors’ knowledge, there are no large-scale experimental results available beyond those mentioned, the small-scale experimental results of Sethy et al. [63] for circular footings in the range of $0^\circ \le \delta \le 20^\circ$ will be utilized. These results are presented in Fig. 11a, along with a best-fit equation for $e/B=$ 0 (${f}_{1}=0.397$ and ${f}_{2}=3$), which perfectly describes the set of data in question. Additionally, considering the 3D finite element results of Singh and Roy [42] and following a similar procedure, the authors derived an ${f}_{1}$ value of 0.087, also for circular footings. Taking the average of these two values, ${f}_{1}$ is calculated to be $0.262$. Assuming the third point (for $B/L=1$) is in close proximity of the 0.262 value, the $B/L -$ ${f}_{1}$ chart in Fig. 11b was drawn, revealing a linear relationship between $B/L$ and ${f}_{1}$. Consequently, the following simple expression for ${i}_{\gamma }$ is proposed:

Fig. 11

a ${{\text{i}}}_{\upgamma } -\updelta$ chart for the small-scale experimental results of Sethy et al. [63] for ${\text{e}}/{\text{B}}=0$ and ${\text{e}}/{\text{B}}>0$, as well as a best fit for ${\text{e}}/{\text{B}}=0$, b ${\text{B}}/\mathrm{L }-$ ${{\text{f}}}_{1}$ chart

$${i}_{\gamma ,B} = {{\alpha }_{\psi }\left[1-\left(1-0.75\frac{B}{L}\right){\tan }\delta \right]}^{3}$$

(28)

Further large-scale experimental results and/or 3D finite element analysis are required to validate this expression.

4.2 Horizontal Load Acting Along the Long Side of the Footing

The previous section discussed how various researchers and standards have focused on refining the ${i}_{\gamma }$ factor in the context of horizontal loading acting along the short side of the footing. Conversely, the scenario of horizontal loading acting along the long side of the footing has received comparatively less attention. The pioneering work in this area was done by the Institute of the German Research Society for Soil Mechanics (Deutsche Forschungsgemeinschaft für Bodenmechanik) through the DEGEBO tests (documented by Muhs and Weiss in 1969 [64]). A primary objective of the DEGEBO tests was to evaluate the accuracy of the DIN standards in addressing load inclination. These tests, which involved loading a 0.5 m × 2 m rectangular footing to failure, demonstrated that for a footing with $L/B=4$, the ${i}_{\gamma }$ factor is equivalent to $1-{\tan }\delta$.

Vesic's [46] interpolation function with the $m$ factor (refer to Table 2) was based on this outcome of the DEGEBO tests. The DIN standard replaced the initial $1-{\tan }\delta$ factor with ${\left(1-{\tan }\delta \right)}^{m+1}$ in 2006, while the EN standard did the same in the recent draft standard prEN1997-3:2023 [53]. AASHTO [52], API [50], EN1997-1:2004 [31] and GEO [32] adopted the form ${\left(1-{\tan }{\delta }_{c}\right)}^{m+1}$, as initially suggested by Vesic [46]. However, not only have these factors been based on a limited number of tests on a footing with a specific aspect ratio ($L/B=4$), but the DEGEBO tests were also conducted on a footing with a width as low as 0.5 m (the scale effect has already been discussed in Sect. 2). Thus, the validity of these experiments can be deemed questionable.

Clearly, the $1-{\tan }\delta$ expression for $L/B=$ 4 (and for any $L/B$ ratio) cannot be correct for the reasons explained in the previous section.

Regarding the $i-$ factors proposed by Meyerhof and Koumoto [38], these are based on the following interpolation function:

$${Q}_{LV}={{\cos}}\delta \left({Q}_{L,\delta =0}-\left({Q}_{L,\delta =0}-{Q}_{L,\delta ={\delta }_{c}}\right)\frac{{\sin\delta }}{{\text{sin}}{\delta }_{c}}\right)$$

(29)

where ${Q}_{L,\delta =0}$ is the bearing capacity of the footing for $\delta =0$ (e.g., ${Q}_{L,\delta =0}=(\uppi +2){c}_{u}{A}_{b}$ for total stress analysis), ${Q}_{L,\delta ={\delta }_{c}}$ is the ultimate sliding resistance of the footing, which occurs for ${\delta }_{c}=90^\circ$ for total stress analysis or effective stress analysis with ${D}_{f}>0$, and $\varphi$ for effective stress analysis with ${D}_{f}=0$. For sands with ${D}_{f}>0$, ${Q}_{L,\delta ={\delta }_{c}}$ also includes lateral sliding resistance and the passive resistance in front of the footing. The terms ${\text{sin}}\delta$ and ${\text{sin}}{\delta }_{c}$ are empirical functions ranging from 0 to 1, controlling the boundary cases. Additionally, ${A}_{b}$ equals $BL$.

For ${i}_{c}$, ${Q}_{L,\delta =0}$ is the same as given above, while ${Q}_{L,\delta ={\delta }_{c}}$=${Q}_{L,\delta =90}={c}_{a}{A}_{b}$.

The procedure for ${i}_{\gamma }$ and ${i}_{q}$ is analogous. In the case of rough surface footings on sand (${D}_{f}=0)$, Meyerhof and Koumoto state that sliding begins when $\delta =\varphi$, ${\delta }_{c}=\varphi$ and ${Q}_{L,\delta ={\varphi }}=0$. This yields:

$${i}_{\gamma }={{\cos}}\delta \left(1-\frac{{\text{sin}}\delta }{{\text{sin}}\varphi }\right)$$

(30)

For an embedded footing (${D}_{f}>0$), the situation is more complex. In every case, sliding is assumed to occur when ${\delta }_{c}=90^\circ$, regardless of the embedment depth and lateral resistance. This presents a “black or white” scenario (${\delta }_{c}=90^\circ$ or $\varphi$), although a “gray” area is a possibility. According to Meyerhof and Koumoto, for a $\varphi$ value greater than 30°, the complex ${i}_{\gamma q}$ factor (not provided herein) can be simplified to:

$${i}_{\gamma q}={{\cos}}\delta \left(1-{\text{sin}}\delta \right)$$

(31)

As shown, Meyerhof and Koumoto’s $i-$ factors also involve an impermissible combination of sliding resistance at the footing-soil interface, Rankine’s passive resistance in front of the footing and Mohr–Coulomb’s bearing capacity failure under the footing. The difference ${Q}_{L,\delta =0}-{Q}_{L,\delta ={\delta }_{c}}$ in Eq. 29 is indicative of a methodological error, where a horizontal force is subtracted from a vertical force. Additionally, the analysis presented in the previous section reveals that ${i}_{\gamma }$ is independent of $\varphi$. Interestingly, the expression ${i}_{\gamma }={{\cos}}\delta \left(1-{\text{sin}}\delta \right)$ (for ${D}_{f}>0$) can be seen as a best-fit expression for $1-{\tan }\delta$ for $\delta \le 30^\circ$, and vice versa. This was likely the starting point for Meyerhof and Koumoto approach.

Taking for granted that ${i}_{\gamma }$ is the same for both directions in square footings (${i}_{\gamma B}={i}_{\gamma L}$; ${f}_{1}\approx 0.25$) and that the horizontal component of the footing loading has no effect on the bearing capacity of an infinite strip if it acts parallel to the long side of the strip (${f}_{1}=0$) and assuming a linear relationship between $B/L$ and ${f}_{1}$ (as in the case of horizontal loading acting along $B$), the following expression could give the ${i}_{\gamma ,L}$ for the case of loading leaning towards the long side of the footing:

$${i}_{\gamma ,L}={\left(1-0.25\frac{B}{L}{\tan }\delta \right)}^{3}$$

(32)

In cases where the horizontal component acts in a direction forming an angle $\theta$ with the direction of $L{\prime}$, ${f}_{1}$ may be calculated as follows:

$${f}_{1}=\sqrt{{\left(0.25\frac{B}{L}\right)}^{2}{{{\cos}}}^{2}\theta +{\left(1-0.75\frac{B}{L}\right)}^{2}{{\text{sin}}}^{2}\theta }$$

(33)

The above was based on Vesic’s interpolation factor $m={m}_{L}{{{\cos}}}^{2}\theta +{m}_{B}{{\text{sin}}}^{2}\theta$, which has been adopted by numerous design standards. The use of the ${{\cos}}\theta$ and ${\text{sin}}\theta$ trigonometric functions is a rational choice, but if raised to the power of 2, the sum of the two terms needs to be under a square root. Ignoring the power of 2 and the square root (i.e., ${f}_{1} = 0.25(B/L){{\cos}}\theta +\left(1-0.75(B/L)\right){\text{sin}}\theta$), on the other hand, leads to different values of ${f}_{1}$ for $\theta$ other than 0 and 90 degrees, which is also not acceptable.

5 The ${{{i}}}_{{{c}}}$ and ${{{i}}}_{{{q}}}$ Inclination Factors

Similar to ${i}_{\gamma }$, various researchers and standards proposed different formulas for the ${i}_{c}$ and ${i}_{q}$ (refer to Table 2). Once again, a comparison of these factors reveals significant discrepancies in their values. Indicative ${i}_{c}$ and ${i}_{q}$ versus $\delta$ charts are provided in Fig. 12a and b for $\varphi =0$.

Fig. 12

a ${{\text{i}}}_{{\text{c}}}$ and b ${{\text{i}}}_{{\text{q}}}$ versus δ charts for φ = 0. The factors marked with * indicate that they have been used with ${\tan\delta }$ instead of the nonrealistic ${\tan }{\updelta }_{{{\text{c}}}_{{\text{u}}}}$, c ${{\text{i}}}_{{\text{c}}}$ versus φ and d ${{\text{i}}}_{{\text{q}}}$ versus φ charts for Schultze’s [25] factors, e ${{\text{i}}}_{{\text{c}}}$ versus δ chart for Van Baars [28] ${{\text{i}}}_{{\text{c}}}$ factor and f ${{\text{i}}}_{{\text{q}}}$ versus δ charts for Van Baars ${{\text{i}}}_{{\text{q}}}$ factor

Fig. 13

a ${{\text{i}}}_{{\text{c}}}$ (Van Baars) versus ${{\text{i}}}_{{\text{c}}}$ (this study) and b the same but for ${{\text{i}}}_{{\text{q}}}$

Analytical expressions for the ${i}_{c}$ factor have been proposed by Green [29] ($\varphi =0$), Schultze [25] and Van Baars [28], while for the ${i}_{q}$ factor by Schultze [25] and Van Baars [28]. Other ${i}_{c}$ and ${i}_{q}$ factors listed in Table 2 are either best fit expressions (e.g., Hansen’s [27] expression, which is essentially a best fit to Green’s [29] expression) or intuitive formulas. To the best knowledge of the authors, there are no experimental results, let alone large-scale ones, available in the literature for these two factors. The same applies to finite element results. Thus, none of the existing ${i}_{c}$ and ${i}_{q}$ factors, whether empirical or analytical, can be verified with existing data. However, some useful observations can be made.

First, as shown in Fig. 12c, Schultze’s [25] ${i}_{c}$ factor equals unity for $\delta =0$ (for any $\varphi$ value) and exceeds unity up to a $\varphi$ value dependent on $\delta$, eventually approaching $+\infty$. On the opposite side of this $\varphi$ value, ${i}_{c}$ is equal to $-\infty$. It reaches a maximum as $\varphi$ increases, and then gradually decreases. Depending on $\delta$, the ${i}_{c}$ factor could be negative for $\varphi$ values. Apparently, the fact that the ${i}_{c}$ factor approaches infinity at the boundary between two consecutive ranges of $\varphi$ values is irrational, while negative ${i}_{c}$ values implying negative bearing capacity are impossible. Similarly, the ${i}_{q}$ factor, as shown in Fig. 12d, equals unity for $\varphi =\delta =0$, but it is zero for $\delta =0$ and $\varphi \to 0$. In this respect, the correct value for both ${i}_{c}$ and ${i}_{q}$ factors for $\delta =0$ and any $\varphi$ value should be unity. However, all ${i}_{q}-\varphi$ curves in Fig. 12d start from zero instead of unity. In the same context, a gradual decrease in the ${i}_{c}$ and ${i}_{q}$ factors is rather expected as $\delta$ increases. Instead, as shown in Fig. 12c and d, in the initial range of $\varphi$ values, the change in the ${i}_{c}$ and ${i}_{q}$ values is abrupt and unrealistic. These peculiar behaviors question the validity of Schultze's factors.

On the other hand, Van Baars’s [28] ${i}_{c}$ and ${i}_{q}$ factors exhibit a seemingly rational behavior, although their validation would benefit from large-scale experimental results and/or finite element analysis. By examining the general trends of the ${i}_{c}$ and ${i}_{q}$ factors in Fig. 12e and f, respectively, it is evident that both factors tend toward zero as $\delta$ approaches 90°. Furthermore, it is interesting that Van Baars’ expressions (see Table 2), which for convenience are given in Eqs. 34 and 35 can be rewritten in the form of Eq. 4.

$${i}_{c}={{{\cos}}}^{2}\delta \left({e}^{-2\cdot \delta \cdot {\tan }\varphi }-\frac{2\delta }{\pi +2}{e}^{-\pi \cdot {\tan }\varphi }\right)$$

(34)

$${i}_{q}={{{\cos}}}^{2}\delta \cdot {e}^{-2\cdot \delta \cdot {\tan }\varphi }$$

(35)

In this context, the authors provide the following approximations:

$${i}_{c}={(1-0.36{N}_{cA}{\tan }\delta )}^{2}$$

(36)

$${i}_{q}={(1-0.59{{N}_{qA}}^{{{\cos}}\delta }{\tan }\delta )}^{0.94}$$

(37)

with ${N}_{qA}={e}^{2\pi \cdot {\tan }\varphi }/{N}_{qR}=\left[\left(1-{\text{sin}}\varphi \right)/\left(1+{\text{sin}}\varphi \right)\right]{e}^{\pi \cdot {\tan }\varphi }$ and ${N}_{cA}=\left({N}_{qA}-1\right){\text{cot}}\varphi$. ${N}_{qR}$ is the well-known Reissner’s [54] factor. The results are presented in Fig. 13.

To validate the existing ${i}_{c}$ and ${i}_{q}$ factors, the authors conducted finite element analyses for ${c}_{u}=$ 100 kPa (and a friction angle, $\varphi$, of $0^\circ$)$,$ as well as for friction angles $\varphi =$ 20° and 30° with cohesions of both $c=$ 10 and 20 kPa. The lateral surcharge was either 0, 17, and 34 kN/m³. The unit weight and the dilation angle of the soil were $\gamma =$ 17 kN/m and $\psi =\varphi$, respectively. The footing was rigid, infinitely long, and two meters wide. The RS2 model from Rocscience used was the same as the one mentioned in Sect. 4.1.1 (Fig. 8). The analysis in question yielded the following ${i}_{c}$ and ${i}_{q}$ factors:

$${i}_{c}={\left(1-{\tan}\left(\frac{45^\circ +\varphi^\circ /2}{100^\circ }\cdot \delta \right)\right)}^{3}$$

(38)

$${i}_{q}={(1-{\tan }\left(2\delta/3 \right))}^{3}$$

(39)

These expressions clearly demonstrate that ${i}_{c}$ depends on both $\varphi$ and $\delta$, while ${i}_{q}$ depends only on $\delta$. Figure 14 illustrates the relationships of ${i}_{c}$ and ${i}_{q}$ against $\delta$. Figure 15a–c show the best-fit ${i}_{c}$ equation on the finite element results. The derived ${i}_{c}$ expressions were ${\left(1-{\tan}\left(0.45\cdot \delta \right)\right)}^{3}$, ${\left(1-{\tan}\left(0.55\cdot \delta \right)\right)}^{3}$ and ${\left(1-{\tan}\left(0.6\cdot \delta \right)\right)}^{3}$ for $\varphi =$ 0°, 20° and 30°, respectively. In Fig. 15d the three coefficients (i.e., the 0.45, 0.55 and 0.6) were plotted against $\varphi$, revealing the coefficient $0.005\varphi +0.45$, which can be rewritten as $\left(45^\circ +\varphi^\circ /2\right)/100^\circ$. Figure 15e,f show the best-fit ${i}_{q}$ equation on the finite element results.

Fig. 14

The proposed a ${i}_{c}$ and b ${i}_{q}$ factors derived from finite element analysis

Fig. 15

a–c show the best-fit ${i}_{c}$ equation on the finite element results. In figure d the three coefficients (i.e., the 0.45, 0.55 and 0.6) were plotted against $\varphi$. e, f show the best-fit ${i}_{q}$ equation on the finite element results

Comparing Fig. 14 with Fig. 12, it becomes evident that the existing ${i}_{c}$ and ${i}_{q}$ factors do not effectively account for the impact of loading inclination on the bearing capacity of footings.

It is also important to be mentioned that Vesic’s function ${m}_{n}={m}_{L}{{{\cos}}}^{2}\theta +{m}_{B}{{\text{sin}}}^{2}\theta$ was based on the interpretation of the DEGEBO tests, which were conducted on sands. The extension of this interpolation function by Vesic himself (and its adoption by others, as shown in Table 2) to the ${i}_{c}$ and ${i}_{q}$ inclination factors is arbitrary, given that an exact analytical solution to the problem is not feasible, and to the authors’ best knowledge, relevant experimental works and 3D numerical examples do not exist. However, it is rational to consider that the aspect ratio of footings would also influence the values of the ${i}_{c}$ and ${i}_{q}$ factors, as potentially indicated by Eqs. 40 and 41, although further investigation is required.

$${i}_{c}={\left(1-{f}_{1}\cdot {\tan}\left(\frac{45^\circ +\varphi^\circ /2}{100^\circ }\cdot \delta \right)\right)}^{3}$$

(40)

$${i}_{q}={(1-{f}_{1}\cdot {\tan }\left(2/2\delta \right))}^{3}$$

(41)

${f}_{1}$ in the equations above could be given by Eq. 33 or a similar one.

6 Design Standards

Table 2 clearly shows that the various design standards rely on Hansen’s [27], Meyerhof’s [48] or Vesic’s [46] load inclination factors. However, these empirical factors are far from being considered reliable for the reasons explained previously. In 2006, DIN4017:2006-03 [51] moved away from the outdated perception of ${i}_{q}$ and ${i}_{\gamma }$ inclination factors depending on the sliding resistance of footing, replacing ${\tan }{\delta }_{c}$ with ${\tan }\delta$. Indeed, the authors found that the ${i}_{\gamma }={\left(1-{\tan }\delta \right)}^{3}$ expression for horizontal loading acting parallel to the small side of the footing perfectly describes the effect of inclined loading (for positive $\delta$ angles). This expression is used by both DIN4017:2006-03 [51] and prEN1997-3:2023 [53] standards. The same cannot be said for the more general ${i}_{\gamma }={\left(1-{\tan }\delta \right)}^{{\text{m}}+1}$ expression for horizontal loading acting at any direction, which is used by these two contemporary standards. This expression dates back to 1975 when Vesic [46] encountered this form based on inadequate and questionable experimental results. The same stand for the ${i}_{q}={\left(1-{\tan }\delta \right)}^{{\text{m}}}$ factor of DIN4017:2006-03 [51] and prEN1997-3:2023 [53] standards. This factor is based on Vesic’s [12] ${i}_{q}={\left(1-{\tan }{\delta }_{c}\right)}^{{\text{m}}}$ intuitive formula, simply replacing ${\tan }{\delta }_{c}$ with ${\tan }\delta$. According to the best knowledge of the authors, there are no experimental or numerical results to support this formula. In addition, in Fig. 16 both the proposed formula for the ${i}_{\gamma }$ factor (Eq. 4 with ${f}_{1}$ of Eq. 33 and ${f}_{2}$=3) and the expression of prEN1997-3:2023 have been drawn in the range of $0\le B/L\le 1$ for $\updelta =10^\circ$, $15^\circ$ and $20^\circ$. The two red points on Fig. 16a indicate the empirical ${i}_{\gamma } = {\left(1-{\tan }\delta \right)}^{2}$ factor. From these charts it is inferred that the intuitive prEN1997-3:2023 ${i}_{\gamma }$ factor is rather insensitive in the aspect ratio of footings. The experience gained from large- and small-scale tests, however, shows the opposite.

Fig. 16

Comparison of the proposed ${i}_{\gamma }$ factor against the expression of prEN1997-3:2023, a $\delta =10^\circ$ and $20^\circ$ for loading acting along $B$ and b $\delta =15^\circ$ for loading acting along $B$ and $L$ (indicated by the notation “B” and “L” respectively)

For the ${i}_{c}$ factor, the various design standards (including the more recent ones) rely on Hansen’s [27] expressions for $\varphi =0$ and $\varphi >0$ from 1961. The ${i}_{c}=0.5+0.5\sqrt{1-{{\tan }\delta }_{{c}_{u}}}$ expression for $\varphi =0$ utilizes the concept of sliding resistance at the footing-soil interface, which as explained previously is erroneous [28]. The ${i}_{c}={i}_{q}-\left(1-{i}_{q}\right)/\left({N}_{q}-1\right)$ expression for $\varphi >0$ has been based on the rule of corresponding states, which is not applicable to the bearing capacity problem [33].

Concluding, the only inclination factor that can be considered reliable is the ${i}_{\gamma }={\left(1-{\tan }\delta \right)}^{3}$. The latter, however, is applicable only to cases where the horizontal loading acts parallel to the smaller side of the footing.

7 Conclusions

This paper provides a comprehensive review of the effects of load inclination and eccentricity on the bearing capacity of shallow foundations. These effects were examined concurrently due to their relation to the loading vector acting on the footing, specifically the inclination and offset from the center, respectively.

Regarding the load eccentricity, expressed by the loading eccentricity factor ${e}_{\gamma }=B^{\prime}/B$, Meyerhof’s intuitive formula ${e}_{\gamma }=1-2{e}_{b}/B$ aligns closely with finite element analyses, albeit being slightly conservative. Analysis of finite element results by the authors introduced a simpler, yet more precise, expression ${e}_{\gamma }=1-1.9{e}_{b}/B$. For the experimentally derived ${e}_{\gamma }$ factors, it was found that they were based on small-scale laboratory tests. Given the well- documented impact of model scale on the bearing capacity of footings, these are considered unreliable.

Regarding loading inclination factors, an initial observation is the presence of a wide variety of factors for each term in the bearing capacity equation. Most are either intuitive formulas or formulas based on small-scale experimental results. From numerical analysis, it was found that for cases of horizontal loading acting along the short side of the footing, all inclination factors (namely, ${i}_{c}$, ${i}_{\gamma }$ and ${i}_{q}$) can be represented by ${\left(1-{f}_{1}\cdot {\tan }\left({f}_{3}\delta \right)\right)}^{3}$. This formulation also ensures smooth transition from the bearing capacity failure to the sliding failure as $\delta$ increases. ${f}_{1}$ is a function of footing’s aspect ratio and the direction of the horizontal loading, while ${f}_{3}$ equals 1 for ${i}_{\gamma }$ and 2/3 for ${i}_{q}$. Only ${f}_{3}$ for ${i}_{c}$ was found to be a function of soil’s friction angle.

An important observation is that Hansen replaced the loading inclination, represented by ${\tan }\delta =H/V$, with an impermissible combination of sliding resistance at the footing-soil interface and Mohr–Coulomb bearing capacity failure under the footing, i.e., $H/{B}^{{{\prime}}}{L}^{{{\prime}}}{c}_{u}$ and $H/(V+{B}^{{{\prime}}}{L}^{{{\prime}}}c{\text{ cot}}\varphi )$ for total and effective stress analysis, respectively. This is evidently incorrect, and, unfortunately, has influenced a significant number of researchers as well as design standards.

Another inclination factor proposed by Hansen [27] and later adopted by many others (including design standards), is the ${i}_{c}$ expression in relation to ${i}_{q}$ and ${N}_{q}$ (${i}_{c}={i}_{q}-(1-{i}_{q})/({N}_{q}-1)$). However, this factor, derived from the principle of corresponding states, is incorrect. Utilizing this principle to adapt a solution for s soil with friction to a soil incorporating both cohesion and friction results in a solution that addresses a scenario with boundary conditions differing from those of the original problem.

Regarding Vesic’s well-known “$m$”- interpolation formula from 1975 it is mentioned that it largely falls short in accurately representing the effect of the direction of the horizontal loading.

Finally, among the numerous expressions for the three inclination factors found in the literature, the only expression that has been proven correct is the ${i}_{\gamma }={\left(1-{\tan }\delta \right)}^{3}$, which is applicable solely in the case of horizontal loading acting parallel to the short side of strip footings.