Bearing capacity of shallow foundations: a focus on the depth factors in combination with the respective N-factors

Abstract

The ongoing refinement of bearing capacity equations remains pivotal in soil mechanics and foundation engineering, reflecting its critical role in ensuring design efficacy and construction safety. This study conducts a thorough evaluation of classical bearing capacity methods—Terzaghi, Meyerhof, Vesic, and Hansen—and methods included in various design standards, such as EN1997:2004, prEN1997:2023, GEO, AASHTO, FHWA, and API. It explores the performance and applicability of these approaches, identifying areas for potential improvement. In response to identified challenges, the paper proposes the integration of a unified depth factor. This new factor is designed to be applicable across all N-terms, providing a more versatile and accurate tool for bearing capacity predictions. Unlike the original depth factors unique to each method, which may not fully address complex soil and footing conditions, the unified depth factor is developed to enhance prediction accuracy for a wide range of conditions, including both flexible and rigid footings under varying flow rules (ψ = 0 and ψ = φ). This depth factor corrects for modeling errors, emphasizing the importance of pairing the correct set of N-factors with their corresponding depth factor. By offering a singular depth factor that aligns with the outcomes of finite element analysis, this paper not only simplifies the computational process but also enhances the accuracy of bearing capacity predictions across a diverse range of soil conditions and footing types. The comparative analysis, based on finite element analysis, validates the proposed method’s effectiveness, showcasing its potential to significantly refine foundation design practices by comparing it with both traditional and newly developed depth factors.

Introduction

The bearing capacity of shallow foundations is one of the major fields of soil mechanics and foundation engineering. Probably the earliest attempt for giving an answer to this problem has been made by Rankine (1857). His simplistic approach with its crude assumptions, however, is far from being considered a method, let alone a reliable one. Besides, his formula ${q}_{u}=\gamma {D}_{f}{K}_{P}^{2}$ gives zero bearing capacity, ${q}_{u}$, for surface footings, a scenario that is implausible.

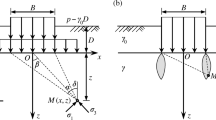
Prandtl (1920) gave an analytical solution for the bearing capacity of a strip punch over a weightless, rigid-perfectly plastic half-space. The strength of the half-space is described by the angle of internal friction, $\varphi$, and the cohesion, $c$. In this solution, Prandtl, introduced the failure mechanism consisting of a triangular active wedge ABC with wedge angle equal to ${45^\circ }+\varphi /2$ (zone I), a log-spiral radial shear zone BCD (zone II), and a triangular passive wedge BDE (zone III), as shown in Fig. 1. Four years later, Prandtl’s solution was extended by Reissner (1924) to account for uniform distributed pressure at the surface of the half space; Reissner’s material was purely frictional.

Fig. 1

The bearing capacity failure mechanism with its three zones (zones I, II, III)

Terzaghi (1943) extended the works of Prandtl and Reissner for considering the self-weight of the triangular wedge (zone I). Also, it was Terzaghi who first expressed the bearing capacity with three separate terms, i.e., for the cohesion, lateral surcharge, and weight of the soil (Van Baars 2018), as shown in Eq. 1.

$${q}_{u}=c{N}_{c}+\frac{1}{2}\gamma B{N}_{\gamma }+\gamma {D}_{f}{N}_{q}$$

(1)

$c$ and $\gamma$ in Eq. 1 are the cohesion and unit weight of soil, $B$ is the width of the strip footing and ${N}_{c}$, ${N}_{\gamma }$, and ${N}_{q}$ are the three $N$-factors for the cohesion, the weight of the triangular soil wedge, and the lateral surcharge term respectively. Terzaghi’s $N$-factors are the following:

$${N}_{qT}=\frac{{e}^{\left(\frac{3}{2}\pi -\varphi \right){\text{tan}}\varphi }}{{2{\text{cos}}}^{2}\left({45}^{o}+\varphi /2\right)}$$

(2)

$$N_{\gamma T}=\left\{\begin{array}{l}\frac{\tan\varphi}2\left(\frac{K_{P\gamma}}{\cos^2\varphi}-1\right):\;\mathrm{Original}\;\mathrm{equation}\\1.74N_{qT}^{0.0707}\tan\left(1.72\varphi\right):\;\mathrm{Best}\;\mathrm{fit}\;\mathrm{to}\;\mathrm{Terzaghi}'\mathrm s\;\mathrm{values}\end{array}\right.$$

(3)

$${N}_{cT}=\left({N}_{qT}-1\right){\text{cot}}\varphi$$

(4)

Terzaghi (1943) did not provide a direct formula for ${K}_{P\gamma }$, but he gave ${N}_{\gamma }$ values in chart form with respect to $\varphi$. A best-fit equation, which aligns perfectly within the range $0^\circ \le \varphi \le 45^\circ$, derived from regression analysis conducted by the author; this is also presented in Eq. 3.

Since Terzaghi’s significant contribution to the problem, a huge number of bearing capacity methods has been proposed in literature, mainly focusing on refining the ${N}_{\gamma }$ factor. In this respect, Taghvamanesh and Moayed (2021) reported 60 different ${N}_{\gamma }$ factors proposed in the literature, covering the time span 1943–2021. But despite this plethora of methods, the earliest ones—namely Terzaghi’s, Meyerhof’s, Hansen’s, and Vesic’s methods—remain the most popular. Indeed, Terzaghi’s solution for general shear failure constituted the basis for the majority, if not all, the available methods, while Vesic’s $N$-factors are generally preferred by the design codes worldwide (e.g. IS6403 1981; API 2000; Kimmerling 2002; EN1997-1 2004; Geotechnical Engineering Office 2006; AASHTO 2020; prEN1997-3:2023 2023).

Meyerhof adopted Prandtl’s (1920) ${N}_{c}$ factor and Reissner’s (1924) ${N}_{q}$ factor, while he suggested his own (Meyerhof 1963) ${N}_{\gamma }$ factor. These are given below:

$${N}_{qR}={{K}_{P}e}^{\pi {\text{tan}}\varphi }$$

(5)

$${N}_{\gamma M}=\left({N}_{qR}-1\right){\text{tan}}\left(1.4\varphi \right)$$

(6)

$${N}_{cP}=\left({{K}_{P}e}^{\pi {\text{tan}}\varphi }-1\right){\text{cot}}\varphi =\left({N}_{qR}-1\right){\text{cot}}\varphi$$

(7)

${K}_{P}=\left(1+{\text{sin}}\varphi \right)/\left(1-{\text{sin}}\varphi \right)$ is Rankine’s (1857) passive earth pressure coefficient. It is mentioned that, according to Meyerhof himself (Meyerhof 1963), the ${N}_{\gamma }$ of Eq. 6 is an empirical, best-fit formula “in good agreement with the theoretical factors derived by Caquot and Kerisel (1966), Lundgren-Odegaard (1953–1961) and Meyerhof (1955)”.

Prandtl’s (1920) ${N}_{c}$ factor and Reissner’s (1924) ${N}_{q}$ factor have also been adopted by Hansen (1970) and Vesic (1973). Hansen’s ${N}_{\gamma }$ factor, which was based on calculations of Lundgren-Mortensen (1953) and Odgaard and Christensen, is given in Eq. 8. Vesic’s (1973; 1975) ${N}_{\gamma }$ factor, which was based on table values given by Caquot and Kerisel (1953), is given in Eq. 9.

$${N}_{\gamma H}=1.5\left({N}_{qR}-1\right){\text{tan}}\left(\varphi \right)$$

(8)

$${N}_{\gamma V}=2\left({N}_{qR}+1\right){\text{tan}}\left(\varphi \right)$$

(9)

Vesic’s (1973) ${N}_{\gamma }$ factor (Eq. 9), which is not an original work but a best fit to the values provided by Caquot and Kerisel (1953) in tabular form, has been checked by the author against the original data (denoted in Table 1 by the symbol ${N}_{\gamma CK}$). In this respect, the author provides an equation (see Eq. 10) that fits better to the same dataset. Equation 10 has also been put in the same comparison (see Table 1).

Table 1 Comparison of the original ${N}_{\gamma }$ values reported by Caquot and Kerisel (1953) against the respective values calculated using Vesic’s (1973) and author’s best-fit formulae (indicated by the symbols ${N}_{\gamma CK}$, ${N}_{\gamma V}$, and ${N}_{\gamma CK,LP}$ respectively). RD stands for “relative difference”

$${N}_{\gamma CK,LP}=\frac{{N}_{qR}}{2.8\mathrm{ sin}\left(\frac{\pi }{4}-\frac{\varphi }{2}\right){\text{tan}}\left(\frac{\pi }{4}-\frac{\varphi }{2}\right)}$$

(10)

Thus, only Terzaghi’s ${N}_{\gamma }$ is the product of original research work. Meyerhof’s, Hansen’s, and Vesic’s ${N}_{\gamma }$ factors are just best-fit expressions on data published by other researchers.

Considering the effect of embedment depth, the bearing capacity formula takes the following form:

$${q}_{u}=c{N}_{c}{d}_{c}+\frac{1}{2}\gamma B{N}_{\gamma }{d}_{\gamma }+\gamma {D}_{f}{N}_{q}{d}_{q}$$

(11)

${d}_{c}$, ${d}_{\gamma }$, and ${d}_{q}$ are the depth factors for the cohesion, the weight of the triangular soil wedge, and the lateral surcharge term respectively.

It is interesting that despite of the tens of $N$-factors suggested in the literature (see Taghvamanesh and Moayed 2021), the depth factors received only minor attention. The depth factors given by Meyerhof, Hansen, and Vesic, as well as those included in the various design codes mentioned earlier, are summarized in Table 2. It is noted that Terzaghi did not suggest any such factor, while Skempton (1984, reprinted), Salgado et al. (2004), Nguyen and Merifield (2012), and Edwards et al. (2005) suggested depth factor only for the cohesion term (i.e., ${d}_{c}$ factor). Edwards et al. did not provide a close formula for ${d}_{c}$ but values in chart form. Lyamin et al. (2007) suggested a bearing capacity formula for sands containing only the the term for the weight of the triangular soil wedge; the effect of the lateral surcharge is taken into account through the ${d}_{\gamma }^{*}$ factor. Benmebarek et al. (2017) suggested depth factors for undrained bearing capacity of circular footings with or without side resistance. Circular footings are out of the scope of the present paper; however, in a bearing capacity analysis, a circular footing could be dealt with the respective square footing.

Table 2 Depth factors incorporated in various methods and design codes for strip footings

In this paper, the initial step involves comparing classical bearing capacity methods of Terzaghi, Meyerhof, Hansen, and Vesic, along with methods included in various design codes such as EN1997-1:2004, prEN1997-3:2023, API, AASHTO, FHWA, IS6403:1981, and GEO (IS6403 1981; API 2000; Kimmerling 2002; EN1997-1 2004; Geotechnical Engineering Office 2006; AASHTO 2020; prEN1997-3:2023 2023) against finite elements using several example cases. Besides, design codes are supposed to represent the best contemporary practices. The paper will subsequently demonstrate that a depth factor in the form of $\kappa \left(1+\lambda \bullet {D}_{f}/B\right)$ or $\kappa \left(1+\lambda \bullet {\left({D}_{f}/B\right)}^{\mu }\right)$, common to all three bearing capacity terms, leads to improved predictions of bearing capacity. Such factors will be proposed both for rigid and flexible footings, and for soils adhering to the associated and non-associated flow rules, with $\psi =\varphi$ and 0, respectively. These proposed depth factors will apply to the classical methods of Terzaghi, Meyerhof, Hansen, and Vesic, with distinct factors tailored to each method. This differentiation is crucial as the depth factors also aim to mitigate errors arising from the derivation of the $N$-factors.

In this paper, the friction angle and cohesion are designated by the generalized symbols $c$ and $\varphi$. The actual application determines whether these refer to the shear strength parameters in the drained or the undrained conditions, $\left\{c\mathrm{^{\prime}}, \varphi \mathrm{^{\prime}}\right\}$ and $\left\{{c}_{u}, {\varphi }_{u}\right\}$, respectively; apparently, in the plane strain problem studied herein, $c$ and $\varphi$ are plane strain values.

${K}_{P}=\left(1+{\text{sin}}\varphi \right)/\left(1-{\text{sin}}\varphi \right)$ is Rankine’s (1857) passive earth pressure coefficient. The factors marked with the symbol † have been derived from the method of characteristics. The $n/a$(not applicable) notation means that there is no provision for the specific factor. If the domain of $\varphi$ is not mentioned, the factor stands for any $\varphi$ value. Lyamin et al.’s (2007) ${d}_{\gamma }^{*}$ factor includes also the influence of lateral surcharge on the bearing capacity of footings; ${d}_{\gamma }$ was calculated from: ${q}_{u}={~}^{1}\!\left/ \!{~}_{2}\right.\gamma B{N}_{\gamma }{d}_{\gamma }+\gamma {D}_{f}{N}_{q}{d}_{q}={~}^{1}\!\left/ \!{~}_{2}\right.\gamma B{N}_{\gamma }{d}_{\gamma }^{*}$

Evaluating existing bearing capacity methods

In this section, the well-established methods of Terzaghi, Meyerhof, Hansen, and Vesic and the methods incorporated in EN1997-1:2004, prEN1997-3:2023, API, AASHTO, FHWA, IS6403:1981, and GEO design codes are compared against finite elements. To assess the $N$- and depth factors of these methods, 56 example cases were considered, 28 for effective stress analysis and 28 for total stress analysis. The corresponding data values can be found in Table 3.

Table 3 Data for the example cases: (a) effective stress analysis, (b) total stress analysis (${\varphi }_{u}$=0)

Rocscience’s RS2 (v11.0.12) was used for obtaining the numerical results for the comparison; RS2 is a commercial program for 2D finite element analysis of geotechnical structures. All examples were solved twice, first considering the footings as perfectly rigid and later as perfectly flexible. This raised the number of different cases considered to 56 $\times$ 2 $=$ 112.

The methods, however, being evaluated adhere to the less conservative associated flow rule ($\psi =\varphi$). Yet, an analysis considering the non-associated flow rule ($\psi <\varphi$) is more representative of the actual soil behavior (Bolton 1986; Loukidis et al. 2008; Mortensen and Krogsbøll 2019). Indeed, fine-grained soils have practically zero dilation angle ($\psi \approx 0$), while loose sands may even exhibit negative values. In such scenarios, the assumption $\psi = 0$ is commonly adopted. As a result, all effective stress analysis examples have been analyzed both for $\psi = 0$ and $\psi =\varphi$, increasing the total number of different cases considered to 168. Given that dilation occurs mainly in dense sands and gravels, the difference in the bearing capacity is expected to be greater for the case of soils with greater friction angles. In this context, Bolton (1986) specified $\varphi ={\varphi }_{crit}+\psi$ as an elementary friction-dilatancy relation; $\psi$ is often taken in the literature equal to 30°, but this is rather a lower boundary on the safe side.

The geometry, typical mesh, and boundary conditions in this plane-strain problem considered are shown in Fig. 2. Favoring reproduction of the example problem, all relevant information is given below (if something is not mentioned, the RS2 default value was used). The “Gaussian elimination” solver type was used. Regarding the “stress analysis” menu, the maximum number of iterations was 1000, and the tolerance was set to 0.001, while the “comprehensive” convergence type was adopted (the “comprehensive” setting means that force, energy, and displacement are checked at the same time). The “mesh type” was set to “graded,” while six-noded triangular elements were used. In addition to the above, the “field stress type” was “gravity” with “stress ratio” in- and out-of-plane defined by Jaky’s (1948) ${K}_{o}=1-{\text{sin}}\varphi$. The “initial element loading” was “field stress and body force.” The problem was solved for static conditions. The shear strength parameters are those given in Table 3 (apparently, the “plastic” material type was chosen). The unit weight, modulus of elasticity, and Poisson ratio of soil were $\gamma =$ 17 kN/m³, $E=$ 20,000 kPa, and $\nu =$ 0.3 respectively.

Fig. 2

Rocscience’s RS2 model showing geometry, loading, mesh, and boundary conditions of the problem

For the elastic constants $E$ and $\nu$, it is widely recognized that they do not influence the bearing capacity of footings. Similarly, the unit weight of soils $\gamma$ does not affect the $N$-bearing capacity factors or the depth factors. Therefore, to simplify, these parameters were kept constant across all examples. It should be noted that some combinations of $c{\prime}-\varphi {\prime}$ in Table 3 may not correspond to real soil cases. However, the effective stress analysis examples in Table 3 are organized into several groups (i.e., nos. 1–7, 8–13, 14–18, 19–20, 21–23, 24–25, and 25–26). Within each group, all parameters remain constant except for one of the shear strength values. The consistency in the results (bearing capacity values) attests to the validity of the finite element models. The total stress analysis examples were also grouped for the same reason.

Some additional important information about the geometry of the finite element models is provided below. The nodes on both sides of the excavation (at the bottom of which the footing is placed) are allowed to move vertically but are restricted horizontally. This setup simulates footings with smooth sides (assumption on the side of safety). However, the outermost nodes of the footings are permitted to move in any direction. The extent of the boundaries was also carefully evaluated. Boundaries that are too close to the footing may result in a significant portion of the stresses returning back to their source (i.e., the footing), whereas the computational cost of modeling large domains is considerable, especially with the appropriate mesh density. The geometry and mesh depicted in Fig. 2 strike a balance between accuracy and computational expense. The mesh is generally uniform, with increased densification in areas where the bearing capacity mechanism is expected to be developed. The discretization density on the foundation surface and near the footings’ boundaries was further increased. A convergence chart for example no. 9 (featuring a rigid footing on a low plasticity clay with $\psi =\varphi$) is presented in Fig. 3. As indicated, the failure load of 1614 kPa (asymptotic value) closely matches the 1602 kPa determined using the finite element model in Fig. 2. The best-fit curve and the asymptotic value in Fig. 3 were found using the exponential decay model $y=a\bullet {e}^{-bx}+c$ and regression analysis ($a=393.6, b=0.199, c=1614)$. It should be noted that the convergence chart in Fig. 3 refers to meshes of uniform density with lateral boundaries extended to twice the width shown in Fig. 2 (e.g., the coordinates of the lower-right corner were [30, − 20]). It is also important to be mentioned that the load in each model was applied in 101 loading steps. The applied load was about 10% greater than the failure load (a preliminary analysis was conducted in each case to determine the appropriate load). This introduces a minor error in the failure load calculation, but less than 1%.

Fig. 3

Convergence chart

For the case of rigid footings, an elastic “liner” element was inserted between the (uniform) loading and the soil. The liner had modulus as high as 300 GPa and thickness 10 m (extreme values for ensuring rigidity), while its Poisson’s ratio and unit weight were 0.2 and 0 (weightless footing) respectively. The “Timoshenko” beam element formulation was adopted. No interface element (“joint” element in RS2) was considered; thus, the footings were rough. Not only does the case of rough footings allow for the direct comparison with Terzaghi’s, Meyerhof’s, Hansen’s, and Vesic’s methods, but also this is more realistic. The author adopts Vesic’s (1973) point of view that the stress and deformation patterns under compressed areas are such that they always lead to the formation of single wedges and that the foundation roughness has little effect on the bearing capacity as long as the applied external loads remain vertical (as in the case considered herein).

All finite element results can be found in Table 4. While results from other methods are not presented in tabular form to conserve space, readers can easily reproduce them. However, these results are depicted in the comparison charts shown in Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12. Four charts are given for each method, more specifically for (a) $\psi =0$ and rigid footings; (b) $\psi =\varphi$ and rigid footings; (c) $\psi =0$ and flexible footings; and (d) $\psi =\varphi$ and flexible footings, although it is supposed that they correspond to rigid footings over soils with $\psi =\varphi$. The total stress analysis examples have been merged with the respective effective stress analysis examples for $\psi =0$.

Table 4 Bearing capacity values for effective and total stress analyses for the cases listed in Table 3 derived from finite element analysis

Fig. 4

Actual versus predicted values for the Terzaghi method. a $\psi =0$; rigid footings. b $\psi =\varphi$; rigid footings. c $\psi =0$; flexible footings. d $\psi =\varphi$; flexible footings

Fig. 5

Actual versus predicted values for the Meyerhof method. a $\psi =0$; rigid footings. b $\psi =\varphi$; rigid footings. c $\psi =0$; flexible footings. d $\psi =\varphi$; flexible footings

Fig. 6

Actual versus predicted values for the Hansen method. a $\psi =0$; rigid footings. b $\psi =\varphi$; rigid footings. c $\psi =0$; flexible footings. d $\psi =\varphi$; flexible footings

Fig. 7

Actual versus predicted values for the Vesic method. a $\psi =0$; rigid footings. b $\psi =\varphi$; rigid footings. c $\psi =0$; flexible footings. d $\psi =\varphi$; flexible footings

Fig. 8

Actual versus predicted values for the EN1997:2004 and GEO methods. a $\psi =0$; rigid footings. b $\psi =\varphi$; rigid footings. c $\psi =0$; flexible footings. d $\psi =\varphi$; flexible footings

Fig. 9

Actual versus predicted values for the API method. a $\psi =0$; rigid footings. b $\psi =\varphi$; rigid footings. c $\psi =0$; flexible footings. d $\psi =\varphi$; flexible footings

Fig. 10

Actual versus predicted values for the EN1997:2023 method. a $\psi =0$; rigid footings. b $\psi =\varphi$; rigid footings. c $\psi =0$; flexible footings. d $\psi =\varphi$; flexible footings

Fig. 11

Actual versus predicted values for the AASHTO and FHWA methods. a $\psi =0$; rigid footings. b $\psi =\varphi$; rigid footings. c $\psi =0$; flexible footings. d $\psi =\varphi$; flexible footings

Fig. 12

Actual versus predicted values for the IS6403 method. a $\psi =0$; rigid footings. b $\psi =\varphi$; rigid footings. c $\psi =0$; flexible footings. d $\psi =\varphi$; flexible footings

To compare different methods, the percent error ($PE=\frac{\left|{\text{measured}}-{\text{real}}\right|}{{\text{real}}}\times 100\mathrm{\%}$) was first calculated for each example. Then, the following indices were used: (a) the mean absolute percentage error ($MAPE=\frac{1}{n}\sum_{i}^{n}{PE}_{i}$) and (b) the standard deviation of $PE$. Additionally, a linear regression line was plotted on each chart with the origin set as the intercept point, noting both the coefficient of the best-fit equation and the coefficient of determination (${R}^{2}$). The four indices are summarized in Figs. 13 and 14, focusing exclusively on methods labeled as “original,” which are applied according to their published specifications, including any depth factors (note that Terzaghi’s method does not include such factors). The optimal values for $MAPE$ and standard deviation $(SD)$ are 0, and for the coefficient of the best-fit equation, it is 1. A coefficient of the best-fit equation below 1 suggests the model tends to yield results on the unsafe side, and vice versa. For the coefficient of determination, ${R}^{2}$, the ideal value is 1. However, even if there is a significant but symmetrical scatter around the regression line, ${R}^{2}$ can still be relatively high, indicating the model captures the overall trend of the data despite wide variations in individual data points. High ${R}^{2}$ values will be used to reject rather than accept a model. Figures 13 and 14 also include histograms for Terzaghi’s, Meyerhof’s, Hansen’s, and Vesic’s methods, as modified by the author, which will be explored in the following section. Putting all alternatives on the same chart facilitates comparison.

Fig. 13

a MAPE and b standard deviation of percent error values for the various methods

Fig. 14

a Coefficient of the best-fit equation and b ${R}^{2}$ values for the various methods

From Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, and 14, the following observations can be made:

• The Vesic original method exhibits a commendable balance of accuracy (MAPE), consistency (standard deviation of percent error), and predictive fit (slope and R²) across both rigid and flexible footings and under varying soil conditions of $\psi =0$ and $\psi =\varphi$. Its performance is notably superior under flexible footings with $\psi =\varphi$, where it shows enhanced accuracy, reduced variability, and strong predictive correlations.

• Surprisingly, Terzaghi’s method, which does not incorporate depth factors, offers a reliable and accurate framework for predicting foundation behavior across a range of conditions. While it exhibits solid performance in both rigid and flexible footings, its standout accuracy and consistency are more noticeable under rigid conditions. The method’s strong linear correlation and substantial explanatory power, as evidenced by the coefficient of best fit equation and R² values, further confirm its applicability in geotechnical engineering designs. When compared to Vesic’s original method, Terzaghi’s shows comparable accuracy and predictive power, especially under rigid footing conditions. However, Vesic’s original method tends to outperform Terzaghi’s under flexible footings for ψ = φ conditions, offering enhanced accuracy, lower variability, and stronger predictive correlations.

• Meyerhof’s original method shows variability in its accuracy, consistency, and predictive fit across different conditions. Compared to Terzaghi’s and Vesic’s original methods, Meyerhof’s method may not consistently offer the same level of precision or reliability, particularly under flexible footings.

• Hansen’s original method reveals significant limitations in its performance, especially concerning accuracy, consistency, and predictive fit. The elevated MAPE values, high variability in predictions, and deviations in the slopes of the regression line collectively underscore Hansen’s challenges in delivering reliable foundation design estimations. When compared with Vesic’s original method, Hansen’s deficiencies become more apparent.

• EN1997:2004, GEO, AASHTO, FHWA, and API show similar challenges with accuracy and consistency, as highlighted by their MAPE and standard deviation values. The slope deviations from the ideal value further question their predictive alignment across varying conditions. When comparing these with Vesic’s original method, Vesic generally offers better accuracy and consistency.

• The IS6403 method demonstrates variability in its performance, with high MAPE and standard deviation values. The predictive fit, measured by the slope and R² values, also suggests potential misalignment with actual foundation behaviors, particularly under rigid footing conditions.

• EN1997:2023 showcases a compelling superiority over all the above methods. It exhibits superior accuracy, lower variability, and stronger predictive correlations.

The proposed depth factors

In the analysis presented below, all three depth factors within the bearing capacity equation have been substituted with a singular depth factor (i.e., a depth factor that is uniform across all three bearing capacity terms). Both linear and non-linear forms of depth factors were explored. As a result, the bearing capacity equation is represented in one of the following forms:

$${q}_{u}=\kappa \left(1+\lambda \frac{{D}_{f}}{B}\right){q}_{u,0}$$

(12)

$${q}_{u}=\kappa \left(1+\lambda {\left(\frac{{D}_{f}}{B}\right)}^{\mu }\right){q}_{u,0}$$

(13)

In these formulas, ${q}_{u,0}$ represents the bearing capacity value derived from the method of Terzaghi, Meyerhof, Hansen, or Vesic, excluding the application of their original depth factors, if present. The coefficients $\kappa$,$\lambda$, and $\mu$ are obtained from regression analysis (in MS Office Excel) based on the finite element results presented in the preceding section. The results are presented in chart form in Figs. 15, 16, 17, and 18. The values of $\kappa$,$\lambda$, and $\mu$ are summarized in Tables 5 and 6. The MAPE, standard deviation of percent error, coefficient (slope) of the best-fit equation, and R² values can be found in Figs. 13 and 14. Based on these, the following observations can be made:

• The depth factor is influenced by the type of analysis (effective or total stress), the dilation angle of soil, and the rigidity of footing.

• The analysis clearly showed that a single depth factor can effectively replace the set of depth factors associated with the three $N$-terms in the basic bearing capacity equation.

• The proposed depth factor, which is able to effectively absorb the modeling errors related to the embedment depth and the assumed failure surface, was successfully applied to Terzaghi’s, Meyerhof’s, Hansen’s, and Vesic’s method. However, it could be used to any similar method.

• Not only does the proposed depth factor simplify the calculations with the use of a single depth factor, but it also improves the prediction of the bearing capacity of footings. This improvement is evident from the values of the statistical indices (MAPE and standard deviation of percent error closer to 0 and slope of the best-fit equation and R² closer to unity).

• The balance of vertical forces considered by Terzaghi (see “Introduction”) ignores the fact whether the footing is rigid or flexible. However, different contact pressures result in different bearing capacity values, as this is evident by the finite element analysis results. In the present paper, $\kappa$,$\lambda$, and $\mu$ coefficients (recall Eqs. 12 and 13) are given for both flexible and rigid footings.

• In addition, $\kappa$,$\lambda$, and $\mu$ coefficients are provided for both the case of $\psi =\phi$ (associated flow rule) and the more realistic, and simultaneously more conservative, non-associated flow rule where $\psi =0$. It is reminded that all methods examined herein refer to the $\psi =\phi$ case.

• The finite element analysis carried out also revealed the strong correlation between the bearing capacity of rigid footings and the respective one of flexible footings. This correlation is illustrated in Fig. 19. The corresponding equation is:

  $${q}_{u,{\text{Flexible}}}=0.95\bullet {q}_{u,{\text{Rigid}}}$$

  (14)

Fig. 15

Actual versus predicted values for the modified Terzaghi method using linear repression analysis: a $\psi =0$, rigid footings; b $\psi =\varphi$, rigid footings; c $\psi =0$, flexible footings; and d $\psi =\varphi$, flexible footings. Panels e to h correspond to the same conditions of ψ and footing rigidity but are derived from non-linear regression analysis. LRA, linear regression analysis; NLRA, non-linear regression analysis

Fig. 16

Actual versus predicted values for the modified Meyerhof method using linear repression analysis: a $\psi =0$, rigid footings; b $\psi =\varphi$, rigid footings; c $\psi =0$, flexible footings; and d $\psi =\varphi$, flexible footings. Panels e to h correspond to the same conditions of ψ and footing rigidity but are derived from non-linear regression analysis. LRA, linear regression analysis; NLRA, non-linear regression analysis

Fig. 17

Actual versus predicted values for the modified Hansen method using linear repression analysis: a $\psi =0$, rigid footings; b $\psi =\varphi$, rigid footings; c $\psi =0$, flexible footings; and d $\psi =\varphi$, flexible footings. Panels e to h correspond to the same conditions of ψ and footing rigidity but are derived from non-linear regression analysis. LRA, linear regression analysis; NLRA, non-linear regression analysis

Fig. 18

Actual versus predicted values for the modified Vesic method using linear repression analysis: a $\psi =0$, rigid footings; b $\psi =\varphi$, rigid footings; c $\psi =0$, flexible footings; and d $\psi =\varphi$, flexible footings. Panels e to h correspond to the same conditions of ψ and footing rigidity but are derived from non-linear regression analysis. LRA, linear regression analysis; NLRA, non-linear regression analysis

Table 5 The proposed linear regression analysis coefficients (see Eq. 12)

Table 6 The proposed non-linear regression analysis coefficients (see Eq. 13)

Fig. 19

Comparison of the finite element results of rigid footings against the respective ones for flexible footings

As shown in Tables 5 and 6, the parameter $\kappa$ varies across all four methods examined, though it remains quite close to 1. In related research, the author (Pantelidis 2023) analytically demonstrated that the three $N$-factors in the bearing capacity equation are directly proportional to the depth of failure. The impact of embedment depth on failure depth can be readily illustrated through common finite element analysis. Since each method is based on its own set of assumptions, $\kappa$ serves as a factor that compensates for relevant modeling errors or decisions: such decisions include the soil’s dilation angle and the footing’s rigidity. Consequently, comparing the derived depth factors directly is illogical because the critical measure is the product of each $N$-factor with its corresponding depth factor, which must yield a consistent value (for example, Terzaghi’s $N$-factors with the proposed depth factor for Terzaghi’s and no other method). This principle applies equally to any published depth factor. Instead, the author provides a comparison with Lyamin et al. (2007) finite-element limit analysis solution for the bearing capacity of footings embedded in sand, which adheres to the associated flow rule. The analysis does not mention either the dilation angle or the rigidity of the footing. It is important to note that some of the errors observed can be attributed to the different assumptions adopted in the various finite element analyses. Also, the author used the weighted average ${N}_{\gamma }$ values provided by Lyamin et al. (average values between the upper and lower bound solutions). The comparison presented in Table 7 encompasses all possible cases and exclusively refers to example nos. 1 to 4 (examples with $c=0$ and ${D}_{f}/B>0$). The average error reported in Table 7 is merely 0.4%.

Table 7 Comparison of the proposed modified method against Lyamin et al. (2007) method. Example nos. 1 to 4 of Table 3. The values in the table indicate the relative error

Two additional comparison tables are presented, focusing on total stress analysis, in Tables 8 and 9, which relate to rigid and flexible footings respectively. In these tables, the method by Salgado et al. (2004) is compared with the proposed modified methods. It is noted that for all methods, ${N}_{c}$ is determined by Eq. 7, which is rather a standard choice, except for the modified Terzaghi method, where ${N}_{c}$ is determined by Eq. 4. The method proposed by Nguyen and Merifield’s (2012) yields very similar results, as their ${d}_{c}$ factor, derived from finite element analysis using Abaqus, closely matches that of Salgado et al. (see Table 2). Salgado et al. conducted their analysis using both upper and lower bound limit analyses. As demonstrated, the relative error with the proposed methods is again very low. It is mentioned that the footing considered by both Salgado et al. and Nguyen and Merifield was perfectly rigid.

Table 8 Comparison of the proposed modified method against Salgado et al. (2004) and Nguyen and Merifield (2012) methods. Example nos. 29 to 36 and nos. 45 to 56 of Table 3. The values in the table indicate the relative error. Case of rigid footings

Table 9 Comparison of the proposed modified method against Salgado et al. (2004) and Nguyen and Merifield (2012) methods. Example nos. 29 to 36 and nos. 45 to 56 of Table 3. The values in the table indicate the relative error. Case of flexible footings

The author also experimented with the depth factors presented in Eqs. 15–19, without, however, further improving the bearing capacity prediction (${f}_{i}$ denotes regression analysis coefficient, $i=$ 1, 2, or 3).

$${q}_{u}={f}_{1}\left(1+{f}_{2}\frac{{D}_{f}}{B}+{f}_{3}{\left(\frac{{D}_{f}}{B}\right)}^{2}\right){q}_{u,0}$$

(15)

$${q}_{u}={f}_{1}\left(1+{f}_{2}\sqrt{{K}_{p}}\frac{{D}_{f}}{B}\right){q}_{u,0}$$

(16)

$${q}_{u}={f}_{1}\left(1+{f}_{2}\bullet {{\text{tan}}}^{-1}\left(\frac{{D}_{f}}{B}\right)\right){q}_{u,0}$$

(17)

$${q}_{u}={f}_{1}\left(1+{f}_{2}\frac{{D}_{f}}{B}\right){q}_{u,0}^{{f}_{3}}$$

(18)

$${q}_{u}={f}_{1}\left(1-{f}_{2}\bullet {e}^{-{f}_{3}{D}_{f}/{\rm B}}\right){q}_{u,0}$$

(19)

The importance of incorporating a depth factor in the analysis is evident in Fig. 20. This figure refers to the total stress analysis example nos. 29 to 40 of Table 3, which contrasts the analytical results derived from Terzaghi’s method (before regression analysis) with the corresponding numerical ones. These examples address rigid footings with varying ${D}_{f}/B$ values (specifically, 0, 0.5, and 1) and a repeating set of undrained shear strength values of soil (namely, ${c}_{u}$=50, 100, 150, and 200 kPa). As shown, the error is greater as the ${D}_{f}/B$ ratio increases (as seen by the divergence of the dashed lines from the $y=x$ line), while for the same ${D}_{f}/B$ value (please focus on any of the three dashed lines of Fig. 20), all points for a specific ${c}_{u}$ value fall on the same ${D}_{f}/B$ line.

Fig. 20

Comparison of the analytical results obtained by Terzaghi’s method prior to regression analysis against the respective numerical ones obtained using RS2. Examples 29 to 40 of Table 3; case of rigid footings

Conclusions

The substantial number of N-factors and depth factors present in the literature underscores the ongoing efforts to refine bearing capacity equations. Upon examining the classical methods and various methods included in design standards, the following observations can be made:

• While Vesic’s original method demonstrates commendable accuracy and consistency across various conditions, it underscores an inherent need for adaptive approaches that further refine predictive capabilities, especially in soil conditions and footing scenarios not covered by traditional methods.

• Terzaghi’s method, although providing a solid foundation for bearing capacity predictions, lacks the depth factor integration for varying soil conditions and footing types.

• The observed variability in Meyerhof’s original method and the limitations in Hansen’s original method serve as clear indicators that despite the strengths of classical methods, there is a pressing need for refined approaches that can provide more accurate, consistent, and reliable predictions.

• Design Standards Methods (EN1997:2004, GEO, AASHTO, FHWA, and API) generally show challenges with accuracy and consistency. Vesic’s original method typically offers better outcomes in these aspects.

• IS6403 method shows considerable variability in its performance, with potential misalignments in predictive fit under rigid footing conditions.

• The superior performance of EN1997:2023 compared to existing methodologies and standards illustrates the substantial advantages that can be achieved with methodological enhancements.

From this study, it becomes clear that incorporating a unified depth factor into the classical methods of Terzaghi, Meyerhof, Vesic, and Hansen significantly enhances the utility and accuracy of these traditional models. Instead of depending on the specific depth factors originally associated with each method, the use of a single, unified depth factor, applicable under various conditions and across all methods, represents a substantial advancement. This innovation achieves compatibility with both flexible and rigid footings and adeptly handles both associated and non-associated flow rules ($\psi =\varphi$ and $\psi =0$), thereby streamlining the application of bearing capacity equations without sacrificing accuracy.

Key enhancements and insights from the present study include:

• Universal depth factor efficiency: The introduction of a universal depth factor remarkably improves the application of bearing capacity equations, offering a more efficient solution. This approach effectively mitigates potential inaccuracies that may arise from the oversimplifications inherent in classical methods or from modeling errors.

• Enhanced prediction accuracy: Utilizing a unified depth factor greatly enhances the accuracy of bearing capacity predictions across various footing types and soil conditions. Its consistency with finite element analysis outcomes highlights the factor’s capability in correcting inaccuracies related to embedment depth and failure mechanism assumptions.

• Streamlining engineering practices: Implementing a single depth factor simplifies foundation design processes, offering a more direct and accurate method for bearing capacity estimation.

• Validation through finite element analysis: The effectiveness of this approach is corroborated by thorough comparisons with finite element analysis results, demonstrating its robustness and reliability under diverse conditions.

These enhancements highlight the significant advantages of applying a unified depth factor to classical bearing capacity methods. This approach not only simplifies the methodology but also ensures a high degree of accuracy and practical applicability.