Abstract
After conducting a comprehensive historical review of presently established methods for computational modeling of multilayered bending plates, the present work introduces a novel 2D multiscale strategy, termed the 2D+ approach. The proposed approach is based on the computational homogenization formalism and is envisaged to serve as an appealing alternative to current methodologies for modeling multilayered plates in bending-dominated situations. Such structural elements involve modern and relevant materials, such as laminated composites characterized by the heterogeneous distribution of low-aspect-ratio layers showing substantial non-linear mechanical behavior across their thickness.
Within this proposed approach, the 2D plate mid-plane constitutes the macroscopic scale, while a 1D filament-like Representative Volume Element (RVE), orthogonal to the plate mid-plane and spanning the plate thickness, represents the mesoscopic scale. Such RVE, in turn, is capturing the non-linear mechanical behavior throughout the plate thickness at each integration point of the 2D plate-midplane finite element mesh. The chosen kinematics and discretization at the considered scales are particularly selected to (1) effectively capture relevant aspects of non-linear mechanical behavior in multilayered plates under bending-dominated scenarios, (2) achieve affordable computational times (computational efficiency), and (3) provide accurate stress distributions compared to the corresponding high-fidelity 3D simulations (computational accuracy).
The proposed strategy aligns with the standard, first-order, hierarchical multiscale setting, involving the linearization of the macro-scale displacement field along the thickness. It employs an additional fluctuating displacement field in the RVE to capture higher-order behavior, which is computed through a local 1D finite element solution of a Boundary Value Problem (BVP) at the RVE. A notable feature of the presented 2D+ approach is the application of the Hill–Mandel principle, grounded in the well-established physical assumption imposing mechanical energy equivalence in the macro and meso scales. This links the 2D macroscopic plate and the set of 1D mesoscopic filaments, in a weakly-coupled manner, and yields remarkable computational savings in comparison with standard 3D modeling. Additionally, solving the resulting RVE problem in terms of the fluctuating displacement field allows the enforcement of an additional condition: fulfillment of linear momentum balance (equilibrium equations). This results in a physically meaningful 2D-like computational setting, in the considered structural object (multilayered plates in bending-dominated situations), which provides accurate stress distributions, typical of full 3D models, at the computational cost of 2D models.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Motivation
Structural materials presenting a multilayer plate morphology have experienced a significant boost in recent decades, due to their appealing mechanical properties, such as high stiffness and strength versus low weight ratios. Additionally, their versatility in design allows customizing them for specific and tailor-made structural applications. Laminated composites are a paradigm of such materials and are used in a large variety of industrial sectors including aerospace, automotive, naval, wind farming, and civil applications, among others.
Despite their increasing popularity, the mechanical behavior of such materials is intricate, especially with complex assemblies covering very diverse constitutive behaviors. Understanding this complexity suggests an examination of the distinct scales and the corresponding dominant physical phenomena taking place therein. For instance, in the laminated composites field, at least three scales can be clearly identified: the macroscopic scale (centimeters to meters), representing the overall structural part; the mesoscopic scale (up to a few centimeters), where through-the-thickness heterogeneity of layers/plies becomes apparent; and the microscopic scale (several micrometers), capturing the interaction between matrix and fibers. This multi-scale character translates into complex deformation mechanisms, leading to distinct failure modes across scales. In this context, single-scale modeling methodologies, aiming at considering the low-scale features and variations in multilayered structural objects, become prohibitive and prevent the implementation of a true bottom-up Materials-by-design approach. In addition, for some very demanding applications (e.g. aerospace materials), structural components are subjected to strict qualification/certification procedures, based on virtual and experimental tests, which essentially operate at macroscopic and mesoscopic levels and require significant economic costs and enormous time consumption. Moreover, this fact often results in material choices based on pre-qualified, rather than optimal, materials for the target application. A computationally efficient virtual testing framework for multilayered plates, focusing on laminated composites, remains prohibitive due to either the high computational cost of 3D representations or the lack of accuracy of the used degenerated 2D kinematics.
This work addresses this issue, by exploring a novel 2D non-linear mechanical modeling of multilayered bending plates, using a suitable ad-hoc two-scale enriched approach. The goal is to assess the computational cost and accuracy of this specific 2D multiscale representation, hereby termed the 2D+ approach, against alternative single-scale 3D representations, and set the basis for its extension and application, in subsequent works, to the efficient computational analysis of high-performance laminated composites.
2 State of the Art: Historical Review on the Topic
In the following, two main modeling scopes are outlined for the analysis of bending-dominated multilayered plates: (i) classical structural theories based on a single-scale approach, and often relying on structural-based hypotheses of geometric and kinematic nature, and (ii) multiscale modeling with a hierarchical treatment of distinct scales based on homogenization theory and other modern computational strategies.
2.1 Structural (Single-Scale) Theories for Multilayered Beams and Plates
In this section multilayered structural objects, essentially constituted by stacked thin layers of different constituents, where the in-plane dimensions result considerably higher than the corresponding thickness (typically one to three orders of magnitude difference), are considered. For this reason, efforts to model this type of structural object as a multilayered two-dimensional plate, endowed with degenerated kinematics, have been very intensive in the computational mechanics community. In the following, we describe the main contributions to single-scale theories such as Equivalent Single Layer (ESL) theories for multilayered beams and plates, Layerwise Theory (LWT) strategies based on three-dimensional elasticity theory, and the so-called Zigzag Theory (ZT) as a multiple model method.
2.1.1 Equivalent Single Layer (ESL) Theories
All ESL theories emerge from three-dimensional elasticity theory by adopting convenient assumptions on the kinematics and stress states through the thickness of the layer. Such assumptions allow the treatment of a 3D (homogeneous or heterogeneous) multilayered beam or plate as a statically equivalent single-layer structure with degenerated kinematics (1D beam or 2D plate). Within these theories, the displacement or stress field can be expressed as a linear combination of functions times the thickness coordinate [1,2,3,4]. The simplest multilayered plate theory is the Classical Plate Theories (CLPT), which can be seen as an extension of classical Kirchhoff plate theory where straight lines normal to the mid surface remain straight and normal to the mid surface after deformation. Within this theory, transverse shear and strain are neglected and only axial strain and bending are considered in the deformation process. First Order Shear Deformation Theory (FSDT) relaxes the normality restriction of CLPT by considering a constant distribution of the transverse shear and strain [5,6,7,8], and can be seen as an extension of the Timoshenko [9] beam and Reissner-Mindlin [3] plate for heterogeneous composite multilayered structures. Within these theories, a bending rotation is added into kinematics and shear corrections are needed to correct the constant distribution of transverse shear. These theories are known to provide inadequate predictions for relatively thick multilayered plates with high-stiffness contrasts between material layers. In general, FSDT tend to underestimate axial stresses at the top and bottom of the beam/plate structure, and shear stresses exhibit high discontinuities between material layers along the thickness. The real through-the-thickness variation of the displacement field is poorly approximated as linearly dependent on the thickness coordinate. The resulting straightness of the transverse normal can be removed considering higher-order displacement fields (i.e. thanks to the use of higher-order polynomials in the expansion of the displacement components through the thickness of the layers [10]). In general, FSDT are seen as highly efficient strategies from a computational standpoint and sufficiently accurate in terms of the global response, but inadequate to correctly capture the transverse strain and stress fields at the layer level. The third-order theory developed by Reddy [11, 12] results in a quadratic variation of transverse shear stresses and strains that vanish at the top and bottom of the structure and, hence, they do not require any shear correction factor as done in FSDT. Higher-order theories [13,14,15,16] result in a higher computational cost and introduce additional unknowns that are difficult to interpret from a physical point of view. Liu and Li showed in [10] that higher-order theories provide a continuous distribution of the displacement and its derivatives with respect to the thickness coordinate. For perfectly bonded layers within the heterogeneous boundary, in-plane displacements are continuous across the interfaces but their first derivatives are discontinuous due to the abrupt stiffness contrast between plies. In other words, in-plane displacement distributions are known to be of a zig-zag nature throughout the thickness. High-order theories (up to the seventh order) are tested in [10], where it is clearly seen how the true zigzag behavior should not be approximated by a considerably high-order polynomial but with layer-wise defined functions (with discontinuous derivatives at the layer interfaces). Transverse stresses are also of utmost importance since their values at interfaces trigger the delamination effect, crucial to assessing the material mechanical performance. Since a continuous strain distribution is obtained in higher-order theories, double-valued interlaminar stresses are obtained at the interfaces when multiplying the single-valued strains by the different material properties of the adjacent layers. Although a post-processing technique can be adopted, as explained in [17], a technique that naturally provides accurate displacements and stresses is preferred.
2.1.2 Layerwise Theories and 3D Elasticity Theory
Most simple ESL types of approaches suffice to model secondary (thin) structures, while primary (thick) structures require a rigorous treatment of thickness effects and accurate predictions of the 3D state of stress, especially at localized regions where damage can nucleate and propagate throughout the structure. In such cases, the analysis requires the use of 3D elasticity theory or the so-called layer-wise theory accounting for the real 3D kinematics and constitutive behavior. In ESL theories, all stresses and, therefore, transverse stresses are discontinuous at layer interfaces due to the choice of continuous displacement functions along the thickness coordinate. This results in an erroneous stress field especially within thick layered structures, since a 3D theory states that transverse stresses \(\sigma _{\text {xz}}\) and \(\sigma _{\text {yz}}\) (with a layer lying on the plane x, y) and the normal stress \(\sigma _{\text {z}}\) within the thickness direction must be continuous at layer interfaces.
Layer-wise theories assume a \(C^0\) displacement field throughout the thickness [18], which results in a discontinuous strain field at various points along the thickness and gives rise to the possibility of continuous transverse stresses at layer interfaces. The displacement layer-wise expansion is constructed as a summation of functions of the in-plane coordinates times a function of the thickness coordinate, which can affect only the in-plane displacement components (partial) or all displacement components (full). Consequently, these theories are able to reproduce the zigzag behavior of the in-plane displacement throughout the thickness. The functions of the thickness coordinate are selected to be layer-wise continuous functions and can be chosen to be one-dimensional Lagrange interpolation functions of the thickness coordinate [18,19,20,21,22,23,24]. The complete displacement field of the plate is constructed by assembling the individual displacement components of each layer. An immediate consequence of such an approach is that the number of displacement variables depends on the number of layers, which indicates that the approach turns out to be computationally expensive for a large stacking of.
A standard discretization of the layer-wise equations using Finite Elements (FE) requires 2D plate elements as interpolation support for the in-plane functions within each layer and 1D elements as interpolation support for the thickness coordinate function. Consequently, a full layer-wise theory shows almost the same integration capability as a standard 3D analysis. Obviously, the thickness of each layer is assigned to each 2D plate. The layer-wise theory involves less data processing than a 3D calculation, and both the in-plane 2D and the transverse 1D meshes can be refined independently whereas a 3D mesh would have to be generated from scratch. Besides this, the 2D type data structure proves to be more efficient when handling element quantities such as stiffness matrices. It should be noted that the conventional 3D finite element model is based on Navier’s governing equations, while the full layer-wise theory is governed by a set of coupled partial differential equations that can be viewed as the semi-discretized version of Navier’s equations and, therefore, an approximation to the exact 3D elastic equations of motion. This approximation tends to Navier’s solution upon mesh refinement or increasing the order of interpolation through the thickness. In general, LWT are regarded as highly accurate strategies in terms of the quality of strain and stress fields within the ply and, obviously, the global response. However, their efficiency in terms of the overall computational cost is regarded as high and just moderately lower than the one of the full 3D analysis.
LWT have been applied to a wide number of problems (see [20] for a thorough review), including progressive failure analysis of multilayered plates. In [25] a non-linear progressive failure analysis of multilayered plates is carried out within the LWT for failure modes I, II, and III employing a stiffness reduction scheme. Delamination in laminated composites has been accounted for in [18], by adding jump discontinuity conditions at the interfaces employing Heaviside functions within the enriched kinematics. Multiple delaminations may be considered by adding an extra degree of freedom per delamination.
2.1.3 Variable Kinematic Formulations
All previous formulations present their own drawbacks and, therefore, there is no unified solution that can be seen as optimal for a general multilayered plate analysis. However, these methodologies can be combined to render an attractive tool capable of studying a wide range of problems with maximum accuracy and minimal cost. Variable kinematic formulations can employ different mathematical models and different levels of discretization at distinct subregions of interest. The way these models can be applied is twofold, leading to the so-called sequential or simultaneous approaches. The former analyzes a global region employing an economical model in the first stage, e.g. based on ESL techniques, in order to determine the displacement field and force boundary conditions, and then performs local analyses with a higher degree of refinement which can eventually involve a full 3D discretization [26, 27]. The latter represents a simultaneous analysis of the entire structure with different subdomains, which in turn are analyzed with distinct mathematical models or levels of domain discretization [28,29,30,31]. An interesting group of techniques within simultaneous variable kinematic approaches consists in superimposing two or more different types of assumed displacement fields within the same integration domain. In general terms, the multiple assumed displacement field can be expressed as the summation of an ESL-type term and a LWT term. The choice of the enrichment function to the layer-wise term gives rise to a great number of contributions, most of them termed zigzag theories [32,33,34,35].
Zigzag theories are seen as a class of variable kinematic formulations incorporating mixed kinematics based on the summation of an ESL displacement field and a LWT displacement field. A zigzag pattern of the in-plane displacements is accounted for, as well as the continuity of the transverse shear stresses along the thickness. A key aspect is that the number of kinematic variables does not depend on the number of layers, and the theory is well suited for FE discretization [33,34,35]. Early zigzag theories on plates were based on adding a piecewise linear displacement function (zigzag function) to a FSDT field [33, 34]. These theories required \(C^1\) continuous shape functions to formulate the FE model and were subsequently modified by Averill [36] using a Timoshenko Beam Theory (TBT) as a baseline with \(C^0\) continuous FE for the discretization. Di Sciuva’s and Averill’s theories suffer from inconsistencies in the physical significance of the transverse shear stress, especially evident at clamped boundaries where the integral of the shear stress does not correspond to the equilibrated shear force. Refined Zigzag Theories (RZT) [37,38,39] have overcome these problems by introducing a unique zigzag function that is prescribed to vanish at the outer surfaces of the laminate structure and does not require continuity of the transverse shear stresses. Within this theory, the transverse shear stresses are not required to be continuous at the layer interfaces. Consequently, if an accurate distribution of the transverse shear stresses is required, a post-process can be performed employing axial stresses by integrating the equilibrium equations. The theory is consistent with the virtual work principle and is free of the shortcomings of previous zigzag theories of Di Sciuva and Averill. Refined zigzag theories RZT have evolved to tackle critical nonlinear effects such as delamination in [40,41,42] by updating the zigzag function according to a damage law. In [40] inter-ply failure is modeled by adding a thin layer between the individual composite plies which constitutes the resin-rich area. A damage model enables tracking of the delamination process. The displacement jumps throughout the interface layers are captured using the zigzag function and are computed as in [43] by relating the interfacial shearing displacement jump to the average shear strain of the resin layer through the thickness of such layer, which is modeled as an explicit isotropic layer between composite plies. A shortcoming of RZT approaches resides in determining transverse shear stresses, which rely on an accurate differentiation of the axial stress fields using Cauchy’s equilibrium in a post-processing stage. Discrepancies are reported when compared to experimental results. In [42] a two-noded beam element is proposed for the analysis of multilayered beams with the capability of reproducing delamination effects without introducing additional kinematic variables as done in [44, 45]. Mode II delamination is modeled in [42] by introducing a very thin interface layer between adjacent materials and is triggered when the material properties of such interface layer are reduced to almost zero compared to those of the adjacent layers. The mechanical properties of the interface layer are modeled following an isotropic damage law as explained in [41]. In order to capture the relative displacement at the edges of the interface between plies, the zigzag function needs to be updated by degrading the interface shear modulus according to the damage evolution. In general, RZT meets some compromise between accuracy and computational efficiency. However, their accuracy in terms of the quality of shear strain and stress fields at the ply level is dependent on the quality of the postprocessing stage. Indeed an accurate determination of the transverse shear is key to nucleating and propagating the delamination behavior and should not be computed in a post-processing stage in order to trigger material non-linearity. This drawback is even more apparent if non-linear material behavior is accounted for at the interfaces and the plies themselves where progressive delamination mechanisms are affected by stress transfer from the damaged plies.
Improved RZT have been derived in [39, 46,47,48] in a linear elastic setting where the computation of accurate out-of-plane shear stresses is integrated into the RZT by means of mixed variational formulations and not as a postprocessing stage. The approach presented in [46] considers a variational formulation that accounts for transverse shear stresses as primary variables. The shear stress profile introduced in the mixed functional is deduced from local three-dimensional equilibrium equations. A similar approach has been introduced in [39, 47] where the RZT is improved for accurate computation of composite beams and plates. The RZT is enriched with Reissner’s Mixed Variational Theorem (cf. [49]) that accounts for the assumed kinematic field by means of the zigzag function and the assumed transverse shear stress deriving from the equilibrium equations. The approach presented in [48] a Hellinger-Reissner (HR) principle is considered together with the kinematic assumptions of the RZT. In this approach stress, moment resultants, and shear forces are introduced as additional degrees of freedom at each node. Results reported in the previous work include linear analysis of thin, thick, and highly heterogeneous plates including delaminated plates with remarkable accuracy compared to available analytical solutions and 3D FE analyses but not accounting for material non-linearity.
To the authors’ knowledge, a RZT with accurate computation of transverse shear stresses has not been devised for the non-linear modeling of delamination processes and intra-ply failure. In this view, the methodology presented in this manuscript and outlined in Sect. 3 represents a novel contribution in this area.
2.2 Multiscale Modeling of Multilayered Bending Plates
Despite considerable efforts to study the behavior of multilayered plates from a multiscale point of view [50,51,52] a fully coupled multi-scale approach is regarded key to simultaneously account for the interactions between different scales depicted by well selected Representative Volume Element (RVE) [53, 54]. Such types of approaches, i.e. computational homogenization approaches [55], have raised considerable interest since a phenomenological closed-form expression is replaced by low-scale simulations nested within the upper-scale analysis. The main attractiveness of the strategy resides in its generality and computational efficiency compared to concurrent multiscale techniques limited to coupled scales problems and often based on domain decomposition methods ([56, 57]). Recent efforts have been focused on providing a unified variational foundation of the approach [58,59,60]. Original Finite Element Square (FE\(^2\)) [53] multi-scale implementations for non-linear materials were done in full dimension setting, i.e. considering the multilayered plate as a 3D body at all scales, disregarding the traditional 2D approaches to plate and shell kinematics. These facts translate into huge computational costs, arising from the nested character finite element solutions at the macro and micro-scale discretizations, for every single time and for every iteration of the analysis. In the last years, a number of strategies were developed for alleviating the problem: (1) Non-uniform Transformation Field Analysis Non-uniform Transformation Field Analysis (NTFA) [61] and Eigendeformation-based reduced order homogenization [62], which relies on strong simplifying hypotheses of the microstructure behavior, leading to large time reductions at the expense of accuracy of the simulation and generality of models to represent, (2) High Performance Reduced Order Modeling High-Performance Reduced Finite Element Square (HPR-FE\(^2\)) [63] is based on the replacement of standard finite element strain modes by selected representative strain modes extracted from a previous (off-line) extensive finite element analysis of the response of a representative volume element RVE. Such a scheme leads to reduced-size nonlinear systems, approximating the original solution upon an increasing number of considered modes. This method is able to accurately represent a wide range of material behaviors, but at a significant reduction in simulation time but still involving a multiplicative cost as the number of scales increases. For instance, the speedups reported in [63] allow for a two-scale coupon analysis within a few hours of computing time, and (3) Artificial neural networks [64] can be used to construct a cheap parameterized surrogate model. Reported results show that the computational cost of these strategies during the online stage can be lower than the one by HPRFE\(^2\) techniques. However, surrogate models derived in this way ignore the physical basis of the problem, and they are unable to simulate material problems governed by input parameters unforeseen in the sampled load trajectories.
Although some alleviation of the involved computational cost can be achieved in these ways, the considered 3D nature of the multilayered plate yields heavy analyses and high computational cost when the realistic geometrical complexity is considered, e.g. for industrial applications. Indeed, within the scope of composite laminated materials, it seems logical to exploit the predominantly 2D spatial dimension of the structure and alleviate the computational cost by considering plate/shell elements with degenerated kinematics. Some authors have elaborated on computational homogenization for shell elements with 3D underlying structures and second-order kinematics involving a high degree of complexity [65, 66]. In the work presented in [67, 68] a 3D macro-structure consisting of several plies is connected to a 3D solid RVE containing fibers within a matrix employing standard computational homogenization techniques. In order to lower the computational cost, hierarchical elements are selected that can change the global and local order of approximation without changing the underlying finite element discretization and, in this way, make efficient use of the computational power. The work presented in [69] constitutes an example of a computational homogenization scheme coupling a seven-parameter shell element to a 3D solid RVE. The upper discretization represents the macro-scale, where a degenerated plate/shell element is employed, and the lower discretization represents a mesoscopic stacking of plies with coupled thickness to the macroscopic structure. The strategy is still partially 3D, not fully exploiting the 2D character of the structure at all levels.
All these methodologies are regarded as highly accurate, in terms of the quality of strain and stress fields at the ply level, but inefficient from a computational standpoint, especially for industrially oriented purposes where reduced computation times are key to designing new material allowables.
3 Proposed Multiscale Approach
As commented above, a drawback of many current multi-layered plates modeling methodologies hinges on their enormous computational cost motivated either by a full 3D macro and/or meso discretization or the adoption of high-order kinematics within the multiscale formulation. For this reason, it seems appropriate to explore a variationally consistent approach based on a computational homogenization scheme accounting for the essential geometrical and kinematic description of the material at all physically relevant scales. This approach is in line with the following reasoning: ... the mechanical response of materials is often governed by specific processes in the material’s microstructure, at one particular spatial scale. Being able to identify this process and capture it in a model that is as simple as possible is extremely rewarding scientifically as well as industrially...[Ron Peerlings, TUEindhoven].
3.1 Brief Description of Hierarchical Multi-scale Material Modeling
Hierarchical mechanical multiscale formulations have gained increasing credit in the Computational Mechanics community during the last decades, as a powerful numerical tool to providing new insights to modeling complex material behavior [53, 55, 60, 63]. They are conceptually established in the following setting:
-
The highly-complex, mechanical behavior of a deformable body, at the observable (upper) material scale, is considered the resultant of the hierarchical interaction of simpler mechanical behaviors in a number of deformable bodies, living in a nested sequence of representative (lower) material scales, conveniently separated by decreasing sizes and appropriately nested. When only two scales are considered the upper scale is commonly termed the macroscopic scale (or, here, the macroscale) and the lower scale is termed the mesoscopic/microscopic scale (or, here, the meso/micro scale).
-
The material at every scale is governed by specific simple mechanical (or physical) laws, in terms of the values and the evolution of some, conveniently identified, scale state-variables, which are aimed at being obtained via computational modeling.
-
A hierarchical-link principle is then postulated for every two consecutive scales (from top to bottom). That link involves some postulated energy equivalence laws, expressed as variational equations, stating the equivalence of the evolution of some entity, for every material point at the upper scale, and the average density of the corresponding entity evolution at the corresponding lower scale, in a specifically shaped and sized domain, termed the Representative Volume Element (RVE). The adequacy and physical significance of that link, in terms of the representation of the material behavior, is, obviously, crucial for the accuracy of the results, which improve asymptotically with the so-called scale separation, understood as the ratio of the typical upper-scale and lower-scale RVE sizes (the larger the better). Solving the resulting variational equations allows determining the evolution of the low-scale variables in terms of the upper-scale ones.
-
Recursive (down to up) computation of the state variables evolution through scales, allows stating the evolution problem at the upper scales, now including all the physical interactions among material scales, which, once solved, provides the (up to down) state variables evolution at all scales.
3.2 Elements of the Approach
The problem tackled here, multiscale non-linear modeling of multilayered-plate structural objects, involves the nested solution (sequentially scale-by-scale) of individual computational problems at every scale (plate-midplane, layers, etc.), and when considered in a full 3D solid context, it yields the aforementioned unaffordable (scale-multiplicative) computational cost (c.f. [63, 70]). The proposed approach, instead, is characterized by the following features (see Fig. 1):
-
It supports the generality and physical consistency of the multiscale setting described in Sect. 3.1.
-
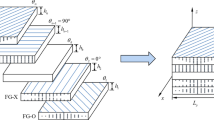
The upper scale domain (macroscale), denoted asFootnote 1\(\Omega ^{\mathcal {M}}\) is constituted by all the material points, belonging to the plate mid-plane (see Fig. 1). The low-scale (mesoscale) Representative Volume element (RVE), denoted as \(\Omega _{\mu }(\textbf{x}^\mathcal {M})\), is constituted by the material points, belonging to the 1D filament (normal to the midplane) at the corresponding macroscale point, \(\textbf{x}^{\mathcal {M}}\), and spanning the plate thickness. The global domain, \(\Omega \), is the one occupied by all particles in the overall geometrical object (the 3D structural plate).
-
The approach introduces the geometrical and kinematic specifications, on the displacement field, typical of ESL formulations (layered plates), thus keeping the structural models in a reduced dimension setting (2D for plates), with high expected reductions in the computational cost compared with 3D solid multiscale formulations.
-
Low-scale kinematics is obtained employing linearization along the mesoscale (thickness) direction where the most relevant heterogeneity takes place. Then, an (unknown) fluctuating displacement field, living at the mesoscale \(\Omega _{\mu }\), is assumed to complement that linearized displacement field providing the displacement field at the mesoscopic scale. That fluctuating displacement is the unknown in the so-called RVE problem, which comes out from the imposition of the hierarchical energy conservation principle (Hill–Mandel Principle).
-
Although at first sight the approach could be viewed as a type of RZT formulation, in which the explicit zigzag function coincides with the low-scale displacement, there is a substantial difference in the origin and role of the displacements obtained in both approaches: in the present multiscale approach no explicit (ad-hoc) law for the aforementioned mesoscopic displacements is imposed; instead, they are point-wise determined by the fluctuating displacements as the solution of a variationally derived RVE problem. While the RZT provides a strong coupling of all the out-of-plane displacement fields (due to the explicit ad-hoc zigzag function), in the proposed approach the warping (zig-zag-like) displacements are obtained in a macroscopic, point-wise, manner as the result of the aforementioned RVE variational problem at every mesoscale domain, \(\Omega _{\mu }(\textbf{x}^{\mathcal {M}})\) (filament) independently from the other filaments.
-
The proposed formulation for the initial, 2D, RVE problem is restricted to fulfill, in a variational format, additional conditions to the resulting fluctuating displacements and, therefore, adjusting the resulting stress distribution. For this purpose, the linear momentum conservation equations (equilibrium equations) are imposed in a weak form in the RVE problem, and an accurate (3D solid) stress distribution is recovered within the considered 2D multiscale approach.
Such an approach is devised to render an efficient computational setting providing: 1) sufficient accuracy to tackle the physically relevant phenomena across the scales, 2) the right stress distribution across the layered structure thickness, and 3) the computational cost benefits of a 2D degenerated kinematics, the natural one for moderately thin structural objects, with the stress accuracy of 3D formulations. In this way, the proposed approach aims to meet an optimal balance between the solution accuracy and the computational efficiency, motivating the authors to use the abbreviation 2D+ approach, synthesizing the cost-efficiency benefits of the 2D multiscale models and the relevant additional accuracy of 3D models.
4 The Multiscale Formulation for Multilayered Bending Plates
4.1 Macroscale Kinematics and Stresses: Macroscopic Displacements, Strains, and Resultant Stresses
Embedded in 3D cartesian coordinate system \(\{{\text {x}},{\text {y}},{\text {z}}\}\), Fig. 1 displays the overall structural object \(\Omega \) (a sufficiently thin plate of lengths \(L_{\text {x}}\), \(L_{\text {y}}\) and depth h), the macroscopic scale domain \(\Omega ^{\mathcal {M}}\) (the plate’s mid-plane in the \(x-y\) space), and the mesoscopic scale RVE domain \(\Omega _{\mu }(\textbf{x}^{\mathcal {M}})\), rendering a plate vertical filament passing through the macroscopic scale domain at a specific point \({\textbf{x}^{\mathcal {M}}}\in {\Omega ^{\mathcal {M}}}\) and spanning the plate thickness h. In this context, these domains can be formally described asFootnote 2
where \({{\mathcal {R}}}\) stands for the set of real numbers, \(L_{\text {x}}\) and \(L_{\text {y}}\) are the plate mid-plane lengths in the \(x-y\) directions, \(\textbf{x}^{\mathcal {M}}\) stands for a specific point of \({\Omega ^{\mathcal {M}}}\), and \(h^{-}(\textbf{x}^{\mathcal {M}})\) and \(h^{+}(\textbf{x}^{\mathcal {M}})\) are, respectively, the distances from the plate-bottom and the plate-top to the plate mid-surface, so that the plate depth is \(h(\textbf{x}^{\mathcal {M}})=h^{-}(\textbf{x}^{\mathcal {M}})+h^{+}(\textbf{x}^{\mathcal {M}})\).
Now let us endow the plate with a degenerated, first-order 3D kinematics (the Reissner-Mindlin plate kinematics including in-plane effects [71]), reading
Multiscale domains: a structural object \(\Omega \), defined for \(\mathbf{{x}}\in [0, L_{\text {x}}]\times [0, L_{\text {y}}]\times [-h^-,+h^+]\) (layered plate), b macro-scale domain \(\Omega ^{\mathcal {M}}\), for any \(\mathbf{{x}}^{\mathcal {M}}\in [0, L_{\text {x}}]\times [0, L_{\text {y}}]\) (plate’s mid plane in the x-y space) and c meso-scale domain \(\Omega _{\mu }(\textbf{x}^{\mathcal {M}})\) defined at a specific macro-scale material point \(\mathbf{{x}}^{\mathcal {M}}\in \Omega ^{\mathcal {M}}\) and any \(z\in [-h^-(\mathbf{{x}}^{\mathcal {M}}),+h^+(\mathbf{{x}}^{\mathcal {M}})]\) (through-the-thickness filament, at the macroscale point \({\textbf{x}^{\mathcal {M}}}\), consisting of a set of layers of different materials)
(see Fig. 2) where, accordingly with the chosen notation, \(\text {u}^{{\mathcal {M}}}_{\text {x}}(\textbf{x}^{\mathcal {M}})\), \(\text {u}^{{\mathcal {M}}}_{\text {y}}(\textbf{x}^{\mathcal {M}})\) and \(\text {u}^{{\mathcal {M}}}_{\text {z}}(\textbf{x}^{\mathcal {M}})\) denote, respectively, the in-plane (in x and y directions) and off-plane (in z-direction) 3D solid displacements at the plate mid surface (\(z=0\)), and \(\theta _{\text {x}}^{\mathcal {M}}(\textbf{x}^{\mathcal {M}})\) and \(\theta _{\text {y}}^{\mathcal {M}}(\textbf{x}^{\mathcal {M}})\) stand for the angles defining the filaments’ rotations at the mid surface. These entities, all of them living at the macroscale domain \(\Omega ^{\mathcal {M}}\), define the herein after termed macro-scale (or macroscopic) displacement vector field \(\mathbb {u}^{\mathcal {M}}(\textbf{x}^{\mathcal {M}})\) as
In addition, the from now on termed macro-scale (or macroscopic) strain vector field \(\mathbb {\epsilon }^{\mathcal {M}}\Big (\mathbb {u}^{\mathcal {M}}(\textbf{x}^{\mathcal {M}})\Big )\), also living in \(\Omega ^{\mathcal {M}}\), can be derived (in Voigt’s notation) as:
where the macroscopic-membrane strain vector \({{\varvec{\varepsilon }}}^{\mathcal {M}}\equiv [\varepsilon ^{{\mathcal {M}}}_{\text {x}},\varepsilon ^{{\mathcal {M}}}_{\text {y}},\varepsilon ^{{\mathcal {M}}}_{\text {xy}}]^T\), the macroscopic-bending strain vector (or pseudo curvatures vector) \({{\varvec{\kappa }}}^{\mathcal {M}}\equiv [\kappa ^{{\mathcal {M}}}_{\text {x}},\kappa ^{{\mathcal {M}}}_{\text {y}},\kappa ^{{\mathcal {M}}}_{\text {xy}}]^T\), and the macroscopic-shear strain vector) \({{\varvec{\gamma }}}^{\mathcal {M}}\equiv [\gamma ^{{\mathcal {M}}}_{\text {xz}},\gamma ^{{\mathcal {M}}}_{\text {yz}}]^T\) can be identified.
Now, from Eqs. (2) and (4), the standard 3D infinitesimal strains \({{\mathbb {E}}}({\textbf{x}^{\mathcal {M}}},z)\) (also in Voigt’s notation), can be computed and expressed in terms of the macroscopic strains as:
where the macroscopic strain entities defined in Eq. (4) have been replaced. In analogy with standard (single-scale) plate formulations, some entities referred to as macroscopic (or macro-scale) stresses, also living in \(\Omega ^{\mathcal {M}}\), are defined as
where \({\textbf{N}}^{\mathcal {M}}\equiv [{\text {N}}^{\mathcal {M}}_{\text {x}},{\text {N}}^{\mathcal {M}}_{\text {y}},{\text {N}}^{\mathcal {M}}_{\text {xy}}]^T\) is termed the membrane resultant stress vector, \({\textbf{M}}^{\mathcal {M}}\equiv [{\text {M}}^{\mathcal {M}}_{\text {x}},{\text {M}}^{\mathcal {M}}_{\text {y}},{\text {M}}^{\mathcal {M}}_{\text {xy}}]^T\) is the bending/torsion resultant stress vector, and \({\textbf{V}}^{\mathcal {M}}\equiv [{\text {V}}^{\mathcal {M}}_{\text {x}},{\text {V}}^{\mathcal {M}}_{\text {y}}]^T\) is the off-plane shear resultant stress vector. The term \({\text {V}}_{\text {z}}^{\mathcal {M}} (\textbf{x}^{\mathcal {M}})\) is never present in common plate formulations, and, as it will be shown below, it does not play any role in the proposed formulation either.
Mimicking the standard plate-formulations and considering a pseudo-time, \(t\in [0,T]\), ruling the evolution of the deformation process (as it is usual in quasi-static structural problems), the macro-scale mechanical work change, in the time interval \([t,t+dt]\), per unit of the time change, dt, and unit of macro-scale measure surface, \(dx\, dy\) (see Fig. 1), i.e. the macroscopic stress power density, \({\dot{\Pi }}^{\mathcal {M}}({{\textbf{x}^{\mathcal {M}}}},t)\), is postulated to be expressible as:
where the upper dot, \(\dot{(\bullet )}\), stands for rate of change of the \((\bullet )\) entity, per unit of time, along a pseudo-time infinitesimal increment, dt.
Remark 1
Notice, at this point, a first relevant difference with the classical Reissner-Mindlin plate theory: the macroscale stresses \(\textbf{N}^{\mathcal {M}}(\textbf{x}^{\mathcal {M}},t)\), \(\textbf{M}^{\mathcal {M}}(\textbf{x}^{\mathcal {M}},t)\) and \(\textbf{V}^{\mathcal {M}}(\textbf{x}^{\mathcal {M}},t)\), also termed the resultant or generalized stresses, are not yet explicitly defined in terms of the continuum mechanics Cauchy stresses (i.e. \(\sigma _x\), \(\sigma _y\), \(\sigma _\text {xy}\),...), living in the structural object domain \(\Omega \) in Eq. (1), but postulated as entities conjugated with the macroscale strains (\({{\varvec{\varepsilon }}}^{\mathcal {M}}\), \({{\varvec{\kappa }}}^{\mathcal {M}}\) and \({{\varvec{\gamma }}}^{\mathcal {M}}\)) to render the stress-power expression in Eq. (7). In fact, the components of vector, \(\mathbb {\Sigma }^{\mathcal {M}}(\textbf{x}^{\mathcal {M}})\), will be identified in Sect. 4.6.1 through the hierarchical-link principle mentioned in Sect. 3.2. Note also that component \({\text {V}}^{\mathcal {M}}_{\text {z}}(\textbf{x}^{\mathcal {M}})\), in Eq. (6), does not contribute in the final statement in Eq. (7) because its conjugate strain, \(\varepsilon _\text {z}\) in Eq. (7), is null (see Eq. (5)).
4.2 Mesoscale Kinematics: Displacements and Strains
Let us now consider the 3D solid displacement field, \(\textbf{u}({\textbf{x}^{\mathcal {M}}},z)\), in Eq. (2), and, its linearization, \(\textbf{u}^{lin}({\textbf{x}^{\mathcal {M}}},z)\), computed as the linear Taylor’s expansion, around a given position in the macroscopic domain, \({\textbf{x}^{\mathcal {M}}}\equiv (x,y)\in \Omega ^{\mathcal {M}}\), and along the RVE domain (z-axis direction). This expansion reads:
and replacing Eqs. (2) into Eq. (8) yields
The linearized strains associated to the linearized displacements in Eq. (9) read (see also Eqs. (5)):
Remark 2
Inspection of the linearized (solid 3D) displacements and strains in Eqs. (9) and (10) shows that they coincide with the original ones, in Eqs. (2) and (5). This could have been naturally expected from the z-linear character of the original Eq. (2), but this emphasizes that the utilized displacement linearization procedure matches the format of the hierarchical multiscale formulation introduced in Sect. 3.2.
4.2.1 Fluctuating (Mesoscale) Displacement Field
Definition of the displacement field at the mesoscopic scale (the mesoscale RVE displacements), \(\textbf{u}_{\mu }({\textbf{x}^{\mathcal {M}}},z)\),Footnote 3 as the linearized expression in Eq. (9), i.e. \(\textbf{u}_{\mu }({\textbf{x}^{\mathcal {M}}},z)=\textbf{u}^{lin}({\textbf{x}^{\mathcal {M}}},z)\), corresponds to the simplest approach in the multiscale modeling [58]. Additional complexity in the kinematic description is then provided by adding the, from now on termed, fluctuating mesoscale-displacements, \(\tilde{\textbf{u}}_{\mu }(z)\), living at the RVE, \(\Omega _{\mu }(\textbf{x}^{\mathcal {M}})\), defined through:
Equation (11(b)) defines the restricted fluctuations space, \(\mathcal {U}_{\tilde{u}}\), which nullifies the mean value on the RVE domain of the fluctuating strain gradient
This confers mathematical consistency to the fluctuating displacements, in Eq. (11), for the subsequently considered multiscale context [58].
Remark 3
Note that all possible second (and higher order) terms in the displacements, \({\textbf{u}}_{\mu }({\textbf{x}^{\mathcal {M}}}z)\), in Eq. (11(a)) are allocated to the displacement fluctuation field \(\tilde{\textbf{u}}_{\mu }(z)\). This is another conceptual difference of the proposed multiscale approach with respect to, alternative, high-order layered-plate formulations [10].
From Eqs. (10) and (11(a)), the corresponding meso-scale strains, \({{\varvec{\varepsilon }}}_{\mu }({\textbf{x}^{\mathcal {M}}},z)\) in the RVE \(\Omega _{\mu }(\textbf{x}^{\mathcal {M}})\), can be decomposed as:
where \({{\varvec{\varepsilon }}}^{lin}\) is that part of the strain emerging from the macro-scale linearization (see Eq. (10)) and \(\tilde{{\varvec{\varepsilon }}}_{\mu }(z)\) (the fluctuating strains vector) is the one arising from the fluctuatingdisplacements, \(\tilde{\textbf{u}}_{\mu }(z)\). To simplify subsequent expressions it is convenient to split them into their in-plane components, \((\bullet )^{\text {inp}}\), and off-plane components, \((\bullet )^{\text {ofp}}\), i.e.
a Fluctuating mesoscale-displacements \(\tilde{\textbf{u}}_{\mu }(z)\) distribution along the RVE (1D-filament). Characterization of b the in-plane stresses, \({{\varvec{\sigma }}}^{\text {inp}}_{\mu }\) \(\equiv [{\sigma }_{\mu _{\text {x}}}, {\sigma }_{\mu _{\text {y}}}, {\sigma }_{\mu _{\text {xy}}}]^T\), and c the off-plane stresses, \({{\varvec{\sigma }}}^{\text {ofp}}_{\mu }\) \(\equiv [{\tau }_{\mu _{\text {xz}}}, {\tau }_{\mu _{\text {yz}}}, {\sigma }_{\mu _{\text {z}}}]^T\)
In summary, the following strain decomposition expressions and variable dependencies are utilized in the subsequent derivations:
where in Eq. (16(b)) the off-plane macroscopic shear strain vector \({{\varvec{\varepsilon }}}_{\mu }^{\text {ofp}}(\textbf{x}^{\mathcal {M}},z)\) has been split into the macro-scale shear \({{\varvec{\gamma }}}^{\mathcal {M}}(\textbf{x}^{\mathcal {M}})\) and z-axial strain counterparts \((\varepsilon _{{\text {z}}}^{\mathcal {M}}=0)\), and the fluctuating shear strain \({\tilde{{\varvec{\gamma }}}}_{\mu }(z)\) and vertical elongation strain \({\tilde{\varepsilon }}_{\mu _{\text {z}}}(z)\) counterparts.
Remark 4
Notice in Eq. (15(a)) that the in-plane components of the fluctuating strains, \(\tilde{{\varvec{\varepsilon }}}_{\mu }^{\text {inp}}\), are null and, thus, the fluctuating displacements (\({\tilde{\textbf{u}}}_{\mu }(z)\equiv [{\tilde{\text {u}}}_{\mu _{\text {x}}},{\tilde{\text {u}}}_{\mu _{\text {y}}},{\tilde{\text {u}}}_{\mu _{\text {z}}}]^T\)) only affect the off-plane components of the fluctuating strains, \(\tilde{{\varvec{\varepsilon }}}_{\mu }^{\text {ofp}}\) in Eq. (15(b)). This fact will be highlighted in subsequent sections.
4.3 Constitutive Model
Associated to the strain field, \({{\varvec{\varepsilon }}}_{\mu }({\textbf{x}^{\mathcal {M}}},z)\), in Eq. (13), the stress field, \({\varvec{\sigma }}_{\mu }({\textbf{x}^{\mathcal {M}}},z)\), is defined at every point, \(({\textbf{x}^{\mathcal {M}}},z)\), of the RVE, \({\Omega _\mu }(\textbf{x}^{\mathcal {M}})\), keeping also the notation in-plane and off-plane to split them (see Fig. 3) i.e.
with
where in Eq. (18) the off-plane stress vector \({{\varvec{\sigma }}}^{\text {ofp}}_{\mu }\) has been split into the shear \({{\varvec{\tau }}}_{\mu }\) and z-axial \(\sigma _{\mu _{\text {z}}}\) components.
The relationship between the mesoscale strains and stresses in Eqs. (13) to (18) is established via appropriate mesoscale nonlinear constitutive models, described here, for simplicity reasons, in terms of generic stress/strain rates in a pseudo-time context, \(t\in [0,T]\). In essence, they are characterized by decoupled in-plane and off-plane stress/strain rate relationships and the corresponding set of (tangent) constitutive tensors, \(\textbf{D}^{\text {inp}}_{\mu }\), \(\textbf{D}^{\text {ofp}}_{\mu }\), \(\textbf{G}^{\text {ofp}}_{\mu }\), and \({ E}_{{\mu }_{\text {z}}}\) as follows:
with
where \(\textbf{D}^{\text {inp}}_{\mu }\) is a \((3\times 3)\) matrix defining the in-plane rate constitutive model and \(\textbf{D}^{\text {ofp}}_{\mu }\) is a \((3\times 3)\) diagonal matrix defining the off-plane constitutive model, which, in turn, can be decomposed into the decoupled off-plane shear constitutive model, ruled by the tangent constitutive operator \(\textbf{G}^{\text {ofp}}_{\mu }\) and the z-axis scalar constitutive model ruled by the tangent Young modulus \(E_{\mu _{\text {z}}}\). For future developments, matrix \(\textbf{D}^{\text {inp}}_{\mu }\) is split into its (\(1 \times 3\)) sub-matrix components, \(\textbf{D}^{\text {inp}}_{\mu _{\text {x}}}\), \(\textbf{D}^{\text {inp}}_{\mu _{\text {y}}}\) and \(\textbf{D}^{\text {inp}}_{\mu _{\text {xy}}}\) as indicated in Eq. (20(a)). Tangent constitutive operators \(\textbf{D}^{\text {inp}}_{\mu }\), \(\textbf{G}^{\text {ofp}}_{\mu }\) and \({E}_{{\mu }_{\text {z}}}\) are to be specified for every different material model.
Remark 5
Note in Eqs. (19) and (20) that: (1) the in-plane and off-plane constitutive models are completely uncoupled (matrix \(\textbf{D}_{\mu }\), in Eq. (19(a)) is block-diagonal), (2) due to this uncoupling, and since the in-plane components of the strains, \({{\varvec{\varepsilon }}}^{\text {inp}}_{\mu }\), do not depend on the fluctuating displacements (see Remark 4) neither the corresponding in-plane components of the stresses, \({\varvec{\sigma }}^{\text {inp}}_{\mu }\) in Eq. (19(b)), depend on the fluctuating displacements and, finally, (3) the tangent off-plane shear constitutive model, described by \(\textbf{G}_{\mu }^{\text {ofp}}\), and off-plane axial (z-axis) constitutive model, described by \(E_{{\mu }_\text {z}}\), are also uncoupled. These facts will be conveniently recalled in the following sections.
4.4 Mesoscale Stress Power Density
In view of the previous definitions, the stress power RVE-average at the mesoscale (mesoscale stress power density) \(\langle \dot{\Pi }_{\mu }\rangle _{{\Omega _\mu }(\textbf{x}^{\mathcal {M}})}\) is defined as:
where the contributions of the rates of the linearized strains, \(\dot{{\varvec{\varepsilon }}}^{lin}({\textbf{x}^{\mathcal {M}}},z,t)\), and the mesoscale fluctuating-strains, \({\dot{\tilde{{\varvec{\varepsilon }}}}}_\mu ({\textbf{x}^{\mathcal {M}}},z,t)\), yield, respectively, the terms \(\langle \langle {\dot{\Pi }}^{lin}_{\mu }({\textbf{x}^{\mathcal {M}}},z,t)\rangle _{\Omega _{\mu }(\textbf{x}^{\mathcal {M}})}\) and \({\langle \dot{\tilde{\Pi }}_{\mu }({\textbf{x}^{\mathcal {M}}},z,t)\rangle _{\Omega _{\mu }(\textbf{x}^{\mathcal {M}})}}\). Then, after substitution in Eq. (21) of the corresponding values in Eqs. (14) to (20), and performing some additional algebraic operations accounting also for Eqs. (4) and (5), the following results are obtained:
where the macroscale strains, \({\mathbb {\epsilon }}^{{\mathcal {M}}}({\textbf{x}^{\mathcal {M}}},t)\), are given in Eq. (4). Also,
where in Eq. (23(a)) the null value of \({\dot{\tilde{{{\varvec{\varepsilon }}}}}}^{\text {inp}}_{\mu }\) has been accounted for (see also Eq. (23(c))) and the off-plane stresses, \({{\varvec{\sigma }}}^{\text {ofp}}_{\mu }\), and fluctuating strain rates, \(\dot{\tilde{{{\varvec{\varepsilon }}}}}^{\text {ofp}}_{\mu }\), vectors have been split into their shear and z-axis components \([{{\varvec{\tau }}}_{\mu },\sigma _{{\mu }_{\text {z}}}]^T\) and \([\dot{\tilde{{\varvec{\gamma }}}}_{\mu }, \dot{\tilde{ \varepsilon }}_{{\mu }_{\text {z}}}]^T\), respectively.
Remark 6
It is emphasized that the mesoscale RVE generalized stresses, \(\mathbb {\Sigma }_{\mu }({\textbf{x}^{\mathcal {M}}},t)\), in Eq. (22(b)), are not, yet, related with the macroscale stresses \(\mathbb {\Sigma }^{\mathcal {M}}({{\textbf{x}^{\mathcal {M}}}},t)\), postulated in Eq. (6). This subject will be tackled in Sect. 4.6.
4.5 Resultant Mesoscale Generalized Stresses and Constitutive Model
The components of the, from now on termed RVE-resultant (or generalized) stresses, \(\mathbb {\Sigma }_{\mu }({\textbf{x}^{\mathcal {M}}},t)\), in Eq. (22(b)), can be readily identified as the in-plane, resultant stresses, \(\textbf{N}_{\mu }({\textbf{x}^{\mathcal {M}}},t)\), bending/torque moments, \(\textbf{M}_{\mu }({\textbf{x}^{\mathcal {M}}},t)\), and off-plane resultant stresses, \(\textbf{V}_{\mu }({\textbf{x}^{\mathcal {M}}},t)\), acting on the RVE, \(\Omega _{\mu }(\textbf{x}^{\mathcal {M}})\) (the plate filaments). They are mechanically computed as the mechanical resultant forces at the RVE center \({\textbf{x}^{\mathcal {M}}}\in \Omega ^{\mathcal {M}}\), in terms of the mesoscale stresses, \({{\varvec{\sigma }}}_{\mu }({\textbf{x}^{\mathcal {M}}},z,t)\), according to Eqs. (17) and (18).
In this context, accounting for the mesoscale constitutive models postulated in Eqs. (17) to (20), the following relationship can be established in terms of the rates of the resultant/generalized stresses, \(\mathbb {\Sigma }_{\mu }({\textbf{x}^{\mathcal {M}}},t)\), in Eq. (22(b)) and the strain measures in Eq. (14):
which can be further elaborated, in view of Eqs. (19), (20) and (22(b)) as
where the macroscale tangent constitutive operator, \({\mathbb D}^{\mathcal {M}} ({\textbf{x}^{\mathcal {M}}},t)\), emerges as
4.6 Hill–Mandel Principle and Stress Homogenization
The classical Hill–Mandel principle [72] or, in a more recent version, the Method of Multiscale Virtual Power (MMVP) [59], for multiscale modeling, is now specified for the multiscale setting in Eq. (1). It is based on:
-
a)
kinematic admissibility of scales, i.e. the mesoscale displacement field arises from the linearization of the macroscopic displacement field, around any given point at the macroscale, along the RVE manifold, supplemented by the fluctuation field, \(\tilde{\textbf{u}}_{\mu }\), in Eq. (11(b)), living at the RVE and considered an additional unknown of the problem (already elaborated on in Sect. 4.2),
-
b)
mathematical duality of the macro/meso scale quantities, and
-
c)
the energy equivalence/conservation across scales utilized to derive the multiscale problem equations from energetic [72] or variational [60] arguments.
4.6.1 Energy Equivalence Across Scales
The energy equivalence/conservation across the macro/meso scales of the plate, at any macroscale point, \({\textbf{x}^{\mathcal {M}}}\in \Omega ^{{\mathcal {M}}}\), and the corresponding RVE (plate filament), \(\Omega _{\mu }(\textbf{x}^{\mathcal {M}})\), in the mesoscale (Hill–Mandel Principle) can be stated as follows:
"the macroscopic stress-power density, \({\dot{\Pi }^{{\mathcal {M}}}({\textbf{x}^{\mathcal {M}}},t)},\) (the work of the macroscopic generalized stresses, \(\mathbb {\Sigma }^{{\mathcal {M}}}({\textbf{x}^{\mathcal {M}}},t)\), at point \(\mathbf{{\textbf{x}^{\mathcal {M}}}}\equiv [x,y]\in \Omega ^{{\mathcal {M}}}\) in the infinitesimal macroscopic domain \(d\Omega ^M\equiv [x,x+dx]\times [y,y+dy]\) conjugated to the macroscopic strain rates, \(\dot{\mathbb {\epsilon }}^{\mathcal {M}}({{ {\textbf{x}^{\mathcal {M}}}}},t)\), during the time interval \([t,t+dt]\), per unit of time increment, dt and unit of macroscopic surface \(dx\,dy\)) equals the total stress power at the corresponding RVE, \({\dot{\Pi }_{\mu }({\textbf{x}^{\mathcal {M}}},t)}_{\Omega _{\mu }(\mathbf{x^{\mathcal {M}}})}\), for ANY possible evolution of the the strain variables"
In the present context, the Hill–Mandel statement is formalized as:
where Eqs. (21), (22) and (23) have been taken into account to obtain Eq. (27(b)). Now, choosing in the previous statement the following (admissible) scenarios:
Equation (27(b)) yields:
and, therefore, the macroscopic stresses, \(\mathbb {\Sigma }^{{\mathcal {M}}}({\textbf{x}^{\mathcal {M}}},t)\), in Eq. (6) are now identified as the resultant (actions on the cross-section) mesoscale stresses, also termed the generalized stresses \(\mathbb {\Sigma }_{\mu }({\textbf{x}^{\mathcal {M}}},t)\), in Eq. (22(b)), i.e.:
The identification in Eq. (30) above is the version, for the present multiscale approach, of the commonly termed stress homogenization procedure.
Remark 7
It is emphasized that the result in Eq. (30), specifically obtained in the proposed multiscale approach, exactly matches, the value for \(\mathbb {\Sigma }^{{\mathcal {M}}}({\textbf{x}^{\mathcal {M}}},t)\) postulated in classical first-order models for plates [71].
Replacement of Eqs. (31) into (27(b)) yields
where the explicit dependence of the fluctuating strains, \(\dot{\tilde{{\varvec{\varepsilon }}}}^{\text {ofp}}_{\mu }\), on the fluctuating displacements, \(\dot{\tilde{\textbf{u}}}_{\mu }\), see Eq. (15(b)), has been emphasized. Also the kinematic restriction in the fluctuating displacements (see Eq. (11(b))) is highlighted. Equation (32) can be further elaborated writing the fluctuating counterpart of the mesoscale energy rate, \({\dot{{\tilde{\Pi }}}}_\mu ({\textbf{x}^{\mathcal {M}}},t)\), as (see Eq. (15(b)))
where Eq. (11(b)) has been considered.
4.7 Variational Statement of the RVE Problem. Euler–Lagrange Equations
Equation (33) can be rephrased in a, totally equivalent, variational manner by replacing the rate terms by variational entities (i.e. \((\dot{\bullet })\rightarrow \delta (\bullet )\)) yielding
Equation (34) can be integrated by parts with respect to the variable z, along the domain \([-h{^-}(\textbf{x}^{\mathcal {M}}),h{^+}(\textbf{x}^{\mathcal {M}})]\), yielding,Footnote 4
where \(\big [\big (\mathbf{\bullet }\big )(z)\big ]^{+h^{+}}_{-h^-}\) stands for the jump of function \((\bullet )\) in the interval \([-h^{-},+h^{+}]\), i.e. \(\big [\big (\mathbf{\bullet }\big )(z)\big ]^{+h^{+}}_{-h^-}\equiv \big (\mathbf{\bullet })(z)\vert _{z=+h^{+}}-\big (\mathbf{\bullet })(z)\vert _{z=-h^{-}}\). Eqs. (35) provide independent BVPs for the following admissible, \({\delta {\tilde{\textbf{u}}}}_{\mu } \in \mathcal {U}_{\tilde{u}}\), scenarios:
Remark 8
Eqs. (36) display the limited ability of the first-order approximations to appropriately represent the actual expected shear stress distribution in plates along the depth. In fact, they establish constant shear stress distributions, \(\tau _{{\mu }_{\text {xz}}}({\textbf{x}^{\mathcal {M}}},z),\tau _{{\mu }_{\text {yz}}}({\textbf{x}^{\mathcal {M}}},z)\) along, the plate depth (z-axis), disregard the heterogeneity of the material along this axis,Footnote 5 see also Fig. 4. This constant shear stress distribution would be in agreement with FSDT approaches as in [5,6,7,8], which can not be accepted to perform a realistic analysis in heterogeneous multilayered plates. For instance, a constant distribution of the shear stress throughout the plate thickness would trigger damage and non-linear phenomena simultaneously at all layers, which is not acceptable from a physical standpoint. Neither the introduced fluctuating displacement field, \({\tilde{\textbf{u}}}_{{\mu }}\) in Eq. (11(a)), alleviates the problem. Higher order theories face the problem by means of an ad-hoc increase of the degenerated kinematics polynomial order along the depth (at the cost, also, of a relevant increase of the computational cost). A solution to this flaw, in the context of the proposed multiscale approach, will be examined in the next sections.
4.8 RVE Problem Rephrased in Rate Form
In a pseudo-time advancing setting, the partial differential equations problems in Eqs. (36) to (37) can also be written in rate form, i.e.
and, undoing the way in Eqs. (34) to (37), it is readily proven that they would emerge from the following variational principle (now in rate form),
where dependencies of the mesoscale stress rate, \(\dot{{\varvec{\sigma }}}^{\text {ofp}}_{\mu }\), on the mesoscale strains rate, \({\dot{\tilde{{\varvec{\varepsilon }}}}}^{\text {ofp}}_{\mu }\), and on the fluctuating displacements, \({\tilde{\textbf{u}}_{\mu }}\), have been displayed.
Remark 9
For deriving Eq. (40), we recall that Eq. (34), ruling the RVE variational problem, is obtained from SCENARIO (II) in the Hill–Mandel Principle (see Eq. (31) and Sect. 4.6.1), where the macroscale strains are frozen, \({\dot{\mathbb {\epsilon }}}^{{\mathcal {M}}}({\textbf{x}^{\mathcal {M}}},t)= \textbf{0}\). Therefore the rate of the linear strains, \({{\varvec{\varepsilon }}}^{lin}\Big (\mathbb {\epsilon }^{\mathcal {M}}(\textbf{x}^{\mathcal {M}}),z\Big )\), in Eq. (10), is nullified i.e.: \({\dot{{\varvec{\varepsilon }}}}^{lin}({\textbf{x}^{\mathcal {M}}},z,t)\equiv \dot{{\varvec{\varepsilon }}}^{lin}\left( {\dot{\mathbb {\epsilon }}}^{{\mathcal {M}}}({\textbf{x}^{\mathcal {M}}},t),z\right) =\textbf{0}\). Therefore, from Eqs. (10) and (19(b, c)),
where terms \(\dot{\tilde{{\varvec{\varepsilon }}}}^{\text {inp}}_{\mu }\) are \(\textbf{0}\) at the mesoscale, thus resulting in a null in-plane micro-scale stress \({\dot{{{\varvec{\sigma }}}}_{\mu }}^{\text {inp}}\).
4.9 Enriched RVE Problem
Equation (40) can be now rephrased as a constrained minimization problem of the functional \({\dot{\tilde{\Pi }}}_{\mu }({{{\tilde{\textbf{u}}}}_{\mu }})\) in the argument \(\tilde{\textbf{u}}_{\mu }\), i.e.
where, from now on, \(\delta [(\bullet );\delta {\tilde{\textbf{u}}}_{\mu }]\) will denote the directional (variational) derivative of \((\bullet )\left( \tilde{\textbf{u}}_{\mu }(z)\right) \) in the direction \(\delta {\tilde{\textbf{u}}}_{\mu }(z)\), i.e.
which will be simplified, when convenient, to \(\delta (\bullet )(\delta {\tilde{\textbf{u}}_{\mu }})\) as indicated in Eq. (45).
4.9.1 Imposing the Linear Momentum (Equilibrium) Equations in Weak Form: Min–Max RVE Problem
After identifying, in Sect. 4.7, that inaccurate stress distributions arise from not imposing the equilibrium (linear momentum conservation) in the formulation, we take advantage of the minimization problem, in Eqs. (42) to (44), to introduce them in the problem as an additional set of restrictions, \(\textbf{R}({\tilde{\textbf{u}}_{\mu }})=\textbf{0}\), forcing the solution to be a local saddle point in the resulting (over-restricted) solution space. The explicit format of \(\textbf{R}({\tilde{\textbf{u}}_{\mu }})=\textbf{0}\) being:
where the classical linear momentum conservation equations (equilibrium equations) in 3D continuum media can be recognized [73]. It is anticipated that the additional restrictions in Eq. (44) are not being imposed in a strong form, like the ones in Eq. (43), but in a weak form, i.e. by adding them to the minimized functional involving a set of Lagrange multipliers, \({{\varvec{\lambda }}}_{\mu }(z,t)\equiv [{\lambda }_{\mu _{\text {x}}},{\lambda }_{\mu _{\text {y}}},\lambda _{\mu _{\text {z}}}]^T(z,t )\). This transforms the original goal function, \({\dot{\tilde{\Pi }}}_{\mu }({\tilde{\textbf{u}}}_{\mu })\), in Eq. (42), into the extended functional (goal functional), \({\dot{{{\tilde{\Pi }}}}}_{\mu }^{\text {ext}}({{\tilde{\textbf{u}}}}_{\mu }, {{\varvec{\lambda }}}_{\mu })\), in the following min-max problem to be solved at every specific time \(t\in [0, T]\)Footnote 6
Resolution of the min-max problem (47), now in terms of \({\dot{\tilde{\Pi }}}^{\text {ext}}_{\mu }({{\tilde{\textbf{u}}}_{\mu }, {{\varvec{\lambda }}}_{\mu }})\), yield the following nested variational problems:
Remark 10
The min-max problem in Eq. (47) gives rise, through the individual variational problems in Eqs. (48) and (49), a two-field variational problem, in the unknowns \({\tilde{\textbf{u}}}_{\mu }(z)\), \({{\varvec{\lambda }}}_{\mu }(z)\), corresponding to directional maximization/minimization of functional \({\dot{\tilde{\Pi }}}^{\text {ext}}_{\mu }({{\tilde{\textbf{u}}}}_{\mu }, {{\varvec{\lambda }}}_{\mu })\) along directions \({\delta {{\varvec{\lambda }}}}_{\mu }\) and \({\delta {\tilde{\textbf{u}}}}_{\mu }\). The intersection of the two manifolds (i.e. the solution of PROBLEM (I) and solution of PROBLEM (II) solved in any sequence) will provide the intended solution (assumed unique) for the considered RVE problem (47).
4.9.2 Analysis of the Variational Problems
PROBLEM (I), in Eq. (48), yields the following variational scenarios:
where dependencies on the fluctuating displacements \({\tilde{\text {u}}}_{\mu _{\text {x}}}\), \({\tilde{\text {u}}}_{\mu _{\text {y}}}\) and \({\tilde{\text {u}}}_{\mu _{\text {z}}}\), in Eq. (11), are specified in the corresponding terms.
Eqs. (50) and (51) can be conveniently elaborated, focusing on their numerical resolution, yielding the following reformulated variational setting, to be fulfilled at the RVE (see Appendix A for a detailed analysis):
Remark 11
Note the natural boundary conditions, in Eq. (52(c)), stating the null value of the off-plane stresses \({{\varvec{\sigma }}}^{\text {ofp}}_{\mu }(z)\equiv [\tau _{\mu _{\text {xz}}},\tau _{\mu _{\text {yz}}},\sigma _{\mu _{\text {z}}}]^T\) at both ends (\(z=-h^-\) and \(z=+h^+\)) of the RVE, \(\Omega _{\mu }(\textbf{x}^{\mathcal {M}})\) (see Fig. 5). This is a relevant consequence of the proposed enriched formulation, which will be subsequently emphasized.
In turn, PROBLEM (II), in Eq. (49), yields an analytical solution for the unknown \({\dot{\tilde{\textbf{u}}}}_{\mu }\) in terms of \({{\varvec{\lambda }}}_{\mu }\) (see Appendix B for a detailed derivation), i.e.
Outline of the Multiscale 2D+ Finite Element setting: a discretization of the macro-scale domain \(\Omega ^{\mathcal {M}}\) (plate mid-plane) using bi-quadratic 2D elements, b scheme of a macro-scale 9-noded quadrilateral finite element, where the mechanical response at each macro-scale integration point is to be obtained by solving the corresponding filament/RVE problem, c mesoscale RVE domain \(\Omega _{\mu }\) (filament) at the macro-scale point \(\textbf{x}^{\mathcal {M}}\), discretized with 2-noded linear 1D elements, d RVE problem scheme
Remark 12
Equation (53) states that the solutions of fields \({\tilde{ \textbf{u}}}_{\mu }\) and \({{ {\varvec{\lambda }}}}_{\mu }\), in the min/max problem in Eq. (47), live in the same functional space, and fulfill the same essential boundary conditions in the z-spatial domain. In addition, in a pseudo-time evolution context, \(t \in [0,T]\), once the solution \({\tilde{ \textbf{u}}}_{\mu }(z,t)\) is determined in the \({{\mathcal {U}}}_{{\tilde{u}}}\times [0,T]\) domain, solution \({{\varvec{\lambda }}}_{\mu }(z,t)\) can be determined in closed form, through simple time differentiation, i.e. \({{\varvec{\lambda }}}_{\mu }(z,t)=\dfrac{\partial {\tilde{ \textbf{u}}}_{\mu }(z,t)}{\partial t}\). Therefore, only the solution \({\tilde{ \textbf{u}}}_{\mu }(z,t)\) is strictly required to be computed (see Sect. 4.9.3).
4.9.3 Coupled RVE Variational Problem
Coupling the results, in terms of the required functional spaces and variational Eqs. (52) and (53), yields the single field variational problem, in terms of the unknown \({\tilde{\textbf{u}}}_{\mu }(z)\), through the following identifications:
yielding, after the replacement \({\delta {{\varvec{\lambda }}}}_{\mu }\rightarrow {\delta {\tilde{\textbf{u}}}}_{\mu }\) in Eq. (52), the following RVE problem:
Remark 13
As for the solution strategy for the RVE problem, in Eqs. (55), the following aspects are highlighted:
-
1.
Problems in Eqs. (55(a–c)) are partially coupled and they can be sequentially solved. Equation (55(a)) only depends on the unknown \({\tilde{\text {u}}}_{\mu _{\text {x}}}\), so it can be solved independently from the other unknowns. The same happens for Eq. (55(b)), which can be solved independently for \({\tilde{\text {u}}}_{\mu _{\text {y}}}\). Finally, by replacing these results into the right-hand side of Eq. (55(c)), \({\tilde{\text {u}}}_{\mu _{\text {z}}}\) can be solved.
-
2.
In addition, the unknown \({\tilde{\text {u}}}_{\mu _{\text {z}}}\) is only involved in the determination of the vertical stress, \(\sigma _{\mu _{\text {z}}}(\varepsilon _{\mu _{\text {z}}}(z))\), see Remark 5, and, for the illustrative examples presented in Sect. 7, it will be neglected.Footnote 7
-
3.
In consequence, the stress component, \(\sigma _{{\mu }_{\text {z}}}\), as well as the corresponding equation to solve it, (55(c)), are considered not strictly necessary for the purposes of this work and they will be omitted in the remaining of it. Also, the RVE variational problem will be restricted to solving the in-plane components of the fluctuating displacements, i.e. \({\tilde{\textbf{u}}}_{\mu }^{\text {inp}}(z)\equiv [{\tilde{\text {u}}}_{{\mu }_{\text {x}}}(z), {\tilde{\text {u}}}_{{\mu }_{\text {y}}}(z)]^T\), and to find the numerical solution of the two uncoupled 1D BVPs, in Eqs. (55(a)) and (55(b)), for every RVE, \(\Omega _\mu (\textbf{x}^{\mathcal {M}})\).
The problem to be solved is then:
where \({{\varvec{\tau }}}_{\mu }(z)\) is the off-plane shear stress vector defined in Eq. (19(c)).
Remark 14
Note that the issue in Eqs. (36) yielding constant shear stress distributions along the plate depth is not present anymore. This is a key result in this work, which opens expectations of achieving high fidelity results, comparable to the ones obtained through 3D approaches, with the adopted 2D degenerated (linear) kinematics for plate formulations in Eq. (2).
5 Meso-scale Finite Element Solution
5.1 Discretization of the RVE PROBLEM
Attention is here restricted to a specific point of the macro-scale \({\textbf{x}^{\mathcal {M}}}\in \Omega ^{\mathcal {M}}\), where the variational problem in Eq. (56) is going to be solved by means of the finite element method. In this context, the RVE domain \(\Omega _{\mu }(\textbf{x}^{\mathcal {M}}){:=}\left\{ z\in {{\mathcal {R}}}\;;\; z\in [-h^{-}(\textbf{x}^{\mathcal {M}}),+h^{+}(\textbf{x}^{\mathcal {M}})]\right\} \) is discretized in a 1D finite element mesh, with \({N^\text {elem}_{\mu }}\) bi-linear (two-noded) elements \(\Omega _\mu ^{(e)}\) and \(N^\text {node}_{\mu }=N^\text {elem}_{\mu }+1\) nodes at positions \({z}_i\) (\(i=1,2,\dots ,N^\text {node}_{\mu }\)), as shown in Fig. 6.
The fluctuating displacement field \({\tilde{\textbf{u}}}^{\text {inp}}_{\mu }(z)\equiv [{\tilde{\text {u}}}_{{\mu }_{\text {x}}},{\tilde{\text {u}}}_{{\mu }_{\text {y}}}]^T (z)\) and its variation \(\delta {\tilde{\textbf{u}}}^{\text {inp}}_{\mu }\), as well as the corresponding fluctuating strains \({\tilde{{\varvec{\gamma }}}}_{\mu }(\tilde{\textbf{u}}^{\text {inp}}_{\mu })\), are interpolated as usual in the FEM context, i.e.:
where \(\tilde{\textbf{d}}_{i}\equiv [{\tilde{\text {d}}}_{\text {x}},\, {\tilde{\text {d}}}_{\text {y}}]_{i}^T=[{\tilde{\text {u}}}_{\mu _{\text {x}}}(z),\, {\tilde{\text {u}}}_{\mu _{\text {y}}}(z)]^T\vert _{z=z_{i}}\) stands for the vector of in-plane fluctuating displacements at the \(i-th\) node. Replacement of Eqs. (57) and (58) into the problem in Eqs. (56), following the standard FEM procedures, yields the RVE problem providing the fluctuation vector \({\tilde{\mathbf{{u}}}}_{\mu }\) as
Remark 15
The problem in Eq. (59), to be solved at the RVE, displays the following features:
-
1.
The RVE solution is driven by the macroscopic strainsFootnote 8\(\mathbb {\epsilon }^{\mathcal {M}}(\textbf{x}^{\mathcal {M}})\), in Eq. (4), which are down-scaled from the local macro-scale point \({\textbf{x}^{\mathcal {M}}}\). The RVE FE problem, in Eqs. (59), is then solved in an inner loop of the upper macro-scale problem, which is fed with those required strains \(\mathbb {\epsilon }^{\mathcal {M}}(\textbf{x}^{\mathcal {M}})\).
-
2.
This yields a local coupling of the mesoscale solution along the corresponding 1D filament \(\Omega _{\mu }(\textbf{x}^{\mathcal {M}})\), with the unique associate sampling point \({\textbf{x}^{\mathcal {M}}}\) at the plate mid-surface, which, in turn, is discretized in 2D elements. This local coupling allows a computational strategy where the mechanical behavior along the width of the plate (RVE/filament) can be simultaneously (in parallel) computed for all the sampling points \({\textbf{x}^{\mathcal {M}}}\) lying at the plate mid-surface, unlike in a full 3D strategy, which couples every integration point along the width with the (large number of) sampling points in the surrounding 3D FE mesh.
-
3.
The kinematic admissibility condition early established in Eq. (11(b)) imposes that the fluctuating displacements must be equal at the top and bottom boundaries of the RVE. Here, the particular case of imposing both fluctuating displacements \({\tilde{\textbf{d}}}_1={\tilde{\textbf{d}}}_{N_{\mu }^\text {node}}=\textbf{0}\) has been adopted. This represents not only the simplest numerical implementation of restriction (11), but also the most meaningful alternative from a physical point of view: it makes the total micro-scale displacements in (11(a)) coincide with the linearized displacements of Eqs. (8) and (9) at the extremes of the RVE and, consequently, allows the fluctuating displacement field at the RVE to be identified as the actual warping of the plate section (i.e. as those displacements withdrawing from the assumption of straightness of the normal to the plate).
5.2 Iterative Resolution of the Discrete RVE Problem
The problem in Eq. (59) can be solved using a standard iterative Newton–Raphson procedure [74] based on their linearization, in a pseudo-time advancing context, along discrete time-steps (\([t, t+\Delta t]\)). The sketch of the procedure to solve the time-step \([t,t+\Delta t]\), is displayed as follows:
where \((\mathbf{\bullet })^{(i+1)}\) stands for the iterative value of \((\mathbf{\bullet })\) at iteration \((i+1)\) and \( \Delta ^{\text{ iter }}(\mathbf{\bullet })^{(i+1)}\equiv (\mathbf{\bullet })^{(i+1)}-(\mathbf{\bullet )}^{(i)}\) for the iterative increment of \((\mathbf{\bullet })\) at iteration \((i+1)\), respectively. Furthermore, \({\tilde{\textbf{K}}}({\tilde{\textbf{d}}}^{(i)})\) stands for the RVE tangent stiffness matrix, which is to be obtained in Sect. 5.3 throughout the linearization of the RVE problem solution.
5.3 Linearization of the RVE Finite Element Problem
Focusing now on the solution of the RVE FE problem in Eqs. (59), and according to the iterative Newton method proposed through (60), we consider the linearization of the incremental solution \(\Delta {\tilde{\textbf{d}}}_{t+\Delta t}\). For this purpose, we define a specific notation for this variational linearization by denoting the variational increment of an entity \(G(\textbf{x}^{\mathcal {M}})={\big (\bullet \big )}\big ({{\textbf{x}^{\mathcal {M}}},{{\phi }}}(\textbf{x}^{\mathcal {M}}),{\mathbb L}\star {\phi }(\textbf{x})\big \vert _{\textbf{x}={\textbf{x}^{\mathcal {M}}}})\), specified at a point \({\textbf{x}^{\mathcal {M}}}\) and in the direction \(\Delta {\phi }(\textbf{x}^{\mathcal {M}})\), as
where the definition of variational derivative in Eq. (45) has been considered. In Eq. (61), \({{\mathbb {L}}}\) stands for a first-order linear differential operator (i.e. involving linear combinations of first derivatives with respect to the argument \(\textbf{x}\)) and symbol \(\star \) denotes the application of the operator \({{\mathbb {L}}}\) on the term contiguous to \(\star \). Using these concepts, in Appendix C, the linearization of the RVE problem solution \({\Delta \tilde{\textbf{d}}}\,({t+\Delta t})\) according to (60) is derived in terms of the RVE problem data increments, \(\Delta {\mathbb {\epsilon }^{\mathcal {M}}(\textbf{x}^{\mathcal {M}})}\equiv \left[ \Delta {{\varvec{\varepsilon }}}^{\mathcal {M}},\,\Delta {{\varvec{\kappa }}}^{\mathcal {M}},\, \Delta {{\varvec{\gamma }}}^{\mathcal {M}}\right] ^T(\textbf{x}^{\mathcal {M}})\), as postulated in Eqs. (59). The results are sketched in the following:
being


where \({\tilde{\textbf{K}}}(\textbf{x}^{\mathcal {M}})\) is the tangent stiffness matrix of the discretized RVE \({\Omega _{\mu }(\textbf{x}^{\mathcal {M}})}\), \({{\mathbb {G}}}\) is a first-order linear differential operator (again, \(\star \) denotes its application to the contiguous previous/subsequent term), and symbol \(\textbf{I}_{3}\) stands for the \((3 \times 3)\) identity matrix. In Eq. (63(c)), the here termed macro/mesoscale coupling tensors \(\textbf{a}^{\varepsilon }(\textbf{x}^{\mathcal {M}})\), \(\textbf{a}^{\kappa }(\textbf{x}^{\mathcal {M}})\) and \(\textbf{a}^{\gamma }(\textbf{x}^{\mathcal {M}})\), result from the coupling of the macroscopic strains and the mesoscale fluctuating displacements. On the other hand, the extended in-plane constitutive matrix \(\textbf{E}^{\text {inp}}_{\mu }\), in Eq. (63(d)), is built in terms of the three sub-matrices (\(\textbf{D}^{\text {inp}}_{\mu _{\text {x}}}\), \(\textbf{D}^{\text {inp}}_{\mu _{\text {y}}}\), \(\textbf{D}^{\text {inp}}_{\mu _{\text {xy}}}\)) that constitute, respectively, the first to the third rows of the in-plane constitutive matrix \(\textbf{D}^{\text {inp}}_{\mu }\) in Eq. (20(a)).
Remark 16
In Eq. (62), the macroscopic strains \({\Delta {{\varvec{\varepsilon }}^{\mathcal {M}}}}(\textbf{x}^{\mathcal {M}})\) and \({\Delta {{\varvec{\kappa }}^{\mathcal {M}}}}(\textbf{x}^{\mathcal {M}})\) are affected by the linear differential operator \({{\mathbb {G}}}\) in Eq. (63(b)). This is a significant feature of the resulting linearization since it involves first derivatives of the strains at the macro-scale and, therefore, second-order derivatives of the macro-scale displacements, consequently affecting the polynomial order of the required finite element discretization at the macro-scale.
6 Macro-scale Finite Element Solution
6.1 Macro-scale Discretization
The macroscale domain \(\Omega ^{\mathcal {M}}\in {{\mathcal {R}}}^2\) in Eq. (1) (see also Fig. 1), is considered now discretized in a mesh of appropriate finite elements, as shown in Fig. 6, by interpolating the macroscopic displacements \(\mathbb {u}^{\mathcal {M}}(\textbf{x}^{\mathcal {M}})\) of Eq. (3), and the corresponding macroscopic strains \(\mathbb {\epsilon }^{\mathcal {M}}(\textbf{x}^{\mathcal {M}})\) of Eq. (4), involving \(N^\text {elem}\) elements and \(N^\text {node}\) nodes, i.e.:
where \(\textbf{d}\) is the global vector of nodal displacements \(\textbf{d}_{i}\), each one involving five degrees of freedom (corresponding to the five components of \(\mathbb {u}^{\mathcal {M}}(\textbf{x}^{\mathcal {M}})\)), \(\textbf{N}_{i}(\textbf{x}^{\mathcal {M}})\) is the diagonal \((5\times 5)\) macroscopic interpolation matrix corresponding to node i, and \(\textbf{I}_5\) stands for the \((5\times 5)\) identity matrix.
Then, the macroscopic strains become interpolated as:
being \({{\mathbb {L}}}^{\mathcal {M}}\), \({\mathbb L}^{\mathcal {M}}_{\varepsilon }\), \({\mathbb L}^{\mathcal {M}}_{\kappa }\) and \({{\mathbb {L}}}^{\mathcal {M}}_{\gamma }\) linear first-order differential operators that can be trivially derived by examining the expressions in Eqs. (3) and (4):
6.2 Macro-scale Finite Element Problem
Applicat‘ standard Virtual Work Principle to the resolution of the (macro-scale) Reissner-Mindlin plate problem is used here [71]. The sketch of the resulting problem, in a pseudo-time advancing setting \(t\in [0,T]\) (with \({\Delta t}> 0\)), and for a generic time-step \([t,t+\Delta t]\subset [0,T]\), is the following:
where \(\textbf{F}^{\mathcal {M}}_{t+{\Delta t}}(\textbf{x}^{\mathcal {M}})\) stands for the external actions on the plate (in-plane/off-plane forces, torques, etc.) acting on the macroscale domain, \(\Omega ^{\mathcal {M}}\), \({{\varvec{{\mathcal {F}}}}}^{int}_{t+{\Delta t}}\) and \({{\varvec{{\mathcal {F}}}}}^{ext}_{t+{\Delta t}}\) stand, respectively, for the internal and external force vectors acting on the discretized macroscopic domain to be balanced at the solution according to Eqs. (67(b)), and Eq. (67(c)) display the rate form of the mesoscale constitutive model displayed in Eq. (25).
Remark 17
In Eq. (67(c)), the following relevant details are emphasized:
-
The macroscopic constitutive model is described, in rate form, highlighting the equivalence of the macroscopic/generalized stresses, \({{\dot{\mathbb {\Sigma }}}}^{\mathcal {M}}({\textbf{x}^{\mathcal {M}}},t+\Delta t)\), and the corresponding RVE generalized stresses, \({{\dot{\mathbb {\Sigma }}}}_{\mu }({\textbf{x}^{\mathcal {M}}},t+\Delta t)\) (i.e. \({{\dot{\mathbb {\Sigma }}}}^{\mathcal {M}}({\textbf{x}^{\mathcal {M}}},t+\Delta t)\equiv {{\dot{\mathbb {\Sigma }}}}_{\mu }({\textbf{x}^{\mathcal {M}}},t+\Delta t)\)) emerging from the stress homogenization in Eq. (30).
-
The implicit functional dependence of the mesoscale fluctuation field, \({\tilde{\textbf{u}}}_{\mu }\), on the macroscale nodal unknowns, \(\textbf{d}_{t+\Delta t}\), emerging from the resolution of the discrete RVE problems in Eqs. (59) and (60), and the discretization of \(\mathbb {\epsilon }^{\mathcal {M}}_{t+{\Delta t}}\) in Eq. (65), i.e. \({\tilde{\textbf{u}}}_{\mu }(t+\Delta t)={\tilde{\textbf{u}}}_{\mu }\left( \mathbb {\epsilon }^{\mathcal {M}}_{t+{\Delta t}}(\textbf{d}_{t+{\Delta t}})\right) \). Accounting for this dependence is a crucial fact for the correct linearization of the macroscale problem, and to achieve quadratic convergence in an iterative Newton-Raphson procedure.
6.3 Linearization of the Macroscale Finite Element Problem
Application of the variational increment concept, in Eq. (61), to the problem in Eq. (67) yields
In a first step, in Appendix D, elaboration on Eqs. (68(b, c)) is done, to obtain the linearization of the macro-scale constitutive equation, i.e. linearization of the macroscopic stresses, \({\mathbb {\Sigma }}^{\mathcal {M}}_{t+\Delta t}(\textbf{x}^{\mathcal {M}})\), in terms of the macroscopic strains, \(\mathbb {\epsilon }^{\mathcal {M}}_{t+{\Delta t}}(\textbf{x}^{\mathcal {M}})\) accounting for the scales coupling/dependence (see also Remark 17). This is done by implicit substitution of the discretized RVE Problem result, \({\Delta {\tilde{\textbf{d}}}}_{t + \Delta t}\left( {\Delta {\mathbb {\epsilon }}}^{\mathcal {M}}_{t+{\Delta t}}(\textbf{x}^{\mathcal {M}})\right) \) in Eqs. (59)–(60), into Eq. (68(c)) and, then, into Eq. (68(b)). The final result reads:
where, in Eq. (69(a, b)), \({{\mathbb {D}}}^{{\text {alg}}}_{t+\Delta t}\), is the algorithmic (consistent) tangent constitutive operator [75] relating the algorithmic computations of the macroscopic stress, \({\Delta {\mathbb {\Sigma }}}^{\mathcal {M}}_{t+\Delta t}(\textbf{x}^{\mathcal {M}})\), and strain, \({\Delta {\mathbb {\epsilon }}}^{\mathcal {M}}_{t+\Delta t}(\textbf{x}^{\mathcal {M}})\), increments, and \({\mathbb D}^{\mathcal {M}}_{t+\Delta t}({\textbf{x}^{\mathcal {M}}})\) and \({\tilde{{\mathbb {D}}}}_{t+\Delta t}\) are, respectively, the contributions from the Taylor solution and the RVE problem to that linearization. In Eq. (69(d)), \({{\mathbb {G}}}\) is the linear differential operator in Eq. (63(b)), and the sub-matrix entities, \({{\varvec{\alpha }}}^{\varepsilon }(\textbf{x}^{\mathcal {M}})\), \({{\varvec{\alpha }}}^{\kappa }(\textbf{x}^{\mathcal {M}})\), and \({{\varvec{\alpha }}}^{\gamma }(\textbf{x}^{\mathcal {M}})\), in Eq. (69(d)), are derived in Appendix D as:
Remark 18
Notice in Eq. (69(d)) that matrix \({\tilde{{\mathbb {D}}}}_{t+\Delta t}(\textbf{x}^{\mathcal {M}})\) contains the linear differential operator \({{\mathbb {G}}}\), which introduces first order derivatives of the macroscale strain increments, \({\Delta {\mathbb {\epsilon }}}_{t+\Delta t}^{\mathcal {M}}(\textbf{x}^{\mathcal {M}})\) (in Eq. (69(a))), through the operation \({{\mathbb {G}}}\star {\Delta {\mathbb {\epsilon }}}_{t+\Delta t}^{\mathcal {M}}(\textbf{x}^{\mathcal {M}})\). This is a very relevant aspect of the formulation because it introduces numerical computation of the first-order derivatives of the macro-strains and, therefore, second-order derivatives of the macro-scale displacements. In consequence, use of either quadratic finite elements at the macro-scale (see Fig. 6)Footnote 9 or smoothing procedures (which should be also conveniently linearized) for lower order elements, is a condition to obtain algorithmic consistency of the linearized problem. Notice, also, that this is a requirement only to obtain exact linearization of the problem.Footnote 10
Remark 19
Matrix entities, \({{\varvec{\alpha }}}^{\varepsilon }(\textbf{x}^{\mathcal {M}})\), \({{\varvec{\alpha }}}^{\kappa }(\textbf{x}^{\mathcal {M}})\), and \({{\varvec{\alpha }}}^{\gamma }(\textbf{x}^{\mathcal {M}})\), in Eq. (70(a)), can be understood as results of the local coupling (dependence) of the macroscopic strain measures, \({{\varvec{\varepsilon }}}^{\mathcal {M}}(\textbf{x}^{\mathcal {M}})\), \({{\varvec{\kappa }}}^{\mathcal {M}}(\textbf{x}^{\mathcal {M}})\), and \({{\varvec{\gamma }}}^{\mathcal {M}}(\textbf{x}^{\mathcal {M}})\), with the RVE problem solution, \({\tilde{\textbf{u}}}^{\text {inp}}_{\mu }\) (in Eq. (56)). In case the simplified Taylor’s solution of the multiscale problem (\({\tilde{\textbf{u}}}^{\text {inp}}_{\mu }=\textbf{0}\)) [60] is considered they nullify, and all macro/meso coupling terms in the formulation disappear. Intermediate values \(\textbf{a}^{\varepsilon }(\textbf{x}^{\mathcal {M}})\), \(\textbf{a}^{\kappa }(\textbf{x}^{\mathcal {M}})\), and \(\textbf{a}^{\gamma }(\textbf{x}^{\mathcal {M}})\), are derived in Appendix C (see Eq. (C.6(c))).
Therefore, the macro-scale FE problem in Eq. (67) can be rephrased as:
The problem in Eq. (71) is ready to be solved through an iterative Newton–Raphson algorithm, mimicking the one in Eq. (60), for the mesoscale case, as follows:
where \((\mathbf{\bullet })^{(i+1)}\) stands for the iterative value of \((\mathbf{\bullet })\) at iteration \((i+1)\) and \( \Delta ^{\text{ iter }}(\mathbf{\bullet })^{(i+1)}\equiv (\mathbf{\bullet })^{(i+1)}-(\mathbf{\bullet )}^{(i)}\) for the iterative increment of \((\mathbf{\bullet })\) at iteration \((i+1)\), respectively. The algorithmic macro-scale problem consistent tangent matrix \(\textbf{K}^{\text {alg}}_{t + {\Delta t}}\), in Eqs. (71(c)) and (72), is obtained by replacing the algorithmic tangent constitutive operator \({\mathbb D}^\text {alg}_{t+\Delta t}({\textbf{x}^{\mathcal {M}}})\) in Eqs. (69(a)) into Eq. (71(c)) and performing the corresponding algebraic and differential operations, i.e.:
Details of the derivation procedure are displayed in Appendix D, the result being:
where the classical Taylor problem contribution [60], \(\textbf{K}^{\text {Taylor}}_{t +\Delta t}\), (i.e. for null fluctuating displacements, \({\tilde{\textbf{u}}}_{\mu }=\textbf{0}\)) and the fluctuations problem contribution, \(\tilde{\textbf{K}}_{t +\Delta t}\), (due to the fluctuating displacements, \({\tilde{\textbf{u}}}_{\mu }\ne \textbf{0}\)) are recovered.
7 Representative Simulations
Numerical tests to check the performance of the proposed 2D+ approach are presented in this section. These tests evaluate two crucial features for the numerical simulation of non-linear multilayered-plate problems: a) the computational efficiency, in terms of the computational cost, and b) the numerical accuracy to evaluate the stresses at representative spatial points. Such features are evaluated by comparing the 2D+ approach results with reference solutions obtained with an equivalent 3D numerical model, considering different stacking configurations of plies and non-linear material behavior.
7.1 Computational Efficiency
A numerical study is conducted on a simply supported squared laminated plate, subjected to a uniform distributed load, as depicted in Fig. 7. The study evaluates speedup factors by comparing the computational time required for 2D+ simulations versus 3D simulations in various scenarios. These speedup factors are assessed with different finite element meshes, and the computational time demanded by each model is estimated on the basis of a single linear-elastic iteration.
The plate, with side length \(L_x=L_y=2\text {m}\), is constituted by a cross-layered plate of \(N_\text {layer}\) orthotropic layers oriented at \(0^\circ \) and \(90^\circ \), as illustrated in Fig. 7. The thickness of each \(i-\)th layer is \(h_i=1.6 \text {mm}\) so the total plate thickness is \(h=h_i \times N_\text {layer}\). The material properties are defined in the material coordinate system, which in turn is assumed to coincide with the global (x, y, z) coordinate system for a zero-degree rotation around the z-axis. Such properties are:
where \(E_i\) stands for the elastic modulus along i-th direction, \(G_{ij}\) corresponds to the shear modulus for the \(i-j\) plane, and \(\nu _{ij}\) is the corresponding Poisson’s ratio, for \(i,j=\{1,2,3\}\). The in-plane rotation of the constitutive properties for each layer is accounted for by means of standard transformation rules (cf. [71] for a detailed insight on the topic).
Simply-supported square plate under a uniformly distributed load, \(q_0\), constituted by \(N_\text {layer}\) layers stacked in a \({[0/90]}_N\) multi-layered configuration, for \(N=N_{\text {layer}}/2\) and \(N_{\text {layer}}=\{8,12,16,20,24,28,32\}\). a 3D setting, b multi-scale 2D setting, and c in-plane FE discretization with \(N^{\text {elem}}=\{16,32,48\}\) elements in each mid-plane direction x, y. Every layer is discretized in 3 1D-linear elements
The symmetry of the problem is exploited to analyze only one in-plane quadrant of the plate, i.e., \({\varvec{x}}\in [L_\text {x}/2, L_\text {x}]\times [L_\text {y}/2, L_\text {y}]\). This reduced domain is then discretized using a regular structured mesh of 27-node tri-quadratic hexahedral elements, for the 3D analysis, and 9-noded bi-quadratic quadrilateral elements at the macro-scale and 2-node linear elements for the micro-scale, for the Multiscale 2D+ model. For both cases, the number of in-plane elements (i.e. located on the plate’s (x,y) plane) is \(N^\text {elem}\times N^\text {elem}\), and the number of elements across the thickness of each layer is kept always constant and equal to three.
A uniform distributed load of magnitude \(q_0\) is applied over the macroscale domain of the Multiscale 2D+ model and over the upper surface of the 3D model. The adopted boundary conditions read
for the 3D model, and
for the Multiscale 2D+ model at the macro-scale. Boundary conditions at the micro-scale are null fluctuating displacements at \(z=\pm h_\text {T}\), representing the simplest alternative within the kinematic admissibility restrictions stated in Eq. (11(b)).
Speedup factorsFootnote 11 are presented in Fig. 8 for different laminate configurations, \(N_{\text {layer}}=\{8,12,16,20,24,28,32\}\), and several in-plane discretizations, \(N^{\text {elem}}=\{16, 32, 48\}\). The results exhibit an increasing speedup factor for finer mesh discretizations. Even for coarse meshes, i.e., \(N^{\text {elem}}=16\), a speedup factor of at least one order of magnitude is observed, while for the finest mesh, i.e. for \(N^{\text {layer}}=32\) and \(N^{\text {elem}}=48\), the Multiscale 2D+ model achieves a remarkable speedup factor of 1800 compared to the full 3D simulation. Based on the obtained results, the speedups attained with a significantly finer in-plane mesh, \(N^{\text {elem}}=100\), are estimated using linear regression for every fixed number of plies, and they are also displayed in Fig. 8. In this case, significant speedup values of up to 4400 could be expected.
Simply supported square plate. Numerical results for a set of increasing mesh discretizations (\(N^{\text {elem}}\)) and a number of layers (\(N_{\text {layer}}\)). The speedup factor for each number of plies is evaluated as the ratio between the computing times of the corresponding 3D analysis and the proposed Multiscale 2D+ approach. The obtained results for \(N^{\text {elem}}=16\), 32, and 48 are represented by circle, square, and triangle markers, respectively. Based on these results, the speedup factor for \(N^{\text {elem}}=100\) is linearly extrapolated and displayed with diamond markers. The corresponding linear regressions for each in-plane mesh discretization are depicted with a solid line, a dashed line, a dot-dashed line, and a dotted line, respectively
7.2 Accuracy Assessment
The multiscale 2D+ approach accuracy is first evaluated by using as a reference problem the one proposed by Pagano [76] with an analytical solution provided by the 3D elasticity theory. This test has been used for accuracy assessments in many composite laminate theories available in the literature, such as [46] or [77].
The accuracy assessment procedure evaluates the agreement between the exact solutions for displacements and the through-the-thickness stresses (from Pagano) versus the Multiscale 2D+ one. For the sake of completeness, the results obtained with a full-3D finite element analysis are included. The study is performed with a square, simply supported laminated plate subjected to a sinusoidal load distributed over the upper surface, as shown in Fig. 9. The geometry of the plate is defined by the in-plane lengths \(L_x=L_y=L\) and the thickness of the laminate, h. Three orthotropic layers [0/90/0] of equal thickness, h/3, constitute the laminate. The considered, non-dimensional, elastic material properties expressed in the material coordinate system, read:
Test from Pagano [76]. The square simply supported [0/90/0] (symmetric cross-layered) plate is loaded with a sinusoidal distributed transverse load \(q_0(x,y)=q_0 \cos (\pi x / L_x) \cos (\pi y/L_y)\) on the upper surface. Due to symmetries of the problem, only one quarter, \(\textbf{x}\equiv [x,y,z]\in \left[ 0, L_\text {x}/2\right] \times \left[ 0, L_\text {y}/2\right] \times [0,h]\) of the plate mid-surface is analyzed. The example is evaluated for the set of slenderness ratios \(\lambda \equiv L_{\text {x}}/h\in \{4,10,20,50,100,200\}\) using a a 3D finite element model discretized with 27-noded tri-quadratic hexahedral element and b a 2D+ multi-scale model discretized with 9-noded quadrilateral elements
As in the previous example, the symmetry of the problem allows us to evaluate a quarter of the plate, i.e., \(\textbf{x}\equiv [x,y,z]\in \left[ 0,\tfrac{L_\text {x}}{2}\right] \times \left[ 0,\tfrac{L_\text {y}}{2}\right] \times [0,h]\). The 2D+ multiscale model is assessed with a structured regular mesh of 9-noded quadrilateral elements at the macro-scale and 2-noded 1D elements at the micro-scale. It is combined with simply supported boundary conditions at the structural scale, i.e.:
and the sinusoidal distributed vertical load \(q(x,y) = q_0\,cos(\pi x /L_x)\,cos(\pi y /L_y)\) also on the 2D macro-scale domain. The full 3D model uses a structured mesh of 27-noded tri-quadratic hexahedral elements. The load is applied over the upper surface of the plate with the following boundary conditions:
Several plates with different slenderness ratios, \(\lambda =L/h\), are considered to evaluate the accuracy of the model, namely \(\lambda =\{4,10,20,50,100,200\}\). When plates of high \(\lambda \) are simulated, the 3D model numerical solutions may be affected by ill-conditioning if excessively high finite element slenderness ratios, \(\lambda _\text {el}\), are used. To avoid this effect, the in-plane 3D model mesh discretization must be progressively increased as \(\lambda \) increases, keeping \(\lambda _\text {el}\) approximately constant. An acceptable \(\lambda _\text {el}=12\) is chosen that leads to the following set of (\(N^\text {elem}\times N^\text {elem}\)) in-plane mesh discretizations: \(N^\text {elem}=\{2, 5, 10, 25, 50, 100\}\) with \(\lambda \in \{4,10,20,50,100,200\}\), respectively. Although the multiscale 2D+ solutions does not suffer from this ill-conditioning effect, we use similar in-plane discretizations (at the macro-scale) to avoid possible biases in the comparative analyses. Each layer is modeled with four elements in the thickness direction, for both the multiscale 2D+ and 3D finite element models.
Solutions of the normalized deflections at the center of the plate, computed as \(\bar{\text {u}}_\text {z} = \text {u}_{\text {z}}(0,0,h)\tfrac{100 E_{2}}{q_0 \lambda ^3\,L}\), are displayed in Table 1. These results show that the Multiscale 2D+ approach performs well in thin and moderately thick plate configurations.
Test from Pagano [76]. In-plane normal stress \(\overline{\sigma }_\text {x}\) distribution throughout the normalized thickness \(\overline{z}=z/h\) of the plate at in-plane point (A, A), located near the center of the plate. Solutions for different slenderness \(\lambda \in \{20,50,100,200\}\) are displayed at the top-left, the top-right, the bottom-left, and bottom-right corners, respectively. The analytical solution from Pagano [76] is displayed in a black solid line, while each Gauss point of the numerical solutions is represented by gray squares and white circles for the 3D analysis and the Multiscale 2D+ approach, respectively
Test from Pagano [76]. Off-plane shear stresses, \(\overline{\tau }_\text {yz}\), throughout the normalized thickness \(\overline{z}=z/h\) of the plate at the in-plane point (A, B), located near the intersection of the midplane \(x=0\) of the plate and the boundary side \(y=L/2\). Solutions for different slenderness ratios \(\lambda \in \{20,50,100,200\}\) are displayed at the top-left, the top-right, the bottom-left, and bottom-right corners, respectively. The analytical solution from Pagano [76] is displayed in a black solid line, while each Gauss point of the numerical solutions is represented by gray squares and white circles for the 3D analysis and the Multiscale 2D+ approach, respectively
Test from Pagano [76]. Off-plane shear stresses \(\overline{\tau }_\text {xz}\) throughout the normalized thickness \(\overline{z}=z/h\) at in-plane point (B, A), located near the intersection of the mid-plane \(y=0\) of the plate and the boundary side \(x=L/2\). Solutions for different slenderness ratios \(\lambda \in \{20,50,100,200\}\) are displayed at the top-left, the top-right, the bottom-left, and bottom-right corners, respectively. The analytical solution from Pagano [76] is displayed in black solid-line, while each Gauss point of the numerical solutions is represented by gray squares and white circles for the 3D analysis and the Multiscale 2D+ approach, respectively
Simply supported rectangular plate, with a constant surface load, \(q_0\), constituted by 10 layers stacked in a sequence \([\text {Stiff}/\text {Soft}]\) or \([\text {I},\text {II}]\) laminate configuration (see Table 2). a 3D setting and b Multi-scale 2D setting. \(L_\text {x}\), \(L_\text {y}\) and h are set to 10 mm, 10 mm, and 0.1 mm, respectively. In this case, stresses are compared at 4 points (A, B, C, and D), the first three separated 0.19 mm from each surface, and the last one located at the center of the quadrant. Due to the symmetries of the problem and the materials, only \(\sigma _\text {x}\), \(\sigma _\text {xy}\), and \(\tau _\text {xz}\) stress distributions are studied at points A and D, while at points B and C, \(\tau _\text {yz}\) and \(\tau _\text {xz}\) are compared, respectively
The through-the-thickness stress distributions are plotted in Figs. 10 to 12 for slenderness ratios \(\lambda \) = 20, 50, 100, and 200. As proposed in Pagano [76], these plots are shown in terms of the normalized thickness coordinate \(\bar{z}=z/h\). The following expressions for the normalized stresses are considered:
In such Figures, the Gauss point solutions for the normalized stresses obtained with the Multiscale 2D+ and the 3D finite element models are compared against the analytical solution. Three specific in-plane locations over the plate are plotted, which are close to the points where each stress component is expected to reach its maximum value (see the highlighted points in Fig. 9). Thus, defining \(A=0.106(L/2)\) and \(B=0.894(L/2)\), we consider the in-plane point (A, A) to evaluate the in-plane stresses \(\overline{\sigma }_\text {x}\) (see the results in Fig. 10), and the in-plane points (A, B) and (B, A) to evaluate the off-plane stresses \(\overline{\tau }_\text {yz}\) and \(\overline{\tau }_\text {xz}\), respectively (cf. Figs. 11 and 12). A close agreement for the in-plane and off-plane stress distributions is achieved for solutions obtained with Multiscale 2D+, analytical, and full-3D analysis.
7.3 Accuracy in Material Non-linear Analyses: Simply Supported Squared Plate Under Distributed Load
The simply supported plate under a uniformly distributed load, q, with dimensions \(L_\text {x}=L_\text {y}=L=10\,\text {mm}\) and slenderness ratio \(\lambda =L/h=100\),Footnote 12 depicted in Fig. 13, is studied. For symmetry reasons, only a quarter of the plate is modeled. The essential boundary conditions imposed at the macro-scale for the 2D+ case are:
An analogous set of boundary conditions for the full 3D analysis can be written as:
The ply materials are endowed with a continuum damage model (cf. [78]). The material parameters for the two plies are described in Table 2.
A \(40\times 40\) in-plane FE discretization for the quarter of the plate is considered in the 2D+ and 3D models. The through-the-thickness RVE discretization of the 2D+ model consists of three 3-node quadratic elements per layer, yielding a total of 30 quadratic elements for both models.
The total load-deflection curves resulting from 2D+ and 3D numerical simulations show good agreement, as depicted in Fig. 14(a). Notably, the 2D+ approach exhibits limited sensitivity to mesh refinement beyond the \(40\times 40\) in-plane discretization. In contrast, the 3D model displays higher sensitivity to in-plane discretization refinement, possibly due to ill-conditioning caused by the 3D element aspect ratio, as mentioned in previous examples. This ill-conditioning demands additional in-plane refinement, particularly when aspect ratios exceed 20. Remarkably, the 2D+ multiscale strategy does not suffer from this limitation.
Simply supported rectangular plate. a Force-displacement structural curves for the 3D and Multiscale approaches, represented by a dashed line with square markers, and a solid line with circular markers, respectively. The control displacement \(\text {u}_\text {z}\) corresponds to the vertical displacement at the center of the plate. b Final displacement field and c the resultant damage field of the plate displayed on the deformed shape for the last step of the non-linear simulation, and d a detailed view of the center of the plate. The displacements have been amplified 5 times
Points A, B, C, and D, in Fig. 13(b), are selected as sampling points for comparison purposes. In such points, we analyze stress states with distinct axial versus transverse shear stress ratios. Damage and stresses (\(\sigma _{\text {xx}}\) and \(\tau _{\text {xz}}\)) at point A are plotted for an intermediate and final step. Damage nucleation starts in the points where tensile and compressive stresses are maximum (top and bottom edges). Axial stresses, \(\sigma _{\text {xx}}\), are plotted in the bottom part of Fig. 15 together with the shear stresses, \(\tau _{\text {xz}}\). Although the shear stresses are negligible compared to axial stresses, an excellent agreement between 3D and 2D+ results is observed. Shear stress distributions, \(\tau _{\text {xz}}\) are shown in Fig. 16. Results obtained with the 2D+ and 3D models are in very good agreement. Note that the magnitude of these stresses is three orders below that of the axial ones.
Simply supported rectangular plate. Top: Damage (d), bottom: axial stresses (\(\sigma _{\text {xx}}\)) and shear stresses (\(\tau _{\text {xz}}\)) at point A, along the thickness of the plate. Steps 10 and 30 are illustrated on the left and right parts of the Figure, respectively. 3D results are plotted in black solid lines, and 2D+ solutions at each Gauss point are plotted with red circles. The shaded regions of the plots with different colors emphasize the positions of the alternating layers (materials I and II in Fig. 13): darker gray indicates stiffer material plies and the soft gray indicates the soft ones
Simply supported rectangular plate. Shear stress (\(\tau _{\text {xz}}\)) distribution at point A along the thickness of the plate. Steps 10 and 30 are illustrated on the left and right parts of the Figure, respectively. 3D results are in black solid lines, and 2D+ Multiscale results are in red circles. The shaded regions of the plots with different colors emphasize the positions of the alternating layers (materials I and II in Fig. 13): darker gray indicates stiffer material plies and the soft gray indicates the soft ones
Simply supported rectangular plate. Axial stresses, \(\sigma _{\text {xx}}\) and \(\sigma _{\text {yy}}\), and shear stresses, \(\tau _{\text {xz}}\) and \(\tau _{\text {yz}}\), distributions, at points C and B, respectively, along the thickness of the plate for the last loading conditions. 3D results are in black solid lines, and 2D+ Multiscale results are in red circles. The shaded regions of the plots with different colors emphasize the positions of the alternating layers (materials I and II in Fig. 13): darker gray indicates stiffer material plies and the soft gray indicates the soft ones
Simply supported rectangular plate. Top: damage (d), bottom: axial stress (\(\sigma _{\text {xx}}\)) and shear stress (\(\sigma _{\text {xy}}\)) distributions at point D along the thickness of the plate. Steps 10 and 30 are illustrated on the left and right of the Figure, respectively. 3D results are in black solid lines, and 2D+ Multiscale results are in red circles. The shaded regions of the plots with different colors emphasize the positions of the alternating layers (materials I and II in Fig. 13): darker gray indicates the stiffer material layers and the soft gray indicates the soft ones
The distribution of axial stresses (\(\sigma _{\text {xx}}\) and \(\sigma _{\text {yy}}\)) and shear stresses (\(\tau _\text {xz}\) and \(\tau _\text {yz}\)) at points B and C are shown in Fig. 17. At the top part of Fig. 17, the through-the-thickness transverse stresses are of a similar order of magnitude to the axial stresses. The solutions provided by the 2D+ and 3D approaches agree very well. Additionally, a close-up view of the shear stress distributions (at the bottom of the Figure) shows that the trends of the curves are well captured, and the possible discrepancies are negligible compared to the magnitude of the axial stresses. Damage (d), axial stress (\(\sigma _{\text {xx}}\)), and in-plane shear stress (\(\sigma _{\text {xy}}\)) for intermediate and final time steps at point D are reported in Fig. 18. A good agreement is observed between the 2D+ and 3D solutions.
Fig. 19 displays the sensitivity of the shear stress (\(\tau _{\text {xz}}\)), at point D, to the in-plane mesh refinement. Like in the previous case, it is noticed that, unlike the 3D solutions, the 2D+ results are insensitive to mesh refinement. Again, this effect is assumed due to the higher slenderness of the 3D finite elements, translating into some degree of ill-conditioning for coarser meshes and decreasing with mesh refinement.
Simply supported rectangular plate. Effects of the mid-plane mesh refinement on the shear stress, \(\tau _{\text {xz}}\) at point D. Results upon mid-plane mesh refinement from \(30\times 30\) (left) and \(40\times 40\) (right) finite elements. 3D results are in black solid lines, and 2D+ Multiscale results are in red circles. The shaded regions of the plots with different colors emphasize the positions of the alternating layers (materials I and II in Fig. 13): darker gray indicates stiffer material plies and the soft gray indicates the soft ones
8 Concluding Remarks
In this work, a novel proposal, the 2D+ approach, to tackle the computational modeling of complex multilayered plates under bending dominated problems has been explored. This proposal follows the hierarchical multiscale formalism as a way to condense the thickness dimension of the problem, from 3D to 2D, via the unique, and well-settled, mechanical context provided by multiscale computational homogenization techniques. Therefore, and according to this formalism, it includes the following ingredients:
-
The mid-plane of the plate stands for the 2D macroscale domain, where the macroscale displacement field is defined via the standard Reissner-Mindlin kinematics for plates (Sect. 4.1).
-
The mesoscale kinematics is modeled through linearization of the macro-scale kinematics along the 1D plate filament, orthogonal to every mid-plane point and spanning the plate width, defining the Representative Volume Element (RVE). This linearized displacement field is then supplemented with the unknown, mesoscale fluctuating displacements field, typical of hierarchical first-order multiscale formulations, with a null gradient average on the RVE: the classical fluctuating displacement restriction (Sect. 4.2).
-
A mechanical energy balance across scales is established by applying the Hill–Mandel principle, i.e.: imposing energy conservation across the scales. This provides 1) a closed-form expression for the macro-scale generalized stresses and 2) the variational RVE problem, supplying the fluctuating displacements at every RVE in an uncoupled way with respect to the other RVEs. This keeps the resulting computational costs in the range of the 2D-plates analyses and allows envisaging large computational cost savings with respect to full 3D modeling (Sect. 4.6.1).
-
The 2D+ approach explores an innovative way for overcoming the traditional problem arising from 2D degenerated kinematics plate theory the distribution of shear stresses along the plate thickness is piece-wise constant, which is in contradiction with what is obtained in 3D analyses (see Sect. 4.9): the RVE problem is enhanced to satisfy the 3D linear momentum balance (equilibrium) equations as an additional (local) restriction along it. This translates into stress solutions that very closely approximate the ones provided by the 3D model, without breaking the aforementioned uncoupling with other RVEs provided by the multiscale setting (Sect. 4.9).
-
The merits of the multiscale 2D+ approach presented in this work are displayed, for bending dominated structural problems in multilayered plates, by comparison with high-fidelity 3D simulationsFootnote 13. These results show that the trade-off between the accuracy of the model and its computational burden compares very favorably with the one in full 3D simulations in the considered setting.Footnote 14 However, the authors are aware that the 2D+ approach, though providing encouraging results, is still restricted to multilayered structural objectsFootnote 15 in bending-dominated scenarios. Research on its possible extension to more general and realistic contexts (e.g. laminated composites) is currently being undertaken.
Notes
From now on super index \((\bullet )^{\mathcal {M}}\), will be used for entities \((\mathbf \bullet )\) living at the macroscale \(\Omega ^\mathcal {M}\).
In the following, small displacements/small-strain kinematics will be considered.
From now on sub-index \((\bullet )_{\mu }\) will denote entities living at the mesoscale domain (i.e., the RVE \(\Omega _{\mu }(\textbf{x}^{\mathcal {M}})\)).
For notation simplicity, dependencies on the pseudo-time, t, will be omitted whenever it is not essential.
Which is, precisely, the main morphological feature exhibited by multilayered plates.
In the following, explicit time dependence of the considered entities will be omitted unless strictly necessary, i.e. \((\bullet )(z,t)\rightarrow (\bullet )(z)\)
However, its consideration is a straight forward generalization of the case considered here.
Thus, from them, all derived entities at the macroscale: stresses, stress and strain derivatives, etc. are obtainable.
The option chosen in the examples of Sect. 7
Thus, to achieve quadratic convergence of Newton’s algorithm in the algorithmic solution procedure.
Numerical simulations have been performed running an in-house MATLAB code on a cluster with 2\(\times \)AMD EPYC 7451 CPUs (with 96 threads) and 1 TB DDR4 RAM, exploiting the most efficient computation strategies for each approach. In particular, the 3D implementation benefits from Matlab’s vectorization, while the 2D+ multiscale code exploits the inherent parallelization of the RVEs’ evaluation at the macro-scale Gauss-point level. In addition, to ensure a fair comparison, a direct solver has been selected to avoid any solver-related effects on the computational cost for each method.
h is the total thickness of the plate.
Which are considered here a sort of high fidelity Direct Numerical Simulation (DNS).
It is emphasized that free edge effects (c.f. [79, 80]) that can potentially initiate inter-layer delamination in multilayered structural materials settings, as in laminated composites, are not accounted yet, in the presented 2D+ approach, which is restricted to multilayered bending-dominated plates.
Delamination effects, and possible local failure in matrix and fiber components, in laminated composites are not considered yet.
Note the uncoupled character of the in-plane stresses (\(\sigma _{\text {x}},\sigma _{\text {y}},\sigma _{\text {xy}}\)) and the off-plane stresses (\(\tau _{\text {xz}},\tau _{\text {yz}},\sigma _{\text {z}}\))
Abbreviations
- CLPT:
-
Classical Plate Theories
- ESL:
-
Equivalent Single Layer
- FE:
-
Finite Elements
- FE\(^2\) :
-
Finite Element Square
- FSDT:
-
First Order Shear Deformation Theory
- HPR-FE\(^2\) :
-
High-Performance Reduced Finite Element Square
- LWT:
-
Layerwise Theory
- MMVP:
-
Method of Multiscale Virtual Power
- NTFA:
-
Non-uniform Transformation Field Analysis
- RVE:
-
Representative Volume Element
- RZT:
-
Refined Zigzag Theories
- TBT:
-
Timoshenko Beam Theory
- ZT:
-
Zigzag Theory
References
Reissner E (1944) On the theory of bending of elastic plates. J Math Phys 23(1–4):184–191. https://doi.org/10.1002/sapm1944231184
Reissner E (1985) Reflections on the theory of elastic plates. Appl Mech Rev 38(11):1453–1464. https://doi.org/10.1115/1.3143699
Reissner E (1945) The effect of transverse shear deformation on the bending of elastic plates. J Appl Mech 12(2):69–77. https://doi.org/10.1115/1.4009435
Mindlin RD (1951) Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates. J Appl Mech 18(1):31–38. https://doi.org/10.1115/1.4010217
Whitney JM, Leissa AW (1969) Analysis of heterogeneous anisotropic plates. J Appl Mech 36(2):261–266. https://doi.org/10.1115/1.3564618
Whitney JM, Pagano NJ (1970) Shear deformation in heterogeneous anisotropic plates. J Appl Mech 37(4):1031–1036. https://doi.org/10.1115/1.3408654
Reissner E (1979) Note on the effect of transverse shear deformation in laminated anisotropic plates. Comput Methods Appl Mech Eng 20(2):203–209. https://doi.org/10.1016/0045-7825(79)90018-5
Reissner E (1972) A consistent treatment of transverse shear deformations in laminated anisotropic plates. AIAA J 10(5):716–718. https://doi.org/10.2514/3.50194
Timoshenko SP (1921) On the correction for shear of the differential equation for transverse vibrations of prismatic bars. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 41(245):744–746. https://doi.org/10.1080/14786442108636264
Liu D, Li X (1996) An overall view of laminate theories based on displacement hypothesis. J Compos Mater 30(14):1539–1561. https://doi.org/10.1177/002199839603001402
Reddy JN (1984) A simple higher-order theory for laminated composite plates. J Appl Mech 51(4):745–752. https://doi.org/10.1115/1.3167719
Reddy JN (1990) A general non-linear third-order theory of plates with moderate thickness. Int J Non-Linear Mech 25(6):677–686. https://doi.org/10.1016/0020-7462(90)90006-U
Whitney JM, Sun CT (1973) A higher order theory for extensional motion of laminated composites. J Sound Vib 30(1):85–97. https://doi.org/10.1016/S0022-460X(73)80052-5
Sun C-T, Whitney JM (1973) Theories for the dynamic response of laminated plates. AIAA J 11(2):178–183. https://doi.org/10.2514/3.50448
Murty AVK (1977) Higher order theory for vibrations of thick plates. AIAA J 15(12):1823–1824. https://doi.org/10.2514/3.7490
Lo KH, Christensen RM, Wu EM (1977) A high-order theory of plate deformation–part 2: Laminated plates. J Appl Mech 44(4):669–676. https://doi.org/10.1115/1.3424155
Lo KH, Christensen RM, Wu EM (1978) Stress solution determination for high order plate theory. Int J Solids Struct 14(8):655–662. https://doi.org/10.1016/0020-7683(78)90004-5
Barbero EJ, Reddy JN (1991) Modeling of delamination in composite laminates using a layer-wise plate theory. Int J Solids Struct 28(3):373–388. https://doi.org/10.1016/0020-7683(91)90200-Y
Barbero EJ, Reddy JN, Teply J (1990) An accurate determination of stresses in thick laminates using a generalized plate theory. Int J Numer Meth Eng 29(1):1–14. https://doi.org/10.1002/nme.1620290103
Li D (2021) Layerwise theories of laminated composite structures and their applications: a review. Arch Comput Methods Eng 28(2):577–600. https://doi.org/10.1007/s11831-019-09392-2
Reddy JN (1987) A generalization of two-dimensional theories of laminated composite plates. Commun Appl Numer Methods 3(3):173–180. https://doi.org/10.1002/cnm.1630030303
Reddy JN, Barbero EJ, Teply JL (1989) A plate bending element based on a generalized laminate plate theory. Int J Numer Meth Eng 28(10):2275–2292. https://doi.org/10.1002/nme.1620281006
Reddy JN (1989) On the generalization of displacement-based laminate theories. Appl Mech Rev 42(11S):213–222. https://doi.org/10.1115/1.3152393
Robbins DH Jr, Reddy JN (1993) Modelling of thick composites using a layerwise laminate theory. Int J Numer Meth Eng 36(4):655–677. https://doi.org/10.1002/nme.1620360407
Reddy YSN, Moorthy CMD, Reddy JN (1995) Non-linear progressive failure analysis of laminated composite plates. Int J Non-Linear Mech 30(5):629–649. https://doi.org/10.1016/0020-7462(94)00041-8
Whitcomb JD, Woo K (1993) Application of iterative global/local finite-element analysis. part 1: Linear analysis. Commun Numer Methods Eng 9(9):745–756. https://doi.org/10.1002/cnm.1640090905
Muheim Thompson D, Hayden Griffin O (1990) 2-D to 3-D global/local finite element analysis of cross-ply composite laminates. J Reinf Plast Compos 9(5):492–502. https://doi.org/10.1177/073168449000900506
Chang F-K, Perez JL, Chang K-Y (1990) Analysis of thick laminated composites. J Compos Mater 24(8):801–822. https://doi.org/10.1177/002199839002400802
Jones R, Callinan R, Teh KK, Brown KC (1984) Analysis of multi-layer laminates using three-dimensional super-elements. Int J Numer Meth Eng 20(3):583–587. https://doi.org/10.1002/nme.1620200316
Pagano NJ, Soni SR (1983) Global-local laminate variational model. Int J Solids Struct 19(3):207–228
Wang ASD, Crossman FW (1978) Calculation of edge stresses in multi-layer laminates by sub-structuring. J Compos Mater 12(1):76–83. https://doi.org/10.1177/002199837801200106
Carrera E (2003) Historical review of zig-zag theories for multilayered plates and shells. Appl Mech Rev 56(3):287–308. https://doi.org/10.1115/1.1557614
Di Sciuva M (1985) Development of an anisotropic, multilayered, shear-deformable rectangular plate element. Comput Struct 21(4):789–796. https://doi.org/10.1016/0045-7949(85)90155-5
Sciuva M (1986) Bending, vibration and buckling of simply supported thick multilayered orthotropic plates: an evaluation of a new displacement model. J Sound Vib 105(3):425–442. https://doi.org/10.1016/0022-460X(86)90169-0
Murakami H (1986) Laminated composite plate theory with improved in-plane responses. J Appl Mech 53(3):661–666. https://doi.org/10.1115/1.3171828
Averill RC (1994) Static and dynamic response of moderately thick laminated beams with damage. Compos Eng 4(4):381–395. https://doi.org/10.1016/S0961-9526(09)80013-0
Tessler A, Sciuva MD, Gherlone M (2007) Refinement of Timoshenko beam theory for composite and sandwich beams using zigzag kinematics. Technical report, NASA
Tessler A, Di Sciuva M, Gherlone M (2009) A refined zigzag beam theory for composite and sandwich beams. J Compos Mater 43(9):1051–1081. https://doi.org/10.1177/0021998308097730
Iurlaro L, Gherlone M, Di Sciuva M, Tessler A (2015) Refined zigzag theory for laminated composite and sandwich plates derived from Reissner’s mixed variational theorem. Compos Struct 133:809–817. https://doi.org/10.1016/j.compstruct.2015.08.004
Groh R, Weaver P, Tessler A (2015) Application of the refined zigzag theory to the modeling of delaminations in laminated composites. Technical report, NASA
Eijo A, Oñate E, Oller S (2013) A numerical model of delamination in composite laminated beams using the LRZ beam element based on the refined zigzag theory. Compos Struct 104:270–280. https://doi.org/10.1016/j.compstruct.2013.04.035
Oñate E, Eijo A, Oller S (2012) Simple and accurate two-noded beam element for composite laminated beams using a refined zigzag theory. Comput Methods Appl Mech Eng 213–216:362–382. https://doi.org/10.1016/j.cma.2011.11.023
Fan C, Jar P-YB, Cheng JJR (2008) Cohesive zone with continuum damage properties for simulation of delamination development in fibre composites and failure of adhesive joints. Eng Fract Mech 75(13):3866–3880. https://doi.org/10.1016/j.engfracmech.2008.02.010
Di Sciuva M, Gherlone M (2003) A global/local third-order Hermitian displacement field with damaged interfaces and transverse extensibility: FEM formulation. Compos Struct 59(4):433–444. https://doi.org/10.1016/S0263-8223(02)00169-1
Sciuva MD, Gherlone M (2005) Quasi-3d static and dynamic analysis of undamaged and damaged sandwich beams. J Sandwich Struct Mater 7(1):31–52. https://doi.org/10.1177/1099636205043821
Auricchio F, Sacco E (2003) Refined first-order shear deformation theory models for composite laminates. J Appl Mech 70(3):381–390. https://doi.org/10.1115/1.1572901
Tessler A (2015) Refined zigzag theory for homogeneous, laminated composite, and sandwich beams derived from reissner’s mixed variational principle. Meccanica 50(10):2621–2648. https://doi.org/10.1007/s11012-015-0222-0
Kutlu A, Dorduncu M, Rabczuk T (2021) A novel mixed finite element formulation based on the refined zigzag theory for the stress analysis of laminated composite plates. Compos Struct 267:113886. https://doi.org/10.1016/j.compstruct.2021.113886
Reissner E (1984) On a certain mixed variational theorem and a proposed application. Int J Numer Meth Eng 20(7):1366–1368. https://doi.org/10.1002/nme.1620200714
Arteiro A, Catalanotti G, Reinoso J, Linde P, Camanho PP (2019) Simulation of the mechanical response of thin-ply composites: from computational micro-mechanics to structural analysis. Arch Comput Methods Eng 26(5):1445–1487. https://doi.org/10.1007/s11831-018-9291-2
Catalanotti G, Camanho PP, Marques AT (2013) Three-dimensional failure criteria for fiber-reinforced laminates. Compos Struct 95:63–79. https://doi.org/10.1016/j.compstruct.2012.07.016
Laux T, Gan KW, Tavares RP, Furtado C, Arteiro A, Camanho PP, Thomsen OT, Dulieu-Barton JM (2021) Modelling damage in multidirectional laminates subjected to multi-axial loading: ply thickness effects and model assessment. Compos Struct 266:113766. https://doi.org/10.1016/j.compstruct.2021.113766
Feyel F, Chaboche J-L (2000) Fe\(_2\) multiscale approach for modelling the elastoviscoplastic behaviour of long fibre SIC/Ti composite materials. Comput Methods Appl Mech Eng 183(3–4):309–330. https://doi.org/10.1016/S0045-7825(99)00224-8
Phu Nguyen V, Lloberas-Valls O, Stroeven M, Johannes Sluys L (2010) On the existence of representative volumes for softening quasi-brittle materials—a failure zone averaging scheme. Comput Methods Appl Mech Eng 199(45–48):3028–3038. https://doi.org/10.1016/j.cma.2010.06.018
Geers MGD, Kouznetsova VG, Brekelmans WAM (2010) Computational homogenization. In: Pippan R, Gumbsch P (eds) Multiscale modelling of plasticity and fracture by means of dislocation mechanics. Springer, Vienna, pp 327–394. https://doi.org/10.1007/978-3-7091-0283-1_7
Allix O, Kerfriden P, Gosselet P (2010) A relocalization technique for the multiscale computation of delamination in composite structures. Comput Model Eng Sci 55(3):271–292
Allix O, Gosselet P, Kerfriden P, Saavedra K (2012) Virtual delamination testing through non-linear multi-scale computational methods: some recent progress. Comput Mater Contin 32(2):107–132
Souza Neto EA, Blanco PJ, Sánchez PJ, Feijóo RA (2015) An RVE-based multiscale theory of solids with micro-scale inertia and body force effects. Mech Mater 80:136–144. https://doi.org/10.1016/j.mechmat.2014.10.007
Blanco PJ, Sánchez PJ, Souza Neto EA, Feijóo RA (2016) The method of multiscale virtual power for the derivation of a second order mechanical model. Mech Mater 99:53–67. https://doi.org/10.1016/j.mechmat.2016.05.003
Blanco PJ, Sánchez PJ, Souza Neto EA, Feijóo RA (2014) Variational foundations and generalized unified theory of RVE-based multiscale models. Arch Comput Methods Eng 23(2):191–253. https://doi.org/10.1007/s11831-014-9137-5
Michel J-C, Suquet P (2009) Non-uniform transformation field analysis: a reduced model for multiscale non-linear problems in solid mechanics. In: Multiscale Modeling in Solid Mechanics, Computational Approaches. Computational and Experimental Methods in Structures, vol. 3, pp. 159–206. Imperial College Press, London. https://doi.org/10.1142/9781848163089_0004
Oskay C, Fish J (2007) Eigendeformation-based reduced order homogenization for failure analysis of heterogeneous materials. Comput Methods Appl Mech Eng 196(7):1216–1243. https://doi.org/10.1016/j.cma.2006.08.015
Raschi M, Lloberas-Valls O, Huespe A, Oliver J (2021) High performance reduction technique for multiscale finite element modeling (HPR-FE2): towards industrial multiscale FE software. Comput Methods Appl Mech Eng 375:113580. https://doi.org/10.1016/j.cma.2020.113580
Rocha IBCM, Kerfriden P, Meer FP (2020) Micromechanics-based surrogate models for the response of composites: a critical comparison between a classical mesoscale constitutive model, hyper-reduction and neural networks. Eur J Mech A Solids 82:103995. https://doi.org/10.1016/j.euromechsol.2020.103995
Geers MGD, Coenen EWC, Kouznetsova VG (2007) Multi-scale computational homogenization of structured thin sheets. Modell Simul Mater Sci Eng 15(4):393–404. https://doi.org/10.1088/0965-0393/15/4/S06
Hii AKW, El Said B (2022) A kinematically consistent second-order computational homogenisation framework for thick shell models. Comput Methods Appl Mech Eng 398:115136. https://doi.org/10.1016/j.cma.2022.115136
Ullah Z, Kaczmarczyk Ł, Zhou X-Y, Falzon BG, Pearce CJ (2020) Hierarchical finite element-based multi-scale modelling of composite laminates. Composites B Eng 201:108321. https://doi.org/10.1016/j.compositesb.2020.108321
Ullah Z, Kaczmarczyk Ł, Grammatikos SA, Evernden MC, Pearce CJ (2017) Multi-scale computational homogenisation to predict the long-term durability of composite structures. Comput Struct 181:21–31. https://doi.org/10.1016/j.compstruc.2016.11.002
Cong Y, Nezamabadi S, Zahrouni H, Yvonnet J (2015) Multiscale computational homogenization of heterogeneous shells at small strains with extensions to finite displacements and buckling. Int J Numer Meth Eng 104(4):235–259. https://doi.org/10.1002/nme.4927
Hernández JA, Oliver J, Huespe AE, Caicedo MA, Cante JC (2014) High-performance model reduction techniques in computational multiscale homogenization. Comput Methods Appl Mech Eng 276:149–189. https://doi.org/10.1016/j.cma.2014.03.011
Oñate E (2013) Structural analysis with the finite element method. In: Linear Statics: Beams, Plates and Shells, vol. 2, p. 864. Springer, New York. https://doi.org/10.1007/978-1-4020-8743-1
Hill R (1963) Elastic properties of reinforced solids: some theoretical principles. J Mech Phys Solids 11(5):357–372. https://doi.org/10.1016/0022-5096(63)90036-X
Zienkiewicz OC, Taylor RL (2005) The Finite Element Method for Solid and Structural Mechanics, 6th ed. edn. Elsevier, Amsterdam. https://doi.org/10.1016/C2009-0-26332-X
Crisfield MA, Tassoulas JL (1993) Non-linear finite element analysis of solids and structures, vol 1. J Eng Mech ASCE 119(7):1504–1505. https://doi.org/10.1061/(ASCE)0733-9399(1993)119:7(1504)
Simo JC, Hughes TJ (2006) Computational Inelasticity, vol. 7, p 392. Springer, New York. https://doi.org/10.1007/b98904
Pagano NJ (1970) Exact solutions for rectangular bidirectional composites and sandwich plates. J Compos Mater 4(1):20–34. https://doi.org/10.1177/002199837000400102
Reddy JN (2003) Mechanics of Laminated Composite Plates and Shells: Theory and Analysis, p. 858. CRC Press, Boca Raton. https://doi.org/10.1201/b12409
Oliver J, Huespe AE, Pulido MDG, Chaves E (2002) From continuum mechanics to fracture mechanics: the strong discontinuity approach. Eng Fract Mech 69(2):113–136. https://doi.org/10.1016/S0013-7944(01)00060-1
Pipes RB, Pagano NJ (1970) Interlaminar stresses in composite laminates under uniform axial extension. J Compos Mater 4(4):538-548
Mittelstedt C, Becker W (2007) Free-edge effects in composite laminates. Appl Mech Rev 60(5):217–245
Acknowledgements
The authors gratefully acknowledge the financial support received from the Spanish Ministry of Science and Innovation through the ’Proyectos de Transición Ecológica y Digital 2021’ programme under grant TED2021-129413B-C21, the ’Generación de Conocimiento 2022’ programme under grant PID2022-140249OB-I00 and the Catalan Agency for Management of University and Research Grants through the ’Convocatòria ajuts d’Indústria del Coneixement: Producte, 2021’ under grant PROD 00016. Dr. Oriol Lloberas-Valls gratefully acknowledges the financial support received from he Spanish Ministry of Science and Innovation, through the ’Consolidación Investigadora 2022’ programme under grant CNS2022-135900. CIMNE is a recipient of a “Severo Ochoa Programme for Centers of Excellence in R &D” grant (CEX2018-000797-S) by the Spanish Ministry of Economy and Competitiveness.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Elaboration on RVE Problem (I)
Following Eq. (48), the problem to be solved is
which can be explicitly written as
yielding the following possible scenarios:
Integration by parts of the left-hand-side in Eqs. (A.3) and (A.4) yields,
From Eqs. (A.1) and (A.5(a–c)), the RVE problem at \(\Omega _{\mu }(\textbf{x}^{\mathcal {M}})\) becomes:
Resolution of RVE Problem (II)
Regarding Eqs. (49(c)), it can be readily proven that:
since the in-plane stress vector, \({{\varvec{\sigma }}}^{\text {inp}}_{{\mu }}\equiv [\sigma _{{\mu }_{\text {x}}},\sigma _{{\mu }_{\text {y}}},\sigma _{{\mu }_{\text {xy}}}]^T\) does not depend on \({\tilde{\textbf{u}}}_{\mu }\), and, therefore \([\delta {{\varvec{\sigma }}}^{\text {inp}}_{{\mu }};\delta {\tilde{\mathbf{{u}}}}_{\mu }]=\textbf{0}\), as it can be concluded from a detailed examinationFootnote 16 of Eqs. (19) and (20). Equation (B.1) can be rewritten in terms of a linear differential operator, \({{\mathbb {L}}}\), as

where symbol (\(\star \)) denotes the application of the differential operator \({{\mathbb {L}}}\) on the contiguous term with respect to (\(\star \)). Application in Eq. (B.2) of the integration by parts (generalized divergence theorem), i.e.,
where matrix \({\mathbb {N}}\) is obtained by replacing any entry, \(\dfrac{\partial }{\partial (\bullet )}\) in \({{\mathbb {L}}}\), with the corresponding entry, \({n}_{(\bullet )}\) in \({\mathbb {N}}\), in terms of the components of the normal vector to the RVE boundary \({\partial \Omega _\mu ({\textbf{x}^{\mathcal {M}}})}\), i.e. \(\textbf{n}\equiv [{n_{\text {x}}},{n_{\text {y}}}, {n_{\text {z}}}]^T\).
Applying Eqs. (B.3) to (B.2) yields

Focusing now on Problem II, after replacement of Eqs. (B.4) into Eq. (49), accounting for the constitutive model in Eq. (19(c)), and some algebraic operations (see also Remark 5), yields the following variational problem:
where condition \({{\varvec{\sigma }}}^{\text {ofp}}_{\mu }=\textbf{0}\Rightarrow {\delta {{{\varvec{\sigma }}}}}^{\text {ofp}}_{\mu }=\textbf{0}\) in \(\partial \Omega _{\mu }({\textbf{x}^{\mathcal {M}}})\) (the natural boundary condition in Eq. (52(c)), see also Eq. (A.6(b)) has been considered. Therefore, from the variational equation (B.5(c)), the following Euler–Lagrange equation emerges:
where the non-singular character of tensor \(\textbf{D}_{\mu }^{\text{ ofp }}\) (see Remark 5) has been taken into account. Further elaboration on Eq. (B.6), since tensor \({\varvec{\lambda }}_{\mu }\) only depends on coordinate z (\({{\varvec{\lambda }}}_{\mu }{\equiv {\varvec{\lambda }}}_{\mu }(z)\)), see Eq. (B.5(a)), yields
Replacement of result in Eq. (B.7) into Eq. (B.6) reads
Finally, z-integration of Eq. (B.8) and consideration of a pseudo-time advancing context, \(t\in [0,T]\), yields
where \(\textbf{c}(t)\) is an arbitrary integration variable. For practical purposes the value \(\textbf{c}(t)=\textbf{0}\); \(\forall t\in [0,T]\) is chosen, this yielding the final solution:
RVE Solution Linearization
Application of the variational increment concept in Eq. (61) to the problem in Eq. (59) yields

and by substitution of Eqs. (C.1(d,e)) into Eqs. (C.1(b,c)), one obtains
where \({{\mathbb {S}}}\) and \({{\mathbb {G}}}\) are linear differential operators, symbol \((\star )\) stands for the application of the operator on the contiguous term, and \(\textbf{I}_{3}\) stands for the (\(3 \times 3\)) identity matrix.
Remark 20
Notice that the extended in-plane constitutive matrix, \(\textbf{E}^{\text {inp}}_{\mu }\), in Eq. (C.3(c)), is built in terms of the three individual sub-matrices (\(\textbf{D}^{\text {inp}}_{\mu _{\text {x}}}\), \(\textbf{D}^{\text {inp}}_{\mu _{\text {y}}}\), \(\textbf{D}^{\text {inp}}_{\mu _{\text {xy}}}\)) constituting the rows of the in-plane constitutive matrix, \(\textbf{D}^{\text {inp}}_{\mu }\), in Eq. (20(a)).
Accounting for the expression of \({\Delta {{\varvec{\varepsilon }}}}^{\text {inp}}_{\mu }\), in Eq. (16(a)), the linearization of the RVE external forces reads
Now, by combining equations (C.1(a)) and (C.2(a)), and accounting for the result in Eq. (C.3), the linearized expression for the fluctuating displacement vector, \({\tilde{\textbf{u}}}_{\mu }\), is obtained through the following sequence of derivations:
where
Macroscale FE Problem Linearization
Application of the variational increment concept, in Eq. (61), to the macroscale finite element problem in Eq. (67) yields
where the tangent operators appearing in Eqs. (D.1(b)) can be readily expressed, accounting from Eqs. (25) and (30), as:
where the values in Eq. (25) have been recalled.
Now, considering some previous derivations:
and replacing Eqs. (D.3(a)) and (D.3(b)) into Eq. (D.3(c)) yields:
where the values \(\textbf{a}^{\varepsilon }({\textbf{x}^{\mathcal {M}}})\), \(\textbf{a}^{\kappa }({\textbf{x}^{\mathcal {M}}})\), and \(\textbf{a}^{\gamma }({\textbf{x}^{\mathcal {M}}})\) are detailed in Eq. (C.6(c)) in Appendix C. Now, replacement of equations (D.4) into Eq. (D.1(b)) yields,
resulting

Equation (D.6) displays the algorithmic linearization of the macroscale constitutive model in terms of the tangent algorithmic constitutive tensor \( {{\mathbb {D}}}^\text {alg}_{t+\Delta t}({\textbf{x}^{\mathcal {M}}})\).
Next step is the linearization of the whole macroscale problem to obtain the macroscale algorithmic stiffness matrix. Equation (D.6(a)) can be rewritten as (see Eqs. (65)–(66)):
and replacing the result in Eq. (D.6) into Eq. (71(c)) yields:
which identifies the algorithmic tangent matrix, \(\textbf{K}^{\text {alg}}_{t + \Delta t}\) of the overall multiscale problem as:
where the classical Taylor problem contribution, \(\textbf{K}^{\text {Taylor}}_{t +\Delta t}\), (i.e. for null fluctuating displacements, \({\tilde{\textbf{u}}}_{\mu }=\textbf{0}\)) and the fluctuations problem contribution, \(\tilde{\textbf{K}}_{t +\Delta t}\), (for \({\tilde{\textbf{u}}}_{\mu }\ne \textbf{0}\)) are recovered.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wierna, P., Yago, D., Lloberas-Valls, O. et al. On the Efficient and Accurate Non-linear Computational Modeling of Multilayered Bending Plates. State of the Art and a Novel Proposal: The \(2\text {D}+\) Multiscale Approach. Arch Computat Methods Eng (2024). https://doi.org/10.1007/s11831-023-10049-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11831-023-10049-4