1 Introduction

Greenhouse gases have become a matter of serious concern in the twenty-first century because of the rapid increase in industrialization which demands a massive amount of power and energy. To meet those energy requirements, coal is widely used in the power sector. The huge consumption of coal for power generation produces greenhouse gases up to 46% worldwide and therefore is considered the single biggest contributor to the greenhouse gases [1]. There exist different CO2 capturing approaches such as pre-combustion capture, oxyfuel and post-combustion carbon capture (PCC). Among these most widely adopted technologies, post-combustion carbon capture has gained a lot of attention due to its ease of application, low capital, and energy requirement [2]. Another most highlighted advantage of this technology is its ability to handle the high volume of CO2 enriched gases and its retrofit nature; therefore, no radical change is required in the current industrial setup to adopt this technology [3]. Numerous techniques such as adsorption [4], membrane separation [5], cryogenics [6], absorption (Chemical and Physical), [7] and calcium looping carbon capture have been proposed and employed by the industries to reduce the emission of CO2 to the atmosphere. Each of the remedial techniques has its limitations and disadvantages that outweigh its advantages. For example, adsorption is a useful technique as it does not discharge liquid waste effluent, however, it does not have a high adsorption capacity for CO2 [8, 9]. Similarly, cryogenics is suitable for the CO2 enriched gaseous stream, but its high energy consumption does not make it an economical choice [10]. Likewise, membrane separation is a simple and cost-effective technique, but the plasticization at high temperature and the trade-off between selectivity and permeability create barriers to its commercialization [11]. Therefore, among various proposed techniques, absorption has emerged as the most effective, mature and reliable CO2 capturing technique with promising capturing capacity [12]. Based on the type of attractive forces between CO2 and the solvent, the absorption process can be classified into two categories, i.e., physical and chemical absorption. The favorable conditions for the physical absorption are the high pressure and low temperature, which require high energy consumption. This high consumption of energy to achieve those conditions results in an increase in the operational cost and thus makes the process uneconomical [13]. On the other hand, chemical absorption involves a chemical reaction between the solvent and the CO2. The intermediate product formed as a result of chemical reaction, which binds the CO2 with the solvent by forming a weak chemical bond. This weak bond can be dismantled to release the captured CO2 when subjected to heat. Moreover, chemical absorption is more advantageous than the physical absorption due to its high absorption capacity and can handle gaseous streams having CO2 partial pressure greater than 15% [14].

The selection of an appropriate solvent is a crucial factor that determines the feasibility as well as the efficiency of the absorption process. Based on the chemical and physical nature of absorption, the solvent can be categorized into chemical and physical solvents. Chemical solvents are those solvents that bind the CO2 molecules by undergoing a chemical reaction with CO2. The efficiency of the solvents can be predicted by their CO2 absorption rate. As the reaction between solvent and CO2 proceeds, the reduction of equilibrium partial pressure occurs, which increases the rate of absorption. One of the highlighted drawbacks of chemical solvents is the high energy consumption for the regeneration of solvent by breaking the bonding between the solvent and the CO2 molecules [15, 16]. On the other hand, for physical solvents, the absorption of CO2 is based on Henry's law, i.e., the amount of CO2 dissolved in the solvent is proportional to the partial pressure of CO2 above the solvent. The favorable condition to absorb the CO2 is high pressure. Therefore, the desorption of gas can be done to regenerate the solvent by reducing the pressure [17].

The gas–liquid mass transfer majorly depends upon the configuration of the chemical reactor. Conventionally, packed bed reactors are being used for the chemical absorption of CO2. This is the simplest configuration in which the CO2-containing gases are passed through the fixed bed of the reactor. There are different packing structures available for this purpose. However, the major disadvantages inherent with this technology are the high capital, operational cost, high thermal efficiency penalty, low mass transfer rate and the use of concentrated amine-based solvent [18,19,20,21]. Lawal et al. [22] studied the post-combustion capturing of CO2 through dynamic simulation and found that at least two packed columns were required with a minimum height up to 7 m and a diameter of 9 m each to achieve the capturing efficiency of CO2 up to 90%. They concluded that this specification of the column will lead to higher capital and operational cost and therefore, will increase the electricity cost by up to 50%. Riboldi and Bolland [23], while studying the performance of the packed bed reactor to capture CO2 emitted from the coal power plant, found that the packed bed reactor imposes higher pressure drop even at a low gas flow rate; thus is not an effective absorber for the CO2 absorption.

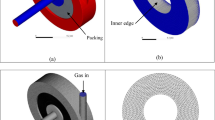
Alternatively, Rotating Packed Bed Reactor (RPB) is a process intensification device which was first introduced by HiGee Technology in 1990s. Rotating packed bed (RPB) has paved its way into various industrial processes such as separation and chemical reaction, distillation, stripping, absorption, production of nanoparticles, etc. The schematic diagram of a typical rotating packed bed is shown in Fig. 1 [24]. During the rotation of RPB, the rotor injects the liquid into the packing. The liquid passes through the packing of the RPB due to the shear force exerted on the liquid by the rotor and split into thin films and droplets which increases its surface area. This increase in the surface area, not only increases the mass transfer rate between the fluids but also reduces the reactor size and energy consumption [25, 26].

Fig. 1
figure 1

Schematic diagram of RBP. 1. Liquid inlet, 2. Gas outlet, 3. Gas inlet, 4. Hull, 5. Packing, 6. Liquid distributor, 7, rotating shaft, 8. Seal, 9. Liquid outlet, 10. Cavity zone [27]

Full size image

The conventional RPB consists of two major components, i.e., the rotor with the porous packing enclosed in a casing and the liquid distributor which inject and distribute the liquid homogeneously in the packing. The centrifugal acceleration produced by the rotor enhances the gas–liquid macromixing and provides better mass transfer between gas–liquid interface.

The RPB can be classified into different categories based on the following criteria.

  1. a.

    Phase contact type (counter-current, co-current, cross current).

  2. b.

    Number of rotor stages

  3. c.

    Type of the rotor

  4. d.

    Rotor orientation

  5. e.

    Type of packing

The selection criteria of RPB among the different types is based on the type of chemical process, the rate of mass transfer, liquid holdup, mean residence time, operational cost, pressure drop, ease of maintenance and the type of fluids [18, 28,29,30]. Furthermore, foam and wire mesh are being used conventionally as packing materials in RPB. The selection of packing material in RPB is based on the viscosity of the fluid. For the high viscosity fluids, wire mesh packing is more effective and provides better mass transfer rate as compared to the counterparts.

To the best of our knowledge, there exist very scarce data in the literature that critically highlights all the efforts made for the study of hydrodynamic parameters using experimental and empirical modelling. Moreover, the current scientific literature lacks to point out the pros and cons of the Computational Fluid Dynamics method to study the hydrodynamic parameters of the RPB, i.e., especially for the mass transfer performance of RPB. The previous studies do not completely address the critical aspects of the hydrodynamics of RPB in a single review such as the effect of different packing structures and RPB designs on the hydrodynamic parameters of the RPB, different approaches to estimate the mean residence time, advantages and disadvantages of different multiphase models, selection of suitable rotating reference frame model for different geometries and the reactive modeling of the CFD. This systematic review aims to critically analyze the experimental and CFD approach to study the hydrodynamics of the RPB. In the first section of the review, the hydrodynamic parameters such as liquid holdup, pressure drop, effective interfacial area, liquid residence time and mass transfer modelling by experimental methods in combination with the empirical modelling is reviewed critically. The later section focuses on the CFD studies, i.e., multiphase modelling of RPB, employment of turbulence models and the reactive modeling of CO2 absorption.

2 Hydrodynamics of RPB

2.1 Experimental Studies

The hydrodynamic modeling provides useful information for all the changes that occur in the process with time. The rate of mass transfer is an important factor for the design and optimization of RPB for post-combustion CO2 capture and depends on the hydrodynamics of the gaseous and liquid phases in RPB [27]. Hence, many researchers have tried to investigate the hydrodynamics of RPB by different non-invasive techniques such as high-speed photography and X-ray computed micro-tomography [31,32,33]. Yang et al. [32] used the X-ray Computed Tomography technique to study the hydrodynamics of CO2 absorption in laboratory-scale RPB. The results were in the form of tomographic cross-sectional images and they found that the rotational speed and the solvent concentration had a considerable effect on the maldistribution of solvent around the packing region in RPB. The intensity of the X-ray was affected by the material of the reactor and was unable to provide any information regarding the flow characteristics of liquid films and liquid droplets. Yan et al. [34] studied the hydrodynamics of RPB by using colored water. The void cavities in the packing were filled with paper to investigate the liquid flow pattern of the colored water in RPB. This approach is cost-effective as it does not require any high-speed camera or the X-ray setup. However, this experimental setup can only capture the film flow within the RPB and no information regarding pore and droplet flow can be achieved using this technique. Likewise, Bongo et al. [35] employed the optical imaging technique by using Particle Image Velocimetry (PIV) to get the visuals of the velocity vectors of the liquid using the projections of the particles carried by the liquid. Burn et al. [36] used non-invasive techniques to study the hydrodynamics of absorptionby investigating the fluid flow using a high-speed stroboscopic photography setup. The Wen et al. [37] used a high-speed camera to capture the film flow behavior in vertical quadrangular fibers and horizontal elliptical fibers (VQHE) and the packing composed of circular fibers (VCHC) in the RPB. The captured image exhibited the transition of liquid ligaments into droplets and liquid film as shown in Fig. 2. However, the non-invasive techniques were unable to provide detailed and accurate flow characteristics of the RPB and were expensive due to the special instrumental setup [34]. The experimental studies to investigate the hydrodynamics of the RPB are shown in Table 1.

Fig. 2
figure 2

Liquid flow transition behavior in the RPB [37]

Full size image
Table 1 Various experimental techniques used to study the hydrodynamics of RPB
Full size table

2.2  Empirical Modeling of Hydrodynamic Parameters

2.2.1 Liquid Holdup

The liquid holdup in the RPB is the ratio of the volume of the packing zone to the volume of the liquid in the packing zone. This is an important hydrodynamic parameter that depicts the resilience of the packing zone to the liquid phase and is a crucial parameter for determining the mass transfer rate as well as the interfacial surface area. The value of the liquid holdup varies in each of the packing zone, i.e., the inner and outer zone has high liquid holdup while the bulk zone has comparatively low liquid holdup [39]. This critical variable primarily depends on various factors such as the inlet velocity of the liquid, solvent concentration, rotational speed and the contact angle of the packing. Yang et al. [32] and Grob et al. [40] used the advanced X-ray and Gamma-ray CT techniques, respectively, to determine the liquid holdup in the RPB. Both techniques have provided key information about the liquid holdup. However, the employment of these techniques is practically and economically not possible due to the expensive technical setup and the complex engineering design constraints in RPB. Therefore, various empirical models have been developed to calculate the liquid holdup in the RPB. However, all of these correlations are non-generic and, therefore, cannot be applied to all packing types and RPB configurations.

Burns et al. [41] placed an electrode in the packing of RPB and used the measurements of electrical resistance between the electrodes to develop the model for the prediction of liquid holdup in a highly porous packing. This model took into account the kinematic viscosity of the solvent and the rotational speed of the RPB. The experimental setup proposed by Burns et al. [41] is complicated and expensive as it requires the special set of equipment. Lin et al. [42] assumed that the liquid flow within the RPB is film flow and developed a correlation for the liquid holdup. The correlation is based on the measurement of the pressure drop and was relatively easy to calculate. Hendry et al. [43] used the empirical correlation (Eq. 1) to determine the liquid holdup in both the counter and co-current setup of the RPB. However, this is the simplest model and does not consider liquid–gas interaction in the RPB and thus, does not predict the accurate liquid holdup in the RPB.

$${\upepsilon }_{\mathrm{L}}=12.159{\mathrm{Re}}^{0.923}{\mathrm{Ga}}^{-0.61}{\mathrm{Ka}}^{-0.019}$$
(1)

As the packing of the RPB is complex and the flow within the different zones cannot be assumed accurately, therefore, all the empirical correlations lag in their reliability and accuracy. Various proposed empirical correlations to determine the liquid holdup are summarized in Table 2.

Table 2 Correlations for liquid holdup estimation in RPB
Full size table

2.2.2 Liquid Residence Time

Liquid residence time is an important aspect as it has significant effect on the mass transfer performance of the reactor and therefore affects the overall efficiency of the reactor. The liquid residence time can be optimized and can be employed for the scale up of the RPB [46]. The liquid residence time in the RPB can be measured by the Residence Time Distribution (RTD) data. Residence Time Distribution characterizes the ability of micro-mixing in the RPB and the study can be performed by monitoring the concentration of the tracer species at the outlet of the RPB over a certain period of time [47]. Guo et al. [46] used an experimental setup for the RTD study on the liquid flow in the RPB. The electrodes were placed on the rotor and the electrical pulse of the tracer species was monitored. They found that the operational parameters such as the liquid flow rate and the rotational speed of the RPB have considerable influence on the RTD. Likewise, Emami‑Meibodi et al. [48] used the conductivity pen to detect the concentration of the tracer species at the outlet of the RPB and proposed a RTD model to calculate the liquid residence time. Their proposed model is a follow:

$$\mathrm{E}\left(\mathrm{t}\right)=\frac{1}{\uptau }$$
(2)
$$\uptau = \frac{\mathrm{V}}{\mathrm{v}}$$
(3)

however the model was based on the assumptions i.e., (i) volume of the pipes is so small that they can be neglected and (ii) there exists a solution gradient the feeding tank. The proposed model shows a good agreement with the experimental data with only a 2.5% difference. The mean residence time (MRT) of the RPB lies within the range of 0.4–1 s [46, 49, 50]. There are various factors other than the operational parameters which may affect the MRT such as the packing structure, RPB design, rate of the chemical reaction, phases interactions, packing wall adhesions, etc. Moreover, the optimum performance of RPB for the absorption of CO2 can be achieved by adjusting the operational parameters, suitable selection of packing and the optimum RPB design [51].

2.2.3 Dry Pressure Drop

Dry pressure drop refers to the loss of gas pressure in the absence of liquid and, therefore, is an essential parameter to be considered to quantify the resistance offered by the packing and energy consumption to run the absorption process in RPB. To overcome the high-pressure drop, additional blowers and fans are required in the upstream, which increases the operational cost of the process [52]. Moreover, this parameter is also important to determine the parasitic load of the CO2 absorption process and, thus, affects the feasibility of the absorption process in the RPB. The dry pressure drop in RPB is always higher than that of the packing bed reactor. But this can be compensated by the smaller reactor requirement due to its high mass transfer efficiency. In general, there are four zones in RPB that have significantly high-pressure drops as shown in Fig. 3

Fig. 3
figure 3

Zones for pressure drop in RPB

Full size image

The main factors to contribute to the pressure drop are (i) the friction forces on gas molecules exerted by the packing and the solvent due to adhesion and the intermolecular forces between gas and the liquid, (ii) centrifugal head and (iii) increase in tangential velocity due to the change in area in the radial direction [53]. The total pressure drop, therefore, is the sum of pressure drop due to friction (\(\Delta {\mathrm{P}}_{\mathrm{f}}\)), centrifugal pressure (\(\Delta {\mathrm{P}}_{\mathrm{ch}}\)) and the (\(\Delta {\mathrm{P}}_{\mathrm{v}}\)), due to sudden change in the area.

Hendry et al. [43] calculated the pressure drop in RPB by the experimental setup and developed one-dimensional pressure drop model. However, the model cannot predict the pressure drop in all RPB’s configurations. Likewise, Lin and Jian [54] studied the effect of operational parameters, i.e. liquid flow rate, gas flow rate and the rotor speed on the pressure drop and found that the pressure drop in the RBP increases with the increase in the gas flow rate and rotor speed but remains unchanged with the change in liquid flow rate. Moreover, they also developed empirical correlation for calculating the pressure drop in the RPB which is as follow

$$\Delta \mathrm{P}=\frac{{\mathrm{F}}_{\mathrm{v}}^{2}}{2}\frac{{\mathrm{a}}_{\mathrm{t}}}{{\left(\upvarepsilon -{\mathrm{h}}_{\mathrm{L}}\right)}^{3}}{\mathrm{f}}_{\mathrm{w}}({\mathrm{R}}_{\mathrm{o}}-{\mathrm{R}}_{\mathrm{i}})$$
(4)

Low pressure drop is favorable for any absorption process in the RPB. Optimum engineering design and selection of suitable packing material can help to achieve the low pressure drop in the RPB [55, 56]. Therefore, a detailed study of the pressure drop is important for the scale-up and the feasibility analysis of this process intensification technique for CO2 absorption.

2.2.4 Effective Interfacial Surface Area

Interfacial surface area is the area of contact between gas and liquid and is the region where the mass transfer between the phases takes place. This important attribute is an essential prerequisite to determine the size of the RPB to achieve the desired rate of the mass transfer between the gas and the liquid [57]. The flow within the RPB is complex and is different from the conventional packed bed reactor. Therefore, various empirical and semi-empirical models have been proposed by the researchers. Im et al. [58] modified the correlation proposed by Billets and Schultes [59] by introducing the centrifugal acceleration in the correlation. Tsai and Chen [60] reported that the effective interfacial surface area can be increased up to 34% by using static baffles in the RPB. This increase in the effective interfacial area increases the overall mass transfer coefficient in the RPB. The correlations proposed for the calculation of RPB are summarized in Table 3.

Table 3 Correlations for the interfacial surface area along with packing specifications
Full size table

2.3 Mass Transfer Modeling of CO2 Absorption

Various experimental methods, in combination with the empirical correlations, have been employed to study the mass transfer performance of the RPB. The mass transfer between gas–liquid interface depends on various factors such as rotational speed (RPM), solvent concentration, contact angle, gas–liquid flow rates and the operational temperature [65]. The mass transfer mechanism inside the RPB is complex and therefore, no theoretical model can be developed to predict the mass transfer coefficient at any stage and zone of contact within the RPB. The volumetric gas and liquid side mass transfer coefficients are the two most important parameters while designing and optimizing the performance of RPB for the absorption process. Researchers have made various assumptions and developed different mass transfer models to predict the mass transfer coefficients at the gas–liquid interface.

Neumann et al. [66], due to the complex packing structure of the RPB, used the gas–liquid effective interfacial area as a considerable variable for the approximation of liquid side mass transfer in the RPB. The effective interfacial area was calculated using the expression below:

$${\mathrm{a}}_{\mathrm{eff}}=\frac{\Delta {\mathrm{n}}_{{\mathrm{CO}}_{2},\mathrm{Pack}}^{.}}{{\mathrm{V}}_{\mathrm{p}}{\mathrm{C}}_{\mathrm{I},{\mathrm{CO}}_{2}}^{\mathrm{IP}}\sqrt{{\mathrm{K}}_{{\mathrm{OH}}^{-}.}{\mathrm{C}}_{{\mathrm{OH}}^{-}.}{{\mathrm{D}}_{{\mathrm{LCO}}_{2}}}_{.}}}$$
(5)

Likewise, Chen et al. [67] proposed the liquid side mass transfer correlation, which was valid for both Newtonian and non-Newtonian fluids. The correlation proposed by the Chen et al. [67] is as follows:

$$\frac{{\mathrm{K}}_{\mathrm{L}}{\mathrm{ad}}_{\mathrm{p}}}{{\mathrm{Da}}_{\mathrm{t}}}\left(1-0.93\frac{{\mathrm{V}}_{\mathrm{o}}}{{\mathrm{V}}_{\mathrm{i}}}-1.13\frac{{\mathrm{V}}_{\mathrm{i}}}{{\mathrm{V}}_{\mathrm{t}}}\right)=0.65{\mathrm{Sc}}^{0.5}{\mathrm{Re}}^{0.17}{\mathrm{Gr}}^{0.3}{\mathrm{We}}^{0.3}$$
(6)

Sun et al. [68] developed a mass transfer model to estimate the overall liquid side mass transfer coefficient for the simultaneous reactive absorption of CO2 and NH3 in the RPB. The predicted mass transfer coefficients were close to the experimental data and were within the bias range of 10%. Various proposed correlations to determine the mass transfer are summarized in Table 4.

Table 4 Mass transfer models reported for the RPB
Full size table

2.3.1 Mass Transfer Modelling of Reactive CO2 Absorption

The absorption of CO2 into an appropriate solvent (such as MEA, K2CO3, etc.) is a physio-chemical process. The absorption of CO2 is considered physical if the absorption is based on Henry’s law and the selectivity of CO2 in a solvent occurs without any chemical reaction [81]. On the other hand, chemical absorption occurs as a result of the chemical reaction between solvent and CO2 [82]. Enhancement factor (E) is a key parameter to predict the nature of absorption, i.e., chemical or physical. The E is the ratio of mass transfer rate due to the chemical reaction to the mass transfer rate without the chemical reaction. The absorption of CO2 is considered as the physical absorption if the E < 1. Likewise, if the E ≥ 1, the absorption is considered as the chemical absorption [83, 84].

Jasmine et al. [85] developed a mass transfer model (Eq. 8) to study the effect of chemical reaction on the mass transfer performance of the RPB using MEA as a solvent.

$${\mathrm{K}}_{\mathrm{G}}\mathrm{a}=\frac{{\mathrm{k}}_{\mathrm{app}}}{{\mathrm{H}}_{{\mathrm{CO}}_{2}-\mathrm{MEA}}}{\upepsilon }_{\mathrm{L}}$$
(7)

The apparent pseudo-first-order reaction rate constant (\({\mathrm{k}}_{\mathrm{app}})\) and Henry’s law constant (\({\mathrm{H}}_{{\mathrm{CO}}_{2}-\mathrm{MEA}})\) were incorporated into the mass transfer model to predict the overall volumetric mass transfer coefficient. They found that the instantaneous reversible reaction affects the mass transfer rate and the predicted results were close to the experimental data. Yi et al. [86] developed a mass transfer model (Eq. 2.9) by considering the effect of reaction between diethanolamine (DEA) and K2CO3.

$${\mathrm{k}}_{\mathrm{L}}={\mathrm{D}}_{\mathrm{L}}\left(\frac{\sqrt{\frac{{\mathrm{k}}_{1}}{{\mathrm{D}}_{\mathrm{L}}}}}{\mathrm{tanh}\left(\left(\sqrt{\frac{{\mathrm{k}}_{1}}{{\mathrm{D}}_{\mathrm{L}}}} \frac{\mathrm{d}}{2}\right)-\frac{2}{\mathrm{D}}\right)}\right)$$
(8)
$${\mathrm{k}}_{1}={\mathrm{k}}_{\mathrm{OH}}{\mathrm{C}}_{\mathrm{OH}}^{-}+{\mathrm{k}}_{\mathrm{DEA}}{\mathrm{C}}_{\mathrm{DEA}}$$
(9)

Based on this model and by comparing the calculated results with experimental data, they concluded that the mass transfer rate is much higher in the end zone region of the RPB as compared to the other regions.

The experimental method is an expensive and time-consuming approach. Furthermore, the results are also very difficult to be reproduced and thus, decrease the validity of the results. Similarly, data obtained by theoretical or analytical approach is not realistic as a lot of assumptions need to be made to simplify the mathematical models due to the complexity of the process. Therefore, the mass transfer rate, liquid holdup, effective interfacial area and pressure drop obtained by the theoretical or analytical methods do not cover all the parameters of consideration and, thus, cannot be used for the practical applications. For the semi-empirical method, there exists very limited data in the literature and cannot be used for determining the mass transfer rate due to lack of generalization in the mathematical models and their respective governing equations.

3 CFD Studies

CFD has proved itself as a cost-effective tool in modern-day engineering as it can solve complex fluid flow problems without compromising the accuracy and reproducibility. It has a promising potential to evaluate the hydrodynamic parameters and mass transfer rate by substantially declining the time and cost. Furthermore, CFD provides a detailed and graphical demonstration of data i.e., occurrence of flow separation or deviation of any set parameter from the maximum or minimum limit, which is not possible to achieve with the rest of the available techniques [87]. CFD analysis of the RPB can provide useful information about the hydrodynamic parameters such as liquid holdup, liquid residence time, pressure drop and liquid dispersion.

3.1 Effect of Operational Parameters on Hydrodynamics of RPB

The liquid holdup is one of the most important parameters to study the hydrodynamics of the RPB. The value of the liquid holdup (\({\upvarepsilon }_{\mathrm{l}})\) determines the resistance offered by the packing to the liquid within the flow domain, the possibility of liquid to be flooded and the gas–liquid interfacial area [51]. Xie et al. [27] investigated the liquid holdup of 50 wt% MEA solution by varying the operational conditions such as the rotational speed, inlet velocity and MEA concentration and found that the rotational speed has a significant effect on the liquid holdup performance of RPB. At higher rotational speed, the MEA ligaments were transformed to tiny droplets and were not under the influence of any resistance offered by the packing. Therefore, the residence time of MEA in the RPB decreased up to 70% when the rotational speed was increased to 1500 rpm, thus also decreased the liquid holdup of MEA. There are various operational parameters that can influence the liquid holdup in the RPB such as the inlet velocity, solvent concentration and packing-solvent contact angle. However, among these parameters, the inlet velocity has a minor effect on the liquid holdup in the RPB [27]. Xie et al. [27] also reported that the concentration of the MEA has a noticeable effect on the liquid holdup as with the increase in concentration, the dynamic viscosity increases considerably. This increase in viscosity improves the adhesion of the solvent with the packing surface, which increases the residence time and the liquid holdup. Similarly, Zhang et al. [88] reported that hydrophobic packings at the entrance of the packing can reduce the liquid holdup up to an optimum level which can avoid the possible flooding of the solvent at the inlet location. They also concluded, as a result of the 3D CFD simulation of RPB, that at low rotational speed, the packing offers noticeable resistance for the incoming liquid and, thus, exhibits high residence time. The effect of different rotational speeds on the liquid holdup can be seen in Fig. 4 and the equations to calculate the mean residence time are summarized in Table 5.

Fig. 4
figure 4

Effect of different operational conditions on the liquid holdup [90, 91]

Full size image
Table 5 Equations for Liquid residence time in RPB
Full size table

Shi et al. [89] used the Residence Time Distribution (RTD) method to calculate the MRT. After the achievement of pseudo-steady state, a tracer with the same physical properties as of the water was injected into the RPB through the inlet with the volume fraction of 1 for a very short instance of time, i.e., 0.01 s. The volume fraction of the tracer at the outlet was then monitored continuously to get the RTD curve. Likewise, Burn et al. [41] calculated the mean residence time as a function of the liquid holdup. The liquid holdup was determined by installing the resistance measuring detectors to measure the liquid holdup resistance in the RPB. The value of the liquid holdup was then used in Eq. 1 of Table 5.

The mass transfer within the RPB depends on how long the gas and liquid come in contact with each other and, therefore, is very crucial in determining the potential of RPB for the CO2 absorption. To achieve an optimum residence time, the gas flow rate is used to tune the gas residence time whereas, the liquid residence time can be tuned by various operational parameters such as the liquid velocity, rotational speed and nature of the packing [92]. Yang et al. [93] studied the liquid residence time by varying the center distance between the packing layers (\(\Delta \mathrm{d}\)) and found that by decreasing the center distance, the liquid residence time increases due to an increase in its surface area which eventually enhances the mass transfer between the gas–liquid phase. This increase in the mass transfer is advantageous to achieve high removal capacity. The effect of the packing structure on the residence time can be seen in Fig. 5.

Fig. 5
figure 5

Effect of packing structure on the residence time: a ∆d = 3 mm; b ∆d = 2.5 mm [91]

Full size image

Whang et al. [94] studied the effect of droplet velocity on the average residence time of the liquid in the RPB and found that change in the rotational speed and liquid inlet velocity can alter the mean residence time of the liquid, as shown in the Fig. 6.

Fig. 6
figure 6

Residence time distribution in RPB at different droplet velocities and rotational speeds. a u0 = 0.5 m/s, N = 300 rpm; b u0 = 0.5 m/s, N = 600 rpm; c u0 = 0.5 m/s, N = 900 rpm; d u0 = 1.5 m/s, N = 600 rpm. [94]

Full size image

Malinowska et al. [95] studied the pressure drop as a function of rotational speed in the porous packing in the RPB using a 3D CFD model. The CFD results of two turbulence model, i.e. RNG \(\mathrm{k}-\upvarepsilon\) and Standard \(\mathrm{k}-\upvarepsilon\) were compared with the experimental data. The CFD results started to deviate from the experimental data with the increase in the gas flow rate. However, the discrepancy was less than 20%, which lies within the acceptable limits of error.

3.2 Effect of Packing Structure on the Hydrodynamics of RPB

The type of the packing structure has a considerable effect on the hydrodynamics and mass transfer efficiency of RPB and is, therefore, considered a key parameter to evaluate the efficiency of RPBs. These packing in general can be categorized as wire mesh and foam packing. The wire mesh structure is subcategorized as structured, unstructured, weaved meshed, knitted meshed and zigzag wire mesh packings. Different packing structures of RPB are shown in Fig. 7. Based on the mass transfer coefficient, wire mesh packing offers more promising performance as compared to its counterparts [67]. Qammar et al. [96] compared the mass transfer efficiency and hydrodynamics of different wire mesh packings by experimental study and found that zigzag wire mesh structure exhibited the highest mass transfer as compared to the conventional wire mesh packing. This packing structure also offers low-pressure drop, which decreases the operational cost and makes the process more economical. The advantages and disadvantages of different RPB packing structures are summarized in Table 6.

Fig. 7
figure 7

a Unstructured wire mesh [97], b structured wire mesh [98], c zigzag wire mesh [96], d foam packing [98] and e knitted wire mesh [98]

Full size image
Table 6 Advantages and disadvantages of different RPB packing structures
Full size table

Moreover, due to the complex packing structure of the RPB, it is difficult to develop an exact packing geometry for the CFD study. Therefore, a lot of simplifications and assumptions are required to be made to develop a simplified structured geometry. Due to these assumptions, accurate prediction of the fluid flow behavior around the packing material cannot be obtained by the CFD study [98]. Square wire mesh packing and circular wire mesh packings are the most widely used geometries for the hydrodynamic study of RPB by CFD. Due to the short computational time and ease of geometry development, 2D geometric models have been employed extensively for the CFD analysis of RPB [50, 89, 93, 98, 102,103,104,105,106]. The different 2D geometry designs of RPB are shown in Fig. 8.

Fig. 8
figure 8

2D CFD models with different packing structures and arrangement (a) square wire mesh packing with no stationary or cavity zone [91], b square wire mesh packing (3 mm \(\times\) 3 mm) with cavity [104], c circular wire mesh packing (\(\mathrm{\varnothing }\)=0.5 mm) with no cavity zone [27] and d square wire mesh packing (0.5 mm \(\times\) 0.5 mm) with cavity [102]

Full size image

However, the prediction of the hydrodynamic parameters such as liquid holdup, residence time and maldistribution with the 2D model is not as accurate as the 3D model. Therefore, various studies have been done so far using the 3D CFD models. Goa et al. [103] used the 3D model to study different characteristics of liquid flow behavior, such as maldistribution of liquid, mean residence time and specific surface area and concluded that the simulated results showed a better agreement with the experimental data compared to the results of the 2D CFD model. However, to reduce the complexity of the 3D model, the packing was simplified without considering the effect of horizontal wire meshes which makes the results less realistic. Likewise, Zhang et al. [107] used the 3D CFD model to study the droplet breakup behavior using a single 3D layer of the packing. They did not study other attributes of liquid flow behavior in a fully developed region of RPB. Despite the complexities in the 3D model, Zhang et al. [88] tried to study the characteristics of liquid flow within the RPB using 3D wire mesh packing (considering the effect of horizontal wire meshes) as shown in Fig. 9 and found that the computed flow pattern obtained as a result of 3D simulation showed a good agreement with the experimental data. However, the difference between the previous CFD data is within 30%, which they claimed is due to the difference in the packing structure.

Fig. 9
figure 9

3D model of RPB as proposed by Zhang et al. [88]: a entire flow domain, b cross-sectional view of the flow domain at 45\(^\circ\) and c cross-sectional view of packing wire

Full size image

3.3 Effect of Different RPB Designs on the Hydrodynamics Parameters

The selection of the appropriate RPB design plays a vital role in the process design and optimization as the employment of the suitable configuration can save energy consumption and can improve the quality of the process. The design of the RPB can significantly affect the hydrodynamic parameters such as the pressure drop, liquid holdup, mean residence time and the liquid dispersion. Bai et al. [108] proposed a novel spherical design of the RPB as shown in the Fig. 10 and studied the effect of operational conditions on the liquid holdup, liquid mean residence time and the pressure drop. Furthermore, they reported that unlike the conventional RPB design, the rotational speed does not have any significant effect on the liquid holdup of the spherical RPB. Similarly, the pressure drop in the spherical RPB was found to be lower than the conventional RPB up to 35%. Therefore, the application of RPB at low rotational speed can reduce the energy consumption for any application. The application of spherical RPB is more suitable which requires very short liquid residence time. However, for the case when the rate of CO2 absorption is low due to slow chemical reaction between the solvent and the CO2 or the diffusion mechanism, this design of the RPB will not be a good selection due to its shorter residence time as compared to the conventional RPB.

Fig. 10
figure 10

Spherical RPB design proposed by Bai et al. [108]

Full size image

The mass transfer efficiency of the RPB can also be intensified by adding any obstacle in the fluid path within the cavity zone of the RPB. Shi et al. [89] used the static baffles in the RPB to reduce the droplet size in the RPB for better dispersion and the mass transfer rate as shown in Fig. 11. The employment of the baffles in the RPB packing can reduce the flow path in the RPB and therefore also reduce the mean residence time of the liquid [109, 110]. Another drawback that limits the application of RPB for the gas–liquid separation is the low angular slip velocity of the gas phase around the rotor. The use of static baffles in the RPB can cope with this drawback of RPB. Sung and Chen [55] developed static baffles in RPB packing and found that using baffles in the packing can provide 117% more volumetric gas-transfer mass transfer coefficient as compared to the conventional RPB.

Fig. 11
figure 11

a Contour of volume fraction with static baffles [89] and b blade baffle design [55]

Full size image

3.4 Multiphase Phase Modeling in RPB

Multiphase models have been used extensively to simultaneously predict the interaction of more than one phase in the RPB. The Volume of Fluid (VOF) and the Eulerian model are the two most commonly used models to predict the flow characteristics (flow pattern) in the RPB.

3.4.1 Eulerian Approach

The Eulerian model has been used extensively for the CFD simulation of the various conventional reactors, such as packed bed reactor and fluidized bed reactor to predict the flow behavior and interaction of multiphase simultaneously. Some prominent advantages of this approach are (i) it does not require too small grids and therefore, can simulate the whole reactor by focusing on the fluid flow throughout the whole bed, (ii) more efficient for steady-state simulation and does not require high computational time and power, (iii) this model assumes both liquid and gaseous phases as individual phases [111]. However, the Eulerian model does not consider the drag forces between the gas–liquid, gas–solid and solid–liquid interfaces and thus is not able to predict the flow behavior around the packing of the RPB accurately [112, 113]. The porous media model has been used extensively in combination with the Eulerian model to predict the flow behavior in packed bed reactor [114, 115]. But due to the high porosity of wire mesh and cylindrical diameter of packing the porous media model cannot be used to predict the flow behavior and gas–liquid interaction in the RPB. Kołodziej and Łojewska [113] experimentally investigated the flow pattern through wire mesh packing and the conventional spherical packing and found that the flow through the wire meshing packing was entirely different from the spherical packing. There are very few studies reported so far, which have used the Eulerian Model for the CFD study of RPB. Lu et al. [112] developed a new porous media model for the CFD analysis of gas–liquid (air–water) two-phase system and found that this model cannot accurately predict the flow behavior within the RPB due to the assumption made to simplify the mathematical model. The application of the Eulerian model and the main findings are summarized in Table 7. Therefore, a more realistic model is required to be developed with minimum assumptions that can accurately predict the flow characteristics such as flow behavior and pattern and should include drag forces, interfacial area and can quantify the mass transfer in the RPB.

Table 7 Main findings of the Eulerian model
Full size table

3.4.2 Volume of Fluid (VOF)

The volume of fluid (VOF) is one of the most capable multiphase models to analyze and track the gas–liquid interface in two-phase flow [102, 117]. This model uses a single set of momentum equations by considering both the liquid and the gas as a single phase and can predict the volume fraction of each fluid (gas and liquid) throughout the domain. The most highlighted advantages of this model are (i) the flow distribution of liquid can be analyzed using this model, (ii) the solution by this model is independent of interaction between different phases and (iii) can analyze all three types of flows, i.e., film flow, rivulet flow and droplet flow within the flow domain [93]. However, there are also some disadvantages associated with the application of this model, such as (i) it cannot be useful for the simulation of a whole reactor as it requires very tiny grids that need more time and computer resources to be simulated, (ii) VOF only emphasizes the numerical solution of liquid that flows along the packing side and (iii) it requires more computational time as compared to the Eulerian model [116]. Shi et al. [89] predicted the flow pattern of the RPB using the Volume of Fluid (VOF) model in combination with the sliding mesh model (SMM) and Reynolds stress model (RSM) to predict the liquid distribution (Fig. 12). They predicted the velocity fields and liquid volume distribution of fluid around the packing area within the RPB. The results showed that VOF was an effective model to understand the liquid–gas interface, which helped to predict the liquid–gas velocity distribution in the RPB.

Fig. 12
figure 12

The maldistribution of the liquid phase in the packing area (t = 0.5 s): a N = 500 rpm, u = 0.5 m/s; b N = 900 rpm, u = 0.5 m/s; and c N = 900 rpm,u = 2 m/s. [89]

Full size image

Xie et al. [27] used Volume of Fluid (VOF) along with the SST k-omega model to investigate the liquid flow behavior in RPB for CO2 (physical) absorption. The results exhibited that the VOF model could successfully simulate the liquid flow pattern by tracking the gas–liquid interface around the packed area of RPB. Based on the validation of simulated data, Xie et al. [27] concluded that the VOF model has promising potential and is capable to analyze the hydrodynamics of industrial RPB using 3D CFD modeling. Ouyang et al. [106] and Guo et al. [103] used realized k-epsilon model in combination with the VOF model to simulate the gas–liquid phases in RPB. They found it an effective approach to capture the gas–liquid interfaces and analyze instantaneous flow information such as liquid film and droplet flow in the RPB. Yang et al. [93] employed the VOF model to study the gas–liquid mass transfer in the RPB. They concluded that the gas–liquid interface cannot be predicted accurately because the computational grids in their conducted study were not small enough to capture the gas–liquid interfaces accurately. The reported research shows that Volume of Fluid (VOF) is the most suitable model to investigate the hydrodynamics of multiphase flow in the RPB [89, 93, 102, 118].

3.4.3 Turbulence Modeling in RPB

There are several factors that affect the accuracy of the CFD results. The selection of an appropriate turbulence model is one among them, and the model selection should be based on its adaptability [38]. The standard k-\(\upvarepsilon\), SST k-\(\upomega\), Reynolds stress model (RSM), and the Detached Eddy Simulation Turbulence Model (DES) are the most commonly employed models for turbulent flow prediction. Each turbulence model has its own limitation and uses the different set of boundary conditions. Guo et al. [102] studied the micro-mixing efficiency in RPB using Reynolds Stress Model (RSM) by simulating the volume fraction of liquid and the concentration distribution. The effect of rotational speed and liquid velocity were studied to investigate their influence on the micro-mixing efficiency of the RPB. The simulated results exhibited good agreement with the experimental data. As the Reynolds Stress Model (RSM) uses five (2D flow) and seven (3D flow) additional equations, it demands more time and computational memory [119]. Xie et al. [27] applied the Standard and SST k-omega model for the closure of the Navier–Stokes equation for simulating the physical absorption of CO2 in RPB using MEA as a solvent. The liquid holdup predicted by the Standard and SST k-omega models was within 5% of the holdup obtained by the RSM model. Yang et al. [120] employed the Realizable k-epsilon and Standard k- epsilon turbulence models to optimize the single (gas) phase flow in the RPB. The standard k- epsilon model showed a better agreement with the experimental data as compared to the Realizable k-epsilon model. However, the agreement was good only for low rotational speed, i.e., rotational speed < 1000 rpm. Table 8 summarizes the multiphase and turbulence model used so far for the CFD analysis of RPB.

Table 8 Multiphase and Turbulence Model used for CFD study of RPB
Full size table

3.4.4 Rotating Reference Frame

The rotational speed of the RPB has a significant effect on the hydrodynamics of the RPB. Therefore, it is necessary to adopt a suitable rotating reference frame model that can incorporate the effect of rotation and can be proven an efficient model in investigating the hydrodynamics of RPB. The sliding mesh model (SMM) is a completely unsteady method that can be employed effectively for the CFD analysis of RPB. Shi et al. [89] used SMM to visualize the liquid pattern in the RPB by generating a dense gravity environment using this model and found that the simulated results showed a good agreement with the experimental data. On the other hand, researchers have also used the moving reference frame for considering the rotation of the RPB [27, 105, 106, 121]. Both the single rotating reference frame and multiple reference frame have been used for this purpose. For the CFD geometry having more than two interfaces, multiple reference frame is the only available model to employ for the unsteady state simulation. For example, Lui et al. [98] concluded that moving reference frame is an effective way to study the flow behavior at the rotor-cavity interface. However, when there is only a single interface, single rotating reference frame can be adapted to study the liquid flow characteristics. Xie et al. [27] employed a single reference frame along with a UDF to control the movement of the inlet to investigate the hydrodynamics of the RPB and concluded that the moving reference frame (MRF) is a useful method when studying the flow behavior at rotor-cavity interface. Both MRF and SMM are found to be effective when simulating the rotating packed bed. However, if the geometry contains more than one zone i.e., stationary and rotating zones, the MRF is the only model available that can be employed to predict the hydrodynamics of gas–liquid in RPB.

3.4.5 Reactive CFD Modeling of CO2 Absorption

There exists very limited data for the CFD analysis of the reactive absorption of CO2 which incorporates the effect of chemical reaction on the mass transfer rate of the RPB. Sebastia-Saez et al. [122] studied the mass transfer rate by employing micro-scale CFD modeling of CO2 absorption in packed bed column using the volume of fluid multiphase model. The formation of the carbamate (RNH+COO−) was considered as the rate-controlling step, which described the complete reaction kinetics of the chemical absorption of CO2. The consumption of the MEA and production of carbamate during the chemical reaction between MEA and CO2 was incorporated into the source terms using the UDF. Considering the formation of the carbamate (RNH+COO−) as an irreversible reaction, the rate of the reaction was calculated by the following equation:

$${\mathrm{R}}_{\mathrm{reaction}}=\mathrm{ K}\left[{\mathrm{CO}}_{2}\right][{\mathrm{RNH}}_{2}]$$
(10)

where, \(\mathrm{K}\) was the forward rate of reaction, which is 24,984 \({\mathrm{m}}^{3}\mathrm{ k}{\mathrm{mol}}^{-1-1}\)[122, 123]. Gbadago et al. [124] studied the reactive absorption of CO2 in industrial packed bed adsorber using the Eulerian (porous media approach) multiphase model in combination with standard k-epsilon turbulence model. The simulated results of pressure-drop and absorption efficiency were compared with the experimental data of the pilot plant absorber. The simulated results showed 5.2% deviation from the experimental data. However, no attempt has been made to study the effect of reaction on the absorption of CO2 in the RPB.

To sum up the discussion, CFD has found its successful application to study the flow characteristics of gas and liquid in the RPB. Unlike the experimental approach, this approach does not require sophisticated engineering tools to predict the hydrodynamics. In addition, a single unit of RPB for the experimental study does not allow any modification in the physical structure of the RPB such as change in packing type, number of injecting nozzles, size of injecting nozzles and the RPB configuration, etc. to study the effect of these parameters on the hydrodynamics of the RPB. Similarly, to scale up the laboratory setup to study the flow characteristics and mass transfer performance of RPB for the industrial application is a time taking approach. On the other hand, CFD is capable of handling these sorts of challenges. Moreover, CFD provides both the visual contours and quantified parameters for the hydrodynamics parameters which provide a better insight of the flow behavior which is favorable attribute for the designing and optimization of the RPB. The comparison of CFD results and the experimental data revealed that CFD has the ability to efficiently predict the mass transfer performance and the hydrodynamics of the RPB on lab scale as well as on the industrial scale. However, predictive potential of CFD is very sensitive to the selection of turbulence model, number of grids and the geometric configurations, i.e., 2D or 3D.

4 Conclusion and Future perspective

The conclusion of the review is as follows.

  1. a.

    The experimental methods have been employed widely to study the hydrodynamics of RPB. However, this approach is expensive and has a lot of engineering problems, such as the installation of technical instruments in RPB for capturing the hydrodynamics of RPB. On the other hand, the analytical correlations used with the experimental methods are based on assumptions that effect the prediction of the hydrodynamics of RPB.

  2. b.

    The application of the rotating packed bed reactor is a promising approach to control the depletion of CO2 into the atmosphere. The process of CO2 absorption can be more cost-effective and efficient by the optimization of process parameters such as rotating speed, solvent concertation, contact angle and the solvent inlet velocity. Mass transfer is one of the most important aspects while considering and optimizing the efficiency of RPB which can be quantified by incorporating an appropriate mass transfer model into the governing equations.

  3. c.

    Among various approaches to study the hydrodynamics of the RPB, CFD is the most effective way to study and investigate the hydrodynamic parameters such as liquid hold up, liquid residence time, pressure drop, etc. The 3D packing structure of RPB is complex, therefore, assumptions have been made in the past to simplify the CFD model. In order to understand the actual hydrodynamics of RPB, 3D CFD model with minimum possible assumptions is required to develop for the in-depth CFD analysis of RPB.

  4. d.

    The Volume of Fluid (VOF) is the most effective model to predict the volume fraction of each CO2 and solvent throughout the flow domain. However, the VOF model requires more computational time as compared to the Eulerian model. Eulerian model in combination with the suitable porous media model can be used to reduce the computational time. However, there exists no suitable porous media that can be used to model the porous mesh packing structure of RPB.

  5. e.

    The selection of a suitable turbulence model is necessary to accurately predict the flow for its adaptability. Reynold Stress Model (RSM) is the most accurate turbulence model for the CFD analysis of RPB. Moreover, this model requires much more computational time as compared to its counterparts. On the other hand, there exist two-equation models such as k-omega and k-epsilon which have also shown a good agreement with the experimental data.

  6. f.

    The validation of the CFD model for the analysis of CO2 absorption is a great challenge nowadays. As there exist no data in the literature which contains the experimental data of CO2 absorption that can be utilized for the model validation.

  7. g.

    The absorption of CO2 is a physio-chemical process. All the previously reported studies have only considered the physical absorption of the CO2 to study the flow characteristics of CO2 and solvent. However, to accurately predict the flow behavior of fluid in RPB, reactive absorption of CO2 must need to be considered and the effect of reaction on mass transfer within the reactor must need to be studied in detail.

  8. h.

    The mass transfer rate in the RPB depends on different RPB configurations. The detail understanding of the fluid behavior in different configurations need to be developed yet to practically utilize the potential of the RPB for the selected applications.