Linear Solvers for Reservoir Simulation Problems: An Overview and Recent Developments

Abstract

Linear solvers for reservoir simulation applications are the objective of this review. Specifically, we focus on techniques for Fully Implicit (FI) solution methods, in which the set of governing Partial Differential Equations (PDEs) is properly discretized in time (usually by the Backward Euler scheme), and space, and tackled by assembling and linearizing a single system of equations to solve all the model unknowns simultaneously. Due to the usually large size of these systems arising from real-world models, iterative methods, specifically Krylov subspace solvers, have become conventional choices; nonetheless, their success largely revolves around the quality of the preconditioner that is supplied to accelerate their convergence. These two intertwined elements, i.e., the solver and the preconditioner, are the focus of our analysis, especially the latter, which is still the subject of extensive research. The progressive increase in reservoir model size and complexity, along with the introduction of additional physics to the classical flow problem, display the limits of existing solvers. Intensive usage of computational and memory resources are frequent drawbacks in practice, resulting in unpleasantly slow convergence rates. Developing efficient, robust, and scalable preconditioners, often relying on physics-based assumptions, is the way to avoid potential bottlenecks in the solving phase. In this work, we proceed in reviewing principles and state-of-the-art of such linear solution tools to summarize and discuss the main advances and research directions for reservoir simulation problems. We compare the available preconditioning options, showing the connections existing among the different approaches, and try to develop a general algebraic framework.

1 Introduction

Reservoir simulators play a central role for the proper management of oil and gas fields during their whole life cycle, from early explorations to decommissioning. These tools have witnessed a constant evolution during the decades, from the first pioneering flow models to the actual general purpose simulators, capable of reproducing a number of physical processes taking place at the subsurface. The drivers of such development include, in particular, the demand for a higher accuracy of the simulation and the ambition of reproducing the most recent and complex field exploitation techniques, such as cutting-edge Enhanced Oil Recovery (EOR) strategies [1,2,3,4] or environmental impact mitigation projects, e.g., Carbon Capture and Storage (CCS) and Carbon Capture, Utilization and Storage (CCUS) [5,6,7]. The expansion of the simulation capabilities, however, goes hand in hand with the explosion of the numerical challenges to be faced and results in a growing complexity of the simulators.

The algorithmic structure of a reservoir simulator includes several different modules, as illustrated in Figure 1. Developing or simply utilizing a simulation tool requires an adequate knowledge of its components, starting from the underlying physical model, which is mathematically described by a set of continuous Partial Differential Equations (PDEs), and the relevant discretization schemes used to convert it into a system of discrete equations that can be solved numerically. The PDEs governing the flow of multiple fluids in a porous medium form a set of nonlinear coupled equations. Non-linearity is frequently treated with a Newton-like scheme, while coupling is addressed with the Fully Implicit (FI) approach. The core of the simulator is the linear solver, which is usually part of a library of different linear algebra tools linked to the code. The Newton iteration requires the solution to a sequence of large-size, often non-symmetric and ill-conditioned, linear(ized) systems of equations. This is the most time and resource consuming task during a full-transient reservoir simulation, generally requiring from 60% to 80% of the total simulation time [8,9,10,11]. Moreover, the fact that a set of simulations is customarily run, for either history matching, production optimization, or uncertainty quantification purposes, can make the computational load not affordable even with the most recent and powerful platforms.

Fig. 1

Typical workflow of an FI reservoir simulator. The red boxes highlight the task and tools reviewed in this work. In the figure, t denotes time, T the end-point simulated time, $\Delta t$ the time increment, $\varepsilon$ the tolerance of the nonlinear solver and ${\varvec{x}}_n^{(j)}$ is the vector gathering the problem unknowns with j the iteration counter and n the time step

It is not unusual that users and programmers of reservoir simulators consider the linear solver library as a “black-box”, supplied with a system of linear(ized) equations and somehow producing the solution. Understanding and managing the linear solver, however, is crucial to have a full control of the simulator and minimize the solution time through an efficient setup.

Roughly speaking, linear solvers can be classified as either direct or iterative, the latter being practically mandatory on modern computational architectures and for the current model sizes. While preconditioned Krylov subspace methods [12] stand out clearly for their flexibility and ease of use, the choice of the preconditioner is key for the overall solver efficiency and robustness.

Since hardware technology and software development are strictly interwoven, the opportunities and challenges of parallel computing must be considered as well, as this has become the standard playground for linear solvers. Multicore CPUs, massively distributed memories and, more recently, GPU-based architectures have strongly impacted the way a linear(ized) system of equations is solved, often stimulating the development of novel techniques specifically designed to fully exploit the new hardware capabilities. In this regard, new supercomputers worldwide are equipped with an increasing number of GPUs and the trend is to take over CPUs, thereby providing most of the peak floating-point performance (see also [13]).

As any other specific simulator, reservoir models are characterized by particular challenges that require a special treatment also from the linear solver viewpoint. Especially in the past two decades, several works have been dedicated to the preconditioning of linear solvers for reservoir simulators, tackling the problem from different perspectives. In this work, we aim at reviewing the current state-of-the-art about linear solvers in reservoir simulators, with particular care devoted to the available options for the preconditioning of Krylov subspace methods. The objective is to fix a standpoint on the state of the research on this topic, also trying to identify and develop a sort of unitary algebraic framework enveloping most of them.

The audience targeted by this paper consists of specialists in reservoir simulation and users of linear solvers. Therefore, before moving on to higher-level discussions of recent advancements in the field, we will try to lay the groundwork by recalling some necessary theoretical fundamentals about Krylov subspace solvers and preconditioning techniques.

The rest of the paper is structured as follows. First, the model problem for reservoir simulation will be presented with its governing PDEs. Based on the associated prototype system of equations, the most efficient iterative solvers will be presented and subsequently the issue of preconditioning addressed. The systems of equations originating in reservoir simulations typically exhibit a mixed elliptic/hyperbolic character, with the pressure block being nearly elliptic and the saturation/concentration part being almost hyperbolic. The preconditioning of such systems leverages this internal partition into elliptic/hyperbolic blocks by establishing a global strategy built on top of local preconditioners, which exploit the specific algebraic properties of each block. This approach is thus based on an interplay between a global preconditioning framework and the local preconditioners. Therefore, after reviewing the most popular preconditioners suitable for local problems, we will consider global techniques. A comparison of the available preconditioning options, with the development of a unifying framework, concludes the paper, along with a discussion of the outlook and future directions.

2 The Model Problem

Reservoir simulation is the generic identification of several different types of models based on flow and transport equations in porous media (see, for instance, [14] for a systematic review). The differences depend on the number of fluid phases being considered, the thermal state of the reservoir, either isothermal or nonisothermal, the presence of fractures or whether hydrocarbon components are modeled or not, just to cite a few common features.

With the aim at being as general as possible, we present here the mathematical model describing the multiphase, multi-component, and nonisothermal flow of compressible fluids in porous media including gravitational and capillary effects. It represents a general mathematical framework from which other models can be derived, usually by neglecting some components. Note that the following model formulation serves only as a reference to introduce the quantities and operators that are typically encountered in the applications of interest. The solving techniques that will be introduced in the sequel are not restricted to a particular model formulation.

2.1 Nonisothermal Multiphase Multi-Component Flow Model

The model describes the flow of a number of fluid components partitioned into three coexisting phases: aqueous, oleic liquid, and gaseous/vapor. The governing equations can be grouped into three sets, namely, conservation, thermodynamic and local constraint equations.

2.1.1 Conservation Equations

In a multi-component nonisothermal flow model, the conservation of both mass and energy is enforced. Let $n_p$ and $n_c$ denote the number of phases and components, respectively, whereas $\Omega$ is the physical domain and t is the time variable spanning the open temporal domain $\mathbb {T} = ]0,T[$. The mass conservation equation is written for each component $c \in \{1, \ldots , n_c\}$ [14, 15]:

$$\begin{aligned}&\frac{\partial }{\partial t} \left( \phi \sum _{\alpha =1}^{n_p} \chi _{c \alpha } \rho _{\alpha } S_{\alpha } \right) + \nabla \cdot \left( \sum _{\alpha =1}^{n_p} \chi _{c \alpha } \rho _{\alpha } {\varvec{v}}_{\alpha } \right) = \nonumber \\&\quad \sum _{\alpha =1}^{n_p} \chi _{c \alpha } \rho _{\alpha } q_{\alpha }, \quad \text {on}\,\, \ \Omega \times \mathbb {T}, \end{aligned}$$

(1)

where $\phi$ is the medium porosity and $\chi _{c \alpha }$, $\rho _{\alpha }$, $S_{\alpha }$ and $q_{\alpha }$ denote the concentration of component c in phase $\alpha$, the relevant phase density, saturation and sink/source term, respectively.

The velocity vector ${\varvec{v}}_{\alpha }$ is provided by Darcy’s equation, rearranged by Muskat and Meres [16] to account for the simultaneous flow of multiple fluids in a porous medium:

$$\begin{aligned} {\varvec{v}}_{\alpha } = - \lambda _{\alpha } K \left( \nabla p_{\alpha } - \gamma _{\alpha } \nabla h \right) , \quad \forall \alpha = \{ 1, \ldots , n_p \}. \end{aligned}$$

(2)

Here K is the permeability tensor, $\lambda _{\alpha } = k_{r \alpha }/\mu _{\alpha }$ is the phase mobility factor, with $k_{r \alpha }$ and $\mu _{\alpha }$ the relative permeability and the dynamic viscosity of phase $\alpha$, $p_{\alpha }$ is the phase pressure, $\gamma _{\alpha }$ is the specific gravity and h is the depth.

The capillary pressure is defined as the difference between the pressures of a non-wetting ($\alpha$) and wetting ($\eta$) phase:

$$\begin{aligned} p_{\alpha } - p_{\eta } = p_{c, \alpha \eta }, \qquad \forall \alpha \ne \eta . \end{aligned}$$

(3)

Typically, $p_{c, \alpha \eta }$ depends non-linearly on the saturation of the wetting phase.

The energy conservation equation reads [14, 17]:

$$\begin{aligned}&\frac{\partial }{\partial t} \left( \phi \sum _{\alpha =1}^{n_p} \rho _{\alpha } S_{\alpha } U_{\alpha } + (1-\phi ) \rho _r C_r T \right) \nonumber \\&\quad + \nabla \cdot \sum _{\alpha =1}^{n_p} \rho _{\alpha } {\varvec{v}}_{\alpha } H_{\alpha } - \nabla \cdot \left( {\kappa _T} \nabla T \right) = \nonumber \\&\quad \sum _{\alpha =1}^{n_p} H_{\alpha } \rho _{\alpha } q_{\alpha }, \quad \text {on} \ \Omega \times \mathbb {T}, \end{aligned}$$

(4)

where $U_{\alpha }$ and $H_{\alpha }$ are the internal energy and enthalpy of phase $\alpha$, respectively, $\rho _r$ and $C_r$ are the density and specific heat capacity of the rock, T is temperature and $\kappa _T$ is the thermal conductivity.

Following the natural variables formulation [18], the phase pressures, $p_{\alpha }$, the phase saturations, $S_{\alpha }$, the molar fractions of the components, $\chi _{c \alpha }$, and temperature, T, are elected as primary unknowns. The material parameters in Equations (1), (2), and (4) generally depend on the position vector and the primary variables through empiric tables or analytical relationships, such as Brooks-Corey’s model [19] for the relative permeability. The nature of these relationships is often nonlinear and, in some cases, hysteretic.

2.1.2 Thermodynamic Equilibrium Equations

A usual assumption in multiphase multi-component models is the instantaneous thermodynamic equilibrium, which prescribes the equality of the fugacities for each component [14, 20]:

$$\begin{aligned}&f_{c \alpha } (p,\chi _{c \alpha }) = f_{c \eta } (p,\chi _{c \eta } ), \nonumber \\&\quad \forall \alpha \ne \eta \in \{1, \ldots , n_p \} \wedge c \in \{1, \ldots , n_c\}. \end{aligned}$$

(5)

Moreover, the following relationships hold:

$$\begin{aligned} z_c - \sum _{\alpha =1}^{n_p} \nu _{\alpha } \chi _{c \alpha }&=0, \quad \forall c \in \{1, \ldots , n_c\}, \end{aligned}$$

(6)

$$\begin{aligned} \sum _{\alpha =1}^{n_p} \nu _{\alpha }&= 1. \quad \end{aligned}$$

(7)

In Equations (6) and (7), $z_c$ is the overall molar fraction of component c and $\nu _{\alpha }$ is the molar fraction of phase $\alpha$:

$$\begin{aligned}&z_c = \frac{\sum _{\alpha =1}^{n_p} \chi _{c \alpha } S_{\alpha } \rho _{\alpha }}{\sum _{\alpha =1}^{n_p} S_{\alpha } \rho _{\alpha }},\\&\nu _{\alpha } = \frac{S_{\alpha } \rho _{\alpha }}{\sum _{\eta =1}^{n_p} S_{\eta } \rho _{\eta }}. \end{aligned}$$

Usually, the fugacity, $f_{c \alpha }$, is a nonlinear function of p and $\chi _{c \alpha }$. Here it is assumed that p and $z_c$ are known, whereas $\chi _{c \alpha }$ and $\nu _{\alpha }$ are not.

In compositional simulations, the phase state of the system is determined with a two-step procedure performed at the element level. At the first stage, the number and type of coexisting phases is evaluated and three possibilities apply: hydrocarbons are present as oleic liquid, gaseous/vapor or both. This evaluation is traditionally carried out by either minimizing Gibbs energy or resorting to the phase stability analysis [15]. Whether the first stage analysis indicates a transition from a single-phase to a two-phase condition, flash calculations are performed, as a second step, in order to determine the $\chi _{c \alpha }$ components and $\nu _{\alpha }$ molar fractions.

2.1.3 Local Constraint Equations

The set of Equations (1)-(7) is under-constrained, hence additional relationships are needed to mathematically close the system. Usually they have a local nature, in the sense that they depend only on the unknowns belonging to a single element, and read:

$$\begin{aligned} \sum _{c=1}^{n_c} \chi _{c \alpha }&= 1, \quad \forall \alpha \in \{ 1, \ldots , n_p \}, \end{aligned}$$

(8)

$$\begin{aligned} \sum _{\alpha =1}^{n_p} S_{\alpha }&= 1. \quad \end{aligned}$$

(9)

The problem outlined by Equations (1), (2), and (4) with the supporting relationships (3), (5)- (9), is well-posed once appropriate initial and boundary conditions are supplied.

2.2 The Numerical Model

The mathematical model, described by the set of governing PDEs and constraint equations defined in Sect. 2.1, is highly nonlinear and requires an appropriate numerical treatment to be solved. Beside the FI method, sequential techniques, such as the classical Implicit Pressure Explicit Saturation (IMPES) [21], the Sequential Implicit (SI) [22,23,24], and, more recently, the Sequential Fully Implicit (SFI) [25,26,27,28,29,30,31,32,33] schemes, have been proposed. These methods leverage the mixed elliptic/hyperbolic character of reservoir problems to decouple the flow and transport processes and tackle them sequentially. This allows to use specialized and efficient solvers for each problem, with the overall success of the method depending on the strength of the pressure/transport coupling. Notice that this factor can change during a transient simulation due to the variable flow conditions that are often experienced in highly heterogeneous media and complex well operations [34]. Recent advancements with the SFI method can prove close to the FI approach in a wide number of applications. The Adaptive Implicit Method (AIM) [11, 35, 36] is another popular approach blending the robustness of the FI method with the computational efficiency of explicit techniques. In this paper, we stick to the FI method because of its unconditional stability, robustness, good convergence rate, and broad use in many academic and industrial simulators. On the other hand, the need for the solution to a sequence of large-size, usually non-symmetric, and possibly ill-conditioned systems of linearized equations makes the FI method computationally expensive and motivates the design of robust and fast linear solvers.

A second key ingredient for the design of a reservoir simulator is the use of appropriate discretization schemes, which allow to convert the governing continuous PDEs into a discrete nonlinear problem. A number of schemes is available from the literature. As to Darcy’s law in Equation (2), a quite common choice is the Two-Point Flux Approximation (TPFA) [21], whose popularity is due to the straightforward implementation, compact stencil and monotonicity. However, an accuracy loss can be observed with non $\mathbb {K}$-orthogonal grids and full-tensor permeabilities (see, for instance, [37,38,39] and references therein). Other schemes have been introduced to cope with this limitation at the cost of a greater complexity, e.g., the Multi-Point Flux Approximation (MPFA) [39,40,41,42,43,44], the family of Mixed Finite Element (MFE) methods with its hybridized version, the Mixed Hybrid Finite Element (MHFE) [45,46,47,48,49,50,51,52], or, more recently, the Mimetic Finite Difference (MFD) method [44, 53,54,55,56,57,58,59,60,61], to mention some. Conversely, the continuity equations (1) and (4) are usually discretized by the Finite Volume (FV) method, where the grid elements are used as control volumes. This guarantees that the mass/energy balance is enforced locally and the velocity field is conservative, the latter being a key requirement for accurate transport computations. Finally, the time dependency is usually addressed by means of low-order Finite Difference (FD) methods, such as the unconditionally stable Backward Euler scheme.

2.3 The Solving Phase

As mentioned earlier, addressing the discretized coupled Equations (1), (2), and (4) with the FI method and a Newton-like linearization technique requires the solution to a sequence of large-size, and possibly ill-conditioned, systems of linear equations at each time step, where all the unknowns, i.e., pressures, saturations, temperature, and molar fractions of the components, are updated simultaneously. For the sake of generality, we can organize the Jacobian matrix and unknown vector in homogeneous blocks, according to the different nature of the variables involved. This approach is also denoted as unknown-wise ordering. While pressures exhibit an elliptic behavior with a global effect on the system solution, saturations and molar fractions of the components have a hyperbolic nature, affecting the solution locally and propagating in time. On the other hand, temperature shows a hybrid character, i.e., elliptic or hyperbolic whether the diffusive or advective component prevails, respectively. In any case, following the subdivision into elliptic (or pressure-like) and hyperbolic (or saturation-like) unknowns, the Jacobian system of equations can be arranged in a $2 \times 2$ prototypical structure:

$$\begin{aligned} \mathcal {A} {\varvec{x}} = {\varvec{b}} \quad \Rightarrow \quad \begin{bmatrix} A_{pp} &{} A_{ps} \\ A_{sp} &{} A_{ss} \end{bmatrix} \begin{bmatrix} {\varvec{x}}_p \\ {\varvec{x}}_s \end{bmatrix} = \begin{bmatrix} {\varvec{b}}_p \\ {\varvec{b}}_s \end{bmatrix}, \end{aligned}$$

(10)

where $A_{pp} \in \mathbb {R}^{n_1 \times n_1}$, $A_{ps} \in \mathbb {R}^{n_1 \times n_2}$, $A_{sp} \in \mathbb {R}^{n_2 \times n_1}$ and $A_{ss} \in \mathbb {R}^{n_2 \times n_2}$.

The properties of the blocks in $\mathcal {A}$ can differ significantly according to the selected discretization schemes. Assessing such properties beforehand is crucial in order to select the most appropriate solver and design an efficient preconditioning strategy for the application at hand. $\mathcal {A}$ is sparse, but the stencil, hence its sparsity degree and structure, may vary substantially with the discretization schemes. From the algebraic stance, important properties are symmetry and definiteness of the leading blocks, while the whole matrix $\mathcal {A}$ is usually non-symmetric. The different reservoir simulation models and available discretization schemes produce linearized systems with the structure shown in Equation (10) and variable properties. This observation motivates why a unique robust and efficient solver is not yet available in literature, but a wide range of methods and preconditioners has been developed.

In the next section, we will review and summarize the most used iterative solvers for reservoir simulators, while in Sect. 4 we will deal with the issue of preconditioning and describe the most common techniques.

3 Linear Solvers

Let us assume existence and uniqueness of the solution of system (10). Of course, simply inverting $\mathcal {A}$, i.e., ${\varvec{x}} = \mathcal {A}^{-1} {\varvec{b}}$, is not an option. The numerical solution to a system of linear equations must be rather carried out with the aid of sparse direct or iterative solvers. In their basic setup, direct solvers recast the system to a triangular structure by a smart sequence of linear combinations of the equations. The interested reader is referred to [62] for an exhaustive survey of such solvers. By distinction, iterative methods build a sequence of approximations converging to the solution by successive corrections. Let $\overline{{\varvec{x}}} \in \mathbb {R}^{n}$, with $n=n_1+n_2$, be the solution $\mathcal {A}^{-1} {\varvec{b}}$ of system (10) and ${\varvec{x}}_0$ an arbitrary guess of $\overline{{\varvec{x}}}$. Iterative methods exploit a recurrent algorithm whose application generates the sequence of vectors ${\varvec{x}}_k$, with k the iteration counter, starting from the seed ${\varvec{x}}_0$. The algorithm converges if $\lim _{k \rightarrow + \infty } {\varvec{x}}_k = \overline{{\varvec{x}}}$, or, alternatively, $\lim _{k \rightarrow + \infty } {\varvec{r}}_k = {\varvec{0}}$, with ${\varvec{r}}_k={\varvec{b}} - \mathcal {A}{\varvec{x}}_k$ the residual vector. In practice, the loop is stopped when ${\varvec{x}}_k$ is “close enough” to $\overline{{\varvec{x}}}$ according to some exit criteria. A typical stopping criterion relies on checking the size of a norm of the residual, $\Vert {\varvec{r}}_k \Vert$, e.g., $\Vert {\varvec{r}}_k \Vert <\tau \Vert {\varvec{r}}_0 \Vert$ for a user-specified tolerance $\tau$.

It is beyond the scope of this work to discuss the pros and cons of direct and iterative solvers. Generally speaking, direct solvers are highly competitive for relatively small-size systems, while iterative methods become more and more efficient as the number of unknowns increases. In this context, by “efficiency” we mean a measure of the computational burden and memory storage required to solve a system of equations at a given precision. For the systems arising from reservoir simulations, Krylov subspace solvers are mandatory in practice because of (i) their low storage requirement, (ii) the small set of computational kernels needed for their implementation, i.e., sparse matrix-by-vector, scalar products, and vector updates only, and (iii) their scalability in parallel simulations [12].

3.1 Krylov Subspace Solvers

Given an arbitrary initial guess, ${\varvec{x}}_0$, and the associated residual, ${\varvec{r}}_0$, Krylov subspace methods look for the approximate solution ${\varvec{x}}_m$ at the m-th step of the recurrent procedure as [12]:

$$\begin{aligned} {\varvec{x}}_m = {\varvec{x}}_0 + {\varvec{y}}, \quad \text {for} \ {\varvec{y}} \in \mathcal {K}_m(\mathcal {A}, {\varvec{r}}_0), \end{aligned}$$

(11)

with $\mathcal {K}_m(\mathcal {A}, {\varvec{r}}_0)$ the so-called Krylov subspace of size m generated by $\mathcal {A}$ and ${\varvec{r}}_0$:

$$\begin{aligned} \mathcal {K}_m (\mathcal {A}, {\varvec{r}}_0 ) = \text {span} \left\{ {\varvec{r}}_0, \mathcal {A}{\varvec{r}}_0, \mathcal {A}^2{\varvec{r}}_0, \ldots , \mathcal {A}^{m-1}{\varvec{r}}_0 \right\} . \end{aligned}$$

(12)

$\mathcal {K}_m(\mathcal {A}, {\varvec{r}}_0)$, also referred to as trial space, is progressively enlarged at each iteration by adding a new vector to the basis ${\varvec{r}}_0$, $\mathcal {A}{\varvec{r}}_0$, $\ldots$, $\mathcal {A}^{m-1}{\varvec{r}}_0$ (Figure 2a). At $m=n+1$, the newly added vector, $\mathcal {A}^n{\varvec{r}}_0$, is linearly dependent with the previous ones and the subspace can be no longer expanded. Hence, $\mathcal {K}_n(\mathcal {A}, {\varvec{r}}_0) \equiv \mathbb {R}^n$ and it necessarily contains $\overline{{\varvec{x}}}$. This entails that, in exact arithmetic, Krylov subspace methods have a finite termination, finding $\overline{{\varvec{x}}}$ at most after n iterations. At each step, ${\varvec{x}}_m$ is computed by orthogonalizing the current residual, ${\varvec{r}}_m$, to a second vector subspace, $\mathcal {T}_m$, also called test space. Depending on the choice of $\mathcal {T}_m$, manifold variants can be defined, and for some of them the iterative solution ${\varvec{x}}_m$ satisfies some optimal properties in the current trial space.

The family of Krylov subspace solvers consists of several different methods. Among them, the most popular techniques used in reservoir simulators are: the Conjugate Gradient (CG), the Generalized Minimum Residual (GMRES) and the Bi-Conjugate Gradient Stabilized (Bi-CGStab). CG is suitable for Symmetric Positive Definite (SPD) systems, while GMRES and Bi-CGStab can be used with any matrix. The interested reader is referred to [63] for a thorough presentation of the solvers’ algorithms. Other solvers are part of the Krylov subspace family, such as Minimal Residual (MINRES) [64] or Orthogonal Minimum Residual (ORTHOMIN) [65] for indefinite and non-symmetric systems, respectively. The latter, in particular, was developed within the reservoir simulation community and enjoyed some popularity during the ’70s and ’80s (see, for instance, [36, 66, 67]), being later shadowed by the introduction of GMRES and Bi-CGStab, as shown, for example, in [68]. These solvers are, in fact, the usual default choice in most of the mainstream commercial simulators, e.g., [11, 69,70,71,72], although ORTHOMIN is still used in Eclipse 100 [71].

Fig. 2

Graphical interpretation of the Krylov subspace $\mathcal {K}_m(\mathcal {A}, {\varvec{r}}_0)$ enlargement within a vector space $\mathcal {Q} = \mathbb {R}^n$

CG for SPD systems was originally introduced by Hestenes and Stiefel [73]. The test space is set equal to the trial space, i.e., $\mathcal {T}_m \equiv \mathcal {K}_m(\mathcal {A}, {\varvec{r}}_0)$. It can be proven (see [12] for details) that the m-th iterate, ${\varvec{x}}_m$, is optimal in the sense that it minimizes the energy norm of the error $\Vert {\varvec{e}}_m \Vert _A = {\varvec{e}}_m^T \mathcal {A} {\varvec{e}}_m$, where ${\varvec{e}}_m = {\varvec{x}}_m - \overline{{\varvec{x}}}$. In other words, it means that ${\varvec{x}}_m$ is the optimal solution within $\mathcal {K}_m(\mathcal {A}, {\varvec{r}}_0)$ with respect to the property above. Since the basis ${\varvec{r}}_0, \mathcal {A}{\varvec{r}}_0, \ldots , \mathcal {A}^{m-1}{\varvec{r}}_0$ is only mildly independent, CG builds an orthonormal basis for $\mathcal {K}_m(\mathcal {A}, {\varvec{r}}_0)$ through the three-term Lanczos recurrence [74]. This allows ${\varvec{x}}_m$ to be generated just by updating the last iteration, while the complete basis of $\mathcal {K}_m(\mathcal {A}, {\varvec{r}}_0)$ is not needed explicitly. This is key for the CG performance, as it allows to keep constant the computational cost of each iteration at a fixed memory footprint. The CG convergence is theoretically controlled by the spectral condition number of $\mathcal {A}$, $\kappa (\mathcal {A})$ [12], i.e., the closer $\kappa (\mathcal {A})$ to 1, the faster the convergence rate.

Selecting $\mathcal {T}_m \equiv \mathcal {A}\mathcal {K}_m(\mathcal {A}, {\varvec{r}}_0)$ gives rise to the GMRES method [75]. With this choice, the 2-norm of the residual, $\Vert {\varvec{r}}_m \Vert _2$, is minimized in $\mathcal {K}_m(\mathcal {A}, {\varvec{r}}_0)$. In contrast to CG, an orthonormal basis for $\mathcal {K}_m(\mathcal {A}, {\varvec{r}}_0)$ has to be explicitly built and stored, thus requiring an increasing memory load and computational cost per iteration. In practice, GMRES is based on a long-term recurrence, which can become not affordable beyond a certain number of iterations. As proved by the Faber-Manteuffel theorem [76], an optimal scheme based on a short-term recurrence does not exist for non-symmetric matrices. Therefore, any attempt to reduce the (full) GMRES memory footprint can jeopardize its optimality and slow down the convergence. However, in order to keep the growth of GMRES computational cost under control, less expensive versions have been devised, in which an upper threshold, l, to the number of basis vectors of $\mathcal {K}_m$ is set. For instance, when such a threshold is reached, the generated vectors are discarded and a new sequence of Krylov spaces, $\mathcal {K}_m(\mathcal {A}, {\varvec{r}}_l)$, is built (Figure 2b). This popular technique is known as restarted GMRES and denoted as GMRES(l). With modern machines, values of l up to 500 are not unusual. Theoretical results about GMRES convergence are available for the full version only and are more complicated than CG. In particular, the GMRES behavior depends not only on the eigenvalue distribution of $\mathcal {A}$, like CG, but also on the condition number of the matrix of the eigenvectors.

Bi-CGStab [77] is another popular method for non-symmetric systems of equations. It is the most effective variant of the Bi-Conjugate gradient (Bi-CG) method [74, 78], which seeks the solution to system (10) by solving simultaneously also the dual system, i.e., $\mathcal {A}^T {\varvec{x}}^* = {\varvec{b}}^*$, for some right-hand side ${\varvec{b}}^*$. The two systems are addressed by orthogonalizing the respective residual to the Krylov dual space, $\mathcal {K}_m(\mathcal {A}^T, {\varvec{r}}_0)$ and $\mathcal {K}_m(\mathcal {A}, {\varvec{r}}_0^*)$, being ${\varvec{r}}_0^*$ the initial residual of the dual system, ${\varvec{b}}^*-\mathcal {A}^T{\varvec{x}}_0^*$. Bi-CGStab is a transpose-free Bi-CG implementation where the usually erratic convergence of the latter is stabilized by a local steepest descent procedure.

In contrast to GMRES, Bi-CGStab is a short-term recurrence like CG, but no optimal property is satisfied by ${\varvec{x}}_m$ at each step. This is also reflected by the convergence profile, which is more erratic than GMRES, despite the local stabilization (Figure 3).

Fig. 3

Converge profiles of (full) GMRES and Bi-CGStab solvers with and without preconditioning. In this application, the simple Jacobi preconditioner (introduced in Sect. 4.2.1) is used. Notice the more erratic convergence of Bi-CGStab compared to the smooth profiles obtained with GMRES

4 Preconditioning Techniques

4.1 General Concepts

Generally speaking, a preconditioner $\mathcal {M}^{-1}$ is an operator that transforms a linear system into an equivalent one, whose properties are such that the solver convergence is accelerated. The system can be either left-preconditioned:

$$\begin{aligned} \mathcal {M}^{-1}\mathcal {A} {\varvec{x}} = \mathcal {M}^{-1} {\varvec{b}}, \end{aligned}$$

(13)

or right-preconditioned:

$$\begin{aligned} \mathcal {A} \mathcal {M}^{-1} {\varvec{y}} = {\varvec{b}}, \qquad {\varvec{x}}=\mathcal {M}^{-1}{\varvec{y}}. \end{aligned}$$

(14)

Both possibilities are commonly used, with right preconditioning often preferred because it preserves the residual vector, ${\varvec{r}} = {\varvec{b}}-\mathcal {A} \mathcal {M}^{-1} \mathcal {M}{\varvec{x}} = {\varvec{b}}-\mathcal {A}{\varvec{x}}$. This can be useful whenever using the residual norm as exit criterion. From a practical viewpoint, opting for left or right preconditioning usually does not affect significantly the convergence rate, unless $\mathcal {M}^{-1}$ is rather ill-conditioned [12]. A third choice, called centered or split preconditioning, is possible if the preconditioner is available in the factorized form $\mathcal {M}^{-1}=\mathcal {M}_2^{-1} \mathcal {M}_1^{-1}$:

$$\begin{aligned} \mathcal {M}_1^{-1} \mathcal {A} \mathcal {M}_2^{-1} {\varvec{y}} = \mathcal {M}_1^{-1} {\varvec{b}}, \qquad {\varvec{x}}=\mathcal {M}_2^{-1} {\varvec{y}}. \end{aligned}$$

(15)

Notice that the preconditioned matrix is never explicitly formed, the only additional requirement being the application of the preconditioner to a vector at each iteration, i.e., the computation of ${\varvec{u}}=\mathcal {M}^{-1}{\varvec{v}}$ for some vector ${\varvec{v}}$.

Though theoretical results are not always available, the convergence of a Krylov solver is generally fast if the eigenspectrum of the preconditioned matrix is clustered far from 0. This can be achieved if the application of $\mathcal {M}^{-1}$ resembles as much as possible that of $\mathcal {A}^{-1}$. Whatever the way the action of $\mathcal {A}^{-1}$ is approximated, a good preconditioner should prove efficient, robust, and scalable. Efficiency is related to the capability of achieving a fast convergence at a low computation and application cost. Robustness concerns the capacity of computing and applying successfully the preconditioner independently of the specific problem at hand. Scalability is a concept related to the use of parallel computers, involving that the number of iterations to converge is insensitive to the problem size. At a deeper level, efficiency, robustness and scalability also rely heavily on the compatibility between the mathematical algorithm and the hardware architecture, whether based, for instance, on CPUs, GPUs, and the number of processing units. As a consequence, for a given problem there is not a unique preconditioning approach, but different options can be equally effective according to the actual resource availability. This explains the eager interest around preconditioning techniques shown by the community of researchers, the abundance of solutions available in the literature and the vastness of the possible designs.

Roughly speaking, preconditioning approaches can be traditionally divided into two categories, i.e., algebraic (or “given a matrix”) and physically based (or “given a problem”) preconditioners [79], but the separating line is often blurred. Purely algebraic preconditioners are meant for a broad use, as “black boxes”, when there is no (or little) knowledge of the underlying physical problem, i.e., the set of PDEs, and its properties. The main advantage is the robustness, but efficiency may not be optimal, since they are not targeted to a specific application. On the other side, physically based preconditioners are specifically designed for the problem at hand, trying to exploit as much as possible the knowledge of the PDEs’ hallmarks and the discretization scheme. Therefore, they can exhibit a great efficiency, but robustness and generalization to other problems is often at risk.

The complexity of reservoir simulation problems, usually expressed with the block structured systems (10), requires the design of articulated, physically based preconditioning frameworks pivoting on local targeted algebraic preconditioners for the blocks and Schur complement, which will be the topic of the next section. Then, the main preconditioning strategies for reservoir simulation problems will be addressed.

4.2 Preconditioners for local problems

In this section, we consider the single-block system of equations

$$\begin{aligned} A {\varvec{x}} = {\varvec{b}}, \end{aligned}$$

(16)

where $A\in \mathbb {R}^{n \times n}$ is nonsingular. Notice the different notation used for single-block and block-structured matrices, A and $\mathcal {A}$, respectively.

4.2.1 Jacobi and Block Jacobi Preconditioners

As previously mentioned in Sect. 4.1, the action of a preconditioner should resemble somehow that of the inverse, $A^{-1}$, of the system matrix, while preserving a workable setup and application cost. Then, a simple algebraic preconditioning approach is to take the inverse of a (possibly significant) portion of A and discard the remaining. If the matrix is diagonally dominant, such a portion might consist of the diagonal only. This gives rise to the so-called Jacobi preconditioner, $M_{\text {J}}^{-1} = \text {diag}(A)^{-1}$, whose action is nothing but a diagonal scaling of A. For general problems, this preconditioner turns out to be pretty ineffective. However, if matrix A is just badly-scaled, as it usually occurs when solving the discrete version of the coupled Equations (1) and (2) in strongly heterogeneous media, Jacobi preconditioner can be helpful for a preliminary coefficient balancing.

A simple strategy to improve the $M_{\text {J}}^{-1}$ performance relies on enlarging the nonzero pattern by taking blocks around the diagonal. This approach, known as Block Jacobi (BJ) preconditioner, is also supported by the observation that the most significant nonzero entries in matrices arising from the discretization of PDEs can be easily clustered around the diagonal by applying proper reordering algorithms [80]. If the block partition induced by BJ preconditioner, $M_{\text {BJ}}^{-1}$, succeeds in gathering the nonzero structure of A, then it may result effective [81, 82]. Figure 4 provides a graphical sketch of the structure of such a preconditioner. Notice that the blocks may also overlap each other.

Fig. 4

Example of BJ preconditioner with three diagonal blocks

The BJ setup consists of extracting the blocks around the diagonal and approximating their inverse. The application of $M_{BJ }^{-1}$ to a vector is carried out by blocks and weighting the contributes in the overlapped portions.

The BJ preconditioner is naturally suitable for parallel computing. A coarse-grained asynchronous parallel version of the application algorithm is, in fact, straightforward. For the inexact application of each block inverse several strategies may apply. If the blocks are sufficiently small, one may think of computing them explicitly, then the application of the preconditioner is nothing but a sequence of effectively parallelizable matrix-by-vector products (see, for instance, [83]). Alternatively, a sparsified version of the block inverse or a direct solver can be used. If the size of the blocks is large, then we can resort to an inner iterative solver, e.g., a Krylov subspace method, which would need, in turn, a set of dedicated local preconditioners for them.

The number of blocks, hence their size, is the main factor governing the preconditioner behavior: the larger the number, and the smaller the block size, the more BJ tends to the native Jacobi preconditioner.

4.2.2 ILU Factorization

ILU stands for Incomplete LU and is thus based on the factorization of a matrix into the product of a lower, L, and an upper, U, triangular factors, which is one of the classical approaches used by direct solvers [12, 84]. Since fill-in takes place in the computation of L and U, for preconditioning purposes a number of entries can be discarded, thus obtaining the inexact (incomplete) factors $\bar{L}$ and $\bar{U}$ (Figure 5), such that:

$$\begin{aligned} M_{ILU } = \bar{L} \bar{U} \approx A. \end{aligned}$$

(17)

This dropping strategy is performed to control the memory footprint and the application cost. In fact, the cost of applying $M_{ILU }^{-1}$ depends linearly on the number of nonzeros stored in $\bar{L}$ and $\bar{U}$.

Fig. 5

Full factorization (b, c) and incomplete factorization with zero fill-in (d, e) of the sparse matrix in (a). In the subpanels, nnz denotes the number of nonzero entries. With respect to the original matrix, the exact factorization requires a larger memory space by a factor 9.11

Notice that the structure of $M_{ILU }$ makes it suitable for split preconditioning as well. $M_{ILU }^{-1}$ is never formed explicitly by inverting and multiplying the two factors because additional fill-in takes place, hence its application to a vector is performed by forward and backward substitutions [12].

Determining the non-zero pattern of the two incomplete factors is key for the ILU effectiveness. Several variants have been introduced in the literature according to the pattern selection strategy. Roughly speaking, they can be subdivided into static and dynamic methods. Static techniques select the entries in $\bar{L}$ and $\bar{U}$ by defining a pattern $\mathcal {P}$ before the factorization begins, while dynamic techniques rely on parameter-controlled dropping strategies that assess and eventually discard the entries during the factorization. In such a way, $\mathcal {P}$ is built as the factorization progresses [85].

The basic static approach takes the nonzero pattern of A, i.e., $\mathcal {P}(A)$, leading to the popular ILU(0) and IC(0) (Incomplete Cholesky for SPD matrices) variants [86, 87]. ILU(0) proves to be a rather efficient preconditioner for matrices obtained from the discretization of both elliptic and hyperbolic problems [88], like some blocks of matrices arising from reservoir simulation applications, though it is not scalable and possibly not robust. A classic static technique to strengthen ILU(0) relies on the level-of-fill concept [89, 90], which ranks the potential entries of the factors according to their likely significance.

Greater flexibility is provided by threshold-based dynamic methods, where the threshold controls either the size of the entries [91, 92], or the number of nonzeros [93], or both [94].

Most of the ILU implementations available in the literature are amenable to be used as black-box preconditioners for Krylov subspace methods, as they do not require any specific knowledge of the problem at hand. This strength of ILU factorizations contributes to explain their popularity for a broad range of applications, including reservoir simulation. In the last three decades, however, the diffusion of parallel computing, along with the demand for models of ever increasing size, brought to light two serious limitations of ILU factorizations. The lack of scalability and the intrinsic sequentiality of both their computation and application, in fact, prevent the full exploitation of modern computing architectures [95]. This issue has been only partially mitigated by specific implementations aimed at uncovering as much parallelism as possible from ILU. Research in this field started from the mid ’80s with a peak in the late ’90s, when several solutions were proposed from graph theory [96] (specifically, graph partitioning techniques like multicoloring [97,98,99,100,101], nested factorization [102,103,104,105,106,107,108], multilevel factorization [109, 110], and level-scheduling [111,112,113,114,115,116]), as well as domain decomposition [8, 117,118,119,120] (Sect. 4.2.4) and reordering strategies (e.g., minimum degree and reverse Cuthill-McKee). Altering the matrix ordering, however, modifies the incomplete factor structure, possibly worsening the numerical stability and thus degrading the overall preconditioning quality, despite the parallel implementation [119, 121, 122]. Alternatively, domain decomposition-based approaches leverage the splitting of the computational grid. ILU factorization is performed independently for the internal unknowns of each subdomain, while the rows belonging to boundary unknowns need to be managed with a greater care.

Level-scheduling is another way to increase the parallelism in the ILU application, though efficiency of such a method is often poor [119, 121]. Other options include the sparse approximation of $\bar{L}^{-1}$ and $\bar{U}^{-1}$ by means of approximate inverse techniques [123] and the possibility of using Jacobi and block Jacobi schemes to iteratively solve lower and upper triangular systems [124]. Numerical tests revealed that the effectiveness of this approach blooms in highly parallel frameworks, but it suffers when the amount of parallelism is relatively low.

A detailed analysis of the different methods is beyond the scope of the paper, however, we refer the interested reader to textbooks [12, 84] or review papers [88, 125] for a thorough discussion and comparison.

Incomplete LU factorizations for reservoir simulation. ILU is a widely used tool in reservoir simulation applications. Most of commercial and academic simulators include ILU in the available preconditioning strategies, either as a standalone algorithm or as part of wider strategies.

Nested Factorization (NF), in particular, is a physics-based variant of ILU that was specifically designed to cope with reservoir simulation needs (see the works by Appleyard et al [102] and Appleyard [103]). The NF concept lies on the observation that the classical five-point or seven-point stencil pattern of the Jacobian, obtained from a TPFA-based discretization in 2-D or 3-D structured grids, respectively, gives rise to a nested tridiagonal structure. In its original formulation, following a natural ordering of the unknowns in a 3-D domain, the outermost diagonal contributions in the Jacobian express the connections between adjacent planes in the grid, whereas, moving towards the main diagonal, we find the inter-line (within each plane) and the inter-cell (within each line) interactions. The NF method leverages this recursive tridiagonal nonzero pattern, resulting in a three-level algorithm that tackles these interactions, one at a time, from the outermost to the innermost. Such an approach is used to both compute and apply the NF preconditioner and is clearly sequential. Around 15 years ago, NF enjoyed a revived interest from the community with some pieces of work dedicated to exposing parallelism from GPU-based implementations with the aid of multicoloring techniques (see, for instance, [106, 107]). Speed-ups between 10 and 20 have been recorded with respect to the classical CPU serial implementation. Though interesting for structured grids, NF can lose attractiveness for unstructured grids or larger-stencil schemes, such as MPFA or MHFE.

NF is the flagship preconditioning tool in Eclipse 100 [71], being used both as a global (for the whole Jacobian matrix) and local (for the pressure block) preconditioner. Other simulators, such as IMEX or STARS [70], tNavigator [69, 126], OPM [127, 128], and TOUGH2/3 [129, 130], embed serial or parallel (to a certain extent) versions of ILU factorizations. Especially in the past, the whole block-structured matrix $\mathcal {A}$ in system (10) was addressed with a single factorization (see, for instance, [8, 36, 67, 104, 105, 117, 131, 132]). Currently, hybrid techniques are preferred, where ILU decompositions are coupled with other preconditioners like BJ (Sect. 4.2.1), domain decomposition (Sect. 4.2.4) and algebraic multigrid (Sect. 4.2.3). In particular, combining ILU factorizations and algebraic multigrid gives rise to a popular version of the Constrained Pressure Residual (CPR) preconditioner (Sect. 4.3.1). The rationale is to exploit the inner block structure of the Jacobian and the elliptic/hyperbolic character of the sub-problems to devise preconditioning techniques that are capable to efficiently address the full range of error components, thus allowing a fast convergence. As a side effect, coupling ILU factorization with a more scalable method, improves the performance of the resulting approach. In fact, ILU shows a limited scalability and its performance tends to degrade as the size of the problem increases (see, for instance, the experimental analysis in [133]) and the heterogeneity/anisotropy of the fluid/rock properties is exacerbated [9, 134], as a result also of the usage of unstructured grids [135]. Ultimately, while level-of-scheduling- or threshold-based variants can still show acceptable results for moderately complex applications [136], challenging real-world problems should be dealt with in a more effective way by exploiting the inherent block structure of the system matrix and consider incomplete LU factorizations as an element of a more comprehensive preconditioning strategy.

4.2.3 Multigrid Methods

Multigrid (MG) methods, originally proposed in the seminal work by Brandt [137] for the solution of elliptic PDEs in regular grids, have enjoyed a great interest from the reservoir simulation community for the past two decades. In particular, the class of Algebraic MG (AMG) has experienced an increasing popularity mostly due to its scalability and flexibility of use.

MG methods leverage a radically different approach than ILU preconditioners. Let us consider the system in Equation (16), obtained from the discretization of an elliptic problem and addressed with a stationary iteration (or fixed-point) scheme [12]. The prototypical structure of these solvers is [84]:

$$\begin{aligned} {\varvec{x}}_{m+1} = {\varvec{x}}_m + C{\varvec{r}}_m, \end{aligned}$$

(18)

where several variants can be derived depending on the choice of the matrix C, such as the classical Jacobi or Gauss-Seidel schemes. We assume that the error at the m-th iterate can be decomposed as:

$$\begin{aligned} {\varvec{e}}_m = {\varvec{e}}_{m,s} + {\varvec{e}}_{m,o}, \end{aligned}$$

(19)

where ${\varvec{e}}_{m,s}$ and ${\varvec{e}}_{m,o}$ are the constant (or smooth) and variable (or oscillatory) components, respectively (see also Figure 6). Recalling Equation (19) and that ${\varvec{r}}_m = A {\varvec{e}}_m$, Equation (18) becomes:

$$\begin{aligned} {\varvec{x}}_{m+1} = {\varvec{x}}_m + C A ({\varvec{e}}_{m,s} + {\varvec{e}}_{m,o}). \end{aligned}$$

(20)

Since matrix A arises from the discretization of an elliptic problem, the row sum is 0, except for the rows associated with Dirichlet boundary conditions, thus implying that $A{\varvec{e}}_{m,s} \approx {\varvec{0}}$. Therefore, once the oscillatory components of the error have been removed, the correction term in Equation (20) becomes negligible and the iterative method stagnates, i.e., ${\varvec{x}}_{m+1} \approx {\varvec{x}}_m$. The effect of stationary iteration schemes on the error is shown in Figure 6. The oscillatory components are flattened in a few iterations and the profile tends to a smooth condition, whereas the overall reduction of the error is not guaranteed a priori. For this reason, fixed-point schemes are referred to as smoothers in the MG literature.

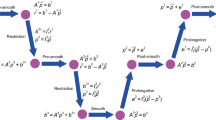
MG methods pivot on the fact that mapping the residual on a coarser grid makes the smooth components of the associated error turn into oscillatory modes, which can be damped by applying again the smoother. These observations are supported by a theoretical background based on Fourier analysis [138]. If a hierarchical sequence of progressively coarser computational grids is available (Figure 7), these steps can be recursively repeated until the size of the system to be solved is small enough to be addressed by a sparse direct solver. The error on the coarsest grid is then prolonged back to the original mesh, with the smoother applied again until convergence. This technique is known as V-cycle and, in its simplest version, comprises only two levels (two-grid cycle).

Fig. 6

Effect of Gauss-Seidel smoothing on the error. The horizontal plane in the panels indicates the smooth component of the error, $e_{m,s}$, at the m-th iterate, whereas the remaining portion to the total is the oscillatory part, $e_{m,o}$ (modified after Rodrigo et al [139])

Fig. 7

Example of multigrid discretization of a square domain with three meshes

The action of projecting the residual into a coarser grid is performed by restriction operators, $R_h^H:\mathbb {R}^{n^h} \rightarrow \mathbb {R}^{n^H}$, where h and H denote two adjacent grids in the mesh hierarchy, the finer and the coarser, respectively, and $n^h$ and $n^H$ the related number of unknowns. Of course, prolongation operators, $P_H^h:\mathbb {R}^{n^H} \rightarrow \mathbb {R}^{n^h}$, are defined as well.

Summarizing, the two main ingredients of an MG method are: (i) the smoother, and (ii) a hierarchy of grids with the relevant restriction and prolongation operators. Notice that the smoother and the restriction operators play a complementary role in MG methods because the former removes the oscillatory modes of the error on a fine grid and the latter injects the remaining smooth components into a coarser grid in order to be further damped. In this regard, the appropriate definition of the coarse space and, by extension, of the restriction operator is crucial. Generally $R_h^H$ is chosen so that $P_H^h$ provides a good interpolation of the error [138].

Though MG techniques were introduced as stand-alone solvers, their most appropriate use is as preconditioners for Krylov methods with a fixed number of pre- and post-smoother iterations. The V-cycle is the most frequent hierarchy, but other variants are available as well, such as the W-cycle [12]. Basically, MG methods comprise two phases: (i) the setup, where the hierarchy of matrices $A_{(j)}$, with $j=1,\ldots ,\eta$, associated with the $\eta$ coarse grids, is built, along with the restriction and interpolation operators, and (ii) the application, carried out, for instance, by the V-cycle. The sequence $A_{(j)}$ can be built by either exploiting a real hierarchy of grids, giving rise to Geometric MG, or introducing restrictions and prolongations in a purely algebraic way by the so-called Galerkin projection, thus defining AMG.

AMG methods gather indirectly information on the grid from the system matrix. Therefore, the grid topology does not need to be supplied and, in contrast with physics-based preconditioners, such as NF, AMG can handle complex domain geometries and anisotropic permeability fields. In fact, a non-zero entry $a_{ij}$ underlies that the unknowns i and j are neighbors and its size is an indicator of the strength of the i-j connection (SoC). This information can be used to separate the fine and coarse unknowns, arranged in the sets F and C, and define a coarsening scheme. The SoC evaluation and the application of the coarsening strategy is performed at each level to determine the sequence of $A_{(j)}$ matrices. Two typical examples are the CF splitting and the Smoothed Aggregation (SA), giving rise to the classical CF AMG [140] and SA AMG [141] versions, but other options apply, such as the more recent Node-root method [142, 143]. Determining coarse spaces by the SoC analysis is not the only available strategy. Multicoloring assisted by heuristic analyses, or independent set ordering techniques [96], have been used as well to classify the unknowns as coarse or fine, but they do not make use of the above information about strong and weak connections. A technique founded on independent set ordering that enjoyed some success is the Algebraic Recursive Multilevel Solver (ARMS) [144, 145].

An interesting AMG technique for reservoir simulators is the Multigrid Reduction (MGR), originally devised by Ries and Trottenberg [146] and Ries et al [147]. Let us consider a two-grid cycle for the sake of simplicity, but the method can be easily extended to a multi-grid setting as well. Differently from standard MG methods, in MGR the C and F sets are disjoint and their union gives the set of the overall unknowns. The system matrix in Equation (16) is reordered following the F-C unknown classification and decomposed using a block $\mathcal {LDU}$ factorization [136, 148, 149]:

$$\begin{aligned} A= & {} \begin{bmatrix} A_{FF} &{} A_{FC} \\ A_{CF} &{} A_{CC} \end{bmatrix} = \nonumber \\&\begin{bmatrix} I_{FF} &{} 0 \\ A_{CF} A_{FF}^{-1} &{} I_{CC} \end{bmatrix} \begin{bmatrix} A_{FF} &{} 0 \\ 0 &{} S \end{bmatrix} \begin{bmatrix} I_{FF} &{} A_{FF}^{-1} A_{FC} \\ 0 &{} I_{CC} \end{bmatrix}, \end{aligned}$$

(21)

where $S = A_{CC} - A_{CF} A_{FF}^{-1} A_{FC}$ is the Schur complement in the coarse space. This term plays a central role for block preconditioning, as we will see in Sect. 4.3.2. Denoting the exact restriction, prolongation and injection operators, respectively, as:

$$\begin{aligned} R_F^C= & {} \begin{bmatrix} D_U&I_{CC} \end{bmatrix}, \ P_C^F = \begin{bmatrix} D_L \\ I_{CC} \end{bmatrix}, \nonumber \\&\text {and}\,\, \ G = \begin{bmatrix} I_{FF} \\ 0 \end{bmatrix}, \end{aligned}$$

(22)

with $D_U = -A_{CF} A_{FF}^{-1}$ and $D_L = -A_{FF}^{-1} A_{FC}$, it is easy to verify that $S=R_F^C A P_C^F$ and $A_{FF} = G^T A G$. Note that, in Equation (22), the terms $D_L$ and $D_U$ serve as decoupling factors of matrix (21). It is difficult to obtain these operators exactly, since the explicit computation of $A_{FF}^{-1}$ is required. Therefore, proper approximations $\tilde{R}_F^C$ and $\tilde{P}_C^F$ should be sought, for instance by replacing $A_{FF}^{-1}$ with the inverse of its diagonal (standard Jacobi preconditioner) or by solving inexactly the sequence of multiple RHS-systems originating $D_U$ and $D_L$, i.e., $A_{FF}D_L=-A_{FC}$ and $A_{FF}^TD_U^T=-A_{CF}^T$. Using the inexact version of the operators in Equation (22), the preconditioner $M_{MGR }^{-1}$ reads:

$$\begin{aligned}&A^{-1} \approx M_{MGR }^{-1} = \tilde{P}_C^F \tilde{S}^{-1} \tilde{R}_F^C + G A_{FF}^{-1} G^T. \end{aligned}$$

(23)

Here, we can recognize the two main ingredients of MG: (i) the coarse-level correction, $\tilde{S}=\tilde{R}_F^C A \tilde{P}_C^F$, and (ii) the smoother $G A_{FF}^{-1} G^T=G(G^T A G)^{-1} G^T$, applied only to the portion of the linear system corresponding to the F-unknowns. A direct connection between Equation (23) and a two-grid approach can be easily established, with the coarse-level correction $\tilde{S}$ corresponding to $A_{(j)}$ in the coarse grid, whereas the smoother corresponds to C in (18). Of course, proper local preconditioners for S and $A_{FF}$ should be provided in Equation (23).

In summary, the main ingredients of AMG are: (i) a coarsening strategy, (ii) restriction and, (iii) prolongation (interpolation) operators, (iv) the smoother, and (v) the application technique [150]. Working on these components gives rise to a considerable number of possible variants. In this regard, AMG methods have attracted a great interest from the scientific community during the last 20 years and are currently object of intense development, see, for instance, [150,151,152,153,154,155,156,157] for a selection of methods.

As to the issue of parallelization, most tasks in the AMG application are matrix-by-vector products and vector updates. Letting aside the direct solution of the coarsest system, a possibly troublesome task is the smoother application. A classical Gauss-Seidel scheme, which requires the solution of a triangular system at each iteration, needs multicoloring and level scheduling approaches, while other smoothers, like BJ (Sect. 4.2.1) and, by extension, Domain decomposition (Sect. 4.2.4), can be much better parallelized. Although the AMG application can be carried out efficiently in parallel, its setup might be expensive as the sequence of $A_{(j)}$ matrices, with the relevant restriction and prolongation operators, is needed. This phase can sometimes jeopardize the method scalability, for example when a large number of computing units is used [158, 159].

AMG for reservoir simulation. Classical AMG methods have been developed to tackle systems of equations originating from elliptic PDEs, where the system matrix is expected to be SPD and, possibly, of M-type. This explains why AMG has found a natural and extensive application as a preconditioner of the elliptic pressure block in system (10) in a broadly used class of multi-stage preconditioning techniques called CPR (see Sect. 4.3.1). Still nowadays it remains the main application of AMG in the context of reservoir simulation.

As an alternative methodology, one can think of applying AMG to the whole block-structured system (10) despite its mixed elliptic/hyperbolic character and non-symmetry. Some arguments can support this approach [160]: (i) whilst the problem is mainly driven by elliptic components (such as pressure in reservoir simulation), AMG should be applicable; (ii) the approach can be extended also to systems incorporating other physics, such as geomechanics or thermal simulations (see, for instance, [161]); (iii) a monolithic preconditioning framework is applied to the full system without the introduction of additional stages; (iv) more information about the simulated physical process can be gathered from the full matrix rather than from one of its portions to obtain more targeted AMG techniques; (v) AMG is highly scalable and the entire linear solver part can be largely parallelized.

Of course, using standard AMG techniques can deliver poor results and specialized tools are thus required. After some early attempts, e.g., [34], significant effort has been spent to achieve comparable or even better performance than CPR-like schemes (see, for instance, the works by Gries and Plum [160] and Gries [162, 163]). The focus was on black oil simulations, with extensions to compositional models, and the advancements have been included in the System-AMG (SAMG) library [140]. Critical for the SAMG efficiency is recognizing the coupling between the different unknown types and applying an effective coarsening strategy. An interesting approach goes under the name of “point-wise AMG” and consists in defining a hierarchy for all the physical unknowns, which can be built from the pressure part. This technique has the potential to address a strong coupling of the unknowns. On the other hand, the smoother plays a crucial role as it is required also to solve somehow for the saturation/concentration unknowns. In this regard, ILU(0) factorization can prove effective, being able to capture the intrinsic coupling between the unknowns, even though its inherent sequentiality can jeopardize the AMG scalability. As mentioned in Sect. 4.2.2, uncovering some form of parallelism on ILU has been, and still is, a topic for research (see, for instance, [122, 124, 164, 165]). In the context of smoothing for AMG, Gries [166] proposed a parallel ILU(0) version based on level scheduling, also known as wavefront elimination [12]. A significant advantage is the equivalence of the resulting incomplete factors to those obtained with the serial algorithm, with no detrimental effects on the factors quality as those brought by other reordering strategies [125]. For unstructured grid, this approach can be more effective than traditional geometric level scheduling and, moreover, the wavefront setup can be recycled whilst the matrix pattern is preserved.

An MGR-based approach for the preconditioning of the full systems arising in fully implicit two-phase flow models and coupled multiphase-flow-poromechanics has been also considered in [148, 149].

The effectiveness of classical AMG algorithms, in terms of scalability and global convergence rate, can be also affected by strong heterogeneity and anisotropy of the rock/fluid properties in diffusion problems or upstreaming in transport models. Advanced AMG methods have been introduced to effectively tackle non-symmetric systems of equations and possible difficulties associated with the medium properties (see, for instance, [143, 167,168,169,170] for recent developments).

A complete and exhaustive review of these methods is far beyond the scope of this work. The interested reader is nevertheless referred to [12, 171, 172], as well as [173, 174] for a selection of textbooks and review papers, respectively. We report also the article by Stüben et al [175], which addresses the transition of AMG methods from academy to industry with abundant historical details and a reference also to reservoir simulation applications.

4.2.4 Domain Decomposition

The introduction of parallel computing was a real breakthrough for numerical modeling, including reservoir simulation, as an increasing amount of resources could be exploited to address larger and more complex problems. Domain decomposition (DD) [176] is one of the most popular methods to take advantage of the parallel computational paradigm. DD relies on the divide et impera concept, i.e., the physical domain $\Omega$ is split into a set of s, preferably equal-size, compact and possibly overlapping, subdomains $\Omega _i$ such that $\Omega = \bigcup _{i=1}^s \Omega _i$, where the problem is addressed locally (see Figure 8). The similarity of subdomain size is geared towards achieving load balance among processors, whereas the compactness aims at reducing the communication overhead. Node (or element) unknowns can be classified as inner or boundary according to their location in a subdomain and renumbered accordingly, as shown in Figure 9a,c.

Fig. 8

Partition of a reservoir model into subdomains

Fig. 9

Two examples (a, c) of domain decomposition with the relevant 5-point stencil matrices (b, d), as obtained from a TPFA discretization. The square domain is subdivided in four subdomains. In panel (a) the boundary elements are shared by neighboring subdomains and are numbered last, whereas in panel (c) the boundary elements are labeled after the internal cells in each subdomain

DD is important at different modeling stages, namely the setup, the discretization and the solving phase [176]. At the last level, DD can be conceived as either a solver or a preconditioner. There are a few different DD strategies for solving a system of equations, such as block Gauss elimination or Schur complement [12], which are used in particular for non-overlapping partitions, but those originating from the Schwarz alternating procedure [177] are perhaps the most popular. These techniques iteratively solve the series of local coupled systems independently of each other, using data from the neighbouring subdomains as boundary conditions. The iterative process ends when the solution on the subdomains stabilizes. Depending on when the overall solution vector is updated, i.e., at the end of the sweep over the subdomains or after each local solution, two variants can be defined: the Additive (AS) or Multiplicative Schwarz (MS) alternating algorithms, respectively (see, for instance, [178,179,180]). Expensive inter-processor communications, unbalanced workloads [181], and especially the low convergence rate [182] are usually important limitations to the use of DD methods as solvers. However, if the process is stopped well before convergence, these techniques can be exploited profitably as preconditioners.

Arranging the equations in system (16) according to the domain partition allows to extract a well-defined block structure from matrix A. The sequence of blocks $A_i$ is clustered along the diagonal and the nonzero off-diagonal blocks $A_{ij}$ denote the interaction between subdomains i and j (see Figure 9). Indeed, the blocks $A_i$ collect unknowns that are neighbours in the physical domain and it is expected, therefore, that strong interactions occur between spatially adjacent unknowns with respect to distant ones. This allows to exploit the knowledge of the domain discretization to obtain more targeted preconditioners.

The AS preconditioner, first introduced for solving SPD elliptic systems, and later extended to nonsymmetric and non-elliptic problems, has found application in the frame of reservoir simulation either as a stand-alone tool or as part of more articulated preconditioning strategies, e.g., [10, 181, 183,184,185,186,187,188]. For instance, AS coupled with ILU is available in Intersect [72, 189] for the preconditioning of the transport problem obtained by the SFI method.

A cheaper version of AS was proposed by Cai and Sarkis [190] and goes under the name of Restricted AS (RAS). The RAS variant exploits a double partition of the domain into overlapping and non-overlapping subdomains (like in Figure 10a) to reduce the communication overhead between processors. In several applications, e.g., the solution to convection-diffusion equations, indefinite complex Helmholtz equations, and compressible Euler’s equation on unstructured grids, the RAS preconditioner proved to perform better than AS [190], as confirmed also in the analyses in [191, 192].

The MS method requires a little more care since the solution vector is updated during the sweep over the processors and not just at the end. Hence, with an overlapping partition, different processors might simultaneously update the same entries. Multicolor techniques may help extracting some parallelism (see, for instance, the simple application in Figure 10).

Fig. 10

Example of domain decomposition in a 2D square setting with the aid of multicoloring. The dashed lines in panel (a) indicate the borders of the overlaps, while the continuous lines refer to a nonoverlapping partition

The design of robust preconditioners is often subjected to mutual influences between different strategies. Multilevel DD is, for instance, an example of contamination between MG and DD, which is motivated with the aim at improving the scalability of single-level DD by including a coarse grid correction. Introducing a hierarchy of grids, in fact, makes multilevel DD a theoretically scalable method. Computational experience, especially in the context of elasticity problems, shows that two levels can be enough when the number of cores is in the thousands, while three levels or more are needed to go beyond this threshold [193]. The basic algorithmic structure of multilevel DD resembles the classical AMG V-cycle, where the smoother is usually an AS preconditioner built upon the subdomain partition in each level. Recent applications of multilevel DD span from the solution of Navier-Stokes equations [194] to elasticity [193], and reservoir simulation problems [159, 187]. In the work authored by Li et al [187], some versions of the V-cycle scheme, obtained by neglecting the pre- or post-smoothing phase are investigated. Nevertheless, the best results are obtained by the full V-cycle. The application of the block inverse in AS/RAS preconditioner is performed via incomplete LU factorization with a different level-of-fill. Gratien [159], instead, focused on the efficient implementation of multilevel DD on modern HPC platforms.

Another promising branch of DD-driven preconditioners, which has gained in popularity in recent years, goes under the name of Nonlinear DD (NDD) preconditioning. Here, the approach to the problem is different, since NDD operates upon the nonlinear system of equations itself, rather than on its linearization through a Newton scheme. Initially introduced in the pioneering work by Cai and Keyes [195] for CFD applications, NDD was later extended to reservoir simulation by Liu et al [196] and Skogestad et al [181]. Reservoir simulation is indeed a challenging bench test, due to the non-linearity given by permeability models and material heterogeneities. The first NDD version exploits the AS approach and is thus denoted as Additive Schwarz Preconditioned Inexact Newton (ASPIN) [197]. A multiplicative version (MSPIN) has been developed as well [198], while a Restricted variant of ASPIN, built upon RAS preconditioner [190], and thus labelled RASPIN, has been introduced in [199]. Preconditioning the nonlinear problem has several attractive features. For instance, considering a typical reservoir simulation scenario like waterflooding, it is expected that the biggest source of non-linearity is mainly located around advancing fronts. Therefore, thanks to the subdomain partition, it is possible to build tailored tools based on the nonlinear degree of each one. The issue of scalability on large parallel machines motivated also the introduction of multilevel version, like the two-level ASPIN in [195]. An exhaustive dissertation on NDD preconditioning is beyond the scope of this paper, which rests on the design of preconditioners for linearized systems, however, the interested reader is addressed to the references herein and the recent works by Klemetsdal et al. [200, 201] for further reading. Moreover, for DD in general, the books [12, 182, 202], as well as the recent review article [203] are also advised.

4.2.5 Multiscale Preconditioners

Originally developed as an alternative to upscaling techniques, in recent years Multiscale (Ms) methods [204] have been successfully reinterpreted as preconditioning techniques as well. Running reservoir simulations directly on the geocellular model, as obtained from high-resolution field characterization, poses a big computational issue in terms of efficiency because they often consist of hundreds of millions of cells with abrupt changes in the material rock properties. Upscaling techniques [205, 206] were introduced to reduce the level of detail of the discretization by building coarser grids with homogenized/averaged properties. With classical upscaling techniques, however, the features of the fine discretization are discarded, thus leading to a possibly significant loss of accuracy. Ms methods have been introduced to overcome this specific limitation. Notice, however, that the separation between the two class of methods, i.e., upscaling and Ms, can be somehow blurred. For instance, Nested gridding techniques [207, 208] allow to switch from coarse to fine scale grids during the solution phase. A coarse partition is used to solve the pressure equation, then local flow problems are considered on each coarse cell to prolong the upscaled solution back to the fine grid.

The theoretical target of such methods is an elliptic problem, in analogy with MG techniques. At the early stages, research focused on the classical pressure equation governing the flow of a single phase in porous media [209]:

$$\begin{aligned} \nabla \cdot \left( K \nabla p \right) = q, \end{aligned}$$

(24)

obtained by simplifying Equations (1) and (2). In the basic setup, two discretizations of a physical domain, referred to as fine and coarse, have to be supplied. The coarse grid is obtained by aggregating neighboring fine cells, in analogy with DD techniques, as shown in [210]. Then, basis functions are numerically constructed to interpolate between the two grids by solving local incompressible flow problems on each coarse cell with simplified boundary conditions, in a similar way as for Nested gridding. This approach is known as harmonic lifting or localization assumption. The final aim is to capture the effect of the local variations in the permeability, while solving the global flow problem only on the coarse grid with averaged values. Once the coarse-scale solution is available, it can be mapped back to the native fine grid by means of the basis functions, thereby obtaining a mass-conservative approximation of the solution on the high-resolution grid, possibly after suitable postprocessing.

We can conceive the problem in a more rigorous algebraic formulation with the aid of restriction and prolongation inter-grid operators [211, 212]. To this end, let us consider a two-grid superimposed partition of the model domain, where $n^F$ and $n^C$ are the number of elements in the fine, $\overline{\Omega }^F$, and coarse, $\overline{\Omega }^C$, grids, respectively. We can define the coarsening ratio $C_r = n^F/n^C$, which is a user-defined parameter governing the size of the coarse problem. The discretized system of equations associated with Equation (24), built upon the native fine grid, reads:

$$\begin{aligned} A_{pp}^F {\varvec{x}}_p^F = {\varvec{b}}_p^F. \end{aligned}$$

(25)

Like in MG techniques, the link between the two levels is algebraically described through restriction $R : \mathbb {R}^{n^F} \rightarrow \mathbb {R}^{n^C}$ and prolongation $P : \mathbb {R}^{n^C} \rightarrow \mathbb {R}^{n^F}$ operators (see also [211,212,213] for the algebraic derivation, as well as [214] for the properties that R and P shall fulfill). The prolongation operator maps the coarse-scale pressure unknowns into the fine ones:

$$\begin{aligned} {\varvec{x}}_p^F \approx \tilde{{\varvec{x}}}_p^F = P {\varvec{x}}_p^C, \end{aligned}$$

(26)

where ${\varvec{x}}_p^C$ denotes the pressure solution on the coarse grid, and $\tilde{{\varvec{x}}}_p^F$ is the fine Ms approximation of ${\varvec{x}}_p^F$. Multiplying both sides of Equation (25) by R and introducing Equation (26) gives the restricted system:

$$\begin{aligned} A_{pp}^C {\varvec{x}}_p^C = {\varvec{b}}_p^C, \end{aligned}$$

(27)

where $A_{pp}^C = R A_{pp} P$ and ${\varvec{b}}_p^C = R {\varvec{b}}_p$. Equation (27) is then solved using either an iterative or direct solver, depending on its size, and the pressure solution mapped back into the fine-scale space by Equation (26). Ultimately, by combining Equations (26) and (27) and isolating $\tilde{{\varvec{x}}}_p^F$, we obtain:

$$\begin{aligned} \tilde{{\varvec{x}}}_p^F = \left( P A_{pp}^{C,-1} R \right) {\varvec{b}}_p^F, \end{aligned}$$

(28)

where $M_{\text {Ms}}^{-1} = P A_{pp}^{C,-1} R$ is the Ms operator. For very large problems, the possibility of realizing a sequence of progressively coarser grids (like in MG) and applying recursively the steps above has been also investigated (see, for instance, [215,216,217]). Multilevel methods can be formulated with dynamic variants [20, 218,219,220] as well, where the local grid refinement method is recast in an Ms framework. The FI system is solved by blending grids with adaptive resolutions so as to preserve a fine discretization only where the solution is expected to change most. Appropriate basis functions for each type of unknowns need to be incorporated to interpolate the solution between the grids. While the approaches advanced in [20, 218,219,220] seem to be promising, applications to non-Cartesian grids are still an unexplored ground as well as their use as preconditioning techniques.

The columns of the prolongation operator, P, are built by gathering the local basis functions computed on each coarse block, while different choices are available for R. Actually, it is the way in which P and R are formed and combined that distinguishes the various Ms techniques. A systematic review of this topic is out of the paper scope, hence we will limit ourselves to some glimpses by referring the reader to the works cited herein. Several methods are available in literature, such as the Multiscale Finite Element (MsFE) [209], Generalized Multiscale Finite Element (GMsFE) [221,222,223], numerical-subgrid upscaling [224,225,226,227], Multiscale Mixed Finite Element (MsMFE) [228,229,230,231], Multiscale Finite Volume (MsFV) [25, 232,233,234,235,236,237] and Multilevel Multiscale Mimetic (M$^3$) [215]. MsFE, MsMFE and MsFV are traditionally the three major variants. We mention, also, the Multiscale Restriction-Smoothed Basis (MsRSB) method, recently developed by Møyner and Lie [238] as the evolution of the MsFV through the incorporation of the SA technique [141], previously introduced in the frame of AMG preconditioners (Sect. 4.2.3).

MsFE was the first Ms method to be devised, with the limitation of the lack of mass conservation at the element level. This is crucial for accurate transport simulations, for instance in multiphase problems, since they rely on conservative velocity fields. The mass-conservative MsMFE and MsFV methods were thus developed to overcome such a drawback and soon gained a great interest within the reservoir simulation community. The interested reader is referred to the paper by Lie et al [239] for an informative discussion of the evolution of the two methods. From the early application to single-phase incompressible subsurface flow problems on Cartesian grids [232], active research allowed to progressively extend the application of Ms methods to advanced models, incorporating the flow of compressible phases with capillarity [234, 240], gravity [240, 241], components [27, 242], sophisticated well controls [243, 244], fractured porous media [245,246,247,248] and unstructured grids [249, 250]. Still, for these more complex models, Ms methods are typically exploited in sequential solving techniques to address the associated pressure equation.

It is quite natural to extend Ms methods as a preconditioner for Krylov subspace solvers, which is nowadays an important research avenue. The work by Lunati et al [213] is one of the first attempts in this direction. To this end, Equation (28) can be reinterpreted as the application, $\tilde{{\varvec{x}}}_p^F$, of the Ms preconditioner $M_{\text {Ms}}^{-1}$ to vector ${\varvec{b}}_p^F$. As to the definition of the restriction operator R, two approaches are usually followed, which correspond to apply the MsFE or the MsFV method. In the first case, $R=P^T$ (Galerkin projection), whereas, in the second, the restriction operator is built in such a way that, upon application, the pressure equations of the fine cells belonging to a coarse block are summed. The first approach (MsFE) is usually preferred since it preserves the symmetry of the problem [183] and the convergence is faster [251], but it does not guarantee the mass conservation at the local level. However, this feature can be easily recovered by performing a last iteration with the MsFV-based operator. In recent years, besides the direct application as pressure-block preconditioner in sequential methods, the Ms operator has been also exploited for the elliptic block, $A_{pp}$, in system (10) in FI schemes [252], as mentioned in Sect. 4.3.1.

The Ms preconditioner must be used as part of a multi-stage strategy, comprising also a smoother. This approach is denoted iterative Ms [245, 253] and usually consists of two stages closely resembling an MG V-cycle. Hajibeygi et al [253] and Zhou and Tchelepi [183] observed, in fact, that $M_{\text {Ms}}^{-1}$ is rank deficient by $n^F-n^C$, therefore it cannot address all the error components and does not yield convergence. Specifically, only the low-frequency (or long-range) modes are deflated, while high-frequency (or short-range) error components have to be treated by a complementing smoother, such as ILU, block ILU or AS. Similar conclusions were also provided by Pasetto et al [254], who used a coarse model based on the Proper Orthogonal Decomposition (POD) of the fine model. Anyway, such a behavior is consistent with the global nature of Ms operators, which rely on approximations at the local level where a smoother usually proves effective. Similarly to AMG, the P operator should provide a good interpolation of the error from the coarse to the fine grid, while avoiding the introduction of oscillatory components in the solution. Several combinations of Ms operator for the global stage and relaxation scheme for the local stage are possible. In this regard, Wang et al [251] found it efficient to blend the MsFE operator (replaced by the MsFV operator at the final step) with an ILU factorization at the fine scale. This setup was also tested by Manea et al [255] in a parallel computing environment and both studies show comparable results with respect to SAMG [140]. The two-stage iterative strategy outlined above sets the basis also for one of the pressure-problem solvers currently implemented in Intersect [72, 256, 257].

The accuracy of the Ms operators largely revolves around: (i) the ability of the basis functions to represent the fine-scale features on the coarse grid, and (ii) the approximation introduced for their computation due to use of homogeneous boundary conditions for the local flow problems. As to the first issue, the coarsening factor $C_r$, the aspect ratio of the coarse cells, and the internal permeability leaps play a prominent role [253]. Generally, it can be beneficial to build coarse grids that adapt to the subsurface geological structure, hence following the medium property distribution, rather than using uniform partitions [249]. High contrasts in the permeability within coarse cells, in fact, can jeopardize the accuracy of the coarse-scale problem equations. To this end, Lie et al [258] proposed to design multiple coarse partitions, each one targeting a specific property, with the aim at representing the fine-scale rock properties in all its aspects at different levels. These concepts have been extended in [214], where three types of basis functions, namely general, static and dynamic are introduced on a likewise number of coarse partitions. General basis functions are built upon regular and homogeneous coarse-scale grids. Static functions, instead, play an important role in grids with different degrees of refinement and irregular cells, thereby adapting to the shape of the reservoir formations or possible flow paths. Finally, dynamic functions aim at characterizing the coupling of pressure and saturation, which is usually confined to advancing fronts or regions experiencing abrupt pressure changes, by developing partitions that follow the solution variation within the domain. Such preconditioning technique appears to be effective, even though possibly expensive.

The second issue, i.e., the inaccuracies caused by weak localization assumptions, is responsible for drawbacks mostly experienced with the MsFV method under specific settings. Large aspect ratios in the cell size, resulting in highly anisotropic transmissivities, and significant permeability leaps, as in channelized media, are responsible of severe monotonicity issues, unreal pressure fluctuations and circular velocity fields [239]. This is a well-known shortcoming and a number of strategies have been devised for its mitigation, for instance by using iterative techniques, possibly with the introduction of additional correction functions (CFs) [253]. For preconditioning purposes, the use of CFs can be thought as a preliminary stage in the iterative MsFV algorithm aimed at dumping the high-frequency components of the error. CFs alone give rise to a non-convergent local solver that usually needs to be complemented by another smoother. While CF helps accelerating the convergence, it also proved to be computationally expensive [251].

As to the efficiency of Ms methods, in multiphase problems the recomputation of the coarse-grid basis functions at every stage of the simulation can be expensive, though being embarrassingly parallel. For incompressible flow, a classical approach consists in updating the basis functions during the simulation whenever changes of the rock/fluid properties have been detected (e.g., near advancing fronts), for instance, by easily setting thresholds [233]. In more general approaches, applicable also to compressible flow problems, basis functions are computed once at the outset of the simulation, and then used in each time step to compute a first guess which can be improved through iterations and smoothers to get rid of any errors induced by global couplings and dynamic changes in the mobilities.

The application of MsFV to unstructured grids presents significant challenges in the computation of the basis functions, since it requires the construction of a second dual-grid upon the coarse partition. The MsRSB method [238, 259] was designed to overcome such a limitation by introducing the more flexible concept of support region, associated with each coarse element, which replaces the dual-cell. The second hallmark of the MsRSB approach regards the computation of the P operator through an iterative technique relying on a simple weighted Jacobi relaxation scheme. Such an iterative approach can be advantageous also for the update of the P operator by exploiting the old version as seed for the recomputation [259]. The interested reader can refer to the book by Lie and Møyner [257] for a detailed description of the transition from MsFV to the MsRSB method.

Ms methods have been the object of an increasing interest within the reservoir simulation community. In late years, much effort has also been spent on extending these techniques as preconditioners for block problems, such as poromechanics [260, 261], coupled flow-poromechanics [262] and flow with heat transfer [263]. Using a similar strategy also for system (10) would entail to compute basis functions for the non-pressure block as well. Even though appealing, this strategy is challenging due to the hyperbolic nature and the strong inherent non-linearity of the problem, as highlighted in [264], and up to date a study on this topic is missing.

4.3 Preconditioners for Reservoir Block Problems

The most effective way to address problems with a structure like the one in Equation (10) is to exploit its block form. After having reviewed some preconditioning techniques for local preconditioners, in this section we will consider methods for reservoir simulation block-structured problems.

4.3.1 Multi-Stage Preconditioners: CPR and CPR-like Schemes

The class of multi-stage preconditioners is definitely one of the most popular for reservoir simulators, with several applications also to multi-physics problems, for instance coupled flow and poromechanics [262, 265, 266]. The rationale is often physics-based and exploits the algebraic properties of single physics in order to build a set of preconditioners, which are applied in an additive or multiplicative sequence. During such an application, the sets of unknowns are repeatedly updated and progressively corrected. The standard preconditioner for commercial reservoir simulators (see, for instance, Eclipse 300 [71], Intersect [72], Nexus [267] and others [11]), as well as academic simulators (like OPM [127, 128], MRST [54, 59, 257], AD-GPRS [15, 17, 268,269,270,271], IPARS [272,273,274] or DARTS [275]), is the two-stage multiplicative Constrained Pressure Residual (CPR). Originally introduced in the early ’80s in the pioneering works by Wallis [276] and Wallis et al [277] as an improvement of the combinative method proposed in [66], CPR was specifically designed to address the linearized systems of equations originating from FI dead-oil models under isothermal conditions [278].

CPR takes inspiration from the IMPES solution strategy [21, 279], where the pressure and saturation equations are decoupled and addressed separately. This is supported by the mixed character of the reservoir problem with respect to pressure-like and saturation-like unknowns. While pressures are associated with an elliptic problem and have a global effect, saturations refer to a hyperbolic problem and their influence on the flow is local. CPR addresses the relevant blocks by means of dedicated preconditioners, tailored upon their specific properties. The traditional CPR preconditioner, $\mathcal {M}_{CPR }^{-1}$, has two stages, namely $\mathcal {M}^{-1}_1$ and $\mathcal {M}^{-1}_2$, involving an approximation of the inverse of $A_{pp}$ and the whole matrix $\mathcal {A}$, respectively. Since $A_{pp}$ has generally the structure of an elliptic problem, an AMG V-cycle (Sect. 4.2.3) is an ideal candidate, as first observed in the seminal works [280] and [134]. In symbols, the restricted pressure approximate solver reads:

$$\begin{aligned} \mathcal {M}_1^{-1} \approx \begin{bmatrix} A_{pp}^{-1} &{} 0 \\ 0 &{} 0 \end{bmatrix}. \end{aligned}$$

(29)

The second-stage preconditioner, instead, is usually an ILU(0) factorization of $\mathcal {A}$:

$$\begin{aligned} \mathcal {M}_2^{-1} = \overline{\mathcal {U}}^{-1} \overline{\mathcal {L}}^{-1} \approx \mathcal {A}^{-1}. \end{aligned}$$

(30)

Due to the inherent limitations of ILU factorization for effective parallel implementations, another choice for $\mathcal {M}_2^{-1}$ is AS, or its less expensive variant RAS [10, 184]. The overall CPR preconditioner is expressed as:

$$\begin{aligned} \mathcal {M}_{CPR }^{-1} = \mathcal {M}_2^{-1} \left[ \mathcal {I} - \mathcal {A} \mathcal {M}_1^{-1} \right] + \mathcal {M}_1^{-1} \end{aligned}$$

(31)

and its application ${\varvec{u}}=[{\varvec{u}}_p \ {\varvec{u}}_s]^T$ to a vector ${\varvec{v}}=[{\varvec{v}}_p \ {\varvec{v}}_s]^T$ can be broken down into four steps, as detailed in Algorithm 1. Here, ${\varvec{u}}^1=[{\varvec{u}}_p^1 \ {\varvec{0}}]^T$ is the first-stage approximation of ${\varvec{u}}$, $\delta {\varvec{u}}=[\delta {\varvec{u}}_p \ \delta {\varvec{u}}_s]^T$ is the correction and ${\varvec{r}}=[{\varvec{r}}_p \ {\varvec{r}}_s]^T$ is the residual. Notice that both usual ingredients of the CPR preconditioner, i.e., AMG and ILU, do not require the knowledge of the domain topology, therefore this preconditioning technique, in conjunction with a Krylov subspace method, can be used as a black-box solver.

Decoupling pressure from saturation. Applying $\mathcal {M}_1^{-1}$ to ${\varvec{v}}$ is equivalent to solve approximately the first block of equations $A_{pp} {\varvec{u}}_p + A_{ps} {\varvec{u}}_s = {\varvec{v}}_p$ by neglecting the coupling between pressure and saturation, i.e., “freezing” the saturations. In order to limit the effect of this approximation, a common strategy is to preliminary decouple pressures from saturations by premultiplying both sides of system (10) by an appropriate operator $\mathcal {F}$. The decoupling process should also have a preconditioning effect on $\mathcal {A}$ and the leading blocks, but this is often difficult to achieve [34].

The $\mathcal {F}$ operator can be conceived as a sort of left preconditioner, whose application might be carried out before system (10) is addressed [17] and, like all preconditioners, its setup and application should be as inexpensive as possible. Alternatively, the decoupling task can be incorporated during the first-stage preconditioner application.

The ideal decoupling operator should read:

$$\begin{aligned} \mathcal {F}_{ex }= \begin{bmatrix} I &{} D \\ 0 &{} I \end{bmatrix}, \end{aligned}$$

(32)

where $D=-A_{ps} A_{ss}^{-1}$. Premultiplying both sides of Equation (10) with $\mathcal {F}_{ex }$ gives:

$$\begin{aligned}&\widetilde{\mathcal {A}} {\varvec{x}} = \widetilde{{\varvec{b}}} \quad \Rightarrow \nonumber \\&\quad \begin{bmatrix} \widetilde{A}_{pp} &{} 0 \\ {A}_{sp} &{} {A}_{ss} \end{bmatrix} \begin{bmatrix} {\varvec{x}}_p \\ {\varvec{x}}_s \end{bmatrix} = \begin{bmatrix} {\varvec{b}}_p - A_{ps}A_{ss}^{-1} {\varvec{b}}_s\\ {\varvec{b}}_s \end{bmatrix}, \end{aligned}$$

(33)

where $\widetilde{A}_{pp} = A_{pp} - A_{ps} A_{ss}^{-1} A_{sp}$ is the reverse, or “primal”, Schur complement of $\mathcal {A}$. Of course, the exact application of $\mathcal {F}_{ex }$ is generally not feasible in practice and it might result in excessive fill-in of $\widetilde{A}_{pp}$. Therefore, cheaper approximations have been introduced, such as the Alternate-Block-Factorization (ABF) [281] or Quasi-IMPES (QI) and True-IMPES (TI) operators [272, 279], borrowed from IMPES method. A systematic review of these techniques can be found in [252] and [282]. In the following, only QI and TI will be briefly presented, since ABF might provide a non-symmetric $\widetilde{A}_{pp}$ that can jeopardize the AMG application. The QI and TI decoupling operator is:

$$\begin{aligned} \mathcal {F}_\text {QI,TI} = \begin{bmatrix} I &{} D_\text {QI,TI} \\ 0 &{} I \end{bmatrix}, \end{aligned}$$

(34)

where $D_{\text {QI}} = - \text {diag}(A_{ps}) \text {diag}^{-1}(A_{ss})$ and $D_\text {TI} = -\text {colsum}(A_{ps}) \text {colsum}^{-1}(A_{ss})$. The operator $\text {colsum}(A)$ returns a diagonal approximation of A with entries equal to the sum of the components in each column of A. These techniques are a trade-off between the need of accuracy and efficiency. Notice, however, that they can be used only if $A_{ps}$ is square, i.e., there are as much pressure-like as saturation-like unknowns. This restrains the relevance of these techniques to specific classes of models and discretization schemes, like standard black-oil simulations discretized with the TPFA. If the above assumption does not hold, other choices are available, for instance by providing sparse approximations of $\mathcal {F}$ through the solution to the multiple RHS-system $A_{ss}^T D^T=-A_{ps}^T$, as proposed in the context of MGR method by Bui et al [148, 149] and adapted to coupled flow-poromechanics applications [283] or MHFE-based flow models [284].

Ellipticity of the pressure subproblem. While decoupling pressure from saturation should improve the effectiveness of the global CPR algorithm, it is also fundamental that the pressure subproblem can be properly tackled by AMG. If not, convergence of CPR-preconditioned Krylov subspace methods can be slow and lack of robustness is sometimes observed. There are two main causes for such a behavior [285]: (i) the diffusive flux preserves the ellipticity of the pressure block, but local source terms, such as fractures and wells, can violate this condition. In some black oil models, due to phase appearance and disappearance [148] or high number of active wells [285], the pressure block can even become indefinite; (ii) the application of the pressure-saturation decoupling factor transforms the original pressure block $A_{pp}$ to $\tilde{A}_{pp}$ of Equation (33), thus potentially worsening, even in a significant way, its native algebraic properties. In summary, AMG may converge slowly or may not converge at all.

As to the first issue, Gries et al [285] proposed the Dynamic Row Sum (DRS) technique to ameliorate the original properties of the pressure block. Applying the DRS method is somehow equivalent to performing an adaptive matrix scaling and can be considered as a preliminary step in the process. The resulting pressure block is a compromise between the one obtained with the IMPES strategy and the necessity of protecting it from troublesome features for AMG. By tuning a couple of parameters, the balance can be shifted towards one of the two extremes.

Regarding the introduction of decoupling factors, we should remember from the previous section that such a decoupling is necessarily approximated since computing and applying $A_{ss}^{-1}$ exactly is too expensive. On top of that, preserving the AMG-friendly properties of the pressure subproblem, for instance diagonal dominance, might be difficult to control. QI and TI operators can be good inexpensive choices [252, 286], but other more sophisticated options are possible (see, for instance, [285]). Notice, however, that early results presented in [285], and later confirmed in [163, 287], show that it is generally better to prioritize the AMG solvability, rather than focusing on the algebraic decoupling between pressure and saturation, in order to have a fast convergence.

Recent advancements Even though CPR is almost 40 years old, the interest around this method is still high. In recent years, the main research directions have focused on: (i) designing CPR-like schemes with more than two-stages [10, 184, 288, 289], (ii) coping with some critical aspects related to the effects of capillarity on the saturation block [266, 290], (iii) extending the CPR preconditioner to general purpose reservoir simulations [17, 286, 291,292,293], and (iv) evaluating the suitability of the Ms operator as an alternative to AMG for the pressure subproblem [214, 217, 252, 255, 294].

In general, an n-stage preconditioner (with $n \ge 2$) can be expressed as:

$$\begin{aligned} \mathcal {M}_{n-stage }^{-1} = \sum _{i=2}^n \mathcal {M}_i^{-1} \prod _{j=1}^{i-1} \left[ \mathcal {I}- \mathcal {A}\mathcal {M}_j^{-1} \right] + \mathcal {M}_1^{-1}. \end{aligned}$$

(35)

A family of CPR-like schemes has been developed in [184] and [10] and applied to black-oil models. Several variants have been designed by swapping the order of the updates in Algorithm 1 or extending the formulation to three and even four stages. Furthermore, the ILU decomposition $\mathcal {M}_2^{-1}$ has been replaced with an RAS approximation, coupled with an additional factorization of the local blocks to improve the parallel degree and scalability of the algorithm. The results show that the most promising scheme has three stages, where the whole problem is tackled first and at the end, whereas the pressure problem is solved only once at the second stage.

The effects of capillarity on the performance of CPR have been investigated in [290]. According to the model used, the saturation block $A_{ss}$ may exhibit a convection-diffusion or a hyperbolic nature. Two- and three-stage CPR variants were considered, whose performance is compared against an AMG applied to the whole Jacobian and a block constraint preconditioner (Sect. 4.3.2). The experimental tests showed that the two-stage CPR is not as efficient as the three-stage variant, which performs very well except when the capillary model leads to an advection-dominated flow. On the other hand, the block constraint preconditioner proved to be competitive with respect to CPR-like methods thanks to its robustness and good scalability. The work by Bui et al [290] has been extended in [266], where poromechanics has been included in the original two-phase flow model. When capillary effects are important and the saturation block exhibits a diffusion dominated nature, the experimental analysis showed that it might be convenient to use an AMG preconditioner rather than a simple Jacobi scaling as obtained from QI decoupling.

As mentioned before, the traditional CPR preconditioner was designed to cope with dead-oil models, however it has been frequently employed for compositional and thermal reservoir simulations as well. In such cases, although new blocks are added to the linearized system (10), the standard approach is to include the additional variables (phase composition and temperature) as saturation-like variables, thus obtaining again a $2 \times 2$ system structure. This choice, however, especially in presence of thermal effects, can worsen the CPR efficiency, requiring more expensive ILU(l) factorizations [293]. The reason is that the additional variables, such as temperature, might not have a local saturation-like effect. This is particularly true when severe thermal diffusion occurs, for instance whenever the fluid flow is slow and the energy equations exhibit a strong elliptic nature [17], which justifies the promotion of temperature as a pressure-like variable. Such an issue was first addressed by Li et al [291, 292], where a novel version of the CPR preconditioner, namely the Enhanced CPR (ECPR), was proposed. With this approach, the set of first-stage unknowns is selected according to the outcome of a preliminary analysis that evaluates the coupling strength between variables. In alternative to CPR, Roy et al [293] designed and tested a block preconditioner, which proved more efficient in diffusion-dominated settings. However, for advection-based simulations the classical CPR remains the method of choice. In [286], the Constrained Pressure-Temperature Residual (CPTR) preconditioner, blending the traditional CPR with block preconditioning, is introduced with the aim at exploiting the strengths of both approaches. The first-stage set of unknowns comprises both pressure and temperature and the application of the relevant preconditioner exploits the $2 \times 2$ inherent block structure of the resulting (1,1) block, instead of computing a single preconditioner, as it will be much clearer in Sect. 4.3.2. In [17], the focus of the problem is expanded from black-oil to multiphase-thermal-compositional-reactive flow in porous media and a novel three-stage preconditioner, namely the CPTR3, which exploits the 3$\times$3 structure of the system matrix, was designed.

In the preliminary work [252], the Authors proposed a CPR-Ms algorithm, where the Ms operator, $M_{\text {Ms}}^{-1}$ in Equation 28, is cast in a V-cycle fashion and used as an approximate pressure solver, $\mathcal {M}_1^{-1}$, replacing AMG. The experimentation on multiphase multi-component flow problems showed some good results for the CPR-Ms preconditioner, while not being always as efficient as the classical CPR-AMG. In a preliminary study, Klemetsdal et al [214] analyzed the performance of a MsRSB-based pressure preconditioner with multiple basis functions built upon both regular and irregular coarse partitions, designed following the shape of the formations and the fluid fronts. The tests proved that this approach is advantageous with respect to algorithms with a single set of basis functions, but a thorough comparison with AMG-based algorithms is missing. By distinction, such an analysis is the driver of the work by Nilsen et al [217], but it is limited to the solution of the pressure block alone. The performance of a MsRSB approximate pressure solver, using two or more grid levels, is evaluated against aggregation and smoothed-aggregation AMG. Hybrid schemes, where Ms and AMG operators are used at different levels, have been considered as well. The results showed that, while Ms-based algorithms often use less iterations to converge, they are more time-consuming than standard aggregation AMG. Hybrid schemes, however, proved to be competing with respect to pure AMG-based algorithms. Therefore, further research is needed to develop a robust and efficient alternative to CPR-AMG preconditioners.

4.3.2 Block Preconditioners

Even though CPR is the academic standard for reservoir simulators with a large use also in commercial software, there is an increasing number of applications where its efficiency and robustness can be questionable. These can include discretizations producing a non-symmetric or indefinite pressure-like block $A_{pp}$, or simulations introducing additional features, such as mechanics, capillarity, temperature, or phase change. To cope with these issues, a growing interest has gathered around block preconditioners, which can be regarded as either an alternative to CPR (see, for instance, [290, 293]) or a mean to improve it (e.g., [17, 286]).

Block preconditioners have been originally introduced since the early ’00s to address the solution of saddle-point matrices [295] that frequently arise in problems like the solution of Navier-Stokes equations [296,297,298,299,300,301], constrained optimization [302,303,304], coupled poromechanics [262, 265, 283, 305,306,307,308,309,310], electromagnetism [311,312,313,314], and contact mechanics [315,316,317], to mention a few applications and some recent related works.

Let us consider the prototype problem (10). The block-$\mathcal {LDU}$ decomposition of $\mathcal {A}$ reads:

$$\begin{aligned}&\mathcal {A} = \mathcal {LDU} \quad \Rightarrow \quad \begin{bmatrix} A_{pp} &{} A_{ps} \\ A_{sp} &{} A_{ss} \end{bmatrix} = \nonumber \\&\quad \begin{bmatrix} I &{} 0 \\ A_{sp} A_{pp}^{-1} &{} I \end{bmatrix} \begin{bmatrix} A_{pp} &{} 0 \\ 0 &{} S \end{bmatrix} \begin{bmatrix} I &{} A_{pp}^{-1} A_{ps} \\ 0 &{} I \end{bmatrix}, \end{aligned}$$

(36)

where $S = A_{ss} - A_{sp} A_{pp}^{-1} A_{ps}$ is the Schur complement. Following Equation (36), the inverse of $\mathcal {A}$ is:

$$\begin{aligned} \mathcal {A}^{-1} = \begin{bmatrix} I &{} -A_{pp}^{-1} A_{ps} \\ 0 &{} I \end{bmatrix} \begin{bmatrix} A_{pp}^{-1} &{} 0 \\ 0 &{} S^{-1} \end{bmatrix} \begin{bmatrix} I &{} 0 \\ -A_{sp} A_{pp}^{-1} &{} I \end{bmatrix} \end{aligned}$$

(37)

and the vector ${\varvec{u}}=\mathcal {A}^{-1} {\varvec{v}}$ therefore reads:

$$\begin{aligned}&\begin{bmatrix} {\varvec{u}}_p \\ {\varvec{u}}_s \end{bmatrix} = \begin{bmatrix} A_{pp} &{} A_{ps} \\ A_{sp} &{} A_{ss} \end{bmatrix}^{-1} \begin{bmatrix} {\varvec{v}}_p \\ {\varvec{v}}_s \end{bmatrix}\nonumber \\&\quad = \begin{bmatrix} A_{pp}^{-1}({\varvec{v}}_p - A_{ps} {\varvec{u}}_s) \\ S^{-1}({\varvec{v}}_s - A_{sp} A_{pp}^{-1} {\varvec{v}}_p) \end{bmatrix}. \end{aligned}$$

(38)

According to Equation (38), the computation of ${\varvec{u}}$ requires the availability of $A_{pp}^{-1}$ and $S^{-1}$, i.e., the solution of two inner systems. If such a solution is carried out inexactly, Equation (38) can be regarded as the application of a block preconditioner of $\mathcal {A}$. This strategy was originally denoted as constraint preconditioning [88], because this technique was often used in connection with constrained optimization problems.

Depending on how $A_{pp}^{-1}$ and $S^{-1}$ are approximated, different variants of constraint preconditioners can be identified. A first approach, introduced by Keller et al [318] for indefinite systems, implies to replace $A_{pp}^{-1}$ with a sparse approximation $M_{pp}^{-1}$, compute explicitly an approximation of S as $\overline{S} = A_{ss} - A_{sp} M_{pp}^{-1} A_{ps}$, and solve exactly the second system in Equation (38) having $\overline{S}$ as matrix. The structure of the resulting block preconditioner, denoted as Exact Constraint Preconditioner (ECP), reads:

$$\begin{aligned} \mathcal {M}^{-1}_\text {ECP} = \begin{bmatrix} M_{pp} &{} A_{ps} \\ A_{sp} &{} A_{ss} \end{bmatrix}^{-1}. \end{aligned}$$

(39)

If $A_{pp}$, hence $M_{pp}^{-1}$, is SPD, this approach has optimal properties for the eigenspectrum of the preconditioned matrix, allowing for the use of CG even for indefinite systems [319]. However, for the sake of efficiency, ECP has to satisfy at least three constraints: (i) $M_{pp}^{-1}$ should be available explicitly, (ii) $\overline{S}$ has to retain a workable sparsity, and (iii) the solution to the system with $\overline{S}$ should be as inexpensive as possible.

A possible remedy to the last issue can arise from the introduction of a sparse approximation $M_S$ of $\overline{S}$, which should be easier to invert. Recalling Equation (37), the Full Inexact Constraint Preconditioner (FICP) is obtained:

$$\begin{aligned} \mathcal {M}^{-1}_\text {FICP}= & {} \begin{bmatrix} I &{} -M_{pp}^{-1} A_{sp} \\ 0 &{} I \end{bmatrix} \begin{bmatrix} M_{pp}^{-1} &{} 0 \\ 0 &{} M_S^{-1} \end{bmatrix} \begin{bmatrix} I &{} 0 \\ -A_{ps} M_{pp}^{-1} &{} I \end{bmatrix} \nonumber \\= & {} \begin{bmatrix} M_{pp} &{} A_{ps} \\ A_{sp} &{} M_S+A_{sp} M_{pp}^{-1} A_{ps} \end{bmatrix}^{-1}. \end{aligned}$$

(40)

This introduces a further approximation, thus causing the loss of the ECP theoretical properties. Notwithstanding, the performance of the FICP preconditioner is usually good in practice and this behavior is theoretically justified, for instance in [320,321,322]. A less expensive FICP variant can be obtained by neglecting one of the two triangular blocks, thus obtaining a lower or upper Triangular Inexact Constraint Preconditioner (TICP), such as:

$$\begin{aligned} \mathcal {M}^{L,-1}_\text {TICP}= & {} \begin{bmatrix} M_{pp}^{-1} &{} 0 \\ 0 &{} M_S^{-1} \end{bmatrix} \begin{bmatrix} I &{} 0 \\ -A_{ps} M_{pp}^{-1} &{} I \end{bmatrix}\nonumber \\= & {} \begin{bmatrix} M_{pp}^{-1} &{} 0 \\ -M_S^{-1} A_{ps} M_{pp}^{-1} &{} M_S^{-1} \end{bmatrix}, \end{aligned}$$

(41)

when the upper block is discarded. An even more inexpensive approximation is obtained by retaining only the central block diagonal factor in Equation (40). TICP has been successfully applied to coupled flow-poromechanics problems in [306], while a suite of ICP/TICP was designed by Chidyagwai et al [323] to tackle mixed Darcy-Stokes flow simulations in porous media. The results show that ICP outperforms TICPs variants in terms of number of iterations and that, for 2D applications, a good scalability can be achieved depending on the choice for $M_{pp}^{-1}$ and $M_S$. Bergamaschi et al [324] provide an interesting comparison between the performance of ECP, ICP and an ILUT preconditioner applied to the whole matrix, for coupled flow-poromechanics problems. The results show that ECP’s performance in terms of solution time is overcome by both ICP and ILUT, due to the inherent high application cost, with ICP standing out clearly.

The availability of a high-quality sparse approximation of $A_{pp}^{-1}$ is often in contrast with the need for an explicit matrix $M_{pp}^{-1}$ guaranteeing the sparse computation of $\overline{S}$. For this reason, another variant was introduced blending two different approximations of $A_{pp}^{-1}$. This is denoted as Mixed Constraint Preconditioner (MCP) [325]:

$$\begin{aligned} \mathcal {M}^{-1}_\text {MCP} = \begin{bmatrix} M_{pp,1} &{} A_{ps} \\ A_{sp} &{} \overline{A}_{ss} \end{bmatrix}^{-1}, \end{aligned}$$

(42)

where $\overline{A}_{ss} = \overline{S} + A_{sp} M_{pp,2}^{-1} A_{ps}$. Here, $M_{pp,1}$ and $M_{pp,2}^{-1}$ represent different approximations of $A_{pp}^{-1}$, where usually the former is implicit and the latter explicit. An MCP extension is the class of Relaxed Mixed Constraint Preconditioner (RMCP) [326], that introduces a relaxation parameter $\omega$ on $\overline{S}$ with the aim at better clustering the eigenspectrum of the preconditioned matrix.

Block preconditioning appears to be a very flexible approach, where the algebraic framework (39)-(42) easily allows for the introduction of proper off-the-shelf local preconditioners according to the specific properties of the problem at hand. Therefore, the field is open to any kind of solution combining ILU, Jacobi, DD, AMG, and many others, including also physics-based approximations specifically related to the actual application. The approximation of the Schur complement is often the most challenging task, mainly because of the term $H = A_{sp} A_{pp}^{-1} A_{ps}$. If $A_{ss}$ prevails, neglecting H is convenient. Otherwise, a natural inexpensive approximation is to use just the diagonal of $A_{pp}$, i.e., $H\simeq \overline{H} = A_{sp} \text {diag}(A_{pp})^{-1} A_{ps}$. In the previously cited work by Roy et al [293], these two options have been tested and proved to be poor approximations for a reservoir problem. On the other hand, for the block preconditioner designed in [290], the latter approximation of H has been judged efficient. The contribution H can also be approximated as a whole, for example by physics-based intuitions such as the “fixed-stress” approach in coupled poromechanical applications [306, 307], or by using restriction and prolongation operators and performing local computations on restricted matrices in a fully-parallel fashion (see, for instance, [327]). Otherwise, Ferronato et al [317] proposed to use the decoupling factors in Equation (37), namely, $G = -A_{ps} A_{pp}^{-1}$ and $F=-A_{pp}^{-1}A_{sp}$, to recast the troublesome H contribution as $G A_{pp} F$. Since the exact computation of F and G factors is not viable, sparse approximations are computed by employing restriction, R, and prolongation, P, operators, which allow for the extraction and efficient solution of restricted systems. These operators control both the efficiency and accuracy of the approximation. Improved strategies to build R and P operators have been developed in [283] and [284]. Alternatively, Roy et al [286, 293] opted to build an approximation of the Schur complement before discretizing the linear problem upon the analytical expression of the single blocks to obtain a mesh-independent preconditioner.

5 CPR and Block Preconditioners: A Common Background

In Sects. 4.3.1 and 4.3.2, we presented multi-stage and block preconditioners separately, as two different approaches for the preconditioning of reservoir-simulation-driven block-structured problems. In fact, these techniques have been developed independently by research groups operating in different fields of numerical modeling, often with limited mutual interactions. CPR was born in the specific frame of reservoir simulation, whereas block preconditioning originated from the numerical analysis of saddle-point matrices and was later specialized in different applications arising, for instance, in coupled poromechanics, constrained optimization and Navier-Stokes equations, just to cite a few. Because of the different scientific contexts they originated from, CPR has a physics-based foundation, while block preconditioners rely on an algebraic approach. Despite these differences, it is possible to identify a common background for the two techniques and show that block preconditioning and the classical two-stage CPR can be somewhat regarded as two sides of the same coin.

We first recall the result of the application of $\mathcal {A}^{-1}$ to a vector ${\varvec{v}}$ in Equation (38):

$$\begin{aligned} \begin{bmatrix} {\varvec{u}}_p \\ {\varvec{u}}_s \end{bmatrix} = \begin{bmatrix} A_{pp}^{-1}{\varvec{v}}_p - A_{pp}^{-1}A_{ps} S^{-1}({\varvec{v}}_s - A_{sp} A_{pp}^{-1} {\varvec{v}}_p) \\ S^{-1}({\varvec{v}}_s - A_{sp} A_{pp}^{-1} {\varvec{v}}_p) \end{bmatrix}. \end{aligned}$$

(43)

Let us now focus on the CPR application following Algorithm 1, where we use the exact inverse of the pressure block $A_{pp}^{-1}$ in the first stage and the exact LU factorization of $\mathcal {A}$ in the second stage. We have:

$$\begin{aligned} {\varvec{u}}^{1} = \mathcal {M}_1^{-1} {\varvec{v}} \quad \Rightarrow \quad \begin{bmatrix} {\varvec{u}}_p^1 \\ {\varvec{u}}_s^1 \end{bmatrix} = \begin{bmatrix} A_{pp}^{-1}{\varvec{v}}_p \\ {\varvec{0}} \end{bmatrix}, \end{aligned}$$

(44)

and the corresponding residual:

$$\begin{aligned} {\varvec{r}}= & {} {\varvec{v}} - \mathcal {A} {\varvec{u}}^1 \quad \Rightarrow \nonumber \\&\begin{aligned} \begin{bmatrix} {\varvec{r}}_p \\ {\varvec{r}}_s \end{bmatrix}&= \begin{bmatrix} {\varvec{v}}_p \\ {\varvec{v}}_s \end{bmatrix} - \begin{bmatrix} A_{pp} &{} A_{ps} \\ A_{sp} &{} A_{ss} \\ \end{bmatrix} \begin{bmatrix} A_{pp}^{-1} {\varvec{v}}_p \\ {\varvec{0}} \end{bmatrix} \\&= \begin{bmatrix} {\varvec{0}} \\ {\varvec{v}}_s - A_{sp} A_{pp}^{-1} {\varvec{v}}_p \end{bmatrix}. \end{aligned} \end{aligned}$$

(45)

The second stage uses the two-level block-LU decomposition of $\mathcal {A}$ [328], which reads:

$$\begin{aligned} \mathcal {A} = \mathcal {L}\mathcal {U} = \left[ \begin{array}{cc} L_{pp} &{} 0 \\ L_{sp} &{} L_{ss} \end{array} \right] \left[ \begin{array}{cc} U_{pp} &{} U_{ps} \\ 0 &{} U_{ss} \end{array} \right] , \end{aligned}$$

(46)

where it is easy to observe that the following conditions hold:

$$\begin{aligned} L_{pp} U_{pp}= & {} A_{pp}, \end{aligned}$$

(47)

$$\begin{aligned} U_{ps}=\, & {} L_{pp}^{-1} A_{ps}, \end{aligned}$$

(48)

$$\begin{aligned} L_{sp}=\, & {} A_{sp} U_{pp}^{-1}, \end{aligned}$$

(49)

$$\begin{aligned} L_{ss} U_{ss}=\, & {} A_{ss} - L_{sp} U_{ps} = S. \end{aligned}$$

(50)

We need to solve the system:

$$\begin{aligned}&\mathcal {LU} \, \delta {\varvec{u}} = {\varvec{r}} \quad \Rightarrow \nonumber \\&\begin{bmatrix} L_{pp} &{} 0 \\ L_{sp} &{} L_{ss} \end{bmatrix} \begin{bmatrix} U_{pp} &{} U_{ps} \\ 0 &{} U_{ss} \end{bmatrix} \begin{bmatrix} \delta {\varvec{u}}_p \\ \delta {\varvec{u}}_s \end{bmatrix} = \begin{bmatrix} {\varvec{r}}_p \\ {\varvec{r}}_s \end{bmatrix}, \end{aligned}$$

(51)

and use the solution to correct the guess of Equation (44):

$$\begin{aligned}&{\varvec{u}} = {\varvec{u}}^1 + \delta {\varvec{u}} \quad \Rightarrow \nonumber \\&\begin{aligned} \begin{bmatrix} {\varvec{u}}_p \\ {\varvec{u}}_s \end{bmatrix}&= \begin{bmatrix} A_{pp}^{-1}{\varvec{v}}_p \\ {\varvec{0}} \end{bmatrix} + \begin{bmatrix} - A_{pp}^{-1} A_{ps} U_{ss}^{-1} L_{ss}^{-1} \left( {\varvec{v}}_s - A_{sp} A_{pp}^{-1} {\varvec{v}}_p \right) \\ U_{ss}^{-1} L_{ss}^{-1} \left( {\varvec{v}}_s - A_{sp} A_{pp}^{-1} {\varvec{v}}_p \right) \end{bmatrix} \\&= \begin{bmatrix} A_{pp}^{-1}{\varvec{v}}_p - A_{pp}^{-1} A_{ps} U_{ss}^{-1} L_{ss}^{-1} \left( {\varvec{v}}_s - A_{sp} A_{pp}^{-1} {\varvec{v}}_p \right) \\ U_{ss}^{-1} L_{ss}^{-1} \left( {\varvec{v}}_s - A_{sp} A_{pp}^{-1} {\varvec{v}}_p \right) \end{bmatrix}. \end{aligned} \end{aligned}$$

(52)

Recalling Equation (50), it is immediately observed that (52) coincides with (43).

Such a result should be no surprise, because the exact CPR application must yield the action of $\mathcal {A}^{-1}$. However, regarding CPR as an inexact application of Equation (43) helps restore a unique framework with block preconditioners. As observed in Sect. 4.3.2, the action of block preconditioning consists of replacing $A_{pp}^{-1}$ and $S^{-1}$ in Equation (43) with proper approximations, or inner local preconditioners, $M_{pp}^{-1}$ and $M_S^{-1}$, respectively, giving rise to either an exact, or inexact, or mixed approach according to the relationship existing between $M_{pp}^{-1}$ and $M_S^{-1}$. Hence, the outcome of the application of any block preconditioner reads:

$$\begin{aligned}&{\varvec{u}}_p^{block } = M_{pp}^{-1} {\varvec{v}}_p \nonumber \\&\quad - M_{pp}^{-1} A_{ps} M_S^{-1} \left( {\varvec{v}}_s - A_{sp} M_{pp}^{-1} {\varvec{v}}_p \right) , \end{aligned}$$

(53)

$$\begin{aligned}&{\varvec{u}}_s^{block } = M_S^{-1} \left( {\varvec{v}}_s - A_{sp} M_{pp}^{-1} {\varvec{v}}_p \right) . \end{aligned}$$

(54)

Equation (52) tells us that the classical CPR can be regarded as a block preconditioner, where $M_{pp}^{-1}$ is an AMG-like approximation of $A_{pp}$ and $M_S^{-1}$ is gathered from the final portion of the ILU decomposition of the full matrix $\mathcal {A}$. As a result, using this smart physics-based intuition, the Schur complement does not need to be computed explicitly, neither in an inexact way. Specifically, CPR can be viewed as a mixed constraint preconditioner because it relies on two different implicit approximations of $A_{pp}^{-1}$, i.e., the already mentioned AMG-like $M_{pp}^{-1}$ and an incomplete factorization, which is indirectly used to assemble the approximated Schur complement, $M_S$. Notice also that the algebraic role of the Schur complement in the preconditioning of block problems has been acknowledged only twenty years after the CPR introduction, with the seminal work by Murphy et al [329].

The algorithm for the CPR application is different from the one used for a standard block constraint approach. This yields a different propagation of the errors associated with the inexact approximations of $A_{pp}^{-1}$ and $S^{-1}$. Let us introduce in Equations (44)-(52) the AMG-like operator $M_{pp}^{-1}$ approximating the pressure-like block $A_{pp}$ and the incomplete global factorization:

$$\begin{aligned} \mathcal {A} \simeq \widetilde{\mathcal {L}} \widetilde{\mathcal {U}} = \left[ \begin{array}{cc} \tilde{L}_{pp} &{} 0 \\ A_{sp} \tilde{U}_{pp}^{-1} &{} \tilde{L}_{ss} \end{array} \right] \left[ \begin{array}{cc} \tilde{U}_{pp} &{} \tilde{L}_{pp}^{-1} A_{ps} \\ 0 &{} \tilde{U}_{ss} \end{array} \right] , \end{aligned}$$

(55)

from which we have the local Schur complement preconditioner $M_S^{-1}=\tilde{U}_{ss}^{-1} \tilde{L}_{ss}^{-1}$. Then, after some algebra, we obtain the outcome of the CPR application as:

$$\begin{aligned}&{\varvec{u}}_p^{CPR } = M_{pp}^{-1} {\varvec{v}}_p\nonumber \\&\quad - \tilde{A}_{pp}^{-1} A_{ps} M_S^{-1} \left( {\varvec{v}}_s - A_{sp} M_{pp}^{-1} {\varvec{v}}_p \right) + {\varvec{e}}_p, \end{aligned}$$

(56)

$$\begin{aligned}&{\varvec{u}}_s^{CPR } = M_S^{-1} \left( {\varvec{v}}_s - A_{sp} M_{pp}^{-1} {\varvec{v}}_p \right) + {\varvec{e}}_s, \end{aligned}$$

(57)

where $\tilde{A}_{pp}^{-1}=\tilde{U}_{pp}^{-1}\tilde{L}_{pp}^{-1}$. Inspection of Equations (56)-(57) in comparison with (53)-(54) reveals that the CPR algorithm introduces two additional contributions, ${\varvec{e}}_p$ and ${\varvec{e}}_s$, which read:

$$\begin{aligned} {\varvec{e}}_p= & {} \left( I_p + \tilde{A}_{pp}^{-1} A_{ps} M_S^{-1} A_{sp} \right) \tilde{A}_{pp}^{-1} E_p {\varvec{v}}_p, \end{aligned}$$

(58)

$$\begin{aligned} {\varvec{e}}_s= & {} - M_S^{-1} A_{sp} \tilde{A}_{pp}^{-1} E_p {\varvec{v}}_p, \end{aligned}$$

(59)

with $I_p$ the identity in the space of pressure-like variables and $E_p$ the error matrix:

$$\begin{aligned} E_p = I_p - A_{pp} M_{pp}^{-1}, \end{aligned}$$

(60)

which gives a measure of the quality of the AMG-like approximation of the pressure block. In other words, CPR differs from a mixed constraint approach only by the two terms (58)-(59), whose size depends on $\Vert {\varvec{v}}_p\Vert$ and $\Vert E_p\Vert$. In general, these two vectors can act in an unpredictable way, either adding new error sources or compensating errors introduced by the selected approximations. Therefore, it is not possible to state a priori which approach is preferable, the result being very problem-dependent.

6 Closing Remarks and Future Directions

The steady expansion in the model size, the introduction of additional physics in classical flow simulators, such as poro- and contact-mechanics, along with the development of more accurate and articulated discretization schemes, contribute to challenge the performance of existing linear solvers for reservoir modeling purposes. In particular, the uninterrupted development of such tools is key for FI simulators, where large-size and ill-conditioned linearized Jacobian systems of equations have to be repeatedly solved during a simulation. This task represents by far the most time and resource consuming kernel of the entire simulator. Krylov subspace methods, such as GMRES and Bi-CGStab, are well-established effective iterative solvers for reservoir problems, provided that appropriate preconditioners are introduced to speed-up convergence. Robustness, computational efficiency and scalability in high-performance computing environments are the targets to be accomplished for an effective inclusion in modern simulators.

The number and complexity of the different possible physical and mathematical variants for reservoirs problems, including multiphase and multi-component processes in possibly nonisothermal conditions, has led to the introduction of a significant amount of solution algorithms, which try to account for as many different situations as possible. For this reason, research in this field is currently very active. The main objective of this work was reviewing the state-of-the-art of the most popular solving techniques used in reservoir simulators. The block-structure of the Jacobian matrices and the different properties of the blocks arising from the governing equations dictate the use of specific articulated strategies. The most successful approaches developed so far are based on either a CPR scheme (Sect. 4.3.1) or a constraint preconditioning method (Sect. 4.3.2), which, on their turn, rely on dedicated local inner preconditioners for the pressure-like block and the Schur complement. Popular preconditioners for the inner problems include incomplete LU factorizations, domain decomposition and multigrid/multiscale methods (see Sect. 4.2).

In Sect. 5, we observed that block preconditioning and the classical two-stage CPR algorithm share a common algebraic background, so that CPR can be regarded as a special variant of the mixed constraint approach, characterized by the use of two implicit approximations of the inverse of the pressure-like block and an implicit factorization of the Schur complement. Other connections between different methods can also be observed. For instance, the structure of the CPR algorithm is equivalent to a two-grid V-cycle without pre-smoothing, where the restricted system coincides with the pressure sub-problem. For this reason, the application of the global ILU preconditioner at the second stage is also referred to in the literature as smoothing step, with a similar effect on the error as in AMG methods [285]. An analogous algorithmic structure is also shared with the two-stage Ms method, where the Ms coarse scale solver is coupled with a relaxation stage. Moreover, the classical two-stage CPR-AMG algorithm can be recovered from the MGR approach of Equation (23) as well, where the F-relaxation is replaced by a global smoothing through ILU, AMG is used as a coarse-grid solver, and $D_L=D_U=0_{CC}$ [148]. Alternatively, the F-C variable partition in the MGR method can be naturally extended to system (10), where the fine and coarse unknowns correspond to the pressure- and saturation-like unknowns. Following this approach, it is straightforward to further notice the connection between MGR and constraint preconditioning [149], as both rely on the same block factorization of the system matrix.

Table 1 Current main research directions. In the table, FE and DG0 stand for Finite Element and Discrete Galerkin methods, respectively

Finally, Table 1 provides a selection of the main research directions that are currently active in the field of preconditioning of reservoir simulation problems. In this regard, CPR still plays a major role, with promising research paths that consider the introduction of new physical variables and the integration with block preconditioning techniques. A reciprocal strategy is also interesting, with CPR considered as a local preconditioner for the flow problem within a broader (block) preconditioning strategy (see, for instance, [265, 266]). The design of efficient preconditioners for such multi-physics problems is a prominent subject for research in the next future.