1 Introduction

At small length scales, most materials are heterogeneous, such as composites, porous media, or polycrystalline aggregates. Accordingly, e.g. polycrystals are composed of several grains which might vary in spatial distribution, size, morphology and crystallographic orientation. In addition, one grain could also consist of a phase mixture. The related heterogeneous structure has a great impact on the microstructural effects and thus results in more complex non-linear constitutive relations. Examples are grain-wise elasto-viscoplastic material behavior or ductile damage behavior related to the grain boundaries. The material behavior’s complexity is increased by microstructural changes which influence the grain’s structure, such as martensitic phase transformations and dynamic recrystallization; see Fig. 1. These effects make it even more difficult to establish appropriate overall constitutive relations to describe the material behavior. Instead of finding such a phenomenological expression, a multiscale approach enables to separately examine the different scales. Within a two-scale simulation approach, the macroscale is used to capture the overall boundary value problem including the external boundary conditions. Meanwhile, the material behavior at the macroscale is determined by the mean response of the smaller scale (microscale). Various methods have been developed to capture the structure, properties and physical behavior of the microstructure and its overall constitutive response. These so-called multiscale schemes may be classified in three major groups: (semi-)analytical methods [169, 214], computational methods [194, 196] and hybrid methods [45, 130].

Fig. 1
figure 1

Ferrite/pearlite-annealed 42CrMo4 steel microstructure: a inverse pole figure illustrating the grain orientations and b image quality map obtained from EBSD measurements illustrating microstructural grain changes, such as phase transformations and recrystallization [99]

Full size image

The focus of the present paper is on one particular computational two-scale technique, namely the FE-FFT-based method. This methodology was first proposed by Spahn et al. [196] and serves as an efficient and powerful alternative compared to the classical computational homogenization method, the FE2 method [129, 144, 167]. The FE-FFT-based method includes a finite element (FE) approach for the macroscale simulation and an evaluation of the behavior at the microscale based on fast Fourier transforms (FFT). The macroscopic material behavior is then defined as volume average of its microscopic counterpart. While the FE approach is widely used in terms of computational mechanics, the FFT-based method is rather new and was introduced by Moulinec and Suquet [155, 156]. It serves as alternative to the classical FE-based simulation of periodic microstructures and is based on solving a global integral equation known as the Lippmann–Schwinger equation [107, 228], which is defined by Green’s function and a polarization stress.

The review paper is structured as follows: after a brief review of the three groups of multiscale techniques (Sect. 2), a review of the FFT-based microstructure simulation is given in Sect. 3. This includes a brief summary of FFT-based algorithms (Sects. 3.2 and 3.3), FFT-based model-order reduction techniques (Sect. 3.4), as well as the applications of the FFT-based simulation (Sect. 3.5). In addition a brief comparison of the FFT-based method to the FE-based method is given in Sect. 3.6. Finally, in Sect. 4, the FE-FFT-based two-scale method is discussed for different applications. The paper ends with a conclusion in Sect. 5.

2 Overview of Multiscale Methods

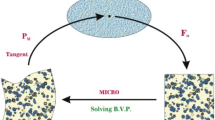
Figure 2 presents the key idea of a multiscale approach in terms of a mechanical boundary value problem considering small strain kinematics. On the macroscale the macroscopic strain \(\bar{\varvec{\varepsilon }}(\bar{\varvec{x}})\) at the macroscopic position \(\bar{\varvec{x}}\) is computed. This macroscopic strain is used on the microscale to compute the overall strain \(\varvec{\varepsilon }(\bar{\varvec{x}},\varvec{x})\) and stress \(\varvec{\sigma }(\bar{\varvec{x}},\varvec{x})\) response. In terms of a spatially resolved microstructure simulation, \({\varvec{x}}\) represents the microscopic position. Vice versa, the resulting macroscopic stress \(\bar{\varvec{\sigma }}(\bar{{\varvec{x}}})\) and macroscopic tangent operator \(\bar{\varvec{\mathbb {C}}}(\bar{{\varvec{x}}})\) are defined as volume averages of their overall counterparts.

Fig. 2
figure 2

Schematic of the two-scale simulation approach incorporating a polycrystalline microstructure

Full size image

Besides this two-scale method, also multiscale methods incorporating more than two scales (for example all the way down to the atomistic level, [170]) exist. Nevertheless we restrict ourselves exclusively to the two-scale method. Doing that, Table 1 and the following three subsections briefly summarize the three different classifications of two-scale methods, the (semi-)analytical, the computational and the hybrid method.

Table 1 Classification of the three major different two-scale methods
Full size table

2.1 (Semi-)analytical Methods

In analytical methods, a deterministic or statistical representation of the microstructure is used. Often, closed form solutions of reference problems serve to compute the overall response of microscopic heterogeneous materials. If an explicit solution for the material behavior is not available but approximated by implicit equations, the method is called a semi-analytical method. In both cases, a spatially resolved visualization of the results on the microscale is not possible.

First attempts to compute the overall macroscopic material behavior of microscopic heterogeneous materials in terms of an analytical homogenization were established by Voigt [214] and Reuss [169]. Whereby Voigt assumes that the strain is constant within the microstructure, resulting in an overall stiffness tensor computed by using the arithmetic mean of the phase-wise stiffness tensor weighted by the corresponding volume fraction, Reuss considers a constant stress in the individual phases. This ansatz results in the computation of the arithmetic mean of the phase-wise compliance tensors again weighted by the corresponding volume fractions. These basic analytical homogenization methods are called “mean field methods”. In the context of statistical methods, the volume fractions of the different phases can be interpreted as first order correlation functions. Since these basic approximations are only related to the volume fractions of certain phases, they are not very accurate in general, but still serve as upper and lower bounds of the averaged material response in terms of homogenization methods. Regarding polycrystalline materials, these bounds are often referred to as the Taylor [203] and Sachs [177] bounds. To generate more accurate homogenized results, the use of a two-point or higher-order correlation function enables the consideration of additional microstructural details [55, 205].

The work of Eshelby [54] deals with an ellipsoidal elastic inclusion embedded in a homogeneous infinite matrix. The present analytic solution for the so-called Eshelby’s inclusion serves as the basis for different more precise mean field approaches [159], such as the Mori-Tanaka model [153] or the double inclusion method introduced in [127]. Furthermore, a self-consistent approximation was introduced in [21, 84, 86, 106] for the simulation of elastic composites and polycrystals. Within this self-consistent approach it is assumed that the material properties of the homogeneous infinite matrix coincide with the overall properties of the composite. An extension of this approach to the computation of the overall properties of non-linear composites is given in [27, 200] and of non-linear polycrystals in [87, 96, 97, 116, 151, 187].

A variational approach for the estimation of the behavior of linear composites with an isotropic microstructure was introduced by Hashin and Shtrikman [81,82,83, 91]. This approach is still based on the assumption of phase-wise constant fields, but in addition the stress state consists of two parts. One part is related to a homogenous reference material and the other part is related to a polarization stress which characterizes the fluctuation within the microstructure. The resulting inhomogeneous partial differential equation is solved by use of Green’s function [158, 197] and hence, yields an integral formulation known as Lippmann–Schwinger equation [107, 228]. For homogeneous and isotropic reference materials which behave elastically, closed-form solutions for the Lippmann–Schwinger equation are available. Compared to the Voigt and Reuss bounds, which do not consider the fluctuation of the stress on the microscale, this variational approach leads to stricter bounds in terms of the overall response of the microstructural material behavior. An extension of the ansatz to anisotropic composites is given in [227] and to non-linear composites in [30, 80, 199, 228]. To further improve the accuracy of the application of the analytical homogenization on microstructures with large variations in their local properties, also second-order homogenization techniques based on incorporating field fluctuations have been proposed in [28, 29, 37, 195].

2.2 Computational Methods

In contrast to (semi-)analytical methods, a computational multiscale method deals with a spatially resolved representation of the microstructure. In this context, the microstructure might be seen as a representative volume element (RVE) and/or unit cell, [44, 80, 85, 161], or a statistically similar RVE, [5, 185]. The macroscopic kinematics serve as an input for the RVE and thus influence the deformation of the microstructure. The macroscopic influence can be prescribed by different possible boundary conditions, such as linear displacements, constant tractions, or combined periodic displacements and anti periodic tractions, [105, 204, 210].

The most common method to solve the related microscopic boundary value problem (BVP) is the finite element method [8, 237]. The performed computational simulation leads to spatially resolved representations of the microstructural fields, like the stress and the strain fields. Accordingly, the volume average of the local microscopic fields determines the required overall macroscopic response, see [85, 137]. Two-scale approaches which use the finite element method to calculate the BVPs on the micro-level as well as on the macro-level are called FE2 methods [58, 194]. To calculate the required overall algorithmic tangent operator closed form expressions were derived in [148, 149]. An overview of recent developments, applications and challenges concerning the FE2 method can be found in [63, 186].

Other microstructural methods in terms of a two-scale full field simulation are for example finite differences (FD)-based [1], Voronoi FE-based [65], virtual element-based [4, 139] and FFT-based solvers [196]. Among these methods, the FFT-based method has proven to be a fast and accurate tool in terms of a computational simulation of periodic microstructures in the recent years. An overview of recent developments, applications and challenges concerning the FFT-based microstructure simulation [155, 156] and the related FE-FFT-based two-scale method [100, 196] is given in Sects. 3 and 4, respectively.

A comparison of the aforementioned analytical and numerical methods is presented in [88, 120]. Concerning the computational methods, Sect. 3.6 gives a brief comparison of the FE- and FFT-based microstructure simulation.

2.3 Hybrid Methods

Hybrid multiscale methods finally combine both, computationally efficient numerical methodologies and theoretical knowledge. In particular, numerical experiments, such as deforming a highly resolved microstructure incorporating different loading conditions, are performed in a pre-processing step to generate microstructural data, such as the point-wise material behavior related to the external loading. Then, the obtained information about the microstructural material behavior is used for the actual micromechanical modeling.

In this context, one methodology is the uniform transformation field analysis (TFA) [45, 59]. It is based on the assumption of piece-wise uniform plastic strain fields to reduce the degrees of freedom during the simulation. Therefore a significant reduction of computational time is gained. A generalization of this method in terms of the non-uniform TFA (NTFA) is given in [60, 61, 141,142,143]. Instead of considering uniform plastic strain fields, the latter quantities are decomposed into a set of plastic modes, which leads to nonuniform plastic strain fields. These modes have to be computed within a pre-processing step. Nevertheless, also the NTFA leads to a highly reduced set of constitutive equations, which again results in a significant reduction of the computational costs.

Another recently developed hybrid multiscale method is the self-consistent clustering analysis (SCA) [31, 130, 131, 221, 231]. This method is derived from the Lippmann–Schwinger equation [107, 228] and based on a clustered microstructure with cluster-wise constant micromechanical fields. A pre-processing step is used to group the highly resolved material behavior into these clusters, see Fig. 3. Under the assumption of constant stress and strain fields during the actual simulation, a significant reduction of degrees of freedom and also a significant reduction of computational times compared to a full field computational two-scale simulation is gained. A generalization of the SCA to finite strain kinematics is given in [232].

Fig. 3
figure 3

Highly resolved two-phase microstructure with a point-wise material behavior, while the inclusion is colored red and matrix is colored blue (left) and clustered microstructure with a cluster-wise constant material behavior, while each color represents one cluster (right) (Colour figure online)

Full size image

3 FFT-Based Microstructure Simulation

The FFT-based microstructure simulation is used in terms of a spatially resolved microstructure simulation. Initially, it was introduced by Moulinec and Suquet based on fixed-point iterations [155, 156]. This basic fixed-point scheme is reviewed in Sect. 3.1. It is followed by an overview of several more efficient FFT-based algorithms and solution methods (Sect. 3.2) and Sect. 3.3, discussing problems related to the Gibbs phenomenon. In addition, recently introduced model order reduction techniques for the FFT-based method are reviewed in Sect. 3.4. Subsequently, Sect. 3.5 provides an overview of different applications of the FFT-based method for the simulation of composite (Sect. 3.5.1) and polycrystalline (Sect. 3.5.2) microstructures, respectively. Finally, a brief comparison to the FE-based microstructure simulation is given in Sect. 3.6. A recapitulation of the FFT-based algorithms, solvers and their applications is also given in Table 2.

3.1 Basic Fixed-Point Scheme

In terms of a spatially resolved microstructure simulation of a mechanical boundary value problem considering small strain kinematics, the overall strain \(\varvec{\varepsilon }(\bar{\varvec{x}},\varvec{x})\) is additively split into the macroscopic part \(\bar{\varvec{\varepsilon }}(\bar{\varvec{x}})\) (see Fig. 2) and a microscopic fluctuating part \(\tilde{\varvec{\varepsilon }}(\varvec{x})\), see Fig. 4. Since the balance of linear momentum holds for the macroscopic as well as for the microscopic scale, the microstructural mechanical boundary value problem is captured by

$$\begin{aligned} \begin{array}{rcl} \text {div}\,\varvec{\sigma }(\bar{\varvec{x}},{\varvec{x}}) &{}=&{} {\varvec{0}} \\ \varvec{\sigma }(\bar{\varvec{x}},{\varvec{x}})&{}= &{} \varvec{\sigma }(\bar{\varvec{x}},{\varvec{x}},\varvec{\varepsilon }(\bar{\varvec{x}},{\varvec{x}}), \varvec{\alpha }(\bar{\varvec{x}},{\varvec{x}}))\\ \varvec{\varepsilon }(\bar{\varvec{x}},{\varvec{x}})&{}=&{}\bar{\varvec{\varepsilon }}(\bar{{\varvec{x}}})+\tilde{\varvec{\varepsilon }}({\varvec{x}}). \end{array} \end{aligned}$$
(1)

Thereby, div\((\cdot )\) represents the divergence operator and the total stress field \(\varvec{\sigma }(\bar{\varvec{x}},{\varvec{x}})\) depends on the macroscopic position \(\bar{{\varvec{x}}}\), the microscopic position \({\varvec{x}}\), the related total strain field \(\varvec{\varepsilon }(\bar{\varvec{x}},{\varvec{x}})\) as well as—related to the observed problem—on some internal variables \(\varvec{\alpha }(\bar{\varvec{x}},{\varvec{x}})\), e.g. the plastic strain and/or a grain orientation. Body forces are neglected within the microscopic BVP since they are already considered within the macroscopic BVP.

Fig. 4
figure 4

Additive split of the total strain into the constant macroscopic part and the fluctuating microscopic part

Full size image

Considering periodic fields and boundary conditions, the microscopic boundary value problem may be solved using spectral methods [125, 158, 159]. Therefore, the inhomogeneous BVP with varying material properties, see Fig. 5 (left), is reformulated as equivalent homogeneous BVP by introducing a microstructure with a homogeneous reference material behavior \(\mathbb {C}^0\), see Fig. 5 (right). Doing this, the equivalent homogeneous BVP reads

$$\begin{aligned} \begin{array}{rrl} \text {div}[\mathbb {C}^0 : \varvec{\varepsilon }(\bar{\varvec{x}},{\varvec{x}}) ]&{}=&{} -\text {div}[\varvec{\tau }(\bar{\varvec{x}},{\varvec{x}})]\\ \varvec{\tau }(\bar{\varvec{x}},{\varvec{x}})&{}:= &{} \varvec{\sigma }(\bar{\varvec{x}},{\varvec{x}})- \mathbb {C}^0 : \varvec{\varepsilon }(\bar{\varvec{x}},{\varvec{x}})\\ \varvec{\varepsilon }(\bar{\varvec{x}},{\varvec{x}})&{}=&{}\bar{\varvec{\varepsilon }}(\bar{{\varvec{x}}})+\tilde{\varvec{\varepsilon }}({\varvec{x}}) \,, \end{array} \end{aligned}$$
(2)

where \(\varvec{\tau }(\bar{\varvec{x}},{\varvec{x}})\) is the so-called polarization stress, which represents the material inhomogeneities within the homogeneous reference material behavior.

Fig. 5
figure 5

Left Inhomogeneous microstructure with spatially varying material properties, such as a spatially depending stiffness tensor \(\mathbb {C}(\bar{\varvec{x}},\varvec{x})\), while body forces are neglected. Right Homogeneous reference microstructure with a constant reference material behavior \(\mathbb {C}^0\), while the inhomogeneities are described in terms of the body force \({\varvec{f}}(\bar{\varvec{x}},\varvec{x})=\text {div}\varvec{\tau }(\bar{\varvec{x}},\varvec{x})\)

Full size image

Equation (2) may be solved by using Green’s function \({\varvec{G}}^0({\varvec{x}}- {\varvec{x}}^\prime )\) or the Lippmann–Schwinger operator \({\mathbb {\Gamma }}^{0}({\varvec{x}}- {\varvec{x}}^\prime )\) [158, 197], respectively, which yields to an integral form known as the Lippmann–Schwinger equation [107, 228]:

$$\begin{aligned} \varvec{\varepsilon }(\bar{{\varvec{x}}},{\varvec{x}})= \bar{\varvec{\varepsilon }}(\bar{{\varvec{x}}}) - \int _\varOmega {\mathbb {\Gamma }}^{0}({\varvec{x}}- {\varvec{x}}^\prime ) : \varvec{\tau }({\varvec{x}}^\prime )\,\mathrm d{\varvec{x}}^\prime \, \end{aligned}$$
(3)

or in a compact notation:

$$\begin{aligned} \varvec{\varepsilon }=\bar{\varvec{\varepsilon }} - {\mathbb {\Gamma }}^{0} *\varvec{\tau }. \end{aligned}$$
(4)

Within Eq. (3) \({\varvec{x}}\) and \({\varvec{x}}^\prime\) represent different positions within the microstructural domain \(\varOmega\) with the side length L, while \(*\) represents the convolution integral in Eq. (4).

The Lippmann–Schweinger equation is solved by transferring it into Fourier space yielding:

$$\begin{aligned} \hat{\varvec{\varepsilon }}(\varvec{\xi }) = \left\{ \begin{array}{lcl} -\hat{\varvec{\Gamma }}^{0}(\varvec{\xi }) \,\hat{\varvec{\tau }} (\varvec{\xi }) &{} \forall &{} \varvec{\xi }\ne {\varvec{0}}\\ \bar{\varvec{\varepsilon }}(\bar{\varvec{x}}) &{} \forall &{} \varvec{\xi }= {\varvec{0}} \end{array} \right. \,, \end{aligned}$$
(5)

while \(({\hat{\cdot }})\) refers to the Fourier representation of the corresponding field depending on the wave vector \(\varvec{\xi }\), which gathers all the considered Fourier modes. The components \(\xi _j (j=1,2,3)\) of this wave vector are defined as

$$\begin{aligned} \xi _j(i)=\frac{2\pi }{L}i \quad \text {with}\quad i=-\frac{N}{2},...,\frac{N}{2}-1 \end{aligned}$$
(6)

for a discretized microstructure with an even number of grid points N and

$$\begin{aligned} \xi _j(i)=\frac{2\pi }{L}i \quad \text {with}\quad i=-\frac{N-1}{2},...,\frac{N-1}{2} \end{aligned}$$
(7)

for a discretized microstructure with an odd number of grid points N.

In Fourier space, Green’s function \(\hat{{\varvec{G}}}^0(\varvec{\xi })\) and the Lippmann–Schwinger operator \({\hat{{\mathbb {\Gamma }}}}^0(\varvec{\xi })\) are explicitly known and just depending on this wave vector and the homogeneous reference material behavior \(\mathbb {C}^0\):

$$\begin{aligned} {\hat{G}}_{ki}^0(\varvec{\xi })=\left( \mathbb {C}^0_{kjil}\,\xi _l\,\xi _j \right) ^{-1} \end{aligned}$$
(8)

and

$$\begin{aligned}&{\hat{\Gamma }}_{ijkl}^0(\varvec{\xi }) \nonumber \\&\quad= \frac{1}{4}\left( {\hat{G}}_{jk,li}^0(\varvec{\xi }) +{\hat{G}}_{ik,lj}^0(\varvec{\xi }) +{\hat{G}}_{jl,ki}^0(\varvec{\xi }) +{\hat{G}}_{il,kj}^0 (\varvec{\xi }) \right). \end{aligned}$$
(9)

The basic fixed-point iteration scheme for the FFT-based microstructure simulation, which makes use of the Fourier representation of the Lippmann–Schwinger equation (5) and the computation of the polarization stress \(\varvec{\tau }(\bar{\varvec{x}},{\varvec{x}})\) in real space (Equation (2)) was introduced by Moulinec and Suquet [155, 156].

Table 2 FFT-based numerical solution methods and applications
Full size table

3.2 Overview and Efficiency of FFT-Based Algorithms and Solution Methods

Recently, two review papers on FFT-based algorithms, solution methods and their applications were published by Schneider [181] and Lucarini et al. [134]. Nevertheless, this subsection briefly sums up the most important developments in this context.

The works presented in [43, 112, 155, 156] deal with the FFT-based basic fixed point scheme for small strain kinematics, reviewed in Sect. 3.1. The generalization of this method to finite strain kinematics is presented in [49, 110]. The rate of convergence of the basic fixed point scheme depends on the contrast between the phases, the choice for the homogeneous reference material behavior, and the material behavior itself (linear or non-linear). While different choices for the homogeneous reference material behavior are generally possible, the best convergence behavior for the fixed point scheme is gained by the arithmetic averages of the phase-dependent Lamé coefficients \(\lambda ^0\) and \(\mu^0\) [92, 156].

Independent of the choice for the reference material behavior, the convergence for the simulation of materials with high phase contrast is very slow and not even ensured for an infinite phase contrast. Improvements concerning the convergence behavior in this context are achieved by a polarization-based solution scheme [56, 146, 213] and a solution scheme based on augmented Lagrangians [122, 145, 146]. These methods are also called accelerated methods. While the polarization-based scheme relies on a reformulation of the Lippmann–Schwinger equation, the scheme based on augmented Lagrangians yields a reformulation of the microscopic BVP in terms of a minimization problem. A comparison of both methods with each other and to the basic fixed point scheme is given in [157]: For a low phase contrast the CPU time of the basic scheme is the shortest. For higher differences between the constituents, the accelerated schemes, are comparable, while the polarization-based scheme suffers at infinite phase contrast. A generalization of the polarization-based solution scheme for the simulation of composites with infinite phase contrast is given in [152]. A comparison of this general scheme to the initially proposed polarization-based scheme and to the solution scheme based on augmented Lagrangians shows, that the initially proposed polarization-based scheme and the solution scheme based on augmented Lagrangians are particular cases of this general polarization-based scheme [154]. Recently, a review of the polarization based schemes including an extension to the simulation of non-linear material behavior was given in [184].

A further accelerated solution strategy based on a conjugate gradient solver was introduced in [233] with a similar convergence behavior as the previous accelerated methods. This solution strategy is based on a linearized Lippmann–Schwinger equation (3). Solving the resulting system of linear equations, the gradient decent method may be used. Using conjugate gradients in this context yields an Krylov subspace method, which is an efficient solution strategy of solving the system of linear equations. This first attempt on FFT-based conjugate gradient solvers suffers at infinite phase contrasts but has the advantage that it is independent of the choice for the reference material behavior. Another solution strategy incorporating the conjugate gradient solver [19], is based on a variational framework which minimizes the energy of Hashin and Shtrikman [82]. This solution scheme also leads to convergence in the case of infinite phase contrast and is compared to the basic fixed point scheme in [20]. A further variational framework, based on a Galerkin discretization of the weak form of the microscopic boundary value problem with trigonometric polynomials, is given in [218]. The extension of the conjugate gradient based solver to capture non-linear material behavior is introduced in [64] and to finite strain kinematics in [92]. In addition, the equivalence of the basic fixed point scheme and a gradient descent method is shown in [92].

For complex material behavior, such as plasticity or damage, the conjugacy of the decent directions might get destroyed, so that the conjugate gradient solver will not converge anymore. Due to that, more stable solution strategies based on the non-linear generalized minimal residual method (GMRES) [189] or the fast gradient method of Nesterov [179] were developed. Recently, also a Barzilai-Borwein basic scheme [180] considering the Barzilai-Borwein step size selection technique for the gradient descent and a FFT-based solution scheme based on the heavy-ball method [53] were introduced. Furthermore, a Quasi-Newton method for a tangent-free FFT-based simulation of a complex non-linear material behavior is presented in [226]. Besides the investigations of these algorithms in the primal formulation of the unit cell problem, the effects of these solvers in a dual formulation [13] are investigated in [225].

Supplementary to the focus on computational efficiency, all these current developments also focus on a memory efficient implementation.

In addition, recent developments deal with the parallel implementation of these solvers using Message Passing Interface (MPI) and OpenMP [46, 76], or high-performance computational platforms integrating a graphics processing unit (GPU) [47, 48].

3.3 Methods to Reduce the Effect of Gibbs Oscillations on Convergence Behavior

Concerning the FFT-based simulations, well known numerical artifacts are oscillations around discontinuities, known as the Gibbs phenomenon [67]. Approaches to tackle this problem use for example a modified Lippmann–Schwinger operator which approximates the differential operator in Eq. (9) with first-order finite difference approximations [9, 113, 229, 230] as introduced by Willot [230]. Investigations by [183] show the equivalence of this modified scheme to a FFT-based finite element discretization which includes linear hexahedral elements with reduced integration. The modified FFT-based scheme may be further improved by using a finite difference discretization on a staggered grid, as shown in [182]. In addition, the artificial oscillations may also be treated by using higher-order finite difference approximations as shown in [211, 212].

Other strategies of smoothing the results around discontinuities are based on regularization strategies [3] or composite voxels [93].

Fig. 6
figure 6

Results for the isotropic linear elastic 3D shear stress field \(\sigma _{12}/\mu _{\mathrm {M}}\) (\(x_{1}\) horizontal, \(x_{2}\) vertical, \(\mu _{\mathrm {M}}\) matrix shear modulus) obtained from different algorithms at a matrix–inclusion interface with discontinuous elastic stiffness phase contrast of \(1000\) for different spectral algorithms and different 3D numerical resolutions \(n^{3}\) with \(n=22\) (left), \(n=42\) (middle left), \(n=82\) (middle right), and \(n=162\) (right). Compared here are algorithms employing finite-difference discretization based on central-differencing (CD), averaged CD (ACD), and averaged-forward-backward-differencing (AFB), which is equivalent to “rotated scheme” (R) of Willot [229]. Displayed for comparison as well are direct Fourier (F; no finite-difference discretization) and standard finite-element (SFE) solutions at the same resolution [95]

Full size image

In Khorrami et al. [95], spectral algorithms are developed and compared for the numerical solution of periodic (quasi-static) elastic mechanical boundary-value problems. To this end, they employ two different approximations / discretizations of (truncated) Fourier series for periodic fields: (i) piecewise-constant approximation of the integrand of the Fourier mode integral, and (ii) trapezoidal approximation of this integral. Given these, a number of algorithms are formulated in the context of (I) Green-function preconditioning of stress divergence, and (II) finite-difference discretization of differential operators (i.e., the basis of the so-called “accelerated schemes”: e.g., Moulinec and Silva [154]). These algorithms solve for displacement (i.e., rather than strain: e.g., Moulinec and Suquet [155]; Suquet [197]; Moulinec and Silva [154]; Willot [229]) via iteration (e.g., fixed-point in the linear, or Newton-Krylov in the non-linear, case). Differential operator discretization is based for example on central-differencing (CD), averaged CD (ACD), and averaged-forward-backward-differencing (AFB). As it turns out, AFB is equivalent to the “rotated scheme” (R) of Willot [229] in the context of trapezoidal discretization. Computational comparisons of these and related algorithms are carried out with the help of the (classic) benchmark case of a cubic-inclusion-matrix composite (e.g., Suquet [197]; Willot [229]) with discontinuous phase contrast at the matrix–inclusion interface (Fig. 6). Related algorithms compared include that of Eloh et al. [52] based on the so-called “discrete Green operator”, which employs piecewise-constant discretization, and Green-function preconditioning in Lippmann–Schwinger form, but not finite-difference discretization. For more information, the interested reader is referred to Khorrami et al. [95].

3.4 Model Order Reduction Techniques for FFT-Based Solvers

Even though the FFT-based simulation of heterogeneous microstructures is already an efficient solution scheme, the computational costs for the simulation of highly resolved complex microstructures is still very intensive. Due to that, a recent research topic is the combination of the FFT-based solvers with model order reduction techniques.

A first FFT-based solver incorporating a model order reduction technique is given in [62] based on a proper orthogonal decomposition (POD), [165]. The POD projects the system equations onto a subspace spanned by a reduced basis of ’small’ dimension. Doing that, so-called ’snapshots’ need to be generated in a pre-processing step considering for example different loadings and loading directions. Subsequently, a snapshot matrix is computed, containing the corresponding strain solutions \(\hat{\varvec{\varepsilon }}\) in Fourier space, followed by a singular value decomposition of this matrix and the computation of a projector operator for a given amount of the largest eigenvalues. This leads to a significant reduction of the computational time, with the drawback of a time consuming pre-processing step for the snapshot generation (but which must be only performed once for a given set of parameters).

Another model order reduction technique for the FFT-based microstructure simulation adapted to the intrinsic character of the spectral solver is based on solving the Lippmann–Schwinger equation in Fourier space (Eq. 5) by considering only a reduced set of Fourier modes. For this purpose, all Fourier modes are arranged on a grid with the lowest Fourier modes in the center. The first idea was to use a fixed, radial sampling pattern on this grid to determine the reduced set of Fourier modes [104]. After solving the Lippmann–Schwinger equation with this reduced set of Fourier modes, a reconstruction algorithm based on the \(TV_1\)-algorithm [23] and a compatibility step was used to generate highly resolved microstructural fields. Since a fixed sampling pattern is used for all computations, no time consuming pre-processing step is necessary. An extension of this algorithm to finite strain kinematics is given in [68]. The accuracy of this model order reduction technique depends on the one hand on the number of considered Fourier modes and on the other hand on the choice of the considered Fourier modes. Due to that, an improved technique for the generation of a reduced set of wave vectors based on a geometrically adapted sampling pattern is proposed in [70]. Considering the same amount of Fourier modes, the solution based on such an adapted reduced set of Fourier modes leads to more accurate microstructural fields even without the reconstruction. A comparison of the stress fields generated by both techniques without the reconstruction and compatibility step is given in Fig. 7. In [70] also a three dimensional extension of this model order reduction technique is given.

Yet another model order reduction technique is proposed in [220] based on low-rank tensor approximations. Within low-rank approximations, tensors are expressed by a smaller set of parameters (e.g. the representation of a second order tensor in terms of a generalized singular value) [140]. The utilization and investigation of different low-rank tensor approximations in terms of the Fourier–Galerkin method [218] again leads to an efficient FFT-based method.

Fig. 7
figure 7

Fixed radial and geometrically adapted set of Fourier modes (top) and corresponding and reference stress distribution in a periodic composite microstructure (bottom)

Full size image

3.5 Application of FFT-Based Simulations

The FFT-based simulation approach was introduced first in the context of computing the micromechanical fields within periodic microstructures of composite materials [155, 156]. The utilization of this method in terms of polycrystalline microstructures is given in [112]. In the past, numerous investigations and improvements for these simulations followed. An overview of microscale simulations of composites or polycrystalline materials in terms of the FFT-based simulation is presented in Sects. 3.5.1 and 3.5.2, respectively.

3.5.1 FFT-Based Simulation of Composite Microstructures

Considering linear or nonlinear mechanical composites with finite phase contrast, such as fiber reinforced materials, the FFT-based method was introduced in [155, 156] as alternative to the common FE-based microstructure simulation. Using the FFT-based method spatially resolved microstructural fields such as the microstructural strain field in a glass fiber reinforced plastic microstructure may be computed, see Fig. 8.

Fig. 8
figure 8

Strain distribution in a periodic glass fiber reinforced plastic microstructure [92]

Full size image

To model composites with infinite phase contrast, such as microstructures with voids or rigids, an extension of the basic fixed-point scheme based on augmented Lagrangians was introduced in [145]. This method is applied in [14, 15] to investigate the effect of the microstructural distribution of voids in composite materials on the plastic overall response. In [89] also a comparison of similar results with the results from analytical homogenization is given. In addition, the effective properties of two-phase composites reinforced by randomly distributed spherical particles are investigated and compared to analytical homogenization methods in [66]. Both studies showed that the analytical models do not provide accurate results for a wide range of phase contrasts and volume fractions. Furthermore, in [128] the FFT-based method is used to predict the material properties in additively manufactured structures and in [32] to display the mechanical fields in thermoplastic polymer composites filled with hollow glass microspheres. Also the effective properties of sheet molding compound composites may be computed in terms of a FFT-based simulation [74].

Besides the investigation on classical composites, the FFT-based method was also used to investigate the behavior of calcium silicate hydrates (C-S-H) in hardened cement paste [193]. The influence of size, distribution and shape of inclusions on the concrete creep properties was shown in [111] and the effect of regular and irregular coarse aggregates in self-compacting high-performance concrete was investigated in [162].

An additional field of the mechanical microstructure simulation is the prediction of the micromechanical damage behavior. In [196] the FFT-based method is combined with continuum damage mechanics to model the failure and progressive damage in composite materials. A similar simulation approach is used to compute the stiffness and strength of medium density fiberboards [192], to capture the progressive damage in 3D braided composites [222] and to capture the damage evolution in porous media, such as sandstone [126]. Instead of the continuum damage approach, the FFT-based method may also be combined with a phase-field approach [2, 22] to model the damage evolution. This approach was used to investigate the brittle fracture in an idealized continuous fiber composite [35, 53] and to analyze the damage initiation in a Silicon carbide (SiC/SiC) composite tube [34].

The FFT-based method furthermore enables to compute the microscopic responses of composite microstructures in different, non-mechanical contexts. This is for example necessary to investigate the behavior of thermoelastic composites [213], the thermal properties of liquid metal elastomeric composites [39], the electrical conduction in periodic composites [230, 233], the electro-mechanically coupled material behavior [73] or the elastic wave propagation in heterogeneous media [26].

3.5.2 FFT-Based Simulation of Polycrystalline Microstructures

A general overview describing anisotropic heterogeneous crystalline materials is given in [173], discussing constitutive laws, kinematics, multiscale techniques and comparisons to experimental results. Considering computational homogenization of polycrystalline microstructures a detailed review is given in [188]. Lebensohn [112] was the first to utilize the FFT-based method in this context incorporating a rigid-viscoplastic material behavior. This full-field simulation approach was for example used to validate analytical methods for the prediction of the effective microstructural response in [3, 18, 117].

Fig. 9
figure 9

Effective equivalent stress–strain curve and microstructural equivalent stress fields \(\text {S}_\text {eq}\) predicted by the EVP–FFT model. For comparison, the results of a FFT-based simulation of a purely elastic (EL-FFT) and a purely viscoplastic (VP-FFT) material model with the same material parameters are shown [122]

Full size image

To generate polycrystalline microstructures, one possibility is to use a Voronoi tessellation as shown in [6, 7, 40]. An advantage of the FFT-based method is the possibility of computing the microstructural fields directly from an image of their microstructure. Therefore, modelling the subgrain texture evolution directly based on polycrystalline microstructures from electron back-scattering diffraction (EBSD)-based orientation imaging microscopy (OIM) was proposed in [118]. Using such polycrystalline microstructures, numerical experiments have been performed to show for example that stress hot spots occur close to grain boundaries [171]. In addition, the influence of the volume fraction and the contiguity of isotropic particles embedded in a polycrystalline matrix phase on the stress and strain-rate fields is investigated in [114]. It showed that the first and second moments of the stress and strain-rate are differently affected by these properties.

A generalization of the rigid-viscoplastic material behavior to an elasto-viscoplastic formulation in terms of a FFT-based microstructure simulation (EVP-FFT) is given by Lebensohn et al. [122] considering the small strain regime and by Eisenlohr et al. [49] considering the finite strain regime. Using this EVP-FFT-based method, further studies modelled the internal lattice strain distributions in stainless steel [94] or in dual phase steel microstructures [24, 41, 163]. Some exemplary results of using this EVP-FFT model are shown in Fig. 9. A modification to include the shear transformation strain associated with deformation twinning is presented in [108, 109, 160]. Another extension of this model is based on augmented Lagrangians [145] for the simulation of void growth in polycrystalline materials [123]. This modified simulation approach is used to investigate the mechanical behavior of metal additive manufactured microstructures [36]. It showed that pores, which result from the additive manufacturing process itself, lead to significant stress hotspots.

Coupling the EVP-FFT-based method with a phase-field model [2, 22] enables the simulation of different additional physical processes. Examples are simulations to capture the recrystallization of polycrystals [33, 236], phase transformations [100] and fracture within polycrystalline microstructures [135], respectively. Further extensions concern the modelling of fatigue crack growth [175, 176], modelling interface decohesion in terms of a nonlocal interphase [190] or a gradient damage approach [191]. Incorporating crystallographic defects in terms of dislocations, introduced in [215], the EVP-FFT-based method was coupled with field dislocation dynamics (FDM) in [9, 10, 42] and discrete dislocation dynamics in [11, 12, 178]. To investigate the grain size on the flow stress of polycrystals, known as the Hall-Petch effect [77, 164], also an intrinsic material length scale associated with the plastic strain gradients may be introduced resulting in a strain gradient crystal plasticity approach [79, 113].

A comparison of the computed micromechanical fields to experimental mechanical fields is given in [166, 201, 202], with the microstructure model directly gained from EBSD measurements. The study confirmed a good correlation between the averaged results obtained from experiments and the results from simulations, while the local microstructural results do agree qualitatively. In addition, a virtual laboratory approach is introduced in [235] to determine the initial yield surface for sheet metal forming operations based on highly resolved microstructural FFT-based simulations and to compare the results to experimental investigations.

An earlier overview of FFT-based simulation of polycrystalline microstructures is given in [115, 121] and the free simulation software DAMASK for the simulation of polycrystalline microstructures based on finite elements or fast Fourier transforms is introduced in [172, 174].

Besides the investigations on polycrystalline metallic microstructures, also the simulation of the micromechanical fields within polycrystalline ice was performed by using a FFT-based method [75, 119, 198].

3.6 Comparison Between FE- and FFT-Based Computational Methods

Compared to finite element simulations one major advantage of FFT-based simulations is the image processing-like character and the associated possibility of directly using images of a real microstructure for the numerical simulation [118, 155, 156]. Therefore, in contrast to the finite element method, it avoids possible difficulties due to meshing of complex microstructures. In addition, several studies [129, 144, 167] showed, that the FFT-based method is more efficient than a classical FE-based microstructure simulation under the condition of periodicity.

A major disadvantage of FFT-based microstructure simulations is the restriction to periodic microstructures. This results from the intrinsic periodic ansatz functions. Nevertheless, considering a multiscale simulation these periodic microstructures are usually desired. In this case no additional effort is needed to prescribe the periodic boundary conditions.

Other disadvantages of the FFT-based basic fixed-point scheme are related to resolution errors due to the Gibbs phenomenon and numerical problems treating composites with high or infinite phase contrasts. These problems were addressed and solved in several works. Solutions concerning the resolution errors are for example elaborated in [3, 93, 211, 229, 230] by using finite difference approximations of the differential operator in Eq. (9) or using composite voxels. Solutions concerning the treatment of microstructures with infinite phase contrast are addressed in [122, 145, 146, 152, 184] using polarization based schemes, solution schemes based on augmented Lagrangians or conjugate gradient solvers.

Based on the Galerkin discretization, introduced in [19, 20, 218] and improved in [216, 219], the analogy of the FFT-based solver to finite element based simulations is finally shown in [38, 179, 234]. This is done by constructing the FFT-based solver using a similar variational basis as for conventional FE methods. Due to that, the constitutive routines of the FE methods may directly be used within the FFT-based framework, while still profiting from the computational efficiency of the FFT-based solver.

4 FE-FFT-Based Two-Scale Simulation

The voxel like character of Fourier spectral solvers results in simple discretization of the underlying microstructure and periodic global ansatz functions intrinsically imply periodic boundary conditions. For this reason, the FFT-based method is a well-suited and efficient solver for the microscopic BVP in terms of a two-scale FE-FFT-based simulation. In this context, the macroscopic BVP is discretized into finite elements while the microscopic BVP is defined by a distinct number of grid points, see Fig. 10. The overall macroscopic material behavior is then defined as volume average of its microscopic counterpart, which yields

$$\begin{aligned}&\bar{\varvec{\varepsilon }}(\bar{{\varvec{x}}}):=\frac{1}{\varOmega }\int _\varOmega \varvec{\varepsilon }(\bar{{\varvec{x}}},{\varvec{x}})\,\mathrm d\varOmega \end{aligned}$$
(10)
$$\begin{aligned}&\bar{\varvec{\sigma }}(\bar{{\varvec{x}}}):=\frac{1}{\varOmega }\int _\varOmega \varvec{\sigma }(\bar{{\varvec{x}}},{\varvec{x}})\,\mathrm d\varOmega \end{aligned}$$
(11)

in terms of small strain kinematics.

Fig. 10
figure 10

Example of a two-scale FE-FFT-based simulation. The FE simulation is used on the macroscale, while the FFT-based simulation is used on the periodic microscale

Full size image

The novel FE-FFT-based two-scale simulation approach was first introduced for modeling progressive damage within fiber-reinforced composites in [196]. As a first approach, the latter authors utilized the basic fixed-point scheme [155, 156] for the FFT-based microstructure simulation within a small strain regime. A more efficient FE-FFT-based two-scale method was proposed in [100] based on augmented Lagrangians [122] for the FFT-based simulation of polycrystalline materials incorporating phase-field-based simulations of microstructural phase transformations.

Considering a two-scale simulation, the computation of the macroscopic tangent operator is essential, but computationally very expensive. One way of computing the macroscopic tangent operator is based on a numerical approximation [100, 103, 196]. Therefore, the linearized stress increment

$$\begin{aligned} \varDelta \bar{\varvec{\sigma }}=\frac{\partial \bar{\varvec{\sigma }}}{\partial \bar{\varvec{\varepsilon }}}:\varDelta \bar{\varvec{\varepsilon }} \end{aligned}$$
(12)

and the perturbed strain field

$$\begin{aligned} \bar{\varvec{\varepsilon }}_\varDelta ^{kl}=\bar{\varvec{\varepsilon }}+\frac{\varDelta {\bar{\varepsilon }}}{2}\left( {\varvec{e}}_k\otimes {\varvec{e}}_l + {\varvec{e}}_l\otimes {\varvec{e}}_k \right) = \bar{\varvec{\varepsilon }}+\varDelta \bar{\varvec{\varepsilon }}^{kl} \end{aligned}$$
(13)

with the perturbation strain \(\varDelta {\bar{\varepsilon }}\) need to be taken into account. Performing a forward difference approximation of the stress increment and considering the definition of the perturbed strain field, the numerical tangent operator yields

$$\begin{aligned} \bar{\mathbb {C}}_{ijkl}=\frac{\partial {\bar{\sigma }}_{ij}}{\partial {\bar{\varepsilon }}_{kl}}\approx \frac{{\bar{\sigma }}_{ij}(\bar{\varvec{\varepsilon }}^{kl}_\varDelta )-{\bar{\sigma }}_{ij}(\bar{\varvec{\varepsilon }})}{\varDelta {\bar{\varepsilon }}}. \end{aligned}$$
(14)

Consequently, in the three-dimensional case, six perturbations are neccessary to compute the numerical tangent operator. These perturbation must be as small as possible in order to obtain an accurate approximation of the analytical tangent operator, while numerical problems due to too small perturbations need to be avoided, which leads to values between \(\varDelta {\bar{\varepsilon }}=10^{-8}\) and \(\varDelta {\bar{\varepsilon }}=10^{-6}\) for the perturbation.

Considering finite strain kinematics, with the macroscopic first Piola–Kirchhoff stress tensor \(\bar{{\varvec{P}}}\) and the macroscopic deformation gradient \(\bar{{\varvec{F}}}\), nine perturbations are needed in general to compute the numerical tangent operator, since \(\bar{{\varvec{F}}}\) is not symmetric. An efficient method based on only six instead of these nine perturbations was proposed in [101, 147].

Another method for the computation of the macroscopic tangent operator is derived by means of the Lippmann–Schwinger equation and can be computed from a system of linear equations, as shown in [72]. To deduce the aforementioned system of linear equations, the linearized stress increment (12) is transformed into

$$\begin{aligned} \varDelta \bar{\varvec{\sigma }}=\frac{1}{\varOmega }\left[ \int _\varOmega \mathbb {C} \, \mathrm d\varOmega + \int _\varOmega \mathbb {C} : \frac{\partial \tilde{\varvec{\varepsilon }}}{\partial \bar{\varvec{\varepsilon }}}\,\mathrm d\varOmega \right] :\varDelta \bar{\varvec{\varepsilon }} \end{aligned}$$
(15)

as shown in [149, 150]. This leads to the definition of the algorithmically consistent macroscopic tangent

$$\begin{aligned} \mathbb {C}^{\text {algo}}:=\frac{1}{\varOmega }\left[ \int _\varOmega \mathbb {C} \, \mathrm d\varOmega + \int _\varOmega \mathbb {C} : \frac{\partial \tilde{\varvec{\varepsilon }}}{\partial \bar{\varvec{\varepsilon }}}\,\mathrm d\varOmega \right]. \end{aligned}$$
(16)

Within this definition, the first part of the equation

$$\begin{aligned} \bar{\mathbb {C}}^V=\frac{1}{\varOmega }\int _\varOmega \mathbb {C} \, \mathrm d\varOmega \end{aligned}$$
(17)

is the effective stiffness tensor as defined by Voigt [214]. In addition, the derivative of the fluctuation strain field \(\tilde{\varvec{\varepsilon }}\) with respect to the macroscopic strain field \(\bar{\varvec{\varepsilon }}\) can be determined by solving the following linear equation system:

$$\begin{aligned} {\mathbb {\Gamma }}^{0}*\left[ \mathbb {C} - \mathbb {C}^0\right] = {\mathbb {\Gamma }}^{0} *\left[ \left( \mathbb {C} -\mathbb {C}^0\right) :\frac{\partial \tilde{\varvec{\varepsilon }}}{\partial \bar{\varvec{\varepsilon }}}\right] -\frac{\partial \tilde{\varvec{\varepsilon }}}{\partial \bar{\varvec{\varepsilon }}}. \end{aligned}$$
(18)

A straight forward extension of this definition of the algorithmically consistent macroscopic tangent operator to finite strains is given in [72] and leads to a speedup of 1.5 to 2 for different material behaviors compared to the aforementioned numerical tangent operator.

Since a two-scale full field simulation is computationally expensive, an efficient and accurate FE-FFT-based simulation procedure was proposed in [102, 103], while the FFT-based microstructure simulation is based on a Newton-Krylov solution scheme [64, 92, 233]. The efficient solution procedure is based on a pre-processing, a processing and a post-processing step. Within the pre-processing step different discretizations of a polycrystalline microstructure with different textures, number of grains and prescribed macroscopic strains are investigated. This leads to a minimal number of grid points, which is necessary to obtain an accurate macroscopic response. The resulting coarsely discretized microstructure is utilized within the actual two-scale simulation, while the history of the macroscopic strain of any point of particular interest is saved. Finally, in the post-processing step, this macroscopic strain and a finely discretized microstructure are used to generate highly resolved microstructural fields for these macroscopic points, see Fig. 11. A generalization of this simulation procedure to finite strain kinematics is given in [69].

Fig. 11
figure 11

Efficient FE-FFT-based two-scale simulation with a coarse discretized microstructure, followed by a post-processing step to generate highly resolved microstructural data

Full size image

Another efficient simulation strategy is based on using highly resolved full field simulations only in macroscopic critical areas. In this context, an algorithm, which uses a database with certain tangent operators for the macroscopic simulation of fiberboards and switches to a full field FE-FFT-based two scale simulation if no appropriate tangent operator is available, was proposed in [192]. A similar approach is presented in [98, 224], in which a FFT-based simulation is used to train a database model in a pre-processing step. Within the actual two-scale FE-FFT-based simulation, this database model is used in general, except for macroscopic critical areas, in which a highly resolved full field simulation is performed to capture the viscoelastic and fatigue behavior of short fiber-reinforced polymers.

Table 3 FE-FFT-based algorithms and applications
Full size table

In contrast to the aforementioned fully coupled concurrent FE-FFT-based simulation approaches, a solution strategy based on an exclusively macroscopic FE simulation followed by an FFT-based simulation of distinct macroscopic integration points was applied in [206]. Doing that, a quantitative understanding of the load dependence of lattice strain evolution during monotonic loading was obtained. In addition, the intergranular strain evolution during biaxial loading [207] and the role of microstructural evolution, such as texture, anisotropy and dislocation density was investigated [208] in a similar manner. Finally, this two-scale simulation approach was used to predict and explain the lattice strain and intensity evolution of microstructures gained from in-situ diffraction experiments [209].

In the following, some more applications of the FE-FFT-based multiscale approach are listed. The utilization of the two-scale simulation approach to magneto-mechanically and electro-mechanically coupled materials at finite strains is given in [168] and [73], respectively. In addition, the FE-FFT-based method was used to investigate the process-structure-property relationship for additive manufacturing in a small strain regime in [132]. The application of the software DAMASK [172, 174] within a multiscale framework has recently been presented in [78]. Finally, investigating braided composite beams in terms of a FE-FFT-based two-scale simulation [57, 223], the FFT-based microstructure simulation based on variational methods [38, 216, 222] was used within the two-scale context, to overcome the poor convergence behavior of FFT-based solvers in terms of composites with high phase contrasts.

An overview of the FE-FFT-based algorithms and their applications is also given in Table 3.

5 Conclusion

For periodic micro-heterogeneous materials, the FFT-based method represents a computational method which is a suitable alternative to classical FE-based methods. In the last two and a half decades this FFT-based method has proven to be a fast and accurate tool in regard of a computational microscale simulation. One major advantage of FFT-based simulations compared to FE-based simulations is the image processing-like character and, connected to that, the possibility to directly employ images of a real microstructure for the numerical simulation. This avoids the meshing of complex microstructures.

Possible problems of the FFT-based method concern the convergence behavior within simulations of microstructures incorporating infinite phase contrasts and artificial oscillations around discontinuities related to the Gibbs phenomenon. These problems were solved by developing accelerated solution methods (e.g. polarization based methods, methods based on augmented Lagrangians, gradient decent methods, or quasi-Newton methods) and using for example finite difference approximations of the Lippmann–Schwinger, composite voxels or a discrete Greens operator, respectively. This leads to a solution scheme, which is even more efficient than the classical FE-based microstructure simulation. Nevertheless, the FFT-based microstructure simulation is exclusively restricted to investigations on periodic microstructures, while there are no further restrictions for the FE-based microstructure simulation.

To generate an even more efficient simulation approach model order reduction techniques for FFT-based solvers were developed recently. These progresses and the intrinsic periodic character of the spectral solver including intrinsic periodic boundary conditions, lead to a well-suited scheme in terms of an efficient and accurate FE-FFT-based two-scale method.