Abstract
For the sake of precise simulation, and proper controlling of the performance of the proton exchange membrane fuel cells (PEMFCs) generating systems, robust and neat mathematical modelling is crucially needed. Principally, the robustness and precision of modelling strategy depend on the accurate identification of PEMFC’s uncertain parameters. Hence, in the last decade, with the noteworthy computational development, plenty of meta-heuristic algorithms (MHAs) are applied to tackle such problem, which have attained very positive results. Thus, this review paper aims at announcing novel inclusive survey of the most up-to-date MHAs that are utilized for PEMFCs stack’s parameter identifications. More specifically, these MHAs are categorized into swarm-based, nature-based, physics-based and evolutionary-based. In which, more than 350 articles are allocated to attain the same goal and among them only 167 papers are addressed in this effort. Definitely, 15 swarm-based, 7 nature-based, 6 physics-based, 2 evolutionary-based and 4 others-based approaches are touched with comprehensive illustrations. Wherein, an overall summary is undertaken to methodically guide the reader to comprehend the main features of these algorithms. Therefore, the reader can systematically utilize these techniques to investigate PEMFCs’ parameter estimation. In addition, various categories of PEMFC’s models, several assessment criteria and many PEMFC commercial types are also thoroughly covered. In addition to that, 27 models are gathered and summarized in an attractive manner. Eventually, some insights and suggestions are presented in the conclusion for future research and for further room of improvements and investigations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the last decades, the necessities of using clean energy sources are rapidly increasing due to the ecological devastating impacts of the fossil fuels [1,2,3,4]. As a result, renewable energy sources (RESs) are targeted to somehow replace the conventional ones due to their advantageous characteristics. Virtually, no emissions, static nature of most RESs types, higher efficiency, availability upon wide range of output power (from mW to MW’s) and convenient for all applications (portable, transportation and stationery). Amongst the several alternatives of RESs; fuel cells (FCs), solar and wind have attracted decision-makers and industry-stakeholders to utilize them as prime energy supplies [1,2,3, 5].
Particularly, FCs have been considered as a new booming energy conversion source as they have penetrated several applications whether portable, stationery or transportation [1, 2, 6]. Depending on the electrolyte type, FCs are categorized and utilized in the market for different applications [1, 2]. Examples of FC types are; (i) Proton exchange membrane FCs (PEMFCs) [7, 8], (ii) Solid oxide FCs (SOFCs) [9, 10], (iii) Molten carbonate FCs (MCFCs) [11], (iv) Phosphoric acid FCs (PAFCs) [8], (v) Alkaline FCs (AFCs) [12, 13] and furthermore. Specifically, the basic characteristics of the latter-mentioned types are illustrated in Table 1.
PEMFCs have distinguished by their flexibility, high power density, short startup time, fast response for load changes, low operating temperatures and pressures and no safety issues. Thus, they have been involved in the widest range of applications, mainly in transportation applications [1, 2, 14,15,16,17,18]. Nevertheless, the expensive cost of PEMFCs hinders their competitive penetration in the market [1, 2].
To appraise the features of PEMFCs systems, several modelling methods have been proposed, such as theoretical [19], empirical [20], and semi-empirical [21] models. Herein, a semi-empirical model, developed by Amphlett is adopted to simulate the polarization characteristics, which are represented by the output current versus voltage (I–V) curve, under various operating situations [21, 22].
In addition, precise PEMFC modelling is crucial for assessing the performance [23], optimum controlling [23], accurate simulating [24], and maximum power tracking [25, 26] of the PEMFCs units. Thus, in the recent years, numerous researchers have attempted to define the unknown parameters of PEMFCs’ model by the aid of several parameter estimation techniques. Examples of these techniques are electrochemical impedance spectroscopy-based approaches [27,28,29], black box-based methods [30, 31], adaptive filter-based techniques [32,33,34], current switching methods [35] and many more.
Nevertheless, these techniques are not broadly utilized because of their plain drawbacks, such as inflexibility and impracticability [7]. Moreover, the PEMFC’s model is high nonlinear, multi-variant and its variables are strongly coupled and severely affected by the operating conditions. Hence, the dynamics and accurate modelling have become more complicated and time-consuming when employed by such conventional techniques [36,37,38,39,40,41,42]. Therefore, there is an imperative demand to derive robust and feasible techniques to tackle such issue.
Since the rapid development of computer-based and artificial intelligence (AI)-based methods, meta-heuristic algorithms (MHAs) have attained distinct results when applied on several highly nonlinear optimization problems [43]. Principally, the problem of defining the unknown parameters of the PEMFCs can be easily dealt with as an optimization task. So, utilizing MHAs, as a reliable and precise tool to obtain the optimal solutions offers low computational effort and high accuracy.
Consequently, numbers of MHAs are employed for extracting the unspecified parameters of PEMFCs. Samples of such approaches are genetic algorithm [44, 45], differential evolution [46, 47], artificial bee colony [48], backtracking search algorithm [49], Biogeography-based optimizer [50], Artificial bee swarm optimizer [51], seeker optimizer [52], Artificial immune system [53], quantum-based optimizer [54], and etc.
Thereupon, an extensive survey article is urgently demanded to summarize these MHAs. A previous survey on several MHAs for PEMFC’s parameter estimation was performed in [5], where only fifteen algorithms are illustrated without methodical classification and comparison among various approaches. Furthermore, detailed discussions and simulation consequences of the algorithms have not been addressed. In addition, another recent survey was undertaken in [7], where only twenty-eight algorithms are discussed. However, it lacks details about the various PEMFC’s models in terms of their classification as well as their applications. Moreover, Amphlett model hasn’t been fully described in terms of mathematical representations.
Thus, a comprehensive literature survey on numerous MHAs implemented for extracting the unknown parameters of PEMFC’s model is undertaken. In-accordance, this paper can represent a unified reference for future in-depth research projects in the same field, while the major contributions can be epitomized as follows:
-
(i)
An overall discussion of various PEMFC models, besides their categories are presented,
-
(ii)
A summarized table gathering twenty-seven up-to-date models with their category-fulfill features,
-
(iii)
A total of thirty up-to-date MHAs with several simulation results are discussed, which are classified into four categories, swarm-based, nature-based, physics-based, and evolutionary-based, respectively, and
-
(iv)
A concluded Table offers the main characteristics of the MHAs, besides the technical specifications and operating conditions of each mentioned paper.
The rest of this paper is structured as follows: an overview of various PEMFC models found in the literature is revealed in Sect. 2. The mathematical model of PEMFC is described in Sect. 3. Section 4 announces some broadly utilized assessment criteria. Numerous MHAs for parameter identification of PEMFC are thoroughly illustrated in Sect. 5. The subsequent discussion is provided in Sect. 6. Finally, Sect. 7 represents the conclusion.
2 PEMFCs’ Generating Unit Models
Accurate modelling plays a significant role when the investigation of the FC’s performance is needed. FC models can be categorized in terms of scale, approach, state, spatial dimensions, and covered phenomena, as depicted in Fig. 1 [55, 56].
A summarized comparison among the various FC model techniques is tabulated in Table 2 [57].
It’s worth saying, some of the recent publications relative to the various FC model specifications are presented in Table 3.
3 PEMFC Mathematical Representation
As previously illustrated, since the FC is a multi-physics device, there are various classifications of the PEMFC models. Each model is constructed to tackle a certain aspect of the PEMFC. In this article, the polarization features’ effects on the PEMFC performance are particularly addressed in terms of the thermodynamics potential, activation, ohmic and concentration losses. The difficulty of modelling the PEMFC polarization characteristics stems from their complexity, multi-variance, and strong coupling. However, the mathematical semi-empirical model deduced by Amphlett and Mann [21, 22] has gain the acceptance through its accurate forecasting the performance of PEMFC in form of I–V polarization curve under several steady state and dynamic operating conditions [5, 7]. Accordingly, numerous researchers have been biased to utilize this model for identifying the performance and the polarization characteristics of the PEMFC.
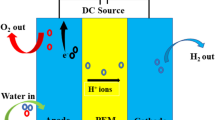
As depicted in Fig. 2, the I–V polarization curve of a single PEMFC can be divided into three regions: activation, ohmic and concentration losses, respectively. At the startup period with light load, a rapid decay of the PEMFC output voltage is noticed. This is due to the initial slow rate of the electrochemical reactions which is represented by the activation losses. Then, a linear decay of the output voltage due to the total resistance seen by the protons and electrons, which is represented by the ohmic losses. Again, the output voltage rapidly falls at higher load conditions due to the excessive water content reducing the concentration of the reactants in both electrodes. This voltage drop is represented by the concentration losses [1,2,3, 5, 7, 85].
Hence, the total output voltage of a single cell \({V}_{o/cell}\) is given by (1) [22]:
where \({E}_{nernst}\) is the cell open circuit voltage in (\(V\)) that is calculated by the Nernst equation. \({V}_{act}\) is the activation over-potential in (\(V\)). \({V}_{\Omega }\) is the ohmic voltage drop and \({V}_{con}\) is the concentration over-potential in (\(V\)).
When connecting \({N}_{C}\) multiple cells in series to form the stack, the stack output voltage \({V}_{o/stack}\) in (\(V\)) is described by (2).
It’s worth mentioning, Eq. (2) assumes that all the connected cells exhibit the same polarization characteristics.
\({E}_{nernst}\) is calculated by the Nernst equation with the addition of the temperature variation effect, which is given by (3) [86].
where \(T\) is the cell operating temperature in (\(Kelvin\)) and \(T\le 100^\circ{\rm C}\). \({P}_{{H}_{2}}\) and \({P}_{{O}_{2}}\) are the partial regulating pressures of the hydrogen and oxygen in (\(atm\)), respectively.
Since \({P}_{{H}_{2}}\) and \({P}_{{O}_{2}}\) vary with the load current values, they are expressed as follows:
While, calculating \({P}_{{O}_{2}}\) is dependable of whether the oxidant is pure oxygen or natural air. Thus, Eqs. (5) and (6) are applied for pure oxygen and natural air, respectively [86].
where \({R}_{{H}_{a}}\) and \({R}_{{H}_{c}}\) are the relative humidity of the vapor at anode and cathode, respectively. \({P}_{{H}_{2}O}\) is the saturation pressure of the water vapor in (\(\mathrm{atm}\)). \({P}_{a}\) and \({P}_{c}\) the anode and cathode inlet pressure in (atm), respectively. \({I}_{cell}\) and \(A\) are the cell current in (\(\mathrm{A}\)) and the membrane effective area in (\({\mathrm{cm}}^{2}\)), respectively.
As \({P}_{{H}_{2}O}\) depends on the cell operating temperature, it’s given by:
To express the reactions slowness when starting to load the cell, the activation losses \({V}_{act}\) is given by:
where \({\varphi }_{j} (j=1\dots .4)\) are defined as the semi-empirical coefficients in (\(V,V{K}^{-1},V{K}^{-1},V{K}^{-1}\)) and \({Co}_{2}\) represents the concentration of the oxygen at the catalytic layer of the cathode in (mol/cm3) which is expressed by:
Also, the concentration of the hydrogen at the catalytic layer of the anode \({C}_{{H}_{2}}\) in (mol/cm3) is described by [87]:
Moreover, the ohmic voltage drop \({V}_{\Omega }\) which exhibits a linear relation in the polarization curve is given by:
where \({R}_{C}\) in (\(\Omega\)) represents the resistance shown by the electrons through the connections to the external circuit. \({R}_{M}\) in (\(\Omega\)) indicates the resistance shown by the protons, through the membrane active area \(A\) in (\({\mathrm{cm}}^{2}\)) and it’s described by:
where the membrane thickness is symbolized by \(l\) in (\(\mathrm{cm}\)). The specific resistivity of the membrane is symbolized by \({\rho }_{M}\) in (\(\mathrm{\Omega cm}\)) and it’s given by:
where \(\gamma\) is a unitless parametric coefficient that indicates the water content in the membrane.
Lastly, the phenomenon, that affects the I–V curve when heavy loading the FC, is the concentration over-potential \({V}_{con}\) or mass transport losses and it’s determined by:
where \(\beta\) is a parametric coefficient in (V), \({J}_{Max}\) and \(J\) are the maximum cell current density and the actual operating current density in (\(\mathrm{A }{\mathrm{cm}}^{-2}\)), respectively.
4 Model Identification and Assessment Criteria
It’s self-explanatory from the aforesaid formulas that for obtaining a fully defined electrochemical-based model, at least seven parameters (\({\varphi }_{1}\), \({\varphi }_{2}\), \({\varphi }_{3}\), \({\varphi }_{4}\), \({R}_{C}\), \(\gamma\), and \(\beta\)) are assigned. Nonetheless, the indispensability, difficulty, and complexity of the model identification process stem from the significant dependence of the model parameters on the operating conditions. As expected, the quality of the polarization curves and the heavy nonlinear characteristics of such model are significantly affected. In addition, the unknown parameters are strongly coupled and aren’t illustrated in the manufacturer’s specifications sheet [57]. Thus, to simply, accurately and with low time-effort define the unknown parameters, it is studied as an optimization problem and solved by numerous optimization techniques. Amongst the various optimization methods, AI-based approaches are widely utilized to obtain the anonymous parameters of the PEMFC model [43]. Summarily, the procedures of modelling of the PEMFCs stacks, depending on the extracted information from the datasheet and the experiment-based data, are depicted in Fig. 3.
Not only the identification method that affects the accuracy of the estimated parameters but also the assessment criteria play a vital role to precisely determine the unknown parameters and fit the calculated I–V curve to the experimental one. Proper picking of the objective function (OF) simplifies the parameter determination process and differentiates among the various model identification methods quantitatively and qualitatively in terms of the acceptable range of results. Thus, a summary of the most utilized OFs in the parameter estimation of PEMFC, is collected in Table 4.
5 MHAs for PEMFC’s model parameters identification
Amongst the various AI-based optimization techniques, MHAs have proven their accuracy and higher computation efficiency when compared with the other conventional optimization techniques [7]. Therefore, MHAs have been adopted to get the optimum solutions for several engineering problems such as power systems problems, as presented in [95,96,97,98,99,100,101,102,103,104]. Besides, depending on the no free-lunch theory [105], many researchers have utilized various algorithms for accurate and effective investigation of the polarization characteristics of the PEMFC, as reported in [5, 7, 16, 57]. It’s worth saying that this section highlights the most recent works regarding presenting a new MHA to identify the undefined parameters of the PEMFC based on the semi-empirical model given in [21, 22]. One can track the procedures depicted in Fig. 4 to implement the MHAs for obtaining the unknown parameters of the PEMFC model. MHAs can be classified into four categories: swarm-based, nature-based, physics-based, and evolutionary-based, respectively. The reader can get a brief knowledge about the technical specifications of the most widely employed PEMFCs types in the commercial market when perusing Table 5. Also, the lower and upper limits of the PEMFC unknown parameters, popularly used in the state-of-art, are encapsulated in Table 6 [57].
5.1 Swarm-Based MHAs
5.1.1 Grasshopper Optimizer (GO)
The GO imitates the behaviors of grasshopper swarms when searching for food. Substantially, to mathematically derive the GO equations, the intermediate forces among the agents are classified as attraction and repulsion forces [106]. Furthermore, GO merits can be summarized as follows: (i) avoiding falling into local minima as GO is strongly capable of balancing between exploration and exploitation, (ii) fast convergence and (iii) simple controlling variables [106, 112]. Thus, it has been utilized in the parameter identification of PEMFC, while promising results are incapsulated in Table 7 in the second row [112].
5.1.2 Grey Wolf Optimizer (GWO)
The GWO mimics the intelligent attitude of grey wolves when attacking their preys. As they live in groups, their tasks are assigned according to the swarm hierarchy where the wolves are divided into four kinds: alpha, Beta, delta, and omega. The hunting process passes through three stages, pursuing and chasing, encircling, and attacking which mathematically represent the exploration, OF evaluation and exploitation phases, respectively [107, 113]. Due to GWO advantages such as simple tuning process and lower computational time and burden, it has been employed in the parameter estimation of the PEMFC model, while the results are gathered in Table 7 in the third row [107].
5.1.3 Salp Swarm Algorithm (SSA)
The SSA mimics the salps collective attitude when searching for food in oceans, where the swarm members are combined to form chains. Mathematically, the salp chains are modeled by classifying the group individuals into leader and followers. Thus, the leader position during the searching process can be formulated as in (15) [108, 114].
where \({X}_{i}^{j}\) denotes the leader position, the food source position in the jth dimension is symbolized by \({S}_{j}\). \({HL}_{j}\) and \({LL}_{j}\) represent the higher and lower limits of the jth dimension, while \({b}_{1}\), \({b}_{2}\) and \({b}_{3}\) are three random numbers, respectively. SSA has the capability of effectively enhancing the initial haphazard solutions and rapidly converging into the optimum ones. As a result, it has been adopted to estimate the undefined parameters of the PEMFC, as elucidated in Table 7 in the fourth row [108].
5.1.4 Shark Smell Optimizer (SSO)
The SSO imitates the hunting mechanism of the sharks when sensing the prey smell. Employing their strong sense of smelling the prey blood, the hunting process depends on three assumptions: (i) the shark velocity is much greater than the prey velocity. So, the prey is assumed stationary. (ii) The blood is uninterruptedly flowed out from the prey to the sea and the propagation of the prey smell particles isn’t affected by the flow of the seawater. (iii) Only one prey (seeking environment) is existed in the search domain [115,116,117]. Accordingly, SSO exhibits the merits of high precision, low computational effort, and high convergence trend. Consequently, its results have outperformed the other conventional algorithms when utilized in the parameter estimation of the PEMFC model, as indicated in Table 7 in the fifth row [117].
5.1.5 Cuckoo Search Optimizer (CSO)
The CSO mimics the brood parasite attitude of cuckoos where the cuckoos put their eggs surreptitiously in the host birds’ nests. Fraudfully, the cuckoos try to empty the nests of the host birds out of their own eggs, keeping only the cuckoos’ eggs to enhance the hatching amount. The cuckoos implement a haphazard strategy to pick the host nest. Furthermore, the basic construction of CSO depends on three concepts, relying on which each cuckoo produces next solutions referring to (16) [118,119,120].
where \({XP}_{i}\) represents the ith egg position, \(\lambda >0\) indicates the step size, the element-wise multiplications are symbolized by \(\oplus\) and \(\varepsilon\) denotes the exponent of Lévy flight.
For the sake of effectively and robustly employ this technique in PEMFC parameter identification, a novel modified approach, called CS-EO, is developed in [119]. In CS-EO, CSO is merged with the explosion operator (EO), derived from fireworks algorithm (FWA). Consequently, the newly proposed hybrid algorithm can effectively improve the search capability and evade from being trapped into local minimum solutions. Eventually, the sixth row in Table 7 elucidates the obtained results from adopting CS-EO in identifying the PEMFC model unknown parameters [119].
5.1.6 Whale Optimizer (WO)
The WO is inspired by the smart attitude of humpback whales when hunting a swarm of small fishes at the ocean surface, which is called bubble net feeding. These whales start the hunting process by diving deeply and surrounding the prey by bubbles. Thereafter, the whales arise to the surface for trapping the small fishes. Consequently, the hunting process mainly includes three phases, encircling prey, making bubbles with various shapes, and looking for the prey. Mathematically, the whales update their positions based on (17)–(18). Upon ending the encircling phase, the whales will try to attack the victim through creating bubbles which mathematically refers to the local exploitation [110, 121].
where \(Y(t)\) is the position vector of the whales, \(t\) refers to the iteration counter, \({Y}_{v}\left(t\right)\) is the position vector of the target victim and \(A\) and \(D\) represents the coefficient vectors.
Due to the robustness, accurateness, and effectiveness of WO, it has been applied for the sake of estimating the unknown parameters of several commercial types of PEMFC, as indicated in Table 7 in the seventh row [110].
5.1.7 Bonobo Optimizer (BO)
The BO is inspired by the social attitudes and reproductive process of Bonobos. Essentially, the Bonobos mating process depends on the fission–fusion concept which describes the techniques used by Bonobos groups for looking for food and other. Moreover, the Bonobos lifestyle is classified into two stages. Firstly, the positive stage (PS) at which all living circumstances are available like food, proper mating, and protection. Secondly, the negative stage (NS) which refers to the lack of these circumstances [122]. Recently, the authors in [122] have utilized BO for the sake of proper identifying the unknow parameters of three commercial PEMFCs, due to its ability to converge to the global solution smoothly and rapidly, while the results are indicated in Table 7 in the eighth row.
5.1.8 Harris Hawk’s Optimizer (HHO)
The HHO mimics the hunting strategy of Harris hawks when chasing their preys (rabbits). Mathematically, like any population-based approaches, HHO is divided into two phases, exploration, and exploitation. In the exploration phase, Harris hawks employ two tactics to discover the prey where the first tactic supposes that the hawks’ position is near to the group members and the prey. On the other hand, the second one assumes that the hawks allocate on stochastic trees [123, 124]. Furthermore, an improved HHO using chaotic equations, called chaotic HHO (CHHO), is presented in [86] where the convergence trend is enhanced. As foreseen, CHHO has been employed for identifying the unknown parameters of several commercial types of PEMFCs, while the results are revealed in Table 7 in the ninth row.
5.1.9 Coyote Optimizer (CO)
Basically, the CO imitates the coyotes’ attitude not only while chasing preys but also the community framework of coyotes and the experiences interchange by the coyotes. Mathematically, the coyote’s population consists of \({N}_{p}\) packs, each pack has \({N}_{c}\) coyotes which is a static number and fixed for all packs. Moreover, each coyote represents a feasible solution for the optimization task and its social circumstance is the cost of the fitness function [125, 126]. CO exhibits advantageous features such as low computational effort, simple tuning variables, and fast convergence trend. Consequently, it has been applied for defining the unspecified parameters of the commercial 250 W PEMFCs stack, while the results are capsulated in Table 8 [127].
5.1.10 Manta Rays Foraging Optimizer (MRFO)
The MRFO is inspired from the menta ray’s mechanism when searching for food (plankton). Hence, the foraging mechanism is subdivided into three phases such as (i) chain foraging, (ii) cyclone foraging, and (iii) somersault foraging. In the chaining phase, the positions of menta rays are updated to the best position of plankton where the plankton exists with high concentration using the mathematical equations given in (19)–(20) [78, 128].
where \({F}_{i,d}\left(it\right)\) denotes the location of the ith member at itth iteration in dth dimension. \(r\) is a randomly generated vector from 0 to 1, \(w\) represents a weight coefficient and \({F}_{b,d}\left(it\right)\) refers to the plankton best location (plankton with high concentration). \({N}_{pop}\) denotes the population size.
It’s worth saying that MRFO requires lesser effort to fine-adjust its controlling parameters. therefore, the authors in [78] have applied it for extracting the unknown parameters of three commercial types of PEMFCs under various operating conditions, where the results are indicated in Table 7 in the tenth row.
5.1.11 Monarch Butterfly Optimizer (MBO)
The MBO mimics the migration mechanism of monarch butterflies which can be achieved by following the subsequent rules. Starting by dividing the whole population into individuals located only in Land 1 or Land 2. Ending by assuming that the movement to the next generation of the MB individuals, having the best fitness, is automatically performed and there is no operator can change them. Hence, this will prevent any deterioration for the MB population and maintain the effectiveness of the population while increasing the generations [129, 130].
However, a major drawback of MBO is that it sometimes gets trapped into local optimum which leads to premature convergence. As a result, a modified MBO (MMBO) has been utilized in [130] to solve this issue. In MMBO, two mechanisms have been integrated with the basic MBO where the first is the mutation operator and the second is the anti-cosine operator, While the procedures of MMBO are revealed in Fig. 5. Accordingly, MMBO has been utilized for tackling the parameter estimation problem of the PEMFCs, while the results are depicted in Table 7 in the eleventh row [130].
5.1.12 Black Widow Optimizer (BWO)
The BWO imitates the distinguished mating attitude of black widow spiders. Fundamentally, this reproductive behavior is composed of an exclusive phase called cannibalism. Thanks to this phase, the individuals with unwanted fitness value are excluded from the circle, resulting in early convergence. While the main phases of BWO are revealed in Fig. 6 [131, 132].
Consequently, BWO has been applied for the parameter estimation of two commercial PEMFCs, while the results are depicted in Table 7 in the twelfth row [132].
5.1.13 Sparrow Search Optimization Algorithm (SSOA)
Fundamentally, the SSOA simulates the collective wisdom, countering the predators and foraging attitudes of sparrows. Specially, the sparrows are divided into two types of producers and scroungers where the producers seek for obtain their food source. On the other hand, the scroungers are fed by the producers [133, 134]. Despite the advantages of SSOA, such as accuracy, stability and robustness, the convergence speed may be slowed down due to haphazardness walk strategy. Thus, an improved version of SSOA, called improved SSOA (ISSOA), has been introduced in [134] to refine this problem. Basically, ISSOA combines the basic SSA with an adaptive learning factor. As a result, ISSOA has been utilized for extracting the unknown parameter of the PEMFCS, while the results are indicated in Table 7 in the thirteenth row [134].
5.1.14 Jellyfish Search Optimizer (JSO)
The JSO is motivated by the search mechanism and movement of jellyfish in the ocean. Specifically, JSO is composed of three concepts: (a) jellyfish track only one governing rule either the ocean current or inside-swarm movement (passive or active) and a time control technique. (b) Jellyfish are interested towards the locations which contains large amount of food. (c) The food quantity is assigned, and its corresponding cost fitness value is determined accordingly [135, 136]. Fewer control parameter and lesser computational efforts and random trials are such the JSO merits. Hence, the authors in [136] has applied JSO in the field of estimating the PEMFCs unknown parameters, while the outcomes are encapsulated in Table 7 in the fourteenth row.
5.1.15 Pathfinder Optimizer (PFO)
The PFO emulates the haphazard motion and performance of animal’s groups following their leader according to their adjoining place, searching for food location or prey. Primarily, PFO is based on the animal competitors’ movement which are gathered in groups. On the other side, the way to the target may be picked by the collaboration between the leader and some competitors who have sufficient information. Moreover, there are four parameters that has been tuned to refine the competitors’ attitude in the exploration phase, which are (a) the oscillation frequency of the competitors, (b) the competitors’ vibration, (c) the communication parameter, and (d) the attraction parameter [137, 138].
PFO has been utilized for extracting the unknown parameters of two commercial PEMFCs. Besides, it has been involved for investigating the steady state and dynamic operation of the PEMFCs, while the results are tabulated in Table 7 in the fifteenth row [138].
5.2 Nature-Based MHAs
5.2.1 Flower Pollination Optimizer (FPO)
Principally, FPO is inspired by the pollination behavior of flowers. Hence, the pollination process can be classified into two techniques, self-pollination (abiotic) and cross pollination (biotic). Herein, the self-pollination, in which pollens of the same flowers inseminate to emanate new flowers via wind as the pollinating medium. While, in the cross pollination, pollens of various flowers inseminate to emanate new flowers via bats, honeybees and birds as the pollinating medium [139].
FPO is characterized by enhancing the convergence tendency, simple variables tuning effort and effectively balancing the global exploration and the local exploitation. Consequently, the authors in [109], have utilized FPO for the parameters estimation purpose of the PEMFC, while the results are indicated in Table 9 in the second row.
5.2.2 Neural Network Optimizer (NNO)
The NNO emulates the artificial neural network (ANN) attitude, in which obtaining the incoming data and the desired data is established first and thereafter forecasting the relation between them. Referring to the ANN framework, it can be divided into two frames feed-forward and frequent NNs. Moreover, it depends on its framework whichever open-loop or closed-loop (feedback). Specifically, in NNO, the targeted solution at a certain iteration is regarded as the output data and the principal aim is to reduce the deviation between this targeted solution and the other forecasted solutions [140, 141].
Additionally, low tuning efforts of the NNO controlling variables and low computation burdens are such the NNO benefits. Hence, the authors in [141] have implemented the NNO to properly define the unknown parameters of the PEMFC, while the results are indicated in Table 9 in the third row.
5.2.3 Firefly Optimizer (FFO)
The FFO is inspired by the social attitude of fireflies when courting mates. Basically, FFO procedures relies on three fundamental assumptions, (i) all the fireflies are considered as hermaphrodite where all the agents in the population seek for the same target. (ii) the attraction possibility of the fireflies is proportional to the intensity of their flashlights. (iii) the brightness strength of a firefly is determined by the objective function [111, 142].
Moreover, FFO procedures are revealed in Fig. 7. In addition, as tabulated in Table 9 in the fourth row, FFO has proven reasonable results in commercial test cases regarding the PEMFC parameter identification [111].
5.2.4 Artificial Ecosystem Optimizer (AEO)
The AEO is inspired by the energy flow in an ecological system on the earth. Specifically, AEO imitates three distinguished attitudes of the living creatures, production, consumption, and decomposition, as revealed in Fig. 8. Mathematically, the production target is to enhance the exploration and exploitation characteristics. Meanwhile, the consumption’s endeavor is to improve the exploration capability. Finally, the decomposition’s objective is to promote the exploitation ability [143, 144].
Moreover, a new modified AEO, called improved AEO (IAEO), is presented in [144], which overcomes the lack of accurate solution related to the basic AEO. Consequently, IAEO has been utilized in the parameter estimation of the PEMFCs. This is due to its ability to effectively fit the computed voltage datasets to the experimental ones, while the results are depicted in Table 7 in the fifth row [144].
5.2.5 Moth-Flame Optimizer (MFO)
Mainly, the MFO mimics the distinguished navigation techniques of moths in night where they can fly with the aid of the moonlight. Using transverse orientation technique, moths fly by keeping a certain angle with respect to the moon [145, 146]. Recently, a proposed algorithm, called without certainty MFO (WCMFO), has been presented in [146] which integrates the uncertainty measurement with the conventional algorithm. Hence, the suggested algorithm has gained more robustness to disturbance with respect to the conventional one. Thus, WCFMO has been employed for extracting the unknown parameters of the PEMFCs with various numbers of unknowns and two OFs, while the results are depicted in Table 10 [146].
5.2.6 Marine Predator Optimizer (MPO)
The MPO is inspired from the foraging process implemented by the marine predators to catch their preys. Particularly, the predators follow the Levy mechanism in case of lack of prey. On the other hand, in case of plentiful prey, the predators follow Brownian movements’ mechanism. According to the ecological impacts, the relative velocity of the prey \(v\) with respect to the predators can be varied relying on the Levy and Brownian mechanisms. Moreover, MPO has exhibited an enhanced global and local search besides, the fast convergence trend [147, 148]. Thus, MPO has been applied for defining the unknown parameters of several commercial PEMFCs, while the results are encapsulated in Table 9 in the sixth row [148].
5.2.7 Slime-Mould Optimizer (SMO)
The SMO is inspired by the natural oscillation state of slime mould. Basically, SMO employs adaptive weights to imitate the concept of generating positive and negative feedback of the spread wave of slime mould. Basically, these feedbacks depend on the bio-oscillator to establish the optimal path for linking food with perfect explorative capability and exploitative tendency [149, 150]. Recently, SMO has been utilized for identifying the unknown parameters of the PEMFCs, while the results are depicted in Table 9 in the seventh row [150].
5.3 Physics-Based MHAs
5.3.1 Multi-Verse Optimizer (MVO)
The MVO is extracted from the multi-verse theory which states that various universes are generated from numerous big-explosions. Each universe is related to each explosion. MVO construction relies on three cosmological concepts, white, black and worm holes. Mathematically, the exploration phase is represented by white and black holes, while the worm holes indicate the exploitation phase [151, 152].
MVO has shown advantageous features such as, simple implementation, less tuning parameters, and less computational effort. Thus, the authors in [152] have encouraged to employ it for identifying the unknown parameters of the PEMFC model, where the results are depicted in Table 11 in the second row.
5.3.2 Atom Search Optimizer (ASO)
Principally, the atoms are the preliminary part that form all the substances. The ASO is inspired by the atoms motion which are moving sustainably based on the classical mechanics. While moving, there are two types of forces that affect the atoms interactions with each other. The first type is the interaction forces deduced from Lennard–Jones potential. While the second one is the constraint forces generated from Bond-Length potential. Referring to Newton’s second law, the atom acceleration \({a}_{i}\) is a function of the atom mass \({m}_{i}\), the interaction \({IF}_{i}\) and the constraint \({CF}_{i}\) forces, as given in (21) [153, 154].
Accordingly, ASO is distinguished by its simple construction and smooth convergent rate. Hence, as expected, it has proven such robustness and accurateness in determining the unknown parameters of the PEMFC model, as illustrated in [154] and revealed in Table 11 in the third row.
5.3.3 Vortex Search Optimizer (VSO)
The VSO simulates the vortex pattern generated by cephalic flow of stirred fluids. This pattern is considered as a set of overlapped circles coordinated in a two-dimensional searching area. Like other metaheuristic approaches, Elementally, VSO is divided into two phases, generation, and replacement. In the generation phase, the existing solution is utilized to produce a group of solutions, while the existing solution is updated in the replacement phase [47, 155]. Furthermore, to improve the computational efficiency and the capability to evade from the local minima, a novel approach called vortex search differential evolution (VSDE) is illustrated in [47]. Thus, VSDE has exhibited robustness and effectiveness in investigating the PEMFC electrical characteristics, while the consequences are arranged in Table 11 in the fourth row.
5.3.4 Fluid Search Optimizer (FSO)
Principally, the FSO simulates the Bernoulli’s law to evaluate the fluid speed relying on the fluid pressure. Where, improving the fluid speed, diminishes the fluid pressure and the potential energy. Herein, the fluid pressure is considered as the fitness function value where improving the fluid pressure, reduces its velocity [156, 157]. Despite all the afore-stated procedures, FSO has an obvious drawback which is the premature convergence. Hence, an improved FSO (IFSO) is proposed in [157] to tackle this problem. Particularly, IFSO is composed of two enhancement techniques, that have been integrated with the basic FSO, which are quasi-oppositional based learning and chaotic concept. IFSO has been applied for tackling the parameter estimation problem of the PEMFCs, while the results are indicated in Table 11 in the fifth row [157].
5.3.5 Equilibrium Optimizer (EO)
The EO emulates the control technique of the balance between mass and volume utilized to evaluate dynamic and equilibrium phases. Particularly, in EO, the search agent is represented by each particle with its concentration. Where, the search agents stochastically update their concentration with respected to the best results, called equilibrium candidates. Furthermore, the mass balance is mathematically described in (22) [158, 159].
where \(V\) refers to the control volume, \(V\frac{d{C}_{in}}{dt}\) represents the mass change rate and \({F}_{r}\) denotes the flow rate. \({C}_{e}\) is the equilibrium phase concentration, \({C}_{in}\) denotes the inside concentration and \({G}_{in}\) symbolizes the inside mass generation rate.
Due to the effectiveness, robustness, and fast convergence trend, EO has been employed for extracting the unknown parameters of various commercial PEMFCs, while the results are tabulated in Table 11 in the sixth row [159].
5.3.6 Gradient-Based Optimizer (GBO)
Mainly, the GBO is inspired by the gradient-based Newton’s concept. Especially, two worthy operators are utilized in GBO, called gradient search approach (GSA) and local escaping coefficient (LEC), respectively. Besides, a group of vectors to explore the search space. Moreover, the exploration features and the convergence trend can be enhanced by implementing the GSA. On the other hand, the LEC is utilized to make GBO evade the local optima problem [160, 161]. Since, GBO has a smooth transition between exploration and exploitation phases and fast convergence features, it has been employed for tackling the parameter estimation issue of the PEMFCs. Hence, the results are revealed in Table 11 in the seventh row [161].
5.4 Evolutionary-Based MHAs
5.4.1 Satin bowerbird Optimizer (SBO)
The SBO is inspired by the satin bowerbirds’ behavior when constructing their own bowers in such a manner to attract satin females during reproduction season. Consequently, various elements like sparkling materials, branches, flowers, and fruits are utilized while building bowers to entice satin females [162, 163]. Owing to the advantageous features of SBO such as algorithm stability and fast convergence trend, it has been employed in [164] to extract the accurate values of the PEMFC unknown parameters, as encapsulated in Table 12 in the second row. Moreover, SBO has shown a significant fitness between the experimental data and the computed ones.
5.4.2 Shuffled Frog-Leaping Optimizer (SFLO)
The SFLO is a memetic evolution-inspired metaheuristic approach which merges the local search mechanism of the particle swarm optimizer (PSO) into the concept of integrating the data obtained from various local searches to a global solution. Mainly, in SFLO, the number of frogs (solutions) represent the agents (population size), where the agents are split into some subgroups called memeplexes. Every memeplex represents a set of frogs carrying out a local search [111, 165].
Finally, SFLO performance in terms of robustness, accuracy and reliability has been proven via parametric statistical tests while identifying the unspecified parameters of many PEMFC types. One can track the results obtained by SFLO in Table 12 in the third row [111].
6 Concluding Discussions
For the sake of helping the reader for simply browsing the various earlier-mentioned MHAs, a comprehensive summary is offered in Table 13. Furthermore, it gives a detailed comparison of thirty MHAs, besides four MHAs that don’t fit to any of the previously-mentioned MHAs’ categories. Essentially, the comparison is divided into two categories, MHA features and PEMFC characteristics. Especially, MHA features include year of application, controlling variables, number of independent runs and statistical performance tests. On the other hand, PEMFC characteristics are represented by model state, number of unknowns, OF, types of plotted curves, various operating conditions and lastly, number of measured I–V dataset points.
As concluded from the mathematical model of PEMFC, the polarization characteristics depends mainly on the operating temperatures and the partial pressures of the fuel and oxidant. Hence, in order to make the reader fully grasp such dependence, two well-known commercial types of PEMFC have been studied under various operating conditions. Particularly, BCS 500 W and SR-12 500 W PEMFCs have been evaluated in terms of I–V and I–P curves, as revealed in Figs. 9a–d and 10a–d; respectively [148]. Generally, as revealed in Figs. 9a–d and 10a–d, it’s clear that the polarization characteristics and the output power of PEMFC are enhanced by increasing the operating temperature at constant pressure. Also, the polarization characteristics are promoted by rising the suppliants’ partial pressures at a constant temperature, as long the minimum and maximum limits haven’t been violated.
7 Conclusions
In this paper, an inclusive survey of various models’ categories of PEMFC has been carried out. In which, 27 models related to such categories have been gathered and summarized. Besides, a detailed PEMFC mathematical model, widely utilized in identifying the PEMFC electrical characteristics, has been totally represented. In addition, a summary of various commercial types of PEMFCs, in terms of their datasheet-extracted parameters, is encapsulated. Moreover, as the paper core work, 34 MHAs, which have been employed for extracting the unknown parameters of PEMFC, have been thoroughly discussed. Particularly, the discussion has covered their based-category, their inspiration, their features, and lastly their results in PEMFC parameter estimation. Consequently, a comprehensive comparison, among these MHAs, has been applied for clearly help the reader to simply investigate their characteristics. Also, the impact of varying the operating conditions on PEMFC output voltage and power have been demonstrated for sake of elaboration.
Lastly, as a future-wise point of view, further development of newly designed PEMFC models, together with novel optimization techniques are crucial for more properly and accurately evaluate the PEMFC performance. In addition, developing new objective functions play a vital role in effectively and precisely assess the performance of the optimization methods.
Data availability
Not applicable.
References
Sharaf OZ, Orhan MF (2014) An overview of fuel cell technology: Fundamentals and applications. Renew Sustain Energy Rev 32:810–853. https://doi.org/10.1016/j.rser.2014.01.012
Karanfil G (2020) Importance and applications of DOE/optimization methods in PEM fuel cells: a review. Int J Energy Res 44:4–25. https://doi.org/10.1002/er.4815
Fathy A, AbdelAleem SHE, Rezk H (2021) A novel approach for PEM fuel cell parameter estimation using LSHADE-EpSin optimization algorithm. Int J Energy Res 45:6922–6942. https://doi.org/10.1002/er.6282
Toghyani S, Afshari E, Baniasadi E, Shadloo MS (2019) Energy and exergy analyses of a nanofluid based solar cooling and hydrogen production combined system. Renew Energy 141:1013–1025. https://doi.org/10.1016/j.renene.2019.04.073
Priya K, Sathishkumar K, Rajasekar N (2018) A comprehensive review on parameter estimation techniques for Proton Exchange Membrane fuel cell modelling. Renew Sustain Energy Rev 93:121–144. https://doi.org/10.1016/j.rser.2018.05.017
Atyabi SA, Afshari E, Wongwises S, Yan W-M, Hadjadj A, Shadloo MS (2019) Effects of assembly pressure on PEM fuel cell performance by taking into accounts electrical and thermal contact resistances. Energy 179:490–501. https://doi.org/10.1016/j.energy.2019.05.031
Yang Bo, Wang J, Lei Yu, Shu H, Tao Yu, Zhang X, Yao W, Sun L (2020) A critical survey on proton exchange membrane fuel cell parameter estimation using meta-heuristic algorithms. J Clean Prod 265:121660. https://doi.org/10.1016/j.jclepro.2020.121660
Inci M, Türksoy O (2019) Review of fuel cells to grid interface: Configurations, technical challenges and trends. J Clean Prod 213:1353–1370. https://doi.org/10.1016/j.jclepro.2018.12.281
Oryshchyn D, Harun NF, Tucker D, Bryden KM, Shadle L (2018) Fuel utilization effects on system efficiency in solid oxide fuel cell gas turbine hybrid systems. Appl Energy 228:1953–1965. https://doi.org/10.1016/j.apenergy.2018.07.004
Chuahy FDF, Kokjohn SL (2019) Solid oxide fuel cell and advanced combustion engine combined cycle: a pathway to 70% electrical efficiency. Appl Energy 235:391–408. https://doi.org/10.1016/j.apenergy.2018.10.132
Ido A, Kawase M (2020) Development of a tubular molten carbonate direct carbon fuel cell and basic cell performance. J Power Sources 449:227483. https://doi.org/10.1016/j.jpowsour.2019.227483
Saebea D, Chaiburi C, Authayanun S (2019) Model based evaluation of alkaline anion exchange membrane fuel cells with water management. Chem Eng J 374:721–729. https://doi.org/10.1016/j.cej.2019.05.200
Wang Y, Leung DYC, Xuan J, Wang H (2017) A review on unitized regenerative fuel cell technologies, part B: unitized regenerative alkaline fuel cell, solid oxide fuel cell, and microfluidic fuel cell. Renew Sustain Energy Rev 75:775–795. https://doi.org/10.1016/j.rser.2016.11.054
El-Hay EA, El-Hameed MA, El-Fergany AA (2019) Improved performance of PEM fuel cells stack feeding switched reluctance motor using multi-objective dragonfly optimizer. Neural Comput Appl 31:6909–6924. https://doi.org/10.1007/s00521-018-3524-z
El-Hay EA, El-Hameed MA, El-Fergany AA (2018) Performance enhancement of autonomous system comprising proton exchange membrane fuel cells and switched reluctance motor. Energy 163:699–711. https://doi.org/10.1016/j.energy.2018.08.104
Ohenoja M, Leiviska K (2020) Observations on the parameter estimation problem of polymer electrolyte membrane fuel cell polarization curves. Fuel cells 20:516–526. https://doi.org/10.1002/fuce.201900155
Miao Di, Chen W, Zhao W, Demsas T (2020) Parameter estimation of PEM fuel cells employing the hybrid grey wolf optimization method. Energy 193:116616. https://doi.org/10.1016/j.energy.2019.116616
Shaheen MAM, Hasanien HM, ElMoursi MS, El-Fergany AA (2021) Precise modeling of PEM fuel cell using improved chaotic MayFly optimization algorithm. Int J Energy Res. https://doi.org/10.1002/er.6987
Giner-Sanz JJ, Ortega EM, Pérez-Herranz V (2018) Mechanistic equivalent circuit modelling of a commercial polymer electrolyte membrane fuel cell. J Power Sources 379:328–337. https://doi.org/10.1016/j.jpowsour.2018.01.066
Busquet S, Hubert CE, Labbé J, Mayer D, Metkemeijer R (2004) A new approach to empirical electrical modelling of a fuel cell, an electrolyser or a regenerative fuel cell. J Power Sources 134:41–48. https://doi.org/10.1016/j.jpowsour.2004.02.018
Amphlett JC, Baumert RM, Mann RF, Peppley BA, Roberge PR (1995) Performance modeling of the Ballard Mark IV solid polymer electrolyte fuel cell. J Electrochem Soc 142:1
Mann RF, Amphlett JC, Hooper MAI, Jensen HM, Peppley BA, Roberge PR (2000) Development and application of a generalised steady-state electrochemical model for a PEM fuel cell. J Power Sources 86:173–180. https://doi.org/10.1016/S0378-7753(99)00484-X
Secanell M, Wishart J, Dobson P (2011) Computational design and optimization of fuel cells and fuel cell systems: a review. J Power Sources 196:3690–3704. https://doi.org/10.1016/j.jpowsour.2010.12.011
Chatrattanawet N, Hakhen T, Kheawhom S, Arpornwichanop A (2017) Control structure design and robust model predictive control for controlling a proton exchange membrane fuel cell. J Clean Prod 148:934–947. https://doi.org/10.1016/j.jclepro.2017.02.033
Rana KPS, Kumar V, Sehgal N, George S (2019) A novel dP/dI feedback based control scheme using GWO tuned PID controller for efficient MPPT of PEM fuel cell. ISA Trans 93:312–324. https://doi.org/10.1016/j.isatra.2019.02.038
Motahhir S, El Hammoumi A, El Ghzizal A (2020) The most used MPPT algorithms: review and the suitable low-cost embedded board for each algorithm. J Clean Prod 246:118983. https://doi.org/10.1016/j.jclepro.2019.118983
Niya SMR, Hoorfar M (2013) Study of proton exchange membrane fuel cells using electrochemical impedance spectroscopy technique—a review. J Power Sources 240:281–293. https://doi.org/10.1016/j.jpowsour.2013.04.011
Taleb MA, Bethoux O, Godoy E (2017) Identification of a PEMFC fractional order model. Int J Hydrog Energy 42:1499–1509. https://doi.org/10.1016/j.ijhydene.2016.07.056
Kheirmand M, Asnafi A (2011) Analytic parameter identification of proton exchange membrane fuel cell catalyst layer using electrochemical impedance spectroscopy. Int J Hydrog Energy 36:13266–13271. https://doi.org/10.1016/j.ijhydene.2010.08.088
Kheirandish A, Motlagh F, Shafiabady N, Dahari M (2016) Dynamic modelling of PEM fuel cell of power electric bicycle system. Int J Hydrog Energy 41:9585–9594. https://doi.org/10.1016/j.ijhydene.2016.02.046
Peng Hu, Cao G-Y, Zhu X-J, Li J (2010) Modeling of a proton exchange membrane fuel cell based on the hybrid particle swarm optimization with Levenberg–Marquardt neural network. Simul Model Pract Theory 18:574–588. https://doi.org/10.1016/j.simpat.2010.01.001
Ettihir K, Boulon L, Agbossou K (2016) Energy management strategy for a fuel cell hybrid vehicle based on maximum efficiency and maximum power identification. IET Electr Syst Transp 6:261–268. https://doi.org/10.1049/iet-est.2015.0023
Ettihir K, Boulon L, Agbossou K (2016) Optimization-based energy management strategy for a fuel cell/battery hybrid power system. Appl Energy 163:142–153. https://doi.org/10.1016/j.apenergy.2015.10.176
Ettihir K, Cano MH, Boulon L, Agbossou K (2017) Design of an adaptive EMS for fuel cell vehicles. Int J Hydrog Energy 42:1481–1489. https://doi.org/10.1016/j.ijhydene.2016.07.211
Chang W-Y (2013) Estimating equivalent circuit parameters of proton exchange membrane fuel cell using the current change method. Electr Power Energy Syst 53:584–591. https://doi.org/10.1016/j.ijepes.2013.05.031
Yang Z, Liu Q, Zhang L, Dai J, Razmjooy N (2020) Model parameter estimation of the PEMFCs using improved Barnacles Mating Optimization algorithm. Energy 212:118738. https://doi.org/10.1016/j.energy.2020.118738
Abdel-Basset M, Mohamed R, El-Fergany A, Chakrabortty RK, Ryan MJ (2021) Adaptive and efficient optimization model for optimal parameters of proton exchange membrane fuel cells: a comprehensive analysis. Energy 233:121096. https://doi.org/10.1016/j.energy.2021.121096
Abdel-Basset M, Mohamed R, Elhoseny M, Chakrabortty RK, Ryan MJ (2021) An efficient heap-based optimization algorithm for parameters identification of proton exchange membrane fuel cells model: analysis and case studies. Int J Hydrog Energy 46:11908–11925. https://doi.org/10.1016/j.ijhydene.2021.01.076
Menesy AS, Sultan HM, Korashy A, Kamel S, Jurado F (2021) A modified farmland fertility optimizer for parameters estimation of fuel cell models. Neural Comput Appl 33:12169–12190. https://doi.org/10.1007/s00521-021-05821-1
Yang M, Zhang L, Li T-Y, Yousefi N, Li Y-K (2021) Optimal model identification of the PEMFCs using optimized Rotor Hopfield Neural Network. Energy Rep 7:3655–3663. https://doi.org/10.1016/j.egyr.2021.06.052
Alizadeh M, Torabi F (2021) Precise PEM fuel cell parameter extraction based on a self-consistent model and SCCSA optimization algorithm. Energy Convers Manag 229:113777. https://doi.org/10.1016/j.enconman.2020.113777
Blanco-Cocom L, Botello-Rionda S, Ordoñez LC, Ivvan Valdez S (2021) Robust parameter estimation of a PEMFC via optimization based on probabilistic model building. Math Comput Simul 185:218–237. https://doi.org/10.1016/j.matcom.2020.12.021
Yang Bo, Wang J, Zhang X, Tao Yu, Yao W, Shu H, Zeng F, Sun L (2020) Comprehensive overview of meta-heuristic algorithm applications on PV cell parameter identification. Energy Convers Manag 208:112595. https://doi.org/10.1016/j.enconman.2020.112595
Rajasekar N, Jacob B, Balasubramanian K, Priya K, Sangeetha K, Sudhakar Babu T (2015) Comparative study of PEM fuel cell parameter extraction using Genetic Algorithm. Ain Shams Eng J 6:1187–1194. https://doi.org/10.1016/j.asej.2015.05.007
Priya K, Sudhakar Babu T, Balasubramanian K, Sathish Kumar K, Rajasekar N (2015) A novel approach for fuel cell parameter estimation using simple Genetic Algorithm. Sustain Energy Technol Assess 12:46–52. https://doi.org/10.1016/j.seta.2015.09.001
Cheng J, Zhang G (2014) Parameter fitting of PEMFC models based on adaptive differential evolution. Electr Power Energy Syst 62:189–198. https://doi.org/10.1016/j.ijepes.2014.04.043
Fathy A, Abd Elaziz M, Alharbi AG (2020) A novel approach based on hybrid vortex search algorithm and differential evolution for identifying the optimal parameters of PEM fuel cell. Renew Energy 146:1833–1845. https://doi.org/10.1016/j.renene.2019.08.046
Zhang W, Wang N, Yang S (2013) Hybrid artificial bee colony algorithm for parameter estimation of proton exchange membrane fuel cell. Int J Hydrogen Energy 38:5796–5806. https://doi.org/10.1016/j.ijhydene.2013.01.058
Askarzadeh A, dos Santos Coelho L (2014) A backtracking search algorithm combined with Burger’s chaotic map for parameter estimation of PEMFC electrochemical model. Int J Hydrogen Energy 39:11165–11174. https://doi.org/10.1016/j.ijhydene.2014.05.052
Niu Q, Zhang L, Li K (2014) A biogeography-based optimization algorithm with mutation strategies for model parameter estimation of solar and fuel cells. Energy Convers Manag 86:1173–1185. https://doi.org/10.1016/j.enconman.2014.06.026
Askarzadeh A, Rezazadeh A (2011) A new artificial bee swarm algorithm for optimization of proton exchange membrane fuel cell model parameters. J Zhejiang Univ-Sci C Comput Electron 12:638–646. https://doi.org/10.1631/jzus.C1000355
Dai C, Chen W, Cheng Z, Li Qi, Jiang Z, Jia J (2011) Seeker optimization algorithm for global optimization: a case study on optimal modelling of proton exchange membrane fuel cell (PEMFC). Electr Power Energy Syst 33:369–376. https://doi.org/10.1016/j.ijepes.2010.08.032
Askarzadeh A, Rezazadeh A (2011) Artificial immune system-based parameter extraction of proton exchange membrane fuel cell. Electr Power Energy Syst 33:933–938. https://doi.org/10.1016/j.ijepes.2010.12.036
Al-Othman AK, Ahmed NA, Al-Fares FS, AlSharidah ME (2015) Parameter identification of PEM fuel cell using quantum-based optimization method. Arab J Sci Eng 40:2619–2628. https://doi.org/10.1007/s13369-015-1711-0
Ang SMC, Fraga ES, Brandon NP, Samsatli NJ, Brett DJL (2011) Fuel cell systems optimisation e Methods and strategies. Int J Hydrogen Energy 36:14678–14703. https://doi.org/10.1016/j.ijhydene.2011.08.053
Asensio FJ, SanMartín JI, Zamora I, Saldañaa G, Oñederra O (2019) Analysis of electrochemical and thermal models and modeling techniques for polymer electrolyte membrane fuel cells. Renew Sustain Energy Rev 113:109283. https://doi.org/10.1016/j.rser.2019.109283
Kandidayeni M, Macias A, Amamou AA, Boulon L, Kelouwani S, Chaoui H (2018) Overview and benchmark analysis of fuel cell parameters estimation for energy management purposes. J Power Sources 380:92–104. https://doi.org/10.1016/j.jpowsour.2018.01.075
Asensio FJ, San Martín JI, Zamora I, Garcia-Villalobos J (2017) Fuel cell-based CHP System modelling using artificial neural networks aimed at developing techno-economic efficiency maximization control systems. Energy 123:585–593. https://doi.org/10.1016/j.energy.2017.02.043
Mu YT, He P, Ding J, Tao W-Q (2017) Modeling of the operation conditions on the gas purging performance of polymer electrolyte membrane fuel cells. Int J Hydrogen Energy 42:11788–11802. https://doi.org/10.1016/j.ijhydene.2017.02.108
Rahgoshay SM, Ranjbar AA, Ramiar A, Alizadeh E (2017) Thermal investigation of a PEM fuel cell with cooling flow field. Energy 134:61–73. https://doi.org/10.1016/j.energy.2017.05.151
Asensio FJ, San Martín JI, Zamora I, Oñederra O (2018) Model for optimal management of the cooling system of a fuel cell-based combined heat and power system for developing optimization control strategies. Appl Energy 211:413–430. https://doi.org/10.1016/j.apenergy.2017.11.066
Ziogou C, Voutetakis S, Georgiadis MC, Papadopoulou S (2018) Model predictive control (MPC) strategies for PEM fuel cell systems—A comparative experimental demonstration. Chem Eng Res Des 131:656–670. https://doi.org/10.1016/j.cherd.2018.01.024
Kahveci EE, Taymaz I (2018) Assessment of single-serpentine PEM fuel cell model developed by computational fluid dynamics. Fuel 217:51–58. https://doi.org/10.1016/j.fuel.2017.12.073
Li S, Yuan J, Xie G, Sunden B (2018) Effects of agglomerate model parameters on transport characterization and performance of PEM fuel cells. Int J Hydrogen Energy 43:8451–8463. https://doi.org/10.1016/j.ijhydene.2018.03.106
Randrianarizafy B, Schott P, Chandesris M, Gerard M, Bultel Y (2018) Design optimization of rib/channel patterns in a PEMFC through performance heterogeneities modelling. Int J Hydrogen Energy 43:8907–8926. https://doi.org/10.1016/j.ijhydene.2018.03.036
Chen J, Huang L, Yan C, Liu Z (2020) A dynamic scalable segmented model of PEM fuel cell systems with two-phase water flow. Math Comput Simul 167:48–64. https://doi.org/10.1016/j.matcom.2018.05.006
Abdollahzadeh M, Ribeirinha P, Boaventura M, Mendes A (2018) Three-dimensional modeling of PEMFC with contaminated anode fuel. Energy 152:939–959. https://doi.org/10.1016/j.energy.2018.03.162
Khan SS, Shareef H, Wahyudie A, Khalid SN (2018) Novel dynamic semiempirical proton exchange membrane fuel cell model incorporating component voltages. Int J Energy Res 42:2615–2630. https://doi.org/10.1002/er.4038
Mohammadi A, Cirrincione G, Djerdir A, Khaburi D (2018) A novel approach for modeling the internal behavior of a PEMFC by using electrical circuits. Int J Hydrogen Energy 43:11539–11549. https://doi.org/10.1016/j.ijhydene.2017.08.151
Kwan TH, Zhang Y, Yao Q (2018) A coupled 3D electrochemical and thermal numerical analysis of the hybrid fuel cell thermoelectric device system. Int J Hydrogen Energy 43:23450–23462. https://doi.org/10.1016/j.ijhydene.2018.10.202
AzimurRahman M, Mojica F, Sarker M, Abel Chuang P-Y (2019) Development of 1-D multiphysics PEMFC model with dry limiting current experimental validation. Electrochim Acta 320:134601. https://doi.org/10.1016/j.electacta.2019.134601
Yang Z, Qing Du, Jia Z, Yang C, Jiao K (2019) Effects of operating conditions on water and heat management by a transient multi-dimensional PEMFC system model. Energy 183:462–476. https://doi.org/10.1016/j.energy.2019.06.148
Sankar K, Aguan K, Jana AK (2019) A proton exchange membrane fuel cell with an airflow cooling system: dynamics, validation and nonlinear control. Energy Convers Manag 183:230–240. https://doi.org/10.1016/j.enconman.2018.12.072
Laribi S, Mammar K, Sahli Y, Koussa K (2019) Analysis and diagnosis of PEM fuel cell failure modes (flooding & drying) across the physical parameters of electrochemical impedance model: using neural networks method. Sustain Energy Technol Assess 34:35–42. https://doi.org/10.1016/j.seta.2019.04.004
Barzegari MM, Rahgoshay SM, Mohammadpour L, Toghraie D (2019) Performance prediction and analysis of a dead-end PEMFC stack using data-driven dynamic model. Energy 188:116049. https://doi.org/10.1016/j.energy.2019.116049
Chen F, Jiao J, Hou Z, Cheng W, Cai J, Xia Z, Chen JCJ (2020) Robust polymer electrolyte membrane fuel cell temperature tracking control based on cascade internal model control. J Power Sources 479:229008. https://doi.org/10.1016/j.jpowsour.2020.229008
Han J, Han J, Ji H, Yu S (2020) “Model-based” design of thermal management system of a fuel cell “air-independent” propulsion system for underwater shipboard. Int J Hydrogen Energy 45:32449–32463. https://doi.org/10.1016/j.ijhydene.2020.08.233
Selem SI, Hasanien HM, El-Fergany AA (2020) Parameters extraction of PEMFC’s model using manta rays foraging optimizer. Int J Energy Res 44:4629–4640. https://doi.org/10.1002/er.5244
Atlam O, Dundar G (2021) A practical Equivalent Electrical Circuit model for Proton Exchange Membrane Fuel Cell (PEMFC) systems. Int J Hydrogen Energy 46:13230–13239. https://doi.org/10.1016/j.ijhydene.2021.01.108
Duan F, Hayati H (2021) Optimal fractional model identification of the polymer membrane fuel cells based on a new developed version of Water Strider Algorithm. Energy Rep 7:1847–1856. https://doi.org/10.1016/j.egyr.2021.03.033
Calili F, Ismail MS, Ingham DB, Hughes KJ, Ma L, Pourkashanian M (2021) A dynamic model of air-breathing polymer electrolyte fuel cell (PEFC): A parametric study. Int J Hydrogen Energy 46:17343–17357. https://doi.org/10.1016/j.ijhydene.2021.02.133
Pinagapani AK, Mani G, Chandran KR, Pandian K, Sawantmorye E, Vaghela P (2021) Dynamic modeling and validation of PEM fuel cell via system identification approach. J Electr Eng Technol 16:2211–2220. https://doi.org/10.1007/s42835-021-00736-2
Prince Abraham B, Kalidasa MK (2021) Influence of catalyst layer and gas diffusion layer porosity in proton exchange membrane fuel cell performance. Electrochim Acta 389:138793. https://doi.org/10.1016/j.electacta.2021.138793
Shen J, Tu Z, Chan SH (2021) Effect of gas purging on the performance of a proton exchange membrane fuel cell with dead-ended anode and cathode. Int J Energy Res 45:14813–14823. https://doi.org/10.1002/er.6757
Jarauta A, Ryzhakov P (2018) Challenges in computational modeling of two-phase transport in polymer electrolyte fuel cells flow channels: a review. Arch Comput Methods Eng 25:1027–1057. https://doi.org/10.1007/s11831-017-9243-2
Menesy AS, Sultan HM, Selim A, Ashmawy MG, Kamel S (2020) Developing and applying chaotic Harris Hawks optimization technique for extracting parameters of several proton exchange membrane fuel cell stacks. IEEE Access 8:1146–1159. https://doi.org/10.1109/ACCESS.2019.2961811
Sun S, Yumei Su, Yin C, Jermsittiparsert K (2020) Optimal parameters estimation of PEMFCs model using Converged Moth Search Algorithm. Energy Rep 6:1501–1509. https://doi.org/10.1016/j.egyr.2020.06.002
Liu E-J, Hung Y-H, Hong C-W (2021) Improved metaheuristic optimization algorithm applied to hydrogen fuel cell and photovoltaic cell parameter extraction. Energies 14:619. https://doi.org/10.3390/en14030619
Chen K, Laghrouche S, Djerdir A (2019) Degradation model of proton exchange membrane fuel cell based on a novel hybrid method. Appl Energy 252:113439. https://doi.org/10.1016/j.apenergy.2019.113439
Sohani A, Naderi S, Torabi F (2019) Comprehensive comparative evaluation of different possible optimization scenarios for a polymer electrolyte membrane fuel cell. Energy Convers Manag 191:247–260. https://doi.org/10.1016/j.enconman.2019.04.005
Danoune MB, Djafour A, Wang Y, Gougui A (2021) The Whale Optimization Algorithm for efficient PEM fuel cells modeling. Int J Hydrogen Energy. https://doi.org/10.1016/j.ijhydene.2021.03.105
Ma R, Yang T, Breaz E, Li Z, Briois P, Gao F (2018) Data-driven proton exchange membrane fuel cell degradation predication through deep learning method. Appl Energy 231:102–115. https://doi.org/10.1016/j.apenergy.2018.09.111
Jiang S, Wang C, Zhang C, Bai H, Xu L (2019) Adaptive estimation of road slope and vehicle mass of fuel cell vehicle. eTransportation 2:100023. https://doi.org/10.1016/j.etran.2019.100023
Ashraf MA, Rashid K, Rahimipetroudi I, Kim HJ, Dong SK (2020) Analyzing different planar biogas-fueled SOFC stack designs and their effects on the flow uniformity. Energy 190:116450. https://doi.org/10.1016/j.energy.2019.116450
Abualigah L, Shehab M, Alshinwan M, Mirjalili S, Elaziz MA (2021) Ant lion optimizer: a comprehensive survey of its variants and applications. Arch Computat Methods Eng 28:1397–1416. https://doi.org/10.1007/s11831-020-09420-6
Khan MJ, Mathew L (2020) Comparative study of optimization techniques for renewable energy system. Arch Computat Methods Eng 27:351–360. https://doi.org/10.1007/s11831-018-09306-8
Behmanesh R, Rahimi I, Gandomi AH (2021) Evolutionary many-objective algorithms for combinatorial optimization problems: a comparative study. Arch Comput Methods Eng 28:673–688. https://doi.org/10.1007/s11831-020-09415-3
Khan MJ (2021) Review of recent trends in optimization techniques for hybrid renewable energy system. Arch Comput Methods Eng 28:1459–1469. https://doi.org/10.1007/s11831-020-09424-2
Sharma M, Kaur P (2021) A comprehensive analysis of nature-inspired meta-heuristic techniques for feature selection problem. Arch Comput Methods Eng 28:1103–1127. https://doi.org/10.1007/s11831-020-09412-6
Emad D, El-Hameed MA, Yousef MT, El-Fergany AA (2020) Computational methods for optimal planning of hybrid renewable microgrids: a comprehensive review and challenges. Arch Comput Methods Eng 27:1297–1319. https://doi.org/10.1007/s11831-019-09353-9
Lachhwani K (2020) Application of neural network models for mathematical programming problems: a state of art review. Arch Comput Methods Eng 27:171–182. https://doi.org/10.1007/s11831-018-09309-5
Tang Z, Hu X, Périaux J (2020) Multi-level hybridized optimization methods coupling local search deterministic and global search evolutionary algorithms. Arch Comput Methods Eng 27:939–975. https://doi.org/10.1007/s11831-019-09336-w
Khan MJ, Mathew L (2017) Different kinds of maximum power point tracking control method for photovoltaic systems: a review. Arch Comput Methods Eng 24:855–867. https://doi.org/10.1007/s11831-016-9192-1
Draz A, Elkholy MM, El-Fergany AA (2021) Soft computing methods for attaining the protective device coordination including renewable energies: review and prospective. Arch Comput Methods Eng. https://doi.org/10.1007/s11831-021-09534-5
Wolpert DH, Macready WG (1997) No free lunch theorems for optimization. IEEE Trans Evol Comput 1:67–82. https://doi.org/10.1109/4235.585893
El-Fergany AA (2018) Electrical characterisation of proton exchange membrane fuel cells stack using grasshopper optimizer. IET Renew Power Gener 12:9–17. https://doi.org/10.1049/iet-rpg.2017.0232
Ali M, Elhameed MA, Farahat MA (2017) Effective parameters’ identification for polymer electrolyte membrane fuel cell models using grey wolf optimizer. Renewable Energy 111:455–462. https://doi.org/10.1016/j.renene.2017.04.036
El-Fergany AA (2018) Extracting optimal parameters of PEM fuel cells using Salp Swarm Optimizer. Renew Energy 119:641–648. https://doi.org/10.1016/j.renene.2017.12.051
Priya K, Rajasekar N (2019) Application of flower pollination algorithm for enhanced proton exchange membrane fuel cell modelling. Int J Hydrogen Energy 44:18438–18449. https://doi.org/10.1016/j.ijhydene.2019.05.022
El-Fergany AA, Hasanien HM, Agwa AM (2019) Semi-empirical PEM fuel cells model using whale optimization algorithm. Energy Convers Manage 201:112197. https://doi.org/10.1016/j.enconman.2019.112197
Kandidayeni M, Macias A, Khalatbarisoltani A, Boulon L, Kelouwani S (2019) Benchmark of proton exchange membrane fuel cell parameters extraction with metaheuristic optimization algorithms. Energy 183:912–925. https://doi.org/10.1016/j.energy.2019.06.1520360-544
Saremi S, Mirjalili S, Lewis A (2017) Grasshopper optimisation algorithm: theory and application. Adv Eng Softw 105:30–47. https://doi.org/10.1016/j.advengsoft.2017.01.004
Mirjalili S, Mirjalili SM, Lewis A (2014) Grey wolf optimizer. Adv Eng Softw 69:46–61. https://doi.org/10.1016/j.advengsoft.2013.12.007
Mirjalili S, Gandomi AH, Mirjalili SZ, Saremi S, Faris H, Mirjalili SM (2017) Salp Swarm Algorithm: a bio-inspired optimizer for engineering design problems. Adv Eng Softw 114:163–191. https://doi.org/10.1016/j.advengsoft.2017.07.002
Abedinia O, Amjady N, Ghasemi A (2016) A new metaheuristic algorithm based on shark smell optimization. Complexity 21:97–116. https://doi.org/10.1002/cplx.21634
Han W, Li D, Yu D, Ebrahimian H (2019) Optimal parameters of PEM fuel cells using chaotic binary shark smell optimizer. Energy Sources Part A Recovery Utilization Environ Effects. https://doi.org/10.1080/15567036.2019.1676845
Rao Y, Shao Z, Ahangarnejad AH, Gholamalizadeh E, Sobhani B (2019) Shark Smell Optimizer applied to identify the optimal parameters of the proton exchange membrane fuel cell model. Energy Convers Manag 182:1–8. https://doi.org/10.1016/j.enconman.2018.12.057
X-S Yang, S Deb (2019) Cuckoo search via Levy flights. In: World congress on nature & biologically inspired computing (NaBIC), pp 210–214. https://doi.org/10.1109/NABIC.2009.5393690
Chen Y, Wang N (2019) Cuckoo search algorithm with explosion operator for modeling proton exchange membrane fuel cells. Int J Hydrogen Energy 44:3075–3087. https://doi.org/10.1016/j.ijhydene.2018.11.140
Inci M, Caliskan A (2020) Performance enhancement of energy extraction capability for fuel cell implementations with improved Cuckoo search algorithm. Int J Hydrogen Energy 45:11309–11320. https://doi.org/10.1016/j.ijhydene.2020.02.069
Mirjalili S, Lewis A (2016) The whale optimization algorithm. Adv Eng Softw 95:51–67. https://doi.org/10.1016/j.advengsoft.2016.01.008
HM Sultan, AS Menesy, S Kamel, M Tostado-Véliz, F Jurado (2020) Parameter identification of proton exchange membrane fuel cell stacks using bonobo optimizer. In: IEEE international conference on environment and electrical engineering and IEEE industrial and commercial power systems Europe (EEEIC/I&CPS Europe), pp 1–7. https://doi.org/10.1109/EEEIC/ICPSEurope49358.2020.9160597
Heidari AA, Mirjalili S, Faris H, Aljarah I, Mafarja M, Chen H (2019) Harris hawks optimization: algorithm and applications. Future Gener Comput Syst 97:849–872. https://doi.org/10.1016/j.future.2019.02.028
Mossa MA, Kamel OM, Sultan HM, ZakiDiab AA (2021) Parameter estimation of PEMFC model based on Harris Hawks’ optimization and atom search optimization algorithms. Neural Comput Appl 33:5555–5570. https://doi.org/10.1007/s00521-020-05333-4
Pierezan J, dos SantosCoelho L (2018) Coyote optimization algorithm: a new metaheuristic for global optimization problems. In: IEEE congress on evolutionary computation (CEC), pp 1–8. https://doi.org/10.1109/CEC.2018.8477769
Abaza A, El-Sehiemy RA, Mahmoud K, Lehtonen M, Darwish MMF (2021) Optimal estimation of proton exchange membrane fuel cells parameter based on coyote optimization algorithm. Appl Sci 11:2052. https://doi.org/10.3390/app11052052
Sultan HM, Menesy AS, Kamel S, Jurado F (2021) Developing the coyote optimization algorithm for extracting parameters of proton-exchange membrane fuel cell models. Electr Eng 103:563–577. https://doi.org/10.1007/s00202-020-01103-6
Zhao W, Zhang Z, Wang L (2020) Manta ray foraging optimization: an effective bio-inspired optimizer for engineering applications. Eng Appl Artif Intell 87:103300. https://doi.org/10.1016/j.engappai.2019.103300
Wang G-G, Deb S, Cui Z (2019) Monarch butterfly optimization. Neural Comput Appl 31:1995–2014. https://doi.org/10.1007/s00521-015-1923-y
Yuan Z, Wang W, Wang H (2020) Optimal parameter estimation for PEMFC using modified monarch butterfly optimization. Int J Energy Res 44:8427–8441. https://doi.org/10.1002/er.5527
Hayyolalam V, Kazem AAP (2020) Black Widow Optimization Algorithm: a novel meta-heuristic approach for solving engineering optimization problems. Eng Appl Artif Intell 87:103249. https://doi.org/10.1016/j.engappai.2019.103249
Singla MK, Nijhawan P, Oberoi AS (2021) Parameter estimation of proton exchange membrane fuel cell using a novel meta-heuristic algorithm. Environ Sci Pollut Res 28:34511–34526. https://doi.org/10.1007/s11356-021-13097-0
Xue J, Shen Bo (2020) A novel swarm intelligence optimization approach: sparrow search algorithm. Syst Sci Control Eng 8:22–34. https://doi.org/10.1080/21642583.2019.1708830
Zhu Y, Yousefi N (2021) Optimal parameter identification of PEMFC stacks using Adaptive Sparrow Search Algorithm. Int J Hydrogen Energy 46:9541–9552. https://doi.org/10.1016/j.ijhydene.2020.12.107
Chou J-S, Truong D-N (2020) A novel metaheuristic optimizer inspired by behavior of jellyfish in ocean. Appl Math Comput 389:125535. https://doi.org/10.1016/j.amc.2020.125535
Gouda EA, Kotb MF, El-Fergany AA (2021) Jellyfish search algorithm for extracting unknown parameters of PEM fuel cell models: Steady-state performance and analysis. Energy 221:119836. https://doi.org/10.1016/j.energy.2021.119836
Yapici H, Cetinkaya N (2019) A new meta-heuristic optimizer: Pathfinder algorithm. Appl Soft Comput J 78:545–568. https://doi.org/10.1016/j.asoc.2019.03.012
Gouda EA, Kotb MF, El-Fergany AA (2021) Investigating dynamic performances of fuel cells using pathfinder algorithm. Energy Convers Manag 237:114099. https://doi.org/10.1016/j.enconman.2021.114099
Samy MM, Barakat S, Ramadan HS (2019) A flower pollination optimization algorithm for an off-grid PV-Fuel cell hybrid renewable system. Int J Hydrogen Energy 44:2141–2152. https://doi.org/10.1016/j.ijhydene.2018.05.127
Sadollah A, Sayyaadi H, Yadav A (2018) A dynamic metaheuristic optimization model inspired by biological nervous systems: neural network algorithm. Appl Soft Comput 71:747–782. https://doi.org/10.1016/j.asoc.2018.07.039
Fawzi M, El-Fergany AA, Hasanien HM (2019) Effective methodology based on neural network optimizer for extracting model parameters of PEM fuel cells. Int J Energy Res 43:8136–8147. https://doi.org/10.1002/er.4809
Yang X-S (2014) Chapter 8—firefly algorithms. In: Nature-inspired optimization algorithms, pp 111–127. https://doi.org/10.1016/B978-0-12-416743-8.00008-7
Zhao W, Wang L, Zhang Z (2020) Artificial ecosystem-based optimization: a novel nature-inspired meta-heuristic algorithm. Neural Comput Appl 32:9383–9425. https://doi.org/10.1007/s00521-019-04452-x
Rizk-Allah RM, El-Fergany AA (2020) Artificial ecosystem optimizer for parameters identification of proton exchange membrane fuel cells model. Int J Hydrogen Energy. https://doi.org/10.1016/j.ijhydene.2020.06.256
Mirjalili S (2015) Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm. Knowl-Based Syst 89:228–249. https://doi.org/10.1016/j.knosys.2015.07.006
Messaoud RB, Midouni A, Hajji S (2021) PEM fuel cell model parameters extraction based on moth-flame optimization. Chem Eng Sci 229:116100. https://doi.org/10.1016/j.ces.2020.116100
Faramarzi A, Heidarinejad M, Mirjalili S, Gandomi AH (2020) Marine predators algorithm: a nature-inspired metaheuristic. Expert Syst Appl 152:113377. https://doi.org/10.1016/j.eswa.2020.113377
Zaki Diab AA, Tolba MA, Abo El-Magd AG, Zaky MM, El-Rifaie AM (2020) Fuel cell parameters estimation via marine predators and political optimizers. IEEE Access 8:166998–167018. https://doi.org/10.1109/ACCESS.2020.3021754
Li S, Chen H, Wang M, AsgharHeidari A, Mirjalili S (2020) Slime mould algorithm: a new method for stochastic optimization. Future Gener Comput Syst 111:300–323. https://doi.org/10.1016/j.future.2020.03.055
Gupta J, Nijhawan P, Ganguli S (2021) Optimal parameter estimation of PEM fuel cell using slime mould algorithm. Int J Energy Res 45:14732–14744. https://doi.org/10.1002/er.6750
Mirjalili S, Mirjalili SM, Hatamlou A (2016) Multi-verse optimizer: a nature-inspired algorithm for global optimization. Neural Comput Appl 27:495–513. https://doi.org/10.1007/s00521-015-1870-7
Fathy A, Rezk H (2018) Multi-verse optimizer for identifying the optimal parameters of PEMFC model. Energy 143:634–644. https://doi.org/10.1016/j.energy.2017.11.014
Zhao W, Wang L, Zhang Z (2019) A novel atom search optimization for dispersion coefficient estimation in groundwater. Futur Gener Comput Syst 91:601–610. https://doi.org/10.1016/j.future.2018.05.037
Agwa AM, El-Fergany AA, Sarhan GM (2019) Steady-state modeling of fuel cells based on atom search optimizer. Energies 12:1884. https://doi.org/10.3390/en12101884
Doğan B, Ölmez T (2015) A new metaheuristic for numerical function optimization: VORTEX Search algorithm. Inf Sci 293:125–145. https://doi.org/10.1016/j.ins.2014.08.053
Dong R, Wang S (2018) New optimization algorithm inspired by fluid mechanics for combined economic and emission dispatch problem. Turk J Electr Eng Comput Sci 26:3305–3318. https://doi.org/10.3906/elk-1803-88
Qin F, Liu P, Niu H, Song H, Yousefi N (2020) Parameter estimation of PEMFC based on improved fluid search optimization algorithm. Energy Rep 6:1224–1232. https://doi.org/10.1016/j.egyr.2020.05.006
Faramarzi A, Heidarinejad M, Stephens B, Mirjalili S (2020) Equilibrium optimizer: a novel optimization algorithm. Knowl-Based Syst 191:105190. https://doi.org/10.1016/j.knosys.2019.105190
Seleem SI, Hasanien HM, El-Fergany AA (2021) Equilibrium optimizer for parameter extraction of a fuel cell dynamic model. Renew Energy 169:117–128. https://doi.org/10.1016/j.renene.2020.12.131
Ahmadianfar I, Bozorg-Haddad O, Chu X (2020) Gradient-based optimizer: a new metaheuristic optimization algorithm. Inf Sci 540:131–159. https://doi.org/10.1016/j.ins.2020.06.037
Elsayed SK, Agwa AM, Elattar EE, El-Fergany AA (2021) Steady-state modelling of PEM fuel cells using gradient-based optimizer. DYNA DYNA-ACELERADO 96:520–527. https://doi.org/10.6036/10099
Moosavi SHS, Bardsiri VK (2017) Satin bowerbird optimizer: A new optimization algorithm to optimize ANFIS for software development effort estimation. Eng Appl Artif Intell 60:1–15. https://doi.org/10.1016/j.engappai.2017.01.006
El-Hay EA, El-Hameed MA, El-Fergany AA (2018) Steady-state and dynamic models of solid oxide fuel cells based on Satin Bowerbird Optimizer. Int J Hydrogen Energy 43:14751–14761. https://doi.org/10.1016/j.ijhydene.2018.06.032
Duan B, Cao Q, Afshar N (2019) Optimal parameter identification for the proton exchange membrane fuel cell using Satin Bowerbird optimizer. Int J Energy Res 43:8623–8632. https://doi.org/10.1002/er.4859
Eusuff M, Lansey K, Pasha F (2006) Shuffled frog-leaping algorithm: a memetic meta-heuristic for discrete optimization. Eng Optim 38:129–154. https://doi.org/10.1080/03052150500384759
Kler D, Rana KPS, Kumar V (2019) Parameter extraction of fuel cells using hybrid interior search algorithm. Int J Energy Res 43:2854–2880. https://doi.org/10.1002/er.4424
Xu S, Wang Y, Wang Z (2019) Parameter estimation of proton exchange membrane fuel cells using eagle strategy based on JAYA algorithm and Nelder–Mead simplex method. Energy 173:457–467. https://doi.org/10.1016/j.energy.2019.02.106
Funding
Open access funding provided by The Science, Technology & Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Institutional Review Board Statement
The study did not involve humans or animals.
Informed consent
The study did not involve humans.
Conflicts of interest
The authors declare no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ashraf, H., Abdellatif, S.O., Elkholy, M.M. et al. Computational Techniques Based on Artificial Intelligence for Extracting Optimal Parameters of PEMFCs: Survey and Insights. Arch Computat Methods Eng 29, 3943–3972 (2022). https://doi.org/10.1007/s11831-022-09721-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11831-022-09721-y