Beyond the Tuned Mass Damper: a Comparative Study of Passive Approaches to Vibration Absorption Through Antiresonance Assignment

Abstract

Vibration absorption is a core research area in the design and control of structures and machines, and exploiting antiresonances is an effective approach for systems under harmonic excitation. This paper proposes a comparative study and a review of the main passive techniques to antiresonance assignment proposed in the recent literature, by discussing them through some numerical examples too. The techniques discussed include the well-known Tuned Mass Damper, which has been widely developed in the literature. However, as the title reveals, great attention is paid to the methods inherited from the field of dynamic structural modification that assign antiresonances without modifying the number of degrees of freedom, by exploiting a proper modification of the system inertial and stiffness parameters. Due to higher mathematical complexity, these approaches have been less investigated in the literature although they are an effective and less invasive approach to antiresonance assignment, especially for machines. To puzzle out the complicated subject matter of antiresonances, their background and their key features are also discussed by reviewing the main theoretical results and their relationship with the assignment techniques. The paper is also enriched with several numerical examples to compare different methods and investigate the features of antiresonances. The concluding remarks of the paper bring together some open issues in this field of research and outlines some possible research directions.

1 Introduction

Vibration absorption has been attractive over the decades to control mechanical systems such as structures or machines. In the case of vibrations due to harmonic excitation, an effective approach is exploiting antiresonances, i.e. those frequencies where the system experiences no (or very small) steady-state vibration at some coordinates. One of the more discussed ways, and probably the oldest one, to perform vibration absorption is the classical tuned mass damper (TMD), also denoted as the dynamic vibration absorber (DVA). The basic and simple idea of such a passive device is that the vibrating motion of a spring-mass system forced by a harmonic excitation can be absorbed by attaching a tuned oscillator to it. This result is commonly credit to Frahm in 1909 [1], who formulated the absorber with reference to an undamped system with one degree of freedom (DOF) excited by an harmonic force. Starting from such a milestone, thousands of developments and applications have been proposed (see e.g. the review in [2,3,4]).

Vibration absorption through passive antiresonance assignment (AA) however can be also solved through the theory of inverse dynamic structural modification (DSM), i.e. methods to compute the inertial, stiffness and damping system parameters ensuring the desired dynamic response. This problem is very interesting since it can be applied both to the design of new systems, and to the optimization of existing ones. Inverse DSM is, in practice, a model-based mechanical design: dynamic models are employed and inverted to compute the optimal parameters leading to the prescribed antiresonances. In the light of this idea, vibration absorption can be achieved both through the addition of TMDs and through the modification of the system parameters. This issue will be discussed in this paper, that provides a critical discussion of the theoretical concepts on AA and of the main passive methods to perform it. A detailed discussion of the most relevant antiresonance properties, such as their existence or locations, is provided to puzzle out this complicated subject matter and to help developing effective solution methods. It should be pointed out that the goal is not just providing a list of papers available in the literature, but rather to show their applicability and help the readers to find the most suitable ones for their applications. Besides discussing the main theoretical points of the quoted methods, some numerical applications are provided, also merging ideas from different techniques.

2 Theoretical Background

2.1 Definitions

Let us consider a linear time-invariant, N-DOF, vibrating system modeled through mass ${\mathbf{M}} \in {\mathbb{R}}^{N \times N}$, stiffness ${\mathbf{K}} \in {\mathbb{R}}^{N \times N}$, and damping ${\mathbf{C}} \in {\mathbb{R}}^{N \times N}$ matrices:

$$ {\mathbf{M}}{\ddot{\mathbf{q}}}\left( t \right) + {\mathbf{C}}{\dot{\mathbf{q}}}\left( t \right) + {\mathbf{Kq}}\left( t \right) = {\mathbf{Bf}}\left( t \right) $$

(1)

${\mathbf{q}}(t) \in {\mathbb{R}}^{N}$ is the vector of the generalized, independent displacements, ${\mathbf{f}}(t) \in {\mathbb{R}}^{N}$ is the force vector and ${\mathbf{B}} \in {\mathbb{R}}^{N \times N}$ is the force distribution matrix. If the excitation force is sinusoidal ($\omega$ is its frequency and $j = \sqrt { - 1}$) the system response is written in the frequency domain as follows:

$$ \left( { - \omega^{2} {\mathbf{M}} + j\omega {\mathbf{C}} + {\mathbf{K}}} \right){\mathbf{q}}\left( {j\omega } \right) = {\mathbf{Bf}}\left( {j\omega } \right) $$

(2)

Hence, the relation between the input force and the displacement of the system is:

$$ {\mathbf{q}}\left( {j\omega } \right) = {\mathbf{H}}\left( {j\omega } \right){\mathbf{Bf}}\left( {j\omega } \right) $$

(3)

where the receptance matrix ${\mathbf{H}}(j\omega )$ is:

$$ {\mathbf{H}}\left( {j\omega } \right) = \left( { - \omega^{2} {\mathbf{M}} + j\omega {\mathbf{C}} + {\mathbf{K}}} \right)^{ - 1} $$

(4)

Let us consider the transfer function $h_{pq} (j\omega )$ from force $f_{q} (j\omega )$, applied at the q-th DOF, to the displacement of the p-th DOF, $q_{p} (j\omega )$:

$$ h_{pq} \left( {j\omega } \right) = \frac{{q_{p} \left( {j\omega } \right)}}{{f_{q} \left( {j\omega } \right)}} = \left( { - 1} \right)^{p + q} \frac{{\det \left( { - \omega^{2} {\mathbf{M}}_{{{\mathbf{\overline{q}\overline{p}}}}} + j\omega {\mathbf{C}}_{{{\mathbf{\overline{q}\overline{p}}}}} + {\mathbf{K}}_{{{\mathbf{\overline{q}\overline{p}}}}} } \right)}}{{\det \left( { - \omega^{2} {\mathbf{M}} + j\omega {\mathbf{C}} + {\mathbf{K}}} \right)}} $$

(5)

Equation (5) introduces the so-called adjunct (or adjoint) system, defined through its mass, damping and stiffness matrices, ${\mathbf{M}}_{{{\mathbf{\overline{q}\overline{p}}}}} ,\,{\mathbf{C}}_{{{\mathbf{\overline{q}\overline{p}}}}} ,\,{\mathbf{K}}_{{{\mathbf{\overline{q}\overline{p}}}}} \in {\mathbb{R}}^{(N - 1) \times (N - 1)}$ that are obtained by removing the q-th row and p-th column from the original ones. The antiresonances of $h_{pq} (j\omega )$ are the frequencies at which the numerator in Eq. (5) is null, and therefore the response of the p-th coordinate vanishes for such an excitation. Antiresonance frequencies will be henceforth denoted as $\omega_{z,i}$ ($0 \le i \le N - 1$). An antiresonance corresponds to a pair of complex and conjugate zeros in the complex plane, $z_{i} ,z_{i}^{*} = - \xi_{z,i} \omega_{z,i} \pm j\omega_{z,i} \sqrt {1 - \xi_{z,i} }$, where $\omega_{z,i}$ is the undamped antiresonance frequency and $\xi_{z,i}$ its damping ratio.

Antiresonances are therefore computed as the eigenvalues of the adjunct system:

$$ \det \left( { - \omega^{2} {\mathbf{M}}_{{{\mathbf{\overline{q}\overline{p}}}}} + j\omega {\mathbf{C}}_{{{\mathbf{\overline{q}\overline{p}}}}} + {\mathbf{K}}_{{{\mathbf{\overline{q}\overline{p}}}}} } \right) = 0 $$

(6)

An alternative formulation is inferred by formulating Eq. (6) as the eigenvalue problem of the adjunct system, by introducing the eigenvector of the adjunct system ${\mathbf{u}}_{{{\mathbf{z,i}}}} \in {\mathbb{C}}^{N - 1}$:

$$ \left( { - \omega_{z,i}^{2} {\mathbf{M}}_{{{\mathbf{\overline{q}\overline{p}}}}} + j\omega_{z,i}^{{}} {\mathbf{C}}_{{{\mathbf{\overline{q}\overline{p}}}}} + {\mathbf{K}}_{{{\mathbf{\overline{q}\overline{p}}}}} } \right){\mathbf{u}}_{{{\mathbf{z,i}}}} = {\mathbf{0}}\,\,\,{\text{with}}\,\,\,0 \le i \le N - 1 $$

(7)

In [5], the physical meaning of the eigenvector of the adjunct system ${\mathbf{u}}_{{{\mathbf{z,i}}}}$ has been explained for undamped systems. Let us consider the response of the p-th coordinate under harmonic excitation applied at the q-th coordinate. Wang demonstrated that the i-th antiresonant response mode ${\mathbf{\varphi }}_{{{\mathbf{z,i}}}}$, i.e. the vector of the steady-state displacement amplitudes under such an excitation, is

$$ {\mathbf{\varphi }}_{{{\mathbf{z,i}}}} = \left( {{\mathbf{e}}_{{\mathbf{q}}}^{T} {\mathbf{GC}}_{{\mathbf{n}}} {\mathbf{u}}_{{{\mathbf{z,i}}}} } \right)^{ - 1} {\mathbf{e}}_{{\mathbf{q}}}^{T} {\mathbf{e}}_{{\mathbf{q}}}^{{}} {\mathbf{C}}_{{\mathbf{n}}} {\mathbf{u}}_{{{\mathbf{z,i}}}} $$

(8)

where ${\mathbf{G}} = \left( {{\mathbf{K}} - \omega_{z,i}^{2} {\mathbf{M}}} \right)$, ${\mathbf{e}}_{{\mathbf{q}}}^{{}}$ is the canonical vector with all null entries except for the q-th, and ${\mathbf{C}}_{{\mathbf{n}}} \in \ker \left( {{\mathbf{e}}_{{\mathbf{p}}}^{T} } \right)$ where e_p is defined similarly to e_q. The calculation of ${\mathbf{\varphi }}_{{{\mathbf{z,i}}}}$ is performed regardless of the normalization of ${\mathbf{u}}_{{{\mathbf{z,i}}}}$. Since $\left( {{\mathbf{e}}_{{\mathbf{q}}}^{T} {\mathbf{GC}}_{{\mathbf{n}}} {\mathbf{u}}_{{{\mathbf{z,i}}}} } \right)^{ - 1} {\mathbf{e}}_{{\mathbf{q}}}^{T} {\mathbf{e}}_{{\mathbf{q}}}^{{}}$ is a scalar, then the i-th adjunct system eigenvector ${\mathbf{u}}_{{{\mathbf{z,i}}}}$ defines the relative amplitude of the steady-state displacements of the system coordinates at the i-th antiresonance frequency (obviously, the displacement at the response DOF, which is not included into ${\mathbf{u}}_{{{\mathbf{z,i}}}}$, is zero).

2.1.1 The Test-Case: Analysis of the Antiresonances for a Sample Receptance

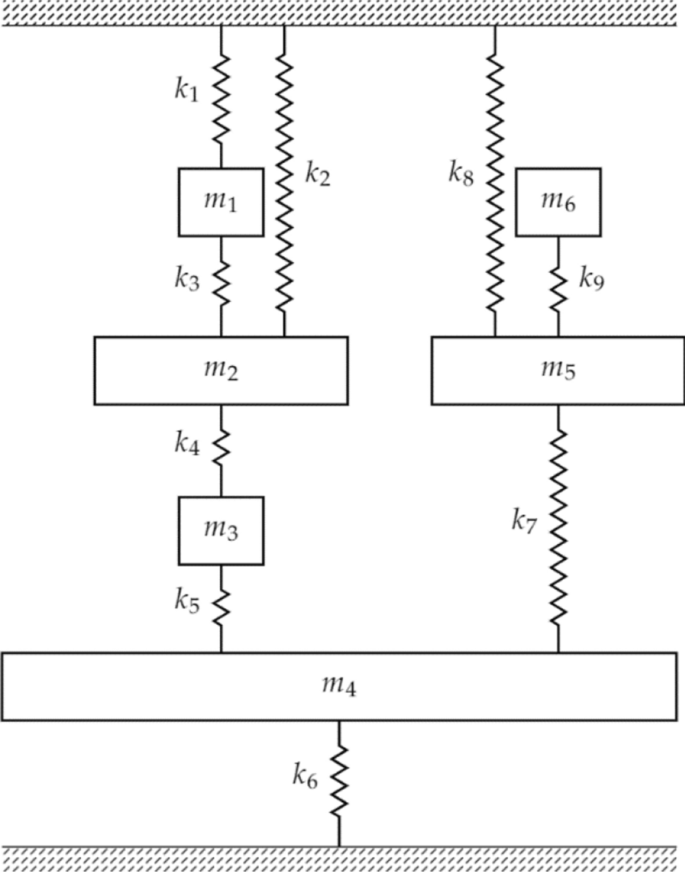
Along this paper, some numerical examples will be proposed through a common benchmark [6,7,8,9] sketched in Fig. 1. The system is made by lumped unitary masses and springs (1 kg for the masses and 1 Nm⁻¹ for the springs). The system will be modified in some sections to provide a clearer explanation of the theories therein discussed.

Fig. 1

Sketch of the six-mass system

Let us consider now, for example, h_3,3(jω). Antiresonances are shown in Table 1 and in Fig. 2. The antiresonant response, computed through Eq. (8), is shown in Fig. 3.

Table 1 Antiresonance frequencies of point-receptance h_3,3(jω)

Fig. 2

Point-receptance h_3,3(jω): magnitude

Fig. 3

Antiresonant response for all the antiresonances of h_3,3(jω)

2.2 Existence and Locations of Antiresonances

2.2.1 Point-Receptances

A key point is the existence of antiresonances. In the case of point-receptances, i.e. a receptance with the same excitation and measurement coordinates (p = q), such an issue is trivial due to ${\mathbf{M}} = {\mathbf{M}}^{T} > 0$, ${\mathbf{C}} = {\mathbf{C}}^{T} \ge 0$ and ${\mathbf{K}} = {\mathbf{K}}^{T} \ge 0$. Indeed, the adjunct system is still symmetric with positive definite or semi-positive definite matrices. Resonances and the antiresonances alternate in the frequency spectrum due to the Cauchy interlace theorem [10]. Therefore, the number of the antiresonances will be exactly N-1. It should be noted that the adjunct system can be interpreted as the original system grounded at the p-th coordinate.

2.2.2 Cross Receptances

In the case of a cross-receptance the excitation and the measurement coordinates are different (p ≠ q). Hence, Eq. (7) no longer represents a physical vibrating system. The eigenvalue problem is not self-adjoint, with asymmetric matrices that might be negative definite, and its eigenvalues can be negative or complex (even in the case of undamped systems), giving rise to complex zeros that must not be considered as antiresonances (see Sect. 2.2.4). Therefore, the number of antiresonances in cross receptances is often lower than N-1.

As a rule of thumb, as the distance between the excitation and the sensor increases, the number of antiresonances decreases [11]. This can be explained through systems modelled through a diagonal mass matrix: the degree of the polynomial $\det \left( { - \omega^{2} {\mathbf{M}}_{{{\mathbf{\overline{q}\overline{p}}}}} + j\omega {\mathbf{C}}_{{{\mathbf{\overline{q}\overline{p}}}}} + {\mathbf{K}}_{{{\mathbf{\overline{q}\overline{p}}}}} } \right)$ decreases as the difference p−q increases, since the number of not-null entries on the main diagonal of ${\mathbf{M}}_{{{\mathbf{\overline{q}\overline{p}}}}}$ decreases. Hence, the number of its possible roots decreases too. In the case of a simply-connected system, i.e. a lumped parameter system where each mass is connected at most to the two adjacent masses and to the frame, the number of antiresonances of $h_{pq} \left( {j\omega } \right)$ is $\left( {N - 1} \right) + \left( {\min \left( {p,q} \right) - \max \left( {p,q} \right)} \right)$ due to the tri-diagonal damping and stiffness matrices, and diagonal mass matrix [12].

In the general case of sparse matrices, as those of systems modeled through finite elements, a general theory about the number and the location of the antiresonances lacks. A useful rule to predict pole-zero interlacing in the low-frequency range of cross receptances has been proposed in [13, 14] for undamped systems. If the modal constants (i.e. the product of the two entries of the i-th eigenvector at the response point ${\mathbf{u}}_{{{\mathbf{r,i}}}} \left( p \right)$ and at the excitation point ${\mathbf{u}}_{{{\mathbf{r,i}}}} \left( q \right)$) of two consecutive modes have the same sign, then there will be an antiresonance $\omega_{z,i}$ between the natural frequencies of the two modes considered:

$$ {\text{sign}}\left( {{\mathbf{u}}_{{{\mathbf{r,i}}}} \left( p \right){\mathbf{u}}_{{{\mathbf{r,i}}}} \left( q \right)} \right) = {\text{sign}}\left( {{\mathbf{u}}_{{{\mathbf{r,i + 1}}}} \left( p \right){\mathbf{u}}_{{{\mathbf{r,i + 1}}}} \left( q \right)} \right)\,\,\, \Rightarrow \,\,\,\omega_{r,i} < \omega_{z,i} < \omega_{r,i + 1} $$

(9)

Intuitively, if the sign of the product of the modal coordinates (i.e. the modal constant) of two consecutive modes for an undamped system is the same, it means that the two coordinates oscillate in-phase. Since a resonance causes a phase decrease of -180°, those coordinates can oscillate in-phase once if-and-only-if an antiresonance frequency increases the phase of + 180°. Modal constants in cross-receptances tends to be positive when the input and the output coordinates are close, since low frequency modes varies slowly in space [12,13,14]. It should be noted that Eq. (9) does not always hold for high frequency modes. In the case of classically damped systems Eq. (9) still holds since the system features real mode shapes. Whenever, non-classical damping arises, if the system is lightly damped just a small phase differences between various parts of the system is introduced hence Eq. (9) can be adopted as an approximate rule.

2.2.3 Numerical Example: Comparison of Point and Cross Receptances

Let us consider the test case and let us compare h_3,3(jω) and h_6,3(jω) (that is equal to h_3,6(jω)). These receptances are the transfer functions of interest to implement collocated or non-collocated controls, respectively. In collocated control, sensor and actuator are placed in the same position, as in a point-receptance. In non-collocated control, sensor and actuator are placed in different positions, as in a cross receptance. Figure 4 shows the root-locus of the two receptances by assuming a proportional controller on the response coordinate. For clarity of representation, the system has been lightly damped in this section. The poles and the zeros alternate along the imaginary axis for h_3,3(jω); in contrast, such a feature is lost for h_6,3(jω). Consequently, h_3,3(jω) is stable for any positive gain, i.e. all the poles will lie to the left half of the complex plane (LHCP) for any positive gain. In contrast, h_6,3(jω). will feature unstable poles in the right half of the complex plane (RHCP) for some gains. This statement is corroborated by the transfer functions in Fig. 5, together with the use of the Bode stability criteria. The pole-zero interlacing is evident for h_3,3(jω), whose phase belongs to the interval [0, − 180°), hence ensuring a positive phase margin (0.313° at the cross frequency 1.060 rads⁻¹) and an infinite gain margin. In h_6,3(jω) the presence of two consecutive pair of poles decreases the phases below the threshold − 180°, thus causing negative phase margin (− 2.23°, with a cross frequency 1.260 rads⁻¹) and reduced gain margin (− 8.54 dB at the cross frequency 0.786 rads⁻¹).

Fig. 4

Comparison of the root-locus for a sample point and cross receptance

Fig. 5

Magnitude and phase comparison between h_3,3(jω) and h_6,3(jω)

Hence, a negative-feedback proportional control on h_6,3(jω) makes the system unstable; stability could be achieved through high-order or state-feedback controllers (e.g. to damp the vibrational modes for avoiding 0 dB crossings at high frequencies). This explanation corroborates the importance of antiresonance to enable stable control in vibrating systems and proves the benefits of collocated control [10].

2.2.4 Complex Zeros of Cross Receptances

Let us consider the adjunct system eigenproblem of a cross-receptance h_pq in an undamped system:

$$ \left( {z_{i} \,{\mathbf{M}}_{{{\mathbf{\overline{q}\overline{p}}}}} + {\mathbf{K}}_{{{\mathbf{\overline{q}\overline{p}}}}} } \right){\mathbf{u}}_{{{\mathbf{z,i}}}} = {\mathbf{0}} $$

(10)

Complex eigenvalues $z_{i}$ might appear in complex conjugate pairs (since $\left( {{\mathbf{M}}_{{{\mathbf{\overline{q}\overline{p}}}}} ,\,{\mathbf{K}}_{{{\mathbf{\overline{q}\overline{p}}}}} } \right)$ are real), $z_{i}^{{}} ,\,z_{i}^{*} ,\,z_{i + 1}^{{}} ,\,z_{i + 1}^{*} = \pm \xi_{z,i} \omega_{z,i} \pm j\omega_{z,i} \sqrt {1 - \xi_{z,i} }$. Unlike imaginary zeros, complex zeros in undamped systems cause no phase change, and no sharp reduction in the magnitude plot of the receptance. Hence, vibration is not eliminated [15]. Under a control perspective, these zeros have no positive effects on stability margins, and the presence of zeros in the RHCP leads to non-minimum phase systems that are difficult to control and experience undershoot. Furthermore, the sensitivity to parameter uncertainty increases in the case of complex zeros [16].

2.2.5 Numerical Example: Complex Zeros

Let us consider the test case by placing a spring k₀ connecting m₁ and m₆. h_3,5(jω) has complex zeros when 0 Nm⁻¹ < k₀ < 1 Nm⁻¹. The zeros of h_3,5(jω) for three sample values of k₀ are reported in Table 2, showing that the complex zeros ± 0.151 ± 1.286j appears when k₀ = 0.1 Nm⁻¹. Additionally, since the numerator of h_3,5(jω) is a 3rd degree polynomial with respect to $\lambda = - \omega^{2}$, $\det \left( {\lambda {\mathbf{M}}_{{{\mathbf{\overline{q}\overline{p}}}}} + {\mathbf{K}}_{{{\mathbf{\overline{q}\overline{p}}}}} } \right) = \lambda^{3} + 6.2\,\lambda^{2} + 11\,\lambda + 6.1$, two antiresonances vanish.

Table 2 Zeros of receptance h_3,5(jω) for different values of k₀

The magnitude and the phase of h_3,5(jω) with k₀ = 0.1 Nm⁻¹ is shown in Fig. 6: the purely imaginary zero is clearly an antiresonance frequency, i.e. it has a sharp notch at such frequency (1.907 rads⁻¹). In contrast, the four complex zeros (1.135 rads⁻¹) just lead to a slight reduction in the receptance magnitude (as highlighted by the dotted vertical line) while the phase is unchanged.

Fig. 6

Cross-receptance h_3,5(jω): magnitude, k₀ = 0.1 Nm⁻¹

2.3 Sensitivity of Antiresonances to Parameter Variations

Sensitivity is a useful tool to understand which model variables have no or negligible impact on antiresonances. This is useful to identify which are the best design variables that impose require small modifications in DSM. On the other hand, a lower sensitivity means that uncertainty on such a parameter will marginally affect the prediction of the antiresonance frequency provided by the numerical model or makes such a frequency robust to variation of the parameter under investigation.

The sensitivity of an antiresonance frequency with respect to an arbitrary parameter x (e.g. a mass or a stiffness) is computed through the relation proposed in [17] for undamped systems:

$$ \frac{{\partial \omega_{z,i}^{2} }}{\partial x} = \frac{{{\mathbf{w}}_{{{\mathbf{z,i}}}}^{T} \left( {\frac{{\partial {\mathbf{K}}_{{{\mathbf{\overline{q}\overline{p}}}}} }}{\partial x} - \omega_{z,i}^{2} \frac{{\partial {\mathbf{M}}_{{{\mathbf{\overline{q}\overline{p}}}}} }}{\partial x}} \right){\mathbf{u}}_{{{\mathbf{z,i}}}} }}{{{\mathbf{w}}_{{{\mathbf{z,i}}}}^{T} {\mathbf{M}}_{{{\mathbf{\overline{q}\overline{p}}}}} {\mathbf{u}}_{{{\mathbf{z,i}}}} }}, $$

(11)

${\mathbf{u}}_{{{\mathbf{z,i}}}}$ and ${\mathbf{w}}_{{{\mathbf{z,i}}}}^{{}}$ are respectively the right and left eigenvectors related to the i-th eigenvalue of the adjunct system.

A different formulation of sensitivity is provided in [6] for undamped systems, without using the system matrices, i.e. by writing sensitivity as a linear combination of natural frequencies and mode-shapes sensitivities. Such a formula also reveals that the sensitivities of the nearest eigenvalues and eigenvectors are the leading contributors to the antiresonance sensitivity.

2.3.1 Numerical Example: Antiresonance Sensitivities

The sensitivity analysis of the antiresonance of h_3,3(jω), with respect to the mass and stiffness parameters of the example (with the original parameters stated in Sect. 2.1.1) is shown in Table 3.

Table 3 Antiresonance frequencies sensitivities of h_3,3(jω)

Let us discuss, for example, the effect of m₁: it just affects the second and the fourth antiresonance frequencies while the remaining ones are unchanged by variations of m₁. A particular situation arises for m₃: since the adjunct system for h_3,3(jω) is obtained by grounding the motion of such mass, any modification of m₃ does not affect all its antiresonance frequencies.

3 AA Through Dynamic Vibration Absorbers and TMDs

3.1 The Frahm’s Dynamic Absorber

In the following of the paper, as usually done in the literature too [18,19,20], DVA and TMD will be used as synonyms. As already mentioned in the Introduction, the basic idea of the TMD is that the vibrating motion of a spring-mass system forced by a harmonic excitation can be absorbed by attaching a tuned oscillator to it. In the formulation proposed by Frahm [1], the absorber is developed with reference to an undamped, single-DOF system excited by an harmonic force (with arbitrary amplitude F₀ and known frequency ω_f). Additionally, he neglected damping of the spring connection between the TMD and the primary system, as sketched in Fig. 7. The equation of motion is:

$$ \left[ {\begin{array}{*{20}c} m & 0 \\ 0 & {m_{a} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\ddot{q}\left( t \right)} \\ {\ddot{q}_{a} \left( t \right)} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {k + k_{a} } & { - k_{a} } \\ { - k_{a} } & {k_{a} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {q\left( t \right)} \\ {q_{a} \left( t \right)} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {F_{0} \sin (\omega_{f} t)} \\ 0 \\ \end{array} } \right\} $$

(12)

Fig. 7

Sketch of the single DOF TMD

The absorber is tuned in such a way that $\omega_{f} = \sqrt {\frac{{k_{a} }}{{m_{a} }}}$, where k_a and m_a are the stiffness of the connection spring and the absorber mass to be chosen. Since there is no energy dissipation in the primary system, vibration is completely confined to the mass of the absorber. The larger the absorber mass is, and the smaller its oscillations are, since $q_{a} \left( t \right) = - \frac{m}{{m_{a} }}\frac{{F_{0} }}{k}\sin (\omega_{f} t)$. Larger absorber masses, although difficult to implement, have another advantage: increasing the mass ratio $\mu = \frac{{m_{a} }}{m}$ shifts the resonance frequency away from ω_f, by increasing the TMD robustness as the excitation frequency differs from the nominal one. Fig. 8 shows the effect of $\mu$ on the amplitude of the primary system. The capability to absorb vibrations quickly degrades as the excitation frequency differs from the nominal one. On the other hand, the presence of damping either in the primary or in the secondary system, downgrades the absorber effectiveness too.

Fig. 8

Influence of the mass ratio on the amplitude of the response of the primary system: m = 1, k = 1, ω_f = ω₀

4 Research Developments on Passive TMDs

Some of the main achievements and issues of passive TMDs are here briefly discussed. Based on the structure and the number of DOFs, three classes can be defined:

• • Single TMDs (TMD): the auxiliary system has a single-DOF (SDOF) and is composed by a mass, a damper and a spring.

• • Multiple TMDs (MTMD): the auxiliary system is composed by more masses, dampers and springs, attached at one point of a SDOF or MDOF primary system.

• • Spatially distributed TMDs (D-MTMD): the auxiliary system is composed by more masses, dampers and springs, with several attachment point to the multi-DOF (MDOF) primary system.

Another classification of TMDs could be done based on the motion of the added coordinates. While “traditional” TMDs are made by translational masses, rotational inertias have been less frequently proposed (see e.g. [21]), although rotational inertias can be effective with small devices. Pendulum TMDs have been proposed too (see e.g. [22, 23]).

The performances of TMDs have been improved recently through the implementation of inerters, to be placed in parallel or in series with the spring-damper arrangement of the TMD to improve the dynamic response and the bandwidth of TMDs, leading to the TMD Inerter (TMDI). Inerters are mechanical devices where the forces applied at their terminals are proportional to the relative acceleration between them [24], thus leading to a virtual mass amplification [25]. The TMDI has been introduced in [26] with three different configurations and the optimal parameters are derived through a global optimization routine. Three different methodologies for the design of TMDI have been proposed in [27]. The analytical solutions for the design of the TMDI with different inerter configurations have been obtained in [28] exploiting the invariant points theory.

Most of the works proposed linear TMDs applied to linear primary systems. Some extensions have been proposed through nonlinear TMDs, usually to cope with nonlinearities in the primary system or to exploit nonlinearities in the auxiliary system (e.g. [29,30,31]). A review is proposed in [32].

4.1 The Single-DOF TMD

To increase the range of frequencies where the absorber is effective, i.e. reducing its sensitivity, a viscously damped spring-mass system can be exploited as a TMD. This has been proposed by Ormondroyd and Den Hartog [33, 34]. The key point is that there are two invariant frequencies of the system response that do not depend on damping, see Fig. 9. Starting from such an observation, analytical expressions of the damper design parameters has been proposed for both the case of mass and base excitation of the primary system (ω₀ is the frequency of primary system without TMD, and $\xi_{d}$ is the damping ratio of the TMD alone, assumed as grounded):

$$ \frac{{\omega_{f} }}{{\omega_{0} }} = \left\{ {\begin{array}{*{20}l} {\frac{1}{1 + \mu }} \hfill & {{\text{(mass}}\,{\text{excitation)}}} \hfill \\ {\frac{1}{1 + \mu }\left( {\sqrt {\frac{2 - \mu }{2}} } \right)} \hfill & {{\text{(base}}\,{\text{excitation)}}} \hfill \\ \end{array} } \right. \quad \xi_{d} = \left\{ {\begin{array}{*{20}l} {\sqrt {\frac{3\mu }{{8\left( {1 + \mu } \right)}}} } \hfill & {{\text{(mass}}\,{\text{excitation}})} \hfill \\ {\sqrt {\frac{3\mu }{{8\left( {1 + \mu } \right)}}} \left( {\sqrt {\frac{2}{2 - \mu }} } \right)} \hfill & {{\text{(base}}\,{\text{excitation)}}} \hfill \\ \end{array} } \right. $$

(13)

Fig. 9

Invariant points on the amplitude of the response of the primary system: m = 1, k = 1, ω_f = ω₀, μ = 0.05

For example, by tuning ω_f accordingly to Eq. (13) it is possible to obtain invariant points with the same amplitude while $\xi_{d}$ is varying, as reported in Fig. 10.

Fig. 10

Invariant points with the same amplitudes: m = 1, k = 1, ω_f = ω₀/(1 + μ), μ = 0.05

The basic theory of Den Hartog is effective if the original system is undamped or lightly damped. As damping increases, invariant points do not exist anymore. Therefore, the parameters in Eq. (13) are no more optimal. Several improvements of Eq. (13) have been proposed to minimize different performance indexes. A comparison of different definition of the optimal ω_f/ω₀ and $\xi_{d}$ for lightly damped SDOF primary systems is proposed in [35] and here summarized in Table 4.

Table 4 Tuning methods for the SDOF-TMD: comparison

Other methods have been developed through approximate solutions usually obtained solving optimization problems. Just to mention some examples, an approach based on the frequency locus has been adopted in [41, 42] to minimize the vibration of the primary system over the whole range of exciting frequencies, while reducing the oscillation of the auxiliary mass of the absorber. A non-linear programming technique is exploited in [43] to minimize the maximum displacement of the primary system, as well as the maximum speed under white noise excitation. In [44], several goal functions over narrow and broad frequency bands are examined, to minimize the absolute or relative displacements, the mass ratio m, or maximize the broadness of the band of attenuation of vibrations. A numerical searching procedure is exploited in [45] to design a TMD for a damped primary system. The authors demonstrated that the higher is the damping on the primary system and the less effective the TMD is in attenuating vibrations.

Four fundamental design topologies have been proposed over the decades for the TMD and here summarized in Table 5. The vibration absorbers are classified first with respect to the main system damping leading respectively to TMDs for US (Undamped main System) or DS (Damped main System). Further, another classifier is related to the position of the absorber dashpot with respect to the absorber mass, leading to the so-called V-TMD (Variant TMD) [46] if the damper is located between the absorber mass and the ground.

Table 5 Topologies of the SDOF-TMD: summary

4.2 Multiple TMDs for Single-DOF Systems

Other arrangements of the classical TMD have been proposed to increase robustness and effectiveness by introducing multiple oscillators to a SDOF primary system. In [53] and [54] the idea of Multiple TMDs (MTMD) is introduced. MTMD consist of more single-DOF oscillators attached to the original system, whose natural frequencies are distributed around the natural frequency of a controlled mode of the structure. A sketch of a MTMD is proposed in Fig. 11a in its parallel topology. Series topologies, as sketched in Fig. 11b, have been proposed too (see e.g. [55]). Clearly, increasing the number of DOFs of the TMD enlarges the achievable performances and allows handling several secondary tasks. Design of MTMDs has been therefore often solved through multi-objective optimization (see e.g. [54] and [56]), also including stochastic representation of the disturbances (see e.g. [55, 57, 58]).

Fig. 11

Sketch of a MTMD: parallel topology (a), series topology (b)

4.3 TMDs for Multi-DOF Systems

The extension of the TMD to MDOF primary systems has been proposed too. In [59] a similar approach as the one of Den Hartog for SDOF systems, is extended to undamped MDOF primary systems, and the optimal absorber location, stiffness and damping are then obtained. It is also proved that the invariant points, defined by Den Hartog, still exist.

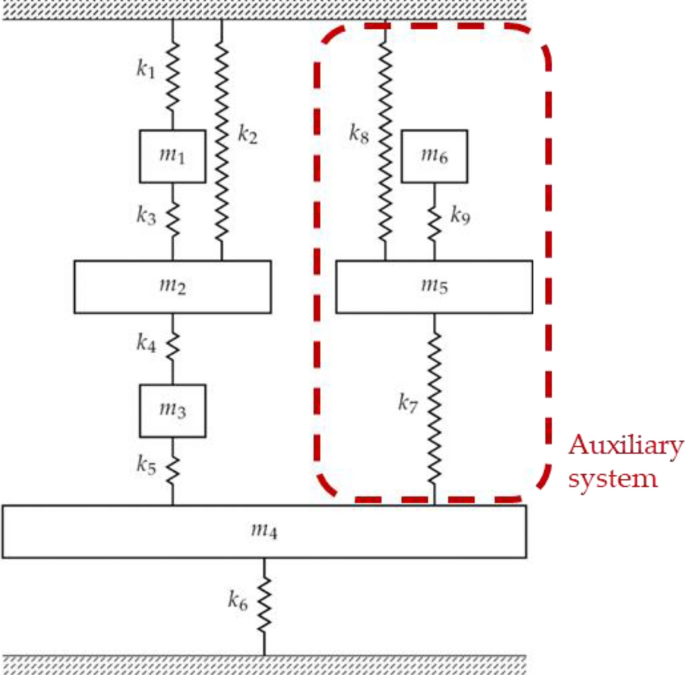
The MDOF TMD has been generalized by Ram and Elhay [60] for both SDOF and MDOF original systems, with MDOF attached auxiliary systems. Let us consider a simply connected vibratory system, the so-called primary system, and suppose that the forced response of the N-th mass to some harmonic excitations ω_f,i (i = 1,…,n_f) should be absorbed. Let us suppose that a N_a-DOF simply-connected system (the secondary system) is attached to the primary one by linking it, without loss of generality, to mass N through a spring (Fig. 12). Let N_a be not smaller than the number of harmonic forces to be absorbed. The meaningful results proved in [60] is that the natural frequencies of the secondary system (obtained assuming fixed boundary constraint at the point of attachment to the original system) are antiresonance frequencies from the forces applied to any DOF of the primary system, to the response of mass N. Hence, at those frequencies, one line and one row of the receptance matrix of the primary system are 0. The design of the suitable masses and springs of the secondary systems is an eigenvalue assignment problem to be solved with state-of-the-art methods. Indeed, paper [60] does not discuss the computational issues of finding the value of masses and springs. The numerical example in Sect. 3.5.1 will provide a deeper insight on this powerful theory, by suggesting a new solution method to the assignment problem.

Fig. 12

Sketch of a primary system with attached a MDOF TMD

Beyond the general theory in [60], MTMDs have been employed in the last decades by several researchers to cope with different tasks. For example, a graphical approach to the design of MTMD to suppress multiple modes have been recently proposed in [61]. In [62], D-MTMDs are exploited to improve the response of a bridge-like structure when it is affected by moving loads. A method to simultaneously tune mass and stiffness of D-MTMD with arbitrary topology, together with the modifications of the parameters of the primary system, is proposed in [63], by exploiting numerical minimization. This method will be discussed in Sect. 4.4.

4.3.1 Numerical Example: Design of a MDOF TMD

Let us assume that the six-mass system is composed by a primary system composed by just masses m₁, m₂, m₃, m_4, and that the subsystem made by m₅, m₆ must be designed to be a simply connected MDOF-TMD for the primary system, as sketched in Fig. 13.

Fig. 13

The sample four-mass system with highlighted its auxiliary system

The assignment of two antiresonances at 0.500 rads⁻¹ and 1.500 rads⁻¹ for all the receptances h_i,4(jω), i = 1,…,4, is performed. As discussed in Sect. 3.5, such antiresonances $\omega_{z,i}^{d}$ will be the resonances of the auxiliary subsystem alone (and grounded), i.e. the solve the following equation

$$ \det \left( { - \left( {\omega_{z,i}^{d} } \right)^{2} \left( {{\mathbf{M}}_{{{\mathbf{5:6}}}} + {\mathbf{\Delta M}}_{{{\mathbf{5:6}}}} } \right) + {\mathbf{K}}_{{{\mathbf{5:6}}}} + {\mathbf{\Delta K}}_{{{\mathbf{5:6}}}} } \right) = 0 $$

(14)

where ${\mathbf{M}}_{{{\mathbf{5:6}}}}$ and ${\mathbf{K}}_{{{\mathbf{5:6}}}}$ are respectively the mass and stiffness matrices of the subsystem composed by auxiliary system itself and ${\mathbf{\Delta M}}_{{{\mathbf{5:6}}}}$, ${\mathbf{\Delta K}}_{{{\mathbf{5:6}}}}$ are the modification matrices employed to assign the prescribed antiresonance frequencies. Besides solving Eq. (14), antiresonances can be also assigned by solving the following eigenproblem (with ${\mathbf{u}}_{{{\mathbf{r,i}}}}$ as the eigenvector):

$$ \left( { - \left( {\omega_{z,i}^{d} } \right)^{2} \left( {{\mathbf{M}}_{{{\mathbf{5:6}}}} + {\mathbf{\Delta M}}_{{{\mathbf{5:6}}}} } \right) + {\mathbf{K}}_{{{\mathbf{5:6}}}} + {\mathbf{\Delta K}}_{{{\mathbf{5:6}}}} } \right){\mathbf{u}}_{{{\mathbf{r,i}}}} = 0 $$

(15)

Two examples are proposed in this Section. The resulting parameter modifications are reported in Table 6 and the antiresonances are listed in Table 7.

Table 6 DSM parameters in different tests

Table 7 Auxiliary system resonance frequencies before and after the modifications in different tests

In the first test proposed it is assumed that just ${\mathbf{\Delta M}}_{{{\mathbf{5:6}}}}$ is allowed, with “large” constraints, and ${\mathbf{\Delta K}}_{{{\mathbf{5:6}}}}$ is set to zero. Indeed, due to the difficulties in solving Eq. (14), only mass modifications have been assumed in the numerical example in [60]. The test has been here also solved through Eq. (15) and through the method proposed in [64] for assigning natural frequencies. It should be noted that the present paper provides the first application of such a method within the frame of the MDOF-TMD proposed by Ram and Elhay and is therefore another contribution of this paper.

A second test including stiffness modification is also proposed, to cope with tighter constraints on the allowable mass modifications that does not allow obtaining the desired antiresonances with just two design parameters. The use of more design parameters, and the availability of numerical methods, are of primary importance to tackle tight constraints. The test has been solved just through Eq. (15) and the method in [64]; the benefits of exploiting numerical solutions are evident.

The analysis of the receptance matrices of the primary system evaluated at the assigned antiresonance frequencies, i.e. ${\mathbf{H}}_{{{\mathbf{1:4}},\bmod }}^{{}} \left( {j\omega } \right)$, shows that they that have a line and a column of zero, as expected:

$$ {\mathbf{H}}_{{{\mathbf{1:4}},\bmod }}^{{}} \left( {0.5\,\frac{{{\text{rad}}}}{s}} \right) = \left[ {\begin{array}{*{20}c} {{0}{\text{.775}}} & {{0}{\text{.356}}} & {{0}{\text{.203}}} & 0 \\ {{0}{\text{.356}}} & {{0}{\text{.622}}} & {{0}{\text{.356}}} & 0 \\ {0.203} & {0.356} & {0.775} & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right]\qquad {\mathbf{H}}_{{{\mathbf{1:4}},\bmod }}^{{}} \left( {1.5\,\frac{{{\text{rad}}}}{s}} \right) = \left[ {\begin{array}{*{20}c} { - 2.171} & { - 0.457} & {1.829} & 0 \\ { - 0.457} & {{0}{\text{.114}}} & { - 0.457} & 0 \\ {1.829} & { - 0.457} & { - 2.171} & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right] $$

(16)

4.4 Discussion on the Attachment Location of TMDs

A proper choice of the attachment location is crucial for ensuring effectiveness of the TMD in MDOF primary systems. A widespread approach [65] states that the optimal TMD attachment location corresponds to the coordinate where the i-th mode shape, i.e. the one that mostly participates to the system response, attains its maximum value. This simplified approach is usually named the “single mode approach” and provides effective placement when using absorbers with adequately small mass and when the primary system eigenfrequencies are well separated.

The “single-mode approach” effectiveness decreases for systems with closely spaced natural frequencies and large absorber mass as demonstrated in [66] in the case of weakly coupled systems. In the light of this limitation, a great contribution is provided in [67], where the attachment location of the TMD is discussed by evaluating the shift in the eigenfrequencies of the modified system caused by the introduction of the TMD as sketched for a sample system in Fig. 14. For a given absorber mass, the device is placed in the location that ensures the largest spectral gap (also called as frequency shift), i.e. the distance between the i-th resonant mode ($\omega_{r,i}$) and the new i-th and (i + 1)-th eigenfrequency close to this mode, respectively $\hat{\omega }_{r,i}$ and $\hat{\omega }_{r,i + 1}$. Let us consider an undamped MDOF primary system with attached an SDOF TMD at the a-th DOF. The modified system receptance matrix is:

$$ {\hat{\mathbf{H}}}\left( {j\omega } \right) = \left( { - \omega^{2} {\mathbf{M}} + {\mathbf{K}} - {\mathbf{e}}_{{\mathbf{a}}}^{{}} \omega^{2} g\left( {j\omega } \right){\mathbf{e}}_{{\mathbf{a}}}^{T} } \right)^{ - 1} $$

(17)

Fig. 14

Neighborhood natural frequencies in a system: (a) without and (b) with the TMD

where $g\left( {j\omega } \right)$ is the transfer function describing the dynamic of the TMD:

$$ g\left( {j\omega } \right) = \frac{{m_{a} \left( {k_{a} + j\omega c_{a} } \right)}}{{ - m_{a} \omega^{2} + j\omega c_{a} + k_{a} }} $$

(18)

The point receptance at the TMD attachment point is:

$$ {\mathbf{e}}_{{\mathbf{a}}}^{T} {\hat{\mathbf{H}}}\left( {j\omega } \right){\mathbf{e}}_{{\mathbf{a}}}^{{}} = \frac{{{\mathbf{e}}_{{\mathbf{a}}}^{T} {\mathbf{H}}\left( {j\omega } \right){\mathbf{e}}_{{\mathbf{a}}}^{{}} }}{{1 - \omega^{2} g\left( {j\omega } \right){\mathbf{e}}_{{\mathbf{a}}}^{T} {\mathbf{H}}\left( {j\omega } \right){\mathbf{e}}_{{\mathbf{a}}}^{{}} }} $$

(19)

The new eigenfrequencies are obtained by solving the roots of the denominator of Eq. (19), i.e. the characteristic polynomial.

The largest spectral gap, $\left| {\hat{\omega }_{r,i + 1} - \hat{\omega }_{r,i} } \right|$, ensures a vibration mitigation of the entire structure within the frequency range that spans from $\hat{\omega }_{r,i}$ to $\hat{\omega }_{r,i + 1}$, regardless of the location of the excitation force. Furthermore, when the new antiresonance ω_z is created through the absorber, the distance between ω_z and the resonance of the modified system that is closest to ω_z should be as large as possible This placement allows for higher robustness of performances by ensuring that small changes in the excitation frequency do not excite vibrational modes close to the antiresonance. Eq. (19) highlights that for $m_{a} \to \infty$ the new natural frequencies are equal to the antiresonances of the point-receptance ${\mathbf{e}}_{{\mathbf{a}}}^{T} {\mathbf{H}}\left( {j\omega } \right){\mathbf{e}}_{{\mathbf{a}}}^{{}}$ (as shown by the direction of the arrows in Fig. 14), hence the maximum spectral gap is limited by the neighboring antiresonances since the flipping of natural frequencies with antiresonances is impossible due to the pole-zero interlacing property of point-receptances (see Sect. 2.2).

The development of the denominator in Eq. (19) through different approximations of ${\mathbf{H}}\left( {j\omega } \right)$ explains the “single-mode approach” in term of spectral gap [67]. Under the approximation of ${\mathbf{H}}\left( {j\omega } \right)$ through one mode, the characteristic polynomial is written as:

$$ 1 - m_{a} \frac{{\omega_{z}^{2} \omega^{2} }}{{\omega_{z}^{2} - \omega^{2} }}\frac{{\left( {{\mathbf{u}}_{{{\mathbf{r,i}}}} \left( a \right)} \right)^{2} }}{{\omega_{r,i}^{2} - \omega^{2} }} = 0 $$

(20)

Hence, fixed m_a, the largest spectral gap from $\omega_{r,i}$ is achieved for the maximum value of $\left( {{\mathbf{u}}_{{{\mathbf{r,i}}}} \left( a \right)} \right)^{2}$. If ${\mathbf{H}}\left( {j\omega } \right)$ is represented through the contributions of all the modes, as in the “multi-mode approach” [67], the characteristic polynomial becomes:

$$ 1 - m_{a} \frac{{\omega_{z}^{2} \omega^{2} }}{{\omega_{z}^{2} - \omega^{2} }}\sum\limits_{k = 1}^{m} {\frac{{\left( {{\mathbf{u}}_{{{\mathbf{r,k}}}} \left( a \right)} \right)^{2} }}{{\omega_{r,k}^{2} - \omega^{2} }}} = 0 $$

(21)

Hence, as demonstrated in [67], the performances of the absorber are improved by choosing an attachment location characterized by a “low activity” on the neighborhood modes ${\mathbf{u}}_{{{\mathbf{r,i - 1}}}} \left( a \right)$ and ${\mathbf{u}}_{{{\mathbf{r,i + 1}}}} \left( a \right)$, besides obtaining “high activity” on the targeted mode. The method still holds for lightly damped systems.

5 Passive Modifications Preserving the Number of DOFs

5.1 Advantages and Disadvantages

There are often some limitations of TMDs due to their practical implementation [68]. Attaching an external structure at a prescribed DOF could be technically infeasible, e.g. because of the size or due to the inaccessibility of the coordinates of interest. Furthermore, introducing a TMD introduces new resonances that may interfere with other excitation frequencies if not properly accounted for. Finally, the masses of the TMD might have large oscillations.

In the light of these issues, a different approach is performing AA by just modifying the existing DOF properties, without changing their number. This idea has been widely adopted for assigning mode shapes and eigenfrequencies (see e.g. [69,70,71]) and lies within the field of dynamic structural modifications. In contrast, it has been less adopted for antiresonances. The main advantage of this approach is that it is simpler under a technical point of view, since it usually relies on just adding (or removing, if possible) masses and springs. This approach can be also seen in the frame of the optimal design of new systems. For example, wise mass distribution can be chosen at the early stage of the design to obtain the desired antiresonances.

The use of this approach is therefore attractive in the case of machines, where layout constraints often do not allow using TMDs. In contrast, it could be difficult to implement in the field of civil engineering, where TMDs have gained more attention. On the other hand, assigning antiresonances without adding new DOFs has some limitations. First, TMDs set to zero one column and one row of the receptance matrix of a multi-DOF system at the tuned frequency, thus achieving vibration absorption for all its coordinates. In contrast, antiresonance is create just for one or a few receptances if no DOFs are added. Additionally, it is sometimes difficult to create new antiresonances, due to constraints on the feasible modifications, and therefore this approach is more effecting in shifting the existing ones. Finally, the assignment of more antiresonance frequencies is a challenging mathematical problem, as discussed in Sects. 4.3 and 4.4. For this reason, less solutions have been proposed in the literature and no review papers have been proposed in the literature.

A first distinction of the possible approaches, that is typical of techniques for DSM ([70]) is between direct and inverse approaches. Direct approaches to AA estimate the effect of some assumed parameter modifications on the antiresonances. Inverse approaches, in contrast, compute the suitable modifications to obtain the desired antiresonances. Clearly, inverse approaches have attracted attentions of researchers in this field: on the one hand they have a greatest practical interest. On the other one, they are more challenging and hence impose wise problem formulations and solutions to handle their ill-posed nature and the difficulties in solving them. In practice, sometimes multiple solutions are possible while sometimes no solution exists. Inverse DSM is a model-based mechanical design ([72]) where dynamic models are inverted to compute the optimal parameters leading to the prescribed antiresonances.

Based on the number of modifications allowed, the methods can be basically classified in the two groups:

• Rank-one modification:

• Higher-rank modifications.

Based on the formulation adopted, the methods can be classified in the following groups:

• Receptance-based methods.

• Methods based on the system matrices.

• Methods based on the sensitivity analysis.

Under a computational point of view, the methods can be classified in the two following groups:

• Analytical methods, that have been developed to solve simpler problems, such as rank-one modifications, without accounting for the presence of constraints on the feasible modifications.

• Numerical methods, that exploit iterative algorithms (such as numerical optimization) to solve more complicate problems (such as higher-rank modifications or multiple assignment) and to handle constraints on the feasible modifications.

A method summary is provided in Table 8.

Table 8 Passive AA techniques preserving the number of DOFs, existing papers comparison

5.2 Rank-One Modifications

The term “rank-one modification” (or “unit-rank modification”) is used to represent the addition and removal of grounded springs (or dampers), springs (or dampers) connecting two DOFs or lumped masses [74, 76, 77].

In the case of a grounding spring modification, [73] introduced a closed-form formula:

$$ k_{g} = - \frac{{\det \left( { - \omega_{z}^{2} {\overline{\mathbf{M}}} + {\overline{\mathbf{K}}}} \right)}}{{\det \left( { - \omega_{z}^{2} {\tilde{\mathbf{M}}} + {\tilde{\mathbf{K}}}} \right)}} $$

(22)

which enables to determine the value of the stiffness k_g attached at the (N-1)-th DOF that enables to absorb the vibration of the N-th DOF of an undamped system excited by an harmonic force at the same coordinate, i.e. for a point-receptance. $\left( {{\overline{\mathbf{M}}},{\overline{\mathbf{K}}}} \right)$ and $\left( {{\tilde{\mathbf{M}}},{\tilde{\mathbf{K}}}} \right)$ are respectively the (N-1)x(N-1) and (N-2)x(N-2) leading sub-matrices of $\left( {{\mathbf{M}},{\mathbf{K}}} \right)$. Clearly, the obtained stiffness is suitable for structural modification if and only if k_g > 0 otherwise active approaches need to be exploited to achieve the AA. Further, the method is effective only for undamped or lightly damped systems.

The general equation of a rank-one modification have been introduced in [74, 77]. Let us consider the modification at the r-th DOF, which is $\Delta g_{r} \left( \sigma \right) = \sigma^{2} m_{r} + \sigma c_{r} + k_{r}$, where m_r, c_r, k_r are respectively a lumped mass, a grounding damper and a grounding spring while $\sigma = j\omega$. The receptance $\hat{h}_{pq} \left( \sigma \right)$ of the modified system, for any p and q, is therefore:

$$ \hat{h}_{pq} \left( \sigma \right) = \frac{{h_{pq} \left( \sigma \right) + \Delta g_{r} \left( \sigma \right)\left( {h_{pq} \left( \sigma \right)h_{rr} \left( \sigma \right) - h_{pr} \left( \sigma \right)h_{rq} \left( \sigma \right)} \right)}}{{1 + \Delta g_{r} \left( \sigma \right)h_{rr} \left( \sigma \right)}}. $$

(23)

The i-th zero of the system after modifications, $z_{i}$, are inferred from the numerator of Eq. (23). Therefore, the suitable value of $\Delta g_{r}$ can be easily computed. A zero of a cross-receptance (p ≠ q, with r ≠ p,q) can be assigned through the following equation:

$$ \frac{1}{{ - \Delta g_{r} \left( {z_{i} } \right)}} = h_{rr} \left( {z_{i} } \right) - \frac{{h_{pr} \left( {z_{i} } \right)h_{rq} \left( {z_{i} } \right)}}{{h_{pq} \left( {z_{i} } \right)}}. $$

(24)

A zero of a point-receptance (p = q, with r ≠ p,q) can be assigned through the following equation:

$$ \frac{1}{{ - \Delta g_{r} \left( {z_{i} } \right)}} = h_{rr} \left( {z_{i} } \right) - \frac{{h_{rq}^{2} \left( {z_{i} } \right)}}{{h_{qq} \left( {z_{i} } \right)}} $$

(25)

The use of Eqs. (24) and (25) in the case of damped system might leads to complex $\Delta g_{r} \left( {z_{i} } \right)$, meaning that damping should be modified too. Indeed, imaginary parts represent the damping modification. Although neglecting such a term causes small shifts of the zero frequency, due to the difficulties in precisely changing damper properties, it is usually neglected in most practical applications, as stated by the Mottershead and Ram themselves in [77].

The strength of this method is that it just requires a few data. In the case of a cross-receptance, it just needs the measure of four receptances of the original system at the frequency of the desired zero. In the case of a point-receptance, just three measures are needed. Additionally, it proves that the minimum number of modifications required to assign one antiresonance is one. On the other hand, it cannot be always adopted if constraints on the feasible modifications are included. In this case, a proper “mix” of the modifications of more parameters overcomes the fact that the solution of Eqs. (24) and (25) is outside the feasible constraints. Multiple assignment cannot be handled too.

Mottershead et al. in [76] extended the idea of receptance based assignment by considering the case of a modification connecting two coordinates r and s. In this case, the unit rank modification is $\Delta g_{rs} \left( \sigma \right) = \sigma c_{rs} + k_{rs}$ and modified system receptance $\hat{h}_{pq} \left( \sigma \right)$ is:

$$ \hat{h}_{pq} \left( \sigma \right) = h_{pq} \left( \sigma \right) - \frac{{\Delta g_{rs} \left( \sigma \right)\left( {h_{pr} \left( \sigma \right) - h_{ps} \left( \sigma \right)} \right)\left( {h_{rq} \left( \sigma \right) - h_{sq} \left( \sigma \right)} \right)}}{{1 + \Delta g_{rs} \left( \sigma \right)\left( {h_{rr} \left( \sigma \right) - h_{rs} \left( \sigma \right) - h_{sr} \left( \sigma \right) + h_{ss} \left( \sigma \right)} \right)}} $$

(26)

Then, by exploiting the theory of the “Vincent’s circle” [82], vibration absorption for a prescribed $\hat{h}_{pq} \left( {\omega_{f} } \right)$ is translated into shifting the Vincent’s circle in such a way that it passes through the origin of the complex plane (or as close as possible) by modifying $k_{rs}$ and $c_{rs}$. Analytical solutions are provided for unit-rank modifications [77]. In contrast, a graphical solution procedure is adopted in the case of higher-rank modifications (i.e. with more design parameters involving more coordinates). The experimental application is proposed too in [76]. The unit-rank modification exploiting passive stiffness (and also active control techniques) has been extended in [83] to perform pole-zero cancellation.

5.2.1 Numerical Example: Rank-One Modification

Let us consider the six-mass system with the original parameters. The goal is to assign an antiresonance at 1.000 rads⁻¹ on h_3,3(jω) (i.e.$z_{i} ,z_{i}^{*} = \pm j1.000$) through one of the following modifications: a lumped mass modification $\Delta m_{4}$, a lumped mass modification $\Delta m_{1}$, or by adding a grounding spring $k_{g4}$ at coordinate 4. Exploiting Eq. (25) leads to: $\Delta m_{4} = 2\,{\text{kg}}$, $\Delta m_{1} = 2\,{\text{kg}}$, $k_{g4} = - 2\,{\text{Nm}}^{{ - 1}}$. Since the spring with negative stiffness cannot be realized through passive springs, unless non-mechanical springs with particular arrangements are adopted (see e.g. [84]), such a solution is infeasible. The zeros of the original system and the ones modified through additive masses are reported in Table 9, while the receptances h_3,3(jω) are shown in Fig. 15. In the light of this issue, approaches using constraints on the feasible values (see Sect. 4.4) can be advantageous.

Fig. 15

Original and modified point-receptance h_3,3(jω): comparison for different DSMs

Table 9 Original and unit-rank modified system antiresonances for h_3,3(jω)

The results in Table 9 can be interpreted through the sensitivity analysis proposed in Sect. 2.3.1. Indeed, $\Delta m_{4}$ do not shift the antiresonance frequencies at 1.176 rads⁻¹ and 1.902 rads⁻¹ since ∂(ω_z,2)²/∂m₁ = ∂(ω_z,4)²/∂m₁ = 0. As for Δm₁, since ∂(ω_z,1)²/∂m₁ = ∂(ω_z,3)²/∂m₁ = ∂(ω_z,5)²/∂m₁ = 0 (as reported in Table 3), the first, the third and the fifth antiresonances frequencies are kept unchanged. Therefore, the antiresonance at 1.000 rads⁻¹ is placed by shifting the second one.

5.3 Receptance-Based Formulations with Higher-Rank Modifications

Given an higher rank modification ${\mathbf{\Delta G}}\left( \sigma \right) = \sigma^{2} {\mathbf{\Delta M}} + \sigma {\mathbf{\Delta C}} + {\mathbf{\Delta K}}$, the receptance matrix of the modified system becomes [77]:

$$ {\hat{\mathbf{H}}}\left( \sigma \right) = \frac{{{\text{adj}}\left( {{\mathbf{I}} + {\mathbf{H}}\left( \sigma \right){\mathbf{\Delta G}}\left( \sigma \right)} \right){\mathbf{H}}\left( \sigma \right)}}{{\det \left( {{\mathbf{I}} + {\mathbf{H}}\left( \sigma \right){\mathbf{\Delta G}}\left( \sigma \right)} \right)}}. $$

(27)

Equation (27) reveals that the receptance of the modified system can be expressed through the receptances of the original one, ${\mathbf{H}}\left( \sigma \right) = \left( {\sigma^{2} {\mathbf{M}} + \sigma {\mathbf{C}} + {\mathbf{K}}} \right)^{ - 1}$. By developing such an equation, in [78] it is demonstrated that the zeros $z_{i}$ of $h_{pq}$ after modification are the solutions of:

$$ h_{pq} \left( \sigma \right)\det \left( {{\mathbf{I}} + {\mathbf{H}}_{{{\mathbf{\overline{q}\overline{p}}}}} \left( \sigma \right){\mathbf{\Delta G}}_{{{\mathbf{\overline{q}\overline{p}}}}} \left( \sigma \right)} \right) = 0, $$

(28)

where subscript pq denotes the pq-th entry of the adjunct matrix, while ${\mathbf{H}}_{{{\mathbf{\overline{q}\overline{p}}}}} \left( \sigma \right)$ and ${\mathbf{\Delta G}}_{{{\mathbf{\overline{q}\overline{p}}}}} \left( \sigma \right)$ are obtained from matrices ${\mathbf{H}}\left( \sigma \right)$ and ${\mathbf{\Delta G}}\left( \sigma \right)$, respectively, by removing the q-th row and the p-th column. ${\mathbf{H}}_{{{\mathbf{\overline{q}\overline{p}}}}} \left( \sigma \right)$ is the receptance matrix of the adjunct system; although it has an “obscure physical meaning”, as the Authors themselves state [78], each entry of such a matrix can be obtained from the receptances of the original system and is useful for design the system modifications.

Equation (28) is a set of non-linear, non-separable, non-convex, multivariate polynomials, that involves products of many design parameters. Hence, its solution is cumbersome and should be performed numerically. For example, in [78] the design problem is solved, to assign a number n_z ≥ 1 of antiresonances $z_{i}$ by replacing it with the following minimization problem:

$$ \mathop {\min }\limits_{{\mathbf{x}}} \left\{ {\sum\limits_{i = 1}^{{n_{z} }} {\alpha_{i} \left( {\det \left( {{\mathbf{I}} + {\mathbf{H}}_{{{\mathbf{\overline{q}\overline{p}}}}} \left( {z_{i} } \right){\mathbf{\Delta G}}_{{{\mathbf{\overline{q}\overline{p}}}}} \left( {z_{i} ,{\mathbf{x}}} \right)} \right)} \right)^{2} } } \right\} $$

(29)

where α_i are the weighting coefficients. x are the design variables, i.e. the admitted modifications. The assignment of natural frequencies can be included through a similar receptance-based formulation, as proposed in the experimental application on a geared rotor-bearing system. The solver provided by function ‘‘fmincon” of Matlab has been adopted in such work. Paper [78] outlines the idea of formulating the AA through multivariate minimization-based problems. The basic idea of minimization-based approaches is that an approximate solution of the exact assignment problem might be sufficient in some cases in which the exact one does not exist or is difficult to compute. On the other hand, numerical solutions enlarge the solvable problems.

A different approach to the solution of a receptance-based formulation has been recently proposed in [9]. The technique assigns more antiresonances at multiple locations for a given force or to assign the zero displacements at a prescribed frequency. The modifications allowed consist of lumped masses or springs; in contrast, the simultaneous modification of masses and springs is not investigated. Constraints on the design variables are not accounted for. The authors, inspired by the formulation of Mottershead et al. in [8], derived a matrix equation for the general case of the attainment of zero displacement at n coordinates (arbitrary denoted through I₁,…,I_n), i.e. $\hat{q}_{{I_{1} }} = \cdots = \hat{q}_{{I_{n} }} = 0$, when several forces $f_{{j_{1} }} ,\ldots,f_{{j_{n} }}$ with the same frequency ω are applied to coordinates $j_{1} ,\ldots,j_{n}$, exploiting n grounding springs at coordinates $i_{1} ,\ldots,i_{n}$:

$${\mathbf{A\beta }} = {\mathbf{0}},$$

(30)

where:

$$ {\mathbf{A}} = \left[ {\begin{array}{*{20}c} {{\mathbf{H}}_{{\mathbf{1}}} \left( \omega \right)} & {\mathbf{0}} \\ {{\mathbf{H}}_{{\mathbf{2}}} \left( \omega \right)} & {\mathbf{I}} \\ \end{array} } \right] \in {\mathbb{R}}^{{2n \times \left( {2n + 1} \right)}} , $$

(31)

$$ {\mathbf{H}}_{{\mathbf{1}}} \left( \omega \right) = \left[ {\begin{array}{*{20}c} {h_{{I_{1} i_{1} }} } & {h_{{I_{1} i_{2} }} } & \cdots & {h_{{I_{1} i_{n} }} } & { - \left( {h_{{I_{1} j_{1} }} f_{{j_{1} }} + h_{{I_{1} j_{2} }} f_{{j_{2} }} + \cdots + h_{{I_{1} j_{n} }} f_{{j_{n} }} } \right)} \\ {h_{{I_{2} i_{1} }} } & {h_{{I_{2} i_{2} }} } & \cdots & {h_{{I_{2} i_{n} }} } & { - \left( {h_{{I_{2} j_{1} }} f_{{j_{1} }} + h_{{I_{2} j_{2} }} f_{{j_{2} }} + \cdots + h_{{I_{2} j_{n} }} f_{{j_{n} }} } \right)} \\ {} & {} & {} & \ddots & {} \\ {h_{{I_{n} i_{1} }} } & {h_{{I_{n} i_{2} }} } & \cdots & {h_{{I_{n} i_{n} }} } & { - \left( {h_{{I_{n} j_{1} }} f_{{j_{1} }} + h_{{I_{n} j_{2} }} f_{{j_{2} }} + \cdots + h_{{I_{n} j_{n} }} f_{{j_{n} }} } \right)} \\ \end{array} } \right] \in {\mathbb{R}}^{{n \times \left( {n + 1} \right)}} , $$

(32)

$$ {\mathbf{H}}_{{\mathbf{2}}} \left( \omega \right) = \left[ {\begin{array}{*{20}c} {h_{{i_{1} i_{1} }} } & {h_{{i_{1} i_{2} }} } & \cdots & {h_{{i_{1} i_{n} }} } & { - \left( {h_{{i_{1} j_{1} }} f_{{j_{1} }} + h_{{i_{1} j_{2} }} f_{{j_{2} }} + \cdots + h_{{i_{1} j_{n} }} f_{{j_{n} }} } \right)} \\ {h_{{i_{2} i_{1} }} } & {h_{{i_{2} i_{2} }} } & \cdots & {h_{{i_{2} i_{n} }} } & { - \left( {h_{{i_{2} j_{1} }} f_{{j_{1} }} + h_{{i_{2} j_{2} }} f_{{j_{2} }} + \cdots + h_{{i_{2} j_{n} }} f_{{j_{n} }} } \right)} \\ {} & {} & {} & \ddots & {} \\ {h_{{i_{n} i_{1} }} } & {h_{{i_{n} i_{2} }} } & \cdots & {h_{{i_{n} i_{n} }} } & { - \left( {h_{{i_{n} j_{1} }} f_{{j_{1} }} + h_{{i_{n} j_{2} }} f_{{j_{2} }} + \cdots + h_{{i_{n} j_{n} }} f_{{j_{n} }} } \right)} \\ \end{array} } \right] \in {\mathbb{R}}^{{n \times \left( {n + 1} \right)}} , $$

(33)

$$ {{\varvec{\upbeta}}} = \left[ {\begin{array}{*{20}c} {k_{{i_{1} }} \hat{q}_{{i_{1} }} } & {k_{{i_{2} }} \hat{q}_{{i_{2} }} } & \cdots & {k_{{i_{n} }} \hat{q}_{{i_{n} }} } & 1 & {\hat{q}_{{i_{1} }} } & {\hat{q}_{{i_{2} }} } & \cdots & {\hat{q}_{{i_{n} }} } \\ \end{array} } \right]^{T} \in {\mathbb{R}}^{{\left( {2n + 1} \right) \times 1}} . $$

(34)

By defining $l = \dim \left( {\mathbf{N}} \right) = \left( {2n + 1} \right) - {\text{rank}}\left( {\mathbf{A}} \right)$, where ${\mathbf{N}} = \ker \left( {\mathbf{A}} \right)$, when l = 1, the stiffness and mass modifications are computed by:

$$ k_{{I_{1} }} = \frac{{{\mathbf{N}}\left( {1,1} \right)}}{{{\mathbf{N}}\left( {n + 2,1} \right)}}, \ldots ,k_{{I_{n} }} = \frac{{{\mathbf{N}}\left( {n,1} \right)}}{{{\mathbf{N}}\left( {2n + 2,1} \right)}} $$

(35)

Alternatively, in the case of lumped mass modifications the method provides the following modifications:

$$ m_{{I_{1} }} = \frac{{{\mathbf{N}}\left( {1,1} \right)}}{{ - \omega^{2} {\mathbf{N}}\left( {n + 2,1} \right)}}, \ldots ,m_{{I_{n} }} = \frac{{{\mathbf{N}}\left( {n,1} \right)}}{{ - \omega^{2} {\mathbf{N}}\left( {2n + 2,1} \right)}} $$

(36)

In the case of l > 1, more combinations of springs (or masses) enable to cope with the prescribed task.

5.4 Higher-rank Modifications with the System Matrices

5.4.1 Assignment of the Antiresonance Frequencies

To overcome the issues in the numerical solution of multi-assignment problem, a different approach has been proposed in [63, 79]: AA is formulated through the eigenvalue problem of the adjunct system, as in Eq. (7). Despite the larger number of equations, such a formulation is easier to solve since just bilinear terms of the unknowns appear. To ensure solvability for higher-rank modifications, also handling the simultaneous assignment of n_z > 1 of antiresonances) and to consider the presence of constraints on the feasible modifications, Eq. (7) has been recast into a constrained least-square minimization of the eigenproblem of the adjunct system:

$$\mathop {\min }\limits_{{{\mathbf{x,y}}}} \left\{ {\sum\limits_{{i = 1}}^{{n_{z} }} {\left\| {\left( {\left( {{\mathbf{M}}_{{{\mathbf{\bar{q}\bar{p}}}}} + {\varvec \Delta} {\mathbf{M}}_{{{\mathbf{\bar{q}\bar{p}}}}} {\mathbf{(x)}}} \right){\omega _{{z,i}}^{{d}}}^{2} - \left( {{\mathbf{K}}_{{{\mathbf{\bar{q}\bar{p}}}}} {\mathbf{ + \Delta K}}_{{{\mathbf{\bar{q}\bar{p}}}}} {\mathbf{(x)}}} \right)} \right){\mathbf{u}}_{{{\mathbf{z,i}}}}^{d} \left( {\mathbf{y}} \right)\,} \right\|_{2}^{2} } ,{\mathbf{x}} \in {\mathbf{\Gamma }}_{{\mathbf{x}}} ,{\mathbf{y}} \in {\mathbf{\Gamma }}_{{\mathbf{y}}} } \right\}.$$

(37)

${\mathbf{\Delta M}}_{{{\mathbf{\overline{q}\overline{p}}}}} {\mathbf{(x)}}$ and ${\mathbf{\Delta K}}_{{{\mathbf{\overline{q}\overline{p}}}}} {\mathbf{(x)}}$ are the mass and stiffness modification of the adjunct system matrices, obtained by removing the q-th row and the p-th column from ${\mathbf{\Delta M(x)}}$ and ${\mathbf{\Delta K(x)}}$; x denotes the design variables vector, whose values are constrained through the set ${{\varvec{\Gamma}}}_{{\mathbf{x}}}$. The adjunct system desired eigenvectors ${\mathbf{u}}_{{{\mathbf{z,i}}}}^{d}$ could be, in principle, fully assigned (leading to a convex problem), or not. In practice, such a requirement is never done since it is too severe and hence it is difficult to satisfy. Therefore, ${\mathbf{u}}_{{{\mathbf{z,i}}}}^{d}$ is usually not assigned or at least, just partially assigned. The formulation in Eq. (37) handles all these possibilities and exploits constraint on the unassigned entries of ${\mathbf{u}}_{{{\mathbf{z,i}}}}^{d}$, that are treated as problem unknowns collected in ${\mathbf{y}}$ to belong to the admissible domain ${{\varvec{\Gamma}}}_{{\mathbf{y}}}$. Since the resulting problem is not convex in the case of partial assignment of ${{\varvec{\Gamma}}}_{{\mathbf{y}}}$ (or no assignment), the achievement of the global optimal solution is performed in [63, 79] by exploiting the idea of homotopy transformation, variable lifting and McCormick’s relaxation. The resulting method is a general tool that can solve the assignment problem in cross and point-receptances of systems with arbitrary topologies (for example with lumped parameters or finite elements) and number of DOFs, as well as with arbitrary topology of the feasible modifications.

Due to its simple formulation and solution the idea outlined in [63, 79] has been extended to solve other AA problems. In [80], the theory is extended to the simultaneous assignment of resonances and antiresonances and to pole-zero flipping on an experimental beam. Such a work exploits a formulation similar to Eq. (37) together with the assignment condition of natural frequencies [64], by imposing of the signs of some entries of ${\mathbf{u}}_{{{\mathbf{z,i}}}}^{d}$ through ${{\varvec{\Gamma}}}_{{\mathbf{y}}}$, ad dictated in Eq. (9).

Besides computing the optimal parameters of the primary system, such a mathematical frame has been extended in [63] to simultaneously handle the design of undamped D-MTMD with arbitrary topology. The equation of motion of the system with the D-MTMD attached and with the primary system modified through ${\mathbf{\Delta M}}$ and ${\mathbf{\Delta K}}$ can be partitioned as follow:

$$\left[ {\begin{array}{*{20}c} {{\mathbf{M}} + \Delta {\mathbf{M}}} & {{\mathbf{M}}_{{{\mathbf{oa}}}} } \\ {{\mathbf{M}}_{{{\mathbf{oa}}}}^{T} } & {{\mathbf{M}}_{{\mathbf{a}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\ddot{\mathbf{q}}}\left( t \right)} \\ {{\ddot{\mathbf{q}}}_{{\mathbf{a}}} \left( t \right)} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\mathbf{K}} + \Delta {\mathbf{K}}} & {{\mathbf{K}}_{{{\mathbf{oa}}}} } \\ {{\mathbf{K}}_{{{\mathbf{oa}}}}^{T} } &{{\mathbf{K}}_{{\mathbf{a}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{q}}\left( t \right)} \\ {{\mathbf{q}}_{{\mathbf{a}}} \left( t \right)} \\ \end{array} } \right\} = {\mathbf{Bf}}\left( t \right), $$

(38)

where (M_a, K_a) are the matrices of auxiliary system (the D-MTMD) while (M + ΔM, K + ΔK) denote the primary (or main) system. The inertial and elastic coupling matrices are M_oa, K_oa. The assignment problem is cast as a minimization problem:

$$\begin{aligned} \mathop {\min }\limits_{{{\mathbf{x,y}}}} \left\{ {\sum\limits_{{i = 1}}^{{n_{z} }} {\left\| {\left( { {\omega _{{z,i}}^{{d}}}^{2} \left[ {\begin{array}{*{20}c} {{\mathbf{M}}^{\prime } \left( {\mathbf{x}} \right)} & {{\mathbf{M}}_{{{\mathbf{oa}}}} \left( {\mathbf{x}} \right)} \\ {{\mathbf{M}}_{{{\mathbf{oa}}}}^{T} \left( {\mathbf{x}} \right)} & {{\mathbf{M}}_{{\mathbf{a}}} \left( {\mathbf{x}} \right)} \\ \end{array} } \right]_{{{\bar{\mathbf{qp}}}}} - \left[ {\begin{array}{*{20}c} {{\mathbf{K}}^{\prime } \left( {\mathbf{x}} \right)} & {{\mathbf{K}}_{{{\mathbf{oa}}}} \left( {\mathbf{x}} \right)} \\ {{\mathbf{K}}_{{{\mathbf{oa}}}}^{T} \left( {\mathbf{x}} \right)} & {{\mathbf{K}}_{{\mathbf{a}}} \left( {\mathbf{x}} \right)} \\ \end{array} } \right]_{{\bar{\mathbf{qp}}}} } \right){\mathbf{u}}_{{{\mathbf{z,i}}}} \left( {\mathbf{y}} \right)} \right\|_{2}^{2} ,{\mathbf{x}} \in \Gamma _{{\mathbf{x}}} ,{\mathbf{y}} \in \Gamma _{{\mathbf{y}}} } } \right\}, \end{aligned}$$

(39)

The modified system matrices are ${\mathbf{M}}_{{}}^{{\mathbf{^{\prime}}}} \left( {\mathbf{x}} \right) = {\mathbf{M}} + \Delta {\mathbf{M}}\left( {\mathbf{x}} \right)$ and ${\mathbf{K}}_{{}}^{{\mathbf{^{\prime}}}} \left( {\mathbf{x}} \right) = {\mathbf{K}} + \Delta {\mathbf{K}}\left( {\mathbf{x}} \right) + \Delta {\mathbf{K}}_{{{\mathbf{ob}}}} \left( {\mathbf{x}} \right)$, with $\Delta {\mathbf{K}}_{{{\mathbf{ob}}}}$ collecting the stiffness modifications at the connections between the original and the auxiliary system. The solution of this problem can be performed through the same method of Eq. (37).

5.4.2 Numerical Example: Higher-rank Modification with System Matrices

Let us consider the six-mass system with the original parameters. The goal is to assign two antiresonances at 1.000 rads⁻¹ and 2.000 rads⁻¹ on h_3,3(jω). Five lumped mass modifications, Δm₁, Δm₂, Δm₄, Δm₅, Δm₆, are assumed. The modifications are constrained such that: 0 kg ≤ Δm_i ≤ 0.5 kg. With these tight constraints, the rank-one modifications computed in Sect. 4.2.1 are infeasible. By solving Eq. (37), the desired antiresonances are exactly assigned with Δm₁ = 0.4019 kg, Δm₂ = 0.3276 kg, Δm₄ = 0.0432 kg, Δm₅ = 0.0311 kg, Δm₆ = 0.1710 kg, as corroborated in Table 10.

Table 10 Original and modified system antiresonances for h_3,3(jω) in the case of higher-rank modification

5.4.3 Assignment of the Antiresonant Response

Exploiting Eq. (7) and the mathematical frame of Eq. (37), it is possible to assign the adjunct system eigenvectors, ${\mathbf{u}}_{{{\mathbf{z,i}}}}^{d}$, which define the steady-state displacements of the system coordinates at the i-th antiresonance frequency as introduced in Sect. 2.1. In the case of complete assignment of ${\mathbf{u}}_{{{\mathbf{z,i}}}}$ Eq. (7) is recast into a constrained linear least-square optimization as follows:

$$\mathop {\min }\limits_{{\mathbf{x}}} \left\{ {\sum\limits_{{i = 1}}^{{n_{z} }} {\left\| {\left( {\left( {{\mathbf{M}}_{{{\mathbf{\bar{q}\bar{p}}}}} {\mathbf{ + \Delta M}}_{{{\mathbf{\bar{q}\bar{p}}}}} {\mathbf{(x)}}} \right) {\omega _{{z,i}}^{{d}}}^{2} - \left( {{\mathbf{K}}_{{{\mathbf{\bar{q}\bar{p}}}}} {\mathbf{ + \Delta K}}_{{{\mathbf{\bar{q}\bar{p}}}}} {\mathbf{(x)}}} \right)} \right){\mathbf{u}}_{{{\mathbf{z,i}}}}^{d} } \right\|_{2}^{2} } ,{\mathbf{x}} \in {\mathbf{\Gamma }}} \right\}$$

(40)

In the (more reasonable) case of partial assignment of the antiresonant response, or when requiring the eigenvector to belong to a prescribed interval, assignment of ${\mathbf{u}}_{{{\mathbf{z,i}}}}^{d} \left( {\mathbf{y}} \right)$ can be performed through Eq. (37), by exactly imposing some entries of ${\mathbf{u}}_{{{\mathbf{z,i}}}}^{d}$ while the remaining ones are required to belong to the feasible domain ${{\varvec{\Gamma}}}_{{\mathbf{y}}}$. The unique example of partial antiresonant response mode assignment in the literature is proposed in [80].

5.5 Sensitivity-Based DSMs

Sensitivity analysis has been used in [81] for the assignment of resonances and antiresonances, by linearizing the relation between the set of the actual resonances and antiresonances (${{\varvec{\Omega}}}_{p}^{{}}$ and ${{\varvec{\Omega}}}_{z}^{{}}$ respectively), the desired ones (${{\varvec{\Omega}}}_{p}^{d}$ and ${{\varvec{\Omega}}}_{z}^{d}$) and the design variables:

$$ \left\{ {\begin{array}{*{20}c} {{{\varvec{\Omega}}}_{p}^{d} } \\ {{{\varvec{\Omega}}}_{z}^{d} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {{{\varvec{\Omega}}}_{p}^{{}} } \\ {{{\varvec{\Omega}}}_{z}^{{}} } \\ \end{array} } \right\} + {\mathbf{Sx}}, $$

(41)

where S is the matrix of the sensitivities with respect to the n_x design parameters, whose finite variation about the original value is collected in vector ${\mathbf{x}} \in {\mathbb{R}}^{{n_{x} }}$:

$$ {\mathbf{S}} = \left[ {\begin{array}{*{20}c} {\frac{{\partial {{\varvec{\Omega}}}_{p}^{{}} }}{{\partial x_{1} }}} & \cdots & {\frac{{\partial {{\varvec{\Omega}}}_{p}^{{}} }}{{\partial x_{{n_{x} }} }}} \\ {\frac{{\partial {{\varvec{\Omega}}}_{z}^{{}} }}{{\partial x_{1} }}} & \cdots & {\frac{{\partial {{\varvec{\Omega}}}_{z}^{{}} }}{{\partial x_{{n_{x} }} }}} \\ \end{array} } \right] $$

(42)

The optimal modifications are computed through the pseudoinverse ($\dag$) matrix, by iterating more times the calculations (including the updating of ${{\varvec{\Omega}}}_{p}^{{}}$, ${{\varvec{\Omega}}}_{z}^{{}}$, S):

$$ {\mathbf{x}} = {\mathbf{S}}^{\dag } \left\{ {\begin{array}{*{20}c} {{{\varvec{\Omega}}}_{p}^{d} - {{\varvec{\Omega}}}_{p}^{{}} } \\ {{{\varvec{\Omega}}}_{z}^{d} - {{\varvec{\Omega}}}_{z}^{{}} } \\ \end{array} } \right\} $$

(43)

Sensitivity-based approaches often provide sub-optimal solutions since linearization holds only for small changes of the design parameters. Hence, large shifts of the antiresonances are hard to handle and iterations of the method updating the sensitivities are needed. On the other hand, iterating does not ensure convergence and defining stopping criteria is not straightforward in the presence of several design variables with constraints on the values, and whenever the achievement of the exact antiresonances is not allowed.

5.5.1 Numerical Example: Sensitivity-Based DSM

Let us assume that it is wanted to assign an antiresonance at $\omega_{z,3}^{d} = 1.000\,{\text{rads}}^{{ - 1}}$ for h_3,3(jω) through Δm₄, as done in Sect. 4.2.1. Exploiting the sensitivity analysis proposed in Sect. 2.3.1 the sensitivity ∂(ω_z,3)²/∂m₄ is used to shift ω_z,4 to the prescribed value:

$$ \Delta m_{4} = \left( {\frac{{\partial \omega_{z,3}^{2} }}{{\partial m_{4} }}} \right)^{ - 1} \left( {\left( {\omega_{z,3}^{d} } \right)^{2} - \left( {\omega_{z,3}^{{}} } \right)^{2} } \right). $$

(44)

Since a large frequency shift is required, the sensitivity based approach leads to the correct mass modification after 5 iterations of Eq. (44) by updating at each iteration the sensitivity ∂(ω_z,3)²/∂m₄. A mass modification Δm₄ = 2 kg is obtained, as provided by the unit-rank receptance based method. The value of Δm₄ for each iteration are: Δm₄ = [0.993; 1.670; 1.961; 1.999; 2.000] kg. The antiresonances obtained after the last iteration are those already proposed in Table 9.

5.6 Choice of the Design Parameters

Sensitivity analysis of the antiresonance frequency with respect to the candidate parameters, as defined in Eq. (11), is a useful approach to identify the most suitable design parameters. Sensitivity analysis is for example adopted to this purpose in [79], to discard some design variables. It should be noted that sensitivity should be sometimes computed with respect to normalized variables, to account for different magnitudes of non-homogeneous parameters (e.g. masses and stiffnesses), leading to the following normalized sensitivity:

$$ \frac{{\partial \omega_{z,i}^{2} }}{{\partial x_{0} }} = \frac{{\partial \omega_{z,i}^{2} }}{\partial x}x_{0} , $$

(45)

where x₀ is the value assumed for normalization, which can be either the original value of the unmodified system (whenever it is greater than 0) or a meaningful value (such as the upper bound of the feasible modifications, or the central values of the bounds) whenever it original value is 0.

Another meaningful tool is the analysis of the left eigenvector of the adjunct system [74]. Indeed, if the i-th left eigenvector of the adjunct system has a zero-entry related to the r-th DOF, then any modification of the parameters of such a coordinate does not modify the i-th antiresonance frequency. Hence, modifications should be done on the coordinates associated to large magnitude in ${\mathbf{w}}_{{{\mathbf{z,i}}}}^{{}}$.

6 Importance and Use of Antiresonances Through Passive Control

6.1 Benefits of Antiresonances in Control

The mathematical features of antiresonances, discussed along this paper, suggest the exploitation of antiresonances for other goals besides vibration absorption. Indeed, the presence of antiresonances in closed loop control has benefits due to the + 180° phase introduced by the pair of zeros related to an antiresonance. In practice, a proper placement of antiresonances can be exploited to perform loop shaping, in lieu of standard lead-lag compensators employed in the loop-shaping process to enhance gain and phase margins [85]. For example, in [80], it is shown that interlacing between resonances and antiresonances can be imposed to cross receptances within a bandwidth of interest, to simplify the use of non-collocated control.

6.2 Practical Applications of AA

Over the decades several practical applications of the AA have been developed. The goal of this Section is to report some meaningful works among the wide range of applications of AA.

6.2.1 Antiresonance Assignment in Buildings and Civil Structures

The assignment of antiresonances by means of TMDs has been deeply studied in civil engineering applications, and therefore it will be marginally addressed in this Section. The readers could refer to the literature reviews [3, 4] and [86] to find hundreds of applications. Just to quote an example, in [87] the authors proposed the application of a tuned mass damper to reduce the response to wind-induced motion of Milad Tower in Tehran.

6.2.2 Antiresonance Assignment in Helicopters

AA is particularly popular in the design of helicopters too, to absorb the rotor induced vibrations at a fixed frequency. In [88] the application of the antiresonance theory for engineering applications in helicopters is discussed placing either passive, semi-active or active TMDs at collocated or non-collocated locations. In [89] the AA in helicopters is studied in order to absorb the rotor induced vibrations. Two methods are provided: the first one performs AA by modifying only the existing stiffness of two fuselage elements by solving a polynomial. While the second method handles the design of appendant structures to create antiresonances. Braun in [90, 91] proposed the development of two experimental “uniaxial antiresonance force isolators” for the reduction of the rotor induced cabin vibrations: AA is exploited to dynamically isolate the helicopter fuselage from the rotor-transmission unit.

6.2.3 Antiresonance Assignment in Industrial Devices and Machines

Some examples can be found in industrial machines. In [92,93,94] the trough of a vibrating feeder is designed in such a way that it acts as a TMD for the feeder body, hence the vibrations on the foundation of the feeder vanish while the vibration frequency and the response amplitude still meet the prescribed requirement in order to feed the material on the vibrating tray. AA by means of Framh’s TMD has been recently exploited in a vibratory conveyor that allows for a sudden stopping of the transport [95].Vibration reduction in rotating mechanical systems have been widely studied and is growing of interest in the recent years, AA seems promising to tackle this problem since a constant harmonic excitation often affects such systems. For example in [84] a vibration absorber combining negative stiffness (due to ring type permanent magnets) with positive stiffness together is proposed in order to suppress the vibration of a rotor system. In [78], an antiresonance frequency to a geared rotor-bearing system is assigned to suppress vibrations at the rotational speed.

AA has been attractive in the design of domestic devices such as washing machines, indeed at the spinning stage those experiences relevant unbalance forces due to the water extraction at high and known frequency. To reduce the vibration amplitude, and possibly completely absorb it, TMDs are sometimes employed. In [96] a rotating ring dynamic absorber is developed enables to reduce the vibration energy in the basket leading to less dynamic loading in the mounts, resulting in less overall noise and vibration of the washing machine structure.

7 A Comparison with AA Through Active Approaches

A relevant feature that is shared by all the quoted passive approaches to AA is that the modified system is guaranteed to remain stable, either when modifying or preserving the number of DOFs [72]. This is due to the symmetric nature of passive modifications that lead to negative real parts of the poles of the modified system, in accordance with the Rayleigh stability criterion [97]. For example, if the number of DOFs is preserved, such real parts are computed as follows:

$$ {\text{Re}} \left( {p_{i} } \right) = - \frac{{\left| {p_{i} } \right|^{2} {\mathbf{u}}_{{{\mathbf{r,i}}}}^{{\mathbf{*}}} {\mathbf{Cu}}_{{{\mathbf{r,i}}}}^{{}} }}{{\left| {p_{i} } \right|^{2} {\mathbf{u}}_{{{\mathbf{r,i}}}}^{{\mathbf{*}}} \left( {{\mathbf{M + \Delta M}}} \right){\mathbf{u}}_{{{\mathbf{r,i}}}}^{{}} + {\mathbf{u}}_{{{\mathbf{r,i}}}}^{{\mathbf{*}}} \left( {{\mathbf{K + \Delta K}}} \right){\mathbf{u}}_{{{\mathbf{r,i}}}}^{{}} }} $$

(46)

where $p_{i}$ is an eigenvalue of the modified system (i.e. a roots of the quadratic pencil $\left( {{\mathbf{M}} + {\mathbf{\Delta M}}} \right)p^{2} + {\mathbf{C}}p + \left( {{\mathbf{K}} + {\mathbf{\Delta K}}} \right)$) and ${\mathbf{u}}_{{{\mathbf{r,i}}}}^{{}}$ is the related eigenvector. A second relevant feature is that passive approaches do not need adopting actuators and sensors, thus performing AA without the need of external energy supply.

On the other hand, all the passive approaches share some disadvantages. First of all, the form of the modifications that can be physically realized is restrictive on the achievable performances, due to their symmetry, positive-definiteness and of the presence of some patterns of non-zero terms in the modification matrices. Secondly, as demonstrated in [98,99,100] the number of antiresonances to be assigned must be matched by the rank of the modification whenever constraints on the feasible modifications are neglected. However, the actual number of assignable antiresonances is often smaller than the rank of the modifications due to presence of constraints on the feasible modifications of parameters. Finally, large shifts of the antiresonances often lead to bulky modifications.

These limitations are recently motivating the research on techniques to AA through active approaches, where springs, dampers and masses are replaced by forces exerted by servo-controlled actuators and computed as functions of the measurements provided by some sensors. Active approaches to AA include semi-active TMDs ([101, 102]), active-TMDs ([103,104,105]), state-feedback techniques ([98]), output feedback techniques ([99, 106]). The advantage of active control is that the achievable performances can be enlarged by exploiting suitable control logics, as well as wise actuator and sensor placements. For example, active control can emulate modifications of mass and stiffness matrices that are asymmetric or sparse. Additionally, the controller gains can be adapted to track changes in the frequency of the external excitation, for adapting the antiresonance frequency.

On the other hand, active control can destabilize the system if spillover on the poles is not properly tackled and if actuators and sensors have reduced bandwidth or are delayed. The latter issue limits the controller gains. Another constraint on the feasible gains should be considered in practice, although some authors erroneously assume that control gains are unbounded: the presence of limits of the actuator force and speed, that often make “active modifications” bulkier than passive ones.

8 Conclusions and Possible Research Directions

This work proposes a comparison and tutorial on the state-of-the-art milestones on vibration absorption through AA. The mathematical background on antiresonances, the adjunct system related eigenproblem and the sensitivities of antiresonances are analysed. The existing passive methods have been introduced, and the main ones have been also applied through a test-case. Some key differences have been discussed between approaches adding additional DOFs and those preserving the number of the existing ones. The numerical results proposed with reference to a 6-mass lumped system clearly highlight all these issues and show the applicability of some methods taken from the literature. Importance of antiresonance frequencies and its applications in different engineering fields has been also proposed to stress the usefulness of the efforts in this research area.

The proposed analysis, together with some numerical applications here provided, enables to summarize the state-of-the art, compare and apply the existing methods by choosing the most suitable for each application or by fusing the ideas and the techniques of more methods. For example, in this paper the general formulation of the MDOF TMD, developed by Ram and Elhay in [60], has been here for the first time solved with a method recently developed for the assignment of natural frequencies.

The critical analysis of literature allows bringing together some open issues in this field of research and outlines some possible research directions. While the theory of TMDs seems to be mature and many papers can be found, less efforts have been done to assign antiresonances without adding new DOFs. In this research area, some issues are therefore partially unsolved, such as robustness and presence of damping. The adaptation of the theories developed for the various developments and arrangements of the TMD might be helpful to extend it. The comparison between passive and active approaches shows that they are not always surrogate approaches due to different features and fields of application. It is expected that semi-active approaches that merges the benefits of both the approaches to overcome their limitations can boost performances, in term of effectiveness, robustness and reduction of energy requirements to perform vibration control.

The ever-growing availability of computational methods, as well as optimization techniques, will further boost the advancements in the research, by leading to improvement of the discussed methods for solving more challenging problems.