A Review on the Developments of Peridynamics for Reinforced Concrete Structures

Abstract

Concrete is the most widely used man made material in the world. Reinforced with steel, it forms a key enabler behind our rapidly urbanising built environment. Yet despite its ubiquity, the failure behaviour of the material in shear is still not well understood. Many different shear models have been proposed over the years, often validated against sets of physical tests, but none of these has yet been shown to be sufficiently general to account for the behaviour of all possible types and geometries of reinforced concrete structures. A key barrier to a general model is that concrete must crack in tension, and in shear such cracks form rapidly to create brittle failure. Peridynamics (PD) is a non-local theory where the continuum mechanics equilibrium equation is reformulated in an integral form, thereby permitting discontinuities to arise naturally from the formulation. On the one hand, this offers the potential to provide a general concrete model. On the other hand, PD models for concrete structures have not focussed on applications with reinforcement. Moreover, a robust model validation that assesses the strengths and weakness of a given model is missing. The objectives of this paper are twofold: (1) to evaluate the benchmark tests involving shear failure for RC structures; and (2) to review the most recent PD theory and its application for reinforced concrete (RC) structures. We investigate these models in detail and propose benchmark tests that a PD model should be able to simulate accurately.

1 Introduction

Whilst the origins of concrete can be traced back several thousand years, the addition of reinforcement to carry tension occurred only in the mid-nineteenth century [26]. Concrete is now our most widely used man made material, and the production of Portland cement approaches 4.1 billion kg per year [143]. This brings economic benefits, and environmental challenges [93, 109].

Concrete presents quasi-brittle behaviour and is usually taken as a homogeneous material at the macroscale. Nevertheless, concrete is clearly a heterogeneous material at the microscale, as it is constituted by different materials such as sand, cement and aggregate. As the structure is loaded, there will be stress concentrations around the aggregates, which can vary due to their different dimensions. This can lead to high values of stresses in localised regions of the RC structure, and potentially causing its early failure.

The behaviour in failure of reinforced concrete (RC) structures can be classified in flexural and shear failure. While flexural failure is a well understood phenomenon, shear failure in RC is still an open problem [30, 160]. Shear failure can broadly be defined when the shear resistance is lower than the flexural strength, leading to a change of direction of the flexural cracks to a diagonal one. Shear failure has brittle behaviour, which can lead to sudden collapse of the RC structure.

Many researches have provided crucial insights for the mechanisms associated with shear failure. The ultimate shear capacity is governed by the combined resistance to shear force offered by (1) the uncracked compressive zone, (2) arch or direct strut action, (3) aggregate interlock, (4) dowel action, and (5) the residual tensile strength in the fracture process zone (FPZ). The contribution of each action to the overall shear resistance is related to parameters such as shear span, beam depth (size effect), and reinforcement ratio. There is no consensus on the relational theory between shear failure and the many influencing parameters. Size effect in shear failure was discussed by Bažant and Kazemi [11]. The ratio between the size of the aggregate and the size of the concrete member is part of the mechanism that constitutes the size effect. Fenwick and Paulay [45] defined the basis of the arch and beam action in RC structures. Kani et al. [76, 77] have showed how the shear capacity can decrease as the span-to-depth ratio varies. Kotsovos [82] has classified the different type of shear failure that can appear in an RC structure.

Numerical models have also been used in the study of RC structures. The first attempts on modelling the quasi-brittle behaviour have used the cohesive formulation developed by Dugdale [38] and Barenblatt [7]. The fictitious crack method was introduced by Hillerborg et al. [59] and further improved by Bažant and Oh [12]. Červenka and Gerstle [22] have used the smeared cracking method in RC structures. Karihaloo and Nallathambi [79] obtained the fracture toughness of plain concrete using 3-point bending tests (3PBT). These models have been successfully used for many concrete structures, but they all rely on assumptions of linear elastic fracture mechanics (LEFM), so an initial crack must exist beforehand, which is often not the case in real RC structures.

Vecchio and Collins [144] developed an alternative formulation which considers compatibility, equilibrium and stress-strain relation to estimate the shear behaviour of cracked RC members. The modified compression field theory (MCFT) assumes that failure will occur when the shear stress on the crack faces required for equilibrium reaches the maximum shear stress that can be transmitted by aggregate interlock in the absence of shear reinforcement. The strain effect comes from the reduction of the failure shear as the tensile strain in the longitudinal reinforcement increases.

A large number of numerical models for RC structures have been obtained, and they have been validated using benchmarks such as other numerical solutions or experimental results. Model verification and validation are two independent processes required for assessing the suitability of a numerical model but they are commonly assumed to be the same process [140]. Model verification is the process to determine how the model represents the developer vision for that particular model and its solution, while model validation is the assessment of how the model represents the real physical model within appropriate levels of accuracy [140]. In this sense, a verified model only satisfies the requirements on how the developer vision is represented in the model, however the developer may not consider all the assumptions that represent the physical problem, hence the importance of an independent model validation.

The issues with model verification and validation have not been explicitly addressed, but they have been an underlying problem in numerical models for RC structures. The International Federation for Concrete (fib) has provided a report with recommendations of using the finite element method (FEM) to model RC structures [44]. Some of the challenges identified in the report are:

• 1. Diversity of theoretical approaches: non-linear, plasticity, fracture, damage mechanics;

• 2. Diversity of behaviour models: compression softening, tension softening, aggregate interlock, confinements effects, and many others;

• 3. Incompatibility of models and approaches: models are developed for specific assumptions/methodologies, and can not be calibrated to other assumptions easily;

• 4. Experience required: analyst experience also affects the results, as shown by [119];

• 5. Too much information: too much data generated in commercial softwares;

• 6. Incomplete knowledge: we still do not have a complete understanding on the behaviour in shear of RC structures;

• 7. Research philosophy: assumptions used in numerical models are not suitable for concrete (for instance, classic continuum mechanics).

From the report presented in [44], it is clear that the developers working on models for RC structures have employed different theories and used different assumptions on how the RC structure should perform. However, a general numerical model will be based on modelling the behaviour of the concrete and its interaction with the reinforcement, rather than making assumptions on how the concrete model should behave.

Peridynamics (PD) is a non-local framework first introduced by Silling [131]. Continuum mechanics partial derivative equations based on stresses are reformulated in an integral form based on forces between bonds over a finite range, which eliminates the need for special assumptions when discontinuities such as cracks are present in the model. The particle-based nature and the presence of physical bonds connecting the particles is an interesting feature that permits different possibilities, such as crack initiation and crack branching. These two phenomena are difficult to capture with standard numerical methods, such as FEM.

Javili et al. [71] have performed an extensive review of the state-of-the-art in PD, concerning both theoretical aspects and applications. Diehl et al. [36] reviewed different benchmarks used to validate PD models for many applications. They evaluated five different works involving concrete structures. For most of these works, the crack patterns obtained with PD correspond as the validation metric, but the failure loading or the load-displacement curves are not in agreement with the actual experiments. The results were normalised using the coefficient of determination $R^2$, which relates data and predictions obtained from the models [35]. The closer $R^2$ is to the value 1, the closer the match between the data and the model. Just one of the investigated works provided a $R^2$ value higher than 0.9. The majority of numerical models on RC structures compare the model results with other benchmarks that cannot be measured quantitatively, for instance, comparing the crack propagation paths. Few models present data for loading and deflections, which represents the behaviour of the RC member and can be quantitatively compared with experimental results.

The objective of this paper is to review the works on PD for RC structures. We discuss the mechanisms of shear transfer, the different types of failure, some of the main results obtained in the field for shear failure and the importance of benchmark tests in Sect. 2. Next we address bond-based PD and its use in RC structures in Sect. 3. In Sect. 4 we discuss the state-based PD theory and the research done on RC structures. We present the conclusions and research questions in Sect. 5.

2 Shear Behaviour and Shear Failure in RC Members

Understanding the behaviour in failure of RC is critical to ensure that the structure will safely withstand the designed load capacity. There are many nomenclatures when approaching failure of RC structures, but the failure modes are generally classified as flexural or shear failure.

Flexural failure is characterised by vertical cracks that appear when the RC structure is loaded. The vertical cracks form cantilever-shaped structures, with the longitudinal reinforcement at the end of these cantilevers. This configuration can resist the loading coming from the reinforcement bars, as have been reported by [76, 77] amongst many others. Design codes provide overall a good prediction of the actual flexural strength of small beams with constant cross-section area. The difference between the prediction of different design codes is about 10% [15, 60]. Nevertheless, the beams used for testing are often much smaller than the normally employed RC beams.

Shear failure in concrete occurs when the shear force exceeds the shear capacity of the section, leading to a sliding diagonal failure. Diagonal failure is usually analysed with a 4-point bending test (4PBT) with longitudinal reinforcement but without shear reinforcement, so diagonal cracks can form in the structure. There has also been works to study how shear failure can develop (or be prevented) due to the use of shear reinforcement. The 4PBT combines two different loading conditions, pure bending between the applied load locations, and constant shear force at the end of the section [82]. A typical 4PBT is illustrated in Fig. 1, where b is the width of the beam, d is the effective depth, a is the shear span, h is the total depth of the beam, $A_s$ is the area of the tensile reinforcement and $\rho$ is the ratio of longitudinal tensile reinforcement $A_s/bd$. The shear-span-to-depth ratio a/d is one of the most important parameters for shear failure behaviour.

Fig. 1

Typical 4-point bending test

There are several known mechanisms that influence shear failure, and they are briefly described in the next sections.

2.1 Shear Transfer Actions

There are two main shear transfer actions that appear in RC beams with longitudinal reinforcement. When vertical cracks start to appear, that zone has a reduced capacity to carry loading. The remaining uncracked concrete forms an arch type compression zone, and it leads to strengthening of the remaining structure rather than weakening. This shear transfer is known as arch action. In this case, the overall behaviour of the structure can be represented by the Strut-and-Tie method [106]. The arch action has a more prominent effect in the shear strength in beams where the shear-span-to-depth ratio is small (typically less than 3). These beams are also denominated as short or deep beam, due to larger values of depth of these RC beams.

On the other hand, if the shear-span-to-depth ratio is larger (typically values between 3 and 8, beams are also denominated slender beams), a different shear transfer mechanism is dominant. The vertical cracks form tooth-like arrangements as described by Kani [77]. This shear transfer is usually defined as beam action. The relation between the reinforcement and the concrete dictates the behaviour of the structure. Other shear transfer mechanisms such as the aggregate interlock, the dowel action, the uncracked compressive zone and the residual stresses can increase the shear strength of the RC member. Each of these mechanisms present complex behaviour, so it becomes clear that obtaining a reliable model for shear failure of RC structures is cumbersome.

Fenwick and Paulay [45] defined the arch and beam action, and concluded that the crack opening resulting in less aggregate interlock in the flexural crack region is the main action responsible for shear failure. Cavagnis et al. [20] have investigated the different shear transfer mechanisms in RC beams using digital image correlation to extrapolate the strain and stresses in the beams. For beams with different shear-span-to-depth ratio, they have verified the existence of arch and beam action, as well as aggregate interlock, dowel action and residual stresses, confirming the findings of Kani [77] and Fenwick and Paulay [45].

Kani [77] has observed that reduction of the bond between the concrete and the reinforcement would increase the shear capacity, as compressive uncracked concrete will be responsible for the remaining capacity of the beam. In such a case, we can see the change of behaviour from the beam to the arch mechanism.

2.2 Shear Transfer Mechanisms

2.2.1 Uncracked Compressive Zone

After flexural cracks have appeared in an RC beam, it is normally assumed that the remaining uncracked compressive zone can provide shear resistance [117]. However, the distribution of the shear stresses in the uncracked concrete depends on the boundary conditions of the compressive zone. If the distribution is constant, it has to take into account the teeth-like shape due to the presence of flexural (or vertical) cracks. If the distribution varies with the compression zone, the shear force is transmitted due to the inclination of the principal stress [160].

The mechanism present in the uncracked compressive zone is not the same as the shear arch action, particularly for slender beams. The arch action will have little influence as the compressive zone is intersected by the diagonal crack, which cannot contribute to shear strength [67].

2.2.2 Aggregate Interlock

Crack surfaces are not smooth in concrete structures. The hardened cement matrix represents most of the crack surface, but an aggregate surface is also present. The aggregate surface can interlock with the crack surface, resisting to displacements along the crack plane, hence leading to shear stresses [145].

Fenwick and Paulay [45] were the first to demonstrate the importance of the aggregate interlock mechanism by comparing crack surfaces of different roughness. One of the most comprehensive works on aggregate interlock was performed by Walraven [145], who proposed a model for the aggregate interlock where the concrete is a two-phase material of aggregate particles embedded into an plastic matrix. The opening and shear in cracks are concurrent rather than independent processes. Walraven’s model assumed that the normal and shear stresses at the crack surfaces depend on the crack width and the shear displacement. Walraven proposed an improved model based on a statistical analysis of the crack surface, the contact areas at the crack surface expressed in terms of the shear displacement, the crack opening and the composition of the concrete mix [146].

To the authors’ best knowledge, the aggregate interlock contribution is not explicitly defined in the design codes.

2.2.3 Dowel Action

Mörsch [111] was the first to suggest that the longitudinal reinforcement can transfer forces in the perpendicular direction from its length, contributing to the shear strength of RC structures.

Kani [76] had also investigated how the bond between the reinforcement and the concrete affects the formation of the beam action.

Olonisakin and Alexander [115] have shown that the yielding of the reinforcement and the debonding between the reinforcement and concrete can limit the influence of the beam mechanism.

2.2.4 Residual Stresses

The softening behaviour of the concrete is partly due to the residual tensile stresses arising at the crack tip. In this case, a fracture process zone (FPZ) can be defined, and the residual stresses in the FPZ are given by a softening law that depends on the crack opening. A common softening bi-linear law was defined by Hordijk [63]. A shear strength component is induced by the residual tensile stresses at the crack tip [67].

Hillerborg et al. [59] introduced the fictitious crack method where a relation between the crack opening displacement and the stress ahead of the physical crack tip. The fictitious crack tip cancels the singularity of the physical crack tip. However, there is much discussion on the influence of residual tensile strength in the shear behaviour of concrete beams [160].

2.3 Influence of the Shear-Span-to-Depth Ratio a/d

Kani [77] is one of the most important names to have analysed the shear failure behaviour in reinforced beams. Kani and his group identified 3 possible beam classification due to the shear-span-to-depth ratio a/d. Figure 2 depicts the observed shear valley, where $M_u$ is the ultimate moment capacity of the beam and $M_{fl}$ is the theoretical flexural capacity, and the Figure summarises their conclusions:

• For values of a/d lower than a minimum $(a/d)_{min}$, the regions delimited by vertical flexural cracks (also known as “concrete teeth”) possess lower capacity than the arch region formed by the acting compressive forces. Hence, a diagonal crack gradually appears in the structure, due to the increasing loading. The structure fails at the full flexural capacity. The arch mechanism has much more influence than the beam mechanism;

• The region delimited $(a/d)_{min}$ and $(a/d)_{TR}$, where $(a/d)_{TR}$ is a transition value of a/d, the capacity of the arch region is lower than the concrete teeth ones, which also implies that sudden collapse will follow once the concrete teeth capacity is exceed;

• For regions beyond the transition value $(a/d)_{TR}$, the concrete beam collapses at the full flexural capacity.

Fig. 2

Kani shear valley

The values for $(a/d)_{min}$ and $(a/d)_{TR}$ vary depending on the concrete compressive strength $f_c$ and the reinforcement ratio. Typical values of $(a/d)_{min}$ are between 2.5 and 3, while $(a/d)_{TR}$ can take values between 5 and 6. From Fig. 2 it is evident the range of values for the shear-span-to-depth ratios where the arch and beam mechanisms are responsible for increasing the shear strength in the RC beam. There is also a point of minimum shear strength, and beams with this $(a/d)_{min}$ ratio present an almost brittle behaviour.

2.4 Types of Shear Failure

Kotsovos [82] has introduced a classification system of the shear failure according to the loading behaviour:

• Type I: flexural failure only, the beam develop its full flexural capacity;

• Type II: a diagonal crack initiates near the tip of the flexural crack closest to the support and propagates toward the load point. The crack can also propagate towards the support along the reinforcement. The flexural capacity reduces with the shear-span-to-depth ratio a/d, decreasing to a critical value dependent upon the area of the reinforcement;

• Type III: a diagonal crack forms independently of the flexural cracks. In this case, the flexural capacity increases from the critical value in Type II to another value, also dependent upon the area of the reinforcement, until it reaches the full flexural capacity again;

• Type IV: failure is caused by a diagonal crack joining the support to the load point, and the beam can develop its full flexural capacity.

The terminology found in the literature for the different types of shear failure is not consistent. For instance, Cavagnis et al. [21] have defined four different developments of the so called critical shear crack:

• Critical shear crack allowing full-arching action to develop;

• Failures following a stable propagation of the critical shear crack;

• Failure triggered by local loss of aggregate interlock capacity due to the propagation of an internal crack;

• Failure triggered by the merging of a secondary flexural crack with a primary flexural crack.

A shear valley similar to the one defined by Kani [77] was obtained using this classification for shear failure in [21]. Figure 3 depicts the different type of shear failure obtained by varying the shear-span-to-depth ratio of longitudinally RC beams, performed by Leonhardt and Walther [89].

Fig. 3

Possible types of shear failure for different a/d ratios. From [60]

The shear failure can be classified as [60]:

• Beam 1: shear-web failure (crack forms in a direct line between applied loading and support)

• Beams 2 and 3: shear-compression failure (flexural cracks appear first, then propagates towards the applied loading; crushing also present; arch shear transfer is more dominant)

• Beams 4, 5, 6, 7, 8: shear-flexural failure (flexural cracks appear first, then propagates towards the applied loading; uncompressive concrete zone may retard crack propagation for some a/d ratios; beam action shear transfer is more dominant )

• Beam 10: flexural failure (full flexural capacity attained)

2.5 Some Results on Shear Failure

Kani and his group analysed hundreds of beams, particularly beams with rectangular and T-shaped cross sections, with longitudinal and also web (shear) reinforcement [76,77,78]. 159 T-beams with longitudinal reinforcement were tested, varying 3 parameters ($f_c$, $\rho$ and a/d). The tests showed that the shear valley is considerably larger in T-beams compared to rectangular beams. For $\rho > 1.88\%$, the flexural capacity increases almost linearly from the minimum flexural capacity at $a/d=3$ until it reaches the full capacity at $a/d \ge 10$ [76]. For $\rho \le 0.90 \%$, the beam maximum capacity when $a/d = 1$ does not reach the full flexural capacity, so that the reinforcement ratio and the concrete compressive strength have increased influence in the shear failure of the T-beam.

Furthermore, 271 beams were investigated to quantify the influence of the web reinforcement and the results presented in [76]. Data from rectangular and T-beams with only longitudinal reinforcement were used for comparison of the differences in the internal failure mechanisms formed. The influence of multiple stirrups was measured, and it becomes clear that much of the internal mechanisms in shear failure are not well understood. There are some clarification points such as [76, 160]:

• Significant dowel forces may develop after the horizontal cracking occurs at the longitudinal reinforcement interface, if the web reinforcement are in the correct locations, i.e., where shear failure could appear. Leonhardt and Walther [88] also showed that closely spaced vertical stirrups would balance out the moment generated by the bond forces due to the presence of a substantial dowel action [76];

• The concrete cover is important, if the cover is too large the effectiveness of the reinforcement is reduced;

• Web reinforcement leads to many well-distributed cracks, rather than larger ones when the stirrups are widely spaced. Smaller cracks do not penetrate into the compression zone, maintaining the aggregate interlock.

Kani and collaborators provided an extensive series of tests for different beams in [76]. However, many researchers have done experiments, for instance, [4, 19, 29, 83, 121] just to mention a few works. The different experiments do not employ the same geometries, reinforcement ratios, concrete type, etc. This issue makes difficult to compare the results amongst different experiments of shear failure. Some researchers have normalised these results from the literature in terms of a common background, forming databases of shear failure tests.

Collins et al. [30] have discussed the research in shear behaviour from 1948 until 2008. They assembled a database with 1849 shear tests from 114 references. About $84 \%$ of the experimental data comes from 4PBT, while only $1\%$ correspond to tests with uniform loading. From the database, 1696 specimens failed in shear and 153 failed in flexure. The empirical ACI expression of shear strength can indicate it decreases as the stresses in the longitudinal reinforcement increases, but the formula does not take into account all the influence of the strain effect [1].

Collins and co-workers also concluded that shear stresses are transmitted across the cracks due to aggregate interlock action [30]. High stress in the longitudinal reinforcement or wider crack spacing will lead to large crack openings, hence lower shear strengths.

The presented database contained 1098 tests for slender beams, where $a/d \ge 2.5$. As mentioned previously, the failure mechanism in slender beams is dictated by beam action. An additional 503 shear failure tests were attributed to short members. The slender beams were compared to a shear stress ratio $\beta$ defined as:

$$\begin{aligned} \beta = \frac{V_{test}}{b_w d \sqrt{f_c'}} \end{aligned}$$

(1)

where $V_{test}$ is the maximum observed shear force of the specimen, $b_w$ is the web width and $f_c'$ is the concrete cylinder strength taken at the date of testing. It was shown that $\beta$ decreases as the specimen becomes larger, and decreases as the stress in the reinforcement increases, showing the presence of a size effect [30]. Collins et al. [30] have also observed that the failure shear stress ratios for short shear spans are much higher than those present in slender beams. There was no evidence of size effect for the short beams specimens.

Additionally, 1343 shear failures were associated to the beam action mechanism. As the specimen depth and the reinforcement stress increase, the shear strength estimation from the ACI 318-08 design code [1] becomes less conservative. High concrete strength or small aggregate size are seen to fail under lower shear stresses, leading to unconservative results.

2.6 Size Effect in RC Structures

Size effects are also a factor that influences shear failure. The definition of size effects and design for quasi-brittle materials can be found in [9] and the references therein.

Jin et al. [73] have investigated the size effect on RC beams subjected to monotonic and low cyclic loading. The size effect was considered by varying the cross-section of the beams, with sides varying from 100 mm to 1000 mm for real specimens and up to 2000 mm using a mesoscale FE model. The beams have longitudinal and transversal reinforcement. Jin et al. study the effect of the statistical size effect, i.e., it depends on the randomness of the material properties. Another type of size effect is based upon the formation of a region with intense strain localisation, which corresponds to the FPZ. The failure patterns are very different for the beams under cyclic or monotonic loading: in the case of the cyclic loading, the failure is more brittle, while the monotonic loading presents a ductile failure. The predicted failure loading was compared with the EC2 [39], the ACI 318-2011 [2] and a Chinese code (GB50010-2010). Jin et al. [73] conclude that the size effect has greater influence on the flexural strength for RC beams under cyclic loading compared to the ones subjected to monotonic loading.

Other authors had different conclusions for the effect of statistical size effects. For instance, Syroka-Korol et al. [138] have analysed the influence of size effects in RC simply supported beams without shear reinforcement using FE models. They focused on both deterministic and statistical size effects for plane stress problems in their work. Additionally, they made particular assumptions for the concrete-reinforcement interface, using models from Akkermann [5], Dorr [37] and the fib Model Code [139]. The Akkermann model [5] has shown to provide the best results compared to the experiments. Syroka-Korol et al. [138] have employed a non-local model to calculate a softening parameter, which also defined the damage zones in the RC beam. A 4PBT was employed for 12 beams with 3 different cross-sections. Both the statistical and deterministic size effects were investigated, and the conclusion was that statistical size effects can be negligible, while deterministic size effects can be easily seen in the structure response. A potential reason for these results can be the use of a 2D plane stress model instead of a 3D as used by [73], or the absence of transverse reinforcement. Furthermore, the randomness in the concrete was focused only in the area of shear failure rather in the entire beam.

Bažant et al. [13] have provided arguments to update the ACI code for shear design of RC beams. They verified that the ACI, CEB-FIB and Japanese design codes present similar shear capacity estimations for small beams, but overestimate it for deep beams. The codes also do not consider that the reinforcement will induce a size effect, using a non-linear FE model to show how the size effect exists and fits the size effect law established in [11]. Moreover, they also suggest that the results obtained by [97] also overestimate the shear capacity of deep beams.

Bentz [14] showed that the size effect has a direct relation to the tensile strength of RC. He showed that the ACI Code [3] has 3 different expressions to evaluate tensile strength due to the modulus of rupture (flexural crack strength), tensile strength of a split cylinder and the shear force required to cause diagonal web-cracking in prestressed members. Bentz has considered that the concrete is highly stressed if 85% of its volume is under the critical tensile strength. The smaller the amount of concrete in tension, the higher the influence of the size effect. Figure 4 illustrates the modulus of rupture, the split-cylinder and uniaxial tensile tests with the highly stressed volume (HSV).

Fig. 4

Uniaxial tests with HSV. Based on [14]

The size effect is most likely governed by the amount of concrete volume in tension, rather than a material or geometrical parameter [14]. The size effect due to the highly stressed concrete comes from the empirical relation:

$$\begin{aligned} k_{sz} = 0.4(1-\log _{10}{\text {HSV} }), \quad \text {HSV}\le 0.032\,\hbox {m}^3 \end{aligned}$$

(2)

where $k_{sz}$ is a scale factor to be used with the design equations for tensile strength from the ACI Code.

For a volume in tension higher than $1\,\hbox {ft}^3$ (or 316 mm per side dimensions), the size effect becomes negligible. Bentz has shown that this relation is sustained well from experimental data. This idea comes from the work of Hunter [69], who demonstrated that concrete specimens with side dimensions superior to 600 mm did not show statistical correlation with the compressive strength. The experimental data used in [14] is provided in the paper.

2.7 Importance of Benchmark Tests in Numerical Models

Traditionally, shear failure has been investigated using 4PBT with longitudinal reinforcement. Researchers have been able to gather the main aspects that dictate shear failure, such as the arch and beam mechanisms [45] and how shear capacity can drastically change with the shear-span-to-depth ratio [77]. Nevertheless, the reasons for the behaviour that leads to shear failure have not been analysed in such depth, for instance, the influence of aggregate interlock [30] or dowel resistance [83], known to have the main influence of shear failure in slender beams. Information about the maximum aggregate size, concrete strength, used rebar are also usually missing in the experiments report, making it complicated to model the underlying mechanisms of shear failure. In this sense, numerical methods have become essential tools in the study of RC structures.

Benchmark tests are important to understand the behaviour of complex problems in a systematic manner. According to the fib guide [44] there are 3 different levels of validation for numerical models:

• 1. Level 1: model calibration with material properties, to ensure that the material properties (such as Young modulus, Poisson ratio, compressive rate in failure $f_c$, etc) are properly used throughout the analysis. One should note that concrete parameters tend to vary depending on the used materials, so a statistical approach can be necessary to obtain meaningful results in the simulation;

• 2. Level 2: validation and calibration with systematically arranged element-level benchmark tests. At this level, we are interested in fundamental tests, where the test data represents a simple physical behaviour of the problem studied. Different experiments may be required in order to capture the behaviour of RC structures.

• 3. Level 3: validation and calibration at structural level. In this case, the numerical model is compared to complex behaviour of experiments, and compared with respect to the load-displacement diagram, shear capacity, deformation at peak load and deformation at failure, just to mention some of the relevant parameters in RC structures.

Most numerical models use validation up to level 2. For example, calibrating material parameters with an uniaxial tensile test data can be considered as level 1 validation. Obtaining a load-displacement curve for a 4PBT and comparing with the experimental one is an example of level 2 validation. Running a simulation of a complex or unconventional RC structure is a case of level 3 validation.

Collins et al. [32] organised a blind competition to evaluate how researchers in RC structures would predict the strength and load-deformation response of 4 orthogonally reinforced panels. Each panel was selected in order to measure different behaviours such as shear transfer, the compression softening and the tension stiffening. This is one of the first attempts to disclose how difficult it is to accurately capture the behaviour in shear of RC structures using numerical models.

The experience of the analyst in RC structures can be important when validating a numerical model. For instance, mesh sensitivity can affect the crack patterns obtained by the end of the analysis. Ingraffea and Saouma [70] introduced a discrete approach to concrete structures, where the mesh is updated after each time step to accommodate the newly formed crack surfaces, since the crack propagation path is not known in advance.

Červenka et al. [24, 25] have provided the most accurate prediction for 4 m thick beam challenge [31] using ATENA [23]. A simple uncertainty model was employed to consider variations of the material properties and non-homogeneities such as the aggregate size in the FE model. It was shown that modelling the aggregate interlock at the crack faces was crucial to obtain the correct prediction. If the aggregate interlock was ignored, a Strut-and-Tie would form instead of the diagonal crack, which would increase the resistance of the deep beam.

Sensitivity analysis should be performed to guarantee that the numerical analysis results are reliable. The FE mesh size itself can introduce a fixed length scale that will influence the results of the analysis [44].

In the next sections we discuss some of the common benchmark tests in concrete structures.

2.7.1 3-Point Bending Test (3PBT)

The 3-point bending test (3PBT) has been used to validate concrete models for many researchers [80, 81, 119]. Normally a specimen with an initial notch is tested so that the results are compared with benchmark parameters coming from the fracture mechanics theory, namely the critical mode I stress intensity factor $K_{Ic}$ when comparing crack propagation, or the fracture energy $G_F$ (also called size-dependent energy) when comparing the load-displacement curves. For instance, Karihaloo [80] describes different methods to obtain $G_F$ using 3PBT with central notch.

Most approaches for theoretical modelling of concrete consider softening behaviour [41]. The softening traction-separation law relates the stress at the FPZ in terms of the crack opening displacement w. Figure 5 illustrate a typical softening law. Note that the initial fracture energy $G_f$ (also denominated size-independent fracture energy) is also a parameter that can be obtained with 3PBT.

Fig. 5

Softening laws for concrete

One should observe that $G_F$ corresponds to the area under the softening curve, while $G_f$ represents only the area under the initial tangent $f_t/w_1$. Microcracks can concentrate in large areas of the specimen, retarding the crack propagation or even completely shielding it [81]. The presence of microcracks is related to the size effect in 3PBT.

The 3PBT with initial notch has also been used to validate numerical models. In this case, the comparison is usually made with the crack propagation path and the load-displacement curves. Due to the size effect related to the fracture energy, different dimensions and loading conditions will provide different values for the fracture energy. In general numerical models do not take the size effect into account. Moreover, numerical models based on linear elastic fracture mechanics (LEFM) do not have the capability of modellng the unnotched 3PBT for instance, as crack initiation is a non-linear problem. A general numerical model for concrete should be able to consider both cracked and pristine structures. Khalipour et al. [81] provides a review of different bending tests used to obtain the fracture energy of concrete and other effective parameters. Le Bellégo et al. [87] have used 3PBT tests to calibrate a non-local model for concrete.

Analysis using commercial softwares should also be able to produce similar results for the same problem, but it is usually not the case, as reported in [44]. Podgorniak-Stanik [119] proposed a 3PBT for two beams one with and one without shear reinforcement. Ten experienced analysts used the same software to predict the load capacity and the corresponding mid-span deflection, and the theoretical calculations for the section moment capacity and the sectional shear capacity. The range of the results provided by the analysts were around $3.5\%$ and $11.1\%$ for the moment capacity and the shear capacity, respectively. The load capacity estimations had a variation of about $17 \%$ for the beam with shear reinforcement, and $28 \%$ when only longitudinal reinforcement was used. However, the mid-span deflection deviation was about $60.4 \%$, since some analysts have considered a brittle shear failure, and others a ductile flexural shear failure. Ideally the assumptions for modelling RC structures should not depend on the analyst, but there are many interpretation on the actual behaviour of RC structures. A general numerical model based that can capture the real behaviour of concrete would produce more consistent results.

2.7.2 4-Point Bending Test (4PBT)

4PBT with longitudinal reinforcement is probably the most used experiment to study shear failure. The 4PBT furnishes a region in the centre with maximum moment, and constant shear force in the areas between the applied loading and the supports. For examples of 4PBT without reinforcement, the reader is referred to [130].

Swartz et al. [136] have tested a 4PBT with a single notch, very similar to the one illustrated in Fig. 6 (only the notch at the top is present, and $Q = 0$). 18 beams were tested, with the notch depth varying from 20 to 70 mm and the notch width was 3 mm. Values of the stress intensity factor for mode I and mode II were measured in the tests. The crack propagation angle observed in the experiments was about $30^\circ$ to $40^\circ$ but it should have been around $70^\circ$ according to the LEFM theory. This indicates that there is another force acting at the crack surfaces, most likely due to the aggregate interlock. Another reason discussed by Swartz et al. [136] about the aggregate interlock effect and friction is that the crack surfaces are under significant compressive stresses by the end of the experiment.

Fig. 6

4PBT used by Swartz et al. [136] and Swartz and Taha [137]

Swartz and Taha [137] have extended the work from [136] to investigate the suitability of fracture mechanics to determine the failure mechanisms in plain concrete structures under complex states of stress. 16 4PBT were performed, with three unnotched beams. The beams were tested with and without an axial force Q to measure its effect in crack propagation and failure loading. The crack propagation paths for each case are seen in Fig. 7. For the beams without axial force, the crack propagation was unstable. The unnotched beams failed in a similar way as in the Brazilian test. For the beams with axial force, the cracks would initiate at the notches in a stable way until the peak load. Then a new crack appears at midspan and almost at mid-depth, which propagated through the beam depth. Application of initial compression did not prevent crack formation.

Fig. 7

Influence of the axial force in the crack propagation paths [136, 137]—case without axial force Q (unstable—left) and with axial force Q (stable—right)

4PBT also furnish information on the possible shear failure modes due to crack propagation, as defined by Kotsovos [82] and the decrease of capacity shown by Kani [76, 77]. The load-displacement curve is perhaps even more important, as numerical models can be able to capture the correct crack patterns formed in failure, but can fail to match the load-displacement curve and therefore the softening behaviour seen in the experiments.

The behaviour of RC structures in shear failure cannot be evaluated by just evaluating a single RC structure. Leonhardt and Walther [89] have proposed a series of tests known as the Stuttgart Shear Tests, where nine 4PBT with different values of a/d were analysed and shear valleys similar to the one reported by Kani were reported. Testing series of beams can provide the necessary insights to validate a general RC model. However, only a single beam was tested for each shear-span-to-depth, so it is not possible to consider how other influencing factors, such as size effects, can be measured. It is important to perform adequate model verification and validation as defined in [140] to assess the limits of the numerical model. Ideally a general model should be able to reproduce the shear valley defined by Kani [77], but it is likely to be valid only for certain shear-span-to-depth ratios, as the shear transfer mechanisms change depending on the a/d ratio.

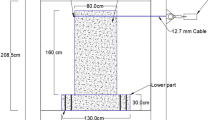
2.7.3 Push-Off Test

Hofbeck et al. [61] have proposed a new test to evaluate shear failure, known as push-off test. The specimen is designed to fail in shear, where shear loading is generated without moment for a certain applied load (see Fig. 8). These tests represent a simplification of a typical shear failure zone in a 4PBT. The advantage is that a smaller scale specimen is required. A drawback for numerical simulation is the use of different types of reinforcement to ensure that the reinforcement is adequately constrained in the structure.

Fig. 8

Typical Hofbeck test specimen

In [61], the tests were performed for specimens with an initial crack in the shear failure zone. Pristine specimens were also tested to quantify the influence of the initial crack.

When a crack is present along the shear plane, there is a reduction of the ultimate shear transfer strength and increase of the slipping, and it is independent from the applied loading. The shear transfer strength depends on the reinforcement ratio and the compressive yield strength $f_y$. A crack in the shear plane sets a limit on the influence of the reinforcement ratio and $f_y$. Significant dowel action is observed in the cracked specimens, even though rubber sleeves were placed around the legs of the stirrups to prevent dowel action.

The shear strength of the initially cracked specimens is not directly proportional to the amount of reinforcement. The data suggests that the slip in the shear plane is higher for the pre-existing crack cases.

An issue present in push-off tests is that there is no standardised test, so different authors make small modifications in the test in order to measure the influence of a particular mechanism. This issue contributes to the lack of unified understanding of shear failure in RC structures.

Mattock and Hawkins [107] showed that the shear strength is achieved in different ways, due to the presence (or not) of an initial crack. The shear strength in cracked specimen depends on shear mechanisms such as the aggregate interlock effect, the dowel action or the axial restraint of the reinforcement crossing the shear plane. In this case, the slip is greater compared to the pristine specimen case, due to the reduction of the ultimate shear stress. For the uncracked case, the shear strength is achieved after several cracks have appeared in the shear plane.

Walraven and Reinhardt [147] have done an extensive study on the mechanism of shear failure in push-off tests. They modified the push-off specimen so the shear failure would appear at different angles, from $0^\circ$ to $75^\circ$. The failure was due to a combination of shear and compression loading. Notably, the failure loading for the specimens that failed mostly due to the shear component was much smaller than any failure loading due to the compression component of loading.

Echegaray-Oviedo et al. [40] also proposed a modified version of the push-off test for initially cracked specimens. The initial crack can be controlled, one of the reasons why is difficult to compare results amongst different push-off experiments. Since the slip displacement is also controlled, it is possible to analyse the micro and macro-roughness at the crack faces. Echegaray-Oviedo et al. [40] mention that better understanding of these conditions can also lead to insights on size effects.

2.8 Summary of RC Structures in Shear

In this section we reviewed important aspects of shear failure and different attempts to investigate this problem. The 4PBT is one of the most used experimental set-ups to measure shear capacity in RC structures. However, empirical and numerical models on shear failure are designed for particular cases, for instance, specific loading, geometries and reinforcement ratios [30]. While these models can show good performance for their chosen benchmark, they can fail to represent well other possible shear failure types, such as defined by Kotsovos [82]. A more consistent approach would be to validate a model against series of tests, such as performed by Leonhardt and Walther [89] for 4PBT or Collins et al. [32] for RC plates.

Additionally, the known mechanisms involved in shear are not represented in the models. For instance aggregate interlock can generate friction at the diagonal cracks, which increases the loading capacity of the structure, but contact models are not normally employed. The bond-slip behaviour at the steel-concrete interface also plays an important role for short beams, where the arch action is the main responsible for the shear capacity. Some authors have modelled this behaviour by refining the discretisation around the reinforcement (for instance, [72]), but overall this behaviour is not implemented explicitly. Analysts should focus on modelling the actual behaviour of RC structures.

Numerical models are based on assumptions coming from continuum and fracture mechanics, but these theories do not represent the behaviour of RC structures during shear failure. Concrete is a particulate material, being composed by sand, aggregates and cement, so a numerical model that does not enforce the same conditions seen in fracture mechanics could provide better results. In this sense, peridynamics (PD) is a framework that is based on continuum mechanics, but does not present discontinuities in the formulation, which permits to model pristine and cracked domains without special assumptions. PD is a particle-based method, so it can model the concrete internal structure easily. For these reasons, PD is a potential numerical method for obtaining a more general approach in modelling RC structures. Several researchers have already employed PD in concrete modelling. We review the PD theory and its application on concrete structures in the next sections.

3 Bond-Based PD

PD was introduced by Silling [131] in order to tackle fracture mechanics problems. The classical definition of continuum mechanics equilibrium equations contain partial derivatives, as can be seen in Eq. (3):

$$\begin{aligned} \nabla \varvec{\sigma } + \mathbf {b}({\mathbf {x}},t) = \rho \ddot{{\mathbf {u}}}({\mathbf {x}},t) \end{aligned}$$

(3)

where $\varvec{\sigma }$ represent the Cauchy stresses, ${\mathbf {x}}$ is a material point, $\mathbf {b}({\mathbf {x}},t)$ are the body forces acting in ${\mathbf {x}}$, ${\mathbf {u}}({\mathbf {x}},t)$ are the displacement field, $\ddot{{\mathbf {u}}}({\mathbf {x}},t)$ stand for the acceleration, and $\rho$ is the mass density.

Partial derivatives pose a difficulty in fracture mechanics, since cracks represent discontinuities in the geometry and also introduce singularities in the stress field at the crack tips in the LEFM theory. For this reason, special assumptions need to be taken in fracture mechanics problems, whether using analytical [10] or numerical [127] approaches. Silling redefined the equilibrium equation in integral form rather than using partial derivatives. The main advantage of this new approach is that discontinuities can be dealt directly with the integral form. Since no modifications are needed, PD can model problems such as crack initiation, a non-linear problem that is not straightforward in LEFM. Another advantage in dynamic problems is that the formulation can also capture crack branching [53] without special assumptions. Crack branching is a particular difficult problem to model with numerical methods, due to the complexity of the physical behaviour that leads to a propagating crack to split into 2 new crack paths. Other authors have used an integral form, namely Eringen [42, 43], Kunin [84] and Rogula [124] are some of the most known authors.

Bond-based is the original PD formulation, described in detail in Silling [131]. The bond interaction is defined by pairwise forces acting in the direction of the bond, which is one of the main characteristic of this framework. This simple assumption also enforces limitations to the material properties, namely a fixed Poisson’s ratio of 1/3 for 2D plane stress problems and to 1/4 for 2D plane strain and 3D problems [131]. This limitation was first described by Love [95]. The pairwise interaction between two particles can be defined as [131, 134]:

$$\begin{aligned} \rho \ddot{{\mathbf {u}}}({\mathbf {x}},t) = \int _{\mathscr {H}} \mathbf {f}({\mathbf {u}}({\mathbf {x}}^{\prime },t)-{\mathbf {u}}({\mathbf {x}},t),{\mathbf {x}}^{\prime } - {\mathbf {x}})dV_{x^{\prime }} + \mathbf {b}({\mathbf {x}},t) \end{aligned}$$

(4)

where $\mathbf {f}$ is the pairwise force function that the particle ${\mathbf {x}}^{\prime }$ exerts on the particle ${\mathbf {x}}$, $\mathscr {H}$ delimits the area of influence of particle ${\mathbf {x}}$. It is usual to adopt the relative position $\varvec{\xi }$ of the two particles in the reference configuration as:

$$\begin{aligned} \varvec{\xi } = {\mathbf {x}}^{\prime } - {\mathbf {x}} \end{aligned}$$

(5)

and the relative displacement $\varvec{\eta }$ is defined similarly as:

$$\begin{aligned} \varvec{\eta } = {\mathbf {u}}^{\prime } - {\mathbf {u}} \end{aligned}$$

(6)

In order to comply with the equilibrium conditions, Eq. (4) must satisfy the balance of linear and angular momentum. The balance of linear momentum is demonstrated if:

$$\begin{aligned} \mathbf {f}(-\varvec{\eta },-\varvec{\xi }) = -\mathbf {f}(\varvec{\eta },\varvec{\xi }) \end{aligned}$$

(7)

which also corresponds to Newton’s third law. The balance of angular momentum is satisfied if:

$$\begin{aligned} (\varvec{\xi } + \varvec{\eta }) \times \mathbf {f}(\varvec{\eta },\varvec{\xi }) = \mathbf {0},\quad \forall \varvec{\eta }, \varvec{\xi } \end{aligned}$$

(8)

is true for every particle. This condition can also be fulfilled if $(\varvec{\xi } + \varvec{\eta })$ is aligned to $\mathbf {f}(\varvec{\eta },\varvec{\xi })$, which is a particularity of the bond-based framework.

The area of influence (also called as family) of a particle is commonly defined as a circumference (in 2D) or a sphere (for 3D) with radius $\delta$, also known as the horizon, with the following property:

$$\begin{aligned} \forall |\varvec{\xi }| > \delta \Rightarrow \mathbf {f}(\varvec{\eta }, \varvec{\xi }) = \mathbf {0}. \end{aligned}$$

(9)

The significance of Eq. (9) is that if an arbitrary particle ${\mathbf {x}}^{\prime }$ is further away the distance $\delta$ from the particle ${\mathbf {x}}$, then ${\mathbf {x}}^{\prime }$ has no influence over ${\mathbf {x}}$. In most cases, a symmetrical horizon is used, but there are particular cases when a non-symmetric horizon has to be employed [112]. Figure 9 illustrates the horizon of particle ${\mathbf {x}}$, the force $\mathbf {f}$ and deformed state $\mathbf {y}$ in the bond-based theory.

Fig. 9

Horizon of a particle in bond-based PD

Two particles interact with each other through a shared bond, which also contains the material properties (stiffness). The bond forces are aligned with the bond and have opposite directions. In the bond-based theory, a bond has the same analogy of a spring in classical continuum mechanics.

We assume that the scalar bond force f depends only on the bond stretch s, defined as:

$$\begin{aligned} s = \frac{|\varvec{\xi } + \varvec{\eta }|-|\varvec{\xi }|}{|\varvec{\xi }|} = \frac{y-|\varvec{\xi }|}{|\varvec{\xi }|} \end{aligned}$$

(10)

Damage is simply introduced into the PD framework through the bond breakage of any two arbitrary particles. In bond-based, the most common damage criterion relies on a critical bond stretch, which is calculated in terms of the horizon size and the material critical energy release rate [131, 134]. Damage evaluation in PD can be determined through a history dependent model, by:

$$\begin{aligned} f(y(t),\varvec{\xi }) = g(s(t,\varvec{\xi }))\mu (t,\varvec{\xi }) \end{aligned}$$

(11)

where $g(s)=c s$, c is a constant and $\mu$ is a history-dependent scalar-valued function, assuming either the values 0 or 1 according to:

$$\begin{aligned} \mu (t,\varvec{\xi }) = \left\{ \begin{array}{ll} 1 &{} \hbox {if } s(t^{\prime },\varvec{\xi }) < s_0 \hbox { for all } 0 \le t^{\prime } \le t, \\ 0 &{} \hbox {otherwise} \end{array} \right. \end{aligned}$$

(12)

In this case, $s_0$ is the critical stretch for bond failure. Failure criterion is usually only defined when the bond is stretched, however we should also assume that failure in compression is possible [155]. Other examples of bond failure criteria in the bond-based theory include a bi-linear model [125, 158], where it is desirable to capture the softening behaviour of the material.

The local damage at a point is defined as:

$$\begin{aligned} \varphi ({\mathbf {x}},t) = 1 - \frac{\int _{\mathscr {H}}\mu ({\mathbf {x}},t,\varvec{\xi })dV_\xi }{\int _{\mathscr {H}} dV_\xi } \end{aligned}$$

(13)

where ${\mathbf {x}}$ has been included as a reminder that the history model also depends on the position in the body. One can see that $0\le \varphi \le 1$, with 0 representing the undamaged state and 1 representing full break of all the bonds of a given particle to all other particles inside the horizon $\delta$. The broken bonds will eventually lead to some softening material response, since failed bonds cannot sustain any load.

As we have seen, there are only two parameters that define the PMB material, the spring constant c and the critical stretch $s_0$. Assuming $\varvec{\eta } = s\varvec{\xi }$, the local strain energy can be expressed as [134]:

$$\begin{aligned} W = \frac{\pi c s^2\delta ^4}{4} \end{aligned}$$

(14)

This relation must be identical to its equivalent in the classical theory, $W = 9ks^2/2$, where k represents the material bulk modulus [134]. The spring constant of the PMB material model is obtained as:

$$\begin{aligned} c = \left\{ \begin{array}{ll} \frac{18 k}{\pi \delta ^4} &{} \text {3D} \\ \frac{12 E}{h \pi \delta ^3(1+\nu )} &{} \text {plane stress/strain} \end{array} \right. \end{aligned}$$

(15)

where E stands for the Young’s modulus, $\nu$ is the Poisson’s ratio and h is the thickness.

Other authors have proposed different constitutive models other than the PMB. For instance, a conical micro-modulus has been used by [17, 53, 92] and it is defined as:

$$\begin{aligned} c = \frac{24E(1-\frac{|\varvec{\xi }|}{\delta })}{\pi \delta ^3 (1-\nu )} \end{aligned}$$

(16)

Huang et al. [65] have introduced a function $g = \left( 1-\left( \frac{\varvec{|}\xi |}{\delta }\right) ^2 \right) ^2$ to account for the weakening of the long-range forces as the distance between the particles increase. Hence, the micro-modulus c assumes the form:

$$\begin{aligned} c = \frac{315E}{8\pi \delta ^3} \end{aligned}$$

(17)

for plane stress problems.

3.1 Surface Effects

The material constants obtained in Eqs. (15)–(17) are only valid for the horizon of the bulk material. In case of particles near surfaces, their neighbourhood around these particles is reduced, leading to an overestimation of the bond stiffness. This issue is known as surface effects in the PD literature, and first reported in Madenci and Oterkus [105]. Figure 10 illustrates the situation of a particle family close to an edge, compared to another particle family completely inside the material.

Fig. 10

Horizon of a particle in the bulk (${\mathcal {H}}_1$) and a particle near a free surface (${\mathcal {H}}_2$)

Le and Bobaru [86] have made a revision of the surface effects correction for bond-based and state-based theories (state-based theory is discussed in Sect. 4). The volume method [132] is the simplest approach, and more effective in the bond-based framework. It is defined in Eq. (18).

$$\begin{aligned} \lambda = \frac{2V_0}{V({\mathbf {x}})+V({\mathbf {x}}^{\prime })} \end{aligned}$$

(18)

with $\lambda$ is the correction factor for the micro-modulus, $V_0$ is the volume (or area for 2D problems) of the horizon in the bulk, $V({\mathbf {x}})$ and $V({\mathbf {x}}^{\prime })$ represent the volumes of particles ${\mathbf {x}}$ and ${\mathbf {x}}^{\prime }$, respectively.

Other methods include the force density [105] (scale the forces so they become equivalent to a particle in the bulk), the energy method [105] (similar to the force density method, it consists in calculating the equivalent strain energy density for the particle close to the surface), the force normalisation [99] (comparing the force to move the particle a small distance from its equilibrium position and comparing it to the corresponding force for a particle in the bulk) and the position-aware method.

3.2 Volume Correction

Another issue in PD arises on how to define the family of a particle, as the particles around the edge of the horizon $\delta$ are not be completely contained, as depicted in Fig. 11.

Fig. 11

Family of a particle with symmetric circumference horizon

Assuming that partially contained particles belong entirely to a given particle family is a source for errors similar to the surface effects. To overcome this problem, a simple rule defined by [64, 105] takes into account the volume of the particle near the edge of the horizon and is given by Algorithm 1, where $vol_{scale}$ is a factor that multiplies the current volume (or area for 2D problems) of particle ${\mathbf {x}}$ during integration.

Seleson [128] compared three common algorithms to calculate the volume of the neighbourhood of particle ${\mathbf {x}}$ and proposed an analytical calculation of partial areas for 2D problems. The partial areas are defined by the intersection of the area of a particle ${\mathbf {x}}^{\prime }$ with the horizon of particle ${\mathbf {x}}$. Convergence and accuracy are improved using the analytical calculation, but some oscillation still remains in the analysis. Seleson [128] has also calculated the centroid location of the partial areas, instead of using the centroid of a square. This simple modification removed the oscillations and improved the convergence of PD.

Seleson and Littlewood [129] have generalised the discussion of [128], addressing convergence and accuracy for 1D, 2D and 3D problems for both bond-based and state-based formulations. They concluded that the partial volume can be used for 3D problems, but the volume is computed numerically rather than analytically. They have also investigated how influence functions can be used to smooth the contributions of the particle volume near the horizon. Polynomial influence functions have shown to be effective in improving the convergence and accuracy, also removing undesirable oscillations.

The reader is referred to [55] for more information on the bond-based PD theory and recent developments.

3.3 Concrete in Bond-Based PD

Table 1 presents a summary of the papers of concrete structures using the bond-based formulation. We compare in terms of the material models(linear, bi-linear, tri-linear), including variations of the bond-based theory such as micropolar [48], damage criterion (condition necessary for a bond to break), benchmarks (how the formulation was validated) and model validation (how the benchmark was compared to the formulation proposed in the papers).

Table 1 Comparison of between RC structures models—bond-based PD

The first paper to tackle concrete structures using PD was from Gerstle et al. [48], where the authors discuss a modification of bond-based PD in order to use different Poisson’s ratios. The proposed modification is a micropolar formulation, where moment densities are introduced into the formulation. A new integral equation has to be considered, and it is given by:

$$\begin{aligned} J_1 \ddot{\theta }= \int _\mathscr {H} \mathbf {m}({\mathbf {x}}^{\prime })-\mathbf {m}({\mathbf {x}}) dV_\xi + \mathbf {m}_b({\mathbf {x}}) \end{aligned}$$

(19)

where $J_1$ is the moment of inertia, $\ddot{\theta }$ is the angular acceleration and $\mathbf {m}({\mathbf {x}})$ is the moment associated to particle ${\mathbf {x}}$. Eq. (19) is to be used conjointly with Eq. (4). The addition of moments to the formulation also enforces that the pairwise forces are no longer in the direction of the bond, but they must have same magnitude and opposite direction. The moment vectors do not have any limitation in terms of magnitude and direction. If a bond could be seen as a spring in the bond-based formulation, it has to be considered as a beam in the micropolar framework.

More recently, Sau et al. [126] have used the micropolar formulation to address RC structures. Sau and co-workers evaluate two problems, a deep simply supported beam and a 4PBT. The failure loading in shear predicted by the American Concrete Institute (ACI) [1] code for a deep beam is 8115 N, while the shear strength obtained during the simulations was 7868 N, where a large crack propagates throughout the beam. However, it is not possible to conclude that the results are valid or not, since there are no values for failure loading of the numerical model, nor actual values of failure loading or crack propagation paths of the deep beam. For the case of a beam with longitudinal reinforcement, the model prediction was not accurate. It has captured some of the behaviour in flexural failure, but there were some inconsistencies, for example, the crack propagation stopped at the transversal reinforcement, which does not happen in the actual experiment. Sau et al. mention that a possible reason for this is the use of a 2D model [126].

Yaghoobi and Chorzepa [155] used an exponential softening law to model fibre reinforced concrete structures. The model was compared with experimental results for the 3PBT, where the ratio of fibre and the position of the initial notch was varied. In all cases, a good agreement was obtained.

Miranda et al. [110] have suggested a modification of the bond-based theory to increase computational efficiency in 3D problems. They define an alternative bond stretch $\bar{s}$ and it is written as:

$$\begin{aligned} \bar{s} = \frac{y^2-|\varvec{\xi }|^2}{2|\varvec{\xi }|} \end{aligned}$$

(20)

and it can be shown that $\bar{s} = \frac{1}{2}s^2+s$. Comparing it to Eq. (10), the computational gain comes from not performing a square-root operation, using the quadratic form to calculate the stretch. For small deformation problems, there is no tangible difference for the bond stretch values whether using Eqs. (20) or (10). To validate the model, an RC beam in a 3-point bending test (3PBT) is shown in [110], and the structure appears to collapse due to shear failure. However, the failure loading is not provided, making difficult to compare the results quantitatively.

Huang et al. [65, 66] have proposed a modification of the bond-based formulation, where the micro-modulus also depends on the distance between the particles. This method takes into account the influence of nearby particles, and the reduction of the contribution of the bond stiffness for the particles that are more distant. Additionally, Huang and co-workers have introduced damping to obtain a quasi-static solution from a dynamic implementation of bond-based PD. The loading was introduced in load steps, to avoid the sudden breakage of bonds near the load application position. A 2D concrete only cantilever subjected to a point load at the end was compared to the analytical solution for the damaged and no damaged cases. The failure loading of the PD analysis was in good agreement with the analytical one.

Gu et al. [51] have used the constitutive models from [66] to analyse the wave dispersion of Brazilian discs under a Split Hopkinson Pressure Bar (SHPB) technique. In this case, the damage in the disc is very diffused. Gu et al. claim that the wave dispersion is reduced with the proposed constitutive model considering the original PMB model.

In [113], the bond-based PD is coupled with a FEM code, where only the area of interest is contained inside a PD region. The other parts of domain are discretised with an irregular FE mesh, in order to reduce the computational costs but retaining the main advantages of PD. A Sequentially Linear Analysis (SLA) is used, where the different criteria for bond breakage are analysed, namely (a) only one bond is allowed to break per iteration, (b) no control on the number of broken bonds per iteration, and (c) limiting the number of broken bonds per iteration. The results show that too many broken bonds can change the crack propagation path. The best approach is to limit the number to broken bonds per iteration a low number. Limiting the bond breakage can change the physical behaviour for a dynamic analysis, but has little influence in a quasi-static one. Nia et al. [113] investigate some examples such as a double cantilever beam and 3PBT with and without holes along the depth of the beam. A single edge notched pure shear test was also performed, in order to evaluate if the correct crack propagation path is obtained.

Aydin et al. [6] have also used SLA with an overlapping lattice model. However, details of the model are not disclosed, and it is not clear which PD formulation was used (although it appears to be a bond-based model combined with truss models).

Li and Guo [92] have used a dual-horizon PD model to investigate fibre-reinforced polymers bonded to a concrete structure. The dual-horizon was first introduced by [122, 123] to tackle the issue of particles with different horizon sizes, and is particularly useful for adaptivity [17, 52] or for irregular particle discretisations [112].

In [161], they propose an implicit implementation of bond-based PD for static problems using a bi-linear relationship between the forces and the stretch in the bonds. A progressive bond damage formulation is proposed when a linear stretch is attained, leading to a gradual reduction of the remaining bond stiffness. Zaccariotto et al. [161] have also analysed a 3PBT and a 4PBT where initial cracks are present.

Yang et al. [158] have proposed a tri-linear bond stretch model for concrete structures, based on a bi-linear model that can be obtained analytically, based on Bazant [8]. Figure 12 illustrate the bi-linear softening law and the tri-linear bond model.

Fig. 12

Bi-linear softening and tri-linear bond models

The crack widths $w_1$ and $w_f$ are obtained by:

$$\begin{aligned} w_1&= 2 \frac{G_f}{f_t} \end{aligned}$$

(21)

$$\begin{aligned} w_f&= \frac{2}{\beta f_t}(G_F-(1-\beta )G_f) \end{aligned}$$

(22)

where $G_f$ is the initial fracture energy, $G_F$ is the fracture energy, and $\beta = 1/4$ (from [149]). We can also assume that $G_F \approx 2.5 G_f$ is a good approximation for a bi-linear model [118]. Let us remark that the softening law is a representation of the residual tensile stress that arises at the crack tip, as defined by [63].

The history-dependent function used to calculate the damage is also modified to consider the softening behaviour and is defined as:

$$\begin{aligned} \mu (t, \varvec{\xi }) = \left\{ \begin{array}{ll} 1, &{} s \le s_0\\ \frac{\mathbf {f}(\varvec{\xi }, \varvec{\eta })}{|f_{max}|} &{} s_0< s < s_c \\ 0, &{} s \ge s_c \end{array} \right. \end{aligned}$$

(23)

A 2D plane stress model was used to simulate 3PBT, with an initial crack at the centre of the specimen. Different beam configurations have been tested experimentally and compared to the bond-based model solution, which provided a good agreement of the load-displacement curve and the maximum and failure loading. Yang et al. [158] have also analysed the influence of the elastic strain energy in determining the fracture energy, and they conclude that the most of the energy comes from the softening phase. They justify the use of a bond-based formulation due to the fact that the Poisson’s ratio has little influence in the structural capacity as this is mainly dictated by the fracture mechanism.

Rossi Cabral et al. [125] attempt to find a physical meaning for the horizon size. Let us remember that the stress intensity factor $K_I$ can be written as:

$$\begin{aligned} K_I = \sigma H \sqrt{\pi a} \end{aligned}$$

(24)

where a is the half-length of the crack and H is a function that depends on the geometry of the problem. For instance, $H = 1$ for a crack of length 2a in an infinite domain. Rossi Cabral et al. [125] propose that the horizon and the stress intensity factor can be related in a similar manner:

$$\begin{aligned} K_I = \sigma \sqrt{\delta } \end{aligned}$$

(25)

In this case, $\delta$ should be related to the FPZ of the material, implying that the horizon must be smaller than the size of the FPZ. If not, the crack will not propagate. This is one of the few studies to link the area of influence of the particle in PD with a physical meaning. Traditionally, the horizon size is defined as $\delta = m \Delta x$ in PD models, where $\Delta x$ is the grid spacing. Bobaru et al. [17] have investigated different aspects on convergence. Rossi Cabral et al. [125] is one of the few studies to establish a physical relation to the horizon size, which was also mentioned by [58] for anisotropic materials.

The fracture energy $G_f$ is defined as a random field, and it is given by a Weibull extreme value distribution such as [125]:

$$\begin{aligned} F(G_f) = 1 - e^{-\frac{G_f}{\beta }^\gamma } \end{aligned}$$

(26)

and $\beta$ and $\gamma$ are the scale and the shape parameters, respectively. The random value of $G_f$ for a bond is taken as the average value between the values of $G_f$ for the bond shared by particles ${\mathbf {x}}$ and ${\mathbf {x}}^{\prime }$.

Rossi Cabral et al. [125] have also introduced a new bi-linear model, where a numerical horizon $\delta '$ is employed with $\delta ' < \delta$ in order to ensure the physical behaviour of the material is respected.

The law descending branch $K_r$ is expressed as:

$$\begin{aligned} K_r = \frac{s_r}{s_p} \end{aligned}$$

(27)

where $s_p$ represents the kinking point of the force-stretch diagram, $s_r$ is the stretch for the fully damaged bond and $K_r \ge 1$. The final bi-linear model is given by [125]:

$$\begin{aligned} \frac{\delta '}{\delta } = \left( \frac{s_0}{s_p} \right) ^2 \frac{1}{K_r} \end{aligned}$$

(28)

The main advantage of this approach is that the change on $\Delta x$ or $\delta '$ do not require additional modifications of the bi-linear law, which is defined in terms of the material parameters E and $G_f$ and the material horizon $\delta$.

Zhang et al. [164] proposed a bond-based model for ultra-high-performance concrete (UHPC) structures using plain and polyvinyl alcohol (PVA) as fibre reinforcement. The PD model used a regular particle discretisation but the bonds were randomly assigned with the mechanical properties and fracture parameters of the PVA or the UHPC depending on the volume fraction. The model was validated with a 3PBT with initial crack, and achieved good agreement with the load-displacement curve of experimental results and similar crack propagation.

Hobbs et al. [60] have analysed RC structures using the bond-based theory for 3D problems. A quasi-static approach using displacement controlled test is employed. The Stuttgart beam series [89] consisting of nine beams with $1 \le a/d \le 8$ has been modelled. Overall the model is able to capture the different shear failure types (shear-web failure, shear-web compression, shear-flexural failure and flexural failure).

Zhao et al. [165] have studied the corrosion-induced fracture in RC structures. The concept of intermidiately-homogenenised PD (IH-PD) defined in [108], where the material properties defined at the bonds (elasticity, fracture energy) vary depending on the volume fraction of the constituent materials. The mechanical properties of the bonds are defined using a stochastic procedure (for more information, see [108]). In [165], the bonds are divided into three types: cement matrix, aggregate, and matrix-aggregate interface. The expansion around the rebar was approximated by a von Mises model due to its simplicity and no requirement to model the rebar itself [153]. The IH-PD model was validated with several examples, where the corrosion-induced cracks agrees well with similar experiments.

Tong et al. [141] proposed an exponential softening law for cohesive quasi-brittle materials. The bond force f is redefined as:

$$\begin{aligned} f = \left\{ \begin{array}{ll} c s, &{} s<s_0 \\ c s_0\left( e^{-k\frac{s-s_0}{s_0}}+\alpha \frac{s-s_0}{s_0} \right) , &{} s > s_0 \end{array} \right. \end{aligned}$$

(29)

where $s_0$ stands for the elastic limit of the bond stretch at the peak force, k governs the reduction of the bond force due to the softening and $\alpha$ controls the residual bond force. While $s_0$ is related to the initial fracture energy $G_f$, k and $\alpha$ are obtained from validation of the load-displacement curve with experimental results. Setting $\alpha = 0$, it can be found that [141]:

$$\begin{aligned} s_0 = \frac{s_c}{\sqrt{1+2/k}} \end{aligned}$$

(30)

The model is also coupled with FEM in the same way as in [162]. The coupled model is validated against a uniaxial test, which presented similar displacement fields to a commercial FE solution. Several values of k and $\alpha$ were tested in different validation experiments, such as the 3PBT with initial notch, double edge notched rectangular plate and L-shaped specimen. Overall the load-displacement curves havea good agreement with the experimental ones.

Gu and Zhang [50] have proposed a modified conjugated bond-based PD for the study of impact problems. Since the original bond-based formulation has material restrictions, the new approach permits the use of any Poisson ratio. A tangential force perpendicular to the bond is introduced, so that rotations are also considered in the formulation. The conjugated bond will break once the bond energy contributions from the normal and tangential forces reach a critical value. The model is used on the impact of a projectile in a concrete dam.

Other works on concrete structures include [116] for impact in an RC panel, [33] for the analysis of notched mortar beams under three-point bending using an extended finite-element method (XFEM), [91] for a 3-phase mesoscale model, and [47] for the analysis of a lap-splice model. Demmie and Silling [34] have modelled the extreme event of an aircraft collinding with an RC structure. Hai and Ren [54] investigated the use of RC slab in underwater explosion environment.

4 State-Based Peridynamics

The PD formulation assumes that any pair of particles interacts only through a central potential which is independent of all the other particles surrounding it. This oversimplification has led to some restrictions of the material’s properties, such as the aforementioned fixed Poisson ratio of 1/4 for isotropic materials. Also, the pairwise force is responsible for modelling the constitutive behaviour of the material, which is originally dependent on the stress tensor. To overcome this limitation, Silling et al. [135] have extended the PD formulation to include vector states. The vector states allow us to consider not only a particle, but a group of particles in the PD framework. Moreover, the direction of the vector states would not be conditioned to be in the same direction of the bond, as in the bond-based theory.

Figure 13 illustrates the particle interaction in state-based PD formulation. The main difference from the bond-based theory is that both horizons ${\mathbf {x}}$ and ${\mathbf {x}}^{\prime }$ are taken into account to the deformation of particle ${\mathbf {x}}$ and ${\mathbf {x}}^{\prime }$. Although the tractions are still in the same direction of the bond between ${\mathbf {x}}$ and ${\mathbf {x}}^{\prime }$, they are no longer the same magnitude. This formulation has been denominated as ordinary state-based PD.

Fig. 13

Particle interaction in state-based PD

One of the particularities of the state-based PD framework is the definition of the vector state. From [135], we assume ${{{\underline{\varvec{A}}}}}$ to be a vector state. Then, for any $\varvec{\xi } \in \mathscr {H}$, the value of ${{{\underline{\varvec{A}}}}} \langle \varvec{\xi } \rangle$ is a vector in the current space, where brackets indicate the vector on which a state operates. The set of all vector states is denoted $\mathscr {V}$. The dot product of two vector states ${{{\underline{\varvec{A}}}}}$ and ${{{\underline{\varvec{B}}}}}$ is defined by:

$$\begin{aligned} {{{\underline{\varvec{A}}}}} \cdot {{{\underline{\varvec{B}}}}} = \int _{\mathscr {H}} {{{\underline{\varvec{A}}}}}_i \langle \varvec{\xi } \rangle {{{\underline{\varvec{B}}}}}_i \langle \varvec{\xi } \rangle \ dV_{\xi } \end{aligned}$$

(31)

The concept of a vector state is similar to a second order tensor in the classical theory, since both map vectors into vectors. Vector states may be neither linear nor continuous functions of $\varvec{\xi }$. The characteristics of the vector states are listed in [135], and they imply the vector states mapping of $\mathscr {H}$ may not be smooth as in the usual PD model, including the possibility of having a discontinuous surface.

In the state theory, the equation of motion (4) is redefined as:

$$\begin{aligned} \rho ({\mathbf {x}}) \ddot{{\mathbf {u}}}({\mathbf {x}},t) = \int _{\mathscr {H}} \{ {{{\underline{\varvec{T}}}}}[{\mathbf {x}},t] \langle {\mathbf {x}}^{\prime } - {\mathbf {x}} \rangle {{{\underline{\varvec{T}}}}}[{\mathbf {x}}^{\prime },t] \langle {\mathbf {x}} - {\mathbf {x}}^{\prime } \rangle \} dV_{{\mathbf {x}}^{\prime }} + \mathbf {b}({\mathbf {x}},t) \end{aligned}$$

(32)

with ${{{\underline{\varvec{T}}}}}$ as the force vector state field, and square brackets denote that the variables are taken in the state vector framework.

To ensure balance of linear momentum, ${{{\underline{\varvec{T}}}}}$ must satisfy the following relation for any bounded body $\mathscr {B}$:

$$\begin{aligned} \int _{\mathscr {B}} \rho \ddot{{\mathbf {u}}}({\mathbf {x}},t)\ dV_{{\mathbf {x}}} = \int _{\mathscr {B}} \mathbf {b}({\mathbf {x}},t)\ dV_{{\mathbf {x}}} \end{aligned}$$

(33)

The balance of angular momentum for a bounded body $\mathscr {B}$ is also required:

$$\begin{aligned} \int _{\mathscr {B}} \mathbf {y}({\mathbf {x}},t) \times (\rho \ddot{{\mathbf {u}}}({\mathbf {x}},t) - \mathbf {b}({\mathbf {x}},t)) dV_{{\mathbf {x}}} = 0, \quad \forall t \ge 0,\ {\mathbf {x}} \in \mathscr {B} \end{aligned}$$

(34)

where

$$\begin{aligned} \mathbf {y}({\mathbf {x}},t) = {\mathbf {x}} + {\mathbf {u}}({\mathbf {x}},t) \end{aligned}$$

(35)

is the deformation vector.

The deformation vector state field is stated as:

$$\begin{aligned} {{{\underline{\varvec{Y}}}}}[{\mathbf {x}},t]\langle \varvec{\xi } \rangle = \mathbf {y}({\mathbf {x}} + \varvec{\xi },t)-\mathbf {y}({\mathbf {x}},t), \quad \forall {\mathbf {x}} \in \mathscr {B},\ \varvec{\xi } \in \mathscr {H},\ t \ge 0 \end{aligned}$$

(36)

The relative position vectors in the deformed configuration $\mathbf {y}_j-\mathbf {y}_k$ with $j=1, 2, \dots , \ N$ associated with material point ${\mathbf {x}}_k$ can be stored in a N-dimensional array as:

$$\begin{aligned} {{{\underline{\varvec{Y}}}}}[{\mathbf {x}}_k,t] = \left[ \begin{array}{c} \mathbf {y}_1 - \mathbf {y}_k \\ \mathbf {y}_2 - \mathbf {y}_k \\ \vdots \\ \mathbf {y}_N - \mathbf {y}_k \\ \end{array} \right] \end{aligned}$$

(37)

The force vector state is defined in the same way as the deformation state as:

$$\begin{aligned} {{{\underline{\varvec{T}}}}}[{\mathbf {x}}_k,t] = \left[ \begin{array}{c} \mathbf {t}_k^1 \\ \mathbf {t}_k^2 \\ \vdots \\ \mathbf {t}_k^N \\ \end{array} \right] \end{aligned}$$

(38)

The relative position vector $\mathbf {y}_j-\mathbf {y}_k$ can be expressed by the deformation state ${{{\underline{\varvec{Y}}}}}$ and the relative position vector ${\mathbf {x}}_j-{\mathbf {x}}_k$ as:

$$\begin{aligned} \mathbf {y}_j - \mathbf {y}_k = {{{\underline{\varvec{Y}}}}}[{\mathbf {x}}_k,t]\langle {\mathbf {x}}_j-{\mathbf {x}}_k\rangle \end{aligned}$$

(39)

Similarly the force density vector $\mathbf {t}_k^j$ that ${\mathbf {x}}_j$ exerts on ${\mathbf {x}}_k$ is defined as:

$$\begin{aligned} \mathbf {t}_k^j({\mathbf {u}}_j-{\mathbf {u}}_k, {\mathbf {x}}_j-{\mathbf {x}}_k,t) = {{{\underline{\varvec{T}}}}}[{\mathbf {x}}_k,t]\langle {\mathbf {x}}_j-{\mathbf {x}}_k\rangle \end{aligned}$$

(40)

The deformation state ${{{\underline{\varvec{Y}}}}}$ is independent, however the force state ${{{\underline{\varvec{T}}}}}$ depends on ${{{\underline{\varvec{Y}}}}}$.

Silling et al. [135] have defined two different formulations using the vector states, called ordinary and non-ordinary. The ordinary state-based theory can be seen as a generalisation of the bond-based, since the forces between the particles are still constrained to the direction of the bond. However, ${{{\underline{\varvec{T}}}}}[{\mathbf {x}}]$ has no longer the same value as ${{{\underline{\varvec{T}}}}}[{\mathbf {x}}^{\prime }]$. Since the bond forces are still aligned with the bond, the balance of linear and angular moment are automatically satisfied. In this sense, the non-ordinary formulation does not suffer from the bond force direction limitation. These differences are illustrated in Fig. 14.

Fig. 14

Differences between traction in the bonds in ordinary and non-ordinary state-based PD

4.1 Material Properties in the Ordinary State-Based PD

The process of obtaining the equivalent material properties in the ordinary state-based formulation is not straightforward. Similar to the bond-based theory, there are no direct equivalences of stresses and strains in the ordinary framework. In this sense, a typical approach is to draw an equivalence between the strain energy for the continuum mechanics theory and the strain energy density in the PD framework. The strain energy density $W^{PD}$ for an ordinary state-based PD is given by [105]:

$$\begin{aligned} W^{PD} = a \lambda _k^2 + b \sum _{j=1}^N \omega _{kj}(|\mathbf {y}_j-\mathbf {y}_k|-|{\mathbf {x}}_j-{\mathbf {x}}_k|)^2 V_j \end{aligned}$$

(41)

where $\lambda _k$ is the dilatation and is defined as:

$$\begin{aligned} \lambda _k = d\sum _{j=1}^N w_{kj} \left( \frac{\mathbf {y}_j-\mathbf {y}_k}{|\mathbf {y}_j-\mathbf {y}_k|} \cdot \frac{{\mathbf {x}}_j-{\mathbf {x}}_k}{|{\mathbf {x}}_j-{\mathbf {x}}_k|} \right) (|\mathbf {y}_j-\mathbf {y}_k|-|{\mathbf {x}}_j-{\mathbf {x}}_k|) V_j \end{aligned}$$

(42)

In this case, the PD material properties are given by the constants a, b and d. These parameters are obtained by solving a series of simple problems with known deformation, such as pure shear, uni-axial deformation, bi-axial deformation [105]. For isotropic materials and some specific anisotropic (e.g. orthotropic) materials, analytical solutions can be obtained. However, analytical solutions are not possible for generally anisotropic materials.

The equivalence between strain energy densities from continuum mechanics and PD framework also poses another inconvenience, as seen in the bond-based theory. Surface effects are also a source for errors in ordinary state-based formulation. Le and Bobaru [86] have also investigated how the different existing methods to tackle surface effects perform, and they have shown that the fictitious node approach generated the best results for state-based models. However, this method is only effective for simple geometries with homogeneous deformations, being difficult to implement in complex geometries and crack problems, limiting the use of this approach. The surface correction reduces the error for bond-based models, but do not eliminate it.

4.2 Non-ordinary State-Based PD

The forces of the bonds in the non-ordinary state-based are not restricted to the direction of the bond. It permits the model to be more general, but it also implies that the balance of linear and angular momentum is not automatically satisfied.

There are different ways to obtain the force-state in the non-ordinary framework, and one of the simplest methods is using correspondence models. In this case, a stress-strain relation from classical continuum mechanics is used as an intermediate step to obtain the traction state at the bonds. The main advantage of the correspondence model is that different material models such as plasticity, cohesive, amongst others, can be used without any modifications. Adopting these material models in bond-based or ordinary state-based require obtaining the equivalent of these classical continuum mechanics parameters into the PD framework. Another particularity of correspondence models is that surface effects correction are not required, since there is no equivalence with strain energy density from continuum mechanics. Silling et al. [135] have shown one way to define a mapping of the stress tensor as a PD force state using the parameters from classical continuum mechanics expressed in the PD framework. The deformation tensor in classical continuum mechanics is expressed as:

$$\begin{aligned} {\mathbf {F}}({\mathbf {x}}) = \frac{\partial \mathbf {y}}{\partial {\mathbf {x}}} \end{aligned}$$

(43)

The non-local deformation tensor is then defined as:

$$\begin{aligned} {\mathbf {F}}({\mathbf {x}})&= \left[ \int _{\mathscr {H}} \omega (|\xi |)({{{\underline{\varvec{Y}}}}}(\xi ) \otimes \xi )dV_{{\mathbf {x}}} \right] \cdot {\mathbf {B}}({\mathbf {x}}) \end{aligned}$$

(44)

$$\begin{aligned} {\mathbf {B}}({\mathbf {x}})&= \left[ \int _{\mathscr {H}} \omega (|\xi |)(\xi \otimes \xi ) dV_{{\mathbf {x}}} \right] ^{-1} \end{aligned}$$

(45)

where ${\mathbf {B}}({\mathbf {x}})$ is the shape tensor, $\otimes$ denotes the dyadic product of two vectors, and $\omega (|\varvec{\xi }|)$ is a dimensionless weight function, used to increase the influence of the nodes closes to ${\mathbf {x}}$. Queiruga and Moridis [120] have investigated how different weight functions affect the error and convergence in PD analysis for 2D problems. The shape tensor becomes a singular matrix if a particle has less than 2 bonds in 2D problems and 3 bonds in case of a 3D problem [58, 148]. Silling [133] highlighted that the shape tensor calculation may suffer in problems with large deformation or when extensive damage is present.

The traction state is defined explicitly as [135]:

$$\begin{aligned} {{{\underline{\varvec{T}}}}}[{\mathbf {x}},t]\langle {\mathbf {x}}^{\prime } - {\mathbf {x}} \rangle = \omega (|{\mathbf {x}}^{\prime } - {\mathbf {x}}|)\mathbf {P}({\mathbf {x}}) {\mathbf {B}}({\mathbf {x}}) ({\mathbf {x}}^{\prime } - {\mathbf {x}}) \end{aligned}$$

(46)

where $\mathbf {P}({\mathbf {x}})$ is the first Piola-Kirchhoff stress.

Some of the earlier works on the non-ordinary state-based PD were performed by Warren et al. [148], where they an explicit formulation for an aluminium bar. Breitenfeld et al. [18] have developed the first implicit formulation for non-ordinary PD for stationary crack problems.

4.2.1 Zero-Energy Modes

Zero-energy modes were first reported by [18], where a few methods were provided to regularise the problem. The addition of an extra term ${{{\underline{\varvec{T}}}}}_z[{\mathbf {x}}]\langle {\mathbf {x}}^{\prime } - {\mathbf {x}} \rangle$ to the bond force is a common method to eliminate the influence of these modes.

Several researchers have investigated the zero-energy modes. Silling [133] approached zero-energy modes as a material instability rather than a numerical instability. Hashim et al. [56] have implemented [133] approach for large deformation problems in an implicit PD non-ordinary formulation. Tupek and Radovitzky [142] investigated the use of alternatives formulation of the correspondence model in order to remove the zero-energy modes and other unrealistic physical behaviour, such as interpenetration. Luo and Sundararaghavan [98] have proposed a stress point method to control the zero-energy modes, where additional stress points are evaluated between different particles.

Yaghoobi and Chorzepa [156] have hypothesised that the zero-energy oscillations come from the poor approximation of the deformation gradient. By using Taylor series expansion, they proposed higher-order approximations through specific values for the influence function, for 1D and 2D problems. However, their approach is only valid for particles in the bulk, therefore particles near the surfaces are still susceptible to spurious oscillations.

Wu and Ren [150] used an averaging process to obtain a displacement field free of zero-energy mode. The proposed method consists of averaging the displacement of a single particle using the displacements of the neighbouring particles as shown in Eq. (47). However, this method does not suppress the oscillations of the stresses and strains.

$$\begin{aligned} \bar{{\mathbf {u}}}({\mathbf {x}})= & {} \int _H \bar{\omega }(|{\mathbf {x}}^{\prime }-{\mathbf {x}}|){\mathbf {u}}({\mathbf {x}}) \ dV_{x^{\prime }} \nonumber \\ \bar{\omega }(|{\mathbf {x}}^{\prime }-{\mathbf {x}}|)= & {} \frac{\omega (|{\mathbf {x}}^{\prime }-{\mathbf {x}}|)}{\int _H \omega (|{\mathbf {x}}^{\prime \prime }-{\mathbf {x}}|)\ dV_{x^{\prime \prime }}} \end{aligned}$$

(47)

Li et al. [90] have proposed a correction term that do not need to be calibrated. The additional bond force comes from the definition of a non-uniform deformation ${{{\underline{\varvec{z}}}}}\langle \varvec{\xi }\rangle = {{{\underline{\varvec{Y}}}}}\langle \varvec{\xi }\rangle - {\mathbf {F}} \varvec{\xi }$ and combining it with the principle of minimum potential energy. The strain energy ratio is also introduced, which corresponds to the energy coming from the additional bond force term. It was also shown that for a specific value of the bond force, the same formulation obtained in [133] is recovered.

Chen et al. [27] have made a retrospective of the most common ways to regularise the zero-energy modes, and propose an innovative approach based on a bond-associated deformation gradient. An alternative mapping to connect the deformation state and the reference configuration is denoted as:

$$\begin{aligned} \underline{\mathbf {Y}}\langle \varvec{\xi }\rangle = {\mathbf {F}}_\xi {{{\underline{\varvec{X}}}}}\langle \varvec{\xi }\rangle \end{aligned}$$

(48)

where ${\mathbf {F}}_\xi$ is the deformation gradient for the bond $\varvec{\xi }$. Additional constraints are necessary to fully define ${\mathbf {F}}_\xi$. A local bond-horizon $h_{x^{\prime }}$ is defined at ${\mathbf {x}}^{\prime }$, as can be seen in Fig. 15.

Fig. 15

Bond-associated horizon

The particles within the horizon $h_{x^{\prime }}$ that are also contained in the horizon of ${\mathbf {x}}$ are used to compute the bond-associated deformation gradient ${\mathbf {F}}({\mathbf {x}})^b$, and it is defined as:

$$\begin{aligned} {\mathbf {F}}({\mathbf {x}})^b = \left( \int _{H_x\cap h_{x^{\prime }}} \omega (|\varvec{\xi }|){{{\underline{\varvec{Y}}}}}\langle \varvec{\xi }\rangle \otimes \varvec{\xi }dV_{x^{\prime }}\right) {\mathbf {B}}({\mathbf {x}})^b \end{aligned}$$

(49)

where $H_x \cap h_{x^{\prime }}$ is the subset of $H_x$ where the approximated deformation gradient is defined. The local shape tensor ${\mathbf {B}}({\mathbf {x}})^b$ is defined in a similar way.

A good approximation of the bond-associated strain energy density can be obtained from the total strain energy density $W({{{\underline{\varvec{Y}}}}})$ and using the ratio of volumes:

$$\begin{aligned} W({{{\underline{\varvec{Y}}}}})^b = \frac{\int _{H_x\cap h_{x^{\prime }}} dV_{x^{\prime }} }{\int _{H_x} dV_{x^{\prime }}} W({{{\underline{\varvec{Y}}}}}) \end{aligned}$$

(50)

The traction force state of the bond-associated deformation gradient can be written as a function of the local variables ${\mathbf {B}}({\mathbf {x}})^b$, ${\mathbf {F}}({\mathbf {x}})^b$, $W({{{\underline{\varvec{Y}}}}})^b$ and $\mathbf {P}({\mathbf {x}})^b = \frac{ W({\mathbf {x}})^b}{{\mathbf {F}}({\mathbf {x}})^b}$. The original traction force state is recoved when $h_{x^{\prime }} \rightarrow H_{x^{\prime }}$.

4.3 Concrete in State-Based PD

Table 2 shows the works on the state-based PD for concrete structures. We analyse both ordinary (OSB) and non-ordinary state-based (NOSB) formulations in the same table.

Table 2 Comparison between RC structures models—state-based PD

In [49], Gerstle presents an extensive review of fracture mechanics and PD. He also proposes the State-based Peridynamic Lattice Model (SPLM). One of the differences from the state-based theory is that the neighbourhood of a particle has hexagonal form (in 2D) or a face-centred cubic lattice (in 3D). This arrangement for the family of a particle leads to a more robust discretisation compared to the one usually obtained from a delimited circumference or a spheric region. The SPLM was first validated for plain concrete using the Brazilian test. Then a 3PBT with longitudinal reinforcement was analysed. The crack patterns appear to be physically consistent, and the failure loading is close to the one predicted by the ACI code [1] for flexural failure. However, when the beam presents shear failure, the predicted failure loading obtained with the lattice PD model is more conservative than the failure loading calculated by the ACI code. One of the possible reasons for this behaviour is that aggregate interlock was not considered in the model [49]. The same problem is repeated adding web reinforcement, so the beam fails due to flexure rather than shear. The SPLM model is able to predict the correct crack pattern, and the failure loading is closer to the ACI prediction for flexural failure.

In [114], a modification of the SPLM model to include a new formulation of damage was proposed, entitled “two-spring damage model ”, where damage can localise in a single lattice, from being a smeared damage in conventional non-ordinary state-based damage models. The idea is to consider two serial springs in any bond connecting two particles. In this sense, the deformation associated with each spring can be very different, for example, the deformation is large one particle but small in the other. They evaluate three different types of experiments (uniaxial tension, uniaxial compression, and the Brazilian test) with material properties obtained from the ACI code [3]. The results are more stable when compared to the previous lattice formulation [49]. The formulation assumes that the bond forces also depend on force states computed at the previous time steps.

Lammi and Min [85] have developed a simple mesoscale model for concrete, in order to capture the material heterogeneity behaviour under a dynamic impact loading.

A model for cohesive crack growth in quasi-brittle materials was developed in [159]. A cohesive zone model (CZM) was defined in the PD sense in order to describe the softening behaviour due to the FPZ. This ordinary state-based model was compared against experimental results and the bond-based model from [28]. The ordinary state-based model was implemented using a dynamic code with damping, in order to obtain the quasi-static solution. A L-shaped panel and a 3PBT were compared to experimental and numerical benchmarks. The PD model was calibrated against the bond-based model from [28] for a symmetric 3-point bending with an initial crack. After calibration, the ordinary state-based model was validated with a L-shaped panel and another 3PBT, where mixed modes arise from the loading conditions. In both cases the PD model crack propagation paths were close to the experimental results, however the loading displacement curve did not agree with the experimental curve during the softening phase.

Yaghoobi and Chorzepa [154] employed an implicit non-ordinary state-based formulation [18] to model fibre-reinforced concrete structures, using a constitutive model for the cementitious matrix [74] and the fibre reinforcement [94], in order to capture the correct softening behaviour. They have validated their model with a 4PBT without notch and a 3PBT with a notch at the centre. The load-displacement curve is similar with the experimental results for a specific amount of fibre-reinforcement in both cases. They have also investigated a fibre-reinforced plate with semi-circle notches when varying the amount of fibre-reinforcement.

Yaghoobi et al. [157] have investigated the mesoscale structure of concrete using a non-ordinary state-based model, were the aggregate, the interfacial transition zone (ITZ), cement, and voids constitute the concrete material. The aggregate particles and voids were randomly distributed across the material. The ITZ has the same stiffness of the aggregate but half of the fracture toughness, so it is designed to break under lower loading, as expected. An isotropic exponential damage model is used to introduce the softening by reducing the stress level as the damage increases:

$$\begin{aligned} \varvec{\sigma }= (1 - D) \mathbf {C} \varvec{\epsilon }\end{aligned}$$

(51)

where $\mathbf {C}$ is the consitutive matrix, $\varvec{\sigma }$ are the Cauchy stresses and $\varvec{\epsilon }$ are the strains.

The damage D is defined in Eq. (52) [157]:

$$\begin{aligned} D&= \left\{ \begin{array}{ll} 0, &{} \text {if }\epsilon _{eq} < \epsilon _0 \\ 1 - \frac{\epsilon _0}{\epsilon _{eq}}e^{-\frac{\epsilon _{eq}-\epsilon _0}{\epsilon _f-\epsilon _0}}, &{} \text {if } \epsilon _0 \le \epsilon _{eq} \end{array} \right\} \end{aligned}$$

(52)

$$\begin{aligned} \epsilon _{eq}&= \frac{k-1}{2k(1-2\nu )}I_1 + \frac{1}{2k}\sqrt{\left( \frac{k-1}{1-2\nu }\right) ^2 I_1^2 + \frac{6k}{(1+\nu )^2}J_2 } \end{aligned}$$

(53)

where $\epsilon _0 = \frac{f_t}{E}$, $\epsilon _f=0.02$, $k=10$ is the ratio between the compressive and tensile strengths, $I_1 = tr(\varvec{\epsilon })$ and $J_2=tr(\varvec{\epsilon }\cdot \epsilon )-\frac{1}{3}tr^2(\varvec{\epsilon })$. The model was only validated qualitatively, due to the 2D nature of the study. Additionally, a size effect study could have been performed as the aggregates are explicitly modelled.

Lu et al. [96] have investigated the anchor bolt pullout problem using a non-ordinary state-based mode. A Drucker-Prager plasticity model was used to model the plastic yielding of the concrete. To avoid large deformation issues during the analysis, a method proposed by Hugues and Winget [68] was adopted.

To obtain the optimum grid spacing and horizon size, they used the model to obtain the solution of a 3D plain concrete beam subjected to a point load at the end. The deflection was in good agreement with the analytical solution and from a FE analysis. Next, they investigate an anchor bolt pullout problem. The steel reinforcement does not appear to be explicitly defined in the model, nor any particular changes in the model due to the large difference on the stiffness between steel and concrete. The load-displacement curves obtained by the PD model do not agree well to the experimental results. Not modelling the steel reinforcement and ignoring the friction generated by the pullout experiment are clear sources of error for this particular test.

Hattori et al. [57] have investigated the use of a correspondence model for steel reinforced concrete structures in 2D plane strain problems. Two examples were analysed, a cantilever beam with reinforcement at the top, and a pull-out test to evaluate the behaviour at the steel-concrete interface. While the model was able to predict the crack pattern for the concrete only structure, the results with the steel reinforcement were very different from the expected failure behaviour. The damage would originate at the interface and propagate therein, ignoring the damage that would appear due to the flexure of the beam. For the pull-out test example, the damage initiates around the interface as expected, but at a very low loading, implying that the interface bonds are breaking too early. The correspondence model from [135] does not take into account different materials. While some authors have been successful in dealing with bi-material problems [163], the difference in the stiffness between the materials was not prominent as the case of RC structures. Differences of 20 times in the Young’s modulus between concrete and steel are common, resulting in non-physical behaviour at the interface.

Another reason for the errors is the difference of wave speeds between steel and concrete. If a particle near the interface share bonds with both concrete and steel particles, the wave speed will propagate with very different speeds, leading to a surface effect at the materials interface.

In [57], the interface was considered to have the same properties as a concrete particle. Still, the interface bonds appear to break under low loadings, which can be associated to the shared bonds between concrete and steel to cause the stresses at the interface to grow in a much faster rate. A possible way to deal with the interface is to reduce the influence of the interface bonds in the calculation of the traction state vector. Using the influence functions of Eq. (54) is a simple way to control the forces at the interface, but the parameter $\gamma$ would need to be calibrated with another benchmark or experimental results, in order to model the interface behaviour [132].

$$\begin{aligned} \bar{\omega }(|\varvec{\xi }|) = \omega (|\varvec{\xi }|) \gamma \frac{\rho _{concrete}}{\rho _{steel}} \end{aligned}$$

(54)

An alternative proposed in [132] to deal with interfaces is the use bond-based, while maintaining the correspondence for the concrete and steel materials.

Wu et al. have analysed impact loading problems with ordinary state-based [152] and non-ordinary state-based [151] PD models. The Holmquist–Johnson–Cook (HJC) model [62] was incorporated into the PD formulation in each case to better represent the damage in the concrete structures. The model was validated with a L-shaped specimen and a 3PBT with offset notch, in order to generate mixed mode crack propagation. In all cases the crack propagation path from the dynamic analysis were similar to the ones found in the literature and other numerical benchmarks. There was good agreement with load-displacement curves.

4.4 PD Differential Operator

Recently, Madenci et al. [101, 102] have introduced the PD differential operator (PDDO). The idea is inspired in combining the advantages of PD with the previous formulations of classical continuum mechanics, where partial derivatives are employed. Effectively, the PDDO expresses function derivatives in integral form, using Taylor series expansion combined with orthogonal functions.

It was stated in [102] that the PDDO have similarities with the reproducing kernel method [16], such as the orthogonality condition. However, the definition of the derivatives is distinct. The use of higher-order derivatives makes this scheme more stable than previous formulations of PD.

Gu et al. [100] have proposed a modification of the non-ordinary state-based formulation to include the PDDO. The derivatives of the stress tensor and the displacements are expressed using the PDDO, where two cases are analysed: 1) first and second-order derivatives are employed in the formulation, and 2) only second-order derivatives are employed. The second approach has shown to eliminate the spurious modes observed in the strong form of the non-ordinary state-based model.

The PD theory [131, 135] was formulated in the strong form. If external forces are required in a PD analysis, they need to be enforced through body forces, which can pose a problem when comparing the solution of the PD analysis with other benchmark solutions. A weak formulation of PD using the PDDO was proposed by Madenci et al. [103], allowing for the use of natural boundary conditions.

The weak formulation can still suffer from instabilities, if the first derivative is used to obtain the internal forces, but the use of second-order derivatives prevents zero-energy modes. An alternative is to use the bond-associated deformation gradient from [27] to stabilise the spurious modes [104]. A different approach for PD using the PDDO employs the least square minimisation technique [101]. This model also shows stability and do not require uniform particle horizon.

To the authors’ best knowledge, the PDDO has not been used for the analysis of concrete structures. Problems with different material properties have not yet been considered in the weak formulation. A generalisation of the weak form for different materials (for instance, anisotropic) would be the first step, then make changes to the formulation to consider more than one material in the same analysis.

5 Conclusions

The purpose of this paper was twofold: (1) to review the mechanisms responsible for shear failure and benchmark tests used in the RC structures research field, and; (2) to review the state-of-the-art on PD for concrete structures. We have reviewed the different types of framework for PD, and how they have been employed in modelling concrete structures. Most of the PD models only consider plain concrete problems. Moreover, the used benchmark tests usually include an initial notch, in order to validate with the fracture energy from the LEFM theory, but most models do not take advantage in using the crack initiation capabilities of the PD framework.

While failure due to flexural behaviour is well understood in RC structures, shear failure is still an open problem. We have discussed some of the most important aspects of shear failure in RC structures. The arch and beam mechanisms provide a good insight on how shear damage appears. The reduction of shear capacity demonstrated with experiments by Kani [77] provides the big picture in shear failure. It is surprising that only few researchers have used the shear valley to validate their models on shear failure. The most common test to assess shear failure is the 4-point bending test (4PBT) with longitudinal reinforcement. While some information is provided for the tests (concrete strength, ratio of reinforcement, geometry), information such as the maximum aggregate size and load-displacement curves are not always reported. The lack of a clear standard for testing also makes difficult to compare the results from different experiments. Databases have been assembled for this purpose, however there are limitations on how to experimental data from different authors can be normalised for comparison.

Different material models have been defined for bond-based and ordinary state-based, including bi-linear and tri-linear softening models. The use of softening models in the material model has improved the results, as observed in [155, 158, 161]. The final result is a PD model that can match the crack patterns and load-displacement curves quite well with the experimental data for the used benchmark problem. However, further validation is necessary to assess the limits of the current PD model. Using series of tests as done by Hobbs et al. [60] can provide a better picture of the capabilities of a PD model. There are too many studies that rely on qualitative analysis only, such as comparison of the crack patterns from the PD model and an experimental result.

The majority of the PD models for concrete structures use the bond-based PD formulation. It appears that the choice on whether PD formulation to be applied in a particular problem depends on the user only. Nevertheless, these formulations have their own particularities, so a given PD framework may be more suitable for a specific type of problem. Bond-based is the simplest PD formulation but it has shown to provide good results for RC structures. Surface effects are present and can be reduced but not completely eliminated. On the other hand, the correspondence model can easily employ complex constitutive models but suffer from zero-energy modes. Only two papers tackled RC problems using state-based theory [49, 57]. It has shown to present issues when modelling failure in RC structures, as the interface between concrete and reinforcement is not represented adequately. Since the theory for correspondence models do not consider that two different materials exist in the same domain, instabilities arise at the interface, which will of course provide inaccurate or unrealistic crack patterns.

The known mechanisms of concrete structures are not enforced in the PD models, such as the friction generated by the aggregates on the crack surfaces and the relative slip between concrete and reinforcement. PD is a particle-based theory, that can incorporate well these aspects in the physical model. This will increase the likelihood to obtain a more general numerical model.

5.1 Research Questions

In this paper, four main challenges have been identified on the use of PD for RC concrete structures: (1) modelling the interface of the reinforcement and the concrete; (2) modelling of the real behaviour of RC structures that present shear failure; (3) ensure correct model validation, and (4) the choice of benchmark tests for validation/calibration.

The interface between the steel and the concrete has an important role for arising diagonal cracks. Little information can be found in the literature on modelling two materials in PD, and it is usually empirical. Aggregate interlock and dowel action are important mechanisms in shear failure that closely depend on the interface. We should investigate the issues arising in modelling the interface steel (ductile, continuum material) and concrete (quasi-brittle, particle-type material) in RC structures. Using bond breaking as the only damage parameter is sufficient for problems where mode I crack propagation is dominant, but it is not able to model possible shear stresses at the crack surfaces due to the aggregate interlock.

To model the relevant aspects in shear failure, we have to incorporate the known mechanisms for shear failure into the model. The residual tensile stresses has been included into PD models using softening laws (bi-linear, tri-linear, exponential), but it is not sufficient to capture the shear failure. The aggregate interlock is known to be an important factor that influences the shear failure in RC structures. It can be incorporated using a contact model at the formed crack surfaces, or by allowing a small number of bonds to heal, so there is resistance to sliding in the direction of the crack plane [75]. Another important shear transfer mechanism is the dowel action, that depends on the interface bonding between the concrete matrix and the steel reinforcement, as well as the yielding in the reinforcement [115].

We need to define tests used for calibration of the model and different tests for validating the model. For instance, a Brazilian test can be used to verify that the material properties used in the numerical model lead to failure at the expected load, with crack propagation also matching experiments. Then a 4PBT such as the experiment reported in [136] can be modelled to calibrate the aggregate interlock effect due to shear stresses at the crack surfaces. Once the numerical model is calibrated with the physics of the problem of interest, we can proceed to validation with another test, say the 4PBT with longitudinal reinforcement. Using different levels of validation as specified in [44] will provide a more accurate and consistent numerical model.

The choice of benchmark test is also important in order to capture the different aspects of behaviour in shear failure. 4PBT are popular since they are relatively easy to perform, and varying the shear-span-to-depth ratio for longitudinally reinforced beams permits to quantify how the model capture the shear transfer mechanisms defined in Sect. 2.2. Using a series of tests as performed by Collins et al. [32] and Leonhardt and Walther [89] also permits to quantify the different failure modes in RC structures that can be modelled.

Push-off tests are also suitable to analyse shear failure, but a standard test must first be defined by the research community. 3PBT with shear reinforcement can also provide additional information, since it will form an asymmetrical diagonal crack when failing in shear.