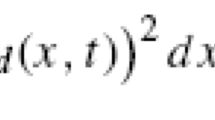Functional determinants for the second variation

Abstract

We study the determinant of the second variation of an optimal control problem for general boundary conditions. Generically, these operators are not trace class and the determinant is defined as a principal value limit. We provide a formula to compute this determinant in terms of the linearisation of the extrenal flow. We illustrate the procedure in some special cases, proving some Hill-type formulas.

1 Introduction

The main focus of this paper is the study of the spectrum of a particular class of Fredholm operators that arise in the context of Optimal Control. Our main result is a formula that relates the determinant of these operators to the fundamental solutions of an ODE system in a finite-dimensional space, in the spirit of Gelfand–Yaglom Theorem.

For operators of the form $1+K$, where K is a self-adjoint compact operator, various ways of defining a determinant function can be found in the literature. Going all the way back to Poincaré, Fredholm and Hilbert. If the operator K one considers is in the so called trace class, i.e. the sequence of its eigenvalues (with multiplicity) gives an absolutely convergent series, a definition of determinant which involves the (infinite) product of its eigenvalues is possible.

In our case, however, the classical approach does not immediately apply since, typically, the operators one encounters are not trace class. In fact, for a large class of optimal control problems, the second variation of the cost functional at a critical point, denoted by Q, can be written as:

$$\begin{aligned} Q(u) = \langle (1+K)u,u\rangle = \int _0^1 \left( -\langle H_t u_t,u_t\rangle +\sigma (Z_t u_t,\int _0^t Z_\tau u_\tau \textrm{d}\tau )\right) \textrm{d}t, \end{aligned}$$

where $u_t$ is an infinitesimal variation of the control and lives in a finite codimension subspace of $L^2([0,1],{\mathbb {R}}^k)$, $\sigma$ is the standard symplectic form on ${\mathbb {R}}^{2n}$, $Z_t$ a $2n\times k$ matrix and $-H_t$ a strictly positive definite $k \times k$ symmetric matrix.

Whenever the compact part K has this particular integral form, there is a non negative real number $\xi (K)$, which we call capacity, for which the following asymptotic relation for the ordered sequence of eigenvalues holds:

$$\begin{aligned} \lambda _n(K) = \frac{\xi (K)}{n} + O(n^{5/3}), \quad n \in {\mathbb {Z}}. \end{aligned}$$

(1)

This is shown in [3] and [10], under some hypothesis on the regularity of the coefficients $H_t$ and $Z_t$. For more details see Sects. 1.1 and 2 and Appendix A.

This symmetry of the spectrum allows us to talk about trace and determinant of the operators K and $1+K$ in the sense of principal value limits. In particular, whenever the compact part of the second variation is trace class, this limit coincides exactly with the usual Fredholm determinant defined for trace class operators. A similar approach has been independently adopted in the works [19, 20] to study the spectrum of Hamiltonian differential operators.

There are, of course, many other ways to define a determinant function for classes of Fredholm operators. For instance, one could apply the theory of regularized determinants, see [27], or rely on the so-called $\zeta -$regularization, see [15] for details. The literature concerning these topics is vast. To mention a few works, one could refer to [24, 25] for Sturm-Liouville problems, to [17] for graphs and to [16] for similar results proved in the general framework of elliptic operators acting on sections of vector bundles. A relation between regularized determinants and $\zeta$-regularization is given in [18].

It is worth pointing out another feature of the construction. Theorem 1 relates the determinant of $1+K$ to the fundamental solution of a finite-dimensional system of (linear) ODEs. This provides a way to compute the determinant and allows to recover some classical results such as Hill’s formula for periodic trajectories. This kind of formulas have important applications since they allow to relate variational properties of an extremal (i.e. the eigenvalues of the second variation), to dynamical properties such as stability. These latter properties are usually expressed through the eigenvalues of the linearisation of the Hamiltonian system of which the extremal we are considering is solution. Take the case of a periodic, non-degenerate trajectory. On one hand, knowing the sign of the determinant amounts to know the parity of the Morse index of the extremal. On the other hand, this sign is completely determined by the number of positive eigenvalues of the linearisation grater than one. Applications of this kind of ideas go back to Poincaré’s result about the instability of closed geodesics and can be found, for example, in [13] or [21]. For several interesting examples of the interplay between parity of Morse index and stability see for instance [11, 12] or [8]. Other related works in this direction are [26, 28] and [22].

Being able to compute the determinant of an operator, without knowing explicitly its spectrum, is also the reason why Gelfand–Yaglom Theorem is an extremely useful tool. In theoretical physics, it finds application in the semiclassical approximation of the wave function. Indeed, using the stationary phase expansion, the contributions to the path integral localize at classical solutions. The quadratic term of the expansion involves the determinant of the Hessian of the classical action. Theorem 1 could be of use in computing this expansion for a broader class of action functionals.

The results are formulated in a quite general framework and the techniques can be applied without virtually any modifications to treat constrained variational problems on compact graphs as already done in [9] to compute the Morse index.

In this paper we will deal exclusively with strictly normal extremals (see Definition 3 in Appendix A). This hypothesis is somewhat restrictive, nevertheless is a priori verified in a consistent number of cases. For instance in Riemannian, almost-Riemannian and contact manifolds. For generic normal extremals of step 2 sub-Riemannian manifolds and in the so called linear quadratic regulator problems to list a few.

The structure of the paper is the following: in Sect. 1.1 we recall the notation and the setting we will use through out the paper and give the full statements of our results. Section 2 contains some information about the second variation and the structure of the space of variation we will employ.

In Sect. 3 we deal with a couple of applications, such as Hill’s formula and the eigenvalue problem for Schrödinger operators. The results deserve some interest in their own, however, the main focus of the section is to provide a worked out example of how to apply the formulas to concrete situations.

The last part of the paper is Sects. 4.1 and 4.2. They are devoted to the proof of Theorem 1. We first prove the result for boundary conditions of the type $N_0 \times N_1$ (Sect. 4.1) and than extend it to the general case (Sect. 4.2). Finally, we give formulas to compute the trace of the compact part of the second variation K (Lemmas 3 and 4) and some normalization constant appearing in Theorem 1.

1.1 Problem statement and main results

We begin this section briefly recalling the setting and the notations that will be used throughout the paper. The reader is referred to [4, 6] for more information on optimal control and sub-Riemannian problems. By an optimal control problem we mean the following data: a configuration space, i.e. a smooth manifold M, a family of smooth (and complete if M is non compact) vector fields $f_u$ defined on it and a cost function $\varphi$. The vector fields $f_u$ depend on a parameter u living in some open set $U \subseteq {\mathbb {R}}^k$. We can think of it as our way of interacting with the system and moving a particle from one state to another. We will always assume that the $f_u$ are smooth jointly in both u and the state variable.

To any function $u(\cdot ) \in L^{\infty }([0,1],U)$ and to any $q_0\in M$ we can associate a trajectory in the configuration space considering the solution of:

$$\begin{aligned} \dot{q} = f_{u(t)}(q), \quad q(0) = q_0. \end{aligned}$$

(2)

We will usually call the function $u(\cdot )$ control.

We can impose further restrictions on solutions of (2) specifying proper boundary conditions. The most general situation that we are going to treat in the paper is the case in which the boundary conditions are given by a submanifold $N \subseteq M \times M$. We say that (a Lipschitz continuous) $\gamma : [0,1] \rightarrow M$ is admissible if it solves (2) for some control u and if $(\gamma (0),\gamma (1)) \in N$. We say that a control u is admissible if the corresponding trajectory, denoted by $\gamma _{u}$, is defined on the whole interval [0, 1] and it is admissible.

Given a smooth function $\varphi : U \times M \rightarrow {\mathbb {R}}$, we are interested in the following minimization problem on the space of admissible curves:

$$\begin{aligned} \min _{\gamma _u\text { admissible}} {\mathcal {J}}(\gamma _u) = \min _{\gamma _u \text { admissible}} \int _0^1 \varphi (u(t),\gamma _{u}(t))\textrm{d}t \end{aligned}$$

(3)

In classical mechanics problems $\varphi$ corresponds to the Lagrangian of the system. In optimal control ones it is usually referred to as the running cost.

It is customary to parametrized the space of admissible curves using the control function $u(\cdot )$ and a finite-dimensional parameter space that takes into account the initial data. We are going to follow this approach. However, we postpone the discussion of the structure of our space of variations to Sect. 2 since it is independent of the main statements.

The wellknown Pontryagin Maximum Principle (see Appendix A) gives a geometric description of critical points u of the restriction of ${\mathcal {J}}$ to the space of admissible controls in terms of suitable lifts of $\gamma _u$ to the cotangent bundle. This lifts are called extremals and satisfy, for some $\nu \le 0$, a Hamiltonian ODE:

$$\begin{aligned} {\dot{\lambda }}_t = \textbf{h}_{u(t)}(\lambda ), \text { where } \,\, h_u(\lambda ) = \langle \lambda , f_u(q)\rangle + \nu \varphi (u,q). \end{aligned}$$

There are two families of critical points. A point u can either be a critical point of the constraints determining the set of admissible controls (giving a so-called abnormal extremal having $\nu =0$) or can be a true critical point of ${\mathcal {J}}$ (giving a normal extremal having $\nu <0$). The two conditions are not mutually exclusive, a critical point can have multiple lifts. We will only consider critical points u which are regular points of the constraints. They are called strictly normal optimal controls and admit no abnormal lift. The associated normal extremal is termed strictly normal extremal.

In this case, the space of variations can be endowed, locally, with a smooth Banach manifold structure. Thus, it makes sense to consider its tangent space. It is a finite codimension subspace ${\mathcal {V}}$ of $L^\infty ([0,1],{\mathbb {R}}^k) \oplus {\mathbb {R}}^{\dim (N)}$.

Suppose that u is critical point of the functional ${\mathcal {J}}$ restricted to the space of variations and consider the Hessian of ${\mathcal {J}}$ at u. It is a quadratic form on ${\mathcal {V}}$. We denote it by $Q(v) = d_u^2{\mathcal {J}}\vert _{\mathcal {V}}(v,v)$ and we will refer to it as the second variation of ${\mathcal {J}}$ at u. Instead of working with the $L^\infty$ topology, we will work with the weaker $L^2$ one since it turns out that the quadratic form Q extends by continuity.

We will further assume that $h_u(\lambda )$ defined above is strictly convex along $(u(t),\gamma _u(t))$ in the u variable, this is the so called strong Legendre condition. Under this assumption and for an appropriate choice of scalar product on $L^2([0,1],{\mathbb {R}}^k)$, it turns out that the quadratic form $(Q-I)(v) = Q(v)-\langle v,v\rangle$ is compact. However, as mentioned, it is in general not trace-class since the asymptotic relation in Eq. (1) holds.

Given an eigenvalue of Q, $\lambda$, denote by $m(\lambda )$ its multiplicity. We define the determinant of the second variation as the following limit:

$$\begin{aligned} \det ( Q) = \lim _{\epsilon \rightarrow 0} \prod _{\vert \lambda -1\vert >\epsilon } \lambda ^{m(\lambda )}, \text { where } \lambda \in \text {Spec}(Q). \end{aligned}$$

As stated in the introduction, the computation of this determinant for general boundary conditions is the main contribution of this work. We provide a formula for this determinant involving essentially two ingredients:

• the fundamental solution of a linear (non autonomous) system of ODE which we call Jacobi equation;

• the annihilator to the boundary condition manifold, a Lagrangian submanifold of $T^*M$.

To state the main Theorem and define precisely the objects above, we need to introduce a little bit of notation. We will just sketch here what is needed for this purpose, further details are collected in Appendix A or given along with the proofs. From now on, assume that a strictly normal extremal $\lambda _t$ with optimal control $\tilde{u}$ is fixed (see Appendix A). As asserted by PMP, it satisfies the following (non autonomous) Hamiltonian ODE:

$$\begin{aligned} h^t_{{{\tilde{u}}}} (\lambda )= h_{u}(\lambda )\vert _{u={{\tilde{u}}}(t)}= \left( \langle \lambda , f_{u}(q) \rangle -\varphi (u, q)\right) \vert _{u={{\tilde{u}}}(t)}, \quad {\dot{\lambda }} = \textbf{h}^t_{{\tilde{u}}}(\lambda ). \end{aligned}$$

The first objects we introduce are the flow of $\textbf{h}_{{\tilde{u}}}^t$ at time t, denoted by ${{\tilde{\Phi }}}_t$, and its differential, denoted by $({{\tilde{\Phi }}}_t)_*$. Note that $\lambda _t$ satisfy $\lambda _t = {{\tilde{\Phi }}}_t(\lambda _0)$. We will use the map ${{\tilde{\Phi }}}_t$ to connect the tangent spaces to each point of $\lambda _t$ to the starting one, $\lambda _0$. This flow, in some sense, plays the role of the choice of a connection (or parallel transport as in Riemannian geometry, see [13]).

The second object we are going to introduce, is a kind of quadratic approximation of our starting system. It is given by a quadratic Hamiltonian on $T_{\lambda _0} T^*M$ (see for detail [1] or [6, Chapters 20 and 21]). To define it, we need to introduce two matrix-valued functions $Z_t \in \textrm{Mat}_{k\times 2\dim (M) }({\mathbb {R}})$ and $H_t \in \textrm{Mat}_{k\times k}({\mathbb {R}})$. They can be computed in terms of ${\tilde{\Phi }}_t$ and the Hamiltonians $h_u$ as shown in (32). The matrix $Z_t$ is the derivative of $\textbf{h}_{u}$ with respect to the control variable along the extremal and, heuristically, represents a linear approximation of the Endpoint map of the original system. On the other hand, $H_t$ is the hessian of $h_u$ with respect to the control variable along the extremal and gives some sort of quadratic approximation of $h_u$. These matrices will be used to get an explicit integral expression of Q, given in Equation (5), and to define Jacobi equation below. Strong Legendre condition can be formulated in terms of $H_t$. We will assume that it is symmetric, positive definite and with uniformly bounded inverse.

Let $\pi : T^*M \rightarrow M$ be the natural projection and set $\Pi :=\ker \pi _*$, the fibers. Define $\delta ^s$ as the dilation by $s \in {\mathbb {R}}$ of $\Pi$. It is determined by the relations $\pi _*(\delta ^s w) = \pi _*(w)$ for all $w \in T_{\lambda _0}T^*M$ and $\delta ^s v = s v$ for all $v \in \ker (\pi _*)$. Let J be some coordinates representation of the standard symplectic form on $T_{\lambda _0} T^*M$. Let us define the following quadratic form:

$$\begin{aligned} \beta _s(\lambda ) = \frac{1}{2}\langle \lambda , J \delta ^sZ_t H_t^{-1}(\delta ^sZ_t)^*J \lambda \rangle , \quad \lambda \in T_{\lambda _0}T^*M. \end{aligned}$$

We will call Jacobi (or Jacobi type) equation the following ODEs system on $T_{\lambda _0} T^*M$:

$$\begin{aligned} {{\dot{\lambda }}} = \mathbf {\beta }_s(\lambda ), \quad \lambda \in T_{\lambda _0}T^*M. \end{aligned}$$

Denote its fundamental solution at time t by $\Phi _t^s$. Here, and for the rest of the paper, we will call fundamental solution any family $\Theta _t$, $t \in {\mathbb {R}}$ of linear maps which satisfies a linear ODE and have initial condition $\Theta _0 = I$.

Remark 1

Whenever PMP’s maximum condition determines a $C^2$ function $h = \max _u h_u$ on $T^*M$, normal extremals satisfy a Hamiltonian ODE on the cotangent bundle of the form ${{\dot{\lambda }}} = \textbf{h}(\lambda )$. Jacobi equation for $s=1$ is closely related to the linearisation of $\textbf{h}$ along the extremal we are fixing. Suppose local coordinates are fixed and let $d^2_{\lambda _t}h$ be the Hessian of h along the extremal. Let $\Psi _t$ be the fundamental solution of:

$$\begin{aligned} {{\dot{\Psi }}}_t = d^2_{\lambda _t}h \, \Psi _t. \end{aligned}$$

It can be shown (see for example [6, Proposition 21.3]) that:

$$\begin{aligned} \Psi _t = ({{\tilde{\Phi }}}_t)_*\Phi _t^1. \end{aligned}$$

The last maps we will need are a family of symplectomorphisms of $T_{\lambda _0} T^*M$ and $T_{\lambda _1} T^*M$. Their definition depends on the choice of a scalar product on each tangent space. Let $g_0$ and $g_1$ be two scalar products on these spaces. Assume that at each $\lambda _i$, $\Pi _i:= \ker (\pi _*) \subseteq T_{\lambda _i}T^*M$ has a Lagrangian orthogonal complement with respect to $g_i$ which we denote by $\Pi _i^\perp$. Denote by $J_0$ and $J_1$ the linear maps determined by $\sigma (v, w) = g_i(J_iv,w)$ for all $v,w \in T_{\lambda _i}T^*M$. For a subspace V, denote by $pr_V$ the orthogonal projection onto V. We set:

$$\begin{aligned} \begin{aligned} A_0^s (\eta )&= \eta + (1-s) J_0^{-1}pr_{\Pi _0^\perp } \eta , \quad \eta \in T_{\lambda _0}(T^*M), \\ A_1^s(\eta )&= \eta + (1-s)\left( J_1^{-1} +{{\tilde{\Phi }}}_*\circ pr_{\Pi _0}\circ {{\tilde{\Phi }}}_*^{-1}\right) pr_{\Pi _1^\perp } \eta , \quad \eta \in T_{\lambda _1}(T^*M). \end{aligned} \end{aligned}$$

(4)

The datum of the boundary condition is encoded in a Lagrangian submanifold of $\big (T^*(M \times M),(-\sigma )\oplus \sigma \big )$, the annihilator of N. It can be thought of as the symplectic version of the normal bundle in Riemannian geometry and is defined as follows. Take a sub-manifold $N \subseteq M \times M$ and consider:

$$\begin{aligned} Ann(N)= & {} \bigcup _{q \in N}\{(\lambda _0, \lambda _1) \in T_q^*(M \times M):{}\\ \langle \lambda _0, X_0 \rangle= & {} \langle \lambda _1,X_1\rangle , \forall (X_0,X_1) \in T_q N\}. \end{aligned}$$

In light of PMP (see Appendix A), critical points of $\mathcal J$ with boundary conditions given by N, lift to the cotangent bundle to curves $\lambda _t$ such that $(\lambda _0,\lambda _1) \in Ann(N)$.

Fix now a complement to $T_{(\lambda _0,\lambda _1)}Ann(N)$, say $V_N$, and denote by $\pi _N$ the projection on $V_N$ having $T_{(\lambda _0,\lambda _1)}Ann(N)$ as kernel. We are ready now to define a function that plays the role of the characteristic polynomial of the Hessian of ${\mathcal {J}}$. For a map f denote by $\Gamma (f)$ its graph, set:

$$\begin{aligned} {\mathfrak {p}}_Q(s) = \det (\pi _N\vert _{\Gamma (A_1^s{{\tilde{\Phi }}}_* \Phi ^s_1A_0^s)}). \end{aligned}$$

With this notation, our main result reads as follows:

Theorem 1

Suppose that $\lambda _t$ is a strictly normal extremal for problem (3) and ${\tilde{u}}$ is its optimal control. Moreover, suppose that $\lambda _t$ satisfies Legendre strong condition, i.e. that $\exists \alpha >0$ such that, $\forall v \in {\mathbb {R}}^k$

$$\begin{aligned} \langle -H_t v, v\rangle \ge \alpha \langle v, v\rangle \end{aligned}$$

and that at least one of the following holds:

• the maps $t \mapsto Z_t$ and $t \mapsto H_t$ are piecewise analytic in t;

• the dimension of the space of controls k satisfies $k \le 2$;

• the operator $I-Q$ is trace class;

Let $\lambda \in \textrm{Spec}(Q)$ and $m(\lambda )$ be its multiplicity. Then, the limits:

$$\begin{aligned} \det (Q) = \lim _{\epsilon \rightarrow 0}\prod _{\vert \lambda -1\vert>\epsilon } \lambda ^{m(\lambda )},\quad \text { tr}(Q-I) =\lim _{\epsilon \rightarrow 0} \sum _{\vert \lambda -1\vert >\epsilon }m(\lambda )(\lambda -1). \end{aligned}$$

are well defined and finite. Moreover, for almost any choice of metrics $g_0$ and $g_1$ we have that ${\mathfrak {p}}_Q(0) \ne 0$ and that:

$$\begin{aligned} \det (I+s(Q-I)) = {\mathfrak {p}}_Q(0)^{-1}e^{s(\text { tr}(Q-I)-{\mathfrak {p}}_Q'(0) )}{\mathfrak {p}}_Q(s). \end{aligned}$$

Remark 2

The hypothesis about the regularity of $Z_t$ and $H_t$ are needed to obtain the asymptotic for the spectrum of $Q-I$ that guarantees the existence of the trace and of the determinant as limits. They can be weakened somehow by requiring that the skew-symmetric $k \times k$ matrix $Z^*_t J Z_t$ is continuously diagonalizable (see [3]).

Remark 3

It is worth pointing out that, under Legendre strong condition, the matrices $Z_t$ and $H_t$ are analytic (or $C^k$) as soon as M, the dynamics $f_u(q)$, the cost $\varphi (u,q)$ and the Hamiltonian function $h = \max _u h_u$ appearing in the statement of PMP are analytic (or $C^{k+1}$) too. Compare with [6, Section 21.4].

Moreover, if $Z_t$ and $H_t$ are at least $C^1$, $Q-I$ is trace class as soon as $\sigma (Z_tv,Z_tw) =0$ for all $t\in [0,1]$ and for all $v,w \in {\mathbb {R}}^k$ (see [10]).

Remark 4

The constants ${\mathfrak {p}}_Q(0)$, ${\mathfrak {p}}_Q'(0)$ and $\text { tr}(Q-I)$ are completely explicit and are given in terms of iterated integrals in Lemmas 4 and 3.

In particular we have the following corollary:

Corollary 1

Under the assumption above, the determinant of the second variation Q satisfies:

$$\begin{aligned} \det (Q) = {\mathfrak {p}}_Q(0)^{-1}e^{\text { tr}(Q-I)-{\mathfrak {p}}_Q'(0) }\det (\pi _N \vert _{\Gamma (\Psi _t)}), \end{aligned}$$

where $\Psi _t = {{\tilde{\Phi }}}_* \Phi _1$ and coincides with the fundamental solution of the linearisation of the extremal flow, whenever the latter is defined.

2 The second variation

The aim of this section is threefold: to define precisely what we mean by $d^2{\mathcal {J}}\vert _{\mathcal {V}}$, to define precisely its domain and to provide the integral representation of this quadratic form we will use throughout the proof section of the paper.

Before going on, a little remark about topology is in order. Up until now we have considered Lipschitz continuous curves and $L^\infty$ controls. Hence, it would be natural to work on the Banach space $L^{\infty }([0,1],{\mathbb {R}}^k) \oplus {\mathbb {R}}^{\dim (N)}$. However, it turns out that, even if $d^2 {\mathcal {J}}\vert _{\mathcal {V}}$ is defined on the latter space, it extends to a continuous quadratic form on $L^2([0,1],{\mathbb {R}}^k)\oplus {\mathbb {R}}^{\dim (N)}$. Moreover, critical points of $d^2 {\mathcal {J}}\vert _{\mathcal {V}}$ in $L^2([0,1],{\mathbb {R}}^k)$ are continuous and thus belong to $L^\infty ([0,1],{\mathbb {R}}^k)$. For this reason (and Fredholm alternative), we will work with $L^2$ controls for the rest of the paper.

Let $n_0,n_1 \in {\mathbb {N}}$ and consider the Hilbert space ${\mathcal {H}}$ (whose scalar product will be defined in the next section) given by:

$$\begin{aligned} {\mathcal {H}} = {\mathbb {R}}^{n_0} \oplus L^2([0,1],{\mathbb {R}}^k)\oplus {\mathbb {R}}^{n_1}. \end{aligned}$$

Let $(\Sigma ,\sigma )$ be a symplectic space and consider a linear map $Z: {\mathcal {H}} \rightarrow \Sigma$ defined as:

$$\begin{aligned} Z(u) = Z_0u_0+\int _0^1Z_t u_t \textrm{d}t +Z_1u_1, \quad u = (u_0,u_t,u_1) \in {\mathcal {H}}. \end{aligned}$$

Suppose that $\Pi \subset \Sigma$ is a Lagrangian subspace transverse to the image of the map Z and define:

$$\begin{aligned} {\mathcal {V}} = Z^{-1}(\Pi ). \end{aligned}$$

For an appropriate choice of Z and $\Pi$ which depends on (2) and (3), the second variation (at a strictly normal critical point) is the quadratic form given in the following definition.

Definition 1

(Second variation) The second variation at ${\tilde{u}}$ is the quadratic form defined on ${\mathcal {V}} \subseteq {\mathcal {H}}$:

$$\begin{aligned} \begin{aligned} Q(u)&= \int _0^1\left( -\langle H_t u_t,u_t\rangle + \sigma (Z_t u_t,\int _0^t Z_\tau u_\tau d \tau +Z_0u_0) \right) \textrm{d}t \\ {}&\quad + \sigma (Z_0u_0+\int _0^1 Z_t u_t \textrm{d}t,Z_1u_1), \end{aligned} \end{aligned}$$

(5)

where $H_t$ stands for a symmetric matrix of dimension k and $\langle ,\,\rangle$ for the standard euclidean inner product of ${\mathbb {R}}^k$.

The definition of this quadratic form may be a bit strange at first glance. Despite the appearances, the way one gets to such an expression is quite natural. The construction is explained in detail in [9]. We will sketch here just the main features, essentially to introduce the notation needed.

The idea is to reduce the problem with boundary conditions N to a fixed points (or Dirichlet) problem for an appropriate auxiliary system. We will consider just the case of separated boundary conditions $N_0 \times N_1$. The general case reduces to this one using the procedure explained in Sect. 4.2.

The first step of the construction is to build the auxiliary system. We always work with a fixed strictly normal extremal $\lambda _t$. Choose local foliations in neighbourhoods of its initial and final points having a portion of $N_0$ and $N_1$ as leaves. This determines two integrable distributions in a neighbourhood of those points. Suppose that said distributions are generated by some fields $\{X_i^j\}_{i=1}^{\dim (N_j)}$ and $j=0,1$. Consider the extended system:

$$\begin{aligned} {{\hat{f}}}^t_u(q) = {\left\{ \begin{array}{ll} \sum _{i=0}^{\dim (N_0)} X_i^0(q)u_0^i, &{}\quad \text { for } t \in [-1,0)\\ f_u(q), &{}\quad \text { for } t \in [0,1]\\ \sum _{i=0}^{\dim (N_1)} X_i^1(q)u_1^i, &{}\quad \text { for } t \in (1,2]. \end{array}\right. } \end{aligned}$$

Denote the initial and final points of our original extremal curve by $(q_0,q_1)$. We will use controls that are locally constant on $[0,1]^c$, this will be enough to reach any neighbouring point of $(q_0,q_1)$ in $N_0\times N_1$. Minimizing our original functional is equivalent to minimize, with Dirichlet boundary conditions, the following one:

$$\begin{aligned} {\mathcal {J}}(\gamma _{(u_0,u,u_1)})= \int _0^1 \varphi (u(t),\gamma _{(u_0,u,u_1)} (t) )\textrm{d}t. \end{aligned}$$

The second step is to differentiate the Endpoint map (see Appendix A) of the auxiliary system. We employ the machinery of Chronological Calculus (see also [6, Section 20.3]), which is standard for fixed endpoints. One of the main steps of this differentiation, is to use a suitable family of symplectomorphism to trivialize the cotangent bundle along the curve we are fixing. This allows us to write all the equations in the tangent space to the initial point, $T_{\lambda _0}(T^*M)$. Let us consider the following functions depending on the parameter u:

$$\begin{aligned} {{\hat{h}}}^t_u(\lambda ) = \langle \lambda , {{\hat{f}}}_u^t(q) \rangle -\varphi _t(u,q), \quad q = \pi (\lambda ). \end{aligned}$$

When an optimal control ${{\tilde{u}}}(t)$ is given, we consider ${{\hat{h}}}^t_{{\tilde{u}}(t)}(\lambda )$ and the Hamiltonian system:

$$\begin{aligned} \dot{{\hat{\Phi }}}_t = \mathbf {{{\hat{h}}}}^t_{{\tilde{u}}(t)}({\hat{\Phi }}_t). \end{aligned}$$

We then define the following functions:

$$\begin{aligned} \begin{aligned} {{\hat{Z}}}_t&= \partial _u \textbf{h}_u^t({\hat{\Phi }}_t(\lambda ))\vert _{\lambda = \lambda _0}, \quad {\hat{Z}}_t: {\mathbb {R}}^k \rightarrow T_{\lambda _0}(T^*M), \\ {{\hat{H}}}_t&= \partial _u^2 h_u^t({\hat{\Phi }}_t(\lambda ))\vert _{\lambda = \lambda _0},\quad {{\hat{H}}}_t: {\mathbb {R}}^k \rightarrow {\mathbb {R}}^k. \end{aligned} \end{aligned}$$

The asymptotic expansions of Chronological Calculus tell us that the second variation at ${{\tilde{u}}}$ is the following quadratic form:

$$\begin{aligned} Q(u) = \int _{-1}^2\langle - {{\hat{H}}}_t u,u\rangle - \int _{-1}^2\int _{-1}^t \sigma ({{\hat{Z}}}_\tau u_\tau , {{\hat{Z}}}_t u_t) \textrm{d}\tau \textrm{d}t. \end{aligned}$$

It is defined on the tangent space ${\mathcal {V}}$ to the variations fixing the endpoints of our curve. This space can be described explicitly as ${\mathcal {V}} = \{v: \int _{-1}^2 {{\hat{Z}}}_t v_t \textrm{d}t \in \Pi \}$, where $\Pi = \ker \pi _*$.

The third step is to specialize this representation to our auxiliary system. Notice that an extremal of the original problem lifts naturally to an extremal of the auxiliary one. If ${{\tilde{u}}}$ is the original optimal control, extending it by zero on $[0,1]^c$ gives the optimal control for the auxiliary problem. Applying the construction just sketched to the extended system, we find that ${{\hat{Z}}}_t$ and ${{\hat{H}}}_t$ are locally constant on $[0,1]^c$. We denote $Z_0$ to be its value on $[-1,0)$ and $Z_1$ the value on (1, 2]. ${{\hat{H}}}_t$ is zero outside [0, 1]. Summing up we have:

$$\begin{aligned} {{\hat{Z}}}_t = {\left\{ \begin{array}{ll} Z_0 &{}\text { for } t \in [-1,0)\\ Z_t &{}\text { for } t \in [0,1]\\ Z_1 &{}\text { for } t \in (1,2]. \end{array}\right. } \quad {{\hat{H}}}_t = {\left\{ \begin{array}{ll} H_t &{}\text { for } t \in [0,1]\\ 0 &{}\text { for } t \in [0,1]^c. \end{array}\right. } \end{aligned}$$

Thus, after the substitution, we recover precisely the operator given in (5).

Remark 5

We always assume that our extremal is strictly normal and satisfies Legendre strong condition. In terms of the matrices $Z_t$ and $H_t$ this means that for $t \in [0,1]$ and some $\alpha >0$:

$$\begin{aligned} X_t:= \pi _*Z_t\, \text { satisfies }\, \int _0^1 X_t^*X_t>0, \quad \langle -H_t v,v\rangle \ge \alpha \langle v,v \rangle , \, \forall v \in {\mathbb {R}}^k. \end{aligned}$$

As a last remark, notice that, by the first order optimality conditions, the map $Z_0$ takes values in the space $T_{\lambda _0}Ann(N_0)$ and the map $Z_1$ in the space $({{\tilde{\Phi }}}^{-1}_1)_*\left( T_{\lambda _1}Ann(N_1)\right)$ ( see PMP in Appendix A and [9]).

2.1 The scalar product on the space of variations

As already mentioned, we will assume through out this paper Legendre strong condition. The matrix $-H_t$ is positive definite on [0, 1], with uniformly bounded inverse. This allows to use $-H_t$ to define an Hilbert structure on $L^2([0,1],{\mathbb {R}}^k)$ equivalent to the standard one. We have still to define the scalar product on a subspace transversal to ${\mathcal {V}}_0 = \{u_0 = u_1=0\}$. A natural choice would be to introduce two metrics, one on $T_{\lambda _0} T^*M$ and one on $T_{\lambda _1}T^*M$, and pull them back to the space of controls using the maps $Z_0$ and ${{\tilde{\Phi }}}_*Z_1: {\mathbb {R}}^n \rightarrow T_{\lambda _i} T^*M$. Let us call any such metrics $g_0$ and $g_1$.

Definition 2

For any $u,v \in {\mathcal {H}}$ define:

$$\begin{aligned} \langle u, v \rangle = -\int _0^1 H_t(u_t,v_t) \textrm{d}t + g_0 (Z_0 u_0,Z_0v_0 ) + g_1( {{\tilde{\Phi }}}_*Z_1 u_1,{{\tilde{\Phi }}}_*Z_1v_1 ). \end{aligned}$$

Since the symplectic form $\sigma$ is a skew-symmetric bilinear form, there exists a $g_i-$skew-symmetric linear operator $J_i$ such that:

$$\begin{aligned} g_i(J_iX_1,X_2) = \sigma (X_1,X_2), \quad \forall X_1,X_2 \in T_{\lambda _i} T^*M, \, i=0,1. \end{aligned}$$

In terms of the symplectic form, the scalar product can be written as:

$$\begin{aligned} \langle u, v\rangle =-\int _0^1 H_t(u_t,v_t) \textrm{d}t + \sigma (J_0^{-1}Z_0u_0,Z_0u_0)+\sigma (J_1^{-1}{{\tilde{\Phi }}}_*Z_1u_1,\tilde{\Phi }_*Z_1u_1). \end{aligned}$$

Now, we use the Hilbert structure just introduced to write the operator K associated with the quadratic form $Q-I$, which is compact. To simplify notation, we can perform the change of coordinates in $L^2$ sending $v_t \mapsto (-H_t)^{\frac{1}{2}} v_t$ and substitute $Z_t$ with $Z_t (-H_t)^{-\frac{1}{2}}$. In this way, the Hilbert structure on the interval becomes the standard one.

We introduce a further piece of notation, call $pr_0$ (respectively $pr_1$) the orthogonal projection on $\text { Im}(Z_0)$ (respectively $\text { Im}({{\tilde{\Phi }}}_*Z_1)$) with respect to the scalar product $g_0$ (respectively $g_1$). Let L be a partial inverse to $\tilde{\Phi }_*Z_1$, i.e. a map $L: T_{\lambda _0} T^*M \rightarrow {\mathbb {R}}^n$ defined by the relation $L {{\tilde{\Phi }}}_* Z_1 v_1 = v_1$. Set:

$$\begin{aligned} \Lambda (u) = L \,pr_1 \,J_1\tilde{\Phi }_*\Big (Z_0u_0 + \int _0^1 Z_tu_t \textrm{d}t+Z_1u_1\Big ). \end{aligned}$$

(6)

Lemma 1

The second variation, as a bilinear form, can be expressed as: $Q(u,v) = \langle u+Ku,v\rangle$ where $u, v \in {\mathcal {V}}$ and K is the operator defined by:

$$\begin{aligned} Ku = \begin{pmatrix} -u_0 \\ - Z_t^*J \left( \int _{0}^t Z_\tau u_\tau \textrm{d}\tau +Z_0u_0\right) \\ -u_1- \Lambda (u) \end{pmatrix} \end{aligned}$$

(7)

where $\Lambda (u)$ is given above, in Eq. (6).

Proof

A quick manipulation of the expression involving the symplectic form in Definition 1, yields the following:

$$\begin{aligned} \begin{aligned}&\int _{-1}^2\int _{-1}^t \sigma (Z_\tau u_\tau , Z_t v_t) \textrm{d}\tau \textrm{d}t = \int _{-1}^0 \int _{-1}^t \sigma (Z_\tau u_\tau , Z_t v_t) \textrm{d}\tau \textrm{d}t \\&\qquad + \int _0^1 \int _{-1}^t \sigma (Z_\tau u_\tau , Z_t v_t) \textrm{d}\tau \textrm{d}t +\int _1^2 \int _{-1}^t \sigma (Z_\tau u_\tau , Z_t v_t) \textrm{d}\tau \textrm{d}t \\&\quad = \int _0^1 \sigma \left( \int _{0}^t Z_\tau u_\tau \textrm{d}\tau +Z_0u_0,Z_t v_t \right) \textrm{d}t\\&\qquad +\sigma \Big (Z_0u_0 + \int _0^1 Z_tu_t \textrm{d}t+Z_1u_1,Z_1v_1\Big ) \\&\quad = \int _0^1 \sigma \left( \int _{0}^t Z_\tau u_\tau \textrm{d}\tau +Z_0u_0,Z_t v_t\right) \textrm{d}t \\ {}&\qquad +g_1 \left( J_1 {{\tilde{\Phi }}}_*\left( Z_0u_0+ \int _0^1 Z_tu_t \textrm{d}t+Z_1u_1\right) ,{{\tilde{\Phi }}}_*Z_1v_1\right) . \end{aligned} \end{aligned}$$

Recall that $Z_t$ is constant on $[0,1]^c$. Moreover, the images of the maps $Z_0$ and $Z_1$ are isotropic subspaces. We used this fact to simplify the expression in the first line. Now, it is clear that in the last term:

$$\begin{aligned} g_1 \Big (J_1{{\tilde{\Phi }}}_*\Big (Z_0u_0 + \int _0^1 Z_tu_t \textrm{d}t+Z_1u_1\Big ),{{\tilde{\Phi }}}_*Z_1v_1\Big ), \end{aligned}$$

only the projection onto the image of ${{\tilde{\Phi }}}_*Z_1$ plays a role. It is straightforward to check that:

$$\begin{aligned} g_1 \Big (J_1{{\tilde{\Phi }}}_*\Big (Z_0u_0 + \int _0^1 Z_tu_t \textrm{d}t+Z_1u_1\Big ),{{\tilde{\Phi }}}_*Z_1v_1\Big ) = g_1({{\tilde{\Phi }}}_*Z_1 \Lambda (u),{{\tilde{\Phi }}}_*Z_1v_1). \end{aligned}$$

Recall that we have normalized $H_t$ to $-1$, thus the first summand can be rewritten as follows:

$$\begin{aligned} \int _0^1 \sigma \left( \int _{0}^t Z_\tau u_\tau \textrm{d}\tau +Z_0u_0,Z_t v_t\right) \textrm{d}t = \int _0^1 \langle Z_t^*J \Big (\int _{0}^t Z_\tau u_\tau \textrm{d}\tau +Z_0u_0\Big ), v_t\rangle \textrm{d}t. \end{aligned}$$

Adding and subtracting $g(Z_0u_0,Z_0v_0)$ and $g(Z_1u_1,Z_1v_1)$ to single out the identity, we obtain the formula in the statement. $\square$

3 Hill-type formulas

Before going to the proof of Theorem 1, we present here some applications of the main result. We deduce Hill’s formula for periodic trajectories and specify it to the eigenvalue problem for Schrödinger operators. In the second sub-section we present a variation of the classical Hill formula for systems with drift. We will mainly deal with periodic and quasi-periodic boundary conditions. Namely, we consider the case $N = \Gamma (f)$ for a diffeomorphism of the state space $f: M \rightarrow M$.

The proofs of this section rely quite heavily on the machinery introduced in Sect. 4.2, in particular in Lemmas 4 and 3. The statements, on the other hand, do not and could shed some light on Theorem 1. Despite the appearance, proofs are rather simple. They reduce to a (long) computation of the normalizing factors appearing in the statement of Theorem 1 and can be skipped at first reading.

3.1 Driftless systems and classical Hill’s formula

In this section, we consider driftless systems with periodic boundary conditions on ${\mathbb {R}}^{n}$ and specify the formulas of Theorem 4 for this class of problems.

First of all, let us explain what we mean by driftless systems. Let $t \mapsto R_t$ be a continuous family of symmetric matrices of size $n \times n$ and let us denote by u a function in $L^\infty ([0,1],{\mathbb {R}}^n)$.

Consider the following family of vector fields $f_u(q)$, their associated trajectories $q_u(t)$ and the action functional ${\mathcal {A}}(u)$:

$$\begin{aligned} \begin{aligned} f_u(q) = u(t), \quad {\left\{ \begin{array}{ll} \dot{q}_u = f_u(q) = u(t),\\ q(0) = q_0 \in {\mathbb {R}}^n. \end{array}\right. }\\ {\mathcal {A}}(u) = \frac{1}{2} \int _0^1 |u|^2-\langle R_t q_u(t),q_u(t) \rangle \textrm{d}t. \end{aligned} \end{aligned}$$

(8)

The Hamiltonian coming from the Maximum Principle takes the following form:

$$\begin{aligned} H (p,q) = \max _{u \in {\mathbb {R}}^k} \langle p,u \rangle -\frac{1}{2}(\vert u\vert ^2 - \langle R_t q,q\rangle ) = \frac{1}{2}(\langle p,p \rangle +\langle R_t q,q \rangle ). \end{aligned}$$

(9)

Let us denote the flow generated by H by $\Psi _t$. Fix a normal extremal $\lambda _t$ for periodic boundary conditions and its optimal control ${{\tilde{u}}} (t)=p(t)$.

We impose periodic boundary conditions, i.e. we take $N = \Delta = \{(q,q)\in {\mathbb {R}}^{2n}: q \in {\mathbb {R}}^n\}$. Let g be a scalar product on ${\mathbb {R}}^n$ which we identify, with a slight abuse of notation, with a symmetric matrix G.

Theorem 2

(Hill’s formula) Let $I+K$ be the second variation at ${\tilde{u}}$ and $\Psi$ the fundamental solution of ${\dot{\Psi }} = \textbf{H} \Psi$ and G the matrix representing the scalar product g. The following equality holds:

$$\begin{aligned} \det (I+K) = (-1)^n (2e)^{-n}\det (G^{-1})\det (1-\Psi ). \end{aligned}$$

Remark 6

If we are working on the interval [0, T] instead of [0, 1] everything remains essentially unchanged. The only difference is that extra factor $T^{-n}$ appears on the right-hand side. In the notation of the proof below this corresponds to the term $\det (\Gamma )^{-1}$.

We can apply the previous result to study boundary value problems for Sturm-Liouville operators. Let us illustrate the case of Schrödinger equation with periodic boundary conditions. Fix, without loss of generality, the normal extremal $(p(t),q(t)) = (0,0)$ and with relative optimal control ${\tilde{u}} = 0$. Consider the cost ${{\tilde{R}}}_t = R_t+\lambda$, for $\lambda \in {\mathbb {R}}$. Consider the second variation of the functional

$$\begin{aligned} {\mathcal {A}}_\lambda (u) = \frac{1}{2}\int _0^1 \vert u_t\vert ^2+\langle (R_t+\lambda ) q_u(t),q_u(t)\rangle \textrm{d}t, \end{aligned}$$

at the point ${{\tilde{u}}} =0$. It is given by the operator $1+K_\lambda$ where:

$$\begin{aligned} \langle K_\lambda (u),u \rangle =\lambda \left( \int _0^1\int _0^t\langle (\tau -t)u(\tau ), u(t)\rangle \textrm{d}\tau \textrm{d}t +\langle u_0,u_0\rangle \right) +\langle K_0(u),u\rangle . \end{aligned}$$

We have the following corollary:

Corollary 2

Let $\lambda \in {\mathbb {R}}$, $\Psi _\lambda$ the fundamental matrix of the lift to ${\mathbb {R}}^{2n}$ of the following ODE on ${\mathbb {R}}^{2n}$:

$$\begin{aligned} \ddot{q}(t) = (R_t+\lambda )q(t). \end{aligned}$$

The determinant of the operators $1+K_\lambda$ can be expressed as:

$$\begin{aligned} \det (1+K_\lambda ) = (-1)^n (2e)^{-n} \det (G^{-1})\det (1-\Psi _\lambda ), \end{aligned}$$

where G is as in the previous statement.

Proof of Theorem 2

We are going now to describe explicitly all the objects involved in Theorem 1. Let us start with the flow ${{\tilde{\Phi }}}$ we use to re-parametrize the space and its differential. It is given by the Hamiltonian:

$$\begin{aligned} \begin{aligned}&h_{{\tilde{u}}(t)}(p,q) = \langle p,{\tilde{u}}(t)\rangle + \frac{1}{2} \langle R_t q, q \rangle \quad \Rightarrow \quad {\left\{ \begin{array}{ll} {\dot{p}} = -R_t q \\ {\dot{q}} = {{\tilde{u}}} (t). \end{array}\right. }\\&{{\tilde{\Phi }}}_t(p,q) = \begin{pmatrix} 1 &{}\quad -\int _0^t R_\tau \textrm{d}\tau \\ 0 &{}\quad 1 \end{pmatrix}\begin{pmatrix} p\\ q \end{pmatrix} +\begin{pmatrix}- \int _0^t \int _0^\tau R_\tau {{\tilde{u}}}(r) \textrm{d}r \textrm{d}\tau \\ \int _0^t \tilde{u} (\tau ) \textrm{d}\tau \end{pmatrix}\\&({{\tilde{\Phi }}}_t)_* = \begin{pmatrix} 1 &{}\quad -\int _0^t R_\tau \textrm{d}\tau \\ 0 &{}\quad 1 \end{pmatrix}. \end{aligned} \end{aligned}$$

The matrix $Z_t$ is the following:

$$\begin{aligned} \quad Z_t = ({\tilde{\Phi }}_t^{-1})_* \partial _u \textbf{h}^t_u = \begin{pmatrix} \int _0^t R_\tau \textrm{d}\tau \\ 1 \end{pmatrix}. \end{aligned}$$

To simplify notation, let us call ${{\hat{R}}} = -\int _0^1 R_\tau \textrm{d} \tau$. The annihilator of the diagonal is simply the graph of the identity. Hence the following map, defined on $(T_{\lambda _0} T^*M)^2$, has the latter as kernel:

$$\begin{aligned} (\eta _0,\eta _1) \mapsto \eta _1-\eta _0. \end{aligned}$$

We will now define $Q^s$ as in Eq. (28) (actually up to a scalar, but this is irrelevant). For $\eta \in T_{\lambda _0} T^*M$ set:

$$\begin{aligned} Q^s(\eta ) = \begin{pmatrix} -1&1 \end{pmatrix} \begin{pmatrix} \eta \\ A_1^s{{\tilde{\Phi }}}_* \Phi _1^s A_0^s\eta \end{pmatrix} =( A_1^s{{\tilde{\Phi }}}_* \Phi _1^sA_0^s -1)\eta \in T_{\lambda _0} T^*M. \end{aligned}$$

It is clear that the kernel of $Q^s$ is precisely the intersection of the graph with the diagonal subspace. Since we are working on ${\mathbb {R}}^{2n}$ we can define the determinant of this map as:

$$\begin{aligned} \det (Q^s) = \det (A_1^s{{\tilde{\Phi }}}_* \Phi _1^sA_0^s -1). \end{aligned}$$

As already mentioned in Sect. 1.1 this function is a multiple of the characteristic polynomial of K. It satisfies (see Sects. 4.1 and 4.2):

$$\begin{aligned} \det (Q^s) = a e^{b s}\det (1+sK), \quad a \in {\mathbb {C}}^*, b \in {\mathbb {C}}. \end{aligned}$$

Let us compute the normalization factors. To do so, we have to evaluate $\det (Q^s)$ and its derivative at $s=0$. This will give us the relations:

$$\begin{aligned} \det (Q^0) = a, \quad a(b+\text { tr}(K)) = \partial _s \det (Q^s)\vert _{s=0}. \end{aligned}$$

We have to work a bit to write down precisely all the quantities appearing in the formulas above. It is straightforward to compute the matrix representations of the maps $A_0^s$ and $A_1^s$. In this setting the projections onto $\Pi _0$ and $\Pi _0^\perp$ are given by:

$$\begin{aligned} pr_{\Pi _0} = \begin{pmatrix} 1 &{}\quad 0 \\ 0 &{}\quad 0 \end{pmatrix}, \quad pr_{\Pi _0^\perp } = \begin{pmatrix} 0 &{}\quad 0 \\ 0 &{}\quad 1 \end{pmatrix}. \end{aligned}$$

Recall that the definition of $A_0^s$ and $A_1^s$ given in (4) depends on the choice of two scalar products $g_0$ and $g_1$. Denote by $G_0$ and $G_1$ their restriction to $\Pi _0^\perp$ and $\Pi _1^\perp$ respectively. We have that:

$$\begin{aligned} \begin{aligned} A_0^s&= \begin{pmatrix} 1 &{}\quad (1-s)G_0\\ 0 &{}\quad 1 \end{pmatrix}, \quad A_1^s = \begin{pmatrix} 1 &{}\quad (1-s)(G_1-{{\hat{R}}}) \\ 0 &{}\quad 1 \end{pmatrix}\\ A_1^s{{\tilde{\Phi }}}_*&= \begin{pmatrix} 1 &{}\quad s{\hat{R}} +(1-s)G_1\\ 0 &{}\quad 1 \end{pmatrix}. \end{aligned} \end{aligned}$$

The value of $\Phi _t^s$ and its derivative at $s=0$ is given in Lemma 4. Here, for the submatrices of $\Phi ^0_t$ and $\partial _s \Phi _t^s\vert _{s=0}$, we use the notation defined in the Lemma 4. In this case, since $Y_t = \int _0^t R_\tau \textrm{d}\tau$ and $X_t =1$, we obtain:

$$\begin{aligned} \begin{aligned} \Phi _t^0&= \begin{pmatrix} 1 &{}\quad 0 \\ \Gamma &{}\quad 1 \end{pmatrix}= \begin{pmatrix} 1 &{}\quad 0 \\ t &{}\quad 1 \end{pmatrix},\\ \partial _s \Phi _t^s\vert _{s=0}&=\begin{pmatrix} \Theta &{}\quad 0\\ \Omega &{}\quad -\Theta ^* \end{pmatrix} = \begin{pmatrix} \int _0^t\int _0^\tau R_\omega \textrm{d}\omega &{}\quad 0 \\ \int _0^t \int _0^\tau \int _r^\tau R_\omega \textrm{d}\omega \textrm{d}r \textrm{d}\tau &{} \quad -\int _0^t \int _0^\tau R_\omega \textrm{d}\omega \end{pmatrix}. \end{aligned} \end{aligned}$$

Let us compute the value of $\det (Q^s)$ in zero. Putting all together we have:

$$\begin{aligned} \det (Q^s)|_{s=0} = \det \left( \begin{pmatrix} 1 &{}\quad G_1 \\ 0&{}\quad 1 \end{pmatrix} \begin{pmatrix} 1 &{}\quad 0 \\ \Gamma &{}\quad 1 \end{pmatrix} \begin{pmatrix} 1 &{}\quad G_0 \\ 0&{}\quad 1 \end{pmatrix} -\begin{pmatrix} 1 &{}\quad 0 \\ 0&{}\quad 1 \end{pmatrix} \right) . \end{aligned}$$

After a little bit of computation we find that $Q_s\vert _{s=0}$ satisfies:

$$\begin{aligned} \begin{aligned}{} & {} Q^s\vert _{s=0} = \begin{pmatrix} G_1 \Gamma &{}\quad G_0+G_1+G_1\Gamma G_0 \\ \Gamma &{}\quad \Gamma G_0 \end{pmatrix}, \,\, \det (Q^s\vert _{s=0} ) = (-1)^n\det (\Gamma )\det (G_1+G_0),\\{} & {} (Q^s\vert _{s=0} )^{-1} = \begin{pmatrix} -G_0(G_1+G_0)^{-1} &{}\quad \Gamma ^{-1}+ G_0(G_1+G_0)^{-1}G_1 \\ (G_1+G_0)^{-1} &{}\quad -(G_1+G_0)^{-1}G_1 \end{pmatrix}. \end{aligned} \end{aligned}$$

We can compute the derivative $\det (Q^s)$ at $s=0$, we find that:

$$\begin{aligned} \begin{aligned} \partial _s Q^s\vert _{s=0}&= (\partial _s A_1^s){{\tilde{\Phi }}}_* \Phi _1^sA_0^s + A_1^s{{\tilde{\Phi }}}_* (\partial _s\Phi _1^s)A_0^s + A_1^s{{\tilde{\Phi }}}_* \Phi _1^s(\partial _sA_0^s)\vert _{s=0} \\&=\begin{pmatrix} ( G_1-{{\hat{R}}})\Gamma &{}\quad G_1- {{\hat{R}}}\\ 0 &{}\quad 0 \end{pmatrix}\begin{pmatrix} 1 &{}\quad G_0\\ 0 &{}\quad 1 \end{pmatrix}\\ {}&\quad +\begin{pmatrix} 1 &{}\quad G_1\\ 0 &{}\quad 1 \end{pmatrix}\left( \begin{pmatrix} \Theta &{}\quad 0\\ \Omega &{}\quad -\Theta ^* \end{pmatrix}\begin{pmatrix} 1 &{}\quad G_0\\ 0 &{}\quad 1 \end{pmatrix}+\begin{pmatrix} 0 &{}\quad G_0 \\ 0 &{}\quad \Gamma G_0 \end{pmatrix}\right) . \end{aligned} \end{aligned}$$

We use now Jacobi formula for the derivative of the determinant of a family of invertible matrices. It reads:

$$\begin{aligned} \partial _s \det (M_s) = \det (M_s) \text { tr}(\partial _s M_s M_s^{-1}). \end{aligned}$$

Without going into the detail of the actual computation, which at this point is just matrix multiplication, we have that:

$$\begin{aligned} \begin{aligned} \partial _s \det (Q^s)\vert _{s=0}&= \det (Q^s)\vert _{s=0} \, \text { tr}(\partial _s(Q^s)(Q^s)^{-1})\vert _{s=0} \\ {}&= \det (Q^s)\vert _{s=0} \, \text { tr}((G_1+G_0)^{-1}(G_0-G_1+{{\hat{R}}})+\Gamma ^{-1}\Omega ). \end{aligned} \end{aligned}$$

The last quantity we have to compute is $\text { tr}(K)$. To do so we use Lemma 3. Mind that in the statement of the Lemma one works with twice the variables, taking as state space ${\mathbb {R}}^{n} \times {\mathbb {R}}^{n}$ and using the symplectic form $(-\sigma ) \oplus \sigma$ on ${\mathbb {R}}^{2n}\times {\mathbb {R}}^{2n}$. The quantities with $\tilde{\,}$ on top always refer to the system in ${\mathbb {R}}^{4n}$, where we have a trivial dynamic on the first factor and the boundary condition we impose are in this case $\Delta \times \Delta$ (see the beginning of Sect. 4.2 for more details). The formula given in the lemma reads:

$$\begin{aligned} \begin{aligned} \text { tr}(K)&= -\dim (N) +\text { tr}[\pi _*^1{{\tilde{\Phi }}}_*^{-1}\,pr_1 \tilde{J}_1{{\tilde{\Phi }}}_* ({{\tilde{Z}}}_0) ]\\ {}&\quad +\text { tr}\left[ \Gamma ^{-1} \left( \Omega + (\pi ^2_*-\pi _*^1){{\tilde{\Phi }}}_*^{-1}\,pr_1 {{\tilde{J}}}_1\tilde{\Phi }_* \left( \int _0^1 {{\tilde{Z}}}_tZ_t^*J\vert _{\Pi } \textrm{d}t\right) \right) \right] . \end{aligned} \end{aligned}$$

(10)

Let us explain all the objects appearing in the formula. $\tilde{\pi }_*^i$ denotes the differential of the natural projection on the $i-$th factor. The matrix ${{\tilde{\Phi }}}_*$ is given here by:

$$\begin{aligned} {{\tilde{\Phi }}}_* = \begin{pmatrix} \begin{pmatrix} 1 &{}\quad 0\\ 0 &{}\quad 1 \end{pmatrix} &{}\quad 0\\ 0 &{}\quad \begin{pmatrix} 1 &{}\quad R \\ 0 &{}\quad 1 \end{pmatrix} \end{pmatrix}. \end{aligned}$$

Moreover the matrices ${{\tilde{Z}}}_0$, ${{\tilde{Z}}}_t$ and ${{\tilde{Z}}}_1$ are:

$$\begin{aligned} {{\tilde{Z}}}_0 = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 1 \end{pmatrix},\quad {{\tilde{Z}}}_t =\begin{pmatrix} 0 \\ 0 \\ \int _0^t R_\tau \textrm{d}\tau \\ 1 \end{pmatrix}, \quad {{\tilde{Z}}}_1 = \begin{pmatrix} 0 \\ 1 \\ -R \\ 1 \end{pmatrix}, \quad {{\tilde{\Phi }}}_*{{\tilde{Z}}}_1= \begin{pmatrix} 0 \\ 1 \\ 0 \\ 1 \end{pmatrix}. \end{aligned}$$

The map $pr_1$ denotes the orthogonal projection onto the image of ${{\tilde{Z}}}_1$. We are using the scalar product $g_0 \oplus g_1$ on $T_{\lambda _0} T^*M \times T_{\lambda _1} T^*M$ to define it. One can check that the following map is the coordinate representation of $pr_1$:

$$\begin{aligned} pr_1 = (G_0+G_1)^{-1}\begin{pmatrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad G_0 &{}\quad 0 &{}\quad G_1\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad G_0 &{}\quad 0 &{}\quad G_1\\ \end{pmatrix}, \\ pr_1 {{\tilde{J}}}_1 = (G_0+G_1)^{-1} \begin{pmatrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ -1 &{}\quad 0&{}\quad 1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ -1 &{}\quad 0&{}\quad 1 &{}\quad 0\\ \end{pmatrix}. \end{aligned}$$

Now everything reduces to some tedious matrix multiplications. The second term in the right hand side of (10) simplifies as follows:

$$\begin{aligned} \text { tr}[\pi _*^1{{\tilde{\Phi }}}_*^{-1}\,pr_1 {{\tilde{J}}}_1{{\tilde{\Phi }}}_* ({{\tilde{Z}}}_0) ] = \text { tr}({{\hat{R}}} (G_0+G_1)^{-1}). \end{aligned}$$

For the third term notice that $(\pi _*^2-\pi _*^1)(\tilde{\Phi }_*)^{-1} pr_1$ is identically zero since ${{\tilde{\Phi }}}_*$ does not change the projection on the horizontal part and we are working with periodic boundary conditions. It follows we are left with $\text { tr}(\Gamma ^{-1} \Omega )$. Summing up we have that:

$$\begin{aligned} \text { tr}(K) = \text { tr}(\Omega \Gamma ^{-1}+ {\hat{R}}(G_0+G_1)^{-1}){-\dim (M).} \end{aligned}$$

It is natural to think of $g_0$ and $g_1$ as restrictions of globally defined Riemannian metrics. Doing so, since we are working with periodic boundary conditions, amounts to choose $G_0= G_1$. Hence the result. $\square$

3.2 System with drift and Hill-type formulas

In this section we give a version of Hill’s formula for linear systems with drift. They are again linear system with quadratic cost of the following form:

$$\begin{aligned} \begin{aligned} f_u(q)&= A_t q +B_t u(t), \quad {\left\{ \begin{array}{ll} \dot{q}_u = f_u(q) =A_t q_u+B_t u(t),\\ q(0) = q_0 \in {\mathbb {R}}^n \end{array}\right. }\\ {\mathcal {A}}(u)&= \frac{1}{2} \int _0^1 |u|^2+\langle R_t q_u(t),q_u(t) \rangle \textrm{d}t. \end{aligned} \end{aligned}$$

(11)

Here $A_t$ is $n\times n$ matrix and $B_t$ a $n\times k$ one, both with possibly non-constant (but continuous) coefficients. The maximized Hamiltonian takes the form:

$$\begin{aligned} H(p,q) = \langle p,A_tq\rangle +\frac{1}{2}\left( \langle B_tB^*_tp,p\rangle +\langle R_t q,q\rangle \right) . \end{aligned}$$

Denote by ${\hat{\Phi }}_t$ the fundamental solution of ${\dot{q}} =A_t q$ at time t. We can lift this map to a symplectomorphism of the cotangent bundle which we denote by ${\underline{\Phi }}_t$. As boundary conditions, we take the following affine subspace of ${\mathbb {R}}^{4n}$:

$$\begin{aligned} N = \Gamma \left( {\hat{\Phi }}+ {\hat{\Phi }}\int _0^1 \hat{\Phi }_r^{-1}B_r{\tilde{u}}(r)\textrm{d}r\right) . \end{aligned}$$

Notice that, since only the tangent space matters in our formulas, the translation is irrelevant and it would be the same as if we considered $\Gamma ({\hat{\Phi }})$. An obvious choice of extremal is the point $\lambda _t = (0,0)$, with control ${\tilde{u}} =0$.

Theorem 3

(Hill’s formula with drift) Suppose that a critical point of the functional given in (11) is fixed and let ${{\tilde{u}}}$ be its optimal control. Let $G_0$ and $G_1$ be our choices of scalar product, $\Gamma := \int _0^1 {\hat{\Phi _\tau }} B_\tau B_\tau ^*\hat{\Phi }^*_\tau \textrm{d}\tau$ and $\Psi _t$ the fundamental solution of ${{\dot{\Psi }}} = \textbf{H} \Psi$. Moreover, define the following matrix:

$$\begin{aligned} G = G_0+{\hat{\Phi }}_t^* G_1 {\hat{\Phi }}_t. \end{aligned}$$

Let $I+K$ be the second variation at ${\tilde{u}}$. The following equality holds:

$$\begin{aligned} \det (I+K) = \frac{(-1)^n e^{-2 \,\text { tr}(G^{-1}G_0)}}{\det (G)\det (\Gamma )} \det (\Psi _t-{\underline{\Phi }}_t). \end{aligned}$$

Proof

The proof is completely analogous to the one of Theorem 2. First of all the Hamiltonian we use to re-parametrize is given as follows:

$$\begin{aligned} h^t_{{\tilde{u}}(t)} = \langle p,B_t {\tilde{u}}(t)+A_tq\rangle +\frac{1}{2}\langle R_t q,q\rangle . \end{aligned}$$

Hence the flow and its differential are given by:

$$\begin{aligned} \begin{aligned} {{\tilde{\Phi }}}_t(p,q) =&\begin{pmatrix} ({\hat{\Phi }}_t^*)^{-1} &{} -({\hat{\Phi }}_t^*)^{-1}\int _0^t {\hat{\Phi }}_\tau ^*R_\tau {\hat{\Phi }}_\tau \textrm{d}\tau \\ 0 &{}{\hat{\Phi }}_t \end{pmatrix}\begin{pmatrix} p\\ q \end{pmatrix} \\ {}&+\begin{pmatrix} -(\hat{\Phi }_t^*)^{-1}\int _0^t{\hat{\Phi }}_\tau ^* R_\tau {\hat{\Phi }}_\tau \int _0^\tau \hat{\Phi }_r^{-1}B_r{\tilde{u}}(r)\textrm{d}r \textrm{d}\tau \\ {\hat{\Phi }}_t\int _0^t \hat{\Phi }_r^{-1}B_r{\tilde{u}}(r)\textrm{d}r \end{pmatrix},\\ ({{\tilde{\Phi }}}_t)_* =&\begin{pmatrix} ({\hat{\Phi }}_t^*)^{-1}_* &{} -({\hat{\Phi }}_t^*)^{-1}\int _0^t {\hat{\Phi }}_\tau ^*R_\tau {\hat{\Phi }}_\tau \textrm{d}\tau \\ 0 &{}{\hat{\Phi }}_t \end{pmatrix}. \end{aligned} \end{aligned}$$

We have to define the map $Q^s$. Similar to the previous case, we can define a map having as kernel the annihilator to the boundary conditions as follows:

$$\begin{aligned} (\eta _0,\eta _1) \mapsto \begin{pmatrix} {\hat{\Phi }}^*_t &{}\quad 0 \\ 0 &{}\quad ({\hat{\Phi }}_t)^{-1} \end{pmatrix} \eta _1-\eta _0 =: T_1 \eta _1 -\eta _0. \end{aligned}$$

Hence:

$$\begin{aligned} \det (Q_s) = \det (T_1 A_1^s{\tilde{\Phi }}_* \Phi _1^sA_0^s-1). \end{aligned}$$

Set as before ${\hat{R}} = - ({\hat{\Phi }}^*)^{-1}\int _0^1 \hat{\Phi }_\tau ^*R_\tau {\hat{\Phi }}_\tau \textrm{d}\tau$, the upper right minor of ${{\tilde{\Phi }}}_*$. A quick computation shows that:

$$\begin{aligned} T_1A_1^s{{\tilde{\Phi }}}_* = \begin{pmatrix} 1 &{}\quad (1-s)\hat{\Phi }_t^*G_1{\hat{\Phi }}_t+ s {\hat{\Phi }}_t^*{{\hat{R}}} \\ 0 &{}\quad 1 \end{pmatrix}:= {{\hat{A}}}^s_1 {{\tilde{\Phi }}}_*. \end{aligned}$$

Hence, up to renaming $G_1$ and $\Gamma$ in the proof of Theorem 2, we have:

$$\begin{aligned} \begin{aligned} \det (Q^s)\vert _{s=0}&= (-1)^n \det (\Gamma )\det ({\hat{\Phi }}_t^*G_1{\hat{\Phi }}_t+G_0) = (-1)^n \det (\Gamma )\det (G), \\ \frac{\partial _s \det (Q^s)}{\det (Q^s)}\vert _{s=0}&= \text { tr}(((\hat{\Phi }_t^*G_1{\hat{\Phi }}_t+G_0)^{-1}(G_0-{\hat{\Phi }}_t^*G_1\hat{\Phi }_t+{\hat{\Phi }}_t^*{{\hat{R}}})+\Gamma ^{-1}\Omega ). \end{aligned} \end{aligned}$$

Now we have to apply Lemma 3 to compute the trace of the compact part of the second variation. Here $pr_1$ and ${{\tilde{Z}}}_1$ are different since we have changed boundary conditions. However we have the same kind of simplification as in the previous case. Let us write explicitly the new objects:

$$\begin{aligned} Z_1 = \begin{pmatrix} 0 \\ 1 \\ 0 \\ {\hat{\Phi }}_t \end{pmatrix},~pr_1 = \begin{pmatrix} 0&{}\quad 0&{}\quad 0 &{}\quad 0 \\ 0 &{}\quad L G_0 &{}\quad 0 &{}\quad L {\hat{\Phi }}_t^* G_1 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0 &{}\quad {\hat{\Phi _tL}} G_0 &{}\quad 0 &{}\quad {\hat{\Phi }}_t L {\hat{\Phi }}_t^* G_1 \end{pmatrix}, ~L =(G_0+{\hat{\Phi }}_t^*G_1{\hat{\Phi }}_t)^{-1}. \end{aligned}$$

In the end, the trace reads:

$$\begin{aligned} \text { tr}(K) = \text { tr}(\Gamma ^{-1}\Omega +{\hat{\Phi }}_t^*{{\hat{R}}}(\hat{\Phi }_t^*G_1{\hat{\Phi }}_t+G_0)^{-1}) -\dim (M). \end{aligned}$$

Contrary to the previous section the two terms do not simplify. We are left with the following equation for b:

$$\begin{aligned} b&= \dim (M) + \text { tr}(({\hat{\Phi }}_t^*G_1{\hat{\Phi }}_t+G_0)^{-1}(G_0-{\hat{\Phi }}_t^*G_1{\hat{\Phi }}_t))\\&= n+ 2\, \text { tr}(G^{-1} G_0)-n = 2\, \text { tr}(G^{-1}G_0). \end{aligned}$$

Hence, the statement follows evaluating $\det (Q^s)$ at $s =1$:

$$\begin{aligned} \begin{aligned} \det (Q^s)&= \det (T_1 {{\tilde{\Phi }}}_* \Phi _1^1-1) = \det ({\underline{\Phi }}_t^{-1}{{\tilde{\Phi }}}_*\Phi _1^1-1)\\&= \det (\Psi _t-{\underline{\Phi }}_t). \end{aligned} \end{aligned}$$

$\square$

4 Proof of the main theorem

In this section, we provide a proof of Theorem 1. First, we work with separated boundary conditions and then reduce the general case to the former. The proof is a bit long so we try to give here a concise outline. The idea is to construct an analytic function f which vanishes precisely on the set $\{-1/\lambda : \lambda \in \text {Spec}(K)\}\subseteq {\mathbb {R}}$. Particular care is needed to show that the multiplicity of the zeros of this function equals the multiplicity of the eigenvalues of K. We do this in Propositions 1 and 2 respectively. We show that this function decays exponentially and use a classical factorization Theorem by Hadamard to represent it as

$$\begin{aligned} f(s) = a s^k e^{b s} \prod _{\lambda \in \text {Spec}(K)}(1+\lambda s)^{m(\lambda )}, \quad a, b\in {\mathbb {C}}, a\ne 0, k \in {\mathbb {N}}. \end{aligned}$$

To prove the general case, we double the variables and consider general boundary conditions as separated ones. In this framework, we compute the value of the parameters a, b and k appearing in the factorization.

4.1 Separated boundary conditions

We briefly recall the notation. We are working with an extremal $\lambda _t$ with initial and final point $(\lambda _0,\lambda _1) \in Ann(N)$, where $N = N_0\times N_1$ are product boundary conditions. We are assuming that $\lambda _t$ is strictly normal and satisfies Legendre strong conditions. We work in a fixed tangent space, namely $T_{\lambda _0}T^*M$, to do so we backtrack our curve to its starting point $\lambda _0$ using the flow generated by the time-dependent Hamiltonian:

$$\begin{aligned} h^t_{{\tilde{u}}}(\lambda ) = \langle \lambda , f_{{\tilde{u}}(t)} (q)\rangle -\varphi _t(q,{\tilde{u}}(t)). \end{aligned}$$

We denote the differential of said flow by ${{\tilde{\Phi }}}_*$. We have a scalar product $g_i$ on $T_{\lambda _i}T^*M$, for each $i=0,1$. We assume that the orthogonal complement to the fiber at $\lambda _i$, $\Pi _i = T_{\lambda _i}T^*_{\pi (\lambda _i)}M$ is a Lagrangian subspace and that the range of $Z_0$ (and ${{\tilde{\Phi }}}_* Z_1$ respectively) is contained in $\Pi _0^{\perp }$ (resp. $\Pi _1^\perp$).

Remark 7

If we fix Darboux (i.e. canonical) coordinates coming from the splitting $\Pi _i \oplus \Pi _i^\perp$ it is straightforward to check that $g_i$ takes a block diagonal form with symmetric $n \times n$ matrix $G^j_i$ on the main diagonal. Similarly, we can write down the coordinate representation of the matrix $J_i$ and find:

$$\begin{aligned} g_i(X,Y) = \left\langle \begin{pmatrix} G^1_i &{}\quad 0\\ 0&{}\quad G^2_i \end{pmatrix} \begin{pmatrix} X_1 \\ X_2 \end{pmatrix}, \begin{pmatrix} Y_1 \\ Y_2 \end{pmatrix} \right\rangle , \quad J_i = \begin{pmatrix} 0 &{}\quad -(G^1_i)^{-1} \\ (G^2_i)^{-1} &{}\quad 0 \end{pmatrix}. \end{aligned}$$

For $s \in {\mathbb {R}}$ (or ${\mathbb {C}}$) we introduce the following symplectic maps:

$$\begin{aligned} \begin{aligned} A_0^s (\eta )&= \eta + (1-s) J_0^{-1}pr_{\Pi _0^\perp } \eta , \quad \eta \in T_{\lambda _0}(T^*M), \\ A_1^s(\eta )&= \eta + (1-s)(J_1^{-1} +{{\tilde{\Phi }}}_*\circ pr_{\Pi _0}\circ {{\tilde{\Phi }}}_*^{-1})pr_{\Pi _1^\perp } \eta , \quad \eta \in T_{\lambda _1}(T^*M). \end{aligned} \end{aligned}$$

(12)

Notice that the transformation $A_i^s$ are indeed symplectomorphisms. In (canonical) coordinates given by $\Pi _i$ and $\Pi _i^{\perp }$ they have the following matrix representation:

$$\begin{aligned} A_i^ s = \begin{pmatrix} 1 &{}&{}\quad (1-s)S_i\\ 0 &{}&{}\quad 1 \end{pmatrix}, \quad S_i^* = S_i. \end{aligned}$$

The last map we are going introduce is two families of dilation in $T_{\lambda _0}(T^*M)$, one of the vertical subspace and one of its orthogonal complement. Let $s \in {\mathbb {R}}$ (or ${\mathbb {C}}$) and let us define the following maps:

$$\begin{aligned} \begin{aligned} \delta ^s: T_{\lambda _0}T^*M \rightarrow T_{\lambda _0}T^*M, \, \quad \delta ^s \nu = s \, pr_{\Pi _0}\nu + pr_{\Pi _0^\perp } \nu , \\ \delta _s: T_{\lambda _0}T^*M \rightarrow T_{\lambda _0}T^*M, \, \quad \delta _s \nu = pr_{\Pi _0}\nu + s \, pr_{\Pi _0^\perp } \nu . \end{aligned} \end{aligned}$$

(13)

Proposition 1

Let $A^s_i$ be the maps given in Eq. (12) and let $\Phi _1^s$ be the fundamental solution of the system:

$$\begin{aligned} {{\dot{\eta }}} = Z_t^s(Z_t^s)^* J \eta , \quad Z_t^s = \delta ^s Z_t, \end{aligned}$$

The operator $I+sK$ restricted to ${\mathcal {V}}$ has non trivial kernel if and only if there exists a non zero $(\eta _0,\eta _1) \in T_{(\lambda _0,\lambda _1)} (Ann(N))$ such that

$$\begin{aligned} A_1^s\circ {\tilde{\Phi }}_*\circ \Phi _1^s \circ A_0^s \, \eta _0 =\eta _1, \end{aligned}$$

In particular, the geometric multiplicity of the kernel of $I+s K$ equals the number of linearly independent solutions of the above equation.

Proof

$I+sK$ has a non trivial kernel if and only if

$$\begin{aligned} \langle u,v\rangle + \langle sKu,v\rangle =0, \quad \forall u, v \in {\mathcal {V}}. \end{aligned}$$

Equivalently if and only if $\exists u$ such that $u+sKu \in {\mathcal {V}}^{\perp }$ (see Lemma 2 below for a description of ${\mathcal {V}}^\perp$). This is in turn equivalent to the following system

$$\begin{aligned} {\left\{ \begin{array}{ll} (1-s)u_0 = v_0 \\ u_t = s Z_t^*J \Big (\int _{0}^t Z_\tau u_\tau \textrm{d}\tau +Z_0u_0\Big ) + Z_t^*J\nu \\ (1-s) u_1 = s \Lambda (u)+v_1 \end{array}\right. } \end{aligned}$$

(14)

Let us substitute $Z_t$ with $Z_t^s = \delta ^s Z_t$. It is straightforward to check, using the definition in (13), that:

$$\begin{aligned} sZ_t^*J \int _{0}^t Z_\tau u_\tau \textrm{d}\tau = (Z_t^s)^*J \int _{0}^t Z^s_\tau u_\tau \textrm{d}\tau . \end{aligned}$$

Moreover $Z_t^*J \nu = (Z_t^s)^* J \nu$ for any $\nu \in \Pi$ and $sZ_t^*JZ_0 = (Z_t^s)^*JZ_0^s$ since $\delta ^sZ_0 = Z_0$.

All the computations we will do from here on are aimed at rewriting (14) as a boundary value problem in $T_{\lambda _0}T^*M\times T_{\lambda _0}T^*M$. Let us start with the second equality in (14). Define:

$$\begin{aligned} \eta (t) = \int _0^t Z^s_\tau u_\tau \textrm{d}\tau +Z^s_0u_0 +\nu , \quad \eta (0) = Z^s_0u_0 +\nu . \end{aligned}$$

The linear constraint defining ${\mathcal {V}}$ implies:

$$\begin{aligned} \begin{aligned} Z_0u_0 +\int _0^1Z_t u_t \textrm{d}t +Z_1u_1 \in \Pi&\iff Z_0u_0 +\int _0^1Z^s_t u_t \textrm{d}t +Z^s_1u_1 \in \Pi \\&\iff \eta (1)+ Z^s_1u_1 \in \Pi _0\\&\iff {\tilde{\Phi }}_*(\eta (1)+ Z^s_1u_1) \in \Pi _1. \end{aligned} \end{aligned}$$

This imposes a condition on the initial and final value of $\eta (t)$. The initial one must lie in $\pi _*^{-1} TN_0$ and final one in $\pi _*^{-1}TN_1$. If we multiply by $Z_t^s$ the second equation in (14), we are brought to consider the following problem:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{\eta }}(t)= Z_t^s(Z_t^s)^* J \eta (t), \\ (\pi _*\eta (0),\pi _*\eta (1)) \in T(N_0\times N_1). \\ \end{array}\right. } \end{aligned}$$

(15)

Now we use the remaining equations in (14) to reduce the space $\pi _*^{-1}(T(N_0\times N_1))$ to a Lagrangian one. Let us reformulate the first and third line in (14) as equations in $T_{\lambda _0} T^*M$ and $T_{\lambda _1}T^*M$. Using the maps $Z_0$ and ${\tilde{\Phi }}_*Z_1$ we obtain:

$$\begin{aligned} {\left\{ \begin{array}{ll} (1-s) Z_0u_0 = Z_0v_0 = pr_0 J_0 \nu ,\\ (1-s) {\tilde{\Phi }}_*Z_1u_1 = {\tilde{\Phi }}_*Z_1v_1 + s{\tilde{\Phi }}_*Z_1\Lambda (u) = pr_1 J_1 {\tilde{\Phi }}_* \nu +s {\tilde{\Phi }}_*Z_1\Lambda (u). \end{array}\right. } \end{aligned}$$

Where we used the fact that $(v_0,v_t,v_1)$ is a vector in ${\mathcal {V}}^\perp$. Notice that, for $u \in {\mathcal {V}}$ we have that:

$$\begin{aligned} s\left( Z_0u_0 +\int _0^1Z_t u_t \textrm{d}t +Z_1u_1\right) = Z_0u_0 +\int _0^1Z^s_t u_t \textrm{d}t +Z^s_1u_1. \end{aligned}$$

This implies that the term $s{\tilde{\Phi }}_*Z_1\Lambda (u)$ can be rewritten as:

$$\begin{aligned} \begin{aligned} s{\tilde{\Phi }}_*Z_1\Lambda (u)&= s\, pr_1J_1{\tilde{\Phi }}_* \left( Z_0u_0 +\int _0^1Z_t u_t \textrm{d}t +Z_1u_1 \right) \\ {}&= pr_1 J_1{\tilde{\Phi }}_*(\eta (1)+Z_1^s u_1-\nu ). \end{aligned} \end{aligned}$$

If substitute $Z_0u_0$ with $pr_{\Pi _0^\perp } \eta (0)$ we end up with the equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} (1-s)pr_{\Pi _0^\perp } \eta (0) = pr_0 J_0 \nu = pr_0 J_0 \eta (0), \\ (1-s) {\tilde{\Phi }}_*Z_1 u_1= pr_1 J_1{\tilde{\Phi }}_*(\eta (1)+Z_1^su_1). \end{array}\right. } \end{aligned}$$

Now we do the same kind of substitution for the term $Z_1^s u_1$. Using the projections on $\Pi _0$ and $\Pi _0^\perp$ and recalling that ${{\tilde{\Phi }}}_*$ sends $\Pi _0$ to $\Pi _1$, we have:

$$\begin{aligned} \begin{aligned} Z_1^s u_1&= s \,pr_{\Pi _0} Z_1u_1 + pr_{\Pi _0^\perp } Z_1u_1 = (s-1)\,pr_{\Pi _0} Z_1u_1 + Z_1u_1.\\ pr_1 J_1 {\tilde{\Phi }}_* Z_1^su_1&= (s-1)\, pr_1 J_1 {\tilde{\Phi }}_*pr_{\Pi _0} Z_1u_1 + pr_1 J_1{\tilde{\Phi }}_*Z_1u_1 \\&= (s-1)\, pr_1 J_1 {\tilde{\Phi }}_* pr_{\Pi _0}Z_1u_1. \end{aligned} \end{aligned}$$

Last equality being due to the fact that the image of ${\tilde{\Phi }}_*Z_1$ is isotropic and thus $J_1\text { Im}({{\tilde{\Phi }}}_*Z_1) \subset \text { Im}( {\tilde{\Phi }}_*Z_1)^{\perp }$. Moreover $\tilde{\Phi }_*Z_1u_1$ coincides with the projection of $-\tilde{\Phi }_*\eta (1)$ on $\Pi _1^\perp$. Thus we are left with:

$$\begin{aligned} {\left\{ \begin{array}{ll} (1-s)pr_{\Pi _0^\perp } \eta (0) = pr_0 J_0 \nu = pr_0 J_0 \eta (0), \\ (1-s)(- pr_{\Pi _1^\perp }{{\tilde{\Phi }}}_* \eta (1) + pr_1 J_1 {\tilde{\Phi }}_* pr_{\Pi _0}Z_1u_1)= pr_1 J_1{{\tilde{\Phi }}}_*\eta (1). \end{array}\right. } \end{aligned}$$

(16)

It is straightforward to check that $pr_1 J_1 {{\tilde{\Phi }}}_* pr_{\Pi _0} Z_1u_1$ depends only on the projection of $Z_1u_1$ on $\Pi _0^\perp$. Moreover, expanding $1 = {{\tilde{\Phi }}}_* \circ \tilde{\Phi }_*^{-1}$ and using the relation $\tilde{\Phi }_*Z_1u_1=-pr_{\Pi _1^\perp }{{\tilde{\Phi }}}_*\eta (1)$, the second equality in (16) can be rewritten as:

$$\begin{aligned} (s-1) pr_{\Pi _1^\perp } {{\tilde{\Phi }}}_* \eta (1) = pr_1J_1 {\tilde{\Phi }}_* \eta (1)+ (1-s) pr_1J_1{{\tilde{\Phi }}}_* pr_{\Pi _0} {{\tilde{\Phi }}}_*^{-1} pr_{\Pi _1^\perp }{{\tilde{\Phi }}}_* \eta (1).\nonumber \\ \end{aligned}$$

(17)

If $s =1$, the equations reduce to $pr_0(J_0\eta (0)) =0$ and $pr_1 J_1 {{\tilde{\Phi }}}_*\eta (1)=0$. Consider the first case, the relation is equivalent to:

$$\begin{aligned} \sigma (\eta (0),Z_0w_0) = g_0(J_0\eta (0),Z_0 w_0) = g_0(pr_0 J_0\eta (0),Z_0 w_0) =0, \, \forall w_0 \in {\mathbb {R}}^{\dim (N_0)}. \end{aligned}$$

Thus we are looking for a solution starting from $T_{\lambda _0} Ann(N_0)$. Similarly setting $s=1$ in the second equality we find that $\eta (1)$ must lie inside $T_{\lambda _1} Ann(N_1)$.

Now, for $s\ne 1$, we want to interpret the boundary conditions as an analytic family of Lagrangian subspaces depending on s. To do so we employ the following linear map defined in (12):

$$\begin{aligned} A_0^s (\eta ) = \eta + J_0^{-1}(1-s) pr_{\Pi _0^\perp } \eta . \end{aligned}$$

If $\eta \in T_{\lambda _0} Ann(N_0)$ we have that $pr_{\Pi _0^\perp } \eta = pr_0 \eta$ and $pr_0 J_0 \eta =0$ and thus:

$$\begin{aligned} \begin{aligned} pr_{\Pi _0^\perp }(A_0^s(\eta ))&= pr_{\Pi _0^\perp }(\eta ) \in \text { Im}(Z_0). \\ pr_0 J_0(A_0^s(\eta ))&= pr_0(J_0 \eta +(1-s) pr_{\Pi _0^{\perp }}\eta ) \\ {}&=pr_0 J_0\eta +(1-s) pr_{\Pi _0^\perp } \eta \\&=(1-s) pr_{\Pi _0^\perp }(A_0^s(\eta )). \end{aligned} \end{aligned}$$

So we have shown that $A_0^s(T_{\lambda _0} Ann(N_0))$ is precisely the space satisfying the first set of equations. A similar argument works for the final point. Let us recall the definition of $A_1^s$ given in (12):

$$\begin{aligned} A_1^s(\eta ) = \eta + (1-s)(J_1^{-1}+{{\tilde{\Phi }}}_* pr_{\Pi _0} \tilde{\Phi }_*^{-1} ) pr_{\Pi _1^\perp } \eta . \end{aligned}$$

Now, we check that the boundary condition for the final point are satisfied if and only if $A_1^s \circ {{\tilde{\Phi }}}_* \,\eta (1)\in T_{\lambda _1}Ann(N_1)$. In fact, take any $\eta$ in $T_{\lambda _1}Ann(N_1)$, it holds:

$$\begin{aligned} \begin{aligned} pr_{\Pi _1^\perp }(A_1^s)^{-1}\eta&= pr_{\Pi _1^\perp }\eta , \\ pr_{\Pi _1}(A_1^s)^{-1}\eta&= pr_{\Pi _1}\eta +(s-1)(J^{-1}_1+{{\tilde{\Phi }}}_* pr_{\Pi _0} {{\tilde{\Phi }}}_*^{-1} ) pr_{\Pi _1^\perp } \eta ,\\ pr_1 J_1 (A_1^s)^{-1} \eta&=(s-1) pr_1 (1+J_1 {{\tilde{\Phi }}}_* pr_{\Pi _0} {{\tilde{\Phi }}}_*^{-1} )pr_{\Pi _1^\perp } \eta . \end{aligned} \end{aligned}$$

It is straightforward to substitute the last equality in (17) and check that indeed $(A^s_1)^{-1}(T_{\lambda _1} Ann(N_1))$ is the right space.

Let us call $\Phi _1^s$ the fundamental solution of (15) at time 1 and denote by $\Gamma (\Phi _1^s)$ its graph. It follows that $s \in {\mathbb {R}} \setminus \{0\}$ is in the kernel of $1+s K$ if and only if:

$$\begin{aligned} \Gamma ({{\tilde{\Phi }}}_* \circ \Phi _1^s) \cap A_0^s(T_{\lambda _0} Ann(N_0))\times (A_1^s)^{-1}(T_{\lambda _1} Ann(N_1)) \ne (0). \end{aligned}$$

which is equivalent to the condition:

$$\begin{aligned} \Gamma (A_1^s \circ \tilde{\Phi }_* \circ \Phi _1^s \circ A_0^s) \cap T_{\lambda _0}Ann(N_0) \times T_{\lambda _1} Ann(N_1)\ne (0). \end{aligned}$$

(18)

Now we prove the part about the multiplicity. Suppose that two different controls u and v give the same trajectory $\eta _t$ solving (15). Since the maps $Z_0$ and $Z_1$ are injective it must hold that $v_0 =u_0$ and $v_1 = u_1$. Moreover, $\int _0^t Z_\tau u_\tau \textrm{d}\tau = \int _0^t Z_\tau v_\tau \textrm{d}\tau$ $\forall \, t \in [0,1]$ and thus:

$$\begin{aligned} Ku = Z_t^* J\int _0^t Z_\tau u_\tau \textrm{d}\tau = Z_t^* J\int _0^t Z_\tau v_\tau \textrm{d}\tau = K v. \end{aligned}$$

However, Volterra operators are always injective and thus $u=v$.

Vice-versa, consider $u = 0$ and see whether you get solutions of the system above that do not correspond to any variation. Since $u_0$ and $u_1$ are both zero we are considering solution starting from the fiber and reaching the fiber. Plugging in $u_t =0$ we obtain:

$$\begin{aligned} 0 = {\dot{\eta }} = Z_t^s(Z_t^s)^*J\eta =Z_t^s(Z_t^s)^*J\nu . \end{aligned}$$

However $pr_{\Pi ^\perp }Z_t^s(Z_t^s)J \nu = X_t X_t^* \nu$ and by assumption the matrix $\int _0^1 X_t X_t^* \textrm{d}t$ is invertible. Thus we get a contradiction. $\square$

The following Lemma was used in the proof of Proposition 1. Gives the orthogonal complement to ${\mathcal {V}}$ inside ${\mathcal {H}}$, using the Hilbert structure introduced in Definition 2. We will denote by the symbol $\perp _i$ the orthogonal complement, in $T_{\lambda _i}T^*M$, with respect to the scalar product $g_i$.

Lemma 2

With this choice of scalar product the orthogonal complement to ${\mathcal {V}}$ is given by:

$$\begin{aligned} {\mathcal {V}}^\perp = \{(v_0,Z_t^* J\nu ,v_1): \nu \in \Pi \}, \end{aligned}$$

where $v_0$ and $v_1$ are determined by the following conditions:

$$\begin{aligned} Z_0v_0 - J_0\nu \in \text { Im}Z_0^{\perp _0},\quad {{\tilde{\Phi }}}_* Z_1v_1 - J_1{{\tilde{\Phi }}}_*\nu \in \text { Im}{{\tilde{\Phi }}}_*Z_1^{\perp _1}. \end{aligned}$$

Proof

Suppose that $u \in {\mathcal {V}}^{\perp }$. Let us test it against infinitesimal variations that fix the endpoints, i.e. such that $u_i = 0$ and $\int _0^1Z_t u_t \textrm{d}t \in \Pi$. Recall that $\Pi$ is Lagrangian, thus the condition $\int _0^1Z_t u_t \textrm{d}t \in \Pi$ can be equivalently formulated as $\sigma (\int _0^1Z_t u_t \textrm{d}t,\nu ) =0$ for all $\nu \in \Pi$. Hence, the subspace $\{u: u_i=0,\int _0^1Z_t u_t \textrm{d}t \in \Pi \}$ is the intersection of the kernels of $u_t \mapsto \int _0^1 \sigma (Z_t u_t,\nu ) \textrm{d}t$. It follows that:

$$\begin{aligned} \langle v, u\rangle = -\int _0^1 \langle v_t,u_t\rangle \textrm{d}t = 0, \, \forall u \in V \iff v_t = \sigma (\nu ,Z_t \cdot ), \quad \nu \in \Pi . \end{aligned}$$

Hence $v_t = Z_t^*J \nu$. Now, take $u \in {\mathcal {V}}$ and compute:

$$\begin{aligned} \langle v, u\rangle = \sigma (\nu , \int _0^1 Z_tu_t \textrm{d}t) +\sigma (J_0^{-1}Z_0v_0,Z_0u_0)+\sigma (J_1^{-1}{{\tilde{\Phi }}}_*Z_1v_1,\tilde{\Phi }_*Z_1u_1). \end{aligned}$$

Since $u \in {\mathcal {V}}$, we have:

$$\begin{aligned} \sigma \left( \nu , \int _0^1 Z_t u_t \textrm{d}t \right) = -\sigma (\nu , Z_0u_0+Z_1u_1). \end{aligned}$$

It follows that:

$$\begin{aligned} \begin{aligned} \langle v, u \rangle&= -\sigma (\nu , Z_0u_0+Z_1u_1)+\sigma (J_0^{-1}Z_0v_0,Z_0u_0)+\sigma (J_1^{-1}{{\tilde{\Phi }}}_*Z_1v_1,{{\tilde{\Phi }}}_*Z_1u_1) \\&= \sigma (J_0^{-1}Z_0v_0-\nu ,Z_0u_0)+\sigma (J_1^{-1}\tilde{\Phi }_*Z_1v_1-{{\tilde{\Phi }}}_*\nu ,{{\tilde{\Phi }}}_*Z_1u_1). \end{aligned} \end{aligned}$$

Since we are assuming that $\int _0^1X_tX_t^*\textrm{d}t >0$, the image of the map $u_t \mapsto \pi _*\int _0^1Z_t u_t \textrm{d}t$ is the whole $T_{q_0}M$. In particular, for any $u_0$, is possible to find variations of the form $(u_0,u_t,0) \in {\mathcal {V}}$. An analogous statement holds for variations of the form $(0,u_t,u_1).$

Hence, if $\langle u, v \rangle = 0$ $\forall u \in {\mathcal {V}}$, then both $\sigma (J_0^{-1}Z_0v_0-\nu ,Z_0u_0)$ and $\sigma (J_1^{-1}{{\tilde{\Phi }}}_*Z_1v_1-{{\tilde{\Phi }}}_*\nu ,\tilde{\Phi }_*Z_1u_1)$ must be zero at the same time.

Moreover, this implies that $v_0$ and $v_1$ are completely determined by the value of $\nu$. Finally notice that:

$$\begin{aligned} \begin{aligned} \sigma (J_0^{-1}Z_0 v_0-\nu ,Z_0 u_0) =0 \, \forall \, u_0&\iff Z_0 v_0-J_0\nu \in \text { Im}(Z_0)^{\perp _0}, \\ \sigma (J_1^{-1}{{\tilde{\Phi }}}_*Z_1 v_1-{{\tilde{\Phi }}}_*\nu ,Z_1 u_1)=0 \,\forall \, u_1&\iff {{\tilde{\Phi }}}_*Z_1 v_1-J_1{{\tilde{\Phi }}}_*\nu \in \text { Im}({{\tilde{\Phi }}}_*Z_1)^{\perp _1}. \end{aligned} \end{aligned}$$

$\square$

Remark 8

If we complexify all the subspaces involved in the proof of Proposition 1, i.e. tensor with ${\mathbb {C}}$ we can take also $s \in {\mathbb {C}}$.

We can reformulate the intersection problem in the statement of Proposition 1 as follows. Let $\pi _{N_1}$ the orthogonal projection, with respect to $g_1$, onto the subspace $T_{\lambda _1} Ann(N_1)^{\perp }$ and define a map $Q^s$ as:

$$\begin{aligned} Q^s: T_{\lambda _0}Ann(N_0) \rightarrow T_{\lambda _1}Ann(N_1)^{\perp }, \quad Q^s(\eta ) = \pi _{N_1}(A_1^s\Phi _1^s A_0^s)(\eta ). \end{aligned}$$

(19)

Let us fix now two bases, one of $T_{\lambda _0} Ann(N_0)$ and one of $T_{\lambda _1}Ann(N_1)$. Construct two $2n \times n$ matrices using the elements of the chosen basis. Let us call the resulting objects $T_0$ and $T_1$ respectively. It follows that $J_1T_1$ is a basis of $T_{\lambda _1} Ann(N_1)^\perp$. Define the function $\det (Q^s)$ as the determinant of the $n \times n$ matrix $T_1^*J_1 A_1^s\Phi _1^s A_0^s T_0$. Clearly, different choices of basis give simply a scalar multiple of $\det (Q^s)$ and thus is well defined:

$$\begin{aligned} \det (Q^s) = \frac{\det (T_1^*J_1 A_1^s\Phi _1^s A_0^sT_0)}{\det (T_0^*T_0)^{1/2} \det (T_1^*J_1J_1^*T_1)^{1/2}}. \end{aligned}$$

Moreover $\det (Q^s) |_{s=s_0} =0$ if and only if there exists at least a solution to our boundary problem. Notice that map $s \mapsto \det (Q^s)$ is analytic in s since the fundamental matrix is an entire map in s (see [3, Proposition 4]). The following Proposition shows that the multiplicity of any root $s_0 \ne 0$ is equal to the number of independent solutions to the boundary value problem.

Proposition 2

The multiplicity of any root $s_0 \ne 0$ of $\det Q^s$ equals the dimension of the kernel of $Q^s$.

Proof

The proof is done in two steps. First, we show that the equation $\det (Q^s)=0$ is equivalent to $\det (R^s) =0$ where $R^s$ is a symmetric matrix, analytic in s. Once one knows this, it suffices to compute $\partial _s R^s$ and show that it is non-degenerate to prove that the multiplicity of the equation is the same as the dimension of the kernel.

Step 1: Replace $Q^s$ with a symmetric matrix Let us restrict to the case $s \in {\mathbb {R}}$, since all the roots are real. As shown in (18) and remarked above, the determinant of the matrix $Q^s$ is zero whenever the graph of $A_1^s {{\tilde{\Phi }}}_*\Phi _1^s A_0^s$ intersect the subspace $L_0 = T_{(\lambda _0,\lambda _1)} (Ann(N_0 \times N_1))$. Suppose that $s_0$ is a time of intersection and choose as coordinates in the Lagrange Grassmannian $L_0$ and another subspace $L_1$ transversal to both $L_0$ and $\Lambda _s:=\Gamma (A_1^s{{\tilde{\Phi }}}_* \Phi _1^s A_0^s)$. This means that, if $(T_{\lambda _0}T^*M)^2 \approx \{ (p,q)| p,q\in {\mathbb {R}}^{2n}\}$, we identify $L_0 \approx \{q=0\}$ and $L_1 \approx \{p=0\}$.

In this coordinates $\Lambda _s$ is given by the graph of a symmetric matrix, i.e. is the following subspace $\Lambda _s = \{(p,R^sp)\}$ where again $R^s$ is analytic in s.

The quadratic form associated to the derivative $\partial _s R(s)$ can be interpreted as the velocity of the curve $s \mapsto \Lambda _s$ inside the Grassmannian, it is possible to compute it choosing an arbitrary base of $\Lambda _s$ and an arbitrary set of coordinates. Invariants such as signature and nullity do not change (see for example [5, 7] or [2]). Take a curve $\lambda _s = (p_s,R^sp_s)$ inside $\Lambda _s$ then one has:

$$\begin{aligned} S(\lambda _s) = \sigma (\lambda _s,{\dot{\lambda }}_s) = \langle p_s, \partial _s R^s p_s\rangle . \end{aligned}$$

Recall that we will be using the symplectic form given by $(-\sigma _{\lambda _0})\oplus \sigma _{\lambda _1}$, in order to have that graph of a symplectic map is a Lagrangian subspace.

Step 2: Replace $\Lambda _s$ with a positive curve We slightly modify our curve to exploit a hidden positivity of the Jacobi equation. We substitute the fundamental solution $\Phi _1^s$ with the following map:

$$\begin{aligned} \Psi ^s = \Psi ^s_1= \delta _s \Phi ^s_1 \delta _{\frac{1}{s}}. \end{aligned}$$

It is straightforward to check that $\Psi ^s$ is again a symplectomorphism and that it is the fundamental solution of the following ODE system at time $t=1$:

$$\begin{aligned} {{\dot{\Psi }}}_t^s = s Z_tZ_t^*J\Psi _t^s, \quad \Psi _0^s = Id. \end{aligned}$$

(20)

On one hand, we are introducing a singularity at $s=0$ but on the other hand we are going to show that the graph of $\Psi ^s$ becomes a monotone curve and its velocity is fairly easy to compute.

First of all, hoping that the slight abuse of notation will not create any confusion, let us introduce a family of dilations similar to the $\delta _s$,$\delta ^s$ also in $T_{\lambda _1}T^*M$. The definition is analogous to the one in (13) but with $\Pi _1$ and $\Pi _1^\perp$ instead of $\Pi _0$ and $\Pi _1^\perp$. We will denote them with the same symbol.

Let us consider the following symplectomorphisms:

$$\begin{aligned} \delta _s A_1^s {{\tilde{\Phi }}}_*\Phi _1^s A_0^s \delta _{\frac{1}{s}} = \delta _s A_1^s {{\tilde{\Phi }}}_* \delta _{\frac{1}{s}} \Psi _s \delta _s A_0^s \delta _{\frac{1}{s}}. \end{aligned}$$

Notice that the dilations $\delta _s$ preserve the subspaces $T_{\lambda _i}Ann(N_i)$ and thus the intersection points between the graph of the above map and the subspace $T_{(\lambda _0,\lambda _1)}Ann(N_0\times N_1)$ are unchanged. Let us rewrite the maps $\delta _sA_0^s\delta _{\frac{1}{s}}$ and $\delta _s A_1^s {{\tilde{\Phi }}}_*\delta _{\frac{1}{s}}$. For the former:

$$\begin{aligned} \delta _sA_0^s\delta _{\frac{1}{s}} = \delta _s(1+(1-s)J_0^{-1}pr_{\Pi _0^\perp })\delta _{\frac{1}{s}} = 1+ \frac{1-s}{s} J_0^{-1}pr_{\Pi _0^\perp } = B_0^s. \end{aligned}$$

For the latter, a computation in local coordinates and the fact that the dilations $\delta _s$ and ${{\tilde{\Phi }}}_*$ do not commute yield:

$$\begin{aligned} \begin{aligned} \delta _sA_1^s{{\tilde{\Phi }}}_*\delta _{\frac{1}{s}}&= \delta _s(1+(1-s)(J_1^{-1} +{{\tilde{\Phi }}}_*pr_{\Pi _0}\tilde{\Phi }_*^{-1})pr_{\Pi _1^\perp }){{\tilde{\Phi }}}_*\delta _{\frac{1}{s}} \\ {}&= \left( 1+ \frac{1-s}{s} J_1^{-1}pr_{\Pi _1^\perp }\right) {{\tilde{\Phi }}}_* = B_1^s{{\tilde{\Phi }}}_*. \end{aligned} \end{aligned}$$

Thus we take, for $s\ne 0$, as curve $\Lambda _s:= \Gamma (B_1^s {{\tilde{\Phi }}}_* \Psi ^s B_0^s)$, the graph of the symplectomorphism just introduced. Notice that $\Psi ^s$ is actually analytic, the singularity at $s=0$ comes only form the maps $B_i^s$.

Step 3: Computation of the velocity Now we compute the velocity of the graph of $B_1^s {{\tilde{\Phi }}}_* \Psi ^s B_0^s$. Take a curve $\lambda _s = (\eta , B_1^s{{\tilde{\Phi }}}_* \Psi ^s B_0^s\eta )$ inside the $\Lambda _s$ and let us compute the quadratic form associated to the velocity:

$$\begin{aligned} \begin{aligned} S(\lambda _s)&=-\sigma (\eta ,\partial _s \eta )+\sigma (B_1^s {{\tilde{\Phi }}}_* \Psi ^s B_0^s\eta ,\partial _s( B_1^s {{\tilde{\Phi }}}_* \Psi ^s B_0^s\eta )) \\&= \sigma (B_1^s {{\tilde{\Phi }}}_* \Psi ^s B_0^s\eta ,(\partial _s B_1^s ) {{\tilde{\Phi }}}_* \Psi ^s B_0^s\eta )+\sigma ( \Psi ^s B_0^s\eta ,(\partial _s \Psi ^s) B_0^s\eta )+\\ {}&\quad +\sigma (B_0^s\eta ,\partial _s(B_0^s)\eta ). \end{aligned} \end{aligned}$$

Let us consider the terms of the type $\sigma (B_i^s x,\partial _s B_i^s x)$. It immediate to compute the derivative in this case, recall that $B_i^s x = x + \frac{(1-s)}{s}J_i^{-1} pr_{\Pi _i^\perp } x$. It follows that $\partial _s B_i^s = -\frac{1}{s^2} J_i^{-1}pr_{\Pi _i^\perp }$ thus the first and last term read as:

$$\begin{aligned} \begin{aligned} \sigma (B_1^s \xi ,(\partial _s B_1^s ) \xi )&= - \frac{1}{s^2}\sigma (\xi , J_1^{-1} pr_{\Pi _1^\perp }\xi ) \\&= \frac{1}{s^2} g_1( pr_{\Pi _1^\perp }\xi , pr_{\Pi _1^\perp }\xi ), \quad \text {where } \xi = {{\tilde{\Phi }}}_*\Psi ^s B_0^s\eta ,\\ \sigma (\partial _s(B_0^s)\eta , B_0^s\eta )&= - \frac{1}{s^2} \sigma (B_0^s \eta , J_0^{-1} pr_{\Pi _0^\perp } \eta ) = -\frac{1}{s^2} g_0(J_0\eta , J_0^{-1} pr_{\Pi _0^\perp } \eta )\\&= \frac{1}{s^2}g_0(pr_{\Pi _0^\perp } \eta ,pr_{\Pi _0^\perp } \eta ). \end{aligned} \end{aligned}$$

Notice we used the fact that $J_i$ (and thus $J_i^{-1}$) is $g_i-$skew symmetric. Now we rewrite the middle term. We present it as the integral of its derivative using the equation for $\Psi _t^s$. Let us use the shorthand notation $x = B_0^s\eta$. We obtain:

$$\begin{aligned} \begin{aligned}&\frac{\textrm{d}}{\textrm{d}t} \left( \sigma (\Psi _t^s x,(\partial _s \Psi _t^s) x)\right) = \sigma (\partial _t\Psi _t^s x,(\partial _s \Psi _t^s) x) + \sigma ( \Psi _t^s x,(\partial _s \partial _t\Psi _t^s) x)\\&\quad = s \sigma (Z_tZ_t ^* J \Psi _t^sx,\partial _s\Psi _t^s x)+s \sigma (\Psi _t^s x,Z_tZ_t^* J \partial _s\Psi _t^sx) \\&\qquad +\sigma (\Psi _t^s x,\partial _s\big (s Z_tZ_t^*\big ) J \Psi _t^sx). \end{aligned} \end{aligned}$$

The first and second term have opposite sign and thus cancel out. What remains is:

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t} \left( \sigma ((\partial _s \Psi _t^s) x, \Psi _t^s x)\right) =\sigma (\Psi _t^s x, Z_t Z_t^* J \Psi _t^s x)= g(Z_t^*J \Psi _t^s x,Z_t^*J \Psi _t^s x). \end{aligned}$$

Integrating over [0, 1] and using the fact that $\partial _s \Psi _t^s \vert _{(0,0)}= 0$ we get that:

$$\begin{aligned} \begin{aligned} \sigma (\partial _s\Psi ^s x,\Psi ^s x)&= \int _0^1 g (Z^*_t J \Psi _t^s x, Z^*_t J \Psi _t^s x) \textrm{d}t. \end{aligned} \end{aligned}$$

Using the notation $\vert \vert \cdot \vert \vert$ to denote the norm with respect to the corresponding metric and summing everything up we find the following expression for the velocity of our curve:

$$\begin{aligned} S_s(\lambda _s) = \frac{1}{s^2} \left( \Vert pr_{\Pi _0^{\perp }}\eta \Vert ^2+\Vert pr_{\Pi _1^\perp } \Psi ^s B_0^s \eta \Vert ^2 \right) +\int _0^1 \Vert Z_t^*J\Psi _t^s B_0^s \eta \Vert ^2 \textrm{d}t. \end{aligned}$$

Since each term of the sum is non-negative $S_s(\lambda _s)$ is zero if and only if each term is zero. From the first one we obtain that $\eta$ must be contained in the fiber. Notice that $B^s_0$ acts as the identity on $\Pi _0$ and thus in this case $\Vert pr_{\Pi _1^\perp } {{\tilde{\Phi }}}_*\Psi ^s B_0^s \eta \Vert ^2 = \Vert pr_{\Pi _1^\perp } \Psi ^s \eta \Vert ^2$.

It follows that $\Psi _t^s B^s \eta =\Psi _t^s \eta$ is a solution of the Jacobi equation (15) starting and reaching the fiber (recall that ${{\tilde{\Phi }}}_*(\Pi _0) = \Pi _1$). Let us consider now the third piece, since the integrand is positive it must hold that for almost any t, $Z_t^*J\Psi _t^s \eta =0$. If we multiply this equation by $Z_t$ we find that:

$$\begin{aligned} Z_tZ_t^*J \Psi _t^s \eta =0 ={{\dot{\Psi }}}_t^s \eta . \end{aligned}$$

It follows that we are dealing with a constant solution starting and reaching the fiber. However, this contradicts the assumption that the matrix $\int _0^1 X_t X_t^* \textrm{d}t$ is non degenerate. In fact, if we substitute a non-zero constant solutions starting from the fiber in (15), we find that $pr_{\Pi _0^\perp } (\eta ) = \int _0^1 X_tX_t^* \textrm{d}t\, \eta \ne 0$ $\square$

The following proposition is proved in [3].

Proposition 3

There exists $c_1,c_2>0$ such that:

$$\begin{aligned} \Vert \Phi _1^s\Vert \le c_1e^{c_2 |s|}\quad \forall \, s \in {\mathbb {C}}. \end{aligned}$$

Moreover $\Phi _t^s$ is analytic and the function $s\mapsto \det (Q^s)$ is entire and satisfy the same type of estimate.

This fact tells us that $\det Q^s$ is an entire function of order $\rho \le 1$. We know its zeros, which are determined by the eigenvalues of K, and thus we can apply Hadamard factorization theorem (see [14]) to present it as an infinite product. It follows that we have the following identity:

$$\begin{aligned} \det (Q^s) = as^k e^{b s}\prod _{\lambda \in Sp(K)} (1+s\lambda )^{m(\lambda )} \quad a, b \in {\mathbb {C}}, a\ne 0, k \in {\mathbb {N}}. \end{aligned}$$

(21)

where $m(\lambda )$ is the geometric multiplicity of the eigenvalue $\lambda$. To determine the remaining parameters it is sufficient to know the value of $\det (Q^s)$ and a certain number of its derivatives at $s =0$ (depending on the value of k). Assume for now that $k=0$, a straightforward computation shows that:

$$\begin{aligned} \det (Q^s)\vert _{s=0} = a, \quad \partial _s\det (Q^s)\vert _{s=0} = a(b+\text { tr}(K)). \end{aligned}$$

(22)

We will compute these quantities in Lemmas 4 and 3 for general boundary conditions. The proofs can be adapted to the case of separated conditions easily.

4.2 General boundary condition

In this section we prove a determinant formula for general boundary conditions $N \subseteq M \times M$. First, we reduce this case to the case of separate boundary conditions. We have to slightly modify the proof of Proposition 1 since, after this reduction, the Endpoint map will not be a submersion anymore. Then, we compute the normalization factors given in (22).

Let us consider $M \times M$ as state space, with the following dynamical system:

$$\begin{aligned} f_u(q',q) = \begin{pmatrix} 0 \\ f_u(q) \end{pmatrix}, \quad (q',q) \in M\times M. \end{aligned}$$

(23)

and boundary conditions $\Delta \times N$. With this definition, any extremal between two points $q_0$ and $q_1$ lifts naturally to an extremal between $(q_0,q_0)$ and $(q_0,q_1)$. However, the Endpoint map of the new system is no longer surjective. In fact, any trajectory is confined to a submanifold of the form $\{{{\hat{q}}}\} \times M$. Thus, even if we started with a strictly normal extremal, we do not get a strictly normal extremal of the new system. However, there is no real singularity of the Endpoint map here: we have just introduced a certain number of conserved quantities. All the proofs presented above work also in this case. We are going to discuss briefly how to adapt them.

Let us start with Pontryagin maximum principle. It implies that the lift of the extremal curve ${\tilde{q}} (t) = (q_0,q(t))$ is the curve ${{\tilde{\lambda }}} (t)= (-\lambda _0,\lambda (t))$. This is because the initial and final covector of the lift must annihilate the tangent space of the boundary conditions manifold. In this case $N_0 = \Delta$ and the annihilator of the diagonal subspace is $\{(\lambda ,-\lambda ): \lambda \in T_{\lambda _0}T^*_{q_0}M\}$. Moreover, by the orthogonality condition in PMP (see Appendix A), we know that $(-\lambda (0),\lambda (1))$ annihilates the tangent space of N.

Thus, if we want to work in one fixed tangent space, we have to multiply the first covector by $-1$. This changes the sign of the symplectic form and we are thus brought to work on $T_{\lambda _0} T^*M \times T_{\lambda _0}T^*M$ with symplectic form $(-\sigma )\oplus \sigma$.

With this change of sign, the tangent space to the annihilator of the diagonal gets mapped to the diagonal subspace of $T_{\lambda _0} T^*M \times T_{\lambda _0}T^*M$ and the tangent space to the annihilator of the boundary conditions N is mapped to the tangent space of:

$$\begin{aligned} A(N) = \{(\mu _0,\mu _1):\langle \mu _0,X_0\rangle =\langle \mu _1,X_1\rangle , \, \forall (X_0,X_1) \in TN\}. \end{aligned}$$

Let us make now some notational remarks. We will still denote by ${{\tilde{\Phi }}}_*$ the map $1 \times {{\tilde{\Phi }}}_*$, which correspond to the new flow we are using to backtrack our trajectory to the starting point.

As explained in Sect. 2, to define the scalar product on our space of variations, it is necessary to introduce two metrics on the tangent spaces to the endpoints of our curve. We will choose them of the form ${{\tilde{g}}}_0 = g_0\oplus g_0$ and ${{\tilde{g}}}_1 = g_0\oplus g_1$ where $g_0$ and $g_1$ are two metrics on $T_{\lambda _0}T^* M$ and $T_{\lambda _1}T^*M$ respectively.

Now we compute the second variation of the new system (23). As a general rule, we will denote all the quantities relative to (23) on $M\times M$, putting a $\tilde{}$ on top. We have:

$$\begin{aligned} {{\tilde{Z}}}_0 u_0 =\begin{pmatrix} Z_0u_0 \\ Z_0u_0 \end{pmatrix}, \quad {{\tilde{Z}}}_1 = \begin{pmatrix} Z_1^0 u_1\\ Z_1^1 u_1 \end{pmatrix}, \quad {{\tilde{Z}}}_t =\begin{pmatrix} 0\\ Z_t \end{pmatrix}. \end{aligned}$$

Notice that ${{\tilde{\Phi }}}_* {{\tilde{Z}}}_1$ maps ${\mathbb {R}}^{\dim (N)}$ to the tangent space to A(N) and we can assume that its image is contained in $\Pi _0^\perp \times \Pi _1^\perp$. We will denote by ${\tilde{pr}}_1$ the orthogonal projection onto the image of $\tilde{Z}_1$.

The domain of the second variation is the subspace ${\mathcal {V}} = \{(u_0,u_t,u_1): {{\tilde{Z}}}_0u_0 + \int _0^1 {{\tilde{Z}}}_t u_t + \tilde{Z}_1u_1 \in \Pi _0\times \Pi _0\}$. Clearly, this equation is equivalent to:

$$\begin{aligned} Z_0u_0+Z_1^0u_1 \in \Pi _0 \quad \text { and } \quad Z_0u_0+Z^1_1u_1+\int _0^1Z_t u_t \textrm{d}t \in \Pi _0. \end{aligned}$$

It follows that the control $u_0$ is completely determined by $u_1$. Moreover, we can assume that $Z_0u_0 = -Z_1^0u_1$ since we are free to choose any system of coordinates and any trivialization of the tangent bundle of the manifolds $\Delta$ and N.

Let $A_i^s$ be the maps given in (12). The following proposition is the counterpart of Proposition 1 for general boundary conditions.

Proposition 4

Let $\Phi _1^s$ be the fundamental solution of the Jacobi system:

$$\begin{aligned} {{\dot{\eta }}} = Z_t^s(Z_t^s)^* J \eta . \end{aligned}$$

The operator $1+sK$ restricted to ${\mathcal {V}}$ has non trivial kernel if and only if there exists a non zero $(\eta _0,\eta _1) \in T_{(\lambda _0,\lambda _1)}A(N)$ such that

$$\begin{aligned} A_1^s\circ {{\tilde{\Phi }}}_* \circ \Phi _1^s \circ A_0^s \, \eta _0 =\eta _1. \end{aligned}$$

(24)

The geometric multiplicity of the kernel equals the number of linearly independent solutions of the above equation.

Proof

The proof is completely analogous to the one of Proposition 1. However, some slight modifications are in order since the Endpoint map is not surjective in this case.

Step 1: Characterize ${\mathcal {V}}^\perp$. The orthogonal complement to ${\mathcal {V}}$ is given by:

$$\begin{aligned} {\mathcal {V}}^\perp =\left\{ (v_0, {{\tilde{Z}}}_t^*J{{\tilde{\nu }}},v_1): \tilde{pr}_1\left( \begin{pmatrix} 2Z_0v_0 \\ 0 \end{pmatrix}+{{\tilde{J}}}_1 {{\tilde{\nu }}}\right) = {{\tilde{\Phi }}}_* {{\tilde{Z}}}_1 v_1 \right\} . \end{aligned}$$

The proof is the same as the one of Lemma 2 and yields $v_t = {{\tilde{Z}}}_t^*J {{\tilde{\nu }}}$. Here, however, we can not separate $v_0$ from $v_1$. Take $u \in {\mathcal {V}}$ and $v\in V^\perp$:

$$\begin{aligned} \langle u, v \rangle&= \sigma \left( \int _0^1 Z_t u_t \textrm{d}t,\nu \right) + {\tilde{g}}_0({{\tilde{Z}}}_0 u_0,{{\tilde{Z}}}_0v_0) + {{\tilde{\Phi }}}^*{{\tilde{g}}}_1 ({{\tilde{Z}}}_1 u_1,{{\tilde{Z}}}_1 u_1) \\&= {{\tilde{g}}}_0({{\tilde{Z}}}_0 u_0, {{\tilde{Z}}}_0 v_0-{{\tilde{J}}}_0 \nu )+ {{\tilde{\Phi }}}^*{{\tilde{g}}}_1({{\tilde{Z}}}_1 u_1, {{\tilde{Z}}}_1 v_1-{{\tilde{J}}}_1 \nu )\\&= g_0 (Z_1^0 u_1, J_0 \nu -2Z_0v_0+Z_1^0v_1) + {{\tilde{\Phi }}}^*g_1(Z_1^1u_1,Z_1^1 v_1-J_1 \nu )=0. \end{aligned}$$

Hence:

$$\begin{aligned} {\tilde{pr}}_1 \begin{pmatrix} 2 Z_0 v_0- J_0 \nu \\ J_1 \nu \end{pmatrix} = {\tilde{pr}}_1 \left( \begin{pmatrix} 2 Z_0 v_0 \\ 0 \end{pmatrix} +\tilde{J}_1 {{\tilde{\nu }}} \right) = {{\tilde{\Phi }}}_* {{\tilde{Z}}}_1 v_1. \end{aligned}$$

(25)

Step 2: Derivation of Jacobi equation. Now we can write down Jacobi equation in a fashion similar to the one of Proposition 1. The system reads:

$$\begin{aligned} {\left\{ \begin{array}{ll} (1-s){{\tilde{Z}}}_0 u_0 = {{\tilde{Z}}}_0v_0,\\ \dot{{{\tilde{\eta }}}}(t) = {{\tilde{Z}}}_t^s({{\tilde{Z}}}_t^s) J {{\tilde{\eta }}}(t), \\ (1-s) {{\tilde{\Phi }}}_* {{\tilde{Z}}}_1 u_1 = {{\tilde{\Phi }}}_* {{\tilde{Z}}}_1 v_1 + s \, {\tilde{pr}}_1 {{\tilde{J}}}_1 {{\tilde{\Phi }}}_* ({{\tilde{Z}}}_0 u_0+\int _0^1 {{\tilde{Z}}}_t u_t \textrm{d}t +{{\tilde{Z}}}_1 u_1). \end{array}\right. } \end{aligned}$$

(26)

Where ${{\tilde{\eta }}}(t) = \int _0^t {{\tilde{Z}}}_t^s u_t \textrm{d}t + {{\tilde{Z}}}_0 u_0 +{{\tilde{\nu }}}$. Arguing as in Proposition 1, we can rewrite the last term of the third equation. We have:

$$\begin{aligned} {pr}_1 {{\tilde{J}}}_1 {{\tilde{\Phi }}}_* \left( {{\tilde{Z}}}_0^s u_0+\int _0^1 {{\tilde{Z}}}^s_t u_t \textrm{d}t +{{\tilde{Z}}}^s_1 u_1\right)&= {pr}_1 {{\tilde{J}}}_1 {{\tilde{\Phi }}}_* (\eta (1)-{{\tilde{\nu }}} +{{\tilde{Z}}}_1^su_1). \\ {{\tilde{\Phi }}}_* Z_1^s u_1 = {{\tilde{\Phi }}}_*Z_1^1 u_1 + s{{\tilde{\Phi }}}_* {\tilde{pr}}_\Pi {{\tilde{Z}}}_1u_1&= {{\tilde{\Phi }}}_*Z_1^1 u_1 + s(\tilde{\Phi }_* {\tilde{pr}}_\Pi {{\tilde{\Phi }}}_* ^{-1}) {{\tilde{\Phi }}}_* \tilde{Z}_1u_1 . \end{aligned}$$

By the equation defining ${\mathcal {V}}$ we have that:

$$\begin{aligned} {\tilde{pr}}_{\Pi ^\perp }{{\tilde{\Phi }}}_*\eta (1) = - \begin{pmatrix} Z_1^0u_1 \\ {{\tilde{\Phi }}}_*Z^1_1u_1 \end{pmatrix} =- {{\tilde{\Phi }}}_*{{\tilde{Z}}}_1 u_1. \end{aligned}$$

Lastly note the the first equation gives $(1-s){{\tilde{Z}}}_0u_0 = (1-s) {\tilde{pr}}_{\Pi ^\perp } \eta (0) = {{\tilde{Z}}}_0 v_0$. Let us now plug all this equations into (26) recalling that ${\tilde{pr}}_{\Pi } + {\tilde{pr}}_{\Pi ^\perp } =1$. The third line now reads:

$$\begin{aligned}&pr_1\bigg (\begin{pmatrix} 2(1-s) {\tilde{pr}}_{\Pi _0^\perp } \eta (0) \\ 0 \end{pmatrix}+{{\tilde{J}}}_1 {{\tilde{\Phi }}}_* ({\tilde{pr}}_{\Pi }\eta (1)-s {{\tilde{\Phi }}}_* {\tilde{pr}}_\Pi {{\tilde{\Phi }}}_*^{-1}{\tilde{pr}}_{\Pi ^\perp }{{\tilde{\Phi }}}_*\eta (1))\\ {}&\quad +(1-s) \tilde{ {pr}}_{\Pi ^\perp } {{\tilde{\Phi }}}_* \eta (1)\bigg )=0. \end{aligned}$$

Writing the equation component-wise and using the fact that, since ${{\tilde{\Phi }}}_*$ preserve the fibers, it holds:

$$\begin{aligned} {{\tilde{\Phi }}}_*pr_{\Pi _0} = {{\tilde{\Phi }}}_* pr_{\Pi _0}{{\tilde{\Phi }}}_*^{-1} {{\tilde{p}}}r_{\Pi _{1}^\perp } \Phi _* + pr_{\Pi _1} {{\tilde{\Phi }}}_*, \end{aligned}$$

we obtain a relation very similar to the one in (16). Namely:

$$\begin{aligned} {\tilde{pr}}_1\begin{pmatrix} -J_0\left( 3(s-1)J_0^{-1} pr_{\Pi _0^\perp } \eta (0)+{{\tilde{\Phi }}}_* pr_{\Pi _0}\eta (0)\right) \\ J_1 \left( pr_{\Pi _1} {{\tilde{\Phi }}}_*\eta (1) + (1-s)( {{\tilde{\Phi }}}_* pr_{\Pi _1} {{\tilde{\Phi }}}_*^{-1}+J_1^{-1}) {pr}_{\Pi _1^\perp } \tilde{\Phi }_* \eta (1)\right) \end{pmatrix}=0. \nonumber \\ \end{aligned}$$

(27)

At this point the argument is again the following. If X belongs to $A(N) + \Pi$ and $\tilde{pr_1} ({{\tilde{J}}}_1 X) =0$, it follows that:

$$\begin{aligned} {\tilde{g}}_1({{\tilde{p}}}r_1 {{\tilde{J}}}_1 X, {{\tilde{Z}}}_1 u_1) = \sigma (X, {{\tilde{Z}}}_1u_1)=0, \, \forall \, u_1 \in {\mathbb {R}}^{\dim (N)}. \end{aligned}$$

Hence X must lie in $\textrm{Im}({{\tilde{Z}}}_1)^{\angle } \cap (A(N)+\Pi )$, which is A(N). Consider the maps $A^s_i$ defined in (12), they preserve $A(N) +\Pi$. Thus we can rewrite (27) as:

$$\begin{aligned} \begin{pmatrix} (A_0^s) ^{-1} \eta (0) \\ A_1^s{{\tilde{\Phi }}}_* \eta (1) \end{pmatrix} \in A(N) \iff \Gamma (A_1^s {{\tilde{\Phi }}}_* \Phi _1^s A_0^s)\cap A(N). \end{aligned}$$

Notice the presence of the inverse of $A_0^s$ due to the sign of the symplectic form.

Step 3: Uniqueness Arguing again as in Proposition 1, to the trivial variation (0, 0, 0) correspond constant solutions of Jacobi equation starting from the fiber. However, since the Endpoint map of the original system is regular, there are no such solutions. Hence the correspondence between $\ker (1+s K)$ and $\Gamma (A_1^s {{\tilde{\Phi }}}_* A_0^s)\cap A(N)$ is one-to-one. $\square$

Now we define an analogous map to the one in Eq. (19). Let $\pi _N$ be the orthogonal projection on the space $T_{(\lambda _0,\lambda _1)}A(N)^\perp$ and consider the map:

$$\begin{aligned} Q^s: \Gamma (A_1^s{{\tilde{\Phi }}}_*\Phi _1^s A_0^s) \rightarrow T_{(\lambda _0,\lambda _1)}A(N)^\perp , \quad Q^s(\eta ) = \pi _N ( \eta ). \end{aligned}$$

(28)

Let $T = (T_0,T_1)$ be any linear invertible map from ${\mathbb {R}}^{2n}$ to the tangent space $T_{(\lambda _0,\lambda _1)}A(N)$. We denote by J the map $(-J_0) \oplus J_1$ representing the symplectic form $(-\sigma _{\lambda _0})\oplus \sigma _{\lambda _1}$. As in the previous section we define the following function:

$$\begin{aligned} \det (Q^s)= \frac{\det (T_1^*J_1A_1^s{{\tilde{\Phi }}}_* \Phi _1^sA_0^s -T_0^*J_0)}{\det (T_0^*J_0J_0^*T_0+T_1^*J_1J_1^*T_1)^{1/2}}. \end{aligned}$$

Remark 9

One could also define (28) as a bilinear form, using just the symplectic pairing. In fact, for $(\eta ,(\xi _0,\xi _1))$ in $T_{\lambda _0}T^*M\times T_{(\lambda _0,\lambda _1)}A(N)$, define:

$$\begin{aligned} {{\tilde{Q}}}^s (\eta ,(\xi _0,\xi _1)) = \sigma (A_1^s\tilde{\Phi }_*\Phi _1^sA_0^s \eta , \xi _1) - \sigma (\eta ,\xi _0). \end{aligned}$$

This form is degenerate exactly when $\Gamma (A_1^s {{\tilde{\Phi }}}_* A_0^s)\cap A(N) \ne (0).$

Proposition 5

The multiplicity of any roots $s_0 \ne 0$ of the equation $\det (Q^s)$ is equal to the geometric multiplicity of the boundary value problem.

Proof

The same proof of Proposition 2 works verbatim. Indeed, we are working with the same curve, $\Gamma (A_1^s {{\tilde{\Phi }}}_* A_0^s)$. $\square$

In the remaining part of this section we carry out the computation of the normalizing factors of the function $\det (Q^s)$. As already mentioned at the end of the previous section a classical factorization theorem by Hadamard (see [14]) tells us that:

$$\begin{aligned} \det (Q^s) = as^k e^{b s}\prod _{\lambda \in Sp(K)} (1+s\lambda )^{m(\lambda )} \quad a, b \in {\mathbb {C}}, a\ne 0, k \in {\mathbb {N}} \end{aligned}$$

where $m(\lambda )$ is the geometric multiplicity of the eigenvalue. We are now going to compute the values of $a,b \in {\mathbb {C}}$ and k.

Theorem 4

For almost any choice of metrics $g_0,g_1$ on $T_{\lambda _i}T^*M$, $\det (Q^s\vert _{s=0}) \ne 0$. Whenever this condition holds, the determinant of the second variation is given by:

$$\begin{aligned} \det (1+ sK) =\det ((Q^s\vert _{s=0})^{-1})e^{s (\text { tr}(K)-\text { tr}(\partial _s Q^s \,(Q^s)^{-1}\vert _{s=0}))} \det (Q^s). \end{aligned}$$

(29)

Proof

We prove the first assertion: for almost any choice of scalar product, $k =0$ and thus $a=\det (Q_1^s|_{s=0})\ne 0$. This is equivalent to a transversality condition between the graph of the symplectomorphism $A_1^s {{\tilde{\Phi }}}_* \Phi ^s A_0^s$ and the annihilator of the boundary conditions N.

We can argue as follows: consider the following family of maps acting on the Lagrange Grassmannian of $T_{\lambda _0}T^*M \times T_{\lambda _1}T^*M$ depending on the choice of scalar products $G_0$ and $G_1$:

$$\begin{aligned} F_G = (A_0^s)^{-1} \times A_1^s\vert _{s=0}, \quad G = (G_0,G_1), G_i>0. \end{aligned}$$

It is straightforward to see that they define a family of algebraic maps of the Grassmannian to itself. For any chosen subspace $L_0$, $F^{-1}_G(L_0)$ is arbitrary close to $\Pi _0 \times \Pi _1$, for $G_i$ large enough. Notice that $\Gamma (A_1^s {{\tilde{\Phi }}}_*\Phi ^s A_0^s) \cap L_0 \ne (0)$ if and only if $\Gamma ({{\tilde{\Phi }}}_* \Phi ^s)\cap F^{-1}_G(L_0) \ne (0)$. Using the formula in Lemma 4 one has that $\Gamma ({{\tilde{\Phi }}}_* \Phi ^s)$ is transversal to $\Pi _0\times \Pi _1$ and thus to $F^{-1}_G(L_0)$ for any fixed $L_0$ and $G_i$ sufficiently large. Now, since everything is algebraic in G and there is a Zariski open set in which the transversality condition holds, the possible choices of $G_i$ for which $k>0$ are in codimension 1.

Let us assume that $k= 0$ and compute b. Differentiating the expression for $\det (Q^s)$ in Eq. (21) at $s=0$ we find that:

$$\begin{aligned} \partial _s \det (Q^s)\vert _{s=0} = a(b+\text { tr}(K)). \end{aligned}$$

An integral formula for the trace of K is given in Lemma 3. The derivative of $\det (Q^s)$ can be computed using Jacobi formula:

$$\begin{aligned} \partial _s \det (Q^s)\vert _{s=0} = a\, \text { tr}(\partial _s Q^s \, (Q^s)^{-1})\vert _{s=0}. \end{aligned}$$

An explicit expression of the derivatives of the map $Q^s$ can be computed using Lemma 4. It follows that $b = \text { tr}(\partial _s Q^s \,(Q^s)^{-1})- \text { tr}(K)$ and we obtain precisely the formula in the statement. $\square$

Before giving the explicit formula for $\text { tr}(K)$ and the derivatives of the fundamental solution to Jacobi equation at $s=0$ we need to make some notational remark and write down a formula for the second variation in the same spirit of Sect. 2 and Eq. (5). We are working on the state space $M \times M$ with twice the number of variables of the original system and trivial dynamic on the first factor and separated boundary conditions. The left boundary condition manifold is the diagonal of $M \times M$ and the right one is our starting N. We apply the formula in Eq. (5) to this particular system, we denote by ${\tilde{Z}}_t$ and ${{\tilde{Z}}}_i$ the matrices for the auxiliary problem, in general everything pertaining to it will be marked by a tilde. Identifying $T_{(\lambda _0,\lambda _0)} T^*(M\times M)$ with $T_{\lambda _0}T^*M \times T_{\lambda _0}T^*M$ we have that:

$$\begin{aligned} {{\tilde{Z}}}_0 u_0 =\begin{pmatrix} Z_0u_0 \\ Z_0u_0 \end{pmatrix}, \quad {{\tilde{Z}}}_1 = \begin{pmatrix} Z_1^0 u_1\\ Z_1^1 u_1 \end{pmatrix}, \quad {{\tilde{Z}}}_t =\begin{pmatrix} 0\\ Z_t \end{pmatrix}. \end{aligned}$$

We still work on the subspace ${\mathcal {V}} = \{(u_0,u_t,u_1): {{\tilde{Z}}}_0u_0 + \int _0^1 {{\tilde{Z}}}_t u_t + {{\tilde{Z}}}_1u_1 \in \Pi \}$. However, it is clear that this equation implies that:

$$\begin{aligned} Z_0u_0+Z_1^0u_1 \in \Pi _0 \quad \text { and } \quad Z_0u_0+Z^1_1u_1+\int _0^1Z_t u_t \textrm{d}t \in \Pi _0. \end{aligned}$$

It follows that control $u_0$ is completely determined by $u_1$. Moreover, we can assume that $Z_0u_0 = -Z_1^0u_1$ since we are free to choose any system of coordinates and any trivialization of the tangent bundle of the manifolds $\Delta$ and N. Technically we are working with different scalar products on each of the copies of $T_ {\lambda _0} T^*M$. However, it is easy to see that on the space ${\mathcal {V}}$ only the sum of these metrics plays a role. We will denote it $g_0$. Now we are ready to state the following:

Lemma 3

The second variation of the extended system, as a quadratic form, can be written as $\langle (I+K ) u,u \rangle$ where K is the symmetric (on ${\mathcal {V}}$) compact operator given by:

$$\begin{aligned} \begin{aligned} -\langle K u, u \rangle&= \int _0^1\int _0^t \sigma (Z_\tau u_\tau ,Z_t u_t) \textrm{d}\tau \textrm{d}t -\sigma \left( Z_1^0u_1,\int _0^1 Z_t u_t \textrm{d}t \right) \\ {}&\quad + \sigma \left( \int _0^1Z_tu_t \textrm{d}t -Z_1^0u_1,Z_1^1u_1 \right) + g_0(Z_1^0u_1,Z_1^0u_1)\\ {}&\quad +({{\tilde{\Phi }}}^*g_1)(Z_1^1u_1,Z_1^1u_1). \end{aligned} \end{aligned}$$

Moreover, define the following matrices:

$$\begin{aligned} \Gamma = \int _0^1 X_t X_t^* \textrm{d}t, \quad \Omega = \int _0^1\int _0^t X_tZ_t^*JZ_\tau X^*_\tau \textrm{d}\tau \textrm{d}t. \end{aligned}$$

Denote by $pr_1$ the projection onto $T_{(\lambda _0,\lambda _1)} A(N)$ and by $\pi ^i_*$ the differential of the natural projections $\pi ^i: T^*M \rightarrow M$ relative to the $i-$th component, $i=1,2$. The trace of K has the following expression:

$$\begin{aligned} \begin{aligned} \text { tr}(K)&= -\dim (N) +\text { tr}[\pi _*^1{{\tilde{\Phi }}}_*^{-1}\,pr_1 \tilde{J}_1{{\tilde{\Phi }}}_* ({{\tilde{Z}}}_0) ]\\ {}&\quad +\text { tr}\left[ \Gamma ^{-1} \left( \Omega + (\pi ^2_*-\pi _*^1){{\tilde{\Phi }}}_*^{-1}\,pr_1 {{\tilde{J}}}_1\tilde{\Phi }_* \left( \int _0^1 {{\tilde{Z}}}_tZ_t^*J\vert _{\Pi } \textrm{d}t\right) \right) \right] . \end{aligned} \end{aligned}$$

Proof

The first part is a straightforward computation combining the expression obtained in Lemma 1 for the second variation with the observation concerning the structure of the maps $Z_0$ and $Z_1$ made before the statement and the choice of the Riemannian metrics.

Now, notice that the codimension of the space giving fixed endpoints variations ${\mathcal {V}}$ for the extended system in ${\mathcal {H}}$ is $2 \dim (M)$. Moreover, it is defined as the kernel of the linear functional:

$$\begin{aligned} \rho : (u_0,u_t,u_1) \mapsto {{\tilde{\pi }}}_* \left( \tilde{Z}_0u_0+\int _0^1{{\tilde{Z}}}_tu_t \textrm{d}t +{{\tilde{Z}}}_1u_1\right) \in T_{\pi (\lambda _0)}M \times T_{\pi (\lambda _0)}M. \end{aligned}$$

It is straightforward to check that the following subspace is $2\dim (M)-$dimensional and transversal to $\ker \rho$:

$$\begin{aligned} {\mathcal {V}}' = \{(u_0, Z_t^*J \nu , 0): \nu \in \Pi , u_0 \in {\mathbb {R}}^{\dim M} \}. \end{aligned}$$

The trace of K on the whole space splits as a sum of two pieces, the trace of $K\vert _{\mathcal {V}}$ and the trace of $K\vert _{{\mathcal {V}}'}$. We can then further simplify and compute separately the trace on ${\mathcal {V}}' \cap \{u_0=0\}$ and its complement ${\mathcal {V}}' \cap \{\nu =0\}$. We are going to compute the trace of K on the whole space and then the trace of $K\vert _{{\mathcal {V}}'}$, determining in this way the value of $K\vert _{{\mathcal {V}}}$.

Consider ${\mathcal {H}} = {\mathcal {H}}_1\oplus {\mathcal {H}}_2$. Where

$$\begin{aligned} {\mathcal {H}}_1 = \{u: u = (0,u_t,0)\}, \quad {\mathcal {H}}_2 = \{u: u = (u_0,0,u_1)\}. \end{aligned}$$

It is straightforward to check that ${\mathcal {H}}_1^\perp ={\mathcal {H}}_2$ for our class of metrics and that ${\mathcal {H}}_1 \equiv L^{2}([0,1],{\mathbb {R}}^k)$. Using Eq. (5), the restrictions of the quadratic form ${{\hat{K}}}(u) =\langle u, K u \rangle$ to each one of the former subspaces read:

$$\begin{aligned} {\hat{K}}|_{{\mathcal {H}}_1} (u) = \int _0^1\int _0^t \sigma (Z_t u_t, Z_\tau u_\tau ) \textrm{d}t \textrm{d}\tau , \quad {\hat{K}}|_{{\mathcal {H}}_2} (u) = \sigma ({{\tilde{Z}}}_0u_0, {{\tilde{Z}}}_1u_1)- \Vert u\Vert _{\mathcal {H}}^2. \end{aligned}$$

The trace of the first quadratic form is zero (see [3, Theorem 2]) whereas the trace of the second part is just $-\dim (N)$. Thus we have that:

$$\begin{aligned} \text { tr}(K\vert _{\mathcal {V}}) = -\dim (N) - \text { tr}(K\vert _{{\mathcal {V}}'}). \end{aligned}$$

To compute the last piece we apply K to a control $u \in {\mathcal {V}}'\cap \{u_0=0\}$ using the explicit expression of the operator given in Lemma 1. Recall that $pr_1$ is projection onto the image of ${{\tilde{\Phi }}}_* {{\tilde{Z}}}_1$. It follows that:

$$\begin{aligned} \begin{aligned} K (u)&= \left( 0,-Z_t^*J\int _0^t Z_\tau u_\tau \textrm{d}\tau ,- L \,pr_1 {{\tilde{J}}}_1{{\tilde{\Phi }}}_*\left( \int _0^1 {{\tilde{Z}}}_tu_t \textrm{d}t \right) \right) \\ {}&= \left( 0,-Z_t^*J\int _0^t Z_\tau u_\tau \textrm{d}\tau ,-\Lambda (u) \right) . \end{aligned} \end{aligned}$$

Now we write K(u) in coordinates given by the splitting ${\mathcal {V}} \oplus {\mathcal {V}}'$. To do so we have first to consider $\rho \circ K(u)$. It is given by:

$$\begin{aligned} \begin{aligned} -\rho \circ K(u)&= {{\tilde{\pi }}}_*\left( \int _0^1 {{\tilde{Z}}}_tZ_t^*J\int _0^t Z_\tau Z_\tau ^*J\nu +{{\tilde{\Phi }}}_*^{-1}\,pr_1 {{\tilde{J}}}_1{{\tilde{\Phi }}}_* \left( \int _0^1 {{\tilde{Z}}}_tZ_t^*J \nu \textrm{d}t \right) \right) \\&= \begin{pmatrix} 0 \\ \Omega \nu \end{pmatrix} +{{\tilde{\pi }}}_*\tilde{\Phi }_*^{-1}\,pr_1 {{\tilde{J}}}_1{{\tilde{\Phi }}}_* \left( \int _0^1 {{\tilde{Z}}}_tZ_t^*J \nu \textrm{d}t\right) . \end{aligned}\nonumber \\ \end{aligned}$$

(30)

Set $\Gamma = \int _0^1 X_t^*X_t \textrm{d}t$, it easy to check that, if $u \in {\mathcal {V}}'$, then

$$\begin{aligned} \rho (u) = \begin{pmatrix} X_0 u_0 \\ \Gamma \nu + X_0 u_0 \end{pmatrix}. \end{aligned}$$

for an invertible matrix $X_0$ which, without loss of generality, can be taken to be identity. It follows that the projection on the first component of $\rho \circ K(u)$ is completely determined by the second term in Eq. (30). Let us call $\pi _*^i$ for $i=1,2$ the projection on the $i-$th component. It follows that an element $(Z_0{{\hat{u}}}_0,Z_t^*J {\hat{\nu }},0) = {{\hat{u}}} \in {\mathcal {V}} '$ has the same projection as K(u) if and only if:

$$\begin{aligned} {\left\{ \begin{array}{ll} {{\hat{u}}}_0 = X_0^{-1} \pi ^1_*{{\tilde{\Phi }}}_*^{-1}\,pr_1 {{\tilde{J}}}_1{{\tilde{\Phi }}}_* (\int _0^1 {{\tilde{Z}}}_tZ_t^*J \nu \textrm{d}t),\\ {\hat{\nu }} = \Gamma ^{-1} \left( \Omega \nu + (\pi ^2_*-\pi ^1_*)\tilde{\Phi }_*^{-1}\,pr_1 {{\tilde{J}}}_1{{\tilde{\Phi }}}_* (\int _0^1 {{\tilde{Z}}}_tZ_t^*J \nu \textrm{d}t)\right) . \end{array}\right. } \end{aligned}$$

In particular the restriction to ${\mathcal {V}}' \cap \{u_0=0\}$ is given by:

$$\begin{aligned} \nu \mapsto \Gamma ^{-1} \left( \Omega + (\pi ^2_*-\pi ^1_*)\tilde{\Phi }_*^{-1}\,pr_1 {{\tilde{J}}}_1{{\tilde{\Phi }}}_* \left( \int _0^1 {{\tilde{Z}}}_tZ_t^*J \textrm{d}t\right) \right) \nu . \end{aligned}$$

A similar strategy applied to ${\mathcal {V}}' \cap \{\nu =0\}$ tells us that the last contribution for the trace is given by the following map:

$$\begin{aligned} u_0 \mapsto X_0^{-1}\pi _*^1{{\tilde{\Phi }}}_*^{-1}\,pr_1 {{\tilde{J}}}_1\tilde{\Phi }_*{{\tilde{Z}}}_0u_0. \end{aligned}$$

It is worth pointing out that indeed the trace does not depend on $X_0$ and that the vector $\int _0^1{{\tilde{Z}}}_t Z_tJ \nu \textrm{d}t$ is the following:

$$\begin{aligned} \int _0^1{{\tilde{Z}}}_t Z_tJ \nu \textrm{d}t = \begin{pmatrix} \begin{pmatrix} 0 \\ 0 \end{pmatrix}\\ \begin{pmatrix} \Theta \nu \\ \Gamma \nu \end{pmatrix} \end{pmatrix}. \end{aligned}$$

In particular, if the boundary conditions are separated (i.e. $N = N_0\times N_1$) the part of the trace coming from ${\mathcal {V}}'\cap \{u_0=0\}$ depends only on the projection onto $T_{\lambda _1}N_1$. $\square$

Lemma 4

The flow $\Phi _t^s\vert _{s=0}$ and its derivative $\partial _s \Phi _t^s\vert _{s=0}$ are given by:

$$\begin{aligned} \Phi _t ^s|_{s=0}= \begin{pmatrix} 1 &{}0\\ \int _0^t X_\tau X_\tau ^* \textrm{d}\tau &{}1 \end{pmatrix}, \quad \partial _s\Phi _t ^s\vert _{s=0}= \begin{pmatrix} \int _0^t Y_\tau X_\tau ^* \textrm{d}\tau &{}0\\ \int _0^t\int _0^\tau X_\tau Z_\tau ^* J Z_r X_r ^*\textrm{d}r \textrm{d}\tau &{} -\int _0^tX_\tau Y_\tau ^* \textrm{d}\tau \end{pmatrix}. \end{aligned}$$

Proof

It is straightforward to check that $\Phi _1^s\vert _{s=0}$ solves the following Cauchy problem:

$$\begin{aligned} {\left\{ \begin{array}{ll} {{\dot{\Phi }}}_t^0 = \begin{pmatrix} 0 &{} 0 \\ X_t X_t^* &{}0 \end{pmatrix} \Phi _t^0,\\ \Phi _0^0 = Id. \end{array}\right. } \end{aligned}$$

Similarly $\partial _s \Phi _1^s\vert _{s=0}$ solves:

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _s {{\dot{\Phi }}}_t^s|_{s=0} = \begin{pmatrix} 0 &{} 0 \\ X_t X_t^* &{}0 \end{pmatrix} \partial _s \Phi _t^s|_{s=0}+ \begin{pmatrix} Y_tX_t^* &{}0\\ 0 &{}-X_tY_t^* \end{pmatrix}\Phi _t^0,\\ \partial _s \Phi _0^s|_{s=0} = 0. \end{array}\right. } \end{aligned}$$

Solving the ODE one obtains the formula in the statement. $\square$

Appendix A

In this appendix we collect some information concerning Pontryagin Maximum Principle (PMP) and the differentiation of the endpoint map used and mentioned throughout the text. Everything is fairly standard material in geometric control theory, the reader is referred to [4, 6, 23] for further details.

1.1 A.1. Pontryagin maximum principle

Let us introduce a useful family of Hamiltonian functions on $T^*M$. They generate a family of Hamiltonian flows which we use to backtrack admissible trajectories $\gamma$ to their initial point. Moreover, they appear in the formulation of PMP and extend the flow of the fields $f_{u(t)}$ to the cotangent bundle. Set:

$$\begin{aligned} h^{t,\nu }_u: T^*M \rightarrow {\mathbb {R}}, \quad h^{t,\nu }_u(\lambda ) = \langle \lambda ,f_u\rangle +\nu \varphi (u,\pi (\lambda )), \quad \nu \le 0. \end{aligned}$$

In particular, if ${{\tilde{\gamma }}}$ is an admissible curve, we can build a lift, i.e. a curve ${{\tilde{\lambda }}}$ in $T^*M$ such that $\pi ({{\tilde{\lambda }}}) = {{\tilde{\gamma }}}$, solving ${{\dot{\lambda }}} = \textbf{h}^{t,\nu }_u(\lambda )$. The following wellknown theorem, Pontryagin Maximum Principle, gives a characterization of critical points of ${\mathcal {J}}$ (as defined in (3)), for any set of boundary conditions N.

Theorem 1

(PMP) If a control ${{\tilde{u}}}\in L^\infty ([0,1],U)$ is a local minimizer for the functional in Eq. (3) there exists a curve $\lambda :[0,1]\rightarrow T^*M$, $\nu \in {\mathbb {R}}$ and an admissible curve $q: [0,1] \rightarrow M$ such that for almost all $t\in [0,1]$

• 1. $\lambda (t)$ is a lift of q(t):

  $$\begin{aligned} q(t) = \pi (\lambda (t)); \end{aligned}$$

• 2. $\lambda (t)$ satisfies the following Hamiltonian system:

  $$\begin{aligned} \frac{d \lambda }{\textrm{d}t} = \textbf{h}^{t,\nu }_{{{\tilde{u}}}(t)}(\lambda ); \end{aligned}$$

• 3. the control ${{\tilde{u}}}$ is determined by the maximum condition:

  $$\begin{aligned} h^{t,\nu }_{{{\tilde{u}}}(t)}(\lambda (t)) = \max _{u\in U} h_u^{t,\nu }( \lambda (t)), \quad \nu \le 0; \end{aligned}$$

• 4. the non-triviality condition holds: $(\lambda (t),\nu )\ne (0,0)$;

• 5. transversality condition holds:

  $$\begin{aligned} (-\lambda (0),\lambda (1)) \in Ann(N). \end{aligned}$$

We call q(t) an extremal curve (or trajectory) and $\lambda (t)$ an extremal.

There are essentially two possibilities for the parameter $\nu$, it can be either 0 or, after appropriate normalization of $\lambda _t$, $-1$. The extremals belonging to the first family are called abnormal whereas the ones belonging to the second normal.

1.2 A.2. The endpoint map and its differentiation

In this subsection, we write down the integral expression for the first and second derivative of the endpoint map. Further details can be found in [6, Section 20.3]. Denote by ${\mathcal {U}}_{q_0}\subset L^{\infty }([0,1],U)$ be the space of admissible controls at point $q_0$ and define the following map:

$$\begin{aligned} E^t: {\mathcal {U}}_{q_0} \rightarrow M,\quad u\mapsto \gamma _{u}(t). \end{aligned}$$

It takes the control u and gives the position at time t of the solution starting from $q_0$ of:

$$\begin{aligned} {\dot{q}} = f_{u(\tau )}(q). \end{aligned}$$

We call this map Endpoint map. It turns out that $E^t$ is smooth, provided that the fields $f_u(q)$ are smooth too.

For a fixed control ${{\tilde{u}}}$ consider the function $h_{{\tilde{u}}}^{t,\nu }(\lambda ):= h_{{\tilde{u}}(t)}^{t,\nu }(\lambda )$ and define the following non autonomous flow which plays the role of parallel transport in this context:

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t} {\tilde{\Phi }}_t = \textbf{h}^{t,\nu }_{{\tilde{u}}}({\tilde{\Phi }}_t), \qquad {\tilde{\Phi }}_0 = Id. \end{aligned}$$

(31)

It has the following properties:

• It extends to the cotangent bundle the flow which solves ${\dot{q}} = f_{{\tilde{u}}}(q)$ on the base. In particular if $\lambda _t$ is an extremal with initial condition $\lambda _0$, $\pi ({\tilde{\Phi }}_t(\lambda _0)) = q_{{\tilde{u}}}(t)$ where $q_{{\tilde{u}}}$ is an extremal trajectory.

• ${\tilde{\Phi }}_t$ preserves the fiber over each $q \in M$. The restriction ${\tilde{\Phi }}_t:\, T^*_qM \rightarrow T^*_{{\tilde{\Phi }}_t(q)}M$ is an affine transformation.

We suppose now that $\lambda (t)$ is an extremal and ${\tilde{u}}$ a critical point of the functional ${\mathcal {J}}$. We use the symplectomorphism ${\tilde{\Phi }}_t$ to pull back the whole curve $\lambda (t)$ to the starting point $\lambda _0$. We can express all the first- and second-order information about the extremal using the following map and its derivatives:

$$\begin{aligned} b_u^t(\lambda ) = (h_u^{t,\nu }-h_{{\tilde{u}}}^{t,\nu })\circ {\tilde{\Phi }}_t(\lambda ). \end{aligned}$$

Notice that:

• $b_u^t(\lambda _0)\vert _{u ={\tilde{u}}(t)} =0 = d_{\lambda _0}\, b_u^t\vert _{u ={\tilde{u}}(t)}$ by definition.

• $\partial _u b_u^t\vert _{u ={\tilde{u}}(t)} = \partial _u (h_u^t\circ {\tilde{\Phi }}_t)\vert _{u ={\tilde{u}}(t)} =0$ since $\lambda (t)$ is an extremal and ${\tilde{u}}$ the relative control.

Thus the first non zero derivatives are the order two ones. We define the following maps:

$$\begin{aligned} \begin{aligned} Z_t&= \partial _u \textbf{b}_u^t(\lambda _0)\vert _{u={\tilde{u}}(t)}: {\mathbb {R}}^k = T_{{\tilde{u}}(t)}U \rightarrow T_{\lambda _0}(T^*M), \\ H_t&= \partial _u^2 b_t(\lambda _0)\vert _{u={\tilde{u}}(t)}: {\mathbb {R}}^k =T_{{\tilde{u}}(t)}U \rightarrow T^*_{{\tilde{u}}(t)}U ={\mathbb {R}}^k. \end{aligned} \end{aligned}$$

(32)

We denote by $\Pi =\ker \pi _*$ the kernel of the differential of the natural projection $\pi : T^*M \rightarrow M$.

Proposition 6

(Differential of the endpoint map) Consider the endpoint map $E^t: {\mathcal {U}}_{q_0} \rightarrow M$. Fix a point ${\tilde{u}}$ and consider the symplectomorphism ${\tilde{\Phi }}_t$ and the map $Z_t$ defined above. The differential is the following map:

$$\begin{aligned} d_{{\tilde{u}}} E (v_t) =d_{\lambda (t)} \pi \circ d_{\lambda _0}{\tilde{\Phi }}_t\bigg (\int _0^t Z_\tau v_\tau \textrm{d}\tau \bigg ) \in T_{q_t}M. \end{aligned}$$

In particular, if we identify $T_{\lambda _0}(T^* M)$ with ${\mathbb {R}}^{2m}$ and write $Z_t = \begin{pmatrix} Y_t \\ X_t \end{pmatrix}$, ${\tilde{u}}$ is a regular point if and only if $v_t\mapsto \int _0^t X_\tau v_\tau \textrm{d}\tau$ is surjective. Equivalently if the following matrix is invertible:

$$\begin{aligned} \Gamma _t = \int _0^t X_\tau X^*_\tau \textrm{d}\tau \in Mat_{n\times n}({\mathbb {R}}), \quad \det (\Gamma _t)\ne 0 \end{aligned}$$

If $d_{{\tilde{u}}} E^t$ is surjective then $(E^t)^{-1}(q_t)$ is smooth in a neighbourhood of ${\tilde{u}}$ and is tangent space is given by:

$$\begin{aligned} \begin{aligned} T_{{\tilde{u}}}(E^t)^{-1}(q_t) =\left\{ v \in L^\infty ([0,1],{\mathbb {R}}^k):\, \int _0^t X_\tau v_\tau d \tau =0 \right\} \\ =\left\{ v \in L^\infty ([0,1],{\mathbb {R}}^k):\, \int _0^t Z_\tau v_\tau d \tau \in \Pi \right\} \end{aligned}. \end{aligned}$$

If the differential of the endpoint map is surjective, the set of admissible control becomes smooth (at least locally) and our minimization problem can be interpreted as a constrained optimization problem. We are looking for critical points of ${\mathcal {J}}$ on the submanifold $\{u \in {\mathcal {U}}: E^t(u) = q_1\}$.

Definition 3

We say that a normal extremal $\lambda (t)$ with associated control ${\tilde{u}}(t)$ are strictly normal if the differential of the endpoint map at ${\tilde{u}}$ is surjective.

It makes sense to go on and consider higher-order optimality conditions. At critical points is well defined (i.e. independent of coordinates) the Hessian of ${\mathcal {J}}$ (or the second variation). Using chronological calculus (see again [6] or [1]) it is possible to write the second variation of ${\mathcal {J}}$ on $\ker dE^t \subseteq L^{\infty }([0,1],{\mathbb {R}}^k)$.

Proposition 7

(Second variation) Suppose that $(\lambda (t),{\tilde{u}})$ is a strictly normal extremal, i.e. a critical point of ${\mathcal {J}}$ for fixed initial and final point. For any $u \in L^{\infty }([0,1],{\mathbb {R}}^k)$ such that $\int _0^1X_tu_t \textrm{d}t =0$ the second variation of ${\mathcal {J}}$ has the following expression:

$$\begin{aligned} d^2_{{\tilde{u}}}{\mathcal {J}}(u) = -\int _0^1 \langle H_tu_t, u_t\rangle \textrm{d}t - \int _0^1\int _0^t \sigma ( Z_\tau u_\tau ,Z_t u_t ) \textrm{d}\tau \textrm{d}t. \end{aligned}$$

The associated bilinear form is symmetric provided that u, v lie in a subspace that projects to a Lagrangian one via the map $u \mapsto \int _0^1 Z_t u_t \textrm{d}t$.

$$\begin{aligned} d^2_{{\tilde{u}}}{\mathcal {J}}(u,v) = -\int _0^1\langle H_tu_t, v_t\rangle \textrm{d}t - \int _0^1\int _0^t \sigma ( Z_\tau u_\tau ,Z_t v_t ) \textrm{d}\tau \textrm{d}t. \end{aligned}$$

Throughout the paper we make the assumption, which is customarily called strong Legendre condition, that the matrix $H_t$ is strictly negative definite and has uniformly bounded inverse. This guarantees that the term:

$$\begin{aligned} \int _0^1-\langle H_tu_t,v_t\rangle \textrm{d}t, \end{aligned}$$

is equivalent to the $L^2$ scalar product.